Modified Interaction-Strength Interpolation Method as an Important Step toward Self-Consistent Calculations

Abstract

The modified point charge plus continuum (mPC) model [Constantin L. A.; Phys. Rev. B 2019, 99, 085117] solves the important failures of the original counterpart, namely, the divergences when the reduced gradient of the density is large, such as in the tail of the density and in quasi-dimensional density regimes. The mPC allows us to define a modified interaction-strength interpolation (mISI) method inheriting these good features, which are important steps toward the full self-consistent treatment. Here, we provide an assessment of mISI for molecular systems (i.e., considering thermochemistry properties, correlation energies, vertical ionization potentials, and several noncovalent interactions), harmonium atoms, and functional derivatives in the strong-interaction limit. For all our tests, mISI provides a systematic improvement over the original ISI method. Semilocal approximations of the second-order Görling–Levy (GL2) perturbation theory are also considered in the mISI method, showing considerable worsening of the results. Possible further development of mISI is briefly discussed.

1. Introduction

The exact exchange–correlation (XC) functional can be formally defined using the adiabatic connection formalism as¹⁻⁷

1

where ρ is the electron density, λ is the electron–electron interaction strength, and

2

is the density-fixed linear adiabatic connection integrand, with Ψ_λ[ρ] being the antisymmetric wave function that minimizes T̂ + λV̂_ee while yielding the density ρ (T̂ and V̂_ee are the kinetic and electron–electron interaction operators, respectively), and U[ρ] being the Hartree energy.

Many accurate hybrid XC functionals are based on, and explained by, this method,^4,6,8−10 which provides a rationale for mixing the Hartree–Fock (HF) exchange with semilocal XC functionals.¹¹ Moreover, the basic Görling–Levy (GL) perturbation theory¹²⁻¹⁴ uses a generalized adiabatic connection formula¹³ to obtain the Taylor expansion of the correlation energy at a small coupling constant (λ → 0). The adiabatic connection formalism also stays behind the more recent and sophisticated double hybrids¹⁵ that are using either the second-order Møller–Plesset¹⁶ (MP2) correlation mixed with fractions of HF exchange and semilocal XC functionals¹⁷⁻²³ into the generalized Kohn–Sham (KS) density functional theory (DFT) scheme^24,25 or GL2 correlation¹³ combined with fractions of KS-DFT exact exchange and semilocal XC functionals²⁶ into the optimized effective potential (OEP) scheme of the true KS-DFT.²⁶⁻²⁹ The adiabatic connection is also of utmost importance for the ground-state calculations of linear-response time-dependent DFT, being part of the so-called adiabatic connection fluctuation-dissipation theorem that provides a framework for high-level, orbital-dependent methods based on XC kernel approximations.³⁰⁻⁴⁵

Here, we focus on the interaction-strength interpolation (ISI) method⁴⁶⁻⁴⁸ that accurately interpolates the weak (λ → 0)- and strong (λ → ∞)-interaction limits that are well known. Thus, in the weak-interaction limit, the GL perturbation theory becomes exact⁴⁶

3

where W₀[ρ] = E_x[ρ] is the exact KS-DFT exchange functional and W₀^′[ρ] = 2E_c[ρ]. On the other hand, the strong-interaction limit is

4

where W_∞[ρ] and W_∞^′[ρ] can be found in the strictly correlated electron (SCE) approach,⁴⁹ but in practice, they have been approximated from the second-order gradient expansion (GE2) of the point charge plus continuum (PC) model.⁴⁶⁻⁴⁸ Starting from the ISI method, several improvements and variants have been proposed.⁴⁹⁻⁶⁵ In particular, we mention the methods of refs (49, 50), which remove the spurious λ^–1 term in the large λ limit of W_λ, keeping the almost same accuracy of the XC energy as the original ISI method. Moreover, correlation energy densities have been constructed from local interpolations along the adiabatic connection curve.^{57,62,63,65−67}

Recently, the modified ISI (mISI) method has been developed,⁶⁵ which solves important failures of the original ISI approach in the tail of the density and in quasi-low dimensional density regimes. The mISI method has been tested on very few atoms showing improved correlation energies over its initial variant. In this article, we assess mISI for molecular systems, using the OEP exact exchange (OEPx) orbitals and densities. Noting that mISI and ISI are pure KS-DFT functionals and not wave function methods, the choice of OEPx orbitals is the most physical, presumably being very close to the true self-consistent ISI orbitals.

The GL2 correlation energy E_c^GL2[ρ] enters the expressions of ISI and mISI functionals, as shown, e.g., in eq 17 of ref (60). Because GL2 depends on all occupied and unoccupied orbitals and orbital energies, its evaluation even with OEPx orbitals is still very expensive. In this sense, semilocal approximations of E_c[ρ] are of interest not only for simplification of the ISI and mISI methods but also for the development of correlation functionals compatible with exact exchange.^68,69 Hence, in our assessment, we also consider the mISI@TPSS-GL2 method that replaces the true GL2 with the TPSS-GL2 meta-generalized-gradient approximation (meta-GGA) correlation functional,⁶⁸ which is one of the most accurate GL2 approximations available nowadays (see Table S12 of ref (70) for a comparison of few GL2 models).

This paper is organized as follows: In Section 2, we show a brief theoretical overview of the methods; in Section 3, we report the computational details; and in Section 4, we present and analyze the results. Finally, in Section 5, we summarize our conclusions.

2. Theoretical Overview of the Methods

Both ISI and mISI functionals have the same W_λ[ρ] integrand in eq 1

5

where X = xy²/z², Y = x²y²/z⁴, Z = xy²/z³ – 1, and x = −4E_c^GL2, y = W_∞, z = W₀ – W_∞ which, in turn, lead to following XC functional expression

6

The ISI functional approximates W_∞ with the GE2 of the PC model, and W_∞^′ has been fitted to the PKZB meta-GGA⁷¹ counterpart such that

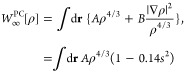7

and

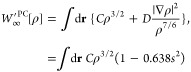8

where s = |∇ρ|/[2(3π²)^1/3ρ^4/3] is the reduced gradient of the density, A = −1.451 and C = 1.535 are the LDA low-density-limit coefficients, B = 0.005317 is the second-order gradient expansion coefficient of the PC model, and D = −0.02558 was fixed from W_∞^′PKZB[ρ] of the He atom.

On the other hand, mISI uses the following expressions⁶⁵

9

and

10

Here, a = 2 is the smallest integer that ensures W_∞^mISI[ρ] ≤ sLL[ρ], where sLL[ρ] = A ∫dr ρ^4/3 – 0.245 ∫dr ρ^4/3s^1/4 is the simplified gradient-dependent bound of Lewin and Lieb.^72,73 Note that W_∞[ρ] still recovers the GE2 of the PC model. Finally, b = 1.3 has been fitted to the correlation energy of the He atom.

By construction, mISI permits local interpolations along the adiabatic connection^57,62 and the adiabatic connection semilocal correlation (ACSC) functional formalism has been constructed.⁶⁵ Thus, for completeness, we will also show results with ACSC GGA correlation functional combined with OEPx.

The ACSC energy per particle ϵ_c^ACSC(r) is defined by E_c[ρ] = ∫dr ρϵ_c^ACSC(r), where⁶⁵

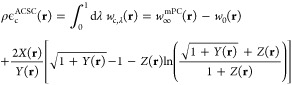11

while

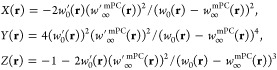12

Here, all energy densities w_λ(r), w_λ^′(r) are defined by W_λ = ∫drw_λ(r) and W_λ = ∫drw_λ^′(r).

The ACSC energy density is a local interpolation along the adiabatic connection, and it is meaningful when all of the energy densities are in the same gauge. Moreover, eq 11 is well defined only when w₀(r) > w_∞^mPC(r),⁶⁵ which is violated by the exact exchange energy density in the conventional gauge of the electrostatic potential of the XC hole,^55,74 but it is satisfied by the exact exchange energy density in the TPSS gauge.^65,74 Thus, all energy densities should be in the TPSS gauge, which is more appropriate for semilocal expressions. Because of their semilocal nature, both w_∞(r) and w_∞^′mPC(r) can be considered to be in the TPSS gauge.

For the ACSC GGA correlation functional, we use w₀^′(r) = 2ρϵ_c and w₀(r) = ρϵ_x^PBE(r) as in ref (65), where ϵ_c and ϵ_x^PBE are the GL2 and exchange energy densities of the popular PBE GGA functional.^65,75

The nonlinear form of the ISI correlation functional expression leads to the increase of size-consistency error,^58,61i.e., the total energy of two nonidentical, distant systems is not equal to the sum of energies of subsystems A and B separately, E_xc^(m)ISI(AB)_R→∞ ≠ E_xc(A) + E_xc^(m)ISI(B). As is generally known, the lack of size consistency may lead to wrong predictions, e.g., for atomization or binding energies of molecular systems.⁷⁶ This feature can be restored, without additional cost, utilizing the sum over fragments idea from ref (61), which allows us to compute the correlation energies of the infinitely far fragments (E_xc(AB)_R→∞) utilizing as ingredients in eq 6 the sum of energies of isolated parts. Then, the size-consistency correction can be written (for considered case) as

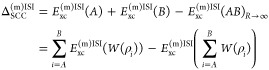13

where W[ρ] = {E_x[ρ], E_c^GL2[ρ], W_∞[ρ], W_∞[ρ]} is a compact notation for all ISI input ingredients (for more technical details, we refer the reader to ref (61)).

3. Computational Details

All methods considered in the present study have been implemented in a locally modified version of the ACES II⁷⁷ program. The ISI, mISI, as well as ACSC and mISI with TPSS-GL2 results have been obtained in a post-self-consistent-field (SCF) manner, using as a reference OEPx SCF converged quantities (i.e., orbitals, orbital energies, and densities). As in our previous studies,^{26,29,60,78−81} to solve the OEPx equation, we have employed the finite-basis set procedure of refs (82, 83). To enable the comparison with GL2 results and avoid problems related to full SCF treatment^78−80,84 (see also the discussion in refs (29, 85, 86)), the reported GL2 results are obtained in the same manner. As reference data, we have utilized the coupled-cluster single double and perturbative triple [CCSD(T)]⁸⁷ results obtained in the same basis set, to make a comparison on the same footing and to reduce basis set-related errors. Additionally, for comparison, we also report the results of the MP2¹⁶ and ab initio DFT OEP2-sc methods.⁸⁸

To assess all methods, we have considered several test cases:

• Correlation energies: evaluated for the set of 9 atoms and 27 small closed- and open-shell molecules from refs (81, 89).

• Thermochemistry data: This set contains atomization energies, i.e., AE6,^90,91 G2 subset⁸⁹ (see the Supporting Information of ref (81) for more details), small radicals,⁹² K9 barrier heights,^91,93 21 isomerization/reaction energies (ISO21),⁷⁶ closed- and open-shell reaction energies listed in refs (81, 94), and the hydrogen transfer reactions (HTR).^81,95 All of the aforementioned calculations have been performed using uncontracted cc-pVTZ basis sets of Dunning⁹⁶ without counterpoise corrections for basis set superposition error (BSSE). In the case of atomization energies, the size-consistency correction from ref (61) was employed.

• Vertical ionization potentials: 32 vertical ionization potentials (VIP)⁷⁹ computed as the energy difference between the neutral and the ionic species.⁹⁷ The computational setup, namely, basis sets and geometries (in the case of molecules), is identical to that in ref (79).

• Noncovalent interactions data: The interaction energies of several types of noncovalent interacting molecular systems also used in our previous studies,⁹⁸⁻¹⁰¹ such as weak interaction (WI), dipole–dipole interaction (DI6), hydrogen-bond interaction (HB6), double-hydrogen-bond interaction (DHB), and charge transfer interaction (CT7). The energies have been obtained using an uncontracted aug-cc-pVTZ¹⁰² basis sets together with the geometries from refs (103−106). All quantities have been calculated without counterpoise corrections for BSSE. In all cases, the size-consistency correction from ref (61) was employed.

• Harmonium atoms: We have performed calculation for various values of ω in the Hooke’s atom model¹⁰⁷ ranging between 0.03 (strong interaction) to 1000 (weak interaction) using a even-tempered Gaussian basis set from ref (108) (N = 8, L = 0, 1). The accuracy of full configuration interaction (FCI) results employing this basis set for all values of ω was cross-checked with the exact ones reported in ref (108) yielding, in total, a mean absolute error (MAE) of 0.002 Ha and a mean absolute relative error (MARE) of 0.06%. Because the ISI formula interpolates between weak- and strong-correlation limits, this test seems to be essential for the assessment of XC formula accuracy.

• Potentials for the strong-interaction limit: We have computed the functional derivatives of original and modified PC W_∞ and W_∞^′ models in a post-SCF manner using OEPx densities. This approach was already successfully utilized in some studies^60,109−111 to investigate the quality of the potentials.

4. Results

Here, we present and analyze results for thermochemistry, noncovalent interactions, and Hooke’s atom^112−115 at various frequencies ω of the harmonic potential. We also investigate the potentials for the strong-interaction limit for a few systems.

4.1. Thermochemistry Results

In Table 1, we present the error statistics (MAE and MARE) of the thermochemistry results. We observe that the mISI method shows a systematic improvement over the ISI method, for all of the tests. On the other hand, GL2 fails badly, being the worst method here. We recall that the GL2¹³ correlation energy expression is

14

where the indices i, j, a, and b are used for occupied and virtual KS orbitals, ε’s are the KS eigenvalues, and v_x^KS and v̂_x are the local, multiplicative KS OEPx and the nonlocal HF exchange potentials, respectively. The first term on the right-hand side of eq 14 is the same as the MP2 correlation energy expression, the only difference being computed using KS OEPx orbitals and orbital energies instead of the HF ones. The last term of eq 14 is small⁸⁰ in comparison to the first one such that E_c^GL2 is approximately E_c evaluated with KS orbitals. A comparison between the MP2 and GL2 results of Table 1 shows huge accuracy differences. In this respect, the ISI and mISI methods show significantly improved performance over GL2. This is a consequence of attenuating the GL2 energy term^60,79,80 in the ISI functional expression. Nevertheless, in general, they are still worse than MP2.

Table 1. Error Statistics (MAE and MARE) of Several Thermochemistry Properties^g.

			@OEPx
	MP2	OEP2-sc	GL2	ISIf	mISIf	mISIe	ACSC
Correlation Energies (9 Atoms and 27 Molecules)
MAEa	24.4	18.4	95.4	42.3	34.9	85.9	73.6
MAREb	10.5	8.7	26.6	10.4	8.3	21.4	16.9
Atomization Energies (27 Molecules)
MAEcI	5.5	8.0	37.8	16.8	15.1	14.8	17.8
MAREb	5.2	7.3	31.6	15.2	13.4	13.2	17.2
Atomization Energies (AE6 Test)
MAEcI	12.2	17.1	82.1	32.7	23.6	25.5	21.0
MAREb	3.7	5.6	23.6	13.6	11.7	7.5	6.9
Atomization Energies (Small Radicals)
MAEcI	6.1	15.7	53.0	21.7	16.6	30.3	34.2
MAREb	3.9	12.1	89.1	17.0	12.2	31.1	46.4
Kinetics (K9 Test)
MAEcI	2.8	14.9	18.9	16.0	15.0	15.9	14.8
MAREb	22.5	46.5	75.9	45.5	37.8	68.3	68.6
HTR Test
MAEcI	13.5	2.2	25.4	14.8	12.2	2.9	2.8
MAREb	143.5	32.6	259.5	150.2	119.0	29.5	34.0
21 Isomerization Energies (ISO21 Test)
MAEcI	0.89	0.39	20.71	12.48	10.97	7.16	6.61
MAREb	7.97	16.59	96.60	42.74	23.87	82.39	84.89
31 Closed-Shell Reaction Energies
MAEcI	2.0	3.0	10.6	4.7	4.6	11.4	10.3
MAREb	46.8	34.5	106.3	54.5	57.3	144.8	125.7
26 Open-Shell Reaction Energies
MAEcI	4.3	3.4	18.3	11.5	10.4	12.2	11.6
MAREb	12.3	12.7	51.5	34.6	29.5	35.6	30.2
32 Vertical Ionization Potentials (VIP)
MAEd	0.2	0.2	1.2	0.6	0.5	0.4	0.4
MAREb	2.4	1.2	9.0	4.9	4.3	3.8	3.6

^aIn mHa.

^bIn %.

^cIn kcal/mol.

^dIn eV.

^eWith TPSS-GL2.

^fCorrected for size-consistency error (see ref (61)).

^gThe best result between ISI and mISI of each line is highlighted in bold style. The full results of all tests are reported in ref (70). The OEP2-sc results are fully self-consistent, the MP2 and (reference) CCSD(T) results are calculated on top of HF orbitals, and the results of the other methods (GL2, ISI, mISI, mISI@TPSS-GL2, ACSC) are computed on top of OEPx orbitals.

On the other hand, mISI@TPSS-GL2, which replaces into the mISI expression the GL2 term with the semilocal TPSS-GL2 variant, is usually worse than mISI, especially for the correlation energies of atoms and molecules. Indeed, more reliable semilocal approximations of GL2 are needed. Finally, the ACSC GGA correlation combined with OEPx exact exchange has a similar accuracy to mISI@TPSS-GL2.

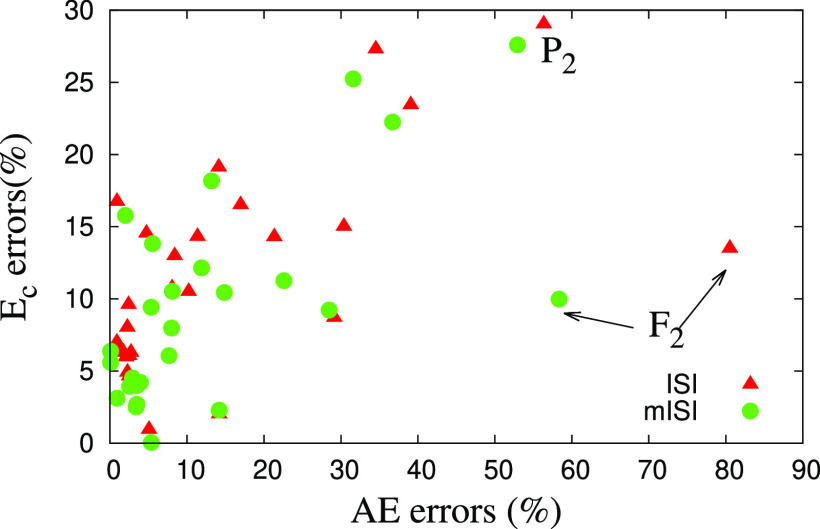
Next, in Figure 1, we show the atomization energy errors versus correlation energy errors for the set of 27 small molecules, used also in Table 1. For almost all of the molecules, the mISI method performs better than the ISI for both properties. We also mention that the worst results are found from F₂ and P₂, which are difficult cases in quantum chemistry, due to their multiconfiguration character.¹¹⁶

Figure 1.

Absolute relative errors (in %) of the atomization energies (AE) versus the ones of the correlation energies, for a set of 27 small molecules BeH, OH, NH₂, NH, NO, PH₂, O₂, S₂, SiH₂, C₂H₅, CH₂, CH₃, CN, COH, CH₄, LiF, Li₂, F₂, CO, CH₂, H₂, CS, LiH, N₂, P₂, NaCl, and H₂O. For the worst cases F₂ and P₂, GL2 fails badly for atomization energies, with errors of 188 and 73%, respectively.

4.2. Noncovalent Interaction Results

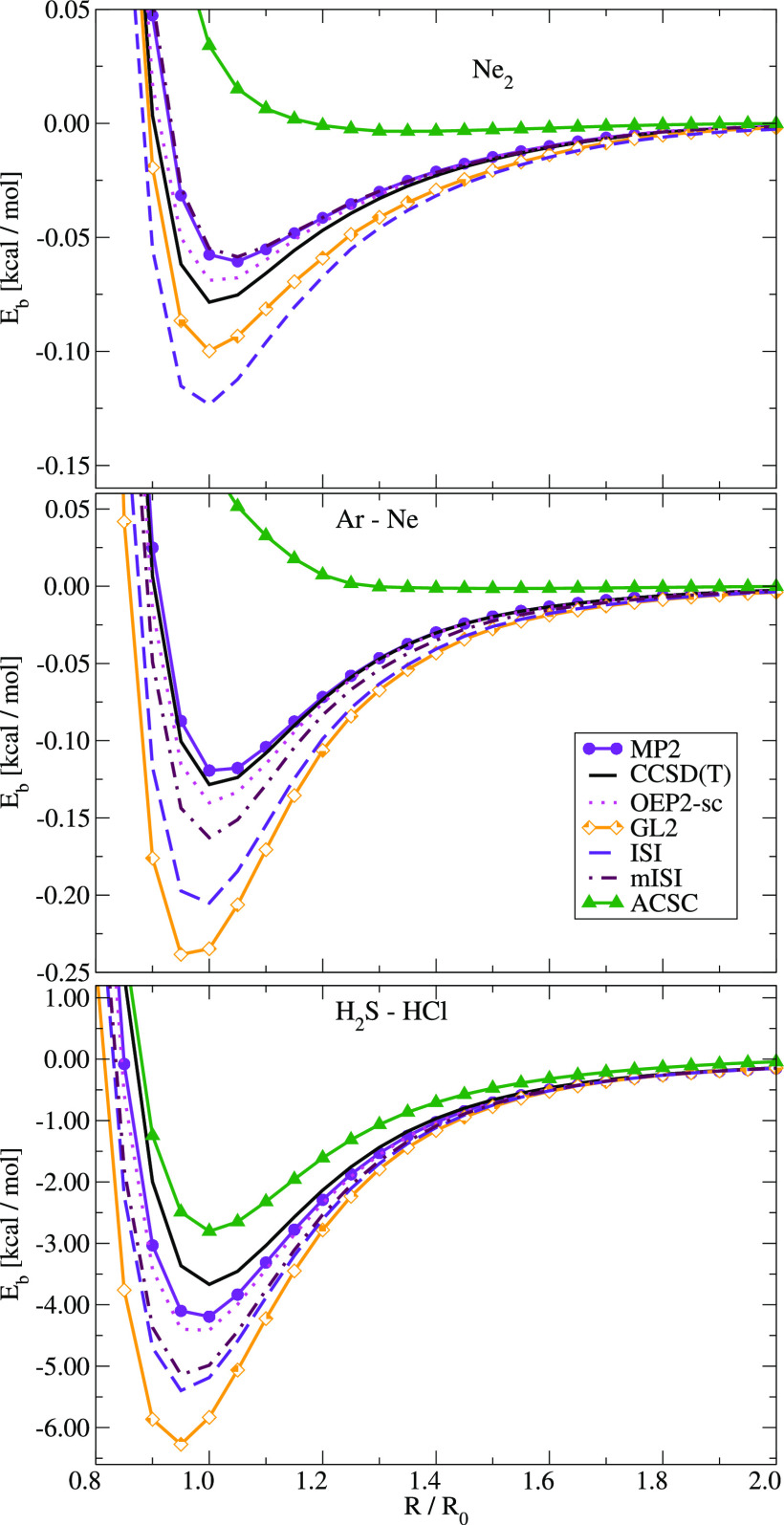
In Figure 2, we report the binding energy curves for three representative cases, namely, Ne₂, Ar–Ne, and H₂S–HCl dimers. In the case of ISI and mISI curves, to enable the comparison with reference results, we have applied the size-consistency correction from ref (61).

Figure 2.

Binding energy curves of Ne₂ (top), Ne–Ar (middle), and H₂S–HCl (bottom) computed using different theoretical methods. In the case of ISI and mISI methods, the size-consistency correction from ref (61) was employed.

First of all, we note that the ACSC gives too shallow binding curves similar to most semilocal functionals. Almost same behavior (not reported) was observed for the mISI@TPSS-GL2 method. The ISI and mISI methods, in turn, reduce the huge overestimation of the GL2 method, with one exception of Ne dimer where ISI gives slightly worse predictions. Nevertheless, also in this case, the utilization of modified point charge plus continuum (mPC) variants of W_∞ and W_∞^′ corrects the predictions. The mISI method, in general, performs better than the ISI method, the results being much closer to reference CCSD(T) and to the ab initio OEP2-sc data.

This finding is further confirmed by the data gathered in Table 2, where we report the error statistics obtained for several classes of noncovalent interacting molecular systems. The overall statistics confirm previous findings. The mISI outperforms the ISI method, giving in the same time results comparable to the OEP2-sc method. The only exception is for the HB6 test, where we observe an inverse trend. However, a closer look at the total energies (used to calculate HB6 binding energies) shows also here very good performance of the mISI method. The MAEs of total energies, calculated for GL2, ISI, and mISI with respect to the CCSD(T) reference, follow the general observed trend mISI (0.11 Ha) < ISI (0.14 Ha) < GL2 (0.28 Ha). This may indicate that the relatively good performance of ISI for the HB6 binding energies can be related to some error balancing between W_∞^PC and W_∞ GE2 terms.

Table 2. MAE and MARE for Noncovalent Interaction Test Sets^e.

			@OEPx
	MP2	OEP2-sc	GL2	ISId	mISId	mISIc	ACSC
WI
MAEa	0.04	0.05	0.51	0.36	0.24	1.96	0.32
MAREb	18.53	17.08	598.63	455.11	426.50	899.71	150.26
HB6
MAEa	0.17	0.27	0.75	0.39	0.70	0.64	0.66
MAREb	1.81	4.32	9.27	4.92	7.28	7.50	6.49
DI6
MAEa	0.45	0.71	2.16	1.41	1.14	1.01	1.09
MAREb	12.85	20.24	64.05	42.53	34.80	38.97	34.77
CT7
MAEa	0.55	1.35	2.54	1.71	1.39	1.94	1.64
MAREb	14.99	40.25	80.36	54.94	44.61	69.62	60.33
DHB
MAEa	0.54	0.85	1.62	0.98	0.79	0.91	1.01
MAREb	8.19	13.18	30.31	18.52	15.17	20.54	20.53
Overall
MAEa	0.38	0.74	1.63	1.05	0.91	1.37	1.03
MAREb	12.58	24.28	154.22	113.00	103.06	195.24	58.49

^aIn kcal/mol.

^bIn %.

^cWith TPSS-GL2.

^dCorrected for size-consistency error (see ref (61)).

^eThe best result between ISI and mISI of each line is highlighted in bold style. The OEP2-sc results are fully self-consistent, the MP2 and (reference) CCSD(T) results are calculated on top of HF orbitals, and the results of the other methods (GL2, ISI, mISI, mISI@TPSS-GL2, ACSC) are computed on top of OEPx orbitals.

We also note that in the case of WI systems, the ISI and mISI methods yield quite large MAE and MARE. This is caused by large errors given by two dimers, namely, He–Ne and He–Ar. We have found that the large overestimation of ISI binding energies is inherited from the GL2 method, which gives energies of 0.90 and 0.83 kcal/mol for He–Ne and He–Ar, respectively. At the same time, the reference CCSD(T) results yield −0.04 and −0.06 kcal/mol for these two cases. To explain this, we have had a closer look at the GL2 total energies involved in the calculation of the binding energy of the He–Ne dimer. It has turned out that while the Ne and He–Ne dimer total GL2 energies largely overestimate the reference CCSD(T) data (approximately by about 80 mHa), the He total GL2 energy gives quite accurate results, being only 6.4 mHa off CCSD(T) data, in consequence, causing the rise of large error in the binding energy. Nevertheless, we note that both the ISI and mISI methods slightly reduce the value of GL2 binding energies for both dimers.

In Table S13 of ref (70), we report additionally the comparison of binding energies obtained from the ISI and mISI methods using HF reference orbitals. Because the MP2 method already provides quite accurate results (MAE = 0.38 kcal/mol, MARE = 12.58%), the improvement seen in ISI and mISI results, which give here overall MAEs of 0.25 kcal/mol (MARE = 10.26%) and 0.29 kcal/mol (MARE = 17.11%), respectively, is not so significant as observed in Table 2.

To conclude, the mISI shows a systematic improvement over the ISI method, and most importantly, both these methods provide significant correction over GL2, which fails badly, being the worst method for all of the tests.

4.3. Hooke’s Atom

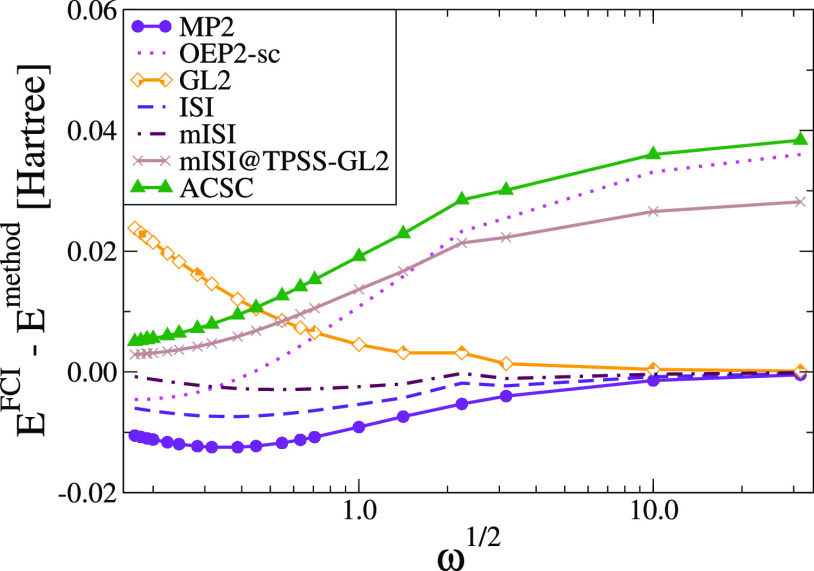
Figure 3 reports the errors in the total energies of harmonium atoms calculated for various values of ω ranging between 0.03 and 1000 for several methods. Because both ISI formulas interpolate between weak- and strong-correlation limits, this type of test can be of utmost importance for checking their accuracy and smooth transition between these two regimes. An inspection of the figure reveals that the best performance is given by the mISI method closely followed by ISI, OEP2-sc, and MP2 results. This indicates that the modified GGA PC formula, which fixes the behavior of ISI functional in the density tail, has a strong impact on the proper description of both regimes. In medium- and weakly correlated limits, we observe really good performance of the GL2 method. This is not surprising because GL2 becomes exact in this regime. On the other hand, in the strongly correlated limit, the GL2 method shows the worst performance of all methods. The ACSC and mISI@TPSS-GL2 give similar performance to the ab initio OEP2-sc method, namely, a small error for ω^1/2 < 1 and a large overestimation for larger values of ω.

Figure 3.

Absolute error on total energies of harmonium atoms for various values of ω.

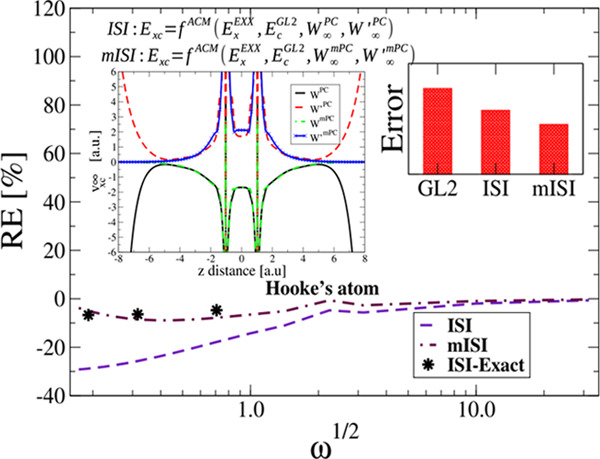
To better see the functional performance at the strong-correlation limit (ω → 0), we report in Figure 4 the relative errors (RE) on the correlation energy. When ω → 0, mISI is the most accurate method being in good agreement with the ISI method computed with exact W_∞ and W_∞^′.⁶² On the other hand, the original ISI, which uses the PC model, gives quite large errors of about 30%, but still much better than GL2, which fails badly, with an error of about 120%. Note that when ω → 0, the density varies rapidly almost everywhere such that the reduced density gradient s is large, and the gradient expansion of the PC model cannot describe this regime.

Figure 4.

Relative error on correlation energies of harmonium atoms for various values of ω. The black dots (denoted with ISI-Exact) show the results of the ISI method computed with exact W_∞ and W_∞^′, taken from ref (62).

4.4. Analysis of Functional Derivatives of W_∞ and W_∞^′

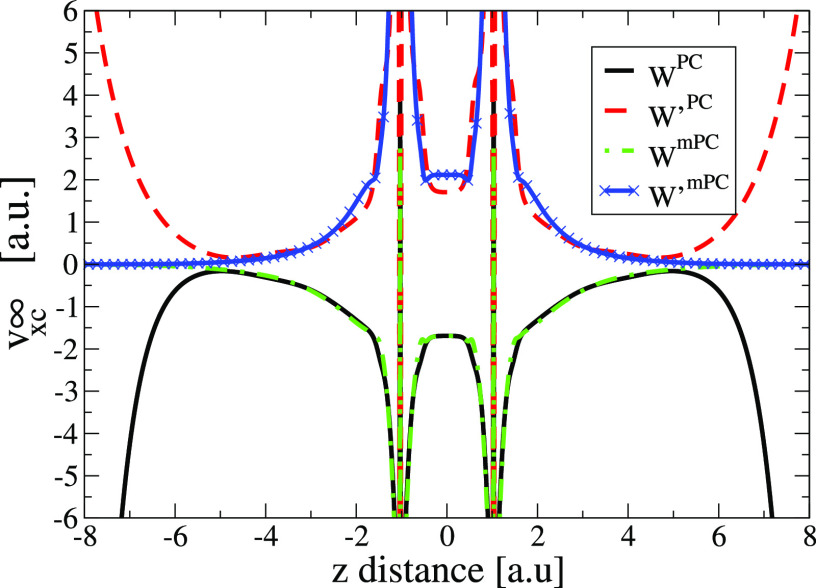
Finally, in Figures 5 and 6, we report the comparison of the functional derivatives of W_∞^PC and W_∞ and their modified counterparts for two representative systems, namely, H^– ion and N₂ molecule.

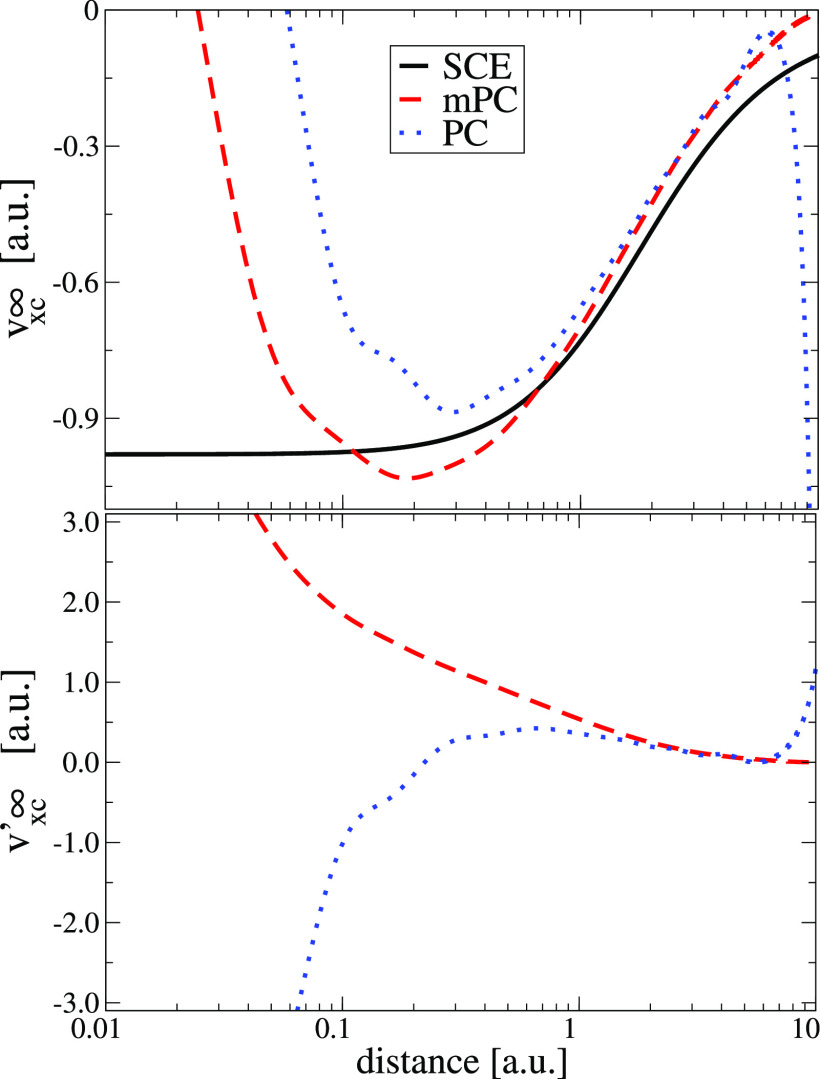
Figure 5.

(Top) Comparison between the exact (SCE) functional derivative of W_∞ and the one computed from PC and modified PC model. (Bottom) Functional derivative of W_∞^′ computed from PC and modified PC model. Both figures are done for H^–.

Figure 6.

Functional derivative of PC and modified PC for N₂ molecule plotted along the bond axis.

Let us turn first our attention to the H^– ion. We note that both mPC and PC W_∞ and W_∞^′ potentials, like any other GGA, diverge on the nuclei, contrary to the exact SCE potential. Furthermore, in the tail of the density, both PC potentials diverge.⁶⁰ This is not the case for mPC potentials where we observe smooth and fast decay to zero in this region. We recall here that the exact SCE potential decays as −1/r in the tail of the density. On the other hand, it was shown recently¹¹⁷ that the functional derivative of an exact W_∞ diverges in the tail for one-dimensional systems. This might indicate that the divergence is an exact feature of W_∞^′ and W_∞ is a more accurate model.

A similar behavior is observed for the N₂ molecule. In the nuclei, both potentials diverge, whereas in the far asymptotic region, the mPC potentials decay quite fast to zero in contrast to the PC potential which diverges.

We note, however, that the utilization of ISI-like functionals in practical KS calculations requires that the functional derivative of the XC functional is finite in the tail. Thus, one needs to remove the divergences of the functional derivative¹¹⁸ despite whether this is an exact or model feature. This step is important toward the fully self-consistent implementation of ISI functionals.¹¹⁸

5. Conclusions

We have presented a small assessment and comparison of ISI and mISI methods showing that the utilization of the modified PC model in ISI formula leads always to the improvement in the results. Moreover, the inspection of functional derivatives of W_∞ and W_∞^′ obtained from the mPC model shows a lack of divergence in the tail of the density, which is a crucial step toward the self-consistent implementation of ISI functionals.

We note that the overall accuracy of the results provided by all ISI-like functionals is not better than other semilocal, hybrid, and double-hybrid functionals.⁵⁸ This is due to the dominant role of the GL2 or MP2 (depending on the reference orbitals used in the evaluation of energy) term in the ISI formula⁶⁰ for most of the chemically important applications. Thus, one possible way to improve the results is to include more terms in eq 3, i.e., third-order GL/MP or higher. This, however, will significantly increase the cost of the method. Another possible path is to substitute the GL2/MP2 term by rescaled GL2/MP2⁷⁶ or one of spin-component-scaled variant^80,119−122 of GL or MP perturbation theory.

Finally, we mention that the mPC, and implicitly the mISI method, can be further improved by considering the Pauli kinetic energy enhancement factor^123−128 as an additional ingredient, which is relevant for one- and two-electron systems,¹²⁹ atomic core,¹²⁹ asymptotic behavior in the tail of the density,¹³⁰ and superior overall performance.¹²⁸ These will be a subject of further studies.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00328.

• Full results for Tables 1 and 2 with accompanying statistical analysis (Tables S1–S13) (PDF)

The authors declare no competing financial interest.