Improved Consensus-Fragment Selection in Template-Assisted Prediction of Protein Structures with the UNRES Force Field in CASP13

Abstract

The method for protein-structure prediction, which combines the physics-based coarse-grained UNRES force field with knowledge-based modeling, has been developed further and tested in the 13th Community Wide Experiment on the Critical Assessment of Techniques for Protein Structure Prediction (CASP13). The method implements restraints from the consensus fragments common to server models. In this work, the server models to derive fragments have been chosen on the basis of quality assessment; a fully automatic fragment-selection procedure has been introduced, and Dynamic Fragment Assembly pseudopotentials have been fully implemented. The Global Distance Test Score (GDT_TS), averaged over our “Model 1” predictions, increased by over 10 units with respect to CASP12 for the free-modeling category to reach 40.82. Our “Model 1” predictions ranked 20 and 14 for all and free-modeling targets, respectively (upper 20.2% and 14.3% of all models submitted to CASP13 in these categories, respectively), compared to 27 (upper 21.1%) and 24 (upper 18.9%) in CASP12, respectively. For oligomeric targets, the Interface Patch Similarity (IPS) and Interface Contact Similarity (ICS) averaged over our best oligomer models increased from 0.28 to 0.36 and from 12.4 to 17.8, respectively, from CASP12 to CASP13, and top-ranking models of 2 targets (H0968 and T0997o) were obtained (none in CASP12). The improvement of our method in CASP13 over CASP12 was ascribed to the combined effect of the overall enhancement of server-model quality, our success in selecting server models and fragments to derive restraints, and improvements of the restraint and potential-energy functions.

Introduction

Modeling protein structures becomes increasingly important with the progress of biological and medical sciences, the main reason for this importance being an insufficient supply of experimental structures. The accuracy of theoretical models has greatly improved over the years.¹ Moreover, relatively inexpensive experiments such as small-angle X-ray/neutron scattering (SAXS/SANS)²⁻⁴ and chemical cross-link/mass spectrometry (XLMS)^5,6 enable us to guide modeling for difficult targets.

Protein-structure modeling used to be divided into knowledge-based and physics-based categories,⁷ which were thought to be clearly separated from each other. Physics-based modeling is guided by the energy function of choice,⁸⁻¹⁰ the engine being the selected method of conformational-space search (usually molecular dynamics and its extensions), while sequence-structure similarity, which is justified by evolutionary relationship, is the basis of knowledge-based modeling.¹ The knowledge-based methods underwent significant progress in recent years, owing to improved contact prediction¹¹⁻¹⁵ and the introduction of deep-learning algorithms.^16,17 However, because there are at least 10% of targets for which no reliable template can be found,¹⁸ the knowledge-based methods routinely use energy functions in such important tasks as model selection and refinement as well as in a limited search of the conformational space in the famous fragment method developed by the Baker group.^19,20 On the other hand, the physics-based methods also use knowledge-based information, e.g., restraints from secondary-structure and contact prediction. Thus, the distinction between the two categories becomes gradually blurred.

Recently,^21,22 we developed a hybrid approach to protein-structure modeling, in which a restrained conformational search is carried out with the coarse-grained physics-based UNRES force field developed in our laboratory,²³ the geometry restraints being taken from the fragments extracted from the knowledge-based models produced by servers. The fragments are selected on the basis of their similarity. This fragment-based approach differs from those applied in, e.g., MODELLER²⁴ or MULTICOM,²⁵ in which restraints derived from whole models are imposed. If the fragments are shared by many server models, they are likely to be good predictions of the corresponding section(s) of a protein. This approach achieved considerable success in the 12th Community Wide Experiment on the Critical Assessment of Techniques for Protein Structure Prediction (CASP12),²⁶ especially in the data-assisted category.²⁷ In this work, we automated the process of fragment selection and also fully applied the Dynamic Fragment Assembly (DFA) pseudopotentials.^28,29 Moreover, we used the OPT-WTFS-2 version of UNRES optimized with 7 training proteins.³⁰ In this paper, we report the results of testing of the improved approach in the 13th Community Wide Experiment on the Critical Assessment of Techniques for Protein Structure Prediction (CASP13) exercise with the regular and oligomeric targets. The results of data-assisted predictions by the KIAS-Gdansk group have been published recently as a part of a joint paper.³¹ The results of our predictions of oligomeric-protein structures in the 46th Community Wide Experiment on the Comparative Evaluation of Protein–Protein Docking for Structure Prediction (CAPRI46) have also been published recently as a part of a joint paper.³²

Methods

Measures of Structure Similarity

In this work, we use the Global Distance Test Score (GDT_TS)^7,33 as a primary measure to compare our models of single protein chains/domains with the respective experimental structures. The GDT_TS is the average of the percentage of residues in the computed structure that are within 1, 2, 4, and 8 Å distances, respectively, from their counterparts in the experimental structure (eq 1).

1

where GDT_Pn is the percentage of the C^α atoms whose distance from the C^α atoms of the experimental structure is below the n Å cutoff.

In the process of the selection of consensus fragments (section Restraint Derivation) and also as a measure of similarity of our models or their sections to the respective experimental structures, we use the α-carbon Root-Mean-Square Deviation (C^α-RMSD or RMSD), which is defined by eq 2.

2

where X_M and X_T are the coordinates of the model (M) and the target (T) structures, n being the number of the reciprocating C^α atoms, whereas R and t are the rotation matrix and the translation vector that minimize the distance between the two structures when applied sequentially to the coordinates of the model, X_M.

For oligomeric structures, the Interface Patch Similarity (IPS), quantified as the Jaccard coefficient and Interface Contact Similarity (ICS),³⁴ quantified as the F1 score,³⁴ are used as the primary measures of the similarity of monomer packing in the model and in the experimental structure. These measures were also used to assess oligomeric-target predictions in CASP12³⁴ and CASP13.³⁵ The IPS is the ratio of the number of interface-patch residues common to the model and to the target and that of the number of all interface residues that occur in the model and in the target. It is defined by eq 3 (ref (34))

3

where I_M and I_T are the sets of residues in the interface patch of the model and of the target, respectively, and |...| denotes the number of elements in a set. The ICS, defined by eq 4, is the harmonic mean of precision (P; the percentage of the correct interchain contacts among all interchain contacts in the model, defined by eq 5) and recall (R; the percentage of correctly reproduced native interchain contacts, defined by eq 6).

4

5

6

where C_M and C_T are the sets of interface contacts present in the model and in the target, respectively.

Apart from IPS and ICS, we also use the global RMSD and GDT_TS (pertaining to the whole oligomer) and the interface RMSD (I-RMSD), which is computed from eq 2 with the set of superposed atoms reduced to those present in the protein–protein interfaces in the experimental structure.

Prediction Protocol

The general protocol of the prediction of protein structures consisted of the same stages as those used in CASP12.²⁶ The procedure consists of the following five stages. In stage 1, models from selected servers are processed to extract the consensus (similar in geometry) fragments and, subsequently, to determine the geometry restraints from these fragments, as described in Restraint Derivation. In this preparatory stage, the DFA pseudopotentials^28,29 are also determined. In stage 2, multiplexed replica exchange molecular dynamics (MREMD) simulations,³⁶⁻³⁸ with the pseudoenergy function consisting of the UNRES force field,²³ DFA pseudopotentials,^28,29 and the restraint terms determined from the selected server models, are carried out to search the conformational space subject to the restraints from the server models. In stage 3, the obtained ensemble of conformations is subsequently processed with the Weighted Histogram Analysis Method (WHAM)³⁹ and, in stage 4, a cluster analysis is performed to select the candidate coarse-grained models (refs (10 and 40) and also Selection of Candidate Predictions). In stage 5, each of the coarse-grained models is subsequently converted to the all-atom representation by using the PULCHRA⁴¹ and SCWRL⁴² knowledge-based algorithms for all-atom backbone and side-chain reconstruction, respectively, and subjected to final refinement at the all-atom level with the AMBER ff14SB force field,⁴³ as described in our earlier work.²⁶ This protocol was applied to all regular targets except for T0997, in which case we carried out the calculations for the dimer only, the initial structures of which were generated with the use of the ClusPro server.^44,45 The final models are converted into the CASP format and submitted. For the oligomeric targets, the procedure differs in that the monomers (which are usually separate targets in the CASP experiments) are usually treated first and then initial oligomer structures are constructed.

In the subsequent subsections, we describe briefly the stages of the procedure summarized above and the pertinent methodology.

Energy Function

To calculate the energy of the systems under study, we use the coarse-grained UNRES model of polypeptide chains and the pertinent force field. UNRES is a highly reduced model, in which a polypeptide chain is represented as a sequence of C^α atoms with two kinds of interaction sites: the united peptide groups (p), each positioned in the middle between two consecutive C^α atoms, and the united side chains (SC) that are attached to the respective C^α atoms (Figure 1). If a residue is glycine, the respective “united side chain” coincides with the C^α atom. The geometry of the chain can be described in terms of the Cartesian coordinates of the C^α atoms and those of the SC centers, in terms of the C^α···C^α and C^α···SC virtual-bond vectors or in terms of the backbone-virtual-bond angles θ, backbone virtual-bond-dihedral angles γ, and the zenith and azimuth angles α and β defining the orientation of a side chain with respect to the local backbone frame (Figure 1). The UNRES energy function (hereafter referred to as U_UNRES) is discussed in detail in ref (23), and its physical origin is presented in detail in our recent work.⁴⁶ In this work, we use the version of the UNRES energy function obtained in ref (30) by calibration with 7 training proteins, which is referred to as the OPT-WTFS-2 force field.

Figure 1.

UNRES model of polypeptide chains. Blue spheres represent the peptide groups (p), spheroids represent the side chains (SC), and small white spheres represent the α-carbon atoms (which are not interaction sites but only serve to assist in chain-geometry definition). The backbone-virtual-bond angle θ_i, backbone-virtual-bond-dihedral angle γ_i, and the two angles α_i and β_i that define the location of the ith side-chain center with respect to the backbone are shown. Reproduced from Zaborowski et al., J. Chem. Inf. Model.2015, 55, 2050 (DOI: 10.1021/acs.jcim.5b00395). Copyright 2015 American Chemical Society.

The complete pseudoenergy function is expressed by eq 7.

7

where e_DFA is the DFA energy (eq 8), V_dist, V_ang, V_dih, and V_SC denote the restraining potentials for the C^α distances, backbone virtual-bond angles, backbone virtual-bond-dihedral angles, and local side-chain coordinates, respectively (eq 9), and the w’s denote the weights of the restraining terms; in this work, we set w_dist = 0.5 and w_ang = w_dih = w_SC = 1.0, respectively. The DFA pseudopotentials and restraint terms are described in detail in Dynamic Fragment Assembly (DFA) Pseudopotentials and Template-Based Restraints, respectively.

Dynamic Fragment Assembly (DFA) Pseudopotentials

The DFA method^28,29 is based on extracting the structural information, specific for the sequence under investigation, from the fragment library and then translating this information into residue-position specific energy terms (pseudopotentials). The DFA pseudoenergy function is expressed by eq 8

8

where e_DFA,dist and e_DFA,angle are to assimilate the local structure of a model to its corresponding fragments²⁹ and e_DFA,nn represents the preferred packing environment around each residue by the number of neighboring C^α atoms from the fragment library.²⁹ For the respective expressions, the reader is referred to the original papers.^28,29

Template-Based Restraints

Restraint Energy Function

The geometric restraints derived from the server models (considered as templates) are imposed on the C^α···C^α distances, the backbone-virtual-bond angles θ, the backbone-virtual-bond-dihedral angles γ, and the local coordinates of the side-chain-direction vectors (Figure 1). The restraint-penalty function consists of log-Gaussian quasi-harmonic terms, which can be expressed by a common formula given by eq 9, which is similar to that adapted from MODELLER²⁴ in our earlier work,^21,22 except that the selected fragments do not have to be common to all templates.

9

Here, V_x is the penalty function imposed on a given set of geometric parameters (C^α···C^α distances, virtual-bond angles, virtual-bond-dihedral angles, or local side-chain coordinates), M_i^incl is the number of templates whose selected fragments contain the geometric parameter with index i, M_i is the number of templates whose selected fragments do not contain the geometric parameter i, M_i^incl + M_i = M, M being the total number of templates, and m₁, m₂, ..., m_Mi^incl are the indices of the templates that contribute to the restraints on the geometric parameter i. x_i and x_i^(m_k) are the values of the ith geometric parameter of a given kind in the calculated and in the m_kth reference structure, respectively, and the σ’s are the standard deviations of the respective Gaussians, which are set as given by eqs 10 and 11.

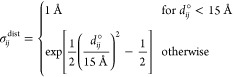10

11

All of the templates contribute to restraints mostly for the template-based modeling (TBM) targets and, consequently, the restraint function given by eq 9 is usually bounded because M^excl > 0; the larger M^excl/M, the shallower is its minimum.

Restraint Derivation

In our earlier work,^22,26 the fragments to derive the restraints from were required to be common to all models gathered from the top servers (GOAL,⁴⁷ BAKER-ROSETTASERVER,¹⁹ Zhang-Server,⁴⁸ and QUARK⁴⁸ in CASP12²⁶), 5 models taken from each server. The underlying assumption was that the parts of the structures, which were similar in top-server models, were likely to be predicted reliably. The fragments were defined as the longest fragments of all templates that superposed within 4 Å C^αRMSD. In this work, we modified the algorithm to select fragments that are not necessarily common to all templates and to select the templates from many servers, based on objective quality assessment, rather than from predefined trusted servers.

Selection of Server Models

The server models were selected on the basis of their quality, assessed by means of the DeepQA server.²⁵ By analyzing the correlation between the DeepQA scores calculated for the CASP12 models and the GDT_TS of these models shown in Figure 2, we divided the regions into 0 < DeepQA < 0.5, 0.5 ≤ DeepQA < 0.7, and DeepQA > 0.7 as low, medium, and high quality regions. Consequently, the selection procedure was as follows. If there were enough (20 or more) server models with DeepQA > 0.7, 20 top-DeepQA-ranked models were selected for further steps. If the DeepQA score was between 0.5 and 0.7, the 20 models were selected on the basis of DeepQA ranking and by eliminating those which had weakly defined secondary structure. If the DeepQA score was below 0.5, the models from the servers best performing in CASP12 [MULTICOM,²⁵ Zhang-server,⁴⁸ QUARK,⁴⁸ RaptorX⁴⁹ (that split in CASP13 into RaptorX-DeepModeller, RaptorX-TBM, and RaptorX-Contact, respectively^50,51), and BAKER-ROSETTASERVER¹⁹ were selected, and the selection process was completed by removing the models with weakly defined secondary structure.

Figure 2.

Plot of the correlation of the GDT_TS of the server models from CASP12 exercise with the respective DeepQA²⁵ values (1486 models). The regression line is GDT_TS = −2.47 (0.57) + 97.5 (1.5) × DeepQA, where the numbers in parentheses are the standard deviations of the parameters, with a standard deviation of σ_{GDT_TS} = 14.8, correlation coefficient r = 0.73, and explained variance r² = 0.54.

A bar plot showing the counts of all server models, the models selected on the basis of DeepQA,²⁵ and those selected from the servers best performing in CASP12 (for which DeepQA was too low to judge model quality) in GDT_TS (which was not known at the prediction time) is shown in Figure 3A. It can be seen that the scoring using DeepQA removed the models of poor quality (with low GDT_TS) to a higher extent than the selection from the best-performing servers. Additional “pruning” of server models resulted from fragment selection described in the next paragraph, because the models which did not share common fragments were rejected. This is illustrated in Figure 3B, in which the counts of models sharing and not sharing common fragments are shown as a function of model GDT_TS (calculated after the completion of the CASP13 experiment). As can be seen, almost all of the models not sharing common fragments and, therefore, removed had GDT_TS < 50, with the peak around 15. Without filtering, the low-quality models would be over-represented and, consequently, the quality of the restraints would deteriorate.

Figure 3.

(A) Bar plot of the counts of all server models submitted to CASP13 (purple), the server models selected using DeepQA²⁵ (green), and those selected from servers that performed well in CASP12 based on visual inspection (light blue). (B) Bar plot of the counts of the server models selected to derive restraints (purple) and rejected (green) as a function of GDT_TS.

A bar plot illustrating the numbers of models selected from particular servers is shown in Figure 4. It can be seen that most of the models from which restraints were derived were the Zhang-server (group 261), QUARK (group 145), and the BAKER-ROSETTASERVER (group 368) models; the models from those servers were also selected by us during the CASP12 experiment.²⁶ However, RaptorX-TBM (group 221) and RaptorX-DeepModeller (group 324), which were not present in CASP12, also have a substantial share.

Figure 4.

Bar plot of the summary counts of models from different servers selected to derive the geometry restraints. The servers are identified in the abscissa by the respective CASP13 group numbers.

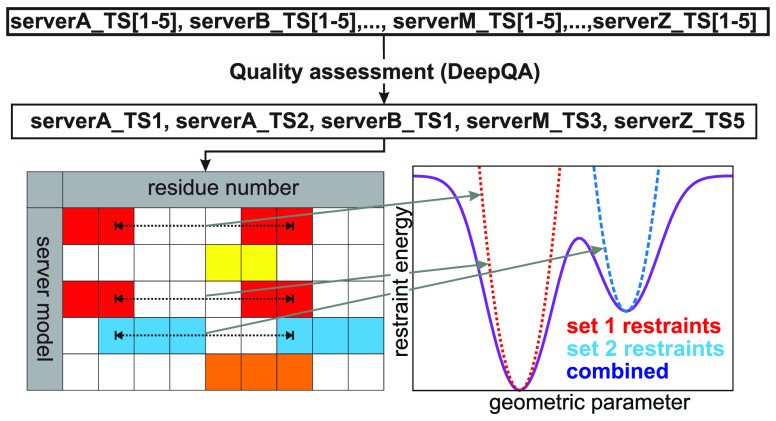
Selection of Fragments

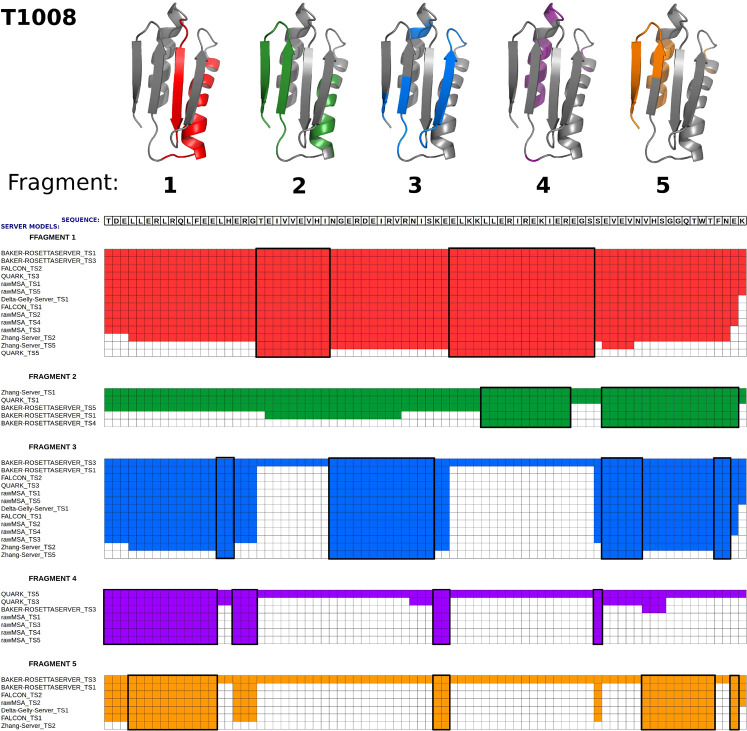
Once the server models (templates) to derive fragments from have been selected, the C^α-RMSD tables ρ_ij^(kl), where i and j are the indices of the first and the last C^α atoms to superpose and k and l are the indices of the templates, are constructed for all pairs of templates. On the basis of these tables, an initial library of fragments common to pairs of models, defined as those for which the corresponding C^α atoms are not farther from each other than the 7 Å C^α distance cutoff, is created. This is done by initially selecting the pairs of contiguous fragments, whose C^α-RMSD is within the 7 Å cutoff, and gradually eliminating the residues whose C^α atoms in one model are farther than 7 Å from those in the other model of the pair. It should be noted that the fragments thus constructed are, in general, noncontiguous. The longest fragment from the library is subsequently selected to initiate the first cluster of templates sharing a common fragment; let the indices of the corresponding templates be k_max and l_max, respectively. To add the next template to the cluster, the other elements of the initial template library sharing the k_max or l_max index are examined, and the one sharing the longest fragment is added to form a cluster of three fragments; the nonoverlapping residues were deleted. The process is continued, until the number of common residues has dropped below 20 (usually, the drop is rapid). The fragment is considered only if it is shared by at least 5 templates. The fragment found is deleted from those elements of the template-pair library, in which it occurs, and the procedure is iterated, until no more fragments with a length of at least 20 residues shared by at least 5 templates can be found. As a result, the clusters of templates, at least 5 members each, sharing fragments of length 20 or more residues are created. The procedure of fragment selection is illustrated in Figure 5.

Figure 5.

Illustration of the scheme of fragment selection with the example of the CASP13 target T1008. In the upper panel, the five selected fragments are marked on the experimental structure of this protein (which was unknown at the prediction time) by red, green, blue, purple, and orange colors, respectively; the remaining part of the protein is colored gray. The panels below depict the history of the determination of these fragments. For fragment 1, the search started with two models with the longest overlapping segments, which were BAKER-ROSETTASERVER¹⁹ models 1 and 3, respectively, and comprised the whole sequence. The models from 9 other servers were found to overlap in the entire sequence range; then, the last residue did not when model 1 from the Delta-Gelly server was added. Finally, 14 server models were found to overlap over 27 residues. The fragment comprises two disconnected sequence parts corresponding to a helix-strand motif shown in red in part 1 of the upper panel and also as two boxes in the panel below. The further addition of models resulted in shortening of the length of the overlapping fragment below the 20 residue cutoff. The found fragment was eliminated from the 14 server models that it occurred in, and the procedure was run again to find the second fragment. This procedure was iterated until no more fragments comprising at least 20 residues and common to at least 5 server models could be found.

MREMD Simulations

To search the conformational space, we used multiplexed replica exchange molecular dynamics (MREMD)³⁷ which, as its predecessor, the replica exchange molecular dynamics (REMD),³⁶ enables us to search the conformational space more efficiently than canonical molecular dynamics (MD). In REMD and MREMD, multiple trajectories are run at different temperatures (T₀, T₁, ..., T_MT). The replicas evolve independently and, after a certain time interval, an exchange of temperatures between the neighboring replicas (j = i + 1) is attempted, the exchange being accepted on the basis of the Metropolis criterion. A single replica and multiple replicas correspond to a given temperature in REMD and MREMD, respectively. The details of MD implementation with UNRES are described in refs (52−54), while the REMD/MREMD implementation with UNRES is described in ref (38).

In this work, we ran trajectories at 12 replica temperatures, 4 trajectories per temperature (48 trajectories per system total). The temperatures were determined with the aid of the Hansmann algorithm,⁵⁵ which maximizes the extent of walk in the temperature space. The replica temperatures thus were 260, 262, 266, 271, 276, 282, 288, 296, 304, 315, 333, and 370 K, respectively. Each trajectory usually consisted of 20 000 000 MD steps with a 4.89 fs step length. The adaptive multistep time-split (A-MTS) algorithm developed in our earlier work⁵⁴ was used. Replicas were exchanged, and snapshots were saved every 10 000 MD steps. The temperature was controlled by the Langevin thermostat, with the solvent friction scaled by 0.01 to speed up simulations, as in our earlier work.⁵³

For single-chain targets, MREMD was fed with all the selected models from the servers, which were distributed between the trajectories to start a production run.

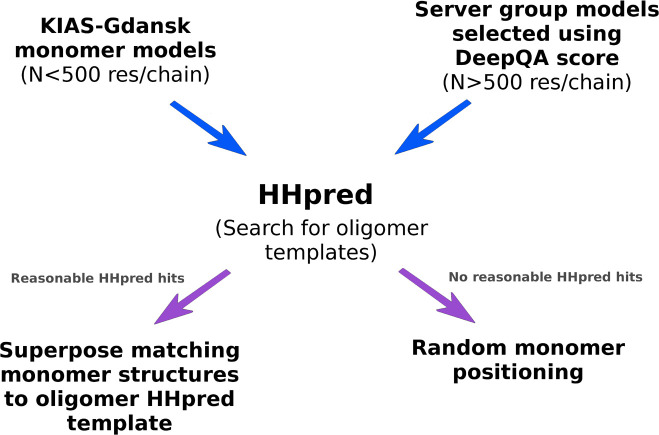
The procedure of the construction of the initial models of the oligomeric structures is illustrated in Figure 6. For not excessively large targets (with monomer chain length of up to 500 residues), the KIAS-Gdansk group models of the respective monomeric structure(s) were used to construct the initial structures of the oligomers. For large oligomeric targets (over 500 residues per monomer chain, which included T0984, T0995, T1003, and T1009), the structures of the monomers were taken directly from server-group models, and the DeepQA score²⁵ was employed to rank the models. Because all large oligomeric targets considered in the CASP13 experiment were very homologous, the DeepQA²⁵ score was high and, therefore, scoring models by using this measure were highly reliable. Five top (according to DeepQA) server models of the monomers were selected for building the initial structures of a respective oligomeric target. Once the monomer building blocks had been selected, they were submitted to the HHpred server⁵⁶ (except for T0997o, in which case the ClusPro server^44,45 was used) to search the PDB for the structures of multimeric proteins with the highest sequence similarity to those of the target oligomeric sequences. If reliable hits were obtained, monomer models (from either the KIAS-Gdansk or server predictions) were superposed on the respective monomers of the oligomer templates found by HHpred (or ClustPro for T0997o) to form the starting structures of the oligomers for UNRES/MREMD simulations. If no reasonable hits were obtained, initial oligomer structures were constructed by random oligomer packing, subject to excluded-volume conditions. The initial models were subsequently distributed to MREMD trajectories to start a simulation.

Figure 6.

Scheme of the construction of initial oligomer-target models. See text for description.

MREMD production simulations for oligomers were carried out with restraints imposed on well-defined structure parts of the monomers (omitting loops, domain linkers, and chain-end regions), instead of using the consensus-fragment-based restraints.

For the smallest targets (with chain lengths less than 100 amino-acid residues), MREMD simulations required up to 2–4 wall-clock hours to accomplish, with 48 cores (1 core per trajectory). For the medium-size targets (up to 200 residues), about 12 wall-clock hours with 384 cores (8 cores per trajectory) were required. For the largest oligomeric targets (1000 residues or more), 48 wall-clock time hours with 576 cores (12 cores per trajectory) were needed. The timings pertain to Cray XC40 of the Interdisciplinary Center of Mathematical and Computer Modeling of the University of Warsaw, ICM (https://kdm.icm.edu.pl/kdm/Okeanos/en), the Intel Xeon E5 v3 cluster at the Informatics Center of the Tricity Academic Computer Network in Gdansk, TASK (https://task.gda.pl/kdm/sprzet/tryton/), and the Intel Xeon cluster at the Academic Computer Center CYFRONET in Krakow (http://www.cyfronet.krakow.pl/komputery/15207,artykul,prometheus.html). Detailed timing and scalability analysis of UNRES runs is presented elsewhere.^57,58

Selection of Candidate Predictions

To select candidate predictions of a given target, the last 200 snapshots from each trajectory (a total of 9600 conformations) were processed by WHAM,³⁹ which was implemented in UNRES in our earlier work.⁴⁰ WHAM enables us to calculate the probabilities of all conformations at a desired temperature and, consequently, ensemble-averaged and thermodynamic quantities, in particular the heat capacity. The temperature at which the conformational ensemble was analyzed (T_a) was determined to be 20 K below the major heat-capacity peak; usually, it ranged from 260 to 300 K. The conformations were then sorted in the descending order of probabilities, and those which constituted together 99% of the ensemble at T_a were subjected to Ward’s minimum-variance clustering⁵⁹ into 5 families of conformations. Subsequently, the fractions (probabilities) of the families of the conformational ensemble at the selected temperature were calculated by using the procedure developed in our earlier work,⁴⁰ and the families were ranked according to decreasing probabilities. This ranking also corresponded to the ranking of the models submitted to CASP. A weighted-average conformation was calculated for each cluster (with weights determined by WHAM), and the conformation of the cluster closest to the average conformation was selected to represent the entire cluster.^10,40 These representative conformations of the five clusters were then converted to all-atom structures.

Results

Regular Targets

In this section, we describe the performance of the KIAS-Gdansk group in the regular 3D prediction of single-chain proteins, Tnnnn, and subunits of multichain proteins, Tnnnnsm, where nnnn and m are the integers denoting target and unit numbers, respectively, including the leading zeros. The rankings and the measures of model quality as well as the GDT_TS plots were taken from the official CASP13 page (http://predictioncenter.org/casp13/index.cgi).

As the KIAS-Gdansk group, we submitted predictions of 71 regular targets (out of 72 targets, which were not canceled or converted to the server-only category), which comprised 127 evaluation units (EUs) out of 131 EUs total, each EU being defined as a protein domain or whole protein molecule. T0999 was skipped by the KIAS-Gdansk group due to its large size and, thereby, not accomplishing the prediction within the 3-week time window.

The assessors divided the CASP12 EUs into 4 difficulty categories, based on the correlation plot between the arithmetic mean of the HHpred score (accounting for the sequence similarity to database proteins),⁶⁰ the LGA (local and global structure alignment) score,³³ and the GDT_TS of the 20 top performing servers. These categories are the template-based modeling (TBM) category [(HHpred + LGA)/2 > 60, GDT_TS > 50 except for the EUs on the boundary of the region], the free modeling (FM) category [(HHpred + LGA)/2 < 60, GDT_TS < 50 except for the EUs on the boundary of the region], and the FM/TBM category for the EUs not belonging to these regions (i.e., with high HHpred/LGA scores but low performance of the top 20 servers or low HHpred/LGA scores and high performance of the top 20 servers, respectively).⁶¹ For the EUs close to the boundary of the TBM or FM regions, the classification was adjusted on the basis of visual inspection. This classification was carried over to CASP13 except that the TBM category was split into TBM-easy and TBM-hard.⁶² To keep the consistency with the CASP12 classification, in the analysis presented in this work, the CASP13 TBM-easy and TBM-hard categories are merged into a single TBM category. Following this classification, our models pertained to 12, 17, and 38 EUs of the TBM, FM/TBM, and FM categories in CASP12 and 50, 12, and 31 EUs of these categories in CASP13, respectively. Because we applied a different protocol than the standard KIAS-Gdansk protocol to the CASP13 target FM/TBM T0997 (see Prediction Protocol), we excluded it from the GDT_TS analysis; this left 11 FM/TBM EUs. The other EUs (23 in CASP12 and 27 in CASP13, respectively) were unclassified or classified as the FM-special category (whole CASP13 targets T1000 and T1002, respectively); usually, these are whole multidomain proteins. We grouped these unclassified and FM-special EUs into the “other” category. It should be noted that many of the unclassified multidomain targets could be FM targets, an example being the CASP10 target T0663, which is composed of two TBM domains, only the complete protein being an FM target.⁶³

We also processed the refinement targets. However, our method has not been designed for refinement, unless substantial rearrangement of the substructures with respect to their packing in the template takes place, which was not the case for CASP13. Therefore, we did not obtain exceptionally good results for any of the refinement targets. In CASP12, we obtained very good results for targets TR872 and TR898, because repacking of α-helices that were incorrectly packed in the templates occurred.²⁶ On the other hand, our group ranked 18th out of 31 groups in the refinement category in CASP13, compared to 29th out of 39 groups in CASP12, which suggests some improvement.

Comparison with the Parent Server Models and with CASP12 Results

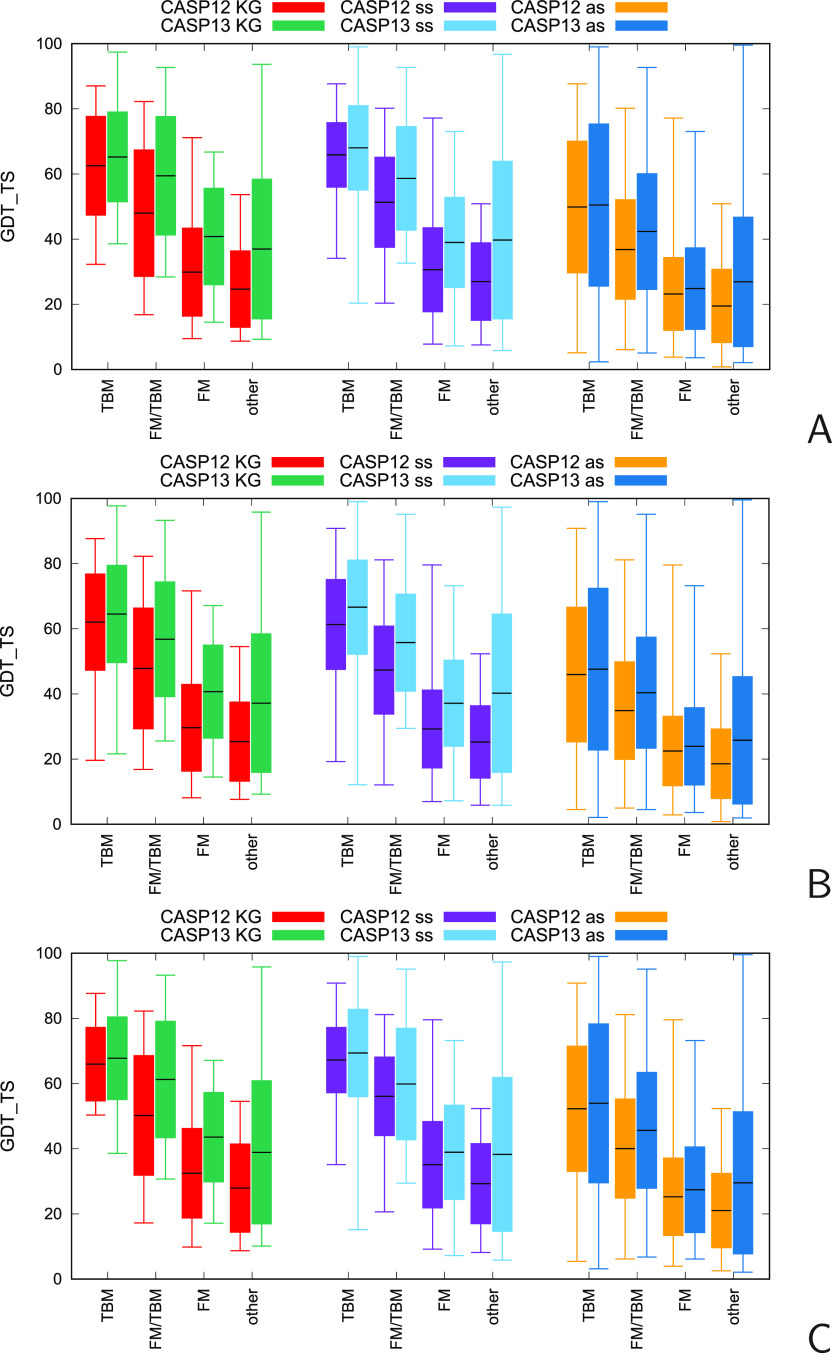
The candlestick plots showing the average, maximum, and minimum values as well as the standard-deviation range of the GDT_TS of the first, all, and the best (with the highest GDT_TS) models obtained by the KIAS-Gdansk group in CASP13 and CASP12 for comparison as well as the corresponding plots for the server models selected to derive restraints and all server models for each of the target-difficulty categories (TBM, FM/TBM, FM, and “other”) are shown in Figure 7. The GDT_TS values and ranks of the first and best KIAS-Gdansk models, together with target categorization with regard to difficulty (TBM-easy, TBM-hard, FM/TBM, FM, and “other”),⁶² are summarized in Table S1, while the minimum, maximum, and average GDT_TS values as well as the standard deviations of the average GDT_TS values, calculated over the KIAS-Gdansk, selected server, and all server models of the respective categories are summarized in Table S2. Figure 8 displays the differences of the GDT_TS of the first, all, and the best KIAS-Gdansk, selected server and all server models from CASP12 to CASP13. The values of these differences, their standard deviations, and significance levels calculated by means of the Student’s test are summarized in Table S3. The GDT_TS differences between the KIAS-Gdansk models and selected server models, the KIAS-Gdansk models and all server models, and the selected server models and all server models, respectively, and their standard deviations are shown in Figure 9 (for the first, all, and the best models). Their values and the significance levels are summarized in Table S4. It should be noted that the standard deviations of the mean differences decrease in the order KIAS-Gdansk > selected server > all server models, which results from the fact that the numbers of models taken to compute averages increase in this order (Table S2).

Figure 7.

Candlestick plots of the GDT_TS of the CASP12 and CASP13 models produced by the KIAS-Gdansk group (left pairs of sticks in panels A–C), server models selected by the KIAS-Gdansk group to derive restraints and select starting models (middle pairs of sticks in panels A–C), and all server models (right pairs of sticks in panels A–C) for the TBM, FM/TBM, FM, and unclassified (other) EUs. Panel A: the KIAS-Gdansk and server “Model 1” predictions; panel B: all KIAS-Gdansk and server models; panel C: best KIAS-Gdansk and server models. The horizontal lines in the middle of each bar correspond to the mean values; the bars range from the mean minus the standard deviation to the mean plus the standard deviation, and the whiskers correspond to the minimum and maximum values. The colors corresponding to each category and CASP experiment are shown above the graphs: KG denotes the KIAS-Gdansk models, ss denotes selected server models, and as denotes all server models, respectively.

Figure 8.

Candlestick plots of the difference of the GDT_TS of the CASP12 and CASP13 models, ΔGDT_TS = GDT_TS(CASP13) – GDT_TS(CASP12), produced by the KIAS-Gdansk group (left), the server models selected by the KIAS-Gdansk group to derive restraints and select starting models (middle), and all server models (right) for the TBM, FM/TBM, FM, and unclassified (other) EUs. The horizontal lines in the middle of each bar correspond to the difference between the means over the CASP13 and CASP12 models of each category, and the bars range from the difference between the means minus the standard deviation of this difference to the difference of the means plus the standard deviation of this difference. The colors corresponding to each category are shown above the graphs: KG denotes the KIAS-Gdansk models, ss denotes selected server models, and as denotes all server models, respectively.

Figure 9.

Candlestick plots of the differences of the GDT_TS of the KIAS-Gdansk and selected server models, ΔGDT_TS(KG,ss) = GDT_TS(KG) – GDT_TS(ss), KIAS-Gdansk and all server models, ΔGDT_TS(KG,as) = GDT_TS(KG) – GDT_TS(as), and the selected server and all server models, ΔGDT_TS(ss,as) = GDT_TS(ss) – GDT_TS(as), in CASP12 and CASP13 for the first (panel A), all (panel B), and best (panel C) models of the TBM, FM/TBM, FM, and unclassified (other) EUs. The horizontal lines in the middle of each bar correspond to the differences between the GDT_TS means over respective categories; each bar ranges from the difference of the mean minus the standard deviation of this difference to the difference of the mean plus the standard deviation of this difference. The colors corresponding to each category are shown above the graphs: KG denotes the KIAS-Gdansk models, ss denotes selected server models, and as denotes all server models, respectively.

As can be seen from Figures 7 and 8 and Tables S2 and S3, the average GDT_TS obtained by the KIAS-Gdansk group in CASP13 increased, for all target-difficulty categories, with respect to CASP12 values,²⁶ regardless of whether the first, all, or the best models are considered. The least increase is observed for the TBM and the biggest, for the FM and “other” models. When considering the “Model 1” predictions (which are the first choices when utilizing predictions as protein-structure models), the GDT_TS increased from 62.51 to 65.23 (by 2.72, 92% significance) for the TBM models, from 47.97 to 58.64 (by 11.47, 97% significance) for the FM/TBM models, from 29.88 to 40.82 (by 10.94, 100% significance) for the FM models, and from 24.66 to 36.97 (by 12.31, 100% significance) for the “other” models (Table S3). Similar GDT_TS increases can be observed for the all and best models (Figure 8 and Table S3). As mentioned in the beginning of Comparison with the Parent Server Models and with CASP12 Results, some of the “other” category models could probably be regarded as another variant of FM; however, because of its being out of clear classification, caution should be exercised when using it to assess the improvement of the prediction methodology. The increase of the GDT_TS difference in the order TBM < FM/TBM < FM/“other” with a jump from TBM to FM/TBM is not surprising, because our methodology is aimed at finding the correct arrangement of the fragments of a structure that is correctly predicted by bioinformatics approaches and not at refining the models of homology targets.

As can be seen from Figures 7 and 8 and from Tables S2 and S3, the GDT_TS values of the selected server and all server models have also increased with respect to CASP12, which is in agreement with the overall improvement of model quality from CASP12 to CASP13.¹⁵ Except for the best models, this increase is significantly smaller for all server models, compared to that for the KIAS-Gdansk and selected server models, which strongly suggests that the procedure of server-model selection developed in this work enabled us to choose the highest-quality models to derive restraints. For the TBM category, the increase seems to be partially due to higher sequence identity, on average, of the CASP13 compared to that of the CASP12 target (see Figure 1A in ref (14)). The constant improvement of the predictions of the FM targets has also been observed from CASP10 to CASP13 (Figure 6 in ref (15)), which probably results from the use of methods for contact or even longer distance prediction, which are steadily improving.^13,15

It can be seen from Figure 8 and Table S3 that the GDT_TS values of the FM/TBM and FM KIAS-Gdansk models increased from CASP12 to CASP13 more than those for selected server models, regardless of whether the first, all, or best models are considered. For the FM category models, the GDT_TS increased by 2.56 units more for the first KIAS-Gdansk models and by 7.28 units more for the best KIAS-Gdansk models, compared to the selected server models. The selected server TBM models improved more than the KIAS-Gdansk models when considering all and the best models, and the selected server models of the “other” category improved more when considering all and the first models. In summary, a greater improvement of the KIAS-Gdansk models compared to that of selected server models was observed in 8 out of 12 instances, which strongly suggests that not only model selection but also improvements of the prediction protocol contributed to the improved performance of the KIAS-Gdansk group in CASP13 (Figure 8 and Table S3), even though our method certainly benefits from the continuing improvement of the server models utilized to derive geometric restraints.

The differences of the GDT_TS values of the KIAS-Gdansk models and those of the selected server models and all server models as well as the GDT_TS differences of the selected server models and all server models are compared in Figure 9A–C (for the first, all, and the best models, respectively) and summarized in Table S4. It can be seen that, in CASP12, the KIAS-Gdansk values were lower than those for the selected server models for all and the best models and slightly higher for the first models (the differences being, however, of low statistical significance, as shown in Table S4). In CASP13, the KIAS-Gdansk models of the FM targets turned out to have higher GDT_TS values than those of the parent servers, the mean differences being 1.83 (93% significance) for the first models, 3.56 (100% significance) for all models, and 4.66 (100% significance) for the best models. The GDT_TS values are also higher than those for the selected server models for the FM/TBM target category, although the differences are of low statistical significance. The selected server models of the TBM targets have higher GDT_TS values, on average, than the KIAS-Gdansk models, regardless of whether the first, all, or the best models are considered, and the “other” category models from selected servers have higher GDT_TS values, except for those averaged over all models (although the statistical significance of the differences is low).

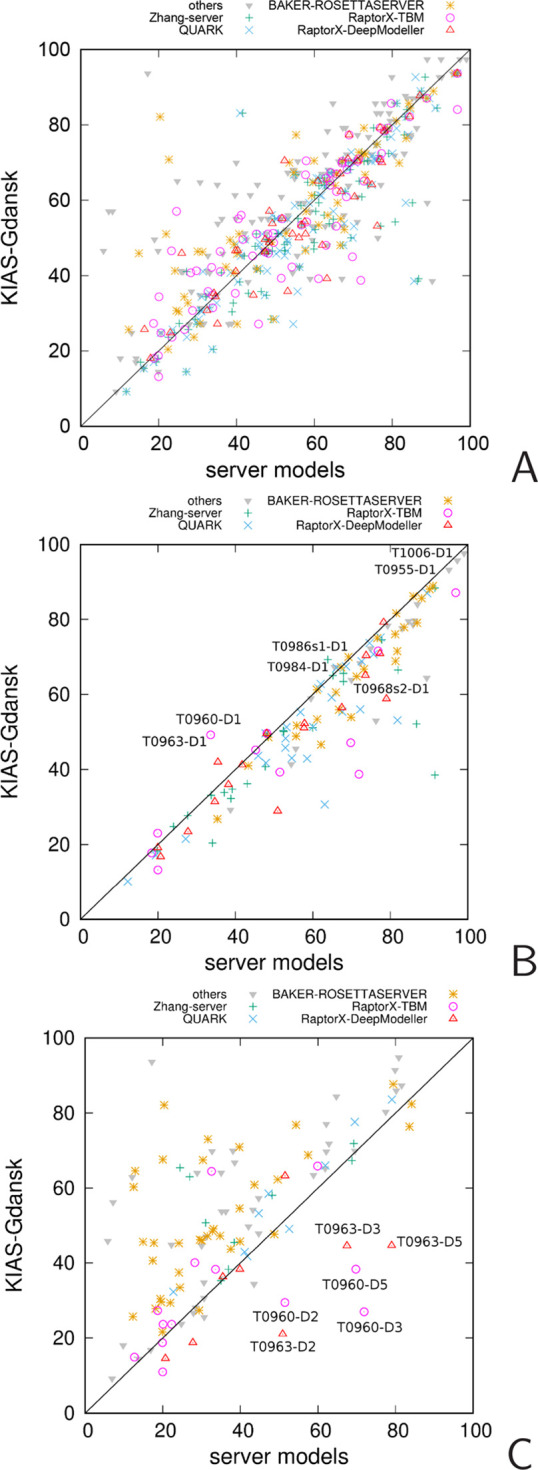
In agreement with the above observations, for many targets, the mean GDT_TS values are higher and the GDT_TS distributions are more focused than those of the server models. This is illustrated by the scatter-whisker plots shown in Figure 10A,B for the targets for which the server models were selected on the basis of DeepQA scoring²⁵ and those from the servers that performed best in CASP12, respectively. It can be seen from Figure 10 that, although the ranges of the server-model GDT_TS (represented by horizontal whiskers) touch higher values than those of the KIAS-Gdansk models, they also comprise small GDT_TS values. Conversely, the highest values of the KIAS-Gdansk model GDT_TS are smaller than those of selected server models but the GDT_TS ranges (the vertical whiskers in the plots) do not contain excessively small values.

Figure 10.

Whiskered scatter plots of the GDT_TS of the KIAS-Gdansk models vs those of the selected server models for targets, for which selection was based on DeepQA²⁵ scoring (A) and those where the servers that performed best in CASP12 were selected (B). Filled red circles represent the mean values; horizontal whiskers represent the GDT_TS ranges of the server models and vertical whiskers, those of the KIAS-Gdansk models.

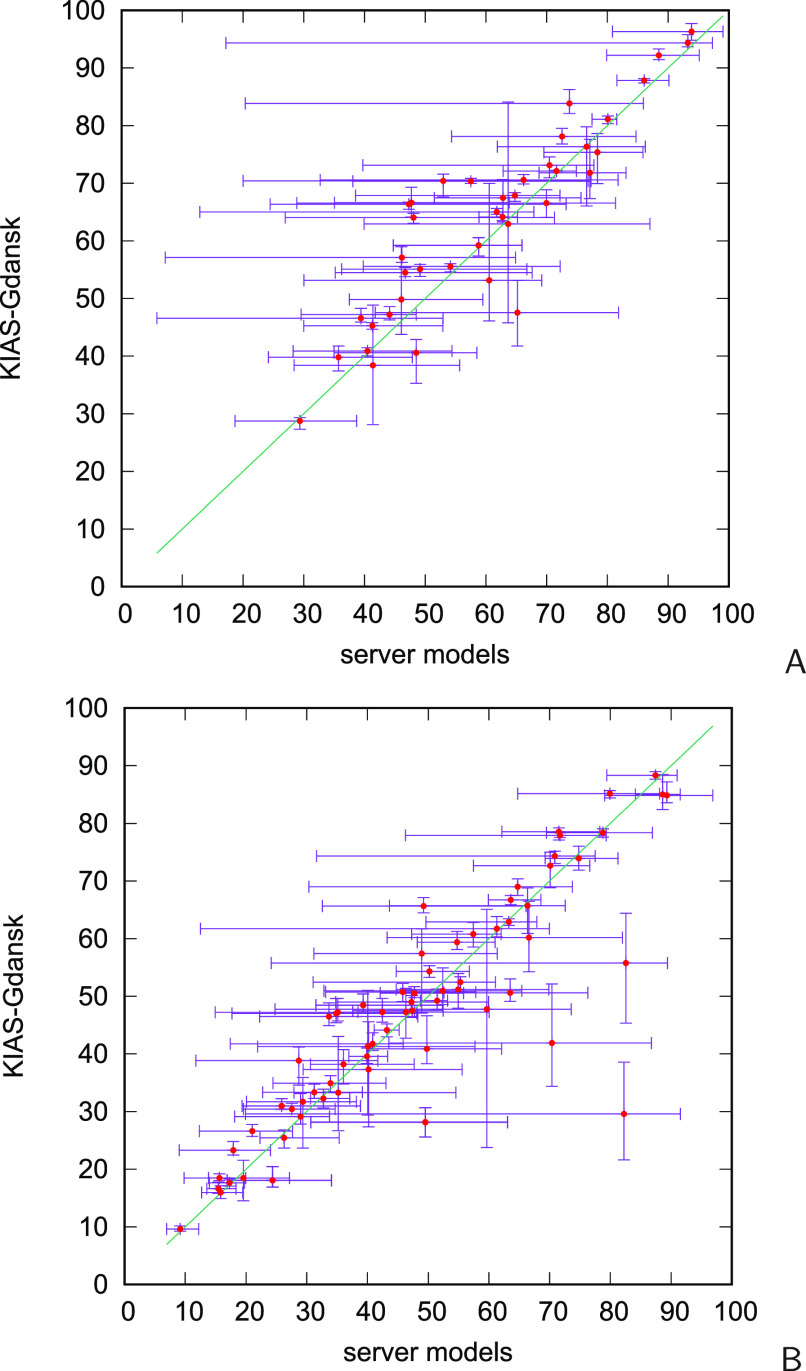
The correlation between the GDT_TS values of the “Model 1”, best and worst server, and KIAS-Gdansk predictions is shown in more detail in Figure 11, in which the points corresponding to the five servers from which the models were the most frequently used to derive restraints are shown as different symbols. As can be seen from Figure 11A, the points corresponding to the “Model 1” predictions are located almost equally on both sides of the diagonal. For the best models (Figure 11B), most of the points are below the diagonal, which means that the majority of the best server models have higher GDT_TS than the KIAS-Gdansk models of the corresponding targets, a conclusion that can also be drawn from Figure 7A. There are, however, several points above the diagonal, and the GDT_TS is distinctively higher for target T0960-D1; this model ranks 12 among all the models of this evaluation unit submitted to CASP13 (see Table S1). The GDT_TS of the worst KIAS-Gdansk models is usually higher than that of the corresponding server models (Figure 11C), an observation that we also made in our earlier work by analyzing the CASP12 KIAS-Gdansk predictions.²⁶ This observation suggests that the restraints from the lowest-quality server models do not influence much of the KIAS-Gdansk models. The reason for this is that these restraints usually correspond to a small number of consensus fragments and do not, therefore, make a substantial contribution to the restraint function (eq 9). On the other hand, there are several points in Figure 11C for which the worst KIAS-Gdansk predictions are worse than the worst server predictions. These points correspond to the evaluation units derived from targets T0960 and T0963, which are viral pyocins (PDB codes: 6CL5 and 6CL6, respectively), for which additional information about the extended shape of the structures was released a few days before the submission deadline. We used this information to impose additional restraints but, because of the large size and trimeric structure of both targets, with chains intertwined in the dimer, we were able to run only short simulations, which were not sufficient to achieve convergence. To obtain the other restraints and to construct the starting structures of targets T0960 and T0963, RaptorX_TBM⁵¹ model 1 and RaptorX_DeepModeller⁵⁰ model 3, respectively, were used.

Figure 11.

Scatter plots of the GDT_TS of the “Model 1” KIAS-Gdansk predictions vs the respective “Model 1” server predictions (A), the best KIAS-Gdansk predictions vs the respective best server predictions (B), and the worst (lowest GDT_TS) KIAS-Gdansk predictions vs the respective worst server predictions (C). The evaluation units for which the KIAS-Gdansk models were remarkably better or remarkably worse compared to server models are marked in the plots. The points corresponding to each of the 5 servers from which the models were most frequently selected by the KIAS-Gdansk group in CASP13 to derive restraints are shown as different symbols, the respective legend being located above the plot.

A detailed comparison of the server and KIAS-Gdansk models of targets T0960 and T0963 is shown in Figure S1 and Table S1. It can be seen that, although many KIAS-Gdansk models are worse than the server models used to derive restraints, there are also models that are better. In particular, for T0960-D1, the GDT_TS of the initial model (RaptorX_TBM⁵¹ Model 1) was 33.59 and the average GDT_TS of the respective KIAS-Gdansk models was 43.13 (49.22 for the best model). The KIAS-Gdansk models of the EUs pertaining to the other large targets that were run as oligomers T0984, T0995, T1003, and T1009 were better than average as shown in Figure S2.

Comparison of the Performance of the KIAS-Gdansk Group with Other Groups

As can be seen from Figure 11, Zhang-server,⁴⁸ QUARK,⁴⁸ and RaptorX-DeepModeller⁵⁰ server predictions have usually higher, while those from BAKER-ROSETTASERVER¹⁹ and RaptorX-TBM⁵¹ have lower GDT_TS values compared to KIAS-Gdansk models. This observation is confirmed by comparing the rankings of the KIAS-Gdansk first and best models with those of the five servers, which are summarized in Table 1 for all types of targets considered. It can be seen that Zhang-server,⁴⁸ QUARK,⁴⁸ and RaptorX-DeepModeller⁵⁰ rank better than the KIAS-Gdansk group for all categories, BAKER-ROSETTASERVER¹⁹ and RaptorX-TBM⁵¹ rank worse for the FM category and for all targets, while RaptorX-TBM also ranks worse for the FM/TBM category. The ranking of the KIAS-Gdansk group has increased compared to CASP12 for all categories except TBM (Table 1), the most significant increase being noted for the FM category. It should be noted that, in CASP12, the KIAS-Gdansk group did not outrank any of the four servers, from which the models were used to derive restraints (Zhang,⁴⁸ QUARK,⁴⁸ BAKER-ROSETTASERVER,¹⁹ or GOAL⁴⁷), while it outranked two of the servers from which the bulk of models were used, BAKER-ROSETTASERVER¹⁹ and RaptorX-TBM⁵¹ in CASP13 for the FM category, regardless of whether the “Model 1” or the best predictions are considered.

Table 1. Rankings and Percentage Rankings (in Parentheses) in the Respective Target-Difficulty Categories and for All Targets of the KIAS-Gdansk Group and of the Server Groups for Which the Models Were Most Frequently Used To Derive Restraints in CASP12 and CASP13^a.

	TBMb		FM/TBM		FM		all
group	CASP12	CASP13	CASP12	CASP13	CASP12	CASP13	CASP12	CASP13
KIAS-Gdansk	32 (26.3%)	33 (33.3%)	33 (26.2%)	25 (25.7%)	24 (18.9%)	14 (14.3%)	27 (21.1%)	20 (20.2%)
	33 (27.0%)	39 (39.4%)	38 (30.2%)	31 (31.2%)	32 (25.1%)	24 (24.5%)	35 (27.3%)	29 (29.3%)
Zhang-Server	17 (13.9%)	4 (4.0%)	8 (6.3%)	10 (10.3%)	13 (10.2%)	6 (6.1%)	3 (2.4%)	5 (5.1%)
	24 (19.7%)	11 (11.1%)	20 (15.9%)	24 (24.7%)	9 (7.1%)	13 (13.3%)	13 (10.2%)	12 (12.1%)
QUARK	23 (18.9%)	6 (6.1%)	16 (12.7%)	7 (7.2%)	12 (9.4%)	4 (4.1%)	14 (11.0%)	4 (4.0%)
	32 (26.2%)	10 (10.2%)	25 (19.8%)	18 (18.6%)	14 (11.0%)	19 (19.4%)	17 (17.3%)	16 (16.2%)
BAKER-ROSETTASERVER	16 (13.1%)	27 (27.2%)	16 (12.7%)	21 (21.6%)	15 (11.8%)	34 (34.7%)	15 (11.8%)	15 (11.7%)
	12 (9.8%)	29 (29.3%)	15 (11.9%)	21 (21.6%)	18 (14.2%)	34 (34.7%)	15 (11.7%)	30 (30.3%)
RaptorX/RaptorX-TBMc		12 (12.1%)		33 (34.0%)		33 (33.7%)		24 (24.2%)
		31 (31.3%)		37 (38.1%)		38 (38.3%)		35 (35.4%)
RaptorX-DeepModellerc		10 (10.1%)		17 (17.5%)		10 (10.2%)		9 (9.1%)
		25 (25.3%)		26 (26.8%)		23 (23.5%)		23 (23.2%)
GOALc	7 (5.7%)		21 (21.6%)		23 (18.1%)		22 (17.2%)
	15 (12.3%)		28 (22.2%)		28 (22.2%)		25 (19.5%)

^aUpper rows: values corresponding to the first models; lower rows: values corresponding to the best models.

^bTo compare with CASP12 in which only the TBM category was present, the combined TMB and TMB-hard rankings of CASP13 appear in this part of the table.

^cNot present in CASP12/CASP13.

It should be noted that there were more participating groups in CASP12 (128) compared to CASP13 (99). Of those groups, 122, 126, and 127, respectively, submitted predictions in the TBM, FM/TBM, and FM categories in CASP12 and 99, 97, and 98, respectively, submitted predictions in these target categories in CASP13. Therefore, for an objective comparison, the relative ranks of the KIAS-Gdansk group, computed as the ranks divided by the number of groups in the respective categories, are also included in Table 1. As can be seen from Table 1, the relative ranks of the KIAS-Gdansk group have also increased for the FM category for both the first and the best models. For the “Model 1” predictions of the FM targets, the relative rank reached the top 14.3% of the submitted models of this category, which is 4.5% higher compared to CASP12. The moderate increase in the relative ranking of the FM models compared to a much more remarkable increase of GDT_TS compared to CASP12 (Figures 7 and 8 and Tables S2 and S3) results from the overall improvement of the server models selected to derive restraints (Figure 7), in particular those from Zhang-server⁴⁸ and QUARK⁴⁸ (Table 1). For the FM/TBM models, the relative ranks change little from CASP12 to CASP13, being slightly higher for the first and slightly lower in CASP13 for the best models (Table 1).

The ranks of the KIAS-Gdansk group in CASP12 and CASP13 and their changes from CASP12 to CASP13 confirm that using the restraints from server models in UNRES simulations produces the best results for the free-modeling targets, which was the aim of the approach.²² The contribution of UNRES improves server models in two ways. First, it results in reorienting the fragments that are improperly packed in the server models and, second, using the multimodal restraint function (eq 9) results in selecting the distances and angles that are compatible with the UNRES energy function. The most important restraints from the server models are the distance restraints, which help to shape the tertiary structures. In this regard, the KIAS-Gdansk group performed worse, both in CASP12 and in CASP13, than the Zhang, Zhang-server, and QUARK groups (the two last of them being server groups). These groups heavily rely on contact prediction. The KIAS-Gdansk group was also outperformed by the new groups that use sophisticated machine-learning methods: A7D from DeepMind⁶⁴ and Destini, which uses an enhanced TASSERVMT protocol.⁶⁵ It was also outperformed, in both CASP12 and CASP13, by the MESHI group that uses a quality-assessment and refinement protocol to select predictions from the server models⁶⁶ and by the wfAll-Cheng group, which is a part of the WeFold co-opetitive experiment⁶⁷ and uses both server models and the models produced by other groups participating in WeFold. In CASP13, the KIAS-Gdansk group was also outranked by the Grudinin group that developed the BROD approach to score server models.⁶⁸ Consequently, the development of the UNRES force field to enhance its power to distinguish the native topology from alternative topologies and to produce higher-resolution structure is needed. On the other hand, it should be noted that some of the groups that performed better than KIAS-Gdansk in CASP12 (e.g., BAKER and BAKER-ROSETTASERVER) were outranked by it in CASP13 in the free-modeling category.

Examples of Predictions

Cartoon drawings of the best KIAS-Gdansk models of the selected FM, FM/TBM, and TBM targets (gray) superposed on the respective experimental structures (rainbow-colored) are shown, together with their GDT_TS and C^α-RMSD values as well as CASP13 ranks, in Figure 12A–D. The models shown are those that have a higher GDT_TS than those of any of the server models selected to derive restraints (the points above the diagonal in Figure 11B) and are in the upper 10% of the models for the respective target. All of the KIAS-Gdansk models shown in Figure 12 overlap very well with the respective experimental structures, which is manifested in their high GDT_TS and low RMSD values. In their free-modeling assessment paper,¹⁵ the CASP13 assessor also featured the KIAS-Gdansk model 1 of T0957s1-D1.

Figure 12.

Cartoon representation (left) of selected KIAS-Gdansk models (gray) superposed on the respective experimental structures (colored from blue to red from the N- to the C-terminus) and the GDT_TS plots of the KIAS-Gdansk models (purple) shown together with other groups’ plots (orange). The GDT_TS plots were downloaded from the CASP13 Web site, http://predictioncenter.org/casp13/results.cgi, and modified to emphasize the lines corresponding to KIAS-Gdansk models and to enlarge the characters in the axis description (A) T0955-D1, 41 residues, PDB: 5WF9, an FM/TBM target, model 4, GDT_TS = 93.3, RMSD = 1.13 Å, rank 15/413; (B) T0968s2-D1, PDB: 6CP9, 116 residues, an FM target, model 1, GDT_TS = 64.8, RMSD = 3.36 Å, rank 39/452; (C) T0984-D1, PDB: 6NQ1, 504 residues, a TBM-easy target, model 2, GDT_TS = 67.3, RMSD = 5.20 Å, rank 1/393; (D) T0986s1-D1, PDB: 6D7Y, 92 residues, an FM/TBM target, GDT_TS = 69.3, RMSD = 3.21 Å, rank 14/443.

The single domain target T0955 (the corresponding EU denoted as T0955-D1; Figure 12A), classified as the FM/TBM type, is a small (41 residue) α + β protein. The servers produced very consistent models, which resulted in only one consensus fragment that encompassed the entire sequence. Our best prediction has a low RMSD and a high GDT_TS and ranked 15 out of 413 submitted models. However, this good result is likely to be caused by including FALCON⁶⁹ model 2 in restraint derivation, which was the best model of this target, in the sets of models from which restraints were derived. On the other hand, all other server models that served to derive the restraints, BAKER-ROSETTASERVER,¹⁹ Delta-Gelly-Server, QUARK,⁴⁸ RBO-Aleph,⁷⁰ slbio_server, and Zhang-Server,⁴⁸ ranked much lower than the KIAS-Gdansk models, which suggests that UNRES either corrected minor inaccuracies of these models or was able to choose FALCON⁶⁹ model 2 to guide the search.

Target T0968s2 is a 116 residue single-domain target (the corresponding EU denoted as T0968s2-D1; Figure 12B), which is a β-sheet unit of a heterotetrameric protein. It has been classified as an FM target. For this target, only short consensus fragments were found comprising at most 31 residues, but the largest discontinuous fragment embraced a 110 residue range. Our model 2 ranked 39 out of 452 models submitted to CASP. Of the server models used to derive the restraints, AWSEM-Suite⁷¹ models 1–5, BAKER-ROSETTASERVER¹⁹ models 1–5, QUARK⁴⁸ models 1, 3, and 5, RaptorX-DeepModeller⁵⁰ model 2, rawMSA, model 3, and Zhang-Server⁴⁸ models 1–5 ranked worse than the KIAS-Gdansk model. Only BAKER-ROSETTASERVER¹⁹ models 2 and 3 had higher ranks than that of our model.

Target T0986s1, a 92 residue, single-domain protein (the corresponding EU denoted as T0986s1-D1; Figure 12C), is an α + β protein, which is a part of a heterodimer. It has been classified as an FM/TBM target. Only short consensus fragments, comprising no more than 26 residues and some discontinuous fragments encompassing a 90 residue sequence range, were found, these being derived from BAKER-ROSETTASERVER¹⁹ models 1–4, Delta-Gelly-Server model 1, FALCON⁶⁹ models 1 and 2, QUARK⁴⁸ models 1–5, rawMSA models 1, 3, and 5, and Zhang-Server models 1–5. Our model 2 ranked 14 out of all models submitted for this target, outranking all server models used to derive restraints except for the BAKER-ROSETTASERVER¹⁹ model 1.

Target T0984, a two-domain α-helical target comprising 752 residues, has been partitioned into two EUs that contain 504 (T0984-D1) and 147 (T0984-D2) residues, respectively. This protein forms a homodimer. We used BAKER-ROSETTASERVER¹⁹ models 1–4, Distill⁷² models 2 and 3, FALCON⁶⁹ model 1, MULTICOM_CLUSTER²⁵ model 1, MULTICOM-Novel²⁵ model 1, QUARK⁴⁸ models 1–4, RaptorX-TBM⁵¹ model 1, Seok-server⁷³ model 1, and Zhang-server⁴⁸ models 1–5 to derive the restraints. Because the target is highly homologous, all server models superposed very well and, therefore, we constructed the consensus fragments by removing the flexible loop regions from the sequence. The KIAS-Gdansk model 1 of T0984-D1 (Figure 12D) is the CASP13 prediction with the highest GDT_TS of this target, and the KIAS-Gdansk models 3 and 4 (not shown) are the second and the third predictions according to GDT_TS, respectively. This target belongs to the TBM-easy category, which demonstrates that UNRES is able to improve the models of the proteins for which very good templates exist; this observation has already been made in our earlier work.²² UNRES simulations were carried out for the dimer of this target (Figure 6). It is likely that packing the monomers in the dimer helped to rectify minor discrepancies between the model and the experimental structure.

Oligomeric Targets

We submitted the models of 23 out of 43 homoligomeric (Tnnnno type) and heteroligomeric (Hnnnn type) targets, where nnnn denotes the target number. The KIAS-Gdansk group ranked 13th out of 23 groups regarding all and 10th out of 20 groups regarding hard oligomeric targets. These rankings are worse compared to CASP12, in which the group ranked 8th out of 33 groups regarding all and 8th out of 19 groups regarding hard targets. However, a target-by-target comparison of rankings turns more in favor of our performance in CASP13. In CASP12, the highest-ranking models of 3 targets (out of 13) were within the upper 10% of the models, while in CASP13, the highest-ranking models of 7 targets (out of 23) were within the upper 10% of all models. Moreover, no KIAS-Gdansk oligomer model scored rank 1 in CASP12, while rank 1 was achieved by our model 4 of H0968, which is a hard oligomeric target³⁵ (our model 2 having rank 2), and model 2 of T0997o, which is a medium-difficult target. Of the 7 KIAS-Gdansk models that are within the 10% of the best models, 4 correspond to hard and 3 to medium-difficult targets; as expected, the approaches with a greater bioinformatics component handle the easy targets much better than our largely physics-based approach. Thus, the overall decrease of KIAS-Gdansk rankings, compared to CASP12, is likely to be caused by greater improvement of other groups’ methods with respect to CASP12 compared to that of our approach.

The candlesticks plots of the Interface Patch Similarity and Interface Contact Similarity, expressed as the Jaccard coefficient (J_C) and F1 score, respectively³⁴ (see Measures of Structure Similarity for definition), averaged over all, first, and the best models of the oligomeric targets, respectively, obtained by the KIAS-Gdansk and other groups in CASP12 and CASP13, respectively, are shown in Figure 13A–E. The corresponding numerical values are collected in Table S5.

Figure 13.

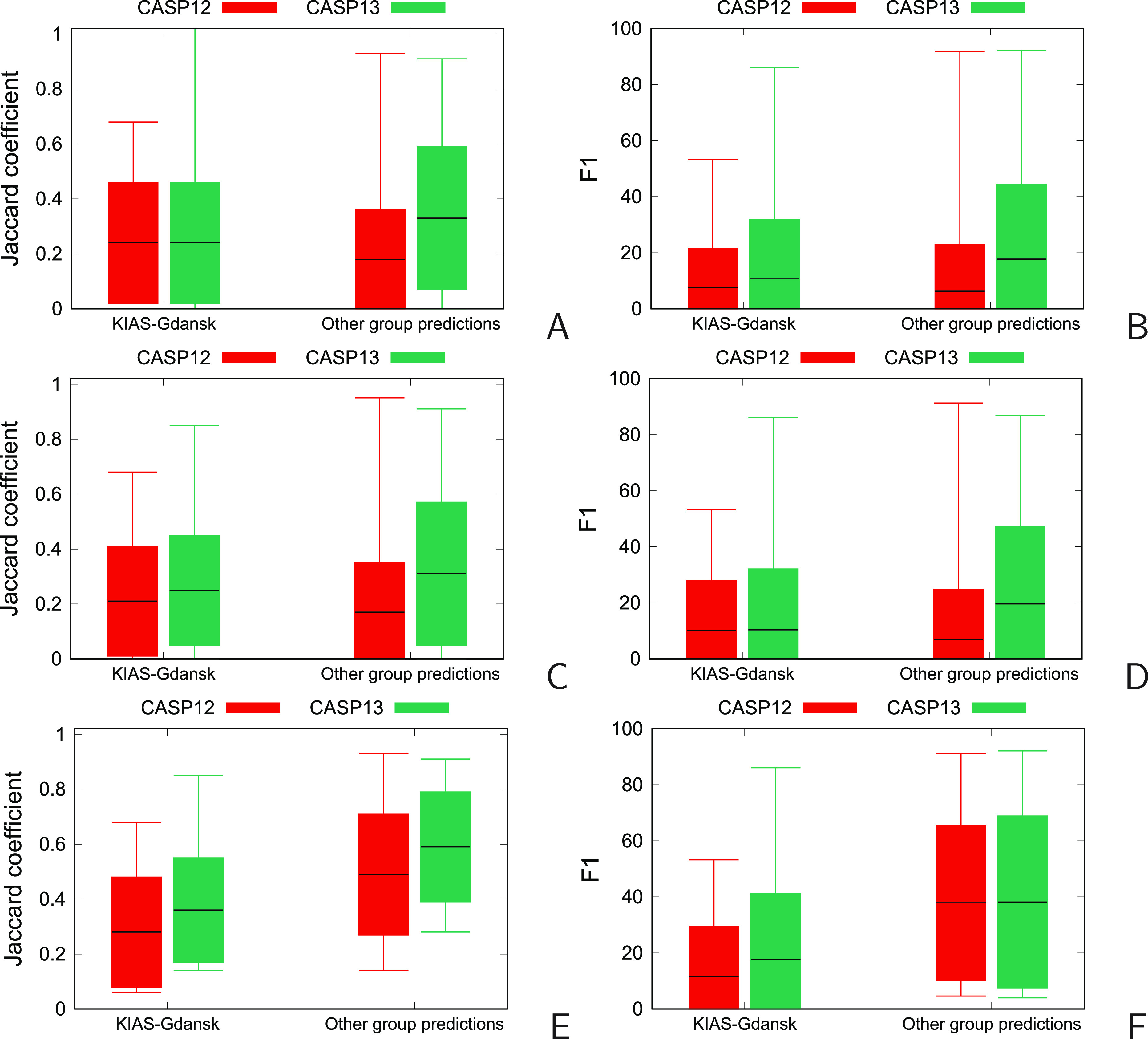
Candlestick plots of the Interface Patch Similarity (IPS), quantified as the Jaccard coefficient^34,35 (A, C, E) and the Interface Contact Similarity (ICS) quantified as the F1 score (B, D, F) of the KIAS-Gdansk models of oligomeric targets (left pairs of sticks) and other group models (right pairs of sticks) obtained in the CASP12 (red) and CASP13 (green) experiments. Panels A and B: all models; panels C and D: “Model 1” predictions; panels D and E: best models (with the highest score as determined by CASP assessors). The horizontal lines in the middle of each bar correspond to the mean values; the bars range from the mean minus the standard deviation to the mean plus the standard deviation, and the whiskers correspond to the minimum and maximum values. The negative values are clipped in all plots.

As can be seen (Figure 13), the average J_C and F1 values of KIAS-Gdansk predictions are lower than those averaged over the respective CASP13 models, regardless of whether “Model 1”, best-model, or all-model average predictions are considered. In CASP12, the J_C and F1 averaged over our “Model 1” predictions and all models were higher than those averaged over other groups’ models (Figure 13A–D); however, the values averaged over our best models were lower than those averaged over other groups’ models (Figure 13E,F). Compared to CASP12, our best-model averages of J_C increased from 0.28 to 0.36 (by 0.08; 88% significance) and the respective F1 values increased from 12.4 to 17.8 (by 5.4; 76% significance). The “Model 1” averages of J_C and F1 are almost the same as those in CASP12, the differences being statistically insignificant (Figure 13A,B). The J_C and F1 values averaged over all KIAS-Gdansk models increased from 0.21 to 0.25 (by 0.05; 89% significance) and from 7.7 to 10.9 (by 3.2; 87% significance), respectively (Figure 13C,D). It should also be noted that the maximum values of J_C and F1 corresponding to the KIAS-Gdansk group models increased with respect to CASP12 (Figure 13A–E). Therefore, net improvement was obtained with respect to CASP12. However, as could also be seen from the comparison of rankings of the KIAS-Gdansk group in CASP12 and CASP13, the increases of the J_C and F1 values of “Model 1” and all-model averages were significantly greater for the other groups. The “Model 1” and all-model averaged J_C increased by 0.15 and 0.13, respectively, and those of F1 increased by 12.7 and 11.5, respectively, all these values having over 99.99% significance. For other groups’ best-model averages, the increases of J_C and F1 from CASP12 to CASP13 were comparable to those of the KIAS-Gdansk group, amounting to 0.10 (98% significance) and 4.5 (74% significance), respectively.

Overall, our methodology has performed worse on oligomeric targets compared to regular targets. One reason for this can be that the protein-docking problem is harder for physics-based methods because of a larger number of degrees of freedom and larger system size, which makes the search of the docking space challenging, in particular when monomer conformations undergo major changes upon docking. Another reason is that UNRES has been parametrized with monomeric proteins only,³⁰ which might overemphasize local-interaction components of the force field relative to long-range components.

In Figure 14A–C, the best KIAS-Gdansk group models for three selected targets, H0968, T1003o, and T1009o, are shown.

Figure 14.

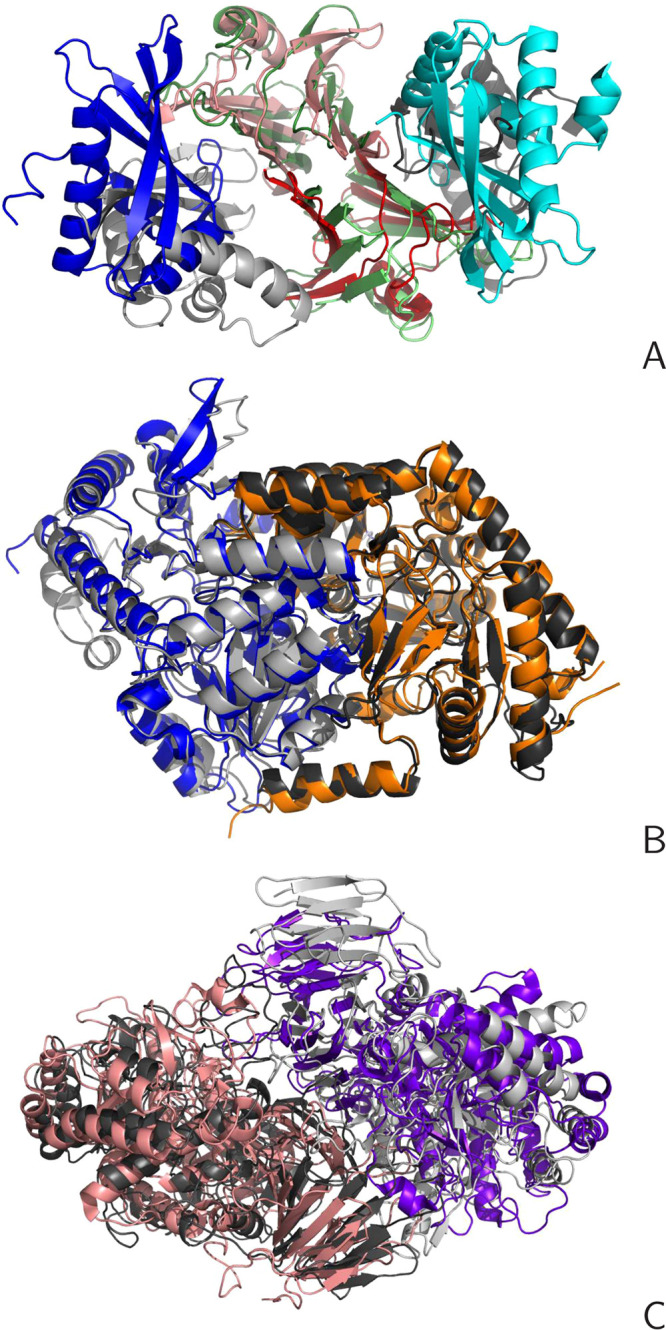
Cartoon representation of sample KIAS-Gdansk models of the oligomeric target (gray) superposed on the corresponding experimental structures (rainbow-colored). (A) Target H0968 (a dimer of heterodimers, monomer chains consisting of 126 and 116 residues, respectively, PDB: 6CP9, hard target), model 4, J_C = 0.30, F1 = 5.3, GDT_TS = 26.3, RMSD = 16.0 Å, I-RMSD = 1.33 Å, rank 1/63. (B) Target T1003o (homodimer, monomer chain consisting of 474 residue, PDB: 6HRH, easy target), model 4, J_C = 0.69, F1 = 61.5, GDT_TS = 82.8, RMSD = 5.20 Å, I-RMSD = 6.45 Å. (C) Target T1009o (homodimer, PDB: 6DRU, monomer chain consisting of 718 residues, medium target), model 4, J_C = 0.39, F1 = 4.8, GDT_TS = 40.0, RMSD = 8.54 Å, I-RMSD = 9.03 Å.

Target H0968 (PDB: 6CP9) is a tetramer composed of two dimers, each of which consists of an α + β-protein and a mainly β-protein (with only a small α-helical section). The largest interface is between the β-structure parts. It has been classified as a hard target,³⁵ for which our model 4 (Figure 14A) is the best of all models of this target submitted to CASP. It can be seen from Figure 14A that the main interface (between β-sheets) is well reproduced, which is also reflected in the low interface RMSD of 1.33 Å. However, the α + β chains have a different orientation compared to that in the experimental structure, which results in comparatively low F1 (5.3) and J_C (0.30) values, as well as comparatively low GDT_TS of the whole oligomer (26.3). Nevertheless, the overall shape of the tetramer is similar to the native shape.

Target T1003o is a homodimer with a monomer size of 474 residues, which has been classified as an easy target.³⁵ The KIAS-Gdansk model 4 of this target is superposed on the 6HRH experimental structure in Figure 14B. This prediction has been ranked 73 out of 164 models. As can be seen, our model matches the experimental structure well, which is reflected by comparatively high F1 (61.5), J_C (0.69), and GDT_TS of the whole complex (82.3).

Target T1009o is a homodimer composed of two large monomers (718 residues each). It has been classified as a target of medium difficulty.³⁵ Our model 4 superposes quite well on the experimental 5DRU structure and ranks 12th out of 126 models. The F1 (4.8) and J_C (0.39) are comparatively low, which suggests that the interface contacts are not modeled very well, but the GDT_TS (40.0) is much higher than that of our model 4 of H0968, which agrees with the overall good superposition of our model on the experimental structure.

Conclusions

In this work, we improved our methodology of bioinformatics-assisted prediction of protein structures with the UNRES force field by introducing server-model selection based on the DeepQA score²⁵ and by developing an automatic protocol for the selection of the consensus fragments illustrated in Figure 5. Moreover, an upgraded version of the UNRES force field³⁰ was used, and DFA pseudopotentials^28,29 were fully implemented in the total pseudoenergy function. In terms of GDT_TS, significant progress was made for regular targets of the FM/TBM and FM category relative to CASP12. For these targets, the average GDT_TS increased by 8.96 and 11.08 GDT_TS units, respectively, for the “Model 1” predictions and by 11.04 and 11.09 units for the best models, respectively (Figures 7 and 8 and Tables S1–S3). The ranking of the KIAS-Gdansk predictions has also increased remarkably for the FM category, for which it reached the top 14.3% of all “Model 1” predictions (compared to 18.9% in CASP12; Table 1). The increase of the KIAS-Gdansk model ranking is even more remarkable in view of the fact that a significant jump in model quality was observed from CASP12 to CASP13, owing to exceptionally good performance of the methods based on deep learning.¹⁵ This progress was achieved owing to the selection of higher-quality server models to derive restraints compared to that in CASP12 (Figure 7), introducing the automatic protocol for fragment selection, improvement of the restraint function to alter the depth of its minima depending on the number of server models contributing to a given geometry restraint (eq 9), implementation of DFA pseudopotentials,^28,29 and using an upgraded version of the UNRES force field.³⁰

The models of the FM targets produced by the KIAS-Gdansk group in CASP13 have definitely higher GDT_TS, on average, than the server models selected to derive restraints, regardless of whether the averages over the first, best, or all models are considered (Figure 9 and Table S4); the differences are 1.83, 3.66, and 3.56 units, respectively, and all differences are statistically significant. For the FM/TBM category, the KIAS-Gdansk models also have higher GDT_TS than those of the selected server models; however, the differences are only 0.80, 1.38, and 2.03 units for the first, best, and all models, respectively; the statistical significance of these differences is low. This is a clear improvement with respect to CASP12, in which the average GDT_TS of only the “Model 1” KIAS-Gdansk predictions was slightly higher than that of the selected server models, irrespective of difficulty category (Figure 9). This result strongly suggests that the improvements of our protein-structure-prediction protocol introduced in this work resulted in improved performance of the method for free-modeling targets, which has been the aim of our approach.

The GDT_TS values of the KIAS-Gdansk models and of the selected server models are significantly greater than those of all server models, irrespective of difficulty category and irrespective of whether the first, the best, or all models are considered. It can, therefore, be concluded that the quality-assessment-based procedure of server-model selection introduced in this work, as opposed to using the top five models from preselected servers,²⁶ enabled us to use the best server models for restraint derivation. We are now working on further improvement of fragment selection by including the information about conserved motifs and sequence-based features (e.g., prediction of disordered regions), which can be obtained by using the tools such as Pse-in-One,⁷⁴ BioSeq-Analysis,⁷⁵ or BioSeq-Analysis2.0.⁷⁶

Some KIAS-Gdansk models, including those of the TBM targets, outperformed those from the servers (Figures 11B and 12). Also, as in CASP12,²⁶ the majority of the worst server models have lower GDT_TS than the worst KIAS-Gdansk models (Figure 11C); exceptions were the models of the targets T0960 and T0963 for which the simulation time was apparently insufficient due to the large target size.

For the oligomeric targets, the KIAS-Gdansk group results are worse, compared to other groups, than those for the regular targets, the average Interface Patch Similarity (J_C) and Interface Contact Similarity (F1)³⁴ being lower than that over all the CASP13 models (Figure 13). The probable reasons for this are (i) larger sizes of oligomeric targets compared to those of the regular targets (this demands a higher simulation time, which is not readily possible for large targets given the 3-week prediction-time window) and (ii) the fact that the UNRES force field used by the KIAS-Gdansk group was calibrated with monomeric proteins.³⁰ Insufficient sampling is also a problem in the prediction of the structure of large regular (monomeric) targets. Nevertheless, improvement with respect to CASP12 has been achieved; in particular, a greater fraction of models (7 out of 23 targets compared to 3 out of 13 targets in CASP13) is within the top 10% of all models and 2 KIAS-Gdansk models have rank 1, while there was no rank 1 model in CASP12.

Apart from the improved selection of high-quality server models, which contributed to the increased performance of the KIAS-Gdansk group relative to CASP12, the improvement of the force-field quality is essential to achieve higher model quality compared to that of the server models from which to derive restraints. Recently, we developed a scale-consistent version of UNRES,⁷⁷ which showed an improved performance in the unassisted and contact-assisted UNRES prediction.⁷⁸ We are now working on improving this version to separate side-chain-specific local and correlation energy terms from the backbone components and to improve the side-chain-interaction potentials. We are also adapting UNRES code to run big targets by introducing cutoff on the interactions, which should alleviate insufficient-sampling problems. To improve the performance of the method on oligomeric targets, we will include oligomeric proteins in force-field calibration.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.9b00864.

• Figure S1: whiskered scatter plot of the GDT_TS of initial models vs KIAS-Gdansk predictions of the T0960 and T0963 targets; Figure S2: whiskered scatter plot of the GDT_TS of the models from the selected servers vs that of the KIAS-Gdansk predictions for the large-size regular targets (T0984, T0995, T1003, and T1009), for which the server models selected on the basis of DeepQA score²⁵ were used as initial models; Table S1: GDT_TS values and rankings of the KIAS-Gdansk first and the best (highest GDT_TS) models of the CASP13 regular targets; Table S2: numbers of EUs and their minimum, maximum, and average GDT_TS values as well as the standard deviations of the GDT_TS for the respective target categories for the KIAS-Gdansk, selected server and all server first, all and best models obtained in the CASP12 and CASP13 experiments; Table S3: differences of the mean GDT_TS values corresponding to the CASP12 and CASP13 experiments for the respective target categories for the KIAS-Gdansk, selected server and all server models (first, all, and best), the standard deviations of these differences, and their statistical significances; Table S4: Differences of the mean GDT_TS values, along with their standard deviations and statistical significances, corresponding to the KIAS-Gdansk models and selected server models, the KIAS-Gdansk models and all server models, and selected server models and all server models (first, all and best); Table S5: difficulties, measures of the fit to the experimental structures, and rankings of the KIAS-Gdansk first and the best (highest GDT_TS) models of the CASP13 oligomeric targets (PDF)

The authors declare no competing financial interest.