How Many Pnicogen Bonds can be Formed to a Central Atom Simultaneously?

Abstract

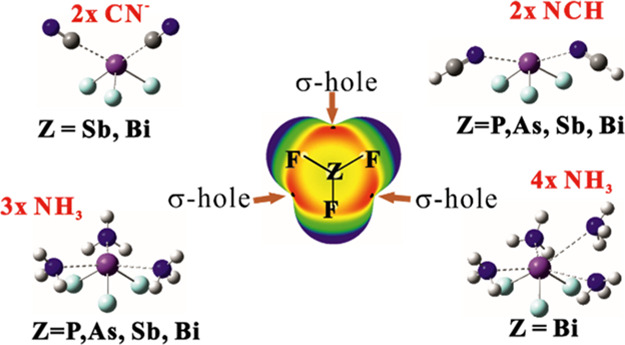
A central ZF₃ molecule (Z = P, As, Sb, Bi) is allowed to interact with a number of nucleophiles exemplified by NCH, NH₃, and NC^– anion. The Z···N pnicogen bond (ZB) to a single base grows stronger for heavier Z atom: P < A < Sb < Bi and follows the NCH < NH₃ < NC^– order for the three bases. The maximum number of ZBs depends on both the nature of the base and pnicogen atom. PF₃ and AsF₃ can pnicogen bond with only a single CN^–; SbF₃ and BiF₃ can interact with two anions but only weakly. The weak NCH nucleophile can engage in a maximum of two ZBs, while three ZBs occur for NH₃. The latter NH₃ maximum can be extended to four ZBs but only for BiF₃. The fourth ZB is somewhat longer and weaker than the others, and the entire (H₃N)₄···BiF₃ complex relies partially on secondary interactions for its stability.

Introduction

In the years following its initial conception, the hydrogen bond (HB) has become one of the most important and far-reaching phenomena for both chemistry and biology.¹⁻⁸ Recent years have witnessed the growth of study of a set of parallel sorts of interactions, replacing the bridging proton of the HB by any set of other elements in the p-block of the periodic table. These electronegative elements are able to attract an electron donor by way of a region of depleted electron density on their periphery, which in turn are commonly referred to as σ- or π-holes.⁹⁻¹⁸ A good deal of work has addressed the factors that contribute to this bonding phenomenon, the strength of the interaction, and the subsidiary part played by monomer deformation, to amplify its role in biological systems, pharmacology, and technology.^1,2,19−30 For example, it is now understood that these noncovalent bonds are stabilized by contributions from charge transfer, polarization, and dispersion, in addition to the electrostatic attraction.

Recent work has described a dual scheme, via either σ- or π-hole, by which a base might bind to the tetrel^31,32 or pnicogen³³ atom of a Lewis acid. As one relevant example, the NH₃ base can interact with a substituted TF₃C₆H₂R₃ (T = C, Si Ge, Sn, Pb; R = H, CH₃, F) acid through either its axial or equatorial σ-hole, with respect to the phenyl ring.³⁴ Likewise, a substituted pyridine base engages in a tetrel bond with the central T atom of TF₄ by first distorting the latter into a trigonal bipyramid arrangement, after which both the axial and equatorial site σ-holes are open to attack.³² A pair of incoming bases can interact with either the σ or π-holes surrounding a TF₄ molecule,³¹ wherein the existence of π-holes depends upon a prior distortion of the tetrahedral TF₄ to a planar configuration.

Moreover, in connection with the latter idea of the presence of multiple noncovalent bonds there is indeed growing interest concerning the clustering of molecules, for instance (PH₂F)_n, (PH₂Cl)_n,³⁵ NH₃, PH₃, and PFH₂³⁶ and HF, FCl,³⁷⁻⁵² wherein such multiple bonds are integral. It has long been recognized that the formation of a HB polarizes each participant and affects their ability to engage in a second such bond. For example, the formation of a AH···BH dimer shifts electron density from BH to AH, making the former a better electron donor. The addition of a third CH molecule to the growing chain can take advantage of this charge shift so that AH···BH···CH is bound by more than the simple sum of the AH···BH and BH···CH bond energies within these respective dimers, a phenomenon known as positive cooperativity. A second factor takes on added importance in the case of certain other noncovalent bonds. The formation of a tetrel bond, for instance, can drastically alter the internal geometry of the Lewis acid. This nuclear rearrangement in turn exerts a very strong influence upon the electrostatic potential surrounding it, which in turn can enhance or inhibit its ability to engage in a second such bond.

The earlier work cited above has documented the ability of the central tetrel atom to engage in two noncovalent interactions simultaneously. Very recent calculations have noted that the hypervalent YF₄ (Y = S, Se, Te, Po) can similarly engage in a pair of chalcogen bonds.⁵³ Two NCH molecules can form a pair of tetrel bonds to a central TF₄ molecule (T = Si, Ge, Sn, Pb).^31,54−56

These earlier findings lead to the natural question as to just how many nucleophiles can be attached to a Lewis acid at the same time. What is the maximum number of such bonds that can be present, and how does this number differ for tetrel, pnicogen, and chalcogen bonds? Surely there will be a point at which simple issues of steric strain will prevent any further bases from approaching. Just how much can the central molecule alter its structure so as to accommodate additional bonds? How might this maximum number depend on the precise nature of the Lewis acid and base molecules? Another issue relates to cooperativity. Does the presence of the first bond strengthen or weaken the second and so on? Does this cooperativity operate through simple electronic polarization or does geometric deformation play an important role?

As a vehicle to begin to answer some of these questions, the work described below considers the pnicogen bonds (ZBs) that might be formed by ZF₃ (Z = P, As, Sb, Bi). As guidance in terms of the formal definition of a pnicogen bond, we employ the IUPAC definitions^57,58 that have been developed for the very similar halogen and chalcogen bonds. These bonds are characterized⁵⁹ by the approach to a pnicogen atom, acting as a Lewis acid, of a nucleophile, which are built upon electrostatic attraction, polarization, and dispersion.

Three different bases are considered. Neutral HCN can engage in a ZB through its N atom, whereas the negative charge on CN^– will naturally lead to a much stronger interaction. This anion also presents the interesting question as to whether it will interact with the Z through its C or N atom; in fact, it is also possible in principle that the negative potential above the CN axis could play the role of the electron donor as well. NH₃ represents an intermediate case. Like HCN, NH₃ is also a neutral molecule so is a weaker nucleophile than CN^–, but its sp³ hybridization makes it stronger than HCN. One, then two, three, and four base units are added sequentially to the ZF₃ molecule, so as to determine how many ZBs are possible for each combination of ZF₃ and base. At the same time, the properties of each complex are monitored to follow changes occurring in each system upon each addition of another base unit.

Methods

The geometries of isolated ZF₃ (Z = P, As, Sb, Bi), NH₃ and HCN molecules, and CN^– anion as well as their ZF₃L_n complexes (L = HCN and CN^–, where n = 1–3) were fully optimized at the MP2 level of theory with the aug-cc-pVDZ basis set.^60,61 This level of theory has been found to be consistent with CCSD(T) with larger basis sets and with available experimental quantities, for complexes stabilized by noncovalent forces.⁶²⁻⁶⁵ Pseudopotentials which include relativistic effects were used for the heavy Sb and Bi atoms.⁶⁶ The absence of any imaginary frequency guaranteed that the generated structures are true minima. Energies were also computed at the CCSD(T)/aug-cc-pVDZ level (using MP2 minima) for purposes of comparison and validation.⁶⁷⁻⁷³ Interaction energies were calculated as the difference in energy between the complex and the sum of monomers (with the same geometries as they adopt within the complex). Binding energies were computed relative to the monomers in their isolated optimized structures. Both quantities were corrected for basis set superposition error (BSSE) using the counterpoise protocol.⁷⁴

All computations were performed via the Gaussian 16 software package.⁷⁵ Molecular electrostatic potential (MEP) analysis was applied to identify and quantify MEP extrema using the WFA-SAS⁷⁶ and MultiWFN programs.^77,78 The electron density topology was analyzed using AIMAll software.⁷⁹ In order to analyze interorbital connections and charge flow between the monomers, the natural bond orbital (NBO) procedure (using GenNBO 6.0) was utilized using the wavefunction generated at the DFT level for MP2 geometries.⁸⁰ The CSD (Cambridge Structural Database, CCDC 2019, ConQuest ver. 2.0.1)⁸¹ was searched for pertinent experimental crystal structures similar to those described here.

Results

Monomers

The ZF₃ (Z = P, As, Sb, Bi) monomers as well as HCN, NH₃, and CN^– anion were fully optimized at the MP2/aug-cc-pVDZ level of theory. All ZF₃ molecules have a pyramidal C_3v structure with a pnicogen Z atom at the apex and three F atoms in the base. As may be seen in the details of these structures in Table S1, the Z–F bond length increases as the Z atom grows in size from 1.630 for PF₃ to 2.016 in BiF₃. The sum of the three θ(F–Z–F) angles in the last column of Table S1 decreases slightly with larger Z, indicating a less planar geometry.

The MEP of each ZF₃ molecule has a similar profile, exemplified in Figure 1 for AsF₃. Each F atom is surrounded by a blue negative region, while a red positive area termed a σ-hole lies opposite each Z–F bond. There is another positive region, but a much less intense one, that lies opposite the Z lone pair, amongst the three F atoms. For lack of a better name, and for convenience in discussion, this latter point is designated as a π-hole here, although the reader must be aware that the ZF₃ molecule is not flat and does not contain a π-electron system per se. The values of V_s,max for these σ and π-holes are listed in the upper portion of Table 1, which shows the expected trend of a more intense positive region for larger Z atoms (with a small irregularity between P and As for the π-holes). The HCN molecule contains a minimum in its MEP on its N atom along the molecular axis, with a V_s,min value of −31.4 kcal/mol, as seen in the lower part of Table 1. The MEP minimum of NH₃ is along its C₃ axis, coincident with its lone pair. Its value is a bit more negative than that of HCN. Because of its negative charge, the MEP of CN^– is much more negative with minima of roughly equivalent intensities on the N and C atoms, as well as along the anion’s equator, its π-region.

Figure 1.

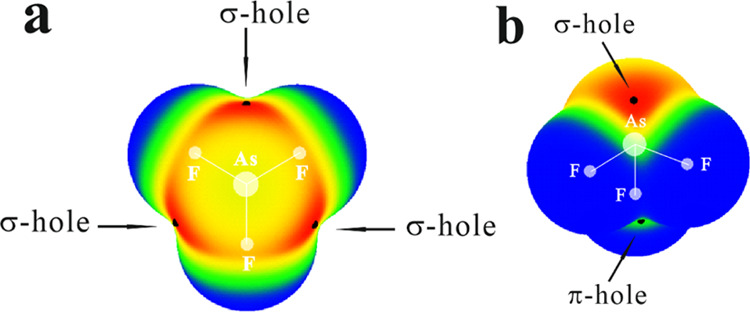
MEP on the 0.001 au isodensity surface at the MP2/cc-pVDZ level of AsF₃ (a, top view and b, bottom view) isolated monomers. Color ranges, in kcal/mol, are red greater than 35, yellow between 15 and 35, green between 0 and 15, and blue below 0 kcal/mol.

Table 1. MEP Maxima (kcal/mol) on the 0.001 au Isodensity Surface of ZF₃ (Z = P, As, Sb, Bi) and HCN and CN^– Monomers, Calculated at the MP2/aug-cc-pVDZ Level of Theory.

molecule	VS,max (Z-F) σ-hole	VS,max π-hole below Z atom
PF3	35.6	9.7
AsF3	43.9	7.1
SbF3	51.6	10.6
BiF3	61.5	12.7

molecule	Vs,min
HCN	–31.4
NH3	–37.7
CN–	–137.7 (N) π
	–136.6 (N)
	–135.5(C)

ZF₃ + 1 Base

The structures of the most stable complexes arising from the addition of a single base to ZF₃ are presented in Figure 2. The neutral HCN approaches N-atom first, toward one of the σ-holes of ZF₃, opposite the F atom labeled F1. As observed in the first column of Table 2, the intermolecular separation R(N···Z) becomes shorter as Z grows larger, despite the increasing van der Waals (vdW) radius of this Z atom. Due in part to the normal transfer of charge from the base lone pair into the σ*(Z–F1) antibonding orbital, r(Z–F1) is consistently the longest bond within the ZF₃ molecule, by between 0.008 and 0.0121 Å. Consistent with the trend of a pnicogen bond toward linearity, the θ(N···Z–F1) angles lie in the 163–171° range. The next column of Table 2 indicates the level of nonplanarity in the ZF₃ subunit, followed by the decrease relative to the unperturbed monomer in the last column. The negative values of ΔΣθ indicate a more pyramidal structure within the dimer. Many of the same trends are seen in the complexes with NH₃ in the next section of Table 2, but the data suggest a stronger interaction. The intermolecular R(N···Z) distances are considerably shorter, in the 2.6–2.8 Å range, and the internal r(Z–F) stretches are of larger magnitude; again r(Z–F1) is longer than r(Z–F2). The θ(N···Z–F1) angles are a bit less linear, but the Σθ angle sums are a bit smaller, indicating somewhat more pyramidality induced within ZF₃.

Figure 2.

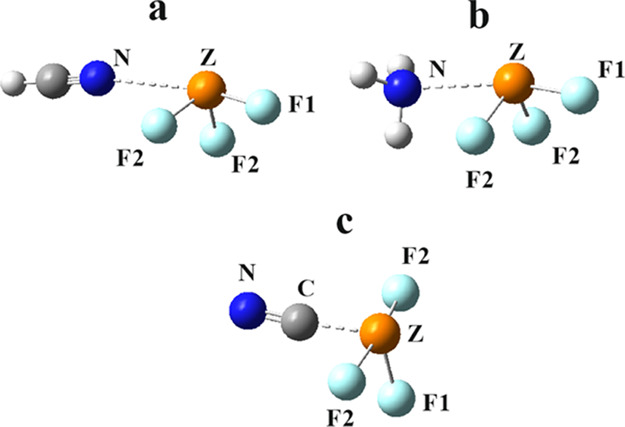
Most stable conformers of HCN, NH₃, and CN^– with ZF₃.

Table 2. Structural Parameters (Distances in Å, Angles in Degs) in Complexes of ZF₃ Plus One Base, Calculated at the MP2/aug-cc-pVDZ Level of Theory.

	R(N···Z)	r(Z–F1)	r(Z–F2)	θ(N···Z–F1)	Σθ(F–Z–F)	ΔΣθ
HCN···ZF3
HCN···PF3	3.032	1.639	1.631	171.3	289.5	–1.7
HCN···AsF3	2.907	1.758	1.749	169.5	285.4	–2.8
HCN···SbF3	2.864	1.933	1.923	162.6	280.6	–3.9
HCN···BiF3	2.860	2.035	2.023	165.5	283.0	–3.6
H3N···ZF3
H3N···PF3	2.780	1.647	1.638	168.5	287.2	–4.0
H3N···AsF3	2.593	1.771	1.759	164.1	282.1	–6.1
H3N···SbF3	2.592	1.945	1.937	155.5	277.0	–7.5
H3N···BiF3	2.670	2.045	2.035	155.4	279.6	–7.0

	R(C···Z)	r(Z–F1)	r(Z–F2)	θ(C···Z–F1/2)	Σθ(F–Z–F)	ΔΣθ
NC–···ZF3
NC–···PF3	1.863	1.675	1.805	99.3/85.0	341.7	50.5
NC–···AsF3	1.978	1.785	1.907	98.0/84.3	339.4	51.2
NC–···SbF3	2.187	1.951	2.046	98.4/82.6	331.7	47.2
NC–···BiF3	2.285	2.049	2.166	89.6/84.5	347.9	61.3

The lowest section of Table 2 lists the same properties for the complexes with the CN^– anion. Importantly, the structures of these complexes are rather different than those with the neutral bases. As seen in Figure 2c, the ZF₃ molecule becomes very nearly planar. This approach to planarity is evident in the last two columns of Table 2 where the sum of the three θ(F–Z–F) angles grows by 50–60° up to nearly 360°. The full charge on this base leads to much shorter intermolecular distances, around 2 Å. In addition, the trend in R(C···Z) is opposite that for the complexes with neutral HCN in that the separation increases as the Z atom grows in size. The stronger binding to the anion is also exemplified by the much longer internal r(Z–F) distances.

The binding energies of these complexes, corresponding to the reaction that forms the dimer from the pair of isolated monomers, displayed in the first two columns of Table 3, reaffirms the indications of the binding strength arising from Table 2. Whereas HCN binds with an energy between 3 and 7 kcal/mol, dimers involving NH₃ are bound by 4.5–13 kcal/mol, and the anion range is considerably larger, 23–39 kcal/mol. In all cases, the binding is enhanced for larger Z atoms. The interaction energies in the next two columns of Table 3 refer to the pure interaction between the monomers which have already been deformed into the geometries they adopt within the complex. As such E_int is more negative than E_b, differing by a deformation energy E_def which is needed to distort each monomer appropriately. There is little deformation involved in the complexation with the neutral bases. However, the large distortion of ZF₃ from its pyramidal structure when complexed with the anion leads to much more negative interaction energies in the bottom segment of Table 3. These deformation energies are the largest for the smaller Z atoms, with E_def rising from 33.9 kcal/mol for BiF₃ up to 55.0 kcal/mol for PF₃, as reported in Table S2. While E_b and E_int obey similar trends for the neutral bases which involve only small deformation energies, there is a reversal for the anion. The binding energies of the NC^–···ZF₃ complexes rise steadily for the P < As < Sb < Bi sequence, but there is no such increase for E_int, which in fact shows a small decrease. It should be mentioned finally that these energetics are not very sensitive to the means of incorporating electron correlation. The CCSD(T) quantities in Table 3 are rather similar to the MP2 values, and all trends are identical.

Table 3. Binding (E_b) and Interaction Energies (E_int) (kcal/mol) of ZF₃ Complexes with HCN and CN^– Calculated at the MP2/aug-cc-pVDZ (I) and CCSD(T)/aug-cc-pVDZ (II) Levels of Theory^a.

	Eb		Eint
	(I)	(II)	(I)	(II)
HCN···ZF3
HCN···PF3	–2.74	–2.51	–2.82	–2.54
HCN···AsF3	–4.09	–3.72	–4.24	–3.80
HCN···SbF3	–5.88	–5.35	–6.15	–5.53
HCN···BiF3	–7.48	–6.95	–7.75	–7.14
H3N···ZF3
H3N···PF3	–4.45	–4.40	–4.87	–4.75
H3N···AsF3	–7.32	–7.05	–8.24	–7.90
H3N···SbF3	–11.70	–11.35	–13.09	–12.71
H3N···BiF3	–13.20	–12.92	–14.31	–13.99
NC–···ZF3
NC–···PF3	–22.68	–20.00	–77.66	–74.64
NC–···AsF3	–30.93	–28.44	–77.79	–75.06
NC–···SbF3	–38.67	–36.70	–74.72	–72.36
NC–···BiF3	–39.24	–37.41	–73.16	–70.74

^aAll values corrected for BSSE.

The AIM diagrams of all of these complexes contain a bond path between the Z and N/C atoms involved in the interaction. The relevant properties of the bond critical point are displayed in Table S3 and reflect the energetics fairly well. For example, the density at this critical point for the two neutral bases rises regularly as the Z atom is enlarged from P to Bi, although there is a small dip from Sb to Bi; ∇²ρ undergoes a similar increase. Just as the interaction energies of the complexes with CN^– diminish with larger Z atom, so do the values of ρ_BCP, although the Laplacian changes are less consistent.

There are also secondary minima for the dimers discussed above. In the case of HCN, this neutral molecule can approach along the C₃ axis, directly opposite the Z lone pair, facilitated by a shallow π-hole in this region. Such a structure is less stable than the σ-hole geometries by the following amounts: 3.6, 5.7, 7.6, and 9.0 kcal/mol for the P, As, Sb, Bi series, respectively. In fact, after correction for BSSE, these alternative structures are barely bound at all, with positive interaction and binding energies. NH₃ can also engage in a similar sort of complex, approaching opposite the Z lone pair, but these structures are quite a bit higher in energy and only those with SbF₃ and BiF₃ are bound after counterpoise correction.

The complexes with the anion have three alternative secondary minima. In addition to the global minimum A in Figure S1, another minimum B occurs when the anion approaches along a σ-hole of ZF₃, causing a lesser degree of deformation. According to Table S4, this structure lies some 1.5–4 kcal/mol higher in energy than A. In configurations C and D, it is the N atom of CN^– that approaches Z rather than C. If the anion approaches a σ-hole, structure C is less stable than A by 2–6 kcal/mol, but this margin rises to the 8–12 kcal/mol level when approaching the π-hole as in D. The energetic edge of geometry A is the smallest for the largest Z atom Bi, where for example, the A conformer involving the σ-hole is more stable than the B π-hole approach by only 1.5 kcal/mol. As one would expect from the diagrams, the transformation of the ZF₃ geometry to a nearly planar configuration structure D leads to high deformation energies as were noted for A, with these values in the 33–53 kcal/mol range reported in Table S5. The less extensive rearrangement within structures B and C leads to much smaller deformation energies, of 11 kcal/mol or less.

Some of these trends would not be easily predictable from a purely electrostatic standpoint, referring to the MEP of each subunit. In the first place, there is little to differentiate the C and N ends of CN^– in terms of V_s,min, as documented in Table 1, so the strong preference for the C end might appear surprising. However, more to the point, the σ-hole of each ZF₃ molecule is far more intense than its π-hole which is at odds with the dominance of the A structure. This preference for the π-hole geometry of the F₃Z···CN^– dimers is particularly notable in that this sort of geometry must overcome a very large deformation energy involved in the rearrangement of the F₃Z unit, indicated above.

MEP diagrams were generated for various dimers, as pertinent to the next step involving addition of a second base. These complexes retain a σ-hole that lies opposite each F2–Z bond, that is, those not occupied by a base. However, the charge transferred from the base to ZF₃ reduces the magnitude of the remaining σ-holes. The values of V_s,max for each of these dimers are provided in Table S6. They remain positive for both neutral bases but are reduced in magnitude by some 11–15 kcal/mol by NCH and by 14–18 kcal/mol for NH₃. The much larger charge transfer from the CN^– anion reverses the previous positive value of V_s,max, making it negative. The charge transferred, even the smaller amount coming from the neutral bases, causes the shallow π-holes of ZF₃ to all become negative. This characterization of the dimer MEPs would predict that the one involving a CN^– anion ought to be incapable of forming a trimer with a second base and those with the neutral bases retain a positive σ-hole; so the formation of a trimer is a possibility.

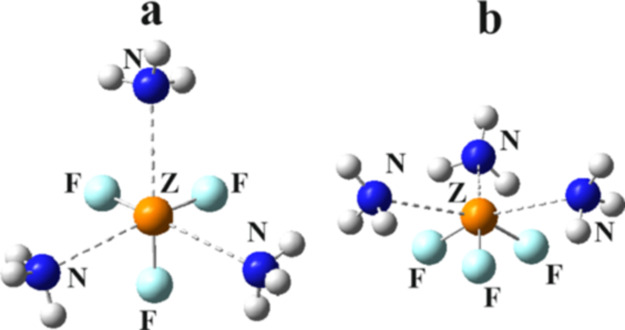
ZF₃ + 2 Bases

The addition of another base molecule to each heterotrimer leads to the structures of the trimers in Figure 3. As in the case of the dimers, it is the N atom of HCN and NH₃ that approaches the central pnicogen and the C of CN^– in the most stable trimers. The structure of each trimer can be thought of as a distorted octahedron. One apex is occupied by the Z lone pair, and the two ligands lie syn to one another, both directly opposite a F atom, designated F1 in Figure 3. As can be seen by the angles in Table 4, these θ(N/C···ZF1) angles are roughly linear. Note that the intermolecular R(N/C···Z) distances are a bit longer in the trimers than in the corresponding dimers. This stretch amounts to some 0.04–0.08 Å for the HCN trimers and 0.05–0.14 Å for NH₃ but is much longer for the trimers involving the CN^– anion, on the order of 0.4 Å. In fact, for the smaller P and As atoms, there is no trimer of the sort illustrated in Figure 3 for a pair of CN^– anions. This failure to form a trimer is likely due first to the negative values of V_s,max for the σ-holes within the CN^–···ZF₃ dimers mentioned above. As another consideration, the P and As atoms have fairly small radii, 1.90 and 1.88 Å, respectively, as compared to 2.47 Å for Sb and 2.54 Å for Bi. The short R(C···Z) distances to this anion (see Table 2) result in overcrowding to the smaller Z atoms, coupled with Coulombic repulsion between the two CN^– anions. For illustrative purposes, if the C atoms are each placed 2 Å from Z, roughly equivalent to these lengths in the dimer, and positioned 90° from one another, they would lie only 1.4 Å from one another, inducing obvious strong steric repulsion. It is no wonder then that this distance stretches to more than 2.5 Å for those trimers that can overcome this repulsive effect. The approach of the ZF₃ geometry toward an octahedron is evident by the Σθ(F–Z–F) sums in Table 4 which lie between 260 and 288°; this sum would be 3 × 90° = 270° for a perfect octahedron. However, these angle sums are notably smaller for the NC^– complexes where the F atoms are forced closer together by the short R(Z···C) contacts. The presence of the base opposite each Z–F1 bond elongates this covalent bond even more than in the dimer.

Figure 3.

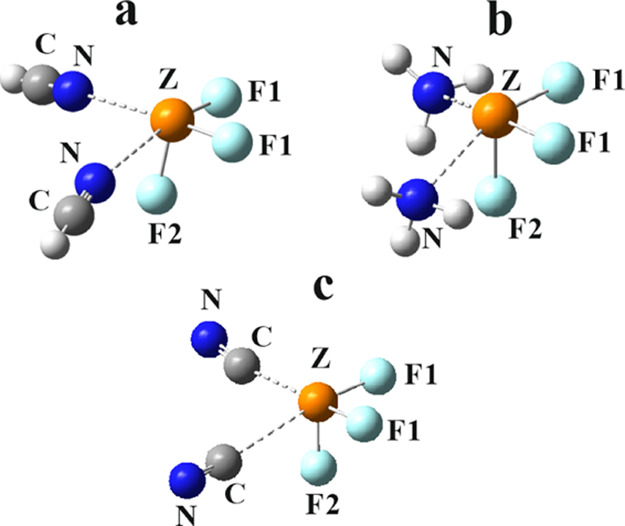
Most stable geometries of trimers including two bases plus ZF₃.

Table 4. Structural Parameters (Å and Degrees) in (HCN)₂···ZF₃ and (CN)₂···ZF₃ Complexes at the MP2/aug-cc-pVDZ Level of Theory.

	R(N···Z)	r(Z–F1)	r(Z–F2)	θ(N···Z–F1)	Σθ(F–Z–F)
(HCN)2···ZF3
(HCN)2···PF3	3.076	1.640	1.632	170.5	288.1
(HCN)2···AsF3	2.968	1.760	1.752	168.4	283.3
(HCN)2···SbF3	2.940	1.937	1.928	161.2	277.6
(HCN)2···BiF3	2.905	2.040	2.029	164.1	279.3
(H3N)2···ZF3
(H3N)2···PF3	2.895	1.652	1.643	166.1	284.4
(H3N)2···AsF3	2.733	1.780	1.767	162.3	278.0
(H3N)2···SbF3	2.688	1.962	1.948	154.1	270.6
(H3N)2···BiF3	2.718	2.066	2.049	154.3	273.4

	r(C···Z)	r(Z–F1)	r(Z–F2)	θ(C···Z–F1)	Σθ(F–Z–F)
(NC–)2···ZF3
(NC–)2···SbF3	2.550	2.059	1.957	166.4	259.2
(NC–)2···BiF3	2.727	2.164	2.057	177.5	269.1

The energetics of formation of these trimers from three separate subunits are compiled in Table 5. As noted above for the dimers, the two separate levels of theory are in good agreement with one another. The addition of a second HCN or NH₃ to form the trimer leads to a significant enhancement of the complexation energies. This magnification is not quite a doubling, lying in the range between 1.6 and 1.9. The situation is quite different for CN^– where the trimer is much more weakly bound. Indeed, the binding energy is positive and only becomes negative when considering the interaction energy. This weak binding of the second anion can be attributed in large part to the Coulombic repulsion between the NC^–···ZF₃ anionic complex and the incoming CN^– anion.

Table 5. Binding (E_b) and Interaction Energies (E_int) (kcal/mol) of ZF₃ Complexes with a Pair of HCN and CN^– Units Calculated at the MP2/aug-cc-pVDZ (I) and CCSD(T)/aug-cc-pVDZ (II) Levels of Theory^a.

	Eb		Eint
	(I)	(II)	(I)	(II)
(HCN)2···ZF3
(HCN)2···PF3	–4.57	–4.14	–4.70	–4.19
(HCN)2···AsF3	–7.19	–6.50	–7.51	–6.70
(HCN)2···SbF3	–10.48	–9.48	–11.06	–9.93
(HCN)2···BiF3	–13.85	–12.86	–14.57	–13.44
(H3N)2···PF3
(H3N)2···PF3	–7.70	–7.74	–8.66	–8.60
(H3N)2···AsF3	–12.90	–12.61	–14.88	–14.49
(H3N)2···SbF3	–20.22	–19.68	–23.28	–22.68
(H3N)2···BiF3	–24.46	–24.00	–27.45	–26.93
(NC–)2···ZF3
(NC–)2···SbF3	10.80	13.06	–4.29	–1.84
(NC–)2···BiF3	–0.63	0.86	–12.92	–11.28

^aAll values corrected for BSSE.

Some of these effects are emphasized when considering the various pairwise interaction energies within the trimers. E₁ and E₂ in Table S7 which reference the interaction of each base with ZF₃ are all negative. In the case of the two neutral bases, these quantities are similar to those in Table 3 for the dimers, but they are reduced for the CN^– trimers, consistent with the R(Z···C) bond stretches. Most important are the interaction energies computed between the two bases, within the geometric context of the trimer. These quantities are only very slightly positive, roughly 1 kcal/mol for HCN and NH₃. However, the Coulombic repulsion between the two anions raises E₃ in Table S7 up to more than +70 kcal/mol, severely reducing the total interaction energy within the full trimer. The difference between the total interaction energy and the sum of pairwise interactions represents a measure of the cooperativity within the trimer. While E_coop is again only slightly positive for HCN and NH₃, less than 3 kcal/mol, it rises to more than 10 kcal/mol for the anions. In other words, the trimerization suffers not only from the pure Coulombic repulsion between the two anions but also by an anticooperative effect.

The various AIM parameters that describe these interactions are displayed in Table S8 where these quantities are again notably larger for the complexes involving the anions than with the neutrals. The bond critical point densities, for example, are in the 0.037–0.047 au range for (NC^–)₂···ZF₃ but only 0.011–0.030 for the neutral analogues. While these AIM descriptors are smaller for the anion trimers than for the corresponding anion dimers, their larger magnitudes when compared to the neutral trimers are consistent with the idea that the anions are intrinsically bonded more strongly than the neutrals, but the overall binding energies suffer from the interanionic repulsions.

Anticipating the possibility of adding a third base, the MEP of the various L₂···ZF₃ trimers was examined. There is a further erosion of the σ-holes relative to the dimers, caused by the charge transfer from the second base. The values of V_s,max contained in Table S9 for the σ-holes are reduced by some 10–17 kcal/mol for the neutral bases, leaving them in the range of only 13–35 kcal/mol. The values for the (NC^–)₂···ZF₃ trimers are very negative, between −120 and −147 kcal/mol, which would of course make it exceedingly difficult for these trimers to accept a third anion.

As was the case for the dimers, there are other alternate minima for the trimers as well. For the CN^– trimers, the other configurations look very much like those in Figure 3, except that the approaching atom can be N rather than C (but only for Z = Sb and Bi). There is not much of a distinction between them in terms of energy. For example, flipping one of the two anions around raises the energy by less than 1 kcal/mol. Very much the same is true if both CN^– anions are rotated around to approach via their N atoms. In addition to the (NH₃)₂···ZF₃ geometry pictured in Figure 3, there are two alternate minima on the surface (see Figure S2). Whereas the two NH₃ molecules in global minimum A occupy two of the four legs of a tetragonal pyramid, they are located nearly opposite one another in geometry B. The latter is higher in energy than global minimum A by 5–19 kcal/mol. A third structure C is similar to A in that the framework is that of a tetragonal pyramid, except that the NH₃ molecules are located at the vertex and on one leg. This sort of geometry only occurs for the two heavier Z atoms Sb and Bi, for which it is 4–6 kcal/mol higher in energy than A.

More than Two Bases

The situation becomes more varied and interesting upon the addition of a third base to form a tetramer with ZF₃. Three CN^– anions will not engage in a stable complex with a central ZF₃. This failure is likely due to the energetic difficulty of adding yet another anion to a ZF₃···(CN^–)₂ complex that already bears a charge of −2. The situation is a bit more nuanced for HCN. Three HCN molecules can form a stable complex with ZF₃, with all positive vibrational frequencies. However, the AIM molecular diagrams in Figure S3 make it clear that only two of the HCN molecules engage in a pnicogen bond with the central Z. For PF₃, the HCN rotates around so that its H participates in a bifurcated H-bond with two F atoms. For the other ZF₃ molecules, the binding is dependent on weak C···F tetrel bonds with the central C of HCN.

It is only NH₃ which can engage in three simultaneous pnicogen bonds with ZF₃. Two views of the structure of these tetramers are displayed in Figure 4, with their corresponding structural parameters in Table 6. Because of the negative cooperativity, the R(N···Z) distances are all a bit longer for the tetramers than for the corresponding trimers. (There is a small amount of asymmetry for PF₃, with three slightly different R(N···P) distances.) There is a further lengthening of the internal Z–F bond lengths, and the pyramidalization of ZF₃ is enhanced relative to the trimers, vis a vis the smaller Σ(F–Z–F) sums.

Figure 4.

Two views of the optimized structure of (H₃N)₃···ZF₃.

Table 6. Structural Parameters (Å and Degrees) in (H₃N)₃···ZF₃ at the MP2/aug-cc-pVDZ Level of Theory.

	r(N···Z)	R(Z–F)	Φ(N···Z–F)	Σ(F–Z–F)	ΔΣ(F–Z–F)
(NH3)3···PF3	2.959	1.657	163.5	282.0	–9.2
	2.954	1.656	163.4
	2.949	1.656	163.2
(NH3)3···AsF3	2.822	1.786	159.6	275.1	–13.1
	2.820	1.786	159.6
	2.820	1.785	159.5
(NH3)3···SbF3	2.789	1.970	150.8	266.5	–18.0
	2.789	1.970	150.7
	2.788	1.970	150.7
(NH3)3···BiF3	2.769	2.081	150.9	268.3	–18.3
	2.769	2.081	150.9
	2.769	2.081	150.9

The energetics of these tetramers are reported in Table 7. Comparison with the data in Table 5 shows that the total complexation energies are larger than in the trimers. There is a certain degree of negative cooperativity, as these quantities are a bit less than 3/2 as would be expected from simple addition of bond energies. The AIM diagrams of these tetramers in Figure S4 confirm that the binding is indeed due to three Z···N pnicogen bonds, although there are some secondary interactions for Z = Bi. The AIM parameters in Table S10 show an increasing ZB strength with growing Z atom, P < As < Sb < Bi, but each is slightly smaller than the corresponding quantity in the trimer, further evidence of negative cooperativity.

Table 7. Binding (E_b) and Interaction Energies (E_int) (kcal/mol) of ZF₃ Complexes with Three NH₃, Calculated at the MP2/aug-cc-pVDZ (I) and CCSD(T)/aug-cc-pVDZ (II) Levels of Theory^a.

	Eb		Eint
	(I)	(II)	(I)	(II)
(H3N)3···ZF3
(NH3)3···PF3	–10.14	–10.32	–11.86	–11.90
(NH3)3···AsF3	–17.39	–17.17	–20.64	–20.30
(NH3)3···SbF3	–27.15	–26.50	–34.68	–31.50
(NH3)3···BiF3	–34.43	–33.92	–40.24	–39.63

^aAll values corrected for BSSE.

A last issue considered was the question as to whether a ZF₃ molecule could engage in a fourth ZB. It was found that a pentamer of this type could only be formed between 4 NH₃ molecules and BiF₃, the largest Z atom considered. The structure displayed in Figure 5 is not symmetric in that there are four unequal R(Bi···N) distances, varying from 2.65 to 3.14 Å. Moreover, the crowded nature of the complex pushes the θ(F–Bi···N) angles away from linearity. Nevertheless, there are indeed four pnicogen bonds present according to AIM analysis, with bond critical point densities between 0.013 and 0.035 au. On the other hand, Figure S5 indicates that these four ZBs are not the only interactions holding the complex together. They are complemented by a set of a N···F pnicogen bond and NH···F HBs. The entire pentamer is held together with a binding energy of −38.7 kcal/mol. This quantity is only slightly larger than the value in the tetramer of −34.4, so one can conclude that the fourth NH₃ is held by only 4.3 kcal/mol. Given this small amount, which depends not only on the four Bi···N ZBs but also on a number of secondary interactions, the ability of BiF₃ to engage in more than three ZBs is in doubt. In addition, the lighter Z atoms do not show any proclivity whatsoever to form more than three ZBs.

Figure 5.

Optimized geometry of (H₃N)₄···BiF₃. Distances in Å.

CSD Survey

A survey of previously derived crystals within the CSD⁸¹ (Cambridge Structural Database) provides some experimental context for the computational data above. In order to provide a comprehensive overview, only trivalent ZR₃ units were considered. The samples were divided into those with all three R substituents a halogen (X) atom, and all others separately. N was chosen as the atom of the approaching nucleophile. In order to rule out covalent Z–N bonds and focus on noncovalent pnicogen bonds, a minimum criterion was set for the R(Z···N) interatomic distance. This threshold was taken at three different values: 110, 120, and 130% of the sum of the covalent radii of the Z and N atoms. The maximum distance which was taken as evidence of a ZB was the sum of the vdW radii.

The data extracted from this survey are presented in Table 8 where each row refers to the number of systems where the indicated number of Z···N pnicogen bonds are present. Taking the first row as an example, there were 7 systems observed where a single pnicogen bond is observed for ZX₃ complexes for which the R(Z···N) distance is at least 110% of the sum of the Z and N covalent bond radii. As the internuclear distance threshold is stretched to 120% and then 130% of this radius sum, the number of such systems is reduced progressively to 5 and then to only 1. Moving down the columns, the number of systems containing two Z···N pnicogen bonds changes to 12, 4, and 4 and then diminishes further to 4, 2, and 1 for the case of three ZBs. It is interesting that there are 9 systems containing four bonds, but this is only true for the very short R(Z···N) contact barely larger than the covalent radii sum, so likely represents a series of slightly stretched covalent bonds.

Table 8. Number of Instances Observed in CSD for Complexes Containing Indicated Number of Z···N Pnicogen Bonds to Central Z Atom^a.

	ZX3			ZR3
number of Z···N contacts	110%	120%	130%	110%	120%	130%
1	7	5	1	285	105	14
2	12	4	4	178	69	7
3	4	2	1b	55	36	10c
4	9	0	0	12	0	0
5	0	0	0	13	0	0

^aX refers to halogen atoms, and R refers to any substituent. Percentages indicate the internuclear Z···N distance as a fraction of the sum of their covalent radii.

^bR(Bi···N) = 2.92 Å, 134% of covalent radii sum.

^c1 with Z = P, 0 with As, 7 with Sb, 2 with Bi.

Relaxation of the restriction of ZX₃ central units to a broader ZR₃, where R can be any substituent of course enlarges the number of such systems observed. The same 110, 120, 130% sequence leads to the rapidly reducing number of 285, 105, and 14 observed single pnicogen bonds. These numbers drop quickly for double and then triple interactions. Again one sees several cases where the 110% threshold would indicate 4 or even 5 pnicogen bonds but none for the more reasonable noncovalent criterion of 120 or 130%. So, while there are certainly numerous systems where a trivalent pnicogen atom engages in 1 or 2 ZBs, this number drops for n = 3. It is questionable as to whether there are any systems containing more than 3 ZBs. Figure S6 illustrates a representative sample of just several of the structures captured from the CSD database.⁸²⁻⁸⁹

Of course, it should be emphasized that the calculations described above pertain to each system in isolation, that is, in vacuo. The crystal structures include effects of neighboring molecules that may modify some of the geometric aspects of each system. So, a reader is cautioned against making precise comparisons.

Discussion and Conclusions

It appears, then, that the number of pnicogen bonds in which a ZF₃ molecule is capable of engaging is dependent upon the nature of the base. The sp hybridization of N in NCH makes it a fairly weak nucleophile. This N can only approach the Z atom to within about 3 Å, and its binding energy reaches a maximum of 7 kcal/mol for Z = Bi. ZF₃ can engage in two ZBs with NCH, but a third such base engages only weakly with the (HCN)₂···ZF₃ and not via a ZB. Its negative charge makes CN^– a powerful nucleophile, binding to ZF₃ by upwards of 20 kcal/mol, as much as 40 kcal/mol for Z = Bi. However, once bound to the Lewis acid, the ensuing NC^–···ZF₃ complex acquires a negative charge which impedes the approach of a second CN^–. Consequently, the second ZB is very weak and only exists at all for the larger Sb and Bi atoms. A base like NH₃, on the other hand, fits into the Goldilocks region of being just right. Its electrical neutrality prevents the acquisition of charge, so there is no Coulombic obstacle to the approach of multiple NH₃ units. It is a strong base, which can approach to within 2.6–2.8 Å of the central Z atom, and is bound by 4–13 kcal/mol, depending on the size of Z. It is thus able to easily engage simultaneously in three ZBs with ZF₃, with an overall complexation energy of 10–34 kcal/mol. A fourth such bond is marginal though. In the first place, it is only the largest Z = Bi that can engage with four NH₃ units. In addition, the entire complex is held together not only by four ZBs but also by a number of secondary interactions. Moreover, the complexation energy of the (NH₃)₄···BiF₃ system is only slightly larger than the smaller (NH₃)₃···BiF₃.

Given the strength of the interaction between CN^– and the central Z atom, it is worth considering whether the addition of this anion to a ZF₃ molecule that is already engaged in a pair of ZBs with two HCN molecules might induce the system to engage in a third ZB. This idea seemed plausible as the incoming CN^– will not be repelled by a (HCN)₂···ZF₃ complex that already contains a single or double negative charge. In order to examine this possibility, the CN^– anion was initially placed in a wide range of positions with respect to each (HCN)₂···ZF₃ complex. Ensuing geometry optimizations led to a variety of situations. For example, in most cases, the anion replaced one of the two HCN units, leaving only two ZBs. In other cases, one or both of the two HCN molecules engaged in a HB with the CN^– anion, or with the F atoms, instead of a ZB with the central ZF₃. However, most importantly, in no case did any of the myriad of initial structures considered optimize to the one containing three ZBs. This result confirms the idea that a third ZB requires a neutral strong base like NH₃.

A prior paper⁹⁰ yielded results that have some relevance to the calculations reported above. While the first four N₂ or NCH Lewis bases attach themselves to a central NH₄⁺ cation via NH···N H-bonds, succeeding base molecules engage via a N···N pnicogen bond.

Aside from the survey of crystal structures described above, there is additional specific experimental verification of some of these ideas. The Cozzolino group⁹¹ has constructed alkoxide cages containing two Sb···O ZBs, each of which is stronger than 7 kcal/mol. The central Sb atom of SbCl₃ engages in three Sb···O contacts short enough to be characterized as ZBs⁹² or in three Sb···S bonds with trithiane;⁹³ three Bi···S bonds with BiX₃ have also been observed quite recently.⁹⁴ Radha et al.⁹⁵ have shown that a Sb atom can engage in three Sb···S ZBs, that complement its three covalent Sb–S bonds. Their analysis also concluded that a bulky alkyl substituent can inhibit the formation of this number of noncovalent interactions. A very recent work⁹⁶ offers further confirmation that with proper formulation of substituents, Bi is capable of three simultaneous ZBs.

The forgoing analysis provides a framework for consideration of multiple pnicogen bonds to a given system, a set of general rules that might be applied to a particular case. As the strength of the base increases, so too does the probability of multiple pnicogen bonds. So, a weak base like NCH might be limited to only two such bonds, whereas a stronger base like NH₃ can engage in three and even four in certain circumstances. In addition, a larger central pnicogen atom is more prone to a greater number of ligands. However, there are secondary issues which might affect these numbers. The overall structural restraints within a crystal, for example, might prevent the central Lewis acid molecule from properly distorting so as to receive a third or fourth ligand. Or the ligands might be large enough that steric repulsions could obstruct the approach of one or more ligands. Another factor is related to the nature of the substituents on the pnicogen atom. The work described above made use of three F substituents which are highly electron-withdrawing and thus enhance the σ-holes that attract the ligands. Less electronegative substituents might be expected to weaken the pnicogen bonds and act to reduce their number. On the other hand, stabilizing interactions between the ligands themselves can promote the ability of the central Z atom to accommodate a larger number of them. The various attractive interactions between the various NH₃ molecules in F₃Bi(NH₃)₄ described above is a case in point. Another example of a special circumstance arises if several of the electron donor atoms are part of a single ligand. Such a situation has been observed wherein SbCl₃ can be induced to engage in as many as five ZBs when all five electron donor O atoms are part of a single crown ether ligand.⁹⁷ While an anion represents a much stronger nucleophile, its charge works against multiple bonding of this type, as was noted above for CN^– because each such anion adds to the electrostatic repulsion between central unit and approaching ligand.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.0c00257.

• Structural parameters of isolated monomers, deformation energies, AIM descriptors of the neutral and anionic complexes, electronic and Gibbs free energy differences, V_s,max of dimers, energies of cooperativity, AIM descriptors of the neutral and anionic trimers, V_s,max of trimers, AIM descriptors of the tetramers, crystal structures of tetra and penta-coordinated complexes (from CSD); and Structural parameters in isolated ZF₃ (Z = P, As, Sb, Bi) calculated at the MP2/aug-cc-pVDZ level of theory (PDF)

The authors declare no competing financial interest.