Phonon Anharmonicity in Bulk T_d-MoTe₂

Abstract

We examine anharmonic contributions to the optical phonon modes in bulk T_d-MoTe₂ through temperature-dependent Raman spectroscopy. At temperatures ranging from 100 K to 200 K, we find that all modes redshift linearly with temperature in agreement with the Grüneisen model. However, below 100 K we observe nonlinear temperature dependent frequency shifts in some modes. We demonstrate that this anharmonic behavior is consistent with the decay of an optical phonon into multiple acoustic phonons. Furthermore, the highest frequency Raman modes show large changes in intensity and linewidth near T ≈ 250 K that correlate well with the T_d→1T ^′ structural phase transition. These results suggest that phonon-phonon interactions can dominate anharmonic contributions at low temperatures in bulk T_d-MoTe₂, an experimental regime that is currently receiving attention in efforts to understand Weyl semimetals.

I. INTRODUCTION

Transition metal dichalcogenides (TMDs) exhibit a wide range of layer-dependent phenomena depending on the choice of the transition metal and chalcogen atoms. Beginning with the discovery of photoluminescence from monolayer MoS₂,^1,2 most studies of TMDs have focused on the semiconducting 2H crystal phase in MoS₂, MoSe₂, WS₂, WSe₂, and MoTe₂.^3–8. However, TMDs can exist in multiple structural phases that exhibit unique electronic properties, including the 2H (α, hexagonal, space group P6₃/mmc), 1T′ (β, monoclinic, space group P2₁/m), and T_d (γ, orthorhombic, space group Pnm2₁) crystal phases.^9–11 The 2H structure is similar to the honeycomb lattice of graphene, but has broken sublattice symmetry and therefore a large bandgap ranging from 1–2 eV. For most TMDs, 2H is the dominant structural phase due to large ligand-field stabilization energies.¹¹ However, for MoTe₂ the ground-state energy difference between the 2H and the 1T′ phases is minimal,^11,12 allowing both to be realized experimentally under ambient conditions. 1T′-MoTe₂ has a distorted octahedral (monoclinic) structure and has been synthesized by a modified growth method^13–16 as well as a low-temperature solution phase synthesis procedure,¹⁷ and has recently been found to be a low-bandgap semiconductor when in few-layer form.¹³ In addition, laser heating can drive MoTe₂ out of the 2H phase into a metallic phase with a Raman spectrum distinct from 1T^′-MoTe₂,¹⁸ a discovery that potentially enables MoTe₂ metal-semiconductor homojunctions as well as phase change memories.¹⁹

1T′-MoTe₂ transitions into T_d-MoTe₂, an orthorhombic phase with broken inversion symmetry, when cooled below T ≈ 250 K. This 1T′→T_d transition in MoTe₂ has been observed in temperature-dependent electrical measurements as hysteresis after a warming/cooling cycle,^15,20–22 low-temperature Raman spectra through the activation of an inversion-symmetry forbidden shear mode,^22,23 X-ray diffraction (XRD) measurements,^24,25 and electron diffraction measurements.²⁶ The lattice constants in T_d-MoTe₂ and 1T′-MoTe₂ are only slightly different^10,15,25 but nevertheless lead to striking modifications of the electronic structure, the most notable of which is the prediction of a type II Weyl semimetal phase.²⁷ This exciting electronic state has also been predicted in WTe₂²⁸ and the alloy Mo_xW_1–xTe₂,²⁹ and recent experimental results have confirmed the presence of the Weyl semimetal state in all three systems.^30–38

The clear importance of T_d-MoTe₂ demands a systematic investigation of its properties and how they evolve under external stimuli. For example, high pressure has been shown to increase the superconducting transition temperature in T_d-MoTe₂ substantially.¹⁵ Thus far there has been little work on understanding how the vibrational properties evolve with temperature^22,23 and the role of electron-phonon or phonon-phonon interactions in 1T′ or T_d-MoTe₂, both of which play important roles in the electronic properties of materials. Understanding the origin of anharmonic effects in MoTe₂ is therefore important for futur explorations of low-temperature phenomena.

Here, we use temperature-dependent Raman spectroscopy to characterize anharmonic contributions to four prominent optical phonon modes in bulk T_d-MoTe₂. Our measurements extend down to 5 K, allowing us to observe departures from the commonly-observed Grüneisen behavior. We find that two phonon modes exhibit modest changes in frequency with temperature, while the remaining two modes exhibit large, nonlinear changes in linewidth, frequency, and intensity. All four modes exhibit a change in frequency and slope around T ≈ 250 K, which correlates well with the T_d→1T′ structural phase transition. These observations are consistent with a regime where anharmonic contributions arising from optical phonon decay into multiple acoustic phonons are substantial.³⁹ Our results are the first studies of phonon anharmonicity in T_d-MoTe₂ and provide crucial information for understanding the low-temperature electronic and vibrational properties of this highly-relevant material.

II. EXPERIMENTAL METHODS

MoTe₂ single crystals were produced by the chemical vapor transport (CVT) method with iodine as the transport agent. First, MoTe₂ powder was synthesized by annealing a stoichiometric mixture of molybdenum (99.999%) and tellurium (99.9%) powders at 750 °C for 72 h in an evacuated and sealed quartz ampoule. To obtain MoTe₂ single crystals, approximately 2 g of polycrystalline MoTe₂ powder and a small amount of iodine (99.8%, 4 mg/cm³) were sealed in an evacuated quartz ampoule of 170 mm in length and 13 mm in diameter. The ampoule was placed in a horizontal furnace with a temperature gradient so that the end containing the MoTe₂ charge maintained a temperature of 1000 °C, while the opposite end was kept at about 950 °C. After 168 hours in the furnace, the ampoule was quenched in ice-water and the MoTe₂ single crystalline platelets were extracted. According to θ − 2θ XRD scans, the platelets crystallized in the 1T^′ form with the lattice parameters a = 6.339(3) Å, b = 3.466(4) Å, c = 13.844(3) Å, and β = 93.84(5)°.

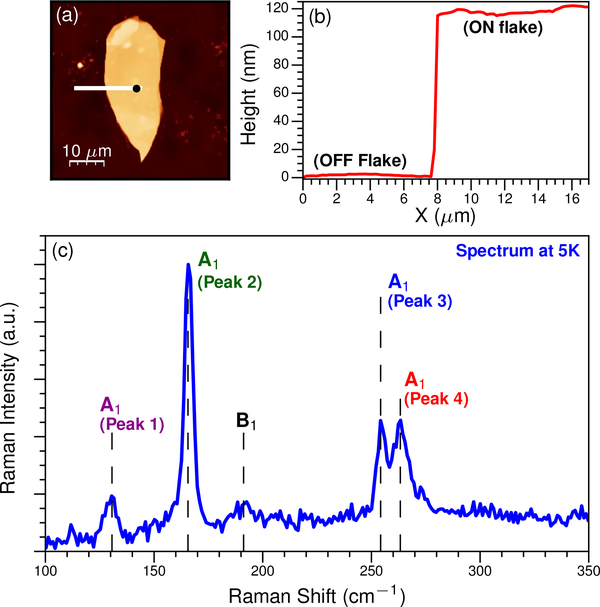
Following structural characterization, the bulk 1T^′-MoTe₂ crystal was mechanically exfoliated using tape and deposited onto Si/SiO₂ substrates with an oxide thickness of 285 nm. Atomic force microscopy (AFM) images (Fig. 1a) indicated that the flake we studied is ≈ 120 nm thick (Fig. 1b) and therefore lies well within the bulk regime, implying that interactions with the substrate can be neglected. It is notable that both the starting crystal and bulk flake we studied were exposed to atmosphere for prolonged periods of time, which is known to oxidize defects in 2H-MoTe₂.⁴⁰ A recent study demonstrated a similar effect in 1T ^′-MoTe₂ where the Raman signal degraded during measurement, presumably due to photooxidation.¹⁶ In order to avoid these effects, we performed all Raman experiments in vacuum and verified that our signal does not degrade after numerous cooldowns and measurements.

FIG. 1.

(a) AFM image of the MoTe₂ flake on a Si/SiO₂ substrate. The black circle on the flake marks the location where Raman spectra were acquired. (b) Height profile of the MoTe₂ flake extracted from (a) along the white line. The flake is over 100 nm thick, which corresponds to the bulk regime. (c) Raman spectra of T_d-MoTe₂ acquired at 5 K. The four peaks examined in this study are labeled along with the symmetry assignments.

Raman measurements were performed from 5 K to 320 K on a home-built, confocal microscope integrated with a closed-cycle cryostat. The excitation source was a 532 nm laser focused through a 0.5 NA long working distance objective with a 50X magnification. Since the sample was excited in a backscattering geometry, we could detect Raman modes with A_g and B_g symmetry for 1T′ and A₁ and B₁ symmetry modes for T_d. The laser spot diameter was ≈ 1.5 μm and the laser power was ≈1.4 mW at the sample for all measurements. Raman scattering from the sample was directed to a 500 mm focal length spectrometer with a LN₂ cooled CCD. The spectrometer and camera were calibrated using a Hg-Ar atomic line source and the spectrometer grating was positioned so that each Raman spectrum included the filtered laser line, allowing us to easily account for any drift in the laser wavelength. The instrumental response function (IRF) for these measurements was ≈ 3.9 cm⁻¹.

III. RESULTS AND DISCUSSION

We present an example Raman spectrum acquired at 5 K in Fig. 1c, at which point MoTe₂ is in the T_d phase. We observe four prominent peaks at ≈ 130 cm⁻¹, 165 cm⁻¹, 254 cm⁻¹, and 264 cm⁻¹, all with A₁ symmetry, which we refer to as Peaks 1–4, respectively. There is also a weak feature at 190 cm⁻¹ that has B₁ symmetry, but its signal is not sufficient for temperature-dependent analysis. These assignments are based on polarization-dependent Raman measurements of the 1T′ phase at 300 K, which will be reported elsewhere, and density functional theory calculations of the phonon eigenspectrum.¹⁷ The Raman tensors for the A_g(B_g) modes and the A₁(B₁) modes are identical in structure for the backscattering configuration used here, which implies that they will evolve into an A₁(B₁) symmetry at low temperature (Supporting Information).

As we increase the sample temperature from 5 K to 320 K, all peaks soften although the magnitude of the redshift is different for each. In Fig. 2a we present temperature-dependent Raman spectra for Peak 2 along with Lorentzian fits (black curves). Fig. 2b shows similar data for Peaks 3 and 4, and all spectra in Fig. 2 have been normalized by the intensity of Peak 2. A similar analysis of Peak 1 is presented in the Supporting Information.

FIG. 2.

Temperature-dependent Raman spectra for (a) Peak 2 and (b) Peaks 3 and 4. Spectra are fit to either a single or double Lorentzian function with a linear background. The sample temperature increases from 5 K (bottom) to 320 K (top). In both panels, the spectra have been normalized by the intensity of Peak 2. Similar data for Peak 1 is presented in the Supporting Information. (c) FWHM of Peaks 1 and 2 extracted from the fits versus temperature. (d) FWHM of Peaks 3 and 4 extracted from the fits versus temperature. (e) Amplitudes of Peaks 3 and 4 extracted from the fits versus temperature. 1σ error bars are included in panels (c) - (e).

We find that the full width at half maximum (FWHM) linewidth of Peak 1 does not change substantially over the entire temperature range (Fig. 2c). The FWHM of Peak 2 is limited by the IRF and also exhibits modest temperature dependence, which suggests that phonon-phonon interactions are weak for these modes. Peaks 3 and 4 exhibit markedly different behavior. As the sample temperature increases, these modes both redshift substantially and the FWHM linewidth of Peak 3 broadens (Fig. 2d). We quantify this behavior by fitting Peaks 3 and 4 to a double Lorentzian function plus a linear background, which allows us to extract the center frequency, amplitude, and linewidth of each mode. At 5 K, the IRF limits the FWHM of Peak 3, which is narrower than Peak 4 (≈ 4 cm⁻¹ versus ≈ 9 cm⁻¹). However, Peak 3 steadily broadens with increasing temperature from 5 K to 250 K, at which point the two modes have similar linewidths. Over the same temperature range, the amplitude of Peak 4 decreases, becoming comparable to that of Peak 3 by 250 K (Fig. 2e). It is notable that observed changes in peak intensity and linewidth correlate well with the T_d→1T′ transition temperature,^{15,20–23,25} suggesting that the relative intensity and linewidth of Peaks 3 and 4 are sensitive to the change in structural phase.

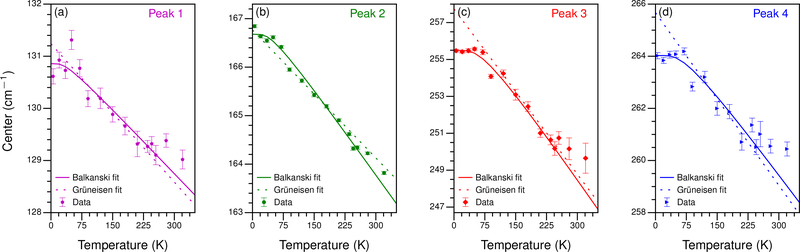
The frequency of all examined Raman peaks softens with increasing temperature (Fig. 3). Temperature-induced shifts in Raman frequencies are typically fit using the linear Grüneisen model:^41–44

$$\omega (T)={\omega }_o+\chi T.$$ (1)

ω(T) is the temperature-dependent phonon frequency, ω_o is the harmonic phonon frequency at 0 K, and χ is the first order temperature coefficient. The Grüneisen model combines the effects of thermal expansion and the phonon self-energy into χ and is sufficient when $T>>\frac{\hslash {\omega }_o}{2k_B}$ where k_B is the Boltzmann constant. At lower temperatures, ω(T) can become nonlinear and Eq. 1 is not necessarily valid. We illustrate this explicitly in Fig. 3, where the dashed line is a fit of Eq. 1 to the data from 100 K to 200 K. While there is good agreement at low T < 100 K for Peaks 1 and 2 (Figs. 3a and 3b), large deviations exist in this range for Peaks 3 and 4 (Figs. 3c and 3d). The fact that the linewidths of Peaks 1 and 2 exhibit comparably little variation suggests that thermal expansion and/or electron-phonon coupling, rather than phonon-phonon interactions, dominate anharmonic effects in these modes. For Peaks 3 and 4, we suggest that thermal expansion of the lattice makes a negligible contribution to the phonon frequency, and instead changes in the phonon self-energy from anharmonic coupling between different phonon branches are the dominant effect.⁴⁵ Theoretical work by Balkanski et al. demonstrated that the temperature dependence of optical phonons can be accounted for by a decay pathway resulting in multiple acoustic phonons.³⁹ ω(T) in this formalism is given by

$$\omega (T)={\omega }_B+A\left(1+\frac{2}{e^x-1}\right)$$ (2)

Where $x=\frac{\hslash {\omega }_B}{2k_{B}T}$ and ω_B is the 0 K harmonic phonon frequency. In the treatment by Ref. 39, the constant A represents an anharmonic contribution to the frequency involving the decay of an optical phonon into two acoustic phonons. At T = 0, ω(0) = ω_B + A, which implies that A represents a third order correction to the phonon self-energy.³⁹ This model has been successfully applied to a variety of nanomaterials to explain nonlinear temperature dependence in optical phonon frequencies.^42,45–48

FIG. 3.

Raman frequency versus temperature for (a) Peak 1, (b) Peak 2, (c) Peak 3, and (d) Peak 4. In each panel, we fit the data to the Grüneisen model (dashed lines) in Eq. 1 from 100 – 200 K and to Eq. 2 (solid lines) from 0 – 250 K. The best fits are extrapolated over the entire temperature range and 1σ error bars are included.

We fit the frequencies of Peaks 1–4 (Figs. 3a - 3d) to Eq. 2 up to 250 K in order to isolate the T_d crystal phase. The extracted values of A, ω_B, χ, and ω_o are summarized in Table I and compared to bulk 2H-MoS₂.⁴⁵ We find that Peaks 3 and 4 have larger values of A which, when combined with the significant changes in FWHM, suggest that phonon interactions dominate the anharmonic coupling. Note that an additional term in Eq. 2 corresponding to fourth order processes has been omitted as it was not required to fit our data.³⁹ Furthermore, we observe that all four modes deviate from both Eqs. 1 and 2 above T ≈ 250 K, which we interpret as the onset of the 1T′ phase with distinct anharmonic behaviors. The unique behavior of Peaks 3 and 4 is attributed to the apparent sensitivity of their atomic displacements to interlayer coupling. As T_d transitions to 1T′, the a and b lattice parameters increase by 0.0198 Å and 0.0375 Å, respectively, while the c lattice parameter decreases by 0.0447 Å.³⁸ This implies that the dominant changes are in the directions of the b lattice vector and the out-of-plane c lattice vector. Furthermore, the angle between the b and c lattice vectors changes from 90° in T_d to 93.84° in 1T′.³⁸ These combined structural changes imply that phonon modes sensitive to interlayer coupling will be most affected by the T_d→1T′ transition. Peak 2 depends only weakly on the number of layers,¹³ and therefore it is expected to respond minimally to changes in layer alignment and separation. In contrast, Peaks 3 and 4 are sensitive to flake thickness¹³ and are therefore likely to respond to changes in the spacing and alignment of the layers during the T_d→1T′ transition.

TABLE I.

Measured values of A, ω_B, χ, and ω_o for Peaks 1–4 along with literature values for bulk 2H-MoS₂.

Mode	Material	Ref.	A (cm−1)	ωB (cm−1)	χ (cm−1/K)a	ωo (cm−1)a
Peak 1	Bulk Td-MoTe2	this work	−0.390 ± 0.027	131.25 ± 0.091	−0.0089 ± 0.004	131.24 ± 0.537
Peak 2	”	”	−0.717 ± 0.009	167.39 ± 0.022	−0.0089 ± 0.001	166.77 ± 0.122
Peak 3	”	”	−3.019 ± 0.094	258.51 ± 0.116	−0.0312 ± 0.002	257.91 ± 0.303
Peak 4	”	”	−2.052 ± 0.105	266.08 ± 0.140	−0.0227 ± 0.003	265.74 ± 0.438
A1g	Bulk 2H-MoS2	45	−5.687	-	−0.0197	-
$E_{2g}^1$	”	”	−3.058	-	−0.0221	-

^aCalculated from fits to data from 100 K to 200 K.

IV. CONCLUSION

In summary, we have investigated anharmonicity of the optical phonon modes in bulk T_d-MoTe₂. Changes in phonon frequency, linewidth, and amplitude are determined for four modes and the results correlate well with the T_d→1T′ structural phase transition. ω(T) is nonlinear for two modes, which is consistent with an anharmonic contribution arising from optical phonon decay into multiple acoustic phonons. The large changes in frequency and linewidth for these two modes as T_d→1T′ indicates they are highly sensitive to interlayer separation and alignment, an observation that is consistent with prior characterizations of their dependence on layer number. All four modes exhibit a change in slope and an increase in frequency at T ≈ 250 K which we attribute to the T_d→1T′ structural phase transition. These results highlight the important, and in some cases dominant, role of phonon-phonon interactions in T_d-MoTe₂. Further studies connecting the atomic displacement of these modes to their anharmonicity are desirable and additional investigation of suspended, few-layer MoTe₂ will illuminate the impact of interlayer coupling on anharmonicity in this exciting material.