Zero-inflated Poisson factor model with application to microbiome read counts

Abstract

Dimension reduction of high-dimensional microbiome data facilitates subsequent analysis such as regression and clustering. Most existing reduction methods cannot fully accommodate the special features of the data such as count-valued and excessive zero reads. We propose a zero-inflated Poisson factor analysis model in this paper. The model assumes that microbiome read counts follow zero-inflated Poisson distributions with library size as offset and Poisson rates negatively related to the inflated zero occurrences. The latent parameters of the model form a low-rank matrix consisting of interpretable loadings and low-dimensional scores that can be used for further analyses. We develop an efficient and robust expectation-maximization algorithm for parameter estimation. We demonstrate the efficacy of the proposed method using comprehensive simulation studies. The application to the Oral Infections, Glucose Intolerance, and Insulin Resistance Study provides valuable insights into the relation between subgingival microbiome and periodontal disease.

1 |. INTRODUCTION

The development of next-generation sequencing (NGS) technologies enables the quantification of microbes living in and on the human body (Hamady and Knight, 2009). Many recent studies have identified that microbial dysbiosis in specific anatomical sites is associated with complex diseases such as type 2 diabetes, prediabetes, insulin resistance, and cardiovascular disease (Dewhirst et al., 2010; Demmer et al., 2015, 2017). However, detecting microbial association remains a formidable problem due to the complexity of microbiome data and a lack of appropriate statistical methods (Li, 2015).

In the motivating Oral Infections, Glucose Intolerance and Insulin Resistance Study (ORIGINS), one goal is to investigate the relationship between subgingival microbial communities and both periodontal disease and biomarkers of diabetes risk. Previous analysis of NGS data in ORIGINS shows expected associations between oral bacterial phyla and markers of inflammation and impaired glucose regulation. However, at the taxa level, few individual bacterial taxa are identified with statistical significance (Demmer et al., 2017) limiting the ability to understand which taxa drive phylum level findings. One of the challenges arises from the high dimensionality of data, requiring multiple testing corrections that result in reduced statistical power. Thus, dimension reduction is often desired to reduce the number of variables subject to hypothesis testing. There are several outstanding challenges for dimension reduction of microbiome NGS data: (a) Library sizes are heterogeneous across samples. (b) Typical data in a microbiome study consist of highly skewed nonnegative sequence counts (Hamady and Knight, 2009), which cannot be directly modeled with Gaussian distributions (Srivastava and Chen, 2010). (c) The data contain excessive zeros. There are two types of zero counts in microbiome data: one is “true zeros” (ie, absence of taxa in samples) and the other is “pseudo-zeros” (ie, the presence is below detection limit). Either true absence or undetected presence of a taxon will lead to excessive zeros in microbiome data.

Factor analysis has been widely used to identify low-dimensional features in high-dimensional data. Typically, original read counts are first converted to compositions (or rarefied) and then transformed. Standard factor analysis is applied to the transformed data to achieve dimension reduction (McMurdie and Holmes, 2014). However, there is significant information loss during the preprocessing step, and the compositional data are still difficult to handle statistically because of the extra constraint on the sum and excessive zeros. McMurdie and Holmes (2014) pointed out that both preprocessing approaches are inappropriate for detection of differentially abundant species. Therefore, standard factor analysis methods are not adequate for analyzing microbiome absolute abundance (ie, sequence read counts) and thus it is desired to bypass the preprocessing procedure and model absolute abundance data directly.

There are some recent developments on modeling sequence read count data. Lee et al. (2013) developed a Poisson factor model with offset. This method can effectively model count-valued data with heterogeneous library sizes, but it fails to take the excessive zeros into consideration. Cao et al. (2017) developed a Poisson-multinomial model to model the high variation arising from excessive zeros. However, the method is not adequate to address the overdispersion from excessive zeros in data (Li, 2015). In order to account for this extra biological variability, established statistical theory shows using a mixture model is necessary (Lu et al., 2005; McMurdie and Holmes, 2014). Very recently, Sohn and Li (2018) built a zero-inflated quasi-Poisson factor model to conquer the inflated zero challenge, but this model relies on a somewhat unrealistic assumption that each taxon has a fixed zero probability despite the heterogeneity in samples. It does not establish any link between the probability of true zeros and the Poisson rate underlying the microbiome read counts, which might lead to inferior results as we will show later.

Intuitively, the probability for a count value being true zero should be lower if the underlying Poisson rate is relatively high. Cao et al. (2017) also presented similar finding when analyzing gut microbiome data. In order to further validate this conjecture, in our motivating ORIGINS data, we assume that each taxon (ie, each column in the dataset) follows a zero-inflated negative binomial (ZINB) distribution. As a result, we could model excessive zeros and potential over dispersion at the same time. In particular, we assume a read count in jth column has probability p_j to be a true zero and probability (1 − p_j) to be from a negative binomial distribution with expectation λ_j and variance $\left({\lambda }_j+{\lambda }_j^2{\varphi }_j\right)$ where ϕ_j is the dispersion parameter. Such a mixture distribution is fitted to each taxon. The relationship between the estimated p_j and log(λ_j) is shown in Figure 1. The negative relationship between the true zero probability and the log rate is well captured by a logistic function (ie, the red solid curve in Figure 1). This figure appears in color in the electronic version of this paper, and any mention of color refers to that version. The above exploratory analysis is only used to investigate the relationship between the probability of true zero and the Poisson/NB rate. In our proposed model, we do not assume different read counts in the same taxon following the same distribution, but rather use separate zero-inflated Poisson (ZIP) models with parameters λ_ij for different values. We remark that having separate λ_ij for each read count compensates the lack of dispersion parameters. We refer interested readers to a more detailed discussion in Collins et al. (2002). These results motivate us to adopt the ZIP distributions (without a dispersion parameter) and propose a link between the true zero probability and Poisson rate.

FIGURE 1. Relationship between fitted true zero probability and log expectation in ZINB for each taxon.

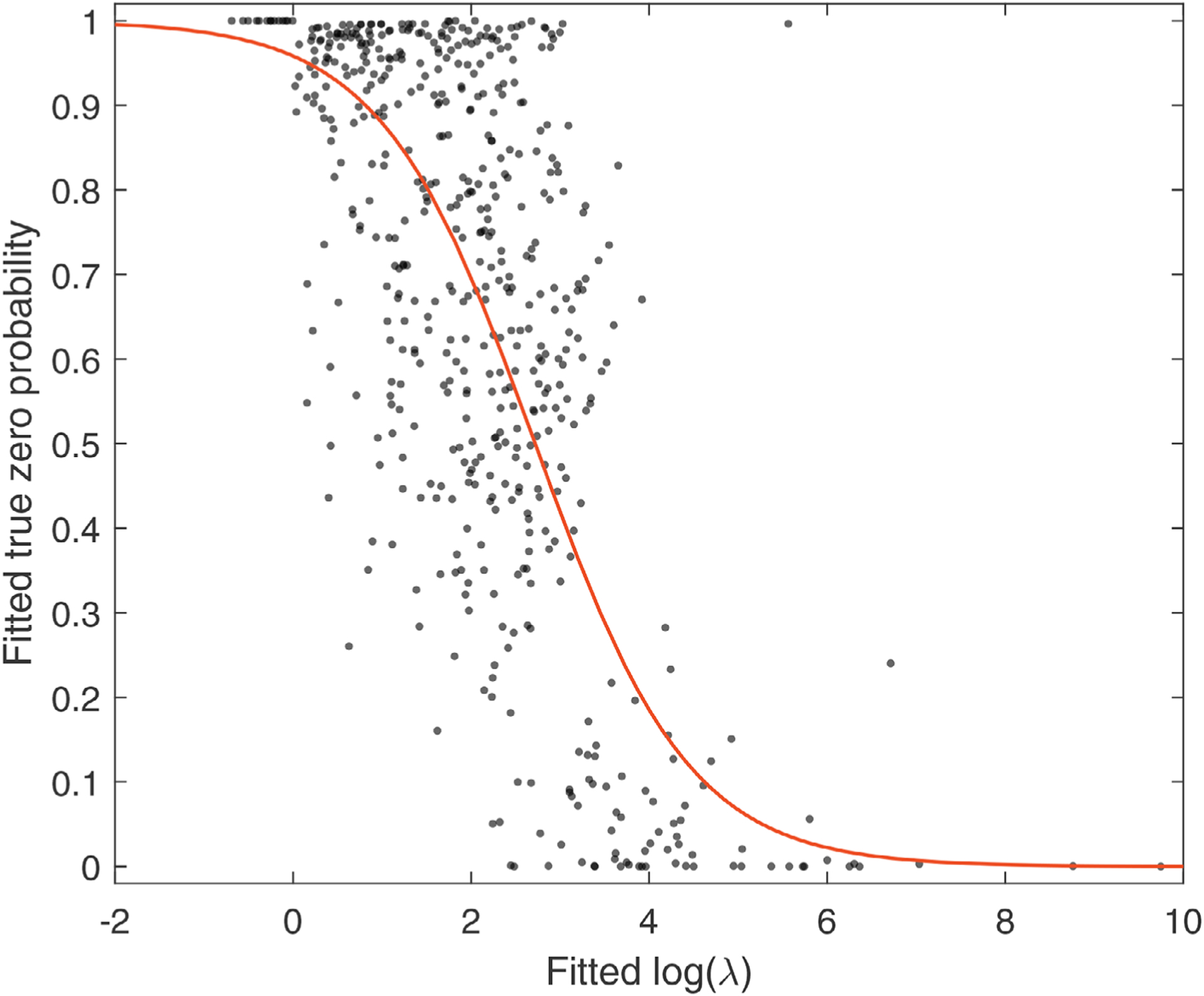
Note. The red curve is the fitted logistic function. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

In summary, we develop a new zero-inflated Poisson factor analysis (ZIPFA) model for reducing the dimension of microbiome data. The model has unique contributions to microbiome data analysis:

• it properly models the original absolute abundance count data;

• it specifically accommodates excessive zero counts in data;

• it incorporates a realistic link between the true zero probability and Poisson rate.

The rest of the paper is organized as follows. In Section 2, we introduce the proposed ZIPFA model first, and then discuss the fitting algorithm and rank selection in the last part of the section. In Section 3, we present simulation studies to compare different methods. The analysis of ORIGINS study and results are in Section 4. Finally, we conclude the paper with discussions in Section 5.

2 |. METHOD

2.1 |. Model setup

In microbiome studies, the absolute sequencing read counts are summarized in a matrix $A\in {\mathbb{N}}_0^{n\times m}$, where n is the sample size and m is the number of taxa. Let A_ij represents the read count of taxon j of individual i (i = 1, …, n; j = 1, …, m). Let N = (N₁, N₂, …, N_n)^⊤ a be vector of the relative library sizes, where

$$N_i=\sum _{j=1}^m{A}_{ij}/\text{median}\left(\sum _{j=1}^m{A}_{1j},\sum _{j=1}^m{A}_{2j},\dots ,\sum _{j=1}^m{A}_{nj}\right).$$

Unlike the absolute library size that depends on the number of measured taxa and sequence depth, the relative library size is scale invariant and performs favorably in numerical studies.

Since excessive zeros may come from true absence or undetected presence of taxa, a mixed distribution is proper to describe A_ij (Sohn and Li, 2018). Previous research points out that it is reasonable to assume each read count A_ij follows a ZIP distribution (Xu et al., 2015):

$$A_{ij}~\{\begin{array}{ll}0,\hfill & \text{with prob}=p_{ij}\hfill \\ \text{Poisson}\left(N_i{\lambda }_{ij}\right),\hfill & \text{with prob}=1-p_{ij},\hfill \end{array}$$

where p_ij (0 ≤ p_ij ≤ 1) is the unknown parameter of the Bernoulli distribution that describes the occurrence of true zeros; λ_ij (λ > 0) is the unknown parameter of the normalized Poisson part, and N_iλ_ij is the Poisson rate adjusted by the subject-specific relative library size N_i. Then let $P=\text{logit}\left(p_{ij}\right)\in {ℝ}^{n\times m}$ and $\Lambda =\text{ln}\left({\lambda }_{ij}\right)\in {ℝ}^{n\times m}$ be the corresponding natural parameter matrices to map parameters p_ij, λ_ij to the real line.

To link the negative relationship between true zero probability p_ij and Poisson rate λ_ij in Figure 1, we propose to use a positive shape parameter τ to build the logistic link by modeling P = −τΛ (ie, logit(p_ij) = −τ ln(λ_ij)). In the setting, ln(λ_ij) and logit(p_ij) are the natural links that linearize the normalized Poisson mean and the Bernoulli probability of true zeros. The probability of A_ij being true zero decreases when λ_ij increases.

To encourage dimension reduction, we assume that matrix $\Lambda \in {ℝ}^{n\times m}$ has a low-rank structure Λ = UV^⊤ with rank K < min(m, n), where $U\in {ℝ}^{n\times K}$ is the score matrix; $V\in {ℝ}^{m\times K}$ is the loading matrix. Then the proposed ZIPFA model with rank K is given by

$$\{\begin{array}{l}{A}_{ij}~\text{ZIP distribution}\hfill \\ \text{logit}\left(p_{ij}\right)=-\tau \text{ ln}\left({\lambda }_{ij}\right)\hfill \\ \text{ln}\left({\lambda }_{ij}\right)=u_{i1}{v}_{j1}+u_{i2}{v}_{j2}+\cdots +u_{iK}{v}_{jK},\hfill \end{array}$$

where u_ij, v_ij are elements of U, V. Here, u_ij represents the jth factor score for the ith individual, and v_ij is the ith taxon loading on jth factor.

Once the factor number K is determined and U, V matrix are estimated, we reduce the dataset dimension from m to K. Score matrix U contains the same sample size as the original dataset A but only K variables. It is much easier to associate the clinical outcomes with the low-dimensional score matrix U through regression analysis. The loading matrix V reflects the composition of the factors in U. Each column in V corresponds to a factor in U and their values show the importance of original taxa in the corresponding factors.

2.2 |. Maximum-likelihood estimation

To begin our discussion, some notation needs to be introduced. Let row vectors a_(i,), u_(i,), v_(i,) denote the ith row of A, U, V. Let column vectors a_(,j), u_(,j), v_(,j) denote the jth column in A, U, V. Let $\tilde{A}$ be the same matrix as A but all 0s are replaced by the column mean.

To estimate the parameters in ZIPFA, we propose to maximize the corresponding total ZIP likelihood L(A):

$$\begin{gathered} L\left(A\right)=\prod _{i,j}L\left(a_{ij};U,V,\tau ,N\right) \\ =\prod _{i,j}\left\{p_{ij}\mathbb{\text{I}}\left(a_{ij}=0\right)+\left(1-p_{ij}\right)\frac{{\left(N_i{\lambda }_{ij}\right)}^{a_{ij}}{e}^{-N_i{\lambda }_{ij}}}{a_{ij}!}\right\}, \end{gathered}$$ (1)

where $\text{ln}\left({\lambda }_{ij}\right)=\sum _{k=1}^K{u}_{ik}{v}_{jk}$ and $\text{logit}\left(p_{ij}\right)=-\tau \text{ ln}\left({\lambda }_{ij}\right)$.

In this expression, the scale parameter τ, the factors U and their scores V are all unknown, which makes direct likelihood maximization over all the unknown parameters prohibitive. Hence, we consider an alternating maximum-likelihood algorithm within the generalized linear model (GLM) framework. Specifically, assuming matrix U is known, we transform the optimization problem into a GLM and find the optimal τ and matrix V that provide maximum L(A); then we fix matrix V and solve for new τ and matrix U that maximize L(A) in a similar GLM. This procedure is repeated to increase the total likelihood L(A) until convergence. Since L(A) has a supremum less than 1, our algorithm is guaranteed to converge. We briefly summarize the model fitting algorithm in the “ZIPFA algorithm” (Algorithm 1) box and its details are in Web Appendix A.

Algorithm 1:

The ZIPFA algorithm

Matrix $A\in {ℝ}^{n\times m}$ is to be decomposed to K factors.

Initialize:

(1) Let $\tilde{A}$ be the same matrix as A but all 0s are replaced by the column mean;

(2) Apply SVD to ln($\tilde{A}$) to obtain the components Uold and Vold.

Update:

(3) Fit zero-inflated Poisson regression with A(u) as the response, U⋆old as the covariates and N(u) as the scaling vector to obtain the estimated Vnew;

(4) Fit zero-inflated Poisson regression with A(u) as the response, V⋆new as the covariates and N(u) as the scaling vector to obtain the estimated Unew;

(5) Apply SVD to Unew VnewT and obtain Uold and Vold;

(6) Repeat from step 3 until convergence.

2.3 |. Zero-inflated Poisson regression

In the ZIPFA algorithm, a special type of ZIP regression has been used in steps 3 and 4 in the “ZIPFA algorithm” (Algorithm 1) box above. Now we will present further discussion about this regression. Let the response variable be Y = (y₁, y, … , y_n)^⊤ (ie, A^(v) or A^(u) in Section 2.2) following a ZIP distribution:

$$Y_i~\{\begin{array}{ll}0,\hfill & \text{with prob}=p_i\hfill \\ \text{Poisson}\left(m_i{\lambda }_i\right),\hfill & \text{with prob}=1-p_i,\hfill \end{array}$$

where m = (m₁, m₂, …, m_n)^⊤ is the known scaling vector (ie, N^(v) or N^(u) in Section 2.2). Let X be an n by p design matrix without intercept column (ie, U^⋆ or V^⋆ in Section 2.2), where column vector X_i denotes the ith row of X; β = (b₁, b₂, …, b_p)^⊤ is the coefficient vector to be estimated (ie, U^s or V^s in Section 2.2).

With the aforementioned relationship between p_i and λ_i, the model satisfies

$$\begin{gathered} \text{ln E}\left(Y_i/m_i\mid X_i\right)=\text{ln}\left({\lambda }_i\right)=X_i^{\top }\beta \text{ and} \\ \text{logit}\left(p_i\right)=-\tau \text{ ln}\left({\lambda }_i\right). \end{gathered}$$

In order to estimate parameters β and τ, we need to write down the likelihood function to maximize it. A latent variable Z = (z₁, z₂, …, z_n) is introduced to indicate whether Y_i is from true zero or not. Define z_i = 1 when Y_i is from true 0; z_i = 0 when Y_i is from Poisson(λ_i) distribution (ie, z_i ~ Bin(1, p_i)). Then the joint likelihood function of Y and Z is as follows:

$$L\left(Y,Z;\beta ,\tau ,X\right)=\prod _{i=1}^n{p}_i^{z_i}{\left\{\frac{{\left(m_i{\lambda }_i\right)}^{y_i}{e}^{-m_i{\lambda }_i}}{y_i!}\left(1-p_i\right)\right\}}^{1-z_i}.$$

Since we introduce a latent variable Z to the expression, it is natural to exploit an expectation-maximization (EM) algorithm for parameter estimation.

E step:

We estimate z_i by its conditional expectation under the current estimates β and τ:

$$\begin{gathered} z_i=\text{E}\left(z_i;\beta ,\tau ,X,Y\right) \\ =\{\begin{array}{ll}\frac{p_i}{p_i+e^{-m_i{\lambda }_i}\cdot \left(1-p_i\right)}\hfill & \text{if }{y}_i=0\hfill \\ 0\hfill & \text{if }{y}_i\ne 0.\hfill \end{array} \end{gathered}$$

When y_i is 0, the conditional expectation of z_i becomes ${\left\{1+\text{exp}\left(\tau X_i^{\top }\beta -m_i{e}^{X_i^{\top }\beta }\right)\right\}}^{-1}$; when y_i is not 0, we know p_i is 0 and thus the conditional expectation of z_i equals to 0.

M step:

Now we need to solve the optimal solution to maximize the conditional expectation of the joint log-likelihood function ln L(Y, Z, β, τ, X) given Y, Z, X. We apply the Levenberg-Marquardt (LM) algorithm in the optimization, for the reason that this algorithm is quite efficient and more robust than the Newton-Raphson method in many cases (Moré, 1978); see Web Appendix B for more technical details.

Finally, we use Frobenius norm of β difference between two iterations to indicate convergence and usually an empirical threshold is 1‰.

2.4 |. Rank estimation

The number of factors K is selected in a data-driven fashion. When prior knowledge about factor number does not exist, we use cross-validation to choose K in practice (Li et al., 2018).

Suppose the candidate rank set is $\mathbb{K}\subset {\mathbb{N}}^{+}$. Let $I_d\in {\mathbb{N}}^{\left(nm\right)}$ be an index set of all elements in A (ie, I_d = (11, 12, …, 1m, …, nm)). Then we randomly divide I_d into r even subsets: $I_d^{\left[1\right]}$, $I_d^{\left[2\right]}$ to $I_d^{\left[r\right]}$. In practice, we usually adopt small r (ie, r = 5) to reduce the probability of the situation that a whole row or column is lost in any subsets. If this happens, we will simply redivide I_d.

Then we calculate likelihood of the model with rank $\kappa \in \mathbb{K}$ in the tth fold (t ∈ r) following the description in Algorithm 2 box. Finally, we sum up the likelihoods of all r folds to obtain the total cross-validation (CV) likelihood of the model with rank κ and calculate the CV likelihood for every rank $\kappa \in \mathbb{K}$. The number of factors κ, which provides the maximum CV likelihood, is the optimal rank.

Algorithm 2:

The ZIPFA cross-validation algorithm in tth fold

Matrix $A\in {ℝ}^{n\times m}$ is to be decomposed to κ factors.

Initialize:

(1) Let $\tilde{A}$ be the same matrix as A but all 0’s and elements corresponding to $I_d^{\left[t\right]}$ are replaced by the column mean of rest values;

(2) Apply SVD to ln $\left(\tilde{A}\right)$ to obtain the components Uold and Vold;

(3) Calculate relative row sum N without elements corresponding to $I_d^{\left[t\right]}$;

(4) Eliminate the elements with index $I_d^{\left[t\right]}$ in A(v) (or A(u)) and note down their locations. Cross out elements in N(v) (or N(u)) on the corresponding location.

Update:

This part remains the same as regular ZIPFA algorithm described before.

CV likelihood:

(5) Obtain Λ(fit) = U(final)V(final)⊤ and calculate P(fit) = −τΛ(fit).

(6) Use the distribution assumption in Section 2.1 to calculate the likelihood of elements in A with index $I_d^{\left[t\right]}$ and sum them up.

3 |. SIMULATION STUDY

In this section, we illustrate the efficacy of our proposed ZIPFA model through a simulation study. We compare our methods with several other singular value decomposition (SVD)-based methods.

3.1 |. Data generation

We generate rank-3 synthetic NGS data of 200 samples (n = 200) and 100 taxa (m = 100) according to the assumption in Section 2.1. The Poisson logarithmic rate matrix Λ = UV^⊤, where $U\in {ℝ}^{m\times 3}$ is a left singular vector matrix, and $V\in {ℝ}^{n\times 3}$ is a right singular vector matrix; see Web Appendix C for data generation in detail. Each row in U corresponds to one sample and each row in V indicates one taxon profile. In Web Figure 1c,d, we applied complete linkage hierarchical clustering to U, V (Eisen et al., 1998). It is clear that both taxa and samples could be clustered into four groups. For settings (1) to (5), we generate matrix A° that $A_{ij}^{°}~\mathit{\text{Poisson}}\left(N_i{\lambda }_{ij}\right)$ where the scaling parameter N_i is set to be 1. Also we need true zero probability p_ij to generate inflated zeros. There are several commonly considered relations between p_ij and λ_ij (Lambert, 1992):

• Setting (1). logit(p_ij) = − τ ln(λ_ij) $\left(p_{ij}=\frac{1}{1+{\lambda }_{ij}^{\tau }}\right)$.

• Setting (2). ln{− ln(p_ij)} = τ ln(λ_ij) $\left(p_{ij}=e^{-{\lambda }_{ij}^{\tau }}\right)$.

• Setting (3). ln{−ln(1 − p_ij)} = τ ln(λ_ij) $\left(p_{ij}=1-e^{-{\lambda }_{ij}^{-\tau }}\right)$.

• Setting (4). ln{−ln(p_ij)} = ln(λ_ij) + ln(τ) $\left(p_{ij}=e^{-\tau {\lambda }_{ij}}\right)$.

Apart from these four linkages, we examine the performance under the setting where each taxon has a fixed true zero probability p_j that is independent of λ_ij (Sohn and Li, 2018):

• Setting (5). p_j ~ Unif(τ − 0.10, τ + 0.10).

In addition, considering that real biological data are some-times over-dispersed, we also explore the simulation settings from Sohn and Li’s (2018) zero-inflated quasi-Poisson latent factor model. Let $A_{ij}^{°}$ to follow a negative binomial distribution with expectation N_iλ_ij and variance $\left(N_i{\lambda }_{ij}+N_i^2{\lambda }_{ij}^2{\varphi }_j\right)$, where ϕ_j is the dispersion parameter. The relationship between true zero probability p_ij and Poisson rate λ_ij is similar to the relationship in setting (4), but it is a positive linkage.

• Setting (6.1). ln{− ln(p_ij)} = − ln(λ_ij) + ln(τ), ϕ_j ~ Unif (0.5, 1.0) (low overdispersion).

• Setting (6.2). ln{2)ln(p_ij)} = − ln(λ_ij) + ln(τ), ϕ_j ~ Unif (1.0, 3.0) (high overdispersion).

For all the settings above, we adjust the total percentage of excessive zeros by setting different τ values. Once p_ij is generated from these settings, our simulated NGS data matrix A can be obtained by replacing $A_{ij}^{°}$ with 0 with the probability of p_ij. Setting (1) is the assumption based on which we develop our model in Section 2 and all the other settings are misspecified situations.

3.2 |. Comparing methods

We compare the proposed method with the following SVD-based methods: (a) log-PCA: We first preprocess the data in a typical way—add a small value (eg, 0.5) to all zeros, and then take a logarithmic value of entries that have been divided by the sum of each row. After that, we apply PCA to the preprocessed matrix. (b) PSVDOS: Poisson singular value decomposition with offset (Lee et al., 2013). This model is based on regular Poisson factor analysis but automatically incorporates sample normalization through the use of offsets. (c) GOMMS: GLM-based ordination method for microbiome samples. This method uses a zero-inflated quasi-Poisson latent factor model and thus is able to handle excessive zeros (Sohn and Li, 2018).

3.3 |. Simulation result

We first check the rank selection performance of our method. In Figure 2, the proposed method provides the maximum CV likelihoods with rank 3 in most settings except for settings (6.1) and (6.2) where the optimal rank is 2. It shows that our method is quite accurate and robust in rank estimation and may underestimate when the model assumption is severely violated.

FIGURE 2. Cross-validation to choose the rank in our simulation. Our method provides maximum CV likelihoods with rank 3 under most simulations settings.

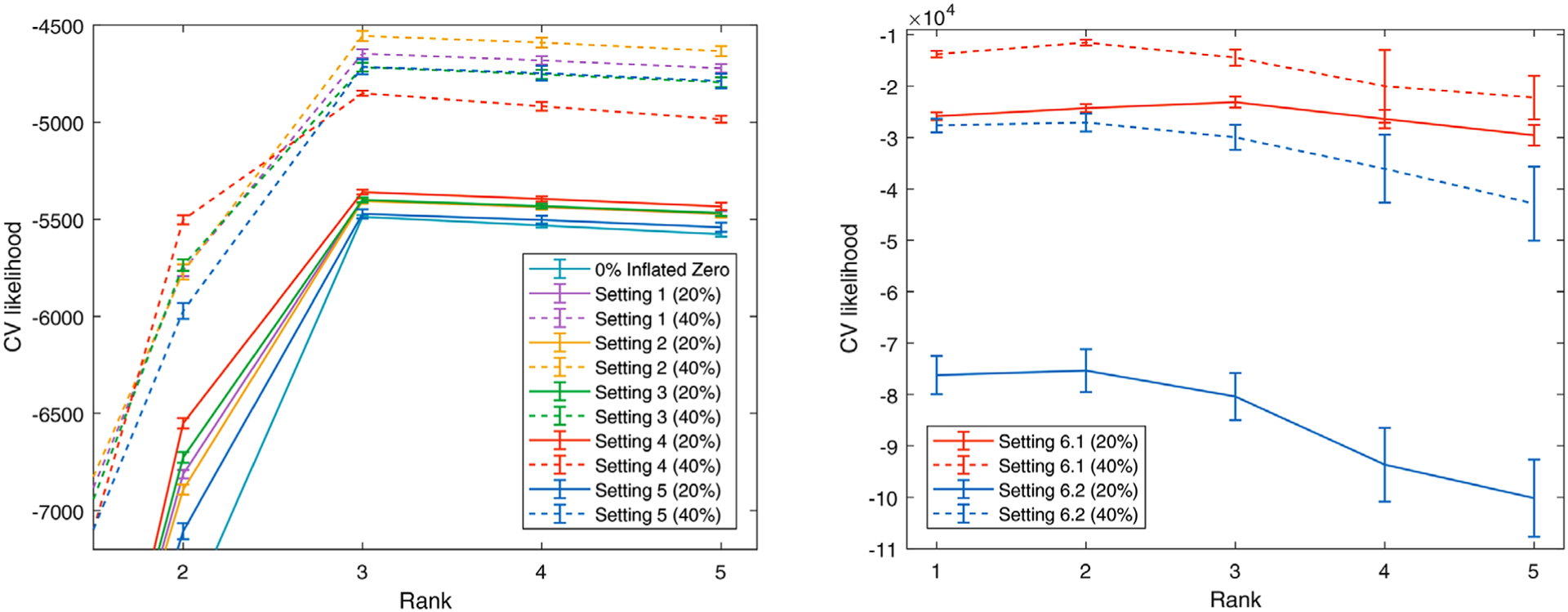
Note. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

Then we compare ZIPFA with other models. For all models, we set their ranks to the true rank 3. GOMMS some-times has diverged results under some situations, so for each simulation setting, we will conduct enough simulation runs to get at least 200 converged results. The method performances are evaluated by the Frobenius norm of error matrix and the clustering accuracy that represents the proportions of taxon/sample that are properly clustered:

$${\text{L}}_2\text{ loss}={\Vert \widehat{U}{\widehat{V}}^{\top }-\Lambda \Vert }_F^2$$

$$\begin{gathered} \text{Clustering accuracy} \\ =\frac{\#\text{ of properly clustered taxa/samples}}{\#\text{ of total taxa/samples}\left(\text{ie, }100\text{ taxa/}200\text{ samples}\right)}, \end{gathered}$$

where $\widehat{U}$, $\widehat{V}$ are estimated score and loading matrices; Λ is the true natural parameter matrix in the simulation.

In Table 1, we list the L₂ loss and the clustering accuracy of taxa and samples under different settings. When there are no true zeros mixed in the data, all four methods have similar performance and are able to separate the underlying clusters. Regarding to the L₂ loss, in the first four settings, when true zero percent is low (20%), all three methods significantly outperform the log-SVD approach, which does not account for the underlying distribution and excessive zeros. When the zero percentage reaches a higher level (40%), PSVDOS becomes worse because it could only capture the Poisson part of the data. ZIPFA has lower or comparable L₂ loss comparing to GOMMS. In setting (5), GOMMS only outperforms ZIPFA when the zero percentage is high (40%) because this setting essentially favors GOMMS by using independent λ_ij and p_ij. In settings (6.1) and (6.2), since the inflated zero probability is positively related with Poisson rate, we obtain negative estimated τ values in our proposed method. Among four methods, log-SVD is always the worst. When the true zero probability is low (20%), ZIPFA, PSVDOS, and GOMMS have comparable performance and GOMMS has insignificant smaller L₂ loss. When the true zero probability is high, our method outperforms all the other methods. As for the clustering results, the proposed method is much more appealing than others in the first five settings. In settings (6.1) and (6.2), log-SVD and our method have the best performance, while GOMMS and PSVDOS fail to recover the clustering information in many cases. Overall, our method performs favorably compared to the competing methods even under overdispersed and/or misspecified simulation settings.

TABLE 1.

Comparison of four methods under different settings

	Zero (%)	ZIPFA		Log-SVD		PSVDOS		GOMMS
L2 loss
	0%	2.35	(1.75)	2.85	(0.22)	2.15	(0.15)	4.47	(0.39)
Setting (1)	20%	4.53	(0.38)	32.84	(1.56)	7.07	(0.67)	6.20	(0.67)
	40%	12.44	(2.18)	171.16	(4.57)	33.93	(2.57)	47.21	(8.82)
Setting (2)	20%	3.94	(0.34)	37.65	(1.79)	7.65	(0.78)	5.60	(0.58)
	40%	28.37	(6.14)	210.88	(4.42)	41.32	(4.59)	26.74	(6.87)
Setting (3)	20%	5.10	(0.41)	29.89	(1.43)	6.74	(0.46)	7.25	(0.77)
	40%	8.99	(1.29)	144.85	(3.93)	30.35	(2.46)	8.14	(0.92)
Setting (4)	20%	7.62	(1.43)	26.56	(1.26)	7.84	(0.54)	10.79	(1.17)
	40%	18.96	(2.63)	95.66	(2.99)	32.34	(1.49)	21.10	(2.64)
Setting (5)	20%	5.16	(0.73)	46.67	(3.25)	11.26	(1.91)	5.29	(0.46)
	40%	18.35	(3.04)	178.06	(7.09)	36.65	(7.33)	6.23	(0.61)
Setting (6.1)	20%	54.30	(3.86)	158.55	(4.09)	55.91	(4.16)	49.64	(16.73)
	40%	108.38	(5.61)	425.31	(4.88)	210.84	(12.82)	475.17	(46.67)
Setting (6.2)	20%	52.50	(3.46)	87.89	(4.29)	32.89	(1.76)	30.50	(2.08)
	40%	111.62	(5.32)	375.38	(6.31)	144.68	(6.80)	256.66	(39.89)
Clustering accuracy by taxa/samples
	0%	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Setting (1)	20%	1.00	1.00	1.00	1.00	1.00	1.00	0.92	1.00
	40%	1.00	1.00	0.91	0.97	0.98	0.86	0.87	1.00
Setting (2)	20%	1.00	1.00	1.00	1.00	1.00	1.00	0.95	1.00
	40%	1.00	1.00	0.66	0.72	0.92	0.77	0.92	1.00
Setting (3)	20%	1.00	1.00	1.00	1.00	1.00	1.00	0.91	1.00
	40%	0.99	1.00	0.99	1.00	0.99	0.94	0.82	1.00
Setting (4)	20%	1.00	1.00	1.00	1.00	1.00	1.00	0.84	1.00
	40%	0.96	1.00	1.00	1.00	1.00	1.00	0.73	1.00
Setting (5)	20%	1.00	1.00	0.99	0.99	1.00	0.91	0.99	1.00
	40%	1.00	1.00	0.77	0.83	0.94	0.82	0.93	1.00
Setting (6.1)	20%	0.86	0.79	0.94	1.00	0.77	0.63	0.48	0.44
	40%	0.65	0.93	0.71	0.75	0.39	0.37	0.41	0.34
Setting (6.2)	20%	0.86	0.62	1.00	0.99	0.92	0.64	0.84	0.69
	40%	0.77	0.73	0.69	0.94	0.48	0.42	0.35	0.34

Note. The best results in each setting are in boldface.

Then in Figure 3, we further explore the performance of the different models for simulated data with different percentages of inflated zeros under setting (1). A typical example of how the fitted results of different models change with increasing inflated zero percentage is shown in Web Appendix D.

FIGURE 3. L₂ loss versus true zero percentage in setting (1).

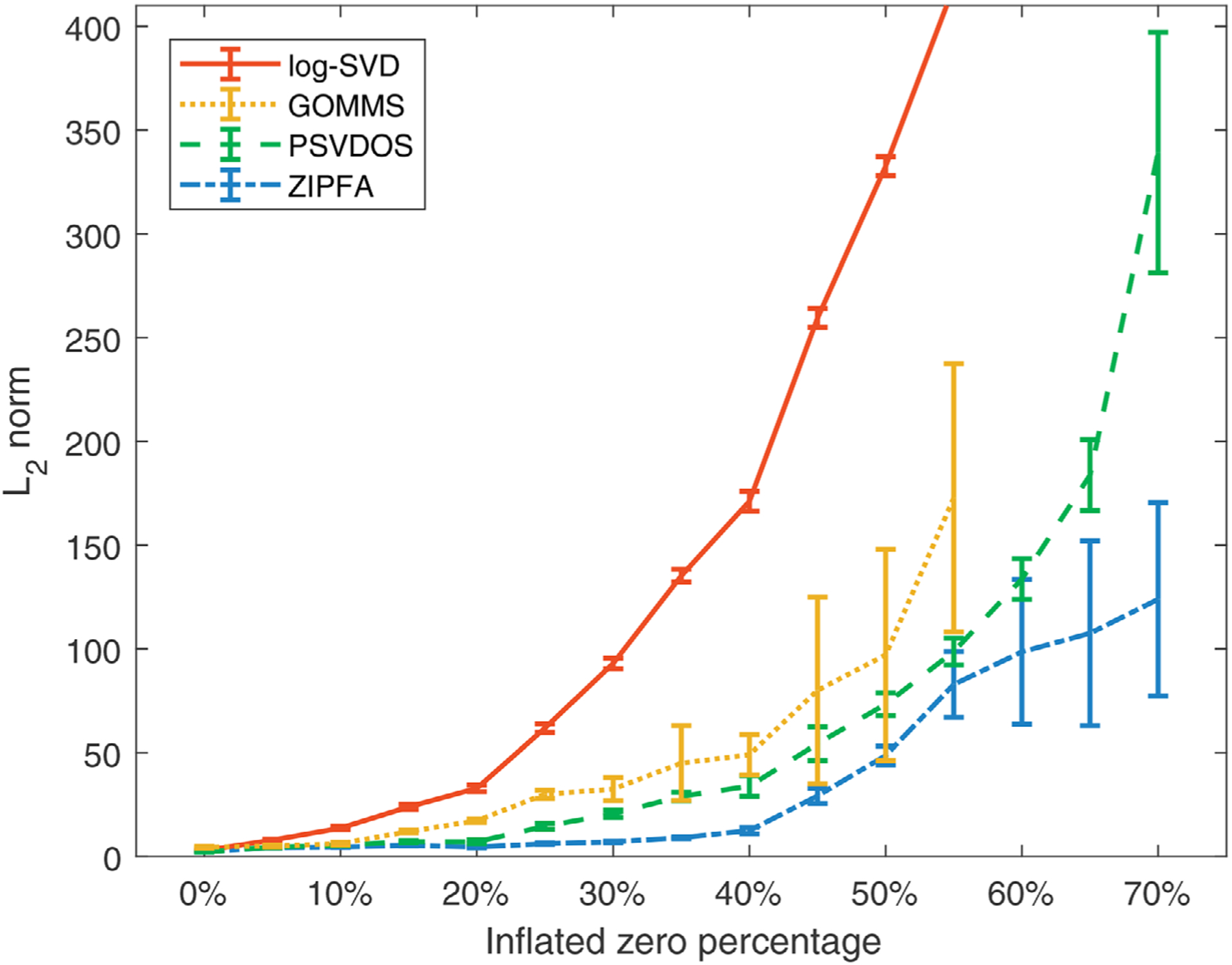
Note. Lower values indicate more accurate fitted results. GOMMS fails to converge when inflated zero percentage exceeds 55%. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

In addition, our proposed ZIPFA has favorable convergence property that it successfully converges within moderate iterations in all simulated situations. GOMMS achieves convergence only for 55%, 52%, 59%, and 71% of the total trials in the first four settings at low zero percentage. When more than half of the data are inflated zeros, we note that GOMMS fails to converge most of the time (>80%).

4 |. APPLICATION TO ORIGINS

4.1 |. Origins data

ORIGINS is a longitudinal cohort study that aims to investigate the cross-sectional association between periodontal microbiota, inflammation, and insulin resistance (Demmer et al., 2015). In this paper, we will focus on the relationship between subgingival microbial community composition and periodontal disease and identify the bacterial genera associated with some disease indicators.

From February 2011 to May 2013, 300 men and women who met the inclusion criteria were enrolled (Demmer et al., 2015). In total, 1,188 subgingival plaque samples (4 samples from 297 participants) were collected from the most posterior tooth per quadrant and were analyzed using the Human Oral Microbe Identification Microarray to measure the abundances of 379 taxa (Demmer et al., 2017). Trained calibrated dental examiners assessed full month attachment loss, probing depth and bleeding on probing at six sites per tooth with a UNC-15 manual probe (Hu-Friedy). Other controlled variables include gender, age, ethnicity, education status, BMI, and smoking history.

4.2 |. Result

We applied 10-fold cross-validation on the data. Web Figure 3 shows that CV likelihood reaches the maximum point at rank equal to 5, so we will use five factors in the following analysis.

We fit a rank-5 ZIPFA to the absolute microbiome data. The algorithm converges after seven iterations (likelihood change <1‰) in 30 seconds (Matlab R2017a, i9–7900X with 32GB memory). The proposed model gives us the estimated score and loading matrix. With such information, we are able to recover the Λ, P matrix according to the model assumption in Section 2.1. The total estimated probability of being zero for each count is ${\widehat{p}}_{ij}+e^{-{\widehat{\lambda }}_{ij}}$. We reorder the larger values in total zero probability matrix to top left, and put the smaller values to bottom right. The heatmap of reordered total zero probability is plotted in Figure 4A and the true data with the same rearrangement are in Figure 4B. We compare the predicted probability of zeros with real data zero distribution to examine the level of similarity. A good resemblance indicates that our methods well captures the structure of the excessive zeros.

FIGURE 4. Comparison of predicted probability of zeros and real zero distribution in the dataset.

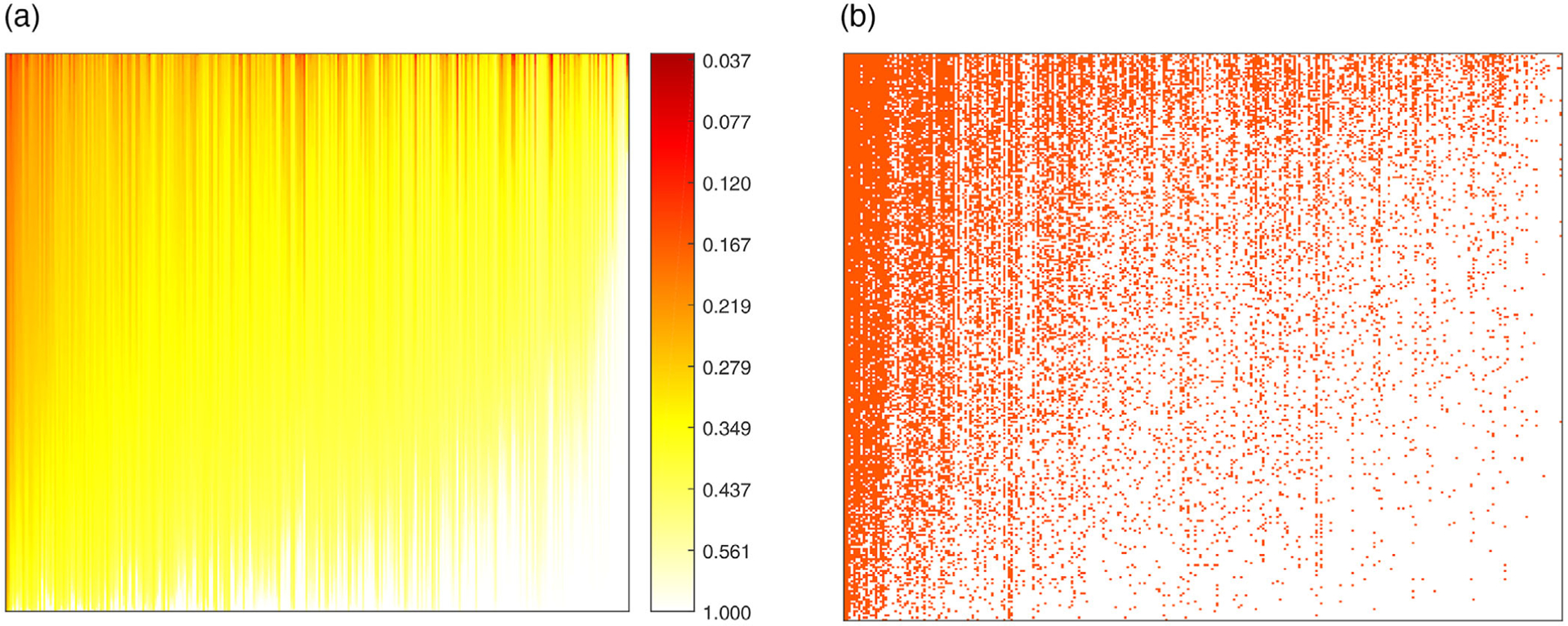
Note. (a) Heatmap of predicted zero probability. (b) Heatmap of the binary real data value. Red points are non-zero values and white points are zeros. Both heatmaps are rearranged in the same row and column ordering. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

In order to find the association between five factors obtained by ZIPFA and three responses (full mouth mean attachment loss, mean probing depth, and bleeding on probing), we fit linear models. In each model, a response variable is regressed on all five factors and six additional covariates including gender, age, ethnicity, education status, BMI, and smoking history. In Web Table 1, P-values corresponding to different factors and response variables are listed. As a comparison, we also demonstrate the result of other methods that we introduce in Section 3.2 including log-SVD, PSVDOS, GOMMS, and two widely used traditional methods including principal coordinates analysis (PCoA) and non-metric multidimensional scaling (nMDS) on Bray-Curtis distance (Bray and Curtis, 1957). nMDS in this case fits the data quite well with stress score 0.098 (Shepard stress plot is in Web Figure 4). The major drawback of PCoA and nMDS is that they are only useful for dimension reduction and data visualization, but cannot identify the explicit relations between the reduced factors and the original taxa. In other words, they cannot provide “loadings” as in a factor model. We observe ZIPFA, log-SVD, PCoA, and nMDS provide significantly associated factors with each response while PSVDOS and GOMMS fail to find a significant factor for “full mouth mean attachment loss.” In particular, factors 2, 3 in our proposed method are significant predictors of all these periodontal disease indicators, which may imply a potential link in oral microbiome composition and periodontal disease.

Due to the nature of distance-based ordination methods, PCoA and nMDS do not help to select taxa that are potentially relevant to periodontal diseases. For the rest of the methods, we further look into the loading vector corresponding to the significant factors to identify important taxa related to periodontal disease. In previous literature, many researchers have studied the associations between subgingival microbiota and periodontal disease. To identify clinically meaningful taxa in the literature, we first searched “microbiome” and “periodontal disease” in “Clinical Queries: Systematic Reviews” on PubMed (National Institutes of Health, 2019) and excluded articles that are not for human beings, studies after inter-vention treatment or focus on other biomarkers instead of taxon species. It turned out that three comprehensive reviews reach our goal. Guerra et al. (2018) examined 170 papers from “Pubmed” and “Scopus” and pointed out three significantly associated taxa: Porphyromonas gengivalis, Theileria mutans, and Aggregatibacter actinomycetemcomitans. Patini et al. (2018) examined 739 articles from “Pubmed,” “Scopus,” “Central” database, and “Web of Science” and listed three associated taxa groups with some, moderate, or strong evidence. We chose taxa in high and moderate evidence group (>3 pieces of evidence) as clinically meaningful taxa. Mendes et al. (2015) examined 440 articles from “Pubmed,” “Scopus,” and “Web of Science” and determined five significantly significant taxa: A. actinomycetemcomitans, Tannerella forsythia, Prevotella intermedia, Capnocytophaga ochracea, and Campylobacter rectus. We plot the absolute loadings of all taxa on the most significant associated factor of ZIPFA and log-SVD in Figure 5 and on the two most significant factors of all four methods in Web Figure 5. The taxa that are potentially clinically meaningful are marked in red (positive association) and green (negative association). Conceptually, those taxa should have large absolute loading values corresponding to the significant factors. In Figure 5, clearly, for ZIPFA, clinically meaningful taxa tend to concentrate on the left with large loading values while for log-SVD, they are more scattered (see Web Table 2 for more details). A permutation test of the mean ranks of the relevant taxa further shows that the difference is significant (P-value = 9.52 × 10⁻⁵). Namely, the result from our method is more consistent with the literature. Similarly, in Web Figure 5, we see that ZIPFA separates the clinically meaningful taxa with larger absolute loadings. Log-SVD fails to pick out most negative associated taxa, and rest of the methods have inferior results as well. Our method also suggests that further investigation into the following taxa is justified: Lachnoanaerobaculum sp. HOT 083, Leptotrichia sp. HOT 219, Neisseria pharyngis, and Prevotella melaninogenica.

FIGURE 5. Absolute taxa loadings on the most significant factor.

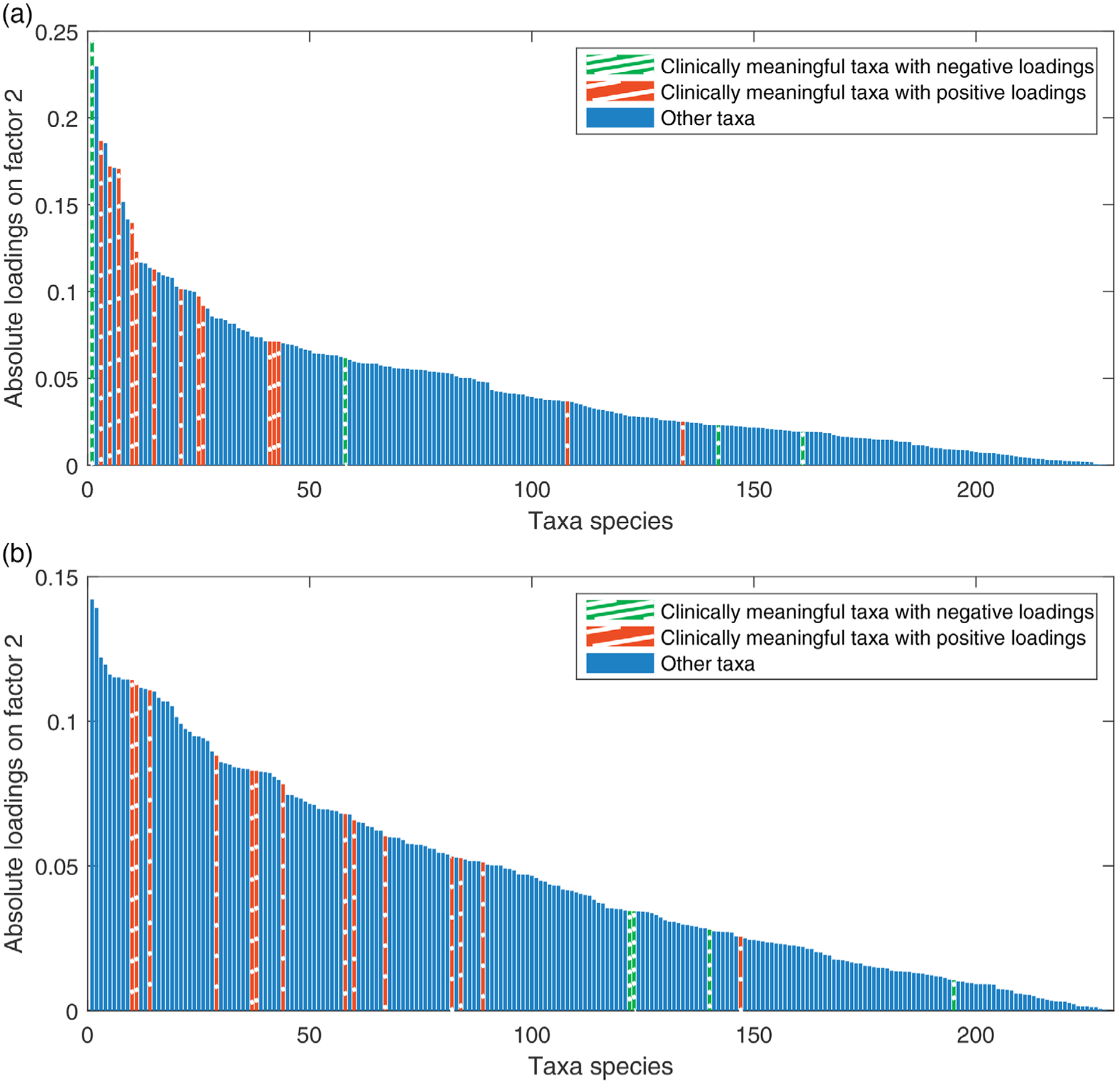
Note. Each bar is a loading value of the factor. Blue or red bars are clinically meaningful taxa in published literature. (a) Loadings on factor 2 of our proposed ZIPFA. (b) Loadings on factor 2 of log-SVD. This figure appears in color in the electronic version of this paper, and any mention of color refers to that version.

5 |. DISCUSSION

Dimension reduction is a common feature of many microbiome analytical workflows (Cao et al., 2017). This paper presents an new method of factor analysis that takes the distribution of counts into full consideration. The proposed model includes one shape parameter (τ) to link the true zero probability and Poisson expectation and achieves satisfactory fitting on the data. In addition, the ZIP regression proposed in Section 2.3 is a new method in zero-inflated regression analysis. We also develop a new CV approach for estimating the rank of the underlying natural parameter matrix. In the ORIGINS analysis, the proposed method identifies microbial profiles that are significantly associated with clinical outcomes and generates new scientific hypotheses for lab research.

There are several future research directions worth studying. While the method is developed for count data in microbiome studies, this idea can be extended to other situations. For example, a ZINB distribution can be considered when the data has extra dispersion (Srivastava and Chen, 2010). We can also change the logistic link function to others if the relationship between logit(p_ij) and ln(λ_ij) is not linear. But how to choose the best link still remains a question. In addition, we can reduce the computation cost of ZIPFA by further optimizing the EM algorithm in the future.