Machine Learning for Rapid Magnetic Resonance Fingerprinting Tissue Property Quantification

Abstract

Magnetic Resonance Fingerprinting (MRF) is an MRI-based method that can provide quantitative maps of multiple tissue properties simultaneously from a single rapid acquisition. Tissue property maps are generated by matching the complex signal evolutions collected at the scanner to a dictionary of signals derived using Bloch equation simulations. However, in some circumstances, the process of dictionary generation and signal matching can be time-consuming, reducing the utility of this technique. Recently, several groups have proposed using machine learning to accelerate the extraction of quantitative maps from MRF data. This article will provide an overview of current research that combines MRF and machine learning, as well as present original research demonstrating how machine learning can speed up dictionary generation for cardiac MRF

I. Introduction

THE Magnetic Resonance Imaging (MRI) signal is sensitive to a variety of tissue properties, including the relaxation time constants T₁ and T₂, diffusion, perfusion, and many others. Most clinical MRI scans are qualitative, meaning the signal is weighted by one or more of these tissue properties. However, the signal intensity at each pixel is not a direct measurement of any tissue property, and consequently the images must be interpreted subjectively. Quantitative MRI, which involves measuring tissue properties on an absolute scale, has recently become more feasible for clinical use due to advances in acquisition and reconstruction methods. Quantitative images, also called maps, can be interpreted objectively and may indicate pathological changes earlier compared to qualitative images [1], [2].

Magnetic Resonance Fingerprinting (MRF) is a technique for quantifying several tissue properties simultaneously [3]. MRF uses a time-varying pulse sequence that causes tissues to produce characteristic signal evolutions depending on their tissue property values, much like a fingerprint. Quantitative maps are reconstructed by matching measured signal evolutions to a dictionary of simulated signals. MRF scans can be highly accelerated because signal matching is robust to incoherent aliasing artifacts.

Although MRF is promising, in some circumstances the process of dictionary generation and signal matching is slow and memory-intensive, which could limit its practical utility. This article will present an overview of quantitative imaging and MRF, followed by a review of state-of-the-art methods that employ machine learning for MRF dictionary generation and signal matching. Finally, a novel application of neural networks will be presented for rapid dictionary generation in cardiac MRF [4]. The article will mainly discuss MRF for T₁ and T₂ quantification, which has been the focus in machine learning research.

II. Traditional Methods for Quantitative MRI

Quantitative MRI methods produce maps where every pixel represents an absolute measurement of a tissue property, such as T₁ or T₂. Traditionally, maps are generated by sequentially acquiring images with different T₁ or T₂ weighting. For instance, images may be collected at different time points after an inversion or saturation pulse to vary the T₁ contrast or with different echo times after a 90° excitation to obtain different T₂ contrast. Then the signal intensity at each pixel is fit to a simple model, such as exponential recovery for T₁ or exponential decay for T₂, to extract a quantitative map. Traditional mapping sequences often suffer from long scan times, which may be uncomfortable for patients and limit scan throughput. They also increase the likelihood of motion artifacts arising from bulk patient movement, respiration, cardiac motion, peristalsis, or flow. Additionally, conventional techniques only measure one tissue property per scan, so maps of different properties may not be spatially registered.

Quantitative methods must also address issues of accuracy, precision, and reproducibility. Different pulse sequences, image reconstruction techniques, or signal models may result in the measurement of different values for the same tissue property. Even the same method may produce different measurements across scanners if it is sensitive to confounding effects that are not accounted for in the signal model. For example, Modified Look-Locker Inversion Recovery (MOLLI) is routinely used in the clinic for cardiac T₁ mapping, but it is also influenced by T₂, off-resonance, magnetization transfer, and heart rate [5], [6]. For this reason, it is recommended to acquire baseline MOLLI T₁ measurements for every scanner [7]. The lack of standardization is a barrier for many conventional quantitative techniques.

III. Overview of Magnetic Resonance Fingerprinting

Magnetic Resonance Fingerprinting (MRF) is a novel technique for quantitative MRI which could potentially address some of the shortcomings of traditional quantitative methods. This section will describe the basic mechanics of MRF and its potential advantages over other techniques. Fig. 1 and 2 summarize the key components of MRF data acquisition and reconstruction, with a focus on T₁ and T₂ quantification. Each step will be described in detail in the following sections.

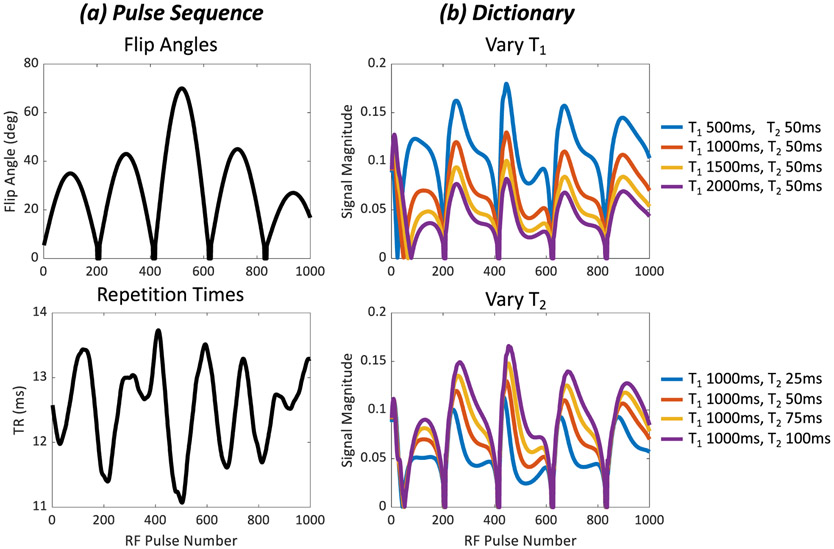
Fig. 1.

Representative MRF pulse sequence and signal evolutions. The example shown is taken from MRF with a FISP readout. In general, the FISP signal is influenced by the flip angle, repetition time, T₁, and T₂ [77]. (a) Varying the flip angles and repetition times sensitizes the MRI signal to both T₁ and T₂. (b) Simulated signal evolutions are stored in a dictionary. The top panel shows signals where T₂ is fixed at 50ms while T₁ is varied from 500ms to 2000ms. The bottom panel shows signals with T₁ fixed at 1000ms while T₂ is varied from 25ms to 100ms.

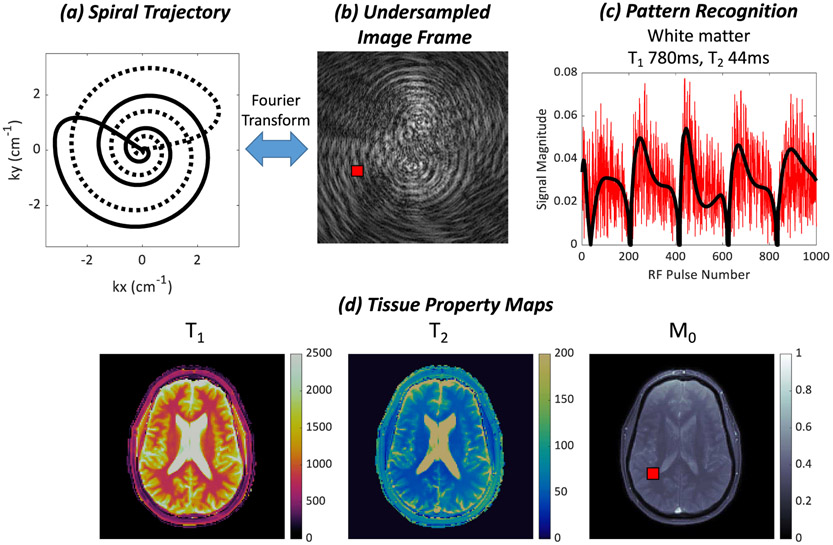
Fig. 2.

(a) MRF data are typically sampled in k-space with a variable density spiral trajectory. The trajectory rotates every TR to sample different parts of k-space, as indicated by the solid and dotted lines. (b) Each image frame is highly undersampled and corrupted by aliasing artifacts. (c) A measured signal evolution from a region in white matter, indicated by the red square in (b) and (d), is plotted in red. The signal is corrupted by noise-like interference due to the undersampling in k-space. The closest matching fingerprint in the dictionary found by dot product matching is plotted in black. (d) Quantitative maps of T₁, T₂, and M₀ are obtained by matching the signal evolution at each pixel to the dictionary.

A. MRF Pulse Sequence

Although many different pulse sequences could be used in conjunction with MRF, all MRF pulse sequence described in the literature use acquisition settings that change throughout the scan (Fig. 1A). MRF pulse sequences deliberately keep signals in a persistent transient state to better distinguish tissues with different T₁ and T₂ values. This approach differs from standard mapping techniques that are mainly limited to producing signals with exponential forms. It also differs from qualitative scans, which are typically used to acquire images after signals have reached steady state. A well-designed MRF sequence uses changing pulse sequence settings to enhance the sensitivity to T₁ and T₂ so that spins with different T₁ and T₂ values will produce measurably different signal evolutions. Similar to human fingerprints, which can be used to identify a unique individual, the measured signal evolution can be used to identify the underlying tissue property values. MRF sequences have many degrees of freedom. They may employ variable flip angles, repetition times (TR), and echo times (TE). Some sequences additionally use magnetization preparation pulses with variable timings, such as inversions or T₂ preparations, to enhance T₁ and T₂ sensitivity. Different imaging readouts have been proposed, including balanced steady-state free precession (bSSFP) [3], fast imaging with steady-state precession (FISP) [8], pseudo steady-state free precession (pSSFP) [9], and quick echo splitting (QUEST) [10].

B. Data Sampling

MRF k-space data are collected at a high temporal resolution in order to characterize the time-varying signal evolutions. Whereas standard mapping sequences collect a handful of high-quality images with different T₁ or T₂ weighting, MRF rapidly acquires hundreds to thousands of highly undersampled images. For instance, the original MRF work employed a variable density spiral k-space trajectory that required 48 interleaves to fully sample the edges of k-space and one interleaf to fully sample the central area of k-space. In many MRF implementations, one undersampled image is collected during a single-shot k-space readout every TR, or roughly every 5-15ms. MRF data are typically sampled using non-Cartesian trajectories (Fig. 2A). The original MRF work used spiral sampling, although radial [9], rosette [11], echo planar imaging (EPI) [12], and other trajectories [13] are also employed. Non-Cartesian trajectories are used for their beneficial properties, including incoherent aliasing when undersampled (Fig. 2B) [14], frequent sampling of the k-space center, robustness to motion [15], [16], and efficient k-space coverage (for spiral) [17]. The trajectory is rotated every TR, often by the golden angle [18], to distribute aliasing artifacts incoherently through time. The artifacts manifest as a noise-like interference superimposed on the signal evolution that ideally does not impede pattern recognition (Fig. 2C). The signal evolution at one voxel location from the aliased image series is referred to as a “fingerprint.”

C. MRF Dictionary

The MRF dictionary is a lookup table of simulated signal evolutions for different tissue property values (Fig. 1B). Dictionaries may be generated using a Bloch equation simulation or extended phase graphs [19]. The only knowledge needed to build the dictionary are the pulse sequence parameters (flip angles, TRs, etc.) and a discrete set of tissue property values which may be found in the measurement data. The tissue property values are selected to cover the expected physiological range, but the total number is limited to save computation time and memory. In most applications, the dictionary is precomputed and reused for all scans, provided the sequence parameters do not change.

D. Pattern Recognition

The final step in the MRF workflow is to compare the measured signal evolutions with the dictionary to extract quantitative maps (Fig. 2D). Dot product matching was the original and simplest method for signal matching in MRF [3]. First, all dictionary entries and measured signal evolutions are divided by their l₂-norms to place them on a similar scale. Next, the dot product is computed between each measured signal and the entire dictionary. Note that MRF signals are generally complex-valued. The dictionary entry that maximizes the absolute value of the dot product is identified as the best match. This process is repeated for each pixel to generate T₁ and T₂ maps. Proton spin density is calculated as the complex coefficient needed to scale the measured signal to its matching fingerprint in the dictionary. More advanced matching techniques have been proposed to mitigate artifacts or reduce scan time using compressed sensing [20], multiscale reconstructions [21], or low-rank matrix completion [22]-[25]. Many of these techniques are iterative and come at the expense of longer reconstruction times.

E. Potential Benefits of MRF over Conventional Quantitative Approaches

One advantage of MRF is that confounding tissue or system properties, which could lead to errors in the quantitative maps if ignored, can be integrated in the dictionary. For example, slice profile imperfections, off-resonance frequency, and ${\mathrm{B}}_1^{+}$ can be explicitly modeled in the Bloch equation simulations [26], [27]. Previous studies have shown that MRF yields accurate T₁ and T₂ measurements in a variety of applications including brain [28]-[31], cardiac [4], abdominal [32], breast [33], musculoskeletal [34], and ocular [35] imaging. T₁ and T₂ measurements using FISP-MRF are reproducible over time [36] and on different MRI scanners at multiple sites in phantom studies [37]. Repeatability studies have been performed using MRF for brain [38] and breast [39] imaging. Looking to the future, cross-vendor and multi-center studies using MRF are needed to ensure the repeatability of measurements made across a variety of MRI scanners. The effect of other phenomena on MRF measurements—such as diffusion, chemical exchange, or magnetization transfer—are less well-studied. However, the incorporation of more complex physical models into the MRF framework could enable measurement of such properties and is an active area of research [40], [41].

IV. Machine Learning and MRF Dictionary Generation

While MRF is a powerful approach to quantitative MRI, MRF does suffer from a number of practical challenges which could be alleviated by the use of machine learning. The two primary areas where machine learning has been applied are the dictionary generation and pattern recognition steps. A summary of recent machine learning methods for MRF is provided in Table I, and each will be discussed in more detail in the following sections. This section begins by describing practical issues with dictionary generation and then summarizes recent work using machine learning to address these problems.

TABLE I.

Summary of recent machine learning approaches for MRF. For each method, the table provides the MRF application (dictionary generation or signal matching), network architecture, the type of data used for training and testing the network, the k-space sampling used to acquire or simulate the training and testing data, and key results reported in the literature.

Method	MRF Application	Network Architecture	Training Data	Testing Data	k-space Sampling	Key Results	Other Notes
MRF-GAN [56]	Dictionary generation	Generative adversarial network (GAN) [55]	Simulated signals	In vivo (brain)	Undersampled spiral	~1000x faster than Bloch equation simulation (7s vs 2hr)	Dictionary included slice profile correction
Neural Network for Cardiac MRF	Dictionary generation	Fully-connected feedforward	Simulated signals with different cardiac rhythms	Simulations, phantom, and in vivo (cardiac)	Undersampled spiral	197x faster than Bloch equation simulation (0.8s vs 158s)	Dictionary included corrections for slice profile and preparation pulse efficiency
DRONE [60]	Signal matching	Fully-connected	Simulated signals with added Gaussian noise	Simulations, phantom, and in vivo (brain)	EPI and undersampled spiral	Faster than dot product matching (10ms vs 3s for EPI; 76ms vs 380s for spiral); More robust to noise than dot product matching
Empirical Artifact Noise Model [65]	Signal matching	Fully-connected	Simulated signals, with added aliasing “noise” from in vivo scans	In vivo (brain)	Undersampled spiral	Robust to aliasing artifacts; Can directly output contrast-weighted images
Complex-Valued Neural Nets [66]	Signal matching	Fully-connected	Simulated signals with added Gaussian noise	Simulated signals with added Gaussian noise	N/A	More accurate signal matching than real-valued network
Deep Learning for MRF [62]	Signal matching	Convolutional neural network (CNN)	Phantom and in vivo (brain)	Phantom and in vivo (brain)	Undersampled spiral	Faster than dot product matching (7-10x using CPU, 47x using GPU)
MRF-CNN [68]	Signal matching	Convolutional neural network (CNN)	Simulated signals with added Gaussian noise	Simulated signals with added Gaussian noise	N/A	More accurate than dot product matching, especially for T2
Spatially-Constrained Quantification [61]	Signal matching	Fully-connected layers followed by U-net [78]	In vivo (brain)	In vivo (brain)	Undersampled spiral	Shorten scan time 4x (23s to 6s) with comparable map quality; 6x faster reconstruction than dot product matching (2.3s vs 14.2s)

A. Practical Challenges

1). Dictionary Simulation Time and Size:

When generating a dictionary with a Bloch equation simulation, processing time scales linearly with the size of the dictionary—that is, the sequence length (number of TRs) and the number of unique combinations of tissue properties for which signal evolutions must be calculated. The total number of signal evolutions Q in a dictionary can be approximated as

$$Q\approx {\prod }_{i=1}^p{N}_i$$ (1)

where N_i is the number of discrete values for tissue property i and p is the number of tissue properties. This formula is an approximation because some tissue property combinations are excluded if they do not occur physiologically, such as T₂ > T₁.

As seen in (1), the dictionary size expands exponentially with the number of tissue properties to be included in the dictionary. Computation time and memory requirements are manageable when the number of tissue properties is small. For example, the FISP-MRF dictionary presented in [8] contains 18,838 fingerprints each with 1000 time points. Here, only the effects of T₁ and T₂ are modeled, as FISP is relatively insensitive to off-resonance frequency, and diffusion effects are ignored for simplicity [42], [43]. However, the dictionary becomes impractically large with more tissue property dimensions. A variation of bSSFP-MRF has been proposed for the simultaneous quantification of T₁, T₂, ${\mathrm{T}}_2^{\ast }$, off-resonance frequency, and intravoxel phase dispersion, which uses a dictionary containing 30 million signals [44]. An application with an even larger dictionary is MRF with intercompartment water exchange (MRF-X) [45]. MRF-X has been proposed to measure relaxation times in two subvoxel compartments (for example, intracellular and extracellular spaces), the volume fraction of each compartment, and the rate of intercompartment water exchange. The MRF-X dictionary has six tissue properties and contains over 500 million signal evolutions with 3000 time points.

Dictionary size also grows when there is a high sampling density along each tissue property dimension. Unlike curve fitting, which produces continuous outputs, the dictionary is simulated at discrete values. Quantization errors in the maps will be more pronounced if the tissue property dimensions are sampled too coarsely. In practice, an intermediate sampling density is chosen to reduce quantization error while also keeping the dictionary to a reasonable size. For example, a typical FISP-MRF dictionary for neuroimaging may have possible T₁ values 20-3000ms (increment 10ms) and 3000-5000ms (increment 200ms), and T₂ values 10-300ms (increment 5ms) and 300-500ms (increment 50ms) [8].

2). Corrections for System Imperfections:

Additional relevant signal dependencies beyond T₁ and T₂ can be modeled in the dictionary calculation step to better describe the behavior of the magnetization, thereby improving accuracy and reproducibility of MRF maps. For instance, RF transmit inhomogeneities (${\mathrm{B}}_1^{+}$), which cause spatially dependent deviations from the expected flip angle, can be included in the signal model [46], [47]. However, this leads to an additional ${\mathrm{B}}_1^{+}$ dimension that must be included in the dictionary, leading to long calculation times and large dictionary sizes. Plug-and-play (PnP) MRF extends this concept further using multiple complementary transmit coil modes to improve the robustness to ${\mathrm{B}}_1^{+}$ at high field [48]. Here, the tradeoff for the improved accuracy in T₁ and T₂ mapping is increased dictionary size, since there is additional ${\mathrm{B}}_1^{+}$ dimension for each transmit channel.

Other corrections use complex physical models that do not change the dictionary size but still require longer to simulate. For example, slice profile correction is implemented by performing a separate Bloch equation simulation for spins at different distances from the slice center [46], [49]. Then the corrected dictionary is obtained by summing the signals over the slice dimension. Another example of a correction that requires more computation time is preparation pulse efficiency [50]. Magnetization preparation pulses, such as inversions and T₂ preparations, are usually implemented with adiabatic pulses due to their insensitivity to B₀ and ${\mathrm{B}}_1^{+}$ inhomogeneities [51]. However, these pulses have long durations during which T₂ relaxation occurs, which may introduce errors if not modeled [52]. The time to generate a typical FISP-MRF dictionary is approximately 30 seconds without these corrections, compared to 3 minutes with corrections for slice profile and preparation pulse efficiency [50]. With an additional ${\mathrm{B}}_1^{+}$ correction, the time scales with the number of possible ${\mathrm{B}}_1^{+}$ values in the dictionary and simulation can easily require more than one hour.

3). Applications Requiring Frequent Dictionary Generation:

While the MRF dictionary can usually be precomputed because the pulse sequence is known a priori, the exact pulse sequence timing is not known in some MRF applications. In these cases, the dictionary can only be generated after the scan is completed and must be calculated anew for each MRF data collection. For example, in cardiac MRF, data are acquired during one phase of the cardiac cycle over several heartbeats to avoid motion artifacts [4]. To obtain accurate T₁ and T₂ quantification, a scan-specific dictionary is simulated that takes into account the subject’s heart rate recorded from an electrocardiogram (ECG) during the scan. MRF sequence optimization is another application that requires frequent dictionary generation [53], [54]. Every time the sequence parameters are updated, a new dictionary must be created to assess its T₁ and T₂ sensitivity.

B. Machine Learning Approaches for MRF Dictionary Generation

Machine learning techniques, and in particular neural networks, are a promising tool for addressing some challenges regarding MRF dictionary generation. Several groups have proposed training neural networks with simulated fingerprints to learn a nonlinear functional mapping that approximates the Bloch equations. Once trained, the network can generate signal evolutions using feedforward calculations that are more than 100 times faster than simulating the Bloch equations. Additionally, neural networks can implicitly learn corrections, such as those for slice profile effects, if they are provided during training. Fast dictionary generation is especially helpful for large-scale dictionaries with many tissue properties or long sequence lengths. Quantization errors could be reduced by using a high sampling density along each tissue property dimension, which would take prohibitively long using a Bloch equation simulation. Neural networks may also aid MRF sequence optimization since new dictionaries can be generated on-the-fly to assess their T₁ and T₂ sensitivity.

1). Generative Adversarial Network for MRF:

One approach for accelerating dictionary generation uses a particular class of neural networks called a generative adversarial network (GAN) [55]. A GAN consists of two competing networks. The generative network creates signal evolutions that imitate actual fingerprints, while the discriminative network attempts to classify whether a signal is real or forged. In [56], the authors implement both networks with four fully-connected hidden layers having 128 neurons. This GAN takes the sequence parameters (flip angles and TRs), and tissue properties (T₁ and T₂) as control variables, and outputs the signal evolution resulting from this combination of factors. The network can be trained using simulated signals, in this case a FISP-MRF sequence with 1000 TRs. Maps that are reconstructed using the GAN approach agree well with maps reconstructed using a dictionary generated by a Bloch equation simulation. A major advantage of the GAN method is speed; in this work, it took only 7s to output a dictionary with 5970 entries using the GAN compared to 2 hours using a Bloch equation simulation with slice profile correction.

2). Neural Network for Cardiac MRF Dictionary Generation:

Section VI will describe a novel approach using a fully-connected neural network that can output a cardiac MRF dictionary in less than one second when given ECG timing information as input. This machine learning approach removes a major bottleneck in cardiac MRF data processing, as there is no need to perform a separate Bloch equation simulation after every scan.

V. Machine Learning and MRF Pattern Recognition

A. Practical Challenges

Dot product matching is an exhaustive search that compares a measured signal evolution with every entry in the dictionary. This approach has the advantage of finding the globally optimal match out of all simulated fingerprints. However, it is prohibitively time-consuming and memory intensive when there are many tissue properties or when there is a high sampling density along each tissue property dimension.

To put the computation time in context, it takes approximately 30 seconds in MATLAB to reconstruct 256x256 T₁ and T₂ maps using a FISP-MRF sequence with 1000 TRs and a dictionary with 18,838 entries [8]. The reconstruction time grows rapidly when there are more tissue properties. Reconstructing six 128x128 tissue property maps for MRF-X by matching to a relatively sparse dictionary with 500 million entries requires more than one day [45].

Other algorithms faster than dot product matching have been proposed. Fast group matching [57] and Fast Library for Approximate Nearest Neighbors (FLANN) [58] both organize the dictionary into a tree-like data structure so that only a fraction of the dictionary is searched. With fast group matching, T₁, T₂, and off-resonance maps for bSSFP-MRF can be reconstructed in 2s, which is 100 times faster than dot product matching. However, these techniques require upfront computation to simulate the entire dictionary and organize it into a clustered data structure. Furthermore, these computations need to be repeated if the pulse sequence changes. MRF-ZOOM is another method that matches signals to a coarse resolution dictionary and iteratively refines the tissue property estimates, avoiding the need to search through and store a high resolution dictionary [59]. However, this method makes assumptions about the matching process, such as convexity, that may not generalize to all MRF sequences.

Another challenge in MRF is that aliasing artifacts are superimposed on the measured fingerprints. Because each individual image frame is highly undersampled, many time frames are usually acquired to obtain robust measurements with dot product matching. The need for long fingerprints leads to longer scan times, but more importantly for this discussion, long pattern matching times as well.

B. Machine Learning Approaches for Pattern Recognition

This section will provide an overview of recent machine learning approaches that improve or accelerate pattern recognition in MRF. One of the most exciting prospects for MRF with machine learning is the potential to bypass the dictionary generation step altogether [60]-[62]. Instead, a neural network can be trained to learn a nonlinear mapping which takes measured signals as inputs and directly outputs tissue property maps. The problem of pattern recognition is no longer an exhaustive search through a dictionary; instead, it becomes a rapid feedforward calculation. This approach has lower memory requirements since only the network weights and biases need to be saved. Another benefit is that the tissue property maps can take on continuous values. This differs from dot product matching, which is prone to quantization errors due to the discrete nature of the dictionary. In some cases, machine learning approaches permits robust signal matching with fewer time points, allowing a reduction in scan time. Additionally, the maps may have less residual aliasing or noise enhancement compared to standard dictionary matching. Several examples of such approaches are discussed below.

1). Fully-Connected Neural Networks:

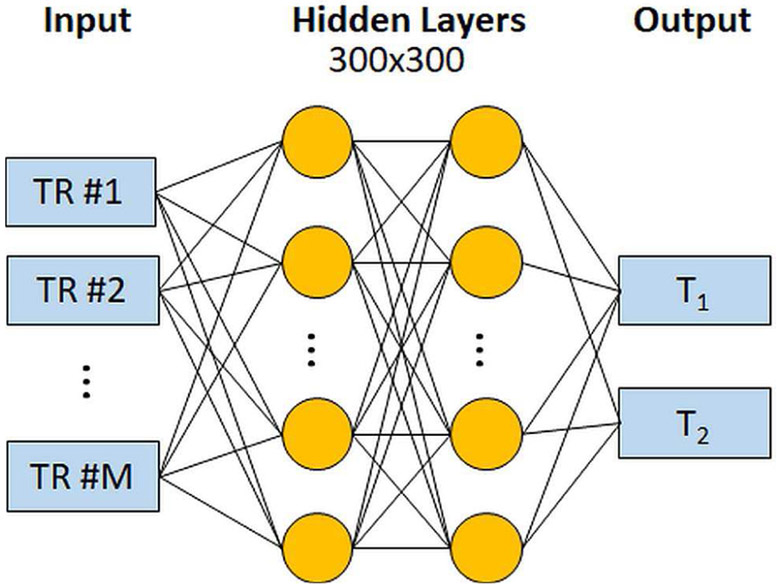
MR fingerprinting Deep RecOnstruction NEtwork (DRONE) uses a feedforward neural network for fast pattern recognition [60]. The neural network architecture is shown in Fig. 3. The network takes the magnitude of a measured signal evolution as input, and provides an estimate of T₁ and T₂ as outputs. This framework has been implemented for two variants of FISP-MRF. The first variant used a Cartesian EPI readout with 25-50 TRs, and the second variant used an undersampled spiral trajectory with 600 TRs. The EPI images are input without preprocessing, whereas the undersampled spiral data are first reconstructed with a sliding window filter to reduce aliasing artifacts [63]. Next, there are two fully-connected hidden layers with 300 neurons, which is followed by the output layer that yields T₁ and T₂ estimates. DRONE was trained with 69,000 signal evolutions simulated using extended phase graphs, and random Gaussian noise was added to promote robust learning [64].

Fig. 3.

Schematic of the DRONE network for MRF pattern recognition. The network takes the magnitude of a measured MRF signal evolution as input. The data are processed by two fully-connected layers with 300 neurons, and it outputs the estimated T₁ and T₂ values.

DRONE reconstructs maps substantially faster than standard dot product matching and with comparable accuracy. The time needed to reconstruct 128x128 T₁ and T₂ maps was 10ms using DRONE compared to 3s with dictionary matching for the EPI sequence. For the spiral sequence, the reconstruction time was 76ms for DRONE compared to 380s with dictionary matching. Notably, the matching time does not scale linearly with sequence length. Although the number of TRs in the spiral sequence is 20 times larger compared to the EPI sequence, the reconstruction time using DRONE is only seven times longer.

Neural networks can also perform pattern recognition directly on highly undersampled MRF data instead of using pre-processing to reduce artifacts. As previously described, the use of undersampled spiral k-space trajectories superimposes a noise-like interference on the measured fingerprints. The noise is modulated by the signal level at each TR and, in general, is not Gaussian. Thus, rather than training a network with simulated signals corrupted by Gaussian noise, an empirical noise model can instead be used. For instance, the authors in [65] employ a neural network with three fully-connected layers, which takes a signal evolution as input and outputs a T₁ or T₂ estimate. To generate training data, artifact noise signatures were found by subtracting measured fingerprints obtained from in vivo MRF scans from their closest matching fingerprints in the dictionary. Training data were generated by simulating 100,000 signal evolutions using the Bloch equations. Empirical noise was added to each signal by randomly selecting an artifact noise signature and SNR level and then adding a random phase shift. When trained with data using the empirical noise model, the network yielded maps comparable to standard dictionary matching. However, the maps had substantial errors when the network was trained with data corrupted by Gaussian noise. Note that this technique takes unprocessed fingerprints as inputs (i.e. signals from the aliased image series), so it is important for the training data to also contain aliasing artifacts due to undersampling of k-space. In comparison, DRONE preprocesses the input with a sliding window filter to mitigate aliasing artifacts, so it is not essential for the training data to be derived from undersampled k-space data.

Although MRF signal evolutions are complex-valued, the majority of machine learning literature focuses on real data. When applying machine learning techniques to MRF, one simple approach is to split the real and imaginary parts of the MRF signals into separate channels, which doubles the number of neurons in the input layer. However, better performance could be obtained by keeping the input in complex form. Recently, a new complex cardiod activation function has been introduced in a neural network for MRF pattern recognition [66]. This activation function is an extension of the rectified linear unit (ReLU) that leaves the input phase unchanged and diminishes the magnitude based on the input phase. It simplifies to a traditional ReLU when the input is real-valued. A neural network that employed this activation function produced more accurate maps compared to networks that split the MRF signals into real and imaginary channels.

2). Convolutional Neural Networks:

A convolutional neural network (CNN) is a subclass of feedforward networks where each neuron performs a convolution using a filter with learned coefficients. CNNs may be appropriate for pattern recognition because specific T₁ and T₂ values are associated with characteristic MRF signal shapes or features.

CNNs have been proposed for pattern recognition for FISP-MRF data collected with an undersampled spiral trajectory [62], [67], [68]. As shown in Fig. 4, this network consists of 4-6 convolutional layers, an average pooling layer, and 4-6 fully-connected layers with ReLU activation functions. The use of convolutional layers and average pooling encourages the network to learn features across different temporal scales. Training data were gathered from both phantom and in vivo brain MRF scans, treating the signal evolution at each pixel location as a separate training example. The proposed CNN was employed to reconstruct maps at a clinical resolution (1.2mm² in-plane) 7-10 times faster than standard dictionary matching on a CPU. It was also found that CNNs with more hidden layers outperformed shallower networks when the MRF scan was undersampled.

Fig. 4.

Diagram of a convolutional neural network (CNN) proposed for MRF pattern recognition. The CNN takes a measured signal evolution from an undersampled MRF scan as input. Although not shown here, the signal is divided into two channels for the real and imaginary parts. Next there are 4-6 convolutional layers (note that only one layer is shown for clarity), an average pooling layer, and 4-6 fully-connected layers (again, only one layer is shown for clarity). The output is an estimate for the T₁ and T₂ value at the target pixel.

3). Spatially-Constrained Tissue Quantification:

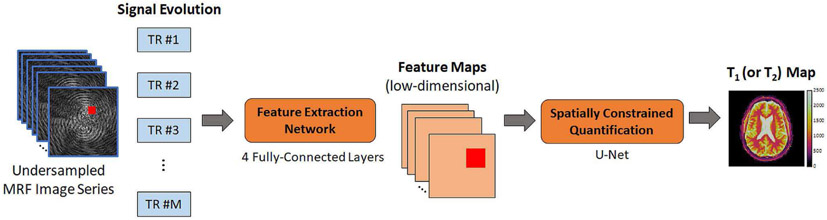
With dot product matching, each measured signal is matched to the dictionary independently of all other signals. However, neighboring pixels often contain similar tissue properties if parts of the image are homogeneous. Furthermore, undersampling in k-space distributes the signal arising from one pixel to many other pixels. These ideas are exploited in Spatially-Constrained Tissue Quantification (SCQ), which is a neural network approach for performing pattern recognition on patches of undersampled MRF images [61]. As shown in Fig. 5, this approach uses two consecutive neural networks. The first subnetwork performs feature extraction on a pixel-by-pixel basis. It transforms signal evolution into a low-dimensional feature vector (in this work, the feature vector has 46 elements). The compression step allows the second network to be smaller, which improves accuracy and reduces the training time. The output of the feature extraction network is used as input to the spatially-constrained quantification network. This subnetwork is implemented as a U-net which first performs convolution and downsampling, followed by upsampling and convolution. Overall, MRF signals from a 54x54 image patch are used to estimate the T₁ and T₂ values at a target pixel location.

Fig. 5.

Schematic of the spatially-constrained tissue quantification (SCQ) network. First, a measured signal evolution is input to a feature extraction subnetwork. The network consists of 4 fully-connected layers, and it outputs a low-dimensional feature vector. This calculation is repeated for each pixel to generate feature maps, which have a lower dimension than the undersampled MRF image series. Next, a block of pixels is input to the spatially constrained quantification subnetwork. This subnetwork is implemented with a U-net, and it uses blocks of data from the feature maps to estimate T₁ or T₂ at a target pixel. Note that a separate SCQ network is trained for each tissue property.

Training data were collected from in vivo brain MRF scans from several volunteers. Dictionary dot product matching was used to generate ground truth T₁ and T₂ maps. Training was divided into two steps. First, the feature extraction subnetwork was trained separately, using the measured MRF signals as inputs and the ground truth T₁ and T₂ values as outputs. Second, the entire network was trained end-to-end using blocks of signals from the in vivo scans. Instead of a conventional mean square error loss function, a relative difference loss function is used so that learning is not dominated by large T₁ and T₂ values.

The SCQ method is considerably faster than standard dot product matching. It took only 2.3s to reconstruct 256x256 T₁ and T₂ maps compared to 14.2s using dictionary matching with SVD compression. This technique also achieved a 4-fold reduction in scan time (from 23s to 6s, or 2304 TRs to 576 TRs) without compromising accuracy in the tissue property maps, whereas standard dot product matching yielded larger errors in both T₁ and T₂ when the scan was shortened.

VI. A Neural Network for Rapid Cardiac MRF Dictionary Generation for Arbitrary Heart Rhythms

As described above, machine learning approaches can dramatically reduce the time needed to reconstruct MRF data and even enable more complex applications of MRF. While machine learning can be deployed to accelerate pattern matching or dictionary generation in MRF, the next part of this article will highlight a specific application where a neural network is used to rapidly calculate dictionaries for cardiac MRF.

A. Introduction

Recently, cardiac MR Fingerprinting (cMRF) was introduced for simultaneous T₁ and T₂ quantification [14]. Several changes were made to the original MRF framework to make the technique robust for cardiac applications. Most relevantly, to reduce motion artifacts, data from one slice are acquired during a 16-heartbeat breathhold, and ECG triggering limits the data acquisition to diastole. One difficulty with ECG triggering is that it introduces pauses on the order of one second between acquisition windows. Relaxation occurs during these pauses that causes cMRF timecourses from different tissues to appear more similar, decreasing the ability of cMRF to accurately measure T₁ or T₂. To counter this problem, inversion pulses with variable inversion recovery times and T₂ preparations with variable echo times are used in cMRF during the ECG trigger delays. Time-varying flip angles are applied during the acquisition window, and the maximum flip angle is kept small (below 25°) to reduce the sensitivity to slice profile imperfections and ${\mathrm{B}}_1^{+}$ inhomogeneities [16].

With an ECG-triggered cMRF acquisition, the subject’s heart rate affects the amount of T₁ relaxation that occurs between each acquisition window. In order to obtain accurate tissue property maps, the ECG signal is recorded and used to simulate a new dictionary specific for each scan. The use of scan-specific dictionaries is different from most other MRF applications, where the pulse sequence is fixed beforehand. In those cases, the dictionary can be precomputed and reused for all future scans.

Frequent dictionary generation is a bottleneck in the cMRF workflow that could limit its practical utility. Any additional complexities in the dictionary simulation will further increase the computation time. For example, modeling slice profile imperfections and preparation pulse efficiency in the dictionary is recommended since it improves the accuracy of the T₁ and T₂ measurements [16]. However, the computation time increases from 30 seconds to 3 minutes with these corrections. Long computation times are a challenge for online reconstruction and can interfere with the fast-paced clinical workflow.

In this work, machine learning is applied to accelerate the process of cMRF dictionary generation. A neural network is trained to learn a functional mapping that takes T₁, T₂, and cardiac rhythm as inputs and rapidly generates a dictionary of signal evolutions. This work is different from prior techniques that combine machine learning with MRF because the sequence timing depends on heart rate and is not fixed. The following sections begin by describing the neural network architecture. The network is trained using signal evolutions generated using the Bloch equations for 1020 simulated cardiac rhythms. Numerical simulations are performed to test the robustness of the network to heart rate variability and missed ECG triggers. A validation study is performed in the ISMRM/NIST system phantom with different artificial cardiac rhythms. Finally, in vivo data are presented from scans of volunteers at 3T comparing myocardial T₁ and T₂ values derived from dictionaries output by the neural network and dictionaries generated by Bloch equation simulations.

B. Materials and Methods

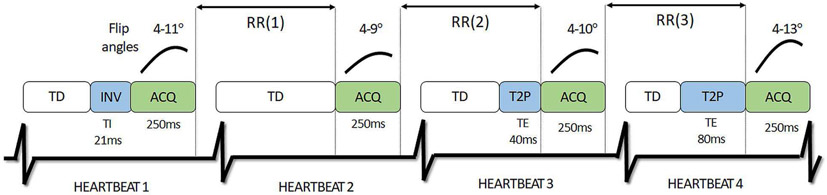
A diagram of the 16-heartbeat cMRF pulse sequence is provided in Fig. 6, which has been described in more detail elsewhere [4], [50]. Note that the inversion and T2-preparation times remain consistent from scan to scan, but the intervals between acquisition modules change depending on the subject’s heart rate.

Fig. 6.

Schematic of the cardiac MRF pulse sequence (only the first four out of sixteen heartbeats are shown for clarity). Each heartbeat consists of a fixed trigger delay (TD). This is followed by an inversion pulse (INV) or T₂ preparation (T2P) for some heartbeats. Next imaging data are collected with variable flip angles during a 255ms acquisition window (ACQ), which is placed near the end of the cardiac cycle. The time between two successive acquisition windows is denoted by the RR interval.

1). Neural Network Architecture:

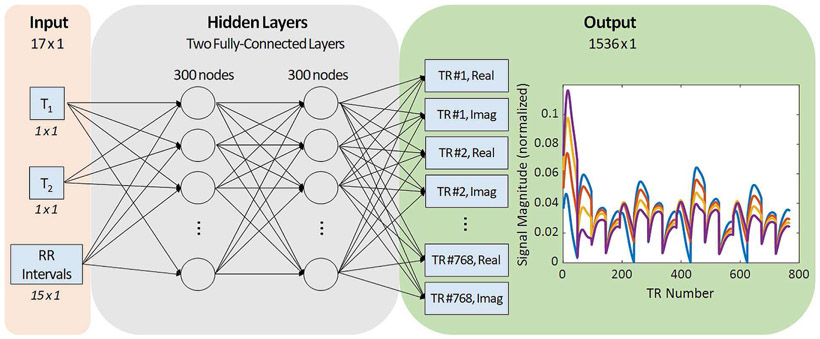
The neural network architecture is shown in Fig. 7. The network takes a 17-element vector as input. The first two elements are the pair of T₁ and T₂ values for which the signal evolution should be computed. The remaining 15 elements contain the RR interval times, which are the times between the end of one acquisition window and the beginning of the next acquisition window (Fig. 6). Even though the scan duration is 16 heartbeats, there are only 15 RR intervals because spins are initially at equilibrium. After generating the training data, as described below, the T₁, T₂, and RR intervals are normalized to the range [−1, 1]. The data passes to two fully-connected layers having 300 neurons. Each fully-connected layer is followed by batch normalization and a ReLU activation function. The final layer is fully-connected with 1536 outputs, corresponding to the real and imaginary parts of the signal evolution for 768 TRs. This network can be used to build a dictionary by sequentially inputting thousands of T₁ and T₂ pairs for a given cardiac rhythm.

Fig. 7.

Diagram of the proposed neural network architecture. The input to the neural network is a 17-element vector containing a T₁ value, a T₂ value, and fifteen RR intervals. Next the input passes through two fully-connected layers with 300 neurons per layer. The output has 1536 nodes corresponding to the real and imaginary parts of the signal evolution at 768 time points. Examples of four representative MRF signal evolutions are plotted in the output panel.

2). Network Training:

The network was trained using signals derived from the Bloch equations for randomly generated cardiac rhythms. To create the training data, the average heart rate was varied from 40 to 120 beats per minute (bpm) with a step size of 5bpm. Random Gaussian noise was added to the RR interval times (not to the signals themselves) to promote the learning of variable heart rates. For each average heart rate, 60 different rhythms were simulated by varying the noise standard deviation from 0% to 50% of the mean RR interval. A total of 4392 timecourses were simulated for each cardiac rhythm with T₁ between 20-3000ms and T₂ between 2-600ms. The specific T₁ and T₂ combinations were different for each cardiac rhythm. Overall, there were 1020 cardiac rhythms x 4392 timecourses, or approximately 4.5 million timecourses in the training dataset. Corrections for slice profile imperfections and preparation pulse efficiency were modeled in the training data [50].

Missed ECG triggers are common during cardiac scans and were explicitly included in the training data. Missed triggering occurs when a subject’s heart rate speeds up, which causes a diastolic acquisition window to extend into systole of the next heartbeat. The scanner waits for this heartbeat to complete before collecting the next block of data, effectively causing a longer than normal pause between acquisition windows. For every cardiac rhythm in the training dataset, each heartbeat was assigned a 5% probability of having a missed ECG trigger, which was modeled by doubling the original RR time.

A separate validation dataset was generated with average heart rates from 40 to 120bpm (step size 20bpm). For each average heart rate, five different rhythms were simulated by adding Gaussian noise to the RR intervals with standard deviation values from 5% to 50% of the mean RR interval. Again, 4392 T₁ and T₂ combinations were simulated for each rhythm, and each heartbeat had a 5% chance for missed ECG triggering. The training and validation datasets did not contain any duplicate signals.

The neural network was implemented with the MATLAB Deep Learning Toolbox. Training was performed using ADAM [69] with a learning rate of 0.001, l₂-regularization of 0.0001, mini-batch size 1024, and a mean square error loss function. A cross-validation check was performed twice per epoch, and the training was terminated when the validation loss was larger than the previously smallest loss more than five times. Overall, it took approximately 9 hours to generate the training and validation datasets using parallelized MATLAB Mex code, and 12 hours to train the network on a CPU. Training ran for 30 epochs before termination.

3). Numerical Simulations:

Monte Carlo simulations were performed to test the accuracy of the network with different cardiac rhythms. The first simulation investigated the robustness of the results to heart rate variability. Ground truth signals were simulated using the Bloch equations with tissue property values representative of myocardium (T₁1400ms and T₂50ms). The average heart rate was varied from 40-120bpm (step size 20bpm). A unique cardiac rhythm was generated for each average heart rate by adding Gaussian noise to the RR intervals with standard deviation from 0% to 50% (step size 5%) of the mean RR interval. A dictionary was output by the neural network, and the best-matching entry was found that maximized the inner product between the ground truth signal and the dictionary after normalization. The simulation was repeated 500 times for each cardiac rhythm, and the average root mean square error (RMSE) for T₁ and T₂ were calculated using the equation

$$RMSE=\mid \frac{T_i^{measured}-T_i^{reference}}{T_i^{reference}}\mid x100\%i\in \{1,2\}$$ (2)

The second simulation investigated the robustness to missed ECG triggering. As before, ground truth signals were simulated using the Bloch equations for T₁ and T₂ values representative of myocardium. The average heart rate was varied from 40-120bpm (step size 20bpm), and noise with standard deviation of 5% of the mean RR interval time was added to each cardiac rhythm. The number of missed triggers during the scan was varied from 0 to 8 (step size of 1). The simulation was repeated 500 times for each case, with different heartbeats randomly selected to have a missed trigger event. Accuracy was assessed by computing the normalized RMSE for T₁ and T₂. All simulations were performed using noiseless cMRF signal evolutions. In addition, the simulations were repeated using ground truth values ranging from T₁ 20-3000ms and T₂ 2-300ms; these results are provided in Supporting File 1.

4). Phantom Validation:

The ISMRM/NIST system phantom [70] was scanned on a 3T Siemens Magnetom Skyra (Siemens AG Medical Solutions, Erlangen, Germany) using a 20-channel head array coil. Only the T₂ layer was scanned since it has physiologically relevant relaxation times. cMRF data were collected while simulating several different artificial cardiac rhythms. In the first set of experiments, data were collected with constant heart rates from 40-120bpm (step size 10bpm). In the second set of experiments, the heart rate was changed halfway through the scan after the eighth heartbeat. In one scan, the heart rate instantaneously changed from 60 to 80bpm, and in another it changed from 80 to 60bpm. All cMRF data were acquired with a 192x192 matrix, 300mm² FoV, and a 255ms diastolic scan window. Data were acquired using a variable spiral trajectory with 48 interleaves and 0^th moment compensation [71], and the trajectory was measured in a separate scan session [72]. Undersampled (R=48) single-shot spiral data from each TR were gridded to the image domain using the non-uniform Fast Fourier Transform (NUFFT) [73].

cMRF maps were reconstructed by dot product matching between the measured data and two different dictionaries, one derived from the Bloch equations and the other generated by the neural network. The mean and standard deviation in T₁ and T₂ were computed within manually drawn ROIs. cMRF measurements from the Bloch equation and neural network approaches were compared with reference values provided by NIST using a linear regression analysis.

5). Cardiac Mapping in Volunteers:

In vivo cardiac scans were performed in 17 volunteers at a medial slice position in short-axis orientation at 3T as part of an IRB-approved, HIPAA-compliant study after obtaining written informed consent. cMRF data were acquired with 34 channels from a cardiac array coil and the built-in spine array. The acquisition window was placed in late diastole based on each subject’s heart rate. Similar to the phantom study, maps were reconstructed using two dictionaries, one derived from the Bloch equations and another output by the neural network. The mean and standard deviation for T₁ and T₂ were computed within ROIs drawn in six medial AHA segments. A Bland-Altman analysis was performed to compare the measurements obtained with the Bloch equation and neural network approaches [74].

C. Results

1). Computation Time and Memory:

The time needed to generate a dictionary with 768 time points and 26,680 T₁ and T₂ combinations is 0.8s for the neural network compared to 158s using a Bloch equation simulation. Note that the dictionary includes corrections for slice profile and preparation pulse efficiency. Saving only the network coefficients requires 2MB of memory compared with 303MB to store the entire dictionary.

2). Numerical Simulations:

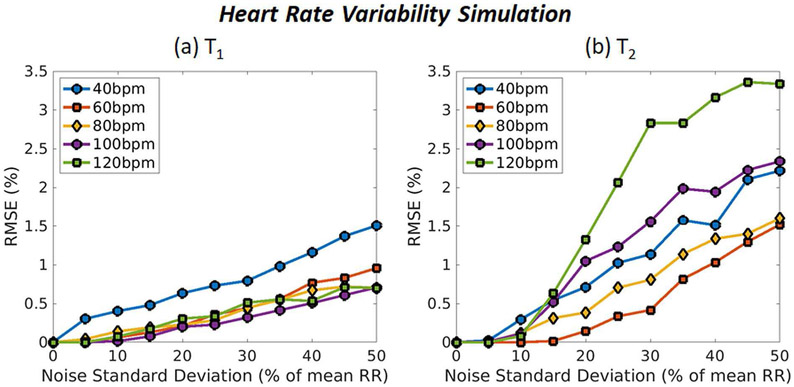
Results from the heart rate variability simulation are shown in Fig. 8. The network is extremely accurate for T₁, with RMSE values less than 1% for average heart rates from 60-120bpm up to a noise level of 50%. Slightly larger errors are seen for the slowest average heart rate of 40bpm, although the RMSE stays below 1% up to a 30% noise level. RMSE values are slightly higher for T₂, with larger errors seen for the highest average heart rate of 120bpm. RMSE values are below 2% for most heart rates even up to a 50% noise level.

Fig. 8.

Monte Carlo simulation results showing MRF accuracy for myocardial (a) T₁ and (b) T₂ under variable heart rate conditions. Results are shown for average heart rates of 40, 60, 80, 100, and 120bpm. The x-axis shows the amount of random Gaussian noise that was added to the RR interval timings as a percentage of the average RR interval, and the y-axis shows the normalized RMSE.

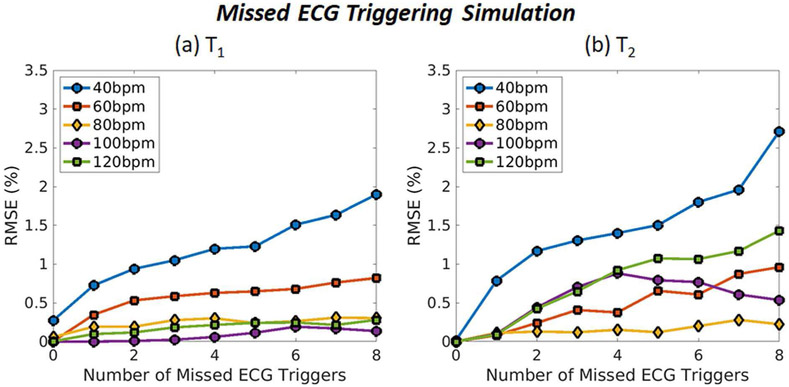
Fig. 9 is a plot of the T₁ and T₂ errors as a function of the number of missed ECG triggers. The RMSE values for T₁ are below 1% for all heart rates between 60-120bpm even when 8 heartbeats have missed ECG trigger events, and they are below 2% when the average heart rate is 40bpm. For T₂, the RMSE values are always below 1.5% for average heart rates between 60-120bpm and below 3% when the average heart rate is 40bpm.

Fig. 9.

Monte Carlo simulation results showing MRF accuracy for myocardial (a) T₁ and (b) T₂ under conditions mimicking missed ECG triggering. Results are shown for average heart rates of 40, 60, 80, 100, and 120bpm. The x-axis shows the total number of missed ECG triggers during the scan, and the y-axis shows the normalized RMSE.

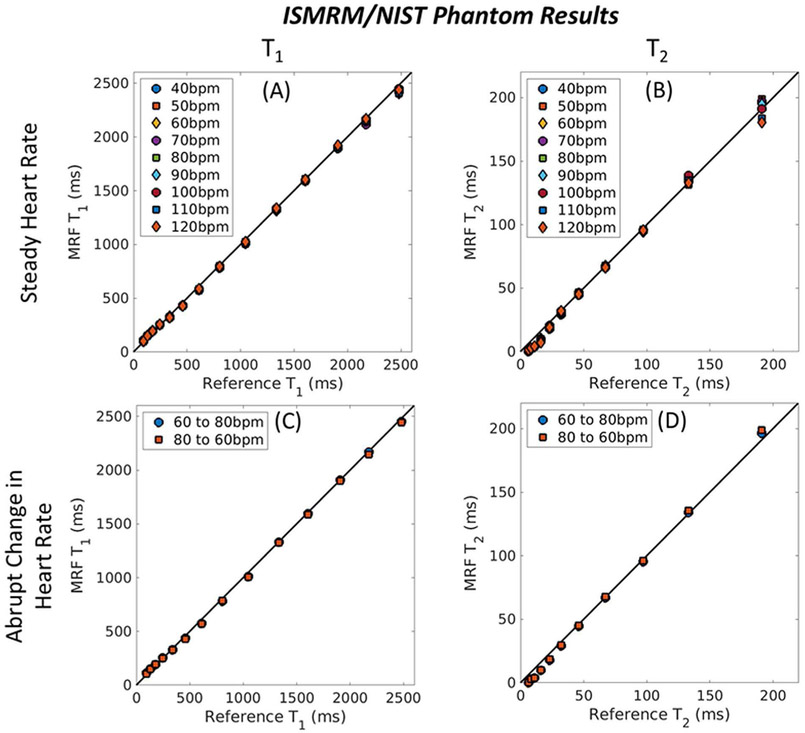
3). Phantom Validation:

As shown in Fig. 10, cMRF measurements using the neural network approach in the ISMRM/NIST system phantom lie close to the identity line (all R² > 0.998), which indicates excellent agreement with the reference values. Good agreement is also seen when an abrupt change in heart rate occurs halfway during the scan, a scenario which does not occurs halfway during the scan, a scenario which does not appear in the training data.

Fig. 10.

cMRF neural net results in the ISMRM/NIST system phantom at 3T with different simulated cardiac rhythms. (a, b) cMRF T₁ and T₂ measurements using a dictionary output by the neural net are shown for constant heart rates from 40-120bpm. (c, d) Measurements are also shown for cases where the heart rate abruptly changed from 60 to 80bpm (and from 80 to 60bpm) halfway during the scan.

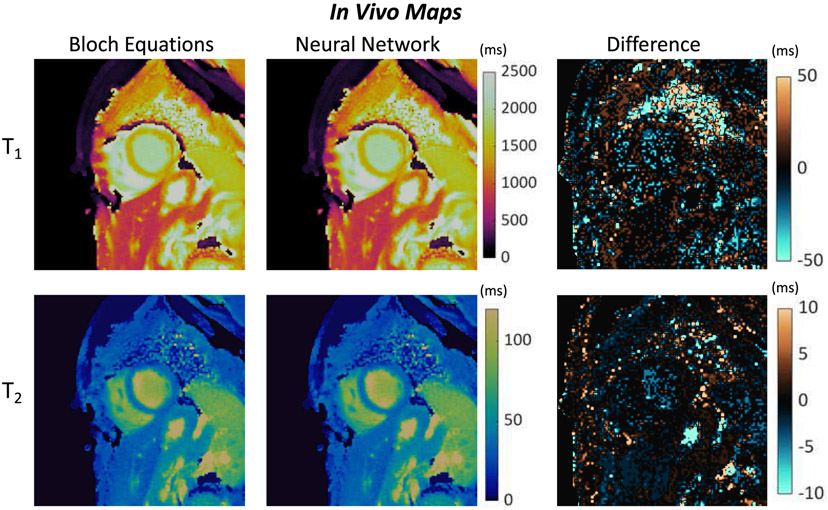
4). Cardiac Mapping in Volunteers:

Representative maps from a volunteer scan are shown in Fig. 11. Visually, the maps reconstructed using dictionaries generated from the Bloch equations and the neural network appear similar. A difference map computed by subtracting the Bloch equation maps pixelwise from the neural network derived maps has a noise-like appearance. There are larger differences in the lungs where signal intensity is low, as well as in some vessels containing fluids with long T₁ and T₂ values.

Fig. 11.

Representative short-axis cMRF T₁ and T₂ maps from a volunteer at 3T. Maps were calculated by matching the measured signals to a dictionary derived from a Bloch equation simulation, as well as a dictionary output by the neural net. Difference maps are also presented (Neural Net – Bloch Equations).

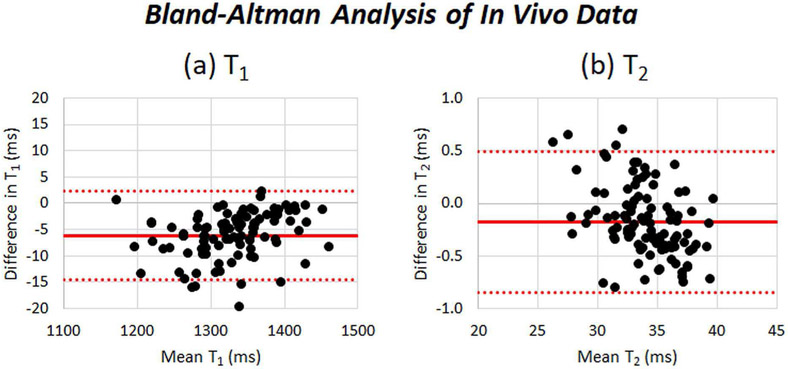
Bland-Altman plots comparing the segment-wise myocardial T₁ and T₂ values derived from the Bloch equation and neural network dictionaries are shown in Fig. 12. For T₁, the bias was 6.1ms with 95% limits of agreement (14.5,2.3)ms, and for T₂, the bias was 0.2ms with 95% limits of agreement (0.9, 0.5)ms. There are 5 outliers (5% of the data) on the T₁ plot and 4 outliers (4% of the data) on the T₂ plot.

Fig. 12.

Bland-Altman analysis comparing myocardial (a) T₁ and (b) T₂ derived from dictionaries using a Bloch equation simulation and dictionaries generated by the neural net. Each data point corresponds to the average T₁ or T₂ measurement calculated within an ROI on a volunteer dataset.

D. Discussion

This work has demonstrated the feasibility of training a neural network to rapidly generate cMRF dictionaries for arbitrary cardiac rhythms. The neural network was able to synthesize a dictionary in less than 1 second, compared to 3 minutes using a Bloch equation simulation. This work removes a major bottleneck in cMRF processing by removing the need to create a new dictionary after every scan. Notably, the network performs well even in the presence of variable or rapid heart rates (Fig. 8) and with missed ECG triggering (Fig. 9), provided these cases are represented in some fashion in the training data.

Machine learning techniques for pattern recognition may be trained using simulated data or data from actual MRI scans. Both approaches have their own advantages. In this work, simulated training data were used, and care was taken to ensure that the training data were representative of actual cardiac rhythms that could be encountered. Random noise was added to the RR interval timings to improve the robustness to heartbeat-to-heartbeat variations. Also, 5% of the training data were corrupted by missed ECG triggers to further improve the network’s generalizability, as shown in the numerical simulation results. One advantage of using simulated data is that a potentially unlimited amount of training data can be generated to improve the learning algorithm. On the other hand, training using actual MRI data may expose the learning algorithm to physical effects that are important to consider yet complicated to simulate.

The neural network introduced here could promote the translation of cMRF into clinical use. Previously, cMRF has been implemented using the open-source Gadgetron platform to perform online reconstructions at the scanner [75], [76]. However, the total reconstruction time was 112s per slice, with 100s needed for dictionary simulation and 12s for gridding and pattern matching. This implementation did not include corrections for slice profile or preparation pulse efficiency, which increase the computation time six-fold. With the proposed neural network, the total reconstruction time could potentially drop to 13s (1s dictionary generation, and 12s gridding and matching), which is not expected to impede clinical workflow. Furthermore, only the network coefficients need to be saved on the reconstruction computer (2MB), which occupy much less space than each dictionary (303MB).

Maps reconstructed with dictionary-based techniques like cMRF suffer from quantization error due to the discrete nature of the dictionary. This work used a relatively dense dictionary with 26,680 tissue property combinations. However, because the neural network outputs timecourses so rapidly, it may be feasible to generate a finer-resolution dictionary with smaller T₁ and T₂ step sizes. Additional work will be performed to investigate how the sparseness of the training data relates to the smallest achievable step size in the dictionary output by the network.

There are several areas that can be explored in future work. The network performance could be improved by training with additional data, either using more simulated cardiac rhythms or a database of ECG recordings. The network could also be modified take additional tissue or scanner properties as inputs, such as ${\mathrm{B}}_1^{+}$. Finally, the overall cMRF reconstruction time could be reduced by developing a neural network that takes undersampled cMRF images as inputs and directly outputs tissue property maps.

VII. Conclusions and Future Directions

This review has summarized several ways machine learning may address practical problems in MRF. First, neural networks may accelerate dictionary generation, which is crucial for applications that quantify many tissue properties simultaneously or require frequent calculation of new dictionaries. Second, machine learning may permit faster, more robust pattern recognition by bypassing dictionary generation altogether and directly estimating tissue property values from measured data. Recent approaches have proposed the use of fully-connected neural networks, convolutional networks, and more advanced network architectures, like U-nets, for pattern recognition. Finally, original research was presented using a neural network to rapidly generate dictionaries for cardiac MRF. This work addresses an important practical bottleneck because scan-specific dictionaries are necessary for accurate myocardial T₁ and T₂ quantification, as the subject’s heart influences the MRF signal evolutions.

Advances in machine learning in the coming years will likely have a large impact on the growing field of MRF. Machine learning can promote the scalability of MRF to quantify a larger number of tissue properties simultaneously. Dictionary sizes and computation times increase exponentially with the number of tissue properties (or dimensions) in the dictionary. For MRF techniques that aim to quantify many properties at once, it can be infeasible to store the dictionary in memory or search for signal matches, even using state-of-the-art hardware. Machine learning techniques may liberate MRF from the curse of dimensionality. In addition, they may facilitate the use of more complex physical models in MRF, such as multi-compartment models for subvoxel tissue characterization [40], [45].

Another emerging area that may profit from machine learning is MRF pulse sequence optimization. Many MRF sequences have been designed empirically. However, optimized sequences promise a host of benefits, including shortened scan times, higher SNR, and improved quantification accuracy. Machine learning technology could automate the selection of flip angles, TRs, TEs, and preparation pulses in MRF sequences, as well as inform the selection of an optimal k-space trajectory. Optimized MRF sequences could potentially be made for specific organs, MRI scan protocols, or even tailored for individual patients.

Image reconstruction for MRF will continue to be an important application for machine learning. Novel reconstruction methods can help achieve targets of higher resolution, shorter scan times, and improved volumetric coverage. Complex-valued neural networks may gain more interest in the future since MRI data are inherently complex, and results suggest that complex networks may outperform real-valued networks [66]. There may also be work using machine learning to exploit the relationship between different tissue properties—for example, by using the correlation between T₁ and T₂ values in the body, rather than estimating each property individually. Finally, machine learning approaches may be developed that combine prior information in the form of previous MRI scans, scans from other imaging modalities, or even a patient’s medical history to glean more information from MRF data.

Biography

Jesse I. Hamilton received his B.S. degree in Biomedical Engineering from Johns Hopkins University in 2012 and completed his Ph.D. thesis in 2017 from Case Western Reserve University on rapid quantitative Magnetic Resonance Imaging techniques. He is currently working as a Research Associate at the University of Michigan. His research interests include Magnetic Resonance Fingerprinting, compressed sensing, parallel imaging, non-Cartesian MRI, and machine learning, with a focus on cardiac imaging.

Nicole Seiberlich is an Associate Professor of Radiology at the University of Michigan. She received her BS in Chemistry from Yale University in 2001, and completed her PhD thesis at the University of Wuerzburg on the topic of novel Magnetic Resonance Imaging techniques in 2008. In 2011, Nicole became a faculty member of Biomedical Engineering at Case Western Reserve University. She later became the Elmer Lincoln Lindseth Associate Professor of Biomedical Engineering, with secondary appointments in the Departments of Radiology, Cardiology, and Electrical Engineering and Computer Science. Her work in rapid MRI is funded by the NIH and NSF. Nicole is a member of the Editorial Board for Magnetic Resonance in Medicine and serves as an Associate Editor for IEEE Transactions in Medical Imaging, and is active in multiple societies including the International Society for Magnetic Resonance In Medicine. She has published more than 50 peer-reviewed manuscripts on the topics of rapid and quantitative MRI, and has been invited to give more than 60 lectures, including the ISMRM/NIBIB New Horizons Lecture. In addition to her professional activities, she has won a number of awards for teaching and mentorship, including the CWRU Diekhoff Award for Excellence in Graduate.