Theoretical Prediction and Synthesis of a Family of Atomic Laminate Metal Borides with In-Plane Chemical Ordering

Abstract

All atomically laminated MAB phases (M = transition metal, A = A-group element, and B = boron) exhibit orthorhombic or tetragonal symmetry, with the only exception being hexagonal Ti₂InB₂. Inspired by the recent discovery of chemically ordered hexagonal carbides, i-MAX phases, we perform an extensive first-principles study to explore chemical ordering upon metal alloying of M₂AlB₂ (M from groups 3 to 9) in orthorhombic and hexagonal symmetry. Fifteen stable novel phases with in-plane chemical ordering are identified, coined i-MAB, along with 16 disordered stable alloys. The predictions are verified through the powder synthesis of Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB₂ of space group R3̅m (no. 166), displaying the characteristic in-plane chemical order of Mo and Y/Sc and Kagomé ordering of the Al atoms, as evident from X-ray diffraction and electron microscopy. The discovery of i-MAB phases expands the elemental space of these borides with M = Sc, Y, Zr, Hf, and Nb, realizing an increased property tuning potential of these phases as well as their suggested potential two-dimensional derivatives.

1. Introduction

Transition-metal borides and carbides have high melting points and are among the hardest compounds known, which are properties required for both bulk and coating applications. When combined with a third element, they can retain or form atomically layered structures. One such example is M_n+1AX_n (MAX) phases (where M is a transition metal, A is an A-group element, and X is C and/or N) of a hexagonal structure with P6₃/mmc symmetry, combining ceramic and metallic attributes.^1,2 The selective removal of the A element, typically Al, upon etching results in the corresponding two-dimensional (2D) material, a so-called MXene,³ which has shown an outstanding potential for a wide range of applications, from energy storage⁴ to electromagnetic interference shielding.⁵

One route to enhancing the materials’ elemental space and the associated range of attainable properties is through alloying. This is exemplified by the recent discovery of in-plane chemically ordered MAX phase alloys, coined i-MAX, which through hexagonal symmetry allow for elemental ordering and the incorporation of metals not found in traditional ternary MAX phases.⁶⁻⁸ A key feature of i-MAX phases is that by employing different etching protocols the resulting 2D MXene can have in-plane chemical or vacancy ordering,⁹ which is valuable for catalysis and energy storage.^6,8 Similar in-plane chemical order in 3D-layered transition-metal borides (MAB phases) has, to this date, not been found.

MAB phases have a large palette of structural variations. From M_n+1AlB_2n with a single layer of Al, n = 1–3 and M is a transition metal (n = 1 in space group Cmmm: Cr₂AlB₂, Mn₂AlB₂, and Fe₂AlB₂; n = 2 in space group Pmmm: Cr₃AlB₄; n = 3 in space group Cmmm: Cr₄AlB₆),¹⁰⁻¹² to MAlB with double layers of Al (MoAlB and WAlB in space group Cmcm)¹² and M₄AlB₄ with double layers of M (Cr₄AlB₄ in space group Immm).¹³ Note that all structures have orthorhombic symmetry. In particular, Fe₂AlB₂ has gained attention as a prospective for a rare-earth free magnetocaloric material with a near-room temperature magnetic phase transition at around 304 K.^14,15

The chemical diversity of MAB phases has so far been limited to M from group 6 to 8 and A commonly being Al. Chemical disorder has previously been investigated for synthesized (M′_1–xMo_x)AlB (Cmcm),¹⁶ with M′ = W and Cr and Fe_2–xMn_xAlB₂¹⁵ (Cmmm), and theoretically studied for Fe_2–xM′′_xAlB₂ (Cmmm), with M′′ = Cr, Mn, Ni, Co.¹⁷ Chemical order has only been investigated theoretically for the M₃AlB₄ structure (Pmmm) with out-of-plane order of M′ and M′′ in M′₂M′′AlB₄ with M′ = Mn, Fe, and Co and M′′ = Cr, Mo, and W.¹⁸ In all cases, the alloying metals encompass the elements found in traditional ternary MAB phases.

All MAB structures display orthorhombic symmetry. The only exception is a recently discovered layered MAB phase, Ti₂InB₂,¹¹ with hexagonal P6̅m2 symmetry (also a hexagonal subgroup of P6₃/mmc). Inspired by this finding and motivated by the previous discovery of i-MAX phases, we here use cluster expansion to theoretically investigate the possibility of chemical ordering in MAB-phase alloys. We also perform systematic phase stability calculations for alloying between M′ and M′′ in M′_2–xM′′_xAlB₂, where M′ and M′′ are Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co in the two known M₂AlB₂ polymorphs, orthorhombic Cmmm and hexagonal P6̅m2. The preference for chemical order and disorder is evaluated for all elemental combinations of M′ and M′′.

We identify 15 novel MAB phases with in-plane chemical order, hereafter referred to as i-MAB phases, that are concluded to be thermodynamically stable up to a temperature of at least 2000 K. To verify these theoretical predictions, we synthesize Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB₂, and material characterization confirms a structure with space group R3̅m (no. 166) displaying the characteristic in-plane chemical ordering of Mo and Y or Sc and Kagomé ordering of the Al atoms. Further theoretical analysis suggests that the formation of i-MAB phases requires a significant difference in size for the two metals and demonstrates a new family of quaternary MAB-phase alloys. Moreover, the approach is expected to be applicable for other hexagonal materials and thus offers opportunities for more versatile chemistry and, in turn, the property tuning of functional materials.

2. Theoretical and Experimental Details

2.1. Density Functional Theory Calculations

All first-principles calculations were performed by means of density functional theory (DFT) and the projector augmented wave method,^19,20 as implemented within the Vienna ab initio simulation package (VASP), version 5.4.1.²¹⁻²³ We used the generalized gradient approximation (GGA) as parametrized by Perdew–Burke–Ernzerhof (PBE)²⁴ to treat the electron exchange and correlation effects. For phases with Cr, Mn, Fe, and Co, we used the spin-polarized GGA version with multiple spin configurations considered. The presented results are for the lowest-energy spin configuration. A plane-wave energy cutoff of 400 eV was used, and the Brillouin zone was integrated by Monkhorst–Pack special k-point sampling with a 2π × 0.05 Å^–1k-point density in reciprocal space.²⁵ The convergence of energy and structure with respect to the k-point density is shown in Figure S1. The total energy is minimized through the relaxation of the unit-cell shape and volume and internal atomic positions until satisfying an energy convergence of 10^–6 eV/atom and a force convergence of 10^–2 eV/Å. Visualization of the atomic structures was done with the VESTA code.²⁶

2.2. Structural Search for Chemical Order and Disorder

To investigate alloying trends within the M-sublattice of M′_2–xM′′_xAlB₂, we used a theoretical approach based on the MIT ab initio phase stability (MAPS)²⁷ code as implemented in the alloy theoretic automated tool kit (ATAT),²⁸ within a high-throughput density functional theory (DFT) framework. In addition, the chemical disorder of M′ and M′′ has been modeled on the M sublattice using the special quasi-random structure (SQS) method.²⁹ Convergence tests show that supercells with 120 atoms or more give a qualitatively accurate representation and a quantitative convergence in terms of calculated formation enthalpies, equilibrium volumes, and lattice parameters.

2.3. Stability Predictions

In this work, we have considered the alloying of M′ and M′′ from group 3 to 9: Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co considering orthorhombic and hexagonal structures of M₂AlB₂. The thermodynamic stability has been investigated at 0 K with respect to decomposition into any combination of competing phases. The most competitive set of competing phases, denoted the equilibrium simplex, is identified using a linear optimization procedure^30,31 which has already been proven to be successful in confirming experimental materials as well as predicting the existence of new ones.³¹⁻³⁶ The stability of a phase is quantified in terms of the formation enthalpy ΔH_cp by comparing its energy to the energy of the equilibrium simplex according to

1

A phase is concluded to be stable when ΔH_cp < 0. Here E(M′_2–xM′′_xAlB₂) represents the chemical order of lowest energy, being the chemically ordered M′_4/3M′′_2/3AlB₂ or the disordered (M′_0.67M′′_0.33)₂AlB₂. When T ≠ 0 K, the contribution from configurational entropy resulting from a disordered distribution of M′ and M′′ on the M sublattice in (M′_0.67M′′_0.33)₂AlB₂ will decrease the Gibbs free energy ΔG_cp^disorder as approximated by

2

where the entropic contribution ΔS, assuming an ideal solution of M′ and M′′ on the M site, is given by

3

where k_B is the Boltzmann constant and y is the concentration of M′′ on the M sublattice.

2.4. Synthesis of Materials

The powders used herein were B (99.999% Sigma-Aldrich), Mo (99.99% Sigma-Aldrich), Al (99.8% Alfa Aesar), Sc (99.99% Stanford Advanced Material), and Y (99.9% Alfa Aesar). To obtain the Mo_4/3Sc_2/3AlB₂ and Mo_4/3Y_2/3AlB₂ powder samples, a stoichiometric amount was mixed in an agate mortar, heated to 1400 °C in an alumina crucible under flowing argon, and held at that temperature for 8 h. After this, the sample was cooled to RT in the furnace and a loosely packed powder was obtained. The powder was crushed and sieved through a 200 mesh sieve (particle size 74 μm). This fine powder was then used for XRD, EDX, and STEM.

2.5. Characterization of Materials

XRD scans of the Mo_4/3Sc_2/3AlB₂ and Mo_4/3Y_2/3AlB₂ powders were carried out on a diffractometer (Panalytical X’pert). The XRD diffractogram of the Mo_4/3Sc_2/3AlB₂ and Mo_4/3Y_2/3AlB₂ powders was analyzed by the Rietveld refinement method using the FULLPROF code.^37,38 Refined parameters were the background parameters, zero shift, scale factors, X and Y profile parameters for peak shape, lattice parameters, and atomic positions for all phases.

Compositional analysis was carried out using energy-dispersive X-ray spectroscopy (Oxford Instrument) on individual Mo_4/3Sc_2/3AlB₂ and Mo_4/3Y_2/3AlB₂ grains.

For the in-plane-ordered Mo_4/3Sc_2/3AlB₂ and Mo_4/3Y_2/3AlB₂ analyses, STEM combined with high-angle annular dark-field imaging (STEM-HAADF) and SAED was performed in the double-corrected Linköping FEI Titan³ 60-300 operated at 300 kV. Fine powder was dispersed onto standard holey amorphous carbon support films suspended by Cu grids (SPI Supplies). Simulated SAED patterns were generated by CrystalDiffract in the CrystalMaker package.

3. Results

3.1. Phase Stability of Ternary M₂AlB₂

The thermodynamic phase stability of the ternary M₂AlB₂ phases are evaluated by assuming both polymorphs: orthorhombic Cmmm (Figure 1a) and hexagonal P6̅m2 (Figure 1b) symmetry. Note that the Cmmm structure contains zigzag chains of boron while P6̅m2 has boron in a flat honeycomb lattice. Figure 1c shows the calculated formation enthalpy ΔH_cp at 0 K for M₂AB₂, with the corresponding identified equilibrium simplex listed in Table S1. The polymorphic crystal structure of lowest energy is identified and indicated in the figure through the displayed form. Only three M₂AlB₂ phases are found to be thermodynamically stable: Cmmm with M = Cr, Mn, and Fe. This is consistent with experimentally known phases (Cr₂AlB₂,³⁹ Mn₂AlB₂,¹⁰ and Fe₂AlB₂⁴⁰) and demonstrates that the predictive thermodynamic phase stability calculations for these types of materials is reliable. Moreover, the hexagonal structure is lowest in energy only for M from groups 4 and 5 but is found not to be stable (ΔH_cp > 0). Ti₂AlB₂ is close to being stable at ΔH_cp = +14 meV/atom, consistent with the theoretical results in ref (11).

Figure 1.

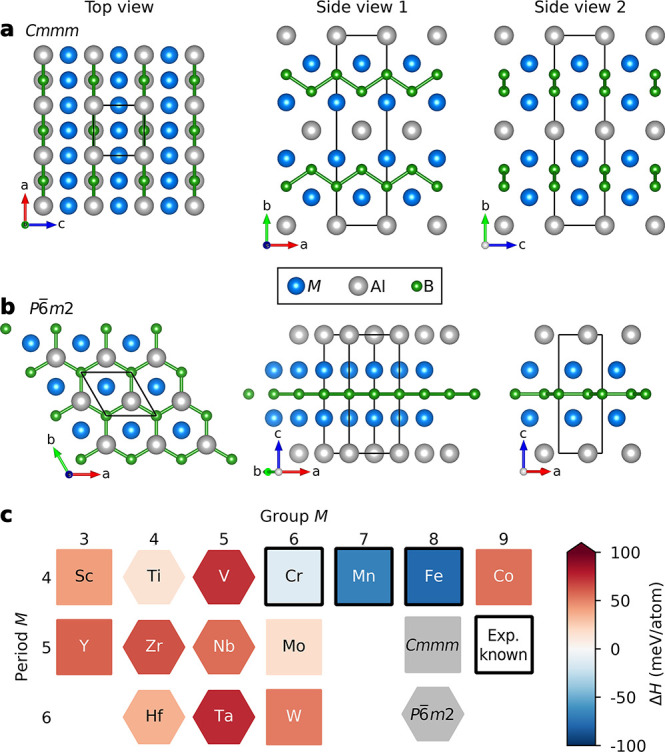
Phase stability of ternary M₂AlB₂. Schematic illustration of M₂AlB₂ with (a) orthorhombic Cmmm and (b) hexagonal P6̅m2 symmetry with unit cells marked by black lines. (c) Calculated theoretical phase stability for M₂AlB₂, identifying whether Cmmm (square) or P6̅m2 (hexagon) is lowest in energy. Experimentally known phases are marked with a black box.

3.2. Identification of Structures with In-Plane Chemical Order upon Metal Alloying

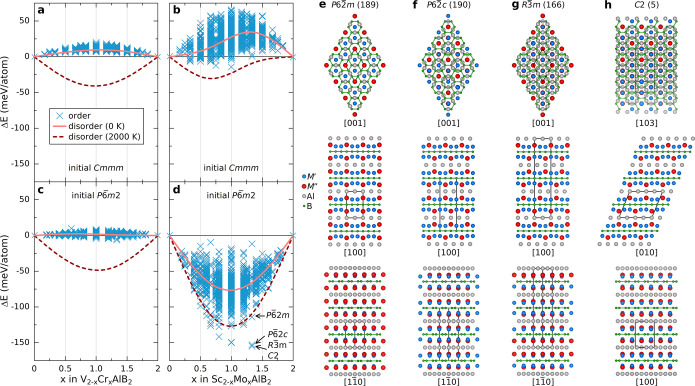
With the exception of one theoretical report on the possible out-of-plane chemical order in M₃AlB₄,¹⁸ there is no study on the chemical order in MAB phases and their alloys. We have therefore investigated M-site alloying of M₂AlB₂ considering the orthorhombic Cmmm and hexagonal P6̅m2 structures. To reveal trends and possible chemical order, we have used the alloy theoretic automated tool kit (ATAT) to generate ∼1200 chemically ordered candidate structures for each material system. Each individual structure was completely relaxed. In addition, we also considered structures with chemical disorder for M′ and M′′. As an example, Figure 2a–d shows the calculated energy difference ΔE of M′_2–xM′′_xAlB₂ with respect to the ternary M′₂AlB₂ and M′′₂AlB₂ phases for two sets of M′ + M′′: Sc + Mo and V + Cr. For the chemically disordered structures, we also include the contribution from configurational entropy for an approximated synthesis temperature of 2000 K. For V_2–xCr_xAlB₂, both the orthorhombic and hexagonal phases show a strong preference for chemical disorder at all x, as concluded from the ordered candidate structures being at higher energy as compared to the disordered structures when an entropy contribution at 2000 K is considered. There is also a rather small spread in energy for the ordered candidates.

Figure 2.

Identification of structures with chemical order. Calculated energy difference between M′_2–xM′′_xAlB₂ and corresponding ternaries M′₂AlB₂ and M′′₂AlB₂ at 0 K as a function of x for chemically ordered (×) and disordered (solid line) candidate structures, assuming (a and b) Cmmm and (c and d) P6̅m2 symmetry of M′_2–xM′′_xAlB₂ for M′ + M′′ being (a and c) V + Cr and (b and d) Sc + Mo. For chemical disorder, the entropy contribution to the Gibbs free energy at 2000 K has also been approximated (dashed line). Comparison of different in-plane chemically ordered candidate structures and a schematic illustration of four stacking sequences identified for Mo_4/3Sc_2/3AlB₂ with (e) P6̅2m, (f) P6̅2c, (g) R3̅m, and (h) C2 symmetry along three zone axes. The unit cells are marked by black lines.

For Sc_2–xMo_xAlB₂, there is a larger spread in ΔE. For the Cmmm structure, most chemically ordered configurations have ΔE > 0, while for P6̅m2, all are negative (ΔE < 0). A comparison of chemically ordered and disordered structures, when also including a contribution from the configurational entropy, reveals that only the hexagonal system prefers chemical ordering, with low-energy candidate structures for 0.5 ≤ x ≤ 4/3. Of special interest are three configurations at x = 4/3, namely, those of P6̅2c, R3̅m, and C2 symmetries. A similar structure with P6̅2c symmetry is found 40 meV/atom higher in energy. These four ordered structures are schematically visualized in Figure 2e–h and all have a characteristic arrangement with M′ situated in a honeycomb lattice and M′′ positioned in the center of the hexagon forming a triangular lattice. The minority M′′ is extended out from the M layer toward the Al layer, in turn displaying an ideal Kagomé lattice. The boron layers are hexagonal. A comparison of the in-plane ordered structures with the original ternary P6̅m2 structure is shown in Figure S2. Phonon calculations of the chemically ordered Mo_4/3Sc_2/3AlB₂ with P6̅2m, P6̅2c, R3̅m, and C2 symmetries reveal that they are all dynamically stable (Figures S3–S6). The in-plane ordered structure in Figure 2e–h shows a close resemblance to i-MAX phases.^6,7 Consequently, we choose to collectively denote the in-plane-ordered MAB phases as i-MAB.

3.3. Phase Stability Screening of Metal Alloys M′_2–xM′′_xAlB₂

For an evaluation of the phase stability of M′_2–xM′′_xAlB₂ ({M′, M′′} = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co), we make two assumptions based on the result presented in Figure 2: (i) for the orthorhombic Cmmm structure, only disorder is considered, while (ii) for the hexagonal systems, disorder in the P6̅m2 symmetry is considered along with identified ordered i-MAB candidates P6̅2m, P6̅2c, R3̅m, and C2. It should be noted that modeling disorder in any of the four identified ordered structures yields results similar to those for P6̅m2 upon relaxation.

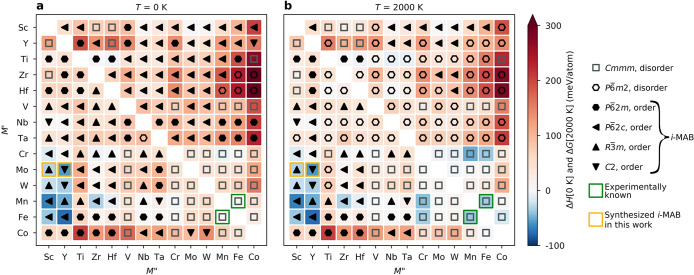
In Figure 3, an overview of the preferred chemical order (crystal symmetry) or disorder is shown for the 182 unique combinations of M′ and M′′. The trends in thermodynamic stability are visualized using a heat map, where M′ and M′′ are listed on the basis of the metal’s periodic group. The background color represents the calculated thermodynamic stability for the chemically ordered/disordered configuration of lowest energy, with the blue region representing stable phases (ΔH_cp or ΔG_cp < 0). We also use a symbol representation to denote the structure of lowest energy: Cmmm with disorder (open squares), P6̅m2 with disorder (open hexagons), i-MAB phases with P6̅2m (filled hexagons), P6̅2c (filled left triangles), R3̅m (filled up triangles), and C2 (filled down triangles) symmetries. In addition, experimentally known quaternary phases are marked by a green square. Identified equilibrium simplexes are listed in Table S2 for all combinations of M′ and M′′.

Figure 3.

Predicted phase stability for M′_4/3M′′_2/3AlB₂ alloys. (a) Calculated formation enthalpy at 0 K and (b) Gibbs free energy of formation at 2000 K. Symbols represent the crystal structure and chemical order of lowest energy for a given M′ and M′′: Cmmm with disorder (open squares), P6̅m2 with disorder (open hexagons), and in-plane-ordered i-MAB phases with P6̅2m (filled hexagons), P6̅2c (filled left triangles), R3̅m (filled up triangles), and C2 (filled down triangles) symmetries. Experimentally known phases are marked with squares: green (prior to this work) and yellow (this work).

Figure 3a depicts the calculated formation enthalpy at 0 K showing that a majority, 132, of the 182 elemental combinations of M′ and M′′ are ordered in a hexagonal structure. Out of these, 15 are stable (ΔH_cp < 0), with M′ mainly coming from groups 6 to 8 (Cr, Mo, W, Mn, and Fe) combined with M′′ from group 3 (Sc and Y). Of the four considered ordered structures, six systems have R3̅m symmetry, six have P6̅2c symmetry, two have C2 symmetry, and only one has P6̅2m symmetry. It should be noted that R3̅m, P6̅2c, and C2 are close in energy, within a few meV/atom, as they are structurally similar on a short-range scale. Another 13 ordered phases are close to stable, or metastable (0 < ΔH_cp < + 25 meV/atom).

For M₂AlB₂ and (Fe_2–xMn_x)₅AlB₂ phases, synthesis is typically performed in the range from 1000 to 1600 °C (1273 to 1873 K). To account for the contribution from configurational entropy to the Gibbs free energy at such temperatures, we use eqs 2 and 3 for the structures modeled with a disordered distribution of M′ and M′′ (SQS). We choose 2000 K as a representative temperature. The heat map in Figure 3b is constructed by comparing ΔH_cp of the chemically ordered candidate structures with ΔG_cp of the disordered Cmmm and P6̅m2, with colors and symbols used in line with Figure 3a.

At 2000 K, the number of chemically ordered and stable M′_4/3M′′_2/3AlB₂ phases is equal to the number identified at 0 K. This indicates that these 15 chemically ordered phases are not only thermodynamically stable with respect to the competing phases but also sufficiently stable toward the formation of chemical disorder at typical synthesis temperatures. This is a key result in the search for experimentally verifiable chemically ordered MAB phases.

Moreover, at 2000 K, the number of stable disordered phases has increased from 1 to 16. These are mainly found for the Cmmm structure, 14 out of 16, with combinations of M and M′′ being Cr, Mn, Fe, and Co. The latter includes the experimentally reported Fe_2–xMn_xAlB₂ (x = 0.67 and 1.33).¹⁵ In addition, 13 ordered and 17 disordered phases are found to be close to stable or metastable (0 < ΔH_cp or ΔG_cp < +25 meV/atom). The additional disordered phases are primarily Cmmm with combinations of M′ and M′′ from groups 6 to 8.

i-MAB is characterized by a 2:1 ratio of M′/M′′ and a size difference where M′′ should be at least 0.2 Å larger than M′. This is illustrated in Figure S11a, showing the calculated ΔH and ΔG (also indicated in Figure 3b) as a function of the atomic size difference between M′′ and M′. Most of the structures with a preference for chemical order (i.e., the i-MAB phases) display this size difference. This is in contrast to the identified preferred Cmmm structures with chemical disorder, where the size difference between M′ and M′′ is within ±0.2 Å. Correspondingly, P6̅m2 with disorder is preferred for −0.6 < r_M′′ – r_M′ < +0.2 Å. Compared to the ternary M₂AlB₂ phases, the large difference in atomic radius of M′ and M′′ in i-MAB induces a change in the out-of-plane coordinates for M′′ toward the Al layer, which in turn induces a change in the Al layer to form an ideal Kagomé lattice. The impact from the electronegativity of M′ and M′′ (Figure S11b) does not show as clear a correlation as found for the size difference between M′ and M′′. This in line with the common features reported for i-MAX phases.^7,41

To summarize selected key results from the thermodynamic stability evaluation of 182 M′_2–xM′′_xAlB₂ phases, a preference for chemical order is found for a 2:1 ratio between the M elements where M′′ is significantly larger than M′ (>0.2 Å). In most cases, this is fulfilled when M′ from groups 6 to 9 is combined with M′′ from group 3 (Sc and Y) and 4 (Zr and Hf). Of particular interest are eight ordered and thermodynamically stable candidates, M′_4/3M′′_2/3AlB₂ where M′ = Mo, W, Mn, and Fe and M′′ = Sc and Y, which allows systematic compositional alterations. However, M′ = Ti, Cr, and Mn and M′′ = Zr, Hf, and Nb are also fundamentally interesting, potentially expanding the elemental space and consequently the properties of these borides.

3.4. Synthesis and Characterization of Chemically Ordered i-MAB Phases

Out of the 15 ordered and stable i-MAB phases predicted in Figure 3b, bulk synthesis was attempted for Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB₂ by the solid-state reaction of a stoichiometric amount of elemental powder. The choice of M′ as Mo and M′′ as Y and Sc was motivated by their predicted stability, thermodynamic (Figure 3) and dynamic (Figures S3–S10), and the identified large size difference between Mo and Y/Sc.

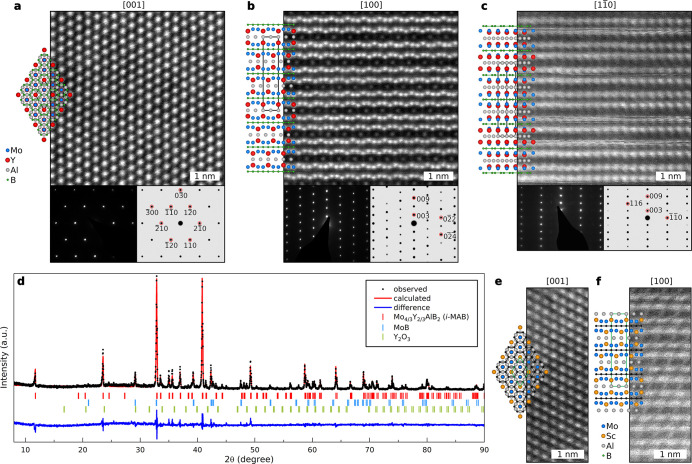
High-resolution scanning transmission electron microscopy (HRSTEM) images of the Mo_4/3Y_2/3AlB₂i-MAB phase along [001], [100], and [11̅0] zone axes are shown in Figure 4a–c, respectively. For the applied imaging conditions, the Mo and Y atoms are the brightest, the Al atoms are less bright, and B is too light to be visible. The schematics to the left of each micrograph show the atomic arrangements expected, assuming hexagonal Mo_4/3Y_2/3AlB₂ in space group R3̅m (no. 166).

Figure 4.

Characterization of synthesized Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB₂i-MAB phases. (a–c) In-plane chemical ordering of the i-MAB phase is evident from HRSTEM images along the [001], [100], and [11̅0] zone axes, respectively, with corresponding measured (left) and simulated (right) selected-area electron diffraction (SAED). Schematics to the left of each image represent the corresponding atomic arrangements considering the hexagonal R3̅m (no. 166) structure. (d) Rietveld refinement of XRD of the sample assuming space group R3̅m (no. 166). (e and f) In-plane chemical ordering of the Mo_4/3Sc_2/3AlB₂i-MAB phase as evident from HRSTEM images along the [001] and [100] zone axes, respectively.

From the top view in Figure 4a, the hexagonal structure is evident. Along the [11̅0] zone axis (Figure 4c), Mo and Y are superimposed, resulting in an average contrast strongly resembling M₂AlB₂ in Figure 1b. Along the [100] zone axis (Figure 4b), a “buckled” M layer consisting of a chemically ordered configuration of Mo and Y is indicated, with Y extending toward the Al layer. The relative contrast differences between Mo and Y are small, and the distinction between the two is not trivial. However, the suggested atomic arrangement is supported by the theoretical predictions and the indirect evidence from the M- and Al-layer interaction. Within the Al layer, spots of different contrast and spatial distribution are seen (Figure 4b) as a result of M′′ (most likely the larger Y atoms) being extended toward the Al layer, which in turn forms a Kagomé lattice, as also shown in the schematic representations in Figure S2. Furthermore, the in-plane-ordered i-MAB structure is also revealed by the measured and simulated selective area electron diffraction (SAED) shown in the insets of Figure 4a–c. Additional simulated SAEDs for all four polymorphs of i-MAB are shown in Figure S12. The structure based on space group R3̅m (no. 166) gives the best agreement with the experimental data.

The X-ray diffraction (XRD) pattern of a sample with nominal composition Mo_4/3Y_2/3AlB₂ is shown in Figure 4d. Rietveld refinement based on space group R3̅m (no. 166) is also included in the graph, with the refinement parameters listed in Table S3. The lattice parameters calculated from the XRD Rietveld analysis, a = 5.44577(9) Å and c = 22.69048(38) Å, are consistent with the theoretical values, a = 5.462 Å and c = 22.755 Å (Table S4). The other ordered candidate structures were also considered, but with resulting lower-quality fitting to the XRD pattern. Figure S14 shows a comparison between the measured XRD pattern and the simulated diffractograms from the four relaxed (using DFT) i-MAB structures, disordered Mo_4/3Y_2/3AlB₂, Mo₂AlB₂, and Y₂AlB₂ with P6̅m2 symmetry. The simulations further support space group R3̅m (no. 166) symmetry.

The metal ratios calculated from the energy-dispersive X-ray spectroscopy spectrum (EDX) are shown in Figure S13 with Mo/Y and (Mo + Y)/Al atomic ratios of 1.9 and 2.0, respectively, which are very close to the ideal ratio of 2.0.

Material synthesis of Mo_4/3Sc_2/3AlB₂ reveals the same i-MAB structure as found for Mo_4/3Y_2/3AlB₂. The schematic illustration and high-resolution STEM (HRSTEM) images (Figure 4e,f and Figure S15) show that the in-plane chemical order is evident only along the [100] zone axis (Figure 4f) where the M layers consist of brighter spots that correspond to Mo, with those that are not as bright corresponding to Sc, extending slightly toward the Al layer. This extension is less pronounced compared to Y in Mo_4/3Y_2/3AlB₂ since the size difference between Mo and Sc is smaller than that for Mo and Y. Along the [11̅0] zone axis, a mixed contribution of both Mo and Sc atoms is seen. This orientation looks identical to the hexagonal M₂AlB₂ shown in Figure 1b. Rietveld refinement of the XRD pattern (Figure S15d) based on space group R3̅m (no. 166), with the refinement parameters listed in Table S5, suggests that the majority of the sample consists of the i-MAB phase. Corresponding lattice parameters calculated from the XRD Rietveld analysis, a = 5.36261(8) Å and c = 22.44267(42) Å, are consistent with the theoretical values, a = 5.383 and c = 22.384 Å (Table S6). Calculated values are obtained at 0 K, while XRD was performed at room temperature. Compositional analysis from EDX gives Mo/Sc and (Mo + Sc)/Al ratios of 1.8 and 1.9, respectively, close to the ideal ratio of 2.0. This is shown in Figure S13. The i-MAB structure of Mo_4/3Sc_2/3AlB₂ is further supported in Figure S16 when comparing the measured XRD pattern with simulated diffractograms of the four i-MAB structures, disordered Mo_4/3Sc_2/3AlB₂, Mo₂AlB₂, and Sc₂AlB₂ with P6̅m2 symmetry. Note that the 110 peak in the XRD pattern at around 19.5°, corresponding to an interplanar distance of 4.5 Å, is a superstructure peak solely due to Mo/Sc chemical ordering which could potentially be quite useful for the identification of other in-plane-ordered 212 MAB phases. This 110 peak does not exist in the ternary Mo₂AlB₂ and Sc₂AlB₂ phases or in disordered Mo_4/3Sc_2/3AlB₂. However, it should be noted that for the Mo_4/3Y_2/3AlB₂i-MAB phase, the 110 peak is of too low an intensity to be visible, which implies that the 110 peak alone should not be used as a distinct fingerprint for claiming an i-MAB structure.

4. Discussion

The family of atomically laminated boride-based ternary materials has crystal structures of tetragonal and orthorhombic symmetry. The recent discovery of Ti₂InB₂ by Wang et al. revealed the first laminated hexagonal structure.¹¹ This hexagonal layered structure is composed of three elements, out of which one is a metal, which do not alone justify it to be classified as a MAX phase or grant an extension of the definition of MAX phases. The composition of hexagonal Ti₂InB₂ is analogous to general formula (MB)_zA_y(MB₂)_x of MAB phases (e.g., orthorhombic Cr₂AlB₂ and Cr₃AlB₄), which is different from the general M_n+1AX_n composition of MAX phases. Furthermore, the B atoms in Ti₂InB₂ occupy Wyckoff sites 1b and 1f with an M layer on each side, forming a honeycomb lattice with strong covalent B–B bonding rather than a triangular lattice such as X in MAX phases. This is due to the B/Ti ratio being 1, which is greater than the X/M ratios (n/(n + 1)) in conventional MAX phases. In principle, the Ti₂InB₂ phase as such could be seen as an extension of the concept of MAX phases but should, in our view, not be considered to be part of the MAX phase family. It should be noted that boron-based MAX phases have recently been discovered by Rackl et al.^42,43

A key requirement for obtaining chemical order upon metal alloying is an underlying hexagonal structure combined with a metal ratio M′/M′′ of 2:1 and a large enough size difference between the alloying metals. The hexagonal symmetry allows for relaxation of the Al layer into a perfect Kagomé lattice. This is a direct consequence of the larger M′′ (Y and Sc herein) being displaced from the smaller M′ (Mo herein) toward the Al layer, which in turn rearranges the relatively loosely bonded Al atoms. This is illustrated in Figure S17. Such relaxation is not possible from a symmetry point of view in tetragonal and orthorhombic structures. The 2:1 M′/M′′ ratio is of particular importance since a hexagonal lattice further allows for chemical order, where the M′ lattice forms a honeycomb lattice combined with a hexagonal M′′ lattice. Note that the Al layer acts as a local mirror plane. Moreover, metal alloying allows for the inclusion of additional elements not found in the traditional M₂AlB₂ phases, as exemplified by Y and Sc for herein stable and verified i-MAB phases but also for predicted stable i-MAB phases with Zr, Hf, and Nb and disordered MAB phases with V, Nb, and Ta. Furthermore, all of the four considered i-MAB candidates (with P6̅2m, P6̅2c, R3̅m, and C2 symmetries) are found to be dynamically stable, as shown for Mo_4/3Sc_2/3AlB₂ and Mo_4/3Y_2/3AlB₂ in Figures S3–S10. This indicates that the in-plane order of M′ and M′′, independent of different stackings, truly forms a stable structure and rules out some as-yet unobserved ordering phenomena stabilizing the synthesized material.

The herein reported discovery of a family of chemically ordered and atomically laminated boride alloys is profound and will from this point forward take inspiration from the hexagonal MAX phases and their 2D derivatives, MXenes. In 2017, metal alloying of a MAX phase revealed the first chemically ordered i-MAX phase, (Mo_2/3Sc_1/3)₂AlC.⁶ Since then, 32 different i-MAX phases have been realized experimentally.^{6−8,41,44−51} Out of these, four have so far been converted to 2D MXenes,^{6,8,9,52−57} displaying properties that are highly promising for energy storage and catalysis. Most importantly, the 3D i-MAX phase alloys can be converted to 2D using the concept of “targeted etching”, realizing either chemical ordering or vacancy ordering depending on the etching protocol.⁹

The similarities between i-MAB and i-MAX phases are many, as illustrated in Figure S17. Both require a 2:1 M′/M′′ ratio, with M′′ being significantly larger than M′, to form in-plane chemical order combining a honeycomb M′ lattice with a hexagonal M′′ lattice. Furthermore, the larger M′′ is displaced toward the Al/A layer, which induces an ideal Kagomé lattice for Al in i-MAB and a Kagomé-like lattice for A in i-MAX. With the vast and recent exploration of i-MAX phases and corresponding 2D MXenes, we expect further exploration of i-MAB phases, which, combined with suitable etching protocols, constitutes an exciting and facile route toward designing novel 2D materials with unprecedented properties.

5. Conclusions

Herein, we have considered the traditional orthorhombic and a recently discovered hexagonal M₂AB₂ crystal structures to investigate the possibility of chemical ordering upon metal alloying of metal borides. Through cluster expansion, four crystal structures exhibiting in-plane chemical order are identified and denoted as i-MAB phases. Combined with high-throughput predictive stability theory, we reduce the 182 hypothetical combinations to 15 predicted chemically ordered and stable i-MAB phases. The theoretical predictions were verified for Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB₂, showing hexagonal R3̅m (no. 166) crystal symmetry consistent with the simulations. Furthermore, we also predict 16 disordered alloys, altogether expanding the elemental space of these borides with five elements (Sc, Y, Zr, Hf, and Nb) not previously used in the ternary counterparts. On the basis of the results shown herein, we have identified a family of chemically ordered boride alloys, and it is reasonable to believe that (i) more i-MAB phases will be discovered, (ii) they have a high potential for conversion to a 2D counterpart through the selective etching of Al and possibly the alloying element, in line with i-MAX phases and their MXenes, and (iii) our combined theoretical approach may be of importance in the identification of chemically ordered structure in other atomically laminated boride-based ternary materials and hexagonal materials in general when metal alloying is considered.

Glossary

Abbreviations

i-MAB

in-plane-ordered quaternary MAB phase

i-MAX

in-plane-ordered quaternary MAX phase

SQS

special quasi-random structure.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c08113.

• Crystallographic data for Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB₂ including atomic coordinates; DFT-optimized crystallographic data and dynamical stability for all Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB candidate structures; equilibrium simplex, powder X-ray diffraction data for samples containing Mo_4/3Sc_2/3AlB₂; simulated powder X-ray diffractograms for all Mo_4/3Y_2/3AlB₂ and Mo_4/3Sc_2/3AlB candidate structures; additional electron microscopy images; additional simulated selected-area electron diffraction patterns; and EDX data (PDF)

The authors declare no competing financial interest.