A monolithic multiphase porous medium framework for (a-)vascular tumor growth

Abstract

We present a dynamic vascular tumor model combining a multiphase porous medium framework for avascular tumor growth in a consistent Arbitrary Lagrangian Eulerian formulation and a novel approach to incorporate angiogenesis. The multiphase model is based on Thermodynamically Constrained Averaging Theory and comprises the extracellular matrix as a porous solid phase and three fluid phases: (living and necrotic) tumor cells, host cells and the interstitial fluid. Angiogenesis is modeled by treating the neovasculature as a proper additional phase with volume fraction or blood vessel density. This allows us to define consistent inter-phase exchange terms between the neovasculature and the interstitial fluid. As a consequence, transcapillary leakage and lymphatic drainage can be modeled. By including these important processes we are able to reproduce the increased interstitial pressure in tumors which is a crucial factor in drug delivery and, thus, therapeutic outcome. Different coupling schemes to solve the resulting five-phase problem are realized and compared with respect to robustness and computational efficiency. We find that a fully monolithic approach is superior to both the standard partitioned and a hybrid monolithic-partitioned scheme for a wide range of parameters. The flexible implementation of the novel model makes further extensions (e.g., inclusion of additional phases and species) straightforward.

1. Introduction

Cancer is an extraordinarily complex disease. Nowadays it is clear that a combined, interdisciplinary effort from all natural sciences is necessary to de-convolute its complexity, advance our understanding of the illness and promote the discovery of new cures [1, 2]. The term “transport oncophysics”, recently coined in [3], describes such a “physical sciences lens” view of cancer as a disease of multiscale mass transport deregulation, which might provide a common background for physicists and doctors. Numerous mathematical models have been proposed to investigate the basic principles underlying cancer progression and predict the outcome of therapies. The comprehensive reviews [4, 5, 6, 7] classify these models into three major categories, namely discrete, hybrid and continuum models. Here, we want to focus on the latter ones, which are especially suited for larger scale systems governed by continuum mechanics. Hence, partial Differential equations can be formulated for the evolution of cancer-related variables such as cell volume fractions or oxygen concentrations, which are typically modeled as continuous fields [4].

Specifically, the more recent continuum multiphase models are more promising than previous simpler single-phase approaches. They take into account that the tumor micro-environment consists of multiple phases, such as Different cell genotypes, interstitial fluid (IF) and the extracellular matrix (ECM). Consequently, a more detailed and natural description with at least one solid and one liquid phase [4] characterizes these approaches. In [4, 8] they are roughly categorized into models based on mixture theory or Thermodynamically Constrained Averaging Theory (TCAT) [9, 10, 11]. Mixture theory models [12, 13] lack a stringent connection between microscale pore mechanics and macroscale closure relations [9]. By contrast, TCAT offers a consistent, rigorous and flexible framework for a systematic development of macroscale formulations from well-known microscale relations. Therefore, the current work will build on the multiphase tumor growth model derived from TCAT and introduced in [14], which will be described briefly hereafter.

The original version of the model [14] consists of four phases, one solid phase, the ECM, and three fluid phases, the interstitial fluid (IF), tumor cells (TC) and healthy cells (HC). The ECM is a mesh-like, porous structure composed mainly of collagen and elastin fibers. In its voids the IF flows and cell migration takes place. The IF is a mixture of water and biomolecules, e.g., nutrients or waste products and permeates the entire domain. TC and HC are only present in the regions with cancerous and healthy tissue, respectively. Additionally, two species are considered, namely oxygen diffusing in the IF and necrotic tumor cells which are modeled as inert. Constitutive relations for tumor growth, necrosis and nutrient, i.e., oxygen consumption have been formulated in [14]. Subsequently, the interactions of the fluid phases have been investigated in [15, 16] and a deformable ECM has been introduced in [17]. Recently, the model has been enhanced with cell lysis and matrix deposition [18].

The models mentioned above allow to study avascular tumor growth and hence exclude a crucial phase in the progression of tumors, namely angiogenesis, which is the formation of blood vessels from a pre-existing vasculature [19]. While it also occurs in other growth processes, it is of fundamental importance in cancer because tumors without their own vascular network are usually confined to a certain size beyond which they cannot grow any further and will become necrotic [20, 21, 22]. Without their own (neo-)vasculature tumors lack nutrients and oxygen. Under these conditions tumor cells produce so-called tumor angiogenic factors (TAF), which diffuse and stimulate the process of angiogenesis. Hereby, endothelial cells (EC), which line the existing blood vessels, migrate from the pre-existing vasculature towards the tumor [23]. The EC proliferate, sprout and finally form a new vascular network supplying the tumor with oxygen and other nutrients. However, this tumor vasculature is structurally and functionally abnormal since tumor vessels are tortuous, dilated and have uneven diameter leading to chaotic blood flow inside the tumor [20, 24, 25]. In addition, the vessels have a high permeability. This leakiness has been identified as a reason for elevated interstitial pressure of tumors because of increased outflow from the vessels [26, 27]. Together with inefficient drainage due to non-functional lymph vessels, this will cause a pressure increase in the interstitial fluid, which might hamper or even inhibit the success of drug delivery [25, 26, 28]. Nowadays, it is well-established that tumor growth is angiogenesis-dependent [21]. Also metastasis, i.e., the spreading of cancer to distinct regions of the body, may occur through the neovasculature developed by angiogenesis. Antiangiogenic cancer therapies to prevent angiogenesis, tumor progression and the metastatic spread are under research [19, 22], which underlines that angiogenesis is an essential trait in cancer progression shared by most tumor types [29]. Hence, modeling the vascular stage including angiogenesis is of utmost importance since together with metastatic tumor growth it is the clinically relevant stage in tumor progression, which actually causes the patient to die [5].

Consequently, angiogenesis has also been investigated through mathematical models. Again three major approaches are discerned in [4, 7], that is, continuum-based or discrete ones and hybrid combinations of the two. On the one hand, continuum models describe blood vessel densities rather than full vascular networks. On the other hand, discrete models resolve blood vessel morphology and blood flow through line segments, continuous curves, interconnected lattice patterns or collections of individual endothelial cells [4]. Two very prominent and often re-used methods are the ones developed by [30], where a continuum approach has been compared to a continuum-discrete approach based on a random walk formulation including migration, proliferation, branching and anastomosis. While earlier attempts did not include a dynamic coupling between angiogenesis and tumor growth, more advanced vascular tumor growth models such as [31, 32, 33] have evolved.

Despite the fact that discrete angiogenesis models are very helpful in investigating the formation of neovasculature in small regions, they seem to be prohibitively expensive in terms of computational cost for large-scale or even patient-specific simulations. The complex morphology of the neovasculature cannot be resolved then and it is questionable if a discrete model provides more relevant insight than a continuum formulation in this case. Hence, our goal in future work is to couple the continuum model presented here with a corresponding 1D model accounting for the existing vasculature, see e.g. [34, 35]. In the context of the continuum multiphase approach discussed above, endothelial cells have been introduced as an additional species in the IF by [36]. However, this approach is not sufficient and flexible enough to resolve the complex coupling between angiogenesis and tumor growth. We will show below that a consistent treatment of the neovasculature as an additional phase instead of a species enables us to resolve the interactions between the fluid phases, the ECM and angiogenesis more clearly. Additionally, the physiologically observed interstitial pressure increase in vascular tumors can be simulated with our extension. Finally, further improvements such as modeling blood flow in the neovasculature are straightforward which was not possible with the species-based version.

The remainder of this paper will be structured as follows: in Section 2, we will extend the avascular model to incorporate the neovasculature as a fifth phase. The coupling between the single fields will be elucidated in Section 3. In addition to the partitioned coupling utilized exclusively so far, a combined monolithic-partitioned as well as a fully monolithic scheme will be introduced. In Section 4, numerical examples will be provided to compare the performance of the presented solution approaches and to show that the novel five-phase-model is capable of simulating important processes of vascular tumor growth. Results and possible further extensions will be summarized in Section 5.

2. The Vascular Multiphase Tumor Growth Model

Our tumor growth model has been derived with Thermodynamically Constrained Averaging Theory. A detailed description of this mathematically intricate and complex procedure can be found in [11]. Here, we just want to emphasize that it is a comprehensive approach which guarantees a consistent relation between microscale and larger scale or homogenized conservation equations.

In addition, in a general porous medium system each phase may consist of multiple species. For instance, the interstitial fluid is not composed solely from water but transports numerous biomolecules. In the TCAT tumor growth model the considered species of the IF are oxygen and TAF. As indicated above, angiogenesis has been introduced into the multiphase model before [36], where endothelial cells have been treated as an additional species in the interstitial liquid. However, this is incorrect since endothelial cells do not qualify as a species diffusing within the IF from a biological point of view. They are not transported by the IF flow as nutrients or TAF. Rather, they have to be modeled as a proper phase with their own velocity and volume fraction as already hinted in [36]. This allows us to define consistent inter-phase exchange terms between the neovasculature and the IF. In the following formulation of the novel vascular multiphase model we will adopt the notation of [17], where α denotes a generic phase, s the solid phase, i.e., the ECM, l the interstitial fluid, h the healthy cells and t the tumor cells. In addition, the (neo-)vasculature is identified with index v and all equations are formulated on the macroscopic level. The components of the multiphase model are sketched in Figure 1.

Figure 1:

Components of the multiphase model

2.1. Modeling of Angiogenesis

The sum of all volume fractions ε^α has to satisfy the relation

$${\epsilon }^s+{\epsilon }^v+{\epsilon }^l+{\epsilon }^h+{\epsilon }^t=1,$$ (1)

where the volume fraction of the (neo-)vasculature ε^v with respect to the total volume has been introduced. In the model developed here the neovasculature can be interpreted as a separate porous network within the ECM, where blood flow takes place. It follows an evolution equation for its independent volume fraction ε^v due to endothelial cell migration and angiogenesis. This volume fraction provides room for blood flow coming from the pre-existing vasculature. However, the pre-existing vasculature and blood flow in the neovasculature is not explicitly modeled at the moment since the blood pressure in the neovasculature is assumed constant hereafter. So far, the fluid in the neovasculature, i. e. blood, only exchanges mass with the IF through transcapillary transport. Appropriate exchange terms depending on blood and IF pressure will be defined below. Still, the present formulation has been chosen to allow a high degree of flexibility for future extensions. Especially a coupling with 1D elements [34] and the corresponding smeared approach [35], describing the capillary bed through capillary volumetric ratios within tissue, lies at hand.

We begin with the definition of the porosity

$$\epsilon ={\epsilon }^l+{\epsilon }^h+{\epsilon }^t,$$ (2)

as the sum of all fluid volume fractions which allows us to get the volume fraction of the ECM from equation (1) as

$${\epsilon }^s=1-\epsilon -{\epsilon }^v.$$ (3)

Correspondingly, saturations of the fluid phases can be defined as

$$S^{\alpha }=\frac{{\epsilon }^{\alpha }}{\epsilon },\alpha \text{= }l\text{, }h\text{, }t\text{,}$$ (4)

which have to follow the relation

$$\sum _{\alpha }{S}^{\alpha }\text{= 1},\alpha \text{= }l\text{, }h\text{, }t.$$ (5)

As in [37] an Arbitrary Lagrangian Eulerian (ALE) form with solid phase velocity

$$v^s={\frac{\partial {\mathit{d}}^s}{\partial t}|}_X$$ (6)

will be employed for the formulation of the governing equations. We refer to material coordinates as X, spatial coordinates as x, displacements as d^s and spatial gradients as ∇. The skeleton or solid phase velocity v^s is then equivalent to the grid velocity in an ALE approach. With that, a formulation of the evolution equation for the neovasculature volume fraction reads as

$${\frac{\partial {\epsilon }^v}{\partial t}|}_X+{\epsilon }^{\mathit{v}}\mathbf{\nabla }\cdot {\mathit{v}}^s+\mathbf{\nabla }\cdot ({\epsilon }^{\mathit{v}}({\mathit{v}}^{\mathit{v}}-{\mathit{v}}^s))=0.$$ (7)

The relative motion of endothelial cells v^v − v^s with respect to the solid phase velocity is approximated as

$${\epsilon }^v(v^v-v^s)\approx -D^v\mathbf{\nabla }{\epsilon }^v+{\epsilon }^v\epsilon S^l{}_{\chi }({\omega }^{TAF\overline{l}})\mathbf{\nabla }{\omega }^{TAF\overline{l}},$$ (8)

which results in a standard formulation governing angiogenesis also applied in [30, 36]. Herein, the first term on the right hand side represents random motion of EC at sprout tips modeled as molecular diffusion with mass diffusivity D^v. The second term accounts for chemotaxis with a varying chemotactic coefficient $\chi ({\omega }^{TAF\overline{l}})$ as in [30] while in [36] it has been chosen to be constant. The latter one is the response of EC on TAF produced by hypoxic tumor cells, i.e., tumor cells which lack oxygen. Its exact form is detailed in Section 2.6. TAF as chemical species diffuse and are advected by the IF, which creates a chemical gradient triggering EC migration. After degrading the venule basement membrane, EC migrate towards the tumor following the TAF gradient as described by the second term in equation (8). So far, we have excluded the haptotactic response of EC on fibronection [30], which would result in a similar additional term depending on the fibronectin gradient. The final equation for angiogenesis, that is, the evolution equation of the neovasculature volume fraction emerges as

$${\frac{\partial {\epsilon }^v}{\partial t}|}_X+{\epsilon }^v\mathbf{\nabla }\cdot v^s-\mathbf{\nabla }\cdot (D^v\mathbf{\nabla }{\epsilon }^v)+\mathbf{\nabla }\cdot ({\epsilon }^v\epsilon S^l{}_{\chi }({\omega }^{TAF\overline{l}})\mathbf{\nabla }{\omega }^{TAF\overline{l}})=0$$ (9)

when inserting (8) in (7). Equation (9) constitutes one governing equation of the five-phase model. The volume fraction of the neovasculature ε^v enters the model as an additional primary variable. Suitable Dirichlet boundary conditions for the neovasculature volume fraction can be applied at positions, where angiogenesis might occur from blood vessels. The coupling to this pre-existing vasculature as in [34, 35] will be a topic of further research while the focus of this contribution lies on the formation of the neovasculature governed by equation (9) and its impact on the multiphase tumor growth model.

2.2. Extensions to the Original Model Equations of the Fluid Phases

Incorporating a fifth phase into the model as described above requires several extensions to the original equations. However, we do not want to repeat all derivations here, the interested reader is referred to [17] for the original model. As opposed to the derivations there, we will employ an ALE formulation. The ALE equation for the balance of mass of the solid phase is given by

$${\frac{\partial [{\rho }^s(1-\epsilon -{\epsilon }^v)]}{\partial t}|}_X+{\rho }^s(1-\epsilon -{\epsilon }^v)\mathbf{\nabla }\cdot v^s=\sum _{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}$$ (10)

Herein, the sum ${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}$ in TCAT notation denotes a generic mass transfer term for all phases k with the solid phase s, which might be used to model ECM deposition, see [18]. Solving equation (10) for the time derivative of porosity results in

$${\frac{\partial \epsilon }{\partial t}|}_X=\frac{(1-\epsilon -{\epsilon }^v)}{{\rho }^s}{\frac{\partial {\rho }^s}{\partial t}|}_X+(1-\epsilon -{\epsilon }^v)\mathbf{\nabla }\cdot v^s-{\frac{\partial {\epsilon }^v}{\partial t}|}_X-\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}}{{\rho }^s}.$$ (11)

For a generic fluid phase α, the balance of mass [17] reads as

$$\frac{\epsilon S^{\alpha }}{{\rho }^{\alpha }}{\frac{\partial {\rho }^{\alpha }}{\partial t}|}_X+S^{\alpha }{\frac{\partial \epsilon }{\partial t}|}_X+\epsilon {\frac{\partial S^{\alpha }}{\partial t}|}_X+\epsilon S^{\alpha }\mathbf{\nabla }\cdot v^s-\mathbf{\nabla }\cdot \left(\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\mathbf{\nabla }{p}^{\alpha }\right)=\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}}{{\rho }^{\alpha }},$$ (12)

where a generalized Darcy equation

$$\epsilon S^{\alpha }(v^{\alpha }-v^s)=-\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\mathbf{\nabla }{p}^{\alpha }$$ (13)

with fluid pressure p^α has been employed. Again, only generic mass transfer terms for all phases k exchanging mass at the interfaces with the phase α have been given, which will be elaborated in Section 2.6. Besides, the viscosity μ_α, relative permeability $k_{rel}^{\alpha }$ and the intrinsic permeability tensor k of the ECM have been defined, which is assumed as isotropic. Inserting the time derivative of porosity (11) in the previous equation and re-arranging terms yields

$$\frac{\epsilon S^{\alpha }}{{\rho }^{\alpha }}{\frac{\partial {\rho }^{\alpha }}{\partial t}|}_X+\frac{S^{\alpha }(1-\epsilon -{\epsilon }^v)}{{\rho }^s}{\frac{\partial {\rho }^s}{\partial t}|}_X+\epsilon {\frac{\partial S^{\alpha }}{\partial t}|}_X-S^{\alpha }{\frac{\partial {\epsilon }^v}{\partial t}|}_X+S^{\alpha }(1-{\epsilon }^v)\mathbf{\nabla }\cdot v^s-\mathbf{\nabla }\cdot \left(\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\mathbf{\nabla }{p}^{\alpha }\right)=\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}}{{\rho }^{\alpha }}+S^{\alpha }\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}}{{\rho }^s}.$$ (14)

Finally, the constitutive equations for fluid and solid phase densities

$$\frac{1}{{\rho }^{\alpha }}\frac{\partial {\rho }^{\alpha }}{\partial {\rho }^{\alpha }}=\frac{1}{K_{\alpha }}\text{and}\frac{1}{{\rho }^s}\frac{\partial {\rho }^s}{\partial {\rho }^s}=\frac{1}{K_s}$$ (15)

with respective bulk moduli and K_α and K_s are employed to obtain

$$\frac{\epsilon S^{\alpha }}{K^{\alpha }}{\frac{\partial {\rho }^{\alpha }}{\partial t}|}_X+\frac{S^{\alpha }(1-\epsilon -{\epsilon }^v)}{K_s}{\frac{\partial {\rho }^s}{\partial t}|}_X+\epsilon {\frac{\partial S^{\alpha }}{\partial t}|}_X-S^{\alpha }{\frac{\partial {\epsilon }^v}{\partial t}|}_X+S^{\alpha }(1-{\epsilon }^v)\mathbf{\nabla }\cdot v^s-\mathbf{\nabla }\cdot \left(\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\mathbf{\nabla }{p}^{\alpha }\right)=\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}}{{\rho }^{\alpha }}+S^{\alpha }\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}}{{\rho }^s}.$$ (16)

In the previous two equations the solid pressure p^s has been employed, whose significance will be elucidated in Section 2.4. Comparing our formulation of the balance of mass with the one of the previous four-phase model [8, 17], three additional terms can be identified, namely, the time derivative of the mass fraction of the neovasculature scaled with the saturation, the additional time derivative of the solid pressure scaled with the negative volume fraction of the neovasculature −ε^v and the additional divergence of the grid velocity scaled with the negative volume fraction of the neovasculature −ε^v. These terms have been introduced since the modified balance of mass of the solid phase (10) incorporates the neovasculature volume fraction. Note also that no saturation gradient multiplied with solid phase velocity v^s is present in the above form as opposed to the one of [17]. This is due to our ALE formulation.

In previous works on the tumor growth model [8, 15, 17] the fluid equations have been specialized consistent with a pre-chosen set of primary variables

$$\mathit{\psi }=[{\psi }^1,\dots ,{\psi }^{n_{\text{fld}}}]$$ (17)

for the n_fld Different fluid phases, where the primary variables ψ^α can be selected from saturations S^α, pressures p^α or Differential pressures p^αβ = p^α − p^β. We wanted to keep our framework as flexible as possible, which is why we allow the user to specify the primary variables suited for the specific problem (as long as they are independent from one another). Assuming an incompressible solid phase (K_s → ∞) and re-writing equation (16) in terms of the chosen generic primary variables ψ^α yields

$$\frac{\epsilon S^{\alpha }}{K^{\alpha }}\sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial {\rho }^{\alpha }}{\partial {\psi }^{\beta }}{\frac{\partial {\psi }^{\beta }}{\partial t}|}_X+\epsilon \sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial S^{\alpha }}{\partial {\psi }^{\beta }}{\frac{\partial {\psi }^{\beta }}{\partial t}|}_X-S^{\alpha }{\frac{\partial {\epsilon }^v}{\partial t}|}_X+S^{\alpha }(1-{\epsilon }^v)\mathbf{\nabla }\cdot v^s-\mathbf{\nabla }\cdot \left(\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial {\rho }^{\alpha }}{\partial {\psi }^{\beta }}\mathbf{\nabla }{\psi }^{\beta }\right)=\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}}{{\rho }^{\alpha }}+S^{\alpha }\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}}{{\rho }^s},$$ (18)

where pressure and saturation derivatives have been transformed to generic primary variables derivatives. For instance, to obtain the reformulation of the time derivative of the saturation the constitutive relations for the pressure-saturation relationships have to be employed, see [15, 16] and Appendix A.

2.3. Species Transport

Chemical species disperse in specific phases, where they are advected and diffused. From TCAT, the balance of mass of a species i with mass fraction ${\omega }^{i\overline{\alpha }}$ in phase α emerges as

$${\rho }^{\alpha }\epsilon S^{\alpha }{\frac{\partial {\omega }^{i\overline{\alpha }}}{\partial t}|}_X+{\rho }^{\alpha }\epsilon S^{\alpha }(v^{\alpha }-v^s)\cdot \mathbf{\nabla }{\omega }^{i\overline{\alpha }}+\mathbf{\nabla }\cdot ({\rho }^{\alpha }\epsilon S^{\alpha }{\omega }^{i\overline{\alpha }}{u}^{i\overline{\alpha }})=\sum _{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{i\kappa \to i\alpha }{M}+{\epsilon }^{\alpha }{r}^{i\alpha }-{\omega }^{i\overline{\alpha }}\sum _{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}.$$ (19)

Herein, u^iα denotes the diffusive velocity of species i. On the right hand side of the equation three distinct mass transfer terms can be discerned: the first one represents transfer of mass of species i in all phases k to the considered species i in phase α and the second one indicates an intra-phase reaction term. The last term is obtained from employing the product rule in the balance of species mass, see e.g. [14]. The relative mass flux in the convective term is again approximated with the generalized Darcy equation (13) and for the diffusive flux Fick’s law with effective diffusivity $D_{\text{eff}}^{i\alpha }$ is employed [14], which results in the final mass balance formulation for species transport

$${\rho }^{\alpha }\epsilon S^{\alpha }{\frac{\partial {\omega }^{i\overline{\alpha }}}{\partial t}|}_X-{\rho }^{\alpha }\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\mathbf{\nabla }{p}^{\alpha }\cdot {\omega }^{i\overline{\alpha }}-\mathbf{\nabla }\cdot ({\rho }^{\alpha }\epsilon S^{\alpha }{D}_{\text{eff}}^{i\alpha }\mathbf{\nabla }{\omega }^{i\overline{\alpha }})=\sum _{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{i\kappa \to i\alpha }{M}+{\epsilon }^{\alpha }{r}^{i\alpha }-{\omega }^{i\overline{\alpha }}\sum _{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}.$$ (20)

The respective mass transfer terms will be detailed in Section 2.6.

2.4. Solid Phase

In porous media the stress tensor σ acting on the solid phase is commonly defined using the effective stress principle as

$${\mathit{\sigma }}_{\text{eff}}^s={\mathit{\sigma }}_{\text{tot}}^s+p^{s}I$$ (21)

where ${\sigma }_{\text{eff}}^s$ and ${\sigma }_{\text{tot}}^s$ denote the effective and total stress, respectively. Furthermore, I is the identity matrix and p^s the aforementioned solid pressure. The solid pressure is the combined pressure of all phases acting on the solid phase. Usually, it is obtained as a weighted sum of the fluid pressures with their respective saturation [38]. A suitable definition of the solid pressure including the neovasculature phase is

$$p^s=\frac{\epsilon }{\epsilon +{\epsilon }^v}\sum _{\beta =1}^{n\text{fld}}{S}^{\alpha }{p}^{\alpha }+\frac{{\epsilon }^v}{\epsilon +{\epsilon }^v}{p}^{\text{blood}}.$$ (22)

The weighted sum of fluid pressures and saturations is the definition of the solid pressure in the previous versions of the model. If no neovasculature exists, the original definition is recovered. If it is present, also the neovasculature with blood pressure p^blood must enter the formulation, which is why the additional term and the additional pre-factors have been introduced. However, blood flow has not yet been included into the model. Therefore, we will assume a constant blood pressure for now. As mentioned before, we plan to enhance the model by also considering blood flow in the future.

Pulled-back into the material configuration and using the second Piola-Kirchhoff stresses S equation (21) can alternatively be written as

$$S_{\text{eff}}^s=S_{\text{tot}}^s+J{F}^{-1}\cdot F^{-T}{p}^s$$ (23)

using the deformation gradient

$$F=I+\frac{\partial d^s}{\partial X}$$ (24)

and its determinant J. The displacements d^s are the primary variable of the solid phase. In the absence of body and dynamic forces the balance of momentum of the solid phase in material configuration is then given by

$${\mathbf{\nabla }}_0\cdot (F\cdot {\mathit{S}}_{\text{eff}}^s-F\cdot J{F}^{-1}\cdot F^{-T}{p}^s)=0$$ (25)

with the material divergence operator ∇₀.

2.5. Summary of the Coupled System

The multiphase model has been implemented in our code in a very general way such that a coupled system with an arbitrary number of fluid phases n_fld and species n_spec can be defined. The governing equations of such a system are summarized here:

$${\mathbf{\nabla }}_0\cdot (F\cdot {\mathit{S}}_{\text{eff}}^s-F\cdot J{F}^{-1}\cdot F^{-T}{p}^s)=0\text{\hspace{1em}\hspace{1em}in}{\mathrm{\Omega }}_{\text{0}}\times [{\text{t}}_0,{\text{t}}_{\mathrm{E}}]$$ (26)

$${\frac{\partial {\epsilon }^v}{\partial t}|}_X+{\epsilon }^v\mathbf{\nabla }\cdot v^s-\mathbf{\nabla }\cdot (D^v\mathbf{\nabla }{\epsilon }^v)+\mathbf{\nabla }\cdot ({\epsilon }^v\epsilon S^l{}_{\chi }({\omega }^{TAF\overline{l}})\mathbf{\nabla }{\omega }^{TAF\overline{l}})=0\text{\hspace{1em}\hspace{1em}in}{\mathrm{\Omega }}_{\text{t}}\times [{\text{t}}_0,{\text{t}}_{\mathrm{E}}]$$ (27)

for α ∈ [1, …, n_fld − 1]:

$$\frac{\epsilon S^{\alpha }}{K^{\alpha }}\sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial {\rho }^{\alpha }}{\partial {\psi }^{\beta }}{\frac{\partial {\psi }^{\beta }}{\partial t}|}_X+\epsilon \sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial S^{\alpha }}{\partial {\psi }^{\beta }}{\frac{\partial {\psi }^{\beta }}{\partial t}|}_X-S^{\alpha }{\frac{\partial {\epsilon }^v}{\partial t}|}_X+S^{\alpha }(1-{\epsilon }^v)\mathbf{\nabla }\cdot v^s-\mathbf{\nabla }\cdot \left(\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial {\rho }^{\alpha }}{\partial {\psi }^{\beta }}\mathbf{\nabla }{\psi }^{\beta }\right)=\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}}{{\rho }^{\alpha }}+S^{\alpha }\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}}{{\rho }^s}\text{\hspace{1em}\hspace{1em}in}{\mathrm{\Omega }}_{\text{t}}\times [{\text{t}}_0,{\text{t}}_{\mathrm{E}}]$$ (28)

for α = n_fld:

$$\sum _{\gamma =1}^{n_{\text{fld}}}\left(\frac{\epsilon S^{\gamma }}{K_{\gamma }}\sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial p^{\gamma }}{\partial {\psi }^{\beta }}{\frac{\partial {\psi }^{\beta }}{\partial t}|}_X\right)-{\frac{\partial {\epsilon }^v}{\partial t}|}_X+(1-{\epsilon }^v)\mathbf{\nabla }\cdot v^s-\sum _{\gamma =1}^{n_{\text{fld}}}\left(\mathbf{\nabla }\cdot \left(\frac{k_{rel}^{\gamma }k}{{\mu }_{\gamma }}\sum _{\beta =1}^{n_{\text{fld}}}\frac{\partial {\rho }^{\gamma }}{\partial {\psi }^{\beta }}\mathbf{\nabla }{\psi }^{\beta }\right)\right)=\sum _{\gamma =1}^{n_{\text{fld}}}\left(\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \gamma }{M}}{{\rho }^{\gamma }}\right)+\frac{{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}}{{\rho }^s}\text{\hspace{1em}\hspace{1em}in}{\mathrm{\Omega }}_{\text{t}}\times [{\text{t}}_0,{\text{t}}_{\mathrm{E}}]$$ (29)

for i ∈ [1,…, n_spec]:

$${\rho }^{\alpha }\epsilon S^{\alpha }{\frac{\partial {\omega }^{i\overline{\alpha }}}{\partial t}|}_X-{\rho }^{\alpha }\frac{k_{rel}^{\alpha }k}{{\mu }_{\alpha }}\mathbf{\nabla }{p}^{\alpha }\cdot \mathbf{\nabla }{\omega }^{i\overline{\alpha }}-\mathbf{\nabla }\cdot ({\rho }^{\alpha }\epsilon S^{\alpha }{D}_{\text{eff}}^{i\alpha }\mathbf{\nabla }{\omega }^{i\overline{\alpha }})=\sum _{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{i\kappa \to i\alpha }{M}+{\epsilon }^{\alpha }{r}^{i\alpha }-{\omega }^{i\overline{\alpha }}\sum _{\kappa \in {\mathcal{J}}_{\text{c}\alpha }}\stackrel{\kappa \to \alpha }{M}\text{\hspace{1em}\hspace{1em}in}{\mathrm{\Omega }}_{\text{t}}\times [{\text{t}}_0,{\text{t}}_{\mathrm{E}}]$$ (30)

Note that the balance of momentum of the solid phase (26) has been formulated w.r.t. the reference or material configuration Ω₀ while all other equations are written in spatial configuration Ω _t. Furthermore, the considered time interval is denoted with [t₀, t_E]. If no angiogenesis occurs, the additional governing equation for angiogenesis (27) with primary variable ε^v is not evaluated and the original formulation is recovered for ε^v = 0. The equation for the last fluid phase (29) is obtained by summing up the mass balances of all involved fluid phases and invoking equation (5), which has also been employed in prior versions of the model. Three fluid phases, namely, tumor cells t, healthy cells h and the interstitial fluid l will be considered and three species, oxygen in the IF, necrotic tumor cells as a part of the tumor cells and TAF dispersed in the IF. In the numerical examples of Section 4 the interstitial fluid will always be the summed-up phase governed by equation (29). Despite that, also this choice is flexible in our framework.

2.6. Constitutive Equations

Additional constitutive relations are necessary to close the governing equations. For the sake of completeness, we have listed all constitutive equations which have been adopted unchanged in Appendix A.

A Perzyna viscoplastic model has been employed in [17, 18, 36] for the ECM remodeling. In this work, the focus does not lie on the ECM behavior which is why we will solely employ hyperelastic materials hereafter even though a Perzyna type model is available in our implementation. Furthermore, we adopt a total Lagrangian formulation as opposed to the updated Lagrangian one applied in the aforementioned papers.

In the previous implementation of the model the porosity has been updated over time using explicit time integration. Here, we propose an alternative approach based on the balance of mass of the solid phase in the material configuration

$${\frac{\partial {\rho }^s(1-\epsilon -{\epsilon }^v)}{\partial t}|}_X=0.$$ (31)

For the sake of simplicity, no source terms in the balance of mass are considered, i.e., no matrix deposition. However, a corresponding mass transfer term can easily be added. Integration gives

$$J\cdot {\rho }^s(1-\epsilon -{\epsilon }^v)={\rho }_0^s(1-\epsilon {}_0-{\epsilon }_0^v)=\text{const}.$$ (32)

with initial density ${\rho }_0^s$, initial porosity ε₀, initial neovasculature volume fraction ε₀ and the Jacobian of the deformation gradient J. With the constitutive equation for the density of the solid phase (15) the ratio of initial and current density can be expressed in terms of the solid pressure and the bulk modulus, which yields

$$\epsilon =1-{\epsilon }^v-\frac{1-\epsilon {}_0-{\epsilon }_0^v}{J}e{}^{-\frac{p^s}{K_s}}.$$ (33)

In case of an incompressible solid phase the previous equation will become

$$\epsilon =1-{\epsilon }^v-\frac{1-\epsilon {}_0-{\epsilon }_0^v}{J}.$$ (34)

In the following, we will assume an incompressible solid phase as in all previous versions of the model. Otherwise, the equation for the solid pressure (22) would become nonlinear and might have to be solved with a local Newton iteration.

For the non-constant chemotactic coefficient $\chi ({\omega }^{TAF\overline{l}})$ of equation (9) we employ the same receptor-namely kinetic law as [30], namely

$$\chi ({\omega }^{TAF\overline{l}})={\chi }_0\frac{{\omega }_{{\chi }_0/2}^{TAF\overline{l}}}{{\omega }_{{\chi }_0/2}^{TAF\overline{l}}+{\omega }^{TAF\overline{l}}}.$$ (35)

The above equation incorporates a decreasing sensitivity of endothelial cells to the TAF gradients if the TAF mass fraction increases. At a mass fraction of ${\omega }_{{\chi }_0/2}^{TAF\overline{l}}$ the sensitivity is exactly half the value of the constant sensitivity ${\chi }_0$.

Finally, a summary of the constitutive equations for the mass transfer terms of equations (27)–(30) is given in Table 1. Here, some of the equations such as the terms for tumor growth ${\stackrel{l\to t}{M}}_{\text{growth}}$, necrosis ε^tr^Nt and nutrient consumption $\stackrel{l\to t}{M}$ are listed, see [14, 15, 17] and Appendix A for an interpretation of the terms. Lysis and ECM deposition as introduced in [18] are not considered in this paper but the two additional mass transfer terms can easily be included.

Table 1:

Mass transfer terms for vascular tumor growth

Entity	Symbol	Term
Extracellular matrix	${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}s}}\stackrel{\kappa \to s}{M}$	= 0
Healthy cells	${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}h}}\stackrel{\kappa \to h}{M}$	= 0
Tumor cells	${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}l}}\stackrel{\kappa \to t}{M}$	= ${\stackrel{l\to t}{M}}_{\text{growth}}$
Interstitial fluid	${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}l}}\stackrel{\kappa \to l}{M}$	= ${\stackrel{l\to t}{M}}_{\text{growth}}+{\stackrel{v\to l}{M}}_{\text{leak}}-{\stackrel{l\to ly}{M}}_{\text{drainage}}$
Necrotic tumor cells	${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}t}}\stackrel{N\kappa \to Nt}{M}+{\epsilon }^t{r}^{Nt}-{\omega }^{N\overline{t}}{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}t}}\stackrel{\kappa \to t}{M}$	= ${\epsilon }^t{r}^{Nt}-{\omega }^{N\overline{t}}{\stackrel{l\to t}{M}}_{\text{growth}}$
Oxygen	${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}l}}\stackrel{n\kappa \to nl}{M}+{\epsilon }^l{r}^{nl}-{\omega }^{n\overline{l}}{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}l}}\stackrel{\kappa \to l}{M}$	= $\stackrel{nl\to t}{M}+\stackrel{nv\to nl}{M_{\text{tc}}}-{\omega }^{n\overline{l}}\left({\stackrel{v\to l}{M}}_{\text{leak}}-{\stackrel{l\to t}{M}}_{\text{growth}}\right)$
Tumor angiogenic factors	${\sum }_{\kappa \in {\mathcal{J}}_{\text{c}l}}\stackrel{TAF\kappa \to TAFl}{M}+{\epsilon }^l{r}^{TAFl}-{\omega }^{TAF\overline{l}}{\sum }_{\kappa \in {\mathcal{J}}_{\text{c}l}}\stackrel{\kappa \to l}{M}$	= $\stackrel{TAFt\to TAFl}{M}-{\omega }^{TAF\overline{l}}\left({\stackrel{v\to l}{M}}_{\text{leak}}-{\stackrel{l\to t}{M}}_{\text{growth}}\right)$

Additional terms have been defined to account for the coupling between angiogenesis and tumor growth. Specifically, the mass balance of the interstitial fluid comprises two supplementary terms, namely the leakage of fluid from the neo-vasculature due to abnormal vessel characteristics and the uptake of interstitial fluid by the lymph system. The first term is defined as

$${\stackrel{v\to l}{M}}_{\text{leak}}={\rho }_l\cdot {\left(L_p\frac{S}{V}\right)}_v\cdot {\langle p^{\text{eff}}-p^l\rangle }_{+}\cdot {\epsilon }^v,$$ (36)

employing a Starling equation with hydraulic conductivity L_p and surface-to-volume ratio S/V for the transcapillary flow as for example given in [28, 31]. A net outflow from the vessels into the interstitial fluid is generated if the effective pressure

$$p^{\text{eff}}=p^{\text{blood}}-\omega ({\pi }^{\text{blood}}-{\pi }^l)$$ (37)

is higher than the fluid pressure p^l. Herein, ω denotes the average osmotic reflection coefficient of the plasma and π^blood and π^l are the osmotic pressures of the plasma and the interstitial liquid, respectively. Macaulay brackets are employed to allow only outflow of liquid into the interstitium and not vice versa. Furthermore, it is assumed that the vessel outflow of (36) is also proportional to the volume fraction of the neovasculature ε^v. We emphasize again that the blood pressure is constant in this version of the model and blood flow is not explicitly modeled. This will be a topic of further research. In addition, the term ${\stackrel{l\to ly}{M}}_{\text{drainage}}$ is employed to model the drainage of interstitial fluid through the lymph system. Functioning lymph vessels remove excessive liquid as well as waste products. However, in many tumors this mechanism is impaired since the proliferating cancer cells compress or even collapse the lymph vessels [20, 27, 28]. Combined with the increased outflow due to the irregular and leaky blood vessels this plays a major role for interstitial hypertension in tumors [20, 27, 28]. We have defined the drainage of liquid as

$${\stackrel{l\to ly}{M}}_{\text{drainage}}={\rho }_l\cdot {\left(L_p\frac{S}{V}\right)}_{ly}\cdot {\langle p^{\text{l}}-p^{\text{ly}}\rangle }_{+}\cdot {\langle 1-\frac{p^t}{p_{\text{coll}}^t}\rangle }_{+},$$ (38)

which is a slightly adapted version of the lymphatic drainage term from [31]. Again, a Starling equation is defined for the outflow of liquid into the lymph system. Additionally, the tumor pressure-induced collapse of the lymph vessels is considered by the last factor of (38). Until the collapsing pressure p^t_coll the drainage capacity of the lymph system decreases linearly. Above this pressure the lymph vessels have collapsed and no uptake of fluid is possible anymore. In the following, we will assume that the lymphatic pressure is small compared to the other pressures of the multiphase system, that is, p^ly ≈ 0. Until now, the lymph system is not explicitly present in the model as a proper phase, which might be a straightforward extension. Analogous to [31] our model can easily be extended employing a lymphatic density or volume fraction. It might then also be possible to model the evolution of the lymph vessel system with a similar equation as (9) also taking into account lymphangiogenesis [39].

As a simplification of the mass transfer relations for species, we will assume that fluid drainage through the lymph system does not influence the mass balance of the species dispersed in the IF, i.e., oxygen and TAF, which implies

$$\stackrel{il\to ily}{M}-{\omega }^{i\overline{l}}\cdot \left(-{\stackrel{l\to ly}{M}}_{\text{drainage}}\right)=0.$$ (39)

If interstitial liquid is drained, the corresponding species is taken up in equal measure by the lymph system.

An important mechanism of angiogenesis is the transport of nutrients to the tumor. In our case the only nutrient present is oxygen dispersed in IF and blood. The transcapillary exchange of this species is modeled by the term

$$\stackrel{nv\to nl}{M_{\text{tc}}}={\omega }_{\text{env}}^{n\overline{l}}{\stackrel{v\to 1}{M}}_{\text{leak}}+{\rho }_l{\left(\frac{S}{V}\frac{D_{tc}}{t}\right)}_v\cdot {\langle {\omega }_{\text{env}}^{n\overline{l}}-{\omega }^{n\overline{l}}\rangle }_{+}\cdot {\epsilon }^v.$$ (40)

Herein, the first summand denotes the flow of oxygen dissolved in the plasma with mass fraction ${\omega }_{\text{env}}^{n\overline{l}}$ due to transcapillary leakage ${\stackrel{v\to l}{M}}_{\text{leak}}$. The second term is employed for the transcapillary diffusion with diffusion coefficient D_tc and blood vessel wall thickness t. Again, it is assumed that this term is proportional to the volume fraction of the neovasculature. More advanced terms for transcapillary oxygen exchange including the haematocrit level in blood have been employed by [32, 40]. The relation for oxygen exchange may be refined once our model is capable of representing blood flow in the neovasculature.

Finally, the production of TAF by tumor cells under hypoxia will be detailed. We assume that all the TAF produced by the living tumor cells are immediately transferred into the interstitial liquid via

$$\stackrel{TAFt\to TAFl}{M}\approx {\epsilon }^t{r}^{TAFt}=(1-{\omega }^{N\overline{t}})\epsilon S^t\cdot {\gamma }_{\text{production}}^{\text{TAF}}\cdot H\left({\omega }_{\text{hyp}}^{n\overline{l}}-{\omega }^{n\overline{l}}\right)\left[\frac{1}{2}+\frac{1}{2}\text{cos}\left(\pi \frac{{\omega }^{n\overline{l}}}{{\omega }_{\text{hyp}}^{n\overline{l}}}\right)\right]$$ (41)

with an intra-phase production term ε^tr^TAFt equivalent to [36]. By employing the Heaviside function H(·) it is ensured that TAF are produced by the living tumor cells at a rate of ${\gamma }_{\text{production}}^{\text{TAF}}$ production only if the nutrient mass fraction falls below the hypoxic limit ${\omega }_{\text{hyp}}^{n\overline{l}}$. Currently, the uptake of TAF through endothelial cells [36] has not been included, however, the extension is straightforward if the results indicate that this term is necessary. Hence, all mass transfer relations summarized in Table 1 have been defined.

3. Numerical Solution and Computational Framework

The original tumor growth model of [8, 15, 17] with the extensions presented in the previous section has been re-implemented in our in-house finite element high performance computing platform [41]. In the following, the efficient solution of the resulting strongly coupled problem will be addressed.

3.1. Space and Time Discretization

The standard Galerkin procedure is employed to obtain the weak form of the governing equations (26)–(30) of the coupled system with n_fld fluid phases and n_spec chemical species. Subsequently, the equations are discretized in space using finite elements [42]. For that, the primary variables of the single fields are interpolated using shape functions. Finally, time discretization with the well-known one-step-theta scheme is performed. More details on space and time discretization can be found in [8, 15, 17, 42].

The time- and space-discrete weak form of the strong formulation (26)–(30) may then be written in terms of discrete nonlinear residuals R at time step n + 1 as

$$R_{n+1}^{\text{s}}(d_{n+1}^s,{\psi }_{n+1},{\mathit{ϵ}}_{n+1}^v)=0\text{with}{R}_{\text{n}+1}^{\text{s}}\in {ℝ}^{{\text{n}}_{\text{nodes}}\cdot {\text{n}}_{\text{dim}}}$$ (42)

$$R_{n+1}^{\text{v,fld}}(d_{n+1}^s,{\psi }_{n+1},{\mathit{ϵ}}_{n+1}^v,{\omega }_{n+1})=0\text{with}{R}_{\text{n}+1}^{\text{v,fld}}\in {ℝ}^{{\text{n}}_{\text{nodes}}\cdot ({\text{n}}_{\text{fld}}+1)}$$ (43)

$$R_{n+1}^{\text{spec}}(d_{n+1}^s,{\psi }_{n+1},{\mathit{ϵ}}_{n+1}^v,{\omega }_{n+1})=0\text{with}{R}_{\text{n}+1}^{\text{spec}}\in {ℝ}^{{\text{n}}_{\text{nodes}}\cdot {\text{n}}_{\text{spec}}}$$ (44)

with nodal primary variables

$$d_{n+1}^s\in {ℝ}^{n_{\text{nodes}}\cdot n_{\text{dim}}},{\psi }_{n+1}\in {ℝ}^{n_{\text{nodes}}\cdot n_{\text{fld}}},{\mathit{ϵ}}_{n+1}^v\in {ℝ}^{n_{\text{nodes}}},{\omega }_{n+1}\in {ℝ}^{n_{\text{nodes}}\cdot {\text{n}}_{\text{spec}}},$$ (45)

which are the discrete form of solid displacements, fluid primary variables, neovasculature volume fraction and species mass fractions at time step n + 1, respectively. Furthermore, n_dim represents the number of spatial dimensions and n_nodes the number of nodes. In this notation R^s is the discrete residual of the solid (42). R^v,fld encompasses both the discrete residual of the equation for the neovasculature (27) as well as the equations for all fluid phases (28) and (29). The third residual term R^spec_n+1 denotes the discrete residual of all present species corresponding to (44). The coupling between these three fields can be resolved either through a partitioned scheme or a monolithic scheme. In the former one iterations between the single-field solvers have to be performed to ensure the nonlinear coupling. By contrast, in the latter one all three fields are solved simultaneously. Previously, the model could only be solved using a partitioned coupling [17]. In the following, we will present three solution strategies for the strongly coupled nonlinear system (42)–(44). If angiogenesis is not considered, the equations reduce to a simpler form without the additional discrete angiogenesis equation and neovasculature volume fraction. However, we want to focus on the more general case including angiogenesis in the following.

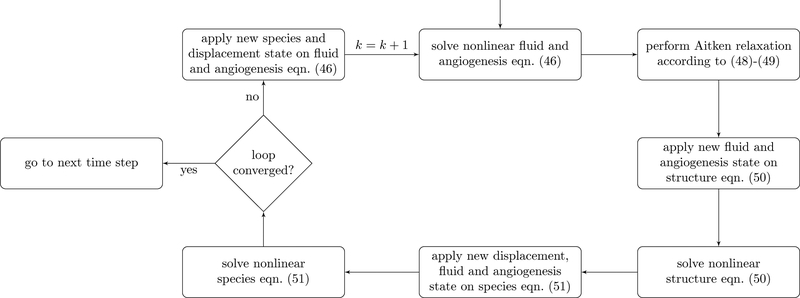
3.2. Partitioned Scheme

The major advantage of partitioned schemes is their flexibility since existing solvers for the single fields can be re-used [43] and their easy implementation compared to monolithic algorithms. Each of the single blocks (42)–(44) is solved individually for its primary variables. Then, the coupling variables are transferred between the fields. Our algorithm for the three-field coupled partitioned scheme is presented in Figure 2. First, the nonlinear problem (43) including the neovasculature equation at the partitioned step k is solved with a Newton scheme

$${\left[\frac{\partial R^{\text{fld,v}}}{\partial {\psi }^v}\right]}_{n+1,k}^i\mathrm{\Delta }{\psi }_{n+1,k}^{v,i+1}=-R_{n+1,k}^{\text{fld,v},i},{\psi }_{n+1,k}^{v,i+1}={\psi }_{n+1,k}^{v,i}+\mathrm{\Delta }{\psi }_{n+1,k}^{v,i+1}$$ (46)

for each Newton iteration i → i + 1. Herein, a nodal primary variable vector ψ^v, which comprises both the generic nodal fluid primary variables ψ as well as the nodal neo-vasculature primary variable ε^v has been defined as

$${\psi }^v=\left[\begin{array}{c}\psi \\ {\epsilon }^v\end{array}\right]$$ (47)

to account for the fact that the nonlinear discrete fluid mass balance equations and the neovasculature evolution equation are solved simultaneously. This fluid and angiogenesis solution is then transferred to the structure equation after performing relaxation with Aitken’s Δ² method [44, 45]. The relaxed solution is constructed as

$${\psi }_{n+1,k}^v={\psi }_{n+1,k-1}^v+{\omega }_k\left({\psi }_{n+1,k}^v-{\psi }_{n+1,k-1}^v\right)$$ (48)

with Aitken relaxation parameter ω_k. This parameter is defined recursively as

$${\omega }_k=-{\omega }_{k-1}\frac{{\left({\psi }_{n+1,k}^v-{\psi }_{n+1,k-1}^v\right)}^T\cdot \left(\left({\psi }_{n+1,k}^v-{\psi }_{n+1,k-1}^v\right)-\left({\psi }_{n+1,k-1}^v-{\psi }_{n+1,k-2}^v\right)\right)}{\Vert \left({\mathit{\psi }}_{n+1,k}^v-{\mathit{\psi }}_{n+1,k-1}^v\right)-\left({\mathit{\psi }}_{n+1,k-1}^v-{\mathit{\psi }}_{n+1,k-2}^v\right){\Vert }^2}.$$ (49)

from the two previous solutions of the partitioned loop. Aitken relaxation significantly improves the convergence behavior and stability of the partitioned scheme. The major advantage of this type of relaxation compared to the one employed in [17, 46] is that the governing equations do not have to be modified. Furthermore, Aitken relaxation is flexible, easy to implement and has only negligible computational cost, which is why it is preferred here. In almost all practical cases, which we investigated, convergence without relaxation was impossible to obtain. The new relaxed state ψ^v_n+1,k is transferred to the structure equation (42), which can in turn be solved with a Newton scheme

$${\left[\frac{\partial R^{\text{s}}}{\partial d^s}\right]}_{n+1,k}^i\mathrm{\Delta }{d}_{n+1,k}^{s,i+1}=-R_{n+1,k}^{\text{s,i}},d_{n+1,k}^{s,i+1}=d_{n+1,k}^{s,i}+\mathrm{\Delta }{d}_{n+1,k}^{s,i+1}$$ (50)

Finally, the solution, i.e., displacements d^s_n+1,k as well as (relaxed) fluid primary variables and neovasculature volume fractions ψ^v_n+1,k are applied to (44). Again, this nonlinear equation is solved with a Newton scheme

$${\left[\frac{\partial R^{\text{spec}}}{\partial \omega }\right]}_{n+1,k}^i\mathrm{\Delta }{\omega }_{n+1,k}^{i+1}=-R_{n+1,k}^{\text{spec,i}},{\omega }_{n+1,k}^{i+1}={\omega }_{n+1,k}^i+\mathrm{\Delta }{\omega }_{n+1,k}^{i+1}$$ (51)

for the n_spec present species, i.e., equation (44) is solved simultaneously for all considered species. However, in the current formulation coupling terms between Different species arise only in the mass transfer terms summarized in Table 1. Lastly, the new species state ω_n+1,k is fed back to the discrete angiogenesis and fluid equation (43). This loop is repeated until convergence has been achieved. Subsequently, the algorithm progresses to the next time step. We assume convergence if the relative change in the solution primary variables from one partitioned iteration step to the next is smaller than a pre-defined tolerance ϵ_part, i.e.,

$$\frac{\Vert {\psi }_{n+1,k}^v-{\psi }_{n+1,k-1}^v\Vert }{\Vert {\psi }_{n+1,k}^v\Vert }<{ϵ}_{\text{part}}\text{\hspace{1em}and\hspace{1em}}\frac{\Vert d_{n+1,k}^s-d_{n+1,k-1}^s\Vert }{\Vert d_{n+1,k}^s\Vert }<{ϵ}_{\text{part}}\text{\hspace{1em}and\hspace{1em}}\frac{\Vert {\omega }_{n+1,k}-{\omega }_{n+1,k-1}\Vert }{\Vert {\omega }_{n+1,k}\Vert }<{ϵ}_{\text{part}}.$$ (52)

Also the single field Newton schemes need a suitable convergence criterion. Naturally, it has to be defined stricter than the partitioned convergence criterion of (52) such that the error in the single field solvers does not influence the convergence of the partitioned loop. Again, we check for relative increments from one Newton step to the next with a single field tolerance of

$${ϵ}_{\text{sf}}=0.01{ϵ}_{\text{part}}$$ (53)

In addition, a further check

$$\frac{\Vert R_{n+1,k}^{\text{fld,v}}\Vert }{\sqrt{n_{\text{nodes}}\cdot (n_{\text{fld}}+1)}}<{ϵ}_{\text{sf}}\text{\hspace{1em}and\hspace{1em}}\frac{\Vert R_{n+1,k}^{\text{spec}}\Vert }{\sqrt{n_{\text{nodes}}\cdot n_{\text{dim}}}}<{ϵ}_{\text{sf}}\text{\hspace{1em}and\hspace{1em}}\frac{\Vert R_{n+1,k}^{\text{s}}\Vert }{\sqrt{n_{\text{nodes}}\cdot n_{\text{spec}}}}<{ϵ}_{\text{sf}}.$$ (54)

guarantees that also the residuals of the single fields have reached convergence within their Newton loop. Here, the RMS norm is employed to have a mesh-independent quantity.

Figure 2:

Algorithm for one time step of partitioned scheme

3.3. Monolithic-partitioned Scheme

From our experience of similar porous medium systems [37, 47] along with the numerical examples of Section 4, most of the computational time is spent in resolving the coupling between the structural deformation and the fluid flow or angiogenesis, respectively. Hence, in a first step, the nonlinear coupling between these two fields (42)–(43) can be resolved monolithically while for the coupling with species transport still a partitioned scheme is employed. The corresponding algorithm is depicted in Figure 3a. Now, a monolithic Newton scheme with the tangent containing off-diagonal derivative terms typical for monolithic algorithms

$${\left[\begin{array}{cc}\frac{\partial R^{\text{s}}}{\partial d^s}& \frac{\partial R^{\text{s}}}{\partial {\psi }^v}\\ \frac{\partial R^{\text{fld,v}}}{\partial d^s}& \frac{\partial R^{\text{fld,v}}}{\partial {\psi }^v}\end{array}\right]}_{n+1,k}^i{\left[\begin{array}{c}\mathrm{\Delta }{d}^s\\ \mathrm{\Delta }{\psi }^v\end{array}\right]}_{n+1,k}^{i+1}=-{\left[\begin{array}{c}{R}^{\text{s}}\\ R^{\text{fld,v}}\end{array}\right]}_{n+1,k}^i,{\left[\begin{array}{c}{d}^s\\ {\psi }^v\end{array}\right]}_{n+1,k}^{i+1}={\left[\begin{array}{c}{d}^s\\ {\psi }^v\end{array}\right]}_{n+1,k}^i+{\left[\begin{array}{c}\mathrm{\Delta }{d}^s\\ \mathrm{\Delta }{\psi }^v\end{array}\right]}_{n+1,k}^{i+1}$$ (55)

is applied to simultaneously solve for the unknown nodal displacements d^s_n+1 and fluid and neovasculature nodal primary variables ψ^v_n+1. These are then applied to the species transport equation, which is again solved by the Newton scheme (51). The species solution is applied on the fluid and the iteration is continued until convergence. The convergence check for the partitioned scheme is given by (52) as before. Relative increments and the residual criterion defined in (54) are employed to assess convergence of the species field and the monolithic Newton scheme (55) with tolerance ϵ_sf defined by (53).

Figure 3:

Algorithms for one time step of hybrid and monolithic coupling

3.4. Monolithic Scheme

Finally, the three-way coupled nonlinear system (42)–(44) can be solved with a fully monolithic scheme resulting in the following Newton scheme

$${\left[\begin{array}{ccc}\frac{\partial R^{\text{s}}}{\partial d^s}& \frac{\partial R^{\text{s}}}{\partial {\psi }^v}& 0\\ \frac{\partial R^{\text{fld,v}}}{\partial d^s}& \frac{\partial R^{\text{fld,v}}}{\partial {\psi }^v}& \frac{\partial R^{\text{fld,v}}}{\partial \omega }\\ \frac{\partial R^{\text{spec}}}{\partial d^s}& \frac{\partial R^{\text{spec}}}{\partial {\psi }^v}& \frac{\partial R^{\text{spec}}}{\partial \omega }\end{array}\right]}_{n+1}^i{\left[\begin{array}{c}\mathrm{\Delta }{d}^s\\ \begin{array}{l}\mathrm{\Delta }{\psi }^v\\ \mathrm{\Delta }\omega \end{array}\end{array}\right]}_{n+1}^{i+1}=-{\left[\begin{array}{c}{R}^{\text{s}}\\ \begin{array}{l}{R}^{\text{fld,v}}\\ R^{\text{spec}}\end{array}\end{array}\right]}_{n+1}^i,{\left[\begin{array}{l}\begin{array}{c}{d}^s\\ {\psi }^v\end{array}\\ \omega \end{array}\right]}_{n+1}^{i+1}={\left[\begin{array}{c}{d}^s\\ \begin{array}{l}{\psi }^v\\ \omega \end{array}\end{array}\right]}_{n+1}^i+{\left[\begin{array}{c}\mathrm{\Delta }{d}^s\\ \begin{array}{l}\mathrm{\Delta }{\psi }^v\\ \mathrm{\Delta }\omega \end{array}\end{array}\right]}_{n+1}^{i+1}.$$ (56)

Compared to the monolithic tangent matrix of the fluid-structure coupling, additional off-diagonal matrices have been added as well as the main-diagonal tangent matrix of the species equation. Note also the zero diagonal matrix $\frac{\partial R^{\text{s}}}{\partial \mathit{\omega }}$ reflecting the fact that no coupling terms of species quantities arise in the structure equation (42). The fully monolithic algorithm of Figure 3b simply requires a solution of the monolithic Newton scheme (56) for each time step until the desired tolerance is met. For that, residuals in RMS norm (54) as well as relative increments (53) are employed with the Newton loop.

3.5. Efficient Solvers for Monolithic Schemes

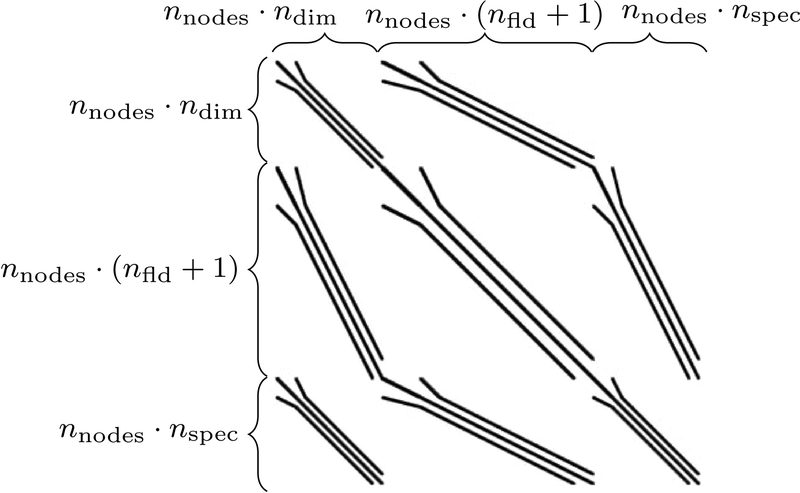
For each Newton step of the monolithic algorithm from Figure 3b, a linear system of equations with 3 × 3 block pattern shown in Figure 4 has to be solved while the monolithic-partitioned approach requires solving the corresponding 2 × 2 sub-system. The distinct fields represented by their respective sparse main-and off-diagonal blocks introduce their Different physical characteristics and parameters into the system often leading to a bad conditioning of the system matrix. Hence, standard iterative linear solvers cannot be applied without sophisticated, problem-specific preconditioners. Efficient preconditioners are a major factor for improving the performance of monolithic algorithms since the linear solver time usually constitutes a considerable amount of the total computational time. The preconditioners employed in this work are based on [43], where an efficient solution framework for an arbitrary number of fields has been developed and applied to thermo- and fluid-structure interaction. We will re-use this implementation here. Recently, it has also been applied to a coupled model of the human lung [48]. A detailed description of these preconditioning techniques is beyond the scope of this contribution but the general idea behind them will be outlined briefly. Basically, they consist of a block Gauss-Seidel (BGS) method combined with an algebraic multigrid (AMG) method. Here, we will exclusively apply the first variant which is termed BGS(AMG) preconditioner in [43]. In an outer iteration the fields are decoupled with the BGS approach and in an inner AMG cycle the single fields are then preconditioned independently. However, a detailed scalability and parameter study for Different solver types as in [43, 48] is beyond the scope and extent of this paper.

Figure 4:

Typical sparsity pattern of monolithic system (56)

4. Numerical Examples

4.1. Performance Comparison between Monolithic and Partitioned Approaches

In this section, we will perform a concise evaluation of the performance of the solution schemes developed above. We have chosen the growth of a multicellular tumor spheroid (MTS) over 120 hours in host tissue within a deformable ECM as a representative benchmark. Similar cases have been studied in [15, 17]. Initial and boundary conditions are given in Appendix B. Our primary interest here is to assess the efficiency of the proposed algorithms, which is why we will not show any significant biological results. In addition, angiogenesis is not present. Furthermore, a simple Saint Venant-Kirchhoff material model is employed for the ECM. However, the results in terms of numerical performance are transferable to the more complicated material laws employed in [17, 18].

The parameters of the benchmark problem have been taken from [17, Table 3, 4, 5] with exception of the value of the Young’s modulus, which we have chosen as E = 400 Pa for the Saint Venant-Kirchhoff material model. The primary variables of the fluid phases are the pressure p^l of the interstitial fluid and Differential pressures p^hl and p^th for the healthy and tumor cells, respectively. A backward Euler scheme, that is, θ = 1, is employed for time discretization with 720 steps of Δt = 600s. The BGS(AMG) method is employed for preconditioning the monolithic systems (55) and (56) in combination with a GMRES iterative linear solver. For solving the linear systems of equations of the single fields in the partitioned scheme also the GMRES method with AMG preconditioners is applied. We employ a strict outer convergence criterion for the monolithic and partitioned schemes of 1.0 · 10⁻⁶, which implies that the single field tolerances for convergence according to (53) are 1.0 · 10⁻⁸. For performance comparison all simulations have been run in parallel on two cores of an Intel Xeon E5–2690 v4 dual socket system which has been specially configured to allow reliable time measurements (cluster-on-die mode and forced C0 state).

Table 3:

Parameters for the fluid phases of the 2D angiogenesis example

Quantity	Symbol	Value	Unit
Density of the fluid phases [15]	ρl, ρh, ρt	1000	kg/m3
HC-IF interfacial tension [15]	σhl	72	mN/m
TC-HC interfacial tension [15]	σth	36	mN/m
TC-IF interfacial tension [15]	σtl	108	mN/m
Coefficient a in saturation-pressure relationship [15]	a	590	Pa
Coefficient b in saturation-pressure relationship [15]	b	1	–
Dynamic viscosity of IF [15]	μl	0.01	Pa/s
Dynamic viscosity of HC and TC [15]	μh, μt	20	Pa/s
Exponent in the relative permeability law for IF [15]	Al	4	–
Exponent in the relative permeability law for HC and TC [15]	Ah, At	2	–
Initial porosity in the domain [15]	ε0	0.8	–
Growth coefficient of tumor cells [17]	${\gamma }_{\text{growth}}^t$	4 · 10−2	kg/(m3s)

Table 4:

Parameters for the species of the 2D angiogenesis example

Quantity	Symbol	Value	Unit
Diffusion coefficient of oxygen in IF [15]	$D_0^{nl}$	3.2 · 10−9	m2/s
Coefficient δ for nonlinear diffusion law of oxygen in IF [15]	δ	2	—
Diffusion coefficient of TAF in IF [36]	DTAFl	3.5 · 10−4	m2/s
Diffusion coefficient of NTC in TC [14]	DNt	0	m2/s
Normal mass fraction of oxygen in tissue [17]	${\omega }_{\text{env}}^{n\overline{l}}$	4.2 · 10−6	—
Critical mass fraction of oxygen [17]	${\omega }_{\text{crit}}^{n\overline{l}}$	1.0 · 10−6	—
Limit mass fraction of oxygen for hypoxia [36]	${\omega }_{\text{hyp}}^{n\overline{l}}$	4.0 · 10−6	—
Necrosis coefficient [17]	${\gamma }_{\text{necrosis}}^t$	1 · 10−2	kg/(m3s)
Consumption related to growth [17]	${\gamma }_{\text{growth}}^{nl}$	2 · 10−4	kg/(m3s)
Consumption related to normal metabolism [17]	${\gamma }_{\text{0}}^{nl}$	3 · 10−4	kg/(m3s)
Production rate of TAF under hypoxia [36]	${\gamma }_{\text{production}}^{\text{TAF}}$	1 · 10−3	kg/(m3s)

Table 5:

Parameters for angiogenesis, transcapillary and lymphatic exchange

Quantity	Symbol	Value	Unit
Diffusion coefficient of neovasculature or EC (half the value of [30])	Dv	5 · 10−15	m2/s
Chemotactic coefficient (see comment in text)	χ0	case 1: 5 · 10−3 case 2: 1 · 10−2 case 3: 2 · 10−2	m2/s m2/s m2/s
Constant for receptor-kinetic law (35) [30]	${\omega }_{{\chi }_0/2}^{TAF\overline{l}}$	1 · 10−10	–
Blood pressure in capillaries [27, 31]	pblood	2660	Pa
Osmotic pressure difference [31]	ω(πblood – πl)	1333	Pa
Hydraulic conductivity for transcapillary flow [31, 50]	Lp,v	2.1 · 10−11	m/(Pas)
Surface-to-volume ratio for transcapillary flow [50]	(S/V)v	2 · 104	m−1
Hydraulic conductivity for lymphatic drainage (see comment in text)	Lp,ly	1 · 10−9	m/(Pas)
Surface-to-volume ratio for lymphatic drainage (same as (S/V)v)	(S/V)ly	2 · 104	m−1
Threshold for lymphatic vessel collapse (see comment in text)	$p_{\text{coll}}^t$	500	Pa
Transcapillary diffusion coefficient over wall thickness (see comment in text)	Dtc/t	case 1: 2 · 10−5 case 2: 1 · 10−5 case 3: 5 · 10−6	m/s m/s m/s

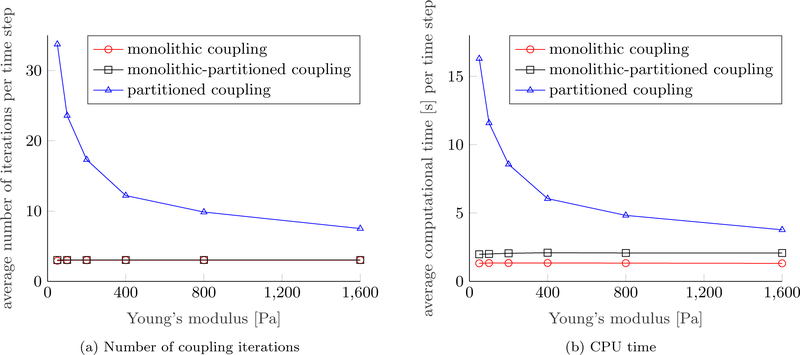
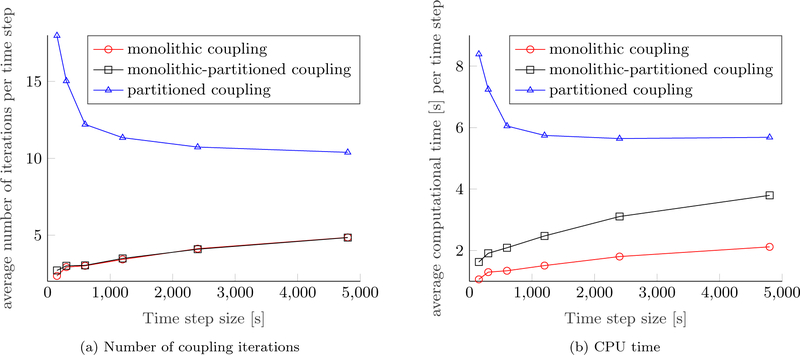
Figure 5 depicts the number of coupling iterations, i.e., the number of Newton steps for the monolithic scheme and the number of partitioned iterations for the partitioned and monolithic-partitioned algorithm, respectively. The schemes which resolve the coupling between the fluid phases and the ECM monolithically exhibit a very stable convergence behavior with three coupling iterations on average compared to the partitioned one, which needs a mean of twelve partitioned steps per time step to converge. Clearly, this behavior is due to the strong coupling between fluid phases and structure. Around time step 300 a necrotic core starts to develop, which means that an additional species, namely, necrotic cells are present. Therefore, the coupling between the fluid phases and the species becomes stronger, such that more partitioned iterations are necessary, which is why the partitioned and hybrid scheme show a peak for their respective number of coupling iterations. Still, the fully monolithic scheme converges within three Newton iterations throughout the simulation except for some time steps at the beginning of the simulation. Naturally, the number of coupling iterations is closely coupled to the CPU time per time step also shown in Figure 5. Evidently, the monolithic-partitioned solution procedure is less efficient in terms of computational time than the fully monolithic one even if the same number of coupling iterations is required since more linear solver calls and element evaluations are needed in total. The small amplitudes in computational time are related to how often the monolithic system (55) has to be evaluated for each time step, which differs slightly for some steps. Still, both monolithic schemes are far superior than the partitioned one with a speed-up of approximately 4.5 and 2.9, respectively. We have also tried to induce a small compressibility of the fluid and solid phases of approximately 10% by reducing their bulk moduli to 10, 000 Pa to test if a slight compressibility was beneficial to the convergence of the partitioned scheme but only an insignificant gain in performance could be achieved. Only for even smaller, yet unrealistic bulk moduli, a substantial effect was present.

Figure 5:

Number of coupling iterations and calculation time per time step

We have conducted a small parameter study on the Young’s modulus of the ECM to further evaluate the efficiency of the distinct approaches. The performances of the Different schemes are shown in Figure 6. The Young’s modulus of the ECM is varied while all other parameters are fixed to the values of [17, Table 3, 4, 5]. A softer ECM effects a stronger coupling between the fluid and solid phases. Consequently, the performance of the partitioned scheme deteriorates considerably as shown by the average number of coupling iterations and the average CPU time per time step in Figures 6a and 6b. Increasing the stiffness of the ECM has an opposing effect leading to smaller deformations and, hence, a weaker coupling, which can more easily be resolved by the partitioned algorithm. By contrast, the performance of the monolithic and monolithic-partitioned algorithm is unaffected by the choice of the Young’s modulus.

Figure 6:

Performance of coupling schemes depending on Young’s modulus

For a rigid ECM, i.e., a non-moving mesh (not shown here) the fully monolithic algorithm’s performance compared to the partitioned coupling was still superior, albeit only by a factor of 1.6, which proves that resolving the coupling between solid and fluid phases is the most challenging part. Hence, this factor seems to be the additional performance gain for resolving the coupling fluid-species with a monolithic scheme. Actually, it is also the difference in performance between the fully monolithic scheme and the monolithic-partitioned scheme from above for a deformable ECM.

Interestingly, the number of monolithic Newton steps decreases even marginally for a softer ECM. This hides the effect that the GMRES iterative linear solver with BGS(AMG) preconditioner needs more iterations and more computational time to resolve the stronger coupling between fluid and structure phases when the ECM is less stiff. In that regard, it is important to emphasize that for systems of larger size than considered here a suboptimal scaling of the employed preconditioner could slightly deteriorate the performance of the monolithic schemes. Even under these circumstances the partitioned algorithm with its large number of coupling iterations can certainly not compete with the monolithic ones.

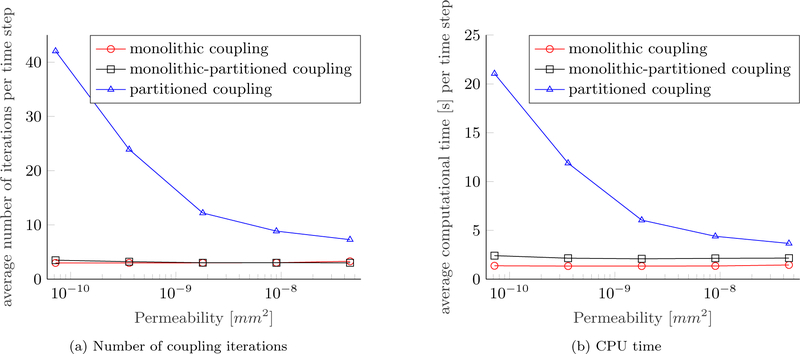
A further study has been conducted on the intrinsic permeability of the ECM. Results are depicted in Figure 7. Again, all other parameters are equivalent to [17, Table 3, 4, 5] and the Young’s modulus is re-set to E = 400 Pa. A similar picture as in Figure 6 emerges. Lower permeabilities lead to a stronger coupling between fluid phases and the solid phase since larger pressures and pressure gradients develop in the computational domain. The lower the permeability of the ECM, the less efficient the partitioned scheme while both monolithic schemes do not show any change in performance. As before, three coupling iterations are needed on average per time step for a wide range of permeabilities while the computational time for the iterative linear solver increases minimally due to the stronger coupling for lower permeabilities. The computational time of the partitioned algorithm decreases for higher permeabilities, however, both monolithic schemes are still faster by at least a factor of 2.5 and 1.7, respectively.

Figure 7:

Performance of coupling schemes depending on permeability

Finally, we have investigated the influence of the time step size Δt. This is due to the fact that [49] found a lower limit for the ratio of time step size and element length Δt/h² to guarantee convergence of a partitioned solution scheme for a consolidation problem of similar type. The existence of this lower limit for a given set of material parameters implies that the time step size cannot be reduced arbitrarily if the mesh is not refined at the same time [17]. With the aim of triggering this instability we have performed a study on the time step size while leaving the material parameters and the mesh unchanged. The results are depicted in Figure 8. The behavior predicted by [49] can be reproduced in this case. Below a time step size of Δt = 600 s the number of coupling iterations starts to increase indicating that the partitioned scheme becomes unstable for the given material parameters and discretization. Still, convergence could be achieved even for the smallest time step size considered in Figure 8, which is probably due to the employed Aitken relaxation. Both monolithic algorithms exhibit a completely Different behavior. If the time step size is decreased, the Newton algorithm converges in less iterations and vice versa, just as expected. Nevertheless, even for the largest time step of Δt = 4800 s the partitioned solution procedure cannot compete with the monolithic algorithms.

Figure 8:

Performance of coupling schemes depending on time step size Δt

As expected the fully monolithic coupling is the most efficient scheme for a wide range of parameter sets. For both monolithic schemes the computational cost is nearly independent of material and simulation parameters in this relatively small yet elucidating example. In the context of tumor growth, where many parameters might be unknown or uncertain, such an efficient algorithm is especially advantageous. The scalability of the monolithic algorithms depends strongly on efficient preconditioners, whose performance has been evaluated in [43, 48]. We expect that the excellent scalability is transferable to the multiphase framework as well. It might also be worth employing the AMG(BGS) preconditioner which is the reversed version of the BGS(AMG) method [43]. Theoretically, it should perform better than the BGS(AMG) variant for strongly coupled problem. We will continue to investigate optimal solvers for the monolithic system.

Despite the fact that the computational effort of the partitioned solution procedure might become prohibitively large for certain parameter combinations, it has proven to be remarkably stable in combination with Aitken relaxation. Obviously, its inferior performance can be attributed to the strong coupling between incompressible fluid and solid phases. If a rigid ECM is considered, the partitioned algorithm is still slower than the fully monolithic one but might be worth considering for a fast implementation of the model. It has to be noted, though, that we have restricted the comparison to a relatively simple example without considering angiogenesis. In more complex scenarios the partitioned algorithm is likely to perform even worse. Finally, the monolithic-partitioned algorithm could be a sensible compromise between computational efficiency and implementational effort for moving meshes. Still, the fully monolithic algorithm is the most efficient which is why we will employ it in the following.

4.2. Two-dimensional Growth of a Vascular Tumor

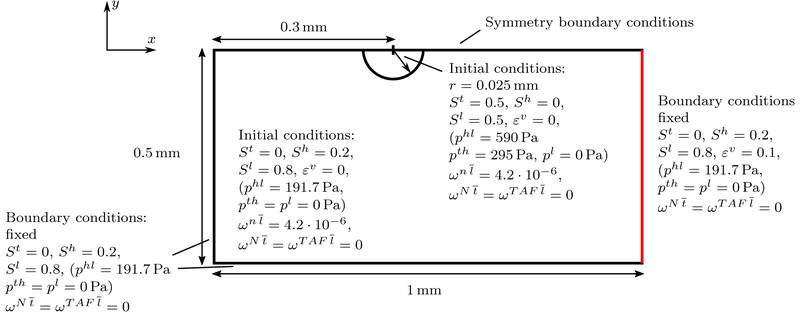
The first numerical example including angiogenesis will be the two-dimensional growth of a tumor. Similar cases have been studied in [32, 36] for their continuum and hybrid approach, respectively. The geometry of the example including initial and boundary conditions is sketched in Figure 9. A circular tumor with initial radius r = 0.025 mm is growing in healthy tissue close to a blood vessel (sketched in red) from which angiogenesis occurs. Here, we have set a Dirichlet boundary condition for the neovasculature volume fraction of ε^v = 0.1 to trigger angiogenesis from the position of the assumed blood vessel. The left, bottom and right boundary of the domain are fixed and appropriate boundary conditions are applied to make use of the symmetry of the problem. Note that oxygen is not prescribed on any boundary of the domain but it is assumed that it is solely provided by the developing neovasculature via transcapillary exchange (40). A Neo-Hookean material law with material parameters given in Table 2 is employed for the ECM. The permeability is slightly smaller than in previous examples. However, the value of [15, 17, 36] (1.8 10⁻¹⁵ m²) has not been obtained from biological data but simply been estimated as this value. Possibly, it might vary for Different ECM and tumor types. With the lower value employed here a smaller tumor with a higher volume fraction of TC emerges. This allows us to illustrate the effect of angiogenesis on the tumor shape more clearly. The value of the Young’s modulus has been increased with respect to the aforementioned contributions since the overall solid pressure calculated with (22) is higher than in previous cases due to the lower permeability, the interstitial fluid pressure increase and the appearance of the blood pressure p^blood in the solid pressure definition. The parameters for the incompressible fluid phases are summarized in Table 3, which are standard parameters also employed in [15, 17, 36]. As in these papers, the primary variables of the fluids are chosen as p^l, p^hl and p^th. Also for the three present species, namely oxygen, TAF and necrotic tumor cells, previously employed parameters have been chosen, see Table 4.

Figure 9:

Geometry, initial and boundary conditions of the 2D angiogenesis example (not to scale)

Table 2:

Parameters for the ECM of the 2D angiogenesis example

Quantity	Symbol	Value	Unit
Density [15]	ρs	1000	kg/m3
Intrinsic permeability of the ECM (see comment in text)	k	1 · 10−15	m2
Poisson’s ratio [15]	v	0.4	–
Young’s modulus (see comment in text)	E	800	Pa

The new parameters governing angiogenesis and transcapillary and lymphatic exchange are given in Table 5. Most of them have been taken from the available literature while some have been slightly adapted. However, the primary goal of this example is to prove the principal applicability of our model to vascular tumor growth and to show its characteristics, capabilities and limitations. Among the many parameters present some will have to be adjusted in the future to reproduce experimental and clinical data. The diffusion coefficient of the neovasculature has been chosen as half the value of [30]. Furthermore, we have assumed that the surface-to-volume ratio (S/V)_ly for lymphatic drainage is equivalent to the one reported for blood vessels. The hydraulic conductivity of the lymphatic system is estimated to be two orders of magnitude higher than the one of the neovasculature. This ensures a correct behavior of a functioning lymph system which drains the liquid leaking from the irregular neovasculature. Only if lymph vessels are destroyed through excessive tumor pressure (38) fluid will accumulate. The collapsing threshold $p_{\text{coll}}^t$ has been set such that a tumor cell saturation of S^t ≈ 0.3 completely inhibits lymphatic drainage. The chemotactic coefficient ${\chi }_0$ and the transcapillary diffusion coefficient over the vessel wall thickness D_tc/t are the key parameters for our vascular model. Three Different combinations of these parameters have been studied to exemplify their effect on the model. We will perform more elaborate studies on these and other parameters but here the goal is only to show the abilities of our novel vascular model.

The domain is discretized with 240 × 120 bilinear elements in space. The time step size is Δt = 1800 s for the one-step-theta scheme with θ = 0.52 over 1152 time steps, i.e., the total simulated time is 24 days. Also the initialization procedure described in Appendix B is employed for this example before the start of the actual simulation.

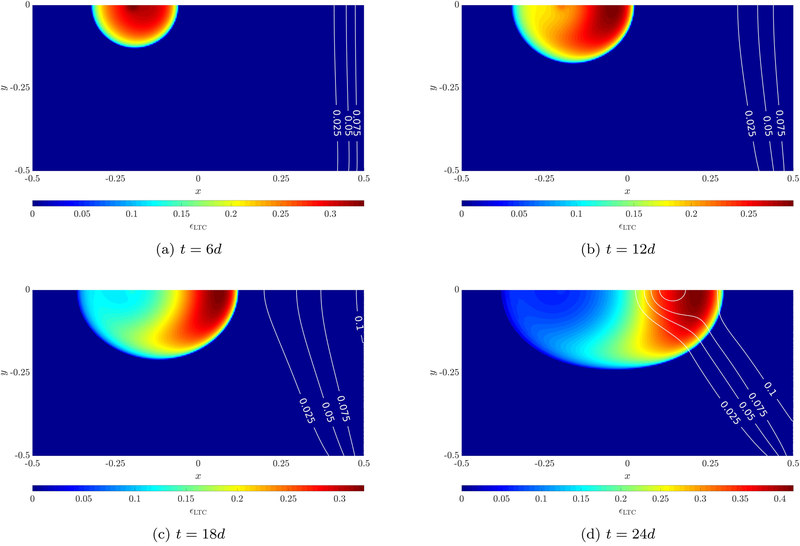
The evolution of the living tumor cell volume fraction ${\epsilon }_{\text{LTC}}=\epsilon S^t\left(1-{\omega }^{N\overline{t}}\right)$ for case 2 is depicted in Figure 10, where also the neovasculature volume fraction ε^v is shown via contour lines. After six days a round tumor emerges while the neovasculature diffuses slightly into the domain and provides oxygen on its right side. This actuates the tumor to evolve unsymmetrically towards the source of oxygen to the right after twelve days, see Figure 10b. A half-moon shape of living tumor cells emerges since in the region further away from the blood vessel necrosis sets in, see also Figure 12a. The tumor continues to progress towards the neovasculature over the course of the simulation (Figures 10c–10d). TAF are constantly produced by the hypoxic tumor cells. After twelve days the chemotactic response of endothelial cells to TAF starts to dominate their migration towards the tumor, which results in the shape of the neovasculature shown in Figures 10c–10d. Most of the oxygen is needed by proliferating tumor cells at the symmetry axis of the domain, hence, here most of the TAF are produced, see Figure 12c, which explains that the neovasculature grows faster in the region close to the symmetry axis. Finally, after 24 days a very well vascularized region with living tumor cells emerges. Qualitatively, these results seem to be in good agreement with the similar angiogenesis example of [32].

Figure 10:

Evolution of living tumor cells and neovasculature (contour lines) for case 2

Figure 12:

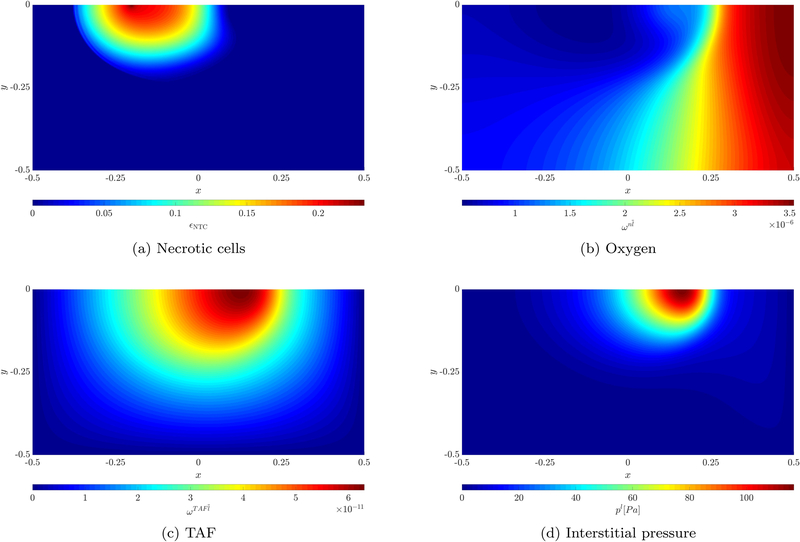
Results of necrotic cells, oxygen, TAF and interstitial pressure for case 2 at t = 24d

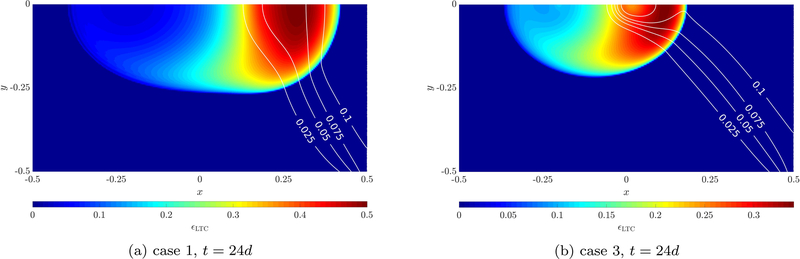
In addition, the necrotic cell volume (or mass) fraction after 24 days ${\epsilon }_{\text{NTC}}=\epsilon S^t{\omega }^{N\overline{t}}$ is depicted in Figure 12a. As already mentioned before, the necrotic region develops on the left in the zone further away from the pre-existing blood vessel and neovasculature. The oxygen mass fraction ${\omega }^{n\overline{l}}$ is plotted in Figure 12b. A large area with a very low oxygen concentration exists in the left part of the domain. During growth the tumor consumes almost all the oxygen there while diffusion of oxygen generated by the pre-existing blood vessel and beginning angiogenesis is not enough to sustain its rapid growth which causes the development of the aforementioned necrotic region. On the right side of the domain an oxygen-rich region is present due to transcapillary exchange of oxygen. Finally, the interstitial pressure is shown in Figure 12d. An increased pressure can be observed in the vascular tumor region. This is due to the leakage of fluid from the irregular neovasculature into the domain. Outside of the tumor region the lymphatic system drains this excessive fluid. However, tumor cells compress the lymph vessels limiting or completely inhibiting drainage. Therefore, interstitial fluid accumulates with the corresponding pressure increase. Thus, there is a net outflow of IF from the vascular tumor region. This increase of interstitial pressure has been physiologically observed and identified as critical to drug delivery to the tumor [26, 27, 28]. Our extensions to the model with the inclusion of angiogenesis modeled by the neovasculature phase and appropriate inter-phase exchange terms enable the simulation of this phenomenon. In the future, we will be able to evaluate the effect of the interstitial pressure increase on drug delivery.

So far, only the parameter set of case 2 has been employed. Now, we want to compare the results with the two other cases. Results after 24 days are given in Figures 11a and 11b, respectively. We have chosen the parameter sets such that two distinct cases evolve. In the first case more oxygen is provided by the vasculature while the sensitivity of endothelial cells to TAF is decreased. This results in faster tumor growth compared to case 2 and 3 since more oxygen is available. At the same time angiogenesis occurs much slower due to the lower chemotactic coefficient and the overall higher oxygen concentration. For case 3 the exact opposite behavior can be observed. Less oxygen is present which slows down tumor growth. Vice versa this leads to faster angiogenesis than in case 1 and 2.

Figure 11:

Evolution of living tumor cells and neovasculature (contour lines) for cases 1 and 3

For a quantitative comparison of the three cases, the volume fractions of all entities have been evaluated at the symmetry axis y = 0. Volume fractions of extracellular matrix (ECM), interstitial fluid (IF), healthy cells (HC), living tumor cells (LTC), necrotic tumor cells (NTC) and neovasculature (NV) are shown in Figure 13. As already evident from the two-dimensional plots from above, tumor growth is fastest for case 1 while the best and fastest vascularization is observed for case 3 due to the chosen parameters as explained before. However, also the largest necrotic zone develops for case 1 since the larger tumor consumes more oxygen which is insufficiently provided in the area further away from the tumor due to slow angiogenesis. For the early stages of growth blood vessels start to grow into the domain and displace HC, IF and to a certain extent also ECM. This is due to the appearance of the blood pressure in the definition of the solid pressure (22). If we had assumed a rigid ECM, the volume fraction of the ECM would have been unaffected by angiogenesis. The inclusion of the neovasculature as an additional phase with its own volume fraction allows us to model the interaction between porosity, ECM and NV volume fraction. With the previous species-based approach [36] such a detailed insight would not have been possible. Later, excessive tumor and IF pressure increase the volume fraction of the fluid phase, i.e., the porosity ε in the proliferating zone. One drawback of the model formulation is that the neovasculature volume fraction is only mildly affected by fluid pressures. In the region with especially high tumor and IF pressure, for example around x = 0.2 in Figure 13k, the neovasculature volume fraction ε^v decreases slightly which is the effect of the grid velocity divergence term from (9) which is positive in this area. In reality, the instable blood vessels of the neovasculature are likely to be compressed more strongly by the tumor. In [31] this has for example been included by a radius adaption depending on the tumor pressure for discrete blood vessels. A similar approach for our continuous representation of blood vessel density can be added once blood flow in the (neo-)vasculature is explicitly modeled.

Figure 13:

Volume fractions of components at symmetry axis y = 0

5. Conclusion

In this contribution we have advanced a dynamic vascular tumor growth model derived from Thermodynamically Constrained Averaging Theory. The model is based on multiphase flow through a deformable solid, the extracellular matrix. It includes important biological phenomena such as nutrient consumption, hypoxia and necrosis. With our continuum representation of the neovasculature as a proper phase with its own volume fraction or blood vessel density angiogenesis has been consistently incorporated. Adequate mass transfer terms and constitutive relations allow us to model chemotaxis, transcapillary leakage and lymphatic drainage. These extensions enable our model to reproduce the physiologically present high interstitial pressure in tumors which has been identified as a major obstacle for successful drug delivery.

However, not all biological phenomena present in tumor growth have been addressed. As already mentioned, an explicit model of blood flow in the neovasculature is still missing. Relevant extensions could be blood vessel collapse due to high tumor pressure, haptotaxis and TAF uptake through endothelial cells. The modular structure of our code with an arbitrary number of species and fluid phases makes the implementation easily extendable. In the future, also the lymph system including lymphangiogenesis might enter it as a proper phase.

As most other vascular tumor growth models, our approach includes many biological and physical parameters. We have taken them as values reported in other contributions or close to them. Nevertheless, extensive validation and comparison with experimental data, which was beyond the scope of this paper, must be a focus of further research to enhance its applicability as a prognostic tool.

For that, we have investigated several coupling methods. While the model was previously only solved with a partitioned approach, we have presented a monolithic-partitioned and a fully monolithic framework. In all cases our fully monolithic scheme was superior in terms of robustness and computational efficiency. The strong coupling between fluid phases and the extracellular matrix severely limits the performance of the partitioned method while the one of the monolithic algorithms does not deteriorate for a wide range of parameters. We have achieved an average performance gain of 4.5 for the fully monolithic and 2.9 for the hybrid coupling compared to the partitioned one in a particular example. Further scalability and parameter studies for Different preconditioners such as the BGS(AMG) or the AMG(BGS) method are necessary to confirm these findings. The latter one might be the method of choice in the future to resolve the strong coupling between structure and fluid phases.

In future work we also plan to include a consistent coupling of the pre-existing vasculature represented as 1D elements with the volume fraction-based neovasculature approach developed here. This model would then be of hybrid and not pure continuum type anymore.

Appendix A. Additional Constitutive Equations and Mass Transfer Terms

For the saturation-pressure relationships S^α(p^αβ) we apply the ones developed in [15, 16] for three-phase flow with pressure difference p^αβ between each pair of fluid phases α, β. The relations are given as

$$p^{hl}(S^l)=p^h-p^l=a\cdot \text{tan}\left[\frac{\pi }{2}{(1-S^l)}^b\right]$$ (A.1)

and

$$p^{th}(S^t)=p^t-p^h=a\frac{{\sigma }_{th}}{{\sigma }_{hl}}\cdot \text{tan}\left[\frac{\pi }{2}{(S^t)}^b\right].$$ (A.2)

Herein, a and b are model constants and σ_αβ the interfacial tension between fluids α and β. The inverses of the above equations are needed for evaluating the derivatives ∂S^α/∂ψ^β w.r.t. generic primary variables ψ^β in (28) and (29) if these are chosen as pressure differences or pressures. The relation for the third phase follows simply as

$$S^h(p^{th},p^{hl})=1-S^l(p^{hl})-S^t(p^{th})$$ (A.3)

in accordance with (5). For the relative permeabilities $k_{rel}^{\alpha }$ the power law

$$k_{rel}^{\alpha }={(S^{\alpha })}^{A_{\alpha }}$$ (A.4)

with A_α > 1 of [15] in accordance with the relative wettability of the fluid phases is re-used. The effective diffusivity $D_{\text{eff}}^{nl}$ of oxygen in the IF is calculated with the same power relationship as [15, 17], namely

$$D_{\text{eff}}^{nl}={(\epsilon S^l)}^{\delta }$$ (A.5)

and TAF have constant diffusivity as in [30, 36]. Viscosity laws of the cell types have been employed in [15] to model cell adherence. This law has been included in our framework, however, we assume constant viscosities here as in [14, 17].

Finally, we summarize the mass transfer terms taken from [15] and listed in Table 1 but not explicitly given in the text. The mass exchange term ${\stackrel{l\to t}{M}}_{\text{growth}}$ is employed for nutrient uptake and consumption of water related to tumor cell growth and is defined as

$${\stackrel{l\to t}{M}}_{\text{growth}}=\left({\gamma }_{\text{growth}}^t{\langle \frac{{\omega }^{n\overline{l}}-{\omega }_{\text{crit}}^{n\overline{l}}}{{\omega }_{\text{env}}^{n\overline{l}}-{\omega }_{\text{crit}}^{n\overline{l}}}\rangle }_{+}\right)\left(1-{\omega }^{N\overline{t}}\right)\epsilon S^t.$$ (A.6)

Nutrient uptake is modeled through the mass transfer relation for oxygen

$$\stackrel{nl\to t}{M}=\stackrel{nl\to nt}{M}=\left({\gamma }_{\text{growth}}^{nl}{\langle \frac{{\omega }^{n\overline{l}}-{\omega }_{\text{crit}}^{n\overline{l}}}{{\omega }_{\text{env}}^{n\overline{l}}-{\omega }_{\text{crit}}^{n\overline{l}}}\rangle }_{+}+{\gamma }_{\text{0}}^{\text{nl}}\text{sin}\left(\frac{\pi }{2}\frac{{\omega }^{n\overline{l}}}{{\omega }_{\text{env}}^{n\overline{l}}}\right)\right)\left(1-{\omega }^{N\overline{t}}\right)\epsilon S^t.$$ (A.7)

The first term represents consumption of oxygen through growth of TC and the second one normal metabolism of TC. Finally, necrosis is accounted for through the intra-phase term

$${\epsilon }^t{r}^{Nt}={\gamma }_{\text{necrosis}}^t{\langle \frac{{\omega }_{\text{crit}}^{n\overline{l}}-{\omega }^{n\overline{l}}}{{\omega }_{\text{env}}^{n\overline{l}}-{\omega }_{\text{crit}}^{n\overline{l}}}\rangle }_{+}\left(1-{\omega }^{N\overline{t}}\right)\epsilon S^t.$$ (A.8)

under hypoxia or nutrient shortage. Note that this term is Different from zero if the oxygen mass fraction falls below the critical value ω^nl_crit while (A.6) and the first summand of (A.7) are only active above this limit. Furthermore, ω^nl_env is the average mass fraction of oxygen in tissue and γ denotes mass transfer rates, see also Tables 3 and 4.

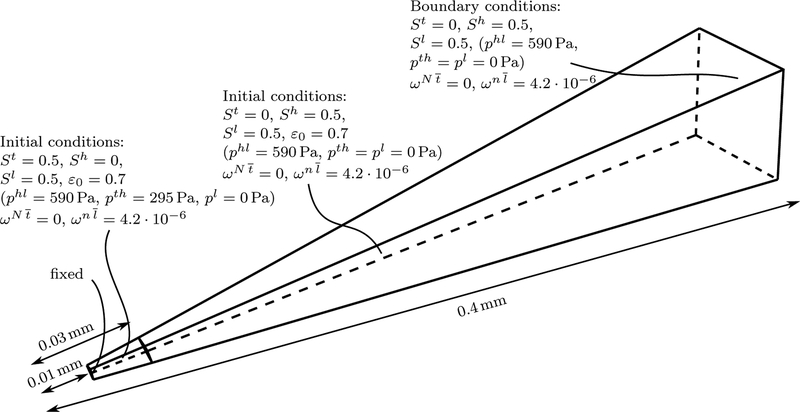
Appendix B. Details on the Setup of the Benchmark Problem

Figure B.14:

Geometry, initial and boundary conditions of the 3D benchmark problem (not to scale)

Figure B.14 depicts geometry, initial and boundary conditions of the benchmark example used throughout Section 4.1. For symmetry reasons only a 9° × 9° segment of the spherical 3D geometry with radius 0.4 mm is considered with appropriate boundary conditions on its side faces. There is an inner region with radius r = 0.03 mm with an initial tumor cell saturation of S^t = 0.5 and a larger outer region where it is zero. 250 linear 3D elements are employed in radial direction resulting in a system consisting of in total 9, 632 degrees of freedom (structure, fluid and species). Before the actual simulation with 720 time steps is started, pressures are linearly increased from p^l, p^t, p^h = 0 in 10 steps until the desired saturations in the sub-domains as shown in Figure B.14 are reached. This is necessary since otherwise the combined solid pressure p^s would act immediately at t = 0. We found that this caused an unstable behavior at the beginning of the simulation such that without this initialization procedure sometimes no convergence was achieved in the first time step. During the initialization the structure deforms slightly such that also the porosity increases from the initial value ε₀ to a value of ε ≈ 0.8 depending on material parameters.