Abstract
In the present work a series of design rules are developed in order to tune the morphology of TiO2 nanoparticles through hydrothermal process. Through a careful experimental design, the influence of relevant process parameters on the synthesis outcome are studied, reaching to the develop predictive models by using Machine Learning methods. The models, after the validation and training, are able to predict with high accuracy the synthesis outcome in terms of nanoparticle size, polydispersity and aspect ratio. Furthermore, they are implemented by reverse engineering approach to do the inverse process, i.e. obtain the optimal synthesis parameters given a specific product characteristic. For the first time, it is presented a synthesis method that allows continuous and precise control of NPs morphology with the possibility to tune the aspect ratio over a large range from 1.4 (perfect truncated bipyramids) to 6 (elongated nanoparticles) and the length from 20 to 140 nm.
Subject terms: Nanoscale materials, Synthesis and processing
Introduction
Titanium dioxide is one of the most studied semiconductor metal oxides, due to its surface and electronic properties providing multisectorial applications that range from healthcare, photocatalysis, smart materials with self-cleaning and self-sterilizing properties and solar energy harvesting (photovoltaics and water photosplitting)1–5. However, it is difficult to correlate the functional properties of TiO2 nanomaterials to the properties at single nanoparticle (NP) level, due to broad size dispersity, the complex morphology and, consequently, the differences in surface properties of material used. In the last decades, intensive experimental and theoretical studies have been conducted on the reactivity of different metal oxides such as TiO2 as a function of the crystal surface exposed and morphology1,2,6–14. The request for different particle shapes, and therefore different surface terminations, stems from the different physico-chemical properties associated to different surfaces, including surface states, which can confer different reactivity and interfacial properties to the material. The possibility to tune the crystal morphology could have a strong impact for several applications, e.g. in photocatalysis the morphology can guide the charge carriers' dynamics15, while in the field of nanocomposites the tribomechanical properties could be adjusted16–19. Nonetheless, the availability of NP materials displaying uniformity at the nanoscale would be beneficial to tune product performance. Moreover, another aspect that should not be overlooked is the possibility to use size and shape-controlled nanoparticles (NPs) with high homogeneity and high stability (both of morphology and of the colloidal suspension) as a reference material for dimensional nano-metrology of real-world, non-spherical NPs. Currently, there is scarcity of certified reference nanoparticles. The few ones, only Au and silica, are rather model nanoparticles, i.e. spherical, monodisperse and generally non-overlapping when prepared on a substrate. The real world of industrial nanoparticles implies complex particle shape, a certain degree of agglomeration/aggregation state, size polydispersity. The nanoparticles presented in the present work constitute a milestone for the reliable but challenging analysis of size and more complex shape of real-world nanoparticles20–22. The synthesis of well-defined and stable NPs as reference materials offers a solid basis for the development of procedures and models to improve the traceability chain, compatibility and comparability of nanoparticle size measurements. This is key for further development in the standardisation of accurate size measurement for non-spherical nanoparticles22. The prediction of final shape and size of a nanocrystal from the synthesis conditions starting from first principles it is currently unfeasible. Under thermodynamic control, the final shape is related to the surface energy of the various crystallographic surfaces. However, these are controlled by the presence of adsorbates that can act as shape controllers23. Concerning anatase synthesis under hydrothermal (HT) conditions, there are several experimental and theoretical studies that suggest various mechanism of TiO2 crystal growth for HT processes24–27. Recently, we proposed a model able to describe the evolution of crystal size and shape during alkaline HT processing of triethanolamine-titanium (IV) complex27. However, a quantitative model able to predict the size and morphology from HT synthesis conditions still does not exist. In this context Machine Learning (ML) is increasingly used for predicting the relationship between determined input parameters and resulting structures or properties from available datasets, without using first principles28–31. Although certain works were already carried out in several fields like synthesis, catalysis, molecular interactions, biology, engineering, etc.32–38, often ML is used to establish the relationship among a structure and a single determined material property only, rather than optimize the conditions to maximize the efficiency of a process39–42. Less frequently, it is used for the material design, i.e. the study of the influence of synthesis parameters on the final morphology of the NPs; and where this has been done, only one final morphological characteristic is taken into account (size or shape)37,43. This occurs because ML approaches are limited by the lack of large pre-existing coherent data sets, especially with regards to material synthesis32. The problem can be partially overcome by using experimental design techniques, which are often employed for building and optimizing regression models able to determine efficiently the set of conditions necessary to obtain a product or process with desired characteristics44–48. The combination of experimental design and ML could allow building a model able to predict/optimize the process parameters even in the presence of a reduced initial data set49–54. Also failed experiments can be useful for this task55. Further, there are recent studies demonstrating the use of ML for classification of materials (or corresponding data)56. Besides the valuable prediction of advanced material properties such as physical, chemical, optical, mechanical, electrical etc., i.e. material discovery, the idea of high-throughput computational materials research is another promising application of ML57.
In the present work we present a quantitative model for the synthesis of TiO2 NPs with “a priori” established shape and size and limited polydispersity. To this aim, we coupled experimental design and ML techniques for the material synthesis, starting from a known HT synthesis method, for which the growth mechanism was investigated27,58. The syntheses of truncated bipyramidal (the equilibrium shape for anatase)1 and elongated anatase NPs were performed using as precursor a titanatrane [Ti(TeoaH)2] (see characterization in Supplementary Information SI, Sect. 2), and triethanolamine as shape controller exploring a quite wide experimental domain, in terms of reaction pH, temperature and reactants concentrations. Then, a mathematical model was developed to generalize and predict NP shape and size. Modelling was carried out in an iterative way with Artificial Neural Network (ANN) and Genetic Algorithm (GA) for the optimization, in the framework of the learning approach59–63. This enabled the formulation of optimized models, which is able to guide the syntheses towards materials constituted of low polydispersity NPs with desired shape and size in an inverse engineering approach. This tool allows identifying well-defined parameters of synthetic procedures once certain particle size and shape are required for a particular application. Moreover, the procedure could be extended to other oxides and materials64. The choice of ANN for process modeling, despite the small dataset, is due to their capability to fit data, without overfitting, which make them reliable, especially for nonlinear dependency between variables, which is our case. ANNs gave better results for some extension of the variables’ variation range resulting in a higher prediction power than classical polynomial regression, even though large datasets are required65. The work follows step by step the creation of the ANN models using the data obtained by the experimental design and their refinement and optimization with the increase of the dataset with further experiments. For each step, a comparison with a second degree polynomial regression was carried out in order to estimate the goodness of the ANN models.
Chart 1 depicts the rationale of this work. The first part is dedicated to the experimental design (defining the desired product characteristics) and the complete morphological characterization of the NPs. The second part describes the development of the ML procedures (in particular ANN modelling) that predict the final characteristics of the NPs, together with their optimization (throughout Genetic Algorithm, GA) and the reverse engineering processes.
Chart 1.
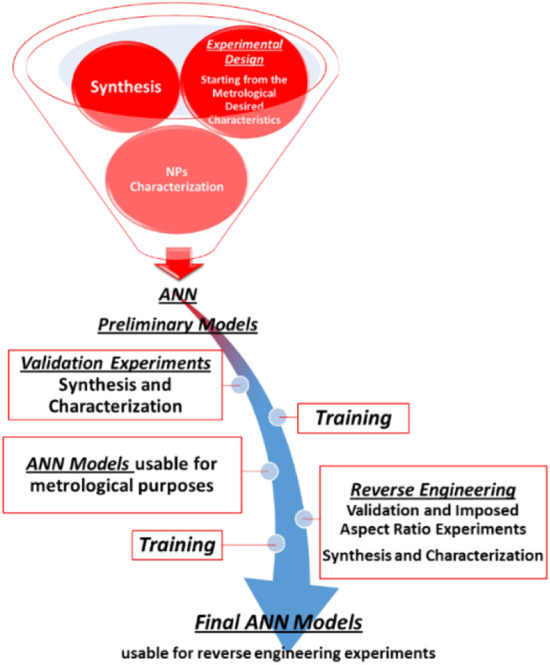
Flowchart of the work process, from the experimental design to the validated and optimized ANN models.
Results
Experimental design and synthesis results
The experimental design technique employed is based on the Responses Surface Method, by using Box Wilson central composite design (CCD)47,66. In SI (Sect. 5), we report the complete explanation of the Experimental Design construction. The experimental plan considers the four independent variables (factors Z1 to Z4), which mainly influence the characteristics of the product:
Z1—[Ti(TeoaH)2] initial concentration;
Z2—Added TeoaH3 concentration as shape controller;
Z3—Initial pH;
Z4—operating temperature.
The experimental ranges studied were from 30 to 120 mM [Ti(TeoaH)2], from 0 to 70 mM added TeoaH3, pH between 8.7 and 12 and temperature values from 135 to 220 °C. The orthogonal fractional CCD is shown in SI (Table S2). The required values for the products characteristics, Y1 to Y3 are:
Hydrodynamic radius (Y1) → RH, max. 25 nm; the choice of the hydrodynamic radius evaluation was done because this parameter allows determining more accurately the polydispersity of NPs. Moreover, RH can be rapidly determined by DLS measurements and then directly compared with the electron microscopy analysis through the Perrin equation (details in SI, Sect. 1). Obviously, RH were determined on stable suspensions and following a standard operative procedure for all samples;
Polydispersity (Y2) → max. 5%, corresponding to 1 nm for Y1 values around 20 nm; the experimental results are expressed as standard deviation (in nm) of the DLS hydrodynamic radius distribution for the relevant mode; for mathematical analysis Y2 is converted in percentages;
Aspect Ratio (p) → required value is 1.5 representing the ratio between major and minor axes of the ellipse that fits to the particle boundaries (for details see Sect. 1—page 3 in SI). The ellipse model for fitting the bipyramids has been chosen due to simplicity (and practicability) reasons.
The experimental program adopted allows the investigation over a large range of operating parameters using a limited number of experiments (Table S2). This will give the possibility of process analysis and mathematical modelling in order to predict final product characteristics in various operating conditions as well as to identify the synthesis conditions for a product with predefined final properties.
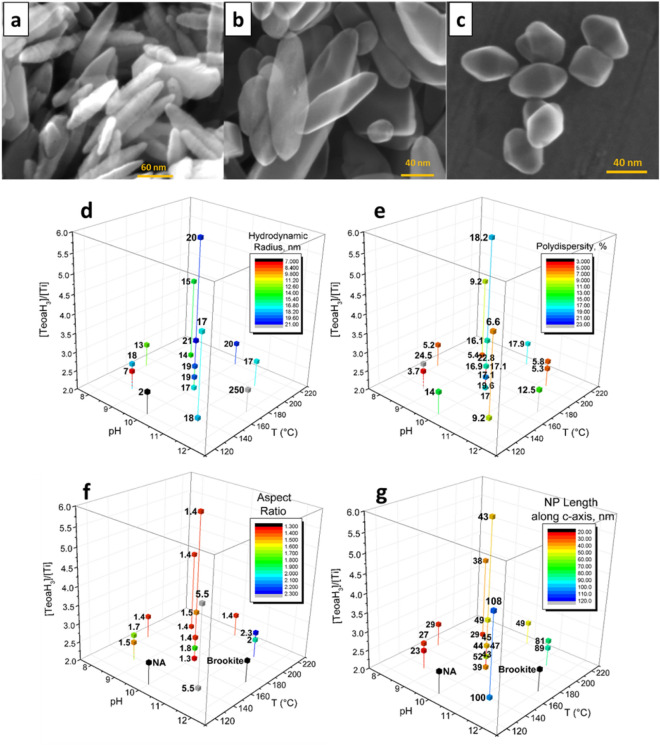
The results of the experimental design, i.e. microscopy measurements, XRD and DLS are described in detail in SI (Sects. 6–8) and summarized in Fig. 1 (together with HR-SEM micrographs of three materials synthetized), where it is possible to gather further insight into the relevance of HT synthesis parameters. The NPs synthetized are characterized by a different elongation along the c axis of the anatase crystal (23–108 nm) (Fig. 1g, Table S3 and Sect. 7 of the SI). The elongation is favored by high pH values in the whole temperature range considered. Very low hydrodynamic radii are expected at low pH and low temperature conditions, in a narrow region of the experimental ranges explored here, while particles with hydrodynamic radius between 10 and 20 nm can be obtained in several working conditions (Fig. 1d, Table S4 and Sect. 8 of the SI). In the whole range of temperatures and pH values, for 65 mM Ti(TeoaH)2 and 40 mM added TeoaH3, the expected RH would never exceed 20 nm. For higher Ti(TeoaH)2 loadings and higher added TeoaH3 concentrations there is a large region in the pH and temperature variation range where particles with RH larger than 20 nm may be obtained. However, even in this case, particle hydrodynamic radius would be limited to 29 nm. As for the hydrodynamic radius, aspect ratios between 1 and 2 are expected in a very wide region of working conditions, whereas high max/min values are favored at initial pH between 11 and 12. In that pH range, the aspect ratio increases with decreasing temperature. Nevertheless, there is a complex interplay among the variables considered that impedes to find other empirical relationships. The polydispersity (%) of NPs is almost always larger than the recommended for metrological applications (5%) (see Table S4), however it must be taken into account that with such complex morphology, polydispersity is even more challenging to be measured accurately, especially for high aspect ratios.
Figure 1.
High-resolution SEM micrographs of selected synthetized materials: HT06 (a), HT08 (b), and HT16 (c). 3D-plots of Hydrodynamic Radius (d), Polydispersity (e), Aspect ratio (f) and NP length along the c-axis (g) experimentally obtained as functions of pH, Temperature and [TeoaH3]/[Ti] relative concentration. The data reported represent the 20 materials obtained following the experimental design.
Artificial neural networks (ANN) modelling
ANN modelling was carried out for the factors’ screening and the analysis of their relative influence upon TiO2 NPs synthesis by HT method. Details about the ANN formulation are presented in Supplementary Information (see Sect. 10).
Three distinct modelling ANN were built to reflect the influence of working parameters upon the characteristics of the bipyramidal anatase synthetized. All three networks have the same architecture: four input neurons, for the four independent variables (Ti(TeoaH)2 concentration (mM), added TeoaH3 concentration (mM), pH and temperature), three neurons in the hidden layer to ensure learning capability, without increasing the number of ANN weights too much, and one output neuron, for the output variable to forecast (the hydrodynamic radius (Y1), the polydispersity (Y2) and the Aspect Ratio (Y3), respectively, Fig. 2). The ANN has 15 total interconnections, avoiding overfitting problems. In this study, the activation function is the sigmoid, and learning algorithm is back-propagating. For each of the three ANNs, from the 20 experimental data, 16 data sets were used for training and 4 data sets for validation and testing. The ANNs were built in the frame of Matlab R2015a software (Math Works, Natick, MA, USA).
Figure 2.
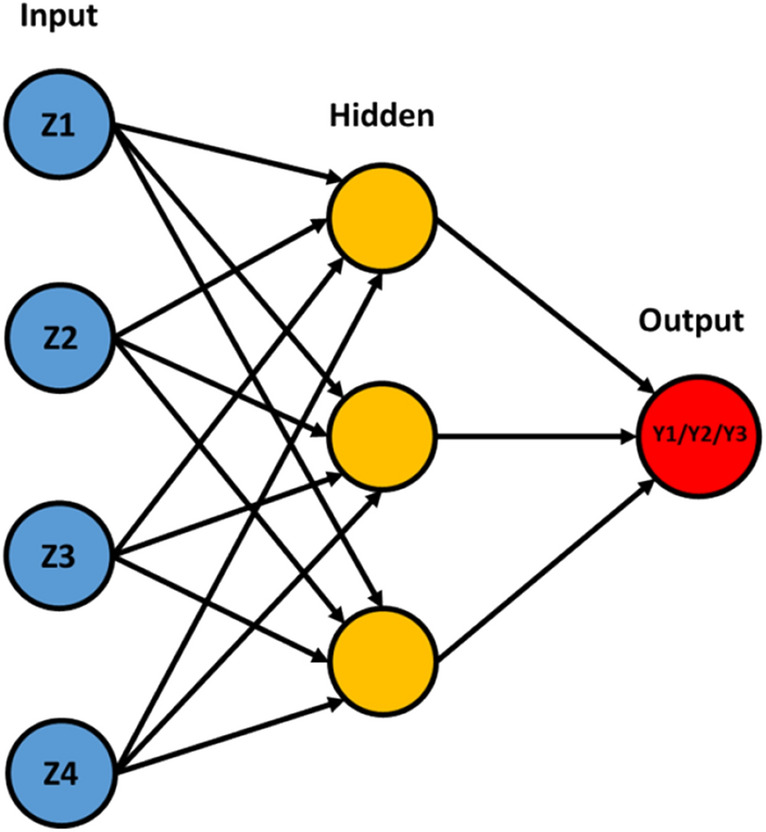
Architecture of the used ANN models, with Z1 to Z4 selected as input neurons and Y1 to Y3 defined as output neurons.
ANN modelling of hydrodynamic radius, polydispersity and aspect ratio were compared at each step with second degree polynomial regression models developed by using the same dataset (see Sect. 9 of the SI for details). In Table 1, we reported the mean relative error of the developed models for hydrodynamic radius, polydispersity and aspect ratio. Table 1 highlights that for the three parameters taken into account, ANN models have always a better prediction ability.
Table 1.
Comparison between the relative mean errors for second degree polynomial models and ANN models.
| ANN (20 experiments) | Polynomial (20 experiments) | ||||
|---|---|---|---|---|---|
| Rh | Polydispersity | Aspect ratio | Rh | Polydispersity | Aspect ratio |
| 2.4% | 9.9% | 2.6% | 12.0% | 18.0% | 2.9% |
Based on the trained ANNs, the influence of process parameters upon the characteristics of particle size distribution (mean hydrodynamic radius, polydispersity) and aspect ratio was investigated. Each network was used to predict the behavior of the system for the experimental range of the operating parameters. The simulations (reported in Figs. S88-S95, SI) revealed that the factors mostly influencing the characteristics of the final product are the pH and the temperature (in this order). These results are in good agreement with the empirical experimental observations.
The validation of the mathematical model was realized by performing 6 new experiments in the range of interest for the operating parameters (Table S5). The experimental outcomes for the obtained TiO2 NPs were compared with predicted ones. The data in Table S6 show a relatively good model prediction capability. In particular, the ANN models mean relative error is better compared with the polynomial models for the prediction of polydispersity.
Refining of the ANN models with the addition of validation experiments
In order to improve the prediction ability of the neural networks, the six validation synthesis were added to the initial 20 experimental points. The neural networks defined for Y1, Y2 and Y3 calculations presented in the previous paragraph were tested for the new set of experimental data (HT-MODEL 01-06). Maintaining the same structure, the ANNs were further trained by using the whole new data set of 26 experiments. Once again, the match of the Polydispersity is the Y parameter suffering from largest deviations. This could be explained by the challenge in measuring accurately the polydispersity index for such non-ideal samples. Table 2 reports the mean relative errors of the developed models (ANN vs Polynomial) for hydrodynamic radius, polydispersity and aspect ratio.
Table 2.
Comparison between the relative mean errors for second degree polynomial models and ANN refined models.
| ANN (26 experiments) | Polynomial (26 experiments) | ||||
|---|---|---|---|---|---|
| Rh | Polydispersity | Aspect ratio | Rh | Polydispersity | Aspect ratio |
| 3.0% | 12.7% | 2.9% | 11.4% | 22.5% | 4.0% |
Table 2 highlights that the ANN models have a significantly higher prediction ability compared to the polynomial regression models.
Reverse engineering ANN models
Reverse engineering is defined as a technique that starts from the product and works through the design/synthesis process in the opposite direction to arrive at product definition statements. Extending this concept to the synthesis of titania NPs, the aim of reverse engineering approach is to find out the particular synthesis conditions enabling to obtain a product with defined RH, polydispersity and aspect ratio. This goal may be realized using mathematical modelling tools and optimization procedures. Therefore, ANN capability to capture the relation between operating condition and final product characteristics was used:
to directly find the corresponding working conditions knowing the product characteristics;
to define a functional dependence on working conditions (X) for each product characteristic (Y).
The optimization tool used is the Genetic Algorithm (GA). This algorithm is inspired from natural evolution and provides a heuristic search of the response surface, identifying the regions where optimum values may be located. Due to their working principle, GA is more robust in the localization of global optima than hill-climbing methods and it is expected to give good results in the case of multimodal objective functions, as it is the case in the present study. The search for best operating conditions for given product characteristics was achieved by formulation of an optimization problems. The definition of the goal was realized in several ways and is reported in SI (Sect. 10). The objective functions were selected based on the cumulated product requirements: minimum mean hydrodynamic radius (Y1), polydispersity (Y2) lower than 5% and Aspect Ratio (Y3) very close to 1.5 corresponding to low truncated anatase NPs. The optimized models were used to estimate the influence of operating parameters on the product characteristics and to propose optimal operating condition for predefined final product characteristics. Based on these predictions five additional validation experiments for the reverse engineering models were carried out together with three imposed aspect ratio experiments, in order to increase also the model potential to indicate the process parameters for elongating the NPs. The new experimental data will contribute to yield more reliable ANN models, capable of covering all the desired ranges of the operating conditions for the HT synthesis of anatase NPs.
The data shown in Table S8 highlight that there is a certain discrepancy between the experimental and the predicted results, especially for the materials with imposed aspect ratio. Therefore, a further implementation of the models for reverse engineering problem was mandatory and an ANN analysis exploiting as input also the 8 new experimental results was carried out. ANN and GA provide together a modelling tool for reverse engineering approach of the crystallization process.
The validation experiments proved that the model can estimate very well product characteristics in the range of the experimental data used in defining the ANN model and less accurate outside this region (for example the conditions for aspect ratio 4.2, see Table S8). The new experiments cover almost completely the whole experimental region and they are all used in the next iteration step to build new ANN models that would better predict the product characteristics starting from operating conditions. The validated optimized reverse-engineering models were built using all the experimental data. New ANN models were built for Y1, Y2, and Y3 using all the data obtained from the synthesis of the experimental design and of the validation experiments. The optimal architecture identified for the new ANNs was similar to the initial ones: 4 neurons in the input layer (Ti(TeoaH)2 initial concentration, TeoaH3 initial concentration, pH and Temperature), 3 neurons in the hidden layer and 1 neuron in the output layer (Y1, Y2 and Y3 respectively). The way in which the optimized models reflect the experimental variation is expressed as relative mean errors percentage in Table 3.
Table 3.
Comparison between the relative mean errors for second degree polynomial models and ANN final models.
| ANN (26 experiments) | Polynomial (26 experiments) | ||||
|---|---|---|---|---|---|
| Rh | Polydispersity | Aspect ratio | Rh | Polydispersity | Aspect ratio |
| 9.1% | 13.9% | 5.6% | 11.9% | 19.5% | 10.1% |
Table 3 confirms that final ANN models built with all the 34 experiments present a higher capacity to predict the results of the synthesis compared with the polynomial models.
Again, these new models can be further employed in solving the inverse problem: find out the operating conditions corresponding to given product characteristics. The higher errors with respect to the previous ones (see Tables 1 and 2) is due to expansion of the ranges of the model with the high imposed aspect ratio experiments, leading to a possible distortion of the model. As already commented earlier, the polydispersity of NPs with such complex morphology is even more challenging to be measured accurately for high aspect ratios. However, the models are able to predict reasonably well the aspect ratio (from 1.4 to 6) and the hydrodynamic radius of the NPs. The comparison of all the data of the final refined models are shown in Tables S9 and S13 of the SI.
ANN model for NPs length along the c-axis direction
Once having seen good results in the ANNs modelling for hydrodynamic radius, polydispersity and aspect ratio, all experimental data were employed for new ANN models, built to reflect the length of the nanoparticles along the c-axis direction dependence on operating parameters (Table S3 column “Major” for the values) and its polydispersity (see SI, Table S10). These new results, unlike RH and polydispersity index, are completely independent on the colloid stability (although the DLS measurements were performed on stable colloids) because in this case the measurands are geometric values obtained from the TSEM micrographs.
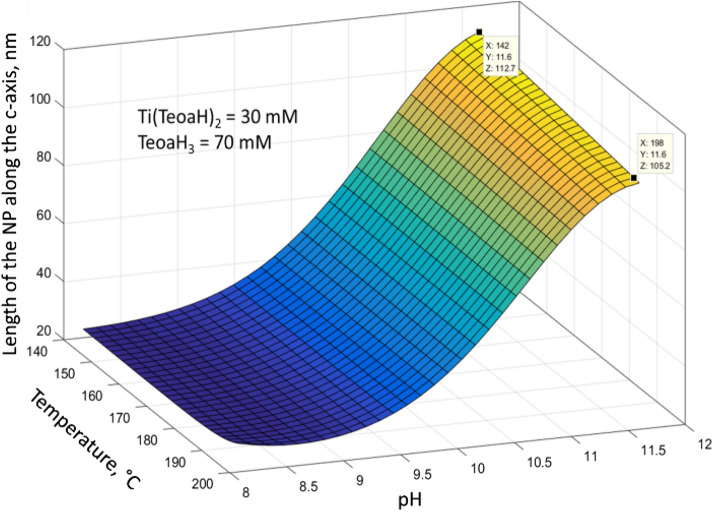
Table 4 displays smaller error between experimental and computed values for the ANN models. The new ANNs can be employed for performing simulations as reported in Fig. 3, where the variation of the length of the nanoparticles along the direction of the c-axis of the crystal is reported as a function of pH and temperature (with precursor and shape controller concentration fixed to 30 mM and 70 mM respectively), the parameters that mainly influence the NPs morphology.
Table 4.
Comparison between the relative mean errors for second degree polynomial models and ANN refined models obtained for the length of the NPs along the c-axis and its standard deviation.
| c-axis length | Standard deviation | ||
|---|---|---|---|
| ANN | Polynomial | ANN | Polynomial |
| 8.5% | 13.5% | 8.9% | 18.1% |
Figure 3.
Variation of the length of the nanoparticles along the direction of the c-axis of the crystal as a function of pH and temperature (image created with Matlab R2015a software (Math Works, Natick, MA, USA), https://it.mathworks.com/products/matlab.html).
It must be underlined, that the length oS3f the NP does not necessarily correspond to the measure of the c-axis intended as average size of crystal domain (D004) as obtained from XRD measurement (Table and in detail in the Sect. 7 of the SI). In particular, the length of the NP seems to be comparable to D004 only for aspect ratios up to 2 (Table S3).
To test the final reliability of all the ANNs model, they were used for predicting the NPs characteristics of a last synthesis, obtaining very good results for almost all the ANN models (Table S12) and each time they performed better compared with the polynomial models. Obviously, each ANN model can be validated with new experiments that consequently can be used to the refine model improving its prediction ability, resulting in an iterative process that can gradually lead to improved reliability.
Discussion
The TiO2 NPs obtained in the experimental design used in the present study have an aspect ratio ranging from 1.4 to 5.5 with sizes from 20 to 110 nm. The hydrodynamic radius values measured with the DLS (RH 7–20 nm) are in fair agreement with the RH values derived from the Perrin formula (RH 9–29 nm), which takes into account the TSEM analysis. Moreover, the comparison of the average size of the crystal domains (D004) obtained by Scherrer Analysis of the 004 XRD peak (c-axis) with the actual length of the nanoparticles obtained by electron microscopy (see Table S3 of the SI) confirms the low defectivity of the nanoparticles along the c-axis for almost all the materials synthetized. The lower D004 values obtained for the more elongated nanoparticles (aspect ratio higher than 2) compared with the nanoparticle length obtained from the microscopy, indicates a higher defectivity of the crystal lattice of these NPs and the possibility to have poly-crystallinity. These new findings further highlight the difficulty to obtain a real strong elongation of the crystal along the c-axis with the exposition of high-energy surface and pay attention to the importance of characterizing nanoparticles in the best possible way before drawing hasty conclusions relying solely on morphology. The final results represented in Fig. 1 highlight some general rules for these kinds of synthesis, in particular: lower pH and temperature conditions lead to lower RH. Alkaline pH (> 11) and low temperature favor the formation of brookite phase and a stronger elongation of the NPs.
The results of the experimental design were used as training set for ANN models to predict the TiO2 NPs size and shape as a function of four HT synthesis process parameters: pH, temperature, precursor and shape controller concentrations. The models were validated with a dataset constituted of 6 validation experiments. The resulting ANN models were used (together with GA) to formulate optimizing problem and propose best operating conditions for given product characteristics. The ANN models were then reverse engineered, to directly find the corresponding working conditions given the NPs characteristics. The models were tested with other experiments that allow the ranges extension, in particular driving the synthesis of NPs with high aspect ratio. This last models lead to a lower prediction accuracy compared with the previous optimized models, but it allows tuning the elongation of the NPs along the c-axis starting from defined synthesis conditions with good predictive capability, especially for aspect ratio > 3. At each step, the ANN models were compared with a second degree polynomial models employed as benchmark for these kind of analysis. Every time, the performances of the ANN models after refinement exceed (in a more or less marked way) the polynomial ones, confirming the good prediction ability of the ANN models (see Tables S9, S12, S13 and S14).
The ANNs built can be further trained with other experiments, in an iterative process that could lead to closer match between the a priori given and experimentally obtained NPs characteristics. In fact, the neurons are usually trained with thousands of input data in its common applications such as data mining, etc. In this work we have seen how ANN can be successfully exploited to predict the morphology of the NPs even starting from a relatively small data set, but obtained through experimental design. The final test confirms the reliability of the model (always better than polynomial models), with the possibility to continuously control the aspect ratio of the anatase NPs from 1.4 to 6. Finally, new ANN models were built in order to reflect the dependence of the length of the nanoparticles along the c-axis and its standard deviation from the synthesis parameters. The new ANNs can be successfully used to modelling and predict (together with GA) the length of the NPs in wide range from 20 to 140 nm.
Conclusions
In conclusion, the statistical analysis of data, model building and refining can help to control the product characteristics. By statistical modelling both polynomial and ANN models are good candidates, but with a slight increase of data the prognosis capacity of ANN is better especially when the process has strong nonlinearities.
The design rules obtained in this study thanks to ANN models are valuable per se, because the NP materials of this kind can find large-scale application in catalysis and energy harvesting, but, more importantly, because these results can be extended to different synthesis procedures or to other materials, e.g. α-Fe2O3 ZnO, WO3, etc., thus, widening the experimental ranges and adding new relevant process parameters. In all these cases, the possibility to rely on materials composed of NPs with low polydispersity in shape and size, enables the more reliable correlation between macroscopic properties and morphology at the nanoscale, with significant benefits for both fundamental and applied research.
Methods
Nanoparticles synthesis
The NPs were synthetized using a known procedure. The required mass of precursor, a complex of Ti with triethanolamine (details in SI), was dissolved in ultrapure water together with the right amount of triethanolamine as capping agent. The pH was adjusted with 1 M carbonate-free NaOH or 1 M HCl, as required. The final solution was then filtered and heated in a Teflon lined stainless steel high pressure autoclave at the set temperature after a N2 sparging of 5 min. Details of the precursor and NPs synthesis and characterization in the Sects. 1–4 of the SI.
Experimental design
The experimental design technique used is a Box Wilson central composite designs (CCD) with 4 factors (n), 8 star points and 4 center points (N0). The experimental plan considered the four independent variables (factors) that mainly influence the product characteristics: Ti (TeoaH)2 initial concentration (Z1), TeoaH3 concentration added as shape controller (Z2), initial pH (Z3), operating temperature (Z4). The output variables are hydrodynamic radius (Y1), polydispersity index (Y2) and the aspect ratio (Y3). Details of the experimental design building in Sect. 5 of the SI.
Mathematical modelling
The best architecture identified for all the ANNs is: 4 neurons in the input layer corresponding to the operating parameters, 3 neurons in the hidden layer and 1 neuron in the output layer. The ANNs were trained in the frame of Matlab R2015a software using backpropagation algorithm as detailed in SI. The hyper-parameters in ANN are the “by default parameters” given in Matlab for the optimization function chosen. The errors (total errors) are explicitly presented by parity plots and detailed in SI. The criterion for adjusting the weights (optimization of the network structure) was the minimization of sum of squared error in the training step. The data sets were used 70–80% for training, and 30–20% for validation and testing to prevent overfitting and test the prediction capability. The ANN were trained and tested in the frame of Matlab R2015a software. The implemented training algorithm, trainlm is used. It is the fastest backpropagation algorithm in the Matlab toolbox and it updates the weight and bias values according to Levenberg–Marquardt optimization. The other hyperparameters are: Number of epach: max 1000, Maximum validation failures 6; Minimum performance gradient 1e-7, Initial Mu 0.001, Mu increasing factor 10, Mu decreasing factor 0.1, maximum Mu 1e10. For the details of the ANN theory and on all the developed ANNs see the Sect. 10 of the SI.
Supplementary information
Acknowledgements
The authors acknowledge funding from: (1) Regione Piemonte, Bando LR34/2004—“Studio preliminare e sviluppo di soluzioni innovative di materiali d’attrito in ambito Automotive”; (2) The project 17NRM04 nPSize has received funding from the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme. (3) SETNanoMetro, EU Project, FP7-NMP-2013_LARGE-7. Project number: 60457. The authors dedicate this work to the memory of Professor G. Martra (17 April 1966–29 September 2020) – University of Torino, Italy—for his fundamental contribution in this paper and his brilliant scientific career that inspired many of the authors of this paper. Thanks Gianmario.
Author contributions
V.M, R.I. and F.P. conceived the research and designed the experiments. F.P. and L.P. performed all the material synthesis and characterization. E.O. and V.D.H. performed the microscopic characterization. R.I. developed the ANN model. F.P. wrote the paper with input from all the authors. F.P., F.S., G.M., V.D.H., A.M.R., R.I. and V.M. revised the manuscript. Correspondence and requests for materials should be addressed to F.P.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Gianmario Martra is deceased.
Contributor Information
Francesco Pellegrino, Email: francesco.pellegrino@unito.it.
Vasile-Dan Hodoroaba, Email: dan.hodoroaba@bam.de.
Supplementary information
is available for this paper at 10.1038/s41598-020-75967-w.
References
- 1.Diebold U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003;48:53–229. doi: 10.1016/S0167-5729(02)00100-0. [DOI] [Google Scholar]
- 2.Yi Z, et al. An orthophosphate semiconductor with photooxidation properties under visible-light irradiation. Nat. Mater. 2010;9:559–564. doi: 10.1038/nmat2780. [DOI] [PubMed] [Google Scholar]
- 3.Lee BH, et al. Reversible and cooperative photoactivation of single-atom Cu/TiO2 photocatalysts. Nat. Mater. 2019;18:620–626. doi: 10.1038/s41563-019-0344-1. [DOI] [PubMed] [Google Scholar]
- 4.Puddu V, Choi H, Dionysiou DD, Puma GL. TiO2 photocatalyst for indoor air remediation: influence of crystallinity, crystal phase, and UV radiation intensity on trichloroethylene degradation. Appl. Catal. B. 2010;94:211–218. doi: 10.1016/j.apcatb.2009.08.003. [DOI] [Google Scholar]
- 5.Dolat D, Quici N, Kusiak-Nejman E, Morawski AW, Li Puma G. One-step, hydrothermal synthesis of nitrogen, carbon co-doped titanium dioxide (N, CTiO2) photocatalysts. Effect of alcohol degree and chain length as carbon dopant precursors on photocatalytic activity and catalyst deactivation. Appl. Catal. B. 2012;1:4. doi: 10.1016/j.apcatb.2011.12.007. [DOI] [Google Scholar]
- 6.Dahlman CJ, Agrawal A, Staller CM, Adair J, Milliron DJ. Anisotropic origins of localized surface plasmon resonance in n-type anatase TiO2 nanocrystals. Chem. Mater. 2019;31:502–511. doi: 10.1021/acs.chemmater.8b04519. [DOI] [Google Scholar]
- 7.Billet J, et al. Size tunable synthesis and surface chemistry of metastable TiO2-bronze nanocrystals. Chem. Mater. 2018;30:4298–4306. doi: 10.1021/acs.chemmater.8b01296. [DOI] [Google Scholar]
- 8.Yuan W, et al. Unveiling the atomic structures of the minority surfaces of TiO2 nanocrystals. Chem. Mater. 2017;30:288–295. doi: 10.1021/acs.chemmater.7b04541. [DOI] [Google Scholar]
- 9.DeRita L, et al. Structural evolution of atomically dispersed Pt catalysts dictates reactivity. Nat. Mater. 2019;18:746–751. doi: 10.1038/s41563-019-0349-9. [DOI] [PubMed] [Google Scholar]
- 10.Hussain H, et al. Structure of a model TiO2 photocatalytic interface. Nat Mater. 2017;16:461–466. doi: 10.1038/nmat4793. [DOI] [PubMed] [Google Scholar]
- 11.Gong XQ, Selloni A, Batzill M, Diebold U. Steps on anatase TiO2(101) Nat Mater. 2006;5:665–670. doi: 10.1038/nmat1695. [DOI] [PubMed] [Google Scholar]
- 12.Pellegrino F, et al. Formic acid photoreforming for hydrogen production on shape-controlled anatase TiO2 nanoparticles: assessment of the role of fluorides, 101}/{001 surfaces ratio, and platinization. ACS Catal. 2019 doi: 10.1021/acscatal.9b01861. [DOI] [Google Scholar]
- 13.Balázs N, Srankó DF, Dombi A, Sipos P, Mogyorósi K. The effect of particle shape on the activity of nanocrystalline TiO2 photocatalysts in phenol decomposition. Part 2: The key synthesis parameters influencing the particle shape and activity. Appl. Catal. 2010;B96:569–576. doi: 10.1016/j.apcatb.2010.03.006. [DOI] [Google Scholar]
- 14.Pellegrino F, et al. Influence of agglomeration and aggregation on the photocatalytic activity of TiO2 nanoparticles. Appl. Catal. B. 2017;216:80–87. doi: 10.1016/j.apcatb.2017.05.046. [DOI] [Google Scholar]
- 15.D’Arienzo M, et al. Crystal surfaces and fate of photogenerated Defects in shape-controlled anatase nanocrystals: drawing useful relations to improve the H2 yield in methanol photosteam reforming. J. Phys. Chem. C. 2015;119:12385–12393. doi: 10.1021/acs.jpcc.5b01814. [DOI] [Google Scholar]
- 16.Gulzar M, et al. Tribological performance of nanoparticles as lubricating oil additives. J. Nanopart. Res. 2016 doi: 10.1007/s11051-016-3537-4. [DOI] [Google Scholar]
- 17.Laad M, Jatti VKS. Titanium oxide nanoparticles as additives in engine oil. J. King Saud Univ. 2018;30:116–122. doi: 10.1016/j.jksues.2016.01.008. [DOI] [Google Scholar]
- 18.Hwang Y, et al. Effect of the size and morphology of particles dispersed in nano-oil on friction performance between rotating discs. J. Mech. Sci. Technol. 2011;25:2853–2857. doi: 10.1007/s12206-011-0724-1. [DOI] [Google Scholar]
- 19.D'Arienzo M, Scotti R, Di Credico B, Redaelli M. Synthesis and characterization of morphology-controlled TiO2 nanocrystals. Stud. Surf. Sci. Catal. 2017;177:477–540. doi: 10.1016/b978-0-12-805090-3.00013-9. [DOI] [Google Scholar]
- 20.Ortel E, et al. Shape recognition of nanoparticles by high-resolution SEM and TSEM. Microsc. Microanal. 2015;21:2401–2402. doi: 10.1017/s1431927615012787. [DOI] [Google Scholar]
- 21.Mino L, et al. Beyond shape engineering of TiO2 nanoparticles: post-synthesis treatment dependence of surface hydration, hydroxylation, lewis acidity and photocatalytic activity of TiO2 anatase nanoparticles with dominant 001 or 101 facets. ACS Appl. Nano Mater. 2018;1:5355–5365. doi: 10.1021/acsanm.8b01477. [DOI] [Google Scholar]
- 22.Babick F, Mielke J, Wohlleben W, Weigel S, Hodoroaba VD. How reliably can a material be classified as a nanomaterial? Available particle-sizing techniques at work. J. Nanopart. Res. 2016;18:158. doi: 10.1007/s11051-016-3461-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bittarello E, Bruno M, Aquilano D. Ab initio calculations of the main crystal surfaces of baryte (BaSO4) Cryst. Growth Des. 2018;18:4084–4094. doi: 10.1021/acs.cgd.8b00460. [DOI] [Google Scholar]
- 24.Penn RL, Banfield JF. Morphology development and crystal growth in nanocrystalline aggregates under hydrothermal conditions: insights from titania. Geochim. Cosmochim. Acta. 1999;63:1549–1557. doi: 10.1016/s0016-7037(99)00037-x. [DOI] [Google Scholar]
- 25.Raju M, van Duin AC, Fichthorn KA. Mechanisms of oriented attachment of TiO2 nanocrystals in vacuum and humid environments: reactive molecular dynamics. Nano Lett. 2014;14:1836–1842. doi: 10.1021/nl404533k. [DOI] [PubMed] [Google Scholar]
- 26.Cho CH, Han MH, Kim DH, Kim DK. Morphology evolution of anatase TiO2 nanocrystals under a hydrothermal condition (pH=9.5) and their ultra-high photo-catalytic activity. Mater. Chem. Phys. 2005;92:104–111. doi: 10.1016/j.matchemphys.2004.12.036. [DOI] [Google Scholar]
- 27.Lavric V, et al. A new model for nano-TiO2 crystal birth and growth in hydrothermal treatment using an oriented attachment approach. Cryst. Growth Des. 2017;17:5640–5651. doi: 10.1021/acs.cgd.7b00302. [DOI] [Google Scholar]
- 28.Coley CW, Green WH, Jensen KF. Machine learning in computer-aided synthesis planning. Acc. Chem. Res. 2018;51:1281–1289. doi: 10.1021/acs.accounts.8b00087. [DOI] [PubMed] [Google Scholar]
- 29.Stein HS, Gregoire JM. Progress and prospects for accelerating materials science with automated and autonomous workflows. Chem. Sci. 2019;10:9640–9649. doi: 10.1039/c9sc03766g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stein HS, Guevarra D, Newhouse PF, Soedarmadji E, Gregoire JM. Machine learning of optical properties of materials—predicting spectra from images and images from spectra. Chem. Sci. 2019;10:47–55. doi: 10.1039/c8sc03077d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Afzal MAF, Sonpal A, Haghighatlari M, Schultz AJ, Hachmann J. A deep neural network model for packing density predictions and its application in the study of 1.5 million organic molecules. Chem. Sci. 2019;10:8374–8383. doi: 10.1039/c9sc02677k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Patra TK, Meenakshisundaram V, Hung JH, Simmons DS. Neural-network-biased genetic algorithms for materials design: evolutionary algorithms that learn. ACS Comb. Sci. 2017;19:96–107. doi: 10.1021/acscombsci.6b00136. [DOI] [PubMed] [Google Scholar]
- 33.Bonk BM, Weis JW, Tidor B. Machine learning identifies chemical characteristics that promote enzyme catalysis. J. Am. Chem. Soc. 2019;141:4108–4118. doi: 10.1021/jacs.8b13879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nielsen MK, Ahneman DT, Riera O, Doyle AG. Deoxyfluorination with sulfonyl fluorides: navigating reaction space with machine learning. J. Am. Chem. Soc. 2018;140:5004–5008. doi: 10.1021/jacs.8b01523. [DOI] [PubMed] [Google Scholar]
- 35.Panapitiya G, et al. Machine-learning prediction of CO adsorption in thiolated, Ag-alloyed Au nanoclusters. J. Am. Chem. Soc. 2018;140:17508–17514. doi: 10.1021/jacs.8b08800. [DOI] [PubMed] [Google Scholar]
- 36.Mansouri Tehrani A, et al. Machine learning directed search for ultraincompressible, superhard materials. J. Am. Chem. Soc. 2018;140:9844–9853. doi: 10.1021/jacs.8b02717. [DOI] [PubMed] [Google Scholar]
- 37.Orimoto Y, et al. Application of artificial neural networks to rapid data analysis in combinatorial nanoparticle syntheses. J. Phys. Chem. C. 2012;116:17885–17896. doi: 10.1021/jp3031122. [DOI] [Google Scholar]
- 38.Ryan K, Lengyel J, Shatruk M. Crystal structure prediction via deep learning. J. Am. Chem. Soc. 2018;140:10158–10168. doi: 10.1021/jacs.8b03913. [DOI] [PubMed] [Google Scholar]
- 39.Eskandarloo H, Badiei A, Behnajady MA. Study of the effect of additives on the photocatalytic degradation of a triphenylmethane dye in the presence of immobilized TiO2/NiO nanoparticles: artificial neural network modeling. Ind. Eng. Chem. Res. 2014;53:6881–6895. doi: 10.1021/ie500253q. [DOI] [Google Scholar]
- 40.Sun B, Fernandez M, Barnard AS. Machine learning for silver nanoparticle electron transfer property prediction. J. Chem. Inf. Model. 2017;57:2413–2423. doi: 10.1021/acs.jcim.7b00272. [DOI] [PubMed] [Google Scholar]
- 41.So S, Mun J, Rho J. Simultaneous inverse design of materials and structures via deep learning: demonstration of dipole resonance engineering using core-shell nanoparticles. ACS Appl. Mater. Interfaces. 2019;11:24264–24268. doi: 10.1021/acsami.9b05857. [DOI] [PubMed] [Google Scholar]
- 42.Patel KA, Brahmbhatt PK. A comparative study of the RSM and ANN models for predicting surface roughness in roller burnishing. Proc Tech. 2016;23:391–397. doi: 10.1016/j.protcy.2016.03.042. [DOI] [Google Scholar]
- 43.Kim E, et al. Materials synthesis insights from scientific literature via text extraction and machine learning. Chem. Mater. 2017;29:9436–9444. doi: 10.1021/acs.chemmater.7b03500. [DOI] [Google Scholar]
- 44.Crump L. Experimental designs. J. Am. Chem. Soc. 1958;80:252–252. doi: 10.1021/ja01534a073. [DOI] [Google Scholar]
- 45.Chew V. Experimental designs in industry. Ind. Eng. Chem. 1959;51:89A–89A. doi: 10.1021/i650590a765. [DOI] [Google Scholar]
- 46.Higgs RE, Bemis KG, Watson IA, Wikel JH. Experimental designs for selecting molecules from large chemical databases. J. Chem. Inf. Comput. Sci. 1997;37:861–870. doi: 10.1021/ci9702858. [DOI] [Google Scholar]
- 47.Palasota JA, Deming SN. Central composite experimental designs: Applied to chemical systems. J. Chem. Educ. 1992;69:560. doi: 10.1021/ed069p560. [DOI] [Google Scholar]
- 48.Dirion B, Cobb Z, Schillinger E, Andersson LI, Sellergren B. Water-compatible molecularly imprinted polymers obtained via high-throughput synthesis and experimental design. J. Am. Chem. Soc. 2003;125:15101–15109. doi: 10.1021/ja0355473. [DOI] [PubMed] [Google Scholar]
- 49.Khorasani AM, Yazdi MRS, Safizadeh MS. Tool Life prediction in face milling machining of 7075 Al by using artificial neural networks (ANN) and Taguchi design of experiment (DOE) Int. J. Eng. Technol. 2011;3:30. doi: 10.7763/IJET.2011.V3.196. [DOI] [Google Scholar]
- 50.Shanmugaprakash M, Sivakumar V. Development of experimental design approach and ANN-based models for determination of Cr(VI) ions uptake rate from aqueous solution onto the solid biodiesel waste residue. Biores. Technol. 2013;148:550–559. doi: 10.1016/j.biortech.2013.08.149. [DOI] [PubMed] [Google Scholar]
- 51.Geyikçi F, Kılıç E, Çoruh S, Elevli S. Modelling of lead adsorption from industrial sludge leachate on red mud by using RSM and ANN. Chem. Eng. J. 2012;183:53–59. doi: 10.1016/j.cej.2011.12.019. [DOI] [Google Scholar]
- 52.Sánchez Lasheras F, Vilán Vilán JA, García Nieto PJ, del Coz Díaz JJ. The use of design of experiments to improve a neural network model in order to predict the thickness of the chromium layer in a hard chromium plating process. Math. Comput. Model. 2010;52:1169–1176. doi: 10.1016/j.mcm.2010.03.007. [DOI] [Google Scholar]
- 53.Rahmanian B, Pakizeh M, Mansoori SA, Abedini R. Application of experimental design approach and artificial neural network (ANN) for the determination of potential micellar-enhanced ultrafiltration process. J. Hazard. Mater. 2011;187:67–74. doi: 10.1016/j.jhazmat.2010.11.135. [DOI] [PubMed] [Google Scholar]
- 54.Kasiri MB, Aleboyeh H, Aleboyeh A. Modeling and optimization of heterogeneous photo-Fenton process with response surface methodology and artificial neural networks. Environ. Sci. Technol. 2008;42:7970–7975. doi: 10.1021/es801372q. [DOI] [PubMed] [Google Scholar]
- 55.Raccuglia P, et al. Machine-learning-assisted materials discovery using failed experiments. Nature. 2016;533:73–76. doi: 10.1038/nature17439. [DOI] [PubMed] [Google Scholar]
- 56.Huo H, et al. Semi-supervised machine-learning classification of materials synthesis procedures. Npj Comput. Mater. 2019 doi: 10.1038/s41524-019-0204-1. [DOI] [Google Scholar]
- 57.Curtarolo S, et al. The high-throughput highway to computational materials design. Nat. Mater. 2013;12:191–201. doi: 10.1038/nmat3568. [DOI] [PubMed] [Google Scholar]
- 58.Deiana C, et al. Shape-controlled TiO2 nanoparticles and TiO2 P25 interacting with CO and H2O2 molecular probes: a synergic approach for surface structure recognition and physico-chemical understanding. Phys. Chem. Chem. Phys. 2013;15:307–315. doi: 10.1039/C2CP42381B. [DOI] [PubMed] [Google Scholar]
- 59.Kalinin SV, Sumpter BG, Archibald RK. Big-deep-smart data in imaging for guiding materials design. Nat Mater. 2015;14:973–980. doi: 10.1038/nmat4395. [DOI] [PubMed] [Google Scholar]
- 60.Marzari N. The frontiers and the challenges. Nat. Mater. 2016;15:381. doi: 10.1038/nmat4613. [DOI] [PubMed] [Google Scholar]
- 61.Zhang Q, Yu H, Barbiero M, Wang B, Gu M. Artificial neural networks enabled by nanophotonics. Light Sci. Appl. 2019;8:42. doi: 10.1038/s41377-019-0151-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rem BS, et al. Identifying quantum phase transitions using artificial neural networks on experimental data. Nat. Phys. 2019;15:917–920. doi: 10.1038/s41567-019-0554-0. [DOI] [Google Scholar]
- 63.Szilagyi B, et al. Piezoelectric-based high performance spray solvent delivery system for desorption electrospray ionization mass spectrometry: systematic design and case studies for high throughput screening of N-alkylation reactions. Chem. Eng. Sci. 2019;195:1010–1020. doi: 10.1016/j.ces.2018.10.046. [DOI] [Google Scholar]
- 64.Kitchin JR. Machine learning in catalysis. Nat. Catal. 2018;1:230–232. doi: 10.1038/s41929-018-0056-y. [DOI] [Google Scholar]
- 65.Pektas AO, Cigizoglu HK. Investigating the extrapolation performance of neural network models in suspended sediment data. Hydrol. Sci. J. 2017;62:1694–1703. doi: 10.1080/02626667.2017.1349316. [DOI] [Google Scholar]
- 66.Wsól VR, Fell AF. Central composite design as a powerful optimisation technique for enantioresolution of the rac-11-dihydrooracin—the principal metabolite of the potential cytostatic drug oracin. J. Biochem. Biophys. Methods. 2002;54:377–390. doi: 10.1016/s0165-022x(02)00138-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.