Abstract
Problems related to unknown or imprecisely measured populations at risk are common in epidemiologic studies of disease frequency. The size of the population at risk is typically conceptualized as a denominator to be used in combination with a count of disease cases (a numerator) to calculate incidence or prevalence. However, the size of the population at risk can take other epidemiologic properties in relation to an exposure of interest and the count outcome, including confounding, modification, and mediation. Using spatial ecological studies of injury incidence as an example, we identify and evaluate five approaches that researchers have used to address “unknown denominator problems”: ignoring, controlling for a proxy, approximating, controlling by study design, and measuring the population at risk. We present a case example and recommendations for selecting a solution given the data and the hypothesized relationship between an exposure of interest, a count outcome, and the population at risk.
Keywords: methodology, spatial, space-time, injury, acute
1. INTRODUCTION
Precise measures of disease frequency are essential for researchers to accurately describe distributions of health and ill-health, to assess associations with putative causal drivers, and ultimately to develop interventions that affect these drivers in order to improve population health (Keyes and Galea, 2014; Porta, 2008). Prevalence and incidence—the primary approaches to measure disease frequency—are calculated similarly, in that both denominate counts of disease cases by the size of population at risk. Researchers collectively invest a great deal of effort to ensure they use valid case counts (Lyons et al., 2008; O’Reilly et al., 2016). Comparatively little attention is paid to measuring the size of the population at risk, yet there are many reasons why the size of the population at risk may be unknown or difficult to measure. Individuals can come and go from populations; precise records are not always available; delineation between populations may be unclear.
Problems related to unknown or imprecisely measured populations at risk can greatly affect researchers’ ability to assess causation. To illustrate this point, Garson (1976) used the simple example of two family physicians, the first of whom reported having seven patients with multiple sclerosis, and the second of whom reported having 25 such patients. Comparison of raw case counts suggests the prevalence of multiple sclerosis is around four-fold greater at the second clinic compared to the first and could justify investigation of possible causes. However, if the first clinic had 1,000 patients and the second had 4,000 patients, there would be no need for further inquiry. Several authors refer to this broad issue as the “denominator problem” and conceptualize the population at risk as a mathematical property of measures of disease frequency (Bartholomeeusen et al., 2005). From this perspective, the primary considerations are whether the population at risk can be defined clearly and measured validly. Once these conditions are met, the population at risk can be used as a denominator to calculate disease frequency or incorporated as an offset variable in a linear model.
1.1. An Epidemiologic Perspective
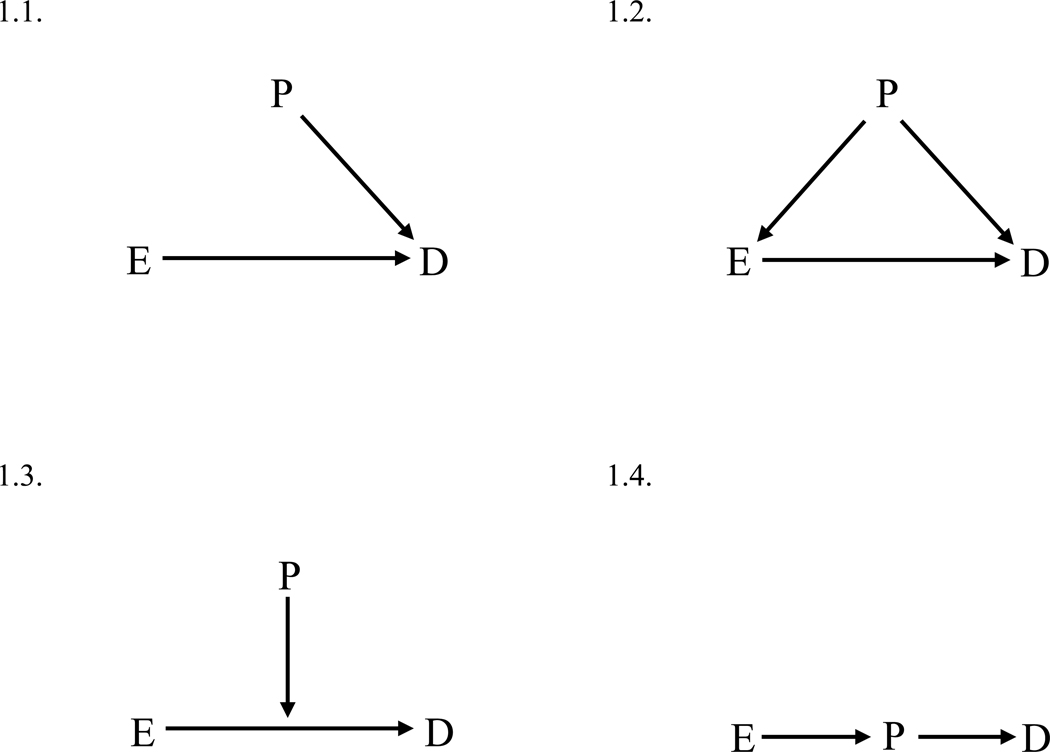
When the population at risk is conceptualized in epidemiologic terms, further essential considerations arise. Fig. 1 presents four possible associations between an exposure, an outcome, and the population at risk. In the simplest scenario (Fig. 1.1), the size of the population at risk is directly causally related to the number of cases (i.e. larger populations generate more outcomes) and is unrelated to the exposure of interest, in which case it is appropriate to use this value as a denominator. However, this approach is not always appropriate. If the size of the population at risk is associated with the exposure of interest and is causally related to the outcome (Fig. 1.2), it may be more useful to consider this value as a confounder. Alternatively, the size of the population at risk may change behavior in a way that modifies associations between the exposure of interest and the outcome (Fig 1.3). For example, studies of bicycle safety document a “safety in numbers” effect (Elvik and Bjørnskau, 2017; Thompson et al., 2015); routine activities theory predicts pedestrian volume will be non-linearly related to the incidence of violent crime (Cohen and Felson, 1979). Studies of these phenomena must necessarily separate the numerator from the denominator to assess statistical interaction. Finally, if the size of the population at risk is on the causal path between the exposure and the outcome (i.e. a mediator), it should not be included in a statistical analysis (Fig 1.4).
Figure 1.
Directed acyclical graphs describing theoretical causal links between an exposure of interest (E), an outcome of interest (D), and the population at risk (P).
Spatial ecological studies are particularly susceptible to variation in the population at risk due to routine human mobility. In this study design, populations are delineated geographically and temporally, and researchers assess associations between social and physical environmental conditions (exposures) and aggregate measures of disease and injury (outcomes) within space-time units. Mobility—defined as the movement of people and resources through space over time—can cause the population at risk to vary considerably within and between units, and the smaller the spatial or temporal partitions, the greater this variation is likely to be. For example, the resident population accounted for 99.99% of pooled variance in the actual number of people present in Australian states and territories on the day of the 2016 Census. Within the much smaller Statistical Area level 2 units (“SA2” units; analogous to US Census tracts), the resident population accounted for 97.43% of variance. This proportion will continue to decrease as spatial units shrink (e.g. SA1 units, blocks, dwellings) and temporal units become briefer (e.g. hours, minutes).
1.2. Study Aims
The aim of this paper is to identify and evaluate methods used to account for the size of the population at risk in population studies of disease frequency in the presence of geographic mobility. For consistency with the extant literature we refer to this issue as the “unknown denominator problem”, though we take an epidemiologic perspective and assess available methods in light of four possible relationships: as a denominator, as a confounder, as an effect modifier, and as a mediator. We focus on studies of acute disease incidence because outcomes with brief induction periods—meaning the interval between an exposure and the first manifestation of a disease (Koepsell and Weiss, 2004)—are well suited to spatial ecological designs. We focus on injury because it is arguably has the most rapid onset of all acute outcomes, because smaller space-time units are often preferable to ensure that the exposure and the outcome are collocated, and because the unknown denominator problem affects smaller space-time units to a greater extent than larger space-time units.
To address our aim, we present a narrative review that identifies and groups the approaches that authors have used to address the unknown denominator problem in spatial ecological studies of injury incidence. We evaluate the strengths and weaknesses of each identified solution and include exemplar publications to illustrate our findings. We then present a guide to assist researchers to determine the best approach for addressing the unknown denominator problem given the available data and the hypothesized associations, and describe a case example in which we implement the available solutions and assess performance in light of the proposed decision tree.
2. NARRATIVE REVIEW
Researchers have used five approaches to address problems related to unknown denominators that arise in spatial ecological studies of injury incidence due to mobility: ignoring, controlling for a proxy, approximating the population at risk, controlling by study design, and measuring the population at risk.
2.1. Ignoring
In some spatial ecological studies of injury incidence, researchers do not attempt to address the unknown denominator problem or they include only the size of the local resident population (Chapman et al., 2016; DiMaggio, 2015; Inada et al., 2020; Wheeler-Martin et al., 2019). These approaches collectively make no attempt to account for temporal and/or spatial variation in the population at risk beyond the number of local residents (Anselin, 2006; Elliott and Wartenberg, 2004). For example, Fink et al. (2018) assessed suicides in the United States per month from 1999 to 2015 (i.e. within nation-months) before and after the suicide of Robin Williams, a well-known comedian. In seasonal time-series analyses, the outcome was undenominated counts of suicides and the exposure measure was a dichotomous variable indicating months before and months after Mr. Williams’ death.
Ignoring the unknown denominator problem is an attractive approach because it requires minimal effort on the part of researchers. The approach assumes that the population exposed is constant across space-time units, which is justifiable when space-time units are very large and variation in the size of the population at risk is likely to be very small compared to the estimated effects, because further efforts to address the problem will not materially enhance internal validity. For example, in the case of Fink et al. (2018), net changes in population due to migration (or births and deaths) will have negligible impact because the resident population is proportionally very large and the additional variation in the population exposed is unlikely to exceed the size of the detected effects. However, as space-time units become smaller, problems may arise if the unmeasured population at risk is unrelated to the exposure but causally related to the outcome (Fig. 1.1), because statistical noise will increase standard errors and thus increase the likelihood of false negative findings. Conversely, confounding by the unmeasured population at risk (Fig 1.2) will most likely increase the likelihood of false positive associations. Importantly, where outcomes reflect individuals’ places of residence rather than the location of the injury event—such as studies aggregating patients within residential ZIP codes based on hospital discharge data (Gruenewald and Remer, 2006)—the residential population is the correct measure and no further adjustment is required.
2.2. Controlling for a Proxy
Another approach occasionally used to address the unknown denominator problem is adding controls to statistical models for proxy variables that are theoretically related to the size of the population exposed. For example, ecological studies commonly find positive associations between on-premise alcohol outlets (e.g. bars) and assault incidence (Campbell et al., 2009); however, alcohol outlets are commonly located in retail zones that attract additional temporary populations, thus the resident population is an inappropriate measure of the population at risk. Grubesic et al. (2013) attempted to address this problem in a cross-sectional study of police-reported assaults within Philadelphia block groups by including statistical controls for other commercial outlets. This proxy measure accounted for retail activity that would inflate the population at risk within block groups.
Using theoretically relevant covariates to account for the unknown denominator problem is a straightforward approach because the requisite data are commonly available from archival sources and the parameter estimates for the covariates are often easy to interpret. One clear advantage is that it allows researchers to explicitly assess confounding (Fig. 1.2) and effect modification (Fig. 1.3). However, this approach assumes that changes in population across space-time units are uniformly related to the control variables. Any residual variation can be conceptualized as measurement error, which implies that the adjusted parameter estimates may still be subject to residual confounding. In the case of alcohol outlets, some retail zones are more popular than others and attendance at retail zones varies seasonally, so the approach is unlikely to wholly account for variation in the population at risk.
2.3. Approximating the Population at Risk
A third approach is to approximate the size of the population at risk within space-time units (Jang et al., 2018; Nesoff et al., 2019). Available approaches include simulation (Løvås, 1994), interpolation or extrapolation from available observations (Edwards et al., 2018; Xie et al., 2018), mathematical estimation based on one or more other factors (Cuthbert, 1994; Feehan and Salganik, 2016; Navin and Wheeler, 1969), and indirect standardization (Anselin, 2006; Elliott and Wartenberg, 2004). For instance, studies of motor vehicle crashes often denominate by the estimated number of vehicle miles travelled within space-time units. Public authorities typically develop these approximations using continuous observations of vehicle counts from carefully sampled roadway sections to extrapolate to larger space-time units (Garrett, 2014). Similarly, Mooney et al. (2016) used mathematical estimation of pedestrian activity for a cross-sectional study of pedestrian injury and roadway conditions at New York City intersections. Because pedestrian injury counts will be higher where there are more pedestrians, the authors estimated pedestrian volume across the city using a kernel density function based on theoretically relevant variables (residential population density, commercial zoning, public transit stops, and public transit ridership). The authors note that similar approximations of pedestrian volume have been validated against observed pedestrian counts (r = 0.62) (Purciel et al., 2009).
Approximations are a flexible approach to account for the population at risk. They allow researchers to incorporate multiple variables that are theoretically related to the population at risk without requiring precise or complete data for all such covariates within all space-time units. However, depending on the method used, approximations can be a time-consuming and computationally intensive to develop, and, importantly, approximations are not precise observations. An approximation that correlates with observed population counts at r = 0.7 may be considered “validated”, but will explain only 49% of variance in the observed counts (Guilford, 1936). Further, when the population at risk is conceptualized as a confounder (Fig. 1.2) or effect modifier (Fig. 1.3) and is adjusted for in a regression model, measurement error in approximations of the population count will be affected by residual confounding. Knowledge of the reliability and validity of the approximation measure is critical because it allows for simulation and sensitivity analyses that can assess the extent of this problem.
2.4. Controlling by Study Design
Some studies address the unknown denominator problem through study design. The case-crossover design (Maclure, 1991) is an efficient epidemiologic solution for studying rare, acute, conditions among individuals by comparing subjects at the time of the outcome to themselves at a different time. In ecological case-crossover studies, spatial units serve as their own controls (i.e. the same spatial unit at a different time). This design, and other similar methods developed in the disciplines of economics and psychology (e.g. regression discontinuity; difference-in-difference) address the unknown denominator problem by comparing space-time units in which the population exposed is likely to vary only slightly (Ashenfelter and Card, 1985; Thistlethwaite and Campbell, 1960). For instance, Coren (1996) compared the incidence of motor vehicle crashes in Canada on Mondays immediately following daylight savings compared to control Mondays one week before and one week afterwards.
Using study designs to account for the unknown denominator problem is a strong approach that can be implemented simply, without the need for additional data to use as controls or to calibrate approximations (Branas et al., 2011). Despite this considerable strength, studies using design solutions may need to exclude many space-time units from the analytic sample, limiting statistical power. Coren (1996) excluded 362 days from each year. Including additional days (e.g. ± 2 Mondays from the case date) would increase the sample size but may introduce problems related to non-linear variation in the population at risk over time. Additionally, design solutions essentially match on the population at risk so it is not possible to assess confounding (Fig. 1.2) or effect modification (Fig. 1.3), which may be important aspects of building a causal narrative.
2.5. Measuring
In some circumstances, it is possible to solve the unknown denominator problem by making the denominator known. Complete population counts may be available from archival sources (e.g. stadium attendance records for a study of alcohol bans at football games; Spaite et al., 1990). Alternatively, researchers can collect the data themselves, which is an approach best used when the population at risk can be observed unobtrusively and when the space-time units are few in number and are very small (Taylor et al., 2019). For example, bicycle traffic volume varies considerably over space (e.g. from street to street) and time (e.g. from hour to hour) (Liggett and Huff, 2016), and concerns related to unknown populations at risk are well documented in the bicycle safety literature (DiGioia et al., 2017; Strauss et al., 2013, 2015; Vanparijs et al., 2015). For a preliminary study of bicycle safety and roadway conditions, van der Horst et al. (2014) installed video cameras at two purposively selected bicycle path intersections in Amsterdam and Eindhoven, Netherlands, and coded 18 hours of film from both sites for traffic volume and near-misses between cyclists within 15-minute units.
Researchers make clear trade-offs when electing to measure the population exposed within space-time units. Notwithstanding problems related to measurement error, the approach wholly eliminates variation in the denominator as a source of bias, and allows researchers to consider the population at risk as a true denominator (Fig. 1.1), a confounder (Fig. 1.2), or an effect modifier (Fig 1.3). However, this prospective design is poorly suited to statistically rare events such as injury. van der Horst et al.’s (2014) solution was to use near-misses as a proxy for injury outcomes; others use events that lie on the causal path between the exposure and the outcome (Thompson et al., 2018). In either case, the outcome is an event other than the injury itself. Furthermore, a complete census covering the study universe is rarely feasible so a sample of space-time units is often necessary, but non-random samples can impede generalizability (Ebrahim and Davey Smith, 2013). van der Horst et al.’s (2014) findings from just two sites are unlikely to generalize even to other sites within these Dutch cities.
3. SELECTING A SOLUTION
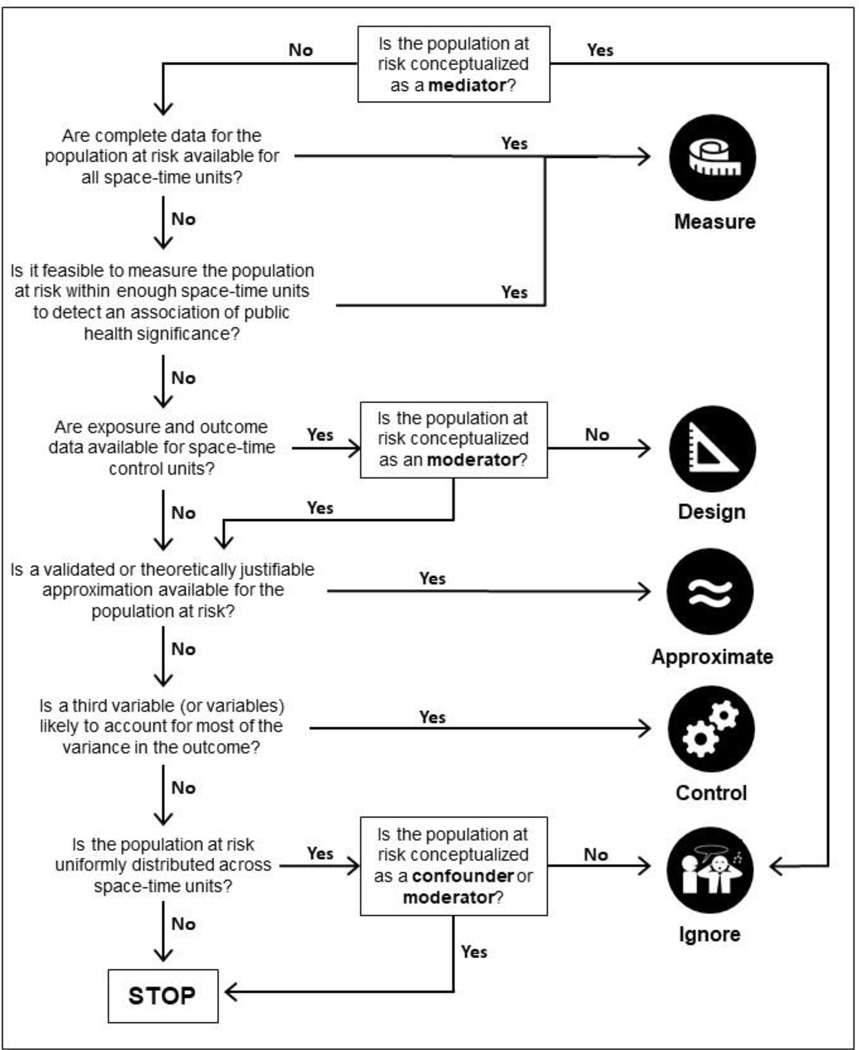
We identified five solutions to the unknown denominator problem that researchers have used to account for unknown denominators that arise due to mobility in spatial ecological studies of injury incidence: ignoring, controlling for a proxy, approximating the population count, controlling by study design, and measuring the population. Fig. 2 suggests an approach for selecting the best solution given the available data and the hypothesized associations between the population at risk and the exposure and outcome of interest. Conceptualized as a mediator, the population at risk should be ignored. Considered as an effect modifier, it should be handled as a controlled proxy, approximated, or directly measured variable. Other approaches mean the assessed associations between the exposure and the outcome reflect the weighted pooled effect across strata. Where the population at risk is thought to be a confounder, a design solution may also be appropriate but the extent of the possible confounding is not measurable. If considered simply to be a denominator, any approach is acceptable, but ignoring the problem is only acceptable if the space-time units are very large. Importantly, the population at risk can have multiple epidemiologic properties at once. Explicitly stating how this variable is conceptualized is critical for understanding the implications of each approach to addressing the unknown denominator problem and in interpreting analytical results. Finally, if none of the five available solutions to the unknown denominator problem are justifiable given the available data and the hypothesized relationships, the best approach is not to proceed with the research effort, lest the analyses yield biased estimates.
Figure 2.
Decision tree for determining the best solution to the unknown denominator problem based on available data and hypothesized relationships between the exposure, the population at risk, and the outcome.
A further essential consideration is the impact of measurement error, which will also depend on how the population at risk is conceptualized in relation to the exposure and outcome variable (Fig. 1). If the population at risk is conceptualized as a denominator unrelated to the exposure and is used to estimate a rate or risk (Fig 1.1), random measurement error in the size of the population at risk (or simply ignoring it) will most likely induce bias to the null. If the population at risk is conceptualized as a confounder, the impact of measurement error will depend on whether this error is differential or non-differential in relation to the outcome. Non-differential error almost always attenuates associations towards null, but differential error can bias associations in either direction (Morgenstern, 1995). If the population at risk is conceptualized as an effect modifier and is explicitly analyzed as such, measurement error can cause the appearance of effect modification where none actually exists or can obscure true effect modification.
4. CASE EXAMPLE: RIDESHARING AND MOTOR VEHICLE CRASHES
To further illustrate the possible solutions to the unknown denominator problem and to demonstrate an application of the proposed decision tree, we now present a case example examining associations between ridesharing services (e.g., Uber, Lyft) and motor vehicle crashes. Previous studies emphasize that ridesharing is associated with fewer alcohol-involved motor vehicle crashes in some municipalities (Brazil and Kirk, 2016; Dills and Mulholland, 2018; Greenwood and Wattal, 2019; Morrison et al., 2018), perhaps because ridesharing replaces some drunk driver trips. However, rideshare services connect owner-operator drivers with prospective passengers through a mobile application using continuous GPS, and distraction due to cell phones is associated with increased crash risks for drivers (Klauer et al., 2010; Harbluk et al., 2007) and pedestrians (Hamann et al., 2017; Stavrinos et al., 2011). Ridesharing may therefore increase motor vehicle crash incidence at trip origins (i.e. pick-up locations) and trip destinations (i.e. drop-off locations). We tested this hypothesis in a recent paper using rideshare trip and motor vehicle crash data for New York City (NYC), aggregated within small space-time areas ( Morrison et al.,2020 ). The unknown denominator problem was an important consideration for these analyses because overall vehicular traffic (the population at risk) will covary with rideshare trip volume and is causally related to crash incidence. Vehicular traffic volume can thus be conceptualized as a confounder. Our published analysis solved the problem using study design solution—specifically, a case-crossover design—whereas here we report the results of statistical analyses that implement all five available solutions. We consider these results in light of the proposed decision tree, the hypothesis, and the available data.
4.1. Method
For a detailed explanation of the methods used for these analyses we refer the reader to our recent publication ( Morrison et al.,2020 ). Briefly, the NYC Taxi and Limousine Commission (2019) provided trip-level rideshare data, including the date, time, trip origin, and trip destination for all rideshare trips in the city. Origins and destinations are masked within NYC Taxi and Limousine Commission taxi zones (n = 258) to protect driver and passenger confidentiality. The New York Police Department provided data for motor vehicle crashes, including the date, time, count of injury victims (motorists, pedestrians, cyclists), and point location (latitude, longitude) for all crashes in which a person was injured and required medical treatment or there was > $1000 of property damage (National Highway Traffic Safety Administration, 2017). We aggregated rideshare trips and injury crashes for 2017 and 2018 within the 258 taxi zones and 17,520 hours; creating a study universe of 4,520,160 taxi zone-hours.
Fixed effects logistic regression models were specified with the space-time units of analysis as taxi zone i at hour t. The outcome Y was a dichotomous indicator for the presence or absence of an injury crash. We modelled the predicted probability (π) of observing outcome Y in unit t as:
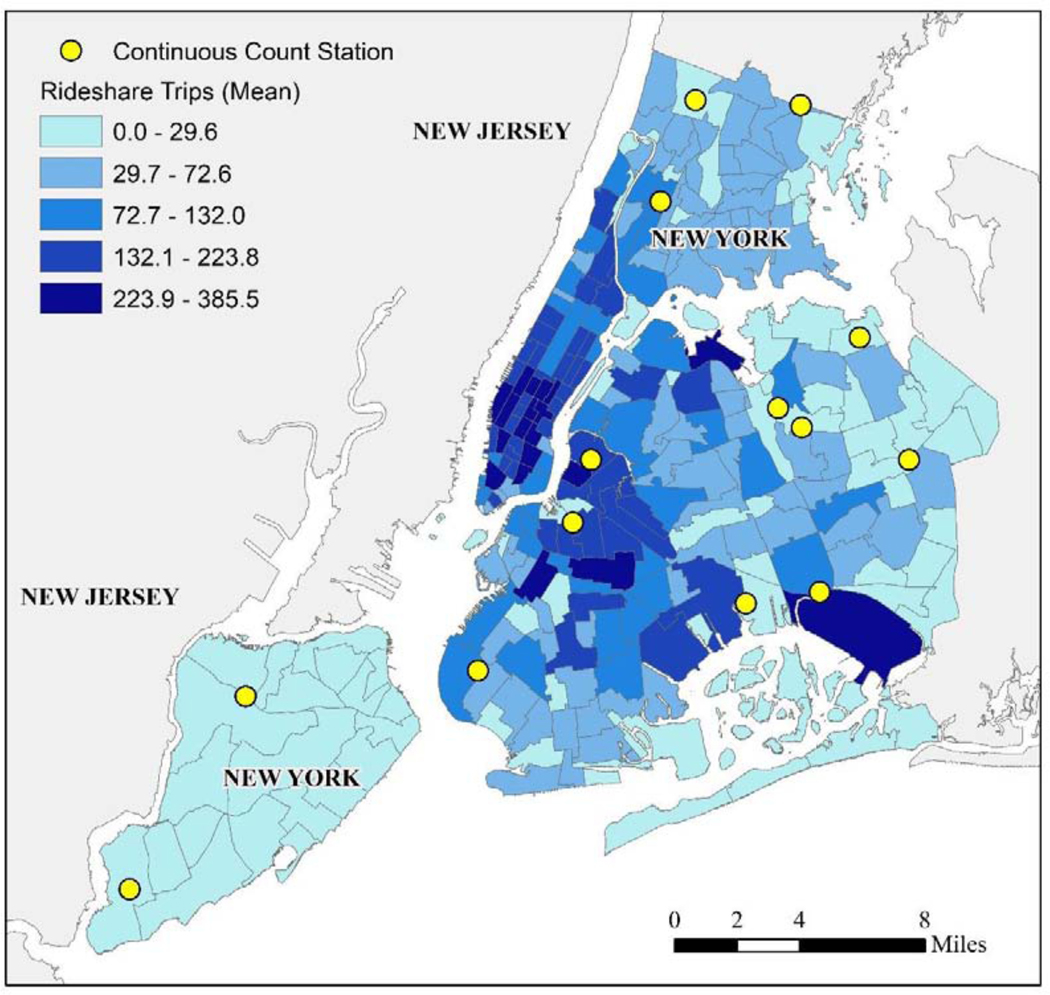
where α was an overall constant term, μi were fixed effects for each taxi zone, and eit was an error term that captured residual variation. The term was a vector of exposure variables that included the exposure of interest (the count of rideshare trip origins) and other variables that accounted for the unknown denominator problem in different ways. Model 1 was an unadjusted analysis implemented on the full sample of taxi zone-hours that ignored the unknown denominator problem. Model 2 controlled for a proxy by including time varying environmental conditions that will affect motor vehicle use (temperature, precipitation, holidays, school days, hour of day, day of week, month-year). Model 3 approximated overall motor vehicle traffic using taxi trip volume. Model 4 was the previously published case crossover analysis that controlled by study design. This approach only included “case” units (taxi zone-hours in which a crash occurred) and matched control units (the same taxi zone precisely 1 week earlier (−168 hours) and 1 week later (+168 hours)) selected with replacement (n = 245,148). Model 5 measured vehicular traffic using data from 14 continuous count stations positioned at fixed sites around NYC. We included taxi zone-hours that contained a continuous count station data (n = 89,384).
The case-crossover design for Model 4 inherently accounted for spatial and temporal dependencies by omitting most units that were adjacent to one another in space and time. We additionally conditioned upon spatial location using a fixed effect for taxi zones because the panel was unbalanced (Greene, 2003) and used robust standard errors to account for nesting within taxi zones. For this demonstration, we used fixed effects for taxi zones and robust standard errors in all five models to ensure consistency and enable comparison of the parameter estimates. This approach is unlikely to fully account for spatial or temporal dependencies when using the full balanced panel of 4,520,160 taxi zone-hours, but the very large number of units meant it was prohibitively computationally intensive to add statistical controls (e.g. in an intrinsically conditional autoregressive [ICAR] model; Besag and Kooperberg, 1995). Therefore, we conducted a simple sensitivity analysis in which we added a spatial autoregressive term (ρWYt), where W is a weights matrix for taxi zones based on queen’s contiguity, such that WYt denotes the row standardized mean odds of injury crashes occurring per hour in adjacent taxi zones (Belotti et al., 2017). Parameter ρ was positive in all models except Model 4. The parameter estimate for the exposure of interest (rideshare trip counts) did not change materially in any of the five models, so we report results for the more parsimonious spatially unstructured models. Nevertheless, results for Models 1, 2, 3 and 5 should be interpreted with caution, due to the potential for false positive findings due to spatial and temporal dependencies. We also report the global Moran’s I for the mean of the residuals.
4.2. Results
There were 83,753 injury crashes that occurred in NYC in 2017–2018. There was a total of 372,957,845 rideshare trips during that period, and on average, there were 81.3 rideshare trips per taxi-zone hour. Table 1 presents the results of the 5 conditional logistic regression models. In Model 1 (ignoring) each 100 additional rideshare trips was associated with 31% increased odds of observing an injury crash (e.g. Model 1: OR = 1.31; 95%CI: 1.30, 1.33). In Model 2 (controlling for a proxy) and Model 3 (approximating) 100 additional rideshare trips was associated with 17% increase in injury crash odds. In Model 4 (controlling by study design) the association of interest was further attenuated (OR = 1.05; 95%CI: 1.03, 1.06). In Model 5 (measuring), the association moved very strongly away from null, indicating that 100 additional rideshare trips was associated with 39.7% increase in injury crash odds (OR = 1.40; 95%CI: 1.24, 1.57). Moran coefficients indicate moderate autocorrelation in Models 1, 2 and 3 (0.281 ≥ I ≥ 0.320) and weak autocorrelation in Model 4 (I = 0.162). Moran’s I was not calculated for Model 5 because the included spatial units were non-contiguous.
Table 1.
Logistic regression models for the odds of observing an injury crash within taxi zone-hours.
| Model 1: Ignore | Model 2: Control* | Model 3: Approximate* | Model 4: Design | Model 5: Measure* | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (n=4,520,160) | (n=4,520,160) | (n=4,520,160) | (n=245,148) | (n=89,384) | ||||||
| OR | 95% CI | OR | 95% CI | OR | 95% CI | OR | 95% CI | OR | 95% CI | |
| Rideshare trips (per 100 increase) | 1.315 | (1.306, 1.325) | 1.169 | (1.156, 1.181) | 1.174 | (1.159, 1.189) | 1.046 | (1.032, 1.060) | 1.397 | (1.241, 1.574) |
| Temperature (per 10 degree increase) | 0.880 | (0.845, 0.916) | 1.057 | (1.048, 1.065) | 1.010 | (1.006, 1.015) | 1.069 | (1.017, 1.123) | ||
| Precipitation (per 0.1 inch increase) | 0.884 | (0.857, 0.913) | 1.110 | (1.092, 1.128) | 1.155 | (1.121, 1.190) | 1.044 | (0.896, 1.217) | ||
| Any holiday | 1.057 | (1.048, 1.065) | 0.879 | (0.845, 0.916) | 0.872 | (0.833, 0.913) | 0.776 | (0.596, 1.011) | ||
| School not in session, not holiday | 1.110 | (1.092, 1.128) | 0.884 | (0.856, 0.913) | 0.933 | (0.900, 0.967) | 0.882 | (0.734, 1.060) | ||
| Taxi trips (per 100 increase) | 0.991 | (0.975, 1.007) | 0.994 | (0.977, 1.011) | 0.639 | (0.530, 0.771) | ||||
| Traffic volume count (per 1,000 increase) | 1.008 | (0.979, 1.038) | ||||||||
| Local Moran’s I (mean of residuals per taxi zone) | 0.281 | 0.320 | 0.317 | 0.162 | n/a | |||||
Model includes fixed effects for hour of day, day of week, and month-year (parameter estimates suppressed)
4.2. Interpretation
For this analysis, the population at risk can be conceptualized as a confounder. According to the decision tree in Fig. 2, we cannot ignore motor vehicle traffic, so we should next consider measuring vehicular traffic within taxi zone-hours. The continuous count stations are a valuable archival source, but variation in traffic volume counts per hour at a single point is unlikely to fully capture variation in traffic volume across the extent of a taxi zone-hour. The decision tree suggests a study design solution is the next best approach to account for confounding by the population at risk. This is a practicable solution for these data. There is a sufficiently large number of crashes, rideshare trips, and space-time units to implement a case-crossover design comparing rideshare trips at taxi zone-hours in which an injury crash occurred to the same taxi zone ± 168 hours. Controlling for a proxy and approximating the population at risk may also be acceptable solutions, but they may be subject to residual confounding.
Results of the five statistical models support the suggestions from the decision tree. The association between rideshare trips and injury crashes estimated in Model 1 (ignoring) is very likely biased away from null. The estimates for Model 2 (controlling for a proxy) and Model 3 (approximating the population count) are attenuated compared to Model 1, suggesting they account for some confounding. However, the estimates for Model 4 (controlling by study design) are further attenuated, indicating that the results for Models 2 and 3 fail to capture some variation in the population at risk. Finally, the estimates for Model 5 (measuring the population) are the furthest from null from among all 5 models. Measuring vehicular traffic flow at a single point appears to capture very little variation in the population at risk across taxi zone-hours, and the smaller sample size yields very wide standard errors. Thus, parameter estimates for ridesharing for Model 4 are most heavily attenuated and this solution likely accounts for confounding by vehicular traffic flow better than the other available methods,
Importantly, it is unclear whether a study design solution fully addresses the unknown denominator problem in this case example. We lack a gold standard against which to validate these results because full observations of vehicular traffic are not available for the full universe of space-time units. Therefore, although we can assert that a study design solution is the best of the five available solutions for this particular research question; we do not know for certain that the parameter estimates from Model 4 are unbiased.
5. CONCLUSIONS
This paper presents five possible solutions available to researchers to address the unknown denominator problem and a decision tree to assist researchers to select the best approach given the available data. We focused specifically on unknown denominators that arise in spatial ecological studies due to geographic mobility. There are other reasons why denominators might be unknown, and there are many other solutions to denominator problems that are not relevant to the current review (e.g. Kreif et al., 2016). For example, denominator problems occur when the population at risk is an unknown subset of the resident population, and indirect standardization—which involves the calculation of adjusted rate ratios comparing incidence in the known population to the incidence in a reference population (Anselin, 2006; Elliott and Wartenberg, 2004)—is a possible solution in such circumstances. Chan et al. (2012) related falls among elderly people to social environmental conditions in Canadian census units, while accounting for the expected incidence given the age and sex distribution of each unit. Identifying and evaluating such methods to address other facets of the unknown denominator problem is an important area for future research.
The unknown denominator problem is frequently an issue for population-level studies of disease frequency. We argue that the relative merits of each approach can be best understood when investigators first articulate the effects of the population at risk within an epidemiological framework. When the causal role of this variable is clearly presented, the results of analyzes that utilize one (or more) of these approaches can be rigorously interpreted.
Figure 3.
Mean rideshare trip origins per hour for New York City taxi zones (n=261), 2017–2018.
Acknowledgments
Funding: This work was supported by the Centers for Disease Control and Prevention (R49-CE003094) and the National Institute on Alcohol Abuse and Alcoholism of the National Institutes of Health (award K01AA026327). The content is solely the responsibility of the authors and does not necessarily represent the official views of the Centers for Disease Control and Prevention or the National Institutes of Health.
Footnotes
Financial Disclosures: CNM has no financial disclosures. AGR has no financial disclosures. CCB has no financial disclosures. GL has no financial disclosures. CM has no financial disclosures. SC has no financial disclosures.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Anselin L How (not) to lie with spatial statistics. American Journal of Preventive Medicine 2006;30(2):S3–S6. [DOI] [PubMed] [Google Scholar]
- Ashenfelter O, Card D. Using the longitudinal structure of earnings to estimate the effect of training programs. The Review of Economics and Statistics. 1985;67(4):648–60. [Google Scholar]
- Bartholomeeusen S, Kim C-Y, Mertens R, et al. The denominator in general practice, a new approach from the Intego database. Fam Pract 2005;22(4):442–47. [DOI] [PubMed] [Google Scholar]
- Besag J, Kooperberg C. On conditional and intrinsic autoregressions. Biometrika 1995;82(4):733–46. [Google Scholar]
- Belotti F, Hughes G, Mortari AP. Spatial panel-data models using Stata. The Stata Journal 2017;17(1):139–180. [Google Scholar]
- Branas CC, Cheney RA, MacDonald JM, et al. A difference-in-differences analysis of health, safety, and greening vacant urban space. American Journal of Epidemiology 2011;174(11):1296–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brazil N, Kirk DS. Uber and metropolitan traffic fatalities in the United States. American Journal of Epidemiology 2016;184(3):192–8. [DOI] [PubMed] [Google Scholar]
- Campbell CA, Hahn RA, Elder R, et al. The effectiveness of limiting alcohol outlet density as a means of reducing excessive alcohol consumption and alcohol-related harms. American Journal of Preventive Medicine 2009;37(6):556–69. [DOI] [PubMed] [Google Scholar]
- Chan WC, Law J, Seliske P. Bayesian spatial methods for small-area injury analysis: a study of geographical variation of falls in older people in the Wellington–Dufferin–Guelph health region of Ontario, Canada. Injury Prevention 2012;18(5):303. [DOI] [PubMed] [Google Scholar]
- Chapman S, Alpers P, Jones M. Association between gun law reforms and intentional firearm deaths in Australia, 1979–2013. JAMA 2016;316(3):291–9. [DOI] [PubMed] [Google Scholar]
- Cohen LE, Felson M. Social change and crime rate trends: a routine activity approach. American Sociological Review 1979;44(4):588–608. [Google Scholar]
- Coren S Daylight savings time and traffic accidents. N Engl J Med 1996;334(14):924–25. [DOI] [PubMed] [Google Scholar]
- Cuthbert JR. An extension of the induced exposure method of estimating driver risk. Journal of the Royal Statistical Society Series A (Statistics in Society) 1994;157(2):177–90. [Google Scholar]
- DiGioia J, Watkins KE, Xu Y, et al. Safety impacts of bicycle infrastructure: A critical review. Journal of Safety Research 2017;61:105–19. [DOI] [PubMed] [Google Scholar]
- Dills AK, Mulholland SE. Ride-sharing, fatal crashes, and crime. Journal of the Southern Economic Assciation 2018;84(4):965–91. [Google Scholar]
- DiMaggio C Small-area spatiotemporal analysis of pedestrian and bicyclist injuries in New York City. Epidemiology 2015;26(2):247–54. [DOI] [PubMed] [Google Scholar]
- Ebrahim S, Davey Smith G. Commentary: Should we always deliberately be non-representative? International Journal of Epidemiology 2013;42(4):1022–26. [DOI] [PubMed] [Google Scholar]
- Edwards JK, Hileman S, Donastorg Y, et al. Estimating sizes of key populations at the national level: considerations for study design and analysis. Epidemiology 2018;29(6):795–803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott P, Wartenberg D. Spatial epidemiology: current approaches and future challenges. Environmental Health Perspectives 2004;112(9):998–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elvik R, Bjørnskau T. Safety-in-numbers: A systematic review and meta-analysis of evidence. Safety Science 2017;92:274–82. [Google Scholar]
- Feehan DM, Salganik MJ. Generalizing the network scale-up method:a new estimator for the size of hidden populations. Sociological Methodology 2016;46(1):153–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fink DS, Santaella-Tenorio J, Keyes KM. Increase in suicides the months after the death of Robin Williams in the US. PLOS ONE 2018;13(2):e0191405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrett M Encyclopedia of Transportation: Social Science and Policy Thousand Oaks, California: SAGE Publications; 2014. [Google Scholar]
- Garson JZ. The problem of the population at risk in primary care. Canadian Family Physician 1976;22:71–74. [PMC free article] [PubMed] [Google Scholar]
- Greene WH. Econometric Analysis (5th Ed.). New Jersey, NJ: Prentice Hall; 2003. [Google Scholar]
- Greenwood BN, Wattal S. Show me the way to go home: an empirical investigation of ride sharing and alcohol related motor vehicle fatalities. MIS Quartlery 2017;41(1):163–187. [Google Scholar]
- Grubesic TH, Pridemore WA, Williams DA, et al. Alcohol outlet density and violence: the role of risky retailers and alcohol-related expenditures. Alcohol and Alcoholism 2013;48(5):613–9. [DOI] [PubMed] [Google Scholar]
- Gruenewald PJ, Remer L. Changes in outlet densities affect violence rates. Alcoholism: Clinical and Experimental Research 2006;30(7):1184–93. [DOI] [PubMed] [Google Scholar]
- Guilford JP. Psychometric Methods. New York, NY: McGraw-Hill; 1936. [Google Scholar]
- Hamann C, Dulf D, Baragan-Andrada E, Price M, Peek-Asa C. Contributors to pedestrian distraction and risky behaviours during road crossings in Romania. Injury Prevention 2017;23(6):370–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harbluk JL, Noy YI, Trbovich PL, Eizenman M. An on-road assessment of cognitive distraction: impacts on drivers’ visual behavior and braking performance. Accident Analysis & Prevention 2007;39(2):372–9. [DOI] [PubMed] [Google Scholar]
- Inada H, Tomio J, Nakahara S, Ichikawa M. Area-wide traffic-calming zone 30 policy of Japan and incidence of road traffic injuries among cyclists and pedestrians. American Journal of Public Health 2020;110(2):237–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jang Y, Kim D, Park J, et al. Conditional effects of open-street closed-circuit television (CCTV) on crime: A case from Korea. International Journal of Law, Crime and Justice 2018;53:9–24. [Google Scholar]
- Keyes K, Galea S. Epidemiology Matters: A New Introduction of Methodological Foundations. 5th ed New York, NY: Oxford University Press; 2014. [Google Scholar]
- Klauer SG, Guo F, Sudweeks J, Dingus TA. An analysis of driver inattention using a case-crossover approach on 100-car data: Final report. Washington, DC: US Department of Transportation National Highway Traffic Safety Administration; 2010. Report No.: DTNH22–00-C–07007. [Google Scholar]
- Koepsell TD, Weiss NS. Induction Periods and Latent Periods Epidemiologic Methods: Studying the Occurrence of Illness. Oxford: Oxford University Press; 2004. [Google Scholar]
- Kreif N, Grieve R, Hangartner D, et al. Examination of the synthetic control method for evaluating health policies with multiple treated units. Health Economics 2016;25(12):1514–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liggett R, Huff H. Bicycle Crash Risk: How Does it Vary, and Why? Caltrans Task No. 2801 2016. University of California, Los Angeles. [Google Scholar]
- Løvås GG. Modeling and simulation of pedestrian traffic flow. Transportation Research Part B: Methodological 1994;28(6):429–43. [Google Scholar]
- Lyons RA, Ward H, Brunt H, et al. Using multiple datasets to understand trends in serious road traffic casualties. Accident Analysis & Prevention 2008;40(4):1406–10. [DOI] [PubMed] [Google Scholar]
- Maclure M The case-crossover design: a method for studying transient effects on the risk of acute events. American Journal of Epidemiology 1991;133(2):144–53. [DOI] [PubMed] [Google Scholar]
- Mooney SJ, DiMaggio CJ, Lovasi GS, et al. Use of Google Street View to assess environmental contributions to pedestrian injury. American Journal of Public Health 2016;106(3):462–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgenstern H Ecologic studies in epidemiology: concepts, principles, and methods. Annual Review of Public Health 1995;16(1):61–81. [DOI] [PubMed] [Google Scholar]
- Morrison CN, Mehranbod C, Kwizera M, Rundle AG, Keyes KM, Humphreys DK. Ridesharing and motor vehicle crashes: a spatial ecological case-crossover study of trip-level data. Injury Prevention, in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison CN, Jacoby SF, Dong B, Delgado MK, Wiebe DJ. Ridesharing and motor vehicle crashes in 4 US cities: An interrupted time-series analysis. American Journal of Epidemiology 2018;187(2):224–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Highway Traffic Safety Administration. Model Minimum Uniform Crash Criteria.United States Department of Transportation; 2017. Accessed December 23, 2019: https://www.nhtsa.gov/mmucc-1 [Google Scholar]
- Navin FPD, Wheeler RJ. Pedestrian flow characteristics. Traffic Engineering and Control 1969;39(9):30–36. [Google Scholar]
- Nesoff ED, Milam AJ, Pollack KM, et al. Neighbourhood alcohol environment and injury risk: a spatial analysis of pedestrian injury in Baltimore City. Injury Prevention 2019;25(5):350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taxi NYC and Commission Limousine. TLC Trip Record Data. NYC Taxi and Limousine Commission 2019. Accessed December 23, 2019: https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page
- O’Reilly GM, Gabbe B, Moore L, et al. Classifying, measuring and improving the quality of data in trauma registries: A review of the literature. Injury 2016;47(3):559–67. [DOI] [PubMed] [Google Scholar]
- Porta M A Dictionary of Epidemiology. 5th ed New York, NY: Oxford University Press; 2008. [Google Scholar]
- Purciel M, Neckerman KM, Lovasi GS, et al. Creating and validating GIS measures of urban design for health research. Journal of Environmental Psychology 2009;29(4):457–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spaite DW, Meislin HW, Valenzuela TD, et al. Banning alcohol in a major college stadium: impact on the incidence and patterns of injury and illness. Journal of American College Health 1990;39(3):125–28. [DOI] [PubMed] [Google Scholar]
- Stavrinos D, Byington KW, Schwebel DC. Distracted walking: cell phones increase injury risk for college pedestrians. Journal of Safety Research 2011;42(2):101–7. [DOI] [PubMed] [Google Scholar]
- Strauss J, Miranda-Moreno LF, Morency P. Cyclist activity and injury risk analysis at signalized intersections: A Bayesian modelling approach. Accident Analysis & Prevention 2013;59:9–17. [DOI] [PubMed] [Google Scholar]
- Strauss J, Miranda-Moreno LF, Morency P. Mapping cyclist activity and injury risk in a network combining smartphone GPS data and bicycle counts. Accident Analysis & Prevention 2015;83:132–42. [DOI] [PubMed] [Google Scholar]
- Taylor N, Mayshak R, Curtis A, et al. Investigating and validating methods of monitoring foot-traffic in night-time entertainment precincts in Australia. International Journal of Drug Policy 2019;66:23–29. [DOI] [PubMed] [Google Scholar]
- Thistlethwaite D, Campbell D. Regression-discontinuity analysis: An alternative to the ex post facto experiment. Journal of Educational Psychology 1960;51:309–17. [Google Scholar]
- Thompson JH, Wijnands JS, Mavoa S, et al. Evidence for the ‘safety in density’ effect for cyclists: validation of agent-based modelling results. Injury Prevention 2019;25:379–85. [DOI] [PubMed] [Google Scholar]
- Thompson J, Savino G, Stevenson M. Reconsidering the safety in numbers effect for vulnerable road users: an application of agent-based modeling. Traffic Injury Prevention 2015;16(2):147–53. [DOI] [PubMed] [Google Scholar]
- van der Horst ARA, de Goede M, de Hair-Buijssen S, et al. Traffic conflicts on bicycle paths: A systematic observation of behaviour from video. Accident Analysis & Prevention 2014;62:358–68. [DOI] [PubMed] [Google Scholar]
- Vanparijs J, Int Panis L, Meeusen R, et al. Exposure measurement in bicycle safety analysis: A review of the literature. Accident Analysis & Prevention 2015;84:9–19. [DOI] [PubMed] [Google Scholar]
- Wheeler-Martin KC, Curry AE, Metzger KB, DiMaggio CJ. Trends in school-age pedestrian and pedalcyclist crashes in the USA: 26 states, 2000–2014. Injury Prevention 2019;injuryprev-2019–043239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie SQ, Dong N, Wong SC, et al. Bayesian approach to model pedestrian crashes at signalized intersections with measurement errors in exposure. Accident Analysis & Prevention 2018;121:285–94. [DOI] [PubMed] [Google Scholar]