A tunable Fabry-Pérot quantum Hall interferometer in graphene

Abstract

Electron interferometry with quantum Hall edge channels in semiconductor heterostructures can probe and harness the exchange statistics of anyonic excitations. However, charging effects present in semiconductors often obscured the Aharonov-Bohm interference in quantum Hall interferometers and make advanced charge screening strategies necessary. Here, we show that high-mobility monolayer graphene constitutes an alternative material system, not affected by charging effects, to perform Fabry-Pérot quantum Hall interferometry in the integer quantum Hall regime. In devices equipped with gate-tunable quantum point contacts acting on the edge channels of the zeroth Landau level, we observe high-visibility Aharonov-Bohm interference widely tunable through electrostatic gating or magnetic field, in agreement with theory. A coherence length of 10 μm at a temperature of 0.02 K allows us to further achieve coherently-coupled double Fabry-Pérot interferometry. In future, quantum Hall interferometry with graphene devices may enable investigations of anyonic excitations in fractional quantum Hall states.

The wave-like behavior of electrons is exemplified in metals and semiconductors by a variety of mesoscopic phenomena stemming from quantum interference effects. Universal conductance fluctuations in coherent conductors or quantum localization due to random scattering are some vivid examples. In two dimensional electron gases, quantum interferences can be precisely tailored and harnessed using the chiral edge channels of the quantum Hall (QH) effect as one-dimensional, coherent electron beams. Electrostatic manipulation and partitioning of QH edge channel trajectories via local gates and quantum point contacts (QPCs) –that is, tunable beam-splitters for electrons–makes it possible to construct on-chip electronic analogues of Fabry-Pérot¹ (FP) or Mach-Zehnder² optical interferometers, usable for quantum information processing³.

The QH Fabry-Pérot configuration in which an edge channel, partially reflected between two QPCs, draws an interfering loop stands as a prominent testbed for anyonic⁴ and non-Abelian interferometry^5–11. Experimentally, the body of work on QH Fabry-Pérot interferometers performed in GaAs heterostructures^12–19 has long faced difficulties due to the Coulomb blockade effect^20–22 that often obscured quantum interference^{12–16,19,23}. The development of novel device architectures that implement various types of screening electrodes to mitigate charging effects^18,24 have recently solved this issue. This led to the long-awaited observation of Aharanov-Bohm oscillations²⁴ in the fractional quantum Hall regime, together with phase jumps²⁵ ascribed to the anyonic statistical exchange phase –a quantity also evidenced via shot-noise measurements²⁶.

Here, we demonstrate that monolayer graphene is a promising alternative platform for QH Fabry-Pérot interferometry, free of charging effects, thereby opening new perspectives for anyon interferometry^24,25. The two-dimensional electron gas of Dirac fermions in graphene exhibits all necessary features for QH interferometry: high-mobility²⁷, fractional quantum Hall effect^28,29 with large energy gaps³⁰, including possible non-Abelian states^31,32, helical edge channels at charge neutrality^33,34, gate-tunability, and versatility of van der Waals heterostructures³⁵. However, gate-tunable QPC –the key component to construct elaborated QH interferometers (see Fig. 1)– has proven challenging to realize due to the gapless band structure of graphene. Depleting the electron gas through electrostatic gating accumulates holes and yields conducting pn junctions that shortcircuit QPC constrictions^36,37. Other alternatives involve partitioning at a pn junction^38,39, or etched constrictions⁴⁰ that yield devices subject to charging effects. We remedy this with the use of high-mobility graphene in the QH regime for which an insulating, broken-symmetry state develops and opens an energy gap at the charge neutrality point separating the conduction band from the valence band³³. This gap is essential for the functioning of split gates as full-fledged QPC with tunable edge channel transmission⁴¹: It suppresses some possible charge transfers at the pn junction surrounding the split-gates (see drawing in Fig. 2d).

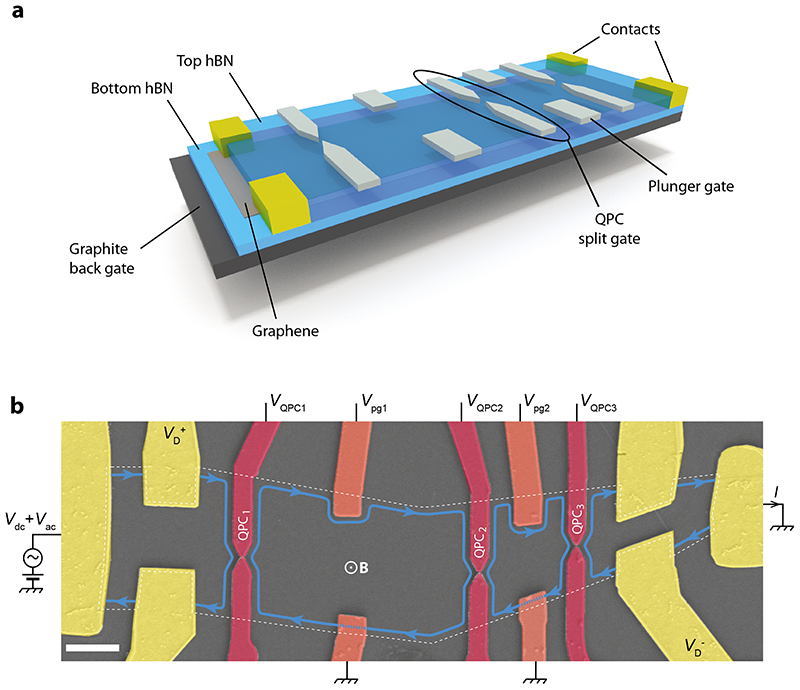
Fig. 1. Graphene quantum Hall Fabry-Pérot interferometer.

a, Schematic of the van der Waals hBN/graphene/hBN/graphite heterostructure equipped with split-gate and plunger-gate electrodes (light gray) atop it. The graphite flake serves as back-gate electrode and the graphene is contacted through edge contacts²⁷ (yellow). Further details about nanofabrication are given in Methods. b, False-colored scanning electron micrograph of the device. The scale bar is 1 μm. Three QPCs define two FP cavities. The interfering quantum Hall edge channel (blue line) propagates along the graphene edges (white dashed line), and along the split-gate (red) and plunger-gate (orange) electrodes, illustrating a configuration in which the gate electrodes deplete the charge carriers and repel the quantum Hall edge channel. The transmissions of the FP cavities are measured through the diagonal differential resistance RD = dV_D/dI, where I is the current measured by an ampmeter and VD the diagonal voltage drop across the contacts $V_{\text{D}}^{+}$ and $V_{\text{D}}^{-}$, in voltage bias configuration using a dc and ac voltage sources, V _dc and V _ac.

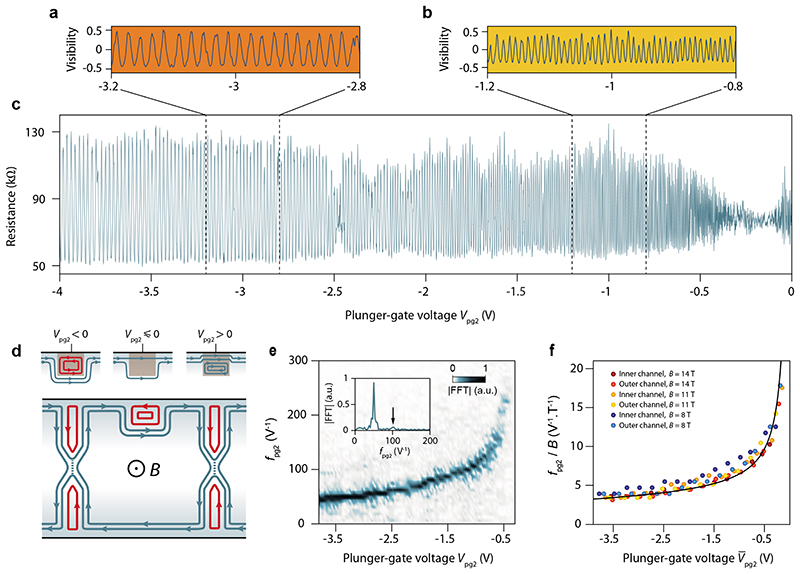
Fig. 2. Gate-tunable quantum interference.

a, b, c, Diagonal resistance oscillations as a function of plunger-gate voltage V _pg2 measured on the small interferometer at 0.015 K and 14 T (with an ac bias voltage of 5μV). The back-gate voltage is set to V _bg = 0.533 V corresponding to a filling factor ν_b = 1.5 in the bulk. The split-gate voltages on QPC2 and QPC3 are tuned to obtain partial transmission of the outer edge channel. The charge neutrality point below the plunger gate is at −0.3 V and corresponds to a suppression of the oscillation amplitude in c due to the divergence of the oscillation frequency shown in e. a and b show zooms on smaller V _pg2 ranges of the resistance oscillations converted in visibility $(R-\overline{R})/\overline{R}$, where $\overline{R}$ is the resistance average. d, Schematics of the QH-FP interferometer illustrating the edge channels configuration for the measurements in c. The black lines represent the physical edges of graphene. The blue (red) lines indicate electron(hole)-like edge channels and the arrows the direction of motion of charge carriers. At the QPC constriction, the dashed line indicates the tunneling of the interfering edge channel. Top sketches: Three configurations for the states around the plunger gate. Left, accumulation of localized hole states repelling the propagating electron edge channels. Middle, depletion of charge carrier density to a filling factor 1 below the gate, which repels the inner edge channel. Right, accumulation of localized electron states that push the propagating edge channels closer to the graphene edge. e, Fourier amplitude of the resistance oscillations in c as a function of V _pg2 and the plunger-gate-voltage frequency ƒ _pg2 obtained by computing the Fourier transform over a small Vpg2 window of 0.16 V sliding over the whole Vpg2 range. Inset : Fourier transform at V _pg2 = –3.28 V showing a well-defined peak at ƒ _pg2 = 50 V⁻¹ and a faint peak at ƒ _pg2 = 100 V⁻¹ indicated by the black arrow. These peaks correspond to first order and second order (two turns in the FP loop) interference processes. f, Evolution of the main peak frequency ƒ _pg2 rescaled by the magnetic field B as a function of ${\overline{V}}_{\text{pg}2}$, the plunger-gate voltage shifted with respect to the voltage that expels the interfering edge channel. The plot gathers a set of experiments performed with different interfering edge states and at different magnetic fields. The collapse of all data points into a single curve is fitted by an electrostatic simulation (see Supp. Section VIII) of the pn-junction displacement with plunger-gate voltage (black line).

Design and characteristics of graphene interferometers

We devised our device on the basis of a high-mobility graphene van der Waals heterostructure made with an hexagonal boron nitride (hBN)-encapsulated graphene monolayer²⁷ resting atop a graphite flake that acts as a back-gate electrode. As depicted in Fig. 1a, three pairs of split-gates of 20 nm gap, on top of the heterostructure, serve as QPCs and define a double FP cavity. Plunger gates located on the edges of each cavity are used to move the trajectory of the interfering QH edge channel and modulate the effective interferometer areas. The device we focus on in this report is shown in Fig. 1b with QPCs highlighted in red and labeled QPC₁, QPC₂ and QPC₃, plunger gates in orange and ohmic contacts in yellow (see Supp. Section III for the design characteristics of the QPC geometry). This triple QPC configuration enables us to operate three FP interferometers that we denote small (QPC₂-QPC₃), medium (QPC₁-QPC₂) and large (QPC1-QPC3) interferometers, whose geometrical areas are 3.1, 10.7 and 13.1 μm², respectively (see Supp. Table S2).

To operate the QH-FP interferometers, the graphene electron gas is subjected to a perpendicular magnetic field, B, to reach the quantum Hall regime. Prior to electron interferometry, each QPC transmission is individually characterized by mapping out the diagonal resistance RD measured across contacts $V_{\text{D}}^{+}$ and $V_{\text{D}}^{-}$ as a function of back-gate and split-gate voltages (see Extended Data Fig.1 and Supp. Section VI). We choose to work at bulk filling fractions ν_b = n_bϕ₀/B (n_b is the bulk charge carrier density, ϕ₀ = h/e is the flux quantum with h the Planck constant and e the electron charge) such that two electron-type edge channels of the zeroth Landau level propagate on the graphene edges, as indicated by a Hall conductance of 2e ² /h (see Supp. Fig. S5). A proper tuning of the split-gate voltages enables us to partially transmit either the inner or outer edge channel at the QPCs. Other configurations with only one electron-type edge channel present in the bulk have also been studied (see Supp. Section XII).

Widely tunable quantum interference

The quantum interferences in the small electronic Fabry-Pérot interferometer readily show up in Fig. 2a-c, which display the oscillatory behavior of the diagonal resistance R_D as a function of the plunger-gate voltage V _pg2. For this measurement performed at B = 14 T, the QH-FP interferometer operates at ν _b = 1.5. We tuned QPC₂ and QPC₃ to a transmission of the outer edge channel T₂ = 0.60 and T₃ = 0.47, respectively, leaving the inner one fully backscattered and localized in the FP cavity (see Extended Data Fig. 2 for the QPCs transmission curves). In this configuration, RD oscillates with about 50% visibility (see Fig. 2a and b) over nearly the whole voltage range spanned by the plunger gate (Fig. 2c), starting around V_pg2 = −0.3 V down to V _pg2 = –4 V. Further oscillations extending to positive V _pg2 values when electrons are accumulated beneath the plunger gate are shown in Extended Data Fig. 3. These results showing more than 280 resistance oscillations demonstrate the high stability and wide tunability of our interferometer.

The oscillatory behavior of the diagonal resistance upon depleting the electron gas beneath the plunger gate is a direct consequence of the modulation δA of the interferometer area defined by the interfering edge channel. Changing the flux through the interferometer via δA yields a variation δφ = 2πBδA/ϕ₀ of the Aharonov-Bohm phase picked up by the electrons. The flux-modulated succession of constructive and destructive electron wave-function interferences is thus reflected in the stark oscillations of the diagonal resistance.

Inspecting the oscillations more closely on a smaller span around two different plunger-gate voltages, V_pg2 = –3 V and –1 V in Fig. 2a and b, respectively, we see that the period depends upon the plunger-gate voltage. This behavior can be tracked by computing the Fourier transform restricted to a small voltage window sliding over the entire V_pg2 range. The resulting Fourier amplitude shown in Fig. 2e as a function of V _pg2 and plunger-gate-voltage frequency ƒ _pg2 displays a single peak that disperses to lower frequency upon decreasing V_pg2 to more negative values. Notice that a second harmonic indicated by the black arrow in the inset of Fig. 2e is also visible, mostly at large negative V _pg2.

The V _pg2-dispersion of the oscillations frequency reflects the electrostatics of the plunger gate. Depleting the graphene electron gas and then accumulating hole states locally under the plunger gate repels the interfering edge channel towards the interior of the QH-FP interferometer as illustrated in the schematics in Fig. 2d, therefore reducing the effective area. The abrupt drop of the oscillation frequency ƒ _pg2 at V _pg2 ≃ –0.3 V corresponds to the expulsion out of the area beneath the plunger gate of the interfering edge channel that was initially propagating along the graphene edge. This expulsion occurs when the graphene beneath the plunger gate reaches charge neutrality (or filling fraction 1 for the inner edge channel interfering case, see Fig. 2d). Notice that near this regime, the apparent reduction of the oscillation amplitude is due to an averaging effect because the oscillation frequency is fast compared to the bandwidth of our measurement apparatus and compared to the plunger gate voltage sweep rate. For more negative V _pg2, ƒ _pg2 decreases more slowly due to the accumulation of holes and the ensuing displacement of the pn junction further away from the plunger gate.

We next demonstrate the plunger gate tuning of the magnetic flux by studying the magnetic field dependence of the oscillations period. The area variation ΔA = ϕ₀/B that yields a change of one flux quantum in the interferometer relates to the plunger-gate voltage period ΔV _pg2 by ΔA = aΔV_pg2, where a is the (non-linear) lever arm of the gate. Since ƒ _pg2 = 1/ΔV _pg2, the quantity ƒ _pg2 /B = a/ϕ₀ depends only on the electrostatic displacement of the pn interface that is encoded in α. Fig. 2f displays ƒ _pg2 /B as a function of V _pg2, gathered from Fig. 2e and from similar data obtained at B = 11 and 8 T, and by measuring the interference of the inner or outer edge channel (see Supp. Fig. S6). Here, ${\overline{V}}_{\text{pg}2}$ is the plunger-gate voltage shifted with respect to the voltage that expels the inner or outer edge channel. Despite a large variation of magnetic field, and hence of oscillations periods, all data collapse onto the same curve, confirming the flux periodicity.

Furthermore, these ƒ _pg2 /B data that are related to the ${\overline{V}}_{\text{pg}2}$-evolution of the lever arm can be compared to numerical simulations of the electrostatic displacement of the pn junction in our device geometry (see Supp. Fig. S7). The resulting computation of α/ϕ₀ shown by the black line in Fig. 2f consistently fits the data and therefore demonstrates the ϕ ₀-periodicity of the oscillations, as expected for the Aharonov-Bohm effect.

Aharonov-Bohm effect vs Coulomb blockade

A critical aspect of QH-FP interferometers lies in the possibility that the resistance oscillations result from charging effects in the FP cavity^20–22, instead of Aharonov-Bohm quantum interference. Thorough studies on this issue showed that these two competing phenomena can be straightforwardly differentiated by the magnetic-field dependence of the gate-induced oscillations^{13,15,19,21,22}: For the Aharonov-Bohm effect, resistance oscillations in the B–V _pg plane shall draw diagonal lines of negative slope, indicating constant flux ϕ = BδA + AδB through the interferometer, whereas a zero or positive slope is expected for the Coulomb blockade effect. This led us to perform systematic measurements of the resistance oscillations as a function of plunger-gate voltage and magnetic-field variation δB. Figure 3 displays two typical resistance maps obtained with the small interferometer (Fig. 3a) and with the large one (Fig. 3b), both at B = 14 T with the outer edge channel interfering. For both cases, resistance maxima and minima draw lines of negative slope: Upon increasing magnetic field the lines go to more negative values of V _pg, hence shrinking the area to maintain the Aharonov-Bohm phase (flux) constant. We observed similar behavior for all configurations, regardless of the interferometer size, magnetic field value, bulk filling factor being 1 or 2, or which edge channel is interfering (see Supp. Sections IX and X). Hence, we can definitely rules out the alternative Coulomb blockade scenario.

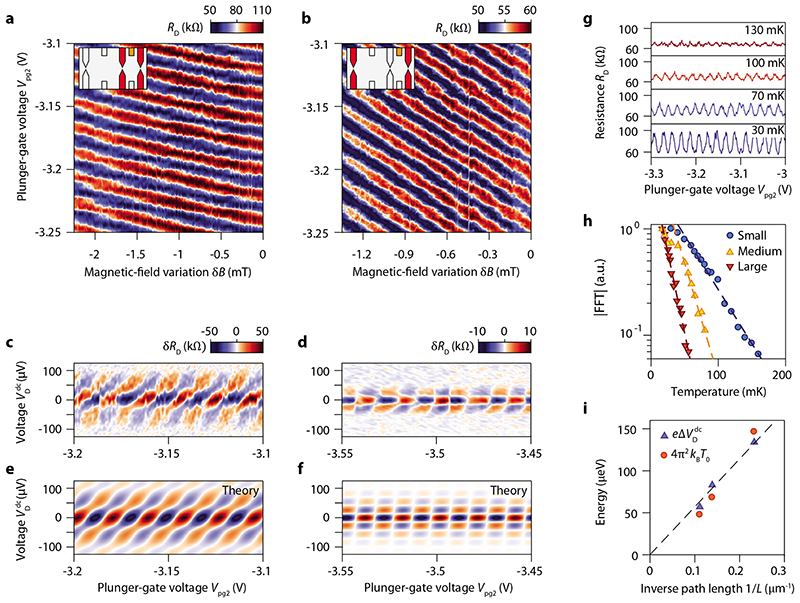
Fig. 3. Aharonov-Bohm effect and energy dependence.

a, b, Diagonal resistance RD versus plungergate voltage V _pg2 and magnetic field variation δB measured at 0.015 K for the small interferometer in a and the large interferometer in b. The inset schematics indicate the active QPCs (in red) and plunger gates (in orange) for the respective measurements. The negative slope in the B – V_pg2 plane is a clear indicator for the Aharonov-Bohm effect in both interferometers. c, d, Differential diagonal resistance variations δRD, after background subtraction, versus measured dc diagonal voltage $V_{\text{D}}^{\text{dc}}$ and plunger-gate voltage V _pg2 for the small interferometer in c and the large interferometer in d. Typical checkerboard patterns are observed with a significant tilt for the smallest interferometer revealing incomplete symmetrization of the voltage bias. e, f, Numerical simulations of resistance oscillations induced by voltage bias and plunger-gate voltage that reproduce the data presented in c and d, respectively. The simulation incorporates an asymmetric potential drop at the two QPCs and an out-of-equilibrium decoherence factor (see Supp. Section XIV). The asymmetry factor is x = 0.2 in e and x = 0.02 in f. g, Temperature evolution of the resistance oscillations versus plunger-gate voltage V _pg2 for the small interferometer. h, Exponential decays of the Fourier amplitude of the resistance oscillations for the small (blue), medium (yellow) and large (red) interferometers. The dashed line is a fit with exp(–T/Tø) giving T₀ = 43, 20, and 14 mK for the small, medium, and large interferometers, respectively. i, Evolution of the energy scales as a function of the inverse of the cavity length L of the three interferometers. The oscillation period with the dc voltage, $\Delta V_{\text{D}}^{\text{dc}}$, of the checkerboard pattern corresponds to the Thouless energy E_Th and is expected to be equal to the energy scale 4π² k _B T ₀ of the temperature-induced blurring of the resistance oscillations⁴. The dashed line is a linear fit highlighting the 1/L scaling of both energy scales. All data in this figure are obtained in a configuration with the outer edge channel interfering at B = 14 T.

The absence of Coulomb blockade even in the small interferometer, whose dimensions are similar to those in GaAs devices that exhibit Coulomb blockade¹³, points to a specificity of the hBN-graphene heterostructure. For our devices, the main source of charging effect mitigation is the close proximity of the graphite back gate electrode. Following the theoretical approach of Ref.²¹, we evaluated the various capacitances involved in our devices and calculated the parameter $\xi =\frac{C_{\text{eb}}}{C_{\text{b}}+C_{\text{eb}}}$ with C_b the bulk-to-gate capacitance and C_eb the edge-to-bulk capacitance, which defines the Aharonov-Bohm (ξ ≪ 1) or Coulomb-dominated (ξ ~ 1) operating regime²¹ (see Supp. Section XIII). For the smallest interferometer, we estimate a charging energy of 18 μeV similar to that of GaAs devices of similar sizes in which Aharonov-Bohm interference in the fractional QH regime has been observed²⁴, and ξ ⋍ 6 × 10⁻³, which is consistent with the absence of Coulomb blockade in our graphene devices. Note that we also observed Aharonov-Bohm interference in two other graphene devices equipped instead with a 285 nm thick SiO₂ back-gate dielectric (see Supp. Section XII). Despite a reduction of about 15 of the back-gate surface capacitance, we estimate for those samples ξ ⋍ 7 × 10⁻² which remains consistent with the Aharanov-Bohm regime. The systematic presence of back-gate electrodes, and to a lesser extent, the close proximity of the top-gate electrodes in hBN-encapsulated graphene therefore provide efficient screening of charging effects that enables to observe Aharonov-Bohm interference.

The magnetic-field period ΔB of the Aharanov-Bohm oscillations provides a direct measure of the effective area A_AB drawn by the interfering edge channel. For the three interferometers we obtained ΔB = 1.32, 0.40 and 0.27 mT corresponding to A_AB = 3.1, 10.4 and 15.0μm², which are consistent with our expected geometrical areas of 3.1 ± 0.4, 10.7 ± 1.2 and 13.1 ± 1.8 μm², substantiating the ϕ ₀-periodicity obtained with the electrostatic analysis of the plunger-gate effect. Notice that the precision of the geometrical areas is limited by the uncertainty in the optical determination of the graphene physical edges position, which could easily explain the small differences with the measured Aharonov-Bohm areas.

Decoherence and thermal broadening

The loss of visibility in QH interferometers is a fundamental question that encompasses several phenomena such as thermal broadening or quantum decoherence by inelastic processes and energy relaxation. We investigated the coherence properties of our interferometers through the joint analysis of the bias and temperature dependence of the visibility. The multiple QPCs configuration enables us to systematically study the coherence properties for three different cavity lengths. We begin with the out-of-equilibrium measurements performed with a dc voltage bias V _dc applied on the source contact (the drain contact is kept grounded). Electrons injected at a finite energy δε above the Fermi energy of the cavity have a phase shift 2πδε2L/hv proportional to twice the length L of the edge channel between the two QPCs and to the edge-excitation velocity v. This additional phase shift that adds up to the Aharonov-Bohm phase can yield theoretically a variety of oscillation patterns as a function of magnetic flux and voltage bias, which depend on the voltage drop across the device (see Supp. Section XIV). For a symmetric drop at the two QPCs (Vd_c/2 and –V _dc/2 on the source and drain), the resistance oscillations draw a checkerboard pattern of the form δR_D ∝ cos(2πϕ/ϕ ₀)cos(2πeV _dc /E _Th). For a fully asymmetric drop (V _dc and 0 on the source and drain) a diagonal strip pattern of the form δR_D ∝ cos(2πϕ/ϕ ₀ – 4πeV_dc/E_Th) is expected instead. In these expressions, the oscillations period as a function of V_dc is governed by the ballistic Thouless energy E _Th = h/τ related to the traveling time τ = L/v between the two QPC_s ^4,22.

For the large interferometer at B = 14 T, the resistance oscillations at finite bias (Fig. 3d) draw a checkerboard pattern similar to those observed in GaAs devices^14,24,42. The resulting oscillations decay quickly as a function of the dc voltage $V_{\text{D}}^{\text{dc}}$ (measured across the diagonal contacts $V_{\text{D}}^{\text{+}}$ and $V_{\text{D}}^{-}$), indicating that some energy relaxation processes are at play at finite bias (see Extended Data Fig. 4 and Suppl. Section XIV). Repeating the measurements on the two other interferometers yields similar patterns (see Supp. Section XIV), though with a notable difference in the form of the checkerboard which tends to be tilted towards a diagonal strip pattern upon reducing the interferometer size, as illustrated in Fig. 3c for the small interferometer. This tilt can be accounted for by an incomplete equilibration of chemical potential carried by the electron flow, which partially maintains the asymmetric voltage drop across the cavity. Calculation of the theoretical FP transmission with an unbalanced voltage drop describes very well the observed tilted checkerboard, as shown in Fig. 3e and f (theoretical analysis and additional data are provided in Supp. Section XIV).

The key parameter extracted from these checkerboards is the Thouless energy of the cavity E_Th = hv/L that is given by the $V_{\text{D}}^{\text{dc}}$-periodicity. The resulting values extracted from Extended Data Fig. 4 and shown in Fig. 3i for the three interferometers are found to consistently scale with 1/L.

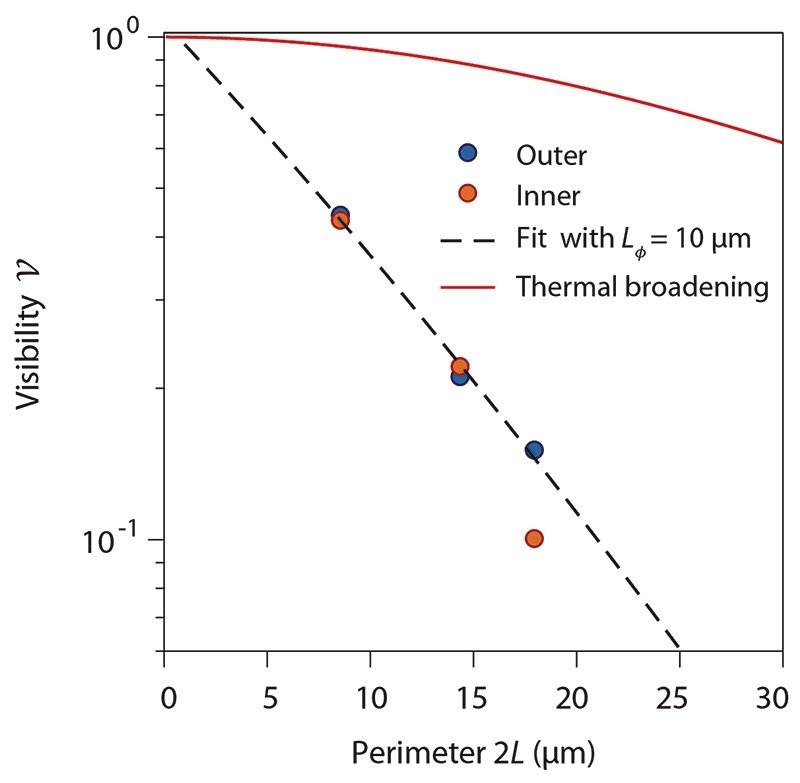
Besides, theory predicts that the temperature dependence of the oscillations visibility also relates to the Thouless energy⁴. The blurring of interference by the thermal broadening of the impinging electrons leads to an exponential suppression of the visibility with temperature, which follows exp(–4π ² k _B T/E _Th) with k _B the Boltzmann constant. In Fig. 3g and h we show the T-dependence of the resistance oscillations for the three interferometers. A clear exponential suppression of the visibilities is obtained in all cases, which is fitted with exp(–T/T₀) (dashed lines in Fig. 3h). The resulting 4π ² k _B T ₀ values that we append to Fig. 3i conspicuously scale as 1/L and are furthermore in excellent agreement with the Thouless energies extracted from the checkerboard patterns, bearing out a visibility limited mainly by thermal broadening. The slope in Fig. 3i further enables us to extract an estimate of the edge velocity v = 1.4 × 10⁵ m.s⁻¹, which is of the same order as that obtained in GaAs devices^14,24,43, though here at a much higher magnetic field. Finally, a phase coherence length of 10 μm at our base temperature can be assessed from the exponential suppression of the visibility with the perimeter of the interferometer, after corrections accounting for thermal broadening (see Extended Data Fig. 5 and Suppl. Section XVI). This global set of data that complies with the theoretical expectations⁴ therefore demonstrates graphene to be a highly tunable, model platform for QH-FP interferometry.

Coherently-coupled double FP interferometer

Here we operate our device in a three QPCs configuration to show that the large FP interferometer remains coherent upon turning on backscattering at the middle QPC. As sketched in Fig. 4a and b, Aharonov-Bohm interference depends upon three fluxes, ϕi,2,3, defined by the three cavity areas (blue, green and yellow in Fig. 4b, respectively). Each of them can be tuned by the magnetic field and one or two plunger gates. Figure 4c displays the resistance of the device for the three QPCs tuned at partial transmission of the outer edge channel, with a total transmission T ⋍ 0.46, upon varying both plunger-gate voltages V _pg1 and V _pg2. The resistance oscillates with both gate voltages and draws a regular pattern characteristic of the flux variation ϕ1 with V _pg1 (blue FP cavity), and ϕ ₂ with V _pg2 (green FP cavity). Coherence through the double interferometer is unveiled in the 2D Fourier transform in Fig. 4e. In addition to the two peaks at frequencies (ƒ _pg1, ƒ _pg2) = (53 V⁻¹,0 V⁻¹) and (0 V⁻¹,60 V⁻¹) corresponding to fluxes ϕ ₁ and ϕ ₂ respectively, a third peak emerges at (ƒ _pg1, ƒ _pg2) = (53 V⁻¹,60 V⁻¹), indicative of a joint modulation by both plunger gates and hence a modulation of the double cavity flux ϕ3. Inspection of the four quadrants of the Fourier transform in Supp. Fig. S17 shows that a fourth peak related to a ϕ ₁ – ϕ ₂ contribution is present but with a lower amplitude than the ϕ3 contribution. This indicates that the ϕ3 peak is mainly the result of the interference process for which electron wavefunctions interfere coherently after passing twice (back and forth) through the partially-transmitting middle QPC (see Supp. Section XVII for a detailed theoretical analysis).

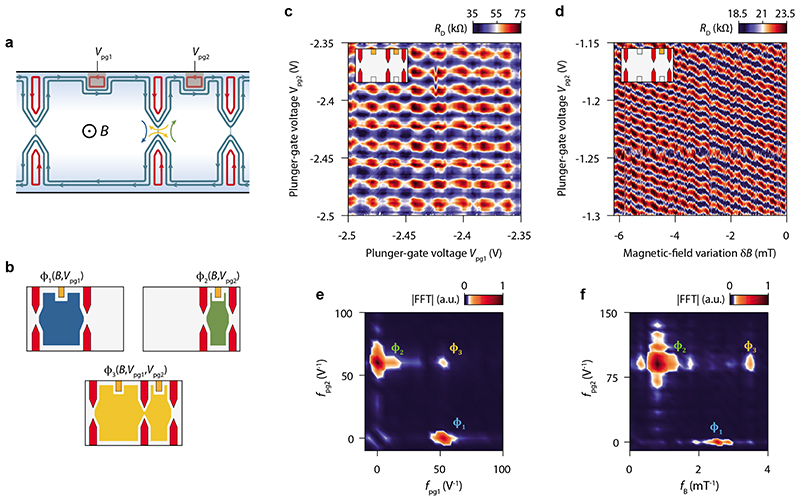
Fig. 4. Coherently-coupled double QH-FP interferometer.

a, Schematics of the double QH-FP interferometer in a configuration of partial backscattering of the inner edge channel at the three QPCs. The central QPC can either reflect an incoming electron from the left cavity (blue arrow) or the right cavity (green arrow), or transmit coherently an electron from one cavity to the other (yellow arrows). In the latter case, electrons pick up the Aharonov-Bohm phase given by the combined areas of the small and medium interferometers. b, Schematics of the cavities involved in the different interference processes depicted in a. ϕi,2,3 are the corresponding Aharonov-Bohm fluxes, indicated with the magnetic field and plunger-gate voltages that modulate them. c, Diagonal resistance versus plunger-gate voltages V _pg1 and V_pg2 (outer edge channel interfering, B = 14 T). d, Diagonal resistance RD versus magnetic field variation δB and plunger-gate voltage V _pg2 (inner edge channel interfering, B = 14 T). The inset schematics in c and d indicate the active QPCs (in red) and plunger gates (in orange) for the respective measurements. e, Fourier amplitude of the resistance oscillations in c versus plunger-gate-voltage frequencies ƒ _pg1 and ƒ _pg2. The three peaks at (ƒ _pg1, ƒ _pg2) = (53 V⁻¹,0 V⁻¹), (0 V⁻¹,60 V⁻¹) and (53 V⁻¹,60 V⁻¹) correspond to the three Aharonov-Bohm fluxes depicted in b. f, Fourier amplitude of the resistance oscillations in d versus magnetic field frequency ƒ_B and plunger-gate-voltage frequency ƒ _pg2. The three peaks of the three Aharonov-Bohm fluxes emerge at (ƒ _B, ƒ _pg2) = (0.79mT⁻¹, 90 V⁻¹), (2.54 mT⁻¹, 0 V⁻¹) and (3.49 mT⁻¹, 90 V⁻¹). In both Fourier amplitude maps, the peak that corresponds to flux ϕ ₃(B, V _pg1, V _pg2) reveals the quantum coherence throughout the two cavities of the double QH-FP interferometer.

Figure 4d shows a complementary measurement where the magnetic field is varied together with the plunger-gate voltage Vpg2 acting on the area of the small interferometer. We observe diagonal stripes similar to those in Fig. 3a and characteristic of the Aharonov-Bohm effect for the small cavity with flux ϕ ₂ (see peak at (ƒ _B, ƒ _pg2) = (0.79 mT⁻¹,90 V⁻¹) in Fig. 4f), but with an additional wiggling. This wiggling results from the Aharonov-Bohm oscillations of the medium interferometer (in series with the small one) via the flux ϕ ₁, which is independent of V _pg2 and corresponds to the peak at (ƒ _B, ƒ _pg2) = (2.54 mT⁻¹,0 V⁻¹) in the Fourier transform (see Fig. 4f). The double cavity flux ϕ ₃, which depends upon both B and V _pg2, leads to a peak at (ƒ_B, ƒ _pg2) = (3.49 mT⁻¹,90 V⁻¹) with a magnetic field periodicity which corresponds to the double cavity area, that is, the sum of the small and medium cavity areas. The precise shape of the wiggling of the diagonal stripes is a direct evidence of the contribution of the double cavity flux (see Supp. Section XVII for an additional measurement configuration).

The observation of the flux periodicity ϕ3, together with a careful Fourier analysis in the four quadrants (see Supp. Section XVII), provides compelling evidence that electron interference occurs through the central QPC at partial transmission, and hence that both FP cavities are coherently coupled. Such a tunable multiple FP interferometer is a building block for more advanced devices envisioned for braiding schemes of non-Abelian anyons⁶.

Conclusions

The high-visibility Aharonov-Bohm interference that we observe with excellent agreement with the non-interacting theory⁴ demonstrates the relevance of graphene for performing prototypical QH-FP interferometry with integer quantum Hall edge channels. The high mobility and the versatility of the graphene van der Waals hetereostructures turn out to be pivotal to harness fine control of QH edge-channel transmissions in QPCs⁴¹, and therefore construct advanced gate-tunable interferometers, as also confirmed in similar devices recently⁴⁴. With further study in the fractional quantum Hall regime, this graphene platform gives new opportunities for anyon physics in QH interferometers, potentially extendable to time-resolved electron quantum optics experiments³. Besides, the recent advances in coupling graphene QH edge channels with superconductivity^45–47 may lead to a variety of novel interferometry devices⁴⁸ in which proximity-induced topological superconductivity could be intertwined with QH interferometry for readout or braiding schemes. Such perspectives could in turn open alternative pathways for quantum-information processing of topological excitations⁴⁹.

Methods

Sample fabrication

hBN/graphene/hBN heterostructures were assembled from exfoliated flakes using the van der Waals pick-up technique²⁷. The substrates are highly doped Si wafers with a 285 nm thick SiO2 layer. For the sample discussed in the main text (BNGr74), the heterostructure is deposited on a thin layer of graphite that serves as a back-gate electrode. Contacts were patterned by electronbeam lithography and metalized by e-gun evaporation of a Cr/Au bilayer after etching of the stack with a CHF₃/O₂ plasma directly through the resist pattern used to define the contacts. The plunger and split gates were obtained with a second electron-beam lithography step and subsequent evaporation of Pd. The graphite layer for sample BNGr74 was also contacted at this step on a purposely uncovered part. Two other samples (BNGr64 and BNGr30) discussed in Supp. Section XII were prepared without graphite-gate electrode but with the hBN/graphene/hBN heterostructure resting directly atop the Si/SiO2 substrate.

Measurements

Measurements were performed in a dilution fridge reaching a base temperature of 0.01 K and equipped with a superconducting solenoid. To ensure good electron thermalization, the fridge is equipped with room-temperature feedthrough filters, highly-dissipative wiring, copper-powder filters at the mixing chamber stage, and cryogenic-compatible capacitors to ground on each line mounted directly on the sample holder. Devices were measured in four-terminal, voltage-bias configuration using an ac voltage of 5 μV and low-frequency lock-in amplifier techniques. Current was measured with a home-made current-voltage converter. Non-linear transport measurements were carried out by adding a dc voltage between source and drain contacts and measuring the dc and ac components of the diagonal voltage V _D. Measurements of the resistance oscillations as a function of magnetic field and plunger-gate voltage were performed by using the current decay of the superconducting solenoid in persistent mode while sweeping the plunger-gate voltage with a 20 bits home-made voltage source. All room-temperature low-noise pre-amplifiers were thermalized in a home-made, temperature-controlled box to get rid of thermal drifts of input voltage offsets.

Extended Data

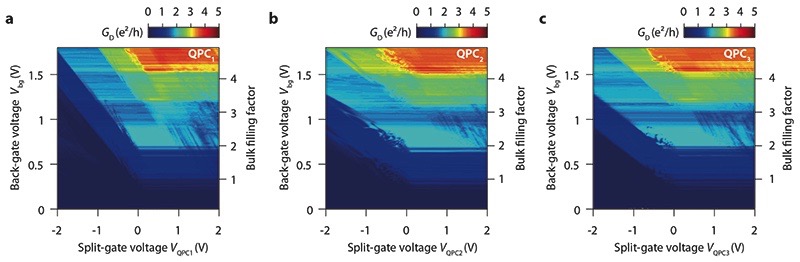
Extended Data Fig. 1. QPC conductance maps at 14 T.

\textbf{a, b, c,} Diagonal conductance $G_{\text{D}}$ versus split-gate voltages, $V_{\text{QPC}}$, and back-gate voltages, $V_{\text{bg}}$, for the three QPCs of the device presented in the main text. During a measurement, only one QPC is studied and the two other sets of split gates are kept floating. The slope of the diagonal stripes corresponds to the capacitance ratio between the QPC constriction and the back gate. This slope is about twice/three times smaller than the zero-field slope for QPC$_2$ and QPC$_3$, but is only slightly smaller for QPC$_1$ (due to the unintentional absence of gap between the two electrodes of this QPC).

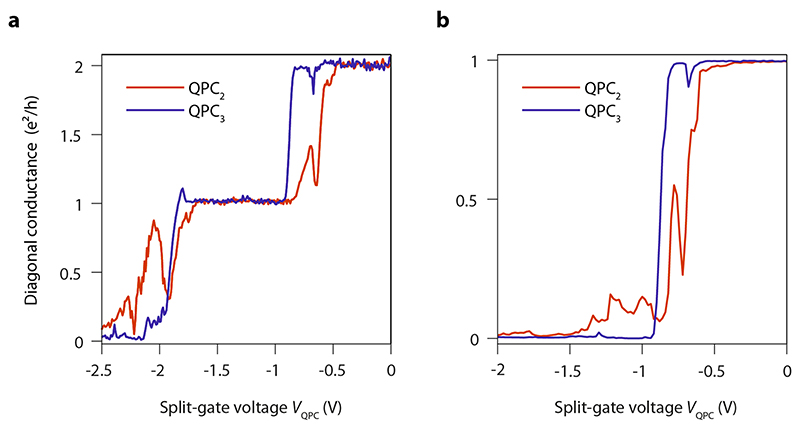
Extended Data Fig. 2. QPC transmission curves at 14 T.

Evolution of the diagonal conductance $G_{\text{D}}$ as a function of split-gate voltages $V_{\text{QPC}}$ at fixed backgate voltage $V_{\text{bg}}$. \textbf{a,} $V_{\text{bg}} =0.88$ V. \textbf{b,} $V_{\text{bg}} = 0.53$ V.

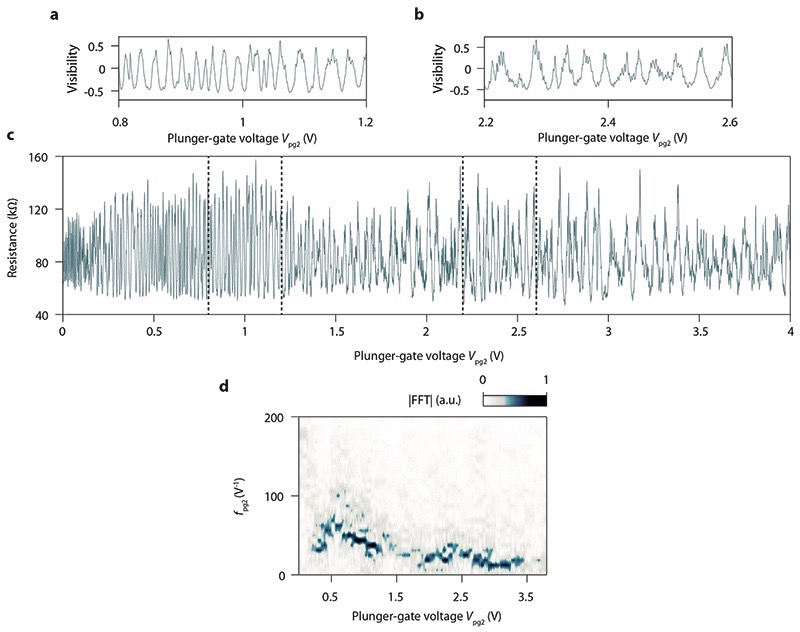
Extended Data Fig. 3. Resistance oscillations at positive plunger-gate voltage.

\textbf{a, b, c,} Resistance oscillations as a function of plunger-gate voltage $V_{\text{pg2}}$ measured in the small interferometer for $V_{\text{pg2}}>0$. These data are the extension of the measurements performed in Fig.~2c of the main text to positive plunger-gate voltage. This corresponds to the accumulation of localized electron states beneath the plunger gate (see inset in Fig.~2c). \textbf{a} and \textbf{b} show zooms on smaller $V_{\text{pg2}}$ ranges of the resistance oscillations converted in visibility $(R-\bar{R})/\bar{R}$, where $\bar{R}$ is the resistance background. \textbf{d,} Fourier amplitude of the resistance oscillations in c as a function of $V_{\rm pg2}$ and the plunger-gate voltage frequency $f_{\rm pg2}$.

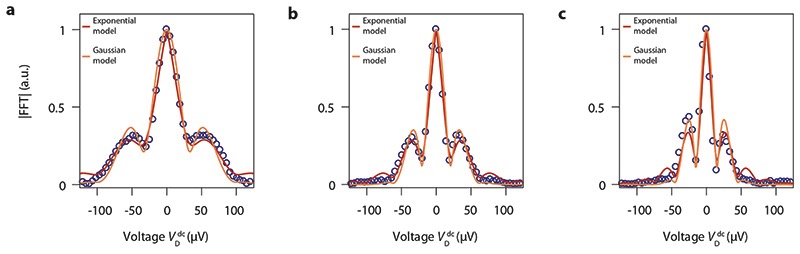
Extended Data Fig. 4. Bias dependence of Aharonov-Bohm oscillations.

\textbf{a, b, c,} Amplitude of the Fourier transform of the oscillations at fixed voltage bias (blue dots) and fits with Suppl. Eq. (S12) (red line) and Suppl. Eq. (S13) (orange line). Fitting parameters are reported in Suppl. Table S3.

Extended Data Fig. 5. Phase coherence length $L_{\phi}$.

Evolution of the best visibilities $\mathcal{V}$ with the perimeter $2L$ of the interferometers obtained in experiments at base temperature with the outer (blue dots) and the inner (red dots) edge channel. The red solid line shows the thermal broadening contribution. The fit of the data (black dashed line) with Suppl. Eq. (S30) and discarding the inner edge channel experiment for the large interferometer, provides a coherence length of 10 $\mu$m at 0.02 K.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.