An efficient and accurate method for modeling nonlinear fractional viscoelastic biomaterials

Abstract

Computational biomechanics plays an important role in biomedical engineering: using modeling to understand pathophysiology, treatment and device design. While experimental evidence indicates that the mechanical response of most tissues is viscoelastic, current biomechanical models in the computational community often assume hyperelastic material models. Fractional viscoelastic constitutive models have been successfully used in literature to capture viscoelastic material response; however, the translation of these models into computational platforms remains limited. Many experimentally derived viscoelastic constitutive models are not suitable for three-dimensional simulations. Furthermore, the use of fractional derivatives can be computationally prohibitive, with a number of current numerical approximations having a computational cost that is $𝒪(N_T^2)$ and a storage cost that is 𝒪(N_T) (N_T denotes the number of time steps). In this paper, we present a novel numerical approximation to the Caputo derivative which exploits a recurrence relation similar to those used to discretize classic temporal derivatives, giving a computational cost that is 𝒪(N_T) and a storage cost that is fixed over time. The approximation is optimized for numerical applications, and an error estimate is presented to demonstrate the efficacy of the method. The method, integrated into a finite element solid mechanics framework, is shown to be unconditionally stable in the linear viscoelastic case. It was then integrated into a computational biomechanical framework, with several numerical examples verifying the accuracy and computational efficiency of the method, including in an analytic test, in an analytic fractional differential equation, as well as in a computational biomechanical model problem.

1. Introduction

Biomechanical analysis has become an area of increasing emphasis in biomedical engineering applications. It has been used for understanding a diverse range of complex problems, such as the surgical intervention strategies for arterial bifurcation [1], the impact of left ventricular assist devices [2,3], the risk of aortic aneurysm rupture [4,5], the repair of the mitral valve in the heart [6,7], as well as the surgical aids for brain surgery [8]. Through biomechanics simulation, devices and procedures can be optimized and personalized to improve design, therapy and patient outcomes [9]. A key component to these types of biomechanical assessments is identifying the appropriate constitutive equations that define the material response. While hyperelastic material models have been developed to describe a range of tissues [10,11], viscoelasticity has been acknowledged as an important component of mechanical response in brain matter [12–14], connective tissues [15,16], fracturing of bone tissues [17], as well as many cardiovascular soft tissues [18], including arterial tissues [19] and myocardium [20,21]. Despite viscoelasticity in soft tissues being widely studied experimentally, its use in computational biomechanics simulations remains relatively uncommon due, in part, to computational challenges.

Viscoelasticity and viscoelastic theory have been topics of interest since the 19th century [22,23]. Early forms of viscoelastic constitutive models used spring and dashpot [24] constructs, e.g., the Maxwell [25] and the Kelvin- Voigt models [26]. To better explain experimental observations, authors began to combine these simple units in series and/or parallel to form more complex systems, such as the generalized Maxwell [23] or generalized Kelvin-Voigt models [27]. These early theoretical works were successfully used to explain the linear viscoelastic behavior in a number of materials, including muscle tissues [28]. A more generalized one dimensional theory was proposed by Green and Tobolsky [29] to explain relaxing media. Extension of these early concepts of viscoelasticity to nonlinear continuum mechanics was addressed by a number of analytic mechanicians, including Truesdell [30], Green and Rivlin [31,32] and Bernstein, Kearsley, and Zapas [33] (see [34] for a review on early works investigating viscoelasticity). Nonlinear viscoelastic theory has been applied to modeling of elastomers [25], rubber materials [35], fiber reinforced materials [36], myocardium [37] as well as brain tissue [38,39]. Extension of these approaches to computational mechanics has been in the works of Simo [40], Le Tallec [41], Holzapfel [19,36,37,42], and De Buhan and Frey [43], amongst others.

While much of the early developments in viscoelasticity (and its numerical application) focused on analogues to spring-dashpot systems, fractional viscoelastic behavior can be seen increasingly in modeling tissue properties [44–46]. Use of these models has been recently presented in lung tissue [47]. The advantage of fractional viscoelasticity is that the method provides a spectrum of relaxation times parameterized through the chosen fractional derivative order, denoted here by α. A simplification of the generalized Maxwell approach with infinite Maxwell elements, the fractional approach has the advantage of being compact, requiring few parameters and being effective at characterizing hierarchical viscoelastic materials exhibiting power-law behavior [48–51]. These benefits are challenged by the need to numerically approximate the fractional derivative, which is often done using cumulative integral approximations that require the storage of all past values of stress with increasingly costly computations in time. Development of efficient approaches to approximate fractional derivatives by Yuan and Agrawal [52], Diethelm [53] and Birk and Song [54] has enabled the efficient extension of fractional models to solid mechanics [55]. However, how these approximations perform in a computational biomechanics context using finite elements presents additional challenges and questions.

In this work, we present a numerical formulation for the constitutive modeling of viscoelastic materials based on a novel and efficient recursive approximation to evaluate fractional viscoelasticity. The proposed approach, utilizes a Prony series (or generalized Maxwell model) as in [54–56] with an additional dashpot element and optimization process to make the computational and storage costs consistent with standard transient methods. An error estimate is derived for the class of Prony approximations, detailing the improved computational accuracy of the proposed method (as well as those previously proposed). The numerical method is then integrated into our finite element framework [57] and shown to be unconditionally stable in the linear viscoelastic setting. Results from this analysis are presented through a series of numerical examples, demonstrating appropriateness of the developed bounds, accuracy and numerical efficiency. While demonstrated in a specific biomechanics setting, this generalized approach lends itself to a wide variety of modeling problems in soft tissues as well as other fractional-time derivative problems.

The paper reviews current techniques for approximating the Caputo derivative, introduces our approximation as well as its error estimates (Section 2). In Section 3, the paper reviews mechanical formulations for viscoelasticity, including fractional approaches, for nonlinear mechanics. The introduced models and approximations are then integrated into a nonlinear mechanics finite element framework (Section 4) which is shown to be unconditionally stable in the linear viscoelastic case (see Appendix A). Convergence, accuracy and computational costs are then evaluated in an analytic example (Section 5), a simplified fractional diffusion system (Section 6) as well as in a biomechanical example of liver tissue (Section 7). The paper finishes with a discussion of the key results and conclusions.

2. Fractional derivatives and their approximations

2.1. Caputo fractional derivative

The concept of fractional calculus started with questions about the generalization of integral and differential operators by L’Hospital and Leibniz [58] from the set of integers to the set of real numbers. Subsequently, many prominent mathematicians focused on fractional calculus (for reviews, see Ross [58] and Machado [59]). Within the field, many different definitions for fractional differential and integral operators of arbitrary order have been introduced [60]. In this work, we focus on the Caputo definition, where the fractional derivative, $D_t^{\alpha }$ (with α ∈ [0, 1]), of a function f can be written as,

$$D_t^{\alpha }f=\frac{1}{\text{Γ}(1-\alpha )}{\int }_0^t\frac{f^{\prime }(s)}{{(t-s)}^{\alpha }}\text{d}s.$$ (1)

The fractional derivative (for α ∉ ℕ), unlike integer derivatives, is a convolution of the past behavior of the function, making it particularly useful for constitutive modeling of viscoelastic materials. The Caputo form (which can be related to other formulations, e.g. Riemann-Liouville) has the advantage that

$$D_t^{\alpha }c=0,\text{for}\text{any}\text{constant}c\in ℝ.$$ (2)

For later analysis, we will assume that the functions f are continuous and two (or more) times differentiable [61], which allows the use of integration by parts to rewrite the Caputo derivative as

$$D_t^{\alpha }f=\frac{1}{\text{Γ}(2-\alpha )}\left(t^{1-\alpha }{f}^{\prime }(0)+{\int }_0^t{(t-s)}^{1-\alpha }{f}^{″}(s)\text{d}s\right).$$ (3)

This form eliminates the weak singularity in the integrand of Eq. (1). For most methods of approximating the fractional derivative, the focus is on the range of α ∈ [0, 1]. However, the Caputo fractional derivative satisfies the semigroup property that is $D_t^{\alpha }{D}_t^{\beta }f=D_t^{\alpha +\beta }f$. As a result, Eqs. (1) and (3) can be extended to a broader range of fractional derivatives by choosing β ∈ ℕ.

2.2. Current methods for numerical approximation of the Caputo derivative

Fractional derivative operators and methods for approximating their effects are well studied in literature. For some recent review of this subject, readers may consider the works of Zeid [62], Guo [63], Weilbeer [64] and Podlubny [60]. Approaches in the literature can be categorized by their method of integration, either cumulative or recursive. Cumulative approaches approximate the Caputo derivative by the direct numerical approximation of the integrals in Eqs. (1) or (3) using some form of a weighted sum over a set of discrete time points. In contrast, recursive approaches first approximate the Caputo derivative by transforming it into a series of ordinary differential equations that have standard discretizations.

Suppose we seek to approximate the α^th-order fractional derivative, $D_t^{\alpha }f(0<\alpha <1)$, of a function f : [0, T] ⟶ ℝ at a series of N_T time points

$$0=t_0<t_1<\cdots <t_{N_T}=T$$

where t_n = nΔ_t, Δ_t denotes the time step size, and that f (t_n) is easily computed given some prior information from previous time points, a straightforward cumulative method to computing the Caputo derivative is through a Riemann sum evaluated using the midpoint point (MP) rule, i.e. the discrete operator, ${\text{D}}_n^{\alpha }$, is

$${\text{D}}_{n,\text{MP}}^{\alpha }f=\frac{1}{\Gamma (1-\alpha )}\sum _{m=1}^n\frac{f\left(t_m\right)-f\left(t_{m-1}\right)}{{\left(t-\left(m-\frac{1}{2}\right){\Delta }_t\right)}^{\alpha }}.$$ (4)

Here the integral in Eq. (1) is approximated at the midpoint of each time interval [t_m−1, t_m] with the derivative computed by central differences. This approach appears effective for α < 0.5, but sees deteriorated convergence for larger fractional orders. Another common method for constructing the fractional order derivative is using the Griinwal–Letnikov (GL) derivative [65]. Using the definition from Scherer et al. [65], the GL derivative with corrections to match the Caputo derivative is

$${\text{D}}_{n,\text{GL}}^{\alpha }f=\frac{1}{{\Delta }_t^{\alpha }}\left[f\left(t_n\right)-\sum _{m=1}^n{C}_m^{\alpha }f\left(t_{n-m}\right)\right]-\frac{t_n^{-\alpha }f\left(t_0\right)}{\Gamma (1-\alpha )},$$ (5)

where $C_m^{\alpha }=C_{m-1}^{\alpha }(1-[\alpha +1]/m),C_1^{\alpha }=\alpha$, is the recursive definition of the real numbered binomial coefficient in the finite difference formula. Another example is given by Diethelm et al. [61,66] where the trapezoidal rule was employed, i.e.

$$\begin{array}{l}{\text{D}}_{n,D}^{\alpha }f=\frac{{\Delta }_t^{-\alpha }}{\Gamma (2-\alpha )}{\displaystyle \sum _{m=0}^n{a}_{m,n}}\left[f\left(t_{n-m}\right)-f\left(t_0\right)\right],\hfill \\ a_{m,n}=\{\begin{array}{ll}1,\hfill & \text{if}m=0,\hfill \\ {(m+1)}^{1-\alpha }-2m^{1-\alpha }+{(m-1)}^{1-\alpha },\hfill & \text{if}0<m<n,\hfill \\ (1-\alpha )n^{-\alpha }-n^{1-\alpha }+{(n-1)}^{1-\alpha },\hfill & \text{if}m=n,\hfill \end{array}\hfill \end{array}$$ (6)

where a_m,n are the weights for the past values of f (t_n). Gao et al. [67] developed a similar method for solving fractional diffusion equations, i.e.

$$\begin{array}{l}{\text{D}}_{n,\text{Gao}}^{\alpha }f=\frac{{\Delta }_t^{-\alpha }}{\Gamma (2-\alpha )}\left(a_0^{\alpha }f\left(t_n\right)-{\displaystyle \sum _{m=1}^{n-1}\left(a_{n-m-1}^{\alpha }-a_{n-m}^{\alpha }\right)}f\left(t_m\right)-a_{n-1}^{\alpha }f\left(t_0\right)\right),\hfill \\ a_m^{\alpha }={(m+1)}^{1-\alpha }-m^{1-\alpha },m\ge 0.\hfill \end{array}$$ (7)

Other cumulative methods have been presented by Murio et al. [68], Yang et al. [69] as well as Liu et al. [70], though many more have been published in the literature.

All the cumulative methods presented here require significant storage costs and have significant computational costs, especially for complex three-dimensional tissue simulations. Storage/memory costs are typically O(N_T) and the computational complexity is often $𝒪\left(N_T^2\right)$, or by best reports 𝒪(N_T log(N_T)), due to the need to sum over the entire time domain. In contrast, the computational cost of transient linear elasticity or hyperelasticity problems is 𝒪(N_T).

One strategy to cope with this limitation is to exploit the fact that the integration weights for numerical approximation of fractional derivatives exhibit a ‘fading memory’, where the weights tend to decay with the number of time steps (or length of time). Hence, some have proposed truncating the approximation, including only the last few weights. However, the accuracy of this approach is fundamentally dependent on the behavior of f and the fractional derivative order α. For example, the weights decay at slower rates for lower α values, requiring more and more terms to avoid inaccuracies due to truncation. More difficult is the dependence on the function f, which is not known a priori in computational simulations. A classic example is to consider a stress relaxation experiment, where an acute action occurring at the beginning of the experiment dictates the response over the entire time course. In this instance, truncation of the series will eventually lead the stress to be zeroed.

Another strategy to reduce computational costs is by use of recursive methods. Such methods mostly follow a similar approach [55]. Namely, the Caputo derivative is approximated using decaying exponentials (or, equivalently, a Prony-series). This approximation step is posited differently depending on the authors. However, a natural rationale for this approximation stems from the relationship between the relaxation spectrum of the Caputo derivative and decaying exponentials via the Laplace transform, i.e.

$$\frac{{(t-s)}^{-\alpha }}{\Gamma (1-\alpha )}={\displaystyle {\int }_0^{\infty }\left[\frac{\sin (\pi \alpha )z^{\alpha -1}}{\pi }\right]}\exp [(s-t)z]\text{d}z.$$ (8)

Here the integral above can be approximated using some form of numerical quadrature, leading to evaluation of the integrand at specific z values that are scaled by associated quadrature weights. Inserting into Eq. (1), we arrive at an equivalent form for a Prony-series comprised of decaying exponentials that can be recast as a series of ordinary differential equations (shown in the following section). One of the earlier works presenting a recursive method for approximating the Caputo derivative was by Yuan-Agarwal [52]. In this case, authors recast the integral based on the above and used Gauss-Laguerre quadrature for integration. Though they presented the idea in the context of a specific fractional differential equation, the idea was clearly generalizable.

The Yuan-Agrawal method has been criticized for slow convergence for certain values of α. Investigation by Diethelm [53] found this to stem from the non-smooth integrand which deteriorated the accuracy of the Gauss-Laguerre quadrature. Instead, Diethelm suggested is his method [56] that Gauss-Laguerre be replaced by Gauss-Jacobi integration by mapping the range of integration from [0, ∞) to [−1, 1] through a change of variables. Aiming for further improvements in the accuracy of these methods, Birk and Song [54] further extended theDiethelm method [56] by altering the mapping onto the [−1, 1] interval and considering the Fourier transform of the fractional operator, showing generally comparable or superior results.

Although the quadrature scheme of these approaches aims to approximate the integral over the entire integration interval, this is not necessarily an advantage. The range of relevant frequencies can be limited based on the corresponding problem and by the size of Δ_t used for simulation. Moreover, as α → 1, the approximation must tend to approach the first order derivative, which becomes increasingly challenging to approximate. In the following sections, we expand on this Prony-based approach by formulating the error estimates, generalizing its form and proposing a new approach for optimizing parameters of the weights and time constants of the associated Prony series.

2.3. Prony approximation of the Caputo derivative

The Prony series approach has been used a number of times in literature [52–54,56,71,72]. Suppose that the fractional derivative can be approximated using N Maxwell elements in parallel, each with their own weight β_k and time constant τ_k (k = 1 … N). Then a Prony-based approximation ${\widehat{D}}_t^{\alpha }f$ to $D_t^{\alpha }f$ can be written as,

$${\widehat{D}}_t^{\alpha }f:={\beta }_0{f}^{\prime }(t)+{\displaystyle \sum _{k=1}^N{\displaystyle {\int }_0^t{\beta }_k}}\exp \left[\frac{s-t}{{\tau }_k}\right]f^{\prime }(s)\text{d}s,$$ (9)

or equivalently, noting that Eq. (9) can be considered the result of the integration factors, we see

$${\widehat{D}}_t^{\alpha }f:={\beta }_0{f}^{\prime }(t)+{\displaystyle \sum _{k=1}^N{q}_k}(t),q_k^{\prime }(t)+\frac{1}{{\tau }_k}{q}_k(t)={\beta }_k{f}^{\prime }(t),$$ (10)

where we introduce N intermediate variables q_k. While Eq. (9) requires approximation of the integral over the entire time domain, Eq. (10) enables discretization of the intermediate variables q_k by standard techniques. Eq. (10) requires 2N + 1 parameters, θ_a = {τ₁, …, τ_N, α ₀, α ₁, …,β _n}. The approximation error of Eqs. (9) and (10) is shown in Lemma 1:

Lemma 1.

Let f : [0, T] ℝ be a real function on the domain [0, T]. If f’ (0) < and f” ∈ L ¹(0, T), then

$$\left(D_t^{\alpha }f-{\widehat{D}}_t^{\alpha }f\right)=\epsilon (t)f^{\prime }(0)+{\displaystyle {\int }_0^t\epsilon }(z)f^{″}(t-z)\text{d}z,$$

and for any t ∈ [0, T]

$$\left|D_t^{\alpha }f-{\widehat{D}}_t^{\alpha }f\right|\le \Vert \epsilon {\Vert }_{0,\infty }\left[\left|f^{\prime }(0)\right|+{\Vert f^{″}\Vert }_{0,1}\right],$$

where the truncation error e is defined as

$$\epsilon (z):=\frac{z^{1-\alpha }}{\Gamma (2-\alpha )}-{\beta }_0+{\displaystyle \sum _{k=1}^N{\beta }_k}{\tau }_k\left(\exp \left[-z/{\tau }_k\right]-1\right).$$ (11)

Proof of Lemma 1

Applying integration by parts to Eq. (9), and the fundamental theorem of calculus to the leading first order derivative term, the Prony approximation to the fractional derivative can be re-written as,

$${\widehat{D}}_t^{\alpha }f=\kappa (0,t)f^{\prime }(0)+{\displaystyle {\int }_0^t\kappa }(s,t)f^{″}(s)ds,$$

where $\kappa (s,t)={\beta }_0-\underset{k=1}{\overset{N}{{\sum }^{\text{}}}}{\beta }_k{\tau }_k\left(\exp \left([s-t]/{\tau }_k\right)-1\right)$. Subtracting this from Eq. (3) leads to

$$\begin{array}{l}\left(D_t^{\alpha }f-{\widehat{D}}_t^{\alpha }f\right)=\frac{1}{\Gamma (2-\alpha )}\left(t^{1-\alpha }{f}^{\prime }(0)+{\displaystyle {\int }_0^t{(t-s)}^{1-\alpha }}{f}^{″}(s)\text{d}s\right)-\kappa (0,t)f^{\prime }(0)-{\displaystyle {\int }_0^t\kappa }(s,t)f^{″}(s)\text{d}s\hfill \\ =\left(\frac{t^{1-\alpha }}{\Gamma (2-\alpha )}-\kappa (0,t)\right)f^{\prime }(0)+{\displaystyle {\int }_0^t\left(\frac{{(t-s)}^{1-\alpha }}{\Gamma (2-\alpha )}-\kappa (s,t)\right)}{f}^{″}(s)\text{d}s\hfill \\ =\left(\frac{t^{1-\alpha }}{\Gamma (2-\alpha )}-\kappa (0,t)\right)f^{\prime }(0)+{\displaystyle {\int }_0^t\left(\frac{z^{1-\alpha }}{\Gamma (2-\alpha )}-\kappa (0,z)\right)}{f}^{″}(t-z)\text{d}z.\hfill \end{array}$$

We deduce that the error in the approximation can be written in terms of ε(t) = t ^1α/Γ(2 - α) — k(0, t). Hence,

$$\begin{array}{l}\left|D_t^{\alpha }f-{\widehat{D}}_t^{\alpha }f\right|=\left|\epsilon (t)f^{\prime }(0)+{\displaystyle {\int }_0^t\epsilon }(z)f^{″}(t-z)dz\right|\hfill \\ \le \left|\epsilon (t)f^{\prime }(0)\right|+\Vert \epsilon {\Vert }_{0,\infty }{\displaystyle {\int }_0^t\left|f^{″}(t-z)\right|}dz\hfill \\ \le \Vert \epsilon {\Vert }_{0,\infty }\left[\left|f^{\prime }(0)\right|+{\Vert f^{″}\Vert }_{0,1}\right],\hfill \end{array}$$

where ‖ · ‖_0,∞ and ‖ · ‖_o,1 denote the L _∞(0, T) and L ¹(0, T) norms, respectively.

Remark 1

Assuming f’(0) = 0 and f” ∈ L ²(0, T), then

$$\left|D_t^{\alpha }f-{\widehat{D}}_t^{\alpha }f\right|\le \Vert \epsilon {\Vert }_0{\Vert f^{″}\Vert }_{0,}$$

where ‖ · ‖₀ is the L ²(0, T) norm.

From Lemma 1, we observe that the error incurred from re-writing the fractional derivative in terms of a finite series of Maxwell elements is governed by ε as well as the behavior of the differentiated function f”. While the behavior of f is unknown in the time domain for forward simulations, we can evaluate its impact on the Prony approximation by directly evaluating ε over the time domain (0, T).

2.4. Discrete prony approximation of the Caputo derivative

The approximation shown in Eq. (10) lends itself to a straightforward discretized form by applying numerical updates to the intermediate variables q_k. We now approximate the first derivative using backward Euler and the integral term using a midpoint approximation, i.e.

$${\widehat{\text{D}}}_n^{\alpha }f:=\frac{{\beta }_0}{{\Delta }_t}\left(f^n-f^{n-1}\right)+{\displaystyle \sum _{k=1}^N{q}_k^n},q_k^n=e_k^2{q}_k^{n-1}+e_k{\beta }_k\left(f^n-f^{n-1}\right),$$ (12)

where e_k = exp[—Δ_t /(2τ_k)] and fⁿ = f(t_n). To simplify the notation from here on, superscripts of the letter n and of expressions of n will be used to denote the n ^th time step of a discretized function. With this definition, we can examine the discretization error between the discrete operator ${\widehat{D}}_n^{\alpha }$ and its continuous counterpart ${\widehat{D}}_t^{\alpha }$, as shown in Lemma 2.

Lemma 2.

Let f : [0, T] → ℝ be a real function in the time domain [0, T] and let f ∈ W^3,∞ (0, T). Assume the time interval [0, T] is divided into equal divisions Δ_t, giving discrete time steps {t₀, …, t_NT} with t_k = kΔ_t and T = N_tΔ_t. The value fⁿ = f(t_n) and the value $q_k^n$ is our approximation to q_k(t_n) based on Eq. (12). Here we assume $q_k^0=q_k(0)$ for all k = 1, …, N, and that β_k, τ_k ∈ ℝ⁺ . Then for any t_n ∈ {t₁, …, t_N}

$$\left|{\widehat{D}}_{t_n}^{\alpha }f-{\widehat{\text{D}}}_n^{\alpha }f\right|\le {\Delta }_t\left({\beta }_0/2+C\left({\theta }_{\alpha }\right){\Delta }_t\right)\Vert f{\Vert }_{W^{3,\infty }(0,T)},$$

where C(θ _α) > 0 is a constant depending on the chosen β_k, τ_k for all k = 1….,N

Proof of Lemma 2

We start by manipulating the ordinary differential equation for q_k in Eq. (10). Applying an integration factor and integrating over a discrete time interval [t_n-1, t_n], we can see that

$$q_k\left(t_n\right)=\exp \left[-\frac{{\Delta }_t}{{\tau }_k}\right]q_k\left(t_{n-1}\right)+{\displaystyle {\int }_{t_{n-1}}^{t_n}{\beta }_k}\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)\text{d}s.$$

Subtracting the discrete approximation shown in Eq. (12), we observe that

$$\left(q_k\left(t_n\right)-q_k^n\right)=\exp \left[-\frac{{\Delta }_t}{{\tau }_k}\right]\left(q_k\left(t_{n-1}\right)-q_k^{n-1}\right)+{\displaystyle {\int }_{t_{n-1}}^{t_n}{\beta }_k}\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)\text{d}s-e_k{\beta }_k\left(f^n-f^{n-1}\right).$$ (13)

We recall the result that for g ∈ W^2,∞ (0, T), one may derive the midpoint relation

$${\displaystyle {\int }_{t_{n-1}}^{t_n}g}(s)-g\left(t_{n-\frac{1}{2}}\right)\text{d}s={\displaystyle {\int }_{t_{n-1}}^{t_n}{\displaystyle {\int }_{t_{n-\frac{1}{2}}}^s(s-z)}}{g}^{″}(z)\text{d}z\text{d}s,$$ (14)

as well as derive an inequality for the truncation error

$$\begin{array}{l}{\displaystyle {\int }_{t_{n-1}}^{t_n}g}(s)-g\left(t_{n-\frac{1}{2}}\right)\text{d}s={\displaystyle {\int }_{t_{n-\frac{1}{2}}}^{t_n}{\displaystyle {\int }_{t_{n-\frac{1}{2}}}^s(s-z)}}{g}^{″}(z)\text{d}z\text{d}s+{\displaystyle {\int }_{t_{n-1}}^{t_{n-\frac{1}{2}}}{\displaystyle {\int }_s^{t_{n-\frac{1}{2}}}(z-s)}}{g}^{″}(z)\text{d}z\text{d}s\hfill \\ \le {\Vert g^{″}\Vert }_{L^{\infty }\left(t_{n-1},t_n\right)}\left[{\displaystyle {\int }_{t_{n-\frac{1}{2}}}^{t_n}{\displaystyle {\int }_{t_{n-\frac{1}{2}}}^s|}}s-z|\text{d}z\text{d}s+{\displaystyle {\int }_{t_{n-1}}^{t_{n-\frac{1}{2}}}{\displaystyle {\int }_s^{t_{n-\frac{1}{2}}}|}}z-s|\text{d}z\text{d}s\right]\hfill \\ \le \frac{{\Delta }_t^3}{24}{\Vert g^{″}\Vert }_{L^{\infty }\left(t_{n-1},t_n\right).}\hfill \end{array}$$

Utilizing the midpoint relation, the second half of Eq. (13) can be written as

$$\begin{array}{l}{\displaystyle {\int }_{t_{n-1}}^{t_n}{\beta }_k}\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)\text{d}s-e_k{\beta }_k\left(f^n-f^{n-1}\right)\hfill \\ ={\displaystyle {\int }_{t_{n-1}}^{t_n}{\beta }_k}\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)-{\beta }_k{e}_k{f}^{\prime }\left(t_{n-\frac{1}{2}}\right)\text{d}s-e_k{\beta }_k\left(f^n-f^{n-1}-{\Delta }_t{f}^{\prime }\left(t_{n-\frac{1}{2}}\right)\right)\hfill \\ ={\displaystyle {\int }_{t_{n-1}}^{t_n}{\beta }_k}\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)-{\beta }_k{e}_k{f}^{\prime }\left(t_{n-\frac{1}{2}}\right)\text{d}s-e_k{\beta }_k{\displaystyle {\int }_{t_{n-1}}^{t_n}{f}^{\prime }}(s)-f^{\prime }\left(t_{n-\frac{1}{2}}\right)\text{d}s.\hfill \end{array}$$ (15)

Note that each integral represents the truncation error of a midpoint approximation, hence

$$\begin{array}{l}\left|{\displaystyle {\int }_{t_{n-1}}^{t_n}{\beta }_k}\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)\text{d}s-e_k{\beta }_k\left(f^n-f^{n-1}\right)\right|\hfill \\ \le \frac{{\beta }_k{\Delta }_t^3}{24}{\Vert {\left(\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)\right)}^{″}\Vert }_{L^{\infty }\left(t_{n-1},t_n\right)}+\frac{e_k{\beta }_k{\Delta }_t^3}{24}{\Vert f^{‴}\Vert }_{L^{\infty }\left(t_{n-1},t_n\right)}\hfill \\ \le \frac{{\beta }_k{\Delta }_t^3}{24}\left(\frac{1}{{\tau }_k^2}{\Vert f^{\prime }\Vert }_{L^{\infty }\left(t_{n-1},t_n\right)}+\frac{2}{{\tau }_k}{\Vert f^{″}\Vert }_{L^{\infty }\left(t_{n-1},t_n\right)}+\left(1+e_k\right){\Vert f^{‴}\Vert }_{L^{\infty }\left(t_{n-1},t_n\right)}\right)\hfill \\ \le {\Delta }_t^3{C}_0\left({\beta }_k,{\tau }_k\right)\Vert f{\Vert }_{W^{3,\infty }\left(t_{n-1},t_n\right)},\hfill \end{array}$$

where $C_0\left({\beta }_k,{\tau }_k\right)=\left({\beta }_k/24\right)\max \left\{{\tau }_k^{-2},{\tau }_k^{-1},\left(1+e_k\right)\right\}$. Inserting the truncation error into Eq. (13), we can see that

$$\begin{array}{l}\left|q_k\left(t_n\right)-q_k^n\right|\le e_k^2\left|q_k\left(t_{n-1}\right)-q_k^{n-1}\right|+\left|{\displaystyle {\int }_{t_{n-1}}^{t_n}{\beta }_k}\exp \left[\frac{s-t_n}{{\tau }_k}\right]f^{\prime }(s)ds-e_k{\beta }_k\left(f^n-f^{n-1}\right)\right|\hfill \\ \le e_k^2\left|q_k\left(t_{n-1}\right)-q_k^{n-1}\right|+{\Delta }_t^3{C}_0\left({\beta }_k,{\tau }_k\right)\Vert f{\Vert }_{W^{3,\infty }\left(t_{n-1},t_n\right)}\hfill \\ \le e_k^2\left|q_k(0)-q_k^0\right|+C_0\left({\beta }_k,{\tau }_k\right){\Delta }_t^3{\displaystyle \sum _{m=1}^n\Vert f{\Vert }_{W^{3,\infty }\left(t_{m-1},t_m\right)}}\hfill \\ \le C_0\left({\beta }_k,{\tau }_k\right)t_n{\Delta }_t^2\Vert f{\Vert }_{W^{3,\infty }(0,T)}\hfill \end{array}$$

making the update formula for $q_k𝒪\left({\text{Δ}}_t^2\right)$. Subtracting the definition of ${\widehat{D}}_{t_n}^{\alpha }$ from ${\widehat{D}}_n^{\alpha }$, we can see that

$$\begin{array}{l}\left|{\widehat{D}}_{t_n}^{\alpha }f-{\widehat{\text{D}}}_n^{\alpha }f\right|=\left|{\beta }_0\left(f^{\prime }\left(t_n\right)-{\Delta }_t^{-1}\left(f^n-f^{n-1}\right)\right)+{\displaystyle \sum _{k=1}^N\left(q_k\left(t_n\right)-q_k^n\right)}\right|\hfill \\ \le {\beta }_0\left|f^{\prime }\left(t_n\right)-{\Delta }_t^{-1}\left(f^n-f^{n-1}\right)\right|+{\displaystyle \sum _{k=1}^N\left|q_k\left(t_n\right)-q_k^n\right|}\hfill \\ \le {\beta }_0\left|\frac{1}{{\Delta }_t}{\displaystyle {\int }_{t_{n-1}}^{t_n}\left(s-t_{n-1}\right)}{f}^{″}(s)ds\right|+C\left({\mathbf{\theta }}_{\alpha }\right){\Delta }_t^2\Vert f{\Vert }_{W^{3,\infty }(0,T)}\hfill \\ \le \frac{{\beta }_0{\Delta }_t}{2}{\Vert f^{″}\Vert }_{L^{\infty }\left(t_{n-1},t_n\right)}+C\left({\theta }_{\alpha }\right){\Delta }_t^2\Vert f{\Vert }_{W^{3,\infty }(0,T)},\hfill \end{array}$$ (16)

where $C\left({\theta }_{\alpha }\right)=\underset{k=1}{\overset{N}{{\sum }^{\text{}}}}{C}_0\left({\beta }_k,{\tau }_k\right)t_n$. Generalizing for any time point completes the proof.

From Lemma 2 we observe the typical discretization errors expected for backward Euler and midpoint based error estimates. The result shows that the discrete approximation converges to the approximate Prony series approximation with 𝒪(Δ_t). Using backward Euler for the first-order derivative term is not necessary, and higher- order approximations could easily be used in Eq. (12). Here we select this form for ease and, in the context of biomechanics simulations, for stability considerations. Combining Lemmas 1 and 2, we can derive an error estimate for this Prony series-based approximation in Theorem 3.

Theorem 3

Given the assumptions of Lemma 2, the error between ${\widehat{D}}_n^{\alpha }f$ and $D_{t_n}^{\alpha }f$ for any t_n ℝ {t₁, …, t_NT} is given by

$$\left|{\widehat{\text{D}}}_n^{\alpha }f-D_{t_n}^{\alpha }f\right|\le \Vert \epsilon {\Vert }_{0,\infty }\left[\left|f^{\prime }(0)\right|+{\Vert f^{″}\Vert }_{0,1}\right]+{\Delta }_t\left({\beta }_0/2+C(\beta ,\tau ){\Delta }_t\right)\Vert f{\Vert }_{W^{3,\infty }(0,T)}.$$

Proof of Theorem 3

This is a straightforward result of the triangle inequality, Lemmas 1 and 2.

Based on this error estimate, we can see that a refinement with Δ_t eliminates the portion of error responsible for discretization, while the appropriate selection of the positive constants used in Eq. (12) can reduce the Prony approximation error given by the truncation ε (as we will later show). We note that decreasing Δ_t will eventually lead to a plateau in the error convergence based on how well the Prony series approximates the true fractional derivative. However, increasing the number of Prony terms N elicits a more complex response. For large Δ_t, the error can become dependent on the second term in Theorem 3 and thus, the constant C(θ _α). This constant, in general, grows with more Prony terms and can have truncation scale factors that grow larger with larger N. However, for sufficiently fine Δ_t, increasing the number of terms shifts the error onto e and thus improves like the truncation error.

2.5. Optimizing the numerical approximation ${\widehat{D}}_t^{\alpha }$

The approximation introduced in Eq. (9) relies on the effective identification of the parameters θ _α that should be chosen to ensure optimal accuracy. Ideally, θ _a would be selected so as to minimize the error between the true Caputo derivative and the approximation in some suitable norm. For example, if we consider the L ²(0, T) norm, then we would seek to minimize the squared error

$$F\left(f,{\theta }_{\alpha },\alpha \right)=\frac{1}{2}{\displaystyle {\int }_0^T{\left[{\widehat{D}}_t^{\alpha }f-D_t^{\alpha }f\right]}^2}\text{d}t,$$ (17)

where F(f, θ _α, α) gives the squared L ²-norm error between the approximate and the true Caputo derivatives for the given function f and set of parameters θ _α. While the parameters θ _α could be chosen to minimize F(f, θ _α, α), this approach presents challenges as we often do not know f prior to simulation. Hence, instead, we must select our approximation to be suitably valid for all f, i.e. we find θ _α such that (for 0 < α < 1),

$$F\left(f,{\mathbf{\theta }}_{\alpha },\alpha \right):=\left\{\min F(f,\phi ,\alpha ),\phi \in {ℝ}^{2N+1}\right\},\text{for}\text{any}f\in W^{2,\infty }(0,T).$$ (18)

The problem posed in Eq. (18) is generally challenging to solve due to the flexibility in the behavior of f. In order to approximately minimize F, suppose we instead consider only those functions f ∈ 𝓕(M) where

$$ℱ(M)=\left\{f\in L^2(0,T)\mid f(t)=\mathrm{Re}\left\{{\displaystyle \sum _{k=1}^M{C}_k}\exp \left(i{\omega }_{k}t\right)\right\},\text{for}\text{some}{C}_0,\dots ,C_M\in ℂ\right\}$$ (19)

represents the set of functions that can be written using a Fourier basis [73]. Here we note that ω_k = kω*, where ω* = 2π/T is the base frequency of f on the time interval [0, T]. In this context, our function f and its fractional derivative (for t » 0) can be written as

$$f(t)=\mathrm{Re}\left\{{\displaystyle \sum _{k=1}^M{C}_k}\exp \left(i{\omega }_{k}t\right)\right\},D_t^{\alpha }f(t)\approx \mathrm{Re}\left\{{\displaystyle \sum _{k=1}^M{C}_k}{\left(i{\omega }_k\right)}^{\alpha }\exp \left(i{\omega }_{k}t\right)\right\}.$$ (20)

In contrast, the approximate fractional derivative ${\widehat{D}}_t^{\alpha }$ based on Eq. (9) can be written as,

$${\widehat{D}}_t^{\alpha }f(t)=\mathrm{Re}\left\{{\displaystyle \sum _{k=1}^M{C}_k}\left({\beta }_{0}i{\omega }_k+{\displaystyle \sum _{m=1}^N{\beta }_m}\left({\tau }_m{\omega }_k\right)\frac{\left({\tau }_m{\omega }_k+i\right)}{{\left({\tau }_m{\omega }_k\right)}^2+1}\right)\exp \left(i{\omega }_{k}t\right)\right\}.$$ (21)

The difference between the true and approximate operators is then simply,

$${\widehat{D}}_t^{\alpha }f(t)-D_t^{\alpha }f(t)\approx \mathrm{Re}\left\{{\displaystyle \sum _{k=1}^M{C}_k}\exp \left(i{\omega }_{k}t\right)\left[{\beta }_{0}i{\omega }_k+{\displaystyle \sum _{m=1}^N{\beta }_m}\left({\tau }_m{\omega }_k\right)\frac{\left({\tau }_m{\omega }_k+i\right)}{{\left({\tau }_m{\omega }_k\right)}^2+1}-{\left(i{\omega }_k\right)}^{\alpha }\right]\right\},$$ (22)

leaving the operator error dependent on the size of the complex number given in the square brackets. This means that for us to obtain a good approximation for any f ∈ 𝓕(M), we must choose θ _α such that we minimize the bracketed term. Hence, we may reduce the minimization problem in Eq. (18) to an analogous normalized system where

$$\frac{1}{k^{\alpha }}{\displaystyle \sum _{m=1}^N{\widehat{\beta }}_m}\frac{{\left(k{\widehat{\tau }}_m\right)}^2}{{\left(k{\widehat{\tau }}_m\right)}^2+1}=\cos \left(\frac{\pi \alpha }{2}\right),{\widehat{\beta }}_0{k}^{1-\alpha }-\frac{1}{k^{\alpha }}{\displaystyle \sum _{m=1}^N{\widehat{\beta }}_m}\frac{k{\widehat{\tau }}_m}{{\left(k{\widehat{\tau }}_m\right)}^2+1}=\sin \left(\frac{\pi \alpha }{2}\right),$$ (23)

for k = 1, …, M. Here, we note that parameters were normalized (with hats) to enable independence from the base frequency, ω* with ${\beta }_0={\widehat{\beta }}_0{\left({\omega }^{\star }\right)}^{\alpha -1},{\beta }_m={\widehat{\beta }}_m{\left({\omega }^{\star }\right)}^{\alpha }$ and ${\tau }_m={\widehat{\tau }}_m/{\omega }^{\star }(m=1,\dots ,N)$. This leads to 2M constraint equations that, if hold, imply equivalence of the true and approximate Caputo derivative. Assuming that our function is composed of many more Fourier terms than the number of Prony terms (i.e. M » N), Eq. (23) leads to a nonlinear over-constrained system that can be solved by optimization.

2.6. Numerical implementation

Resulting parameters for approximating different fractional derivatives can be found in the MATLAB [74] codes provided as supplementary material. Here optimized parameters can be returned for values of N ∈ [3,15] and α ∈ [0, 1] for a specified base frequency ω*. Codes and examples are also provided showing how the approximation can be utilized for approximating the Caputo derivative. Other methods, such as the midpoint (MP) or Grünwald–Letnikov (GL) approximations, are also provided.

3. Large deformation viscoelastic solid mechanics

3.1. Review of kinematics and kinetics

In this section, we briefly review the kinematics and kinetics for hyperelastic materials. Let Ω ₀ ⊂ ℝ³ denote the reference configuration of a three-dimensional solid (coordinates X) and Γ₀ denote its boundary. The boundary is split into groups ${\text{Γ}}_0={\text{Γ}}_0^N{\cup }^{\text{}}{\text{Γ}}_0^D$ based on either loading (subscript N) or displacement boundary conditions (subscript D). Over a time interval t ∈ [0, T], the configuration of the body becomes Ω(t) ⊂ ℝ³, with physical coordinates x. The coordinates are related by

$$x(t)=u(t)+X,x_i(t)=u_i(t)+X_i.$$ (24)

The mapping in Eq. (24) is assumed to be bijective with u : Ω ₀ x [0, T] → ℝ³ denoting the material displacements. Note that X and x are the vector positions, with components X_i and Xi. The deformation gradient F defines the local mapping of infinitesimal vectors, which is given by

$$\mathit{\text{F}}=\frac{\partial \mathit{\text{x}}}{\partial \mathit{\text{X}}}=\frac{\partial u}{\partial \mathit{\text{X}}}+\mathit{\text{I}},F_{ij}=\frac{\partial u_i}{\partial X_j}+{\delta }_{ij},$$

where I is the identity tensor. The determinant J = det F defines the relative change in volumes, providing key information about material growth/decay. The right and left Cauchy-Green tensors [75], defining the material stretch, are

$$\mathit{\text{C}}={\mathit{\text{F}}}^T\mathit{\text{F}},\mathit{\text{B}}=\mathit{\text{F}}{\mathit{\text{F}}}^T.$$

The deformation gradient and the left and right Cauchy-Green tensors comprise a common set of measures used to characterize the constitutive behavior of a material. For a hyperelastic material, the strain-energy density function is given by Ψ = Ψ(C), which defines the stored energy resulting from material deformations. From the second law of thermodynamics, the strain-energy function can be related to the second Piola-Kirchhoff stress tensor (PK2) as

$$S=2\frac{\partial \Psi (C)}{\partial C},S_{ij}=2\frac{\partial \Psi \left(C_{ij}\right)}{\partial C_{ij}},$$ (25)

which, in turn, is related to the first Piola-Kirchhoff and Cauchy stress tensors (P and σ, respectively) by push forward operations on PK2. In this case,

$$\sigma =\frac{1}{J}{\mathit{\text{FSF}}}^T=\frac{1}{J}\mathit{\text{P}}{\mathit{\text{F}}}^T.$$ (26)

For isotropic biomechanical materials, the strain-energy function is often defined using invariants of C [76],

$$I=C:I,II=C:C,III=\det C$$ (27)

with Ψ = Ψ(I, II, III). For incompressible materials, the third invariant III is constrained to 1 by splitting the strain-energy function into a deviatoric (Ψ_d) and a volumetric components with Ψ = Ψ_d + p(III ^1/2 − 1), where p : Ω × [0, T] → ℝ denotes the hydrostatic pressure. Often the strain-energy function takes exponential forms, as seen in the Fung model [10]. However, with many tissues exhibiting anisotropic material response [77], additional invariants have been introduced to denote stretch with respect to specific microstructural directions. These laws can be naturally extended, but for the purposes of this work, we will focus on more simple isotropic forms.

3.2. Extension of hyperelastic to viscoelastic models

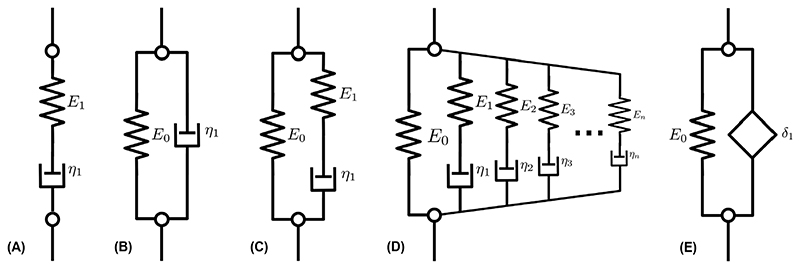
For constitutive modeling of viscoelastic behavior, a number of model approaches have been presented in the literature. Fig. 1 illustrates some of the common models introduced, particularly for linear viscoelastic materials, using spring, dashpot or spring-pot elements. Extension of these forms toward nonlinear material models has become more common, with models following the analogy presented in Fig. 1. For example, following the template of the linear models, a nonlinear viscoelastic Maxwell model (Fig. 1A) could be written as

$$S+\frac{{\eta }_1}{E_1}{S}^{\prime }={\eta }_1{S}_v^{\prime }$$ (28)

and the nonlinear viscoelastic Kelvin-Voigt model (Fig. 1B) as,

$$S=E_0{S}_e+{\eta }_1{S}_v^{\prime }.$$ (29)

Fig. 1. Illustration of spring, dashpot and spring-pot elements used to compose viscoelastic models.

Examples include the (A) Maxwell, (B) Kelvin-Voigt, (C) Standard Linear, (D) Generalized Maxwell and (E) Fractional Kelvin-Voigt models.

Here S _e denotes a symmetric tensor denoting the hyperelastic response of the material, while S _v denotes the symmetric tensor encoding the viscoelastic response. Note that these stresses denote the non-hydrostatic components, which can be included based on the application. Commonly, both take a similar form to hyperelastic materials commonly encountered in the literature. These models provide an exponential decay in the viscoelastic phenomena, which can yield viscoelastic response times that are incompatible with experimental data. Other formulations, such as introduced by Schapery et al. [78], provide a more generalized view for characterizing material response. Another example is the model developed by Freed and Diethelm [46], i.e.

$$\mathit{\text{S}}(t)=\left({\mu }_{\infty }+\left({\mu }_0-{\mu }_{\infty }\right)\right)G(t)\frac{\partial \Psi (\mathit{\text{E}})}{\partial \mathit{\text{E}}}+\left({\mu }_0-{\mu }_{\infty }\right){\displaystyle {\int }_0^{t}M}(t-s)\frac{\partial \Psi (\mathit{\text{E}})}{\partial \mathit{\text{E}}}\text{d}s,$$ (30)

where G(t) is a relaxation function and M(t) is a memory function for the history dependency.

An alternative approach, that has been successful in the experimental literature, is use of fractional elements [44,45]. This is due to the progressive memory exhibited by these models following a power spectrum commonly observed in biological tissues for moderate frequencies. In this case, we can envision development of nonlinear fractional viscoelastic models, such as the fractional Kelvin-Voigt model (Fig. 1E), e.g.

$$S=E_0{S}_e+{\eta }_1{D}_t^{\alpha }{S}_v.$$ (31)

Here α = 0 reduces to a pure elastic response and α = 1 converts the equation into the nonlinear viscoelastic Kelvin-Voigt model shown above. The advantage of this approach is the generality of its application and ability to capture the dynamic viscoelastic behavior of tissues with the addition of the fractional differential operator.

3.3. Conservation of mass and momentum

With an appropriately defined constitutive model, the conservation of mass and momentum for an incompressible solid material is given by [77],

$${\partial }_t(\varrho Jv)-{\nabla }_X\cdot (FS)=Jb,\text{in}{\Omega }_0\times [0,T],$$ (32)

$$J-1=0,\text{in}{\Omega }_0\times [0,T]$$ (33)

where ∂_t is the Lagrangian derivative (taken with respect to fixed coordinates X), ϱ is the material density, v = ∂_t u is the material velocity, and [0, T] is the time interval of interest. The mechanical system is then subject to an initial condition and boundary conditions, e.g.

$$u(\cdot ,0)=u_0,v(\cdot ,0)=v_0\text{in}{\Omega }_0,$$ (34)

$$v(\cdot ,t)=v_D,\text{on}{\Gamma }_0^D\times [0,T],(FS)\cdot N=t_N\text{on}{\Gamma }_0^N\times [0,T]$$ (35)

where u₀, v₀ : Ω ₀ → ℝ³ are given initial conditions, $v_D:{\text{Γ}}_0^D\to {ℝ}^3$ given information about the rate of deformation on the boundary ${\Gamma }_0^D$, and $t_N:{\text{Γ}}_0^N\to {ℝ}^3$ is given information about the applied traction on boundary ${\text{Γ}}_0^N$. All examples considered herein assume that no history of deformation is present in the material for t < 0 (e.g., the fractional derivative is defined w.r.t. t = 0).

4. Finite element approximation for viscoelastic solid models

This section reviews the integration of the nonlinear fractional viscoelastic model into a finite element solid mechanics framework. For development and discretization of the weakform system, we follow the typical mixed finite element u – p formulation [79,80] (Section 4.1) and extend it to account for the discrete fractional order model (Section 4.2). A summary of the implementation steps is provided in Section 4.3. The linearized system is introduced in Section 4.4, and stability estimates are proven for the discrete problem.

4.1. Continuous and discrete weakform system

The weak formulation for the mechanical system follows the typical procedure. Multiplying Eqs. (32)–(33) by test functions w and q, respectively, integrating and applying integration by parts, the weak problem can be written as: find (u(t), v(t), p(t)) ∈ 𝒰 × 𝒱 _D × 𝒫 such that,

$$\left({\partial }_t(\varrho vJ),y\right)+\left(FS,{\nabla }_{X}y\right)-\langle t_N,y\rangle -(Jb,y)+(q,J-1)+\left(v-{\partial }_{t}u,w\right)=0,$$ (36)

for all (w, y, q) ∈ 𝒰 × 𝒱 ₀ × 𝒫 and all times t ∈ [0, T]. Here, 𝒰, 𝒱 and 𝒫 denote appropriate spaces [81], their subscripts D and 0 denote spaces equipped with appropriate Dirichlet or zero Dirichlet conditions on ${\text{Γ}}_0^D$, and the operators (·, ·) and 〈·,·〉 denote the inner products on Ω ₀ and ${\text{Γ}}_0^N$, respectively.

A discrete-in-time discretization of Eq. (36) can be considered using Backward Euler for temporal derivative approximations. Here we define a series of time steps ${\left\{t_n\right\}}_{n=0}^{N_T}$ (as seen in Section 2.2), where the superscript n denote a variable quantity at time t_n, and the Backward temporal operator, δ_tfⁿ = (fⁿ — Δ^n-1)/A_t. Defining appropriate inf-sup compatible discrete spaces, denoted with the subscript h (in later results, we use ℚ² - ℚ² - ℚ¹ Taylor-Hood elements [82]), the discrete weak form of Eq. (36) can be written as: find $\left(u_h^n,v_h^n,p_h^n\right)\in {𝒰}^h\times {𝒱}_D^h\times {𝒫}^h$ such that,

$$\left({\delta }_t\left(\varrho v_h^n{J}^n\right),y_h\right)+\left(F^n{S}^n,{\nabla }_X{y}_h\right)-\langle t_N,y_h\rangle +\left(q_h,J^n-1\right)-\left(J^n{b}^n,y_h\right)+\left(v_h^n-{\delta }_t{u}_h^n,w_h\right)=0,$$ (37)

for all (w_h, y _h, q_h) ∈ ${𝒰}^h\times {𝒱}_0^h\times {𝒫}^h$ and n = 1, …, N_T. We note that, under the scheme presented, the solution for $u_h^n$ can be implicitly defined based on $v_h^n$ as

$$v_h^n={\delta }_t{\mathit{\text{u}}}_h^n$$

at node points.

4.2. Stress discretization and integration with the Prony approximation

Evaluation of the discrete finite element equation in Eq. (37) follows the typical procedure applied in finite element mechanics. Namely, the weighted residual equations are evaluated using an appropriate form of quadrature based on the element type and computational complexity of the integrand. In the context of fractional viscoelastic models, as introduced in Section 3.2, the only additional challenge is determining a scheme for handling the viscoelastic stress tensor. Using the Prony approximation introduced in Eq. (12), the fractional Kelvin-Voigt model can be written as,

$$S^n=S_e^n+{\beta }_0{\delta }_t{S}_v^n+{\displaystyle \sum _{k=1}^N{Q}_k^n}+p_h^n{S}_p^n,$$ (38)

where $S_e^n=S_e\left(C^n\right),S_v^n=S_v\left(C^n\right)$, $S_v^n=S_v\left(C^n\right),S_p^n=J^n{\left[C^n\right]}^{-1}$ and $Q_k^n$ is defined by the update formula,

$$Q_k^n=e_k^2{\mathit{\text{Q}}}_k^{n-1}+{\beta }_k{e}_k{\Delta }_t{\delta }_t{\mathit{\text{S}}}_v^n.$$

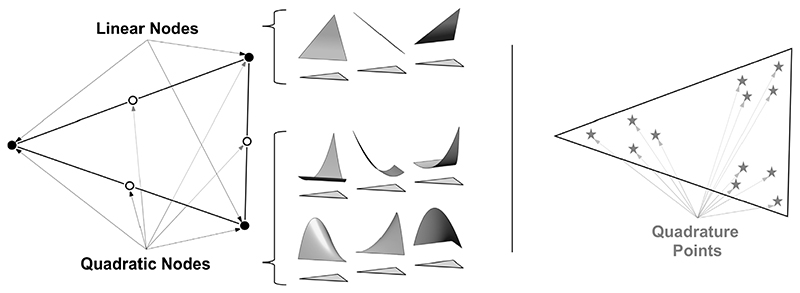
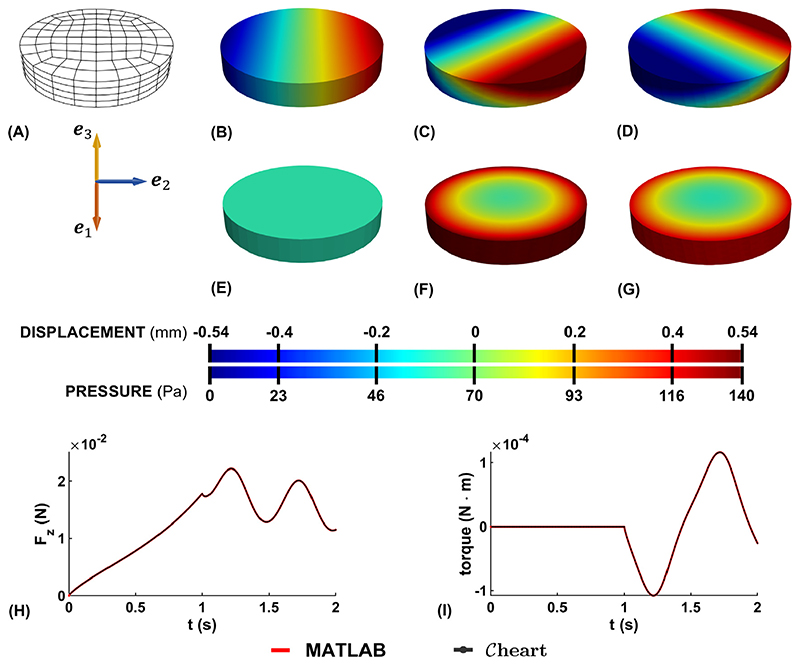
The approximation for the current value of the second Piola-Kirchhoff stress given in Eq. (38) introduces the intermediate variables, Q _k, representing the evolution of the material history due to different Prony terms. Within a finite element discretization, Eq. (38) could be realized weakly, interpolating Q _k using basis functions. However, this form does not ensure equivalence to the original form observed in Eq. (37). Instead, the values of Q _k are discretized at quadrature points where the residual equation (and, consequently, the stress) must be evaluated. Fig. 2 illustrates this strategy for the Taylor–Hood ℙ² – ℙ¹ mixed-problem on triangles using an appropriate quadrature rule [83]. We note that this illustration, though for triangles, similarly applies to other Taylor-Hood approximation spaces on different element types (e.g. quadrilateral, tetrahedra, hexahedra) with the corresponding appropriate quadrature rules. In Fig. 2 we see the mixed element showing node points for displacement, velocity and pressure as well as the quadrature points at which values of Q _k are stored.

Fig. 2.

Illustration of element level discretization for fractional viscoelasticity for Taylor-Hood triangular elements. (Left) View of standard mixed ℙ² – ℙ¹ Taylor-Hood triangular finite element scheme and corresponding linear (pressure) and quadratic (displacement, velocity) nodal Lagrange basis functions. Selection of quadrature used to approximate the viscoelastic intermediate variables, Q.

For practical implementation purposes, it is convenient to re-arrange Eq. (38) to consolidate terms based on their dependence on the current time step and past time step, e.g.

$$S^n=S_e^n+\gamma S_v^n+p_h^n{S}_p^n-\gamma S_v^{n-1}+{\displaystyle \sum _{k=1}^N{e}_k^2}{\mathit{\text{Q}}}_k^{n-1},$$ (39)

where $\gamma ={\beta }_0/{\text{Δ}}_t+\underset{k=1}{\overset{N}{{\sum }^{\text{}}}}{\beta }_k{e}_k$ From Eq. (39), the first three terms depend on n while the latter two terms depend on variables at n - 1. As a result, to iteratively solve Eq. (37), one needs to evaluate the last two terms once per time step. While the first three terms vary at each iteration, the complexity of computing these terms over a standard hyperelastic formulation is the addition of $\gamma S_v^n$.

4.3. Solution procedure

The computational model framework presented was implemented into C heart [57], a custom multiphysics finite element solver used in a range of biomechanics applications [81,84–87]. The solution procedure follows the Shamanskii-Newton-Raphson (SNR) method [88] shown in Algorithm 1. Due to the formulation devised in Section 4.1, the final linearized system is written for variables $v_h^n$ and $p_h^n$ with the current displacement calculated as discussed previously. In this case, our residual functional can be written as,

$$R\left(v_h^n,p_h^n;w_h,q_h\right):=\left(\varrho {\delta }_t\left(v_h^n{J}^n\right),w_h\right)+\left({\mathit{\text{F}}}^n{S}^n,{\nabla }_X{w}_h\right)-\langle t_N,w_h\rangle +\left(q_h,J^n-1\right)-\left(J^n{b}^n,w_h\right).$$ (40)

Owing to the fact that $v_h^n$ can be expressed as the weighted sum of vector basis functions (and similar for $p_h^n$, but using scalar basis functions), Eq. (40) can be written as

$$R\left(X^n;Y\right)=R\left({\Phi }_v{V}^n,{\Phi }_p{P}^n;{\Phi }_{v}W,{\Phi }_{p}Q\right)$$

where Xⁿ = (Vⁿ, Pⁿ) denotes the coefficients of our solution and Y = (W, Q) the weights of our test functions. Finally, the vector residual function can be expressed as the gradient with respect to Y, e.g.

$$R\left(X^n\right)={\nabla }_{Y}R\left(X^n,Y\right)=\mathbf{0}.$$ (41)

Algorithm 1 Viscoelastic Mechanics Algorithm.

1: Given initial condition X ⁰ (and Q ⁰ at all quadrature points).

2: Compute J _β = Δ_x R(X ⁰), [J_β]^-1.

3:

4: for (n = 1 : N) do

5: 

6:      Set X^{n ,0} = X^{n -1}.

7:      Compute R(Xⁿ’⁰).

8:      Compute r = ‖ R(Xⁿ’°)‖.

9:      Set k = 0.

10:

11:      while (r > T OL) do

12:

13:          Compute δX = -[J_β]⁻¹ R (X^n,k).

14:          Find min _α∈[0,1]‖R(X^n,k + α δX)‖.

15:          Set X ^n,k+1 = X ^n,k + α δX.

16:          if (‖R(X ^n,k+1)‖ > γ r or k > ITER) then

17:              Compute J_β = Δ_x R (X ^n,k+1), [J_β]⁻¹.

18:          Compute r = ‖R (X ^n,k+1)‖.

19:          Set k = k + 1.

20:      Update $Q^n=e_k^2{Q}_k^{n-1}+{\beta }_k{e}_k{\text{Δ}}_t{\delta }_t{S}_v^n$ at quadrature points.

4.4. Stability of the discrete weak form system

In this section, stability is analyzed for linear incompressible fractional viscoelastic materials shown in Eqs. (42) and (43). The problem depends on the parameters ϱ, E, Ƞ ∈ ℝ⁺ which, for ease, we take as positive spatiotemporal constants denoting the material density, elastic stiffness and fractional viscoelastic stiffness, respectively.

$$\varrho {\partial }_t(v)-{\nabla }_X\cdot \Sigma =b,\text{in}{\Omega }_0$$ (42)

$${\nabla }_X\cdot v=0,\text{in}{\Omega }_0$$ (43)

$$\mathit{\text{u}}(\cdot ,0)={\mathit{\text{u}}}_0,v(\cdot ,0)=v_0,\text{in}{\Omega }_0$$ (44)

$$v=\mathbf{0}\text{on}{\Gamma }_0^D,\mathit{\text{Σ}}\cdot \mathit{\text{N}}=\mathbf{0},\text{on}{\Gamma }_0^N$$ (45)

Here b denotes body forces and u ₀ and v ₀ are given initial conditions. All examples considered herein assume that no history of deformation (e.g. the fractional derivative is defined w.r.t. t = 0). The constitutive model for the linear elastic material is given by

$$\Sigma =EDu+\eta D_t^{\alpha }(Du)+pI.$$ (46)

with $D(\cdot )=\frac{1}{2}\left({\nabla }_X(\cdot )+{\nabla }_X{(\cdot )}^T\right)$. Mirroring the discretization strategy of Section 4, we can derive the discrete weakform equation for the problem in Eqs. (42)–(45) as: For every n = 1, …, N_T, find $\left(u_h^n,v_h^n,p_h^n\right)\in {𝒰}^h\times {𝒱}_0^h\times h$ such that,

$$\left(\varrho {\delta }_t{v}_h^n,y_h\right)+\left({\Sigma }^n,{\nabla }_X{y}_h\right)-\left(b^n,y_h\right)+\left(q_h,{\nabla }_X\cdot v_h^n\right)+\left(v_h^n-{\delta }_t{u}_h^n,w_h\right)=0$$ (47)

for all (w_h, y _h, q_h) ∈ ${𝒰}^h\times {𝒱}_0^h\times {𝒫}^h$. Here we assume $u_h^0=u_0,v_h^0=v_0$, and $Q_k^0=\mathbf{0}$ for each k = 1, …, N (e.g. no history of deformation is assumed). Σⁿ is given by Eq. (48), which utilizes the approximate fractional derivative denoted by ${\widehat{D}}_n^{\alpha }$.

$${\Sigma }^n=E\mathit{\text{D}}{\mathit{\text{u}}}_h^n+\eta {\widehat{\text{D}}}_n^{\alpha }\left(\mathit{\text{D}}{\mathit{\text{u}}}_h\right)+p_h^n\mathit{\text{I}}$$ (48)

Examining the stability of Eq. (47), it can be shown that the state variables satisfy the stability estimates given in Lemmas 4 and 5 in Appendix A.

5. Analytical evaluation of the Prony-based method

5.1. Comparison of truncation error of fractional differentiation approaches

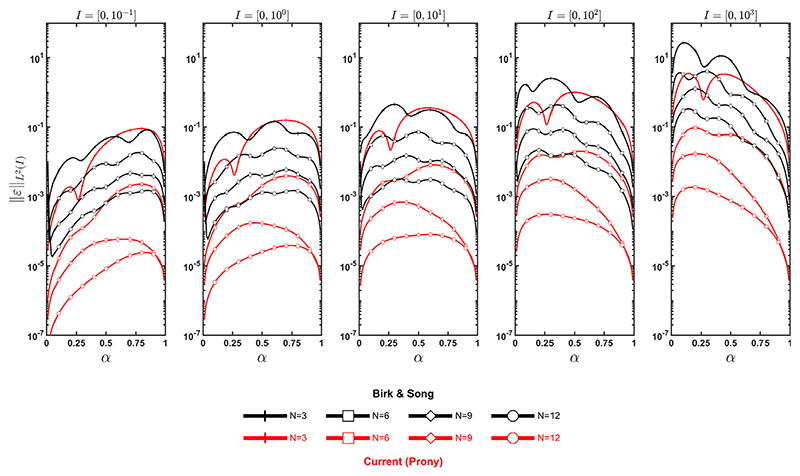
The truncation error gives a more broad view of the errors and convergence the methods without a given function or differential equation. For the Prony-based method, this is given in Eq. (11). As can be seen in Lemma 1 and Theorem 3, the truncation error, when scaled by the derivative of a given function, serves as a lower-bound for the approximation error of the method. As such, we directly compared the truncation errors of the Prony-based method against that of the integral approach in Birk and Song [54] (Fig. 3), for different time intervals and number of Prony terms, N ∈ {3, 5, 6, 9, 12}.

Fig. 3.

Examination of the L ²(I) norm error of the truncation error ε for different time intervals, I = [0, T]. Each plot shows parameters selected by the optimization approach here and the integral approach in Birk and Song [54], for N ∈ {3, 5, 6, 9, 12}.

The most immediate observation is that, the Prony-based method outperforms the method of Birk and Song in all cases when N ≥ 6. When N = 3, both methods perform similarly. Both methods also show that the overall truncation error increases with the duration of the time interval as expected when interpolating a larger range. Also of interest is that the trend for increasing alpha changes with time interval. As shown in Fig. 3, for smaller time intervals the error increases with increasing alpha, while at longer time intervals the error decreases with increasing alpha. Approximation errors increasing with α is a familiar issue to most methods for approximating the fractional derivative and the latter case is likely related to the effect of α increasing the rate of relaxation, causing the values of the fractional derivative to decay over larger time intervals.

5.2. Evaluation of approximation errors using polynomial function

In this section, we aim to examine the accuracy and convergence of the Prony-based method (Eq. (12)) in comparison to a few other methods in the literature. For this purpose, we here consider a basic example of approximating the fractional derivative of a polynomial series, i.e.

$$p(t)={\displaystyle \sum _{k=1}{b}_k}{t}^{k-1},D_t^{\alpha }p(t)={\displaystyle \sum _k{b}_k}\Gamma (1-k)\frac{k-1}{k-\alpha }{t}^{k-1-\alpha },$$ (49)

where b_k are the given parameters (given under Fig. 4). Different methods are used to approximate the fractional derivative of p, where the L ²-norm of the error with the analytic solution is then computed. All methods considered in this section were implemented in MATLAB [74].

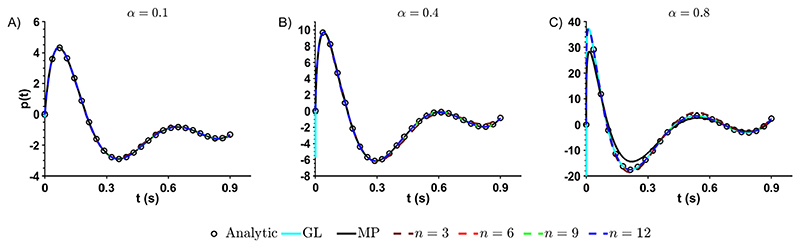
Fig. 4.

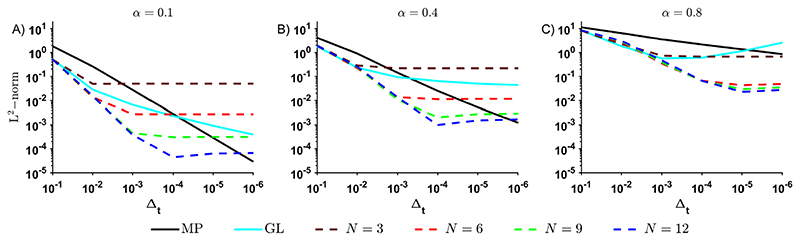
Examples of approximating the fractional derivative of a polynomial (with {b ₁ … b ₈} = {2.17, 101.54, -977.47, 3368.61, -5636.44, 4937.49, -2191.59, 398.40}) using the midpoint rule versus the Prony-based method with N ∈ {3, 6, 9, 12} terms for (A) α = 0.1, (B) α = 0.4 and (C) α = 0.8.

Table 1 compares the computation time of the Prony-based method in Eq. (12) with a representative cumulative approach, in this case, the midpoint (MP) rule (Eq. (4)). From this, we observe that the computation time for the midpoint rule grows as $𝒪\left(N_T^2\right)$, with N_T denoting the number of time steps. As a consequence, the midpoint rule Eq. (4) takes ≈ 13 min to complete the problem with Δ_t =1e-5 in comparison to about 3 s for the Prony-based method. This disparity stems from the use recursive updates of intermediate variables, qk, in the Prony-based method resulting in a temporal scaling of O(N_T). Minimal increase in compute time is observed with increasing Prony terms despite the N -dependent workload required for the computation of the fractional derivative operation (computation time grows 15% from N = 3 to N = 12). This likely stems from the efficiency of vectorized operations in MATLAB.

Table 1.

Computational cost of approximating the fractional derivative of the polynomial in Eq. (49) with the midpoint rule versus the Prony-based method with N ∈ {3, 6, 9, 12}. Here the time interval for the calculation is [0, 0.9] and α = 0.4.

Δt (s)	Midpoint (s)	Prony (s)
		N = 3	N = 6	N = 9	N = 12
1e–4	8.16	0.28	0.27	0.30	0.33
5e–5	29.25	0.53	0.58	0.60	0.61
1e–5	785.14	2.58	2.64	2.87	3.01

For the Prony series parameters, we selected the optimized values from Section 2.5 on a time interval of 9 s, 10 times the time domain. This can significantly improve the error estimates in Theorem 3 by reducing ε(z) and C(β, τ), and being more inclusive of the frequencies of the Prony series that are larger than the time domain but still relevant to the problem (see Appendix B for more details).

Fig. 5 illustrates the accuracy of the proposed, midpoint and Griinwald–Letnikov methods. Here the accuracy of the Prony approximation is examined for different α, N and Δ_t (Δ_t =1e-4 case shown in Fig. 4). Visibly, six or more Prony terms appear to perform well for the polynomial function, but three Prony terms generally yield noticeable errors. As predicted by the truncation error in Fig. 3, the accuracy of the Prony approximation deteriorates with increasing α, especially for α > 0.5, limiting the Δ_t convergence as shown in Theorem 3. However, this deterioration is also observed in the midpoint method, where limited convergence with Δ_t is observed at α = 0.8. The Gninwald-Letnikov method is significantly better in this regard, where convergence of the Griinwald–Letnikov method is on par or better than the Prony-based methods for N = 12 for sufficiently large N_T. However, as observed in Fig. 5, the Grunwald-Letnikov method seems to diverge as Δ_t approach 0. This is due to a singular behavior in the Griinwald–Letnikov method (Eq. (5)) when the number of time points N_T is small. Precisely, when N_t = 0, i.e. when taking the fractional derivative at time zero, the resulting value behaves as $f(0)/{\text{Δ}}_t^{\alpha }$ (Fig. 4). This singularity is always present and decreases quickly with increasing N_T, and indicates the reliance of this method on knowing the value of the function being differentiated, making it unsuitable for solving differential equations without further corrections. The Prony-based method for N > 3 generally shows convergence for all α values, with errors plateauing based on the truncation error derived in Lemma 1 (see Table 2). This is most visibly obvious for α = 0.1 (Fig. 5A). For the N = 3 case, truncation errors vastly exceed time discretization errors, resulting in no appreciable convergence with time step refinement. It is noticeable that the Prony-based method performs better than the midpoint rule before reaching the truncation error in all cases tested. Larger number of Prony terms can significantly reduce this truncation error, illustrating the importance of choosing a sufficient number of terms for the problem depending on the required degree of accuracy.

Fig. 5. The convergence of the approximation of the fractional derivative of polynomials when using the midpoint rule versus the Prony series for (A) α = 0.1, (B) α = 0.4 and (C) α = 0.8.

Table 2.

Comparing the approximation error for the fractional derivative of polynomials when using the midpoint (MP) rule versus the Prony series. Here Δ_t = 0 denotes the norm, ∥ε∥₀, of the truncation error predicted in Lemma 1.

	Δt	MP	GL	Prony					Birk and Song
				N = 3	N = 6	N = 9	N = 12		N = 3	N = 6	N = 9	N = 12
α = 0.1	1e–1	1.84e0	5.24e–1	5.07e–1	5.14e–1	5.14e–1	5.14e–1		4.73e–1	4.95e–1	5.12e–1	5.14e–1
	1e–2	2.64e–1	2.86e–2	4.96e–2	1.37e–2	1.49e–2	1.56e–2		2.99e–1	6.78e–2	2.77e–2	1.84e–2
	1e–3	2.76e–2	6.64e–3	5.04e–2	2.76e–3	4.45e–4	3.81e–4		3.01e–1	7.42e–2	2.23e–2	7.31e–3
	1e–4	2.81e–3	2.35e–3	5.04e–2	2.74e–3	3.03e–4	4.47e–5		3.01e–1	7.46e–2	2.24e–2	6.81e–3
	1e–5	2.86e–4	9.19e–4	5.04e–2	2.75e–3	3.13e–4	6.39e–5		3.01e–1	7.46e–2	2.24e–2	6.78e–3
	1e–6	2.93e–5	3.92e–4	5.04e–2	2.75e–3	3.14e–4	6.69e–5		3.01e–1	7.46e–2	2.24e–2	6.77e–3
	0	–	–	5.04e–2	2.75e–3	3.14e–4	6.71e–5		3.01e–1	7.46e–2	2.24e–2	6.77e–3
α = 0.4	1e–1	4.12e0	1.80e0	1.95e0	1.91e0	1.91e0	1.92e0		2.73e0	2.22e0	1.99e0	1.94e0
	1e–2	9.12e–1	2.36e–1	2.88e–1	2.25e–1	2.48e–1	2.58e–1		1.23e0	5.25e–1	3.34e–1	3.22e–1
	1e–3	1.43e–1	9.34e–2	2.21e–1	1.38e–2	1.08e–2	1.35e–2		1.21e0	4.74e–1	1.63e–1	7.59e–2
	1e–4	2.53e–2	6.46e–2	2.21e–1	1.14e–2	2.04e–3	9.88e–4		1.21e0	4.17e–1	1.43e–1	4.39e–2
	1e–5	5.27e–3	5.05e–2	2.21e–1	1.17e–2	2.76e–3	1.53e–3		1.21e0	4.12e–1	1.38e–1	4.31e–2
	1e–6	1.22e–3	4.42e–2	2.21e–1	1.18e–2	2.90e–3	1.68e–3		1.21e0	4.12e–1	1.37e–1	4.34e–2
	0	–	–	2.21e–1	1.18e–2	2.92e–3	1.69e–3		1.21e0	4.12e–1	1.37e–1	4.35e–2
α = 0.8	1e–1	1.13e1	8.46e0	8.14e0	8.37e0	8.42e0	8.47e0		8.22e0	9.10e0	9.38e0	9.36e0
	1e–2	6.42e0	1.84e0	2.27e0	2.79e0	2.92e0	3.06e0		4.54e0	5.35e0	5.90e0	5.53e0
	1e–3	3.54e0	5.66e–1	7.41e–1	3.52e–1	3.86e–1	4.71e–1		4.48e0	2.80e0	3.19e0	3.70e0
	1e–4	2.16e0	6.11e–1	6.75e–1	6.67e–2	6.50e–2	6.62e–2		3.98e0	1.71e0	2.41e0	2.07e0
	1e–5	1.36e0	1.14e0	6.75e–1	4.34e–2	2.98e–2	2.29e–2		2.85e0	1.70e0	1.13e0	1.42e0
	1e–6	8.56e–1	2.58e0	6.75e–1	4.90e–2	3.54e–2	2.76e–2		2.89e0	1.25e0	1.10e0	7.39e–1
	0	–	–	6.75e–1	4.98e–2	3.64e–2	2.87e–2		2.89e0	8.03e–1	2.63e–1	8.89e–2

In addition to the midpoint rule, we also examined the method of Birk and Song [54], which also uses a Prony series approximation. The method presented in this work performs similarly or better for all α and N (see Table 2). This is consistent with our theoretical analysis in Fig. 3, which shows that the method presented here has better performance with N > 3 in nearly all scenarios. This improved performance stems from the increased error in the Prony approximation, causing errors to plateau with time step refinement earlier as predicted in Lemma 1 (see Table 2). The performance gain is more significant for larger α and larger N as predicted. In the Prony-based method presented in this work, the integral is done with Prony terms with frequencies that are comparable with the domain of the simulation, whereas in the method of Birk and Song approximates the complete range of frequencies by Gauss-Jacobi weights (which need not be optimal). As a result, the method of Birk and Song does not see as much improvement in accuracy with an increase in N.

6. FE approximation of fractional differential equations

While Section 5 demonstrates the efficacy of the Prony approximation for given known differentiable functions, it does not give an indication of how well the method performs for solving a fractional differential equation. To examine this, we replicated Example 1 of Gao et al. [67], i.e.

$$\begin{array}{l}{D}_t^{\alpha }u-\frac{{\partial }^{2}u}{\partial x^2}=f(x,t),\text{for}x\in [0,1],t\in [0,1],\hfill \\ f(x,t)={(x-1)}^2{e}^{-x}{t}^3\left[\Gamma (4+\alpha )\frac{{(x-1)}^2}{6}-\left(21-10x+x^2\right)t^{\alpha }\right]-4x^2{(x-1)}^2\left(14x^2-14x+3\right),\hfill \\ u(x,0)=x^4{(x-1)}^4,\hfill \\ u(0,t)=t^{3+\alpha },u(1,t)=0\hfill \end{array}$$ (50)

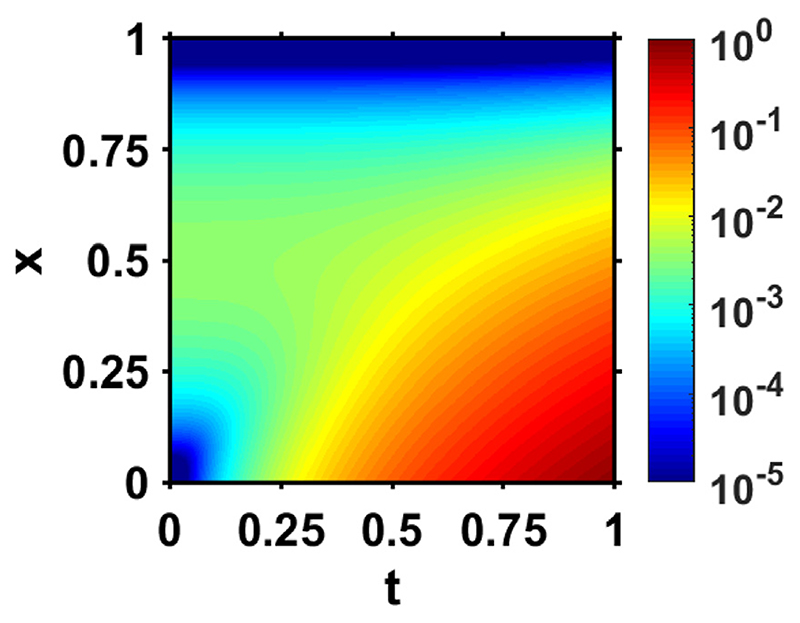
The problem above has the unique analytic solution given in Eq. (51) and shown in Fig. 6. The major feature is a cubically growing source term at x = 0, which decays to 0 at x = 1 with a smaller concave quartic polynomial spanning x ∈ [0, 1].

$$u\left(x,t\right)={\left(x-z\right)}^4\left(e^{-x}{t}^{3+\alpha }+x^4\right)$$ (51)

Fig. 6. The solution of the Prony series approximation of the fractional differential equation example Eq. (50) with three Prony terms, α = 1/2, Δ _x = 1/2500 and Δ_t = 1/2500.

Following Gao et al. [67], Eq. (50) is solved using linear finite elements in space. Further, to make results comparable, we use the same error norm, i.e.

$$E\left(h,{\Delta }_t\right)=\underset{x\in [0,1]t\in [0,1]}{\max }\underset{\text{analytic}}{\max }(x,t)\mid$$ (52)

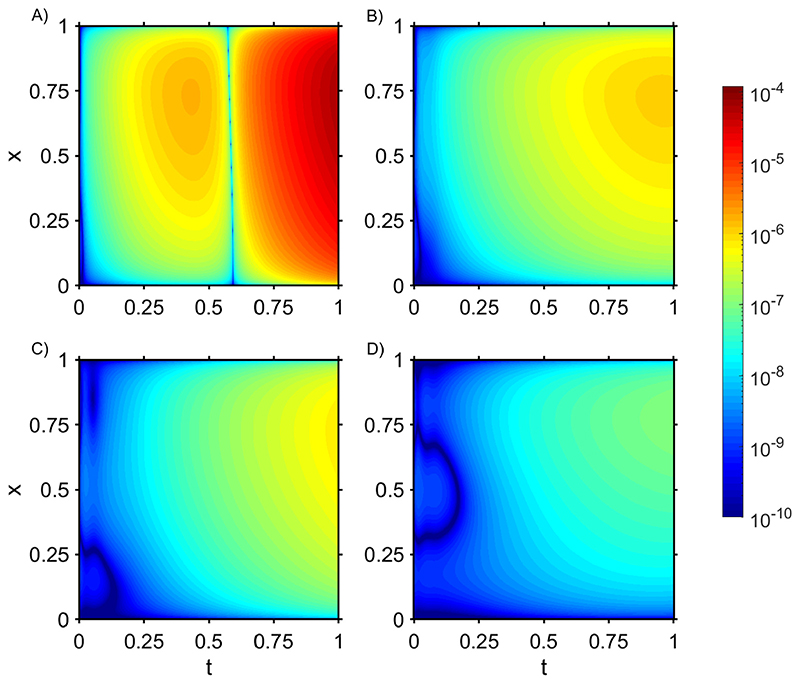
and replicate the results from Table 1 (temporal refinement) and Table 2 (spatial refinement) of Gao et al. [67] (see Tables 3 and 4, respectively). We also obtained Prony series parameters for the time interval of t ∈ [0, 100], by a factor of 100 times the time domain of the FE problem, to improve the error estimates (see Appendix B). Spatiotemporal errors are also shown in Fig. 7 for Δ_t = 1/2500, h = 1/2500 and a varying number of Prony terms. As expected, the error improves with an increasing number of Prony terms.

Table 3. Reproducing Table 1 from Gao et al. [67] using the Prony-based method Eq. (12) for refinement in time with a constant h = 5e–5.

			Gao et al. [67]			Prony approximation
						N = 3			N = 6			N = 9			N = 12
α	h	Δt	E(h, Δt)	log2		E(h, Δt)	log2		E(h, Δt)	log2		E(h, Δt)	log2		E(h, Δt)	log2
1/2	1/20 000	1/10	8.48e–4	1.41		2.13e–3	1.62		3.33e–3	1.26		3.73e–3	0.96		3.96e–3	0.74
		1/20	3.19e–4	1.44		6.94e–4	1.54		1.39e–3	1.73		1.91e–3	1.53		2.36e–3	1.25
		1/40	1.17e–4	1.46		2.39e–4	1.03		4.17e–4	1.94		6.64e–4	1.86		9.94e–4	1.73
		1/80	4.26e–5	1.47		1.17e–4	0.44		1.09e–4	2.03		1.83e–4	1.98		3.00e–4	1.92
		1/160	1.53e–5	1.48		8.60e–5	0.14		2.67e–5	2.21		4.64e–5	2.08		7.92e–5	1.99
		1/320	5.49e–6	*		7.82e–5	*		5.79e–6	*		1.10e–5	*		2.00e–5	*
2/3	1/20 000	1/10	1.91e–3	1.26		4.52e–3	1.52		6.78e–3	0.99		7.40e–3	0.72		7.88e–3	0.56
		1/20	7.96e–4	1.29		1.58e–3	1.65		3.42e–3	1.58		4.51e–3	1.31		5.33e–3	1.00
		1/40	3.25e–4	1.31		5.04e–4	1.31		1.14e–3	1.90		1.82e–3	1.78		2.67e–3	1.59
		1/80	1.31e–4	1.32		2.04e–4	0.69		3.07e–4	2.07		5.28e–4	2.01		8.85e–4	1.91
		1/160	5.26e–5	1.32		1.26e–4	0.24		7.28e–5	2.53		1.31e–4	2.32		2.35e–4	2.13
		1/320	2.10e–5	*		1.07e–4	*		1.26e–5	*		2.64e–5	*		5.36e–5	*

Table 4. Reproducing Table 2 from Gao et al. [67] using the Prony-based method Eq. (12) for refinement in space with a constant Δ_t = 5e–5.

			Gao et al. [67]			Prony approximation
						N = 3			N = 6			N = 9			N = 12
α	h	Δt	E(h, Δt)	log2		E(h, Δt)	log2		E(h, Δt)	log2		E(h, Δt)	log2		E(h, Δt)	log2
1/2	1/10	1 /20 000	1.50e–2	2.00		5.95e–3	2.06		6.02e–3	2.01		6.02e–3	2.01		6.01e–3	2.01
	1/20		3.75e–3	2.00		1.43e–3	2.22		1.50e–3	2.00		1.50e–3	2.00		1.50e–3	2.00
	1/40		9.38e–4	2.00		3.07e–4	3.24		3.75e–4	1.99		3.75e–4	1.99		3.74e–4	2.00
	1/80		2.35e–4	2.00		3.25e–5	-0.75		9.47e–5	1.95		9.44e–5	1.96		9.37e–5	2.00
	1/160		5.86e–5	*		5.47e–5	*		2.45e–5	*		2.43e–5	*		2.35e–5	*
2/3	1/10	1 /20 000	1.37e–2	1.99		5.67e–3	2.08		5.77e–3	2.00		5.77e–3	2.00		5.77e–3	2.00
	1/20		3.44e–3	2.00		1.35e–3	2.31		1.44e–3	1.98		1.44e–3	1.97		1.44e–3	1.98
	1/40		8.61e–4	2.00		2.71e–4	3.33		3.66e–4	1.92		3.67e–4	1.90		3.67e–4	1.91
	1/80		2.15e–4	2.00		2.68e–5	–1.58		9.67e–5	1.71		9.81e–5	1.66		9.75e–5	1.68
	1/160		5.37e–5	*		8.01e–5	*		2.96e–5	*		3.11e–5	*		3.05e–5	*

Fig. 7.

The absolute value of the residuals from the Prony series approximation of the fractional differential equation example Eq. (50) shown in color with α = 0.5, Δ _t = 1/2500, Δ _x = 1/2500, and (A) 3, (B) 6, (C) 9, or (D) 12 Prony terms in the approximation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Examining temporal refinement (with h = 5e-5), the Prony-based method presented here has better convergence at smaller Δ_t; however, the results from Gao et al. show smaller initial errors (see Table 3). This improved error for larger Δ_t comes with additional computational expense requiring storage of the solution for all time points. Additionally, we observe that the truncation error due to the Prony approximation results in small errors, meaning that temporal convergence is observed even for N = 3 up to Δ_t > 1/160. Further, at coarse time discretizations, the Prony-based method shows increasing errors for increasing N. While counter-intuitive, this is explained by Theorem 3. With increasing N, the discretization error is scaled by C(β, τ) which generally grows with N. This results in slow convergence until the approximation errors asymptotically converges to the error bounds. However, optimal convergence is still achieved with Δ_t refinement.

In the case with refinement in space (with Δ_t = 5e-5), both methods have similar convergence rates but the Prony-based approach has smaller initial errors due to better convergence with Δ_t (Table 4). Interestingly, but not unexpectedly, the number of Prony terms does not affect the convergence rate with refinement in space due to the fractional derivative being taken with respect to time only. However, additional Prony terms are still important, as an insufficient number of terms limits the lower bound of the errors, as seen for N = 3.

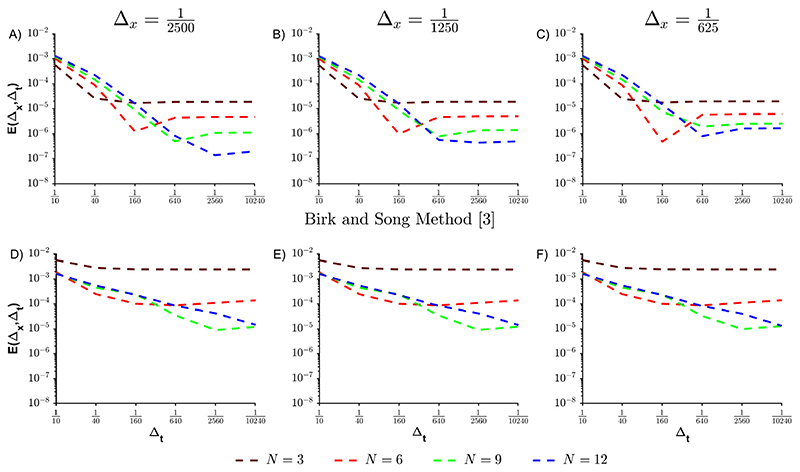
Fig. 8A, B and C shows spatiotemporal convergence for a range of time and discretizations. For fine spatial grids, we observe that errors approach the limit predicted by Lemma 2 and adhere to the results of Theorem 3. Coarsening spatial refinement, we can observe spatial errors shift the lower bound for higher values of N. Fig. 8D, E, and F presents a similar analysis utilizing the weights from Birk and Song [54]. Once again, the Prony-based method presented in this work performs better, where the convergence rates are improved and lower bounds for the Prony-based approximation are one (N = 9) to two (N = 3) orders of magnitude lower.

Fig. 8.

Convergence of the solution of the fractional diffusion equation with α = 0.3 using the Prony-based method Eq. (12) with refinement in time and (A) Δ _x = 1/2500, (B) 1/1250 and (C) 1/625 versus using the method of Birk and Song [54] with refinement in time and (D)Δ_x, = 1/2500, (E) 1/1250 and (F) 1/625.

7. Fractional approximation applied to biomechanics in the liver

7.1. Finite element model for the mechanical testing of livers

In order to investigate the efficacy of the proposed method for simulating fractional viscoelasticity in soft tissues, here we model an experiment executed by Tan et al. [89] on ex vivo bovine liver tissue. Briefly, cylindrical liver samples of height H = 2.7 mm and radius R = 10 mm were tested in a rheometer at a range of compressions, shear strains and frequencies. The behavior of the ex vivo liver sample can be effectively modeled using a viscoelastic exponential model [90] of the form

$$S=\delta \text{Dev}\left[D_t^{\alpha }{S}_v\right]+pJ{C}^{-1},S_v=\exp [b(II-3)]\mathit{\text{C}}.$$ (53)

The first term denotes the deviatoric component of the stress depending on the fractional derivative of S _v which follows a similar form to a typical hyperelastic material model of the right Cauchy-Green strain (see Section 3.1). The second component denotes the hydrostatic stress, depending on the pressure variable, p. Here Dev[A] = A − (A : C/3)C ⁻¹ denotes the deviatoric operator. The model can be fit to match the behavior of the ex vivo liver from [89] by three parameters: the linear scaling parameter 3, the nonlinear response parameter b, and the fractional derivative a. Following the parameterization process in [90], parameters α = 0.2, b = 1.5 and δ = 126.4Pa were observed to provide the best fit to the data (see Fig. 9).

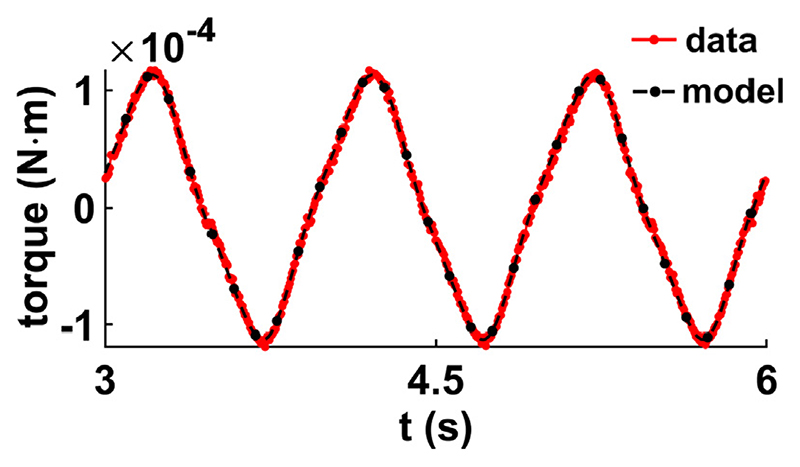
Fig. 9. Comparison of the model and experimental data from Tan et al. [89] at 10% compression and 25% shear strain, showing efficacy of the fractional viscoelastic model.

Here we focus on a single test case, where a sample was compressed by 10% and subsequently sheared at a frequency of 1 Hz around its axis with a shear strain amplitude of 25%. In this case, the reference domain is the cylindrical region ${\text{Ω}}_0=\left\{x\in {ℝ}^3\mid \sqrt{x_1^2+x_2^2}\le R,0\le x_3\le H\right\}$. The boundary Γ₀ is split into a bottom surface, top surface, and side surface ${\text{Γ}}_0={\text{Γ}}_0^b\cup {\text{Γ}}_0^t\cup {\text{Γ}}_0^w$, respectively. Assuming pure compression and shear, the deformation

$$u(t)=\left[\begin{array}{l}\frac{X_1}{\sqrt{\lambda (t)}}\cos \left(\psi (t)X_3\right)-\frac{X_2}{\sqrt{\lambda (t)}}\sin \left(\psi (t)X_3\right)-X_1\hfill \\ \frac{X_1}{\sqrt{\lambda (t)}}\sin \left(\psi (t)X_3\right)+\frac{X_2}{\sqrt{\lambda (t)}}\cos \left(\psi (t)X_3\right)-X_2\hfill \\ X_3(\lambda (t)-1)\hfill \end{array}\right],\psi (t)=\frac{\gamma {\lambda }^{3/2}(t)\sin (2\pi f\widehat{t})}{\sqrt{X_1^2+X_2^2}},$$ (54)

where the compression, λ, and the shear angle, ψ X ₃, were chosen to mimic the experimental conditions. Here compression took place over the first 1s, e.g. λ(t) = 1 - 0.1min(t, 1). Additionally, the angular displacement was applied after compression, t = max(0, t - 1), with an oscillatory frequency f = 1 Hz and a maximal shear strain of Xy. Torque readings were acquired during the shearing process.

This problem provides the ability to verify the finite element implementation outlined in Section 4. The analytical stresses could be computed using Eqs. (54) and (53). Applying Eq. (26), the predicted torque, τ, and normal traction, t_N, can be calculated by

$$\tau (t)={\displaystyle {\int }_{{\Gamma }^t}{e}_3}\cdot [x\times (\sigma \cdot n)]d\Gamma ,t_N(t)={\displaystyle {\int }_{{\Gamma }^t}{e}_3}\cdot [\sigma \cdot n]d\Gamma ,$$ (55)

where Γ^t is upper boundary of the physical domain Ω, n = e ₃ the outward normal, and e _k is the k^th-base vector for rectangular-Cartesian coordinates. These quantities were computed in MATLAB R2018b and in-house software Cheart. In MATLAB, a reference solution for the torque and normal traction were computed using the Grimwald- Letnikov method [65] (Eq. (5)) with a small time-step Δ_t =1e-5. A sweep over time-step size and the number of Prony terms was also applied to examine computing times and computational accuracy.

For the finite element implementation in Cheart, a curvilinear hexahedral mesh (with 9072 elements) was used to approximate τ ₀. The inf-sup stable ℚ² ℒ ℚ² ℒ ℚ¹ scheme was used to solve for u, v and p (with 77,425 quadratic nodes and 10,309 linear nodes). Eq. (54) was applied as boundaries conditions on ${\text{Γ}}_0^b$ and ${\text{Γ}}_0^t$ with no boundary conditions applied on ${\text{Γ}}_0^w$. Model torque and normal traction were exported along with the solution.

7.2. Accuracy and convergence

The accuracy and convergence of the Grimwald-Letnikov and Prony approximations are shown in Table 6, with the latter examined for N ∈ {3, 6, 9, 12}. When the number of Prony terms is N = 3, there is little improvement in the stress accuracy with temporal refinement reflecting inherent limitations in the approximation quality with so few terms. However, increasing to N = 6, we see the stagnation in convergence shift to Δ_t =1e-3. Further increases to N = 9 and N = 12 exhibit continued convergence even for the finest time step size, as predicted from Theorem 3

Table 6.

Accuracy and convergence of the Prony approximation with Δ_t and N applied to the ideal analytic solution. Percentage errors were measured relative to the GL with a refined time-step size of Δ_t = 1e-5. The percentage errors reported in the table correspond to the L ²(0, T) norm difference in (1,3)-Cauchy stress component normalized by the L ²(0, T) norm of the (1,3)-Cauchy stress component predicted by the reference solution.

Δt (s)	Prony error (%)
	N = 3	N = 6	N = 9	N = 12
1e–2	2.26e0	5.05e–1	6.51e–1	7.01e–1
5e–3	2.06e0	1.52e–1	2.50e–1	3.27e–1
1e–3	2.00e0	1.01e–1	1.30e–2	1.97e–2
5e–4	1.99e0	1.04e–1	8.79e–3	4.86e–3

The deformation and pressure from the FEM simulation can be observed in Fig. 10 (with N = 9 and Δ_t =1e-3). The simulated displacements were within 1e-6 of their analytic counterparts. The FEM simulation was further verified against the Grimwald-Letnikov implementation in MATLAB. The torque and normal force from both implementations are shown in Fig. 10, showing both forward model and the analytically computed behavior are consistent. Here, an error of 1e-3 was observed for the torque and 2e-4 was observed in the normal traction force.

Fig. 10. Illustration of the FEM solution of the liver model under deformation and shear.

(A) Sample mesh; u₂-component of the deformation at (B) compressed state (t = 1s) (C) compressed and sheared state (counter-clockwise, t = 1.25 s) (D) compressed and sheared state (clockwise, t = 1.75 s); Hydrostatic pressure at (E) compressed state (t = 1s) (F) compressed and sheared state (counter-clockwise, t = 1.25 s) (G) compressed and sheared state (clockwise, t = 1.75 s); The bottom panels show the force (H) and torque response (I) of a sample under compression and shear.

7.3. Computational cost

Table 5 presents the cost performance of the Prony approximation (Eq. (12)) compared to the Grimwald-Letnikov method (Eq. (5)) over the time domain t e [0, 2]. Time step Δ_t was chosen to vary between 1e-2 and 5e-5. For time steps larger than 1e-4, the Grimwald-Letnikov and Prony approach (for n = 3, 6, 9, 12 terms) is comparably fast. However, as Δ_t shrinks further, the Grimwald-Letnikov approach becomes increasingly expensive to compute $(𝒪\left(N_T^2\right)$ versus O(N_T)), with storage costs of O(N_T) vs O(N) (N is the number of Prony terms).

Table 5.

Comparison of solving speed for the Grunwald-Letnikov (GL) and Prony approximation methods (MATLAB implementation). The time results reported correspond to calculations for a single point on the outer edge of the cylinder. All methods were run in serial on a DELL PRECISION M4800 quad-core Intel(R) Core(TM) i7-4810MQ CPU @ 2.80 GHz.

	Δt (s)	GL (s)	Prony (s)
			N = 3	N = 6	N = 9	N = 12
α = 0.2	1e–2	0.029	0.054	0.044	0.051	0.047
	5e–3	0.052	0.086	0.093	0.097	0.094
	1e–3	0.202	0.406	0.429	0.442	0.561
	5e–4	0.492	0.818	0.871	0.890	0.933
	1e–4	5.728	4.676	4.169	4.348	4.530
	5e–5	17.706	8.392	8.369	8.859	9.088
	1e–5	770.569	38.051	37.888	39.370	41.773

Finally, we sought to examine the added computational cost of simulating the viscoelastic model compared to a classical hyperelastic model (see Table 7). Here the compute time of the viscoelastic model in Eq. (53) was compared with the hyperelastic model resulting if α = 0 in Eq. (53). It is notable that the computational time for both hyperelastic and viscoelastic material models does not increase proportionally with the number of time steps, likely due to a reduction in the required number of Newton-Raphson iterations per time step. Further, while the computational cost of the viscoelastic model is larger, this does not lead to a significant increase in computational time, with the differences observed being within ≈16%. Additionally, varying the number of Prony terms does not significantly impact the computational time, as seen in Table 7. While increasing N increases the computational work, the added cost for residual and matrix calculations is minor relative to the basic computational expense for simulating large deformation mechanical systems.

Table 7.

Comparison of compute times for a hyperelastic and fractional viscoelastic solutions in 𝒞heart with (left) changes in Δ_t (N = 9) and (right) changes in N (Δ_t = 1e-3). All times are reported in seconds and based on simulations run using 16 cores on a 3.8 GHz Titan A399 AMD RYZEN Threadripper 32 core system.

Model	Δt
	1e–2	1e–3	1e–4
Hyperelastic	170.43s	672.71s	2899.40s
Viscoelastic	190.24s	669.65s	3365.30s
Viscoelastic
N = 3	N = 6	N = 9	N = 12
655.69s	684.74s	669.65s	677.85s

8. Discussion

8.1. Computational cost

The biggest advantage of this Prony based method for approximating Caputo fractional derivatives Eq. (12) is computational efficiency. The historical integral required typically leads to an accumulating computational cost and demands smaller time steps by introducing nonlinearity into the system in the form of the strain history, thus becoming a heavy burden in viscoelastic simulations. The method developed herein allows a bounded storage cost for the strain history by an approximation using Prony series. The parameters can be precomputed from the a values and are independent of the strain history itself, which only leaves the cost of summing over the Prony series at each time step, which is small. The number of Prony terms necessary is dependent on the required accuracy of the approximation. However, for the example we have tested, six or fewer terms are sufficient for a wide range of cases. We find this cost to be only a fraction of the cost of the overall simulation, but can reduce the cost of simulating later time steps by several magnitudes. A well-bounded cost for the historical integral also removes a limitation on the full duration of the simulation, making it applicable to a wider range of applications.

8.2. Accuracy and convergence

The number of terms to use in the Prony-based method (Eq. (12)) is the decision between the truncation error, lower-bound for the approximation, and the loss in accuracy at larger Δ_t due to the C(β, τ) term. Increasing the number of Prony terms will lower the resulting truncation error at the cost of larger error terms. The Prony-based method has superior computational costs and better convergence rates when above the truncation error (Lemma 1) in comparison to classical non-recursive methods (Fig. 5). It is noted that in some cases, the discretization error introduced by the coefficient C(β, τ) (Lemma 2) can cause the solution to be initially less accurate at large Δ_t (Tables 3 and 4). However, this factor remains to be small and the savings in the computational cost are much more significant factor. Against competing methods such as the Birk and Song method [54], the Prony-based method has better convergence for six or more Prony terms or quadrature points and at higher α, and is competitive otherwise (Fig. 3) in examples tested.

8.3. Other methods

One common approach to improve the computational efficiency of traditional methods is by truncating the historical data. As noted by Diethelm et al. [61], it is typical that the weights in fractional derivative approximations exhibit some form of fading memory. For this reason, terms in the history are neglected to reduce computational costs. While it is true that terms that are further in the past will decay more, and in a way becomes small enough to be negligible, the length of the history also will increase. As such, truncation cannot be done negligently. For example, for α = 0.3 and if the method presented by Diethelm et al. [61] in Eq. (6) is truncated to 12 terms, the sum of the absolute value of the first 12 weights on the domain t ∈ [0, 1] is always 1.66353, independent of Δ_t (assuming Δ_t < 1/11). In comparison, the sum of the remaining weights are 0.16037, 0.248329, 0.292299, and 0.314331 for Δ_t = 1e-2, 1e-3, 1e-4 and 1e-5 respectively. The weight of the truncated history actually increases faster than the rate of decay due to fading memories. This effect is more significant for lower values of α, and thus care must be taken for how the truncation is done. The number of terms to keep needs to increase over time, depending on the problem.

Another similar method has been presented by Jiang et al. [91]. The major differences between the two methods are: (i) the approximation of the integral in the discretized case and (ii) the method of computing the parameters of the Prony series. For the approximation of the integral, this is largely a choice. However, we do note that in the method of Jiang et al. [91], holding the input function constant will still lead to a small but non-zero increase in the history terms when the solution should be zero on a stationary pure viscoelastic body. Jiang et al.’s method of computing the Prony series parameters [91] is designed with the goal of targeting a desired error of the approximation. However, the bounds on the number of terms are typically in the hundred for even modest desired error (e.g., 1e-4). The algorithm provided by Jiang et al. [92] can reduce this number, but it is still larger than the Prony-based method. In addition, the algorithm presented select from a list of frequencies based on Eigenvalues of the least squares system, which do not necessarily include the optimal frequencies. The method presented in this work (Eq. (12)) outputs a desired number of Prony terms, which is more desirable for ease of implementation and application.

8.4. Other applications

Although this method is described for the constitutive modeling of viscoelastic materials, fractional derivatives have a wide range of other applications. The most common application of fractional calculus in the literature is in regard to viscous fluid flows. The parallels to viscoelasticity are obvious and its use along with viscoelasticity to solve complex biomechanical systems is also very common. Also common is the application of acoustic waves traveling through viscous media. Another interesting and useful application is in edge detection in image analysis. The use of fractional derivatives can improve thin edge detection and tolerance to noises [93]. One other important application is in PID controllers, where the feedback loops are on fractional order. An interesting example of this is in path tracking of self driving vehicles [94]. Some other common and interesting applications are summarized by Dalir and Bashour [95].

8.5. Practical guidance

The cost of computing the parameters of the Prony series can be expensive and are best precomputed then imported at the time of use. However, since each of the parameters as a function of α is smooth, one method is to generate a set of Prony series parameters for well-spaced values of α, which can then be interpolated for more specific values of α. Indeed, we used this method for the MATLAB and C heart [57] implementations. The number of Prony terms to use is quite flexible. N < 4 is not recommended, but six is typically sufficient for most problems. Increasing N further will also not significantly negatively impact the solution and the computational cost of the problem. It should be noted that due to the necessity of approximating the derivative of the function to be uniform for each time interval, smaller time steps are necessary for the convergence of the solution in finite element simulations. One should choose step sizes such that the derivative is expected to be constant. Also, we have found that the velocity is unstable under second-order schemes in transient viscoelasticity simulations, but is stable under first-order schemes, as shown in Appendix A.

9. Conclusion

In this work we present a novel method for the finite element approximation of fractional nonlinear viscoelastic materials. Application of fractional viscoelastic models can present computational challenges, with many methods requiring prohibitive storage and computational expense. To overcome these issues, a new approximation to the Caputo fractional derivative is introduced, resulting in a fixed storage cost and making the computational time scale linearly with the number of time steps. Error estimates are derived for this approximation, demonstrating the efficacy of the approximation. Estimates are demonstrated to be accurate through numerical examples, where comparable or better convergence behaviors with refinement in time are observed compared to current state-of-the-art methods. The fractional approximation was then introduced into a nonlinear transient finite element mechanics implementation. The numerical problem was shown to be unconditionally stable for simple linear fractional viscoelasticity, and observed stable for nonlinear viscoleasticity through verified numerical examples. The computational cost of this fractional derivative implementation is comparable to the standard hyperelastic model, despite the historical integral (~16% more), and it was able to accurately approximate the solution in all examples considered. This method can significantly simplify the implementation of fractional viscoelastic models in general, and provides a pathway for applications of viscoelastic soft tissue models for the efficient simulation of complex biomechanical systems. While developed in the context of viscoelastic modeling, the Caputo approximation introduced has potential applications in solving the many other problems involving fractional derivatives.