Flexible proton density (PD) mapping using multi-contrast variable flip angle (VFA) data

Abstract

Quantitative proton density (PD) maps measure the amount of free water, which is important for non-invasive tissue characterization in pathology and across lifespan. PD mapping requires the estimation and subsequent removal of factors influencing the signal intensity other than PD. These factors include the T1, T2* relaxation effects, transmit field inhomogeneities, receiver coil sensitivity profile (RP) and the spatially invariant factor that is required to scale the data. While the transmit field can be reliably measured, the RP estimation is usually based on image post-processing techniques due to limitations of its measurement at magnetic fields higher than 1.5 T. The post-processing methods are based on unified bias-field/tissue segmentation, fitting the sensitivity profile from images obtained with different coils, or on the linear relationship between T1 and PD. The scaling factor is derived from the signal within a specific tissue compartment or reference object. However, these approaches for calculating the RP and scaling factor have limitations particularly in severe pathology or over a wide age range, restricting their application.

We propose a new approach for PD mapping based on a multi-contrast variable flip angle acquisition protocol and a data-driven estimation method for the RP correction and map scaling. By combining all the multi-contrast data acquired at different echo times, we are able to fully correct the MRI signal for T2* relaxation effects and to decrease the variance and the entropy of PD values within tissue class of the final map. The RP is determined from the corrected data applying a non-parametric bias estimation, and the scaling factor is based on the median intensity of an external calibration object. Finally, we compare the signal intensity and homogeneity of the multicontrast PD map with the well-established effective PD (PD*) mapping, for which the RP is based on concurrent bias field estimation and tissue classification, and the scaling factor is estimated from the mean white matter signal. The multi-contrast PD values homogeneity and accuracy within the cerebrospinal fluid (CSF) and deep brain structures are increased beyond that obtained using PD* maps. We demonstrate that the multi-contrast RP approach is insensitive to anatomical or a priori tissue information by applying it in a patient with extensive brain abnormalities and for whole body PD mapping in post-mortem foetal imaging.

1. Introduction

MR proton density (PD) mapping quantifies the amount of free water protons (Cercignani et al., 2018, chapter 4; Neeb et al., 2008), which is crucial for measuring water volume fraction employed in tissue composition models (Edwards et al., 2018; Mezer et al., 2013; Weiskopf et al., 2015). Although lipid, protein and nucleic acids in cellular structures contain a large pool of non-aqueous protons (30% of protons in white matter), those are MRI-invisible due to the short T2 (Cercignani et al., 2018, chapter 4). Currently there is an increasing interest in using quantitative PD mapping to accurately determine the tissue (patho-) physiological composition (Mezer et al., 2013). In fact, recent studies demonstrated that PD maps improve lesion detection in multiple sclerosis (Gracien et al., 2016), hepatic encephalopathy (Shah et al., 2008) and peritumoral oedema (Blystad et al., 2017).

Despite many clinical studies use fast spin-echo sequences to acquire high resolution PD-weighted images (Chong et al., 2016; Fuchs et al., 2014; Jones et al., 1992; Oikawa et al., 2002), in this work we will focus on quantitative PD, which is typically estimated from gradient-echo images. Quantitative PD mapping requires knowledge of relaxation effects (T1, T2*), inhomogeneities in the transmitted radio-frequency field (B1⁺), receiver sensitivity profile (RP) and a spatially invariant scaling factor that yields PD values between 0 and 100 p.u.(Cercignani et al., 2018, chapter 4). However, the approaches currently used for the estimation of both the RP and scaling factor can be inaccurate in case of severe pathology or anatomical changes (Volz et al., 2012a, 2012b). Here we propose to perform PD mapping based on a data-driven method for the estimation of RP inhomogeneity and map scaling. This approach can be applied on ex-vivo samples and in case of pronounced brain pathologies because it is independent from anatomical nor tissue information.

At high field strengths (≥3 T) the measurement of the RP is problematic due to the fact that the magnetic field measured in receive mode is not equal to the one measured in transmit mode, since the simple reciprocity of both fields cannot be assumed at field strengths higher than 1.5 T (Watanabe et al., 2011; Volz et al., 2012b). The RP estimation can be performed using different image processing techniques. Weiskopf and colleagues (Weiskopf et al., 2013) used the bias correction approach embedded in the SPM unified image segmentation (Ashburner and Friston, 2005; Weiskopf et al., 2011), which has been shown to provide reliable RP correction for the PD estimates in the brain (Volz et al., 2012a). However, where anatomical priors employed for tissue segmentation are either inaccurate (e.g. in case of severe anatomical abnormalities) or do not exist (PD mapping in the body), the RP estimation will be inaccurate or unavailable with this approach. Similarly Wang and colleagues computed the PD and RP sensitivity map (Wang et al., 2018) assuming that cortical grey and white matter have specific T1 values, and used the iso-intense images for each tissue class to fit the RP with a quadratic function. The method was successfully tested on healthy subjects and stroke patients, but it might fail for diseases such as tumours or lesions affecting the WM (Wang et al., 2018).

Another approach for determining the RP is by using the well-known linear relationship between T1 and PD values (Fatouros et al., 1991; Fatouros and Marmarou, 1999; Gelman et al., 1999; MacDonald et al., 1986), as proposed by Volz and colleagues (Volz et al., 2012b). This procedure has been shown to provide reliable PD values in healthy brains (Volz et al., 2012b; Abbas et al., 2014), but any areas with pathological changes to be masked, precluding the accurate estimation of RP sensitivity in the presence of undetected brain abnormalities or lesions (Volz et al., 2012b). Mezer and colleagues (Mezer et al., 2013) estimated the RP sensitivity by combining the multi-channel coil information, and applying the linear relationship between T1 and PD values over many small, overlapping volumes to regularise the fitting procedure (Volz et al., 2012b; Baudrexel et al., 2016). However his approach might be inaccurate when tumours or other diseases lead to major changes in local tissue properties (Baudrexel et al., 2016).

To avoid any dependency on the anatomy, the RP can be calculated using methods such as the nonparametric non-uniform intensity normalization (N3) algorithm (Sled et al., 1998). This method iteratively derives a slow varying multiplicative field that maximizes the frequency content of the tissue intensity distribution by using a B-spline approximation. Recently a variation of N3, called N4ITK, has been proposed in order to improve the robustness and speed of the B-spline interpolation (Tustison et al., 2010). Both N4ITK and N3 can be applied to any organ or pathological data since they do not require anatomical information, although the use of a binary mask can improve the accuracy of RP estimation over the volume of interest (Sled et al., 1998; Tustison et al., 2010). To the best of our knowledge those methods have not been used for the RP estimation in PD mapping studies.

The scaling factor is usually derived from the mean intensity of a specific tissue class such as the white matter (WM) (Weiskopf et al., 2011) or the cerebrospinal fluid (CSF) (Mezer et al., 2013, 2016; Volz et al., 2012b). If the scaling is based on the WM, the mean intensity is assumed to be equal to 69 p.u. (Weiskopf et al., 2013), in the case that the CSF is used for the scaling, the mean signal is set to 100 p.u. (Volz et al., 2012b). These values are a reasonable approximation in healthy brains, but they are likely to introduce error when WM or CSF signal means are hard to estimate or altered by pathological or developmental processes, limiting the applicability of these PD mapping methods. Moreover using the CSF as a scaling factor might be difficult with short TR acquisitions due to the low signal amplitudes.

Here we propose a PD mapping approach based on a well-established multi-echo FLASH (fast low angle shot) dataset acquired with a multi-contrast variable flip angle (VFA) protocol for multi-parameter mapping (MPM) (Weiskopf et al., 2013). Aiming to utilise all available data, we employed all the contrasts for the PD map estimation including the magnetization transfer (MT) weighted scan in the MPM protocol. After correcting the multi-echo images for relaxation effects, we determined the RP using a non-parametric algorithm based on N4ITK (Tustison et al., 2010). The effectiveness of this approach was evaluated using data with different receiver coils and comparing the PD values obtained. To derive a scaling factor independent from any tissue model, we used the signal of an external calibration object, i.e., a plastic tube filled with water doped with Gadolinium. The new PD mapping approach was applied both on healthy brain data where it could be evaluated against existing methods and on a post-mortem foetal dataset to demonstrate its wide applicability. Finally, we assessed the maps values and homogeneity by analysing the different factors that contribute to the PD values distribution comparing the multi-contrast PD approach with the well-established PD mapping (Weiskopf et al., 2013). This was performed within brain tissue classes, using voxel-wise comparison and computing signal entropy and variance as measures for the map homogeneity.

2. Method

2.1. Data acquisition

10 healthy subjects (32 ±5years) were scanned using a 3 T Prisma (Siemens, Erlangen, Germany) with a 64 channel radio-frequency (RF) receiver coil and a two channel transmit body coil. Written informed consent was obtained prior to study according to the approval requirements of the local Ethics committee.

A plastic tube (size 10 cm × 1.5 cm) filled with a solution of 0.09 mg/ml Gadolinium was placed on the right temple of the subjects’ head for calibration purposes (Sasaki et al., 2005). The Gadolinium employed in this study was the Dotarem® (gadoterate meglumine) manufactured by Guerbet’s and was introduced to reduce the water T1, increasing signal levels in the T1w images while keeping almost unaltered T2* values, the solution concentration was chosen based on Sasaki and colleagues (Sasaki et al., 2005).

Three 3D multi-echo FLASH datasets with predominant PD-, T1-and MT-weighting (respectively PDw, T1w, MTw) (Weiskopf et al., 2013) were acquired with spatial resolution of 1 mm³, using the following repetition time (TR) and flip angle (α) (PDw: TR/α = 24.5 ms/6°; T1w: TR/α = 24.5 ms/21°). PDw and T1w images were acquired at eight equidistant echo times (TE) between 2.3 and 18.7 ms, while MTw was acquired at six equidistant TE between 2.3 and 14.04 ms. The field of view (FOV) was 256 x 240 x 176 mm and the matrix size 256 x 240 x 176. To correct for non-linearity in the RF transmit chain, RF spoiling was performed during the acquisition. RF spoiling was performed by transmitting pulses with different phases in order to linearly increase the phase differences between subsequent pulses by a phase increment of 137°, as previously optimised by Lutti and Weiskopf to obtain stable T1 values in grey and white matter (Lutti and Weiskopf, 2013). Parallel imaging (Roemer and Edelstein, 1989) was used along the phase-encoding (PE) direction (acceleration factor 2 GRAPPA reconstruction (Griswold et al., 2002)), 6/8 partial Fourier was used in the partition direction. The acquisition time for each weighted set was approximately 5.2 min.

3D echo-planar imaging (EPI) spin-echo (SE) and stimulated echo (STE) images were used to calculate maps of the transmit field B1⁺ (Lutti et al., 2012, 2010) and correct for the effect of RF transmit inhomogeneities on the quantitative maps (Helms and Dechent, 2009; Weiskopf et al., 2013). The image resolution was 4 mm isotropic, matrix size 64 × 48 × 48 and FOV = 256 × 192 × 192 mm along readout × PE × partition direction, parallel imaging using GRAPPA factor 2 × 2 in PE and partition direction, TR = 250 ms, acquisition time 1.3 min. The flip angles of the SE/STE refocusing pulses were decreased from 230°/115°-130°/65° and in steps of 10°/5°.

To correct the RF transmit field maps for geometric distortion and off-resonance effects, a B0 map was acquired using a two-dimensional double-echo FLASH sequence (Lutti et al., 2012, 2010). The acquisition parameters were: 64 axial slices, slice thickness = 2 mm, inter-slice gap = 1mm, matrix = 64 x 64, FOV = 192 x 192 mm, α = 90°, TR = 1020 ms, TE1/TE2 = 10/12.46 ms, acquisition time ~2 min.

2.2. Estimation of R1 and MT maps

Quantitative R1 and MT maps were calculated as described in (Weiskopf et al., 2013) using an in-house code running under SPM12 (http://www.fil.ion.ucl.ac.uk/spm) and Matlab2015b (Mathworks, Sherborn, MA, USA). In brief, the magnitude images of each weighted set were first co-registered to remove potential motion effects, and then averaged across echoes to increase the signal-to-noise ratio (SNR) (Helms and Dechent, 2009). The three mean images were employed to estimate the apparent R1 and the semi-quantitative MT saturation using an approximation of the Ernst equations for dual flip angle measurements using the FLASH signal (Helms et al., 2008b, 2008a; Helms and Dechent, 2009; Weiskopf et al., 2013). The quantitative R1 maps were computed from the apparent R1 by correcting the flip angle for inhomogeneities in the local RF transmit field using B1⁺ maps and imperfect RF spoiling (Helms et al., 2008a, 2008b; Preibisch and Deichmann, 2009). The semi-quantitative MT saturation was corrected for R1 dependency and for residual RF inhomogeneities using a semi-empirical approach described by Weiskopf and colleagues (Weiskopf et al., 2013).

2.3. Estimation of PD* and standard PD maps

The PD* maps were calculated as described in (Helms et al., 2008a; Weiskopf et al., 2013) using the T1w data averaged over all echoes, the R1 and B1⁺ maps. The RP correction was based on the UNICORT method which determines the RP using the bias correction approach implemented in the segmentation step of SPM12 (Ashburner and Friston, 2005; Weiskopf et al., 2011). Finally the maps were scaled by setting the mean WM signal equal to 69 p.u. (Weiskopf et al., 2013). As the data were not corrected for R2* signal decay, the final parameter map was called PD*.

Additionally, we removed the R2* dependency by extracting the TE = 0 signal for the T1w data (as described below for the multi-contrast approach) and using that instead of the T1w data averaged over all echoes in the aforementioned approach. The final map was called standard PD.

2.4. Estimation of multi-contrast PD maps

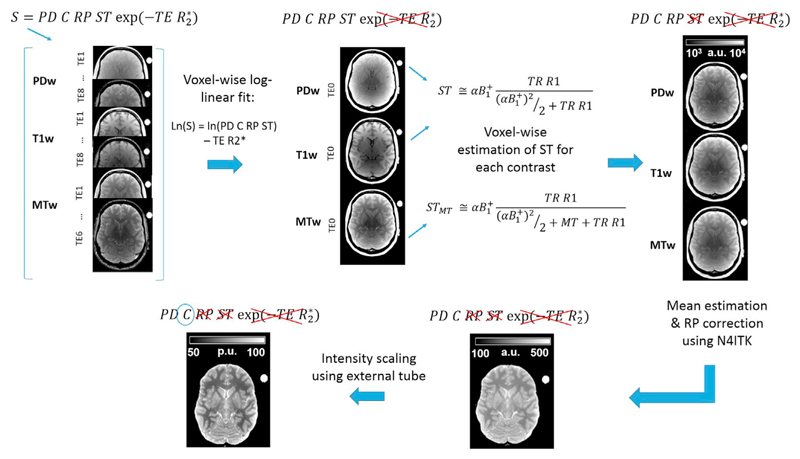
Fig. 1 shows the workflow for the estimation of the multi-contrast PD maps.

Fig. 1.

Workflow and signal equation for multi-contrast PD estimation. The signal (S) of FLASH multi-echo PDw, T1w, and MTw images was combined and corrected for R2* relaxation. The resulting PDw and T1w images were corrected for R1 and inhomogeneity in the transmit magnetic field (B1⁺) by computing voxel-wise the steady state (ST) term. MTw images were corrected for ST_MT computed using the magnetisation saturation (MT) term. This led to three maps representing the signal amplitude common to the three FLASH datasets. The mean of the three images was corrected for the receiver profile (RP) using N4ITK, and scaled using the median signal of the external calibration object (C).

The estimation of the multi-contrast PD was based on the signal equation of the FLASH sequence used to acquire the data (Brown et al., 2014; Volz et al., 2012b):

$$S=S_{TE0}exp\left(-TE{R}_2^{\ast }\right)=PDCRPSTexp\left(-TE{R}_2^{\ast }\right)$$ (1)

Where PD is the proton density to be estimated, RP is the receiver profile sensitivity, C is a spatially invariant scaling constant and TE is the echo time of the acquired signal. ST is the steady state term dependent on T1 (=1/R1) relaxation and nominal flip angle (α) corrected for transmit inhomogeneities (B1⁺). Under the approximation for small α and TR R1≪1, ST can be written as follows (Helms et al., 2008a):

$$ST\cong \alpha B_1^{+}\frac{TRR1}{{\left(\alpha B_1^{+}\right)}^2/2+TRR1}$$ (2)

In case a magnetisation saturation pulse is present during the signal acquisition, the ST_MT term is given by (Helms et al., 2008b):

$$S{T}_{MT}\cong \alpha B_1^{+}\frac{TRR1}{{\left(\alpha B_1^{+}\right)}^2/2+MT+TRR1}$$ (3)

where MT is the magnetisation transfer saturation.

To remove the R2* relaxation component we computed voxel-wise the linear dependence of the log of the signal intensities for each echo time, using the model described in Eq (4):

$$\begin{array}{l}\ln \left(\mathit{S}\right)=\ln \left(S_{TE0}\right)-TE{R}_2^{\ast }+\epsilon =\mathit{X}\beta +\epsilon \hfill \\ \mathit{S}=\left[\begin{array}{ccc}{S}_{MT\left(TE1\right)}\left(v{x}_1\right)& \cdots & S_{MT\left(TE1\right)}\left(v{x}_n\right)\\ ⋮& \ddots & ⋮\\ S_{MT\left(TE6\right)}\left(v{x}_1\right)& \cdots & S_{MT\left(TE6\right)}\left(v{x}_n\right)\\ S_{PD\left(TE1\right)}\left(v{x}_1\right)& \cdots & S_{PD\left(TE1\right)}\left(v{x}_n\right)\\ ⋮& \ddots & ⋮\\ S_{PD\left(TE8\right)}\left(v{x}_1\right)& \cdots & S_{PD\left(TE8\right)}\left(v{x}_n\right)\\ S_{T1\left(TE1\right)}\left(v{x}_1\right)& \cdots & S_{T1\left(TE1\right)}\left(v{x}_n\right)\\ ⋮& \ddots & ⋮\\ S_{T1\left(TE8\right)}\left(v{x}_1\right)& \cdots & S_{T1\left(TE8\right)}\left(v{x}_n\right)\end{array}\right]\text{X}=\left[\begin{array}{cccc}1& 0& 0& -T{E}_1\\ ⋮& ⋮& ⋮& ⋮\\ 1& 0& 0& -T{E}_6\\ 0& 1& 0& -T{E}_1\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& ⋮& -T{E}_8\\ 0& 0& 1& -T{E}_1\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& 1& -T{W}_8\end{array}\right]\beta \hfill \\ =\left[\begin{array}{ccc}\ln \left(S_{MT\left(TE0\right)}\left(v{x}_1\right)\right)& \dots & \ln \left(S_{MT\left(TE0\right)}\left(v{x}_n\right)\right)\\ \ln \left(S_{PD\left(TE0\right)}\left(v{x}_1\right)\right)& \dots & \ln \left(S_{PD\left(TE0\right)}\left(v{x}_n\right)\right)\\ \ln \left(S_{T1\left(TE0\right)}\left(v{x}_1\right)\right)& \dots & \ln \left(S_{T1\left(TE0\right)}\left(v{x}_n\right)\right)\\ R_2^{\ast }\left(v{x}_1\right)& \dots & R_2^{\ast }\left(v{x}_n\right)\end{array}\right]\hfill \end{array}$$ (4)

Where S is the matrix concatenating the signal of the co-registered MTw, PDw and T1w dataset acquired at different echo times for every voxel (vx₁, vx₂ …, vx_n), X is the design matrix whose elements are the contrast-specific regressors and the echo time dependency, β contains the contrast-specific estimates of the log of the signal intensities at TE = 0 (S_TE0) and the R2* estimate, and ε represents the model residual. This model assumed a mono-exponential signal decay with TE and that R2* was common between the different image contrasts. The fitting procedure was performed in Matlab2015 as a robust fit with a bisquare weighting function (robustfit.m), using a similar approach to that employed by Weiskopf and colleagues (Weiskopf et al., 2014a,b).

Then, the S_TE0 image of the T1w and PDw contrasts was divided voxel-wise by the ST term calculated according to Eq. (2), using the R1 and B1⁺ maps, while the S_TE0 image of the MTw contrast was divided by the ST_MT term computed according to Eq. (3) using the R1, MT and B1⁺ maps. The R1 and MT maps were estimated as described previously in section.

2.5. Estimation of R1 and MT maps

After this step we obtained three images, one for each contrast, corresponding to the product of PD, RP and C terms (see Eq. (1) and Fig. 1) and therefore differing only in stochastic noise in case of an accurate fit to the data. Since the C and RP terms are common to the three images derived from each contrast set, we averaged those ones to increase the stability of the final PD values.

The RP was determined from the mean image applying the non-parametric bias estimation provided by the N4ITK approach available in the advanced normalisation tools (ANTs, http://stnava.github.io/ANTs/) (Tustison et al., 2010). N4ITK was applied with default settings on the skull-stripped images iteratively eight times. The number of N4ITK iterations was optimised using a root mean square (RMS) analysis described in section Assessment and optimisation of RP correction using N4ITK. Skull removal was performed to improve the RP estimation accuracy by applying the Brain Extraction Tool (Smith, 2002) from FMRIB Software Library v5.0 (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) on the MT images using default settings.

In order to obtain PD values between 0 and 100 p.u., the RP corrected map was divided by the median intensity of the plastic tube filled with Gd solution and multiplied by 100, under the assumption that the solution had PD values of 100 p.u. The reproducibility of the map scaling with respect to the position of external calibration was tested in a separate experiment reported in Appendix A.

2.6. Assessment and optimisation of RP correction using N4ITK

Aiming at optimising the number of iterations required for the RP removal, and the robustness of this process across different experimental set-ups, we scanned three healthy controls using a 64 and 20 channel head receiver coil. Owing to the higher density of the 64 channel coil this has an RP with a higher spatial frequency and therefore is more challenging for bias field correction methods. We applied a different number, from one to ten, of N4ITK iterations to estimate the RP correction and then generated multi-contrast PD maps. Firstly, we assessed the stability of the RP removal for each coil by estimating voxel-wise the difference between PD maps computed with n and n+1 iterations of N4ITK (where n = 1,2, …9) for the RP correction for each subject. Secondly, we calculated the root mean square (RMS) value within voxels belonging to the brain mask for each difference map. Finally, we quantified the voxel-wise PD value changes across the two receiver coils for each number of N4ITK iterations and we estimated the RMS map within voxels belonging to the brain mask.

For the following analyses we used the data acquired with the 64channel receiver coil and n = 8 iterations.

2.7. Estimation of one-contrast PD map

In order to test the applicability of our method in the absence of MTw contrast, we computed the PD map for one subject using only the PDw images, the R1 and B1⁺ maps. We applied the model described by Eq. (1), estimating the S_TE0 for the PDw dataset, and we removed the ST term computed using Eq. (2). The final image was skull-stripped, corrected for the RP by applying N4ITK iteratively eight times with default settings and scaled using the same procedure described in the section Estimation of multi-contrast PD maps.

2.8. Homogeneity of PD maps

Then we assessed the intensity homogeneity of the multi-contrast PD, PD* and standard PD maps by using the Shannon’s entropy as a measure of the intensity distribution scattering, and the variance as an estimator of the distribution spread (Mangin, 2000). Entropy and variance were estimated within cerebrospinal fluid (CSF), white matter (WM) and grey matter (GM) separately. Subject-specific tissue masks were derived from tissue probability maps (voxel with GM or WM probability >0.9) estimated from the MT maps using the SPM12 segmentation approach (Ashburner and Friston, 2005). The Wilcoxon test was applied to compare entropy and variance across PD estimation methods within tissue class, statistical significance was set to p < 0.05.

To evaluate the effect of using three contrasts on the signal variability, we computed the variance and entropy within each tissue class for the PD*, multi-contrast and one-contrast PD maps.

2.9. Voxel-wise statistical comparison of PD values

To identify systematic PD value differences and determine their spatial distribution we compared voxel-wise the multi-contrast PD with PD*, and the multi-contrast PD with the standard PD in the brain. The maps were spatially registered to standard MNI space using subject-specific diffeomorphic estimates (Ashburner, 2007), derived for the MT images, without scaling by the Jacobian determinants. A combined tissue probability weighting and Gaussian smoothing procedure (Draganski et al., 2011) was used with a 6 mm FWHM isotropic smoothing kernel. Statistical comparison was performed applying a paired t-test with threshold at p < 0.05 after family-wise error (FWE) correction.

2.10. In vivo experiment: focal epilepsy and porencephalic ventricle dilation

To demonstrate the applicability of the new multi-contrast PD mapping approach, we scanned an 11-year old patient with focal epileptic seizures and a porencephalic dilation of the right ventricle. Written informed consent was obtained prior to study according to the approval requirements of the UK National Research Ethics Service.

The MRI acquisition protocol and the estimation of PD* and multi-contrast PD maps were identical to the experiment performed on the healthy controls.

2.11. Post-mortem experiment: post-mortem foetus

Post-mortem MRI (PM-MRI) as part of minimally invasive autopsy is an increasingly important clinical application of MRI (Arthurs et al., 2015a, 2015b; Griffiths et al., 2005; Norman et al., 2016; Papadopoulou et al., 2016; Shelmerdine et al., 2017) where quantitative mapping could be useful e.g. in the determination of autolysis. To demonstrate the general applicability of the new multi-contrast PD mapping approach, we scanned a 24 week gestation foetus who underwent PM-MRI at our centre. Written informed consent was obtained for clinical pre-autopsy PM-MRI as part of our institution’s clinical post-mortem assessment. The foetus was stored in a mortuary at 4 °C, for PM-MR it was positioned in the 64 channel head coil in the supine position, and wrapped in insulating material to aid temperature stability.

The entire foetus was scanned with similar settings and acquisition protocol described above for the healthy subjects, except for the use of Hanning filter set to medium and no partial Fourier sampling. These two protocol changes were introduced for decreasing Gibbs ringing artefacts due to high intensity changes in neighbouring tissues.

The PD map estimation was performed over the whole foetus body applying the previously described processing steps with the exception of the skull-stripping for the RP correction. The RP estimation was based on the N4ITK algorithm applied only on voxel belonging to the head, body and plastic tube.

We could not compute the PD* map due to the absence of either brain or whole body anatomical information about tissue distribution required by the SPM RP estimation.

3. Results

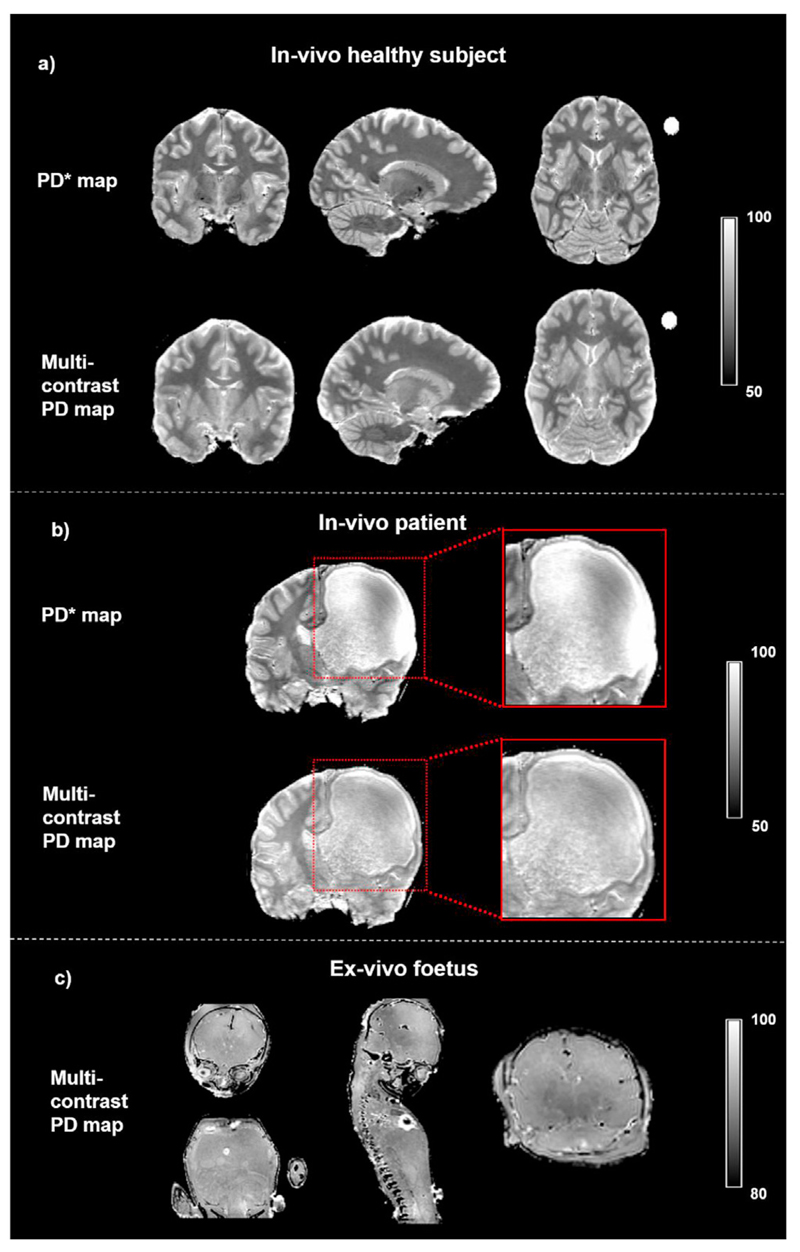
On visual inspection the multi-contrast approach provided homogeneous PD maps over the whole brain of the healthy volunteers and focal epilepsy patient, and over the whole body of the post-mortem foetus, as shown in Fig. 2.

Fig. 2. Examples of effective proton density (PD*) map, and multi-contrast PD map.

(a) Maps computed for a healthy subject. (b) Maps computed for a paediatric patient with a porencephalic dilation of right frontal lateral ventricle. The magnification shows the grey and white matter regions where the PD* map fails to provide homogenous RP correction resulting in blurred tissue contrast, while the same regions are correctly delineated on the multi-contrast PD. (c) Whole body example of multi-contrast PD map obtained from a post-mortem unfixed foetus.

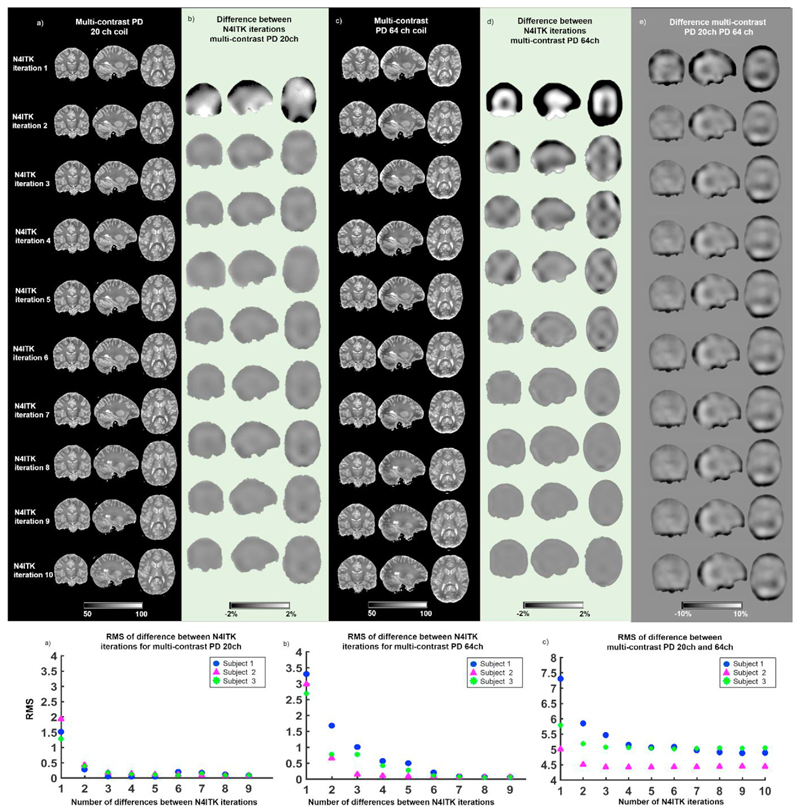
3.1. Effects of receiver coil and number of N4ITK iterations

To evaluate the stability of the PD maps estimated with RP correction obtained using different numbers of N4ITK iterations, we quantified the RMS PD value changes with successive iterations. This was performed for the datasets acquired with the 20 and 64 channel receiver coils. We observed that after the eight N4ITK iteration the PD changes between successive number of iterations were smaller than 2% (see Fig. 3b), and there was minimal RMS variation for the multi-contrast maps estimated with the 20 channel coil data (see Fig. 3f). For the multi-contrast maps obtained with the 64 channel coil data, we found PD variations smaller than 2% between iteration and negligible RMS change after the eight iteration (see Fig. 3d,g).

Fig. 3. Multi-contrast PD maps estimated using data acquired with the 20 and 64 channel (ch) receiver coils using different numbers of N4ITK iterations for RP removal.

(a) Example of multi-contrast PD map estimated using data acquired with 20 channel coil. Each row displays the PD map corrected for RP sensitivity using a different number of N4ITK consecutive iterations (one to ten). (b) PD changes between different numbers of N4ITK iterations for the 20 channel dataset. Each row displays the spatial changes between consecutive numbers of iterations. (c) Example of multi-contrast PD map estimated using data acquired with 64 channel coil and different number of N4ITK iterations. (d) PD changes between different numbers of consecutive N4ITK iterations for the 64 channel dataset. (e) Difference between the multi-contrast PD maps acquired with the 20 and 64 channel coils for each number of N4ITK iterations used for the RP removal. (f) Root mean square (RMS) of the PD changes between different numbers of consecutive N4ITK iterations for the 20 channel coil data in three healthy subjects. (g) RMS of the PD changes between different numbers of consecutive N4ITK iterations for the 64 channel coil data of three healthy subjects. (h) RMS of the PD changes between the 20 channel coil dataset and the 64 channel coil one for each iteration of N4ITK in three healthy subjects.

Aiming at assessing the effectiveness of RP removal by comparing data acquired with different bias fields, we calculated voxel-wise the difference between the multi-contrast PD maps obtained with the 20 channel coil and the 64 channel coil for each N4ITK iteration. We found that the differences between maps were greatest in the occipital and frontal regions (see Fig. 3e), but were stable after the forth iteration as measured by the RMS displayed on Fig. 3h and by visual inspection of the spatial data in Fig. 3e.

The results of the following analyses were based on data acquired with the 64channel receiver coil and n = 8 iterations.

3.2. Homogeneity of PD maps

The signal entropy and variance estimated for each tissue class (WM, GM, and CSF) were used as summary measures of the PD map histograms. To disentangle the effects of R2* signal decay, RP correction method and number of contrasts employed in the PD map estimation on the homogeneity of the intensity distribution, we performed comparison of variance and entropy between the PD* and multi-contrast PD maps, multi-contrast PD and standard PD maps, multi-contrast PD and one-contrast PD ones.

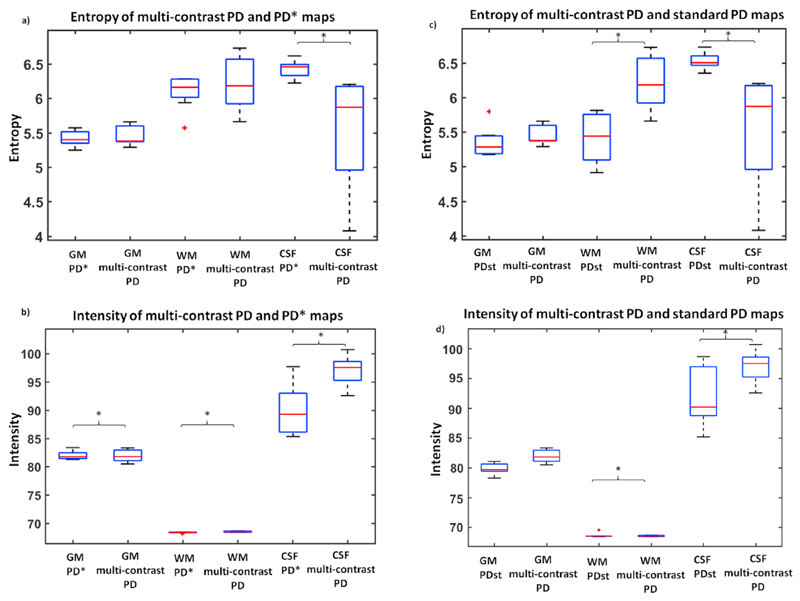
3.3. Comparison of multi-contrast PD vs PD* maps

Significantly higher entropy was found in PD* compared to multi-contrast PD within the CSF, while similar values were observed across the two methods in WM and GM, as reported on Table 1 and Fig. 4a. Significantly higher variance was found in multi-contrast PD compared to PD* maps in WM and GM, while significant lower values were observed in CSF for the multi-contrast PD maps, as reported on Table 1 and Fig. 4b.

Table 1.

Tissue-specific entropy and variance estimated for the PD* maps and multi-contrast PD in subjects native space within the cerebrospinal fluid (CSF), grey matter (GM) and white matter (WM). The measures were statistically compared using the Wilcoxon ranked test.

Tissue class	Entropy			Variance
	PD*	Multi-contrast PD	Wilcoxon test p-value	PD*	Multi-contrast PD	Wilcoxon test p-value
	Entropy± SD	Entropy± SD		Variance ±SD	Variance ±SD
CSF	6.45 ± 0.13	5.70 ± 0.90	0.007	385 ± 151	209.72 ± 77.5	0.009
GM	5.45 ± 0.14	5.46 ± 0.18	0.367	18.2 ± 1.94	38.68 ± 8.64	0.008
WM	6.01 ± 0.4	5.96 ± 0.49	0.242	4.28 ± 0.25	11.24 ± 1.20	0.008

Fig. 4. Assessment of intensity uniformity for the effective proton density (PD*), multi-contrast PD and standard PD (PDst) maps within grey matter (GM), white matter (WM), and cerebrospinal fluid (CSF) for in-vivo data.

(a) Entropy estimated within GM, WM and CSF for the multi-contrast and PD and PD* maps. Significantly (*) higher entropy was found in PD* compared to multi-contrast PD over CSF. (b) Multi-contrast and PD and PD* median and variance estimated within GM, WM and CSF. Significantly (*) higher variance was found in multi-contrast PD compared to PD* over GM, WM and CSF. (c) Entropy estimated within GM, WM and CSF for the multi-contrast PD and standard PD maps. Significantly (*) higher entropy was found in standard PD compared to multi-contrast PD over CSF, and in the multi-contrast PD over WM. (d) Multi-contrast and PD and standard PD median and variance estimated within GM, WM and CSF. Significantly (*) higher variance was found in multicontrast PD compared to standard PD over WM and CSF.

3.4. Comparison of multi-contrast PD vs standard PD maps

To remove the R2* effect on the intensity homogeneity, we compared the entropy and variance of the multi-contrast PD with the ones computed for standard PD maps. Significant lower entropy and variance were observed in the multi-contrast PD when compared to the standard PD within the CSF, as reported on Table 2 and Fig. 4c and d. Significant lower entropy and variance were found for the standard PD compared to the multi-contrast PD within the WM, as reported on Table 2 and Fig. 4c and d.

Table 2.

Tissue-specific entropy and variance estimated for the standard PD (PDst) and multi-contrast PD maps in subjects’ native space within the cerebrospinal fluid (CSF), grey matter (GM) and white matter (WM). The measures were statistically compared using the Wilcoxon ranked test.

Tissue class	Entropy			Variance
	PDst	Multi-contrast PD	Wilcoxon test p-value	PDst	Multi-contrast PD	Wilcoxon test p-value
	Entropy± SD	Entropy± SD		Variance ±SD	Variance ±SD
CSF	6.53 ± 0.19	5.70 ± 0.90	0.007	309 ± 113	209.72 ± 77.5	0.009
GM	5.35 ± 0.22	5.46 ± 0.18	0.1	39.1 ± 11.7	38.68 ± 8.64	0.2
WM	5.37 ± 0.43	5.96 ± 0.49	0.004	4.59 ± 3.1	11.24 ± 1.20	0.007

3.5. Effect of the number of weighted contrast datasets used to calculate PD

To assess the effect on the map homogeneity of the number of contrasts employed in the PD estimation, we estimated the tissue class specific variance and entropy for the PD*, one-contrast, and multi-contrast PD maps. We found lower entropy and variance for the multi-contrast PD with respect to the one-contrast map for all tissue classes in a single subject analysis, as shown on Table 3 and Fig. 6b in the supplementary material. Moreover we observed lower entropy for all tissue classes and lower variance within the CSF for the multi-contrast PD with respect to the PD* maps.

Table 3.

Tissue-specific entropy and variance estimated for the PD* maps, and one-contrast and multi-contrast PD within the cerebrospinal fluid (CSF), grey matter (GM) and white matter (WM) for a single healthy control.

Tissue class	Entropy			Variance
	PD*	One-contrast PD	Multi-contrast PD	PD*	One-contrast PD	Multi-contrast PD
CSF	6.47	6.22	6.17	440	320	300
GM	5.57	5.68	5.37	20	70	50
WM	6.28	6.16	6.1	4	14	10

3.6. Voxel-wise statistical comparison of PD values

The voxel-wise comparison, performed on GM and WM separately, showed regional intensity differences between the multi-contrast PD and PD* maps, and between the multi-contrast PD and standard PD ones.

3.7. Multi-contrast PD vs PD* maps

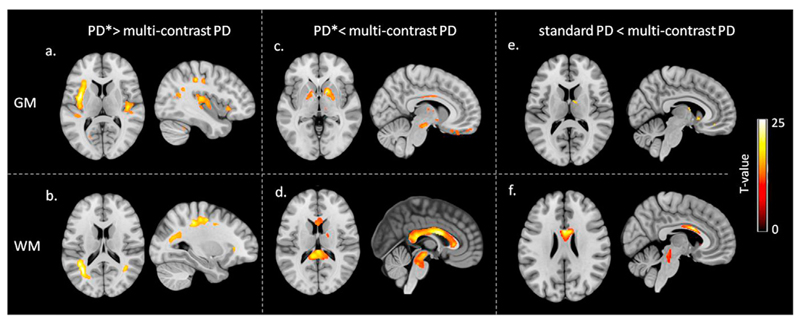
Significantly higher PD values were found in the insula and along visual and sensory-motor tracks for PD* compared to multi-contrast PD maps (see Fig. 5a and b and Table 4). Higher values were found in pallidum, brain stem and corpus callosum for multi-contrast PD maps compared to PD* (see Fig. 5c and d and Table 4).

Fig. 5.

Voxel-wise comparison of effective in-vivo proton density (PD*) with multicontrast PD maps, and between standard PD and multi-contrast PD maps in grey matter (GM) and white matter (WM). The statistical maps of paired t-test at statistical threshold of p_FWE < 0.05 are displayed on T1w image in standard MNI space. (a) Higher PD* values compared to multicontrast PD in GM. (b) Higher PD* values compared to multi-contrast PD in WM. (c) Higher multi-contrast PD values compared to PD* in GM. (d) Higher multi-contrast PD values compared to PD* in WM. (e) Higher multi-contrast PD values compared to standard PD in GM. (f) Higher multi-contrast PD values compared to standard PD in WM.

Table 4.

Summary of the main differences relative to the whole brain voxel-wise comparison between the multi-contrast PD and PD* maps, and between Multi-contrast PD and standard PD. Coordinates are reported in MNI standard space.

Analysis			Region	Coordinates (mm)			T-value
				x	y	z
PD* > Multi-contrast PD		GM	Left motor cortex	–33	–18	42	23
			Right motor cortex	–32	–18	–5	22
			Left insula	–38	–2	8	21
			Right insula	44	18	–3	18
		WM	Left motor track	–25	–34	46	19
			Right motor track	30	–35	41	13
			Left visual track	–36	–56	14	13
			Right visual track	41	–53	17	12
Multi-contrast PD > PD*		GM	Left globus pallidus	–15	–3	0	14
			Right globus pallidus	23	–6	–3	23
			Left orbitofrontal cortex	–17	42	–30	20
			Right orbitofrontal cortex	9	27	–24	15
			Left substantia nigra	–10	–17	–12	10
			Right substantia nigra	8	–18	–17	12
			Left inferior temporal pole	–59	–23	–27	17
			Right inferior temporal pole	44	–30	–27	12
		WM	Corpus callosum	2	6	23	27
			Pons nuclei	2	–32	–26	13
Multi-contrast PD > standard PD		GM	Right nucleus lateroponderalis	12	–6	14	15
			Right caudate	6	13	–3	22
		WM	Corpus callosum	5	8	24	30
			Pons nuclei	2	–30	–17	20

3.8. Multi-contrast PD vs standard PD maps

Significantly higher PD values were found in the corpus callosum and in the posterior region of the brain stem for the multi-contrast maps with respect to standard ones (see Fig. 5f and Table 4). Moreover significantly higher PD values were observed in the right nucleus lateroponderalis of the thalamus and right caudate for the multi-contrast maps compared to the standard ones, as reported on Fig. 5e and Table 4.

3.9. In vivo experiment: focal epilepsy and porencephalic ventricle dilation

Fig. 2b shows a coronal slice from the dataset acquired on the patient with focal epilepsy and porencephalic ventricle dilation. The right hemisphere porencephalic cyst is enclosed by a thin cortical layer (in the lateral and frontal neighbouring regions) and by white matter (in the posterior and inferior neighbouring regions). Those grey and white matter regions are accurately delineated on the multi-contrast PD map, while the PD* fails to provide correct tissue contrast. This is due to the different behaviour of the RP estimation methods in the presence of a severe anatomical abnormality. While N4ITK employed by the multi-contrast PD map, does not make any assumption on the voxel distribution across tissue classes, the bias estimation used for PD* calculation is hampered by the inaccurate tissue segmentation.

3.10. Post-mortem experiment: post-mortem foetus

Fig. 2c illustrates a single slice for the multi-contrast PD map estimated on the post-mortem foetus. Although strong susceptibility artefacts are visible around the heart due to the presence of air, the map shows homogeneous PD values over the whole body illustrating that the method described allows PD mapping in various applications. The potential to produce PD maps in the absence of anatomical information regarding tissue distribution was demonstrated by the PM foetus MRI dataset, for which the PD* maps are not available due to their requirement for the a-priori information.

4. Discussion

In this study, we propose a framework for PD estimation based on minimal anatomical information, suitable for multiple applications including healthy and diseased brains with widespread pathology. To achieve this, the RP determination was based on a non-parametric algorithm for the correction of the intensity non-uniformity, while the scaling factor was based on an external calibration object. Additional experiments were carried out to test the PD values reproducibility with respect to the position of the calibration object, the receiver coil employed for acquiring the data and the number of iterations of the N4ITK bias field correction. Aiming to fully correct the PD map for transverse relaxation effects and decrease the PD value variability, we employed all the acquired data points using a well-established multicontrast VFA protocol. Nonetheless we also tested the applicability of our method in the absence of MTw contrast.

We evaluated the PD values and homogeneity separating the main effects of R2* signal decay, RP correction method and number of contrasts. Finally, we demonstrated the wide applicability of the new multi-contrast PD mapping on a severely damaged brain and on a post-mortem foetus.

4.1. RP estimation with N4ITK

The RP sensitivity for the multi-contrast PD was estimated using information about the volume of interest and a B-spline interpolation of the intensity distribution. In the following section the different factors affecting the RP estimation are discussed along with their impact on the resulting homogeneity of the PD maps.

4.2. Motion effects

The presence of motion during the scan acquisition could induce the variation of RP sensitivity between the different image contrasts. This has been corrected previously using repeated RP measurements (Papp et al., 2015) although these are limited by the assumption of B1⁺/B1^- reciprocity. To address this case the N4ITK bias correction could be applied to each contrast after the removal of the ST or ST_MT term and any differences, due to movement between each weighted image acquisition, could be corrected.

4.3. Effects of receiver coil and number of N4ITK iterations

The spatial variability of the RP for a particular RF coil could impact the accuracy of the PD maps. To account for those effects we acquired data with different receiver coils and we compared the resulting multicontrast PD maps.

To evaluate the effectiveness of RP correction, data were obtained using 20 and 64 channel receiver head coils. We estimated the multi-contrast PD maps using data acquired with the 20 and 64 channel coils, and tested the effect of different numbers of N4ITK iterations. PD map differences estimated within the same coil showed that low density coils required less N4ITK iterations to remove the bulk of RP sensitivity profile with respect to the maps obtained from higher number of channels. This is expected due to the fact that higher density RF coils have more localised sensitivity profiles leading to an RP with increased spatial variation. However the same number of iterations was required for both the 20 and 64 channel multi-contrast PD maps in order to obtain negligible RP changes. Effective RP correction should reduce changes in PD maps estimated with different RF coils. The systematic PD value differences between receiver coils suggest that N4ITK provides a less robust RP correction when a larger number of receiver channels or more highly localised coils are used.

4.4. Comparison between multi-contrast PD and an established PD mapping method

In the following sections we discuss the factors contributing to the homogeneity and PD value differences between methods. The homogeneity was assessed using tissue class specific entropy and variance, while PD value comparison was performed using voxel-wise statistical analysis.

4.5. Effects of R2*: comparison of multi-contrast PD vs PD* maps

The presence of R2* dependency could modify the PD values distribution, affecting the homogeneity assessment across different RP estimation methods. To analyse the main effect of R2* on the PD maps estimation we compared variance and entropy between the PD* and multi-contrast PD maps. The increased variance observed in GM for the multi-contrast PD maps was mainly driven by voxels in brain regions where high susceptibility-related static magnetic field gradients are present (e.g. temporal poles and orbitofrontal regions) leading to the rapid local R2* decay and poor model fit. This could be improved by increasing image spatial resolution or improved fit regularisation.

The main effects of R2* dependency on voxel-wise comparison were the reduced PD values in the deep brain structures and the increased values along the visual and motor tracks when comparing the PD* maps to the multi-contrast PD ones. The results in the deep GM regions can be explained by the presence of high iron content (Aquino et al., 2009; Langkammer et al., 2010; Ordidge et al., 1994), that decreases the intensity of the PD* maps. While the results along the visual and motor tracks could be ascribed to the presence of tightly packed and heavily myelinated tracts leading to a form of anisotropy and residual R2* contrast dependency related to the fibre orientation with respect to the main magnetic field (Bender and Klose, 2010; Cherubini et al., 2009; Denk et al., 2011).

4.6. Effects of RP correction and scaling method: comparison multi-contrast vs standard PD maps

Aiming to assess the effect of the RP estimation method, we compared entropy and variance across the multi-contrast PD and standard PD (PD* corrected for R2* effects) maps. The PD values homogeneity and accuracy, measured through the entropy and variance, for the multi-contrast technique within CSF were increased beyond that obtained using state-of-the-art SPM12. As PD mapping can be used for the estimation of the water volume fraction in tissue property models and g-ratio ( Berman et al., 2018; Mezer et al., 2013), obtaining CSF values around 100 p.u. indicates reliable measurements are provided by the PD map to characterise the percentage of observed water protons (Mezer et al., 2016). Moreover the correct delineation of CSF from PD map could benefit advanced diffusion approaches where accounting for the presence of water compartmentalisation and free water volume fraction is important for accurately modelling diffusion in different micro-structural compartments (Kaden et al., 2016; Zhang et al., 2012).

As expected, in healthy controls the WM homogeneity for the standard PD was increased compared to the multi-contrast PD. This is due to the RP estimation for PD* maps being based on SPM unified bias-field/tissue segmentation, that explicitly minimises the signal variability in those tissue classes, although strict regularization and boundary conditions are used to preserve structural variability (Ashburner and Friston, 2005; Weiskopf et al., 2011). Additionally, the scaling factor used in the PD* maps was based on the mean WM signal, which further decreases the intensity variability in this tissue class between subjects. However, the standard PD approach for the RP calculation and the map scaling excludes the possibility of biological signal variability within WM that can occur in brain development and in pathology (Gracien et al., 2016; Mezer et al., 2013; Shah et al., 2008) leading to scaling errors that could potentially result in erroneous GM PD differences.

The main effects of the RP correction method and scaling factor on the PD values were the increased intensity of the multi-contrast PD with respect to both standard PD and PD* maps in the corpus callosum and pons nuclei. This might be mainly driven by different methods applied to estimate the RP. While SPM bias correction minimises the intensity variation over each tissue class, N4ITK reduces the intensity distribution over the whole volume of interest leading to potential inaccurate RP estimation in regions where RP inhomogeneities are stronger.

4.7. Effect of the number of weighted contrast datasets used to calculate PD

Finally, the use of a different number of contrasts could alter the variability of PD values with the expectation that PD variability should be reduced by using a greater amount of data for its calculation. To assess the effect of the number of contrasts employed in the PD estimation on the map homogeneity, we estimated the tissue specific variance and entropy for the one-contrast, and multi-contrast PD maps. The observed lower entropy and variance for the multi-contrast PD for all tissue classes indicates that using more images with differing tissue contrast decreases the signal variability, and increases the accuracy of the PD estimates. This decrease in variance also indicates that the model used is sufficient to remove contrast effects.

4.8. PD estimation in pathology

While correcting the PD* map for R2* signal decay provides a suitable approach for estimating free water content in healthy brains, it could be inaccurate in case of abnormal tissue property changes happening in brain development or pathological conditions. We demonstrated that our multi-contrast PD maps improved tissue delineation in the presence of abnormal anatomical structures, such as ventricle dilation due to a porencephalic cist. This improvement was mainly due to the approach used for the RC profile estimation and the external probe employed for scaling. However, it is noted that the cist CSF delineation provided by both the multi-contrast PD and PD* map was hampered by the presence of Gibbs artefacts.

The multi-contrast approach enabled the PD map estimation for the whole body of a post-mortem foetus. Although our primary interest was in PD mapping within the brain, this example was used to highlight how this method can be more generally applied. There is an increased role of post-mortem MRI for autopsy which can provide information regarding cause of death or major pathology, but can also be used to advance medical research and knowledge in answering specific ante mortem questions (Thayyil et al., 2013). In this regard, quantitative imaging such as PD measurements may have an important role to play.

4.9. Limitations and outlook

The majority of the existing techniques (Abbas et al., 2014; Mezer et al., 2016; Volz et al., 2012b; Wang et al., 2018) employ two main contrasts to estimate PD and the voxel-wise R1 required for the PD mapping. As we showed with the one-contrast PD map, the PD mapping approach described in this work can be applied both where multiple contrasts are available and where only T1w and PDw images are present. For the multi-echo VFA images obtained for multi-parameter mapping, utilising all datasets improves the PD maps by reducing their variance within tissue class. This is important both for robustness against motion artefacts (Weiskopf et al., 2014a,b) and for fast data acquisition methods using partial k-space sampling, such as partial Fourier, parallel acquisition or compressed sensing, that can reduce SNR in the raw images (Bilgic et al., 2011; Griswold et al., 2002; Johnson, 2017; Lustig et al., 2007; Vasanawala et al., 2010).

Despite the neurobiological and anatomical plausibility of our findings, there are certain methodological limitations of note. Most importantly, the assumption of a mono-exponential signal decay described by R2* may be violated in some brain areas, particularly those suffering from susceptibility artefacts (Neeb et al., 2006). In those regions the mono-exponential fit is potentially unstable and can significantly increase the noise level (Neeb et al., 2006). However, high spatial resolution (here 1 mm³ was used) reduces the effects of susceptibility artefacts on the signal decay due to a reduced within voxel spin phase coherence loss (Weiskopf et al., 2007). Despite possible limitations related to the R2* estimation in regions with susceptibility artefacts, we observe that our method provides PD values in deep brain structures unaffected by the R2* relaxation effects.

The RP correction method employed in this study allows the PD mapping estimation pipeline to be more generally applied across different applications, albeit the robustness of the bias correction is influenced by the number of channels present in the receiver coil. In the brain, a relatively small effect of channel count was found on the PD values when comparing a 20 and 64 channel head/neck receiver array. The use of receiver coils with very strong spatial variations or comparisons made between PD maps acquired with different RF coils could therefore be biased by inaccurate RP estimation.

PD is an important parameter for mapping water volume fraction during lifespan and in different pathologies. The procedure presented here allows the delineation of both local and global changes making PD suitable for characterising brain maturation, aging and pathology both in the brain and beyond (Ayata and Ropper, 2002; Baierl et al., 1988; Blystad et al., 2017; Hagiwara et al., 2017; Jurcoane et al., 2013; McAllister et al., 2017; Mezer et al., 2013). Our results are particularly relevant for studies focusing on PD mapping in the presence of pronounced pathologies that cause the failure of tissue segmentation algorithms or hamper the correct fit between PD and T1. Notably, the RP correction and the scaling method used in this study are independent from the subject’s anatomy and can be used for any organs.