The Case Time Series Design

Abstract

Modern data linkage and technologies provide a way to reconstruct detailed longitudinal profiles of health outcomes and predictors at the individual or small-area level. While these rich data resources offer the possibility to address epidemiologic questions that could not be feasibly examined using traditional studies, they require innovative analytical approaches. Here we present a new study design, called case time series, for epidemiologic investigations of transient health risks associated with time-varying exposures. This design combines a longitudinal structure and flexible control of time-varying confounders, typical of aggregated time series, with individual-level analysis and control-by-design of time-invariant between-subject differences, typical of self-matched methods such as case–crossover and self-controlled case series. The modelling framework is highly adaptable to various outcome and exposure definitions, and it is based on efficient estimation and computational methods that make it suitable for the analysis of highly informative longitudinal data resources. We assess the methodology in a simulation study that demonstrates its validity under defined assumptions in a wide range of data settings. We then illustrate the design in real-data examples: a first case study replicates an analysis on influenza infections and the risk of myocardial infarction using linked clinical datasets, while a second case study assesses the association between environmental exposures and respiratory symptoms using real-time measurements from a smartphone study. The case time series design represents a general and flexible tool, applicable in different epidemiologic areas for investigating transient associations with environmental factors, clinical conditions, or medications.

Background

Observational studies aim to discover and understand causal relationships between exposures and health outcomes through the analysis of epidemiologic data.¹ Paramount to this objective is removing biases due to the non-experimental setting, in the first place confounding. It is, therefore, no surprise that traditional approaches based on cohort and case–control methods have been complemented with, and extended by, alternative study designs and statistical techniques applicable in specific contexts. An active area of research is so-called self-matched studies, which investigate acute effects of intermittent exposures by comparing observations sampled at different times within the same unit. These include individual-level designs such as the case–crossover,² the case-only,³ the case–time–control,⁴ the exposure–crossover,⁵ and the self-controlled case series,⁶ among others. An alternative but related epidemiologic method for aggregated data is the time series design, applied in particular in environmental studies.⁷ A thorough overview of self-matched methods is provided in a recent publication by Mostofsky and colleagues.⁸

This landscape is likely to be transformed further by ongoing technologic and methodologic developments in data science, which offers unique opportunities for epidemiologic investigations, for instance through electronic health records linkage,⁹ exposure modelling,¹⁰ and real-time measurements technologies.^11,12 Ultimately, these data resources can be used to reconstruct detailed longitudinal profiles with repeated measures of health outcomes and various risk factors, offering the chance to investigate complex aetiological mechanisms and to test elaborate causal hypotheses. However, existing self-matched methods present limitations in this context, and new analytical techniques must be developed for epidemiologic investigations in these intensive longitudinal and big data settings.¹³

In this contribution, we present the case time series design, a novel self-matched method for the analysis of transient changes in risk of acute outcomes associated with time-varying exposures. This innovative design combines the longitudinal modelling structure of time series analysis with the individual-level setting of other self-matched methods, offering a flexible and generally applicable tool for modern epidemiologic studies. First, we introduce the case time series design and its features, including the design structure, modelling framework, estimation methods, and key assumptions. Later, we assess the methodology in a simulation study that evaluates its performance under various data generating scenarios. Then, we demonstrate its application through two real-data epidemiologic analyses. In a final discussion section, we describe the epidemiologic context, advantages, and limitations, and areas of further development. We add documents for reproducing real-data examples and the simulation study as eAppendix 1–3 in the online supplementary material, with an updated version complemented with and R scripts available at the personal website and GitHub webpage of the author (see ‘Data and Code’).

A Novel Self-Matched Design

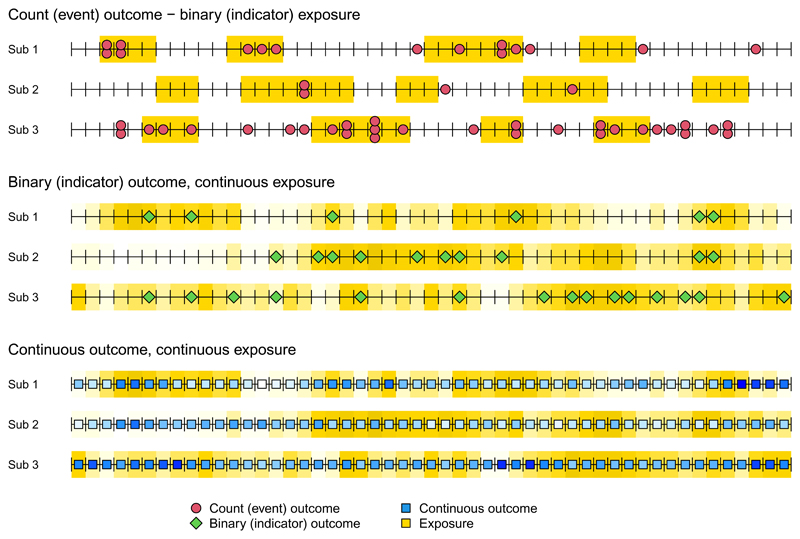
The study design proposed here, called case time series, is a generally applicable tool for the analysis of transient health associations with time-varying risk factors. This novel design considers multiple observational units, defined as cases, for which data are longitudinally collected over a pre-defined follow-up period. The main design feature that defines the case time series methodology is the split of the follow-up period in equally spaced time intervals, which results in a set of multiple case-level time series. Data forming the series can originate from actual sequential observations or be reconstructed by aggregating or averaging longitudinal measurements, but, eventually, they are assumed to represent a continuous temporal frame. A graphical representation is provided in Figure 1, showing case-specific time series data with various types of measurements of outcome and exposure collected for multiple subjects.

Figure 1.

Graphical representation of data configurations for the case time series design applied in the analysis of transient health risks of time-varying exposures. The figure represents three examples of data for three subjects (cases) followed for a period of time, with equally spaced measures of outcome and exposure that form case-level time series. This setting allows the definition of predictors and time axes as unique and sequential observations. The three examples illustrate different measures of outcome and exposure. The former is represented as counts (top), a binary indicator (middle), or a continuous measure (bottom). Similarly, exposure can be represented by a simple binary episode indicator (top), or continuous term (middle and bottom). Continuous variables are represented by shaded colours. The graphical representation demonstrates the potential of the case time series design to be applied in various research areas for modelling associations defined by different types of measurements.

The case time series data setting provides a flexible framework that can be adapted for studying a wide range of epidemiologic associations. For instance, outcomes, exposures, and other predictors can be represented by either indicators for events, episodes, or continuous measurements that vary across units and times, as in Figure 1. The time intervals can be of any length (from seconds to years), depending on the temporal association between outcome and exposures and on practical design considerations. A case is a general definition, and it can represent a subject or other entities such as a geographic area to which observations are assigned, thus allowing analyses to be conducted either at individual level or with aggregated data. Eventually, the case time series structure combines characteristics of various other study designs: it allows individual-level analyses of transient risk associations as in traditional self-matched methods, but it retains the longitudinal temporal frame typical of time series data, with ordered repeated measures of outcomes, exposures, and other predictors. As discussed below, this flexible design setting offers important advantages.

Modelling Framework

A case time series model can be written in a regression form by defining the expectation of a given health outcome y_it for case i at time t in relation to a series of predictor terms. Algebraically, the model can be written as:

$$g\left[\text{E}\left(y_{it}\right)\right]={\xi }_{i(k)}+f\left(x_{it},\ell \right)+{\displaystyle \sum }_{j=1}^J{s}_j(t)+{\displaystyle \sum }_{p=1}^P{h}_p\left(z_{ipt}\right)$$ (1)

The definition in Eq. (1) resembles a classic time series regression model traditionally used in environmental epidemiology, where the ordered and sequential nature of the data allows the application of cutting-edge analytical techniques.⁷ Specifically, the function f(x, ℓ) specifies the association with the exposure of interest x, defined either as a binary episode indicator or as a continuous variable, optionally allowing for non-linearity and complex temporal dependencies along the lag dimension ℓ. These complex relationships can be modelled through distributed lag linear and non-linear models (DLMs and DLNMs), which can flexibly define cumulative effects of multiple exposure episodes.¹⁴ The term(s) S_j represent functions expressed at different timescales to model temporal variations in risk associated to underlying trends or seasonality, among others.¹⁵ Other measurable time-varying confounders z_p can be modelled through functions h_p, and these can include for instance age or time since a specific intervention. The two sets of terms S_j and h_p ensure a strict control of temporal variation in risks over multiple time axes. The outcome y can represent binary indicators, counts of rare or frequent events, or continuous measures. The analysis can be performed on multiple cases i = 1, …, n, with intercepts ξ_i(k) expressing baseline risks for different risk sets, optionally stratified further in time strata k = 1,…, K_i nested within them, allowing an additional within-case control for temporal variations in risk.

Estimation

The estimation procedures in case time series analyses rely on estimators and efficient computational algorithms provided by the general framework of fixed-effects models.¹⁶ These were developed in econometrics and often applied in panel studies with repeated observations.^10,17 Fixed-effects methods allow the estimation of coefficients for the various functions in Eq. (1), without including the potentially high number of case/stratum-specific intercepts ξ_i(k), treated as nuisance (or incidental) parameters.¹⁶

Fixed-effects estimators are available for the three main types of outcomes and distributions within the extended exponential family of generalized linear models (GLMs). Specifically, for continuous outcomes with a Gaussian distribution, the estimation procedure involves mean-centring and a simple correction of the degrees of freedom. For event-type indicator or count outcomes following a Bernoulli and Poisson distribution, respectively, estimators for fixed-effects models with canonical logit and log links can be defined through conditional likelihoods for logistic and Poisson regression.^18,19 These are forms of partial likelihoods that are derived by defining reduced sufficient statistics for ξ_i(k), obtained by conditioning on the total number of events within each of the n cases or n × K strata.

The main advantage of fixed-effects models is that the effect of any unmeasured predictor that does not vary within each risk set is absorbed by the intercept ξ_i(k), and therefore the related confounding effect is controlled for implicitly by design, as in other self-matched methods.⁸ In addition, the within-case design offers important computational advantages, especially from a big data perspective. First, the analysis is restricted to informative strata, i.e. cases and risk sets with variation in both outcome and exposure. Second, the estimators are based on efficient computational schemes, where the conditional or fixed-effect likelihood is defined by the sum of parts related to multiple risk sets, and the corresponding nuisance parameters ξ_i(k) are not directly estimated.

Key assumptions and threats to validity

As discussed above, the case time series framework has interesting design and modelling features that offer important advantages. On the other hand, its self-controlled structure, while appealing, only operates within an elementary causal framework and requires relatively strict assumptions to protect against key threats to validity. Specifically, the main requirements are the following:

1. Distributional assumptions on the outcome. The outcome y_it must represent conditionally independent observations originating from one of the standard family distributions, for instance, Poisson counts, Bernoulli binary indicators, or Gaussian continuous measures.

2. Outcome-independent follow-up period. The period of observation for each case i must be independent of a given outcome, meaning that the follow-up period cannot be defined or modified by the outcome itself.

3. Outcome-independent exposure distribution. The probability of the exposure x_t must be independent of the outcome history prior to t, meaning that the occurrence of a given outcome must not modify the exposure distribution in the following period.

4. Constant baseline risk conditionally on measured time-varying predictors. The baseline risk along the (strata of) follow-up period of each case i must be constant, meaning that variations in risks must be fully explained by model covariates.

These requirements enable valid conditional comparison of observations at different times within the follow-up of each case. Departures from these assumptions can produce imbalances in the temporal distribution of the outcome, the exposure, or unmeasured risk factors, thus determining spurious associations.

Some of these assumptions have been separately described in the literature of self-matched designs and fixed-effects models.^20–23 Specifically, Assumption 1 dictates that outcomes must occur independently, and in particular that the occurrence of a given outcome level or event must not modify the risk of following outcomes.²⁴ This assumption indirectly implies that outcomes are recurrent, and non-recurrent events can only be analysed if rare in the population of interest.^25,26 Assumptions 2 and 3 are those posing more limitations to the application of self-matched methods, as for many associations of interest an outcome can modify both the follow-up period and exposure distribution.^27,28 These requirements often restrict the case time series designs to the analysis of exogenous exposures, which are by definition outcome-independent, and for which the observation period can be extended even beyond a terminal event, as in bi-directional case–crossover schemes.²⁹ Assumption 4 requires a constant baseline risk to ensure conditional exchangeability between observations within each risk sets,^20,30,31 requiring that relevant time-varying confounders are included and all the terms in Eq. (1) are correctly specified.

Importantly, the design setting described above is not suited to represent complex causal scenarios characterised by dynamic mechanisms between time-varying terms. Specifically, feedback between outcomes and between outcome and exposure are forbidden by Assumptions 1 and 3, respectively, while more generally exposure–confounder feedback cannot be validly handled through traditional regression-based methods for longitudinal data.³²

Simulation Study

We evaluated the performance of the case time series design in a set of simulated scenarios that involved various data-generating processes and assumptions (Table). Detailed information on the simulation settings, definitions, and additional results are provided in eAppendix 3 (online supplementary material). Briefly, we simulated and analysed data for 500 subjects followed up for one year, testing the method in terms of relative bias, coverage, and relative root mean square error (RMSE) in 50,000 replications. The basic scenario involves an outcome represented by repeated event counts and binary indicators of exposure episodes associated with a constant increase in risk in the next 10 days.

Table.

Results of the simulation study, with ten scenarios representing increasingly complex data settings (Scenarios 1-10), and four additional scenarios simulating data where the key design assumptions are violated (Scenarios 11-14). The table reports empirical figures of relative bias (%), coverage, and relative root mean square error (RMSE, %) in 50,000 replications. A detailed description of the scenarios, definitions, and additional results and graphs are provided in the supplementary material [Appendix A].

SCENARIO	RELATIVE BIAS	COVERAGE	RELATIVE RMSE
SCENARIO 1: BASIC	0.0%	0.951	8.8%
SCENARIO 2: RARE OUTCOME/EXPOSURE	−4.5%	0.951	86.0%
SCENARIO 3: CONTINUOUS EXPOSURE	−0.1%	0.950	15.2%
SCENARIO 4: BINARY OUTCOME	0.3%	0.949	9.1%
SCENARIO 5: CONTINUOUS OUTCOME	0.0%	0.950	14.7%
SCENARIO 6: COMMON TREND	−0.1%	0.950	28.8%
SCENARIO 7: SUBJECT-SPECIFIC TREND	0.1%	0.948	35.2%
SCENARIO 8: UNOBSERVED BASELINE CONFOUNDER	0.2%	0.951	25.8%
SCENARIO 9: TIME-VARYING CONFOUNDER	−0.2%	0.949	35.1%
SCENARIO 10: COMPLEX LAG STRUCTURE	0.0%	0.950	29.2%
SCENARIO 11: OUTCOME-DEPENDENT RISK	−18.9%	0.738	24.7%
SCENARIO 12: OUTCOME-DEPENDENT FOLLOW-UP	16.8%	0.797	22.7%
SCENARIO 13: OUTCOME-DEPENDENT EXPOSURE	11.1%	0.744	14.4%
SCENARIO 14: VARIATION IN BASELINE RISK	40.7%	0.222	43.3%

The first part of the simulation study (Scenarios 1-10) evaluates the performance of the new design in recovering the true association under increasingly complex data settings. Specifically, the scenarios depict different outcome and exposure types, the presence of common or subject-specific trends, time-invariant and time-dependent confounders, and more complex lag structures. Results in the Table indicate that the case time series design provides correct point estimates and confidence intervals in almost all ten scenarios. The small underestimation in Scenario 2 is consistent with the asymptotic bias of maximum likelihood estimators originating from the extreme unbalance of expected events between risk and control periods, previously described and defined analytically in the self-controlled case series literature.³³ eFigure 1 (online supplementary material) shows that the case time series models can correctly recover the true association, both in the basic Scenario 1 with constant risk and no confounding, and in the more complex Scenario 10 representing varying lag effects, strong temporal trends, and highly correlated confounders.

The second part of the simulation study (Scenarios 11-14) illustrates basic applications, but where each of the four assumptions, in turn, does not hold. Specifically, Scenario 11 describes the case where the occurrence of an outcome can change the risk status of a subject and temporally reduce their underlying risk. This can occur for instance when the event results in the prescription of drugs or therapies. This induces a form of dependency in the outcome series that violates Assumption 1 and, in this example, results in a negative bias (Table). Scenarios 12 simulates a different situation, namely when the outcome event carries a risk of censoring the follow-up, for instance, if it increases the probability of death. This contravenes Assumption 2 and generates a bias in the opposite direction. In Scenario 13, the outcome event reduces instead the probability of exposure episodes in the following two weeks, a situation that can occur for example if the event results in hospitalization or lifestyle changes. Here Assumption 3 does not hold, and the estimators are again biased upward. Finally, Scenario 14 illustrates the case of unobserved periods of lower baseline risk within the follow-up, for instance corresponding to holiday periods with a reduced probability of an outcome being reported. This undermines the conditional exchangeability requirements of Assumption 4 and induces a large positive bias.

Illustrative Examples

This section illustrates the application of the case time series design in two real-data examples. These case studies are described here only for illustrative purposes, and they are not meant to offer substantive epidemiological evidence on the associations under study. Detailed information on the setting and sources of data can be found in the cited references. Documents in the online supplementary material (eAppendix 1 and 2) provide notes and R code that reproduce the steps of these analyses using simulated data, and they offer details on the specific modelling choices.

Flu and Myocardial Infarction

The first example replicates a published analysis that assessed the role of influenza infection as a trigger for acute myocardial infarction (AMI).³⁴ The data, retrieved by linking electronic health records from primary care and cohort databases for England and Wales, include 3,927 acute MI cases with at least one flu episode in the period 2003-2009. A representation of a sub-interval of the follow-up for six subjects is reported in eFigure 2 (online supplementary material). The original analysis relied on the self-controlled case series design to examine the association, using exposure windows in the 1-91 days after each flu episode and controlling for trends using 5-year age strata and trimester indicators. Limitations of this approach are the use of stratification to describe smooth continuous dependencies and the fact that multiple flu episodes experienced by some subjects resulted in the long exposure windows to overlap (see eFigure 2), requiring ad-hoc fixes that can generate biases.³⁵ Conversely, the rarity of the exposure, with most of the subjects experiencing a single flu episode, prevents the application of the case–crossover design, as most control sampling schemes would generate non-discordant case–referent sets.

We replicated the analysis with a case time series design, splitting the follow-up period of each subject into daily time series (see eAppendix 1, online supplementary material). We fitted a fixed-effects Poisson model to estimate the flu–AMI association while controlling for underlying trends across multiple time scales. The model includes smooth functions to define the baseline risk, specifically using natural splines (with two knots at the interquartile range) for age and cyclic splines (with three degrees of freedom) for seasonality. More importantly, we applied DLMs defined by either splines (with knots at 3, 10, and 29 lags) or step functions (with strata 1-3, 4-7, 8-14, 15-28, and 29-91 lags) to describe temporal effects along with the exposure window.

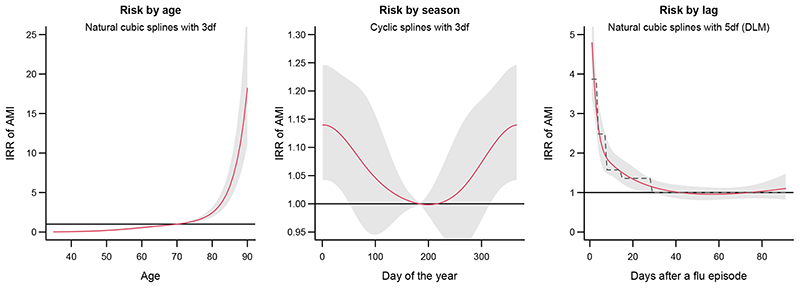
Results are reported in Figure 2. The left and middle panels display the variation in risk of AMI by age and season, showing how the case time series design allows modelling baseline trends fluctuating smoothly across multiple time axes. The right panel illustrates the risk after a flu episode within the selected lag period, as estimated using a DLM with spline functions. The graph indicates a high risk in the first days after a flu episode, which then attenuates and disappears after approximately one month. The same panel also includes the fit of the alternative DLM defined by step functions, which assumes a constant risk within exposure windows (see also eFigure 3 in the online supplementary material). This specification matches the stratification approach in the original self-controlled case series analysis,³⁴ although the case time series design with DLMs accounts for cumulative effects of potentially overlapping periods of flu episodes.

Figure 2.

Results of the analysis on the association between influenza infection and acute myocardial infarction (AMI), as incident rate ratio (IRR) and 95% confidence intervals. The three panels show the AMI risk by age (left) and by season (middle), and the lag-response curve representing the risk in the 1-91 days after a flu episode (right). The latter is estimated in the main model using natural splines (continuous red line), with superimposed the results from an alternative model using step functions (dashed grey line).

Environmental exposures and respiratory symptoms

The second example illustrates a preliminary analysis of the role of multiple environmental stressors in increasing the risk of respiratory symptoms using smartphone technology. Data were collected within AirRater, an integrated online platform operating in Tasmania that combines symptom surveillance, environmental monitoring, and real-time notifications.¹² A smartphone app allowed the self-reported recording of respiratory symptoms and the reconstruction of personalized exposure series by linking geo-located positions with high-resolution spatio-temporal maps derived from environmental monitors (see Figure 3). Standard cohort analyses based on between-subject comparisons are unsuitable in this complex study setting, characterized by continuous recruitment, high dropout rates, and intermittent participation (see eFigure4 in the online supplementary material). Similarly, the frequent and highly seasonal outcome pose problems in adopting a case–crossover design, with issues in selecting control times and about the assumption of constant within-stratum risk. Finally, the presence of multiple continuous exposures prevents the application of the self-controlled case series design, either in its standard or extended forms.^36,37

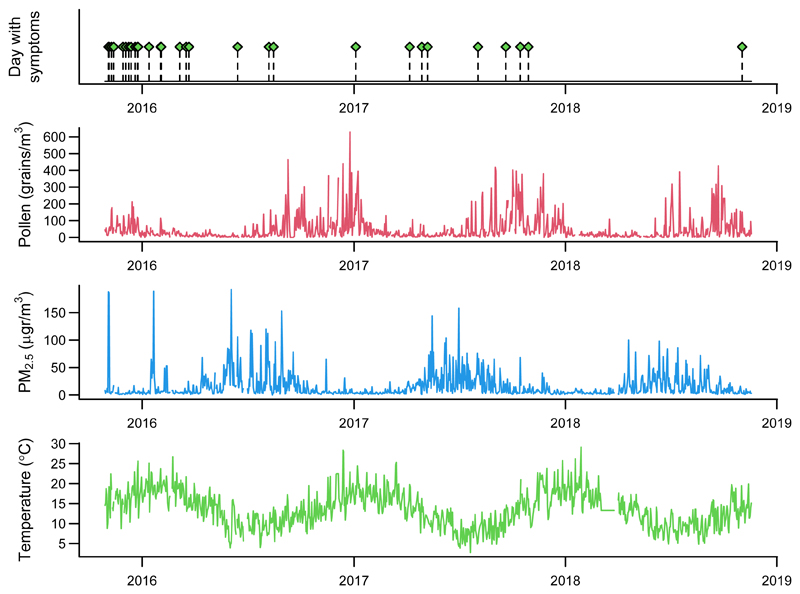
Figure 3.

Graphical representation of the individual time series of a subject participating in the AirRater study on the association between environmental exposures and respiratory symptoms. The four panels (from top to bottom) display the daily series of indicators of allergic events and levels of the three environmental stressors, represented by pollen (grains/m³), PM₂.₅ (μg/m³), and temperature (°C).

We, therefore, applied a case time series design (see eAppendix 2, online supplementary material). The analysis included 1,601 subjects followed between October 2015 and November 2018, with a total of 364,384 person–days. The event-type outcome was defined as daily indicators of reported respiratory symptoms and associated with individual exposure to pollen (grains/m³), fine particulate matter (PM_2.5, μg/ m³), and temperature (°C) (Figure 3). We modelled the relationships using a fixed-effects logistic regression over a lag period of 0-3 days, using an unconstrained DLM for the linear association with PM_2.5, and bi-dimensional spline DLNMs for specifying non-linear dependencies with pollen and temperature.^14,38 A strict temporal control was enforced by using subject/month strata intercepts, natural splines of time (with 8 df/year), and indicators of the day of the week, thus modelling individually varying baseline risks on top of shared long-term, seasonal, and weekly trends.

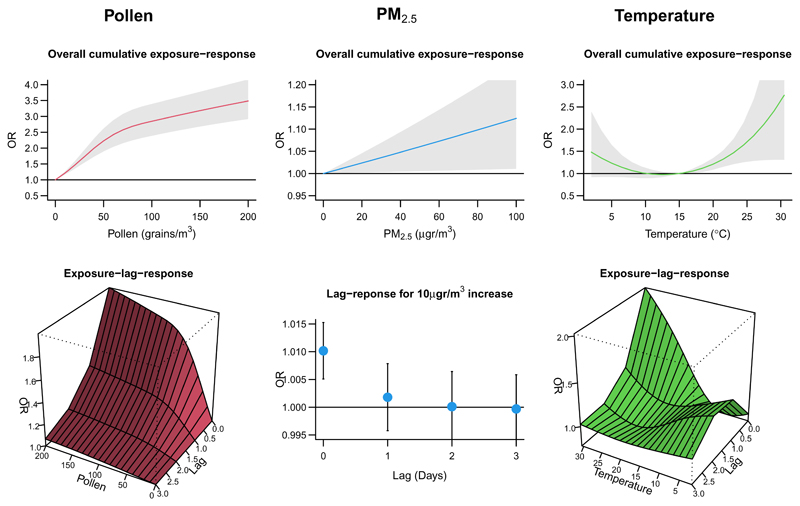
Figure 4 shows the preliminary results, with estimated associations reported as odds ratios (ORs) from the model that includes simultaneously the three environmental stressors. The graphs display the overall cumulative exposure-response relationships (top panels), interpreted as the net effects across lags, and the full bi-dimensional exposure-lag-response associations (bottom panels)^14,38. The lefthand panels indicate a positive association between risk of allergic symptoms and pollen, with a step increase in risk that flattens out at high exposures, and a lagged effect up to 2 days. The middle panels suggest an independent association with PM_2.5, where the risk is entirely limited to the same-day exposure. Finally, results in the righthand panels show a positive association with high ambient temperature, with the OR increasing above 1 beyond daily averages of 15°C.

Figure 4.

Results of the analysis on the association between environmental exposures and respiratory symptoms, as odds ratio (OR) and 95% confidence intervals. The three columns of panels show estimated associations with pollen (left, grains/m³), PM_2.5 (middle, μg/m³), and temperature (right, °C). The top row of panels displays the net risk cumulated in the lag period 0-3 days as overall cumulative exposure-response associations, assumed linear for PM_2.5 and non-linear for pollen and temperature. The bottom row of panels shows instead the full exposure-lag-response associations, represented as the bi-dimensional risk surface for pollen and temperature or the lag-specific risks for a 10 μg/m³ increase in PM_2.5.

Discussion

The novel case time series methodology offers a general modelling framework for the analysis of epidemiologic associations with time-varying exposures. The design is adaptable to various data settings for the analysis of highly informative longitudinal measurements, and it is particularly well-suited in applications with modern data resources such as individual-level exposure models and real-time technologies.

The main feature of methodology is a flexible scheme that embeds a longitudinal time series structure in a within-subject design, providing unique modelling advantages. For instance, the sequential order of observations offers the opportunity to assess complex temporal relationships with multiple exposures, where patterns of cumulative effects for linear or non-linear dependencies can be easily modelled. Furthermore, the time series and self-controlled features offer a structure that enables strict control for confounding: time-invariant and time-varying factors can be adjusted for by stratifying the baseline risk between and within subjects, respectively, while residual temporal variations can be directly modelled through time-varying predictors that represent confounders or shared trends across multiple time axes.

The new design complements and extends the already rich set of self-matched methods for observational studies described in the epidemiological literature.⁸ Previous methodological contributions have highlighted links and similarities between various designs,^{18,21,29,30,39–41} and ultimately these can be seen as alternative approaches to model the same risk associations. However, each method relies on different sets of assumptions and modelling choices, which explain in part their separate areas of application. The case time series methodology, nevertheless, offers a general framework that combines and extends features of existing designs, with important advantages. For example, it borrows flexible modelling tools from aggregated-data time series design, but it implements them in individual-level analyses that allow a finer reconstruction of outcomes, exposures, and other risk factors. It is applicable to assess associations with multiple continuous predictors as the case–crossover design, and it can model recurrent events, either common or rare, as the self-controlled case series analyses, but it can be extended to the analysis of outcomes represented by binary indicators or continuous measures, simply assuming different distributions. Finally, its time series structure allows the application of sophisticated techniques such as smoothing methods and distributed lag models, characterized by well-defined parameterizations, computational efficiency, and standard software implementations. A thorough and critical comparison of the case time series methodology with alternative approaches will be provided in future contributions.

Together with other self-matched methods, the new case time series design is based on strict assumptions to protect against key threats to validity. However, these conditions are not always met in practice, and their violations can lead to important biases. Specifically, the requirement that both exposures and follow-up periods are independent of the outcome poses severe limitations to the application of the method, in particular in clinical and pharmaco-epidemiologic studies. In fact, the temporal distribution of endogenous predictors such as behaviours, clinical therapies, or drug prescriptions are often modified by an outcome event. In contrast, the case time series and other self-controlled designs are well suited for the analysis of exogenous exposures such as environmental factors, as discussed before. Extension to test and relax these strong assumptions have been developed for the self-controlled case series design,^27,28 but further research is needed to implement and assess their validity in case time series models. Conversely, the new design is well suited to control for temporal confounding that can invalidate the assumption of constant baseline risk, through the stratification of the follow-up period and the inclusion of lagged and smooth continuous terms in the model.

Other limitations and areas of current research must be discussed. First, as a method based on a within-subject comparison, the case time series design is ideal for investigating phenomena with short-term changes in risk relative to the study period, while it is less suitable for the analysis of long-term effects and chronic exposures. In fact, while it is in theory possible to extend indefinitely the lag period within the follow-up interval, there is a limit to which the model can disentangle long-lagged effects from seasonal and other trends.⁴² In addition, the splitting of the follow-up period in individual-level time series produces a substantial data expansion, with considerable computational demand especially in the presence of a high number of subjects or long study periods. Schemes based on risk-set sampling, previously proposed for cohort and nested case–control studies,^43–45 are currently under development to address this issue. Finally, the simulation study and the two real-data examples presented basic epidemiological relationships between time-varying variables. However, more complex causal dependencies, involving, for instance, dynamic feedback or multiple pathways, explicitly violate the strict assumptions underpinning the case time series design, and cannot be modelled in the proposed framework. The definition, limitations, and potential extensions of fixed-effects models and related designs within a general causal inference setting is an area of current research.²³

In conclusion, the case time series design represents a novel epidemiologic method for the analysis of transient health associations with time-varying exposures. Its flexible modelling framework can be adapted to various contexts and research areas, for instance in clinical, environmental, and pharmaco-epidemiology, and it is suitable for the analysis of intensive longitudinal data provided by modern data technologies.

Data and code

Online supplemental material includes documents for simulating data with the same features of the datasets used in the two case studies, and for reproducing the steps and results of the analyses presented in the article. An updated version complemented with scripts of the R statistical software is available at https://github.com/gasparrini/CaseTimeSeries.