Experimental quantum speed-up in reinforcement learning agents

Abstract

As the field of artificial intelligence advances, the demand for algorithms that can learn quickly and efficiently increases. An important paradigm within artificial intelligence is reinforcement learning [1], where decision-making entities called agents interact with environments and learn by updating their behaviour based on obtained feedback. The crucial question for practical applications is how fast agents learn [2]. While various works have made use of quantum mechanics to speed up the agent’s decision-making process [3, 4], a reduction in learning time has not been demonstrated yet. Here, we present a reinforcement learning experiment where the learning process of an agent is sped up by utilizing a quantum communication channel with the environment. We further show that combining this scenario with classical communication enables the evaluation of such an improvement, and additionally allows for optimal control of the learning progress. We implement this learning protocol on a compact and fully tuneable integrated nanophotonic processor. The device interfaces with telecom-wavelength photons and features a fast active feedback mechanism, allowing us to demonstrate the agent’s systematic quantum ad-vantage in a setup that could be readily integrated within future large-scale quantum communication networks.

Rapid advances in the field of machine learning (ML) and in general artificial intelligence (AI) are paving the way towards intelligent algorithms and automation. An important paradigm within AI is reinforcement learning (RL), where decision-making entities called ‘agents’ interact with an environment, ‘learning’ to achieve a goal via feedback [1]. Whenever the agent performs well (i.e., makes the right decision), the environment rewards its behaviour, and the agent uses this information to progressively increase the likelihood of accomplishing its task. In this sense, an agent ‘learns’ by ‘reinforcement’. RL has applications in many sectors, from robotics [5, 6] to the healthcare domain [7], to brain-like computing simulation [8] and neural network implementations [6, 9]. Also the celebrated AlphaGo algorithm [10], able to beat even the most skilled human players at the game of Go, employs RL.

At the same time, quantum technologies have experienced remarkable progress [11]. At the heart of quantum mechanics lies the superposition principle, dictating that even the simplest, two-dimensional quantum system is described by a continuum of infinitely many possible choices via a state vector |ψ〉 = α|0〉 + β|1〉 with |α|² + |β|² = 1, while only two possible states, |0〉 and |1〉, exist classically. Advantageous RL algorithms [12, 13] inspired by quantum mechanics have been successful in aiding problems in quantum information processing, e.g., decoding of errors [14–16], quantum feedback [17], adaptive code-design [18], quantum state reconstruction [19], and even the design of quantum experiments [20, 21]. Conversely, quantum technologies have enabled quadratically faster decision-making processes for RL agents via the quantization of their internal hardware [3, 4, 22, 23].

In all of these applications, agent and environment interact entirely classically. Here, we consider a novel RL setting where they can also interact quantumly, formally via a quantum channel [2]. We therefore introduce a quantum-enhanced hybrid agent capable of quantum as well as classical information transfer. This makes it possible to achieve and quantify a quantum speed-up in the agent’s learning time with respect to RL based solely on classical interaction.

We realize this protocol using a fully programmable nanophotonic processor interfaced with photons at telecom wavelengths. The setup enables the implementation of active feedback mechanisms, thus proving suitable for demonstrations of RL algorithms. Moreover, such photonic platforms hold the potential of integrating RL quantum speed-ups in future quantum networks thanks to the photons’ telecom wavelengths. A long-standing goal in the development of quantum communication lies in establishing a form of ‘quantum internet’ [24, 25], a highly interconnected network able to distribute and manipulate quantum states via optical links. We therefore envisage AI and RL to play important roles in future quantum networks, including a potential quantum internet, much in the same way that AI forms integral part of the internet today.

Quantum-Enhanced Reinforcement Learning

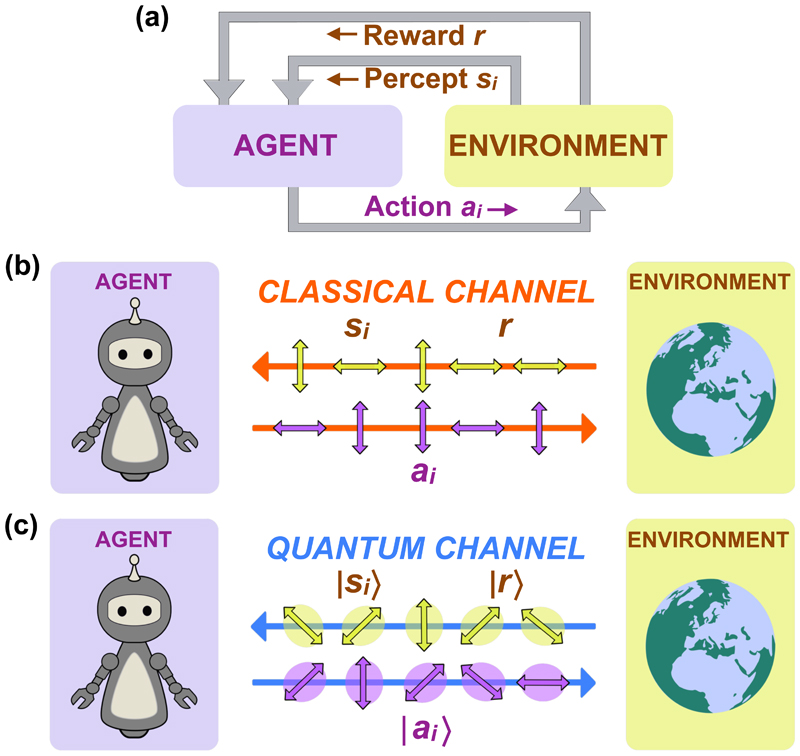
The conceptual idea of RL is shown in Fig. 1(a). A decision-making entity called agent interacts with an environment by receiving perceptual input (‘percepts’) s _i, and outputting specific ‘actions’ a _i accordingly. Different ‘rewards’ r issued by the environment for correct combinations of percepts and actions incentivize agents to improve their decision-making, and thus to learn [1].

Fig. 1.

Schematic of a learning agent. (a) An agent interacts with an environment by receiving perceptual input s _i and outputting actions a _i. When the correct a _i is chosen, the environment issues a reward r that the agent uses to enhance its performance in the next round of interaction. (b) Agent and environment interacting classically, i.e., using a classical channel, where communication is only possible via a fixed preferred basis (e.g., vertical or horizontal photon polarization). (c) Agent and environment interacting via a quantum channel, where arbitrary superposition states are exchanged.

Although RL has already been shown amenable to quantum enhancements, the interaction has so far been restricted exclusively to classical communication, meaning that signals can only be composed from a fixed, discrete alphabet. For signals carried by quantum systems (e.g., single photons considered here) this corresponds to a fixed preferred basis, e.g., ‘vertical’ or ‘horizontal’ photon polarization, as shown in Fig. 1(b).

In general, it has been shown that granting agents access to quantum hardware (while still considering classical communication) does not reduce the learning time, although it allows to output actions quadratically faster [3, 4]. To achieve reductions in learning times, quantum communication becomes necessary.

We therefore consider an environment and a quantum-enhanced hybrid agent with access to internal quantum (as well as classical) hardware interacting by exchanging quantum states |a _i〉, |s _i〉, and |r〉, representing actions a _i, percepts s _i, and rewards r, respectively. Such agents may behave ‘classically’, i.e., use a classical channel, or ‘quantumly’, meaning that communication is no longer limited to a fixed preferred basis, but allows for exchanges of arbitrary superpositions via a quantum channel, as shown in Fig. 1(c). In general, agents react to (sequences of) percepts |s _i–1〉 with (sequences of) actions |a _i〉 according to a policy π(a _i|s _i–1) that is updated during the learning process via classical control.

Within this framework, we focus on so-called [2] deterministic strictly epochal (DSE) learning scenarios, also called episodic instead of epochal [1]. Here, ‘epochs’ consist of strings of percepts $\overrightarrow{s}$ = (s ₀, …,s _L–1) with fixed s ₀, actions $\overrightarrow{a}$ = (a ₁, …, a _L) of fixed length L, and a final reward r, and both $\overrightarrow{s}$ = $\overrightarrow{s}$ ($\overrightarrow{a}$) and r = r($\overrightarrow{a}$) are completely determined by $\overrightarrow{a}$. Therefore, no explicit representation of the percepts is required in our experiment (see Methods). A non-trivial feature of the DSE scenario is that the effective behaviour of the environment can be modelled via a unitary U _E [2] on the action and reward registers A and R as

$$U_{\text{E}}\left|\overrightarrow{a}{\rangle }_{\text{A}}\right|{0\rangle }_{\text{R}}=\{\begin{array}{c}\left|{\overrightarrow{a}\rangle }_{\text{A}}\right|{1\rangle }_{\text{R}}\text{if}r\left(\overrightarrow{a}\right)>0\\ \left|{\overrightarrow{a}\rangle }_{\text{A}}\right|{0\rangle }_{\text{R}}\text{if}r\left(\overrightarrow{a}\right)=0\end{array}.$$ (1)

U _E is similar to a generalized controlled-NOT gate such that in case of rewarded action sequences (r($\overrightarrow{a}$) > 0), the reward state is flipped. U _E can therefore be used to perform a quantum search for such sequences.

A hybrid agent can choose between quantum and classical behaviour in each epoch. In classical epochs, the agent prepares the state |$\overrightarrow{a}$〉_A|0〉_R, where $\overrightarrow{a}$ is determined by sampling from a classical probability distribution p($\overrightarrow{a}$) determined by its policy π. With a winning probability

$$\epsilon ={\sin }^2\left(\xi \right)={\displaystyle \sum _{\left\{\overrightarrow{a}|r\left(\overrightarrow{a}\right)>0\right\}}p\left(\overrightarrow{a}\right)},$$ (2)

with ξ ∈ [0, 2π], the agent receives a reward and updates its policy according to a rule, presented in Eq. (4), based on projective simulation [26] (see also Methods). In quantum epochs, the following steps are performed:

1. The agent prepares the state |ψ〉_A|–〉_R, with $|{\psi \rangle }_{\text{A}}={\displaystyle {\sum }_{\overrightarrow{a}}\sqrt{p\left(\overrightarrow{a}\right)}|{\overrightarrow{a}\rangle }_{\text{A}}}=\cos \left(\xi \right)|{\ell \rangle }_{\text{A}}+\sin \left(\xi \right)|{w\rangle }_{\text{A}}$, and sends the state to the environment. |𝑤〉_A and |ℓ 〉_A are superpositions of all winning (rewarded) and losing (non-rewarded) action sequences, respectively, and |–〉_R = (|0〉_R – |1〉_R)/$\sqrt{2}$.

2. The environment applies U _E from Eq. (1) to |ψ〉_A|–〉_R, flipping the sign of the winning state:

   $$U_{\text{E}}\left|{\psi \rangle }_{\text{A}}\right|{-\rangle }_{\text{R}}=\left[\cos \left(\xi \right)|{\ell \rangle }_{\text{A}}-\sin \left(\xi \right)|{w\rangle }_{\text{A}}\right]|{-\rangle }_{\text{R}},$$ (3)

   and returns the resulting state to the agent.

3. The agent performs a reflection U _R = 2 |ψ〉〈ψ|_A – 𝟙_A over the initial state |ψ〉_A.

The last step leads to amplitude amplification similar to Grover’s algorithm [27] and thus to an increased probability sin²(3ξ) [28] to find rewarded action sequences (see Methods). In our experiment, the hybrid agent performs a single query (and thus a single step of amplitude amplification) during a quantum epoch. However, the general framework allows for multiple steps of amplitude amplification in consecutive quantum epochs.

While quantum epochs lead to an increased winning probability, they do not reveal the reward (or corresponding percept sequence, in general). The reward can be determined only via classical test epochs, where the obtained action sequence is used as input. Thus, the hybrid agent alternates between quantum and classical test epochs, updating its policy every time a reward is obtained after a test epoch. Such agents accomplish their task of finding winning action sequences faster, and hence learn faster than entirely classical agents. This approach allows us to quantify the speed-up in learning time, which is not possible in the general setting discussed in [2]. The learning speed-up manifests in a reduced average learning time 〈T〉_Q, i.e., the average number of epochs necessary to achieve a certain winning probability P _L. In general, a quadratic improvement can be achieved if the maximal number of coherent interactions between agent and environment scales with the problem size (see Methods).

Experimental Implementation

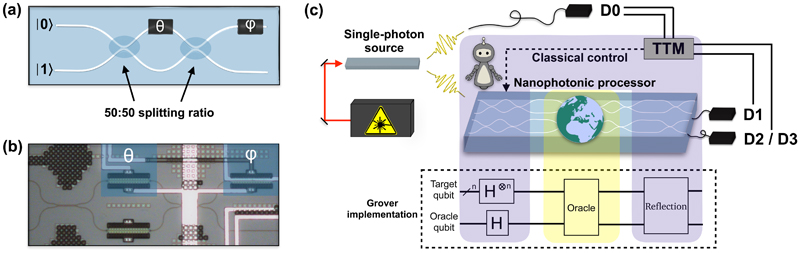
Quantized RL protocols can be compactly realized using state-of-the-art photonic technology [29]. Nowadays, integrated photonic platforms hold the advantage of providing scalable architectures where many elementary components can be accommodated on small devices [30]. Here, we use a programmable nanophotonic processor comprising 26 waveguides fabricated to form 88 Mach-Zehnder interferometers (MZIs). An MZI is equipped with two configurable phase shifters as shown in Figs. 2(a), (b), and acts as a tuneable beam splitter. Information is spatially encoded onto two orthogonal modes, |0〉 = (1, 0)^T and |1〉 = (0, 1)^T, which constitute the computational basis.

Fig. 2.

Experimental setup. (a) Single programmable unit consisting of a Mach-Zehnder interferometer (MZI) equipped with two fully tuneable phase shifters, one internal allowing for a scan of the output distribution over θ ∈ [0, 2π], and one external dictating the relative phase ϕ ∈ [0, 2π] between the two output modes. This makes the MZI act as a fully tuneable beam splitter and allows for coherent implementation of sequences of quantum gates. (b) Image of a single MZI in the processor. The third phase shifter in the bottom arm of the interferometer is not used. (c) Overview of the setup. A single-photon source generates single-photon pairs at telecom wavelength. One photon is sent to a single-photon detector D0, while the other one is coupled into the processor and undergoes the desired computation. It is then detected, in coincidence with the photon in D0, either in detector D1 or in D2/D3 after the agent plays the classical/quantum strategy (see Fig. 3 for more details). The coincidence events are recorded with a custom-made time tagging module (TTM). Different areas of the processor are assigned to either the agent or the environment, that can perform a Grover-like quantum search to look for rewarded action sequences in quantum epochs. The agent has access to a classical control that updates its policy.

As illustrated in Fig. 2(c), pairs of single photons are generated (at telecom wavelengths) from a single-photon source. One photon is coupled into a waveguide and then detected by single-photon detectors D1, D2 or D3, while the other one is sent to D0 for heralding (i.e., clicks in detectors D1, D2 or D3 are registered in coincidence with clicks in D0). The detectors are superconducting nanowires with efficiences of up to ~90% (see Methods for experimental details). The processor is divided into three regions, where the first and last are assigned to the agent, and the middle region to the environment, in order to carry out, in quantum epochs, steps 1-3 listed above. The agent is further equipped with a classical control mechanism (a feedback loop) that updates its learning policy.

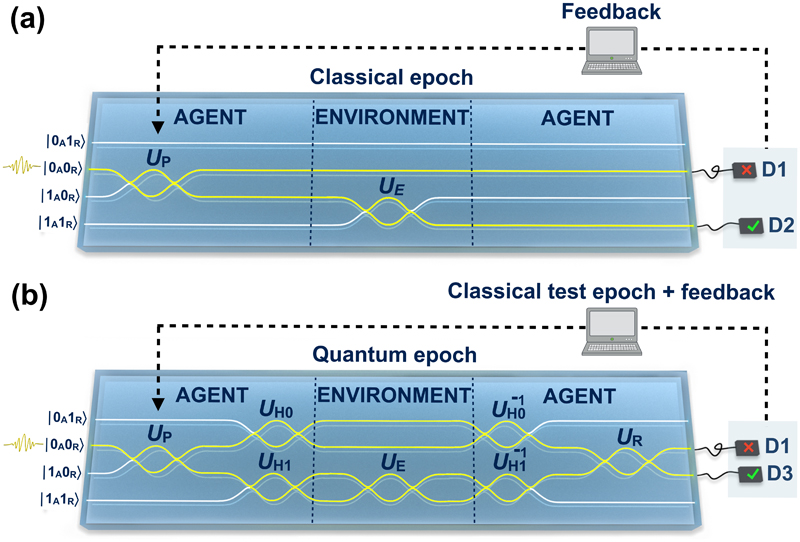
In our experiment, we represent the winning and losing action states |𝑤 〉_A and |ℓ 〉_A by a single qubit via |0〉_A = |ℓ 〉_A and |1〉_A = |𝑤 〉_A, and use another qubit to encode the reward (|0〉_R, |1〉_R). This results in a four-level system, where each level is a waveguide in our processor, as shown in Fig. 3. The winning probability for the agent is initially set to ε = sin²(ξ) = 0.01, representing a single rewarded action sequence out of 100. After a single photon is coupled into the mode |0_A0_R〉, the agent creates the state |ψ〉_A = (cos(ξ)|0〉_A + sin(ξ)|1〉_A)|0〉_R by applying a unitary U _P. Next, it can decide to play classically or quantum-mechanically.

Fig. 3.

Circuit implementation. One photon is coupled into the |0_A0_R〉 waveguide and undergoes different unitaries depending on whether a classical (a) or a quantum (b) epoch is implemented. The waveguides highlighted in yellow show the photon’s possible paths. Identity gates are represented by straight waveguides. Only the part of the processor needed for the computation is represented.

Classical strategy. The environment flips the reward qubit only if the action qubit is in the winning state via U _E, see Fig. 3(a). Next, the photon is coupled out and detected in either D1 or D2 with probability cos²(ξ) and sin²(ξ), respectively. If D2 is triggered (i.e., the agent has been rewarded), a feedback mechanism updates the policy π by updating the winning probability ε _j after having obtained j rewards as

$${\epsilon }_j=\frac{1+2j}{100+2j}.$$ (4)

π is related to p($\overrightarrow{a}$), and therefore to ε, via Eq. (A.1) (see Methods).

Quantum strategy. The hybrid agent uses this strategy to speed up its learning process. After the reward qubit is rotated to |–〉_R via U _H0 and U _H1, the environment acts as an oracle via U _E as in Eq. (3). Consecutively, the agent reverses the effect of U _H0 and U _H1, and performs the reflection U _R, see Fig. 3(b). Measuring in the computational basis of the action register then leads to the detection of a rewarded action sequence with increased probability sin²(3ξ) in D3. For practical reasons, the classical test epoch is implemented only in software (see Methods). The update rule remains the same as in the classical case.

In general, any Grover-like algorithm faces a drop in amplitude amplification after the optimal point is reached. Since different agents will reach this optimal point in different epochs, one can identify the probability ε = 0.396 until which it is beneficial for all agents to use a quantum strategy, as they will observe more rewards than in the classical strategy on average (see Methods). When this probability is surpassed, it is advantageous to switch to an entirely classical strategy. This combined strategy thus avoids the typical amplitude amplification drop without introducing additional overheads in terms of experimental resources.

Results

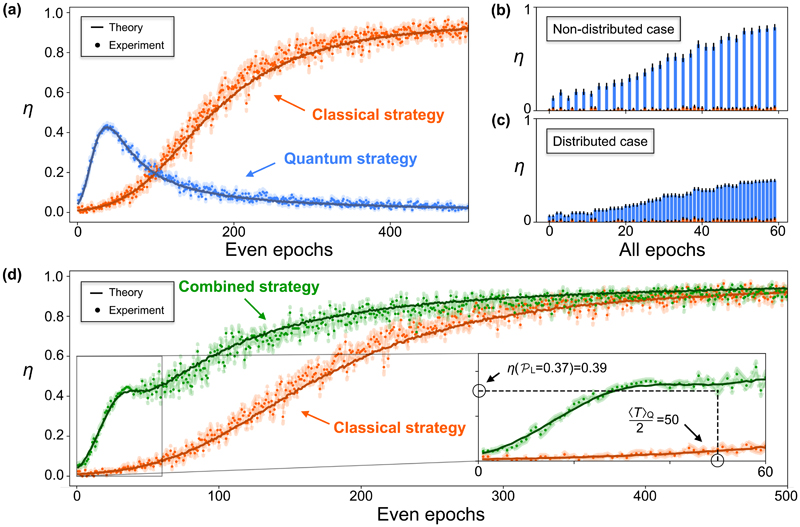
At the end of each classical epoch, we record outcomes 1 and 0 for the rewarded and non-rewarded behaviour, respectively, obtaining a binary sequence whose length equals the number of played epochs in the classical learning strategy and half of the number of played epochs in the quantum strategy (as here two epochs, quantum and classical test, are needed to obtain the reward). For a fair comparison between these scenarios, in the quantum strategy the reward is distributed (i.e., averaged) over the quantum and classical test epochs. The reward is then averaged over different independent agents. Fig. 4 shows this average reward η for the different learning strategies.

Fig. 4.

Behaviour of the average reward η for different learning strategies. The solid line represents the theoretical data simulated with n = 10,000 agents, while the dots represent the experimental data measured with n = 165 agents. The shaded regions indicate the errors associated to each single data point. (a) η of agents playing a quantum (blue) or classical (orange) strategy. (b) η accounting for rewards obtained only every second epoch in the quantum strategy, compared to (c) the case where the reward is distributed over the two epochs needed to acquire it. (d) Comparison between the classical (orange) and combined (green) strategy, where an advantage over the classical strategy is visible. Here, the agents stop the quantum strategy at their best performance (at ε = 0.396) and continue playing classically. The inset shows the point where agents playing the quantum strategy reach the winning probability P _L = 0.37, after 〈T〉_Q = 100 epochs.

The theoretical data is simulated for n = 10,000 agents and the experimental data obtained from n = 165. Fig. 4(a) visualizes the quantum improvement originating from the use of amplitude amplification in comparison with a purely classical strategy. For completeness, the comparison between not distributing and distributing the reward over two epochs in the quantum strategy is shown in Figs. 4(b), (c).

When ε = 0.396, η for the quantum strategy starts decreasing, as visible in Fig. 4(a). Our setup allows the agents to choose the favorable strategy by switching from quantum to classical when the latter becomes advantageous. This combined strategy outperforms the purely classical scenario, as shown in Fig. 4(d). As previously discussed, a certain winning probability P _L has to be defined to quantify the learning time. Choosing P _L = 0.37 (note however, that any probability below ε = 0.396 can be chosen), the learning time 〈T〉 for P _L decreases from 〈T〉_C = 270 in the classical strategy to 〈T〉_Q = 100 in the combined strategy. This implies a reduction of 63%, which fits well to the theoretical values $T_{\text{C}}^{\text{theory}}=293$ and $T_{\text{Q}}^{\text{theory}}=97$, accounting for small experimental imperfections.

In general, hybrid agents can experience a quadratic speed-up in their learning time if arbitrary numbers of coherent Grover iterations can be performed [31], even if the number of rewarded actions is unknown [32].

Methods

I. Quantum enhancement in reinforcement learning agents

Here, we present an explicit method for combining a classical agent with quantum amplitude amplification. Introducing a feedback loop between classical policy update and quantum amplitude amplification, we are able to determine achievable improvements in sample complexity, and thus in learning time. Additionally, the final policy of our agent has properties similar to those of the underlying classical agent, leading to a comparable behaviour as discussed in more detail in [31] (a paper dedicated to discuss the theoretical background of the hybrid agent more specifically).

In the following, we focus on simple deterministic strictly epochal (DSE) environments, where the interaction between the agent and the environment is structured into epochs. Each epoch starts with the same percept s ₀, and at each time step i an action-percept pair (a _i, s _i) is exchanged. Many interesting environments are epochal, e.g., in applications of RL to quantum physics [21, 36–38] or popular problems such as playing Go [10]. At the end of each epoch, after L action-percept pairs are communicated, the agent receives a reward r ∈ {0, 1}. The rules of the game are deterministic and time independent, such that performing a specific action a_i after receiving a percept s _i–1 always leads to the same following percept s _i.

The behaviour of an agent is determined by its policy described by the probability π(a _i|s _i–1) to perform the action a _i given the percept s _i–1. In deterministic settings, the percept s _i is completely determined by all previously performed actions a ₁, …, a _i such that π(a _i|s _i–1) = π(a _i|a ₁, …, a _i–1). Thus, the behaviour of the agent within one epoch is described by action sequences $\overrightarrow{a}$ = (a ₁, …, a _L) and their corresponding probabilities

$$p\left(\overrightarrow{a}\right)={\displaystyle \prod _{i=1}^L\pi \left(a_i\mid a_1,\dots ,a_{i-1}\right).}$$ (A.1)

Our learning agent uses a policy based on projective simulation [26], where each action sequence $\overrightarrow{a}$ is associated with a weight factor h($\overrightarrow{a}$) initialized to h = 1. Its policy is defined via the probability distribution

$$p\left(\overrightarrow{a}\right)=\frac{h\left(\overrightarrow{a}\right)}{{\displaystyle \sum _{\overrightarrow{a}\prime }h\left(\overrightarrow{a}\prime \right)}}.$$ (A.2)

In our experiment, the initial winning probability ε, i. e., the probability to choose rewarded action sequences (r($\overrightarrow{a}$) > 0), is given by

$$\epsilon ={\displaystyle \sum _{\left\{\overrightarrow{a}\mid r\left(\overrightarrow{a}\right)>0\right\}}p\left(\overrightarrow{a}\right)=\frac{{\displaystyle \sum _{\left\{\overrightarrow{a}\mid r\left(\overrightarrow{a}\right)>0\right\}}h\left(\overrightarrow{a}\right)}}{{\displaystyle \sum _{\left\{\overrightarrow{a}\right\}}h\left(\overrightarrow{a}\right)}}},$$ (A.3)

and is set to 1/100. If the agent has chosen the sequence $\overrightarrow{a}$, it updates the corresponding weight factor via

$$h\left(\overrightarrow{a}\right)\to h\left(\overrightarrow{a}\right)+\lambda r\left(\overrightarrow{a}\right),$$ (A.4)

where λ = 2 in our experiment and r($\overrightarrow{a}$) = 1 (0) if $\overrightarrow{a}$ is rewarded (non-rewarded). Thus, the winning probability after the agent has found j rewards is given by Eq. (4). In general, the update method for quantum-enhanced agents is not limited to projective simulation and can be used to enhance any classical learning scenario, provided that p($\overrightarrow{a}$) exists and that the update rule is solely based on the observed rewards. We generalize the given learning problem to the quantum domain by encoding different action sequences $\overrightarrow{a}$ into orthogonal quantum states |$\overrightarrow{a}$〉 defining our computational basis. Additionally, we create a fair unitary oracular variant of the environment [2], whose effective behaviour on the action register can be described by Ũ _E as

$${\tilde{U}}_{\text{E}}|\overrightarrow{a}\rangle =\{\begin{array}{cc}-|\overrightarrow{a}\rangle & \text{if}r\left(\overrightarrow{a}\right)>0\\ |\overrightarrow{a}\rangle & \text{if}r\left(\overrightarrow{a}\right)=0\end{array}.$$ (A.5)

The unitary oracle Ũ _E can be used to perform, for instance, a Grover search or amplitude amplification for rewarded action sequences by performing Grover iterations

$$U_{\text{G}}=\left(2\left|\psi \rangle \langle \psi \right|-\text{𝟙}\right){\tilde{U}}_{\text{E}}$$ (A.6)

on an initial state |ψ〉. A quantum-enhanced agent with access to Ũ _E can thus find rewarded action sequences faster than a corresponding classical agent defined by the same initial policy π(a _i|s _i–1) and update rules.

In general, the optimal number k of Grover iterations $U_{\text{G}}^k|\psi \rangle$ depends on the winning probability ε via k ~ 1/$\sqrt{\epsilon }$ [27]. In the following, we assume that ε is known at least to a good approximation. This is for instance possible if the number of rewarded action sequences is known. However, a similar agent can also be developed if ε is unknown by adapting methods from [32] as described in [31].

I.1. Description of the agent

A quantum-enhanced hybrid agent is constructed via the following steps:

1. Given the classical probability distribution p($\overrightarrow{a}$), determine the winning probability ε = sin²(ξ) based on the current policy and prepare the quantum state in the action register:

   $$|\psi \rangle ={\displaystyle \sum _{\left\{\overrightarrow{a}\right\}}\sqrt{p\left(\overrightarrow{a}\right)}}|\overrightarrow{a}\rangle$$ (A.7)

   $$=\cos \left(\xi \right)|\ell \rangle +\sin \left(\xi \right)|w\rangle .$$ (A.8)
   Here, the quantum states

   $$|\ell \rangle ~{\displaystyle \sum _{\left\{\overrightarrow{a}|r\left(\overrightarrow{a}\right)=0\right\}}\sqrt{p\left(\overrightarrow{a}\right)}}|\overrightarrow{a}\rangle ,$$ (A.9)

   $$|w\rangle ~{\displaystyle \sum _{\left\{\overrightarrow{a}|r\left(\overrightarrow{a}\right)>0\right\}}\sqrt{p\left(\overrightarrow{a}\right)}}|\overrightarrow{a}\rangle ,$$ (A.10)

   contain all losing and winning components, respectively. In our experiment, we identify $|\ell \rangle \stackrel{\wedge}{=}|0\rangle$ and $|w\rangle \stackrel{\wedge}{=}|1\rangle$. The task assigned to the agent is to (learn to) perform the winning sequences |𝑤 〉 via policy update. This translates to a maximization of the obtained reward.

2. Apply the optimal number k $\left(\sqrt{\epsilon }\right)$ of Grover iterations leading to

   $$|{\psi }^{\prime }\rangle =U_{\text{G}}^k|\psi \rangle ,$$ (A.11)

   and perform a measurement in the computational basis on |ψ′〉 to determine a test action sequence $\overrightarrow{a}$.

3. Play one classical epoch by using the test sequence $\overrightarrow{a}$ determined in step 2 and obtain the corresponding percept sequence $\overrightarrow{s}$($\overrightarrow{a}$) and the reward r($\overrightarrow{a}$).

4. Update ε, and thus the classical policy π, using the rule in Eq. (4).

There exists a limit P on ε determining whether it is more advantageous for the agent to perform k Grover iterations with k $\left(\sqrt{\epsilon }\right)$ ≥ 1 or sample directly from p($\overrightarrow{a}$) (therefore k $\left(\sqrt{\epsilon }\right)$ = 0) to determine $\overrightarrow{a}$. In the latter case, the agent would interact only classically (as in step 3) with the environment.

After each epoch, a classical agent receives a reward with probability sin² (ξ). A quantum-enhanced agent can instead use one epoch to either perform one Grover iteration (step 2) or to determine the reward of a given test sequence $\overrightarrow{a}$ (step 3). After k Grover iterations, the winning probability is sin²[(2k + 1)ξ] [28] (see next section). Thus, for k = 1, the agent receives a reward after every second epoch with probability sin² (3ξ). Therefore, we define the expected average reward of an agent playing a classical strategy as η _C = sin²(ξ) and of an agent playing a quantum strategy with k = 1 as η _Q = sin²(3ξ)/2. For ε < P, η _Q > η _C, meaning that the quantum strategy proves advantageous over the classical case. However, as soon as η _Q = η _C (at P = 0.396), a classical agent starts outperforming a quantum-enhanced agent that still performs Grover iterations.

Determining the winning probability ε exactly as in the example presented here is not always possible. In general, additional information like the number of possible solutions and model building helps to perform this task. Note that a P smaller than 0.396 should be chosen if ε can only be estimated up to some range. To circumvent this problem, methods like Grover search with unknown reward probability [32], or fixed-point search [39], can be used to determine if and how many steps of amplitude amplification should be performed [31].

I.2. Enhancement of the winning probability

After a quantum epoch, the amplitude sin(ξ) of the winning state |𝑤 〉 increase to sin(3ξ). Here, we derive this result. The projections onto the winning and losing subspaces are given by $P_w={\displaystyle {\sum }_{\left\{\overrightarrow{a}\mid r\left(\overrightarrow{a}\right)>0\right\}}|\overrightarrow{a}\rangle }\langle \overrightarrow{a}|$ and $P_{\ell }={\displaystyle {\sum }_{\left\{\overrightarrow{a}\mid r\left(\overrightarrow{a}\right)=0\right\}}|\overrightarrow{a}\rangle }\langle \overrightarrow{a}|$, respectively, which are orthogonal and sum to Identity. Therefore, the initial state (A.8) can be decomposed into a normalized winning |𝑤 〉 ∝ P _𝑤 |ψ〉 and losing |ℓ 〉 ∝ P _ℓ|ψ〉 component, and the unitary (A.6) implementing one Grover iteration can be written as

$$U_{\text{G}}=\left(2\left|\psi \rangle \langle \psi \right|-\text{𝟙}\right)\left(P_{\ell }-P_w\right).$$ (A.12)

Now, let us investigate the effect of U _G on an arbitrary real superposition

$$|\alpha \rangle =\sin \left(\alpha \right)|w\rangle +\cos \left(\alpha \right)|\ell \rangle$$ (A.13)

in the plane spanned by |𝑤 〉 and |ℓ 〉. Using the trigonometric addition theorems, the application of one Grover iteration to |a〉

$$U_{\text{G}}|\alpha \rangle =\sin \left(\alpha +2\xi \right)|w\rangle +\cos \left(\alpha +2\xi \right)|\ell \rangle$$ (A.14)

can be identified as a rotation of 2ξ in the plane. Assuming α = ξ, we therefore find the amplitude of |w〉 to be sin(3ξ), and thus obtain a winning probability sin²(3ξ). Implementing k Grover iterations leads to sin²[(2k + 1)ξ].

I.3. Learning time

We define the learning time T as the number of epochs an agent needs on average to reach a certain winning probability P _L. The hybrid agent can reach P with fewer epochs on average than its classical counterpart. However, once both reach P, they need on average the same number of epochs to reach P + ΔP with 0 ≤ ΔP < 1 –P. Therefore, we choose P _L ≤ P in order to quantify the achievable improvement of a hybrid agent compared to its classical counterpart. In our experiment, we choose P _L = 0.37 to define the learning time.

Let l _J = {$\overrightarrow{a}$ ₁, …, $\overrightarrow{a}$ _J〉 be a time-ordered list of all the rewarded action sequences an agent has found until it reaches P _L. Note that the actual policy π _j, and thus p _j, of our agents depend only on the list l _j of observed rewarded sequences of actions, and this is independent of whether they have found them via classical sampling or quantum amplitude amplification. As a result, a classical agent and its quantum-enhanced hybrid version are described by the same policy π(l _j) and behave similarly if they have found the same rewarded action sequences. However, the hybrid agent finds them faster.

In general, the actual policy and overall winning probability might depend on the rewarded action sequences that have been found. Thus, the number J of observed rewarded action sequences necessary to learn might vary. However, this is not the case for the experiment reported here. In our case, the learning time can be determined via

$$T\left(J\right)={\displaystyle \sum _{j=0}^{J-1}{t}_j,}$$ (A.15)

where t _j determines the number of epochs necessary to find the next rewarded sequence $\overrightarrow{a}$ _j+1 after it has observed j rewards. For a purely classical agent, the average time is given by

$${\langle t_j\rangle }_{\text{C}}=\frac{1}{{\epsilon }_j}.$$ (A.16)

This time is quadratically reduced to

$${\langle t_j\rangle }_Q=\frac{\alpha }{\sqrt{{\epsilon }_j}}$$ (A.17)

for the hybrid agent. Here, α is a parameter depending only on the number of epochs needed to create one oracle query Ũ _E [2] and on whether ε _j is known. In the case considered here, we find α = π/4. As a consequence, the average learning time for the hybrid agent is given by

$${\langle T\left(J\right)\rangle }_{\text{Q}}={\displaystyle \sum _{j=0}^{J-1}\frac{\alpha }{\sqrt{{\epsilon }_j}}}\le \alpha \sqrt{J}\sqrt{{\langle T\left(J\right)\rangle }_{\text{C},}}$$ (A.18)

where we used the Cauchy-Schwarz inequality and equations A.15 and A.16. The classical learning time typically scales with 〈T〉_C ~ A ^K for a learning problem with episode length K and the choice between A different actions in each step. The number J of observed rewarded sequences in order to learn depends on the specific policy update and sometimes also on the list l _J of observed rewarded action sequences. For an agent sticking with the first rewarded action sequence, we would find J = 1. However, typical learning agents are more explorative, and common scalings are J ~ K such that we find

$${\langle T\left(J\right)\rangle }_{\text{Q}}\sim \sqrt{\log \left({\langle T\left(J\right)\rangle }_{\text{C}}\right)}\sqrt{{\langle T\left(J\right)\rangle }_{\text{C}}}$$ (A.19)

for these cases. This is equivalent to a quasi-quadratic speed-up in the learning time if arbitrary numbers of Grover iterations can be performed.

In more general settings, there exist several possible l _J with different length J such that the learning time 〈T(J)〉 needs to be averaged over all possible l _J, which again leads to a quadratic speed-up in learning time [31].

I.4. Limited coherent evolutions

In general, all near-term quantum devices allow for coherent evolution only for a limited time and are thus limited to a maximal number of Grover iterations. For winning probabilities ε = sin²(ξ) with (2k + 1)ξ ≤ π/2, performing k Grover iterations leads to the highest probability of finding a rewarded action.

Again, we assume that the actual policy of an agent only depends on the number of observed rewards an agent has found. As a consequence, the average time a hybrid agent limited to k Grover iterations needs to achieve the winning probability P < sin²[π/(4k + 2)] is given by [31]

$${\langle T\left(J,k\right)\rangle }_{\text{Q}}={\displaystyle \sum _{j=0}^{J-1}\frac{{\alpha }_{0}k+1}{{\sin }^2\left[\left(2k+1\right){\xi }_j\right]}},$$ (A.20)

with α ₀ determining the number of epochs necessary to create one oracle query Ũ _E. For α ₀ = 1, k ≫ 1 and (2k + 1)ξ _J ≪ π/2 we can approximate the learning time for the hybrid agent via

$${\langle T\left(J,k\right)\rangle }_{\text{Q}}\approx {\displaystyle \sum _{j=0}^{J-1}\frac{1}{4k{\epsilon }_j}}=\frac{{\langle T\left(J\right)\rangle }_{\text{C}}}{4k},$$ (A.21)

where we used sin x ≈ x for x ≪ 1. In general, it can be shown [31] that the winning probability P _k = sin²[π/(4k + 2)] can be reached by a hybrid agent limited to k Grover iterations in a time

$${\langle T\left(k\right)\rangle }_{\text{Q}}\le \gamma \frac{{\langle T\rangle }_{\text{C}}}{k},$$ (A.22)

where γ is a factor depending on the specific setting.

In our case, Eq. (A.20) can be used to compute the lower bound for the average quantum learning time, with α ₀ = k =1. For the classical strategy, Eq. (A.16), together with Eq. (A.15), is used. Thus, given P _L = 0.37, the predictions for the learning time in our experiment are $T_{\text{Q}}^{\text{theory}}=97$ and $T_{\text{C}}^{\text{theory}}=293$.

II. Experimental details

A continuous wave laser (Coherent Mira HP) is used to pump a single-photon source producing photon pairs in the telecom wavelength band. The laser light has a central wavelength of 789.5 nm and pumps the single photon source at a power of approximately 100 mW. The source is a periodically poled KTiOPO₄ non-linear crystal placed in a Sagnac interferometer [40, 41], where the emission of single photons occurs via a type-II spontaneous parametric down-conversion (SPDC) process. The crystal (produced by Raicol) is 30 mm long, set to a temperature of 25 °C, has a poling period of 46.15 μm and is quasi-phase matched for degenerate emission of photons at 1570 nm when pumping with coherent laser light at 785 nm. As the processor is calibrated for a wavelength of 1580 nm, we shift the wavelength of the laser light to 789.75 nm in order to produce one photon at 1580 nm (that is then coupled into the processor) and another one at 1579 nm (the heralding photon).

The processor is a silicon-on-insulator (SOI) type, designed by the Quantum Photonics Laboratory at MIT (Massachusetts Institute of Technology) [30]. Each programmable unit on the device acts as a tuneable beam splitter implementing the unitary

$$U_{\theta ,\varphi }=\left(\begin{array}{cc}{e}^{i\varphi }\sin \frac{\theta }{2}& e^{i\varphi }\cos \frac{\theta }{2}\\ \cos \frac{\theta }{2}& -\sin \frac{\theta }{2}\end{array}\right),$$ (A.23)

where θ and ϕ are the internal and external phases shown in Figs. 2(a), (b), set via thermo-optical phase shifters controlled by a voltage supply. The achievable precision for phase settings is higher than 250 μrad. The bandwidth of the phase shifters is around 130 kHz. The waveguides, spatially separated from one another by 25.4 μm, are designed to admit one linear polarization only. The high contrast in refractive index between the silicon and silica (the insulator) allows for waveguides with very small bend radius (less than 15 μm), thus enabling a high component density (in our case 88 MZIs) on small areas (in our case 4.9 x 2.4 mm). Given the small dimensions, the in-(out-)coupling is realized with the help of Si ₃ N ₄ – SiO ₂ waveguide arrays (produced by Lionix International), that shrink (and enlarge) the 10 μm optical fibers’ mode to match the 2 μm mode size of the waveguides in the processor. The total input-output loss is around 7 dB. The processor is stabilized to a temperature of 28 °C and calibrated at 1580 nm for optimal performance. To reduce the black-body radiation emission due to the heating of the phase shifters when voltage is applied, wavelength division multiplexers with a transmission peak centered at 1571 nm and bandwidth of 13 nm are used before the photons are sent to the detectors. In our processor, two external phase shifters in the implemented circuits were not responding to the supplied voltage. These defects were accounted for by employing an optimization procedure.

The single-photon detectors are multi-element superconducting nanowires (produced by Photon Spot) with efficiencies up to 90% in the telecom wavelength band. They have a dark count rate of ~ 100 c.p.s, low timing jitter (hundreds of ps) and a reset time < 100 ns [42]. Coincidence events are those detection events registered in D0 and at the output of the processor that fall into a temporal window of 1.3 ns (the coincidence window), and are found using a time tagging module (TTM). In more detail, in order to record coincidences and then update the agent’s policy accordingly, the following steps are performed in the classical/quantum strategy (after initially setting h _𝑤 = ${\displaystyle {\sum }_{\left\{\overrightarrow{a}\mid r\left(\overrightarrow{a}\right)>0\right\}}h\left(\overrightarrow{a}\right)}=1$ and h _ℓ = ${\displaystyle {\sum }_{\left\{\overrightarrow{a}\mid r\left(\overrightarrow{a}\right)=0\right\}}h\left(\overrightarrow{a}\right)}=99$ such that ε = 0.01):

1. The TTM records the time tags for photons in D0, D1 and D2/D3.

2. A Python script converts the time tags into arrival times, and it iterates through until it finds a coincidence event between either D0 and D1, or D0 and D2/D3.

3. If a coincidence event between D0 and D1 (or D0 and D2/D3) is first found, a 0 (1) is sent to another Python script controlling the MZIs’ phase shifters operating on a different computer. If a 0 is sent, the ratio ε = h _𝑤/(h _ℓ + h _𝑤) remains unchanged. If a 1 is sent, h _𝑤 is updated as h _𝑤 + 2, which follows the update in Eq. (4). In the quantum strategy, this step also includes the implementation of a classical test epoch.

Implementing classical test epochs on hardware would require ‘testing’ the measured action state, i.e., using the measured action sequence as input and making the environment act via U _E, thus leading to detection of a reward |0〉_R or |1〉_R. However, since this simple circuit works in very close agreement with theoretical predictions (its visibility exceeds 0.99), this part has been implemented in software only.

The update rate is ~ 1 Hz for both the classical and quantum epochs, and can be reduced up to the phase shifters’ bandwidth.

Conclusions

We have demonstrated a novel RL protocol where an agent can boost its performance by allowing quantum communication with the environment. This enables a quantum speed-up in its learning time and optimal control of the learning process. Emerging photonic technology provides the advantages of compactness, tunability and low-loss communication, thus proving suitable for RL algorithms where active feedback mechanisms, even over long distances, need to be implemented. Future scaled-up implementations of our protocol rely on a linearly increasing number of waveguides with the action space size when considering action sequences of length L = 1, and the use of just a single photon. In this case, a learning task with N different actions requires a processor with 2N modes, while 3N + 1 or maximally $\frac{\pi }{4}\sqrt{N}\left(3N+1\right)$ gates are needed for a single or multiple rounds of amplitude amplification, respectively. In general, multiple photons will be required to deal with a combinatorially big space of action sequences of arbitrary length L. We envision our protocol to aid specifically in problems where frequent search is needed, e.g., network routing problems, where, for instance, tens of qubits, waveguides and detectors would be employed to represent search spaces of 10⁴ elements. In general, the development of superconducting detectors, on-demand single-photon sources [33], or the large-scale integration of artificial atoms within photonic circuits [34] suggest significant steps towards scalable multi-photon applications. Although photonic architectures are particularly suitable for such learning algorithms, our theoretical background is applicable to different platforms, e.g., trapped ions or superconducting qubits. Here, future implementations can feature the implementation of agent and environment as spatially separated systems, and a light-matter quantum interface for coherent exchange between them [24, 35].

Data Availability

All the datasets used in the current work are available under the DOI 10.5281/zenodo.4327211.