Skip to main content
NCBI home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2022 Mar 1.
Published in final edited form as: Magn Reson Med. 2021 Oct 22;87(3):1289–1300. doi: 10.1002/mrm.29048

QSMxT: Robust masking and artifact reduction for quantitative susceptibility mapping

Ashley Wilton Stewart 1,2,✉, Simon Daniel Robinson 2,3,4,5, Kieran O’Brien 1,2,6, Jin Jin 1,2,6, Georg Widhalm 7, Gilbert Hangel 5,7, Angela Walls 8, Jonathan Goodwin 9,10, Korbinian Eckstein 5, Monique Tourell 1,2, Catherine Morgan 11,12,13, Aswin Narayanan 2, Markus Barth 1,2,14, Steffen Bollmann 1,2,14
PMCID: PMC7612305  EMSID: EMS140944  PMID: 34687073

Abstract

Purpose

Quantitative susceptibility mapping (QSM) estimates the spatial distribution of tissue magnetic susceptibilities from the phase of a gradient-echo signal. QSM algorithms require a signal mask to delineate regions with reliable phase for subsequent susceptibility estimation. Existing masking techniques used in QSM have limitations that introduce artifacts, exclude anatomical detail, and rely on parameter tuning and anatomical priors that narrow their application. Here, a robust masking and reconstruction procedure is presented to overcome these limitations and enable automated QSM processing. Moreover, this method is integrated within an open-source software framework: QSMxT.

Methods

A robust masking technique that automatically separates reliable from less reliable phase regions was developed and combined with a two-pass reconstruction procedure that operates on the separated sources before combination, extracting more information and suppressing streaking artifacts.

Results

Compared with standard masking and reconstruction procedures, the two-pass inversion reduces streaking artifacts caused by unreliable phase and high dynamic ranges of susceptibility sources. It is also robust across a range of acquisitions at 3 T in volunteers and phantoms, at 7 T in tumor patients, and in an in silico head phantom, with significant artifact and error reductions, greater anatomical detail, and minimal parameter tuning.

Conclusion

The two-pass masking and reconstruction procedure separates reliable from less reliable phase regions, enabling a more accurate QSM reconstruction that mitigates artifacts, operates without anatomical priors, and requires minimal parameter tuning. The technique and its integration within QSMxT makes QSM processing more accessible and robust to streaking artifacts.

Keywords: quantitative susceptibility mapping (QSM), QSM masking, QSM pipeline, QSM software, quantitative imaging

1. Introduction

Quantitative susceptibility mapping (QSM) is an MRI method that aims to calculate the degree of magnetization induced in tissues when placed in a magnetic field. Recovering a magnetic susceptibility distribution requires a series of post-processing techniques applied to gradient-echo (GRE) phase data. 1 Compared with related techniques currently used in clinical brain imaging such as susceptibility weighted imaging (SWI), 2 QSM provides improved detection and unambiguous differentiation of iron and calcium deposits, enhanced characterization of pathological iron and myelin variations, and unique brain morphology detail within deep brain nuclei. 3,4 QSM applications include brain imaging to study tumors, 5 hemorrhage, 6–8 Huntington’s disease, 9 multiple sclerosis, 10–13 Alzheimer’s disease 14,15 and Parkinson’s disease, 16,17 as well as applications outside the brain such as quantifying liver iron, 18,19 identifying calcifications in the prostate 20 and imaging cartilage in joints. 21

QSM reconstruction classically involves several independent phase processing steps, including phase combination from multiple coils, 22 phase unwrapping, 22 background field removal, 23 and dipole inversion. 1,3 One critical step that is often neglected in the QSM literature is signal masking. Signal masks in QSM are necessary to identify the regions containing reliable phase signal for the background field removal and dipole inversion steps. Including unreliable voxels introduces errors in the background field estimation and erroneously strong susceptibility values as well as streaking artifacts throughout the final susceptibility map. Most QSM literature cites the Brain Extraction Tool (BET) from the FMRIB Software Library (FSL) for mask generation. 24 BET segments the brain in the magnitude signal by applying locally adaptive forces to a deformable model, evolving it to fit the brain surface. Using a BET-generated brain mask for QSM has several limitations that impact reconstruction quality and utility. First, the assumption of normal brain anatomy for masking is not always warranted and impacts the application of QSM in patients with brain tumors or traumatic brain injuries. 25,26 Second, areas such as the medulla and lower brainstem are specifically excluded. Another tenuous assumption is that all brain voxels contain sufficiently reliable phase for QSM despite rapid signal decay with increasing echo time (TE), especially near the brain boundary and strong susceptibility sources such as vessels and lesions. Reconstructing QSM in such areas and across high dynamic ranges of susceptibility values is challenging, with most reconstruction algorithms introducing pervasive streaking artifacts without sufficient regularization. However, strong regularization causes loss of detail throughout the susceptibility map. Despite this, and even in multi-echo acquisitions, a single brain mask is often used, ignoring the behavior of the phase signal and potentially introducing artifacts, especially at later TEs.

Recent QSM algorithms such as preconditioned total field inversion (TFI), 27 STAR-QSM, 28 QSMART, 29 and superposed dipole inversion (SDI) 7 address the problem of high dynamic range. Preconditioned TFI estimates background and local fields simultaneously within a single optimization, reducing error propagation, and suppressing streaking artifacts. The others resolve weak and strong susceptibility sources in separate inversion steps so that artifacts are avoided or specifically excluded after a combination step. STAR-QSM reconstructs strong sources first using a high regularization factor before simulating the phase shifts caused by these sources using the dipole forward model. These phase shifts are then subtracted from the original phase so that subtle sources can be reconstructed in the second pass with a lower regularization factor before combination. QSMART, on the other hand, uses a different mask for each inversion, and both can be performed in parallel. The first reconstruction uses a full brain mask, while the second uses a brain mask with vasculature removed. Vasculature is identified by applying a Frangi vessel enhancement filter on the echo-averaged magnitude image. The remaining method, SDI, performs a single QSM reconstruction using a brain mask, before generating a second mask by thresholding the QSM result to remove strong, positive susceptibility sources. The second mask is used for a second QSM reconstruction, with both results combined by superposition. The currently existing QSM techniques have limitations, as they use masks generated using anatomical priors for brain imaging, and require application-specific regularization parameter tuning. These limitations narrow the application potential for each method and reduce their robustness across diverse acquisitions.

In this paper, a robust masking technique and two-pass reconstruction procedure are presented. Two-pass QSM aims to mitigate streaking artifacts throughout susceptibility maps using the magnitude signal or spatial phase coherence to separate reliable from less reliable sources. Since the technique is based on thresholding, it does not require anatomical priors, is easily automated, and is robust to pathology. These features enable users to explore many applications otherwise requiring bespoke or cumbersome manual techniques impractical for large datasets. Moreover, two-pass QSM was integrated into a fully automated QSM framework, QSMxT. 30 QSMxT automates all steps from raw data preparation to QSM reconstruction, group space and template generation, as well as region of interest analyses across large datasets, with all required dependencies. Support for parallel processing on multicore or cluster computing systems ensures QSMxT is both practical and scalable, and its availability on every operating system via a modular and containerized ecosystem makes it computationally reproducible and deployable.

2. Methods

2.1. Data and acquisition

The accuracy of each masking and inversion method with respect to a ground truth and in the presence of strong susceptibility sources was investigated using the QSM challenge 2.0 in silico head phantom. 31,32 The phantom was adapted to include four high-susceptibility lesions: a cortical lesion, two subcortical lesions in close proximity to each other, and a brainstem lesion. Each lesion was given a spherical shape with a 2.5 mm radius, and was assigned a uniform susceptibility of 1 ppm. Like the original QSM challenge 2.0 simulation, the phantom is based on a segmented MP2RAGE dataset with 0.64 mm resolution downsampled to 1 mm using k-space cropping. The simulation was adapted to use a single echo with TE = 4 ms, as well as a background field and phase wraps. Each method was also tested against the original QSM challenge 2.0 data to generate scores, enabling comparisons to other state-of-the-art techniques. 31,32

A GRE dataset of a gel phantom containing tooth pieces and gold fiducial markers was acquired. The phantom was 12 × 8 × 3 cm3 in size and made from Liquid Soft Plastic (U-Make-Em Soft Plastics, Australia) poured into a plastic container before heating to solidify. Two gold markers were placed into the phantom, including a pure gold marker (Riverpoint Medical, Portland, Oregon, United States) measured at 1 × 3 mm2, and a Gold Anchor MR+™ with 1.5% iron (Naslund Medical, Huddinge, Sweden), measured at 0.4 × 0.2 mm2. The dataset was acquired with 1.1 × 1.1 × 1.2 mm3 resolution, TE = 3.69/7.40/11.11/14.82 ms, TR = 25.0 ms, TA = 11:16, FA = 45.0°, flow compensation disabled, and pixel bandwidth = 400.0 Hz. Data were acquired using a MAGNETOM Skyra 3T scanner (Siemens Healthcare, Erlangen, Germany) with a 32-channel spine coil on software version VE11. Phased array channels were combined using the Prescan Normalize plus Adaptive Combine approach. 33 The acquisition setup and sequence were chosen in order to evaluate their use in an on-going prostate imaging study.

GRE datasets from 46 volunteers were acquired with 1 mm isotropic resolution, spatial coverage 18 × 22.4 × 17.6 cm3 (RPI), TE = 5.84/10.63/15.42/20.21/25.00 ms, TR = 29.9, TA = 12:17, FA = 15°, flow compensation enabled, and pixel bandwidth = 310.0 Hz. T1-weighted datasets were also acquired with 1 mm isotropic resolution and TE = 2.96 ms. Data were acquired using a MAGNETOM Skyra 3T scanner (Siemens Healthcare, Erlangen, Germany) with a 64-channel head/neck coil on software version VE11. Phased array channels were combined using the Prescan Normalize plus Adaptive Combine approach 33 . Data were approved by the ethics committee of the South Australian Health and Medical Research Institute (SAHMRI).

GRE datasets from 6 brain tumor patients were acquired with 0.3 × 0.3 × 2.9 mm3 resolution, spatial coverage 16.56 × 23.2 × 22.8 cm3 (RPI), TE = 3.31/6.62/9.93/12. 49/15.05/17.61/20.17/22.73/25.29/27.85 ms, TR = 31.0 ms, TA = 12:30, FA = 10°, flow compensation disabled, and pixel bandwidth = 523.0 Hz. Data were acquired using a 7T whole-body research scanner (Siemens Healthcare, Erlangen, Germany) with a 1-channel Tx 32-channel Rx head array coil (Nova Medical, Wilmington, MA, USA), on software version VB17. Phased array channels were combined using ASPIRE. 34 Data were originally acquired for another study investigating an improved acquisition for susceptibility weighted imaging (CLEAR-SWI, Ref. [35]), and were approved by the ethics committee of the Medical University of Vienna.

2.2. QSMxT architecture

The new, two-pass QSM approach was implemented as part of the QSMxT framework within a modular reconstruction and analysis ecosystem. 30 The first module consists of a continuous integration system using GitHub actions to automatically build software containers, including the container required for the QSMxT framework. The QSMxT container incorporates the FMRIB Software Library (FSL) v6.0.4, 36 FastSurfer, 37 ANTS 2.3.4, 38 Julia v1.5.3, 39 Bidscoin v2.3, 40 Python v3.8, 41 TGV-QSM v1.0.0, 42,43 the Python packages pydicom, 44 nibabel, 45 seaborn 46,47 and NiPype, 48 the Julia packages ArgParse 49 and MriResearchTools, 50 as well as the QSMxT NiPype workflow. 30 QSMxT runs natively on Linux operating systems and high-performance clusters (HPCs), only requiring Singularity 51 as a dependency. A lightweight Linux desktop is also provided (neurodesk.github.io), conveniently accessible via a browser interface that runs on Windows, MacOS, and Linux, only requiring Docker as a dependency.

QSMxT first identifies and converts DICOM series to the NIfTI format, following the Brain Imaging Data Structure (BIDS) conventions where specified. 40 Then, the NiPype QSM pipeline processes images from each subject from the BIDS directory to produce QSMs (including a combined multi-echo QSM). If T1-weighted images are available, an additional NiPype pipeline segments these and registers them to the QSM space for each subject and exports susceptibility statistics for each segmented ROI. A final NiPype pipeline generates and registers all subjects to a common group space and produces QSM and magnitude templates using minimum deformation averaging 52 (see Figure 1).

Figure 1.

Figure 1

Open in a new tab

QSMxT processing pipeline and outputs after automated conversion to the Brain Imaging Data Structure standard. Outputs for each subject include masks, T1-weighted images, segmentations registered to the quantitative susceptibility mapping (QSM) space, QSM images, as well as quantitative data for analysis and figure generation. Outputs for the whole group include magnitude and QSM templates

2.3. QSM reconstruction and two-pass QSM

The phase unwrapping, background field removal, and dipole inversion steps are achieved using the TGV-QSM algorithm. 42 QSM algorithms incorporating TGV have been shown to be quantitatively stable across echo times compared to others, 53 and achieved competitive results in the QSM challenge 2.0. 54 TGV-QSM has an open-source implementation in Python, 43 making it conveniently accessible for high-performance computing compared to other QSM tools that use proprietary software such as MATLAB.

QSM reconstruction is achieved using a two-pass QSM procedure that performs two parallel QSM reconstructions per echo, with the first including more reliable susceptibility sources, and the second including reliable as well as less reliable sources (see Figure 2). The first reconstruction uses a mask produced by thresholding and binarizing the magnitude signal using a percentile of the signal distribution. The 50th percentile was chosen as the threshold for all reconstructions after testing against a single acquisition and tweaking the threshold to minimize the appearance of artifacts in the final result (see Figure 3). The thresholding operation automatically excludes areas with short T2∗ times, including strong and artifact-inducing susceptibility sources. The second reconstruction uses the same set of masks after applying the hole-filling algorithm from Fslutils 36 to fill any gaps from the first set, enabling less reliable sources to be included. A combined QSM image is then produced by filling gaps from the first QSM image using the second. After a combined QSM image is reconstructed for each echo, a final weighted average is produced by summing the combined QSMs and dividing them by the pixel-wise sum of the filled masks. A single-pass version of the reconstruction was also used for comparison using only filled threshold-based masks. By separating reliable from less reliable susceptibility sources, the two-pass technique aims to provide a substantial reduction in streaking artifacts. As an alternative to the magnitude signal, the spatial phase coherence can also be used as an input to the thresholding operation. This was necessary for the in silico head phantom because the simulation does not generate a magnitude signal that fully reflects the added susceptibility sources. However, since a reduced signal in the magnitude image may not necessarily reflect susceptibility-induced dephasing, a mask based on the phase coherence may have a theoretical advantage for QSM. Spatial phase coherence was computed as the quality map produced by the phase-unwrapping method, Rapid Opensource Minimum Spanning TreE AlgOrithm (ROMEO). 55 The quality map is a weighted combination of the first- and second-order spatial phase gradients in three dimensions in each voxel.

Figure 2.

Figure 2

Open in a new tab

Two-pass QSM masking and reconstruction process for one subject with one echo. A mask is initially produced by thresholding either the magnitude or the spatial phase coherence. A second mask is then produced after applying the hole-filling algorithm. Both masks are then used in parallel QSM reconstruction steps before combination. The images shown were produced using the QSM challenge 2.0 data, and are included for illustrative purposes

Figure 3.

Figure 3

Open in a new tab

QSM results from a volunteer brain (3 T; multi-echo; axial slice) calculated using two-pass QSM with a range of magnitude signal thresholds. The slice shown intersects the top portion of the lateral ventricles. At some thresholds, dark artifacts are visible toward the center of the brain caused by the dephased signal in the lateral ventricles. With a threshold set to the 50th percentile of the magnitude distribution, the artifacts are kept to a minimum

Two-pass QSM was also compared to the standard approach of brain masking, which applies BET 24 to the first-echo magnitude image to produce a brain mask. QSM is then reconstructed for each echo using the mask before averaging. BET was run with robust brain center estimation enabled (to run BET iteratively) and with other settings left at their defaults. To improve performance at 7 T, a homogeneity correction was applied to the magnitude prior to masking. 50,56

2.4. Template building

QSMxT generates magnitude and QSM templates using an implementation of a minimum deformation averaging method for atlas construction called Volgenmodel. 52 A template is initially constructed using the magnitude images from all subjects, and the estimated transformations are subsequently applied to the susceptibility maps to produce a QSM template. QSM templates were generated for the volunteer brains for each masking technique to qualitatively assess the group-level effects of each.

2.5. Segmentation and quantitative analysis

If T1-weighted images are available, QSMxT segments these using FastSurfer 37 and registers the T1-weighted image to the magnitude in the QSM space. QSM statistics for each ROI are then exported. This segmentation and analysis pipeline was tested using the volunteer brains for quantitative analysis across a large group.

3. Results

The adapted in silico head phantom was used to assess each masking and inversion method with respect to a ground truth. The threshold-based masks used for two-pass QSM successfully included all introduced lesions, whereas the BET-generated mask excluded the brainstem lesion (see Figure 4, blue arrows). Furthermore, the two-pass QSM result contained no visually apparent streaking (see Figure 4), and had significantly lower reconstruction error near the introduced lesions compared to single-pass QSM, with rapidly decreasing error with distance from each lesion (see Figure 5 and Supporting Information Figure S1). Running single-pass QSM without the lesions present resulted in a similar error near the lesion locations to two-pass QSM. In reconstructions where the lesion was present, the reconstruction error inside the lesion was higher, as TGV-QSM is known to systematically underestimate susceptibility sources. 57

Figure 4.

Figure 4

Open in a new tab

In silico head phantom ground truth and QSM reconstructions using single- and two-pass QSM (7 T; single-echo; simulated; sagittal slice). The zoomed area (yellow rectangle) shows a cortical and two subcortical lesions in close proximity. Two-pass QSM reduces streaking artifacts near the lesions (green arrow), and includes more anatomical detail in the brainstem due to threshold-based masking, allowing the brainstem lesion to be recovered (blue arrow). The difference image illustrates that two-pass QSM primarily mitigates the star-shaped streaking artifacts surrounding the lesions

Figure 5.

Figure 5

Open in a new tab

A, Sagittal brain segmentation of the in silico head phantom, with highlighted ROIs in the vicinity of the introduced lesions. B, Susceptibility error in each ROI using three processing methods. All reconstructions used threshold-based masks based on the spatial phase coherence

Against the original QSM challenge 2.0 data, the single-pass reconstruction using a BET mask scored 112 for the overall detrended RMSE metric, whereas two-pass QSM using threshold-based masks scored an improved 99.9, effectively moving from rank 96 to 90 among the stage 1 submissions. The CalcStreak metric also reduced from 0.136 to 0.077, moving from rank 88 to 45 for that metric within the same set of submissions. 58

Two-pass QSM was further tested in vitro using the gel phantom (see Figure 6). The strong susceptibility sources in the phantom caused significant streaking when all sources were included in a single-pass inversion. However, all visible streaking was successfully mitigated after the two-pass combination step.

Figure 6.

Figure 6

Open in a new tab

QSM results using the gel phantom (3 T; multi-echo; axial slice). On the left is a photo of the gel phantom containing a Gold Anchor MR+™ with 1.5% iron content (yellow square), a pure gold fiducial marker (blue square), and a tooth piece (green square). The latter three images depict the same slice from the magnitude, as well as single- and two-pass QSM results. The two-pass QSM image has a clear reduction of streaking artifacts surrounding the strong sources

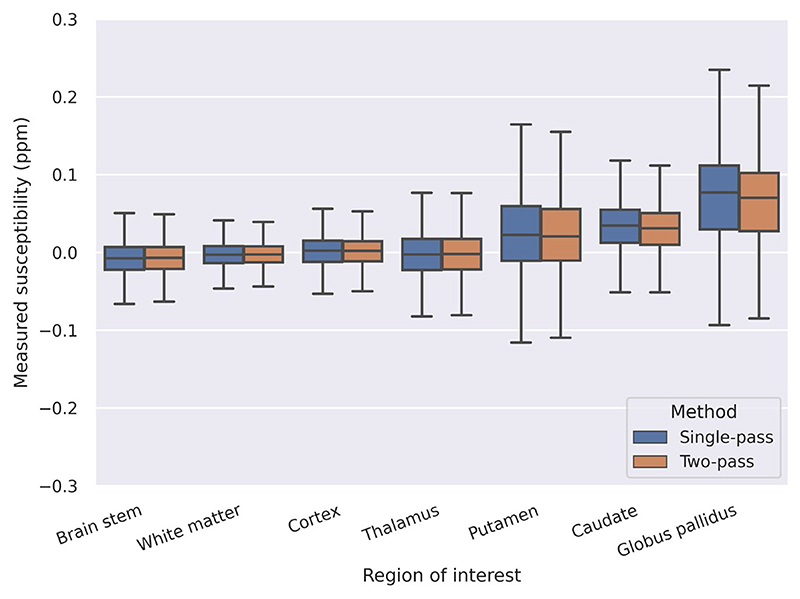
The QSM templates generated using volunteer brains were used to examine the systematic, group-level influence of the masking and reconstruction technique on QSM results (see Figure 7). Two-pass QSM systematically reduces the streaking that occurs near the brain boundary, particularly around the superior and transverse sagittal sinuses, with dipole-shaped reductions of artifacts visible when compared to single-pass QSM with BET-generated masks. A range of ROIs were also analysed across all subjects, with both methods producing similar quantitative measurements (see Figure 8 and Supporting Information Table S1).

Figure 7.

Figure 7

Open in a new tab

QSM templates generated using 46 volunteer brains (3 T; multi-echo; coronal slice). When BET-generated masks are used, strong artifacts near the transverse and superior sagittal sinuses are visible (left; arrow). The artifacts are mitigated using two-pass QSM (center; arrow), with dipole-shaped streaking visible in the difference image (right; arrow)

Figure 8. Measured susceptibility values in 46 volunteer brains across seven ROIs using single-pass and two-pass QSM. Both methods used threshold based masking, and produced similar quantitative measurements across all ROIs tested.

Figure 8

Open in a new tab

The brain tumor data were used to assess the performance of two-pass QSM at 7 T and in clinical cases. As such, BET regularly failed to mask the whole brain, sometimes missing crucial tumor and cortical detail (see Figure 9). Furthermore, two-pass QSM mitigated the shadow artifacts within tumors, generating more plausible QSM values (see Figures 9 and 10).

Figure 9.

Figure 9

Open in a new tab

QSM results of a brain tumor patient computed using single- and two-pass QSM (7 T; multi-echo; axial slice region). The BET-generated mask excluded part of the tumor included by thresholding (yellow rectangle), as well as areas of the cortex (pink arrow). The two-pass inversion suppresses streaking artifacts near the tumor (orange arrow), and potentially near veins where some differences can be seen (aquamarine arrow)

Figure 10. QSM results of a brain tumor patient (7 T; multi-echo; axial slices) computed using single- and two-pass QSM. Significant reductions of artifacts can be seen near vessels and within tumors after two-pass combination (yellow arrows).

Figure 10

Open in a new tab

4. Discussion and Conclusions

A novel two-pass masking and QSM reconstruction procedure has been presented that separates susceptibility sources using masks based on the MRI signal. Compared with BET-generated masks, the threshold-based technique includes more anatomical detail without priors, including in the cortex, the brainstem, and tumors (see Figures 4 and 9). The gel phantom experiment further demonstrates the threshold-based technique’s invariance to anatomy, and that it may have potential in non-brain data (see Figure 6). The two-pass reconstruction mitigates the streaking artifacts caused by high dynamic ranges of susceptibility values (see Figures 4, 6, 9, and 10) and signal decay with TE (see Figure 7). The improved accuracy in the in silico head phantom and QSM challenge 2.0 metrics confirms that the artifact reductions lead to a more accurate QSM reconstruction (see Figure 5 and Supporting Information Figure S1). Furthermore, in the simulation, two-pass QSM was found to not introduce significant errors in the normal-appearing white matter surrounding the lesion, with a similar error to single-pass with no lesions present, and similar values across a range of ROIs in volunteers (see Supporting Information Figure S1, Figure 8 and Supporting Information Table S1). The reduction of artifacts allows the boundaries of strong sources, including vessels and veins, to be depicted with greater clarity, facilitating object identification, segmentation and quantitative analysis. The two-pass QSM technique and its masking strategies are automated within the open-source QSM framework, QSMxT, which was used for all results presented with default parameters across all datasets. This demonstrates the robustness of the technique in its application across multiple acquisitions and hardware configurations. Finally, the conceptual simplicity of the thresholding operation makes it straightforward to implement in conjunction with any QSM algorithm requiring a mask.

Several other multi-stage QSM reconstruction techniques exist with similar artifact mitigation results, including pre-conditioned TFI, 27 QSMART, 29 STAR-QSM, 28 and SDI. 7 However, the two-pass QSM technique provides two novel features: first, it does not require anatomical priors for brain masking or source separation, including optimized and application-specific filters, making it potentially useful across a much wider array of applications. Second, our experiments indicate that it requires minimal parameter tuning across applications and datasets, potentially making automation over large datasets more practical, and with the potential to be used in clinical datasets with high dynamic ranges and wider anatomical variability.

The two-pass technique has been shown to perform well using magnitude-based masks or masks based on the spatial phase coherence. Whether an improved QSM reconstruction may be achieved using a particular masking technique or a combination thereof has not been systematically investigated, and is an area of future work. A comparison between the techniques using the in silico head phantom would require modifications to the phantom such that the generated magnitude signal realistically reflects the presence of strong susceptibility sources. It is hypothesized that phase-based masking may have benefits in low-SNR acquisitions, as the degree of phase coherence does not directly reflect the strength of the signal. Furthermore, the robustness of the two-pass technique and invariance to anatomy is based on results across multiple imaging resolutions, field strengths, pathology, and in simulations and phantoms. Robustness in QSM applications more broadly across the human body or in other animals is yet to be investigated.

To make the two-pass technique accessible and computationally reproducible in the QSM community, it was integrated into the new QSM framework, QSMxT. Existing QSM processing frameworks have limited scalability, with most tools only able to process one subject at a time, and with manual intervention required between steps. Furthermore, the lack of QSM tools with integrated segmentation and analysis hampers the use of QSM among researchers, especially those less experienced with segmentation and quantitative MRI. QSMxT requires only a single dependency to run and is compatible with every operating system. QSMxT can also take advantage of HPC systems to process many datasets and computational steps in parallel. With a single command, QSMxT can run one of several pipelines to standardize input data, reconstruct multi-echo susceptibility maps using two-pass QSM, generate a group space along with QSM and magnitude templates, and provide full segmentations and quantitative outputs. QSMxT significantly lowers QSM’s barrier to entry, providing researchers with a complete set of tools to include QSM in their studies.

Supplementary Material

Supporting Information

Acknowledgements

We thank the participants involved in this study. MB acknowledges funding from Australian Research Council Future Fellowship grant FT140100865 and SR from the Marie Skłodowska-Curie Action MS-fMRI-QSM 794298. This research was funded by the Australian Research Council Training Centre for Innovation in Biomedical Imaging Technology (project number IC170100035) and funded by the Australian Government. Additional support was provided by the Austrian Science Fund (FWF): 31452 and KLI-646. The authors acknowledge the facilities and scientific and technical assistance of the National Imaging Facility, a National Collaborative Research Infrastructure Strategy (NCRIS) capability, at the Centre for Advanced Imaging, the University of Queensland. We wish to acknowledge QCIF for its support in this research by providing high performance computing and storage resources.

Funding information

Austrian Science Fund, Grant/Award Number: 31452 and KLI-646; H2020 Marie Skłodowska-Curie Actions MS-fMRI-QSM, Grant/Award Number: 794298; Australian Research Council, Grant/Award Number: FT140100865 and IC170100035

Footnotes

CONFLICT OF INTEREST

Kieran O’Brien and Jin Jin are employees of Siemens Healthineers in Australia. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationship that could be construed as a conflict of interest.

Data Availability Statement

We facilitate the reproducibility of our study by providing the full implementation of the pipeline (https://github.com/QSMxT/QSMxT, commit hash 6308062). The pipeline can be executed in NeuroDesk (https://neurodesk.github.io/).

References

  • 1.Schweser F, Deistung A, Reichenbach JR. Foundations of MRI phase imaging and processing for quantitative susceptibility mapping (QSM) Z Med Phys. 2016;26:6–34. doi: 10.1016/j.zemedi.2015.10.002. [DOI] [PubMed] [Google Scholar]
  • 2.Haacke EM, Xu Y, Cheng Y-CN, Reichenbach JR. Susceptibility weighted imaging (SWI) Magn Reson Med. 2004;52:612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
  • 3.Deistung A, Schweser F, Reichenbach JR. Overview of quantitative susceptibility mapping. NMR Biomed. 2017;30:e3569. doi: 10.1002/nbm.3569. [DOI] [PubMed] [Google Scholar]
  • 4.Wang Y, Spincemaille P, Liu Z, et al. Clinical quantitative susceptibility mapping (QSM): biometal imaging and its emerging roles in patient care. J Magn Reson Imaging. 2017;46:951–971. doi: 10.1002/jmri.25693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Deistung A, Schweser F, Wiestler B, et al. Quantitative susceptibility mapping differentiates between blood depositions and calcifications in patients with glioblastoma. PLoS One. 2013;8:e57924. doi: 10.1371/journal.pone.0057924. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Chen W, Zhu W, Kovanlikaya I, et al. Intracranial calcifications and hemorrhages: characterization with quantitative susceptibility mapping. Radiology. 2014;270:496–505. doi: 10.1148/radiol.13122640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Sun H, Kate M, Gioia LC, Emery DJ, Butcher K, Wilman AH. Quantitative susceptibility mapping using a superposed dipole inversion method: application to intracranial hemorrhage. Magn Reson Med. 2016;76:781–791. doi: 10.1002/mrm.25919. [DOI] [PubMed] [Google Scholar]
  • 8.Chang S, Zhang J, Liu T, et al. Quantitative susceptibility mapping of intracerebral hemorrhages at various stages. J Magn Reson Imaging. 2016;44:420–425. doi: 10.1002/jmri.25143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Chen L, Hua J, Ross CA, et al. Altered brain iron content and deposition rate in Huntington’s disease as indicated by quantitative susceptibility MRI. J Neurosci Res. 2019;97:467–479. doi: 10.1002/jnr.24358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Langkammer C, Liu T, Khalil M, et al. Quantitative susceptibility mapping in multiple sclerosis. Radiology. 2013;267:551–559. doi: 10.1148/radiol.12120707. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Chen W, Gauthier Susan A, Gupta A, et al. Quantitative susceptibility mapping of multiple sclerosis lesions at various ages. Radiology. 2013;271:183–192. doi: 10.1148/radiol.13130353. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Eskreis-Winkler S, Deh K, Gupta A, et al. Multiple sclerosis lesion geometry in quantitative susceptibility mapping (QSM) and phase imaging. J Magn Reson Imaging. 2015;42:224–229. doi: 10.1002/jmri.24745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Schweser F, Ana LRDM, Hagemeier J, et al. Mapping of thalamic magnetic susceptibility in multiple sclerosis indicates decreasing iron with disease duration: a proposed mechanistic relationship between inflammation and oligodendrocyte vitality. NeuroImage. 2018;167:438–452. doi: 10.1016/j.neuroimage.2017.10.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Ayton S, Fazlollahi A, Bourgeat P, et al. Cerebral quantitative susceptibility mapping predicts amyloid- β-related cognitive decline. Brain. 2017;140:2112–2119. doi: 10.1093/brain/awx137. [DOI] [PubMed] [Google Scholar]
  • 15.Tiepolt S, Schäfer A, Rullmann M, et al. Quantitative susceptibility mapping of amyloid- β aggregates in Alzheimer’s disease with 7T MR. J Alzheimers Dis. 2018;64:393–404. doi: 10.3233/JAD-180118. [DOI] [PubMed] [Google Scholar]
  • 16.Acosta-Cabronero J, Cardenas-Blanco A, Betts Matthew J, et al. The whole-brain pattern of magnetic susceptibility perturbations in Parkinson’s disease. Brain. 2017;140:118–131. doi: 10.1093/brain/aww278. [DOI] [PubMed] [Google Scholar]
  • 17.Langkammer C, Pirpamer L, Seiler S, et al. Quantitative susceptibility mapping in Parkinson’s disease. PLoS One. 2016;11:e0162460. doi: 10.1371/journal.pone.0162460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Jafari R, Sheth S, Spincemaille P, et al. Rapid automated liver quantitative susceptibility mapping. J Magn Reson Imaging. 2019;50:725–732. doi: 10.1002/jmri.26632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Sharma Samir D, Hernando D, Horng Debra E, Reeder SB. Quantitative susceptibility mapping in the abdomen as an imaging biomarker of hepatic iron overload. Magn Reson Med. 2015;74:673–683. doi: 10.1002/mrm.25448. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Straub S, Emmerich J, Schlemmer H-P, et al. Mask-adapted background field removal for artifact reduction in quantitative susceptibility mapping of the prostate. Tomography. 2017;3:96–100. doi: 10.18383/j.tom.2017.00005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Wei H, Dibb R, Decker K, et al. Investigating magnetic susceptibility of human knee joint at 7 Tesla. Magn Reson Med. 2017;78:1933–1943. doi: 10.1002/mrm.26596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Robinson SD, Bredies K, Khabipova D, Dymerska B, Marques JP, Schweser F. An illustrated comparison of processing methods for MR phase imaging and QSM: combining array coil signals and phase unwrapping: phase image combination and unwrapping. NMR Biomed. 2017;30:e3601. doi: 10.1002/nbm.3601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Schweser F, Simon DR, de Rochefort L, Li W, Bredies K. An illustrated comparison of processing methods for phase MRI and QSM: removal of background field contributions from sources outside the region of interest. NMR Biomed. 2017;30:e3604. doi: 10.1002/nbm.3604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Fennema-Notestine C, Burak OI, Clark CP, et al. Quantitative evaluation of automated skull-stripping methods applied to contemporary and legacy images: effects of diagnosis, bias correction, and slice location. Hum Brain Mapp. 2006;27:99–113. doi: 10.1002/hbm.20161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Speier W, Iglesias JE, El-Kara L, Tu Z, Arnold C. In: Medical Image Computing and Computer-Assisted Intervention-MICCAI 2011 (Lecture Notes in Computer Science) Fichtinger G, Martel A, Peters T, editors. Springer; Berlin, Heidelberg: 2011. Robust skull stripping of clinical glioblastoma multiforme data; pp. 659–666. [DOI] [PubMed] [Google Scholar]
  • 27.Liu Z, Kee Y, Zhou D, Wang Y, Spincemaille P. Preconditioned total field inversion (TFI) method for quantitative susceptibility mapping. Magn Reson Med. 2017;78:303–315. doi: 10.1002/mrm.26331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Wei H, Dibb R, Zhou Y, et al. Streaking artifact reduction for quantitative susceptibility mapping of sources with large dynamic range. NMR Biomed. 2015;28:1294–1303. doi: 10.1002/nbm.3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Yaghmaie N, Syeda Warda T, Chengchuan W, et al. QSMART: quantitative susceptibility mapping artifact reduction technique. NeuroImage. 2021;231:117701. doi: 10.1016/j.neuroimage.2020.117701. [DOI] [PubMed] [Google Scholar]
  • 30.Stewart AW, Bollmann S, Shaw T. QSMxT/QSMxT: release for QSMxT paper preprint. 2021 [Google Scholar]
  • 31.Marques JP, Langkammer C, Meineke J, Milovic C, Bilgic B, Schweser F. QSM Reconstruction Challenge 2.0. 2019 doi: 10.1002/mrm.28754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Marques JP, Meineke J, Milovic C, et al. QSM reconstruction challenge 2.0: a realistic in silico head phantom for MRI data simulation and evaluation of susceptibility mapping procedures. Magn Reson Med. 2021;86:526–542. doi: 10.1002/mrm.28716. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Vladimír J, Kannengiesser SAR. Adaptive coil combination using a body coil scan as phase reference; ISMRM 22nd Annual Meeting & Exhibition; Milan, Italy. 2014. https://cds.ismrm.org/protected/14MProceedings/files/4406.pdf . [Google Scholar]
  • 34.Eckstein K, Dymerska B, Bachrata B, et al. Computationally efficient combination of multi-channel phase data from multi-echo acquisitions (ASPIRE) Magn Reson Med. 2018;79:2996–3006. doi: 10.1002/mrm.26963. [DOI] [PubMed] [Google Scholar]
  • 35.Eckstein K, Bachrata B, Hangel G, et al. Improved susceptibility weighted imaging at ultra-high field using bipolar multi-echo acquisition and optimized image processing: CLEAR-SWI. NeuroImage. 2021;237:118175. doi: 10.1016/j.neuroimage.2021.118175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. FSL. NeuroImage. 2012;62:782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
  • 37.Henschel L, Conjeti S, Estrada S, Diers K, Fischl B, Reuter M. FastSurfer-a fast and accurate deep learning based neuroimaging pipeline. NeuroImage. 2020;219:117012. doi: 10.1016/j.neuroimage.2020.117012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Avants BB, Tustison NJ, Stauffer M, Song G, Wu B, Gee JC. The insight ToolKit image registration framework. Front Neuroinform. 2014;8:44. doi: 10.3389/fninf.2014.00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Bezanson J, Edelman A, Karpinski S, Shah VB. Julia: a fresh approach to numerical computing. SIAM Rev. 2017;59:65–98. [Google Scholar]
  • 40.Gorgolewski Krzysztof J, Auer T, Calhoun Vince D, et al. The brain imaging data structure, a format for organizing and describing outputs of neuroimaging experiments. Sci Data. 2016;3:1–9. doi: 10.1038/sdata.2016.44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Van Rossum G, Drake FL., Jr . The Python Language Reference. Network Theory Limited; 2014. [Google Scholar]
  • 42.Langkammer C, Bredies K, Poser BA, et al. Fast quantitative susceptibility mapping using 3D EPI and total generalized variation. NeuroImage. 2015;111:622–630. doi: 10.1016/j.neuroimage.2015.02.041. [DOI] [PubMed] [Google Scholar]
  • 43.Langkammer C, Bredies K, Poser BA, et al. TGV QSM algorithm. Python Source Code; 2015. http://www.neuroimaging.at/pages/qsm.php . [Google Scholar]
  • 44.Pydicom. 2021. https://github.com/pydicom/pydicom .
  • 45.Brett M, Hanke M, Markiewicz C, et al. nipy/nibabel: 2.3.0. 2018 doi: 10.5281/zenodo.1287921. [DOI] [Google Scholar]
  • 46.Hunter JD. Matplotlib: a 2D graphics environment. Comput Sci Eng. 2007;9:90–95. [Google Scholar]
  • 47.Waskom M. Seaborn: statistical data visualization. 2020. https://seaborn.pydata.org .
  • 48.Gorgolewski K, Burns Christopher D, Madison C, et al. Nipype: a flexible, lightweight and extensible neuroimaging data processing framework in python. Front Neuroinform. 2011:5. doi: 10.3389/fninf.2011.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Baldassi C. carlobaldassi/ArgParse.jl. 2021. https://github.com/carlobaldassi/ArgParse.jl .
  • 50.Eckstein K. korbinian90/MriResearchTools.jl. 2020. https://github.com/korbinian90/MriResearchTools.jl .
  • 51.Kurtzer GM, Sochat V, Bauer MW. Singularity: scientific containers for mobility of compute. PLoS One. 2017;12:e0177459. doi: 10.1371/journal.pone.0177459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Janke AL, Ullmann JFP. Robust methods to create ex vivo minimum deformation atlases for brain mapping. Methods. 2015;73:25. doi: 10.1016/j.ymeth.2015.01.005. [DOI] [PubMed] [Google Scholar]
  • 53.Biondetti E, Karsa A, Thomas DL, Shmueli K. Investigating the accuracy and precision of TE-dependent versus multi-echo QSM using Laplacian-based methods at 3T. Magn Reson Med. 2020;84:3040–3053. doi: 10.1002/mrm.28331. [DOI] [PubMed] [Google Scholar]
  • 54.Bilgic B, Langkammer C, Marques JP, Meineke J, Milovic C, Schweser F. QSM reconstruction challenge 2.0: design and report of results. Magn Reson Med. 2021;86:1241–1255. doi: 10.1002/mrm.28754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Dymerska B, Eckstein K, Bachrata B, et al. Phase unwrapping with a rapid opensource minimum spanning tree algorithm (ROMEO) Magn Reson Med. 2021;85:2294–2308. doi: 10.1002/mrm.28563. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Eckstein K, Simon DR. A Simple homogeneity correction for neuroimaging at 7T; Proceedings of the International Society for Magnetic Resonance in Medicine; Montreal, Canada. 2019. Abstract #2716. [Google Scholar]
  • 57.Zhou D, Cho J, Zhang J, Spincemaille P, Wang Y. Susceptibility underestimation in a high-susceptibility phantom: dependence on imaging resolution, magnitude contrast, and other parameters. Magn Reson Med. 2017;78:1080–1086. doi: 10.1002/mrm.26475. [DOI] [PubMed] [Google Scholar]
  • 58.Bilgic B, Langkammer C, Marques José P, Meineke J, Milovic C, Schweser F, editors. 2019 QSM reconstruction challenge. Metrics and submission information. 2020 doi: 10.5281/zenodo.3687198. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
EMS140944-supplement-Supporting_Information.pdf (269.7KB, pdf)

Data Availability Statement

We facilitate the reproducibility of our study by providing the full implementation of the pipeline (https://github.com/QSMxT/QSMxT, commit hash 6308062). The pipeline can be executed in NeuroDesk (https://neurodesk.github.io/).

RESOURCES