Surface-tension-induced budding drives alveologenesis in human mammary gland organoids

Abstract

Organ development involves complex shape transformations driven by active mechanical stresses that sculpt the growing tissue ^1,2. Epithelial gland morphogenesis is a prominent example where cylindrical branches transform into spherical alveoli during growth^3–5. Here we show that this shape transformation is induced by a local change from anisotropic to isotropic tension within the epithelial cell layer of developing human mammary gland organoids. By combining laser ablation with optical force inference and theoretical analysis, we demonstrate that circumferential tension increases at the expense of axial tension through a reorientation of cells that correlates with the onset of persistent collective rotation around the branch axis. This enables the tissue to locally control the onset of a generalized Rayleigh-Plateau instability, leading to spherical tissue buds⁶. The interplay between cell motion, cell orientation and tissue tension is a generic principle that may turn out to drive shape transformations in other cell tissues.

The transformation from tubular ducts into terminal spherical alveoli is ubiquitous in the organ development of higher organisms³. The mammary gland is a unique example that relies on this shape change to undergo repeated postnatal cycles of expansion, alveologenesis and involution⁷. This self-organization of spherical structures is reminiscent of hydrodynamic instabilities driven by surface tension, first described by Lord Rayleigh and Joseph Plateau in passive isotropic fluids⁶. Specifically, a column of fluid always breaks up into droplets that have a smaller surface-to-volume ratio. When the fluid column is not surrounded by air but by an elastic medium, a shape instability occurs only if the surface tension can overcome the ensuing elastic stresses, resulting in pearling^8–10. This is a compelling picture considering the fluid-like behaviour of tissues^1,11–14 and the key role of cortical tension in duct development¹⁵. However, the classical pearling of isotropic fluids occurs on a global scale, as a long-wavelength instability without any defined spatial localization. In contrast, controlled development of tissue requires spatially localized shape transformations that are regulated by cell activity. Since cells are able to move, orientate and generate forces, a plausible hypothesis is that these properties enable local changes in the tension field and that this is the mechanism to locally control fluid shape instabilities.

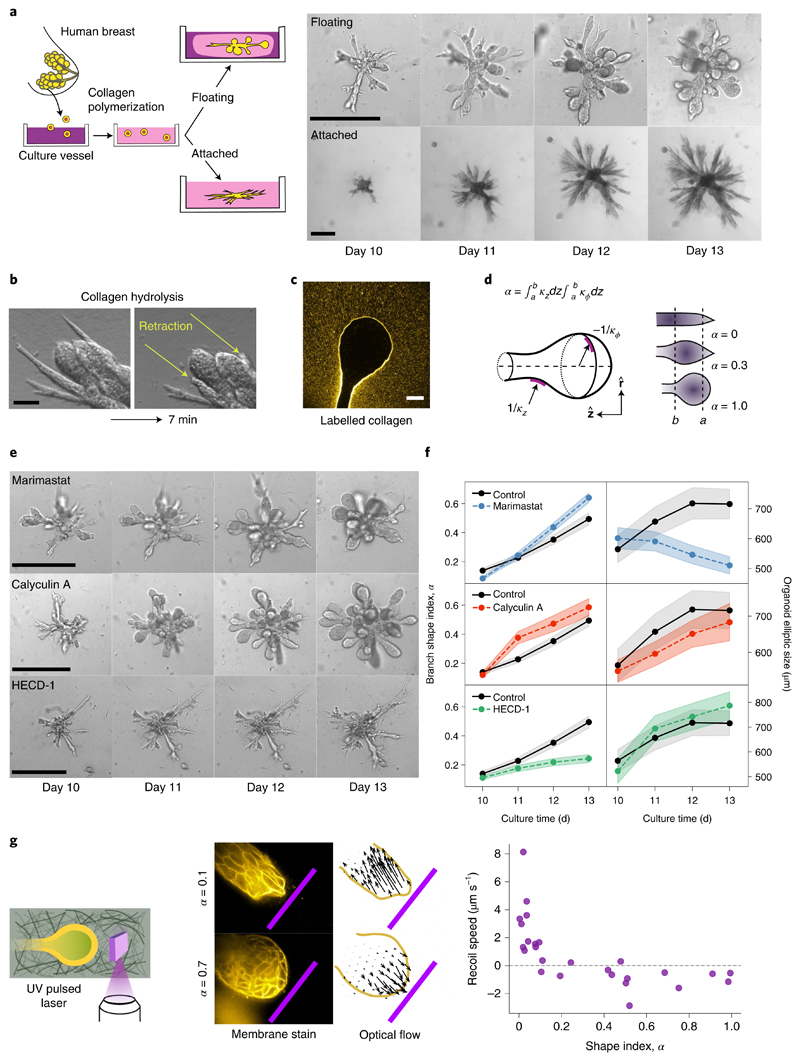
To understand the nature of such shape transformations, we exploit an organoid assay from primary cells that recapitulates the architecture of the human mammary gland, with its characteristic arrays of spherical alveoli^4,16,17. In this assay, single primary human mammary epithelial cells are seeded into collagen I matrices and develop into highly branched organoids over a time period of two weeks (Fig. 1a). The resulting organoid morphology crucially depends on the adhesion of the elastic collagen matrix to the enclosing culture vessel⁴. In the attached gels, branches stay cylindrical and their length continuously increases (Fig. 1a, lower row), while in floating gels, about 50% of the branches develop round alveoli at their ends (Fig. 1a, upper row, and Supplementary Table 1). Starting around day 10, the average alveolus becomes spherical within 3–4 days (Fig. 1a).

Fig. 1. Morphology of human mammary gland organoids depends on the mechanical interaction with the ECM.

a, Primary cells from reduction mammoplasty are seeded in collagen I gels and allowed to grow for up to 20 days. As a function of the attachment of the matrix, different morphologies are obtained. Scale bars, 100 μm. b, Organoids behave like liquids. After collagen hydrolysis by collagenase treatment, branches flow into the organoid body within a few minutes. Scale bar, 50 μm. c, Organoids grown in fluorescent collagen are completely surrounded by a layer of compacted collagen. Scale bar, 50 μm. d, To characterize the branch shape, we introduce the shape index α defined in terms of the axial and circumferential curvatures, namely, ${\kappa }_Z={\partial }_Z^{2}R/{\left[1+{\left({\partial }_{Z}R\right)}^2\right]}^{\frac{3}{2}}\text{and}{\kappa }_{\varphi }=-R^{-1}/{\left[1+{\left({\partial }_{Z}R\right)}^2\right]}^{\frac{1}{2}},$ respectively (Supplementary Section B1). Here, R ≡ R(z) refers to the local tube radius as a function of the axial coordinate z. To avoid irregular shapes of the branch tip, the integration region was taken at a distance of a = 30 μm from the tip. The upper bound b = 100 μm corresponds to the typical size of the alveoli on days 12–14. e, Effect of several biochemical perturbations on the development of organoids grown in floating gels. Calyculin A increases contractility, marimastat inhibits matrix metalloproteinases and HECD-1 antibody blocks cell–cell adhesion. f, Time evolution of average branch shape index α and overall organoid size (n_branches = 215, 95, 211 and 119 and n_organoids = 33, 23, 28 and 24 for control, marimastat, calyculin A and HECD-1, respectively). The shaded regions correspond to ±s.e. g, To determine the mechanical interaction between the branch tip and ECM, we ablate a 30-μm-high, 100-μm-wide and 1-μm-thick ECM region near the branch tip. Cylindrical branches recoil within 1 s away from the cut, revealing pulling tension (top); in contrast, round alveoli expand towards the cut, showing compressive ECM forces (bottom). The pink bar represents the ablated region (100 μm wide). Arrows, optical flow. Scale bar, 50 μm. Far right, recoil speed of the branch tip as a function of the shape index.

To understand this shape transformation, we asked whether organoids behave like solids or fluids in the absence of the extracellular matrix (ECM). We found that enzymatic digestion of the collagen matrix leads to a dramatic loss of organoid structure: within minutes, cylindrical branches flow towards the organoid body (Fig. 1b and Supplementary Video 1). Thus, organoids behave like fluids and crucially depend on the elasticity of the ECM for the stability of the branches. Observation of alveoli grown in fluorescent collagen revealed that they are enveloped by a compacted collagen cage similar to the one around cylindrical branches (Fig. 1c and Supplementary Fig. 1)¹⁷. This suggests that the organoid deforms and compacts the surrounding collagen by exerting mechanical stresses above the plastic yield threshold, rather than by proteolysis and degradation^18–20. To corroborate this hypothesis, we investigated the effect of inhibiting enzymatic ECM degradation by adding the metalloproteinase inhibitor Marimastat¹⁷ right at the onset of alveologenesis. To quantify the degree of sphericity at the branch end, we defined a 'shape index' α (Fig. 1d and Supplementary Section B1). We found that the addition of Marimastat has no effect on the formation of spherical alveoli, which proceeds at the normal rate despite a drastic inhibition of the tubular branch growth (Fig. 1e,f, top row). To investigate the role of mechanical stresses, we increased cell contractility by the addition of calyculin A. As a result, this leads to a faster formation of alveoli (Fig. 1e,f, middle row). Next, we sought to diminish epithelial tension by the addition of antibody HECD-1 against E-cadherin. As a result, branches fail to become round and instead develop long, thin extensions (Fig. 1e,f, lower row). We conclude that alveologenesis involves a plastic deformation of the encasing ECM driven by epithelial contractility.

To determine the mechanical interaction between developing branches and the ECM, we performed UV laser ablation of the collagen network in close proximity to the branch tips and alveoli (Fig. 1g). We found that straight, cylindrical branches react with a fast recoil towards the organoid body, indicating a catastrophic loss of the pulling tension generated by cell contractility¹⁷. In contrast, spherical alveoli exhibited a slight expansion towards the cut, revealing a compressive (negative) stress in the ECM.

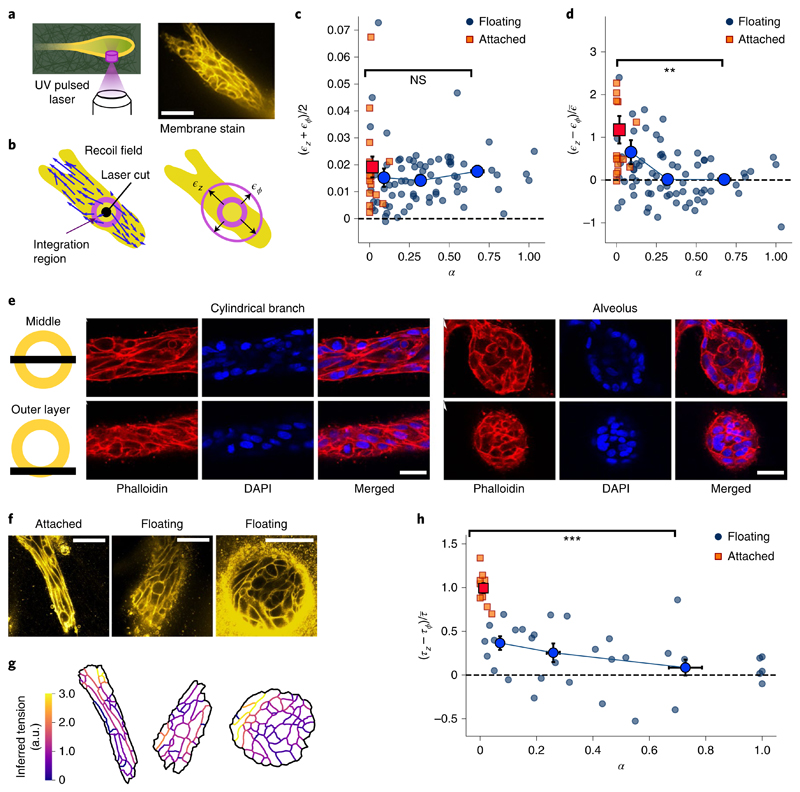
Next, we applied laser ablation to the cells themselves (Fig. 2a). While a majority of cylindrical branches in floating gels are not stable but are actually undergoing alveologenesis (Fig. 1a,f), branches in the attached gels remain cylindrical. Therefore, we used branches in the attached gels as a stable control. Immediately after ablation, the cell boundaries surrounding the cut move away with a fast recoil (Supplementary Video 2). We characterized the recoil response by axial strain ϵ_z and circumferential strain ϵ_ϕ (Fig. 2b and Methods). The overall response (ϵ_z+ϵ_ϕ)/2 is the same for all shapes and gel boundary conditions, indicating that spherical alveoli, branches undergoing alveologenesis and stable cylindrical branches maintain a similar contractile tonus (Fig. 2c). Next, we turned to the recoil strain difference (ϵ_z – ϵ_ϕ) to assess tension anisotropy. We found that branches in the attached gels react with a considerable axial bias (Fig. 2d, red squares). In floating gels, the response is less biased and decreases with an increasing shape index, eventually becoming isotropic for spherical alveoli (Fig. 2d, blue circles). To confirm that the stresses leading to these responses originate from actomyosin activity, we ablated organoids after disruption of the actin network by adding cytochalasin D. The recoil response after laser ablation was significantly lower and no longer axially biased (Supplementary Fig. 2 and Supplementary Video 3).

Fig. 2. Alveoli are under isotropic tension and cylindrical branches are under axially biased tension.

a, We ablate a cylindrical region with a diameter of 10 μm and height of 30 μm, cutting through the ECM and the outer cell layer. From the recoil, we estimate the axial and circumferential elastic strains. Scale bar, 50 μm. b, Displacement field induced by the cut. We integrate the optical flow over an annular region to obtain the recoil strains. c, Mean recoil (ϵ_z+ϵ_ϕ)/2 as a function of shape index α, both in attached (n = 16) and floating (n = 73) gels. d, Recoil anisotropy (ϵ_z – ϵ_ϕ) as a function of shape index α for the same experiments as in c (P value, 8 × 10⁻⁴). To compare with the force inference data in h, we scaled by the mean recoil averaged over the whole dataset, namely, $\overline{\epsilon }=0.017.$ e, Confocal microscopy of actin and nuclei in a cylindrical branch and a spherical alveolus. Top: slice through the middle plane. Bottom: slice through the outer cell layer. f, Cell membrane stains. Scale bars, 50 μm. g, From the membrane segmentations, we computed the tensions using the curvilinear-boundary force inference method. h, Inferred tension anisotropy (τ_z–τ_ϕ) as a function of shape index α, both in attached (n = 10) and floating (n = 32) gels (P value, 2 × 10⁻⁷). Note that we assume $\overline{\tau }=1.$ NS, not significant; **P < 0.010; ***P < 0.001.

Since cortical tension is mainly determined by the actin cortex located along the cell boundaries^21,22, we turned to confocal microscopy of the actin cytoskeleton and the cell boundaries. In straight cylindrical branches, we found that the cells are highly elongated and aligned parallel to the branch axis; in contrast, in mature alveoli, the cells are less elongated (Fig. 2e,f). We found that the distribution of boundary angles is strongly anisotropic in attached gels and becomes increasingly isotropic as organoids develop into spheres in floating gels (Supplementary Fig. 3). To compute the relative cortical tension from these images, we used the curvilinear-boundary force inference method (Fig. 2g)^23,24. We found that tension is axially biased in attached gels. This bias decreases in floating gels as the branches become rounder (Fig. 2h). These results quantitatively agree with our laser ablation experiments (Fig. 2d and Supplementary Fig. 5), indicating that the spatial arrangement of cell boundaries is linked to the anisotropy of cortical tension in mammary gland organoids.

Can we explain the observed constant mean recoil $\overline{\epsilon }$ from the arrangement of cell boundaries (Fig. 2c)? Considering each cell as a force dipole²⁵ oriented at an angle θ relative to the branch axis, we decompose the cellular tension into an isotropic part τ₀ and an anisotropic part Δτ (Supplementary Section B2). For a distribution P(θ) of different cell orientation angles, the population-averaged tension tensor is then given by

$$\begin{array}{l}\overline{\tau }\equiv \left[\begin{array}{cc}{\overline{\tau }}_z& \ddots \\ \ddots & {\overline{\tau }}_{\varphi }\end{array}\right]\\ ={\displaystyle \underset{-\pi }{\overset{\pi }{\int }}d\theta P\left(\theta \right)\left[\begin{array}{cc}{\tau }_0+\text{Δ}\tau {\cos }^2\left(\theta \right)& \text{Δ}\tau \cos \left(\theta \right)\sin \left(\theta \right)\\ \text{Δ}\tau \cos \left(\theta \right)\sin \left(\theta \right)& {\tau }_0+\text{Δ}\tau {\sin }^2\left(\theta \right)\end{array}\right]}.\end{array}$$ (1)

The trace of this surface tension tensor is constant, that is, ${\overline{\tau }}_z+{\overline{\tau }}_{\varphi }=2{\tau }_0+\Delta \tau ,$ and independent of the distribution of cell orientation, in agreement with our experiments. The tissue can, therefore, make trade-offs between axial and circumferential tension by reorienting the cells.

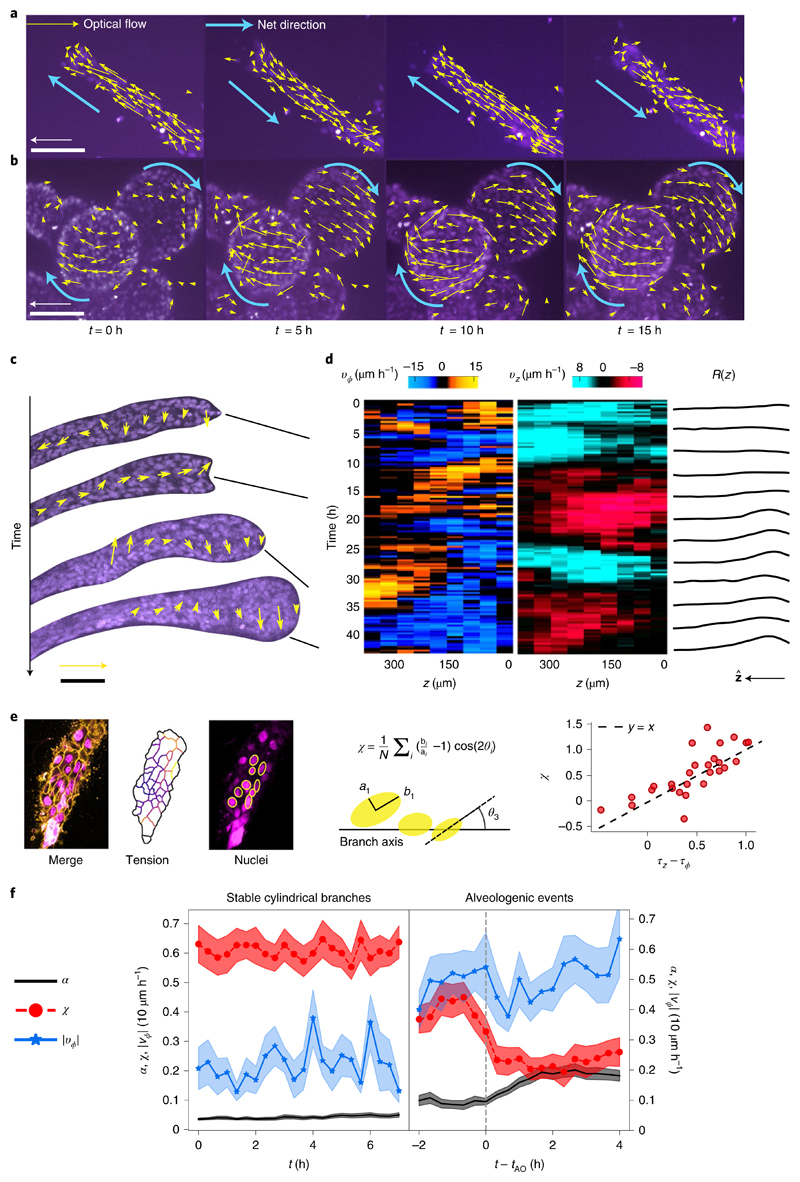
To directly observe the reorientation of the cells, we followed the time course of cell movements by staining the cell nuclei. In cylindrical branches, cells collectively move parallel to the branch axis in a back-and-forth manner (Fig. 3a). In contrast, we observed that mature spherical alveoli perform a persistent collective rotation around the branch axis lasting for at least 20 h without direction reversal and no preferred chirality (Fig. 3b, Supplementary Video 4 and Supplementary Figs. 6 and 7). The observation of branches at early stages of alveologenesis (α ≃ 0.3) revealed that the rotational motion did not arise in a single step, but through transient bouts of localized rotation interspersed with phases of longitudinal translation (Fig. 3c,d). However, rotation broadly correlated with increasing sphericity of the branch end and longitudinal motion coincided with a partial recovery of the cylindrical shape; alveologenesis thus proceeded with superimposed oscillations (Fig. 3d, right, and Supplementary Video 5). Based on the understanding that strong cell–cell adhesion would explain the high spatial coherence of motion, we live-imaged organoids treated with HECD-1. We found that translation and rotation stop within 15–24 h after antibody addition in 73% of the observed branches (n = 15; Supplementary Video 6). Thus, longitudinal translation, rotation and alveologenesis are collective phenomena that require long-range force transmission via E-cadherin junctions, as previously described for a small number of human mammary epithelial cells spontaneously forming spherical aggregates²⁶ and other epithelial cell types in circular confinement²⁷.

Fig. 3. Alveoli undergo collective rotation.

a, Characteristic back-and-forth movement parallel to the axis in a cylindrical branch. Arrows show optical flow for a 20 min time step. Scale bar, 100 μm. Arrow, 30 μm h⁻¹. b, Spherical alveoli rotate for at least 20 h. Scale bar, 100 μm. c, Observation of cell dynamics during alveologenesis shows that rotation is spatially limited to the distal end, correlating with the location of the nascent alveolus. Notice the coexisting opposite rotation senses at time t = 33 h. Scale bar, 100 μm. Arrow, 30 μm h⁻¹. d, Mean circumferential velocity v_ϕ(z, t), mean axial velocity v_z(z, t) and local radius R(z, t) along the branch for the experiment shown in c. e, Nuclei elongation can be used to infer tension anisotropy. We defined a nuclear anisotropy parameter χ by averaging a function of the nucleus elongation b_i/a_i and angle θ_i over several nuclei located at the lower z slices. This parameter may be positive for the elongated nuclei aligned parallel to the branch axis, zero for isotropic distributions or round nuclei, and negative for circumferential alignment. Comparing this parameter with the tensions obtained from force inference in double-stained branches, we found that χ is approximately equal to the tension anisotropy $\left({\tau }_z-{\tau }_{\varphi }\right)/\overline{\tau }.$ f, Sample-average shape index α, nuclear bias χ and absolute circumferential velocity |v_ϕ| as a function of time for two different scenarios: stable cylindrical branches, where α < 0.1 throughout (n = 11, left), and alveologenic events aligned relative to the onset time t_AO (n = 24).

To clarify the causal role of branch rotation in alveologenesis, we undertook a full characterization of the time course of branch shape, cell migration and cortical tension. We used cell nuclei shapes as a proxy for cell tension and found a linear relation between the tension anisotropy (inferred from the cell boundaries) and the anisotropy parameter χ (characterizing the elongation and orientation of nuclei) (Fig. 3e). As a control measurement, we observed stable branches that remained cylindrical for at least 8 h with an average constant tension anisotropy χ ≃ 0.65 and a predominantly axial motion (Fig. 3f, left). As we turned to the onset of the shape transformation, we defined an alveologenic event as an increase in shape index by at least 0.1 within 2 h, starting at onset time t_AO from a low value of α < 0.1 (Supplementary Fig. 4). We found that already within 2 h before alveologenesis, these branches displayed a lower anisotropy parameter (χ ≃ 0.45) and an increased rotational activity |ν_ϕ| compared with the control (Fig. 3f). At onset time t_AO, a robust decrease in nuclear anisotropy precedes the increase in shape index α by about 1 h (Fig. 3f, right, red traces; also see Supplementary Videos 7 and 8). This dynamic data quantitatively agrees with the laser ablation and force inference experiments, supporting our hypothesis of a tension-driven shape transformation (Supplementary Fig. 5).

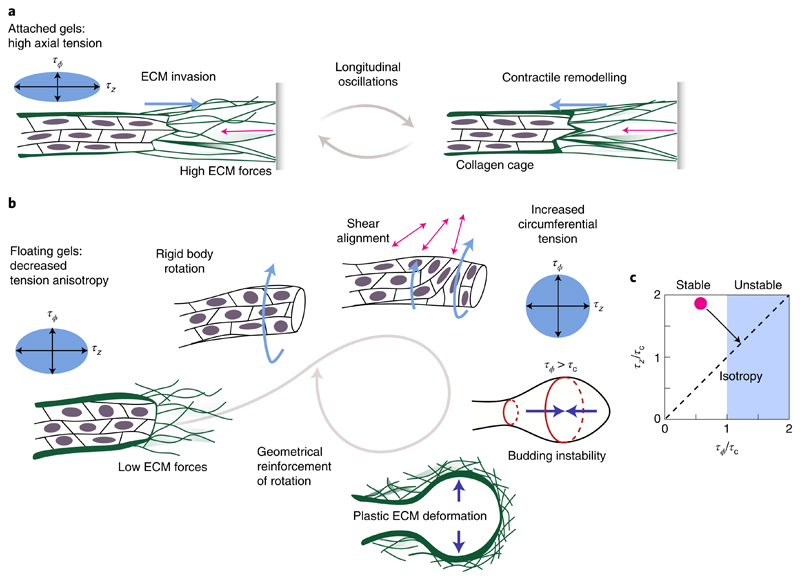
In general, polar matter (such as motile cells) aligns and collectively forms migrating groups to minimize shear²⁸. In a constrained cylindrical geometry like organoid branches, cells can enter an axial translational motion that requires periodic cell repolarization (Fig. 4a). To maintain this motion, cells have to remain axially aligned in the elastic ECM, which could occur due to the cellular sensing of fixed boundaries²⁵. The longitudinal back-and-forth movement of elongating branches (Fig. 3a and Supplementary Video 4) can then be understood from the generic tendency of planar epithelia to move along the principal stress direction²⁸. In floating gels, the ECM cannot support high stresses and thus cells reorient freely (Fig. 4b). Then, the state that minimizes shear corresponds to collective rotation, which runs without cell repolarizations and also arises spontaneously in constrained planar epithelia^29,30. When the cells reorient, there is an increase in circumferential tension at the expense of axial tension (equation (1)), which finally drives the formation of a stable spherical alveolus.

Fig. 4. A hydrodynamic model with anisotropic tension and ECM elasticity can explain the shape transition.

a, In attached gels, high ECM forces are balanced by anisotropic tension and cells move parallel to the branch axis. b, In floating gels, the onset of collective rotation is most likely a consequence of the decreased tension anisotropy, which is in agreement with flat epithelial dynamics²⁸. The resulting surface shear aligns cells in the circumferential direction, increasing τ_ϕ at the expense of τ_z. c, Stability analysis for a fluid cylinder surrounded by an elastic shell. The cylindrical shape becomes unstable for τ_ϕ > τ_c ≃ Eh, where E and h correspond to the elastic modulus and thickness of the collagen cage, respectively. Through cell reorientations, the tissue can increase circumferential tension at the expense of axial tension, thus taking the initially stable cylindrical organoid (red dot) into the unstable regime (black arrow).

How can a shift from axially biased surface tension, namely, (τ_z – τ_ϕ) > 0, towards isotropic surface tension, that is, (τ_z – τ_ϕ) ≈ 0, induce a shape transformation as observed in our experiments? Consider a cylindrical branch as a long, rotationally symmetric, fluid cylinder with radius R, surrounded by an elastic shell with modulus E and thickness h that idealizes the collagen cage. Since the cell layer of the organoid branch forms an interface between a fluid and the ECM, there must be a stress balance between the viscous normal stresses due to fluid flow $\left({\sigma }_{\text{visc}}^{\text{rr}}\right),$ hydrostatic pressure p₀, generalized Laplace pressure due to circumferential tension τ_ϕ, and axial tension τ_z, and elastic stresses Δp_el due to the collagen cage:

$${\sigma }_{\text{visc}}^{\text{rr}}=p_0-\frac{{\tau }_{\varphi }}{R}+{\tau }_z{\partial }_z^{2}R+\text{Δ}{p}_{\text{el}}.$$ (2)

Thus, fluid flows and the corresponding viscous stresses arise whenever the right-hand side of equation (2) is unbalanced. Analysing the linear stability of the tubular branch with respect to small deviations from its cylindrical shape, we find that a shape transformation appears above a critical circumferential tension of τ_ϕ > τ_c = Eh (Fig. 4c and Supplementary Section B3). In terms of tension anisotropy, this criterion is equivalent to $\chi <{\chi }_{\text{c}}=2-2{\tau }_{\text{c}}/\overline{\tau };$ the critical anisotropy parameter corresponding to the alveologenesis onset is χ_c ≃ 0.35, as shown in Fig. 3f. Estimating that τ_c is of the order of 4–7 mN m⁻¹ (Supplementary Section B3), we finally obtain $\overline{\tau }\simeq 5-8{\text{mNm}}^{-1},$ which is of the same order as the typical cortical tension of contractile cells (0.3–4.0 mN m⁻¹ (ref. ³¹)) and organoids (10 mN m⁻¹ (ref. ³²)). Thus, a redistribution of tension from the axial to the circumferential direction—resulting from a simple reorientation of cells (equation (1))—is sufficient to trigger the shape transformation. Note that this remains a dynamic process with extensive cell motility: in early phases of alveologenesis, tension isotropification at the branch tip can be perturbed and transiently reversed by the back-and-forth migration of stalk cells, which actively drags the branch towards the organoid centre and restores axial cell reorientation (Supplementary Videos 5 and 8 and Supplementary Fig. 4b). Thus, the organoid shape change is not monotonic. On long timescales, however, the spherical geometry is stabilized by collective cell rotations and plastic deformation of the surrounding ECM. Finally, once the alveolus is approximately spherical, the Laplace pressure (τ_ϕ + τ_z)/R decreases with increasing radius; as a consequence, under a constant, osmotically balanced hydrostatic pressure difference p₀ and a plastic ECM response, isotropic alveoli keep growing. The presented results show that the shape transformation underlying alveologenesis in human mammary gland organoids can be understood as a budding instability triggered by a decrease in tension anisotropy. This mechanism amounts to a global feedback loop: tissue shape and ECM forces determine epithelial motion, which, in turn, influences the symmetry of the tension tensor, which ultimately feeds back to the tissue shape via hydrodynamics (Fig. 4). The mechanism presented here may turn out to be of general importance for complex shape tranformations in organogenesis.

Methods

Cell culture

Organoids were prepared as described previously⁴. Briefly, mammary gland tissue was obtained from healthy women undergoing reduction mammoplasty at the Nymphenburg Clinic for Plastic and Aesthetic Surgery, in accordance with the regulations of the ethics committee of the Ludwig-Maximilians-Universitat Munchen, Munich, Germany (proposal no. 397-12). The ductal tree was minced, enzymatically digested and cryopreserved. Before each experiment, cells were unfrozen and seeded in collagen gels. The cells were initially cultured in mammary epithelial cell growth medium (MECGM, PromoCell) supplemented with 1% pen/strep (Invitrogen), 0.5% fetal calf serum (FCS) (Pan Biotech), 3 μM Y-27632 (Biomol) and 10 μM forskolin (Biomol). After 5 days, the medium was changed to MECGM supplemented with 1% pen/ strep and 10 μM forskolin. Organoids were prepared from four different donors (Supplementary Table 1).

Three-dimensional collagen I gels

Organoids were grown in collagen I gels from rat tail (Corning). Freshly unfrozen single-cell suspensions were mixed with MECGM medium, ×11 HEPES and collagen solution; pH 7.5 was attained by the addition of 1 M NaOH. Final collagen concentration was 1.3 mg ml⁻¹. The mixture was gently but thoroughly mixed before deposition on slides (ibidi). After polymerization for 1 h in an incubator at 37 °C, an equal volume of medium was added to the gel. Organoids were grown in 3% oxygen atmosphere. For enzymatic digestion of the collagen matrix (Fig. 1c), to the gel, we added an equal volume of medium containing 0.01 U ml⁻¹ collagenase (Sigma). Within ~20 min, the collagen fibres were no longer visible in the Hoffman contrast images and the debris diffused freely, indicating complete hydrolysis of the matrix.

Biochemical perturbation

Organoids were grown under normal conditions for 9 days; on culture day 10, medium containing either 0.5 nM calyculin A (Gibco), 10 μM Marimastat (Santa Cruz Biotechnology) or HECD-1 (abcam) at a ratio of 1:50 was added. Fresh drug was replenished in a second medium change on day 12. Organoids were imaged by bright-field Hoffman contrast microscopy. To determine the organoid size, we manually drew ellipses tightly enclosing the structures and defined the size as the mean of the elliptic axes.

Laser ablation

Laser ablation of collagen and organoids was performed with a custom setup based on the one described in ref. ³³. Briefly, a pulsed 355 nm laser with 400 ps pulse duration and 25 mW average power (Teem Photonics) was shone on the sample through a PL APO ×40/1.1 NA water immersion objective (Leica). Two galvanometric mirrors were used to tilt the beam and control the spot position in the focal plane. To cut along the z direction, we simultaneously acquired three-dimensional stacks, displacing the sample with a piezo stage (ASI). Stack height along z was 30 μm and the number of slices per stack was 10. To maximize the acquisition rate, we used Micro-Manager's fast sequence mode³⁴, controlling the stage with the camera FIRE signal. Image exposure time was 50 ms, corresponding to a stack acquisition time of 0.5 s.

For organoid ablation experiments, the laser spot was displaced in a circular fashion, cutting a circle with a diameter of 10 μm and a height of 30 μm. We performed these experiments on culture days 14–15 for both floating and attached gels. The cuts induced a fast recoil of the surrounding tissue. We determined the displacement field of the recoil by comparing the slices at a given z position in the initial, unperturbed configuration and 3 s after the cut. Specifically, we calculated the corresponding optical flow using the OpenCV implementation of the Farneback algorithm³⁵. The axial and circumferential components of the displacement field were integrated over an annular region surrounding the cut to obtain the total displacement. The inner radius of the annular region was 15 μm, chosen such that artifacts stemming from ablation bubbles were avoided. The outer radius of the annular region was determined by the branch width and was typically 30 μm. The data showed considerable scatter that seemed to be intrinsic variability in the rearrangement of cell boundaries after the cut, rather than noise in the image processing algorithm.

Confocal microscopy

The laser ablation setup was equipped with a spinning disk unit (Yokogawa); a scientific complementary metal-oxide-semiconductor (sCMOS) camera (Andor); and 488, 561 and 638 nm lasers (Cobolt) for fluorescence confocal imaging, as well as an XYZ translation stage (ASI), a temperature control device and a gas incubation system to maintain 5% CO₂ and 3% O₂ (ibidi). Before the laser ablation experiments, organoid membranes were stained with 1X CellMask Deep Red (Invitrogen). For time-lapsed microscopy, cell nuclei were stained with 10 μM SiR-DNA (Spirochrome).

Nuclear anisotropy parameter

Organoids were stained with 10 μM SiR-DNA and imaged by confocal microscopy using an HC FLUOTAR L ×25/0.95 W VISIR water immersion objective (Leica). Since alveologenic events are rare, we devised a procedure that allowed for several days of continuous, simultaneous imaging of many structures (10–13) without evaporation of the water layer between the slide and objective. Basically, we enclosed the objective and sample slide with a party balloon filled with 25 ml water. In this way, we acquired the images shown in Supplementary Videos 6-8. To calculate the anisotropy parameter from the branch images, we manually drew ellipses around 5–15 nuclei located at low-z slices using ImageJ software. Ellipse parameters were exported and further processed using Python scripts. Rotation velocities were calculated by the optical flow³⁵.

Statistical analysis

Data are presented as mean ± standard error (s.e.). To compare tension estimations from branches with different shapes, data were pooled according to the shape index and compared with Student's t-test (two-tailed, unpaired). Here P < 0.05 was considered significant: *P < 0.050, **P < 0.010, ***P < 0.001.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Supplementary Material

The online version contains supplementary material available at https://doi.org/10.1038/s41567-021-01336-7.

Data availability

Microscopy data that support the findings of this study are available in Zenodo at https://doi.org/10.5281/zenodo.5076123. Source data are provided with this paper. All other relevant data supporting the key findings of this study are available within the article and Supplementary Information or from the corresponding authors upon reasonable request.

Code availability

The code used for analysing the data of this study is available in Zenodo at https://doi.org/10.5281/zenodo.5076123.