Physics-driven coarse-grained model for biomolecular phase separation with near-quantitative accuracy

Abstract

Various physics- and data-driven sequence-dependent protein coarse-grained models have been developed to study biomolecular phase separation and elucidate the dominant physicochemical driving forces. Here, we present Mpipi, a multiscale coarse-grained model that describes almost quantitatively the change in protein critical temperatures as a function of amino-acid sequence. The model is parameterised from both atomistic simulations and bioinformatics data and accounts for the dominant role of π–π and hybrid cation-π/π–π interactions and the much stronger attractive contacts established by arginines than lysines. We provide a comprehensive set of benchmarks for Mpipi and seven other residue-level coarse-grained models against experimental radii of gyration and quantitative in-vitro phase diagrams; Mpipi predictions agree well with experiment on both fronts. Moreover, it can account for protein–RNA interactions, correctly predicts the multiphase behaviour of a charge-matched poly-arginine/poly-lysine/RNA system, and recapitulates experimental LLPS trends for sequence mutations on FUS, DDX4 and LAF-1 proteins.

Introduction

Under certain conditions, macromolecules within cells demix into membraneless organelles. These organelles, often termed biomolecular condensates, are sustained by the physicochemical process of liquid-liquid phase separation (LLPS) [1, 2] The ensuing condensates play important roles in cellular function as well as dysfunction [3]; therefore, delineating the mechanisms of intracellular LLPS is now an active area of research. Intracellular LLPS is principally driven by biomolecular multivalency, i.e. the ability of multidomain proteins, intrinsically disordered proteins/regions (IDPs/IDRs), ribonucleic acids (RNA) and chromatin to engage multiple interaction partners simultaneously. This multivalency is, in turn, predominantly encoded in the chemical makeup of the macromolecules in question. It is well-established that both hydrophobic and electrostatic interactions are important drivers of biomolecular LLPS, including charge–charge, π–π, cation–π, dipole–dipole and non-polar interactions. Additionally, there is strong evidence that certain chemical building blocks have a bigger stake in biomolecular LLPS than others [4–7]. Biophysical models for studying LLPS must therefore be able to capture the correct balance between these myriad driving forces. In this paper, we aim to achieve precisely this.

Together, the stickers-and-spacers framework of Pappu and colleagues [8, 9] and the quantitative experimental phase diagrams of Mittag and colleagues position aromatic residues as being chief drivers of biomolecular phase separation [4, 10]. Moreover, it is evident that even within the subset of aromatic residues, tyrosine, for example, is a stronger contributor than phenylalanine to LLPS stability [7, 10–12], perhaps because it has more side-chain binding modes than phenylalanine: in addition to forming aromatic π–π contacts, tyrosine can form strong hydrogen bonds via its phenol group.

The dominant role of π–π interactions in LLPS was also suggested by Vernon et al. [13], who, via a comprehensive survey of the protein data bank (PDB), identified an abundance of planar π–π contacts involving not only aromatic but also non-aromatic residues in protein structures. Additionally, in recent work, π–π interactions emerged as a major driver of LLPS at both low and high salt concentration [7]. Specifically, our atomistic simulations revealed that, for proteins, the strongest pairwise interactions arise when the two amino acids in question both possess π electrons in their side chains, including both aromatic or non-aromatic residues with sp²-hybridised groups [7].

The role of hydrophobic π–π contacts in LLPS is even more obvious when we consider differences in the strengths of cation–π interactions. Notably, cationic residues, namely arginine and lysine, have been shown to act as unequal contributors to LLPS [6, 7, 14–16]: arginine establishes appreciably stronger cation–π and charge–charge interactions due to the presence of the guanidinium group [6, 7, 13, 16–18]. Furthermore, Pappu and colleagues have recently demonstrated that the free energy of hydration of arginine is considerably less favourable than that of lysine; thus, although they both carry the same charge, arginine is significantly more hydrophobic than lysine [16]. Since π–based contacts play such a dominant role in biomolecular LLPS, achieving the correct balance of these interactions is essential for making quantitative predictions.

Complementing experimental and theoretical work, computer simulations have provided a unique lens for probing biomolecular LLPS. Because LLPS is a collective phenomenon, coarse-graining is essential to reduce the system dimensionality while retaining essential physicochemical information and allowing sufficient sampling of phase space in computationally tractable time scales. There are numerous possible approaches for parameterising biomolecular coarse-grained models [21], from ‘bottom-up’ strategies that rely on higher-resolution models [9, 10, 22–24], to ‘knowledge-driven’ approaches that aim to reproduce experimental properties using a data-based parameterisation [25–27], to ‘top-down’ strategies that account for emergent behaviour by approximating fundamental physical forces [28, 29], to combinations of these [30, 31]. Coarsegrained models can also be broadly classed as ‘system-specific’, bottom-up parameterisations focussing on finding an optimum representation for a particular system using fine-grained simulations as a reference, often derived in a systematic way using for instance iterative Boltzmann inversion [32, 33] or force matching [34, 35], and ‘transferable’, either bottom-up or top-down parameterisations, aiming to achieve a generally applicable potential.

Developing a coarse-grained model involves invoking multiple approximations and making design decisions (e.g. type of model, resolution, bead characteristics, types of interaction) that are more or less appropriate depending on the question being investigated. As discussed by Choi et al. [9], there is no unequivocal reason that makes one scheme intrinsically superior to others: each approach has its advantages and drawbacks. For instance, systematic multiscale coarse-graining from higher-resolution models [23, 36] by construction results in an excellent description of the system under investigation and allows us to work out precisely what underlying building blocks have been coarse-grained. However, system-specific coarse-graining does not generally result in a unique solution [37] and requires sufficiently long simulations of the entire system of interest to be run with an expensive high-resolution potential. Indeed, bulk phase behaviour can be significantly different between a machine-learned potential and the underlying quantum-mechanical potential-energy surface even for systems much simpler than biomolecules [38], illustrating the significant challenge of this approach. Similarly, transferable data-driven or machine-learning-based approaches can give excellent agreement with the data they were parameterised from, but, since in such high-dimensional problems, many solutions are similarly good, careful curation is required to obtain statistically meaningful results for a specific system, and even these may still not be transferable to similar molecules [39]. On the other hand, a transferable ‘physics-based’ approach to interaction parameters provides us with a simple way of rationalising complex behaviour based on relatively simple interactions. However, it risks introducing our biases of which interactions are important into the predictions of the model, and the predictions and rationalisations of observed behaviours with such models can therefore be to some extent self-fulfilling.

Various coarse-graining strategies have now been applied to gain insights into the problem of biomolecular LLPS. For example, the mean-field stickers-and-spacers model can be parameterised to reach quantitative agreement with experimental phase diagrams of specific proteins, providing a tool to dissect the driving forces behind the observations [4, 8–10]. A different approach, pioneered by Mittal, Best and colleagues [28], combines residue-level coarse-grained models with direct-coexistence simulations [20], offering a transferable method to predict protein phase diagrams and augmenting our ability to link molecular sequences to their experimental phase behaviour.

Inspired by previous computational work and guided by the accumulated knowledge of the LLPS interaction landscape, we set out to design a chemically accurate coarse-grained model for predicting biomolecular LLPS. Specifically, the model aims to achieve optimal strengths of protein–protein and protein–RNA interactions. We demonstrate that our model can accurately predict biomolecular phase separation while achieving quantitative agreement with experiment, recapitulating post-translational modification effects, and even capturing more complex features such as sequence-dependent multiphasic compartmentalisation. Simulations using our model are particularly simple to set up since all its components are already implemented in open-source software.

In what follows, we first describe the design of our multiscale π–π model (termed ‘Mpipi’) for probing phase separation of biomolecules. We outline the use of atomistic potential-of-mean-force (PMF) calculations coupled with bioinformatics data for yielding a chemically accurate interaction scale for coarse-grained simulations [Fig. 1]. We then assess the balance of key interactions in the Mpipi model alongside other commonly used residue-based coarse-grained models. Finally, we present benchmarks for several LLPS systems and directly compare our predictions with other models and against quantitative experimental phase diagrams and other experiments.

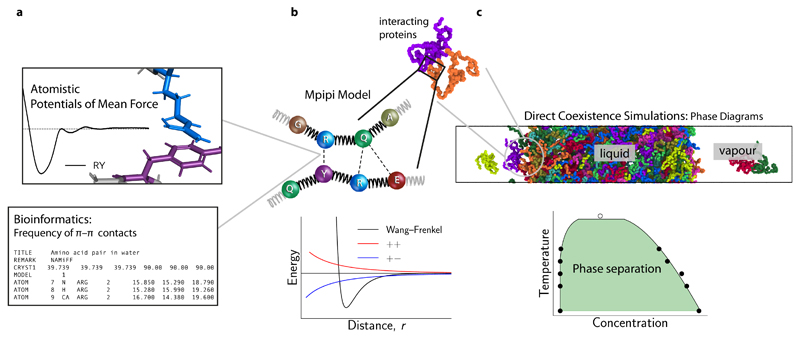
Figure 1. Designing a coarse-grained model for LLPS from potential-of-mean-force calculations and bioinformatics data.

a (Top) Potential of mean force (PMF) of selected amino-acid (or nucleic-acid) pairs are computed in all-atom simulations with explicit solvent and ions. The computed curves provide a free energy of interaction for the pair in question. (Bottom) The frequencies of π–π contacts for amino acids are obtained from bioinformatics work [13]. Together, these data are used to parameterise the pairwise interactions in the Mpipi model. b (Top) In the Mpipi model, each amino acid (or nucleic acid) is represented by a unique bead. The potential energy is computed as a sum of short-ranged pairwise terms, electrostatic interactions and bonded interactions modelled as harmonic springs. (Bottom) Short-ranged pairwise and electrostatic interactions are computed via a Coulomb term with Debye–Hückel screening (red and blue curves) and the Wang–Frenkel potential [19] (black curve), respectively. c To study biomolecular phase behaviour, we use direct-coexistence molecular-dynamics simulations [20] and compute phase diagrams in the temperature–concentration (or density) space.

Results

Designing coarse-grained models for biomolecular LLPS

We have designed a residue-level coarse-grained model for predicting biomolecular phase behaviour (Fig. 1a–c) that captures the fundamental Van der Waals and electrostatic interactions of a ‘top-down’ approach and the interaction strengths obtained from ‘bottom-up’ atomistic simulations and bioinformatics data. In the Mpipi model, each amino (or nucleic) acid is mapped onto a unique bead (Fig. 1b) based on simulation and experimental data. Following Dignon et al. [28], the potential energy of molecules is computed as the sum of a harmonic bond energy, Debye–Hückel and short-ranged energy terms (Methods), which account for π–π, cation–π and other non-ionic interactions. The main differences between the Mpipi model and other sequence-based coarse-grained models for LLPS are (1) the functional form of short-ranged terms, (2) the parameterisation of short-ranged interactions, and (3) the relative contribution of long-ranged electrostatics and short-ranged terms to the total energy. Specifically, for short-range interactions, we use the recently developed Wang–Frenkel [19] pair potential (Fig. 1b; see Methods), which accounts for key physical interactions, namely a short-ranged excluded-volume repulsion and a longer-ranged attraction which gradually decays to zero. The Wang–Frenkel potential has several advantages [19] over Lennard-Jones-like potentials that are commonly adopted in molecular simulations. We outline these and how our model is fitted within the Wang–Frenkel framework in the Methods section.

When deciding on the energy scale for short-ranged interactions, our main objective is to achieve the correct balance of π–π and non-π-based contacts. To this end, we combine bioinformatics data and atomistic short-ranged free energy estimates (Fig. 2a–d). In the Methods section, we explain our parameterisation of short-ranged pairwise contacts and long-ranged charge–charge interactions (Fig. 2e).

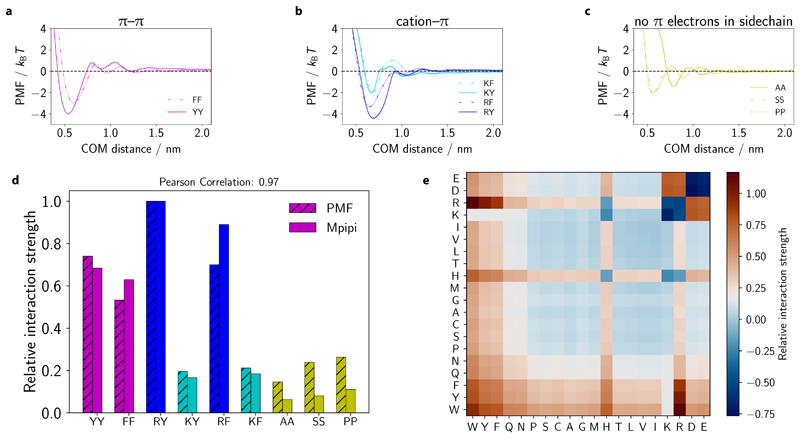
Figure 2. Obtaining the correct balance of π–π and non-π-based interactions in the Mpipi model.

a–c PMF calculations at 150 mm NaCl salt concentration for π–π, cation–π and non-π-based interactions, respectively, as a function of the centre-of-mass (COM) distance. Statistical errors (mean±s.d.) are given as error bands, and are only just larger than the line width. They were computed via Bayesian bootstrapping of 3 independent simulations. Each pair is labelled using one-letter amino-acid codes (SI Table I). d Comparison of relative interaction strengths of selected residue pairs (SI Table I) from the PMF calculations with those implemented in the Mpipi model, relative to the Arg–Tyr (RY) interaction. Values are computed by taking the integral of the curves in a–c and the integral of the Wang-Frenkel potential only (between σ and 3σ) for the PMF and Mpipi sets, respectively; for the PMF data only the leftmost well is considered. These correspond to mean energies in the high-temperature limit. e Summary of relative interaction strengths in the Mpipi model. These relative interaction strengths include electrostatic interactions and are computed by numerically integrating Eq. (8) and normalising the result by the RY interaction strength.

Cation–π, π–π and non-π interactions in residue-level models

To validate our model parameters, we first compare the Mpipi model with seven other residue-level coarse-grained models for LLPS, namely the KH (Kim–Hummer) [28], HPS-KR (hydrophobicity scale) [28], FB-HPS [26] and HPS-Urry [29] models, as well as the HPS model with augmented cation–π interactions [schemes (i) and (ii)] [40]. We also include analyses for TSCL-M2, the M2 parameter set of Tesei et al. [27] proposed while our work was under review. Das et al. [40] recently provided a thorough comparison of the KH, HPS-KR, HPS+cation–π(i) and HPS+cation–π(ii) models. Below, we briefly discuss the key features of all models and then evaluate them in terms of the balance of π–π, cation–π and non-π-based interactions.

A key difference between Mpipi and other residue-level models is the parameterisation of short-ranged interactions. In the KH model [28, 41], short-ranged interactions (ε_ij) are based on residue contact statistics of folded proteins. The energy scale of the KH model was tuned to reproduce approximately the radii of gyration of selected unfolded proteins/IDPs [28]; here, we utilise parameter set D [28] for interactions involving disordered proteins. The KH model has been successfully used to predict LLPS propensities for variants of the N-terminal domain (NTD) of the DEAD-Box Helicase 4 (DDX4) protein [40] and to describe qualitatively the phase behaviour of the proteins Fused in Sarcoma (FUS) and Lethal-And-Feminizing-1 (LAF-1) [28].

The next model, HPS-KR [28] is perhaps the most widely used sequence-based continuum model for studying biomolecular LLPS. In this model, short-ranged interactions are based on the hydrophobicity scale of Kapcha and Rossky [42], and each amino acid is assigned a λ_i value which accounts for its ‘hydrophobicity’, and residue–residue contacts (λ_ij) are determined by the arithmetic mean of the λ_i values of each residue [43]. Additionally, the absolute energy scale of the model was optimised to reproduce experimental radii of gyration (R_g) of an IDP subset. However, as previously noted [40], the HPS-KR model is inconsistent with experimental data when accounting for the balance between Arg and Lys interactions. An improved version of the HPS model, HPS-Urry [29], was recently parameterised, which employs instead the hydrophobicity scale of Urry et al. [44] to determine λ_ij. Moreover, two free parameters (μ and Δ) are introduced to scale and shift the λ_ij values; these are optimised to reproduce experimental R_g [29]. Recently, Dannenhoffer-Lafage and Best [26] also reparameterised the short-ranged interactions in the HPS-KR model by employing machine-learning techniques. Their model, FB-HPS, was optimised against experimental R_g of unfolded, phase-separating and intrinsically disordered proteins.

Prior to these studies, Das et al. [40] augmented the HPS-KR model so as better to account for cation–π interactions. They presented two schemes: scheme (i), where Arg/Lys–π interactions are scaled uniformly, and scheme (ii), where they vary. Notably, the authors comment that despite these changes, the augmented models fail to capture fully the experimental LLPS propensities of their test set of proteins [40]. In another study, it was demonstrated that the HPS+cation–π(i) model can reasonably reproduce experimental trends of selected RNA binding proteins [45]. Here, we have considered these augmented models to achieve a more complete view of how cation–π interactions contribute to biomolecular LLPS.

Recently, Tesei and coworkers [27] used experimental data to reparameterise the hydrophobicity scale of HPS-KR via a Bayesian parameter-learning procedure. The M2 parameter set predicted well both single-molecule and collective behaviours of the tested IDPs; we have therefore included benchmarks for this parameter set in our work.

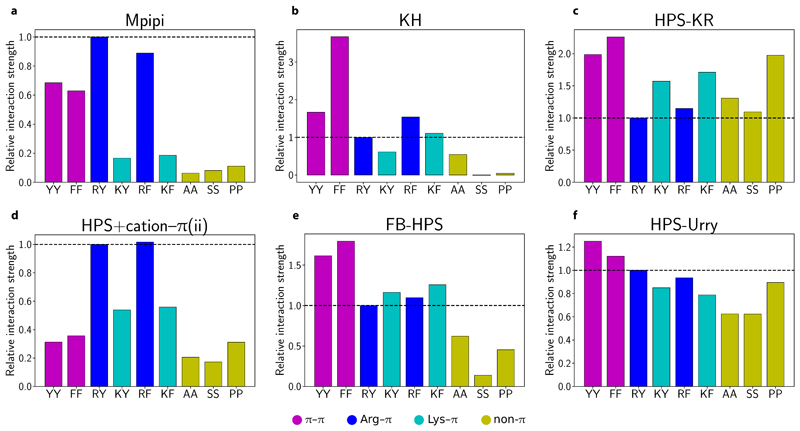
Fig. 3 summarises the relative contributions of selected π–π and non-π-based interactions for the residue-level coarse-grained models assessed in this work (see SI Fig. S5 and SI Fig. S6 for the HPS+cation–π(i) and TSCL-M2 models). The relative interaction strengths are obtained by computing the integral of the curves of the short-ranged potential (with consistent limits of σ–3σ). In the Mpipi, KH, FB-HPS and TSCL-M2 models, aromatic residue pairs (magenta bars in Fig. 3a,b,e and SI Fig. S6a) are generally considerably stronger than residue pairs not involving π contacts (dark yellow bars in Fig. 3a,b,e and SI Fig. S6a). Hence, consistently with the stickers-and-spacers framework, YY and FF are expected to act as stickers, while AA, SS and PP should behave as spacers in these models. Interestingly, in the FB-HPS model, glycine (see Figure 4 of Dannenhoffer-Lafage and Best [26]), which is normally classified as a spacer, has an interaction strength that is stronger than even the aromatic residues. While this result is attributed to glycine forming strong backbone π–π contacts [26], mutational studies have consistently found that replacing sticker-like residues with Gly significantly suppresses biomolecular LLPS [10, 11]. The stronger contacts for Gly arising from the machine-learning algorithm optimisation [26] may be a result of how commonly occurring glycine is in many proteins, particularly those for which experimental radii of gyration are available.

Figure 3. Relative contributions of π–π, cation–π and non-π-based interactions in different residue-level models.

a–f Relative interaction strengths [Eq. (8)] for selected residue pairs (see SI Table I for one-letter amino-acid codes) in Mpipi, KH, HPS-KR, FB-HPS, HPS+cation–π(i) and HPS+cation–π(ii) models. For each model, the data set is normalised relative to the corresponding Arg–Tyr (RY) interaction. In each plot, a horizontal dashed line at the RY interaction strength is provided for comparison purposes. Aromatic π–π interactions are coloured in magenta, Arg–π in blue, Lys–π in cyan and non-π-based interactions in dark yellow.

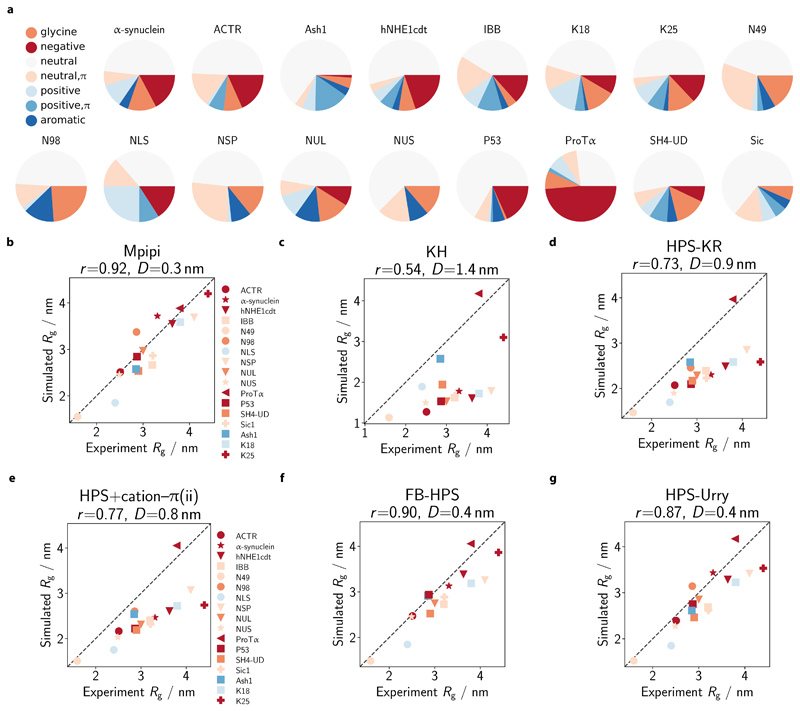
Figure 4. Comparison of single-molecule radii of gyration with experiment.

a Composition of simulated IDPs. We select 17 IDPs for which experimental radii of gyration (R_g) are available (see SI Sec. S2.1 and SI Table III) and assess the composition of the IDPs in terms of the proportion of glycine (orange), neutral (dark yellow; no net charge at pH 7 and no π electrons in side-chain: A, C, I, L, M, P, S, T, V), neutral with π (green; no net charge at pH 7 with π electrons in side chain: N, Q), positive (cyan; without π electrons in side-chain: K), positive with π (blue; with π electrons in side-chain: H, R), negative (red: D, E) and aromatic (magenta: F, W, Y) residues. b–g Comparison of simulated and experiment R_g. R_g values are computed at 300 K in each model. Each protein is coloured based on its dominant residue class (as categorised in a and excluding the ‘neutral’ class). The broken line represents the ‘perfect fit’ line. For each model, the Pearson correlation coefficient r and the root mean squared deviation D are reported in the respective figure title.

With regards to Tyr versus Phe, a survey of the PDB [13], our atomistic PMF calculations (Fig. 2d) and experiments [10–12] all suggest that Phe–Phe contacts are weaker than Tyr–Tyr ones. By contrast, the KH, HPS-KR, FB-HPS, HPS+cation–π(i) and HPS+cation–π(ii) models all predict stronger Phe–Phe contacts than Tyr–Tyr interactions (Fig. 3). The trend for the KH model is particularly striking, with the weighted interaction energy of FF predicted to be about twice that of YY (Fig. 3b). Taken together, we do not expect these models to reproduce LLPS propensities faithfully as far as Tyr vs Phe mutations are concerned.

We also examine the relative strengths of cation–π interactions in the coarse-grained models, again focussing on the contributions of cation–π contacts versus aromatic π–π contacts and Arg–π contacts compared to Lys–π ones. The HPS+cation–π(ii) (Fig. 3d) and the TSCL-M2 (SI Fig. S6a) models are most similar to the Mpipi model in terms of the relative contributions of Arg–π and Lys–π contacts. While in the KH model, Arg–π interactions are also stronger than Lys–π ones, the overall strength of these is low, which makes Arg–π interactions closer in strength to spacer-type interactions (Fig. 3b); thus, the dominant role of these interactions may not be properly accounted for in the KH model. The HPS-Urry model also captures the overall trend for Arg –vs Lys–π contacts (Fig. 3f); in addition, the weights of these interactions are more similar than those encoded in Mpipi, HPS+cation–π(ii) and TSCL-M2. The opposite trend is found in both the HPS-KR and the FB-HPS models, where Lys–π interactions are now stronger than Arg–π interactions. Moreover, in the HPS-KR model, non–π-based interactions are comparable to (or even stronger than) cation–π interactions (Fig. 3c). We therefore speculate that the HPS-KR model might represent an upper bound in terms of predicting LLPS propensities of proteins. Strikingly, in the HPS+cation–π(i) model, cation–π interactions convincingly dominate all other types of interaction (SI Fig. S5). LLPS systems driven by cation–π interactions are thus likely to be over-stabilised with this model [40].

Estimating single-molecule radii of gyration

Certain single-molecule properties of proteins, such as R_g in the context of coil-to-globule transitions, are often governed by similar driving forces as bulk LLPS [46–48], and coiling transitions are sometimes used as a proxy for the upper critical solution temperature (T_c) [24]. Importantly, the strong correlation between single-molecule dimensions and T_c has been used as a target for optimising coarse-grained LLPS models. It is often assumed that models that correctly reproduce experimental R_g of single proteins (at infinite dilution) should accurately predict homotypic LLPS propensities.

Accordingly, we tested the ability of Mpipi to recapitulate experimental R_g of IDPs (Fig. 4a; see also SI Sec. S2.1 and SI Table III). The set of IDPs has a good distribution of net charge: from –44e for ProTα to +16e for Ashl, where e is the elementary charge. These proteins therefore provide an indirect measure of how well electrostatic and short-ranged pairwise interactions are balanced in the coarse-grained models. Most of the proteins in our test set largely comprise neutral residues that lack π electrons in their side-chains. Proteins amenable to single-molecule experiments are likely to have a high content of these neutral residues that lack π electrons, since these residues form weaker contacts and so the resulting proteins are less prone to aggregation and self-assembly. Notwithstanding the dominance of this class, the test set of proteins does exhibit appreciable variation in protein composition.

Fig. 4b–g compares simulated R_g with experiment R_g for each coarse-grained model we have considered. Each protein is coloured according to its dominant residue class, using the same colouring code as Fig. 4a but ignoring the neutral class. The Mpipi, FB-HPS (Fig. 4f), HPS-Urry (Fig. 4g) and TSCL-M2 (SI Fig. S6b) models achieve the closest match with experiment. This result is not unexpected for the last three models, since they were all optimised to reproduce experimental R_g values, and several proteins in the current study were used either to train or to validate the respective model parameters. Importantly, compared to HPS-KR, HPS-Urry and TSCL-M2 both perform better at predicting single-molecule radii of gyration. Thus, in this regard, these models fulfil their goal of offering an improvement over their common predecessor.

Notably, Mpipi (Fig. 4b), whose parameters were not optimised on R_g data but rather on physicochemical information, is able to predict the R_g values to within a root mean squared deviation of 0.3 nm for the tested IDPs. Fits to the bioinformatics data and atomistic PMFs therefore appear to be physically sound, at least with respect to capturing sequence-dependent single-molecule chain dimensions.

While the HPS+cation–π(ii) (Fig. 4e), HPS-KR (Fig. 4d) and HPS+cation–π(i) (SI Fig. S5) models yield reasonable agreement with experiment, all generally predict more compact proteins than experiments. Interestingly, the KH model (Fig. 4c) gives the poorest agreement with experiment, perhaps because short-ranged pairwise interactions in the KH model were obtained from residue-residue contacts in folded proteins and may thus overestimate the relative strengths of such interactions.

Recapitulating the phase behaviour of A1-LCD variants

To ascertain the extent to which the Mpipi potential is able to capture the bulk properties of protein solutions, we compute the critical solution temperatures for a series of variants of the LCD of the heterogeneous nuclear ribonucleoprotein A1 (hnRNPA1), referred to here as A1-LCD, whose experimental phase diagrams were recently determined [10].

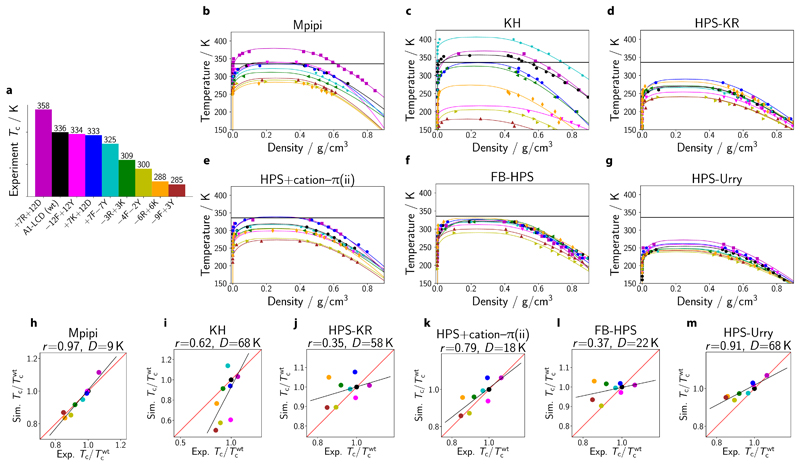
We estimate the experimental critical temperatures [Fig. 5a] of a range of A1-LCD variants, using the fitting procedure described in SI Sec. S2.2. The variants’ sequences are given in SI Sec. S2.2, following the nomenclature of Bremer and co-workers [10]. For each model, we show the computed phase diagrams in Fig. 5b–g, and the correlation between simulation and experimental values in Fig. 5h–m. The corresponding data for the HPS+cation-π(i) and TSCL-M2 models are provided in SI Fig. S5d,e and SI Fig. S6d,e, respectively.

Figure 5. Recapitulating the phase behaviour of A1-LCD variants.

a Nine variants of the A1-LCD (including the wild-type) are studied in this work. Variants are prepared following Bremer et al. [10] Experimental critical temperatures are estimated as described in SI Sec. S2.2. The colour of each variant used in panel a is also used in all remaining panels. b–g Phase diagrams for A1-LCD variants obtained via direct-coexistence simulations using the Mpipi, KH, HPS-KR, HPS+cation–π(ii), FB-HPS and HPS-Urry models, respectively. Estimation of critical points of simulated phase diagrams is described in the Methods section. Curves are derived from empirical fits of the data to Eqs (6) and (7); typical errors are discussed in SI Sec. S8.4. h–m Simulated critical temperature T_c relative to the critical temperature of the wild type $(T_c^{wt})$ shown against the experimental analogue. The Pearson correlation coefficient r and the root mean squared deviation D are provided above each graph. The red lines correspond to a perfect fit to the experimental data, while the black lines represent the linear regression fit.

Although the fitted linear regression has a positive gradient for the eight models considered, indicating that, broadly speaking, all the models capture some of the underlying physics, the Pearson correlation coefficient varies significantly across the models. Mpipi achieves a Pearson correlation coefficient (r) of 0.97 (Fig. 5h), indicating that the parameterisation works well not only for single-molecule properties (Fig. 4), but also accounts for bulk behaviour. The HPS-Urry (Fig. 5m; r = 0.91), TSCL-M2 (SI Fig. S6e; r = 0.80) and HPS+cation–π(ii) (Fig. 5k; r = 0.79) models also achieve high correlation with experiment. By contrast, the FB-HPS model, which was parameterised principally on R_g data, performs quite well when predicting the radius of gyration, but the improvement of its predictions of the phase behaviour of the A1-LCD variants relative to the underlying HPS-KR potential ((Fig. 5j; r = 0.35) is only marginal ((Fig. 5l; r = 0.37). Although R_g properties do correlate with phase behaviour in experiment, there are evidently several parameterisations of coarse-grained models which are able to capture one property but not the other.

Coarse-graining necessarily entails integrating out some degrees of freedom and so interaction ‘energies’ are therefore approximate free energies. It is thus not likely that such models could capture faithfully the behaviour of protein systems far from the temperature range in which they were parameterised. Nevertheless, given that all the models were parameterised to reproduce protein behaviour close to room temperature, we may also consider the agreement between the experimental and simulation temperature scales. To this end, we can compare the deviation of the experimental and simulation critical temperatures. For the A1-LCD wild type, this can be visualised by comparing the solid horizontal black lines in Fig. 5b–g, representing the experimental critical solution temperature of the A1-LCD wild type, to the maximum temperature of the binodals in black, the simulation results for the same system. In addition, a quantification of the deviation between the experimental and simulation results is given by the difference in slope between the black linear fits shown in Fig. 5h–m and the y = x lines shown in red, as well as by the root mean squared deviation between the experimental and simulation critical temperatures (D).

These comparisons demonstrate that, at least within the range of experimental data available, Mpipi (D=9 K), HPS+cation-π(ii) (D=18 K) and TSCL-M2 (D=19 K) give good quantitative predictions for A1-LCD (i.e. high Pearson coefficients and small D values). Lastly, although HPS-Urry achieves good agreement with experiment when considering the Pearson coefficients, its range of predicted critical temperatures is smaller than in experiment, which results in a relatively large root mean squared deviation.

LLPS of other proteins and multiphasic compartmentalisation

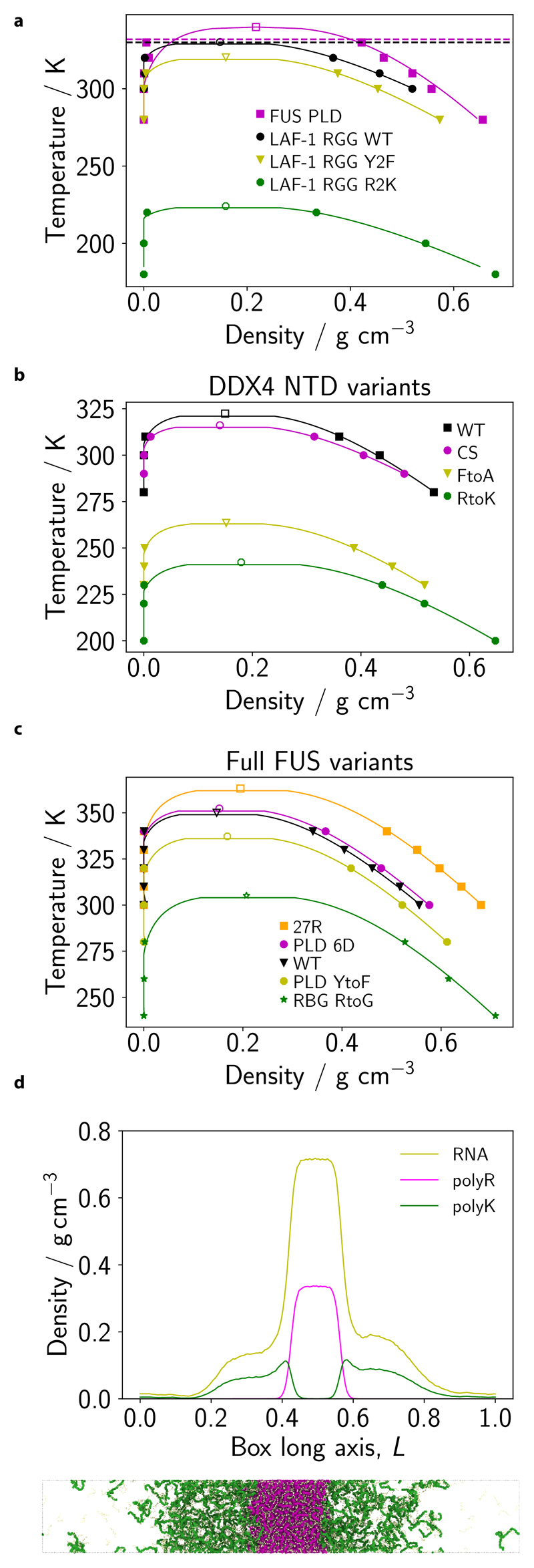
To probe the model’s transferability, we test its performance for other well-studied IDRs of RNA-binding proteins. Specifically, we compute phase diagrams for the prion-like domain (PLD) of FUS protein, three variants of the arginine/glycinerich (RGG) domain of LAF-1 (Fig. 6a), and four variants of the DDX4 NTD (Fig. 6b). We also compute phase diagrams for five variants of the full-length FUS protein (SI Sec. S2; Fig. 6c). For all these systems, Mpipi achieves good qualitative agreement with experiment and in some cases achieves quantitative accuracy as well. We provide a full account of these results in SI Sec. S7.

Figure 6. Predicting LLPS propensities of other proteins and multiphasic compartmentalisation.

a Temperature–density phase diagrams for FUS PLD, LAF-1 RGG (WT) and two other variants of LAF-1 RGG for the Mpipi model. Filled symbols represent simulation data, while empty symbols depict estimated simulation critical points (see Methods). The horizontal dashed lines represent estimated T_θ (temperature of the coil-to-globule transition) for FUS PLD (magenta) and LAF-1 RGG (WT) (black) obtained with the Absinth potential. b, c Same as in a, but for four DDX4 variants and full FUS variants, respectively. d We simulate a mixture of PolyK (50 residues; 128 chains), PolyR (50 residues; 128 chains) and RNA (10 residues; 1280 chains) with an extended Mpipi model (see Methods and SI Fig. S4). The density profile along the simulation box’s long axis (L; normalised) is given for each mixture component. A simulation snapshot is provided below the density plot. The colour code in the snapshot is consistent with that used in the density plot. The mixture is simulated at T/T_c ≈ 0.8, where T_c is the critical temperature for liquid-vapour phase separation.

Finally, beyond predicting critical temperatures, achieving the correct balance of interactions is essential to recapitulate more complex condensate behaviours. Inside cells, condensates are multicomponent systems and can have complex molecular architectures that are meaningful to their functions (e.g. the nucleolus), and the variance in the chemical makeup of biological phase-separating systems can give rise to multilayered architectures [49]. For example, Fisher and Elbaum-Garfinkle [6] recently demonstrated that charge-matched mixtures of polyarginine (polyR), poly-lysine (polyK) and polynucleotides formed multiphasic droplets in which arginine is positioned towards the centre of the condensates and lysine is concentrated at the interface.

To investigate this behaviour in simulations, we extend Mpipi to include parameters for RNA (Methods and SI Fig. S4) and study the phase-separation behaviour of a mixture of polyK, polyR and polyU RNA. Consistent with experiments, our simulations recapitulate multiphase droplet architectures (Fig. 6d). Interestingly, we find that the density of the Argrich region at the droplet core is significantly higher than the Lys-rich phase density towards the interface; these results also agree well with experiment [6]. For comparison, we also simulate this mixture using the extended HPS-KR model which includes parameters for RNA [50]; however, using this model, multiphase droplets are not stabilised (SI Fig. S8a). This result is not especially surprising since, as noted above, the balance between Arg and Lys interactions in HPS-KR is incorrect [29, 40].

More broadly, we speculate that it is generally difficult to account for multiphasic behaviour if the standard arithmetic mixing rules for interaction strengths are utilised. Collectively, our work suggests that it is not sufficient to obtain the correct trends for short-ranged pairwise terms: one must also achieve the right balance of these interaction parameters to yield quantitative accuracy.

Discussion

While the balance of interactions in our current model is in agreement with several experimental and computational studies, there is conflicting evidence on the exact ordering of certain key interactions. For example, Bremer and colleagues [10] report weaker Arg–π contacts than the corresponding π–π ones, while our work and the work of Wang et al. [11] appear to favour the view that Arg–aromatic interactions are stronger than analogous aromatic–aromatic ones. Furthermore, the data suggest that, in some cases, the precise ordering of these interactions within coarse-grained models is fundamental to recapitulate the observed behaviours, while in other cases an approximate ordering could suffice. For example, in FUS protein we find that the LLPS propensities of the full-length protein versus its PLD domain are highly sensitive to the relative ordering of these interactions [7], whilst our current benchmarks reveal that for the A1-LCD variants, all models that favour Arg–π and π–π contacts over the non-π-based contacts achieve a high Pearson correlation, regardless of the precise ordering of Arg–π and π–π contacts. Hence, we postulate that the ordering of these and other interaction strengths is likely to be context specific, and a system-specific coarse-graining strategy may be necessary to achieve good agreement with experiment in some cases. Consequently, one set of measurements, be it experiments or simulations, will be unlikely to yield the complete picture.

A key assumption in our work is that differences in LLPS propensities of biomolecules can be captured via pairwise amino-acid interactions. This approximation allows us to construct a transferable coarse-grained model that can capture several qualitative and quantitative trends for phase-separating systems, especially for those characterised in vitro. However, in crowded intracellular environments, three- and higher-body energy terms may become important; accordingly, co-operative interactions can reshape the phase boundaries of LLPS systems [5, 51]. It is therefore important to consider carefully the contribution of such co-operative interactions in intracellular LLPS systems.

As we discussed above, interaction energies in coarse-grained potentials are in fact effective free energies, and they should in principle depend on temperature. In particular, since we have not considered explicit protein–solvent interactions, the solubility of all proteins studied increases with increasing temperature, even when other effects, such as hydrogen bonding, could result in significantly different phase behaviour as the temperature is lowered. This can even result in complete mixing at low temperatures, leading to a lower critical solution temperature or re-entrant phase behaviour, especially in multi-component systems [52–54].

Capturing such effects within computational models can further extend our ability to elucidate the driving forces for intracellular LLPS and to probe the ensuing material properties. The current parameterisation of the Mpipi potential is not able to account for such phase behaviour; as an extension of the current work, an approach similar to that of Dignon and co-workers [55] for the HPS-KR model, involving an explicit temperature dependence of the interaction strengths, could be undertaken to enable successful simulations of a broader range of proteins to be performed.

This work highlights the promise that multiscale coarsegrained models can prove robust in delineating the link between chemical changes in biomolecules and their emergent collective behaviour. In particular, the ability of Mpipi to predict quantitatively both single-molecule radii of gyration (which are computationally inexpensive to determine) and the collective behaviour of proteins and RNA in solution (which is computationally more expensive) makes it a prime candidate for efficiently assisting the design of experiments and for gaining physical insight into LLPS at the microscopic scale. Our approach therefore augments the set of rigorous tools that are narrowing down the gap towards achieving a predictive quantitative description of the influence of amino-acid sequence in biological phase behaviour. Alongside experimental advances, theoretical work, and other computational approaches, the Mpipi model has the potential to help discover the molecular mechanisms underpinning phase separation and to provide biophysical understanding of how biomolecular condensates are formed, sustained and regulated.

Methods

Atomistic PMF calculations

To quantify the relative contributions of different types of interactions at physiological salt, we perform atomistic potential-of-mean-force (PMF) computations for a subset of residue pairs, namely WW, YY, FF, RY, RF, KY, KF, AA, SS, PP, RE, RD, KE, KD. All residue pairs from our previous work [7] were recomputed at 150 mm salt concentration, and we have included additional pairs. We also perform PMF calculations for four RNA dimer pairs (SI Sec. S4).

Preparation of structures

Amino acids and nucleic acids are modelled using the AMBER ff03ws force field [56]. This force field is well-suited for probing protein-protein interactions. For modelling the solvent (water) and ions, we use the JC-SPC/E-ion/TIP4P/2005 force field [57], as in our previous work [7]. The N- and C-terminal ends of each amino acid are capped with acetyl and N-methyl capping groups, respectively. Pairs of amino acids are orientated with their side-chains facing each other, based on the most common arrangements observed in protein structures. In cases where the interaction preference is uncertain, multiple arrangements are tested to determine the strongest interaction mode.

Each dimer is then immersed in a cubic box containing TIP4P/2005 water molecules (ca. 960–11,020 molecules) with a minimum distance of 1 nm between the dimer and the edge of the box. Na⁺ and Cl^– ions are added to achieve a salt concentration of ~ 150 mm, as well as to produce charge-neutral systems. The resulting systems are then minimised (force tolerance = 500 J mol^–1 pm^–1), with positional restraints of 200 J mol^–1 pm^–2 applied in each dimension to all heavy atoms.

Umbrella sampling

The interaction between each dimer is probed with umbrella sampling. For production runs, positional restraints of 1 J mol^–1 pm^–2 in directions perpendicular to the pulling direction are used to constrain heavy atoms. The centre-of-mass (COM) distance between interacting pairs is restrained with a harmonic umbrella potential (pulling force constant 6 J mol^–1 pm^–2). All bonds with hydrogens are constrained using the LINCS algorithm, permitting an integration time step of 2 fs. Periodic boundary conditions were used during molecular dynamics (MD) simulations. Electrostatics are computed using particle-mesh Ewald summations with a Coulomb cutoff of 0.9 nm. For each umbrella sampling run, approximately 40 windows, spaced at 50 pm from 0.1 nm to 2nm, are used per pair. Each window is simulated for 10 ns. Three independent simulations are conducted for each umbrella sampling window (i.e. an aggregate simulation time of 30 ns per window). Umbrella sampling data is analysed using the weighted histogram analysis method (WHAM)The first 1 ns of simulations is used for equilibration and is not included in the WHAM analysis. Error analysis is performed using the Bayesian bootstrap method. All atomistic simulations and analyses are carried out using the Gromacs simulation package.

Although we focus on COM distances for fixed molecular orientations in PMF calculations, we ultimately map these to Cα–Cα distances of the coarse-grained potential. The effective free energy as expressed with different order parameters may not be the same and depends on the jacobian determinant of the transformation. However, our choice of order parameter cannot affect observable properties of the system, and the two distances are related by a simple linear relationship for a fixed molecular orientation. Provided we use the PMFs in a self-consistent manner, the resulting ratios of interaction strengths should not depend on this choice of order parameter.

Cation–π charge refitting

Cation–π interactions involve significant polarisation of π electron clouds of aromatic side-chains in the proximity of cationic side-chains (i.e. arginine and lysine), especially at physiological salt conditions. There have been many efforts to capture correctly cation–π interactions in atomistic force fields, both with fixed-charge and polarisable force fields (see discussion by Liu and co-workers [58]). Recently, Paloni et al. demonstrated that the fixed-charge AMBER 99SB-disp force field was able to account for Arg/Lys–π interactions for the DDX4 NTD [59]. In another study, Liu and colleagues used quantum-mechanical calculations to reparameterise the Lennard-Jones parameters in the CHARMM36 force field to model cation–π pairs [58]. Their modified parameters led to improved descriptions of the selected folded proteins [58], achieving a closer match to experimental crystal structures.

In this work, to model cation–π interactions atomistically, we follow our previous approach [7] and first refit the charges on tyrosine and phenylalanine side chains. Specifically, the dimers (Arg/Lys–Phe/Tyr) are first optimised using constrained geometry optimisations at MP2/6-31G(d) level of theory, where the backbone and capping group heavy atoms are frozen. The electrostatic surface potential (ESP) is then computed for respective optimised pairs at HF/6-31G(d) level. These calculations are carried out using the Gaussian 09 code. Finally, the restrained electrostatic potential method in AMBER is used to refit the side-chain charges of Tyr and Phe to the ESPs from the quantum-mechanical calculations; charge symmetry of the rings is maintained during the refitting procedure. The refitted charges are then used when probing the pairwise interaction strengths via umbrella sampling, as described above.

Mpipi model

In the Mpipi model, each amino acid or nucleic acid is represented by a single bead, with corresponding mass, molecular diameter (σ), charge (q), and an energy scale reflecting the relative planar π–π contact frequency (ε). We broadly follow the approach of Dignon et al. [28] to compute the potential energy of a given protein or RNA molecule as

$$E_{\text{Mpipi}}=E_{\text{bond}}+E_{\text{elec}}+E_{\text{pair}}.$$ (1)

The bond energy is computed by using a harmonic bond potential,

$$E_{\text{bond}}={{\displaystyle \sum _{\text{bonds}i}\frac{1}{2}k\left(r_i-r_{i,\text{ref}}\right)}}^2,$$ (2)

where the spring constant k is set to 8.03 J mol^–1 pm^–2 and r_i is the bond length: reference bond lengths, r_i, _ref, of 381 pm and 500 pm are used when bond i connects two protein and two RNA beads, respectively. The electrostatic contribution to the potential energy is computed using a Coulomb term with Debye–Hückel electrostatic screening,

$$E_{\text{elec}}={\displaystyle \sum _{i,j}\frac{q_i{q}_j}{4\text{π}{\epsilon }_{\text{r}}{\epsilon }_0{r}_{ij}}}\exp \left(-\kappa r_{ij}\right),$$ (3)

where ε_r = 80 is the relative dielectric constant of water, ε₀ is the electric constant and K^–1 = 795 pm is the Debye screening length, corresponding to a monovalent salt concentration of 0.15 m to be consistent with the PMF calculations. We use a Coulomb cutoff of 3.5 nm. The dielectric constant and the Debye length control the range of ionic interactions and determine the relative importance of charges relative to all other interactions. A more careful treatment of electrostatics, perhaps in the spirit of Wessen and co-workers [60], would be an important next step to consider in the development of more accurate potentials.

Finally, the non-bonded interactions between protein/RNA beads are modelled via the Wang–Frenkel (WF) potential [19]. The WF potential between two beads of types i and j a distance r apart is given by

$${\varphi }_{ij}\left(r\right)={\epsilon }_{ij}{\alpha }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r}\right)}^{2{\mu }_{ij}}-1\right]{\left[{\left(\frac{R_{ij}}{r}\right)}^{2{\mu }_{ij}}-1\right]}^{2v_{ij}},$$ (4)

where

$${\alpha }_{ij}=2v_{ij}{\left(\frac{R_{ij}}{{\sigma }_{ij}}\right)}^{2{\mu }_{ij}}{\left[\frac{2v_{ij}+1}{2v_{ij}\left({\left\{\frac{R_{ij}}{{\sigma }_{ij}}\right\}}^{2{\mu }_{ij}}-1\right)}\right]}^{2v_{ij}+1},$$ (5)

and σ_ij, ε_ij and μ_ij are parameters specified for each pair of interacting beads. We use v_ij = 1 and R_ij = 3σ_ij. The total pairwise energy E_pair is then taken as the sum over all pairs of beads evaluated within their respective interaction ranges (i.e. R_ij, at which ϕ_ij vanishes).

Most importantly, the Wang–Frenkel potential is finite-ranged, vanishing quadratically to zero at the user-specified cutoff distance, and so obviates the need for truncating and shifting the potential. This key feature makes the Wang–Frenkel potential better suited for numerical calculations and removes any ambiguities or inconsistencies that may arise from one implementation to the next. For example, Lennard-Jones-based potentials can exhibit significant undesirable finite-size effects as a function of the cutoff distance and subsequent tail corrections [61]. The computational performance of the Wang–Frenkel potential is comparable to the Lennard-Jones potential for the same cutoff; although we have not done this here, if one wished to simulate particularly large systems, the Wang–Frenkel potential’s more flexible functional form affords an opportunity for optimising the distance at which the potential vanishes, which could enable a significant computational boost without degrading performance. Moreover, although from its scaling properties, the Lennard-Jones potential appears at first glance to account for London dispersion interactions, in reality this is not the case in solution, where the potential accounts for many interactions in a coarse-grained way; a further advantage of the Wang–Frenkel potential is that it removes this misleading appearance of physicality.

To obtain the parameters that appear in the WF parameterisation, we first determine relative planar π–π contact frequencies of the amino acids from the work of Vernon etal. [13], determine Ashbaugh–Hatch-styleLennard-Jones interactions following Dignon et al. [28], and from these obtain the initial WF parameters. The steepness of the repulsive region of the potential and the width of the attractions can easily be modulated in this framework by allowing the μ parameter to take values larger than unity. We next adjust the values of ε_ij by a suitable multiplicative factor so that the integrals of the well depths of the PMF curves of residue pairs i and j approximate their WF analogues, including any screened charge–charge interaction (SI Fig. S3) if relevant to ensure that the overall interaction energy is correctly taken into account [62]. We provide a full parameter listing in SI Table XI, and a Lammps implementation in the supporting data. Although it has been suggested [26, 43] that simple arithmetic combination rules are often sufficient, unlike in previous models, the pairwise interactions for those residue pairs which dominate the phase behaviour are explicitly specified, giving the model greater flexibility. There is no a priori reason to assume that coarse-grained interactions between unlike species will be well described by an arithmetic mean of homotypic interactions, and, in particular, we find that the heterotypic interactions of arginine and lysine can be significantly different from the mixing-rule prediction. Parameters for the nucleic acids are determined directly by fitting the respective PMF well depths and widths to the WF framework (see below). Both disordered proteins/regions and RNA are modelled as fully flexible polymers.

Validation simulations use various previously reported models. Mostly, these are based on the functional form introduced in the work of Dignon et al. [28]. The bonded and electrostatic contributions to the potential are given by the same functional form in each case, although with slightly different constants (SI Table X).

Background on the parameterisation of Mpipi

To parameterise the non-bonded short-ranged terms described via the Wang–Frenkel potential, we first determine the relative π–π contact frequencies for amino acids from the work of Vernon et al. [13] (SI Table I), who predict the planar π–π contact frequencies from a survey of approximately 6000 high-resolution structures in the PDB. We utilise these contact frequencies as an initial energy scale for short-ranged interactions in our model.

We then refine this initial energy scale using atomistic PMF calculations, focussing on aromatic π–π (Fig. 2a), cation–π (Fig. 2b) and a subset of non-π-based (Fig. 2c) interactions. Pappu, Mittag and colleagues position aromatic ‘stickers’ as the chief drivers of biomolecular LLPS [4, 8–10]; our recent findings are also consistent with the stickers-and-spacers model, where we predict that aromatic π–π interactions constitute dominant forces in LLPS even at extremely high salt concentrations [7].

In this work, we compute the PMF between YY, FF (Fig. 2a) and WW (SI Fig. S2) at physiological salt concentration (see Methods) and find that, in agreement with the bioinformatics data [13] and experiments [10–12], the relative strength of aromatic π–π interactions increases in the order FF<YY<WW (magenta bars in Fig. 2d and SI Fig. S2). Importantly, we find that aromatic π–π interactions are at least twice as strong as non-π-based interactions (dark yellow bars in Fig. 2d). The latter interactions include non-polar, polar and special residues (e.g. Pro) and are commonly categorised as spacers [4, 8, 11]. Interestingly, Bremer et al. predict that the disparity in spacer–spacer and sticker–sticker residue interaction strengths can be as high as 1:8 [10]. Our fitted spacer-type interactions represent a compromise between the predictions of Bremer and co-workers [10] and those suggested by our PMF calculations [Fig. 2e].

We next concentrate on interactions between basic residues (Arg and Lys in particular) and aromatics. These ‘cation–π’ interactions also make significant contributions to LLPS of biomolecules. In an early bioinformatics survey, Gallivan and Dougherty [63] revealed that Trp was most likely to form cation–π interactions, followed by Tyr and then Phe. Song et al. [64] subsequently used experiments and simulations to demonstrate significantly higher binding strengths for RW interactions compared to RY/F ones, with RY slightly stronger than RF.

Furthermore, recent work by Wang et al. [11] suggests that Arg–Tyr interactions may be stronger drivers of LLPS than Tyr–Tyr contacts; our PMF calculations agree that Arg–Tyr interactions are stronger than Tyr–Tyr. However, whether cation–π interactions are indeed stronger contributors to protein LLPS than π – –π interactions remains contested: the work of Bremer et al. [10] and single-residue solubility measurements [65] suggest instead that Tyr–Tyr interactions are stronger than Arg–Tyr contacts. A potential source of error in the relative ordering of interactions in our work might come from the approximate nature of atomistic PMFs simulations and the use of a pairwise energy to describe an interaction that is likely affected by co-operative effects. Reassuringly, despite the differences, in all cases, both cation–π and π–π interactions are significant.

A further important consideration is the balance of Arg–π and Lys–π interactions. The differences between Arg–π and Lys–π contacts were highlighted by Gallivan and Dougherty [63], who reported a higher percentage of Arg–π contacts in protein structures. We recently proposed that Arg–π interactions are best described as hybrid cation-π/π–π, whereas Lys–π contacts represent ‘purer’ cation–π interactions [7]. This distinction arises largely from the presence of π electrons in the Arg side-chain [6, 7, 13, 16–18], which enable Arg residues to interact much more strongly with n-binding partners than Lys can [6, 7, 15, 16]. The dominance of Arg over Lys in these interactions is also consistent with the less favourable hydration free energy recently reported for Arg versus Lys [16]. An earlier study by Kumar et al. revealed that, whereas Lys–π interactions are more favourable in the gas phase, in solution Arg establishes stronger interactions with aromatic rings than Lys, the latter being dominated by electrostatics and therefore weakened by the surrounding dielectric medium [66]. Collectively, our PMF calculations and previous studies all suggest a preference for Arg–π interactions over Lys–π contacts in biomolecular systems. Accordingly, we reparameterise cation–π interactions so that the relative weights in our model more closely match those suggested by the atomistic simulations (Fig. 2d). A summary of the relative interaction strengths between amino-acid pairs is provided in Fig. 2e. These interaction strengths correspond to the average interaction energy in the high-temperature limit relative to a fixed (albeit arbitrary) energy of zero obtained by numerically integrating Eq. (8). The integration over the energy well in this high-temperature limit enables the relative interaction strength to account, at least approximately, for both enthalpic and entropic contributions.

Direct-coexistence simulations

Proteins/RNA are represented via the Mpipi model (or other residue-level coarse-grained model) and direct-coexistence [20] simulations are used to compute their phase diagrams. In such simulations, the high- and low-density fluid phases are simulated in the same simulation box delimited by an interface.

The target number of copies of the protein are placed in an elongated box, which is initially simulated at high temperature and then cooled down to the desired temperature. Canonical-ensemble simulations are then run at temperatures below the estimated critical temperatures for each system. A relaxation time of 5 ps is typically used for the Langevin thermostat and an integration time step of 10 fs is used for all coarse-grained simulations. Calculations are carried out using Lammps. We discuss the effect of finite-size effects [9, 67, 68] below.

Estimation of critical points on phase diagrams

Critical temperatures are estimated using the law of coexistence densities,

$${\left({\rho }_{\text{high}}\left(T\right)-{\rho }_{\text{low}}\left(T\right)\right)}^{3.06}=d\left(1-T/T_c\right),$$ (6)

and critical densities are computed by assuming that the law of rectilinear diameters holds,

$${\rho }_{\text{high}}\left(T\right)+{\rho }_{\text{low}}\left(T\right)=2{\rho }_c+2A\left(T-T_c\right),$$ (7)

where ρ_high(T), ρ_low(T) and ρ_c are the densities of the high-density and low-density phases and the critical density, respectively; T_c is the critical temperature and d and A are fitting parameters.

Data analysis

When comparing relative interaction strengths, we compute the average energy in the high-temperature limit, i.e. assuming that the well depth is much smaller than k_BT for each individual interaction. For each pair of amino-acid residues, we compute

$${\epsilon }_{\text{avg}}={\displaystyle {\int }_{\sigma }^{3\sigma }\varphi \left(r\right)}\text{d}r+{\displaystyle {\int }_{\sigma }^{3.5\text{nm}}{E}_{\text{elec}}\left(r\right)}\text{d}r,$$ (8)

where ϕ(r) is the Wang–Frenkel potential [Eq. (4)] and E_elec (r) is the Coulomb energy [Eq. (3)], if relevant. We then normalise the result by the interaction strength of the RY (Arg–Tyr) pair. We compute the integral in Eq. (8) in one-dimensional space, i.e. not including the 4πr² volume element, since we wish to compare these strengths to PMF calculations, where a constrained approach was used. However, including a spherical-polar volume element does not significantly affect the appearance of Fig. 2e.

To assess the agreement between simulation results and experiment for a given observable X (where X is either the critical temperature or the radius of gyration), we compute both a Pearson correlation coefficient (r), which is a measure of deviation from a linear fit to the data and is a good measure of the quality of the ordering of the predictions, and a root mean squared deviation D, whose square we define as

$$D^2=\frac{1}{n}{{\displaystyle \sum _{i=1}^n\left[X_i\left(\text{experiment}\right)-X_i\left(\text{simulation}\right)\right]}}^2,$$ (9)

where n is the number of data points. D is a measure of the absolute deviation from experimental results.

Radii of gyration computation

We compute single-molecule radii of gyration (R_g) for the protein sequences presented in SI Sec. S2.1. Each protein was simulated in a large cubic box (ca. 60 nm × 60 nm × 60 nm). Canonical-ensemble simulations were then performed at 300 K for 5 μs, with a time step of 10 fs. A Langevin thermostat was used, with a relaxation time of 50 ps. R_g measurements were made every 100,000 time steps (i.e. 1 ns). The first 1000 fs part of simulation was not used in the estimation of R_g values. Simulations were run using Lammps.

Estimation of the coil–globule transition temperature

We have estimated the coil–globule transition temperature T_θ with ABSINTH [69], a continuum solvation all-atom model of proteins. To determine this temperature, we simulated a single protein in a spherical cell with explicit ions, and determined the temperature at which there is a sudden change in the radius of gyration as a function of temperature [24].

Finite-size scaling

Finite-size effects can play a significant role in direct-coexistence simulations [67]. To ascertain that phase-diagram calculations with direct-coexistence simulations yield robust results, we first confirmed that reducing the system size by approximately 30 % yields the same phase diagrams, within error bars, for the hnRNPA1 variants and FUS-LCD as the results reported above. Since there is no difference in the predicted critical temperatures, we hypothesised that finite-size effects are not dominant in our simulations. To test this hypothesis more carefully, we investigated the finite-size scaling behaviour of the FUS-LCD system systematically. In SI Fig. S7, we show two sets of results for this system. We first tested the effect of the size of the cross-sectional area of the interface, starting from a particularly small area of 4 nm × 4 nm, i.e. with box dimensions only just larger than the largest cutoff distance in the interparticle potential of 3.5 nm. SI Fig. S7a shows a considerable spread in individual values, but with the possible exception of the smallest system size, there is no significant difference in the mean density computed across the entire high-density portion of the density profile, which is needed for the phase diagram. In other words, a cross-sectional area of approximately 10 nm × 10 nm used in the majority of phase-diagram calculations appears to be more than sufficient to avoid significant finite-size effects.

Next, we tested the finite-size scaling of the bulk of the system, by keeping a constant cross-sectional area and increasing the length of the long box dimension at a constant density, i.e. by increasing the number of chains in the system. We show these results in SI Fig. S7b. For the very smallest system size considered here, with a z-axis dimension of 11 nm, the density profile is close, but not exactly consistent with that of the larger systems. This is not especially surprising, since the ‘long’ box dimension is only marginally longer than the remaining two, and the interface is considerably more fluxional as a result. However, from the 22 nm simulation onwards, the high-density profile has a flat region that changes in width, but not the mean density, suggesting that finite-size effects are negligible beyond this point. The system sizes used in our phase-diagram calculations are shown in SI Table IX. All sizes are well beyond the point where finite-size effects dominate the system’s behaviour.

One caveat here is that the results for FUS-LCD we show in SI Fig. S7 correspond to a temperature just above 80 % of the critical temperature. The interface naturally becomes less well defined as the critical point is approached, and data points very close to the critical temperature are not usually very robust. However, such data points are not necessary to obtain to estimate the critical temperature from a fit to Eqs (6) and (7).

Implementation of parameters for RNA

We have parameterised an initial set of RNA nucleotide parameters that is compatible with the Mpipi model for proteins. Here, nucleotide–nucleotide interaction strengths are derived by first performing atomistic PMF calculations for homo-dimer pairs (SI Fig. S4a,b). We use dimers instead of monomers since it is more straightforward to study homodimers than single nucleic acid monomers in standard protein/RNA force fields; from these simulations we extract the relative weights of RNA nucleotide–nucleotide interactions. Specifically, we compute the base–base binding free energies, which encode the short-range pairwise terms in the Mpipi model.

To map the PMFs to our Mpipi model parameters, we first fitted the weighted atomistic interaction energies (i.e. the integral of the PMF curves at 298.15 K; Eq. (8)) to the corresponding Wang–Frenkel weighted interaction energies at the same temperature. This procedure involves performing a linear fit between known WF interaction energies in our model and their atomistic counterparts (i.e. for the set in SI Fig. S2a). The fit parameters were then used to determine the corresponding weights for the RNA nucleotides. Next, using an iterative procedure, we determined the WF parameters (i.e. ε and μ) for each RNA bead that yield the target binding strengths.

Each RNA bead is then described by a unique set of WF parameters and a charge of –0.75 e. Finally, we reduced the ε in the WF part of the potential for the RNA beads until self-assembly for PolyA/PolyG RNA (50 beads; 64 chains) [i.e. nucleotides with stronger base-stacking propensities] was sufficiently destabilised at 200 K. In subsequent work, we aim to refine our RNA parameters (including short-ranged binding strengths, bond constants and angular constants).

Data Availability

All relevant supporting data are available in the Figshare data repository at doi:10.6084/m9.figshare.16772812 [70]. Source data for Figures 2–6 are available with this manuscript.

The data for this study were generated with the simulation codes aand algorithms outlined in SI Table XIV, using the supporting code [70], alongside standard command-line tools.

Code Availability

Lammps input scripts and parameter files are available in the Figshare data repository at doi:10.6084/m9.figshare.16772812 [70].