Tractography in the presence of multiple sclerosis lesions

Abstract

Accurate anatomical localisation of specific white matter tracts and the quantification of their tract-specific microstructural damage in conditions such as multiple sclerosis (MS) can contribute to a better understanding of symptomatology, disease evolution and intervention effects. Diffusion MRI-based tractography is being used increasingly to segment white matter tracts as regions-of-interest for subsequent quantitative analysis. Since MS lesions can interrupt the tractography algorithm’s tract reconstruction, clinical studies frequently resort to atlas-based approaches, which are convenient but ignorant to individual variability in tract size and shape. Here, we revisit the problem of individual tractography in MS, comparing tractography algorithms using: (i) The diffusion tensor framework; (ii) constrained spherical deconvolution (CSD); and (iii) damped Richardson-Lucy (dRL) deconvolution. Firstly, using simulated and in vivo data from 29 MS patients and 19 healthy controls, we show that the three tracking algorithms respond differentially to MS pathology. While the tensor-based approach is unable to deal with crossing fibres, CSD produces spurious streamlines, in particular in tissue with high fibre loss and low diffusion anisotropy. With dRL, streamlines are increasingly interrupted in pathological tissue. Secondly, we demonstrate that despite the effects of lesions on the fibre orientation reconstruction algorithms, fibre tracking algorithms are still able to segment tracts that pass through areas with a high prevalence of lesions. Combining dRL-based tractography with an automated tract segmentation tool on data from 131 MS patients, the corticospinal tracts and arcuate fasciculi could be reconstructed in more than 90% of individuals. Comparing tract-specific microstructural parameters (fractional anisotropy, radial diffusivity and magnetisation transfer ratio) in individually segmented tracts to those from a tract probability map, we show that there is no systematic disease-related bias in the individually reconstructed tracts, suggesting that lesions and otherwise damaged parts are not systematically omitted during tractography. Thirdly, we demonstrate modest anatomical correspondence between the individual and tract probability-based approach, with a spatial overlap between 35 and 55%. Correlations between tract-averaged microstructural parameters in individually segmented tracts and the probability-map approach ranged between r = .53 (p < .001) for radial diffusivity in the right cortico-spinal tract and r = .97 (p < .001) for magnetisation transfer ratio in the arcuate fasciculi. Our results show that MS white matter lesions impact fibre orientation reconstructions but this does not appear to hinder the ability to anatomically reconstruct white matter tracts in MS. Individual tract segmentation in MS is feasible on a large scale and could prove a powerful tool for investigating diagnostic and prognostic markers.

1. Introduction

Accurate quantification of white matter damage in multiple sclerosis (MS) is important for an improved characterisation of the disease burden (Barkhof et al., 2009). While the hallmark of MS pathology is focal inflammatory demyelinating lesions, correlations between the number and volume of lesions and disability scores are low (Barkhof, 1999, 2002) and disability can be better explained by the anatomical location of lesions and of diffuse microstructural damage outside of lesions (Charil et al., 2003; Kolind et al., 2012). Accurate assignment of damage to specific anatomical white matter tracts is important for several reasons (Lin et al., 2005). Firstly, the relationship between functional and structural (derived using tractography) brain networks in MS is not yet fully established and is likely to offer important insights into disease pathophysiology. Secondly, the ability to measure longitudinally microstructural changes within tracts allows the relationship between focal demyelination and distant white matter pathology in relevant pathways to be established. Finally, tract-based quantitative measures are likely to have utility in early clinical trials, for example studying the effect of remyelinating agents on axonal preservation within the visual pathway following optic neuritis, or the study of specific rehabilitation interventions on relevant white matter tracts (Bonzano et al., 2014).

Anatomical localisation of white matter tracts in vivo currently relies on diffusion-weighted MRI and fibre tracking (Catani et al., 2002; Jeurissen and Leemans, 2017). The reconstruction of individual tracts is based on combining prior anatomical knowledge of the tract location with diffusion MRI-based evidence about fibre orientations in the imaging voxels. Early tractography work was performed by producing streamlines that follow the principal eigenvector of the diffusion tensor (e.g. Basser et al. (2000); Mori et al. (1999)), while more recent work relies on the estimation of the fibre orientation distribution function (e.g. Tournier et al. (2004)). Tractography can be combined with an extraction of tract-specific microstructural metrics (Jones et al., 2005, 2006) to be used for investigating individual differences or longitudinal changes in tract-specific microstructure (e.g. Lin et al. (2005); Metzler-Baddeley et al. (2011)). Tractography is also a useful tool for cortical or sub-cortical functional parcellation at an individual level (Mars et al., 2011; Tomassini et al., 2007).

Focal brain pathology, such as demyelinating white matter lesions in MS, can affect tractography. MS lesions are characterised by fibre loss and consequent increase in extracellular water associated with tissue destruction, which is reflected in the diffusion profile (Filippi et al., 2001). During tractography, at each step of streamline reconstruction, angle and amplitude criteria are in place to avoid spurious tracking. Early tractography studies used fractional anisotropy (FA) as a criterion for streamline termination. As FA is significantly decreased in white matter lesions in MS (Filippi et al., 2001), applying tractography to data from MS patient has been recognized as being problematic (Ciccarelli et al., 2008; Inglese and Bester, 2010). In the absence of a strategy to overcome the problem of streamline termination (such as employed by Lagana et al. (2011), Tench et al. (2002) and Wang et al. (2018)), the reconstructed tracts may lack anatomical accuracy, e.g. by premature termination of tracking (Ozturk et al., 2010). For this reason few studies apply tractography in brains affected by MS (other examples are Lin et al. (2005); Reich et al. (2007, 2010)).

More recent advances in tractography algorithms do not rely on the estimated fibre orientation from the diffusion tensor (which yields one fibre orientation estimate per voxel), but employ deconvolution approaches that yield multiple fibre orientations per voxel (e.g. Tournier et al. (2004)). This advanced approach could permit the reconstruction of streamlines through MS lesions, given that enough fibres are present to generate a peak in the estimated fibre orientation distribution (FOD). However, it is possible that due to the fibre loss in lesions, the peak amplitudes may fall below the threshold normally used for termination of tracking. On the other hand, lowering the FOD amplitude threshold could lead to the tract reconstruction following spurious peaks, such as those arising from noise, since lesions are characterised by an increased component of water with isotropic diffusion, which can compromise orientation estimates (Dell’Acqua et al., 2010). Due to the ill-posed nature of the tractography process, reducing false positives streamlines is a significant challenge (Jeurissen and Leemans, 2017) and therefore needs to be considered when assessing tractography methods in pathological tissue. To our knowledge, tractography results obtained with spherical deconvolution approaches in MS patients have not been assessed systematically.

Due to the challenges related to tractography in pathological tissue, an alternative approach for obtaining tract-specific measures in MS was suggested (Pagani et al., 2005; Hua et al., 2008). First, tracts are reconstructed in the native space of brains of healthy volunteers and then normalized to a common reference space, where a tract-probability map is created. Then, the data from patients are aligned with the same common reference space. To get a tract-specific measure of damage, the probabilistic atlas is used to calculate a weighted average for the microstructural metric of interest.

While the probability-map based method has the advantage that individual tracts are only reconstructed in healthy brains, there are also considerable short-comings. The approach relies on inter-subject co-registration of the images by normalising them to a common reference space. This normalisation is generally performed based on structural images, e.g. T1-weighted images, on which white matter appears homogeneous (Hua et al., 2008; Pagani et al., 2005; Reich et al., 2010). The approach therefore implicitly assumes that white matter tract anatomy is consistent across individuals and in states of health and disease. However, this assumption is unlikely to hold. Tract location and shape vary even between healthy individuals (Wassermann et al., 2012), and in MS white matter atrophy is well described (Ge et al., 2001) and could affect some tracts more than others (Kezele et al., 2008). Applying a probability mask may yield measures of microstructural damage that are likely to include information from other tracts in the vicinity and may therefore not be anatomically precise. This imprecision could be the explanation for the low correlations between individual tractography and probability-based measures that have previously been reported for some tracts (Reich et al., 2010). Another explanation could be that the individual tractography omits damaged parts of the tract, leading to not-representative and biased estimates.

In this work, we evaluate methods for performing individual tractography in multiple sclerosis patients with focal white matter lesions. Using simulations as well as in vivo data sets from patients, we compared the effect of MS pathology on the performance of three tractography algorithms: (i) DTI based tracking; (ii) Constrained spherical harmonic deconvolution (CSD)-based tracking and (iii) damped Richardson-Lucy-based tracking. Then, we reconstruct cortico-spinal tracts (CST) and arcuate fasciculi (Arc) in a large number of patients to evaluate the practical implications of tracking through white matter regions with a high prevalence of lesions.

2. Methods

2.1. Data acquisition

2.1.1. Simulated data

We simulated diffusion data for a virtual pulse sequence comparable to our in vivo sequence (Section 2.1.3), with a conservative SNR estimate of 20:1 for non-diffusion weighted images (see Supplementary Section 1), using Camino’s datasynth (Hall and Alexander, 2009). The virtual pulse sequence was a twice-refocussed spin echo (TRSE) sequence with TE = 94.5 m s, b-value = 1200 s/mm², δ1: 11.2 m s, onset δ1: 15.2 m s, δ2: 17.8 m s, onset δ2: 31.7 m s, δ3: 17.8 m s, onset δ4: 75.3 m s, gradient amplitude: 40 mT), sampling 40 uniformly distributed gradient directions (Camino 40), and 6 non-diffusion weighted images at the beginning.

We simulated data for a number of tissue substrates, all characterised by impermeable parallel cylinders with a shape parameter of 2 and scale parameter of 5 x 10⁻⁷, which corresponds to a mean radius of 1 μm and standard deviation of 0.7 μm. The parameters used in the simulation were: 500,000 walkers (numbers of spins simulated), uniformly distributed across the substrate, cylinder permeability 0, tmax = 5000.

To assess the effect of fibre loss and increased extracellular volume fraction, as seen in lesion pathology, we simulated substrates that differed in their intracellular volume fractions, by varying the number of cylinders placed in the substrate. We simulated various substrates (cubes of the length 50 x 10⁻⁵ m), that only differed in their cylinder density (0–40,000 cylinders placed in substrate), yielding intracellular volume fractions of about 0–80%. For each substrate type, we simulated 20 different substrates (by choosing different seed values), and for each substrate we simulated 100 voxels that only differed in their noise.

We simulated substrates with a single fibre population as well as substrates with two fibre populations crossing at 90°. To simulate crossing fibres, we ran the exact same simulation, but rotating the acquisition scheme around the x-axis by 90°.

2.1.2. Participants

In total, data from 135 right-handed MS patients, who took part in a large-scale imaging project (Lipp et al., 2017, 2019), contributed to this study. The project was approved by the NHS South-West Ethics and the Cardiff and Vale University Health Board R&D committees. All participants provided written informed consent.

Diffusion data were available for 131 patients. A subset (29 patients) of the large cohort had been age- and gender-matched to 19 healthy controls, who underwent the same scanning protocol. For all analyses, for which pathological tissue was compared to healthy control tissue, data from the two matched groups (N = 29 patients and N = 19 controls) were considered. This was done to eliminate the risk of aging-related changes to WM microstructure acting as a confound. For analyses regarding the in vivo tract segmentation, data from all 131 patients were considered to ensure a representative lesion probability distribution across the brain. We indicate the sample size used for each analysis in the respective tables and figures. Data from the healthy controls were used for creating the tract probability maps as well as a shape model that was used for automatic tract segmentation for the larger cohort of patients, as described below. The clinical and demographic characteristics of the whole patient cohort, matched patient subset and controls are presented in Table 1.

Table 1. Demographic and clinical characteristics of the cohorts investigated.

Characteristics are provided for all multiple sclerosis patients (MS), as well as the subgroup of patients (Subgroup MS) matched to and healthy controls (HC). Unless otherwise indicated, descriptive statistics provided are means and standard deviations (SD). For statistical comparison between the two cohorts (All MS vs HC) and the sex- and age-matched groups (Subgroup MS vs HC), Chi-square tests were computed for categorical variables, Kruskall-Wallis tests for skewed variables (9 hole peg test and timed 25 foot walk), and unpaired t-tests for the rest. P values for group differences are provided. Acronyms: RR = Relapsing-remitting, P = progressive MS (includes primary and secondary progressive patients), EDSS = Extended Disability Status Scale, MSIS-29 = Multiple Sclerosis Impact Scale 29 items, 9-HPT: 9 hole peg test, T25-FW: timed 25 foot walk, PASAT = Paced Auditory Serial Addition Test (3 and 2 s version), DMT = disease-modifying treatment, BDI = Beck Depression Inventory, MFIS = Modified Fatigue Impact Scale. Normalized brain and grey matter volume was calculated using SIENAX (Smith et al., 2002).

Variable	All MS	Subgroup MS	HC	All MS vs HC (p)	Subgroup MS vs HC (p)
N	131	29	19
Age (years)	44.5 ± 9.4	39.2 ± 11.3	40.5 ± 11.0	.0929	.6954
Sex (F/M)	85/46	17/12	12/7	.8830	.7533
Education (years)	15.6 ± 3.9	15.9 ± 3.9	20.0 ± 4.8	< .0001	.0021
Disease duration (years)	12.4 ± 7.5	7.6 ± 4.3	–	–
Disease course (RR/P)	105/26	29/0	–	–	–
EDSS score (median/iqr)	4.0 ± 1.5	4.0 ± 2.0	–	–
MSIS-29 scale	65.6 ± 29.5	48.3 ± 16.9	–	–
9-HPT (right) in sec. (across 2 trials) median/iqr	25.4 ± 11.7	21.9 ± 3.6	18.7 ± 2.2	< .0001	.0012
T25-FW in sec. (across 2 trials) median/iqr	8.5 ± 9.8	5.3 ± 1.4	4.3 ± 0.9	.0669	.0071
PASAT 3s	39.9 ± 14.0	44.5 ± 12.2	51.0 ± 6.4	.0009	.0379
PASAT 2s	27.5 ± 11.6	31.1 ± 8.6	33.9 ± 7.1	.0195	.2424
DMT (Yes/No)	43/88	13/16	–	–	–
Depression (BDI)	12.5 ± 10.4	8.2 ± 8.6	4.6 ± 5.1	.0016	.1123
Fatigue (MFIS)	39.6 ± 20.7	27.7 ± 19.3	21.1 ± 13.3	.0003	.2093
Normalized GM volume (cm3)	594.4 ± 63.2	613.1 ± 47.9	645.8 ± 39.9	.0010	.0176
Normalized whole brain volume (cm3)	1173.5 ± 115.9	1196.4 ± 109.5	1230.0 ± 87.0	.0432	.2665
T2-hyperintense lesion volume (cm3)	4.2 ± 4.6	2.8 ± 2.4	–	–	–

2.1.3. MRI acquisition

In vivo MRI data were acquired on a 3T General Electric HDx MRI system with an eight channel receive-only head RF coil (GE Medical Systems, Milwaukee, WI). We acquired the following sequences: a T2/proton-density weighted and a fluid-attenuated inversion recovery (FLAIR) sequence for lesion identification and segmentation, a T1-weighted sequence for identification of T1-hypointense MS lesions and for registration, and a twice-refocussed diffusion-weighted sequence (40 uniformly distributed directions (Camino 40), b = 1200 s/mm²), and a 3D MT sequence. Latter was used to calculate an additional microstructural parameter independent of the diffusion-weighted images. The acquisition parameters of all scan sequences are reported in Supplementary Table 1.

2.2. Data analysis

2.2.1. Algorithms for resolving fibre orientation

We compared three algorithms for recovering fibre orientational information. Firstly, as done in previous MS work (Hua et al., 2008; Reich et al., 2010), fibre orientation was estimated using the first eigenvector of the diffusion tensor. The diffusion tensor was derived by robust non-linear least squares fitting (Chang et al., 2005), using ExploreDTI v.4.8.3.

Additionally, we employed two fibre orientation distribution (FOD) deconvolution algorithms, which have been developed to overcome some of the limitations related to tensor-based tracking: a constrained spherical deconvolution (CSD, Tournier et al. (2007)), and a modified damped Richardson-Lucy algorithm (dRL, Dell’Acqua et al. (2010)). Deconvolution methods work by characterising a response function for a single fibre orientation. This response function is then deconvolved from the observed signal. The reason for considering both CSD and dRL is that previous work (Parker et al., 2013b) showed that while CSD performs better than dRL when resolving crossing fibres in voxels with low FA, it also more frequently produces spurious peaks and is more sensitive to mis-calibrations of the FOD.

The constrained spherical convolution (CSD; Tournier et al. (2007)) was implemented using in-house scripts. The single fibre response function was calculated from voxels with an FA > 0.8, as done in previous work (Tournier et al., 2004). For the simulated data, the CSD response function was estimated from voxels with FA > 0.8 in the single fibre population data set. Spherical harmonics were resolved up to the 6th order. During the tractography process, we employed an FOD amplitude threshold of > 0.1 that has been previously optimised (Jeurissen et al., 2013).

The modified damped Richardson-Lucy algorithm (dRL) was implemented with a fibre response shape parameter of α = 1.5x10⁻³mm²/s according to Dell’Acqua et al. (2010), using in-house scripts. Note that we fitted harmonics up to the 8th order to the discrete dRL estimates, to increase computational efficiency, while allowing to track along all potential directions rather than only along the discretely estimated directions. The FOD amplitude threshold was set to > 0.05 (Parker et al., 2013b).

2.2.2. Analysis of simulated data

For each simulated voxel, we applied the three algorithms. From the resulting estimated fibre orientation profiles, we tested whether peaks could be correctly identified: a) along the true underlying direction(s) along which the cylinders had been placed; and b) along false directions (the direction(s) orthogonal to the long axis of the simulated cylinders). For each substrate type and algorithm, the proportion of simulated voxels in which the reconstructed peak orientation closest to the simulated orientation subtended an angle of less than 45° and reached the specified amplitude threshold (dRL: > 0.05, CSD: > 0.1, tensor: FA > 0.2) was determined. Additionally, the orientation dispersion of the detected peaks as a measure of algorithm precision was calculated using Basser et al. (2000)’s coherence measure to an average dyadic tensor which was calculated across all identified peaks (Jones, 2003). The dispersion measure can take values between 0 (all peaks point in exactly the same direction) and 1 (the detected peaks are uniformly distributed on the unit sphere).

2.2.3. In vivo lesion mapping and segmentation

Damage was quantified in three tissue-states, which were expected to vary in their underlying microstructural damage: normal appearing white matter, T2-weighted white matter hyperintense lesional tissue without T1-weighted hypointensity, and T1-weighted white matter hypointense lesional tissue with corresponding T2-weighted hyper-intensity, as reported elsewhere (Lipp et al., 2019). Briefly, normal appearing white matter was defined as FSL FAST (Zhang et al., 2001) segmented (80% thresholded) white matter at least 5 mm away from lesions. We classified lesional voxels as T1-weighted white matter hypointense if their signal intensity lay at least 1.5 interquartile ranges below the lower quartile of the distribution in normal appearing white matter. All other lesional voxels were classified as T2-weighted white matter hyperintense lesional tissue without T1-weighted hypointensity. Further, we restricted all three tissue classes to lesion-susceptible white matter (white matter with > 5% lesion probability, as defined by a lesion probability map derived from our data, also see Lipp et al. (2019)).

2.2.4. MT processing

The MTR was calculated voxel by voxel with the equation MTR = [(S₀-S_MT)/S₀]x100, whereby S₀ represents the signal without the off-resonance pulse and SMT represents the signal with the off-resonance pulse. The MTR images in native space were skull-stripped using FSL BET and non-linearly registered to the respective skull-stripped T1-weighted images using Elastix (Klein et al., 2010).

2.2.5. Diffusion preprocessing

The DTI data were preprocessed in ExploreDTI (v 4.8.3; Leemans et al. (2009)). Data were corrected for head motion, distortions induced by eddy currents and EPI-induced geometrical distortions by registering each diffusion image to the corresponding T1-weighted anatomical image (Irfanoglu et al., 2012) using Elastix (Klein et al., 2010), with appropriate reorientation of the diffusion encoding vectors (Leemans and Jones, 2009). The anatomical image was first skull stripped and down-sampled to 1.5 mm in order to reduce computation times during further processing of the diffusion data. RESTORE (Chang et al., 2005) was used to account for outliers.

2.2.6. Tractography algorithm

For the subsample of 29 patients and the healthy control group, whole brain tractography was performed in native space with all three algorithms, using an adaptation of CSD-based streamline tractography (Jeurissen et al., 2011; Tournier et al., 2004, 2007, 2008). Seed points were evenly distributed across vertices of a 2 mm isotropic grid and propagated in 1 mm steps with streamline length constraints of 20–500 mm. The diffusion tensor/fODF peaks were resolved at each new location and only the FOD peak direction that is closest to the previous stepping direction was extracted (Newton optimization on the sphere (Jeurissen et al., 2011)). In the case of CSD/dRL-based tracking, tracking was terminated if the fODF threshold fell below the defined threshold or the direction of streamline changed through an angle greater than 45° between successive steps. In the case of tensor-based tracking, instead of an FOD amplitude threshold, an FA threshold of 0.2 was used. The same procedure was then repeated by tracking in the opposite direction from the initial seed-points.

2.2.7. Individual tract segmentation

For the purpose of this paper, the CST and arcuate fasciculi were segmented. The CST originates from motor and premotor cortices and runs to midbrain and medulla, passing the corona radiata and internal capsule (Al Masri, 2011), whose periventricular spaces are common spots for lesions (Kincses et al., 2010). The arcuate fasciculi connect the perisylvian cortex of the frontal, parietal, and temporal lobes (Catani and Thiebaut de Schotten, 2008).

Three-dimensional tractograms for specific white matter tracts were extracted from the whole-brain tractograms by applying multiple way-point of interest gates (Catani et al., 2002), drawn on colour-coded fibre orientation maps (Pajevic and Pierpaoli, 1999). We applied tract reconstruction protocols to the tractograms obtained with dRL from the matched 29 patients and 19 healthy controls. All tract segmentations for a given tract were performed by the same operator (CST: EP, Arcuate fasciculus: SG).

To segment the CSTs, AND gates were placed in the primary motor cortex (identified on the T1-weighted image) and in the brain stem (identified as the blue colour of the pons in the anterior part of the brain stem in the axial slice of a first eigenvector-colored FA image (Pajevic and Pierpaoli, 1999)). This protocol is comparable to Mole et al. (2016). Left and right CST were segmented separately.

Left and right arcuate fasciculi were segmented separately. To do so, each time first a coronal slice of a first eigenvector-colored FA image was identified, in which the posterior commissure was visible. Then a SEED gate was drawn in the arcuate fasciculus, identified as a green triangle lateral to the corpus callosum. Additionally, an AND gate was drawn where the arcuate fasciculus bends, identified as the blue/purple appearing ipsilateral to the SEED gate on an axial slice at the height of the posterior commissure. Example tract delineations for an individual brain are shown in Supplementary Fig. 1.

To assess inter-operator spatial agreement, another operator (SP) dissected all tracts in the data from the first five healthy controls, and spatial overlap Dice coefficient scores were calculated (see also Dice (1945); Zijdenbos et al. (1994) as follows: First the tracts were exported to binary NIfTI files, then the number of voxels for each operator’s tract and the number of voxels overlapping in both operators’ tracts were counted using the AFNI function 3DOverlap (Cox, 1996). Finally, Dice coefficients (in percent) were calculated using the equation:

$$100\hspace{0.17em}\times \hspace{0.17em}\frac{2\hspace{0.17em}\times \hspace{0.17em}\#\hspace{0.17em}\text{overlapping}\hspace{0.17em}\text{voxels}}{\#\hspace{0.17em}\text{voxels}\hspace{0.17em}\text{in}\hspace{0.17em}\text{tract}\hspace{0.17em}1\hspace{0.17em}+\hspace{0.17em}\#\hspace{0.17em}\text{voxels}\hspace{0.17em}\text{in}\hspace{0.17em}\text{tract}\hspace{0.17em}2}$$

In the healthy control data, the approach of Parker et al. (2013a) was used to construct a shape model for each tract in each hemisphere from the manually segmented tracts. The resulting models were then used to automatically extract the tracts of interest for all patients and controls (To do this, dRL-based whole brain tractograms were computed for all patients). All automatically segmented tracts were visually inspected and spurious streamlines were removed if necessary. To validate the automated protocol, for each of the 29 patients and 19 controls with both manually dissected and automatically dissected tracts, we calculated the spatial agreement between the two tract masks.

2.2.8. Tract probability maps

For both patients and controls tract probability maps were computed, which indicate each voxel’s likelihood of being part of an individual’s tract. Each tract was first converted to a binary voxel-wise mask, indicating which voxels a tract intersected. To exclude voxels with only minimal streamlines, the 25% of voxels with lowest number of streamlines were ignored during this process. The exported tracts of each participant were registered to MNI space. This was done by first registering each participant’s structural high-resolution T1-weighted image to MNI space, using ANTs SyN (Avants et al., 2008) and then applying the warp to the tract NIfTI file (which had already been registered to the high resolution structural scan as part of the pre-processing pipeline). From the binary tract masks in MNI space, we computed probability maps for each tract and hemisphere. The probability maps for controls were then used to employ the probability-map based approach for obtaining tract-specific microstructural measures.

2.2.9. Extraction of microstructural damage within tracts

For individual tracts, we computed the microstructural parameters (FA, RD, MTR) at each point along the individual streamlines (Jones et al., 2005) by trilinear interpolation of the surrounding voxels. We then computed probability-weighted averages (Reich et al., 2010) of the tracts, after normalising the parameter maps to MNI space (which was done by applying the warp obtained for the T1-weighted image to the parameter maps). The two approaches are comparable in that voxels with higher tract probability will contribute more strongly to the computed average.

2.2.10. Comparison between individual tracts and probability map-based approach

Firstly, we investigated the anatomical correspondence between the two approaches. We calculated weighted Dice coefficients between individual tract masks (in MNI space) and tract probability maps as done in Hua et al. (2008).

Secondly, we checked whether individually dissected tracts are biased, by omitting damaged parts of the tract. This was done by comparing tract-averaged microstructure of individually dissected tracts to averaged microstructure from the group probability maps. If there was a bias towards the healthy part, the individual measures should indicate less damage than the probability-based measures.

Additionally, we implemented Bland-Altman analysis (Altman and Bland, 1983), similar to Kuchling et al. (2018).

2.2.11. Statistical analysis

All statistical analyses were performed in Matlab R2015a. The following functions were used: ttest2 for calculation of unpaired t-tests, ranksum for calculation of Kruskall-Wallis tests, crosstab for calculation of Chi-square tests, corrcoef for calculation of Pearson correlation co-efficients. Calculation of Dice scores was also performed in Matlab, using the equation provided above.

3. Results

3.1. Comparison of the fibre orientation reconstruction algorithms

3.3.1. Simulation results

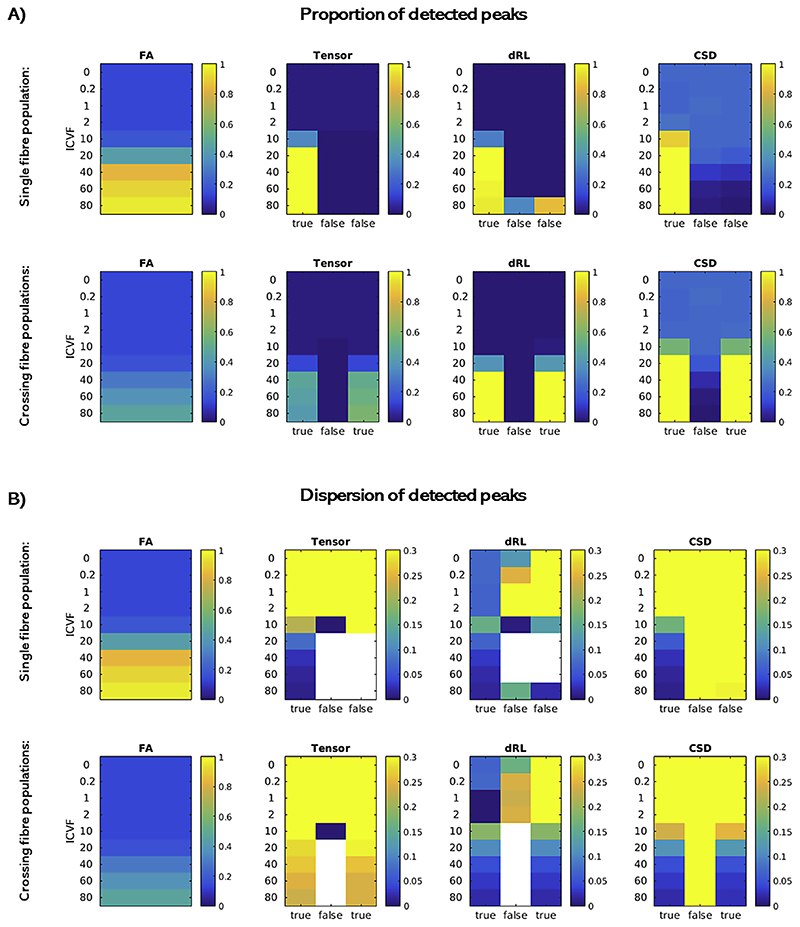
Single fibre population. All three algorithms could successfully reconstruct the peak of the simulated fibre orientation in almost 100% of substrates with an intracellular volume fraction of at least 20%, which corresponded to an FA value of around 0.5. The dispersion of successfully reconstructed true peaks consistently lay below 0.15 (Fig. 1). In substrates with intracellular volume fraction below 10%, all algorithms failed to resolve the peak orientation reliably. Here, CSD-based peak detection resulted in a significant number of false positive peaks (up to 25%). On the other hand, the tensor-based approach produced a maximum of 2% false positives. dRL produced less than 0.01% false positives, with the exception of substrates with a single fibre population and the highest simulated fibre content (80% intracellular volume fraction). Inspection of the discrete FOD suggests that this is a truncation artifact of the harmonics that occurred due to the lack of orientation dispersion in the closely packed simulated cylinders. This is something that would only occur in the simulation scenario, as the substrates were simulated with perfectly parallel cylinders, which is a simplification of the axonal arrangement in vivo, where orientation dispersion occurs even in the most systematically packed regions (Mollink et al., 2017).

Fig. 1. Comparison of the three fibre orientation reconstruction algorithms in simulated data.

Simulated substrates varied in their intracellular volume fraction (ICFV). The parallel cylinders in each substrate were aligned with the z-axis (single fibre population), or with the z- as well as the y-axis (crossing fibre populations). A: For each approach (tensor-based, dRL and CSD), we calculated the percentage of all voxels within each substrate type for which the ‘true’ underlying fibre configuration peak(s) could be detected. As a control, we also calculated this percentage for ‘false’ peaks (orthogonal to the true peak(s)). In each case, the left-most plot shows the FA for each substrate type. B: Dispersion across all detected peaks of a substrate type was calculated. Dispersion was high across wrongly detected peaks, while for substrates with higher intracellular volume fraction, the true detected peaks by dRL and CSD consistently showed dispersion of < .15.

Crossing fibres. In simulated substrates with two fibre populations crossing at 90°, by definition, the tensor-based approach only ever reconstructed one of the two peaks. For both dRL and CSD, a minimum total intracellular volume fraction of 40% was needed to consistently detect both true peaks (Fig. 1), corresponding to a minimum of 20% per fibre population, which is consistent with what we found in the single fibre population scenario. In substrates with low fibre content, CSD again produced false positives in up to 25% of the voxels, while the false positive rate in the tensor or dRL implementation was negligible. In substrates with intracellular volume fraction above 10%, the dispersion for the truly detected peaks again lay below 0.15, with the exception of the tensor-based approach in the crossing fibre condition, where the tensor could not reliably represent either of the true fibre orientations.

3.1.2. In vivo results

For each algorithm investigated, we explored its performance within various tissue types: healthy control tissue, normal appearing white matter, white matter lesions that only appear T2-hyperintense, and white matter lesions that also appear T1-hypointense. An example of reconstructed tensor and FOD in an area of severe white matter lesion is shown in Fig. 2.

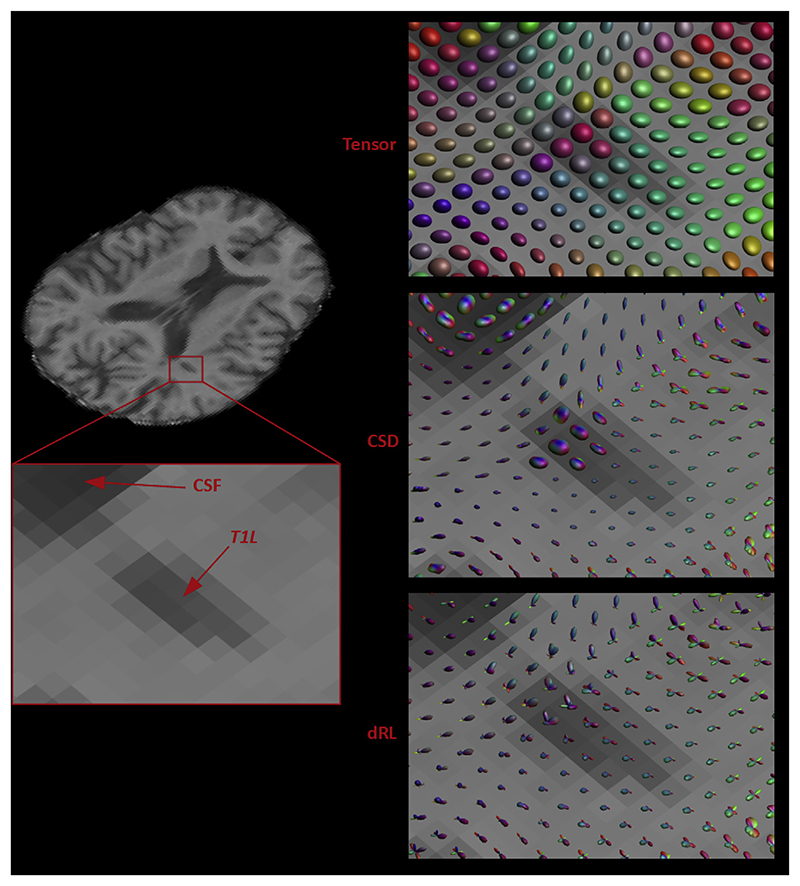
Fig. 2. Example for fibre orientation reconstruction in a patient with severe white matter damage.

Left: an axial slice of the T1-weighted scan of an MS patient is shown, highlighting an area around the posterior corona radiata that is affected by T1-hypointense lesional pathology. Right: Voxel-wise tensor (top) and FODs (middle: CSD; bottom: dRL) are shown in this area, which includes normal appearing white matter, a T1-hypointense white matter lesion and CSF in the lateral ventricle. The increased isotropic diffusion that is found in the most hypointense voxels of the lesion is reflected by tensor and FOD shapes that are comparable to the shapes found in CSF. The less hypointense voxels of the lesion show FOD shapes comparable to normal appearing white matter, but decreased in peak amplitude.

On average, the FA and FOD amplitude of continued streamlines in T1-hypointense lesional tissue were slightly lower when comparing to streamlines in lesional tissue without T1-weighted hypointensity. However, overall there were no strong and systematic differences between tissue types (Table 2). On the other hand, with an increasing level of pathology, an increasing number of premature streamline terminations was observed due to the amplitude threshold not being met. This was only the case for the tensor-based approach and dRL (Table 2). In contrast, using CSD, with an increase in pathology, more streamlines were terminated due to the angle criterion. This indicates that while CSD is equally likely to find peaks passing the amplitude threshold in pathological tissue, these peaks are most likely to be spurious.

Table 2. Comparison of the three fibre orientation reconstruction algorithms in vivo.

For each algorithm (tensor, dRL, CSD) and each tissue type (Ctrl, NAWM, T2L, T1l), we calculated voxel-wise averages of the following parameters: the number of streamlines found in a voxel, the average FA/FOD amplitude across all streamlines found in a voxel, the number of streamline terminations due to the amplitude threshold in a voxel, and the number of streamline terminations due to the angle threshold in a voxel. The mean ± SD of these measures across healthy controls (Ctrl; N = 19) and patients (NAWM, T2L, T1L; N = 29 of the MS subgroup) are reported. The values across different tissues types were statistically compared (unpaired t-test between Ctrl vs NAWM tissue; paired t-tests for T2L vs NAWM, and T1L vs T2L) and t and p statistics are provided for each comparison. Acronyms: Ctrl: Control tissue, NAWM: normal appearing white matter, T2L: T2-weighted white matter hyperintense lesional tissue without T1-weighted hypointensity, T1L: T1-weighted white matter hypointense lesional tissue with corresponding T2-weighted hyperintensity.

Ctrl		NAWM	T2L	T1L	NAWM vs Ctrl	T2L vs NAWM	T1L vs T2L
Average number of streamlines per voxel
Tensor	32.31 ± 3.35	30.66 ± 4.23	33.48 ± 6.72	30.77 ± 9.52	t = −1.43, p = .16	t = 2.64, p = .01	t = −1.55, p = .13
dRL	38.14 ± 5.91	39.40 ± 5.09	42.68 ± 8.61	40.41 ± 11.25	t = 0.79, p = .44	t = 2.6, p = .02	t = −1.3, p = .20
CSD	63.37 ± 10.22	66.12 ± 8.77	70.70 ± 13.18	70.69 ± 18.86	t = 0.99, p = .33	t = 2.4, p = .02	t = −0.01, p = .996
Average peak amplitude (FOD amplitude/FA) of all streamlines per voxel
Tensor	0.71 ± 0.03	0.68 ± 0.03	0.67 ± 0.04	0.64 ± 0.06	t = −3.1, p = .003	t = −1.1, p = .29	t = −2.4, p = .03
dRL	0.22 ± 0.02	0.21 ± 0.02	0.21 ± 0.02	0.20 ± 0.03	t = −1.1, p = .29	t = −0.2, p = .99	t = −2.7, p = .01
CSD	0.42 ± 0.04	0.43 ± 0.05	0.43 ± 0.06	0.42 ± 0.06	t = 0.78, p = .44	t = 0.64, p = .53	t = −2.2, p = .04
Average number of streamline terminations due to amplitude threshold
Tensor	0.32 ± 0.01	0.24 ± 0.04	0.51 ± 0.26	0.97 ± 0.47	t = −8.7, p < .0001	t = 5.8, p < .0001	t = 8.5, p < .0001
dRL	0.23 ± 0.01	0.25 ± 0.02	0.36 ± 0.11	0.70 ± 0.33	t = 5.9, p < .0001	t = 5.2, p < .0001	t = 6.9, p < .0001
CSD	0.97 ± 0.03	0.87 ± 0.09	0.81 ± 0.19	0.80 ± 0.28	t = −4.7, p < .0001	t = −1.7, p = .10	t = −0.38, p = .71
Average number of streamline terminations per voxel due to angle threshold
Tensor	0.10 ± 0.01	0.13 ± 0.02	0.16 ± 0.07	0.08 ± 0.07	t = 6.4, p < .0001	t = 2.0, p = .05	t = −6.4, p < .0001
dRL	0.58 ± 0.02	0.71 ± 0.08	0.74 ± 0.20	0.53 ± 0.23	t = 7.2, p < .0001	t = 0.86, p = .39	t = −5.3, p < .0001
CSD	1.37 ± 0.09	1.41 ± 0.12	1.76 ± 0.59	2.04 ± 0.76	t = 1.1, p = .26	t = 3.2, p < .01	t = 2.9, p = .0074

Counterintuitively, all algorithms produced more streamlines in lesions than in normal appearing white matter, with no significant differences between the two lesional tissue types. This result could be due to an increase of spurious streamlines within lesions, but also due to the preferential localisation of lesions in fibre-rich areas. To check whether the latter might be an explanation for our results, we registered the voxelwise ‘number-of-streamline’ maps from healthy controls to MNI space, and performed voxel-wise correlations between the average number of streamlines and the lesion probability observed in the patients. (This was done for voxels with at least 5% lesion probability, which is the criterion we used to restrict the normal appearing white matter ROI). There were small, but significant correlations, indicating that areas with higher lesion probability in patients also have higher streamline probability in controls (dRL: r = .10, p < .0001, CSD: r = .26, p < .0001, tensor: r = .18, p < .0001).

3.1.3. Considerations of other parameters

As the performance of CSD has been reported to be particularly good at higher b-values (Tournier et al., 2007), we repeated the simulation analyses with b = 2000 s/mm² by increasing the simulated gradient strength, while keeping all other parameters the same. This led to an even higher false positive rate for CSD (Supplementary Fig. 2).

The FOD amplitude threshold that was employed for CSD was based on previous work (Jeurissen et al., 2013). Increasing the amplitude threshold from 0.1 to 0.3 eliminated the spurious peaks in the simulated data at b = 1200 s/mm², but did not affect the comparisons in vivo (Supplementary Table 2).

3.2. Individual tract segmentation in MS

3.2.1. Evaluation of the tract segmentation methods

Average Dice coefficients of around 80% in healthy controls demonstrate high spatial overlap between manually segmented tracts from two independent operators, indicating robust tract reconstruction protocols (Supplementary Fig. 3). To validate the segmentations obtained from the automatic segmentation tool, we also quantified the spatial overlap between automatically segmented tracts and the available manually segmented tracts. The overlap was slightly lower than for the inter-rater analysis, but still showed an average Dice coefficient of > 60%, in both patients and healthy controls (Supplementary Fig. 4). Correlations of tract-specific microstructural metrics extracted from manually vs automatically segmented tracts were high, ranging from r = .85 (p < .001) to r = .98 (p < .001) (Supplementary Table 3 and Supplementary Fig. 5).

3.2.2. Cortico-spinal tracts

Overlaying the tract probability map in patients with the lesion probability map (Fig. 3 top) confirms that despite the high lesion probability in that region, the individually segmented tracts run through these areas. In all controls and more than 90% of the patients (123/131 for the left and 130/131 for the right), both CSTs could be reconstructed.

Fig. 3. Tract probability.

Tract probability maps for patients (red-yellow) are overlaid with lesion probability maps (blue-lightblue). Data from 123 to 130 patients contributed to the map for the left and right CST, respectively, and data from 130 to 122 patients contributed to the map for the left and right Arc, respectively. The lesion probability map is the same as reported in Lipp et al. (2019). Both maps are thresholded between 5 and 50%. Maps for the CST (top) and Arc (bottom) show that areas of high lesion probability overlap with the tracts. This suggests that the investigated tracts go through areas with increased likelihood of lesions, potentially affecting the tracking. R indicates the right hemisphere. Acronyms: CST: cortico-spinal tract, Arc: arcuate fasciculus.

3.2.3. Arcuate fasciculi

As evident from overlapping tract and lesion probability maps (Fig. 3 bottom), the medial part of the arcuate fasciculus runs is a common location for lesions. In all controls and patients both arcuate fasciculi could be reconstructed, with the exception of the left arcuate fasciculus in 1 patient and the right arcuate fasciculus in 9 patients.

3.3. Characteristics of patients without successful reconstruction

There was no overlap between patients for whom one or both CSTs could not be reconstructed and patients for whom one or both arcuate fasciculi could not be reconstructed. This suggests that failure to reconstruct was not purely a result of poor data quality. To test whether the patients for whom tract reconstruction failed were characterised by deviant clinical parameters, we compared them to the rest of the patients and did not find any differences between groups (Supplementary Table 5).

3.4. Testing for bias in the individually reconstructed tracts

We extracted average microstructural parameters from individually segmented tracts and from the tract-probability maps that were computed in healthy control data. Average FA and MTR were systematically higher, and average RD was systematically lower in individually reconstructed tracts than with the probability map-based tracts (Table 3), also illustrated by the estimated bias in the Bland-Altman analysis (Supplementary Table 4)). However, the extent to which measures from individual and probability-based tracts differed was similar in patients and controls, as shown by the non-significant interaction terms Table 3. The non-significance of the individual statistical tests was further supported by the fact that for which group the average bias was stronger in (as indicated by the sign of the t-statistics in the respective comparison) was inconsistent between measures and tracts (see Supplementary Fig. 6 for boxplots of the bias distributions of the two groups). This indicates that while individually reconstructed tracts systematically differ from the tract probability map, this is the case for both patients and controls, and therefore cannot be attributed to the presence of MS lesions. Statistical comparison between the tract-averaged metrics in patients vs controls (Supplementary Table 6) suggest lower FA and higher RD in the tracts of patients than in the tracts of healthy controls, with no statistically significant differences in MTR. The statistics slightly differed depending on whether the probability-based or individual approach is used for the comparison.

Table 3. Systematic differences between individually segmented and probability-based tracts.

For each patient and control group and for each tract, Mean ± SD microstructural metrics (FA, RD and MTR) were extracted from the probability-based (Prob.), as well as for the individually dissected tract mask. To check for systematic differences between individual and probability-based approaches, a paired t-test was calculated for each tract - t and p statistics are reported. To test whether a systematic difference is likely the result of a bias towards the healthy part of the tract in the individual dissections, the difference measure was compared between patients and controls. t and p values are reported for this interaction. Boxplots for the difference measures are shown in Supplementary Fig. 6. Data from 123 to 130 patients and 19 controls contributed to the analysis for the left and right CST, and data from 130 to 122 patients and 19 controls contributed to the analysis for the left and right Arc, respectively. Acronyms: l: left, r: right, CST: cortico-spinal tract, Arc: arcuate fasciculus, FA = fractional anisotropy, RD = radial diffusivity (in 10⁻³ m²/s), MTR = magnetisation transfer ratio.

	MS			HC
FA
Tract	Prob	Individual	Prob vs Individual	Prob	Individual	Prob vs Individual	Interaction
CST1	0.42 ± 0.02	0.51 ± 0.04	t = -33.01, p < 0.0001	0.42 ± 0.02	0.50 ± 0.02	t = -20.13, p < .0001	t = -0.02, p = .98
CSTr	0.42 ± 0.02	0.51 ± 0.03	t = -55.76, p < .0001	0.42 ± 0.01	0.51 ± 0.01	t = -22.16, p < .0001	t = 0.6l, p = .54
ARC1	0.31 ± 0.02	0.41 ± 0.03	t = -75.80, p < .0001	0.32 ± 0.02	0.42 ± 0.02	t = -35.42, p < .0001	t = -0.97, p = .33
ARCr	0.32 ± 0.02	0.40 ± 0.03	t = -52.59, p < .0001	0.34 ± 0.01	0.41 ± 0.02	t = -18.80, p < .0001	t = -1.72, p = .09
RD (in 10-3 m2/s)
Tract	Prob	Individual	Prob vs Individual	Prob	Individual	Prob vs Individual	Interaction
CST1	0.65 ± 0.05	0.58 ± 0.06	t = 15.48, p < .0001	0.64 ± 0.04	0.56 ± 0.03	t = 7.79, p < .0001	t = -0.43, p = .67
CSTr	0.66 ± 0.05	0.58 ± 0.04	t = 18.62, p < .0001	0.65 ± 0.04	0.55 ± 0.02	t = 9.15, p< .0001	t = -1.48, p = .14
ARC1	0.71 ± 0.05	0.61 ± 0.06	t = 46.14, p < .0001	0.66 ± 0.02	0.57 ± 0.03	t = 24.70, p< .0001	t = 0.74, p = .46
ARCr	0.68 ± 0.05	0.61 ± 0.06	t = 34.93, p < .0001	0.64 ± 0.02	0.57 ± 0.03	t= 17.13, p < .0001	t = 0.75, p = .46
MTR
Tract	Prob	Individual	Prob vs Individual	Prob	Individual	Prob vs Individual	Interaction
CST1	0.40 ± 0.01	0.42 ± 0.02	t = -25.61, p < .0001	0.40 ± 0.01	0.42 ± 0.01	t = -12.08, p < .0001	y = 0.92, p = .34
CSTr	0.39 ± 0.01	0.42 ± 0.01	t = -38.68, p < .0001	0.40 ± 0.02	0.42 ± 0.01	t = -16.15, p < .0001	t= 1.91, p = .06
ARC1	0.39 ± 0.02	0.42 ± 0.02	t = -54.32, p < .0001	0.40 ± 0.02	0.42 ± 0.02	t = -35.46, p < .0001	t= 1.02, p = .31
ARCr	0.39 ± 0.02	0.41 ± 0.02	t = -33.96, p < .0001	0.40 ± 0.02	0.42 ± 0.02	t = -19.15, p<.0001	t = l.72, p = .09

3.5. Anatomical correspondence between individually segmented and probability-based tracts

We quantified the anatomical overlap between the individually dissected tracts and the group probability map with a probability weighted overlap score (see Hua et al. (2008)). In both patients and controls, spatial overlap varied between tracts, with median scores of around 55% for the CST and of around 35% for the arcuate fasciculus (Fig. 4). The individual variability suggested that for some patients only 10% of voxels were shared between individual tract mask and probability mask, while for others it was 75%.

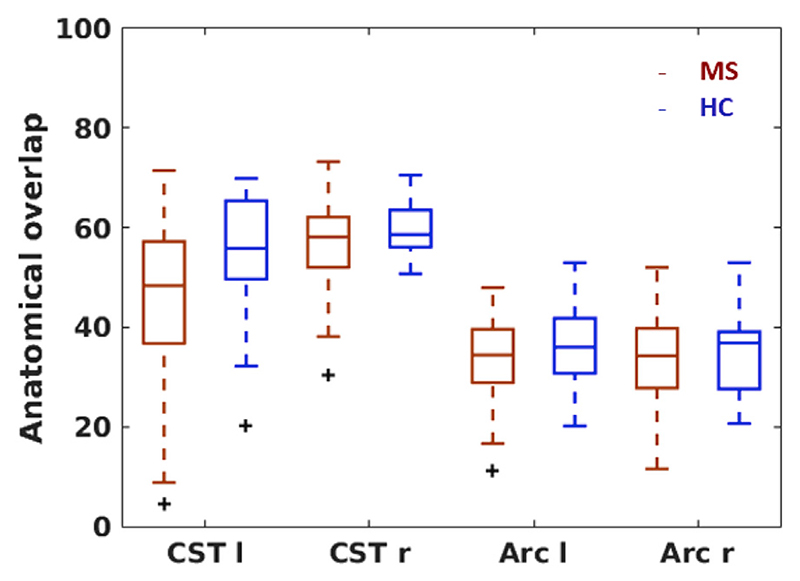
Fig. 4. Anatomical overlap.

An overlap score between the tract probability map and the individual tract mask (registered to MNI space) were calculated. Each time, boxplots for patients (red) and controls (blue) are presented for each tract. Mean ± SD of the weighted Dice coefficients (converted to %) are 45±14 (MS) and 55±13 (HC) for the left CST, 57±8 (MS) and 60±6 (HC) for the right CST, 45±8 (MS) and 36±8 (HC) for the left Arc, and 32±9 (MS) and 35±8 (HC) for the right Arc. Data from 123 to 130 patients and 19 controls contributed to the plot for the left and right CST, respectively, and data from 130 to 122 patients and 19 controls contributed to the map for the left and right Arc, respectively. Acronyms: l: left, r: right, CST: cortico-spinal tract, Arc: arcuate fasciculus.

3.6. Correspondence in tract-specific microstructure of individual and probability-based approach

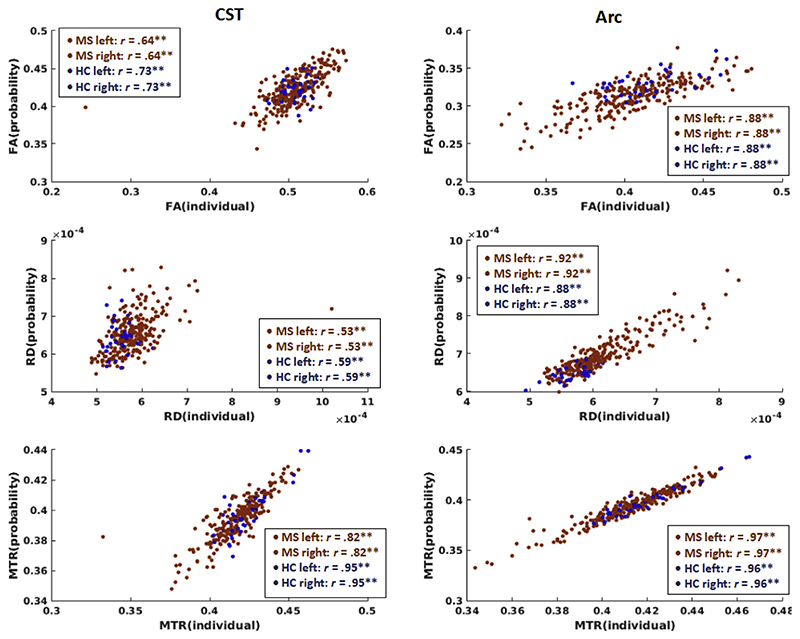
We also assessed the agreement between tract-based estimates of microstructural damage between the individual and the probability-map approach. Correlations were very high for the arcuate fasciculus, ranging from r = .88 (p < .001) to r = .97 (p < .001), and lower for CST, ranging from r = .53 (p < .001) to r = .95 (p < .001). Results were similar for patients and controls (Fig. 5).

Fig. 5. Correlations between tract-specific microstructure from individually segmented and probability-based tracts.

For each microstructural metric (top row: FA, middle row: RD and bottom row: MTR) and tract (CST: left column, ARC: right column), the correlation between individual approach and probability-based approach is shown. Data were collapsed across hemispheres for plotting. Pearson correlation coefficients are provided for each group and hemisphere separately. MS data points are plotted in red, HC data points in blue. Data from 123 to 130 patients and 19 controls contributed to the plot for the left and right CST, respectively, and data from 130 to 122 patients and 19 controls contributed to the plot for the left and right Arc, respectively. **p < .0001. Acronyms: CST: cortico-spinal tract, Arc: arcuate fasciculus.

To complement the previous analysis, we also performed Bland-Altman analysis (Altman and Bland, 1983; Kuchling et al., 2018) for both tracts and all metrics, collapsing across hemispheres. The plots (Supplementary Fig. 7) and values (Supplementary Table 4) again illustrate the systematic difference between approaches and shows that the difference between the two method lies in the range of 0.05 and 0.13 for FA, between −0.18 x 10⁻³m² / s and 0.02 x 10⁻³m² / s for RD and between 0.01 and 0.04 for MTR. Low to medium correlations show that the difference between methods depends on the magnitude to some extent.

4. Discussion

In this work we revisited the challenges of tracking through pathological tissue. We showed that the presence of MS lesions affects fibre orientation reconstruction algorithms differentially: during tensor- and dRL-based tracking, streamlines are more likely to stop, while CSD is more likely to produce spurious streamlines. Even though the CST and arcuate fasciculi run through regions that are frequently affected by MS lesions, we were able to successfully perform individual tract segmentation in a large patient cohort. The segmented tracts did not show a systematic bias in the estimation of microstructural integrity, when compared to a frequently employed approach based on tract probability maps. While tract-averaged microstructural measures showed medium to high correlations between the two approaches, the anatomical correspondence was limited, highlighting the potential benefits of individual tract reconstruction.

4.1. MS pathology affects fibre orientation reconstruction algorithms differentially

To compare fibre orientation reconstruction algorithms under controlled conditions, we simulated tissue substrates that varied in the number of fibres they contained, providing a simplified model of damage in MS. Lesions are characterised by a variety of pathological processes, with fibre loss likely being the change that is the most significant for tractography. Fibre loss could lower the amplitude of the FOD peaks, which are followed during streamlining. At the same time, the associated increase in extracellular water is likely to impact on the diffusion profile, which could further complicate the identification of peaks. Indeed, in our simulated substrates with intracellular volume fractions below 10%, none of the algorithms could reliably identify the true underlying fibre orientations. With intracellular volume fractions above 10%, all three algorithms were consistently successful, with the exception of the tensor-based approach under crossing fibre conditions due to its inherent constraint that it can only ever reconstruct one peak. The main difference between CSD and dRL, in both the single and crossing fibre scenarios, was the false positive rate. With the specified FOD amplitude thresholds, only CSD, but not dRL, produced a substantial amount of spurious peaks in substrates with lower fibre content and low FA. This could be a result of a mismatch between responses in high-FA calibration tissue and the target responses (Parker et al., 2013b).

The findings from the simulations were largely supported by in vivo data from MS lesions. DRL seemed to be more conservative than CSD, with an increase in streamline termination in lesions due to low FOD amplitudes. Premature termination was most pronounced in T1-hypointense lesions, presumably due to the particularly high fibre loss found in this lesion type (Sahraian et al., 2010). dRL has previously been shown to perform worse in tissue with crossing fibres and low FA (Parker et al., 2013b), which could be the reason for the increased streamline terminations in lesions. Even though CSD may be able to resolve fibres better under these conditions (Parker et al., 2013b), our results suggest that it may also be more sensitive to the increased isotropic diffusion in lesions than dRL, producing false positive peaks and consequently spurious streamlines. Even though CSD’s performance at resolving crossing fibres has been reported to be better for data obtained at high b-values (Jeurissen et al., 2013), in our case, increasing the b-value during the simulation led to an even higher false positive rate in CSD. It is possible that the FOD threshold for peak detection, which we based on previous studies (Jeurissen et al., 2013; Parker et al., 2013b) is not universally optimal for all types of data, SNRs, diffusion-weightings etc. In our case, increasing the FOD threshold from 0.1 to 0.3 reduced the false positives rate during the simulations, but did not change the behaviour of the algorithm in vivo. It is likely that optimal tractography parameters for simulated data are not the same optimal parameters for in vivo data, as simulations are often simplified, e.g. in our case the fibres in the simulated substrates lacked orientation dispersion. Systematic and thorough parameter tuning in pathological in vivo data could potentially help to optimise the use of CSD in MS lesions, but was out of scope of this study.

Choosing the algorithm for tract segmentation in vivo, we considered the following: Firstly, dRL seems to be the more conservative algorithm, which leads to streamline termination in lesions with high fibre loss, potentially producing tract reconstructions that at least partially omit lesions. CSD produces more streamlines in lesions, but a considerable number of them may be spurious, which also hinders the correct reconstruction of tracts that pass through lesions. The second consideration was theoretical. In contrast to dRL, CSD requires the response function used for the deconvolution to be calibrated from voxels with single underlying fibre populations, which are generally identified through their high FA. In MS, high FA voxels are likely voxels with preserved white matter integrity. However, the single fibre response function is then applied to the lesional tissue, which could lead to problems with FOD reconstruction and tracking in lesional tissue. Estimating a separate ‘pathological’ single fibre response function from the average response in lesioned voxels is unlikely a sensible alternative, as lesional tissue is highly heterogeneous. In comparison to CSD, dRL is more robust to miscalibrations of the single fibre response function (Parker et al., 2013b). For this reason, for the purpose of this paper, we performed the in vivo whole-brain tractography in MS using dRL.

4.2. Fibre tracking in MS allows to reconstruct tracts that go through areas with high lesion probability

Even though the CSTs and arcuate fasciculi pass through white matter regions that are frequently affected by lesions, we successfully segmented these tracts in individual brains from a large cohort of MS patients. A previously introduced automated tract extraction algorithm made this a feasible endeavour (Parker et al., 2013). Unlike the automated approach using tract probability maps (Reich et al., 2010), this method learns the shape and approximate location of a tract from training data and uses the resulting model to identify and segment tracts from whole-brain tracto-grams, obtained with the same tractography pipeline as in the training data. We found that the automated approach produces tracts that are realistic with regard to their shapes and anatomical location and that show high spatial overlap with manually segmented tracts. In all our spatial agreement analyses, for some individuals the spatial overlap between tracts obtained through different methods was low. This suggests that even when standard manual segmentation protocols are robust in most cases, the process is not completely objective and there is still room for error when drawing anatomically-defined waypoints. The advantage of the automatic segmentation tool we used here is its robustness to day-to-day variability of the rater’s performance and its feasibility for individual tract segmentations in large cohorts. It should be noted that the automatic tract segmentation is still affected by some subjectivity, as it would still capture systematic biases in the rater’s segmentations that were used to create the shape models.

An obvious reason to exert caution about individual tract segmentation in MS, even when done in an automated manner, is that, if lesions or otherwise damaged parts of the tract are left out by the tracking algorithm, then there would be a systematic bias in tract-averaged micro-structural parameters towards values from healthier tissue. We found that individually segmented tracts show higher FA, lower RD and higher MTR than when employing probability-based tract masks, therefore, more intact microstructure in individually segmented tracts. This is not a surprising result, as the tractography algorithm will preferentially produce streamlines in voxels with high white matter and fibre density. In contrast, the probability-map approach considers all voxels in the probability map, independent on the underlying white matter in an individual patient. However, importantly, the reported systematic difference between individual and probability-map based tracts we found was comparable between patients and controls. This finding suggests that there is no additional disease-related bias in the individual tract segmentations. While the simulation and tissue comparison results suggest that the fibre orientation reconstruction algorithms could further be optimised for tracking through lesions, our tract segmentation results suggest that dRL may be a promising method for tractography in MS.

4.2.1. The anatomical correspondence of individual and probability-based approach is modest

Previous studies have suggested using a probability-based approach of investigating microstructure in specific white matter tracts in MS. Here, we showed that the spatial overlap between tract probability maps obtained from healthy controls, and individually segmented tracts of individuals is modest, with averages ranging from 35% for the right arcuate fasciculus to 60% for the right CST, with similar results for patients and controls. The stronger agreement for the CST suggests that there may be more individual variability in tract shape and localisation in the arcuate fasciculus. In both cases, the variability in individual tracts is likely to be partially also a result of the normalisation of individual brains to MNI space, which does not necessarily align tracts within the homogeneously appearing white matter.

Other methodological factors are likely to play a role as well. Even though the anatomical correspondence between individual and probability-based approach was lower than the correspondence between manual and automatic segmentations and the correspondence between manual segmentations of different operators, latter methodological differences also affected the tract anatomy. Without ground truth data available, it is difficult to conclude which methods give the most accurate tract segmentations (Schilling et al., 2019). Evaluating the accuracy of tractography in MS brains for which the ground truth is known is unlikely to ever be possible. Here, we show that tractography methods developed for healthy tissue can be used to anatomically segment tracts without introducing patient-specific biases. The biases that may be inherent to the tractography method itself will still be there and will also affect the tract probability maps that are used in atlas-based approaches.

4.2.2. The correlation of tract-specific microstructure in individually segmented vs probability-based tracts is high

Despite the difference in spatial location and systematic difference in average microstructural parameters, the correlation of the microstructural information between the individual and probability-map based approaches was high, particularly for the arcuate fasciculus. This indicates a large overlap in the individual variability that is captured by the two approaches, not necessarily, that the measurements are interchangeable in all applications (Altman and Bland, 1983). Correlations between microstructural parameters from individually segmented tracts vs atlas-based estimations have previously been reported to be tract-dependent (Reich et al., 2010). Some of our correlations were also lower, e.g. only 25% between the two approaches were shared in RD measures of the right CST. Low correlations for tensor-based measures, such as RD, could be influenced by their sensitivity to the macroscopic tract shape and individual differences in tract morphometry (De Santis et al., 2014). This hypothesis is corroborated by the result that the correlation between individual and probability-based approach in the CST was highest for MTR, a microstructural metric that does not show this sensitivity to tract morphometry.

Individual tract segmentation may not bring large benefits compared to the probability-based approach, when average microstructural parameters of a tract as a whole are of interest. This can be the case for studies looking at global effects within specific tracts (e.g. Bonzano et al. (2014)). Here, averaging microstructural measures should be less noisy and provide more statistical power and spatial accuracy than voxel-based approaches. However, the advantage of individual tract segmentation is that it does not limit the analysis to tract-specific average measures. Other features of the tract can also be studied, such as tract shape, tract-specific atrophy (Wang et al., 2018) or the spatial variation along a tract (Jones et al., 2005; Yeatman et al., 2012). Very precise anatomical assignment of lesions to specific white matter specific tracts could also open doors for clinical questions, for example on how the appearance or disappearance of lesions in specific tracts is associated with the presence or resolution of specific symptoms or with potential secondary damage, such as pathology in the cortical regions that are directly connected by a tract.

4.2.3. Anatomical generalisability

In this work, we focussed on the CST and arcuate fasciculus, because they are comparatively easy to reconstruct and pass areas of high lesion probability, which challenges the tracking predominantly through challenging the FOD estimation. This allowed us to focus on the potential problem of MS lesions for the reconstruction of these tracts. To what extent the results generalise to other tracts is likely to depend on the nature of the tract, as other tracts come with other challenges. An example is the optic radiation, which is also a tract often affected by MS (Kuchling et al., 2018), and hard to reconstruct due to the Meyer’s loop (Chamberland et al., 2018). Here, recent developments in tractography also aim to improve the tracking process itself rather than the FOD estimation, may come in hand, such as anatomically constrained tractography (Horbruegger et al., 2019) and microstructure informed tractography (Schurr et al., 2018). To what extent these methods are beneficial in MS is also starting to be explored (Horbruegger et al., 2019; Kuchling et al., 2018; Schurr et al., 2018).

While the strength of tractography lies in its robustness to individual differences in tract size and shape, successful delineation depends on the employed tractography algorithm and parameters, and the anatomically accurate placement of waypoint of interest gates. Therefore, a widely used alternative for studying group differences or brain-behaviour correlations is the off-the-shelf whole-brain analyses tool tract-based-spatial-statistics (TBSS; Smith et al. (2006)). Despite its name, TBSS does not reconstruct individual tracts, but instead aligns participants’ FA maps and produces a skeleton, characterised by high average FA values. Voxel-wise group statistics are calculated within the skeleton and interpreted consulting WM atlases. TBSS has been shown to be sensitive to picking up damage in specific tracts in MS (Kuchling et al., 2018), however, the anatomical accuracy of TBSS results can be limited even in healthy individuals (Bach et al., 2014). To what extent the anatomical accuracy of TBSS may be limited by the effect of MS lesions on the skeleton projection remains to be investigated.

4.2.4. Limitations and future directions

Under the conditions of this study, CSD produced more spurious peaks than the other algorithms. However, this is not to say that the algorithm does not have benefits which could aid tractography in MS patients. For example, CSD has previously been shown to outperform dRL when resolving crossing fibres under low FA conditions (Parker et al., 2013b). We only assessed the performance of the algorithms in the context of tractography, where not all FOD peaks are reconstructed and considered simultaneously. Instead, at each point along the streamlining process, the closest detected peak to the current streamline direction is followed, assuming that the tangent to the streamline minimally subtends the best estimate of fibre orientation. To mimic the tractography process in our simulation, the 45° angle threshold employed during streamlining was also employed when assessing the proportion of successfully detected peaks. This is a comparatively lenient threshold for assessing peak detection accuracy, with an additional measure of dispersion confirming orientational agreement between the detected peaks. While under these specific conditions, CSD produced a large number of false positives, at this point we are not in a position to comment of the suitability of CSD for other types of analyses, such as fixel-based analysis (Raffelt et al., 2015).

We employed standard tractography protocols that have been optimised in healthy tissue, and that are compatible with clinically feasible diffusion MRI acquisitions. It is likely that optimising tractography for MS could benefit from fine-tuning of some of the parameters for pathological tissue, and also from data with higher angular resolution and multiple diffusion weightings. For example, the sensitivity of CSD to the increase in isotropic diffusion in lesions may be partly counteracted using multi-shell - CSD, which considers several tissue compartments (Jeurissen et al., 2014). Transitioning to multi-shell acquisitions could allow the benefits of such advanced deconvolution methods to be explored.

Simulations produced a simplified version of pathology, and other factors such as permeability, could also be considered to make the scenario more realistic (e.g. Nedjati-Gilani et al. (2017)). Ideally, also fibre orientation dispersion is introduced, which is currently not possible with the Camino software package used in the current study.

The probability-based approach depends on inter-subject co-registration of the images by normalising them to a common reference space. To do this, we chose T1-weighted based co-registration, as this is most successful for aligning pathological brains (Avants et al., 2008), and to make our results comparable to previous studies (Reich et al., 2010). However, in future studies, this normalisation step could be further improved, e.g. in the form of multi-modal registration by white matter parametric maps, such as FA maps.

Last but not least, while comparable to similar recent methodological studies (e.g. Horbruegger et al. (2019); Kuchling et al. (2018)), the sample size of our healthy control group small compared to the patient group, posing some limitation with regard to statistical power in some of the analyses.

4.2.5. Conclusions

Accurate anatomical assignment of damage to specific white matter tracts is important for clinical research. In MS research, tractography-based anatomical segmentation in individual patients is rarely performed, with probability-based approaches often being the method of choice to avoid potential effects of MS lesions on tractography algorithms. We show that MS pathology indeed affects the fibre orientation reconstruction that is done during tractography, with different algorithms being affected differently - lesions led to an increase in streamline interruptions with dRL, and an increased number of spurious streamlines with CSD. Nevertheless, fibre tracking through MS lesions is possible, and can even be used to reconstruct tracts that go through areas with high lesion probability. The resulting tracts do not seem to systematically omit lesional tissue. A problem with tractography in general is that the anatomical localisation of the tract does depend on the specific method used to segment individual tracts. The anatomical overlap between individual tracts and tract probability methods is quite low, however, this may not be an issue if the aim of the research is to obtain tract-averaged microstructural parameters. For studying tract shapes, tract-specific atrophy and along-tract profiles, individually segmenting tracts is necessary. We showed that this is feasible, even in large scale clinical studies. Further improvements of the algorithms to maximize anatomical accuracy could lead to powerful tools to investigate diagnostic and prognostic markers.

Data and code availability statement

The data described in this manuscript are not available in the public domain, as this would not comply with the institutional ethics approval for the project under which the data were acquired. Direct requests for pseudoanonymized data can be considered, and will be dependent on the agreement on an appropriate inter-departmental data transfer agreement that includes the conditions for sharing and re-use.

The analysis approach of this study is based on previously published methods (Jeurissen et al., 2011; Leemans et al., 2009). The methods employed in this paper can be reproduced with implementations in various software packages: preprocessing of the data and tensor and non-negativity constrained super-resolved spherical deconvolution-based tracking (Tournier et al., 2007) can be reproduced with ExploreDTI (http://www.exploredti.com/). An implementation of non-negativity constrained super-resolved spherical deconvolution-based tracking (Tournier et al., 2007) can also be found in MRTrix (https://mrtrix.readthedocs.io/en/latest/). A dRL-plugin for ExploreDTI, which was used in this paper, can be shared upon reasonable request. dRL-based tracking is also implemented in the software package StarTrack (https://www.mr-startrack.com/).