Abstract
Optical remotely sensed data are typically discontinuous, with missing values due to cloud cover. Consequently, gap-filling solutions are needed for accurate crop phenology characterization. The here presented Decomposition and Analysis of Time Series software (DATimeS) expands established time series interpolation methods with a diversity of advanced machine learning fitting algorithms (e.g., Gaussian Process Regression: GPR) particularly effective for the reconstruction of multiple-seasons vegetation temporal patterns. DATimeS is freely available as a powerful image time series software that generates cloud-free composite maps and captures seasonal vegetation dynamics from regular or irregular satellite time series. This work describes the main features of DATimeS, and provides a demonstration case using Sentinel-2 Leaf Area Index time series data over a Spanish site. GPR resulted as an optimum fitting algorithm with most accurate gap-filling performance and associated uncertainties. DATimeS further quantified LAI fluctuations among multiple crop seasons and provided phenological indicators for specific crop types.
Keywords: Gap-filling, Machine learning, Vegetation phenology, Remote sensing
1. Introduction
Quantifying the spatiotemporal variability of the Earth has always been an essential requirement for many applications in remote sensing, geodesy and geodynamics (Hamblim and Christiansen, 2010). Improving its knowledge may help to better comprehend and model the global environmental change. The usage of optical remote sensing time series has opened the door to global-scale monitoring of seasonal changes in vegetated areas through their spectral properties (Reed et al., 2009; Ramachandran et al., 2011; Gutman and Masek, 2012; Liang, 2019; Pricope et al., 2019). To achieve that, the generation of continuous fields in time and space starting from irregularly distributed data is of critical importance. Given the current viability of multiple Earth observation missions (e.g., the Sentinels), a growing number of monitoring agencies and Earth System sciences depend on the influx of continuous satellite data, i.e. gap-free data. In reality, however, the need for continuous data is often unfulfilled, for multiple causes (Kandasamy et al., 2013; Weiss et al., 2014): (1) inadequate climatic conditions (clouds, snow, dust and aerosols), (2) instrumentation errors, (3) losses of image data during data transmission, or (4) low temporal resolution (i.e. long interval needed to revisit and acquire data for the exact same location), among others. They degrade the availability/quality of spectral/temporal information required to retrieve land surface properties. Therefore, the impact of missing data on quantitative research can be serious, leading to biased estimates of parameters, loss of information, decreased statistical power, increased standard errors, and weakened of findings (Dong and Peng, 2013). For this reason, spatiotemporal reconstruction of areas with gaps from satellite imagery is becoming a crucial step for monitoring purposes (Schwartz, 2013), and for the knowledge of the life cycle of vegetation, i.e. vegetation phenology (White et al., 2005; Rezaei et al., 2017). Although a variety of gap-filling methods can perform this task (see review in Zeng et al. (2020)), the difficulty lies in the choice of the one that best reproduces the actual surface to identify the precise date when a phenological event occurs.
Vegetation phenology quantification over agricultural lands is widely used for yield determination, and to improve management and timing of field works (planting, fertilizing, irrigating, crop protection or harvesting) (Mulla, 2013; Sakamoto et al., 2005). Distinct phenological parameters are of interest to the scientific community, private companies, and farmers, such as dates of start and end of growing season (SOS and EOS, respectively), maximum peak, seasonal amplitude defined between the base level and the maximum value for each individual season, length of the season, etc (Jönsson and Eklundh, 2004). As reported by multiple studies (Sobrino and Julien, 2011; Richardson et al., 2013; Atzberger, 2013), these parameters are extremely sensitive to changes in vegetation cycles due to climate change, and these changes can have a profound impact in the agricultural production.
Time series analysis of vegetation’s phenological trends is a powerful and practical tool that comprises a diversity of methods for reconstructing, modeling and analyzing time series data (e.g. vegetation indices or biophysical variables) in order to extract meaningful statistics and other characteristics from the data such as autocorrelation, trend or seasonal variation (Tang et al., 2016). Numerous studies have dealt with the retrieval of phenological phases from remotely sensed data (White et al., 2009; Julien and Sobrino, 2009; Tan et al., 2011; Broich et al., 2015; Berra et al., 2019). In the era of the Sentinels, where large amounts of data are available, these methods must be accurate, robust and fast. Hence, there is a compelling need to identify next-generation time series algorithms to be integrated into an operational processing chain. Of specific interest is the emergence of machine learning regression algorithms (MLRAs). MLRAs tend to behave as highly adaptive and versatile fitting algorithms (Verrelst et al., 2015, 2019) and can thus replace conventional fitting functions, e.g. for enabling more accurate estimation of phenology trends, or for identifying multiple seasons within a time series. However, their performances need to be evaluated against standard time series processing methods, such as those available in established software packages.
Several sophisticated time series software packages have been developed over time, with capabilities of identifying phenology trends or disturbances, e.g. TIMESAT (Jönsson and Eklundh, 2004), BFAST (Verbesselt et al., 2010), TIMESTATS (Udelhoven, 2011), SPIRITS (Eerens et al., 2014), BeeBox (Arundel et al., 2016), phenor (Hufkens et al., 2018), pyPhenology (Taylor, 2018), CroPhenology (Araya et al., 2018), FORCE (Frantz, 2019), Earth Engine App (Li et al., 2019), EO Time Series Viewer (Jakimow et al., 2020). In most cases, these packages are freely available to process time series but they also face some limitation such as the need to use regular time series with more than one phenological cycle, the absence of graphical user interface (GUI) or being merely addressed to advanced users. Also, these packages provide limited tools for gap-filling and smoothing purpose, and above all, are not yet adapted to the emergence of MLRAs.
In general, modeling phenological evolution represents a challenging task mainly because of time series gaps and noisy data (D’Odorico et al., 2015; Kuenzer et al., 2015), coming from different viewing and illumination geometries, cloud cover, seasonal snow and low temporal resolution (Weiss et al., 2014; Mariethoz et al., 2012). For that reason, the use of reliable gap-filling fitting functions and smoothing filters is frequently required for retrievals at the highest feasible accuracy (Chen and Boccelli, 2018; Jönsson et al., 2018). To avoid all these drawbacks, time series studies typically use the regular composite Normalized Difference Vegetation Index (NDVI) product from the MODerate resolution Imaging Spectroradiometer (MODIS) (e.g. Gong et al., 2015; Zhao et al., 2009).
Nevertheless, a critical aspect in time series analysis is that remote sensing products are generally spatially and temporally discontinuous. This implies that the ability to process irregular time series becomes indispensable for studying land surface phenology. Given that most time series data are spatiotemporally irregular, some questions arise:
Can we cope with this irregularity and achieve a reasonably accurate reconstruction of phenological stages by taking advantage of latest MLRAs?
How can we benefit from the new, high spatiotemporal resolution remote sensing data (e.g. the Sentinel constellation) to improve understanding of dynamic changes of land surfaces?
With ambition to tackle these questions and offer solutions to the community, in this paper we present a novel and generic scientific time series toolbox that serves as an alternative to existing toolboxes. The so-called Decomposition and Analysis of Time Series Software (DATimeS) is a stand-alone image processing GUI toolbox written in MATLAB. This toolbox can model and analyze regular and irregular time series data from complete images, specific region of interest or single pixels in multiple formats (e.g., geotiff, ENVI). It encompasses a suite of powerful mathematical fitting algorithms such as MLRAs (e.g., decision trees, kernel-based methods, neural networks) as well conventional fitting methods such as harmonic analyses (HA) (i.e. Fourier Transform (Roerink et al., 2000; Zhou et al., 2012, 2015)) and non-linear least squares regression, i.e. double logistic function (Richardson et al., 2009). With these smoothing and fitting algorithms, spatiotemporal gap-filling can be achieved. DATimeS enables to perform advanced time series tasks for: (1) the generation of spatially continuous maps from discontinuous data, i.e. gap-filling, and (2) detection of heterogeneous spatial patterns of phenological indicators (i.e., crop key growth stages) throughout multiple seasons.
The remainder of the paper is structured as follows. Section 2 provides the general concept of DATimeS, section 3 outlines the modules of the toolbox and describes the theoretical framework of the algorithms available. Section 4 provides a demonstration case of reconstructing leaf area index (LAI) time series from Sentinel-2 acquisitions and estimating phenological indicators over crop areas. Discussion is presented in Section 5, whereas conclusions and future work lines are finally presented in section 6.
2. DATimeS: general aspects
The DATimeS toolbox is developed in MATLAB (version R2011b or later is required), which has the advantages of being easy to use and source code changes can be applied without much effort. Although MATLAB faces some limitations as being a commercial software and not as much optimized in speed as opposed to other programming languages, DATimeS can be either operated independently (i.e., without a license) through a runtime engine called the Matlab Compiler Runtime, or it can be run as part of the ARTMO scientific software package (Verrelst et al., 2011, 2012). Matlab is widely used by the science and engineering community. Its processing speed should not be considered a drawback since today’s computer hardware is fast enough to guarantee software efficient performances.
The core functioning of DATimeS involves multiple time series smoothing and fitting algorithms. On the one hand, the toolbox provides state-of-the-art MLRAs as well as conventional methods available in other distinguished time series toolboxes (e.g., TIMESAT, TimeStats, SPIRITS). On the other hand, its environment offers sophisticated new modeling techniques for vegetation phenology. Users do not need advanced processing knowledge to take full advantage of these capabilities since it has a friendly GUI for non-programmers.
DATimeS is primarily designed to process time series of vegetation indicators derived from satellite spectral measurements. However, other types of raster data such as meteorological index, radar data, and eddy co-variance carbon flux data or data as acquired by airborne sensors or drones can also be processed. Its processing firstly leads to cloud-free composite images for any chosen time sampling, e.g. every 10 days. Subsequently, phenology variables can be derived such as the start and end of a growing season.
3. Modules
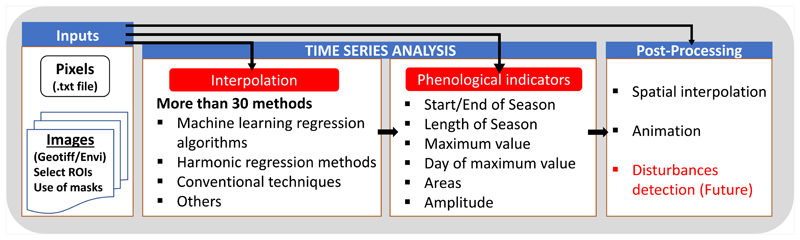
DATimeS software is structured in multiple modules. The modular architecture, which has been inherited from the ARTMO toolbox, offers the following advantages: (1) it guides the user through the processing steps, i.e. subsequent processing modules are activated once current module has been completed, (2) modules can be easily modified or extended without affecting the main architecture, (3) and new modules with new functionalities can be easily added to the toolbox. An overview of the DATimeS’ modules contained in this first official version (v.1.06) is shown in Fig. 1.
Fig. 1. Hierarchical design of DATimeS.
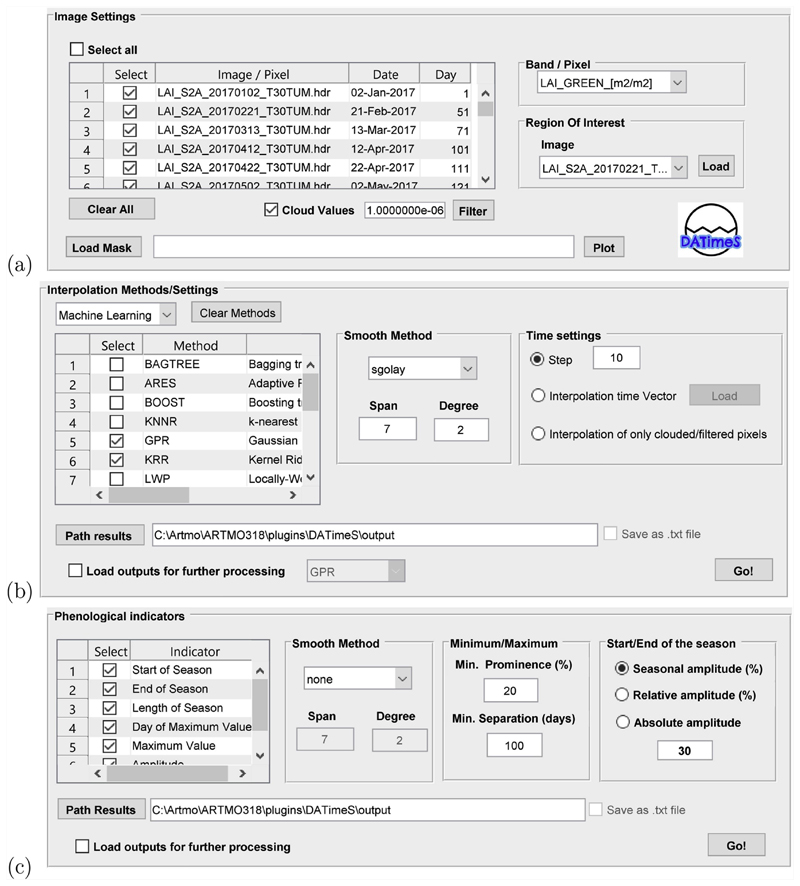
The first module, ”Input”, is responsible for reading the data. Time series processing for spatiotemporal analysis can take place either on a single pixel, or on a stack of images. For single pixels, a.txt file is required. Imagery can be entered in TIFF or ENVI format from a specific folder. When loaded, the data will appear sorted in the DATimeS main window (Fig. 2a).
The second module, ”Time Series Analysis”, is in charge of constructing composite images with any time step by applying the gap-filling (e.g. due to clouds) using a broad variety of advanced interpolation and smoothing methods. Besides, it enables to calculate all kinds of phenological indicators. The GUIs corresponding to this module are shown in Fig. 2b and c.
The third module, ”Post-processing”, improves the obtained maps by spatial interpolation and provides the possibility to create videos, thus enabling animation of temporal trends.
Fig. 2. DATimeS graphical user interface.
a) Main window of DATimeS. b) Panel designed for gap-filling. It is divided into three logical areas: interpolation algorithms, smoothing methods and time settings. c) Panel for phenological indicators estimation.
3.1. Input data
3.1.1. Single pixels
The first option that DATimeS offers is the possibility to analyze and process single time series. Data must be provided as.txt file accordingly to specific format rules: dates need to be provided in YYYYMMDD format, YYYY being the four-digit year, MM the two-digit month and DD the two-digit day in the month. The text file can encompass multiple pixels, sorted as columns, so that any of these columns can be analyzed. The DATimeS manual (see http://artmotoolbox.com) provides a complete overview and more in-depth explanation of the format rules.
3.1.2. Supported image formats
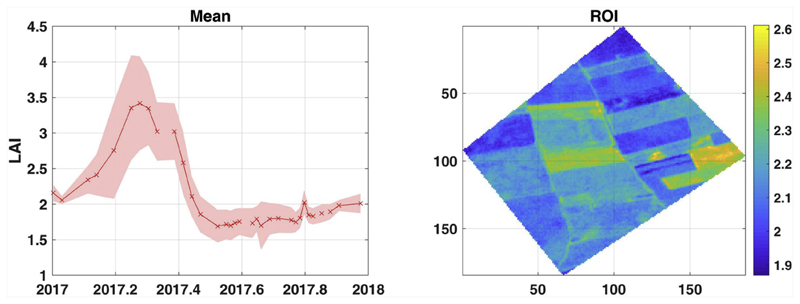
Imagery can be loaded in two formats: ENVI or TIFF files. First, complete multiple images are loaded as long as their spatial dimensions match. Then, they can be completely processed. A subset within the area covered by the loaded images can be also defined. Two possible options are provided: (1) to apply an earlier created mask or, (2) to define directly a region-of-interest (ROI). In the latter case, the user can draw a ROI on a selected image and band (in case the loaded images contain of multiple bands), and create a new mask. Subsequent processing will then only take place within the selected region. It should be noted that the images belonging to a time series must contain their acquisition date. In case of ENVI format, it must be included in the header file. In case of TIFF, the TIFF ”DATETIME” tag will be looked for. Finally, the loaded images will appear into the main window, sorted according to dates (see Fig. 2a). The time evolution of the mean and standard deviation of pixels within the ROI, along with the map of pixel values for the selected image, can be easily obtained by clicking on Plot (see Fig. 3).
Fig. 3.
Evolution of mean LAI and its standard deviation (red shadow area) along the temporal range (left), and map of pixels of the chosen image (right). The study area is located near the city of Valladolid, north-west Spain, where the landscape is characterized by an intensive dryland agricultural system where arable land comprises up to 80% of the available area. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
3.1.3. Filtering option: cloud thresholding and masking
Regardless of the type of input data (i.e., single pixel time series or images), the time series data can be inspected on missing values, typically due to cloud cover. The first step is to identify the cloudy pixels and to remove by setting their weight to zero. Two ways to define cloud values are implemented:
Using a fixed value, e.g., in case clouds have been labeled with a fixed value.
With a thresholding filter, where the user must provide a minimum and maximum value to filter out pixels that fall outside these boundaries.
Once having the images loaded, an earlier-created mask can also be applied to the analysis. The mask can be a.mat, ENVI or TIFF file and must match the spatial size of the image stack. Again, the masked region can be plotted for the selected image and band by clicking on Plot, same as displaying a full image.
3.2. Time series analysis
After having inputted pixel or image data, the Time Series Analysis module can be activated. This is composed of two parts: (1) the interpolation and (2) the phenological indicators submodules, and described below.
3.2.1. Interpolation
The interpolation is the main processing step of DATimeS: it allows to perform the time series gap-filling (e.g. in case of a single pixel as loaded by the.txt file) and generate composite maps (in case images were loaded). In the Interpolation submodule (Fig. 2b), the key option is the selection of the interpolation strategy.
About 30 interpolation algorithms have been brought together and categorized according to the following methods: (1) machine learning regression algorithms (MLRAs), (2) harmonic regression methods, (3) conventional interpolation methods, and (4) others. Their complete list is reported below, in Table 1.
Table 1. Interpolation methods implemented in DATimeS.
| INTERPOLATION METHODS | |
|---|---|
| MLRA | Bagging trees (BAGTREE) |
| Adaptive Regression Splines (ARES) | |
| Boosting trees (BOOST) | |
| k-nearest neighbors regression (KNNR) | |
| Gaussian Process Regression (GPR) | |
| Kernel Ridge Regression (KRR) | |
| Locally-Weighted Polynomials (LWP) | |
| Support Vector Regression (SVR) | |
| Neural networks (NNIPL) | |
| Random forests (RF2) | |
| Boosting random trees (RF1) | |
| Structured Kernel Ridge Regression with linear Kernel (SKRRlin) | |
| Relevance Vector Machine (RVM) | |
| Sparse Spectrum Gaussian Process Regression (SSGPR) | |
| Structured Kernel Ridge Regression with RBF kernel (SKRRrbf) | |
| Decision trees (TREE) | |
| Variational Heteroscedastic Gaussian Process Regression (VHGPR) | |
| Harmonic | Offset + Harmonic analysis |
| Offset + Harmonic analysis + Linear Term | |
| Offset + Harmonic analysis + Linear Term | |
| Offset + Harmonic Analysis using Sliding Window | |
| Conventional Methods | Linear, Polynomial, Nearest, Next, Previous, Pchip, Spline |
| Othters | Double Logistic curve |
-
Machine learning regression algorithms. A suite of MLRAs have been implemented in DATimeS (see Table 1). For a complete overview and more in-depth discussions of the algorithms we refer to the following publications: Smola and Schölkopf (2004); Camps-Valls et al. (2006); Rasmussen and Williams (2006); Thayananthan et al. (2006); Lázaro-Gredilla et al. (2014); Verrelst et al. (2019). Their source code is freely available and can be found at: https://github.com/IPL-UV/simpleR.
Among the multiple MLRA approaches, special attention deserves the Gaussian processes regression (GPR) (Rasmussen and Williams, 2006). GPR carries out a non-parametric modeling developed in a Bayesian framework and provides uncertainty intervals along with the mean estimates (Verrelst et al., 2013). This distinct feature, which is not shared by other machine learning algorithms, can open a unique source of information to assess the robustness of the predictions at various temporal scales.
-
Harmonic Regression methods. Four Fourier-based techniques have been implemented to reconstruct the seasonal leaf development (see Table 1). The first (and simplest) algorithm, named Fourier1, is based on the general equation (Roerink et al., 2000; Zhou et al., 2012):
where y is the reconstructed time series, an and bn are the amplitudes of the cosine and sine terms, t is the time, ωn = 2π/P is the angular frequency, P is the period, and a0 is a constant offset which accumulates the low-frequency part of the signal. Applying the method of least squares, the amplitude coefficients (an, bn) are estimated. The second and third approaches, named Fourier2 and Fourier3 (Equations (2) and (3), respectively), are similar to Equation (1), with the difference that linear and quadratic terms have been included into the algorithms.(1) (2) (3) In the fourth approach, named Fourier4, the estimates are obtained using a sliding window to account for the amplitude and phase time variability, i.e. changes in seasonality of vegetation variables. Essentially, the longer time series is divided into shorter segments of equal length (NL) and then the Fourier coefficients are computed separately on each shorter segment using Equation (1). Consequently, the tabulated epoch for each fit is the middle date of the window. Finally, the amplitude variation is modeled as continuous piecewise liner functions, which is defined to have linear variations between “nodes” at selected times. The length of the sliding window (NL) and the displacement between the subsequent fits (ND) are specified by the user and have to be sufficiently large to separate the main signal from the noise and high frequency signals (e.g. NL = 365 days, ND = 30 days). This technique provides an optimal tradeoff between quality and computational cost.
Conventional interpolation methods. Apart from the above-mentioned algorithms, DATimeS also includes various types of conventional interpolation techniques (Akima, 1970, 1974; Olivier and Hanqiang, 2012; Lepot et al., 2017) (see Table 1). They are favorable when speed is the main concern and not accuracy.
-
Others: Double logistic curve. Finally, a double logistic curve method has been implemented, which is commonly used in phenology studies (Beck et al., 2006; Hird and McDermid, 2009; Atkinson et al., 2012). This algorithm, also known as Sigmoid, uses a double-sigmoidal model (Richardson et al., 2009) by combining two regular sigmoidal functions to characterize the phenological metrics of different vegetation indices, as shown here:
(4) Here, the double-sigmoidal model is uniquely determined by six parameters, two midpoints (c, d) and two slope parameters (d, e), a maximum value (b), and a base level (a). The difference between parameters b and a gives the seasonal amplitude. These parameters are estimated using a non-linear least squares regression. For this reason, DATimeS uses an iterative algorithm reducing the error sums of squares (SSE) to converge on a single solution. The iterations continue until the algorithm converges to the minimum SSE, or reaches the maximum number of iterations permitted. To account for the seasonal variability and the complex behaviour of time series, this function is divided in three overlapping intervals around maxima and minima: one is aligned to the left minimum, another is placed on the central maximum, and the latter is fixed to the right minimum. To guarantee the continuity and the convergence of the reconstructed time series, the estimate parameters are modeled as continuous piecewise linear functions.
3.2.2. Interpolation and smoothing processing options
Before starting the gap-filling procedure, a compulsary step is to define the output time settings, i.e. the days to which data is interpolated. In this context, three options are possible:
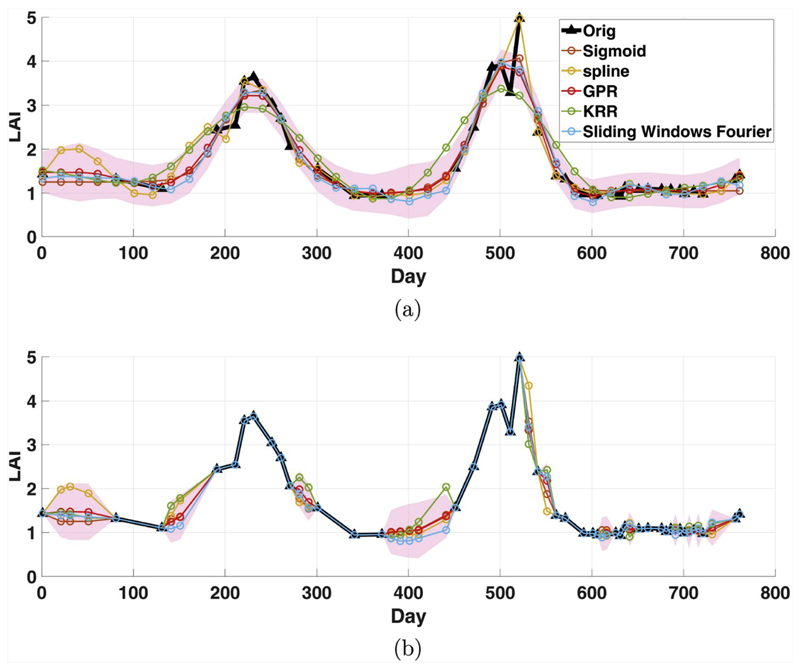
Fixed time step: interpolating to a higher or low frequency (e.g., each 20 days, see Fig. 4a).
Interpolation time vector: User-defined dates as provided by a text (. txt) file.
Interpolation of only clouded/missing/filtered pixels: With this option only those pixels labeled as clouds or fitered out by the thresholding criteria will be filled up at the original dates. All other pixels keep their original value. An example of this option is provided in Fig. 4b.
Fig. 4.
Original and reconstructed time series of LAI using several gap-filling techniques. The example applies different time settings. Interpolated values of time series at a higher sampling frequency (every 20 days) (top). Interpolated values are computed only for embedded missing values in the input time series (bottom). The GPR uncertainties are shown in red shade areas. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
A key feature of DATimeS is that multiple interpolation methods can be selected at once for running in a sequence fashion, so their performances can be visually compared. Information about processing time is also provided. The interpolation methods can be additionally combined with a smoothing method to facilitate the calculation of the gap-filling and phenological metrics, but that is not mandatory. If selected, smoothing is applied before the interpolation. When data collected over time include some noisy behaviour, smoothing techniques can be helpful to mitigate the effect of these variations. DATimeS features six different smoothing techniques (see description in Table 2). They are based mainly on moving average, locally weighted scatter plot and Savitzky-Golay algorithms (Press et al., 1993). The number of data points for calculating the smoothed value as a combination of nearby values can be controlled using the span argument (see middle panel in Fig. 2b). As such, the greater the value of span, the smoother the fitted curve. In case of Savitzky-Golay, the optimal choice of polynomial order can be controlled using the degree argument. In any event, it should never be bigger than span.
Table 2.
Description of different smoothing methods (Press et al., 1993) included on DATimeS. Source: MathWorks.
| Filter | Description |
|---|---|
| Moving | A low pass filter with filter coefficients equal to the reciprocal of the span. |
| LOWESS | Local regression using weighted linear least squares and a 1st degree polynomial model. |
| LOESS | Local regression using weighted linear least squares and a 2nd degree polynomial model. |
| Savitzky-Golay | A generalized moving average with filter coefficients determined by an unweighted linear least-squares regression and a polynomial model of specified degree. The method can accept nonuniform predictor data. |
| RLOWESS | A robust version of ‘lowess’ that assigns lower weight to outliers in the regression. The method assigns zero weight to data outside six mean absolute deviations. |
| RLOESS | A robust version of ‘loess’ that assigns lower weight to outliers in the regression. The method assigns zero weight to data outside six mean absolute deviations. |
3.3. Phenological indicators
Spatiotemporally-explicit knowledge of vegetation phenology is critical to understand the change trend of natural seasonal phenomena and serve for agricultural production and global change studies (Yu et al., 2017; Tang et al., 2015; Ren et al., 2017). In this regard, this module has the capability to estimate multiple phenological indicators using primarily satellite remote sensing data, although likewise other type of time series data could be used. The estimation settings for phenological indicators can be inspected in Fig. 2c. In this step the user can choose among the following phenological metrics (Fig. 5): (1) amplitude (difference between the maximum and the average of the left and right minimum values per season), (2) maximum value (largest value per cycle), (3) day of maximum value (when the largest value per cycle occurs), (4) start of season (SOS), (5) end of season (EOS), (6) seasonal integral (area under the curve between SOS and EOS), and (7) length of season (difference between SOS and EOS). Moreover, DATimeS also provides the user with the freedom of choosing whether or not to incorporate smoothing prior to the parameter estimation. To optimize the provided gap-filling algorithms, this module is recommended to be applied after the interpolation step so that cloud-free composite images are created, and trends become evident for easy phenological metrics derivation. However, it is also possible to go directly to this step.
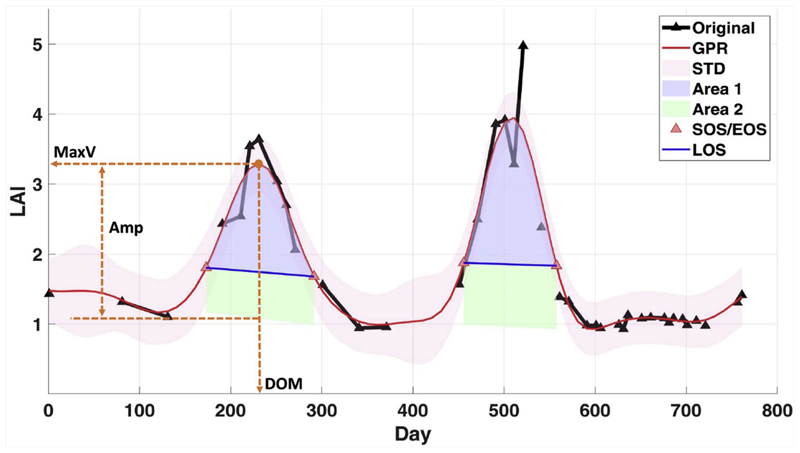
Fig. 5.
Automatic identification of some seasonal patterns computed in DATimeS by using the reconstructed LAI curve (red line) with GPR. Red shade area shows the associated GPR uncertainties (standard deviation). Purple and green colors indicate the areas under the curve between SOS/EOS (red triangles) and the left/right minimum values, respectively. Blue lines show approximately the length of seasons (LOS). Maximum value (MaxV), day of maximum value (DOM) and amplitude (Amp) are represented with orange dashed lines. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
The computational strategy follows multiple steps. When running the phenological module for each pixel within an image it: (1) extracts time series data, (2) identifies automatically individual growing seasons within each year, (3) locate specific points within the growing season (e. g. SOS, EOS, peak), (4) calculate data value and day of year for growing season points of interest, (5) compute integrals and cumulative integrals, and (6) store the estimates in output ENVI or Tiff files.
The determination of the number of seasons (seasonal decomposition) is analogous to previous approaches (Araya et al., 2018; Jönsson and Eklundh, 2004; Hill and Donald, 2003), i.e. making use of local maximum and minimum of the curve to identify the change of state. When three consecutive local minimum, maximum and minimum points are detected, one season is extracted. To be able reducing contributions from undesired artifacts at low frequencies, this search needs to be optimized with specific constraints. In DATimeS, these spurious estimates can be masked using a prominence threshold. The prominence of a peak is the minimum vertical distance that the signal must descend on either side of the peak before either climbing back to a level higher than the peak or reaching an endpoint. Accordingly, peaks not meeting the specified prominence value are discarded in advance as noise. Additionally, users can also discard the minimum/maximum peaks that are very close to each other. When the separation value is greater than zero, DATimeS selects the largest local maximum/minimum and ignores all other local maxima/minima within the specified separation in time.
After the time series decomposition, each individual growing season is analyzed to detect specific phenological events (e.g. SOS and EOS) based on conventional threshold methods, analogous to Jönsson and Eklundh (2004); Lloyd (1990); Delbart et al. (2006); White and Nemani (2006); Wu et al. (2010); Huang et al. (2019). Three different methods have been implemented in DATimeS: (1) seasonal, (2) relative, and (3) absolute amplitude. In the former case, the SOS/EOS are identified where the left/right part of the curve reaches a fraction of the seasonal amplitude along the rising/decaying part of the curve. An example of this method is shown in Fig. 5. The second approach is similar to the previous one, but now a mean amplitude is estimated considering the minimum/maximum values of all seasons. Consequently, the SOS/EOS correspond to dates where the curve reaches a percentage of this relative amplitude. In the latter method, the SOS/EOS is determined when each growing season reaches an absolute value.
3.4. Post-processing
In the post-processing module, the following options are provided: (1) spatial interpolation, and (2) time series animation. The spatial interpolation module offers the option of applying spatial interpolation methods when the earlier-developed phenological indicators maps are not completely spatially resolved. In such case, the phenological metrics estimation becomes impossible due to noisy data, especially in case no temporal gap-filling and smoothing methods have been applied. Then, the post-processing step is recommended to generate continuous maps over space through standard spatial interpolation techniques (linear, cubic, nearest and natural neighbor).
In the animation option, satellite images taken over time are integrated and stitched together as a video, which enables users to visually detect changes, map trends, and quantify differences on the selected area or region. For this purpose, the use of cloud-free composite images, which were previously estimated in the Interpolation module, are preferable since it produces a smooth time lapse of cloud-free land surface phenology.
4. Demonstration cases
4.1. Study area and data
Having described the functioning of DATimeS, in this section we present two experiments making use of the different DATimeS modules. The ROI selected for the study is a crop region in Castile and Leon, in North-West of Spain. The area shown in Fig. 6 was selected as part of a wider validation region of Sensagri H2020 Project (Amin et al., 2018), for which a highly detailed land-cover map is yearly retrieved by using a random forest classifier on satellite imagery time series. The classifier distinguishes between 50 specific crop types, being 35 of them arable crops, 7 are irrigated crops and 8 for permanent crops (Gómez et al., 2018). The scene selected for the demonstration cases is mainly characterized by an intensive dryland agricultural system where the arable land comprises up to 80% of the available area.
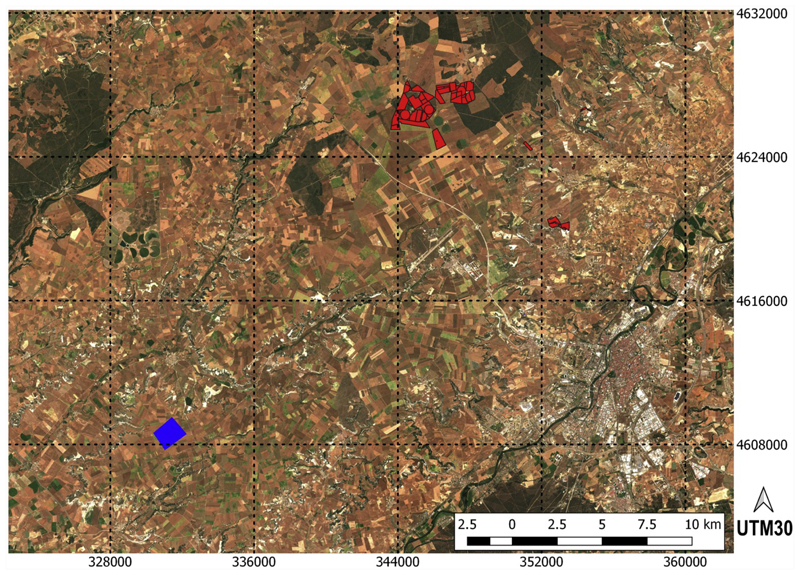
Fig. 6.
RGB image of the crop ROIs in Castile and Leon region, Northwest Iberian peninsula, from Sentinel 2 capture of 2016, June 26th. Pixels inside the blue region are used for the interpolation experiment. Pixels inside red area are used for the phenological indicators analysis between different crops and seasons. (For inter-pretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
For the experiments, we used green leaf area index (LAI) generated from atmospherically corrected S2 imagery using the GPR model developed in the framework of SENSAGRI project (Amin et al., 2018). The time series consists of 127 unevenly spaced and largely cloud-free acquisitions between November 2015 to September 2019.
4.2. Testing interpolation fitting algorithms
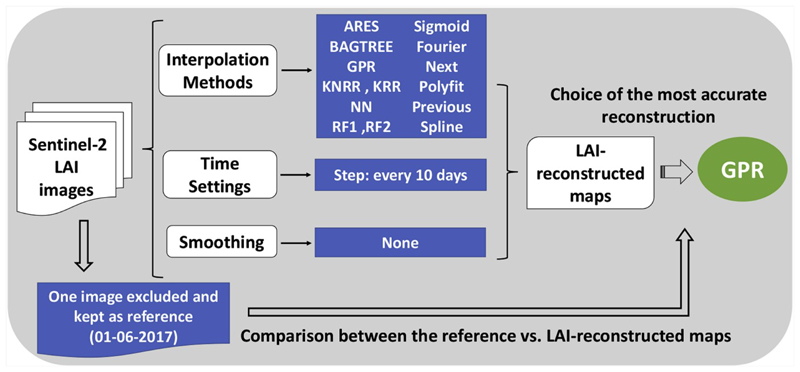
First, we evaluate the performance of multiple fitting algorithms (parametric and non-parametric regressions) in terms of reconstruction effectiveness and processing time. For this experiment we used a region composed essentially of wheat, barley, green peas, forage, potato, sunflower and oats (blue polygon in Fig. 6). The pursued approach is sketched in Fig. 7. First, we kept out one map from the LAI time series to be used as reference for assessment purposes, being the date 01-06-2017. Next, a selection of the most powerful and hence promising interpolation algorithms were run to reconstruct the LAI information on the date of the reference image. Finally, we calculated the goodness-of-fit statistics of reference map vs reconstructed map and also the global and per-pixel processing time performances.
Fig. 7. Schematic diagram representing the processing steps undertaken in the interpolation experiment.
It is important to point out that parametric and non-parametric algorithms have different modeling assumptions. By definition, parametric regression algorithms assume an explicit relationship between response (dependent) and explanatory (independent) variables using a finite number of parameters. On the contrary, for non-parametric regressions the information is derived from the training data without any assumption about their statistical distribution or variable interrelations, making the number of parameters (theoretically) infinite. Parametric models such as linear regression, logistic regression, and harmonic algorithms are typical examples of “learners” with a fixed size of parameters. Conversely, algorithms such as K-nearest neighbor, decision trees, or GPR are considered non-parametric since the number of parameters grows with the size of the training set. Therefore, the statistical assessment measures used in this study are: coefficient of variation R2, root mean square error RMSE and relative RMSE (RRMSE [%]). An overview of validation results and processing time is provided in Table 3.
Table 3. Goodness-of-fit statistics and processing time for the reference vs. LAI-reconstructed map as produced by the gap-filling methods for 17,218 pixels.
| Methods | RMSE | RRMSE [%] | R2 | Time | |
|---|---|---|---|---|---|
| Total (min) | Per pixel (sec) | ||||
| ARES | 0.500 | 19.387 | 0.041 | 25.533 | 0.089 |
| BAGTREE | 0.482 | 18.661 | 0.572 | 263.050 | 0.917 |
| GPR | 0.153 | 5.940 | 0.913 | 23.100 | 0.081 |
| KNRR | 0.522 | 20.216 | 0.137 | 6.883 | 0.024 |
| KRR | 0.187 | 7.230 | 0.826 | 5.450 | 0.019 |
| NN | 0.248 | 9.628 | 0.696 | 771.824 | 2.689 |
| RF1 | 0.341 | 13.199 | 0.836 | 34.049 | 0.119 |
| RF2 | 0.539 | 20.872 | 0.684 | 58.397 | 0.204 |
| Sigmoid | 0.187 | 7.250 | 0.925 | 313.117 | 1.091 |
| Fourier1 | 0.360 | 13.961 | 0.338 | 0.383 | 0.001 |
| Fourier2 | 0.351 | 13.597 | 0.380 | 0.413 | 0.001 |
| Fourier3 | 0.350 | 13.549 | 0.389 | 0.226 | 0.001 |
| Next | 0.539 | 20.872 | 0.684 | 0.317 | 0.001 |
| Polyfit | 0.492 | 19.056 | 0.002 | 0.467 | 0.002 |
| Previous | 0.472 | 18.283 | 0.849 | 0.333 | 0.001 |
| Spline | 0.158 | 6.121 | 0.896 | 0.333 | 0.001 |
The map reconstruction results suggest the following:
The error estimates (RMSE, RRMSE) provide a description of the algorithms’ image reconstruction capability. The most accurate reconstruction was obtained with GPR with a relative error of 5.9% and a R2 of 0.913. The second best reconstruction was obtained with the spline interpolation. The following top-performing methods are KRR and then sigmoid; the rest of methods perform substantially poorer. A remark hereby is that a perfect reconstruction is virtually impossible to achieve, not only due to the sources of noisiness in original data, but also because of the smoothing effect that the fitting methods have on the original series (Atkinson et al., 2012).
The recorded processing time indicates that the Fourier and the conventional interpolation methods are extremely fast; processing the subset took about half a minute. Conversely, the accurate sigmoid took significantly longer, being about one thousand times slower.
Taking both accuracy and processing speed into account, GPR and spline interpolations turn out to be the most efficient interpolators, with GPR more accurate but spline faster by a factor of 70.
Based on the above results, GPR resulted as the preferred method for gap-filling purposes. Besides, it is the only method that also provides associated uncertainties. We therefore used this method for subsequent calculation of the phenological indicators to fill up some remaining missing values.
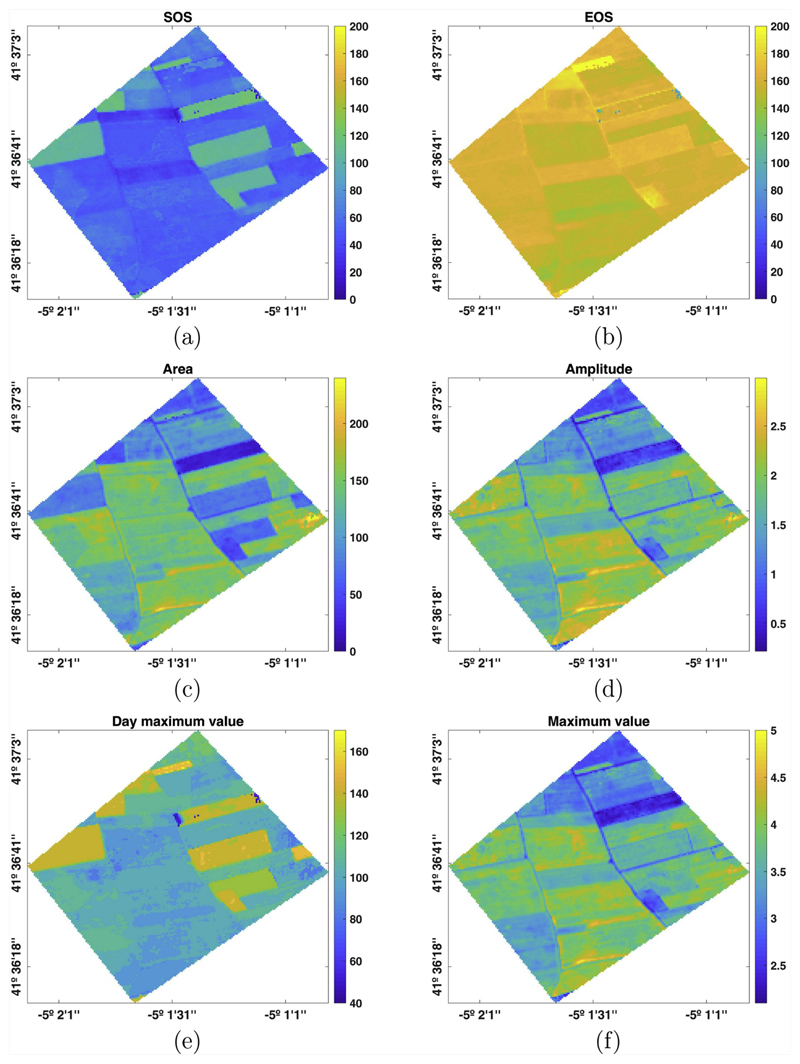
The DATimeS maps of the phenological indicators for the year 2017 are shown in Fig. 8. The field-scale consistency of the result can be easily appreciated by visually inspecting the results. In the SOS map it can be clearly viewed that some crops started their growing season later. The EOS map is consistent as well, leading to homogeneous parcels in terms of length of season. Also, the day corresponding to the maximum value well resembles the pattern of the start of season. Probably of more interest are the indicators amplitude, maximum value and area. These indicators are usually related to crop’s productivity (Zhang and Zhang, 2016). Also within-field variations can be observed in these maps, which is extremely useful for smart farming applications (Das et al., 2019), e.g. for precision fertilizing.
Fig. 8.
Maps of phenological indicators estimated by using reconstructed Sentinel-2 LAI images with GPR. Spatial interpolation was only applied for pixels with no strong seasonal signal.
4.3. Phenological metrics between different crops and seasons
Keeping the most accurate interpolation method obtained in Section 4.2 in mind, in this second case study we use GPR to achieve a spatiotemporal reconstruction LAI maps and compare the phenological indicators of specific crop types throughout multiple seasons. The region chosen for the study corresponds to a dryland farming area containing crops of barley, beet, potato, rape and wheat (red polygons in Fig. 6).
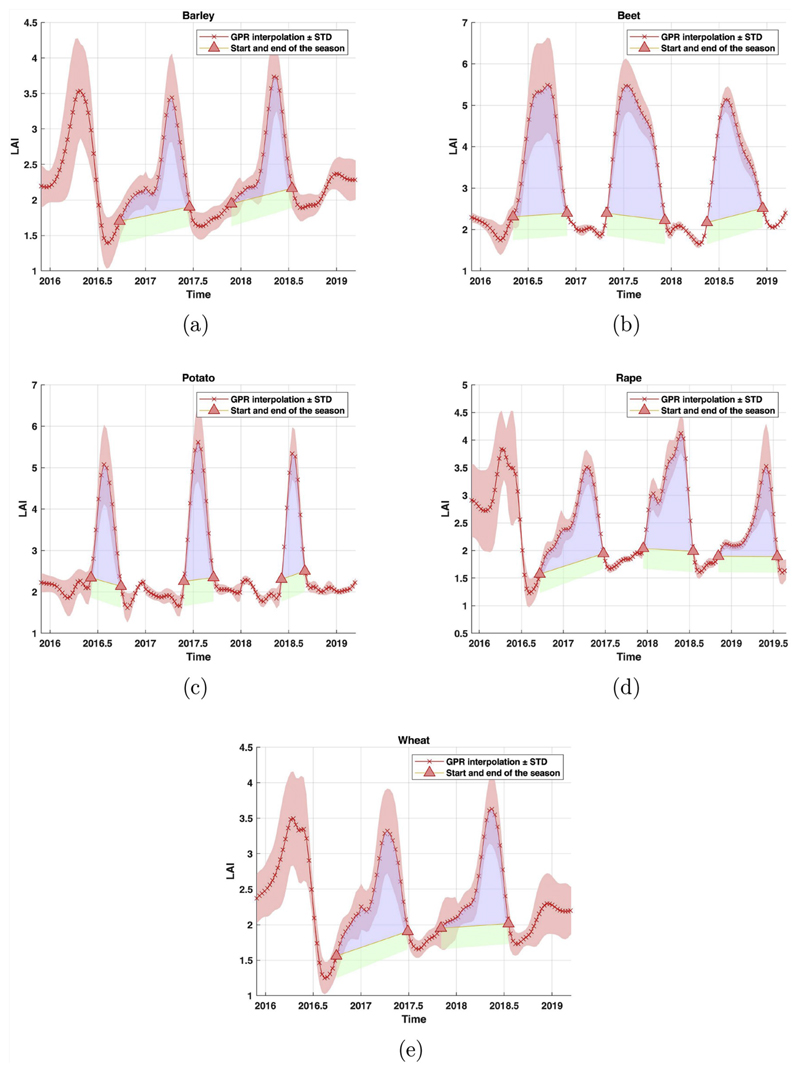
The main steps of the experiment have been the following: (1) training an independent GPR model for each pixel of the ROI using its corresponding LAI time series, (2) providing interpolated LAI values with its associated uncertainty estimates for each input time t (every 10 days) and pixel, subsequently (3) estimating the mean LAI time series and their variance using the interpolated values of pixels belonging to the same crop type, and finally (4) extracting the phenological indicators for each crop and season. The results obtained for the five aforementioned crop types are shown graphically in Fig. 9 and reported numerically in Table 4.
Fig. 9.
Modeling LAI time series of different crop types by using GPR method. The green and blue colors represent the area under the curve between SOS and EOS. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.
Table 4. The phenological metrics derived from the mean LAI of different crop types (wheat, barley, colza, beet and potato) between November 2015 to September 2019.
| Crop type | Season | SOS | EOS | LOS | DOM | Max Value | Amp | Area |
|---|---|---|---|---|---|---|---|---|
| Wheat | 1 | 273 (29-09-2016) | 180 (29-06-2017) | 273 | 102 (12-04-2017) | 3.320 | 1.869 | 268.065 |
| 2 | 307 (03-11-2017) | 200 (19-07-2018) | 258 | 137 (17-05-2018) | 3.627 | 1.936 | 231.180 | |
| Barley | 1 | 268 (24-09-2016) | 169 (18-06-2017) | 267 | 102 (12-04-2017) | 3.439 | 1.928 | 234.089 |
| 2 | 329 (25-11-2017) | 196 (15-07-2018) | 232 | 127 (07-05-2018) | 3.733 | 1.975 | 198.765 | |
| Rape | 1 | 264 (20-09-2016) | 175 (24-06-2017) | 276 | 102 (12-04-2017) | 3.502 | 2.053 | 299.794 |
| 2 | 348 (14-12-2017) | 200 (19-07-2018) | 217 | 147 (27-05-2018) | 4.121 | 2.483 | 339.334 | |
| 3 | 309 (05-11-2018) | 200 (19-07-2019) | 256 | 152 (01-06-2019) | 3.524 | 1.920 | 221.604 | |
| Beet | 1 | 126 (05-05-2016) | 333 (28-11-2016) | 207 | 258 (14-09-2016) | 5.487 | 3.691 | 507.208 |
| 2 | 119 (29-04-2017) | 341 (07-12-2017) | 222 | 192 (11-07-2017) | 5.464 | 3.717 | 581.870 | |
| 3 | 137 (17-05-2018) | 350 (16-12-2018) | 213 | 207 (26-07-2018) | 5.126 | 3.278 | 441.477 | |
| Potato | 1 | 158 (06-06-2016) | 273 (29-09-2016) | 115 | 208 (26-07-2016) | 5.078 | 3.343 | 241.555 |
| 2 | 148 (28-05-2017) | 261 (18-09-2017) | 113 | 202 (21-07-2017) | 5.614 | 3.900 | 277.928 | |
| 3 | 156 (05-06-2018) | 245 (02-09-2018) | 90 | 197 (16-07-2018) | 5.340 | 3.456 | 195.900 |
Although at first glance the temporal evolution of mean LAI profiles seems to indicate that each crop presents almost identical patterns throughout the multiple seasons, a more careful analysis of phenological indicators reveals that meaningful changes took place. For wheat, similar to barley, the dates of SOS/EOS determined from season 1 occurs roughly one month before those of season 2. They further show a reduction in LOS of about 15 and 35 days, respectively. Consequently, the areas derived from the profiles of season 2 are approximately 15% lower than those of season 1. As for potato, mean LAI shows good agreement in SOS over the different seasons. Conversely, season 3 presents a slight decrease in LOS of around 24 days. Also noteworthy is that season 2 stands out for being the year with the highest values of area (277.9 [m2/m2d]), LAI (5.6 [m2/m2])) and amplitude (3.9 [m2/m2])). For rape, the phenological metrics derived from the LAI time series changed significantly across the 3 seasons, specially in SOS with values ranging from 264 to 348 DOY. This crop also exhibits the shortest growing season (217 days) and the largest area (339.3) at season 2. Finally, the temporal course of beet shows good agreement in SOS/EOS, with differences less than 13%. Contrarily, a substantial mismatch exists in DOM where the fluctuation of measured value lies between 192 and 258 DOY.
The explanation of the seasonal variability of crop temporal patterns is not straightforward as they are deeply related to the weather evolution during each crop season in terms of temperature fluctuations and precipitation events. Effects from climate change are leading to a general increase of temperature and a reduction of the number of rain events, with extreme precipitations always more frequent and severe. Because of the sensitivity of agriculture to the variations of weather and climate conditions, they are likely to have substantial direct and indirect effects on crop production and yield. Therefore, easy monitoring of changes in vegetation phenology becomes critical to assess alteration of land ecosystem productivity and seasonal variations.
5. Discussion
Having outlined the key modules of DATimeS, some general reflections are worth mentioning. A first aspect is the streamlined, modular processing of the toolbox. The required steps are essentially loading the time series, drawing a subset, selecting the interpolation to run and choosing the date to reconstruct an image. The data filling does not have to be restricted to LAI or another vegetation property. Phenological studies are typically carried out with spectral indicators such as NDVI, but in a broader context, any kind of continuous data can be processed, including proximal sensing time series (Guo et al., 2019; Marino and Alvino, 2014) coming from flux towers (Gamon, 2015)), land surface temperature (Li et al., 2013) or microwave acquisitions (Marzahn et al., 2012).
Besides, the inclusion of machine learning fitting methods provides a benchmark as opposed to conventional gap-filling methods. Not only may it lead to more accurate reconstructions (Table 3), it is also adaptive towards unevenly spaced data over multiple seasons. Particularly GPR is of interest, as its associated uncertainty estimates provides per-pixel information of the gap-filling confidence. Typically, the longer the gap between two consecutive input samples, the higher the uncertainty. However, the provided gap-filling techniques offer different performances. Each method has its own advantages and drawbacks, which depend strongly on the characteristics of the input time series (Atzberger and Eilers, 2011; Zeng et al., 2020), i.e. a method that fits well with some data can be unsuited for a different set of data points. This implies that GPR is not necessary top performing in all situations, and in other situations alternative gap-filling methods could achieve more efficient performances. For that reason, it is recommended to analyze first the behaviour of the fitting methods on single pixels (e.g., as detailed in section 4.2). For instance, conventional harmonic analysis is only suitable for stationary data, and without aperiodic extreme behaviors. Contrarily, MLRA algorithms are effective to account for the amplitude and phase time variability.
Concerning the appropriate length of time series, even if there is no limit of amount of data, the accuracy of the time series reconstruction increases with the data size. The main limitation of the interpolation module is the high time consuming and computational cost of specific algorithms; especially NN but also the double logistic curve.
The toolbox is expected to be practical for a wide range of users interested in detecting vegetation phenology. Specifically, a comprehensive familiarity of crop dynamics is essential in agricultural applications whereby the phenological indicators can be related to essential sources of information including start of senescing, harvest day, productivity estimates, irrigation management, nutrient management, health management, yield prediction and crop type mapping (Alam et al., 2012; Jayawardhana and Chathurange, 2016). An example of such variability has been provided in section 4.3 (Table 4 and Fig. 9), where fluctuations of a specific crop are evident along consecutive seasons. They are likely generated by changes in precipitation, insect pests, plant diseases, or even by a changing climate. Nonetheless, these are complex dynamics that need to be studied further.
Finally, despite that DATimeS is written in MATLAB, additional methodologies as multi-sensor fusion (Pipia et al., 2019) based on open-source Python package (GPy, 2012) (Warmerdam, 2008) will be added to the Matlab-based GUI in the future release. For that, a basic Python distribution will be also included in the installing package.
6. Conclusions and future work
The presented DATimeS is a stand-alone toolbox for time series analysis that brings together versatile MLRA algorithms and conventional interpolation techniques (e.g., harmonic analyses, double logistic curve, among others). DATimeS aims to be a generic and innovative time series toolbox that provides sufficient flexibility to capture the principal vegetation features without imposing too heavy computational or inferential burdens, for gap-filling and subsequent phenological analysis. In comparison to other GUI times series toolboxes, DATimeS is state of the art, through the: (1) ability to process unevenly spaced satellite image time series, (2) possibility to select over twelve different machine learning fitting methods for time series prediction (some methods include associated uncertainties, e.g. GPR), and (3) provision and analysis of phenological indicators over multiple growing seasons. The preliminary assessment of the multiple interpolation methods using Sentinel-2 LAI time series demonstrated the potential of GPR as optimum algorithm to successfully reconstruct vegetation indices and retrieve reliable phenological indicators.
At the same time, DATimeS keeps being improved and extended in various ways. The following upgrades are in the pipeline: new supported image formats (e.g. NetCDF and the native format of Sentinel imagery JPEG2000), more phenological indicators (e.g. growth rate between SOS and maximum value for each individual season), aggregated processing on a per-field scale when a land cover map is loaded, and latest tools related to harvest trends and automatic disturbances detection. We also foresee that more conventional and latest gap-filling methods will be implemented, such as Whittaker smoother (Eilers, 2003) and Multi-Output Gaussian Process regression (MOGP) (Álvarez et al., 2012) The latter is a cutting-edge machine learning tool which is able to stress the dependencies among any kind of multiple but related data collections. It could be beneficial to establish the synergy between vegetation descriptors from multiple sensors, e.g. fusing Sentinel-1 with Sentinel-2 data (Pipia et al., 2019). We also aim to provide DATimeS in batch processing mode as alternative to the Matlab-based GUI. First steps towards reaching these goals are already underway. Finally, DATimeS is made freely available to registered users for scientific purposes. It can be freely downloaded from the ARTMO web page: http://artmotoolbox.com.
Supplementary Material
Acknowledgements
The authors acknowledge constructive comments provided by the reviewers that helped to improve the quality of the manuscript. This work was supported by the European Research Council (ERC) under the ERC2017-STG SENTIFLEX project (Grant Agreement 755617). The research leading to these results has received funding from European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement 730074.
Footnotes
Software availability
Software name: DATimeS (Decomposition and Analysis of Time Series software)
Developer: Santiago Belda (santiago.belda@uv.es)
Institution: Image Processing laboratory (IPL), University of Valencia, Spain
Year first official release: 2019
Hardware requirements: PC
System requirements: Microsoft Windows
Program language: Standalone image processing GUI toolbox written in MATLAB
Program size: 1.73 GB
Availability: http://artmotoolbox.com
License: Free for non-commercial use
Documentation and support for users: Manual and tutorial with test data
Declaration of interest
None.
References
- Akima H. A new method of interpolation and smooth curve fitting based on local procedures. J ACM. 1970;17:589–602. doi: 10.1145/321607.321609. [DOI] [Google Scholar]
- Akima H. A method of bivariate interpolation and smooth surface fitting based on local procedures. Commun ACM. 1974;17:18–20. doi: 10.1145/360767.360779. [DOI] [Google Scholar]
- Alam MM, Strandgard MN, Brown MW, Fox JC. Improving the productivity of mechanised harvesting systems using remote sensing. Aust For. 2012;75:238–245. doi: 10.1080/00049158.2012.10676408. [DOI] [Google Scholar]
- Álvarez MA, Rosasco L, Lawrence ND. Kernels for vector-valued functions: a review. Foundations and Trends in Machine Learning. 2012;4:195. doi: 10.1561/2200000036. [DOI] [Google Scholar]
- Amin E, Verrelst J, Rivera-Caicedo JP, Pasqualotto N, Delegido J, Verdú AR, Moreno J. The Sensagri Sentinel-2 LAI green and brown product: from algorithm development towards operational mapping; IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium; 2018. pp. 1822–1825. [Google Scholar]
- Araya S, Ostendorf B, Lyle G, Lewis M. Cropphenology: an R package for extracting crop phenology from time series remotely sensed vegetation index imagery. Ecol Inf. 2018;46:45–56. doi: 10.1016/j.ecoinf.2018.05.006. [DOI] [Google Scholar]
- Arundel J, Winter S, Gui G, Keatley M. A web-based application for beekeepers to visualise patterns of growth in floral resources using MODIS data. Environ Model Software. 2016;83:116–125. doi: 10.1016/j.envsoft.2016.05.010. [DOI] [Google Scholar]
- Atkinson PM, Jeganathan C, Dash J, Atzberger C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Rem Sens Environ. 2012;123:400–417. doi: 10.1016/j.rse.2012.04.001. [DOI] [Google Scholar]
- Atzberger C. Advances in remote sensing of agriculture: context description, existing operational monitoring systems and major information needs. Rem Sens. 2013;5:949–981. [Google Scholar]
- Atzberger C, Eilers PH. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. International Journal of Digital Earth. 2011;4:365–386. [Google Scholar]
- Beck PS, Atzberger C, Høgda KA, Johansen B, Skidmore AK. Improved monitoring of vegetation dynamics at very high latitudes: a new method using MODIS NDVI. Rem Sens Environ. 2006;100:321–334. doi: 10.1016/j.rse.2005.10.021. [DOI] [Google Scholar]
- Berra EF, Gaulton R, Barr S. Assessing spring phenology of a temperate woodland: a multiscale comparison of ground, unmanned aerial vehicle and Landsat satellite observations. Rem Sens Environ. 2019;223:229–242. doi: 10.1016/j.rse.2019.01.010. [DOI] [Google Scholar]
- Broich M, Huete A, Paget M, Ma X, Tulbure M, Coupe NR, Evans B, Beringer J, Devadas R, Davies K, Held A. A spatially explicit land surface phenology data product for science, monitoring and natural resources management applications. Environ Model Software. 2015;64:191–204. doi: 10.1016/j.envsoft.2014.11.017. [DOI] [Google Scholar]
- Camps-Valls G, Bruzzone L, Rojo-Alvarez JL, Melgani F. Robust support vector regression for biophysical variable estimation from remotely sensed images. Geosci Rem Sens Lett IEEE. 2006;3:339–343. doi: 10.1109/LGRS.2006.871748. [DOI] [Google Scholar]
- Chen J, Boccelli DL. Real-time forecasting and visualization toolkit for multi-seasonal time series. Environ Model Software. 2018;105:244–256. doi: 10.1016/j.envsoft.2018.03.034. [DOI] [Google Scholar]
- Das V, Sharma S, Kaushik A, et al. Views of Irish farmers on smart farming technologies: an observational study. Agri Engineering. 2019;1:164–187. [Google Scholar]
- Delbart N, Toan TL, Kergoat L, Fedotova V. Remote sensing of spring phenology in boreal regions: a free of snow-effect method using NOAA-AVHRR and SPOT-VGT data (1982-2004) Rem Sens Environ. 2006;101:52–62. doi: 10.1016/j.rse.2005.11.012. [DOI] [Google Scholar]
- D’Odorico P, Gonsamo A, Gough CM, Bohrer G, Morison J, Wilkinson M, Hanson PJ, Gianelle D, Fuentes JD, Buchmann N. The match and mismatch between photosynthesis and land surface phenology of deciduous forests. Agric For Meteorol. 2015;214-215:25–38. doi: 10.1016/j.agrformet.2015.07.005. [DOI] [Google Scholar]
- Dong Y, Peng C. Principled missing data methods for researchers. Springer Plus. 2013;2(1):1–17. doi: 10.1186/2193-1801-2-222. 222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eerens H, Haesen D, Rembold F, Urbano F, Tote C, Bydekerke L. Image time series processing for agriculture monitoring. Environ Model Software. 2014;53:154–162. doi: 10.1016/j.envsoft.2013.10.021. [DOI] [Google Scholar]
- Eilers PHC. A perfect smoother. Anal Chem. 2003;75:3631–3636. doi: 10.1021/ac034173t. [DOI] [PubMed] [Google Scholar]
- Frantz D. Force-landsat + Sentinel-2 analysis ready data and beyond. Rem Sens. 2019;11 doi: 10.3390/rs11091124. [DOI] [Google Scholar]
- Gamon JA. Reviews and syntheses: optical sampling of the flux tower footprint. Biogeosciences. 2015;12:4509–4523. doi: 10.5194/bg-12-4509-2015. [DOI] [Google Scholar]
- Gómez V, Medina V, Bengoa J, García D. Accuracy assessment of a 122 classes land cover map based on Sentinel-2, Landsat 8 and Deimos-1 images and ancillary data; IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium; 2018. pp. 5453–5456. [Google Scholar]
- Gong Z, Kawamura K, Ishikawa N, Goto M, Wulan T, Alateng D, Yin T, Ito Y. MODIS normalized difference vegetation index (NDVI) and vegetation phenology dynamics in the inner Mongolia grassland. Solid Earth. 2015;6:1185–1194. doi: 10.5194/se-6-1185-2015. [DOI] [Google Scholar]
- GPy. GPy: a Gaussian process framework in python. 2012. http://github.com/SheffieldML/GPy .
- Guo Y, Zhou Y, qing Zhou L, Liu T, gang Wang L, zheng Cheng Y, He J, qing Zheng G. Using proximal sensor data for soil salinity management and mapping. Journal of Integrative Agriculture. 2019;18:340–349. doi: 10.1016/S2095-3119(18)61937-9. [DOI] [Google Scholar]
- Gutman G, Masek JG. Long-term time series of the Earth’s land-surface observations from space. Int J Rem Sens. 2012;33:4700–4719. doi: 10.1080/01431161.2011.638341. [DOI] [Google Scholar]
- Hamblim W, Christiansen E. Earth Dynamic System. Pearson; 2010. [Google Scholar]
- Hill MJ, Donald GE. Estimating spatio-temporal patterns of agricultural productivity in fragmented landscapes using AVHRR NDVI time series. Rem Sens Environ. 2003;84:367–384. doi: 10.1016/S0034-4257(02)00128-1. [DOI] [Google Scholar]
- Hird JN, McDermid GJ. Noise reduction of NDVI time series: an empirical comparison of selected techniques. Rem Sens Environ. 2009;113:248–258. doi: 10.1016/j.rse.2008.09.003. [DOI] [Google Scholar]
- Huang X, Liu J, Zhu W, Atzberger C, Liu Q. The optimal threshold and vegetation index time series for retrieving crop phenology based on a modified dynamic threshold method. Rem Sens. 2019;11 doi: 10.3390/rs11232725. [DOI] [Google Scholar]
- Hufkens K, Basler D, Melaas TME, Richardson A. An integrated phenology modelling framework in R. Methods in Ecology and Evolution. 2018;9:1276–1285. doi: 10.1111/2041-210X.12970. [DOI] [Google Scholar]
- Jakimow B, van der Linden S, Thiel F, Frantz D, Hostert P. Visualizing and labeling dense multi-sensor earth observation time series: the EO time series viewer. Environ Model Software. 2020:104631. doi: 10.1016/j.envsoft.2020.104631. [DOI] [Google Scholar]
- Jayawardhana W, Chathurange V. Extraction of agricultural phenological parameters of Sri Lanka using MODIS, NDVI time series data; International Conference of Sabaragamuwa University of Sri Lanka 2015 (ICSUSL 2015); 2016. pp. 235–241. Procedia Food Science. [DOI] [Google Scholar]
- Jönsson J, Eklundh L. Timesat - a program for analysing time-series of satellite sensor data. Comput Geosci. 2004;30:833–845. doi: 10.1016/j.cageo.2004.05.006. [DOI] [Google Scholar]
- Jönsson P, Cai Z, Melaas E, Friedl MA, Eklundh L. A method for robust estimation of vegetation seasonality from Landsat and Sentinel-2 time series data. Rem Sens. 2018;10 doi: 10.3390/rs10040635. [DOI] [Google Scholar]
- Julien Y, Sobrino JA. Global land surface phenology trends from GIMMS database. Int J Rem Sens. 2009;30:3495–3513. doi: 10.1080/01431160802562255. [DOI] [Google Scholar]
- Kandasamy S, Baret F, Verger A, Neveux P, Weiss M. A comparison of methods for smoothing and gap filling time series of remote sensing observations - application to MODIS LAI products. Biogeosciences. 2013;10:4055–4071. doi: 10.5194/bg-10-4055-2013. [DOI] [Google Scholar]
- Kuenzer C, Dech S, Wagner W. Remote sensing time series revealing land surface dynamics. Remote Sensing Time Series. 2015;22 doi: 10.1007/978-3-319-15967-6. [DOI] [Google Scholar]
- Lazaro-Gredilla M, Titsias MK, Verrelst J, Camps-Valls G. Retrieval of biophysical parameters with heteroscedastic Gaussian processes. Geosci Rem Sens Lett IEEE. 2014;11:838–842. doi: 10.1109/LGRS.2013.2279695. [DOI] [Google Scholar]
- Lepot M, Aubin JB, Clemens FH. Interpolation in time series: an introductive overview of existing methods, their performance criteria and uncertainty assessment. Water. 2017;9 doi: 10.3390/w9100796. [DOI] [Google Scholar]
- Li H, Wan W, Fang Y, Zhu S, Chen X, Liu B, Hong Y. A Google Earth Engine-enabled software for efficiently generating high-quality user-ready Landsat mosaic images. Environ Model Software. 2019;112:16–22. doi: 10.1016/j.envsoft.2018.11.004. [DOI] [Google Scholar]
- Li ZL, Tang BH, Wu H, Ren H, Yan G, Wan Z, Trigo IF, Sobrino JA. Satellite-derived land surface temperature: current status and perspectives. Rem Sens Environ. 2013;131:14–37. doi: 10.1016/j.rse.2012.12.008. [DOI] [Google Scholar]
- Liang L. Reference Module in Earth Systems and Environmental Sciences. Elsevier; 2019. Phenology. [DOI] [Google Scholar]
- Lloyd D. A phenological classification of terrestrial vegetation cover using shortwave vegetation index imagery. Int J Rem Sens. 1990;11:2269–2279. doi: 10.1080/01431169008955174. [DOI] [Google Scholar]
- Mariethoz G, McCabe M, Renard P. Spatiotemporal reconstruction of gaps in multivariate fields using the direct sampling approach. Water Resour Res. 2012;48 doi: 10.1029/2012WR012115. [DOI] [Google Scholar]
- Marino S, Alvino A. Proximal sensing and vegetation indices for site-specific evaluation on an irrigated crop tomato. European Journal of Remote Sensing. 2014;47:271–283. doi: 10.5721/EuJRS20144717. [DOI] [Google Scholar]
- Marzahn P, Rieke-Zapp D, Ludwig R. Assessment of soil surface roughness statistics for microwave remote sensing applications using a simple photogrammetric acquisition system. ISPRS J Photogrammetry Remote Sens. 2012;72:80–89. doi: 10.1016/j.isprsjprs.2012.06.005. [DOI] [Google Scholar]
- Mulla D. Twenty five years of remote sensing in precision agriculture: key advances and remaining knowledge gaps. Biosyst Eng. 2013;114:358–371. doi: 10.1016/j.biosystemseng.2012.08.009. [DOI] [Google Scholar]
- Olivier R, Hanqiang C. Nearest neighbor value interpolation. Int J Adv Comput Sci Appl. 2012;3 doi: 10.14569/ijacsa.2012.030405. [DOI] [Google Scholar]
- Pipia L, Muñoz-Marí J, Amin E, Belda S, Camps-Valls G, Verrelst J. Fusing optical and SAR time series for LAI gap filling with multioutput Gaussian processes. Rem Sens Environ. 2019;235:111452. doi: 10.1016/j.rse.2019.111452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in FORTRAN; the Art of Scientific Computing. second ed. Cambridge University Press; New York, NY, USA: 1993. [Google Scholar]
- Pricope N, Mapes K, Woodward K. Remote sensing of human environment interactions in global change research: a review of advances, challenges and future directions. Rem Sens. 2019;11 doi: 10.3390/rs11232783. [DOI] [Google Scholar]
- Ramachandran B, Justice C, Abrams M. Land Remote Sensing and Global Environmental Change. Vol. 11 Springer; New York: 2011. [Google Scholar]
- Rasmussen C, Williams C. Gaussian Processes for Machine Learning. The MIT Press; 2006. [Google Scholar]
- Reed B, Schwartz M, Xiao X. Remote sensing phenology: status and the way forward. Phenology of Ecosystems Processes. 2009;231 doi: 10.1007/978-1-4419-0026-5-10. [DOI] [Google Scholar]
- Ren S, Chen X, An S. Assessing plant senescence reflectance index-retrieved vegetation phenology and its spatiotemporal response to climate change in the inner Mongolian grassland. Int J Biometeorol. 2017;61:601–612. doi: 10.1007/s00484-016-1236-6. [DOI] [PubMed] [Google Scholar]
- Rezaei EE, Siebert S, Ewert F. Climate and management interaction cause diverse crop phenology trends. Agric For Meteorol. 2017;233:55–70. doi: 10.1016/j.agrformet.2016.11.003. [DOI] [Google Scholar]
- Richardson A, Keenan T, Migliavacca M, Ryu Y, Sonnentag O, Toomey M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric For Meteorol. 2013;169:156–173. [Google Scholar]
- Richardson AD, Braswell BH, Hollinger DY, Jenkins JP, Ollinger SV. Near-surface remote sensing of spatial and temporal variation in canopy phenology. Ecol Appl. 2009;19:1417–1428. doi: 10.1890/08-2022.1. [DOI] [PubMed] [Google Scholar]
- Roerink GJ, Menenti M, Verhoef W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int J Rem Sens. 2000;21:1911–1917. doi: 10.1080/014311600209814. [DOI] [Google Scholar]
- Sakamoto T, Yokozawa M, Toritani H, Shibayama M, Ishitsuka N, Ohno H. A crop phenology detection method using time-series MODIS data. Rem Sens Environ. 2005;96:366–374. doi: 10.1016/j.rse.2005.03.008. [DOI] [Google Scholar]
- Schwartz M. Phenology: an Integrative Environmental Science. Vol. 2. Springer; Netherlands: 2013. [DOI] [Google Scholar]
- Smola AJ, Schölkopf B. A tutorial on support vector regression. Stat Comput. 2004;14:199–222. doi: 10.1023/B:STCO.0000035301.49549.88. [DOI] [Google Scholar]
- Sobrino J, Julien Y. Global trends in NDVI-derived parameters obtained from GIMMS data. Int J Rem Sens. 2011;32:4267–4279. doi: 10.1080/01431161.2010.486414. [DOI] [Google Scholar]
- Tan B, Morisette JT, Wolfe RE, Gao F, Ederer GA, Nightingale J, Pedelty JA. An enhanced TIMESAT algorithm for estimating vegetation phenology metrics from MODIS data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. 2011;4:361–371. doi: 10.1109/JSTARS.2010.2075916. [DOI] [Google Scholar]
- Tang H, Li Z, Zhu Z, Chen B, Zhang B, Xin X. Variability and climate change trend in vegetation phenology of recent decades in the greater Khingan mountain area, northeastern China. Rem Sens. 2015;7:11914–11932. doi: 10.3390/rs70911914. [DOI] [Google Scholar]
- Tang J, Körner C, Muraoka H, Piao S, Shen M, Thackeray S, Yang X. Emerging opportunities and challenges in phenology: a review. Ecosphere. 2016;7 [Google Scholar]
- Taylor S. pyphenology: a python framework for plant phenology modelling. Journal of Open Source Software. 2018;3:827. doi: 10.21105/joss.00827. [DOI] [Google Scholar]
- Thayananthan A, Navaratnam R, Stenger B, Torr PHS, Cipolla R. In: Computer Vision - ECCV 2006. Leonardis A, Bischof H, Pinz A, editors. Springer Berlin Heidelberg; Berlin, Heidelberg: 2006. Multivariate relevance vector machines for tracking; pp. 124–138. [Google Scholar]
- Udelhoven T. Timestats: a software tool for the retrieval of temporal patterns from global satellite archives. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing. 2011;4:310–317. doi: 10.1109/JSTARS.2010.2051942. [DOI] [Google Scholar]
- Verbesselt J, Hyndman R, Newnham G, Culvenor D. Detecting trend and seasonal changes in satellite image time series. Rem Sens Environ. 2010;114:106–115. doi: 10.1016/j.rse.2009.08.014. [DOI] [Google Scholar]
- Verrelst J, Camps-Valls G, Munoz-Marí J, Rivera JP, Veroustraete F, Clevers JG, Moreno J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties - a review. ISPRS J Photogrammetry Remote Sens. 2015;108:273–290. doi: 10.1016/j.isprsjprs.2015.05.005. [DOI] [Google Scholar]
- Verrelst J, Malenovskŷ Z, Van der Tol C, Camps-Valls G, Gastellu-Etchegorry JP, Lewis P, North P, Moreno J. Quantifying vegetation biophysical variables from imaging spectroscopy data: a review on retrieval methods. Surv Geophys. 2019;40:589–629. doi: 10.1007/s10712-018-9478-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verrelst J, Rivera J, Alonso L, Moreno J. ARTMO: an automated radiative transfer models operator toolbox for automated retrieval of biophysical parameters through model inversion; Proceedings of 7th EARSeL Workshop on Imaging Spectrometry; 2011. [Google Scholar]
- Verrelst J, Rivera JP, Moreno J, Camps-Valls G. Gaussian processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. ISPRS J Photogrammetry Remote Sens. 2013;86:157–167. doi: 10.1016/j.isprsjprs.2013.09.012. [DOI] [Google Scholar]
- Verrelst J, Romijn E, Kooistra L. Mapping vegetation density in a heterogeneous river floodplain ecosystem using pointable CHRIS/PROBA data. Rem Sens. 2012;4:2866–2889. doi: 10.3390/rs4092866. [DOI] [Google Scholar]
- Warmerdam F. The Geospatial Data Abstraction Library. Open Source Approaches in Spatial Data Handling. 2008;2:87–104. doi: 10.1007/978-3-540-74831-1_5. https://gdal.org . [DOI] [Google Scholar]
- Weiss DJ, Atkinson PM, Bhatt S, Mappin B, Hay SI, Gething PW. An effective approach for gap-filling continental scale remotely sensed time-series. ISPRS J Photogrammetry Remote Sens. 2014;98:106–118. doi: 10.1016/j.isprsjprs.2014.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White MA, De Beurs KM, Didan K, Inouye DW, Richardson AD, Jensen OP, O’Keefe J, Zhang G, Nemani RR, Van Leeuwen WJD, Brown JF, et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982 to 2006. Global Change Biol. 2009;15:2335–2359. doi: 10.1111/j.1365-2486.2009.01910.x. [DOI] [Google Scholar]
- White MA, Hoffman F, Hargrove WW, Nemani RR. A global framework for monitoring phenological responses to climate change. Geophys Res Lett. 2005;32 [Google Scholar]
- White MA, Nemani RR. Real-time monitoring and short-term forecasting of land surface phenology. Rem Sens Environ. 2006;104:43–49. doi: 10.1016/j.rse.2006.04.014. [DOI] [Google Scholar]
- Wu Wb, Yang P, Tang Hj, Zhou Qb, Chen Zx, Shibasaki R. Characterizing spatial patterns of phenology in cropland of China based on remotely sensed data. Agric Sci China. 2010;9:101–112. doi: 10.1016/S1671-2927(09)60073-0. [DOI] [Google Scholar]
- Yu L, Liu T, Bu K, Yan F. Monitoring the long term vegetation phenology change in northeast China from 1982 to 2015. Sci Rep. 2017;7 doi: 10.1038/s41598-017-14918-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng L, Wardlow BD, Xiang D, Hu S, Li D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Rem Sens Environ. 2020;237:111511. doi: 10.1016/j.rse.2019.111511. [DOI] [Google Scholar]
- Zhang X, Zhang Q. Monitoring interannual variation in global crop yield using long-term AVHRR and MODIS observations. ISPRS J Photogrammetry Remote Sens. 2016;114:191–205. doi: 10.1016/j.isprsjprs.2016.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao B, Yan Y, Guo H, He M, Gu Y, Li B. Monitoring rapid vegetation succession in estuarine wetland using time series MODIS-based indicators: an application in the Yangtze river delta area. Ecol Indicat. 2009;9:346–356. doi: 10.1016/j.ecolind.2008.05.009. [DOI] [Google Scholar]
- Zhou J, Jia L, Hu G, Menenti M. Evaluation of harmonic analysis of time series (HANTS): impact of gaps on time series reconstruction; Second International Workshop on Earth Observation and Remote Sensing Applications; 2012. [DOI] [Google Scholar]
- Zhou J, Jia L, Hu G, Menenti M. Reconstruction of global MODIS NDVsI time series: performance of harmonic analysis of time series (HANTS) Rem Sens Environ. 2015;163:217–228. doi: 10.1016/j.rse.2015.03.018. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.