Prediction of Broad-Spectrum Pathogen Attachment to Coating Materials for Biomedical Devices

Abstract

Bacterial infections in healthcare settings are a frequent accompaniment to both routine procedures such as catheterization and surgical site interventions. Their impact is becoming even more marked as the numbers of medical devices that are used to manage chronic health conditions and improve quality of life increases. The resistance of pathogens to multiple antibiotics is also increasing, adding an additional layer of complexity to the problems of employing safe and effective medical procedures. One approach to reducing the rate of infections associated with implanted and indwelling medical devices is the use of polymers that resist the formation of bacterial biofilms. To significantly accelerate the discovery of such materials, we show how state of the art machine learning methods can generate quantitative predictions for the attachment of multiple pathogens to a large library of polymers in a single model for the first time. Such models facilitate design of polymers with very low pathogen attachment across different bacterial species that will be candidate materials for implantable or indwelling medical devices such as urinary catheters, cochlear implants, and pacemakers.

Introduction

Bacterial infections are a large and re-emerging global healthcare issue because of aging populations, the evolution of multi- and pan-antibiotic resistant pathogens, increasing numbers of immunocompromised patients, and developments in and the use of medical devices. Immune responses abate with aging, and concurrent medical conditions mean that hospitalizations are increasing and nosocomial infections are becoming more prevalent.^1,2 Antibiotic resistance is a major global healthcare challenge, and the increased use of implantable and indwelling medical devices is hampered by the risk of bacterial infections, especially by multiantibiotic resistant pathogens.^3,4 Additionally, wound infections, traumatic burns, suppressed immune responses due to HIV infection or organ transplantation, and increased survival of patients with serious, chronic conditions such as cystic fibrosis and diabetes add to the overall burden of infection.

Health care-associated infections affect around 4.1 million patients in Europe and around 1.7 million patients in the USA per year, according to World Health Organization.⁵ Bacterial colonization of, and subsequent biofilm formation on, medical devices are particularly problematic given the rapidly growing number of patients requiring, for example, catheterization, stents, cochlear implants, pacemakers, and other major and minor surgical interventions.^1,3,4 New materials are needed for medical device applications that prevent infection by broadly resisting attachment and subsequent formation of antibiotic tolerant biofilms by diverse pathogens. These materials have advantages over those that incorporate antibiotics including: efficacy against strains resistant to incorporated antibiotics; low antibiotic resistance pressure; and enduring performance because the active components cannot leach away. Consequently, a substantial amount of research and development is now being conducted to identify new types of materials, chiefly polymers, that prevent bacterial colonization and hence biofilm development. The current status has been summarized in recent reviews.^6–12 In spite of some promising outcomes, given the immense size of materials space, it is essential that automated and high throughput materials synthesis and assessment methods be adopted to identify suitable materials quickly and allow their use in medical devices.¹³

Clearly, it would be ideal if we fully understood the diverse sensing and signaling mechanisms that bacteria employ to determine whether they are near or on a surface and whether that surface is suitable for attachment and biofilm formation. Such knowledge would allow the direct, rational design of surfaces that do not support bacterial colonization. As recent articles on this topic indicate,^14,15 mechanistic information is still far from complete. Pathogens use sophisticated, diverse strategies to colonize a surface that involve multiple surface appendages and macromolecules including pili, flagellar, proteins, and exopolysaccharides.^14,16–18 Attachment can be reversible or irreversible and mature biofilms disperse, releasing bacterial cells to search for new attachment sites.¹⁹ Pathogen interactions are modulated by surface physicochemical interactions²⁰ and involve substantial changes in gene expression through an integrated network of bacterial sensing and signaling systems that operate at transcriptional and post-transcriptional levels and involve, e.g., multiple two-component sensor regulators, mechanosensors, quorum sensing systems, riboregulatory networks, and second messenger molecules (e.g., cyclic diguanylate).^14–18,21 Consequently, we are not yet at the point where sufficient information is available to permit the rational design of low attachment surfaces as an effective and reliable strategy for new materials discovery. High throughput experimentation is a practical alternative to rational design in the majority of situations where the primary aim is to discover translatable materials to solve real clinical problems. However, high throughput synthesis and assessment of materials is not sufficient to guarantee discovery of the best materials.

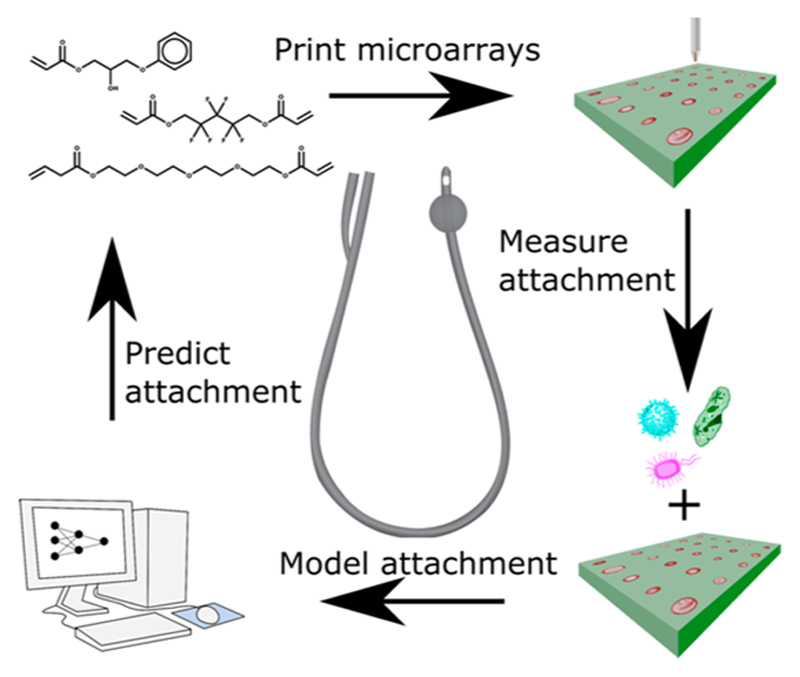
An experimental high throughput materials discovery campaign was undertaken to identify new acrylate polymers with reduced attachment and biofilm formation, initially using a single strain belonging to each of three major pathogen species but subsequently using multiple clinical isolates.²² Pseudomonas aeruginosa (PA), Staphylococcus aureus (SA), and uropathogenic Escherichia coli (UPEC) attachment was compared with existing commercial medical device materials such as silicone rubber and silver-containing hydrogel coatings. Acrylate polymers presented in a microarray format (see Figure 1) were screened to identify promising materials that minimized bacterial attachment and biofilm formation in vitro and in an in vivo foreign body infection model.^22,23 Some of these materials are now undergoing regulatory approval for use as urinary catheter coatings.

Figure 1.

Schematic of the processes employed in the microarray fabrication, pathogen screening, modeling of data, and prediction of pathogen attachment for new polymers.

Data-driven computational modeling methods that extract useful information from large data sets are an important adjunct to accelerated synthesis and testing technologies. The experiments generated large, information rich data sets derived from many hundreds of polymers and more than 20 000 assays. These data were used in the current work to extract useful information on relationships between polymer surface chemistry and bacterial attachment and to predict attachment of multiple pathogens on materials not used to generate the models. We previously employed sparse feature selection and Bayesian Regularized Artificial Neural Network (BRANN) approaches to generate quantitative and predictive models of the attachment of each of the three pathogens to diverse acrylate materials.²⁴ These have important advantages over other modeling techniques. They are very resistant to overtraining and overfitting, as they automatically generate sparse models and select sparse sets of relevant molecular features with optimum predictive capabilities. Although linear models of the relationships between surface chemistry and bacterial attachment reported by Hook et al.²³ showed some predictive abilities for pathogen attachment, nonlinear neural network-based models are often significantly more robust and predictive and were used in the current study. Sanni et al.²⁵ also used the highest performing (lowest bacterial attachment) subset of the monomers reported in the Hook et al.²³ study and used here, correlating bacterial cell attachment with a composite parameter composed of contributions from the lipophilicity and molecular flexibility of the monomer units.

There is often a lack of clarity, even within the quantitative structure—property relationships (QSPR) modeling community, on the two main purposes of machine learning and other statistical methods that model the relationships between the properties of molecules or materials and their biological effects. One aim is to understand the details of the molecular interactions and mechanisms underlying the biological phenomena being modeled. The other aim, now dominant in drug discovery and materials design, is to be able to predict the biological response of materials yet to be synthesized, allowing very large virtual libraries of synthetically feasible materials to be prioritized for subsequent synthesis and testing and discovering useful materials more quickly. This aim is driven by the need to translate novel materials with previously inaccessible properties into real medical applications. It is this aim that our current research is pursuing. These disparate but synergistic uses of models have been elucidated recently by Fujita and Winkler.²⁶ QSPR models can also be used as fitness functions in evolutionary processes that allow materials to evolve toward one or more desirable properties.²⁷

Given our previous success in generating computational models capable of making quantitative predictions of attachment of a single pathogen to a polymer library, here, we report for the first time a single computational model that can predict the polymer attachment of multiple pathogens simultaneously. It should be noted that these experiments and models predict the attachment of single pathogen strains to polymers not mixtures of different pathogens. The approach we have taken is similar to multitask networks,^28,29 which have proven to be successful in predicting the biological activities of small molecules against several targets. Multitask models potentially have wide applicability in materials science and medicine as they can identify materials with low attachment for a range of important pathogens and strains, rather than for a single pathogen strain. We compare the performance of the multipathogen model to that of the three, single pathogen strain computational models. Such models may also lead to general rules that relate low attachment to specific types of surface chemistry of polymers. A similar computational approach is used in small molecule drug discovery to find alternative drug targets.³⁰

Experimental Methods

Polymer Library and Pathogen Attachment Data

Data for pathogen attachment to a polymer library containing 496 acrylate copolymers and homopolymers were obtained from Hook et al.²³ Acrylate polymers were used because of the robustness and reliability of this type of polymer when used in the microarray format in our hands.^{23,24,31–33} Homo- and copolymers were generated by combinatorial reaction of different ratios of each monomer prior to UV-initiated polymerization. The nomenclature adopted for the copolymers is as follows: 1A(30%) means the polymer is composed of 70% of monomer 1 and 30% of monomer A by volume.

The bacterial attachment was measured using the fluorescence of bacteria transformed with green fluorescent protein. The brightness of the green fluorescence was proportional to the number of bacteria on the spot. As some polymers show a degree of autofluorescence, we removed the background signal from an equivalent microarray immersed in fresh uninoculated media

$$F=F_{\text{polymer+bacteria }}-F_{\text{polymer }}$$ (1)

As the fluorescence spanned several orders of magnitude, we modeled the logarithm of the fluorescence, log F.

Two additional new polymer arrays were used to validate blind predictions of the models, the gold standard for assessing the utility of computational models.³⁴ These arrays were constructed as described previously by Hook et al.²³ using the monomers and proportions shown in Figures S6 and S7 and Tables S6 and S7. Measurements of pathogen attachment were obtained using the same bacterial strains but transformed to express mCherry protein instead of GFP. This change in protocol was made to minimize problems with autofluorescence of polymers and to improve the signal-to-noise ratio and lower detection limits. However, this meant that a direct quantitative comparison between the bacterial attachment predictions of the models for GFP-transformed bacteria and those with bacteria expressing mCherry could not be made. For these validation experiments, the following screening protocol was adopted. The fluorescently tagged bacteria were grown for 12 h in LB (Luria—Bertani, Oxoid, UK) and used to inoculate RPMI-1640 defined medium (OD₆₀₀ = 0.01) containing the microarray slides. These were incubated at 37 °C with shaking at 60 rpm for 72 h; the slides were removed and washed with phosphate buffered saline (PBS, 15 mL) at room temperature three times for 5 min each, then rinsed with distilled H₂O, and air-dried. Fluorescence was measured with a GenePix Autoloader 4200AL scanner, using red laser 635 nm and red emission filter. The data were screened as described above before modeling and are summarized in Tables S6 and S7.

Polymer microarrays may contain errors due to monomer carry over between spots despite washing procedures and other types of printing errors, and cell attachment may be heterogeneous due to poor presentation on the slide. We identified likely problematic replicates in the arrays using modified Thomson’s tau. This identifies suspect measurements using the variance between data point replicates.

$$\tau =\frac{t_{a/2}\times (n-1)}{\sqrt{n}\times \sqrt{n-2+t_{a/2}{}^2}}$$ (2)

where n = sample size, t_a/₂ = critical student’s t test value at a with sample size n — 2. We chose a = 0.05, viz., statistical significance at 95% level. Data points were omitted if δ > τ × S where S is standard deviation of the sample and δ is the absolute difference of a data point and the sample mean. Replicates identified by this process were discarded, and values of the remaining replicates were averaged for the modeling studies.

The analyses also required the removal of polymers having log F values below 5.6, the detection limit of the pathogen attachment assay, as we did not have information on what their actual fluorescence/ attachment values were. It was also necessary to remove a few model outliers, a process that must be done carefully and objectively. Polymers with low fluorescence values that were <2.5σ of the background fluorescence were removed. These two steps eliminated 89 polymers from the PA data set, 18 from the SA data set, and 409 from the UPEC data set. Four additional outliers were identified from the models. Polymers 1A(30%), 5F(15%), and 9D(15%) for the PA attachment model and 5D(10%) for the SA attachment model had fluorescence values that were inconsistent with the fluorescence of copolymers with similar compositions and were poorly predicted by the models.

The acrylate monomer library used to screen the three pathogens is shown in Figure S1, and a schematic of the screening and modeling process is provided in Figure 1. The identities and structures of the monomers used to generate the additional smaller and larger polymer arrays used to valid model predictions are summarized in Figures S2 and S3.

Quantitative Modeling

Data sets were partitioned into training and test sets containing 80% and 20% of data points, respectively. The splitting was done by using k-means clustering (generating k clusters related by descriptor similarity and choosing the cluster mean for the test set). This ensures that the test set spans the same range of descriptors and attachment levels as the training set so that predictions outside of the domain of the models do not occur. It also ensures reproducibility of results for others wishing to replicate our work. The PA attachment data set contained 404 polymers after removal of data points below the detection threshold and outliers. The data was divided into a training set of 323 polymers and a test set of 81 polymers. The SA attachment data set consisted of 477 points for modeling (after statistical assessment), split into 382 polymers in the training set and 95 points in the test set. The protocol for measuring attachment of UPEC was different from that of the other two pathogens, as artificial urine was added to the culturing protocol to simulate the service environments that urinary catheters will encounter. This increased the variance in the measured bacterial fluorescence and resulted in a lower degree of attachment of UPEC to the polymers compared to that of SA and PA. UPEC also forms weaker adhering biofilms compared to PA and SA. Consequently, the UPEC data set only contains 87 polymers after omitting those below the detection limit (the majority), with experimental artifacts, or with unusually high variability in replicates. This data set was partitioned into 70 points for the training set and 17 for the test set. After removal of outliers and polymers with fluorescence below the detection limit, the resulting 968 multipathogen attachment polymer data set was split into a training set of 774 points and a test set of 194 points.

Molecular descriptors were calculated from the Dragon 7.01 package using SMILES strings to represent the structures of monomers.³⁵ We generated 3839 constitutional, structural, and physicochemical descriptors that were dependent only on 2D structures. We and others^{36– 38} have shown that consideration of monomer or small oligomer structures alone can often provide good descriptions of polymer performance without consideration of other structural properties such as molecular weight, polydispersity, degree of branching copolymer block size, etc. Copolymer descriptors were calculated as a linear combination of monomer descriptors weighted by the proportion of each monomer in the copolymer.²⁴ Highly correlated descriptors (r² > 0.95) and those with low variance in the data set were removed, to provide 1640 final descriptors. The most relevant descriptors were identified by multiple linear regression with expectation maximization (MLREM), an extremely sparse method of identifying features.39 The sparsity was adjusted by a parameter, β, to obtain a model with the lowest standard error of prediction (SEP) for all three pathogens. This resulted in a set of descriptors shown in Table S1.

We have also used experimental time-of-flight secondary ions mass spectrometry (ToF-SIMS) ion peaks derived from analysis of the surfaces of the polymer spots in the library as descriptors. These data were also obtained from Hook et al. and contained surface characterization of one spot from the six replicates.²³ The assignment of the identities of the peak ions and association with the polymer structures is described by Hook and Scurr.³² The water contact angle (WCA), a measure of surface polarity, was also measured in this paper and employed here as an experimental descriptor. Experimental data used for modeling are shown in Table S3.

The multipathogen models were generated from a data set that combined all three pathogen attachment data sets, using an indicator variable as a descriptor to distinguish between the presence (1) and absence (0) of a specific pathogen. A Bayesian regularized Neural Network with Gaussian prior (BRANNGP) was used to generate the pathogen attachment models.⁴⁰ The neural network consisted of one input, one hidden, and one output layer. The number of nodes in the hidden layer was varied from 2 to 10. However, previous reports⁴¹ have shown that less than five hidden layer nodes are sufficient in almost all cases and that specifying larger numbers of nodes results in almost identical models because of the Bayesian regularization.⁴¹ The best model for each case was identified as the one with the lowest test set standard error of prediction (SEP), as is best practice.⁴² However, the standard error of estimation (SEE) for the training set prediction and the r² value for the training and test set predictions were also reported.

To ensure that the neural network was not biased by the order in which the data were presented during training, we shuffled the order of the rows. Shuffling of the data order has essentially no effect on the quality of the model generated. We also checked for overfitting (something Bayesian regularized neural networks are relatively immune to)⁴¹ or chance correlations by randomly redistributing only the y-values. This gave models with r² values very close to zero, as would be expected.

As described above, the predictions of pathogen adhesion of two new polymer libraries were complicated by a change in experimental protocols after generating, measuring, and modeling the data using GFP-modified bacteria. Pathogens genetically modified to express the mCherry fluorescent protein were used to check the prediction of the models for a new polymer array containing homo- and copolymers. This prevented a direct, quantitative validation of model predictions. The logarithm of the mCherry intensities was autoscaled (normalized), and three classes (low, medium, and high attachment) were defined for each normalized set of data by inspection of the distributions in the histograms (see Figure S4). Truth tables were generated from the class membership of attachment of PA and UPEC to each polymer in the array.

Results

The attachment of each of P. aeruginosa (PA), S. aureus (SA), and uropathogenic E. coli (UPEC) to the polymer microarray was modeled using two classes of descriptors: experimentally measured time-of-flight secondary ion mass spectrometry (ToF-SIMS) peak intensities and water contact angles (WCAs); computed molecular descriptors (from DRAGON).³⁵ These descriptors describe the surface chemistry of the polymer spots on the arrays. While WCA has been found to be a poor predictor of bacterial attachment across diverse libraries when used alone,²³ we wanted to investigate its utility when combined with the molecularly rich information from ToF-SIMS experiments.⁴³

Individual models predicting the attachment of each pathogen to the same polymer library were reported by Epa et al. using computed molecular descriptors specifically chosen to be chemically interpretable.²⁴ The aim of this prior work was to generate models that provided some insight into the relationship between surface chemistry and pathogen attachment, as well as making quantitative prediction of bacterial attachment of new materials. More arcane molecular descriptors generally provide improved predictive power at the expense of loss of chemical interpretability. Given the added complexity of modeling surface chemistry-polymer attachments relationships for several pathogens simultaneously, in this work, we chose descriptors solely for their ability to generate the most accurate predictions of pathogen attachment. We employed indicator variable descriptors to allow the entire set of pathogen attachment data to be used to train multipathogen attachment models that predict the performance of polymer libraries for all three pathogens (see Experimental Methods).

Here, we compare the performance of multipathogen attachment models with those that predict attachment of single pathogens. We reiterate that these experiments and models predict the attachment of single pathogen strains to polymers not coincident mixtures of pathogens, as often occurring in infections. Model performance was assessed by the ability of each model to recapitulate the attachment performance of polymers in a test set not used to train the models. We also compared the performance of experimental ion peak and water contact angle descriptors with computed molecular descriptors for single and multipathogen attachment models, to assess whether the extra effort involved in ToF-SIMS experiments was justified by higher model accuracy or interpretability.

Pathogen Attachment Models Based on Computed Molecular Descriptors

The results of modeling the attachment of the three individual pathogens and the attachment of all three pathogens simultaneously to the polymer library are summarized in Table 1. These models were generated by a Bayesian neural network (BRANN), and a linear multiple regression (MLR) model was also included for comparison. Clearly, the BRANN multipathogen model had significantly lower standard error of prediction (SEP) than the linear model, so it predicted the attachment to polymers in the test set more accurately (the r² was also higher than the linear model). This is consistent with earlier studies of models predicting each pathogen separately.^{23, 24}

Table 1. Statistics of Pathogen Attachment Neural Network (BRANN) Models Based on Molecular Descriptors^a.

				training set		test set
model	Nhidden	Neff	Ndes	SEE	r2	SEP	r2
multipathogen (MLR)		22	22	0.30	0.59	0.28	0.60
multipathogen	7	488	41	0.16	0.86	0.19	0.81
P. aeruginosa	8	246	30	0.17	0.88	0.17	0.87
S. aureus	7	310	18	0.12	0.87	0.14	0.78
uropathogenic E. coli	7	33	18	0.30	0.78	0.24	0.94

^aN_eff is the number of effective adjustable weights, N_des is the number of descriptors employed, N_hidden in the number of nodes in the hidden layer, SEE is the standard error of estimation, SEP is the standard error of prediction, and r² is the squared correlation coefficient of the predictions.

Multipathogen Model

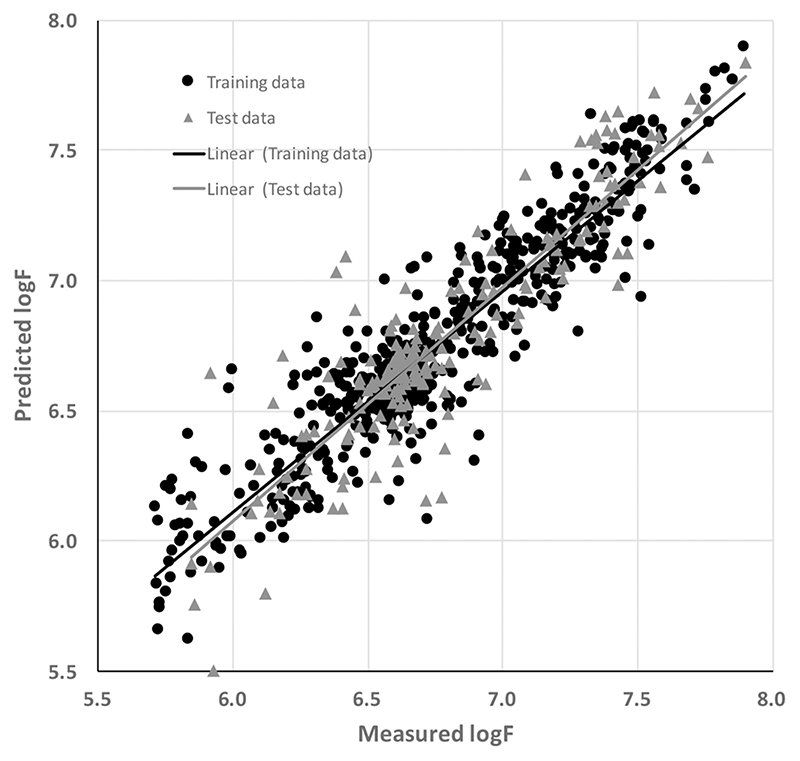
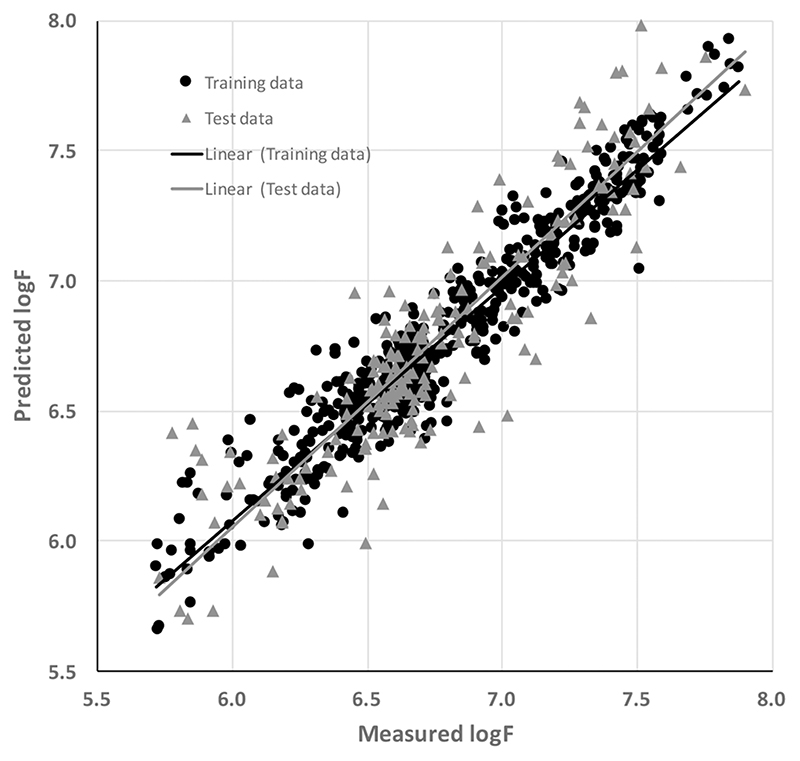
The best multipathogen attachment model was generated by a BRANN neural network model that employed 7 neurons in the hidden layer and 41 descriptors. The training set standard error of estimation (SEE) and test set standard error or prediction (SEP) values were 0.16 and 0.19 log F, respectively, for this model. The training and test set predictions had r² values of 0.86 and 0.81, indicating a high level of statistical significance and showing that the model was robust and strongly predictive. Figure 2 illustrates the performance of the multipathogen model in predicting the attachment of bacteria to the polymer library.

Figure 2.

Measured and predicted attachment (estimated using the log of the GFP fluorescence, log F) of the multipathogen attachment model employing computed molecular descriptors.

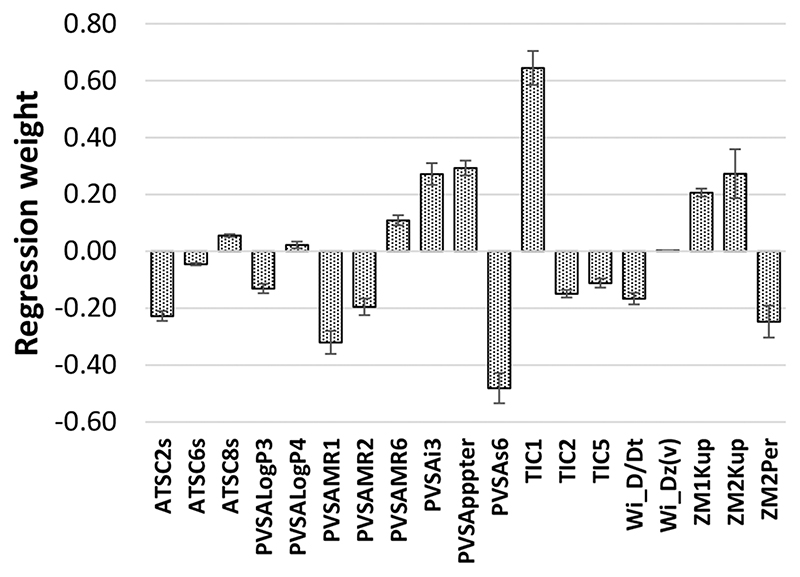
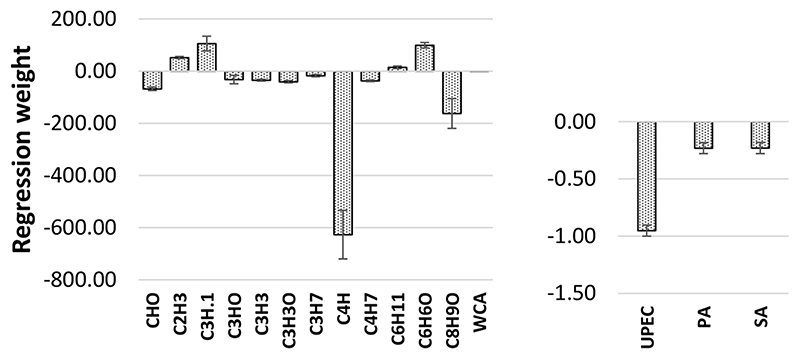
The linear MLR multipathogen attachment model was also statistically significant (r² ~ >0.5, Table 2),⁴⁴ but the standard errors of prediction were larger (0.28 log F) than the nonlinear BRANN model (0.19 log F). The linear models were derived to elucidate the likely contributions of the descriptors to the models. The contributions of the computed molecular descriptors to the multipathogen model are summarized in Figure 3. The main purpose of this and related figures in the paper is to show which descriptors make positive or negative contributions to the attachment of one or more pathogens, to provide a qualitative measure of the size of the contribution and to make inferences of the role of surface chemistry where possible.

Table 2. Statistics of Pathogen Attachment BRANN Models Based on ToF-SIMS Molecular Ion Peaks and WCA Values^a.

				training set		test set
model	Nhidden	Neff	Ndes	SEE	r2	SEP	r2
multipathogen (MLR)		16	16	0.31	0.55	0.33	0.52
multipathogen (BRANN)	5	378	79	0.12	0.76	0.21	0.74
P. aeruginosa	6	173	57	0.14	0.92	0.22	0.81
S. aureus	8	259	19	0.11	0.88	0.14	0.84
uropathogenic E. coli	2	44	10	0.24	0.87	0.24	0.84

^aSee Table S3 for ToF-SIMS descriptors used in the models.

Figure 3.

Weights of the descriptors in the linear multipathogen attachment model. The error bars represent the standard errors in the parameter estimations from the MLR model. See Table S2 for an explanation of these descriptors and Discussion for the relevance to the model.

Single Pathogen Strain Models

Models relating pathogen attachment to surface chemistry were also generated for each pathogen separately. The model that best predicted PA attachment to polymers in the test set was derived using a neural network with 8 nodes in the hidden layer and 30 descriptors. The training set SEE was 0.17 log F and r² was 0.88, while the test set had an SEP of 0.17 log F and an r² of 0.87. This suggests that the model was not overtrained and was quite robust. The SA attachment model had a training set SEE of 0.12 and a test set SEP of 0.14 and an r² of 0.87 and 0.78 for predictions of attachment to polymers in the training and test sets, respectively.

Despite the smaller data set size of the UPEC attachment study, a statistically valid and predictive model was obtained. The model used two neurons in the hidden layer and 18 descriptors. The training and test set SEE and SEP values were 0.30 and 0.24, respectively, and the r² for the training set was 0.78 and for the test set was 0.94. The graphs showing the correlations between the measured and predicted attachment for the individual pathogen models employing computed molecular descriptors are shown in Figure S5.

Pathogen Attachment Models Based on ToF-SIMS Ion Peak Descriptors

Experimentally measured ToF-SIMS ion peaks and water contact angles (WCA) were also used as descriptors in the pathogen attachment models to assess their efficiency relative to the computed descriptors. The results of modeling the three individual pathogen data sets and the combined multipathogen data sets with the experimental ToF-SIMS analysis and WCA data are summarized in Table 2. A linear MLR attachment model for multiple pathogens is included for comparison and to allow the contributions of ion peaks to the model to be evaluated.

Multipathogen Model

As with the pathogen attachment model generated using computed molecular descriptors, the best performing attachment model employed a neural network (BRANN) with 5 neurons in the hidden layer and 79 descriptors. This model contained more effective weights but fewer descriptors than the same model using computed molecular descriptors. The training and test sets were predicted with good accuracy, with SEE and SEP values of 0.12 and 0.21 log F and r² values of 0.76 and 0.74, respectively. Values of r² above 0.7 show that it is possible to generate a good combined model for the attachment of all three pathogens to the polymer library using data obtained from experimental techniques: ToF-SIMS and WCA.³³ Figure 4 illustrates the performance of this multipathogen model in predicting the attachment of bacteria to the polymer library.

Figure 4.

Measured and predicted attachment (estimated using the log of the GFP fluorescence, log F) of the multipathogen attachment model employing ToF-SIMS ion peak features and WCA from experiments as descriptors.

As with the linear multipathogen attachment model based on computed molecular descriptors, the experimental descriptors also generated a linear (MLR) model of multipathogen attachment of lower statistical significance (r² > 0.5, Table 2).⁴⁴ The standard error of prediction was larger (0.33 log F) than the nonlinear model (0.21 log F) and larger than that of the linear multipathogen attachment model using computed molecular descriptors (0.28 log F). The contributions of the experimental descriptors to the linear model are summarized in Figure 5.

Figure 5.

Weights of the descriptors in the linear multipathogen attachment model (different scales for the ToF-SIMS ion peaks, WCA, and the indicator variables for the three pathogens). The error bars represent the standard errors in the parameter estimations from the MLR model.

Single Pathogen Strain Models

The best PA attachment model was obtained using a neural network containing 6 neurons in the hidden layer and 57 descriptors. The training and test sets were well predicted by this model, with SEE and SEP values of 0.14 and 0.22 log F and r² values of 0.92 and 0.81 for training and test sets, respectively. The number of descriptors in the model is higher than in the other bacterial attachment models for SA and UPEC. The optimal SA attachment model was obtained from a BRANN model that used 8 neurons in the hidden layer and 19 descriptors. Again, the training and test set attachment was well predicted by the model, with SEE and SEP values of 0.11 and 0.14 log F for training and test sets. The corresponding r² values for these predictions were 0.88 for the training set and 0.84 for the test set. The low standard errors, high r² values, and the similarity in the prediction efficacy of the training and test set data show that this model of SA attachment to the polymer library using experimental features is robust and predictive. The quality of the models is similar to those reported previously by Epa et al.,²⁴ which had an SEP = 0.12 log F and r² = 0.85 for the test set. The most predictive UPEC attachment model for the polymer library was obtained also using a neural network with 2 neurons in the hidden layer and 10 descriptors. This model predicted attachment of UPEC with SEE and SEP values of 0.24 and the r² values of 0.87 and 0.84 for training and test sets. The relatively small number of experimental descriptors and excellent model metrics show that there are few key molecular features important for UPEC attachment to the polymer surface. The model SEE and SEP values of 0.24 are significantly better than those reported by Epa et al.²⁴ (0.43 and 0.48), presumably because the descriptors employed were more efficient than the chemically interpretable set used in the earlier study. In our study, r² for the training set was higher than that in Epa et al.’s model (0.87 vs 0.58), while r² for the test set was slightly lower at 0.84 versus 0.73 in the Epa et al.²⁴ study. However, as we have shown previously, the standard errors are a more robust measure of model predictivity than the r² values.⁴² The graphs showing the correlations between the measured and predicted attachment for the individual pathogen models employing experimental descriptors are shown in Figure S6.

Discussion

We would first like to clarify that the term multipathogen should not be confused with the term polymicrobial, which describes a situation where a number of bacterial species and strains coexist (common in many infections). By multipathogen, we mean we have tested one bacterial species and strain at a time. We have not performed experiments where we mix several strains together and examine their collective behavior.

Single versus Multipathogen Models

The attachment of the three pathogens to the polymer library is reasonably well correlated with each other, with r² values greater than 0.5 for all species, as Table 3 shows. UPEC attachment shows good correlation with PA and SA, while PA and SA attachment are correlated to a slightly lesser extent. The significance of the pathogen indicator variables (1 when pathogen present and 0 when absent) to the attachment models was interesting. Only the UPEC indicator variable was statistically significant in the models, and the weights of the PA and SA indicator variables were similar and much smaller. Given the caveat that we are only examining single strains of each pathogen, we might imply that PA and SA may have more similar structure-property relationships and levels of attachment compared to UPEC.

Table 3. Correlation Matrix (r²) for the Attachment of the Three Pathogens to the Polymer Library.

	PA	SA	UPEC
PA	1.00	0.52	0.66
SA	0.52	1.00	0.72
UPEC	0.66	0.72	1.00

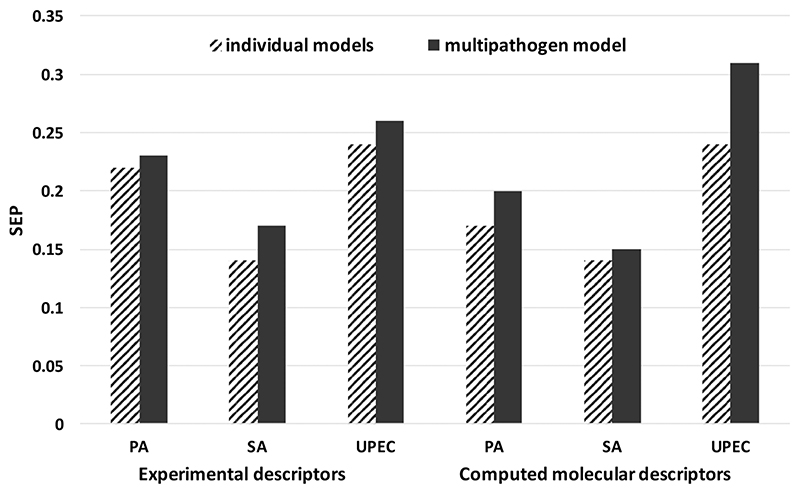
The differences between the single pathogen and multipathogen models for the two types of molecular descriptors are summarized in Tables 1 and 2. It is clear that there are not large differences in the predictive power of the single pathogen models compared to the multipathogen model for each family of descriptors. This is illustrated graphically in Figure 6, which summarizes the SEP values for pathogen attachment generated by pathogen-specific models or the by the multipathogen model. Clearly, the test set SEP values for predicted attachment from single pathogen models are similar to those from the multipathogen models. This suggests strongly that multipathogen models are effective and have quantitative predictive power that is similar to the individual pathogen models. Consequently, it should be feasible to generate models that can make accurate quantitative predictions of pathogen attachment to materials for more than three pathogens. The fact that such models can be derived relatively simply by use of indicator variables as descriptors shows that the structure-activity (attachment) relationships between the pathogens may be described well by a nonlinear additive function such as a log-linear relationship. There is also a degree of inductive transfer of knowledge (a type of “read across”) where internal models predicting the adhesion of each pathogen learn from each other.⁴⁵ It has been proposed relatively recently that multitask machine learning models have improved generalization performance because they use information from related tasks as an inductive bias.⁴⁶ The efficacy of the multipathogen model may also be aided by the moderate correlations between the attachment of the three pathogens to the polymer library. Bacterial pathogens whose attachment to polymers are not as strongly correlated with each other may not be predicted as reliably by future multipathogen models.

Figure 6.

Standard errors of prediction values for the test set for single pathogen versus multipathogen models generated using molecular descriptors or experimental surface analytical ToF-SIMS descriptors.

Models Using Computed versus Experimental Descriptors

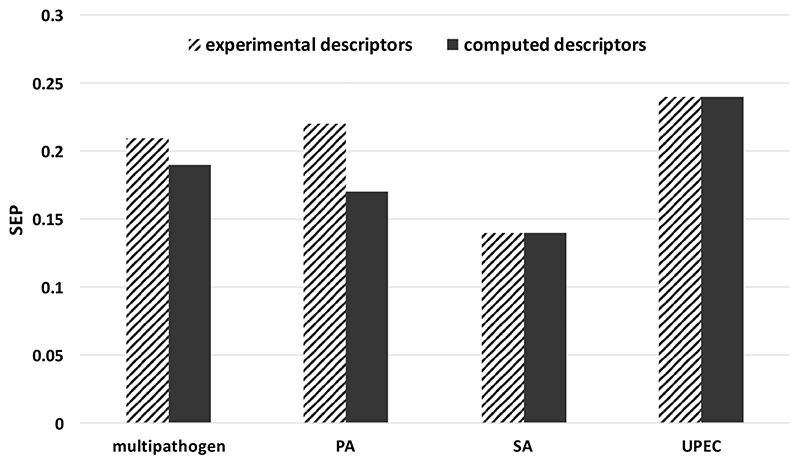
The results summarized in Tables 1 and 2 suggest that nonlinear models derived from computed and experimental descriptors have similar abilities to predict attachment of pathogens to polymers in the test set (SEP values of 0.19 and 0.21 log F). However, the linear model of pathogen attachment based on computed molecular descriptors had significantly better predictive power than that based on experimental ToF-SIMS and WCA descriptors (0.28 versus 0.33 log F). Consequently, it may be argued that it is not essential to obtain ToF-SIMS data for model generation, unless these types of experimental descriptors provide additional insight into the role of surface chemistry on pathogen attachment compared with computed molecular descriptors. Table 4 summarizes the statistics of the two multipathogen models. Figure 7 compares the performance of the two descriptor types in predicting the attachment of the test set.

Table 4. Statistics of Multipathogen Attachment Models^a.

				training		test
descriptor set	N hidden	N eff	Ndes	SEP	r 2	SEE	r2
computed	7	488	41	0.16	0.86	0.19	0.81
experimental	5	378	79	0.12	0.76	0.21	0.74

^aSee Tables S1 and S3 for details of the descriptors used in the models.

Figure 7.

Test set SEP values for the four pathogen attachment models for the two types of descriptors. The experimental descriptors were dominated by ToF-SIMS ion intensities, and the WCA did not play a significant role.

The model using experimental ToF-SIMS ion peaks uses a less complex neural network architecture but more descriptors than the model using computed molecular descriptors. However, the number of effective weights in the model, derived from the Bayesian regularization, are similar. It is clear that both methods for encoding the molecular characteristics of the polymers generated very good, robust, and predictive attachment models, and the model quality is similar. The SEP values for all models derived using computed molecular descriptors are equal to or lower than those derived using experimental descriptors, as Figure 7 shows. The performance of the UPEC model using ToF-SIMS ions peak and computed molecular descriptors are comparable despite the model derived from ToF-SIMS descriptor being sparser (10 relevant descriptors compared to 18).

The weights of the descriptors in the linear multipathogen models gives some insight into the role surface chemistry plays in attachment of the three pathogens. The unweighted contributions the computed descriptors made to the model are shown in Figure 3. Curiously, in this linear model, the contributions that the PA and SA indicator variables made to the model were very similar, suggesting similar structure−property relationships at the polymer surfaces and similar levels of pathogen attachment, despite having fundamentally different cell surfaces and signal transduction machineries (Gramnegative vs Gram-positive). In spite of being easy to calculate and capable of generating a robust model that makes good predictions of the attachment of pathogens to polymers, the molecular descriptors are quite arcane and difficult to interpret in terms of surface chemistry. The majority of computed descriptors make negative contributions to the attachment model, meaning that, when these molecular properties are larger, pathogen attachment is reduced. The largest negative contribution was from the PVSAs6 descriptor, and the most positive contribution was from the TIC1 descriptor. The PVSAs6 descriptor is one of a group of P-VSA-like descriptors that is defined as the amount of the molecular van der Waals surface area (VSA) having a property P in a certain (binned) range.⁴⁷ TIC1 is the first order neighborhood total information content of the molecule, a measure of molecular (graph) complexity. It is related to Shannon entropy.⁴⁸

The unweighted contributions the sparse experimental descriptors make to this model are summarized graphically in Figure 5. Significantly, WCA makes a negligible contribution to pathogen attachment in either individual or multipathogen models. Previously Hook et al. had also found no correlation between contact angle and pathogen attachment.23 Conventional wisdom teaches that reduced bacterial attachment often requires bound water in hydrophilic structures. As noted by Hook et al.,23 previously, these relatively hydrophobic materials clearly do not function by that mechanism. This is consistent with the poor predictive power provided by a surface wettability parameter across these diverse material libraries for eukaryotic and prokaryotic cells, discussed in detail elsewhere.⁴³

In the multipathogen attachment models using the ToF-SIMS surface analysis data, the indicator variables for the pathogen identity were also significant, with the UPEC indicator variable making a much larger negative contribution to the model than the PA and SA indicator variables. This may be due to the significantly lower average attachment of UPEC to the polymer library. The C₄H⁺ ion peak made the largest negative contribution to the model, approximately 3 times larger than the next most significant ion peaks (Figure 5). The dominance of hydrocarbons in the ion fragments associated with negative loadings is consistent with the view that monomers with pendent hydrocarbon groups bonded to the ester moiety are more resistant to bacterial attachment. The exceptions are the C₂H₃⁺, C₃H^-, C₆H₁₁⁺, and C₆H₆O⁺ ions that made positive contributions to the model. The C₂H₃⁺ fragment ion is present in the spectra of all polymers and is likely to have contributions from both the backbone and the polymer pendant groups. The C₃H⁻ peak is present at elevated intensities in the mass spectra of monomers 7 and 14 and is consequently assigned to a fragment of an aromatic ring. C₆H₁₁⁺ could be an aliphatic chain or a cyclohexane ring fragment (e.g., from monomer 5), but it makes negligible contribution to the multipathogen linear model in any case. The C₆H₆O⁺ ion fragment comes mostly from the phenol fragment present in monomer 7. These contributions toward the log F model imply that small aliphatic groups (all hydrophobic) on the meth/acrylate polymer were correlated with low bacterial attachment, as was previously reported by Hook et al. and Epa et al.^23,24 The more hydrophilic phenolic fragment C₆H₆O⁺ appears to enhance attachment of pathogens in the multipathogen model, again consistent with these previous studies. It was conjectured that the functional groups in the polymer facilitated hydrogen bonding with peptidoglycans, teichoic acids, proteins, lipopolysaccharides, lipoteichoic acids, or exopolysaccharides present on the bacterial cell surface or that are components of the biofilms.

There is relatively little difference between the test set standard errors of prediction (Figure 6) for models using computed or experimental descriptors (ToF-SIMS ion peak dominated). Models derived from experimental descriptors have larger prediction errors for the PA attachment but smaller errors for UPEC models (this may also be an artifact of the small training set size of this data set). Clearly, the computed descriptors avoid the need for further experiments, but the experimental descriptors may be easier to interpret in terms of how the surface chemistry of the polymers influences pathogen attachment. Generally, for quantitative structure-property relationship (QSPR) methods, the use of computed molecular descriptors is desired as it allows properties of new molecules to be predicted prior to synthesis. The use of experimentally derived data may be useful in cases where the characterization experiments have been carried out for another purpose or where other synthesis or processing properties have a significant effect on their performance.

As mentioned previously, work on bacterial attachment modeling has been reported Epa et al.,²⁴ Hook et al.,²³ and Sanni et al.²⁵ The simplest modeling approach was by Sanni et al.,²⁵ where the authors generated a linear attachment model using a composite descriptor derived from the log of the octanol/water partition coefficient (log P) and number of rotatable bonds in the monomer. The model was derived from only (meth)acrylate materials containing hydrocarbon pendant groups, and it failed to predict attachment for other chemistries that promoted greater biofilm formation. The predictions inside this restricted chemical space domain of applicability had an r² of 0.67, good for such a simple linear model.

Hook et al.²³ employed a partial least squared (PLS) linear method using ions obtained from ToF-SIMS experiments to find the relationship between surface chemistry and bacterial attachment. The authors were able to make relatively good models for PA and SA with r² values of 0.68 and 0.76, respectively, while PLS analysis failed to find a statistically valid predictive model for UPEC (r² < 0.3). In this paper, we were able to make substantially improved quantitative models predicting the polymer attachment of all three pathogens (see Table 3). This shows that sparse selection of features, combined with an optimal nonlinear modeling method BRANN, can create significantly improved predictive models compared to those generated by PLS or other linear methods with the same or similar sets of descriptors.

Epa et al.’s²⁴ sparse selection of computed, interpretable molecular descriptors generated bacterial attachment models consistent with those of the current study, presented in Table 2. It is interesting to note that, despite different sets of descriptors being used, models of similar quality were obtained.

Model Predictions of Pathogen Attachment to a New Polymer Array

Prediction of the attachment properties of test sets partitioned from a large data set and never used to generate the model is a pragmatic way of measuring the predictive power of computational models. However, the ultimate test is to predict the attachment properties of new polymers. The models derived for bacterial attachment from computed molecular descriptors were used to estimate bacterial attachment for two new libraries, one containing 61 polymers made from 12 monomers Table S6) and the other containing 368 polymers derived from 21 monomers (Table S7). Attachment data were obtained for PA and UPEC. As explained in the Experimental Methods, these polymer attachment experiments used a different fluorescent protein, mCherry instead of GFP, to generate the data used to validate model predictions. Differences between the different fluorophores meant that quantitative comparisons between the predicted and measured pathogen attachment to these new monomers could not be made, and classification methods were employed. Predictions were made for low, medium, or high pathogen attachment of polymers in the two new libraries based on the distribution of predicted log F values. Predictions of the multipathogen and single pathogen attachment (log GPF fluorescence) models were also normalized and assigned to the low, medium, and high attachment classes. Prediction accuracy was assessed by use of truth tables, and the percentage of class membership was correctly predicted.

As the truth tables for classification by models in Figure S7 show, the individual pathogen attachment models had similar accuracies to those for the multipathogen models for predicting the class membership of the new materials in both new polymer arrays. The class membership for attachment of PA to the larger polymer library was predicted with accuracies of 60% and 71% for the multipathogen and specific PA models, respectively. The class membership prediction accuracies were slightly lower for the smaller validation polymer library. In this case, PA attachment was predicted with 55% and 40% accuracies for the multipathogen model and specific PA model, respectively. Given that classes would be assigned correctly 33% of the time by chance, the specific PA model attachment to the smaller polymer library predictions are not statistically significant but those of the multipathogen model are. Adhesion of UPEC to polymers is generally lower, and the experimental error is larger; however, both models predicted the class membership with reasonable accuracies (39% and 46% for multipathogen and single pathogen models, respectively). Although this study did not allow us to assess the predicted pathogen attachment to new polymer libraries quantitatively, it does strongly suggest that the models have useful predictive capabilities that will be helpful in selecting improved materials with the ability to resist the attachment and biofilm formation for multiple pathogens.

Conclusions

We have shown that it is possible to predict the individual attachment of three important pathogens to a library of copolymers using a single model that employs a specific set of descriptors. This model can predict the attachment of each pathogen to the polymers with accuracies similar to those of models specifically trained to predict a single pathogen. This offers the possibility of developing a generalized description of the response of multiple bacterial strains to materials. This could ultimately become a framework with which new materials with broad pathogen resistance can be designed and optimized, rather than relying on “one-pathogen-at-a-time” modeling methods now widely used. Such new materials promise reduced materials-associated infections in the clinic and more broadly in other nonclinical applications where formation of biofilms is problematic. We anticipate the multipathogen modeling approach may be extendable to more than three pathogens and to experiments where several bacterial species (or strains) are coexisting. This will open the way for a comprehensive predictive capability that could be used to assess the suitability of novel materials for highly effective implantable materials.

Supplementary Material

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.7b14197.

Abbreviations

SA

Staphylococcus aureus

PA

Pseudomonas aeruginosa

UPEC

uropathogenic Escherichia coli

QSPR

quantitative structure-property relationships BRANN, Bayesian Regularized Artificial Neural Network MLR, multiple linear regression SEP, standard error of prediction

SEE

standard error of estimation

ToF-SIMS

time-of-flight secondary ions mass spectrometry WCA, water contact angle

log P

logarithm of the octanol/water partition coefficient MLREM, multiple linear regression with expectation maximization