Using fit functions in computational dielectric spectroscopy

Abstract

This work deals with the development of an appropriate set of fit functions for describing dielectric spectra based on simulated raw data. All these fit functions are of exponential character with properly chosen co-functions. The type of the co-functions is different for translation, rotation and their coupling. As an alternative to multi-exponential fits we also discuss Kohlrausch-Williams-Watts functions. Since the corresponding Fourier-Laplace series for these stretched exponentials has severe convergence problems, we represent their Fourier-Laplace spectrum as a Havriliak-Negami expression with properly chosen parameters. A general relation between the parameter of the Kohlrausch-Williams-Watts and the Havriliak-Negami parameters is given.

The set of fit functions is applied to the concrete simulation of the hydrated ionic liquid 1-ethyl-3-methyl-imidazolium triflate with H₂O. The systematic variation of the water mole fraction permits to study the gradual transition from a neutral molecular liquid to molecular ionic liquids.

I. Introduction

Among the physico-chemical properties of molecular ionic liquids [MIL] accessible to experiments,^1–6 dielectric spectra^7–11 are of special importance: On the one hand they enable a description of MILs at the macroscopic level in terms of collective motion involving all possible couplings between species and molecules. On the other hand the frequency-dependent generalised dielectric constant [GDC] may serve as a global characterization of solvation properties. In fact, the results of “solvation spectroscopy” can be interpreted in dielectric terms.^12–14

Due to the inherent collectivity of dielectric spectra, their interpretation is far from trivial. Very often, different contributions from various species or various types of motion, e.g. rotation and translation, superimpose and interact in a complicated manner leading to rather broad spectra extending over several orders of magnitude in frequency.^9,10,15,16 In this situation detailed computer simulation have proven to be a valuable tool for interpretation.^9,16,17 This computational dielectric spectroscopy in turn needs an appropriate computer-adapted dielectric theory in order to convert the simulation box to a piece of dielectric material. As one cannot mimic the behaviour of a macroscopic sample in finite simulation box the inherent Coulomb forces have to be handled with great care. In fact, these forces are modified in a way in order to reproduce the behaviour of a large sample by the small simulation box. This is the art of “Finite system electrostatics”.^18–21 Among the different modifications of Coulomb forces available the Ewald technique taking periodic boundary conditions seriously has been found to have the lowest size dependence.^20–26

The proper treatment of size dependence, however, is only one part of the story. The time dependence is important, too. Based on “Linear Response Theory”²⁷ one needs the time correlation functions [TCF] of collective dipole moments and currents to compute the dielectric spectra via Fourier-Laplace transform of TCFs.²⁸ These TCFs are evaluated from time series of the corresponding collective properties obtained from the trajectories of atomic coordinates and velocities. Practical calculations have shown that simulations shorter than several dozens of nanoseconds are inappropriate to yield reliable TCFs. Even for TCFs confined to the picosecond range this long-term simulations are essential to achieve the necessary statistical quality.

The concept of using fit functions copes with the dual problem: On the one hand it removes numerical noise. On the other hand the complex time behaviour can be described with a few motional parameters, i.e. amplitudes, time constants, frequencies and time shifts. In this way the respective TCFs can be revived from these parameters even if the corresponding raw simulation data are not available any more. Another advantage of fit functions is their independence of time step between two function values. As a result, the fit functions can be computed at very high frequencies without any problems as opposed to the numerical Fourier-Laplace transform of the unfitted TCF.

The basis of all fit functions used in the present work is the exponential function which guarantees the decay to zero of all compound functions. This is essential for the Fourier-Laplace transform. The present study shows that this basic exponential function can be augmented by co-functions which are typical for the type of collective motion to which they refer: rotation, translation and their cross-term. The self-developed program GENDICON converts the TCFs to dielectric spectra on the basis of the raw correlation data as well as the fit functions.

The capability of the program GENDICON can be demonstrated by applying it to the concrete system ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water which was chosen for the following reasons: As the anion has a major influence on the properties of a MIL we have first selected triflate $\left[{\text{CF}}_3{\text{SO}}_3^{-}\right]$ because of its high polarity. This high polarity is caused by the large differences in electronegativity of the constituent atoms. Furthermore, the direction of dipole coincides with the C–S bond which is the major axis of the molecule. Since most cations in MILs are substituted imidazoliums we chose 1-ethyl-3-methyl-imidazolium [EMIM⁺]. This asymmetric cation has the advantage of short side chains reducing the viscosity.

Since the time constants of TCFs scale roughly with the viscosity,^9,29 their decay to zero is better realised in more fluid systems. The addition of water to ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$ further reduces the viscosity. With varying mole fraction x_H2O the systems change from neutral molecular liquids to molecular ionic liquids. This gradual change may be regarded as a severe test of the fit procedure to cover a diversity of motional parameters and phenomena. Last but not least, ionic liquids are highly recognized solvents in separation or purification of biomolecules.^30–33

II. Theory

The theory section is divided into two parts: The first part deals with the theoretical background of the generalised dielectric constant. It mentions the prerequisites of the computational dielectric spectroscopy and describes decomposition of the generalised dielectric constant into rotational and translational components. The rotational contributions are attributed to the dielectric permittivity ϵ(ω) whereas the translational contributions are assigned to the dielectric conductivity ϑ₀(ω).

The second part concerns the computation of the generalized dielectric constant Σ(ω) and its components by means of fit functions. Since Molecular dynamics simulations are able to compute each contribution to the dielectric spectrum separately, proper choices of the fit function for each component can be made. Furthermore, the fit functions represent the time-dependent correlation functions and describe their relaxation in time. When transferred to the frequency-dependent dielectric spectrum, the peak structure of diverse correlation functions may look similar on a logarithmic frequency scale but their origin and thereby their time behaviour may be completely different. Therefore, the second part of the theory section tries to give insights which fit function may be appropriate for a certain frequency regime.

A. The generalised dielectric constant

The frequency-dependent GDC Σ(ω) is the susceptibility relating the dielectric polarization to the strength of the Maxwell field E. It can be measured experimentally by various techniques.^15,34–36 From a theoretical point of view, it may be expressed in terms of the Fourier-Laplace transform of the equilibrium total dipole moment of the sample M_tot

$$\text{Σ}(\omega )={\text{Σ}}^{\ast }(\omega )-{ϵ}_{\infty }=\frac{4\pi }{3V{k}_{B}T}ℒ\left[-\frac{d}{dt}{\langle M_{tot}(0)\cdot M_{tot}(t)\rangle }_{eq}\right].$$ (1)

As the left hand side of this equation refers to the constitutive relation involving the Maxwell field E, the right hand side stems from the application of Linear Response Theory giving the susceptibility with respect to the applied external field E_ext. Consequently, the dielectric field factor E/E_ext had to enter Eq. (1) which depends on the respective boundary conditions and results from the “Finite system electrostatics” used in simulation studies.^18,21,37,38 For so-called “conducting boundary conditions”, e.g. Particle-Mesh-Ewald with carefully chosen parameters, the local field factor equals unity.^18,39,40

The collective dipole moment M_tot(t)

$$M_{tot}(t)={\displaystyle \sum _i{\displaystyle \sum _{\alpha }{q}_{i,\alpha }\cdot r_{i,\alpha }(t)}}$$ (2)

is the total dipole moment of the sample including all atoms α of the molecules i.^9,41 Since the sum over all partial charges q_i,α is zero, M_tot(t) is uniquely defined. For the interpretation M_tot(t) may be decomposed into a translational part M_J(t)

$$M_J(t)={\displaystyle \sum _i{\displaystyle \sum _{\alpha }{q}_{i,\alpha }\cdot r_{cm,i}(t)={\displaystyle \sum _i{q}_i\cdot r_{cm,i}(t)}}}$$ (3)

and a rotational part M_D(t)

$${\mathbf{\text{M}}}_D\left(t\right)={\mathbf{\text{M}}}_{tot}\left(t\right)-{\mathbf{\text{M}}}_J\left(t\right)={\displaystyle \sum _i{\displaystyle \sum _{\alpha }{q}_{i,\alpha }}}\left({\mathbf{\text{r}}}_i,\alpha \left(t\right)-{\mathbf{\text{r}}}_{cm,i}\left(t\right)\right).$$ (4)

Here, r_cm,i(t) and q_i are the center of mass of molecule i and its charge, respectively. From these definitions one immediately see that M_J(t) merges all atoms α with their partial charges q_i,α to a molecule i with charge q_i = q_i,α represented by its center of mass r_cm,i(t). Hence, only charged species contribute to the collective translational motion M_J(t). M_D(t) contains all non-translational motions of charged and neutral molecules, e.g. all kinds of rotations and molecular vibrations. Since the rotations about the center of mass dominate, M_D(t) is called “collective rotational dipole moment” in the following text. Both quantities are uniquely defined and their sum exactly yields M_tot(t).

This decomposition of M_tot(t) results in a splitting of the time correlation function Φ_tot = 〈M_tot(0)·M_tot(t)〉:⁴²

$${\text{Φ}}_{tot}(t)={\text{Φ}}_D(t)+{\text{Φ}}_J(t)$$ (5)

$${\text{Φ}}_D(t)=\langle M_D(0)\cdot M_D(t)\rangle +\langle M_D(0)\cdot M_J(t)\rangle$$ (6)

$${\text{Φ}}_J(t)=\langle M_J(0)\cdot M_J(t)\rangle +\langle M_D(0)\cdot M_J(t)\rangle$$ (7)

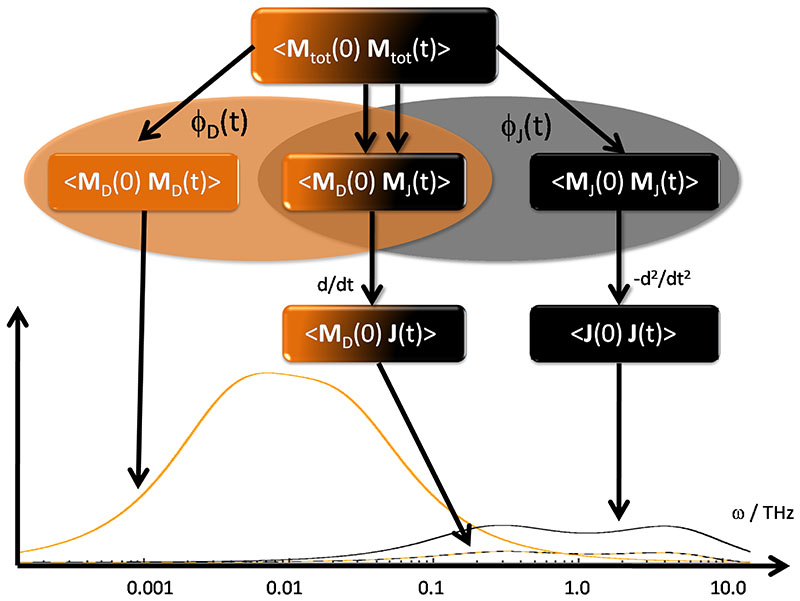
and is visualized in Fig. 1. Both, the rotational part Φ_D(t) [shown with orange background] and the translational part Φ_J(t) [black background] contain the cross-correlation 〈M_D(0) · M_j(t)〉 representing the coupling of rotation and translation at the mesoscopic level which cannot be described independently by auto-correlation functions alone.^9,41,43

Fig. 1.

The autocorrelation function of the total collective dipole moment 〈M_tot (0) · M_tot(t)〉 is decomposed into a rotational part Φ_D(t) [displayed with orange background] and a translational part Φ_J(t) [displayed with black background]. Because of toroidal jumps the correlation functions containing the collective translational dipole moment M_j(t) are transferred to functions involving the current J(t). Each correlation function affects the dielectric loss spectrum at different frequencies. The pure rotational 〈M_D(0) · M_D(t)〉 resides in the low frequency regime. The translational contributions from 〈J(0) · J(t)〉 are located at much higher frequencies. However, this separation in frequency space is not complete. There exists a common overlag region. The rotational-translational coupling 〈M_D(0) · J(t)〉 has more or less the same frequency range as the translational contributions.

As the Fourier-Laplace transform

$$ℒ[f(t)]={\displaystyle \underset{0}{\overset{\infty }{\int }}f(t)e^{i\omega t}dt}.$$ (8)

is a linear operation the decomposition of Φ_tot results in

$$ℒ\left[-\frac{d}{dt}{\text{Φ}}_D(t)\right]=\langle M_D^2\rangle +i\omega {ℒ}_{DD}(\omega )-{ℒ}_{DJ}(\omega )$$ (9)

$$ℒ\left[-\frac{d}{dt}{\text{Φ}}_J(t)\right]=ℒ\left[-\frac{d}{dt}\langle M_J(0)\cdot M_J(t)\rangle \right]-{ℒ}_{DJ}(\omega )$$ (10)

The details of the derivation of Eq. (9) can be found in Appendix A. The abbreviations ${ℒ}_{DD}(\omega ),{ℒ}_{DJ}(\omega )$ and ${ℒ}_{JJ}(\omega )$ are defined by

$${ℒ}_{DD}(\omega )=ℒ\left[\langle M_D(0)\cdot M_D(t)\rangle \right]$$ (11)

$${ℒ}_{DJ}(\omega )=ℒ\left[\langle M_D(0)\cdot J(t)\rangle \right]$$ (12)

$${ℒ}_{JJ}(\omega )=ℒ\left[\langle J(0)\cdot J(t)\rangle \right].$$ (13)

The cross-contribution ${ℒ}_{DJ}(\omega )$ and the translational contribution ${ℒ}_{JJ}(\omega )$ are already given in terms of the current J(t) representing the derivative of the collective translational moment M_j(t) defined in Eq. (3):

$$J(t)=\frac{d{M}_J(t)}{dt}={\displaystyle \sum _i{q}_i\cdot v_{cm,i}(t)}$$ (14)

with v_cm,i(t) being the velocity of the ith center of mass. The use of the current is more appropriate for simulation studies since J(t) [as opposed to M_j(t)] does not suffer from “jumps” of individual molecules due to the periodic boundary conditions. In other words, molecules leaving the simulation box on one side enter the box at the opposite side during simulation. Thereby, their coordinates r_cm,i(t) changed dramatically [causing huge, more or less instantaneous changes of M_j(t)] but their velocities v_cm,i(t) are not affected. Since these “jumps” have severe consequences on the statistics of the 〈M_J(0) · M_J(t)〉, one should use 〈J(0) · J(t)〉 instead. Therefore, the Fourier-Laplace transform of 〈M_j(0) · M_j(t)〉 may be completely reformulated in terms of the current:

$$ℒ\left[-\frac{d}{dt}\langle M_J(0)\cdot M_J(t)\rangle \right]=\frac{i}{\omega }{ℒ}_{JJ}(\omega )$$ (15)

A short derivation of the last equation is given in Appendix A.

Assembling Equation (1), (9) and (15) we get the final expression for the GDC

$$\text{Σ}(\omega )=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_D^2\rangle +i\omega {ℒ}_{DD}(\omega )-2{ℒ}_{DJ}(\omega )+\frac{i}{\omega }{ℒ}_{JJ}(\omega )\right)$$ (16)

$$=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_D^2\rangle +i\omega {ℒ}_{DD}(\omega )-{ℒ}_{DJ}(\omega )+\frac{i}{\omega }\left({ℒ}_{JJ}(\omega )+i\omega {ℒ}_{DJ}(\omega )\right)\right)$$ (17)

The different contributions to the GDC in Eq. (16) may be arranged into two groups: One with the pre-factor i/ω and one without. This equation may be compared to the experimental relation:

$$\text{Σ}(\omega )=ϵ(\omega )-{ϵ}_{\infty }+4\pi \frac{i\sigma (\omega )}{\omega }$$ (18)

In principle, the equation used in experiments contains an electronic contribution represented by ϵ_∞ which is visible in the high-frequency limit [above 10 THz]. However, in classical molecular dynamics simulations, these electronic contributions are neglected making ϵ_∞ unity.⁴⁴

Accordingly, the different contributions to the GDC in Eq. (16) can be assigned to ϵ(ω) as well as to the conductivity σ(ω) in Eq. (25)

$$ϵ(\omega )-1=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_D^2\rangle +i\omega {ℒ}_{DD}(\omega )-{ℒ}_{DJ}(\omega )\right)$$ (19)

$$\sigma (\omega )=\frac{1}{3V{k}_{B}T}\left({ℒ}_{JJ}(\omega )+i\omega {ℒ}_{DJ}(\omega )\right)$$ (20)

$\omega \cdot {ℒ}_{DD}(\omega )$ and consequently ϵ(ω) affects the low-frequency regime of the GDC as schematically depicted in Fig. 1. The frequency regime of ${ℒ}_{DJ}(\omega )$ overlaps with that of $\omega \cdot {ℒ}_{DD}(\omega )$ to a certain degree but lasts for longer frequencies. ${ℒ}_{JJ}(\omega )$ resides at frequencies in the THz regime.

The last two equations can be seen as the motivation for the “arbitrary” decomposition of M_tot: Despite the marginal cross term ${ℒ}_{DJ}(\omega ),$ the dielectric permittivity ϵ(ω) is built up by the rotational collective dipole moment M_D(t). The time derivative of the translational collective dipole moment M_j(t) almost exclusively determines the conductivity σ(ω). However, the influence of the conductivity σ(ω) on the GDC is indirect since the ratio σ(ω)/ω enters the spectrum of the GDC. Therefore, we introduce the dielectric conductivity

$$\vartheta (\omega )=4\pi \frac{i\sigma (\omega )}{\omega }$$ (21)

$$=\frac{4\pi }{3V{k}_{B}T}\left(\frac{i}{\omega }{ℒ}_{JJ}(\omega )-{ℒ}_{DJ}(\omega )\right)$$ (22)

Unfortunately, ϑ(ω) diverges for ω → 0 in the same manner as 4πiσ(ω)/ω in the experimental equation (18). This is in accordance with the experimental situation that a static field applied to a system of charged particles leads to an infinite GDC. Hence, both the experimenter and we subtract 4πiσ(0)/ω from the dielectric spectrum to get rid of the divergence. This is denoted by the index 0 in the following equations:

$${\text{Σ}}_0(\omega )=\text{Σ}(\omega )-4\pi \frac{i\sigma (0)}{\omega }$$ (23)

$$=ϵ(\omega )-1+4\pi \frac{i(\sigma (\omega )-\sigma (0))}{\omega }$$ (24)

$$=ϵ(\omega )-1+{\vartheta }_0(\omega )$$ (25)

with

$${\vartheta }_0(\omega )=4\pi \frac{i(\sigma (\omega )-\sigma (0))}{\omega }$$ (26)

$$=\frac{4\pi }{3V{k}_{B}T}\left(\frac{i\left({ℒ}_{JJ}(\omega )-3V{k}_{B}T\sigma (0)\right)}{\omega }-{ℒ}_{DJ}(\omega )\right)$$ (27)

This correction removes the overall translational drift of the ions but not all translational motion. At the theoretical level, it only affects the real part of ${ℒ}_{JJ}(\omega ).$ The imaginary part of ${ℒ}_{JJ}(\omega ).$ remains unchanged. Consequently, the correction applies to the imaginary part of ϑ(ω) whereas the real part is not affected.

The difference between the dielectric conductivity ϑ₀(ω) and the conductivity σ(ω) is more than dividing σ(ω) by the frequency ω: First, it shifts the contribution from σ(ω), e.g. peaks in the dielectric loss spectrum, to smaller frequencies. Second, and even more important, is the non-vanishing static limit⁴¹

$${\vartheta }_0(0)=\underset{\omega \to 0}{\lim }{\vartheta }_0(\omega )=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_J^2\rangle +\langle M_D(0)\cdot M_J(0)\rangle \right)$$ (28)

in contrast to

$$\underset{\omega \to 0}{\lim }\frac{\sigma (\omega )}{\omega }=\infty .$$ (29)

In principle, ϑ₀(ω) characterizes the frequency-dependent collective translational motions of ions. For example, this may include intermolecular vibrations of ions, ion cage librations or the translation of ion aggregates. ϑ₀(ω) does not involve contributions from collective motions of neutral species, e.g. water, which also may be present but they do not contribute to the collective translational dipole moment M_j(t) according to Eq. (3).

From Eq. (19) the static limit of the dielectric permittivity can be easily read

$$ϵ(0)-1=\underset{\omega \to 0}{\lim }ϵ(\omega )-1=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_D^2\rangle +\langle M_D(0)\cdot M_J(0)\rangle \right)$$ (30)

and represents the rotational contribution to the static GDC. Uniting the equations (28) and (30) the static GDC ϵ_stat is given by

$${ϵ}_{stat}-1=\underset{\omega \to 0}{\lim }{\text{Σ}}_0(\omega )$$ (31)

$$=ϵ(0)-1+{\vartheta }_0(0)$$ (32)

$$=\frac{4\pi }{3V{k}_{B}T}\left(\langle M_D^2\rangle +\langle 2M_D(0)\cdot M_J(0)\rangle +\langle M_J^2\rangle \right)$$ (33)

$$=\frac{4\pi }{3V{k}_{B}T}\langle M_{tot}^2\rangle$$ (34)

The derivation of this expression shows that the dielectric conductivity ϑ₀(ω) although residing in the high frequency regime finally makes a significant contribution ϑ₀(0) to the static GDC ϵ_stat. This demonstrates that in charged, dipolar systems the dielectric conductivity ϑ₀(ω) is an equal partner of the permittivity ϵ(ω).⁴⁵

At this point a caveat is necessary: Eq. (34) is a theoretical relation connecting the static dielectric constant ϵ_stat with the mean squared fluctuations of the total collective dipole moment M_tot(t). One should not forget, however, that M_tot(t) suffers from toroidal jumps of its translational component M_j(t). Hence, a computation of ϵ_stat directly from $\langle M_{tot}^2\rangle$ is not feasible. Rather, one has to trace back the way to the total current as derived from Eq. (9) to (27) and displayed in Fig. 1.

Our program GENDICON provides the real and imaginary part of the dielectric spectra of the conductivity σ(ω), the dielectric conductivity ϑ₀(ω), the dielectric permittivity ϵ(ω) and the GDC Σ₀(ω), separately. All dielectric quantities [ϵ(ω), ϑ₀(ω) and Σ₀(ω)] are traditionally in units of 4 πϵ₀ with ϵ₀ = 8.854187 · 10^-12AsV⁻¹m⁻¹ being the vacuum permittivity [or electric constant]. The dielectric spectra may be calculated in GENDICON by the numerical Fourier-Laplace transform or more elegantly by the use of fit functions which are described in the next section.

B. Fit functions

Bearing in mind that for a collective property every point along the trajectory provides a single value only, because averaging over particles, residue, etc is not possible, these extreme demand on simulation length can be easily understood. This explains why TCFs of collective dipole moments are still noisy for simulation length of hundred nanoseconds. In order to smooth this statistical roughness, TCFs are often fitted to analytical expressions. A first overview of the fit functions used in this work is given in Table I. The next paragraphs deal with each fit function separately.

Table I.

The computed correlation functions were fitted with the corresponding fit function f(t) In the top part of the table the corresponding ${ℒ}_{DD}(\omega ),{ℒ}_{DJ}(\omega )$ and ${ℒ}_{JJ}(\omega )$ are used to calculate $ℒ\left[-\frac{d}{dt}{\text{Φ}}_D(t)\right]$ and $ℒ\left[-\frac{d}{dt}{\text{Φ}}_J(t)\right]$ by means of Eq. (9) and (15). At the bottom of the table $ℒ\left[-\frac{d}{dt}{\text{Φ}}_D(t)\right]$ is calculated directly.

correlation function	fit function f(t)	$ℒ[f(t)]$
〈MD(0) · MD(t)〉	${\displaystyle \sum _k{A}_k\cdot e^{-t/{\tau }_k}}$	${\displaystyle \sum _k\frac{A_k\cdot {\tau }_k}{1-i\omega {\tau }_k}}$	(Debye)	→ $\to {ℒ}_{DD}(\omega )$
〈MD(0) · J(t)〉	${\displaystyle \sum _k{A}_k{t}^{{\gamma }_k-1}\cdot e^{-t/{\tau }_k}}$	${\displaystyle \sum _k\frac{{\tilde{A}}_k}{{\left(1-i\omega {\tau }_k\right)}^{{\gamma }_k}}}$	(Cole - Davidson)	→ $\to {ℒ}_{DJ}(\omega )$
〈JD(0) · J(t)〉	${\displaystyle \sum _k{A}_k\cos \left({\omega }_k\cdot t+{\delta }_k\right)e^{-t/{\tau }_k}}$	${\displaystyle \sum _k\frac{A_k\cdot {\tau }_k\left(\cos \left({\delta }_k\right)\cdot \left(1-i\omega {\tau }_k\right)-{\omega }_k{\tau }_k\sin \left({\delta }_k\right)\right)}{{\tau }_k^2{\omega }_k^2+{\left(1-i\omega {\tau }_k\right)}^2}}$		→ $\to {ℒ}_{JJ}(\omega )$
correlation function	fit function f(t)	$ℒ\left[-\frac{d}{dt}f(t)\right]$
〈MD(0) · MD(t)〉	A ·e-(t/τ)β	$\frac{A}{{\left(1-{\left(i\omega {\tau }^{hn}\right)}^{{\alpha }^{hn}}\right)}^{{\gamma }^{hn}}}$	(Havriliak-Negami)

The application of the set of fit functions for the rotational and translational correlation functions is not limited, however, to 〈M_D(0) · M_D(t)〉 and 〈J(0)·J(t)〉, but can be applied to the correlation functions of their subcomponents, too.

1. Fitting 〈M_D(0) · MD(t)〉 multi-exponentially

Quite generally, TCFs Φ(t) obey⁴⁶

$$\frac{d\text{Φ}(t)}{dt}=-{\displaystyle \underset{0}{\overset{t}{\int }}\mathcal{K}\left(t^{\prime }\right)\cdot \text{Φ}\left(t-t^{\prime }\right)d{t}^{\prime }}$$ (35)

For a simple Markovian process the kernel $\mathcal{K}\left(t^{\prime }\right)$ is a δ-function, i.e. $\mathcal{K}\left(t^{\prime }\right)=\lambda \cdot \delta \left(t^{\prime }\right).$ As a result, the corresponding TCF Φ(t) becomes mono-exponential. In order to cope with complex dynamics a distribution of relaxation times ρ(t′) is assumed for the TCF

$$\text{Φ}(t)={\displaystyle \underset{0}{\overset{\infty }{\int }}\rho \left(t^{\prime }\right)e^{-t/t^{\prime }}d{t}^{\prime }.}$$ (36)

The easiest distribution function ρ(t′) is a sum of δ-functions. As a result, Φ(t) is a super-position of exponential functions. For example, one may fit the autocorrelation function of the collective rotational dipole moment with such a superposition:

$$\langle M_D(0)\cdot M_D(t)\rangle \simeq {\displaystyle \sum _k{A}_k\cdot e^{-t/{\tau }_k}}$$ (37)

The number of exponential terms depends on the TCF under investigation and the precision desired. This may require up to four terms in this work. As the amplitudes A_k determine the height of the peaks in the imaginary part of the dielectric spectrum, the careful determination of the amplitudes and their correct sum is crucial. Due to the linearity of the Fourier-Laplace transform the multi exponential fit results in a superposition of Debye processes.

$$ℒ\left[{\displaystyle \sum _k{A}_k\cdot e^{-t/{\tau }_k}}\right]={\displaystyle \sum _k\frac{A_k{\tau }_k}{1-i\omega {\tau }_k}\simeq {ℒ}_{DD}(\omega )}$$ (38)

Since the imaginary part of the Fourier-Laplace transform displays maxima at ω_k = 1/τ_k the distribution of relaxation times $\rho \left(t^{\prime }\right)={\displaystyle \sum _k{A}_k\cdot \delta \left(t^{\prime }-{\tau }_k\right)}$ can be recognized. As similar relaxation times result in a single broad peak in the spectrum, they are not a real problem. However, an increasing number of exponentials impedes a reasonable interpretation.

In order to keep the number of fit parameters at the minimum one could alternatively use so-called “Kohlrausch-Williams-Watt” [KWW] functions⁴⁷ which model the spread of exponentials by a single parameter β

$$\langle M_D(0)\cdot M_D(t)\rangle \simeq A\cdot e^{-{(t/\tau )}^{\beta }}.$$ (39)

In principle, the Fourier-Laplace transform can be computed by two series as illustrated in Appendix B. For the sake of simplicity and stability GENDICON uses the Havriliak-Negami function to compute

$$ℒ\left[-\frac{d}{dt}A\cdot e^{-{(t/\tau )}^{\beta }}\right]\simeq \frac{A}{{\left(1-{\left(i\omega {\tau }^{hn}\right)}^{{\alpha }^{hn}}\right)}^{{\gamma }^{hn}}}.$$ (40)

The parameters α^hn, γ^hn and τ^hn can be expressed in terms of τ and β of the KWW function according to:

$$\begin{array}{l}{\alpha }^{hn}\hfill \\ {\gamma }^{hn}\hfill \\ {\tau }^{hn}\hfill \end{array}\}=a(\tau )e^{-\beta /b(\tau )}+c(\tau )$$ (41)

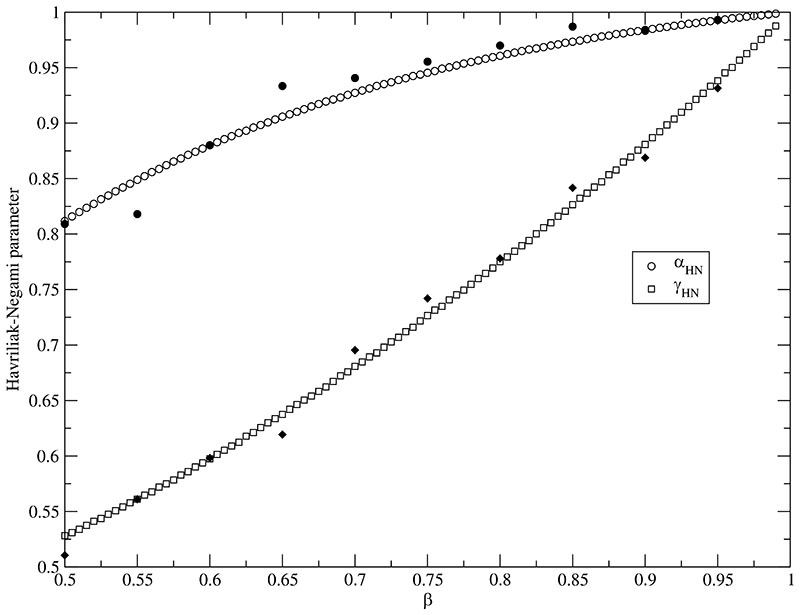
a(τ), b(τ) and c(τ) for α^hn, γ^hn and τ^hn can be found in Table II. These parameters are gained from fits of the numerical Fourier-Laplace transforms of a series of KWW-functions. Therefore, β was varied from β = 0.500 up to 1.000 with a step size of Δβ = 0.005 and τ was varied from τ = 100 ps up to τ = 900 ps with a step size of Δτ = 100 ps. This range of KWW parameters corresponds to the expected functions in dielectric spectra. The KWW function of each combination of these β and τ-values was calculated until f(t) = e^−(t/τ) was less than 10⁻⁴ in order to avoid chirp effects of the numerical Fourier-Laplace transformation. Furthermore, the function was calculated each Δt = 10⁻⁴ ps. This data series was used to evaluate the spectrum from 10 MHz to 100 THz according to Eq. (40) and fitted to the Havriliak-Negami function. It turned out that the dependence of α^hn, γ^hn and τ^hn on β was exponentially at each τ as visible in Fig. 2 and fitted according to Eq. (41). In Fig. 2 the fitted α^hn and γ^hn from Ref. 48 are additionally displayed as filled circles and squares, respectively. These parameters were gained by fitting the distribution of the KWW [see Eq. (65)] and the Havriliak-Negami function. Although their method is more indirect, the results are very close to our method of direct fitting the dielectric spectrum. Varying τ resulted in a slight shift of the parameters a(τ), b(τ) and c(τ) and was fitted linearly.

Table II.

Interpolation of the Havriliak-Negami parameters: α^hn, γ^hn and τ^hn can be approximated by a(τ)e^{−β/b(τ)+c(τ)} from the KWW-function f(t) = e^−(t/τ)β with the KWW parameter τ and β.

	a(τ)	b(τ)	c(τ)
α hn	-23·10−5 τ-1.24	-2.1·10−5 τ+0.29	-0.44·10−5 τ+1.04
γ hn	-11·10−5 τ+0.34	15.·10−5 τ-0.86	17.·10−5 τ-0.091
τ hn	9.7·τ+284.	5.·10−5 τ+0.28	0.528·τ+9.9

Fig. 2.

Fitted Havriliak-Negami parameter α_HN and γ_HN as function of the KWW parameter β at τ = 500 ps. The open symbols represent the fit in this work. The filled symbols are taken from Ref. 48.

2. Fitting 〈J(0) · J(t)〉 with damped oscillators

As opposed to the monotonic behaviour of the collective rotational dipole functions the TCFs involving the current relax within few picoseconds and are oscillatory in nature. Since a single damped oscillation already corresponds to a more complicated kernel⁴⁶

$$\mathcal{K}\left(t^{\prime }\right)=\lambda \cdot e^{-t^{\prime }/\zeta },$$ (42)

a superposition⁴⁵ of them is given by a multi-exponential phase-shifted cosine functions

$$\langle J(0)\cdot J(t)\rangle \simeq {\displaystyle \sum _k{A}_k\cos \left({\omega }_k\cdot t+{\delta }_k\right)e^{-t/{\tau }_k}}$$ (43)

which represents damped oscillators. The relaxation times τ_k are found to be much shorter than those of 〈M_D(0) · M_D(t)〉.

The corresponding Fourier-Laplace transform of this superposition of the damped oscillators reads

$$\begin{array}{c}ℒ\left[{\displaystyle \sum _k{A}_k\cos \left({\omega }_k\cdot t+{\delta }_k\right)e^{-t/{\tau }_k}}\right]={\displaystyle \sum _k{A}_k{\tau }_k\frac{\cos \left({\delta }_k\right)\cdot \left(1-i\omega {\tau }_k\right)-{\omega }_k{\tau }_k\sin \left({\delta }_k\right)}{{\tau }_k^2{\omega }_k^2+{\left(1-i\omega {\tau }_k\right)}^2}}\\ \simeq {ℒ}_{JJ}(\omega )\end{array}$$ (44)

and is also tabulated in Table I.

The real part of that Fourier-Laplace transform reads

$$\begin{array}{c}Re\left[{ℒ}_{JJ}(\omega )\right]\simeq {\displaystyle \sum _k\frac{A_k{\tau }_k}{2}(\frac{\cos \left({\delta }_k\right)-{\tau }_k\left({\omega }_k-\omega \right)\sin \left({\delta }_k\right)}{1+{\tau }_k^2{\left({\omega }_k-\omega \right)}^2}}\\ +\frac{\cos \left({\delta }_k\right)-{\tau }_k\left({\omega }_k+\omega \right)\sin \left({\delta }_k\right)}{1+{\tau }_k^2{\left({\omega }_k+\omega \right)}^2})\end{array}$$ (45)

and gives a zero frequency-limit

$$\underset{\omega \to 0}{\lim }\mathrm{Re}\left[{ℒ}_{JJ}(\omega )\right]=3V{k}_{B}T\sigma (0)\simeq {\displaystyle \sum _k{A}_k{\tau }_k\left(\frac{\cos \left({\delta }_k\right)-{\tau }_k{\omega }_k\sin \left({\delta }_k\right)}{1+{\tau }_k^2{\omega }_k^2}\right)}$$ (46)

As suggested by Eq. (27) one has to correct the real part of the Fourier-Laplace transform by 3Vk_BTσ(0) for the computation of the dielectric conductivity. This way, $\underset{\omega \to 0}{\lim }Im\left[{\vartheta }_0(\omega )\right]$ becomes zero for the used fit function.

The imaginary part of ${ℒ}_{JJ}(\omega )$) can be approximated by

$$\begin{array}{c}Im\left[{ℒ}_{JJ}(\omega )\right]\simeq {\displaystyle \sum _k\frac{A_k{\tau }_k}{2}(\frac{-\sin \left({\delta }_k\right)-{\tau }_k\left({\omega }_k-\omega \right)\cos \left({\delta }_k\right)}{1+{\tau }_k^2{\left({\omega }_k-\omega \right)}^2}}\\ +\frac{\sin \left({\delta }_k\right)+{\tau }_k\left({\omega }_k+\omega \right)\cos \left({\delta }_k\right)}{1+{\tau }_k^2{\left({\omega }_k+\omega \right)}^2})\end{array}$$ (47)

The contribution to the static value of the GDC stems from the zero frequency limit of the imaginary part of ${ℒ}_{JJ}(\omega )$ and can be computed

$$\begin{array}{c}\underset{\omega \to 0}{\lim }\mathrm{Re}\left[{\vartheta }_0(\omega )\right]=\frac{4\pi }{3V{k}_{B}T}\underset{\omega \to 0}{\lim }\frac{Im\left[{ℒ}_{JJ}(\omega )\right]}{\omega }\\ \simeq \frac{4\pi }{3V{k}_{B}T}{\displaystyle \sum _k\frac{A_k{\tau }_k^2}{{\left({\tau }_k^2{\omega }_k^2+1\right)}^2}\left(\cos \left({\delta }_k\right)\left({\tau }_k^2{\omega }_k^2-1\right)+2{\tau }_k{\omega }_k\sin \left({\delta }_k\right)\right).}\end{array}$$ (48)

Please note that the correction of Eq. (27) only applies for the real part of ${ℒ}_{JJ}(\omega ).$ What about non-charged species? Since they possess no net charge, their corresponding 〈J(0) · J(t)〉 will be zero all the time. Consequently, all their amplitudes Ak of the 〈J(0) · J(t)〉 -fit function are zero and the corresponding contribution to the static translational value ϑ₀(0) reduces to zero as one can see from the equation above. The influence of charged species are mainly characterized by the time constants τ_k.

3. Fitting 〈M_D(0) · J(t)

In contrast to the TCFs 〈M_D(0) · M_D(t)〉 and 〈J(0) · J(t)〉 the influence of the cross-correlation between the collective rotational dipole moment and the current, namely 〈M_D(0) · J(t)〉, is generally of marginal importance for the dielectric spectra. Nevertheless, 〈M_D(0) · J(t)〉 can often be fitted according to

$$M_D(0)\cdot J(t)\simeq {\displaystyle \sum _k{A}_k\cdot t^{{\gamma }_k-1}\cdot e^{-t/{\tau }_k}}$$ (49)

with a short time constant τ_k.^49,50 The co-factor $t_k^{{\gamma }_k-1}$ ensures that the cross-correlation starts at 0 for γ_k-values greater than one. Therefore, fitted γ_k less than one are unrealistic since they result in an infinite value of the TCF at t = 0.

The corresponding Fourier-Laplace transform of Eq. (49) is a superposition of so-called Cole-Davidson functions: ^49–52

$$ℒ\left[{\displaystyle \sum _k{A}_k{t}^{{\gamma }_k-1}{e}^{-t/{\tau }_k}}\right]={\displaystyle \sum _k{A}_k\cdot \text{Γ}\left({\gamma }_k\right){\left(\frac{{\tau }_k}{1-i\omega {\tau }_k}\right)}^{{\gamma }_k}}$$ (50)

$$={\displaystyle \sum _k\frac{{\tilde{A}}_k}{{\left(1-i\omega {\tau }_k\right)}^{{\gamma }_k}}\simeq {ℒ}_{DJ}}$$ (51)

The general expression (49) includes the special case of pure exponentials inthe time domain or equivalently Debye processes in the frequency domain. Specifying γ_k = 1, however, enforces more than one exponential term in order to secure that the amplitudes of these exponential functions A_k sum up to zero.

III. Methods

In this study six aqueous mixtures of the MIL $\text{MIL}{\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$ with a water mole fraction x_H2O between 0.653 and 0.974 were simulated over 40 ns with the molecular dynamics program package CHARMM⁵³ under constant volume and temperature [T = 300 K] with a time step of Δt =1 fs. The cubic simulation boxes [V =(67.0 Å)³] are generated by a procedure described in Ref. 54 with the ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water compositions tabulated in Table III. Nonbonded and image lists were updated heuristically using a 12 Å neighbour list distance. Lennard-Jones energies and forces were smoothly switched off between 9 and 10 Å. The electrostatic interactions were calculated by the Particle-Mesh Ewald method,^55,56 using a r_EW =10 Å cutoff for the real-space part interactions. In order to achieve the so-called “conducting boundary conditions” the damping constant κ has to be evaluated by the following integral Q:^18,21,57

$$Q={\left(\frac{\kappa }{\sqrt{\pi }}\right)}^3{\displaystyle \underset{0}{\overset{r_{EW}}{\int }}4\pi r^2{e}^{-{\kappa }^2{r}^2}dr}$$ (52)

Table III.

Composition and dielectric properties of the ${\text{EMIM}}^{+}{}^{-}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixtures under investigation. Please note that ${\text{EMIM}}^{+}{}^{-}{\text{CF}}_3{\text{SO}}_3^{-}$/water mix ϵ_start - 1 = ϵ(0) - 1 + ϑ₀(0)

mole fraction xH2O	ion pairs	water	viscosity [mPas]	ϵ(0)	ϑ0(0)	ϵstart
0.974	200	7428	0.5	63.9	1.9	65.8
0.932	400	5489	1.4	44.0	6.4	50.4
0.899	500	4467	2.2	33.5	6.8	40.3
0.852	600	3444	4.5	24.9	2.7	27.6
0.785	700	2561	7.5	20.4	3.5	23.9
0.653	800	1504	22.5	12.5	2.8	15.3

with κ being the lowest real number so that Q equals unity with a very high numerical precision. In our case, this procedure leads to a κ-value of 0.410 Å⁻¹ which is higher than the values proposed by molecular dynamics program packages.

The cationic force field parameters are taken from Ref. 58,59 which involve Lennard-Jones parameter from the AMBER force field.⁶⁰ The partial charges are changed to the values reported in Ref. 61. gained by a distributed multipole analysis⁶² at the MP2/6-31G** level. The change of the EMIM⁺ partial charges generally results in a viscosity closer to the experimental value, e.g. in Ref. 29. The anionic force field parameters stems from Ref. 63 without any further modification. For water, the TIP3P model of Jorgensen is employed.⁶⁴ All bond lengths are kept fixed by the SHAKE algorithm,⁶⁵ whereas bond angles and torsions are left flexible.

IV. Results

In a first step the trajectory data representing the time series of coordinates and velocities have to be converted to the collective rotational dipole moment M_D(t) and the collective current J(t). Because of the difference in the genuine dynamic range these two time series are treated differently: M_D(t) is evaluated each 50 fs for the elapsed simulation time period of more than 40 ns from the stored trajectory files. The time graining of J(t) is much finer, indeed, J(t) is computed for each time step of 1 fs but only for a time period of 10 ns synchronously with the integration of motion performed by the molecular dynamics program CHARMM⁵³. This procedure of data reduction, i.e. the storage of J(t) time series instead of the plethora of atomic velocities at each time step, enables the very long evaluation period of the above mentioned 10 ns.

In a second step the respective auto- [〈M_D(0) · M_D(t)〉 and 〈J(0) · J(t)〉] as well as the cross- [〈M_D(0) · J(t)〉] correlation functions are computed. In case of the latter a duplicate time series of M_D(t) analogously to J(t) with afiner resolution of 1 fs is used. All these TCFs are fitted according to the formulae described in the Theory section. The corresponding fit parameters for the six ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixtures are given in Tables IV, V and VI. In this way, the dependence on the mole fraction x_H2O is visible from the trend of the fit parameters.

Table IV.

Fit parameters of the auto-correlation function of the collective rotational dipole moment 〈M_D(0) · M_D(t)〉 according to $f(t)={\displaystyle \sum _k{A}_k\cos \left({\omega }_{k}t+{\delta }_k\right)e^{-t/{\tau }_k}}.$

x H 2 O	A1 [D2]	τ1 [ps]	A2 [D2]	τ2 [ps]	A3 [D2]	τ3 [ps]	A4 [D2]	τ4 [ps]
0.974	0.17	794	12.3·104	12.84	6.14·104	5.41	994	0.09
0.932	5.00	60.0	9.45·104	22.51	2.80·104	6.09	2022	0.20
0.899			8.25·104	25.77	0.959·104	3.50	1374	0.14
0.852	1680	398	5.47·104	41.77	0.989·104	7.16	2400	0.30
0.785	1410	2500	4.05·104	90.27	1.12·104	12.26	2206	0.25
0.653	15300	223	1.32 104	41.51	0.289 104	1.85

Table V.

Fit parameters of the current-current auto-correlation function 〈J(0) · J(t)〉 according to $f(t)={\displaystyle \sum _k{A}_k{t}^{{\gamma }_k-1}{e}^{-t/{\tau }_k}.}$ ω₃ and δ₃ are zero.

x H 2 O	A1 [D2 ps−2]	ω1 [ps−1]	δ 1	τ1 [ps]	A2 [D2 ps−2]	ω2 [ps−1]	δ 2	τ2 [ps]	A3 [D2 ps−2]	τ3 [ps]
0.974	1.89·104	17.016	-1.293	0.059	67.1·104	0.160	1.524	0.235	-14.7	13.2
0.932	5.12·104	16.415	-1.099	0.071	97.8·104	0.233	1.519	0.216	-78.9	6.0
0.899	8.71·104	14.912	-1.144	0.065	105·104	0.299	1.519	0.194	-149	10.0
0.852	9.22·104	16.833	-1.124	0.072	143·104	0.324	1.520	0.183	-191	3.6
0.785	11.9·104	17.240	-0.954	0.082	233·104	0.217	1.545	0.169	-134	6.2
0.653	13.9 104	18.359	-1.009	0.084	271 104	0.285	1.543	0.142	-262	3.8

Table VI.

Fit parameters of the cross-correlation function 〈M_D(0) · J(t)〉 according to $f(t)={\displaystyle \sum _k{A}_k{t}^{{\gamma }_k-1}{e}^{-t/{\tau }_k}.}$ The index 1 corresponds to the first peak of the cross-correlation function whereas the second index characterizes the tail of the TCF at longer times. ϵ_MDJ is the contribution of this cross-correlation function to the static dielectric constant. The number in brackets corresponds to the share of 2ϵ_MDJ in ϵ_start

x H 2 O	A1 [D2 ps−γ1]	τ1 [ps]	γ 1	A2 [D2 ps−γ2]	τ2 [ps]	γ 2	ϵMDJ
0.974	-3.58·104	0.192	3.25	-550	2.0	1.77	0.72 (2.2%)
0.932	-9.11·104	0.159	3.13	-495	3.8	1.44	1.22 (4.8%)
0.899	-20.4·104	0.133	3.28	-452	3.2	1.33	0.87 (4.3%)
0.852	-32.3·104	0.121	3.37	-380	3.3	1.30	0.79 (5.7%)
0.785	-46.4·104	0.107	3.35	-330	3.1	1.25	0.66 (5.5%)
0.653	-56.1·104	0.095	3.30	-300	3.0	1.17	0.55 (7.2%)

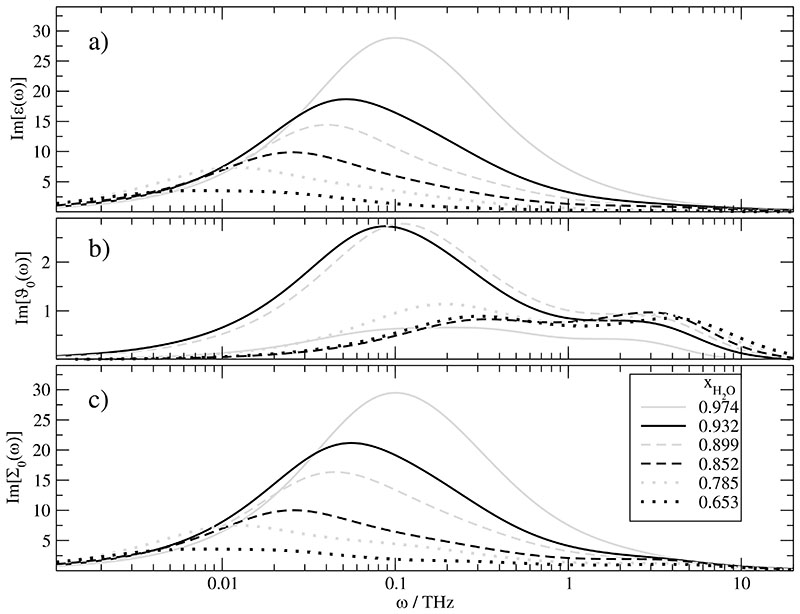
In a third step the fit functions are Fourier-Laplace transformed in order to yield the spectrum of the dielectric permittivityϵ(ω) and the dielectric conductivity ϑ₀(ω). The superposition of both spectra gives the frequency-dependent GDC Σ₀(ω). The final test of a proper fitting procedure is the juxtaposition of Σ₀(ω) [as visible in Fig. 3] built up from the contributions of the fit functions and that obtained by numerical Fourier-Laplace transformation which can be considerably facilitated by means of a chirp function described in Appendix C.

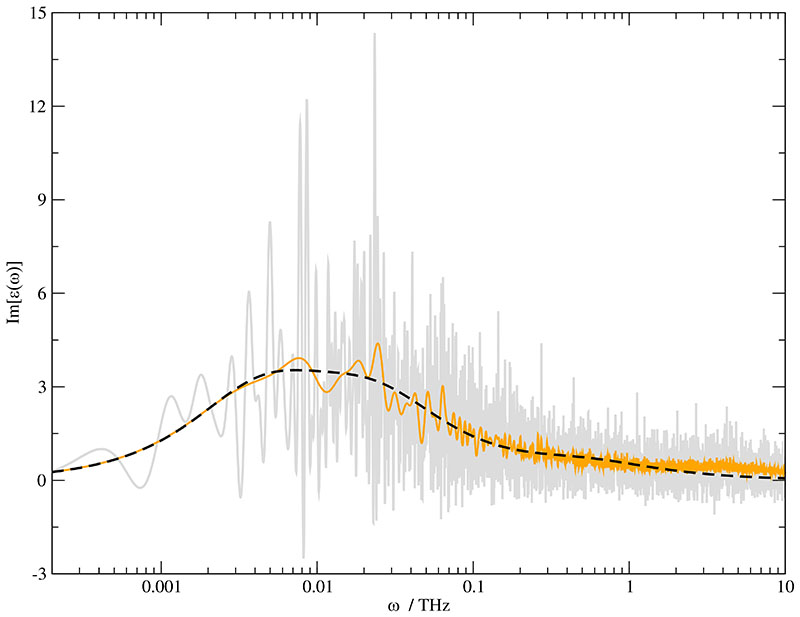
Fig. 3.

Im[ϵ(ω)] of the ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixture with a water mole fraction x_H2O =0.653. The gray line represents the spectrum of the pure data. The application of a chirp function with t₀ = 1000 ps and τ =100 ps changes the spectrum to the orange solid line. The black dashed line represents the fit with three exponential functions with the parameter given in Table IV.

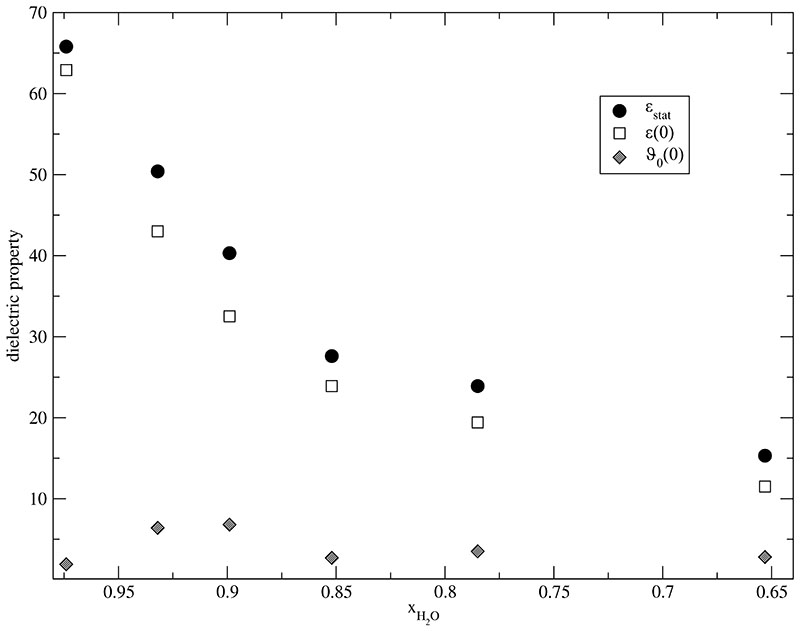
The static limit of Σ₀(ω) is the experimentally accessible static dielectric constant ϵ_stat. We emphasize that both low frequency limits ϵ(0) and ϑ₀(0) contribute to ϵ_stat as can be read directly from Table III. While their sum is experimentally accessible the static dielectric permittivity and the static dielectric conductivity can not be measured by experiments independently. In fact, they serve as an explanatory device to figure out the amount of rotation and translation. In case of our mixtures the rotational part plays the dominant role. This is in accordance with the large amount of water, a highly polar dielectric medium. The ratio of rotational [open squares] and translational [grey diamonds] contribution is displayed in Fig. 4 for different mole fractions x_H2O. As water is a highly polar dielectric medium whereas MILs – despite of their net charge – are low conducting materials, the dependence of ϵ(0) on x_H2O is strong as compared to that of ϑ₀(0). Upon superposition this strong dependence is almost maintained for ϵ_stat.

Fig. 4.

Static dielectric properties of the ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixtures. The overall static dielectric constant ϵ_stat consists of its rotational ϵ(0) and its translational contribution ϑ₀(0).

It would be tempting to compute ϵ_stat by averaging over independent snapshots along the trajectory. However, this procedure might work for ϵ(0) but will fail to evaluate ϑ₀(0) and consequently ϵ_stat: One might think that the static dielectric conductivity could be obtained by averaging ${\text{M}}_J^2$ over snapshots according to Eq. (28). However, this approach overlooks the finiteness of simulated samples which implies toroidal jumps of the coordinates of the charged species due to periodic boundary conditions. As velocities do not suffer from toroidal jumps, the computation of the static limit of the dielectric conductivity via the current J(t) is the only way to cope with this problem. The rotational component ϵ(0) is not plagued with that problem because the corresponding collective dipole moment M_D(t) is not made up by absolute coordinates but by coordinate differences which cancel toroidal jumps.

As a result the computation of a static quantity requires a time series. This is no additional effort, however, as our focus is on the full frequency-dependent dielectric spectrum Σ₀(ω) which inevitably requires sufficiently long time series. While experiments are restricted to the frequency-dependent GDC Σ₀(ω) as a whole, our simulation enable the separate computation of the rotational ϑ(ω) and the translational part ϑ₀(ω).

A. ϵ(ω)and 〈M_D(0) · M_D(t)〉

The main contribution of dielectric constant ϵ(ω) stems from the auto-correlation of the collective rotational dipole moment 〈M_D(0) · M_D(t)〉. A Fourier-Laplace transform of the raw data of 〈M_D(0) · M_D(t)〉 is not desirable since the integration ofstatistical errors ofthe TCF at very long times leads to blurred spectra. This can be circumvented up to a certain degree by restricting the TCF to a specific time or using chirp functions. The simplest method which we used our articles is the Fourier-Laplace transform of the corresponding fit functions. As mentioned in the fitting section before, 〈M_D(0) · M_D(t)〉 can be fitted multi exponential. Commonly, one starts with the longest relaxation time constant and subtract this exponential function from the pure correlation data. The remaining residuals are fitted exponential again. This procedure is repeated until the sum of amplitudes A_k reaches the first value of the numerical correlation data. As visible in Table IV this procedure results in up to four exponential terms. Larger number of exponential term causes no problems in the computation of the spectrum since unimportant exponentials are often more or less invisible in the dielectric loss spectrum Im[ϵ(ω)] but they sometimes impedes a reasonable interpretation of the data. Nevertheless, the sum of all A_k should represent the initial value of 〈M_D(0) · M_D(t)〉 in order to give the right static dielectric constant ϵ(ω = 0).

With the given fit parameters in Table IV the dielectric loss spectrum Im[ϵ(ω)] can be computed easily and is shown in Fig. 5a for the six ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixtures under investigation. With the exception of the last two mixtures with a water mole fraction of x_H2O of0.785[grey dotted line] and 0.653 [black dotted line], the dielectric spectrum Im[ϵ(ω)] can be fitted with a Havriliak-Negami function with the parameters in Table VII. With decreasing water content, the maximum of the corresponding peak decreases. Consequently, the corresponding amplitude of the Havriliak-Negami fit decreases, too. This is quite expected since water has a very high dipolar density. Furthermore, the location of the peak is shifted to lower frequency and leads to increasing values of the fitted τ^hn. Interestingly, this τ^hn seems to depend linearly on the water mole fraction x_H2O. This is surprising since the exponential time constants [which were used to construct the spectrum] are normally scaled by the viscosity²⁹ which does not scale linearly with the water mole fraction x_H2O. The Havriliak-Negami α^hn-parameter is more or less constant whereas γ^hn decreases with decreasing x_H2O.

Fig. 5.

Imaginary part of the dilectric spectra of the ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixtures: a) dielectric constant ϵ(ω). b) dielectric conductivity ϑ₀(ω). Please note that the y-axis is enlarged in order to distinguish the spectra of different mole fraction x_H2O. c) Overall generalized dielectric constant Σ₀(ω).

Table VII.

Fit of Im[ϵ(ω)] to the Havriliak-Negami function Eq. (40). Because of the peak-shoulder structure of Im[ϵ(ω)] for x_H2O=0.785 and 0.653, a fit with a single Havriliak-Negami function was not possible.

x H 2 O	A	α HN	γ HN	τHN [ps]
0.974	63.3	0.955	0.979	9.86
0.932	43.4	0.967	0.820	21.3
0.899	32.3	1.02	0.716	32.3
0.852	23.7	0.993	0.671	54.2
0.785
0.653

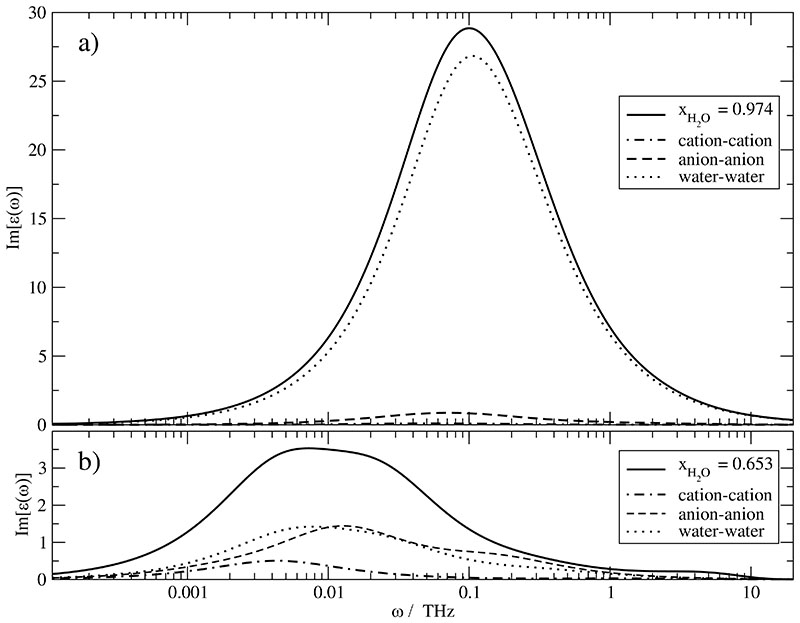
In order to elucidate the characteristics of ϵ(ω) at a given mole fraction x_H2O we have computed separately the contribution from the cations, anions and water. This speciesspecific composition is shown for the highest mole fraction x_H2O = 0.974 in Fig. 6a and the lowest x_H2O = 0.653 in Fig. 6b. The behaviour of intermediate systems changes gradually from Fig. 6a to Fig. 6b for the main peak [as visible by the Havriliak-Negami parameters of the overall peak in Table VII]. The shoulder at lower water mole fractions above 1 THz emerges from the shift of the main peak to lower frequencies due to the increasing viscosity. In contrast, the “shoulder” is covered by the main peak at x_H2O = 0.974.

Fig. 6.

Decomposition of the imaginary part of the ϵ(ω) spectrum of the ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixtures into molecular contributions at two different mole fractions: a) x_H2O =0.974 and b) x_H2O =0.653. The contribution of the cross-correlation 〈MD(0) · J(t)〉 is part of the overall black line but not shown as single contribution.

As already pointed out for the static dielectric permittivity the water component makes the dominant contribution at x_H2O = 0.974 visible by the black dotted line in Fig. 6a. Cationic and anionic contributions are marginal. This situation changes dramatically for x_H2O = 0.653: Intra- and intermolecular water-water and anion–anion interactions are now of comparable size and even the cation–cation contribution is discernible but of lower importance. Furthermore, it is slightly shifted to lower frequencies. The significant contribution of more than one species to ϵ(ω)complicates the spectrum and thus rules out the possibility of a description by a single Havriliak-Negami function at frequencies between 3 GHz and 30 GHz.

It should be noted that the total ϵ(ω)[black line] is more than the sum of the three contributions mentioned above since there are interactions between the cations, anions and water as well as translational-rotational coupling discussed later. This becomes obvious in Fig. 6b at the left and right wings. The low-frequency wing up to 2 GHz the sum of the cation-cation, anion-anion and water-water contribution is certainly below the overall spectrum [black line]. In other words, the interspecies cross-terms make a significant positive contribution. This is reversed at the high-frequency wing above 100 GHz.

B. ϑ₀(ω)and 〈J(0) · J(t)〉

A reliable fit of the current auto-correlation function 〈J(0) · J(t)〉 is much more delicate than that of 〈M_D(0) · M_D(t)〉. In principle, two terms of Eq. (43) are sufficient to reproduce the overall shape of 〈J(0) · J(t)〉 at first sight. When calculating the static conductivity from these two terms, however, the resulting value is too high. As shown in Ref. 45 one needs at least a third exponential term [ω₃ and δ₃ equal zero] to get a consistent value of σ(0). This fact demonstrates that fit functions have to be used very carefully: The third component does not affect the shape of 〈J(0) · J(t)〉 in a visible manner due to its low amplitude but contributes to ϑ₀(ω) significantly. This comes from the very high time constant τ₃ compared to τ₁ and τ₂.

Once, the fit parameters have been determined carefully, the spectrum of the dielectric conductivity ϑ₀(ω) displayed in Fig. 5b is readily obtained. There are two striking features: On the one hand the peak heights of ϑ₀(ω) are smaller by almost one order of magnitude as compared to ϵ(ω). This is hidden in Fig. 5 by the fact that the scaling of subfigure Fig. 5b was spread in order to discern the spectra for the various mole fractions x_H2O. On the other hand there is no gradual change from the highest to the lowest water mole fraction. This comes from the simultaneous change of the viscosity and the number of charge carrier as a function of x_H2O. At low x_H2O there are many ions, e.g. 800 ion pairs for x_H2O =0.653. However, they are moving in a high viscous system of 22.5 mPa s [refer to Table III]. In contrast, at x_H2O =0.972 fewer ions, i.e. 200 ion pairs, are moving in a more fluid system with a simulated viscosity of 0.5 mPa s. This complex interplay is even more complicated when considering the contribution of the cross-correlation 〈M_D(0) · J(t)〈 to the dielectric conductivity spectrum.

C. Σ₀(ω) and 〈M_D(0) · J(t)

The strong influence of viscosity shows up again in the size of this cross term 〈M_D(0) · J(t)〉. In pure ionic liquids the collective dipole moment M_D(t) and the current J(t) relax on a different time scale. The addition of water to this ionic liquid significantly enhances the rotation as can be seen from the τ₂ time constant of 〈M_D(0) · M_D(t)〉 in Table IV. As a consequence, the frequency domain of rotation shifts upwards and the overlap with translation becomes stronger. This does not only enhance the cross term 〈M_D(0) · J(t)〉 by a factor of roughly four compared to pure ionic liquids⁴¹ but even more important changes the principle character of the GDC Σ₀(ω)in Fig. 5c. As the dielectric permittivity and the dielectric conductivity are now closer in frequency space their superposition leads to a single peak structure which can be fitted by a single Havriliak-Negami function. Decreasing x_H2O a considerable broadening of the peak is observed hampering the Havriliak-Negami fit. At the lowest mole fraction x_H2O =0.653 the extent of broadening is almost that of a pure ionic liquid.

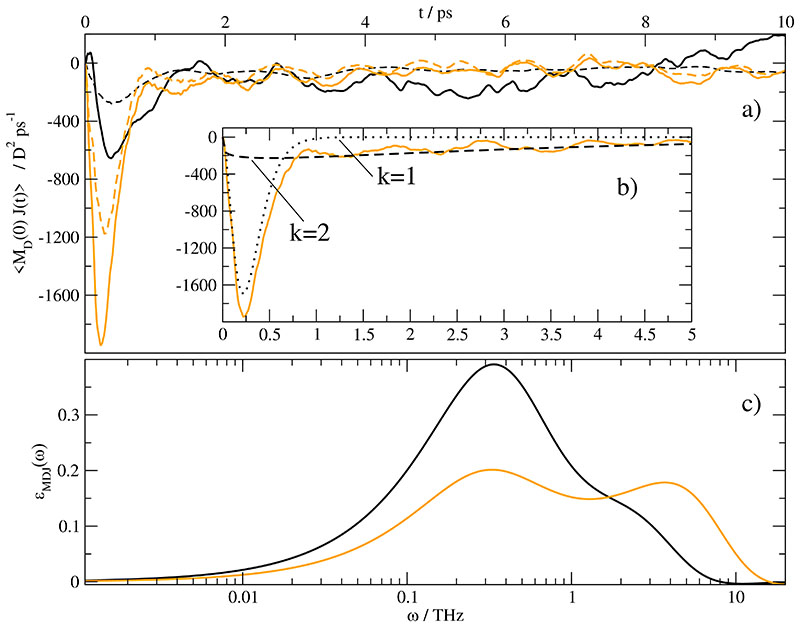
This rise in importance of the rotational-translational coupling represented by 〈M_D(0) · J(t)〉 justifies a closer inspection. The raw TCFs are given in Fig. 7a for x_H2O =0.974 and x_H2O =0.653 as black and grey solid line, respectively. First, the overall TCF is negative as opposed to pure ionic liquids.⁴¹ Second, the sharp initial peak at 0.25 ps is followed by a shoulder lasting over several picoseconds. This shoulder is not present in 〈M_D(0) · J(t)〉 of pure ionic liquids. Third, the initial negative peak is almost equally shared between the ions and water. This can be seen in Fig. 7a: The two dashed lines represent the contribution of $M_D^{\pm }(0)\cdot J(t).$ In other words, the correlation between the collective dipole moments of the cations and anions with the current. The solid line, however, correlates the total rotational dipole moment $\left[M_D(t)=M_D^{+}(t)+M_D^{-}(t)+M_D^0\right]$ with the current. Its peak heights is roughly double that of $M_D^{\pm }(0)\cdot J(t).$ In other words, the collective reorientation of neutral water molecules correlate with the ionic current in the same way as the reorientation of the ions themselves. One must admit that the number of water molecules clearly overrules the number of ions. Nevertheless, the coupling between water rotation and ion translation is an interesting fact.

Fig. 7.

a) Cross-correlation 〈M_D(0) · J(t)〉 of ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixture with x_H2O = 0.974 [black line] and x_H2O = 0.643 [orange line]. The solid lines represent the correlation of the total collective rotational dipole moment M_D (t) with the current J(t) whereas the dashed lines stand for the correlation of the ionic collective rotational dipole moment $M_D^{+}(t)+M_D^{-}(t)$ with the current J(t). b) Fit of 〈M_D(0) · J(t)〉 of ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water 2 at x_H2O = 0.643 according to $f(t)=\underset{2}{\overset{k}{{{\displaystyle \sum }}^{\text{}}}}{A}_k{t}^{{\gamma }_k-1}{e}^{-t/{\tau }_k}$ with the parameters given in Table VI. The orange line are the same data as a), the black dotted line and dashed line represent k = 1 and k = 2 contribution of f(t), respectively. The sum of both contributions is displayed as dash-dotted line. c) Contribution of the above mentioned cross-correlation 〈M_D (0) · J(t〉 to the dielectric spectrum of ϵ(ω). Please note that this contribution is part of ϑ₀(ω) additionally.

As mentioned in the Theory section the cross-correlation 〈M_D(0) · J(t)〉 can be fitted according to $f(t)={\displaystyle \sum _k{A}_k{t}^{{\gamma }_k-1}{e}^{-t/{\tau }_k}}$ resulting in a sum of Cole-Davidson peaks in the dielectric spectrum. In the case of cross terms, however, the fit is rather complicated due to bad statistics: Although the final TCF extends over a few picoseconds one has to use a time series of 10 ns to obtain reasonable raw data. The statistics can be improved when calculating 〈M_D(0) · J(t)〉 and 〈J(0) · M_D(t)〉 independently. From a theoretical point of view these two functions should be equal but of opposite sign. Therefore, an additional averaging over these two series is possible. Under these preconditions a tentative fit with two components according to Eq. (49) can be made. For the special case of x_H2O =0.653 this fit is shown in sub figure 7b. The first [k = 1, black dotted line] fit component is confined to the first peak of the total grey curve. It is characterized by a very small relaxation constant τ₁ =0.095 ps and a large γ₁-value of 3.30. Consequently, it appears as maximum around 4 THz in the spectrum shown in Fig. 7c. The maximum at 0.3 THz stems from the second fit component [k = 2, dashed line] of sub figure 7b. This second component describes the decay of 〈M_D(0) · J(t)〉 over several picoseconds with a time constant of τ₂ =3.0 ps and γ2-value of 1.17. This long-term tail of 〈M_D(0) · J(t)〉 seems to be an intrinsic feature of hydrated ionic liquids because it was not observed in pure ionic liquids.⁴¹ As a result, the contribution of 〈M_D(0) · J(t)〉 to the static dielectric constant ϵ_stat is higher than in pure ionic liquids. It is important to note that the difference of τ₁ and τ₂ has a strong influence on the spectrum but the difference of respective γ-values is of minor importance.

Quite general, the rotational-translational cross term 〈M_D(0) · J(t)〉 is characterized by large fluctuations. Therefore, its demand on statistical accuracy is very high. Even for time series extending over 10 ns as used here may be even not sufficient. In the light of these facts the above considerations are of tentative nature. Fortunately, the absolute contribution of these cross terms to the static GDC ϵ_stat is about 5% on average for the hydrated ionic liquids, and even less than this for pure ionic liquids.

V. Conclusion

The use of fit functions in computational dielectric spectroscopy is investigated both, from a theoretical and a practical point of view. Although not derived from first principles the presented fit functions may be classified and made plausible in terms of memory kernels. For the simplest possible memory kernel, a δ-function, the corresponding correlation function decays exponentially. This exponential behaviour is common to all fit functions used here. In fact, they differ by appropriate co-functions desscribing their specific features:

Collective rotational correlation functions can be represented multi-exponentially. Consequently, their co-function is merely the amplitude and their Fourier-Laplace spectrum is a superposition of Debye processes residing in the frequency regime from several MHz up to roughly 1 THz. Debye peaks in the dielectric loss spectrum in the MHz regime correspond to very slow rotational relaxations on a nanosecond time scale. The upper limit of 1 THz stems from fast relaxations with time constants of approximately 1 ps. The accuracy of multi-exponential fits can be easily improved: The higher the number of exponential terms, the better the fit. While this poses no problems for the Fourier-Laplace transform, it hampers interpretation because of the large number of parameters. Therefore, Kohlrausch-Williams-Watt functions may be better as they model the diversity of exponents by a stretching parameter β. Their use facilitates interpretation but introduces the problem of badly converging series representations in Fourier-Laplace space. Therefore, we presented formulae for the conversion of Kohlrausch-Williams-Watt parameters τ and β to the set of three Havriliak-Negami parameters α_HN, γ_HN and τ_HN.

The damped, oscillatory character of the collective current correlation functions is modelled by cosine functions with time shifts as co-functions. The actual fit procedure with this type of functions is rather delicate. While usually two terms are sufficient to reproduce the overall shape of the current correlation function, corresponding integrated values are highly sensitive to fit parameters. Therefore, one has to add a third, pure exponential term in order to secure a reliable reproduction of physical properties. From a principle point of view damped oscillator functions corresponds to an exponential memory kernel. Their Fourier-Laplace transform are voluminous but straightforward. These functions are only used in the high frequency regime of the dielectric loss spectrum beyond roughly 1 THz. Hence, their exponential damping constant is in the subpicosecond time regime typically for current-current correlation functions. Furthermore, these analytical formulae give the correct low-frequency behaviour.

The time behaviour of collective rotational-translational coupling is quite different from the two pure modes of motion. Collective rotational as well as translational correlation functions decay from an initial value to zero, rotation strictly monotonically and translation oscillatory. However, their cross term raises from zero to an extrema and decays afterwards. Therefore, we have used a completely different co-function t^γ−1 mimicking a distributionlike behaviour. Upon Fourier-Laplace transform this type of functions gives the well-known Cole-Davidson spectra. From these arguments it becomes quite obvious that Cole-Davidson fits of the low and high-frequency end of the dielectric loss spectrum are inappropriate since the relaxation of the collective rotation and translation is not distribution-like as depicted in Fig. 7a.

The fitting procedure of all individual components should always be checked by a numerical Fourier-Laplace transform of the corresponding time correlation functions.

The equipment of fit functions was applied to ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$/water mixtures with water mole fractions x_H2O from 0.974 to 0.653. As a first result, the static generalised dielectric constant ϵ_stat is dominated by rotational contributions and hence by the water component. This explains the monotonic decrease of ϵ_stat as well as ⏑(0) with decreasing x_H2O. On the contrast, the translational contribution ϑ₀(0) does not behave monotonically. This comes from the competence of the number of charge carriers with the viscosity.

On the frequency scale Im[ϵ(ω)] shows more or less a single peak structure which — for not too small x_H2O — can be fairly described by Havriliak-Negami model. Thereby, the γ_HN and τ_HN are again monotonically decreasing func tions of the water mole fraction. In case of τ_HN, the dependence is almost linear. A decomposition into species finds the cationic contribution at lower frequencies, whereas that of water and anions resides at almost the same frequency.

As already found for the static value the complete Im[ϑ₀(ω)] spectrum does not gradually change with mole fraction. In principle, it maintains its double-peak structure but the relative height of the two maxima changes. Furthermore, the first maxima fall in the same frequency range as Im[ϵ(ω)]. The coupling between collective rotation and translation is higher than in pure ionic liquids but still below 5% of the static generalised dielectric constant ϵ_stat.

As a final summary the complete spectrum of the generalised dielectric constant is the sum of the collective rotational and translational spectrum ranging from 1 GHz to 10 THz. These spectra of the hydrated ${\text{EMIM}}^{+}{\text{CF}}_3{\text{SO}}_3^{-}$ change from a more or less single peak [resembling a spectrum of a neutral molecular liquid] at high water mole fractions to a sustained plateau-like spectrum known from pure molecular ionic liquids.