Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2023 Jan 12.
Published in final edited form as: Nat Ecol Evol. 2022 Jan 13;6(3):307–314. doi: 10.1038/s41559-021-01644-4

Ecological network complexity scales with area

Núria Galiana 1,2,✉, Miguel Lurgi 1,3, Vinicius A G Bastazini 1,4, Jordi Bosch 5, Luciano Cagnolo 6, Kevin Cazelles 7, Bernat Claramunt-López 5,8, Carine Emer 9,10, Marie-Josée Fortin 11, Ingo Grass 12, Carlos Hernández-Castellano 5,8, Frank Jauker 13, Shawn J Leroux 14, Kevin McCann 7, Anne M McLeod 14, Daniel Montoya 1,15,16, Christian Mulder 17, Sergio Osorio-Canadas 5,18, Sara Reverté 5, Anselm Rodrigo 5,8, Ingolf Steffan-Dewenter 19, Anna Traveset 20, Sergi Valverde 21,22, Diego P Vázquez 23,24, Spencer A Wood 25, Dominique Gravel 26, Tomas Roslin 27,28, Wilfried Thuiller 29, José M Montoya 1
PMCID: PMC7614050  EMSID: EMS159330  PMID: 35027724

Abstract

Larger geographical areas contain more species—an observation raised to a law in ecology. Less explored is whether biodiversity changes are accompanied by a modification of interaction networks. We use data from 32 spatial interaction networks from different ecosystems to analyse how network structure changes with area. We find that basic community structure descriptors (number of species, links and links per species) increase with area following a power law. Yet, the distribution of links per species varies little with area, indicating that the fundamental organization of interactions within networks is conserved. Our null model analyses suggest that the spatial scaling of network structure is determined by factors beyond species richness and the number of links. We demonstrate that biodiversity–area relationships can be extended from species counts to higher levels of network complexity. Therefore, the consequences of anthropogenic habitat destruction may extend from species loss to wider simplification of natural communities.

Research on the spatial scaling of biodiversity has historically focused on the increase of species richness with area1–3 and on other components of biodiversity, such as functional or phylogenetic diversity4–6. The species–area relationship (SAR) is essential to estimate species richness in a region and species loss following habitat destruction and range contraction7–9. Ecological communities are, however, more than disconnected collections of species. Instead, they can be represented as networks, with species as nodes and interactions among species as links10. Ecological interactions are fundamental to predict ecosystem responses to environmental changes11–13 and to sustain important ecosystem functions14–16. Understanding how the structure of interaction networks changes with area is, thus, crucial to fully characterize the spatial scaling of biodiversity and to predict ecosystem responses to human activities.

The influence of spatial processes on the organization of interaction networks has long interested ecologists17–19. However, research on the spatial scaling of network structure has been scarce20–22. This scaling concerns two hierarchical levels: the number of building blocks within communities (species and their interactions) and the relationships between them. The scaling of the number of links (biotic interactions) with area has been previously predicted20 by unifying the SAR with the well-established scaling of the number of links with species richness23–26. Similarly, recent theoretical research has shown that a number of network–area relationships (NARs) can emerge from different spatial mechanisms and assembly processes, such as different SARs across trophic levels or dispersal limitation21. Yet empirically documenting the specific shape of these relationships and assessing their potential universality across biomes, interaction types and spatial domains remains a major challenge.

The power function of the form S ≈ cAz, where c is the intercept and z is the slope in logarithmic space, has been found to describe the increase in species richness (S) with area (A) across all ecosystem types1,27, with parameter z varying substantially with the spatial extent studied27–29. Whether other aspects of network complexity can be captured by the same functional form, and how the parameters of such scaling vary with network properties and spatial extent, are questions of fundamental importance for characterizing the effects of area loss on biodiversity. Similarly, as many aspects of network structure can change with species diversity and network connectance (the proportion of realised interactions among all potential ones)30–33, it is important to determine whether the spatial scaling of network structure is a trivial consequence of the increase of species richness with area, or whether such scaling of network properties follow rules beyond those applying to species richness.

We compiled 32 datasets from different ecosystems across the globe describing interaction networks (including both mutualistic and antagonistic interactions) within two spatial domains: regional and biogeographical. The regional domain represents communities for which sampling was conducted locally in a replicated fashion within narrow spatial extents (maximum spatial extent of ~1,000 km2). The biogeographical spatial domain includes datasets for which the sampling units span much broader areas, encompassing multiple biomes (Methods and Supplementary Text 1). Thus, biogeographical data comprise communities exposed to larger environmental heterogeneity, stronger dispersal barriers and historical contingencies, which combine to produce diversity patterns at large spatial scales. Hence, we expected a priori the scaling relationships for the biogeographical domain to be steeper than those for the regional domain, as within the biogeographical domain, species assemblages can be evolutionarily less related and exhibit greater turnover of species and links. Each dataset contained interaction data, using different methodologies to document pairwise interactions. To characterize changes in network properties with changes in area, we sequentially aggregated the sampling units available, scoring the structure of the network at each step of the aggregation procedure (Methods).

Results and discussion

The spatial scaling of network complexity

We found that network complexity increased with area at all levels: at the level of the number of building blocks (species and links) and at the level of their combinations (links per species; Fig. 1, Table 1 and Supplementary Table 1). For all datasets, the relationships followed a power-law function, regardless of the spatial extent of observation or interaction type. Within both the regional and biogeographical domain, we found that an extended power function best describes the scaling of network complexity with area (Methods and Supplementary Table 1). This function has the form N = cA(zA−d), where N is a given network property, A is area and c, z and d are fitted parameters, where z represents the slope of a given NAR in log–log space (the scaling exponent) and d controls the strength of the asymptotic flattening.

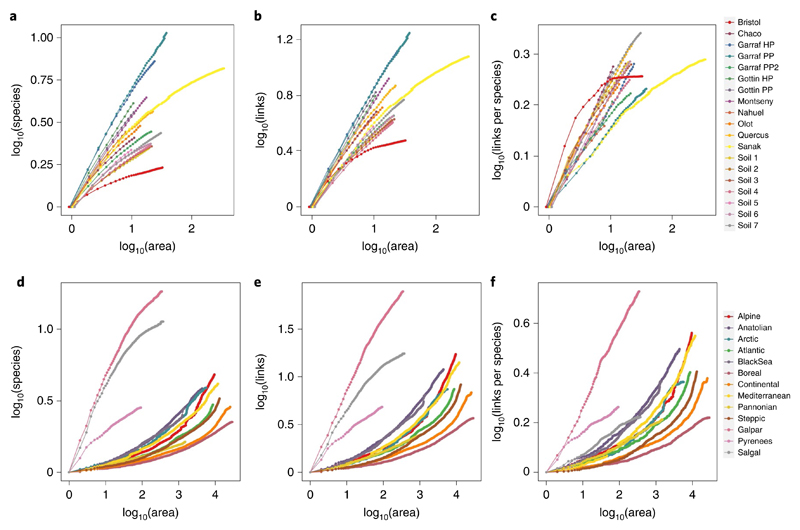
Fig. 1. Spatial scaling of network complexity.

Fig. 1

Open in a new tab

a–f, The relationship of species (a,d), links (b,e) and links per species (c,f) with area for regional (a–c) versus biogeographical (d–f) networks. For each dataset, each point represents the mean value of the analysed network property across the total amount of replicates in the aggregation procedure for a given area. For all datasets, all network properties have been rescaled to start at 0 for visualization purposes. In the biogeographical domain, three datasets show a linear-concave increase of the number of species, network links and links per species with area, similar to those observed in the regional domain; these differences may be explained by differences in sampling methods among datasets (Methods and Supplementary Text 1).

Table 1.

Parameter estimates for the fit of the extended power model (N = cA(zA−d)) to the network properties analysed. Mean and standard deviation of d and z are shown for each network property analysed in both spatial domains

Network property Parameter Spatial domain
Regional Biogeographical
Species d 0.08 ± 0.03 −0.38 ± 0.78
z 0.48 ± 0.12  0.05 ± 0.41
Links d 0.07 ± 0.03 −0.19 ± 0.13
z 0.72 ± 0.10  0.41 ± 0.63
Links per species d 0.05 ± 0.11 −0.31 ± 0.57
z 0.26 ± 0.10  0.08 ± 0.11
Indegree d 0.04 ± 0.12 −0.27 ± 0.22
z  0.31 ± 0.13  0.07 ± 0.19
Open in a new tab

The model fit was performed on the original data in arithmetic space and not on the rescaled properties.

We found systematic differences in the shape of the scaling relationships between the regional and biogeographical domains. All measures of network complexity followed a linear-concave increase with area size in the regional domain (z » d > 0) while in the biogeographical domain, the increase was convex for most datasets (z > 0 > d) (but see Supplementary Figs. 7 and 8). The biogeographic domain also showed larger variability across datasets than the regional domain, suggesting lower predictability at larger spatial extents (Supplementary Table 3).

The number of links increased faster with area than did the number of species, within both the regional and biogeographical domains. Importantly, whether links increase faster than species with area will depend on how the number of links scales with species richness20,21. Previous empirical studies23–26 have used a power function to relate the increase of the number of links with species richness and found the value of the scaling exponents to lie between 1 and 2 (refs. 25,26)—coining the expressions of the ‘link–species scaling law’34 versus ‘constant connectance hypothesis’24, respectively. Consistent with previous work, we found the increase in the number of links with an increase in species richness to follow a power law in all datasets (Fig. 2 and Supplementary Table 2). The exponents were larger for the biogeographical (mean ±s.d.: z = 1.78 ± 0.20) than for the regional domain (z = 1.60 ± 0.20). For both spatial domains, the scaling exponents of the links-per-species relationship were thus clustered between 1.5 and 2, but with substantial variability in specific values (Fig. 2 and Supplementary Table 2). The high variation observed suggests that the species richness of a community may carry little information on how the number of links will change with area. Instead, the scaling of the number of links with species richness may need to be established on a network-specific basis20.

Fig. 2. Scaling of the number of links with species richness.

Fig. 2

Open in a new tab

a,b, For networks spanning both regional (a) and biogeographical (b) spatial domains, the number of links scales with species following a power law (Supplementary Table 2). Each point represents the mean values across all replicates in the aggregation procedure. Note that for visualization purposes, all x and y values in all datasets have been rescaled to start at 0. To allow convenient comparison with the constant connectance hypothesis and the link–species scaling law, the slope of each log–log relationship is provided in Supplementary Table 2. Note that for constant connectance, the slope equals 2, as the number of links in a web increases approximately as the square of the number of trophic species: L≈S2. For the link-species scaling law, the slope equals 1, as the number of links per species in a web is constant and scale invariant at roughly two: L ≈ 2S).

The unpredictability of vertical diversity

Within a network, the links can be organized in multiple ways. In our dataset, the mean number of resources used by a consumer (mean indegree (L/Sc)) increased with area. The general shape of the relationship was similar to that of the other complexity measures analysed, that is, linear-concave in the regional domain and convex in the biogeographical domain (Fig. 3 and Supplementary Table 1). Still, compared with the relationships observed for other network properties, we observed greater variability in indegree–area relationships within spatial domains (Supplementary Table 3). This variability is driven partially by the variability in changes in consumer-to-resource ratios with area observed across datasets (Supplementary Table 1). Although previous studies have shown a consistent increase of the slope of SARs with trophic level35,36, we did not observe any consistent increase or decrease of the consumer/resource richness ratio with area at any of the spatial domains (Supplementary Table 1). These findings suggest that the spatial scaling of vertical diversity properties, such as the proportion of species per trophic level, might be system specific.

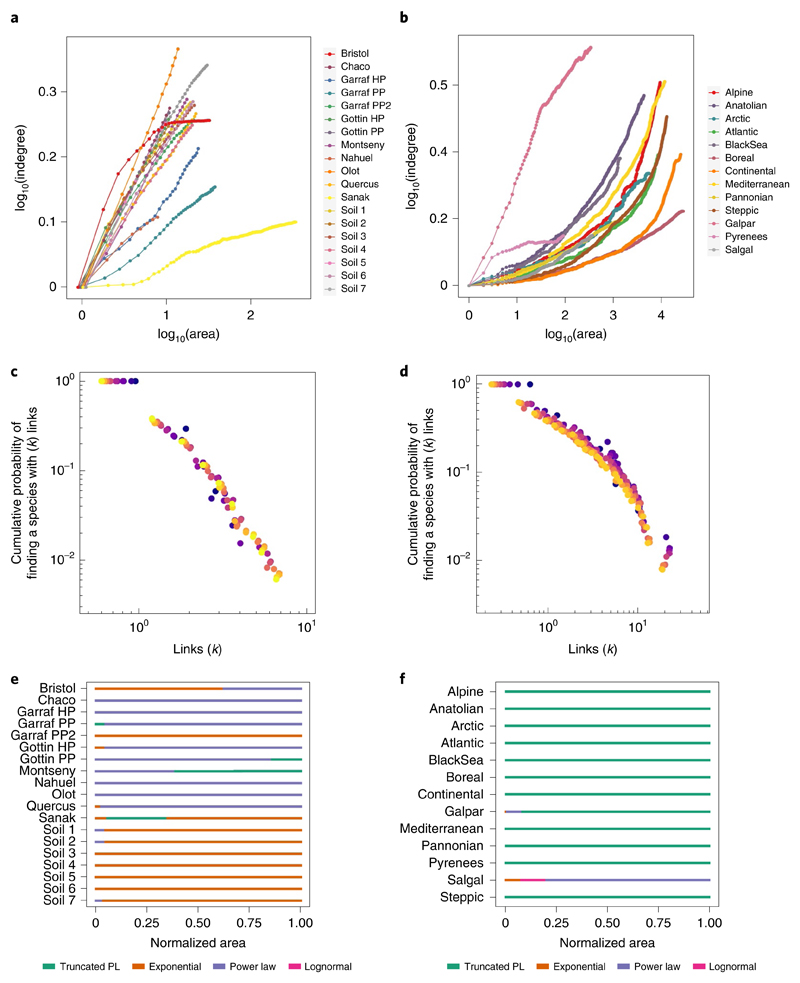
Fig. 3. Spatial scaling of mean indegree and network degree distribution.

Fig. 3

Open in a new tab

a,b, The mean number of resources per consumer (mean indegree) increases with area within both regional (a) and biogeographical (b) spatial domains. Each point represents the mean value across every replicate in the aggregation procedure at a given area. Note that for visualization purposes, all x and y values in all datasets have been rescaled to start at 0. The shape of the network degree distributions is consistent across area at both regional and biogeographical domains. c,d, Two datasets are shown as illustration: Garraf-PP (c, regional) and Galpar, (d, biogeographical) (Supplementary Text 1). The cumulative probabilities of finding a species in the network that has k links to resources in the network are normalized by the mean number of links per species in the network. One replicate for a subset of areas is shown for each dataset to facilitate visualization. Each colour represents network degree distribution for a given area, from dark blue, representing the smallest area (1 spatial unit), to yellow, representing the largest area for each dataset (40 spatial units for Garraf-PP and 373 spatial units for Galpar). Notice that the starting point of each distribution changes with area, indicating that at smaller spatial scales, the most specialized species of the network have more interacting partners than at larger spatial scales. Yet the shape of the degree distribution is preserved. e,f, The top-ranked model describing the degree distribution of each ecological network across the area range for regional (e) and biogeographical (f) domains. Although the degree distribution of most ecological networks was characterized by the same function along the range of areas, the specific shape of each function changed with area (Supplementary Fig. 4). Area values were rescaled between 0 and 1.

The scale invariance of degree distributions

Beyond the network properties considered in the preceding, other network properties were more consistent across scales. The degree distribution of ecological networks is typically highly skewed, with many specialist species and few generalists37,38. This skewness may influence the stability and robustness of communities38, and it is tightly linked to widely studied network properties, such as nestedness (the degree to which specialist species interact with subsets of the species interacting with generalists)39,40. Previous theoretical work has suggested that the skewness of ecological networks is preserved across spatial scales21, an expectation borne out in our data. Despite variability in the degree distribution across datasets, the same function provided a good fit to the degree distribution of most ecological networks across the full range of areas (Methods and Fig. 3). Although we observed variation in the parameters of the functions (Supplementary Fig. 4), the consistency in the fundamental shape suggests that community robustness to species loss (independently of whether it is high or low) may be maintained across spatial scales.

Disentangling the effect of species richness

Given the influence of species richness and network connectance on many aspects of network structure30–33, we aimed to investigate whether network structure changes with area beyond those changes associated with the increase in species richness and links with area. To do so, we generated random networks with two different null models, as reflecting the case where the spatial scaling of network structure emanates from the spatial scaling of species richness alone (with no change in links per species) or the spatial scaling of both species richness and links, respectively. In both models, we started from the metaweb (the overall network pooled across all original networks within each specific study) then randomly drew the same number of species as observed in the original local networks. In null model 1, local random networks were drawn as random subsets of the metaweb, picked to have the same species richness as the observed local networks. In other words, after randomly selecting a given number of species from the metaweb, we kept only interactions among this subset of species, thereby determining the number of links of the network generated. Thus, this procedure mimics a scenario where random local networks have the same number of species as the observed local networks, but the number of links and the associated network properties may differ. In null model 2, we preserved both species richness and the number of interactions observed in the original networks but distributed the links randomly among the species (Methods). Accordingly, null model 2 mimics a scenario where a change in area causes a potential change in indegree and network degree distribution, while not affecting the number of either species or links. For each of the 100 randomizations under each scenario, we then scored each of the complexity metrics defined in the preceding: species, links, links per species, indegree and network degree distribution.

The observed spatial scaling of network structure in the original networks differed substantially from the results generated by the null models. The number of links in empirical networks increased more slowly with an increase in the number of species than expected from a random sample of species from the metaweb (null model 1) (Supplementary Fig. 5). This slower increase is driven by the fact that local original networks show greater complexity (more links per species) than random networks. This result suggests that the scaling of the number of links is shaped by factors beyond the species richness of a community, such as evolutionary constraints, phenological matching or competition. By contrast, other structural properties, such as mean indegree and degree distributions, are consistent with the pattern derived from null model 1 (Supplementary Figs. 5 and 6 and Supplementary Tables 5 and 6). The consistency indicates that these network properties might be inherited from the metaweb and that the co-occurrence structure of species in the empirical data is not meaningfully impacting the degree distribution. This interpretation is supported by patterns observed under null model 2. When links are reshuffled randomly among selected species from the metaweb, the pattern is substantially different from the observed one: here, both the mean indegree and network degree distributions of the randomized networks strongly deviate from that of their original counterparts (Supplementary Figs. 5 and 6 and Supplementary Tables 5 and 6). Similarly, the observed spatial scaling of the consumer/resource ratio was poorly predicted by both null models.

Overall, our null model analyses suggest that the spatial scaling of network structure is determined by factors beyond species richness and the number of links. With a change in area, we see changes in important features of ecological networks—such as vertical diversity, consumer specialization and degree distribution—well beyond those expected if changes were driven by the number of species and/ or links alone.

The fragility of biotic interactions

In conclusion, our analyses of multiple interaction networks from different biomes, interaction types and spatial domains allowed us to explore the generality in the spatial scaling of several structural properties of ecological networks. Our results demonstrate how previously established biodiversity–area relationships can be extended from species counts2,3,27 to higher levels of network complexity. The increase in the number of interactions in which each species is involved when area increases indicates that trophic interactions might be more vulnerable to habitat loss than to species richness41,42. Therefore, the consequences of anthropogenic habitat destruction may extend from species loss to wider simplification of natural communities43–45, with further consequences for the functioning of ecosystems14–16,46,47. The systematic scaling of network complexity with area suggests that trophic interactions will be lost with habitat destruction in a predictable manner, and describing the factors shaping this sequence allows us to better anticipate the effects for ecosystem functioning. Importantly, the scaling of the number of interactions with species richness proved variable across datasets, and our null model analysis indicated that other complexity metrics cannot be predicted from species richness alone. Both of these patterns suggest that we need network-specific knowledge on the relationship between links and species to accurately predict the effects of habitat loss on network complexity. To estimate the spatial scaling of the number of links, a general understanding of the SAR may still suffice if it is supplemented by informed assumptions regarding the scaling exponent of the links–species relationship. For such assumptions, our current results will form a useful point of departure, given their foundation in a wide set of scales and biomes.

Future studies should put effort towards unravelling the potential ecological mechanisms affecting the slopes of NARs, as well as disentangling the importance of the methodological aspects (Supplementary Figs. 7 and 8 and Supplementary Table 7), as has been widely done for SARs27. Explicitly investigating the effect of habitat heterogeneity, for example, would help elucidate the effect of area, not only on network size and the number of links, but also on its modular structure. Such insight is urgently needed, given that heterogeneous landscapes are likely to promote the emergence of compartments within networks48,49. Similarly, it is important to investigate how our observations could inform predictions about the effects of habitat loss caused, for example, by link extinction debt or changes in trophic regulation41,42. Yet it is also fundamental to understand how our predictions of the effects of habitat loss on network structure would resemble those obtained by direct experiments of habitat destruction. Gaining a deeper understanding of the mechanisms behind NARs will allow us not only to anticipate the potential consequences of habitat loss, but also to provide management recommendations with a solid foundation in the structure and functioning of natural ecosystems.

Methods

To measure NARs for ecological communities from different biomes across the world, we used 32 empirical datasets comprising species recorded in different localities and with different types of interactions. This is a comprehensive synthesis of spatial interaction network datasets. Depending on the study, local observations span either a regional or biogeographical spatial extent. Our analysis allowed us to identify universalities in the ways network properties change with area for datasets comprising different interaction types. To evaluate whether there are universalities in the ways that networks of ecological interactions scale across space, we quantified the exponents of the relationships between all network properties analysed with area when fitted to a power function. The spatial scaling of network degree distributions was assessed by fitting four different distributions at each spatial domain and comparing the best fit across the entire range of areas. In addition, we used two different null models to disentangle the effects of the spatial scaling of species richness on the patterns observed in other complexity metrics.

Data classification

Thirty-two datasets comprising species distributions and their interactions were obtained from different sources and classified into two categories according to the geographical extent covered: regional or biogeographical spatial domain. The main features of the type of data considered in each category, including sampling method, location and interaction types, are briefly described in the following. Additional details about each dataset can be found in Supplementary Text 1

Regional spatial domain

Datasets in this category are distinguished from biogeographical networks by their geographical extent and sampling methods. Regional-domain data were collected with locally replicated samples over relatively narrow spatial extents up to ~1,000 km2. Sample units are generally the same size or a series of localities of roughly equal size. A total of 19 datasets were considered in the regional domain, covering different ecosystems and geographical locations across the globe. The datasets are networks describing plant–pollinator interactions and host–parasitoid interactions from Mediterranean scrublands located in Garraf (three datasets50,51) and forests located in the natural parks of Montseny (1 dataset52) and Olot (1 dataset53) in Catalonia, Spain; host–parasite interactions networks describing insect herbivores (gallers and leaf miners) of the pedunculate oak (Quercus robur) and their parasites in a temperate forest in Finland (1 dataset54); plant–pollinator interactions from a temperate forest in Argentinian Patagonia (1 dataset55); soil food webs from agroecosystems across the Netherlands (7 datasets56); terrestrial food webs within small islands of a temperate saltmarsh mudflat in southeastern England (1 dataset57); intertidal food webs from the northeastern Pacific in Alaska, USA (1 dataset22); networks of plant–pollinator interactions and host–parasitoid interactions in fragmented calcareous grasslands in central Germany (2 datasets58); and networks of plant–leaf miner–parasitoid interactions from forest fragments embedded in an agricultural matrix landscape in central Argentina (1 dataset59).

Biogeographical spatial domain

Datasets from this category span broad (biogeographical) spatial extents. There are two types of biogeographical datasets: (1) datasets where local communities are built on the basis of the information of the presence of all species found in each location and where the interactions between species have been inferred from literature review and expert knowledge and (2) datasets where local communities are built on the basis of direct observations of ecological interactions at each locality. The datasets of type (1) comprise the European terrestrial vertebrate trophic network (food web60) divided among 10 biogeographical regions that characterize each region according to its climatic conditions (local communities for this dataset are defined at the 10 km × 10 km grid level (10 datasets)) and the terrestrial vertebrate food web of the Catalan Pyrenees (1 dataset12), where local communities are also defined at the 10 km × 10 km grid level. The datasets of type (2) comprise networks of plant–herbivore interactions and herbivore–parasitoid interaction sampled from plants of the genus Salix and spanning a large latitudinal gradient from Italy to northern Norway (2 datasets61).

Building NARs

To analyse the spatial scaling of network structure, we built NARs for each dataset described. The procedure to generate NARs was slightly different between spatial domains.

Regional spatial domain

The spatial extent was rescaled for each dataset. The smallest spatial scale considered was a single sampling unit. The spatial scaling of network structure was defined by sequentially aggregating each of the sampling units available until all replicated samples were considered. The aggregated sampling units are not contiguous, given that the specific location of each was not considered. We analysed network structure at each step of the aggregation procedure. Given that the order in which sampling units (local communities) are aggregated might generate a bias in the aggregation procedure, we replicated the procedure 100 times for each dataset where the aggregation order was randomly generated without replacement.

Biogeographical spatial domain

The fundamental difference between the two spatial domains considered is that biogeographical data span large spatial extents, thus comprising communities exposed to large environmental gradients. This environmental heterogeneity suggests potential differences in scaling patterns compared with communities sampled regionally, which cover smaller geographical extents. Due to the large spatial extent covered by these datasets, an aggregation procedure where each aggregated sampling unit is randomly selected in space, independently of its location, would generate a fast accumulation of species and links at small areas due to the large heterogeneity among the sampling units (Supplementary Fig. 8 and Supplementary Table 7), generating a fast accumulation of species and links at small areas. For this reason, we employ an aggregation method based on neighbouring cells while still preserving the statistical power of randomizing across replicated aggregation instances (see Supplementary Fig. 8 and Supplementary Table 7 for results based on the random aggregation of sites). Two types of data comprise this category: those for which species presences and their interactions were recorded in the field from single georeferenced locations across the latitudinal gradient61 and those where species presences were extracted from species distributions maps and interactions were inferred on the basis of the joint condition of species co-occurrence in space and an indication that the two species interact, as extracted from the literature60. The latter datasets, therefore, include all potential interactions between species, which are not necessarily realized locally. Local sampling units of these latter datasets were defined as the 10 × 10 km cells on a gridded map. The spatial scaling of network structure is thus simulated by merging adjacent cells of the map in an increasing manner. Starting from a randomly chosen cell, subsequent communities occupying larger areas were defined as collections of neighbouring cells forming increasingly larger clusters of cells, chosen in anticlockwise fashion from the starting cell (spiral fashion). Thus, the sampling units that are aggregated are contiguous. We measured network properties at each step of the aggregation procedure. We repeated the aggregation procedure 100 times. For datasets with georeferenced locations, the spatial scaling of network structure was defined by sequentially aggregating the closest communities (in terms of Euclidean distance) to the starting point.

Network properties

We analysed the spatial scaling of network complexity at both spatial scales measuring the number of species (S), the total number of links (biotic interactions; L) present in the network and the number of links per species (L/S). We also quantified the relationship between species richness and the total number of links in the network (links–species scaling). Specialization was measured at the network level by computing the mean indegree (mean number of resources utilized by a consumer; L/Sc) of the community (also known as generality or diet breadth in food webs).

To further assess how the structure of ecological networks scales across space in different ecosystems, we examined their degree distribution. The degree distribution P(k) of a network is defined as the probability of finding a species that has k links to resources in the network. Degree distributions provide a notion of how links are structured across the network, and their shape has been related to different aspects of community stability37,38,46,62. In particular, scale-free degree distributions are considered the hallmark of network organization, conferring stability properties to ecological communities. We fitted four different functions that have been identified as typical of the shapes observed indegree distributions in ecological networks: power law, truncated power law, lognormal and exponential38,63. After fitting these distributions to the network of interactions built for each spatial scale analysed, for each dataset, the most parsimonious one as measured by Akaike information criterion (AIC) was recorded as the best representation of the data. We did that for each replicate of each dataset, selecting the distribution that was best ranked in most of the replicates. Looking at whether the top-ranked distribution (the lowest AIC) changes with area provides insights into the scale invariance of this network property. In addition, we looked at the changes of the parameters involved in each function with area (Supplementary Fig. 4).

NARs fitting

After constructing NARs on the basis of the 100 replicates for each dataset, we analysed the scaling relationships by fitting a suite of functions that have traditionally been used to quantify SARs64,65(see Supplementary Table 4 for the full set of functions tested). These scaling functions incorporate in different ways the network property as the response variable and area as the predictor variable, using a characteristic exponent, or a variation of it, to define the relationship of network properties to area size. For example, the power law (N = cAZ) relates N (a network property) to area (A) using a constant c and a scaling exponent (z). Similarity in the fitted parameters obtained for different datasets was then used to evaluate universalities in NARs. Scaling functions in Supplementary Table 4 were fitted to each dataset (after network properties were calculated at each spatial extent) using the sar package in R65. We used R2 and P values to assess goodness of fit. Comparison across models and selection of the best-supported model was done with AIC. Among all fitted functions, we focused on the top five models that were best supported and selected (if possible) the best-ranked model from the power family to facilitate comparisons among datasets. We note that the functions were fitted to the original data in arithmetic space and that the rescaling of the properties to start at 0 was performed for visualization purposes alone.

Null models

To understand the contribution of species richness and the number of links for the spatial scaling of the associated network properties analysed, we used two null models. For null model 1, we checked for each dataset the number of species present in each spatial unit, and we randomly picked the same number of species from the corresponding metaweb. We then built the network for those species taking from the metaweb all the interactions present among the selected species. Thus, the resulting assemblages can differ from the original networks in the number of links between species and, in turn, in the associated network properties analysed. By contrast, for null model 2, we checked both the number of species and the number of links present in each spatial unit and randomly distributed those links between the selected species. While networks built with null model 1 can potentially preserve part of the structure from each metaweb given that the selected species preserve the links they have in the metaweb, networks built with null model 2 can be considered random networks given that there is no inherited structure from the metaweb. Thus, null model 1 allows us to determine the contribution of the identity of the species (with their respective links) to the observed patterns, while null model 2 allows us to further test whether there is any contribution of area into network structure beyond species richness and the number of links. For both null models, we generated networks of different sizes by adding the number of species of the subsequent spatial units of each dataset. At each step of species addition, we calculated all network metrics. We replicated the procedure 100 times for each dataset. We evaluate the resulting NARs (where area is the number of spatial units from which we extracted the number of species) by fitting a power function, as we did for the original networks. We finally compared the spatial scaling of network properties with those obtained in the original networks (Supplementary Figs. 5 and 6 and Supplementary Tables 5 and 6).

Supplementary Material

Supplementary Material

Acknowledgements

We thank J.-F. Arnoldi, M. Barbier and Y. Zelnik for numerous discussions that improved the quality of this paper. This work was supported by the TULIP Laboratory of Excellence (ANR-10-LABX-41 and 394 ANR-11-IDEX-002-02) to J.M.M., by a Region Midi-Pyrenees project (CNRS 121090) to J.M.M., and by the FRAGCLIM Consolidator Grant (726176) to J.M.M. from the European Research Council under the European Union’s Horizon 2020 Research and Innovation Program. The study was also supported by Spanish MICINN projects CGL2009-12646, CSD2008-0040 and CGL2013-41856 to J.B. and A.R. C.E. was funded through the São Paulo Research Foundation (FAPESP 2015/15172-7). V.A.G.B. was funded by National Funds through FCT—Foundation for Science and Technology under the Project UIDB/05183/2020. W.T. received funding from the ERA-Net BiodivERsA—Belmont Forum, with the national funder Agence National pour la Recherche (FutureWeb: ANR-18-EBI4–0009 and BearConnect: ANR-16-EBI3-0003).

Footnotes

Author contributions

N.G., J.M.M. and M.L. designed the research with contributions from all co-authors. N.G. and M.L. conducted research and analysed the data. J.B., L.C., B.C.-L., C.E., I.G., C.H.-C., F.J., D.M., C.M., S.O.-C., S.R., A.R., I.S.-D., A.T., D.P.V., S.A.W., T.R. and W.T. contributed the data. J.M.M., V.A.G.B., K.C., M.-J.F., S.J.L., K.M., A.M.M., D.G., T.R., S.V. and W.T. supported research. N.G. and J.M.M. wrote the manuscript with substantial contributions from D.G., T.R. and W.T. and feedback from all co-authors.

Competing interests

The authors declare no competing interests.

Peer review information Nature Ecology & Evolution thanks Jonathan Chase and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Reprints and permissions information is available at www.nature.com/reprints.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Reporting Summary. Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

All datasets analysed during the current study are available online at https://doi.org/10.5061/dryad.zcrjdfndg66, https://github.com/nuriagaliana/Ecological-network-complexity-scales-with-area or https://github.com/mlurgi/global-network-area.

Code availability

Custom code used to perform the analyses are available online at https://doi.org/10.5281/zenodo.5758580, https://github.com/nuriagaliana/Ecological-network-complexity-scales-with-area or https://github.com/mlurgi/global-network-area.

References

  • 1.Arrhenius O. Species and area. J Ecol. 1921;9:95–99. [Google Scholar]
  • 2.MacArthur RH, Wilson EO. The Theory of Island Biogeography. Princeton Univ. Press; 1967. [Google Scholar]
  • 3.Rosenzweig ML. Species Diversity in Space and Time. Cambridge Univ. Press; 1995. [Google Scholar]
  • 4.Smith AB, Sandel B, Kraft NJB, Carey S. Characterizing scale-dependent community assembly using the functional-diversity-area relationship. Ecology. 2013;94:2392–2402. doi: 10.1890/12-2109.1. [DOI] [PubMed] [Google Scholar]
  • 5.Mazel F, et al. Multifaceted diversity-area relationships reveal global hotspots of mammalian species, trait and lineage diversity. Glob Ecol Biogeogr. 2014;23:836–847. doi: 10.1111/geb.12158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Dias RA, et al. Species richness and patterns of overdispersion, clustering and randomness shape phylogenetic and functional diversity-area relationships in habitat islands. J Biogeogr. 2020;47:1638–1648. [Google Scholar]
  • 7.Pereira HM, et al. Scenarios for global biodiversity in the 21st century. Science. 2010;330:1496–1501. doi: 10.1126/science.1196624. [DOI] [PubMed] [Google Scholar]
  • 8.Pimm SL, Russell GJ, Gittleman JL, Brooks TM. The future of biodiversity. Science. 1995;269:347–350. doi: 10.1126/science.269.5222.347. [DOI] [PubMed] [Google Scholar]
  • 9.Simberloff D. In: Tropical Deforestation and Species Extinction. Whitmore TC, Sayer JA, editors. Chapman Hall; 1992. pp. 75–89. [Google Scholar]
  • 10.Jordano P. Chasing ecological interactions. PLoS Biol. 2016;14:e1002559. doi: 10.1371/journal.pbio.1002559. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Montoya JM, Woodward G, Emmerson MC, Solé RV. Press perturbations and indirect effects in real food webs. Ecology. 2009;90:2426–2433. doi: 10.1890/08-0657.1. [DOI] [PubMed] [Google Scholar]
  • 12.Lurgi M, López BC, Montoya JM, Lopez BC. Novel communities from climate change. Philos Trans R Soc Lond B. 2012;367:2913–2922. doi: 10.1098/rstb.2012.0238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Tylianakis JM, Tscharntke T, Lewis OT. Habitat modification alters the structure of tropical host-parasitoid food webs. Nature. 2007;445:202–205. doi: 10.1038/nature05429. [DOI] [PubMed] [Google Scholar]
  • 14.Montoya JM, Rodriguez MÁ, Hawkins BA. Food web complexity and higher-level ecosystem services. Ecol Lett. 2003;6:587–593. [Google Scholar]
  • 15.Reiss J, Bridle JR, Montoya JM, Woodward G. Emerging horizons in biodiversity and ecosystem functioning research. Trends Ecol Evol. 2009;24:505–514. doi: 10.1016/j.tree.2009.03.018. [DOI] [PubMed] [Google Scholar]
  • 16.Thompson RM, et al. Food webs: reconciling the structure and function of biodiversity. Trends Ecol Evol. 2012;27:689–697. doi: 10.1016/j.tree.2012.08.005. [DOI] [PubMed] [Google Scholar]
  • 17.Cohen JE, Newman CM. Community area and food-chain length: theoretical predictions. Am Nat. 1991;138:1542–1554. [Google Scholar]
  • 18.Schoener TW. Food webs from the small to the large: the Robert H. MacArthur Award lecture. Ecology. 1989;70:1559–1589. [Google Scholar]
  • 19.Post DM, Pace ML, Hairston NG. Ecosystem size determines food-chain length in lakes. Nature. 2000;405:1047–1049. doi: 10.1038/35016565. [DOI] [PubMed] [Google Scholar]
  • 20.Brose U, Ostling A, Harrison K, Martinez ND. Unified spatial scaling of species and their trophic interactions. Nature. 2004;428:167–171. doi: 10.1038/nature02297. [DOI] [PubMed] [Google Scholar]
  • 21.Galiana N, et al. The spatial scaling of species interaction networks. Nat Ecol Evol. 2018;2:782–790. doi: 10.1038/s41559-018-0517-3. [DOI] [PubMed] [Google Scholar]
  • 22.Wood SA, Russell R, Hanson D, Williams RJ, Dunne JA. Effects of spatial scale of sampling on food web structure. Ecol Evol. 2015;5:3769–3782. doi: 10.1002/ece3.1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Pimm SL, et al. Food web patterns and their consequences. Nature. 1991;350:669–674. [Google Scholar]
  • 24.Martinez ND. Constant connectance in community food webs. Am Nat. 1992;139:1208–1218. [Google Scholar]
  • 25.Ings TC, et al. Ecological networks-beyond food webs. J Anim Ecol. 2009;78:253–69. doi: 10.1111/j.1365-2656.2008.01460.x. [DOI] [PubMed] [Google Scholar]
  • 26.Montoya JM, Solé RV. Topological properties of food webs: from real data to community assembly models. Oikos. 2003;102:614–622. [Google Scholar]
  • 27.Drakare S, Lennon JJ, Hillebrand H. The imprint of the geographical, evolutionary and ecological context on species-area relationships. Ecol Lett. 2006;9:215–227. doi: 10.1111/j.1461-0248.2005.00848.x. [DOI] [PubMed] [Google Scholar]
  • 28.Preston FW. Time and space and the variation of species. Ecology. 1960;41:611–627. [Google Scholar]
  • 29.Turner WR, Tjørve E. Scale-dependence in species-area relationships. Ecography. 2005;6:721–730. [Google Scholar]
  • 30.Bengtsson J. Confounding variables and independent observations in comparative analyses of food webs. Ecology. 1994;75:1282–1288. [Google Scholar]
  • 31.Vermaat JE, Dunne JA, Gilbert AJ. Major dimensions in food-web structure properties. Ecology. 2009;90:278–282. doi: 10.1890/07-0978.1. [DOI] [PubMed] [Google Scholar]
  • 32.Dunne JA, et al. Parasites affect food web structure primarily through increased diversity and complexity. PLoS Biol. 2013;11:e1001579. doi: 10.1371/journal.pbio.1001579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Poisot T, Gravel D. When is an ecological network complex? Connectance drives degree distribution and emerging network properties. PeerJ. 2014;2:e251. doi: 10.7717/peerj.251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Cohen JE Briand. Fredeiri Trophic links of community food webs. Proc Natl Acad Sci USA. 1984;81:4105–4109. doi: 10.1073/pnas.81.13.4105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Roslin T, Várkonyi G, Koponen M, Vikberg V, Nieminen M. Species-area relationships across four trophic levels—decreasing island size truncates food chains. Ecography. 2014;37:443–453. [Google Scholar]
  • 36.Holt RD, Lawton JH, Polis GA, Martinez ND. Trophic rank and the species-area relationship. Ecology. 1999;80:1495–1504. [Google Scholar]
  • 37.Dunne JA, Williams RJ, Martinez ND. Food-web structure and network theory: the role of connectance and size. Proc Natl Acad Sci USA. 2002;99:12917–12922. doi: 10.1073/pnas.192407699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Montoya JM, Pimm SL, Solé RV. Ecological networks and their fragility. Nature. 2006;442:259–264. doi: 10.1038/nature04927. [DOI] [PubMed] [Google Scholar]
  • 39.James A, Pitchford JW, Plank MJ. Disentangling nestedness from models of ecological complexity. Nature. 2012;487:227–230. doi: 10.1038/nature11214. [DOI] [PubMed] [Google Scholar]
  • 40.Valverde S, et al. The architecture of mutualistic networks as an evolutionary spandrel. Nat Ecol Evol. 2018;2:94–99. doi: 10.1038/s41559-017-0383-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Valiente-Banuet A, et al. Beyond species loss: the extinction of ecological interactions in a changing world. Funct Ecol. 2015;29:299–307. [Google Scholar]
  • 42.Janzen DH. The deflowering of central America. Nat Hist. 1974;83:49–53. [Google Scholar]
  • 43.Mendoza M, Araújo MB. Climate shapes mammal community trophic structures and humans simplify them. Nat Commun. 2019;10:5197. doi: 10.1038/s41467-019-12995-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Emer C, et al. Seed dispersal networks in tropical forest fragments: area effects, remnant species, and interaction diversity. Biotropica. 2020;52:81–89. [Google Scholar]
  • 45.McWilliams C, Lurgi M, Montoya JM, Sauve A, Montoya D. The stability of multitrophic communities under habitat loss. Nat Commun. 2019;10:2322. doi: 10.1038/s41467-019-10370-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.McCann KS. The diversity-stability debate. Nature. 2000;405:228–233. doi: 10.1038/35012234. [DOI] [PubMed] [Google Scholar]
  • 47.Fig T, Mccann K, Hastings A, Huxel GR. Weak trophic interactions and the balance of nature. Nature. 1998;395:794–798. [Google Scholar]
  • 48.Pimm SL, Lawton JH. Are food webs divided into compartments? J Anim Ecol. 1980;49:879–898. [Google Scholar]
  • 49.Macfadyen S, Gibson RH, Symondson WOC, Memmott J. Landscape structure influences modularity patterns in farm food webs: consequences for pest control. Ecol Appl. 2011;21:516–524. doi: 10.1890/09-2111.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Reverté S, et al. Spatial variability in a plant-pollinator community across a continuous habitat: high heterogeneity in the face of apparent uniformity. Ecography. 2019;42:1558–1568. [Google Scholar]
  • 51.Torné-Noguera A, Arnan X, Rodrigo A, Bosch J. Spatial variability of hosts, parasitoids and their interactions across a homogeneous landscape. Ecol Evol. 2020;10:3696–3705. doi: 10.1002/ece3.6158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Hernández-Castellano C, et al. A new native plant in the neighborhood: effects on plant-pollinator networks, pollination, and plant reproductive success. Ecology. 2020;101:e03046. doi: 10.1002/ecy.3046. [DOI] [PubMed] [Google Scholar]
  • 53.Osorio S, Arnan X, Bassols E, Vicens N, Bosch J. Local and landscape effects in a host-parasitoid interaction network along a forest-cropland gradient. Ecol Appl. 2015;25:1869–1879. doi: 10.1890/14-2476.1. [DOI] [PubMed] [Google Scholar]
  • 54.Kaartinen R, Roslin T. Shrinking by numbers: landscape context affects the species composition but not the quantitative structure of local food webs. J Anim Ecol. 2011;80:622–631. doi: 10.1111/j.1365-2656.2011.01811.x. [DOI] [PubMed] [Google Scholar]
  • 55.Vázquez DP, Simberloff D. Changes in interaction biodiversity induced by an introduced ungulate. Ecol Lett. 2003;6:1077–1083. [Google Scholar]
  • 56.Mulder C, Den Hollander HA, Hendriks AJ. Aboveground herbivory shapes the biomass distribution and flux of soil invertebrates. PLoS ONE. 2008;3:e3573. doi: 10.1371/journal.pone.0003573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Montoya D, Yallop ML, Memmott J. Functional group diversity increases with modularity in complex food webs. Nat Commun. 2015;6:7379. doi: 10.1038/ncomms8379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Grass I, Jauker B, Steffan-Dewenter I, Tscharntke T, Jauker F. Past and potential future effects of habitat fragmentation on structure and stability of plant-pollinator and host-parasitoid networks. Nat Ecol Evol. 2018 doi: 10.1038/s41559-018-0631-2. [DOI] [PubMed] [Google Scholar]
  • 59.Cagnolo L, Salvo A, Valladares G. Network topology: patterns and mechanisms in plant-herbivore and host-parasitoid food webs. J Anim Ecol. 2011;80:342–351. doi: 10.1111/j.1365-2656.2010.01778.x. [DOI] [PubMed] [Google Scholar]
  • 60.Maiorano L, Montemaggiori A, Ficetola GF, O’Connor L, Thuiller W. TETRA-EU 1.0: a species-level trophic metaweb of European tetrapods. Glob Ecol Biogeogr. 2020;29:1452–1457. [Google Scholar]
  • 61.Kopelke J, et al. Food-web structure of willow-galling sawflies and their natural enemies across Europe. Ecology. 2017;98:1730. doi: 10.1002/ecy.1832. [DOI] [PubMed] [Google Scholar]
  • 62.Sole RV, Montoya M. Complexity and fragility in ecological networks. Proc R Soc Lond B. 2001;268:2039–2045. doi: 10.1098/rspb.2001.1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 63.Broido AD, Clauset A. Scale-free networks are rare. Nat Commun. 2019;10:1017. doi: 10.1038/s41467-019-08746-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 64.Guilhaumon F, Mouillot D, Gimenez O. mmSAR: an R-package for multimodel species-area relationship inference. Ecography. 2010;33:420–424. [Google Scholar]
  • 65.Matthews TJ, Triantis KA, Whittaker RJ, Guilhaumon F. sars: an R package for fitting, evaluating and comparing species-area relationship models. Ecography. 2019 doi: 10.1111/ecog.04271. [DOI] [Google Scholar]
  • 66.Galiana N. Ecological network complexity scales with area. Dryad. 2021 doi: 10.5061/dryad.zcrjdfndg. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Material
EMS159330-supplement-Supplementary_Material.pdf (25.6MB, pdf)

Data Availability Statement

All datasets analysed during the current study are available online at https://doi.org/10.5061/dryad.zcrjdfndg66, https://github.com/nuriagaliana/Ecological-network-complexity-scales-with-area or https://github.com/mlurgi/global-network-area.

Custom code used to perform the analyses are available online at https://doi.org/10.5281/zenodo.5758580, https://github.com/nuriagaliana/Ecological-network-complexity-scales-with-area or https://github.com/mlurgi/global-network-area.

RESOURCES