Over and above frequency: gamma oscillations as units of neural circuit operations

Abstract

Gamma oscillations (˜30–150 Hz) are widespread correlates of neural circuit functions. These network activity patterns have been described across multiple animal species, brain structures and behaviors, being usually identified based on their spectral peak frequency. Yet, despite intensive investigation, whether gamma oscillations implement causal mechanisms of specific brain functions or represent a general dynamic mode of neural circuit operation remains unclear. In this Perspective we review recent advances in the study of gamma oscillations towards a deeper understanding of their cellular mechanisms, neural pathways, and functional roles. We discuss that a given gamma rhythm does not per se implement any specific cognitive function but rather constitutes an activity motif reporting the cellular substrates, communication channels and computational operations underlying information processing in its generating brain circuit. Accordingly, we propose shifting the attention from a frequency-based to a circuit-level definition of gamma oscillations.

Introduction

Oscillatory dynamics are ubiquitous signatures of operating neural circuits. Multiple types of oscillations have been described across animal species and neural structures, being commonly associated with a large array of behaviors, computations, and codes, in the sensory, cognitive, and motor domains. Notably, it has been proposed that the fast rhythms marking the gamma frequency band, broadly defined from ˜30 to ˜150 Hz, modulate action potential timing, neuronal population synchrony and cross-structural communication channels for selective processing and routing of information ^1–6. Yet, despite the wealth of research on this topic, the extent to which gamma oscillations report mechanisms of neural operations remains unclear, and a unifying view is still missing.

Gamma oscillations differ in spectral properties, cellular substrates, brain states and behavioral correlates. Different methods are used to record these rhythms, ranging from non-invasive whole-brain techniques such as electro- or magneto-encephalography (E/MEG) to intracranial recordings of extracellular potentials, multiunit spiking activity or single cell membrane dynamics ^7–12. The common way of identifying gamma oscillations is then based on their spectral peak frequency and their generation is typically attributed to the circuit where the electrode is placed. Although this approach has led to considerable progress, it is increasingly clear that gamma oscillations form a complex set of rhythms that are generated by different cellular substrates and circuits, featuring distinct, yet overlapping, frequencies ^9,13–23. Oscillations recorded by the same electrode and of similar frequency can yet originate from different underlying rhythm generating circuits and be volume conducted to the recording electrode from different current generators ^24–26. At the same time the frequency of the gamma oscillation generated by the same circuit may vary depending on the inputs that drive it ^27,28. Recording gamma oscillations away from their current generators introduces the added complication of mixing of signals, contamination from extrinsic sources and volume conduction of electric fields ^1,29,30. These nuances regarding the measurement and classification of gamma oscillation patterns call for a more principled approach to investigate them, over and above an ill-defined frequency band.

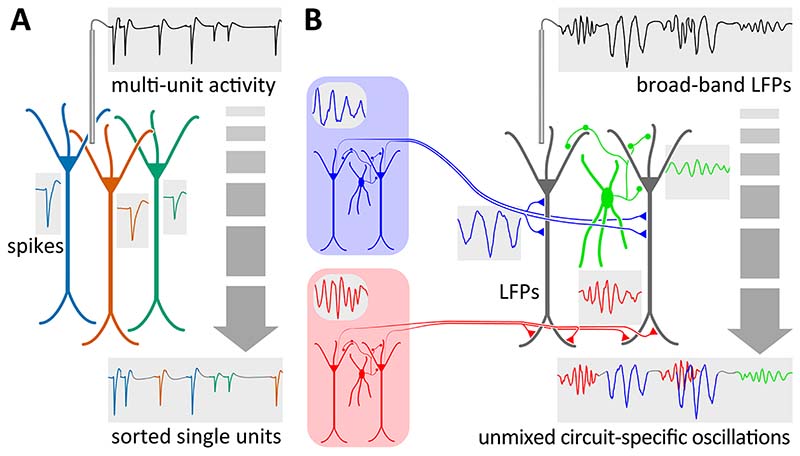
Accordingly, in this Perspective we review recent advances in the analysis, recording and manipulation of neural oscillations that indicate a roadmap for addressing these challenges and reaching a better understanding of the diversity of gamma frequency patterns. Notably, we propose shifting the attention from a frequency-based to a circuit-level definition of gamma oscillations, focusing on two anatomically based defining features, namely their underlying rhythm-generating and current-generating circuitries. Such a mindset draws from the analogy with the problem of ‘spike sorting’ (Figure 1). Extracellular electrodes allow to simultaneously record action potentials (‘spikes’) of many neurons in the surrounding tissue. Spike sorting then aims to assign each spike to an individual neuron (i.e., a ‘unit’), allowing to replace coarse population activity (i.e., ‘multiunit firing’) readout by fine-grain dynamics and interactions among individual neurons (Figure 1A). Mechanisms of active generation of the action potential and transmembrane current generation are both localized to the cell body of one neuron. Likewise, gamma oscillations emerge from different rhythm generating circuits that each give rise to different current sources. In turn, these mix in the extracellular space, yielding mesoscopic local field potentials (LFPs) (Figure 1B). Importantly, and in contrast to spikes, the identification and labeling of gamma oscillations require tracing back the current generators (synaptic currents giving rise to measured LFP oscillations) to the rhythm generators (the neural circuit generating the oscillatory pattern). This requires knowledge of anatomy, connectivity and biophysics of the underlying circuits ³¹. We thus propose that the ‘sorting’ of gamma oscillations and the identification of their rhythm- and current-generating substrates will move the field forward as the progress in spike sorting and cell type electrophysiological identification is currently doing. In line with this, instead of merely reporting changes in the overall gamma power in a given brain area during a given condition, we would shift towards discriminating gamma oscillatory patterns that reflect circuit-level motifs of activity and interactions among defined neuronal populations.

Figure 1. Sorting network gamma oscillations: an analogy with neuron spike sorting.

A) Action potentials discharged by nearby neurons are recorded on the same electrode, resulting in an aggregated signal of multi-unit activity (MUA). Spike sorting relies on sampling of the action potentials by an array of recording sites that allow assigning each action potential to an individual neuron (color-coded single-units), notably using spike waveform features. B) Likewise, multiple oscillations generated by different rhythm-generating circuits project repetitive volleys of synchronous action potentials via axonal pathways to their downstream targets, producing synaptic current-generating sources that sum up in the extracellular space and give rise to the recorded local field potentials (broad-band LFPs). These individual (color-coded) oscillations can then be demixed and assigned to their generating sources and subcellular domains, notably using their spectro-temporal and spatial characteristics.

Gamma oscillations as mesoscopic readouts of operating circuits

The discovery of the electrical nature of neural communication has been central to the field of systems neuroscience where assessing the selectivity of neuronal activity allows studying mechanisms at the nexus of brain and behavior. Following the pioneering work of Richard Caton who reported electrical impulses from the brains of animals using a galvanometer ³², Hans Berger made the seminal observation of the low frequency electroencephalogram (EEG) waves featuring alpha (8-12 Hz), delta (1-4 Hz), and theta (5-10 Hz) rhythms in the human brain ³³. From there on, neural oscillations have been widely examined using their frequency range, localization of origin, or brain state dependency. In vivo approaches, including electrophysiology, opto/chemogenetic and imaging, now allow linking individual neuron activities to network dynamics across spatio-temporal scales. Neuronal population synchrony appears as a theoretically predicted and experimentally demonstrated principle of organization for various neural operations, and at the same time allowing experimental measurement and dissection of network dynamics ^34–36. A remarkable observation is that many features of neural rhythms are evolutionary preserved, enabling to identify homologous oscillations across a wide range of species, from reptiles to birds to mammals ^37–39. This generalization stems from conservation of neural circuits, intrinsic neuronal properties and neuromodulatory correlates of behavioral and brain states associated with these rhythms, suggesting that both the mechanisms and functional roles of these oscillations could be conserved across a wide range of species. This generalization of slow rhythms, from animals to humans, also provides a framework for translational research of cognitive functions and neural pathologies ^37,40–42.

In contrast to slow-frequency oscillations, the discovery of the faster (>30 Hz) gamma rhythm counterparts took much longer. Except for early observations of beta and “faster-than-beta” oscillations in humans ^43,44, it was only much later that robust gamma rhythms in olfactory bulb ^45,46 and visual cortex ¹⁷ were reported, bringing gamma oscillations into the focus of research. However, by then, the term “gamma” already encompassed a large array of oscillations in the wide ˜30–150 Hz frequency band. One primary challenge compared to other rhythms is that gamma oscillations typically do not appear as one clear peak in the power spectrum ^7,22,23,30 and both their generating mechanisms and their biological relevance differ from that of the slow ones. Historically though, gamma oscillations were treated in a similar way as the slow rhythm, namely, as a spectral band.

Slow neural rhythms, such as those mentioned above, are typically brought about by the coordinated activity of multiple cell types that rely on upstream and/or local pacemaker circuits ^1,47. Divergent connectivity allows distributed or local circuits to be synchronized by a global rhythm, giving rise to macroscopically measurable oscillations. For example, theta (5–10 Hz) oscillations appear in the rodent hippocampus during active locomotion where they are sustained over second-long timescales ⁴⁸. During these periods, most hippocampal neurons receive rhythmic synaptic inputs that elicit coordinated transmembrane currents, giving rise to the observed theta rhythmic field potentials and corresponding frequency peak in the power spectrum ^49,50. However, this same reason makes it a daunting task to isolate the contribution of specific cells to the global rhythm ⁵¹. Gamma oscillations are, on the other hand, typically more localized in time and space as they reflect the synchronous activation of smaller ensembles of cells ^18,52–54. This could offer an advantage for their mechanistic investigation since the generating circuit can be dissected. Various analysis methods are considering this spatio-temporal selectivity to distinguish gamma oscillations (Box 1) (see reviews dedicated to this topic; e.g., ^47,55–57).

Box 1. Extracting gamma oscillations.

The electrical potential reflecting neural oscillators spread by volume conduction and can be captured by nearby electrodes. Therefore, at any point in the brain, the raw LFPs are typically composed of multiple superimposed oscillations generated by different sources that can overlap in both frequency and time. Various decomposition techniques have been designed and employed to detect and disambiguate co-existing oscillations.

One of the most common approaches is the use of linear/Fourier-based filters to isolate oscillations in frequency bands determined by the user, based on past work and/or observations of the raw signals. For example, one might filter CA1 LFPs from 20 to 50 Hz to extract slow gamma oscillations while filtering the same LFP signal from 50 to 90 Hz to extract mid gamma oscillations. This comes with the assumption that each oscillation of interest is (1) mostly contained within the defined frequency band (in the Fourier sense), and (2) the interference caused by other oscillations in that specific band is negligible. Violation of such assumptions has consequences for the study of co-existing oscillations and hinders the uncovering of yet unknown oscillators. Of note, parametrizing the LFP (or EEG) power spectra can separate the aperiodic components (or ‘1/f’) and putative oscillations, without the need to pre-define specific frequency bands ¹¹². However, while frequency-based dissociation of different gamma sources is possible, it does not provide a principled way to uniquely assign an oscillation to generating circuit.

Another approach to reveal different oscillators is to explore both their frequency and temporal dynamics, i.e., by studying how their features vary over time. This is often achieved using time-frequency representations of LFPs by filtering these signals in narrower frequency bands (computed with common linear filters, the continuous wavelet transform or multi-taper short-time Fourier-transform) and computing the instantaneous amplitude (spectral power) of these components at each frequency ¹¹³. Decomposition techniques, such as factor analysis (e.g., ³⁰) and independent component analysis (ICA) (e.g., ²⁴), can be employed to reduce the dimensionality of the spectrograms to a set of spectral patterns. These techniques combine correlated frequencies in a broad spectrogram into components that are statistically orthogonal or independent from each other, and therefore potentially reflect different oscillators. Another strategy consists in detecting local maxima in the 2D (frequency versus time) representation of spectrograms, thus detecting isolated and transient oscillatory bursts (e.g., ^30,72), which generalizes conventional detection of oscillations in one, typically broad, predefined frequency band ^52,114.

Additional to the frequency content and temporal dynamics, spatial distribution provides key information for decomposing and attributing oscillatory signals to their anatomical sources. This can be achieved by dense sampling covering the anatomical sources that provide spatial information that allows discriminating different oscillators. Thus, the underlying cellular basis of an oscillatory pattern would be identified by their spatial profile. In contrast to a single channel-based detection this approach does not require a high detection threshold to avoid spurious out-of-band contamination and is less affected by volume conduction. Spatial information has been particularly successful for the analysis of hippocampal CA1 signals since different sources generated by afferent synaptic pathways, that convey gamma oscillations from the upstream generators, are segregated along the somato-dendritic axis (Figure 2). At least three dominant oscillatory components can be isolated using current source density analysis (CSD) and blind source separation techniques such as ICA ²⁹. Likewise, ICA has been applied to isolate layer-specific gamma oscillations in other structures such as the hippocampal dentate gyrus ⁹³ and the neocortex ²⁶. Joint use of space-time-frequency spectral content allows statistical decomposition that benefits from all the above-mentioned features allowing unique identification of different gamma patterns ³⁰.

The initial description of gamma rhythms had focused on sensory input driven oscillations. Controlled presentation of olfactory or visual stimuli activates downstream circuits in a predictive manner, allowing direct raw data observation and statistical quantification of gamma oscillations. However, in the absence of controlled timing and strength of circuit activation, gamma oscillations appear to emerge in a stochastic manner, with variable power, frequency and timing influenced by multiple sources of excitability fluctuation. Gamma oscillations also appear during different states of vigilance, from active behavior to awake rest to sleep or anesthesia. This highlights that gamma frequency patterns are neither uniquely coupled to specific brain states (as their slow counterparts) nor exclusively support specific functions. They might rather reflect a dynamic mode of operating circuits that could, potentially, serve different functions in different behavioral and brain states^{2,22,26,30,52,58,59}.

Building from all these features, we propose an analogy between gamma frequency patterns and action potentials as elementary units of collective neural activity (see also ^60–62). Of course, analogies have their own intrinsic limitations. But for the purpose of this Perspective, distinct neuron types emerge when comparing action potential waveforms, refractory periods, inter-spike intervals or firing rates. Different cell types can also exhibit similar action potential waveforms while further defined by their molecular profile, anatomical location, post-synaptic recipients, or synaptic inputs. Similarly, gamma oscillations can be uniquely identified by the rhythm-generating circuit they emerge from and current circuit they are recorded from, while the power, frequency and temporal dynamics of gamma bursts generated by the same oscillator may yet vary (e.g., as a function of behavioral states). In direct analogy with spike sorting of neurons based on triangulation of their anatomical localization, distinct gamma oscillators can be identified by their anatomical location and the properties of the circuit they emerge in. As nearby neurons produce multi-unit activity that cannot be fully interpreted unless they are individually sorted, so is the mixing of gamma signals generated by temporally correlated neighboring circuits. Thus, the spectral profile of gamma power is not a full descriptor of the underlying circuits. It is also important to note that, contrary to the discrete, all-or-none nature of action potentials, the amplitude of gamma oscillations is graded. This indicates that the underlying circuits operate at varying strengths or levels of synchrony rather than in an ON or OFF manner. Instead, driven by various external inputs gamma rhythm-generating circuit acts as a nonlinear integrator of this input. Variable synchrony and frequency of the oscillation could be compared to the emergence of a burst in a single neuron with variable inter-spike interval and duration in response to variable input. Further, contrary to action potentials that come from a well-defined and discrete unit (i.e., the corresponding neuron limited by its cell membrane that clearly defines the anatomical substrate), gamma oscillations emerge from the stochastic synchronization of interconnected neurons within specific circuits, and in this respect are not ‘real’ physical units. Due to stochastic nature of synchronization, all neurons in the population do not participate in every cycle of the oscillation, but the global output of the population of similarly projecting neurons active at every cycle gives rise to the transmembrane currents that generate the LFP signal with macroscopically invariant spatial structure. Moreover, no circuit is exclusive to a specific oscillation, similar to how the firing of specific neurons is not limited to a certain temporal pattern and rate. For example, the networks generating hippocampal gamma oscillations overlap with those involved in other oscillatory events such as sharp-wave ripples and theta oscillations ^50,63. The ‘anatomical substrate’ of gamma oscillations is furthermore complicated by the temporal overlap of oscillations generated by interconnected circuits making their circuit-level isolation difficult and requiring knowledge of their biophysical mechanisms and anatomical connectivity. Accordingly, here we highlight that the ‘oscillogenesis’ of different gamma frequency patterns pertains to dynamical, yet well-defined, neural circuits, which defines their mechanistic basis. We thus suggest that future research would need to uncover these underlying dynamic mechanisms along their functions.

Box 2. Spike-to-LFP and LFP-LFP coupling.

In addition to their presence in LFPs, genuine oscillatory patterns are observable in the spiking activity of their corresponding circuits. Relating spiking activity to an oscillation of interest is crucial to the understanding of its origin. For example, demonstrating that neurons in a circuit are coupled to an LFP oscillation adds evidence that such oscillatory activity is either generated by that circuit or driven by the afferent circuit, as opposed to being recorded by volume conduction. Studying the timing (e.g., by means of spiking preferred phase) of principal cells and interneurons relative to an oscillation provides further insight into its generation mechanism.

Multiple statistics have been developed to characterize LFP-to-LFP ^115–118 and spike-to-LFP phase coupling ^116,119,120, capturing the level of consistency between the fluctuations in phase and/or amplitude of two LFP signals, or between the firing of a neuron and the phase of an oscillation (Figure 3A). The more concentrated the distribution of spike-phases, the higher the coupling. Note that this approach involves the computation of the instantaneous phase of the LFP signal filtered in different narrow frequency bands. Alternatively, coupling might be quantified as the coherence between LFPs and spike time series (Figure 3B).

The presence of an oscillation might also be derived from the analysis of inter-spike intervals (ISI) distribution or auto/cross-correlograms of the spike trains, which are the time-domain analogues of the LFP spectral analysis. Auto- or cross-correlations of rhythmically firing neurons reveal the dominant oscillation frequency, comparable to the LFP spectrum, but precise circuit specificity. Likewise, triggered averages or peri-event histogram analyses, an equivalent of the cross-spectrum, can be used to visualize oscillatory pacing of spike trains (Figure 3C). When appropriately normalized and corrected these quantities are equivalent to spike-LFP coherence.

In addition to being generated by the local circuitry, gamma coupling often reflects cross-area communication. Simply stated, a “source” region produces a gamma rhythm and "projects” its rhythmic output to a “target” circuit. The gamma-paced spiking in the source region causes field post-synaptic potentials (fPSP) in the target region with the same periodicity, generating time-delayed gamma currents that are reflected in the local LFPs and potentially entrain target neurons. This implies that a local gamma oscillatory signal in the source region is coherent with LFP in the target region, both reflecting connectivity between areas and not necessarily the interaction. Thus, demonstrating phase-coupling between oscillators in two connected circuits A and B requires decomposing the signal in B into an afferent gamma (originated in upstream region A) from the local gamma oscillatory signal generated by the circuit B. Another possible scenario for LFP-LFP coherence between circuits A and B is that a third circuit C projects its gamma pattern to both A and B, giving rise to coherent gamma signals despite no direct coupling between A and B oscillators. As a typical confound, distant gamma sources and non-neuronal (e.g., EMG) sources can volume conduct to both circuit A and B, giving rise to a spurious high coherence.

In contrast to LFP signals, spiking activity can be directly attributed to the circuit it is recorded in. A tight temporal relationship between gamma LFP patterns featuring circuit A and spiking activities recorded in circuit B is robust support that A is driving B, and potentially for direct coupling between the two circuits. Likewise, gamma-timescale cross-correlation or coherence in the gamma band of the unit firing in A to unit firing in B is robust evidence of interaction between A and B. At the same time, phase coupling of units firing in A to gamma frequency patterns in B is a robust support for gamma LFP patterns in B being directly generated or indirectly driven by the oscillator in A. It is important to note that since conduction delay for action potential propagation from A to B is typically longer than recurrent delay within A, local gamma patterns in A will thus be causal to those in B, with this asymmetry providing an electrophysiologically-derived connectivity metric. Similar directionality can be, under some circumstances, inferred from the unit-LFP phase spectra.

Towards a circuit-based definition of gamma oscillations

Experimental and theoretical work have synergistically suggested several candidate generating mechanisms for - and identified key features of - gamma oscillations. For instance, in the interneuron gamma (ING) model, gamma frequency patterns emerge from a mutual inhibition between inhibitory GABAergic neurons in response to a tonic excitatory drive to the network. In the pyramidal-interneuron gamma (PING) model, a tight excitation-inhibition (E-I) balance involving the ubiquitous motif of reciprocally connected excitatory-inhibitory cells allows an alternation between fast excitation and delayed feedback inhibition to generate gamma oscillations ^1,19,64–69. Consistent with this, the frequency of gamma oscillations depends on the fast GABAa and glutamate AMPA synaptic time constants ^11,70. Moreover, gamma oscillations decohere as spatial scale increases because both conduction delays and heterogeneous connectivity preclude synchronization over large distances ^22,60,71. High amplitude gamma is also typically transient, instantiating bursts that typically last 50–100 milliseconds ^{14,24,30,72,73}. Finally, the power and frequency of gamma bursts both depend on the synaptic time constants of neuronal interactions, the underlying circuit motifs, the temporal structure and strength of the excitatory and inhibitory population drives, and the neuromodulatory states ^{1,18,21,53,70,74}. Hence, while under certain conditions (e.g., a strong sensory stimulus inducing high network synchrony) the central frequency of gamma oscillations emerging in a circuit might appear relatively stable over time, the heterogeneity of the inputs constantly impinging that circuit can lead to moment-by-moment variation of some features, including frequency. Moreover, gamma oscillations can be generated by local neuronal interactions (e.g., recurrent excitatory-inhibitory synaptic connections) or inherited from afferent synaptic inputs (i.e., generated by an upstream network), which hinder their attribution to a particular circuit without additional information. Afferent gamma frequency inputs originating from multiple upstream circuits can also mix in the target (recorded) region where they converge, together with local gamma oscillations, making their separation a necessary step for further analysis. These confounds highlight again the importance of distinguish between the current generators of a particular gamma pattern (i.e., transmembrane currents in the region where oscillations are recorded) and their rhythm generator (which can be local as the current generation but also in a distant afferent region). If temporally isolated and transient, anatomically localized and frequency defined, then gamma oscillations can be identified as local maxima of the spectral power. These considerations have allowed separation of multiple neocortical and hippocampal gamma generators ^30,72. In contrast, gamma detection solely based on the power of one band-pass filtered raw signal risks contamination by other (e.g., volume conducted) sources and can be biased by the selection of a given frequency band, requiring high threshold to avoid spurious out-of-band contamination. Some of the caveats and proposed solutions that will be discussed here in regard of gamma oscillations, can also be applied to the study of other brain rhythms. A prominent example are hippocampal theta-frequency (5-10 Hz) oscillations and those commonly present in the EEG from frontal-midline cortical regions. These patterns, despite having similar spectral profile have completely disparate generating mechanisms and functional correlates ⁷⁵.

Investigating gamma oscillations thus requires distinguishing their internal generating mechanisms from the externally observable signals. Leveraging again the analogy used above, both the generation of gamma rhythms and the intracellular mechanisms generating action potentials cannot be directly observed. The mean-field synaptic transmembrane currents produced by the synchronous firing of the excitatory and inhibitory populations at every gamma cycle give rise to periodically repeated responses macroscopically observable as oscillatory frequency patterns. Moreover, neurons receiving gamma currents can be either members of the local oscillating circuit (recurrent sources) or of the remote circuits (afferent sources), producing multiple copies of a gamma burst. The smaller the gamma-generating circuit and the sparser the activity of the generating population, the smaller the power of the corresponding oscillation (both locally and remotely). The larger the degree of convergence of the gamma oscillator circuit to the downstream circuit and the stronger the synaptic connectivity in respective synapses, the larger the afferent signals. Thus, the power of gamma frequency patterns is a complex function influenced by the properties of both the oscillator (e.g., E-I circuitry) and its target structure (e.g., synaptic connectivity to cellular recipients) ^76,77. Such a complex relationship between the gamma generator and the readout signals qualitatively differentiates the gamma bursts from the action potentials, which exhibit relatively stable properties for a given neuron. The spatio-temporal features of the gamma mesoscopic (e.g., LFP) readout thus provide both pros and cons for their interpretation. Furthermore, as gamma oscillations can be detected both locally and in remote locations, the attribution of oscillatory signals to their original circuit remains ill-defined without additional information. As mentioned above, afferent gamma oscillation sources originating from multiple upstream circuits can mix in the downstream target region. Likewise, afferent gamma sources can mix with the local recurrent and volume conducted ones, making their separation a necessary step for further analysis.

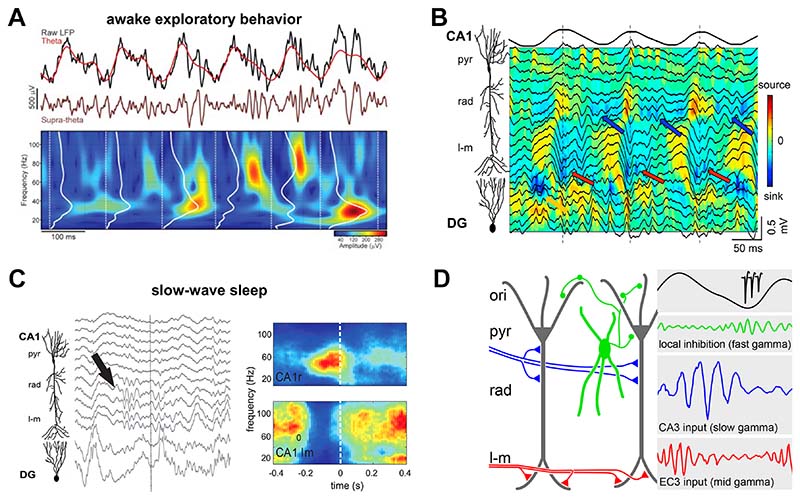
To illustrate the diversity of gamma oscillations we are focusing on two regions of the mammalian brain where considerable progress has been made to identify the underlying cellular substrates: the CA1 region of the hippocampus and the primary visual cortex. The hippocampal CA1 presents an important advantage for the study of network oscillations: its principal (pyramidal) cells form parallel layers of cell bodies and dendritic trees where synaptic inputs are stratified. Synchronous EPSPs and IPSPs at gamma timescales elicit transmembrane currents that add up in the extracellular space to generate mesoscopic fluctuations of the LFPs ^31,53. The stratification of different synaptic inputs along the dorso-ventral CA1 axis and the alignment of dendritic compartments across the pyramidal cell population facilitate the summation of transmembrane currents in the extracellular space, giving rise to large amplitude LFPs with a stereotypical laminar profile ^7,78,79. In other structures, such as the neocortex, where neurons are not as well aligned as in CA1, the spatial discrimination of gamma oscillations becomes more challenging ^17,23,26,30. Synaptic and circuit time constants and the cycle-by-cycle balance of excitation and inhibition modulate the amplitude and frequency of gamma oscillations ^18,70. Distinct gamma oscillations have been related to selective synaptic current sources along the radial axis of CA1 pyramidal cells (Figure 2). The two main excitatory inputs to CA1 arise from the neighboring area CA3 and from the entorhinal cortex layer 3, that target respectively the proximal (stratum radiatum) and distal (stratum lacunosum moleculare) apical dendritic domains. CA3 generates slow gamma oscillations (30–50 Hz) through the interaction of recurrent excitatory connections between pyramidal cells and feedback inhibition from perisomatic-targeting basket cells ^53,80,81. This then ‘projects’ slow gamma oscillations to CA1, where they are recorded with largest amplitude in the stratum radiatum ^19,22,29,52. Similarly, gamma oscillations of faster frequency (60–100 Hz) are generated by recurrent circuits in the layer 3 of entorhinal cortex and are projected to the stratum lacunosum-moleculare of CA1 ^14,24,82. Although these oscillations are generated in regions upstream of CA1, local interneurons play an important role in modulating them and in their efficacy to entrain somatic action potentials ^11,83,84. In addition, and despite its lack of dense recurrent excitatory connections, CA1 also generates its own gamma oscillations. These have faster frequency (100–150 Hz) than the ones previously mentioned and are supported by local recurrent interaction between pyramidal cells and perisomatic-targeting fast-spiking interneurons ^19,22,85,86. These three hippocampal CA1 gamma patterns are also coupled to different phases of the pyramidal layer theta rhythm, indicating a temporal segregation of inputs to CA1 pyramidal cells ^{13,14,22,24,82,87–89}. In addition, the same gamma oscillations appear in non-theta states (e.g., slow-wave sleep; Figure 2C; e.g. see ⁵⁸), indicating that it is the generating circuit that underlies a particular gamma frequency pattern. As briefly discussed here, a large body of experimental evidence converges on both the existence and circuit mechanisms of different gamma-band oscillations in the CA1 region. Despite this broad agreement, some reports differ in the specific behavioral correlates of these oscillations (such as their modulation by theta rhythms or animal locomotion during exploration) or their proposed functions ^{14,22,24,73,82,87–92}. Furthermore, the analysis of gamma oscillations can be confounded due to other sources of activity that also generate spectral power in the gamma frequency band, such as spikes, electromyographic artifacts (EMG) or theta harmonics (see Box 3). Switching to a circuit-based definition of gamma oscillations and incorporating specific experimental and computational approaches for their study could clarify most differences across these observations, which could be heightened when studying gamma oscillations in other brain structures.

Figure 2. Diversity of gamma oscillations: example of the hippocampal CA1 region.

A) Example of co-occurring theta (top) and gamma (middle) CA1 oscillations (black trace: raw LFPs; color-coded traces: corresponding theta and supra-theta signals) during spatial exploration. Spectrogram at the bottom showing spectral features of hippocampal gamma oscillations. Adapted from ²⁴. B) Depth profile of hippocampal theta and gamma oscillations (black traces) and underlying current sources (color map) during learning. Blue arrows show slow frequency gamma oscillations in the proximal apical dendrites of CA1 pyramidal cells (stratum radiatum, rad). Red arrows mark mid frequency gamma oscillations in the distal dendrites (stratum lacunosum-moleculare, l-m). Adapted from ⁹³. C) Left, depth profile of hippocampal LFP traces during slow wave sleep (note slow gamma during down state, arrow); right, average spectrogram for CA1 stratum radiatum (top) and lacunosum-moleculare (bottom) triggered on the entorhinal up state onset. Note similar spectral content of the slow/medium gamma in the dendritic domains innervated by CA3/EC3 to those during theta state. Adapted from ⁵⁸. D) Schematic showing that entorhinal cortex layer 3 (EC3) input to distal CA1 apical dendrites elicits mid frequency gamma oscillations (red) at the peak of CA1 pyramidal layer theta (black trace), while CA3 inputs to proximal CA1 apical dendrites elicits slow gamma oscillations (blue) at the descending theta phase. Fast gamma oscillations (green) during theta troughs are generated by a local excitatory-inhibitory circuit motif.

Box 3. Slower rhythms modulate gamma oscillations.

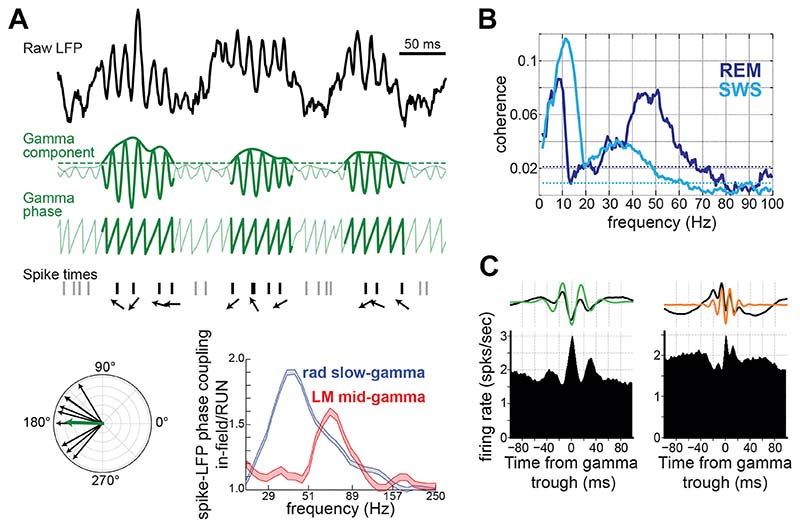
Slower rhythms provide a natural pacing of gamma oscillatory burst rate or, equivalently, the amplitude modulation of gamma power. This gives rise to the well-known power-phase correlation or cross-frequency coupling (CFC) phenomenon ^7,135–137. As we cannot describe a neuron just by its firing rate at a given phase of a slow rhythm, so we cannot describe a gamma pattern by its frequency that has the largest power modulation by the phase of a slow rhythm, or maximal CFC strength. The mean power spectrum, under typical non-stationary conditions, is ill-defined and reflects a combination of sparse gamma occurrence and power statistics. CFC metrics are bivariate statistics that quantify non-stationary gamma dynamics better than average spectrum, but should, in general, only be seen as descriptive statistics and not unique identifiers of the oscillators. While convenient to reveal temporal dynamics of the gamma oscillators, CFC metrics alone generate a bias towards those gamma patterns that are more strongly and consistently modulated by the slow rhythms. For example, hippocampal dendritic gamma sources give rise to specific bands in CFC in CA1 stratum radiatum at ˜30-50 Hz and lacunosum-moleculare at ˜60-90 Hz reflecting strong theta-modulated gamma frequency inputs originating in the hippocampal CA3 and MEC layer 3. Contaminants of LFPs, such as spike leakage or EMG can, respectively, positively or negatively, bias CFC at broad range of frequencies above 50 Hz ^13,138,139. Furthermore, bivariate analyses relating fast and slow spectral components of the signal might be affected by harmonic artefacts ¹⁴⁰. When assuming that a complex signal can be described as a sum of sine waves, performing a spectral decomposition of such a function of time using linear filters can produce harmonics (a set of mathematically produced sine waves whose frequencies are a multiple of the frequency of the original signal). This is especially pronounced for strongly asymmetric nonlinear waveforms, such as those featuring hippocampal theta cycles. In this case, theta harmonics could bleed into the gamma frequency band, potentially confounding some cross-frequency coupling analyses, notably phase-phase coupling measures ^140–142. For gamma amplitude to theta phase coupling, this is less of a concern as the gamma range starts around the third theta harmonic (˜32 Hz) where the harmonics are orders of magnitude below the power of slow gamma oscillations (provided the recording is near the gamma source). Furthermore, it has been shown (in rats) that the amplitude of slow gamma is negatively correlated to speed ^24,143,144 while the amplitude ¹⁴⁵ and asymmetry ¹⁴⁶ of theta are positively correlated, showing a clear disambiguation between theta harmonics and slow gamma power. Moreover, phase coupling analysis reveals that spike coupling starts at gamma range but not around the first theta harmonics (˜16Hz or 24Hz) which are stronger than the following ones (>30Hz) (Figure 3A,B). In the same line, triggering spiking activity by a single trough of gamma per theta cycle clearly reveals three cycles (at least) of rhythmic modulation in hippocampal firing activity matching the corresponding gamma frequency (Figure 3C), whereas a saw-tooth like waveform would be present if theta harmonics significantly explained the gamma range coupling. Finally, LFPs from CA3 and EC present strong slow ^22,147 and mid ⁸² gamma amplitude modulation by theta phase, respectively; yet no contamination indicating harmonic artifacts below gamma frequencies are observed (which would include the first two theta harmonics), demonstrating that in fact harmonic artifacts are orders of magnitude weaker than the modulation of genuine gamma oscillations. Nevertheless, it is good practice to evaluate in each dataset if theta harmonics are contaminating the gamma range. Notably, visual inspection of raw traces, spectrograms using small windows (100-200 msec), and tests as those mentioned above should help to determine if energy observed within gamma frequency range comes solely from the non-linearity of lower frequency signals (such as theta) rather than genuine gamma rhythmic patterns of activity. Further methodologic development for capturing the space-time-frequency localized non-stationary nature of neural oscillations, and handling of non-linear wave shape of slow oscillations, will help the field to study gamma patterns moving forward (e.g., ^146,148,149).

Advances of recording technologies and data analysis methods, as well as control of the sources of variability and input parameters have resulted in rapid progress towards the dissection of the origin of gamma oscillations in sensory thalamo-cortical circuits. A central difference between the dynamics of hippocampal gamma oscillations and those in sensory neocortices is the source of excitability that modulates them. While brain state, locomotion speed and task demand modulate the engagement of different hippocampal circuits and their control allows for measuring their modulatory role of the gamma dynamics, experimental control of timing and parameters of the sensory stimuli and their presentation in different brain states present an opportunity for investigation of gamma oscillations in the sensory thalamo-cortical circuits. Layer and frequency specific gamma oscillation generators have been reported in vitro ^94–96. In vivo, recordings in rodents, cats and primates revealed differential spectral content and differential laminar neuronal entrainment by spontaneous and evoked gamma oscillations ^26,97,98. While layer-specific hippocampal gamma oscillations tend to be prevalent at relatively broad frequency ranges, gamma oscillations in thalamo-cortical circuits can be narrower bands. In particular, narrow-band gamma (50-70 Hz) in the mouse visual system has been a focus of intense research in recent years. Anatomical rhythm generators of this oscillation pattern have been identified in the dorsal lateral geniculate nucleus and its current generators are in layer 4 of primary visual cortex ²¹. Their expression is robustly induced by visual stimulation, similar to how early neonatal gamma in somatosensory thalamo-cortical circuit is evoked by the whisker stimulation ⁹⁹. They have been shown to be modulated by brain state and arousal level ^26,76,100, as well as active locomotion ^101,102. Controlling parameters of the visual stimulus revealed that high luminance modulates narrow-band gamma power ^21,103, which is practically absent in darkness. Visual stimulus contrast decreases narrow-band gamma power ²¹, while promoting broadband-gamma oscillations ^96,104,105. This is reminiscent of sensory-triggered gamma oscillations in other thalamo-cortical circuits, such as whisker stimulation-triggered early neonatal gamma in somatosensory areas ⁹⁹.

A prominent role for rapid changes in behavioral states and sensory inputs as sources of excitability fluctuation in thalamo-cortical circuits provides mechanistic insights into the basis for non-stationary oscillations. Visual stimulus presentation induces sustained narrow band gamma oscillations in the visual cortex, which peak frequency, in turn, can vary with stimulus parameters ^21,27,106 and attentional state ¹⁰⁷. However, spontaneously emerging gamma oscillations under naturalistic states and stimuli are associated with non-stationary transient gamma bursts ^28,61. Future analysis of the anatomical circuits contributing to thalamo-cortical gamma oscillations and their modulation by diverse sources will provide an important temporal framework for dissecting the role of gamma patterns in coordinating information processing and flow in sensory systems across animal species ^108–110.

In this section, we have reflected on the definition of gamma oscillations where, instead of solely focusing on peak frequencies, one would also consider the underlying cellular substrates. For example, in the context of hippocampal gamma oscillations, one would probe and validate ‘CA3→CA1 stratum-radiatum gamma frequency inputs’ instead of detecting ‘slow gamma’ from bulk signals and assuming neural pathway and process from the frequency band. The CA3 to CA1 gamma frequency input is a well-defined anatomical-physiological entity while slow gamma oscillations can yet be generated by different cellular sources and can have distinct functional correlates, even within the hippocampus itself ^90,93,111. This shift in definition has several advantages. First, it would unequivocally ascribe a mesoscopic gamma pattern to the operation of a well-defined circuit. Indeed, the frequency and other spectro-temporal properties of an oscillation can largely vary, because of the related biological variables and detection approaches. But the cellular substrates do not. This would also prevent a given term creating confusion between different neural oscillatory phenomena that have similar frequency but distinct mechanisms or functions as they are produced by different circuits. Likewise, oscillations generated by the same neural substrates and mechanisms in distinct species (e.g., humans versus rats versus mice) would then be considered analogous even if their frequency band is not the same. Here, the relevant question will no longer be ‘what is the function of x-Hz gamma’ where x is a frequency value, but ‘what is the gamma-reported function of a specific neural circuit and pathway’ (e.g., the CA3→CA1 pathway).

About the computational function of gamma oscillations

While important progress continues to be made on the characterization of network oscillations, the central question about the functional relevance of those spanning the wide gamma band yet remains uncertain. What are the neural operations reported by gamma patterns? Do gamma dynamics provide any mechanistic insights into information processing? What possible computational benefits does the temporal structure provided by gamma oscillations bring? The fine-timescale coordination of neural population firing within and across regions is the expected basis for effective computation in gamma oscillations. Discrete gamma patterns could indeed constitute elementary “units” of neural computations, but they need to be assessed with respect to their host circuit where afferent inputs, balance of excitation and inhibition and local connectivity are all dynamically interacting. While we do not intend to overview this vast topic here, we aim to provide a biophysical and anatomical backdrop to the proposed computations that gamma could serve.

Gamma oscillations are thought to aid the precise orchestration of spatio-temporal patterns in the recruited neural populations, thereby providing the basis for neural coding ¹²¹. While appealing and supported by theoretical and experimental evidence, this tenet yet faces the instability and variability of oscillation frequency and sparseness of neuronal firing. Ensemble synchrony likely underpins attractor dynamics that give rise to low-dimensional representations in many circuits, including the olfactory bulb, motor cortex and hippocampus ^122,123. Surround suppression of competing cell assemblies by gamma recruited inhibition can provide means for selective resonance of the circuit to a specific input ⁷⁴. Other hypothesis of gamma synchronization posits that excitation/inhibition balance yields a gain control function ¹⁸. Constructive interference between gamma-synchronization of a circuit with an afferent gamma-rhythmic input could also aid information transfer, as put forth by the communication through coherence hypothesis ¹²⁴. The commonly reported mismatch between synchronization frequencies in LFP-LFP and spike-LFP metrics (e.g., ²²) between source and target remains to be resolved. Fine-timescale synchrony is also a good candidate for synaptic plasticity ^125–127. While the computational role of pairwise plasticity (Hebbian or Spike Timing Dependent Plasticity, STDP) is well-understood, higher-order plasticity rules associated with different physiological conditions and conduction delays yet remain to be further investigated ¹²⁸. The existence and variability of axonal conduction delays across regions remain a major anatomical constraint that need to be considered ¹²⁹. In fact, STDP over long and variable conduction delays can result in desynchronization ¹³⁰. This problem takes special relevance when considering zero-lag long-range synchronization, which is suggested to contribute to the integration of neural representations (binding; ¹³¹). While long conduction delays are a major impediment to achieve zero-lag synchronization between two brain areas, this can still be accomplished by introducing a third, upstream structure projecting to both areas ¹³². In this setting, the strength of connectivity between the three areas and the dynamic control of firing in the upstream structure can determine the type of synchrony, ranging from zero-lag to out-of-phase coupling ¹³³.

The periodic nature of neural oscillations is appealing for theories of their function (e.g. temporal coordination of spiking), in addition to their practical use for detection and characterization. Yet, it is not strictly necessary for most of the proposed functions. For example, the periodicity of theta oscillations in the rodent hippocampus has been long-assumed essential for the orchestration of spatial coding and learning; but recent work suggests that it is synchrony, not periodicity, that is a necessary component of the theta-like dynamics organizing spatial coding in the bat hippocampus ¹³⁴. It follows that neither the exact frequency nor its stability within a gamma oscillatory transient might be functionally critical. Similarly, increased level of synchrony does not necessarily imply a computational advantage: robustness might come at the expense of flexibility. Moreover, sparse spatio-temporal activation of distributed ensembles may not give rise to mesoscopically observable gamma patterns. High neuronal synchronization might result in strong gamma power yet not associated with qualitatively different ensemble activation. Taken together, this evidence suggests that gamma oscillations do not report one but many different computations, which can also be dynamically weighted on a moment-by-moment basis. Identifying and testing the specific computational function(s) reported by gamma oscillations thus require robust unbiased methods that are invariant across experimental paradigms, brain states and animal species. Achieving this will pave the road to develop a comprehensive framework linking circuit motifs, neural dynamics, and computations.

Figure 3. Spiking activity coupling to gamma oscillations.

A) Mean vector length method for coupling quantification. Raw LFPs are filtered for the extraction of a gamma signal, which is then used to compute the instantaneous gamma phase. The distribution of the phases sampled by the spike times of a given neuron is next analyzed in a polar plane, where each spike-sampled phase is represented by a vector (phasor) with that corresponding angle. The more consistent is the firing of the neuron, the more concentrated this distribution is around a given mean phase. Thus, the spike-to-phase coupling is quantified as the length of the mean phasor. Non-coupled neurons produce phasors homogenously distributed around the polar plane that cancel out when averaged, whereas phasors obtained for highly coupled neurons stack up, resulting in larger mean vectors. A threshold might be applied to the instantaneous amplitude of gamma to avoid using spikes when the oscillation is not present in the signal, as shown in this figure. Bottom right panel shows coupling strength (relative measure for spikes inside- over outside of place fields) of CA1 place cells calculated for signals in CA1 strata radiatum and lacunosum-moleculare, estimated by ICA (adapted from ⁸². Copyright 2010 Society for Neuroscience). B) (Magnitude-Square) Coherence between neocortical LFPs and spike train of a local neuron during REM (darker blue) and slow-wave sleep (lighter blue). These results show how oscillation frequency of the same oscillator, localized near the cell, revealed by spike-LFP coupling, can vary depending on the behavioral state (adapted from ³⁰). C) Spike coupling to different gamma oscillations revealed by time-domain analysis. Top panels show CA1 raw and filtered LFP averaged around slow (left) or mid (right) gamma troughs. Bottom panels show firing rate of CA1 principal cells aligned to the same gamma troughs. Importantly, for this analysis a single trough of gamma is taken per theta cycle. Note that instantaneous rates of these cells oscillate around the trough of each gamma paced by its corresponding rhythm (adapted from ²⁴).

Experimental approaches for investigating gamma oscillations

The brain features non-linear dynamics linked to the structural connectivity, functional properties and biophysical constraints of its composing elements. As it happens with many other complex systems, it is not feasible to study a particular aspect of it in isolation. To understand the functional relevance of gamma oscillations, one would ideally manipulate these rhythms while other variables in the system (e.g., neuronal firing rates) remain fixed. Unfortunately, this is not possible due to the inter-dependency between the various components of the underlying neural circuitry. In this section, we summarize recent developments enabled by novel experimental approaches to study the mechanisms and functions of gamma oscillations and suggest a roadmap for future studies.

Obtaining experimental evidence for any particular role(s) of gamma oscillations would require first to pursue their identification. A well-known example and success story of network pattern study is provided by hippocampal ripples that emerge as 150-250 Hz oscillatory bursts in the hippocampal CA1 region driven by CA2/3 sharp-waves ^63,151. Decades of work have documented how temporally structured firing activity (in the form of neuronal sequences or short-timescale coactivations), emerging and organized by these mechanistically well described oscillatory bursts, relate to memory and other higher-order functions. Notably, it is the anatomical localization and not the precise frequency that provided selectivity of the research on ripples. Drawing from this successful case study, meticulous dissection of anatomically and temporally defined readouts of gamma-paced neuronal activity will report circuit-specific computations and their relevance to behavior and information processing. Such readouts can be obtained using LFP recordings as an effective low-dimensional sampling of population-level firing structure. The hippocampus provides again a useful illustration on the progress in the identification of the cellular mechanisms of gamma oscillations. Classical studies have focused on the importance of local circuit interactions, in particular recurrent connections between excitatory and inhibitory cells, for the generation of gamma oscillations ^64–66. In vitro experiments have demonstrated that the local circuitry is sufficient for the generation of gamma oscillations ^67,152. Both in vitro and in vivo studies have highlighted the importance of perisomatic inhibition mediated by fast GABAa post-synaptic inhibitory potentials (IPSPs) in synchronizing the rhythmic output of pyramidal cells (‘rebound from inhibition’) ^11,53. Reciprocal interactions between excitatory cells driving local interneurons and delayed feedback inhibition became the canonical model for gamma generation (‘E-I model’) ^153–155. In vivo optogenetic studies have confirmed parvalbumin-expressing basket cells as a key cellular element in gamma generation ^156–158. Most of these studies focused on local mechanisms of gamma oscillations. Gamma oscillations have also been implicated in mediating inter-regional communication (Figure 4). Early studies performing surgical lesions or pharmacological inactivation, demonstrated the importance of extrinsic inputs for the generation of hippocampal gamma oscillations. In a classical study, Bragin et al., surgically de-afferentiated the rat hippocampus from all its entorhinal inputs and showed a strong reduction in gamma oscillations in the dentate gyrus ⁷. In this study, theta oscillations were also affected, illustrating the tight relationship between both signals and their dependence on the entorhinal inputs. More recent studies have employed optogenetic manipulations to transiently perturb entorhinal inputs to the hippocampus. Fernandez-Ruiz et al., entrained GABAergic cells in either the medial or lateral portions of the rat entorhinal cortex with a spurious gamma frequency stimulation pattern, disrupting their natural gamma spike timing ⁹³. This manipulation, in turn, reduced power and CFC of different anatomically-distinct gamma oscillations in the hippocampal dentate gyrus while global theta oscillations were relatively spared. Furthermore, perturbation of the fast gamma synchrony between medial entorhinal cortex and dentate gyrus impaired spatial learning, while perturbation of the slow gamma synchrony between lateral entorhinal cortex and dentate gyrus impaired object learning. Despite these selective physiological and behavioral effects, one may not conclude that the ‘functions’ of fast and slow dentate gyrus’ gamma oscillations are spatial and object learning, respectively. Rather, the conclusion would be that fast and slow gamma oscillations report the functional interactions between the dentate gyrus and upstream (medial and lateral) entorhinal cortices, and that such coordination is necessary for those behaviors in which these neural pathways are implicated (e.g., spatial and object learning). This way, spatio-temporally localized gamma bursts can be conceived as the elementary units reporting ensemble dynamics and interactions in these circuits, in an analogous manner to action potentials mediating communication among individual neurons. In this case, the perturbation of the endogenous rhythm generation in the particular gamma oscillators provided the means to study the function of a specific circuit, and to shed light into network processing of different information streams. Despite their multiple uses and advantages, optogenetic interventions also have important limitations for the study of oscillations. Due to the interconnected nature of neural circuits, perturbing one of its elements (e.g., a defined cell type) is likely to induce additional physiological and behavioural effects that complicate the interpretation. Furthermore, using optogenetic stimulation to induce oscillations may result in stronger synchrony over a larger volume of tissue that what happen during endogenous oscillations.

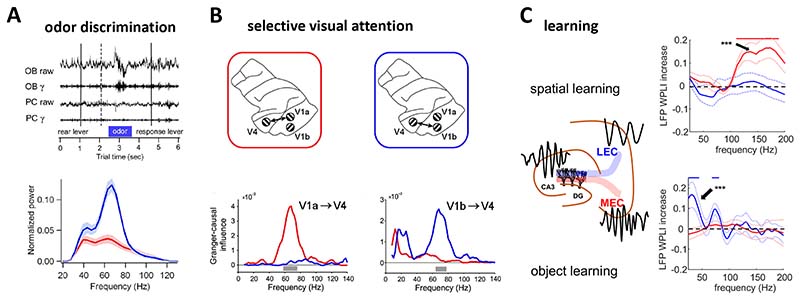
Figure 4. Behavioural modulation of gamma synchrony.

A) Fine odour discrimination is associated with stronger gamma oscillations in the rat olfactory bulb (top: wide-band and gamma filtered LFP traces from rat olfactory bulb and its main target region, the piriform cortex, around the time of odour presentation) compared to coarse odour discrimination (bottom blue and red curves are average power spectra for olfactory bulb responses during fine and coarse odour discrimination respectively; ¹⁶⁶. B) Monkey higher-order visual cortex (V4) displays synchronized gamma oscillations with primary visual cortex (V1) neural population representing behaviourally relevant visual stimulus, but not those linked to irrelevant stimulus ¹⁰⁷. The plots on the bottom indicates directional influence of different areas within V1 on V4 gamma oscillations (as supported by Granger causality) depending on which of two simultaneously presented grating stimuli the monkey was attending to. C) Synchronized fast gamma oscillations appear in the rat dentate gyrus and medial entorhinal cortex during spatial learning (top). However, during object learning, coherent gamma oscillations of slower frequency appear between the dentate gyrus and lateral entorhinal cortex (bottom) ⁹³. Plots on the right show the increase in LFP-LFP gamma synchrony between rat entorhinal cortical areas and the hippocampal dentate gyrus during different learning tasks as compared to baseline conditions.

Ascribing a specific behavioral or cognitive function to ‘gamma oscillations’ remains complicated. The specific role of a particular oscillation is not invariant to its neural substrate but rather depends on the function of the circuit that generates it. Yet, since gamma oscillations emerge from determined neural circuits, the instantaneous amplitude of such rhythms can be used as proxies for the strength of interactions in those networks. This is particularly convenient for studying the function of a brain pathway or area in behaving animals. As a notable example, the two main excitatory inputs to hippocampal CA1 are associated with different gamma oscillations: CA3 input to proximal apical dendrites of CA1 pyramidal cells typically relates to slow gamma, whereas entorhinal layer 3 input to distal apical dendrites is associated with mid gamma (Figure 2). Consistent with this, optogenetic silencing of the CA3→CA1 pathway during learning reduces the power of CA1 slow – but not mid – gamma ^91,92 (but see also ¹⁵⁹). During REM sleep, hippocampal network dynamics also display prominent theta and nested gamma oscillations. During this state, the strength of entorhinal gamma frequency input to CA1 is enhanced and the firing of some CA1 pyramidal cells shifts to the opposite theta phase compared to the awake state, consistent with the phase of entorhinal layer 3 inputs ^82,160,161. The theta rhythm, both during locomotion and REM sleep, strongly modulates hippocampal gamma oscillations (Box3). The contamination by theta harmonics has led some authors to debate the existence of slow gamma ¹⁶². Yet, a large body of converging evidence supports the existence of distinct slow gamma oscillations localized to CA1 stratum radiatum. Most notably, the same gamma patterns are observed during non-theta states, such as slow wave sleep ⁵⁸ or anaesthesia ²⁹ (Figure 2). Furthermore, the frequency range of the “slow” CA3 gamma frequency input can extend up to 80 Hz as evidenced by CA3 unit to CA1 LFP coherence ²² (Figure 3A; and Box 3). Memory demands and environment novelty also influence the strength of these two (slow and mid) gammas frequency inputs and the coordination of CA1 with upstream CA3 or entorhinal ensembles. During spatial memory retrieval, both CA1 slow gamma power and CA3-CA1 slow gamma coherence increase, suggesting a role of the CA3→CA1 pathway in mediating the recall of previously formed memories ^{22,24,59,82,92}. On the other hand, the power of entorhinal mid-gamma frequency input has been shown to be enhanced during first-time exposure to (novel) information ^24,73,82,163. Despite this distinct modulation by behavioral task demands, concluding that the function of slow gamma is to solely mediate recall and mid-gamma encoding remains complicated. The dynamic interplay between both gamma frequency inputs determines the precise timing of action potential discharge of CA1 pyramidal cells ^24,164. The phase of firing of CA1 cells within the theta cycle thus varies as a function of the relative strength of CA3 and entorhinal inputs (and associated interneuron activation), contributing to the gradual shift of theta phase preference of CA1 spikes within their place fields (‘phase precession’) ^82,88,165. Theta phase of CA1 firing can influence which downstream targets read out hippocampal inputs, providing a potential mechanism for routing information to different circuits.

A promising approach for the interrogation of circuit functions and oscillations is to perform selective manipulations timed by the ongoing neural activity in a ‘closed-loop’ manner. This approach has been successfully applied to the study of sharp-wave ripples. Closed-loop disruption or stimulation of hippocampal ripples respectively impaired or improved spatial memory performance ^150,167,168 and the consolidation of newly-formed hippocampal cell assemblies ¹⁶⁹, supporting their long-time hypothesized roles. This approach has not yet been widely applied to gamma oscillations. Kanta et al. performed closed-loop optogenetic stimulation in the mouse basolateral amygdala (BLA) by detecting gamma bursts ¹⁷⁰, reporting opposite effects on memory performance depending on gamma phase when stimulation was delivered. Although the cellular mechanisms of BLA gamma remain elusive, this illustrates the importance of timing external manipulations to features of ongoing neural dynamics. The observation of interregional gamma phase entrainment of neuronal spiking has led to the proposal that gamma coherence mediates selective communication between brain areas ¹²⁴. The ‘communication through coherence’ hypothesis poses that those inputs arriving at particular phases are preferentially integrated by target neurons, functionally coupling upstream and downstream regions. Numerous correlational studies have provided support for the relation between interregional gamma synchrony and neuronal communication ^{3,12,14,90,93,107,131,171–173}. A recent study tested this idea by optogenetically perturbing interhemispheric prefrontal cortex gamma synchrony ¹⁷⁴. Disrupting the phase synchronization of parvalbumin interneurons across hemispheres impaired rule learning in mice, but not if stimulation was delivered at the opposite gamma phase. However, interregional gamma interactions can be more complex, and usually the observation of coherent LFP oscillations or spike entrainment across areas without accessing the underlying cellular mechanisms is not enough to make functional inferences. Gamma coherence across regions can reflect feedforward inhibition or presence of synaptic connectivity rather than synchronization of principal cells ^64,83. Gamma frequency inputs to the distal dendrites of pyramidal cells undergo low-pass frequency filtering in their propagation to the soma due to the properties of the cell membrane, thus reducing the efficacy of those inputs to rhythmically entrain somatic action potentials ^22,175. On the other hand, gamma resonant properties of the target network can transform a tonic input into an output gamma rhythmic pattern of spiking ^106,109,176. The relevance of frequency-specific gamma resonance has been further illustrated by experiments in which constant optogenetic stimulation of neocortical pyramidal cells induced gamma oscillations and unit firing entrainment ^109,177. Thus, to understand the role of gamma synchrony it is necessary to determine its cellular mechanisms in both upstream and downstream regions. Recording, and selectively manipulating, input spiking patterns, dendritic integration, as reflected by gamma oscillations, and output spiking, will enable the understanding of input-output transformation in neural circuits (Figure 5).

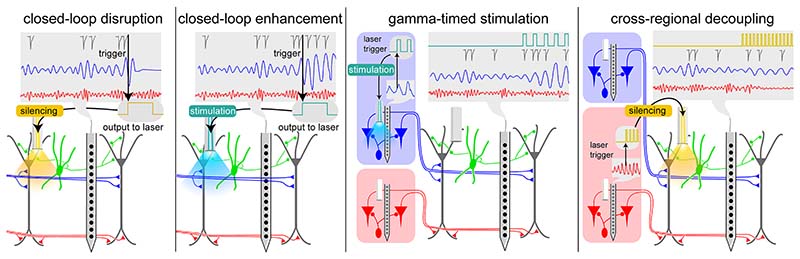
Figure 5. Proposed experimental manipulations to study gamma oscillations.

High-density recordings in upstream and downstream areas allow recording input patterns (upstream spike trains), input integration (postsynaptic potentials in target neurons) and firing output of target neurons. Such recordings combined with closed-loop optogenetic manipulations allow for the dissection of input-output signal transformation in neural circuits. A gamma pattern (blue trace) generated by a specific synaptic pathway can be optogenetically disrupted (A) or enhanced (B) to probe the function of that pathway. To test the role of the precise timing of spikes for inter-areal communication, optogenetic stimulation of target neurons (gray) can be timed by the phase of gamma oscillations in a projecting area (blue) to increase their synchrony (C). In a similar manner, two connected neuronal populations that normally display gamma coherence can be decoupled by transient inhibition timed by the phase of ongoing gamma oscillations (D). Neurons, oscillations, and spikes are color-coded according to the circuit generating them. Silicon probes and optic fibers are depicted in each region. Blue and yellow trapezoids indicate optogenetic activation and silencing respectively. Vertical black arrows indicate event detection.

Conclusions and future perspectives

We have discussed in this Perspective that gamma oscillations represent units of operating neural circuits. Yet, a given gamma oscillation does not per se implement any specific function (e.g., attention or memory recall), but rather reports the underlying computations and communication channels for information processing. A first step towards reaching a comprehensive mechanistic understanding of gamma patterns is the identification of their diversity in the brain regions of interest, in terms of both biological implementation and activity dynamics. In line with this, we propose a shift from a definition of gamma oscillations based on their peak frequency to one based on their neuronal substrates, pathways and mechanistic underpinnings. We believe that this approach will contribute to move the field forward in a similar manner as recent progress in classifying and identifying neuronal cell types. Considering all the factors and challenges that influence the study of gamma frequency patterns, from the gamma-band dynamics generated in a circuit to the (local or remote) gamma LFP readout signals, we would like to conclude by highlighting four considerations for future studies (Figure 5). First, gamma patterns when recorded far from the source that generates them, can be influenced by the effects of volume conduction and contamination by non-local sources of activity. Multichannel cross-laminar recordings provide the principled means of anatomical localization and source separation that are essential for identification of oscillatory patterns generated by distinct circuit generators. Second, to relate gamma patterns to circuit operations, it is helpful to also record the action potentials discharged by neurons in both upstream and downstream regions along the pathway of interest, and to examine the temporal relationships between these spikes and gamma oscillations. Third, the occurrence, frequency and magnitude of gamma oscillations are modulated by brain and behaviour states, but these changes are typically not restricted to specific generators (and different oscillatory circuits are often densely interconnected). Thus, studying a gamma pattern of interest across a variety of states and behaviours and in relation to other rhythmic patterns in the same circuits may provide important insight. Fourth, leveraging from recent and future advances in cell-type-selective and neural-input-defined tools with real-time signal processing for closed-loop manipulations could provide much needed increased spatial and temporal resolution to investigate specific gamma oscillations. Over and above such challenges, the study of well-defined gamma patterns will offer an invaluable window to study circuit-level mechanisms of information processing during behaviour.

Materials Availability

This Perspective did not generate new materials, data or codes.