Abstract
Advances in functional magnetic resonance spectroscopy (fMRS) have enabled the quantification of activity-dependent changes in neurotransmitter concentrations in vivo. However, the physiological basis of the large changes in GABA and glutamate observed by fMRS (>10%) over short time scales of less than a minute remain unclear as such changes cannot be accounted for by known synthesis or degradation metabolic pathways. Instead, it has been hypothesized that fMRS detects shifts in neurotransmitter concentrations as they cycle from presynaptic vesicles, where they are largely invisible, to extracellular and cytosolic pools, where they are detectable. The present paper uses a computational modelling approach to demonstrate the viability of this hypothesis. A new mean-field model of the neural mechanisms generating the fMRS signal in a cortical voxel is derived. The proposed macroscopic mean-field model is based on a microscopic description of the neurotransmitter dynamics at the level of the synapse. Specifically, GABA and glutamate are assumed to cycle between three metabolic pools: packaged in the vesicles; active in the synaptic cleft; and undergoing recycling and repackaging in the astrocytic or neuronal cytosol. Computational simulations from the model are used to generate predicted changes in GABA and glutamate concentrations in response to different types of stimuli including pain, vision, and electric current stimulation. The predicted changes in the extracellular and cytosolic pools corresponded to those reported in empirical fMRS data. Furthermore, the model predicts a selective control mechanism of the GABA/glutamate relationship, whereby inhibitory stimulation reduces both neurotransmitters, whereas excitatory stimulation increases glutamate and decreases GABA. The proposed model bridges between neural dynamics and fMRS and provides a mechanistic account for the activity-dependent changes in the glutamate and GABA fMRS signals. Lastly, these results indicate that echo-time may be an important timing parameter that can be leveraged to maximise fMRS experimental outcomes.
Keywords: Magnetic resonance spectroscopy, FMRS, Glutamate, GABA, Mathematical modelling, Mean field model
1. Introduction
Understanding how neurochemistry affects human physiology in health and disease is of central importance to clinical and neuroscientific fields. However, the need for non-invasive methods to quantify neuro-transmitter activity in humans makes this question inherently challenging. Magnetic resonance spectroscopy (MRS) allows quantification of brain metabolites non-invasively, providing a method to directly measure the concentrations of the brain’s major neurotransmitters (NT), glutamate (Glu), and γ - aminobutyric acid (GABA) in vivo (Rae, 2014). However, it is not clear how to interpret the resulting signals in terms of the underlying cellular mechanisms. Here, we use mean-field theory to provide a macroscopic level account of the basis of Glu and GABA functional MRS (fMRS) signal changes in response to stimulation. We then use the model to predict the precise metabolic pools that give rise to activity-dependent changes in the fMRS signal.
Traditionally, MRS has been used to provide a static snapshot of neurotransmitter levels in the brain, predominantly used to allow comparison between healthy and diseased states. However, there is increasing use of MRS to quantify time-resolved metabolic responses to stimuli on much shorter timescales of seconds to minutes, so-called functional MRS (see (Jelen et al., 2018; Mullins, 2018) for reviews). Following earlier work in the visual system, fMRS applications have now been expanded to a range of other paradigms including motor, cognitive, and pain stimuli (as reviewed by Jelen et al., 2018; Mullins, 2018). In many of these studies, the authors report changes in neurochemical concentration of 10–14% in response to short bouts of stimulation. In addition to studies focussed on healthy volunteers, the utility of fMRS techniques in clinical populations is also increasingly being explored. For example, a recent fMRS study in the anterior cingulate cortex showed that the expected increase in Glu in response to a Stroop task was significantly reduced in people with schizophrenia and major depressive disorder (Taylor et al., 2015). Given that this region has been substantially implicated in schizophrenia, with increased Glu and glutamine (Gln) levels observed commonly, fMRS is therefore able to significantly aid our understanding of the pathophysiological processes of these complex diseases (Bustillo et al., 2010; Théberge et al., 2002). Therefore, understanding the physiological basis for differences in the neurochemical response between healthy and diseased states is crucial to optimize clinical treatments.
MRS uses technology similar to magnetic resonance imaging (MRI), but the MRS signal is directly proportional to the concentration of metabolites within the specified region of interest (voxel). Nonetheless, the physiological basis of activity-dependent changes in the fMRS neurotransmitter signal remains unclear (Jelen et al., 2018; Mullins, 2018). Focusing on Glu initially, the most widely-accepted explanation is that an increased MRS-Glu signal reflects increased metabolic turnover (for example, via the anaplerotic pathway) (Rothman et al., 2003). However, it remains controversial as to whether these processes are able to account for the large changes observed in the MRS signal (>5%) over short time scales of seconds to minutes (Jelen et al., 2018; Mullins, 2018). For example, (Jelen et al., 2018) argue that changes in Glu of 6% or more in a minute cannot be explained by synthesis/degradation, since calculations based on the cerebral metabolic rate of glucose utilisation 0.26 mM min−1 (Hyder et al., 2016) could not produce the same magnitude of change in such a short time (even under the unrealistic assumption that all glucose is metabolized to glutamate). For reference, we note that if functional changes in Glu represent newly synthesized glutamate, which removes carbon from the cycle, it must be replaced by anaplerosis. Using known rates of glutamate synthesis from (Shen et al., 1999), an acquisition duration of 5 mins would yield synthesis of Glu via the anaplerotic pathway to account for an increase of 0.2 mM. These relate to an increase of 2% assuming an average concentration of 10 mM in the human brain, less if degradation was also taken into account.
A major source of neuronal Glu is via flux through the Glu-Gln cycle, which has been shown in animals to exhibit rate increases in response to neural stimulation and thus can reasonably be expected to do the same in humans (Sibson et al., 1998). Upon exocytosis into the cleft, Glu is quickly taken up by nearby astrocytes and converted to Gln (a non-neuroactive species), Gln is then returned to the neuron where it is converted back to Glu and packaged into vesicles (Mangia et al., 2012). Supported by observations of varying Glu-MRS visibility in different compartments (Kauppinen et al., 1994; Kauppinen and Williams, 1991; Pirttilä et al., 1993) and on the echo-time dependence of fMRS signal changes, Jelen et al. proposed that fMRS detects compartmental shifts (in Glu) due to neural activation, as it moves from pre-synaptic vesicles to more visible synaptic, extracellular and astrocytic pools (Jelen et al., 2018). Glu will naturally cycle through these compartments as it passes through the stages of release, reuptake and vesicular repackaging in response to neural firing. It has been estimated that up to 30% of Glu is invisible to MRS at any one time (Kauppinen et al., 1994; Kauppinen and Williams, 1991; Pirttilä et al., 1993) due to it being tightly bound to macromolecular structures in the vesicles, including monotopic, polytopic, and associated membrane proteins (Südhof, 1999), causing faster T2 relaxation (Kauppinen et al., 1994; Kauppinen and Williams, 1991). In the case of the inhibitory transmitter GABA, the process is less complex in that released GABA is returned to the presynaptic cell largely via reuptake mechanisms where it is repackaged into vesicles (Olsen and DeLorey, 1999). Vesicle refilling has been shown to occur in an activity-dependent manner (Li et al., 2020). Importantly, maximal rates of release and refilling are not equivalent; for example in a hippocampal slice experiment, it was estimated that quanta are released from occupied sites at a rate of 0.72 s−1, whereas the rate of refilling an empty site occurs at the rate 0.11s−1. Therefore, it could be that neural activation drives a shift of Glu (or GABA) between states that are more or less visible to MRS via the recycling processes described above and that this shift between states contributes to the change in fMRS signal at short time scales. Here, we develop a neural mass model with compartmental NT dynamics to investigate how changes in neural activity might affect the fMRS signal under the hypothesis that vesicular NT contributes minimally to the MRS signal at standard echo times used empirically. Specifically, we wish to test how much of the fMRS signal change can be explained by shifting of NT between compartments over short timescales of less than 1 min. We interrogate the model with a range of stimulation types intended to mimic visual, pain, and transcranial direct current stimulation (tDCS) and test the model predictions against empirical data found in the literature. The model allows us to link cellular level mechanisms of neural activity and NT dynamics with their systems-level observations via the MRS signal.
To achieve this, we develop a model of interacting populations of excitatory (E) and inhibitory (I) neurons intended to represent a generic cortical MRS voxel. We start with a microscopic-level model of neural activity based on the well-established Hodgkin-Huxley formalism (Hodgkin and Huxley, 1952). We explicitly incorporate a multi-compartment description of the movement of neurotransmitters between pools based on work by Tsodysks and Markram (Tsodyks and Markram, 1997). This multi-compartment model of NT dynamics assumes a fixed absolute quantity of NT that cycles between three pools: effective, inactive or readily releasable in an activity-dependent manner. We interpret these pools to correspond to, respectively, NT found instantaneously in the cleft upon cell activation or in the extracellular space (ECS); NT undergoing recycling or other biological processes (cytosolic compartment); and NT packaged in vesicles ready for release. Essentially, the model accounts for the simplified dynamics of the release-reuptake-repackaging cycles described above. We obtain a macroscopic systems-level approximation of the neurotransmitter activity by deriving the mean-field reduction of the system dynamics under the Laplace approximation (Marreiros et al., 2008, 2009). This allows us to formulate a description of the average response of a population of neurons to stimulation and the associated population-level changes in NT concentrations where the population density assumes a Gaussian form. We do not account for absolute (total) changes in NT concentration due to metabolic flux over the short timescales under investigation here as it is our aim to understand how much of the change in MRS signal could theoretically be accounted for by considering only the movement of NT between compartments of differing MR-visibility.
We simulated three types of stimuli to apply to the model: acute pain, visual, and current stimulation to emulate the most common fMRS studies. We used the model output to make predictions about how the cells microscopic activity translates to changes in the fMRS measurement under the assumption that the vesicular pool of NT exhibits very short T2 relaxation and therefore contributes minimally to the overall signal at standard echo times found in the literature. Finally, we compare our findings to empirical data. In doing so, we provide a mechanistic account for the change in observed NTs concentrations during cognitive fMRS studies.
2. Theory
We model a cortical region as a local network composed of two densely interconnected populations of spiking excitatory and inhibitory neurons. The neurons are coupled through excitatory α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) and inhibitory (GABA) synapses. Glu acts on postsynaptic AMPA receptors to excite the cell and depolarise it, whereas GABA acts on GABA receptors to hyperpolarise and inhibit the cell. A key component of the spiking model is that we account for the dynamics of both GABA and Glu during synaptic transmission. This allows us to study how the dynamics of the NT themselves vary in response to stimulation and predict how the functional MRS signal in turn would be affected.
Our aim is to relate the NT activity in the model to MRS-derived measurements of GABA and Glu, which are acquired over large voxels in the brain containing billions of neurons. Using a network model comprised of individual cells, this would entail simulating considerable numbers of coupled nonlinear differential equations. Rather, we derive a mean-field reduction of the spiking network model. This reduction describes the evolution of the ensemble of neurons representing a local population, in terms of the dynamics of the average states of the ensemble. We follow Marreiros et al. to approximate the average ensemble behaviour under the Laplace approximation (Marreiros et al., 2008, 2009), see Appendix for derivation.
2.1. Microscopic model dynamics
2.1.1. Extended Hodgkin-Huxley model
We begin by defining the equations governing the behaviour of the individual neurons that comprise the network. Experimentally, it has been found that neocortical pyramidal cells exhibit dense reciprocal connectivity within a local region as well as strong connections with pyramidal cells in different regions via AMPA and N-methyl-D-aspartate (NMDA) receptor-mediated transmission (Czeiger and White, 1993; Elhanany and White, 1990; Johnson and Burkhalter, 1996; Mountcastle 1997; Somogyi et al., 1998; Szentágothai, 1983). Inhibitory cells receive excitatory input from pyramidal cells mainly via AMPA receptor-mediated transmission (Bartos et al., 2007). Similarly, GABAergic synapses have been found to mediate inhibitory connections on to pyramidal cells and inhibitory basket cells (Freund and Katona, 2007 ; Molaee-Ardekani et al., 2010). Therefore, we base the model structure on these principles and define 2 populations of cells; an excitatory population and an inhibitory population coupled via AMPA, and GABA-mediated connections. We note that the inclusion of NMDA receptors did not substantially alter the model behaviour and therefore were omitted. The E-population has NE neurons, and the I-population has NI neurons.
A single neuron is modelled using an extended form of the classical Hodgkin-Huxley (HH) neuronal model (Hodgkin and Huxley, 1952). This model was chosen so as to be able to tune the excitatory and inhibitory neurons with data acquired directly from the biology (using (Pospischil et al., 2008)) in order to test the effect of stimulation on the biologically realistic networks. The HH model is a conductance model that describes the evolution of the membrane potential of a neuron as being the sum of currents which pass through the cell membrane. The standard HH model accounts for leak, sodium and potassium currents, and we have extended the model to include AMPA and GABA-receptor-mediated currents in addition to this. The standard equations describing the evolution of the membrane potential for a single HH neuron j are given by (adapted from (Pospischil et al., 2008), see also (Destexhe, 1997 ; Kobayashi and Kitano, 2016)), where is the time derivative of x at time t :
| (1) |
where
| (2) |
| (3) |
| (4) |
In Eqs. (1) to (4), where α ∈ {E, I} denotes the membrane potential of an excitatory or inhibitory cell j respectively. Where α does not appear as a superscript for a variable, this implies that the parameter is the same regardless of the cell type. All parameter values are listed in Table 1. Changes in the membrane potential are driven by incoming signals from connected excitatory and inhibitory neurons k in the form of GABA and Glu concentrations in the cleft, as well as external current-based inputs. C is the specific capacitance of the membrane; Iext,j is the external input current; Iint,j encompasses the voltage-dependent leak, sodium and potassium currents, respectively, which are responsible for the action potential generation; gL, , are the mean leak, sodium and potassium conductances; , VNa, VK are the associated reversal potentials. The voltage-mediated gating variables m, n, and h represent the fraction of open channels of each current type and are represented by standard exponential functions detailed in the Appendix. In order for the model to generate activity we added an extra input term to the excitatory population only for all simulations as without this input the model does not generate spontaneous activity, similar to (Kobayashi and Kitano, 2016; Pospischil et al., 2008). The synaptic input currents are given by the AMPA (IA), and GABAA (IG) receptor mediated synaptic input currents which will have either an excitatory or inhibitory effect on the cell. Following (Zou and Destexhe, 2007), we consider GABAA receptors only as the majority of inhibitory postsynaptic potentials are mediated by GABAA receptors (Destexhe, 1997). They are highly sensitive to GABA and can be fully saturated by GABA released from a single vesicle; whereas GABAB require stronger stimuli to respond (Destexhe, 1997 et al., 1994; Thompson, 1994). The respective mean synaptic conductances are gA, and gG; with , representing the AMPA and GABA receptor reversal potentials. The binary connectivity matrices γE and γI represent maps of excitatory or inhibitory connections between neurons, so is the (j, k) element of the matrix which is equal to 1 if neuron j is connected to k, and 0 otherwise. ωEα, ωIα are the dimensionless parameters that represent the synaptic weights between the cell types, as in (Deco et al., 2014). and are the synaptic gating variables for each connected synapse k and depend on the population type (excitatory and inhibitory, respectively).
Table 1. Parameter values used in the simulations unless stated otherwise in the text. T2 values for ’visible’ compartments are standard values measured at 3 T. The parameters B and Vmax are normalised values.
| Parameter | Definition | Values | Reference |
|---|---|---|---|
| C | membrane capacitance | 0.01 F/m2 | (Pospischil et al., 2008) |
| gL | leak membrane conductance | 3 S/m2 | (Pospischil et al., 2008) |
| potassium membrane conductance | 0.006 S/cm2, 0.002 S/cm2 | (Pospischil et al., 2008) | |
| sodium channel conductance | 0.056 S/cm2, 0.01 S/cm2 | (Pospischil et al., 2008) | |
| adjust spike threshold | −58 mV, −68 mV | (Pospischil et al., 2008) | |
| leak reversal potential | −70 mV, −56 mV | (Pospischil et al., 2008) | |
| VNa, Vk | Na/K reversal potential | 50 mV, −90 mV | (Pospischil et al., 2008) |
| gA, gG | quantal conductance | 25 nS, 10 nS | (Destexhe, 1997; Zou and Destexhe, 2007) |
| aA, cA | rate constants AMPA receptors | 1.1 s−1 M−1, 180 s−1 | (Destexhe and Pare, 1999; Destexhe, 1997; Zou and Destexhe, 2007) |
| aG, CG | rate constants GABA receptors | 5 ms−1 M−1, 166 s−1 | (Destexhe and Pare, 1999; Destexhe, 1997; Zou and Destexhe, 2007) |
| reversal potentials | 0 mV, −80 mV | (Destexhe and Paré, 1999; Destexhe, 1997) | |
| ωEE, ωEI, ωIE | coupling strengths | 2 | - |
| ωII | coupling strengths | 0 | - |
| U | fraction of NT released | 0.01 | (Tsodyks et al., 1998) |
| B | normalised value for concentration conversion | 10 mM | - |
| N 0 | lower bound preventing further vesicle packaging | 0.7 | est from (Kauppinen et al., 1994; Kauppinen and Williams, 1991; Pirttilä et al., 1993) |
| τx | rate constant | 3 ms | (Tsodyks and Markram, 1997; Tsodyks et al., 1998) |
| τr | rate constant | 1800 ms | (see Results) |
| Vmax, Vtr, σV | max firing rate, firing threshold | 1, 2 mV, 5 mV | (Destexhe et al., 1994) |
| T2 (Glu, visible), T2 (Glu, invisible) | T2 constant | 181 ms, 5 ms | (Ganji et al., 2012), estimate |
| T2 (GABA, visible), T2 (GABA, invisible) | T2 constant | 88 ms, 5 ms | (Edden et al., 2011), estimate |
| TE (Glu), TE (GABA) | echo time | 30 ms, 68 ms | typical values used empirically |
| excitatory input current | 5.3 mA | - |
The synaptic gating variables p for AMPA and GABA mediated channels are given by the following kinetic differential equation (Destexhe, 1997):
| (5) |
Where β ∈ {A, G} denotes the type of synaptic receptor (AMPA or GABA), represents the concentration of active NT acting instantaneously on receptor type β in the synaptic cleft of an afferent connection from a neuron k of population α where α ∈ {E, I} and relates to Glu or GABA respectively. Finally, aβ and cβ are rate constants specified in Table 1.
In standard conductance-based models, the synaptic currents are a function of the firing of presynaptic neurons, which are in turn functions of the membrane potentials. Closing this loop allows for the membrane potential to be determined self-consistently. However, this type of modelling sidesteps the explicit modelling of neurotransmitter dynamics. In our case, for the membrane potential to be computed self-consistently, the dynamics of the neurotransmitters need to be expressed as a function of the pre-synaptic firing. In the next section, we describe the equations governing neurotransmitter cycling activity.
2.1.2. Neurotransmitter cycling
Upon activation, excitatory neurons release Glu into the postsynaptic cleft which rapidly binds to postsynaptic receptor sites and then is very quickly taken up by surrounding astrocytes. Within astrocytes Glu is amidated to Gln by glutamine synthetase and released into the extra-cellular space. Gln, a non-neuroactive species, is then taken up by the presynaptic neuron where it is converted back into Glu via phosphate-activated glutaminase (PAG) and repackaged into vesicles. In addition to this, cytosolic Glu concentrations are also synthesised by the anaplerotic pathway via the tricarboxylic acid cycle (TCA) cycle.
In the case of inhibitory cells, released GABA is primarily taken up at the presynaptic terminal ready to be repackaged into vesicles. Synaptic GABA is also taken up into astrocytes where it is metabolised via the TCA cycle to succinate and then to Glu and finally Gln. In a similar way to the glutamatergic synapse, Gln is then released into the extracellular space and transported back to the presynaptic cell where it is converted back to Glu via PAG and finally to GABA via glutamic acid decarboxylase (GAD) after which it is packaged into vesicles ready for re-release. In addition to these two processes, cytosolic GABA is also synthesised by the anaplerotic pathway via TCA cycle as in the glutamatergic cell.
In this paper, we do not account for absolute changes in NT concentration due to metabolic flux in response to stimulation. Instead, we focus on movement of NT between cellular environments that are more or less visible to MRS to ascertain whether this shift in concentration is enough to explain the magnitude of change that we observe in the MRS signal over short timescales.
To account for the above mechanisms surrounding neurotransmitter recycling in the model, we make the following assumptions:
Neurotransmitter is released into the cleft in an activity-dependent manner and is rapidly removed so that it can no longer act on the postsynaptic cell.
Once removed from the cleft, neurotransmitter is assimilated into the cytosolic neurotransmitter concentration.
Cytosolic neurotransmitter is then repackaged into the vesicles; the temporal evolution of this process depends on both the level of cytosolic transmitter and neural activity (Li et al., 2020).
We note here that for Glu, the situation is more complex as it is recycled via astrocytic conversion to Gln. Accounting for this extra step is an area for further work but we note here that in many MRS studies the combined measure Glx (which includes the Glu and Gln peaks) is used to approximate the Glu concentration and in these cases the model predictions are particularly relevant. Additionally, we note that Glu is present in approximately 4 times the concentration of Gln in the brain (see Ramadan et al., 2013).
We employ the kinetic model of Tsodysks and Markram (Tsodyks and Markram, 1997) which characterises the transition of NT between the 3 states: R (the fraction of releasable transmitter in the bouton - the vesicular pool), X (the fraction of effective transmitter in the cleft) and N (the remaining proportion of ”inactive ” transmitter which for our purposes we assume to be cytosolic neurotransmitter awaiting repackaging into vesicles), see Fig. 1. For each spike, a proportion of NT is released from the vesicles into the cleft after which it is cleared, returned to the cytosol and repackaged into the vesicles. The equations describing the temporal evolution of NT in each compartment (for an excitatory cell the equations describe Glu cycling, and for inhibitory cells GABA cycling) for cell k are given by:
| (6) |
| (7) |
| (8) |
| (9) |
where
| (10) |
Fig. 1. Neurotransmitter cycling.
Schematic diagram of generalised NT cycling process as per the kinetic model of Tsodyks and Markram (Tsodyks and Markram, 1997). The presynaptic cell is shown in pink and the postsynaptic in blue. Steady state (top): the presynaptic cell fires an action potential releasing NT (GABA or Glu) into the cleft. NT is characterised as belonging to one of three states: NT in the vesicular pool (R), where the NT is packaged in the vesicles ready to be released into the cleft upon activation; NT in the extracellular space (X), where it has been released into the cleft and is acting at receptor sites on the postsynaptic cell; and NT in the cytosolic pool (N), is awaiting repackaging into the vesicles. Decreased firing (left): if the firing rate is reduced, the NT will start to accumulate in the vesicles due to the mismatch between the rate of exocytosis and the rate of repackaging into the vesicles. A shift of NT from the cytosol to the vesicles will result in a decreased MRS signal as we assume the vesicular compartment is largely invisible to MRS. Increased firing (right): if the firing rate increases, then NT from the vesicles will be used more quickly. Upon exocytosis it will transfer rapidly from the cleft to the cytosol and start to accumulate there. A shift of NT from the vesicles to the ECS and the cytosol will result in an increased MRS signal under the current hypothesis.
Where Eq. (8) is a conservation rule ensuring that the total amount of NT at any point in time is constant, and denotes the spike train of presynaptic neuron k firing action potentials at times q. With each presynaptic spike, a fraction U of the total available neuro-transmitter stored in the vesicles (R) is released into the cleft/ECS (X). NT is cleared from the cleft with time constant τx and is assimilated in the cytosol (N) via Eq. (8). The transmitter in the cytosol (N) undergoes recycling and repackaging into the vesicles at a rate τr. H in Eq. (10) is the Heaviside function and determines when the cytosolic compartment has reduced to 70% under which no further repackaging can occur. Eqs. (6) to (8) describe the proportion of the total NT in each of the pools which are multiplied by an absolute concentration, B, to convert the proportion of NT to a concentration in the cleft into a concentration in mM, denoted (Eq. (9)). Therefore, the concentration of neurotransmitter acting on the postsynaptic cell j (via Eq. (5)) from presynaptic cell k is given by . As before, α ∈ {E, I} determines whether NT is Glu or GABA. We adapt the model by including a lower bound N0 set to 70% (Eq. (6)) which defines a lower bound to the fraction of cytosolic NT below which no further vesicular packaging occurs (and can practically be thought of as ensuring that no more than 30% of the total NT is packaged in the vesicles, based on (Kauppinen et al., 1994; Kauppinen and Williams, 1991; Pirttilä et al., 1993).
As there is a considerable mismatch between the rate of exocytosis and the rate of recycling into the vesicles ready for release, a natural consequence of these equations is that during increased stimulation there is a shift of transmitters from a relatively MR-invisible compartment (vesicles) to a detectable compartment in the cytosol of astrocytes and neurons resulting in an increased MRS signal for that metabolite (see Fig. 1). The opposite effect occurs when firing is reduced.
2.2. Macroscopic model dynamics
2.2.1. Mean-Field model
A typical MRS signal is acquired from a large voxel of brain tissue (in the region of cm 3) making it a macroscopic measure of activity. The goal of this paper is to describe the evolution of NT dynamics in terms of what is measured using MRS and therefore the model must also account for activity at this spatial scale. So far, the model equations account for the activity of a neuron. To model the behaviour of a network of billions of connected neurons using these equations would be computationally prohibitive. Rather, we derive a mean-field reduction of these large-scale neuronal network under the Laplace approximation following (Marreiros et al., 2008, 2009), please see Appendix for details. This method allows us to look at the average activity over a large population of cells rather than modelling each cell individually and is a method borrowed from statistical physics commonly used to simplify neural network computation meaning that we can make meaningful comparisons between the model output and the MRS signal obtained from a neural network contained within typical voxel.
The Laplace approximation allows us to summarise the density dynamics of an ensemble of neurons using the method of moments (Rodriguez and Tuckwell, 1996, 1998) where the population density assumes a fixed Gaussian form. The mean-field model (MFM) expresses the time evolution of the mean activity of each population of neurons (excitatory and inhibitory) within the local spiking network described previously by averaging over the activity of all cells within each population. This is achieved by expressing the state variables by their mean values and replacing the sum over spikes found in (Eqs. (6) to (7)) with an averaged value (firing rate) calculated using a sigmoidal input-output function (Abbott and Chance, 1995). The key point to note is that under the mean field assumption, the states of all neurons in a population are affected by the averaged state of all neurons in a connected population. It is not possible for a single neuron in a population to directly affect another individual neuron in the same or another population. In the MFM, we consider only the first statistical moment of the distribution, the mean, while discounting higher order moments thus equating the system to a neural mass model (Marreiros et al., 2009). The model architecture, intended to account for a generic cortical voxel, comprises an excitatory and an inhibitory population of cells, these are both self- and inter-connected, see Fig. 2. Both populations are capable of receiving excitatory (AMPA receptor-mediated) and inhibitory (GABA receptor-mediated) inputs.
Fig. 2. Schematic of the mean-field model.
The MFM is intended to approximately represent a generic cortical MRS voxel. It consists of an excitatory (E) and inhibitory (I) population representing the averaged activity of billions of cells. These are both self and inter-connected via the weights ωEE, ωII, ωEI, ωIE. All connection strengths are fixed. Inhibitory connections are mediated via GABA receptors and excitatory connections via AMPA receptors.
Under the mean-field assumption and Laplace approximation, the equations have a similar structure and parameter interpretation as in the single-neuron model, but with state variables replaced with their population averages and the input train of spikes replaced by a sigmoidal activation function. The equations of motion for the means of the state variables for each population α ∈ {E, I} are given below where μx defines the mean-field quantity for variable x:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Variables x are as defined previously with μx representing their mean-field quantity with α ∈ {E, I} and β ∈ {A, G} where E and I refer to the excitatory and inhibitory populations and A and G to AMPA and GABA receptor types. For example, defines the mean membrane potential for population α at time t. Iint refers to the voltage-mediated currents, Iext, I0 determine the external input currents, and IA, IG refer to the AMPA and GABA-receptor mediated currents. C is the mean membrane capacitance, the mean conductances gL, , gA, gG and reversal potentials for the leak, Na, K, AMPA and GABA currents are as previously defined. Likewise, define the mean synaptic gating variables for each conductances (standard equations representing the initial three are detailed in the Appendix). define the mean proportion of NT in each of the compartments X, R, N for each population. NT is cleared from the cleft with time constant τx, and undergoes repackaging into the vesicles at a rate τr. Here the weights ωE/I denote the coupling strength between the populations. The values for ω and I0 were chosen to obtain spontaneous activity for each population, as in (Deco et al., 2014).
S is a sigmoidal function which transforms the mean membrane potential of all cells within a population to an averaged firing rate. Essentially, it represents the cumulative distribution of the membrane’s depolarisation (or its deviation from resting levels) under Gaussian assumptions with mean and variance σV. Vmax relates to the maximal firing rate of the presynaptic cells which is normalised to 1 as in (Wilson and Cowan, 1972, 1973), for example, and can be thought of as converting the mean membrane potential to a fractional (percentage) firing rate. Vtr is a voltage threshold that defines the point at which the function is half-activated, while σV determines the steepness of the curve. We also note that in the present study, all connections are assumed to be instantaneous and therefore conduction delays between distant cortical areas are neglected. The full system of equations can be found in the Appendix and parameter values in Table 1.
3. Methods and materials
3.1. Input types
Understanding how stimulation interacts with ongoing brain dynamics is important to optimise therapeutic and rehabilitation strategies (Malerba et al., 2017). In order to generate model predictions for a range of experimental scenarios, we modelled three different stimulus input types. These were: tDCS, as it allows the inclusion of negative/inhibitory inputs; visual stimulation, as this is one of the most common stimulus types used in fMRS studies; and pain, as painful stimuli have been shown to elicit the largest changes in Glu and GABA in fMRS studies (Mullins, 2018). The major distinction between the input types is which cell population is targeted by the stimulation. Beyond that, we note that current stimulation is not thought to induce cell firing, so must be less than 5 mA as that is the minimum input required to cause excitatory cell firing in the model. Therefore, we consider sensory stimulation to occur for stimulus intensities greater than 5 mA in the current model.
3.1.1. Electrical stimulation (tDCS)
To model the effects of tDCS, we applied the stimulus to both the excitatory and inhibitory populations following (Molaee-Ardekani et al., 2021) who recently showed that extending a tDCS-style input to inhibitory interneurons as well as excitatory pyramidal cells allowed them to simulate evoked potentials that were much closer to physiological data. Here we used as in (Bonaiuto and Bestmann, 2015 ; Molaee-Ardekani et al., 2021). We note that the effects of electrical stimulation depend on a number of factors such as current field and cell orientation (Berzhanskaya et al., 2013 ; Rahman et al., 2015 ; Tranchina and Nicholson, 1986), and acknowledge that this is an area for future work.
3.1.2. Visual stimulation
To model vision, we applied the input only to the excitatory population, as in (Wilson, 2003), formally . We account for the temporal properties of visual stimuli and allow the stimulus to flicker at 2 Hz.
3.1.3. Pain
To model acute pain, we applied a depolarising stimulus equally to both the excitatory and inhibitory populations of the model following (Song et al., 2021), formally . We do not account for the temporal properties of the stimulus as these are beyond the scope of this paper.
3.2. Observation model
In this paper, we focus on 1H-MRS which is commonly used to analyse the chemical composition of tissue in vivo with the resulting signal reported as an average over the tissue volume and in time. The mean-field model presented here determines the distribution of NT in each of the 3 compartments at any point in time. The predicted MRS signal for each metabolite then is the time average (over the recording period) of the sum of the signal of the 3 compartments. The predicted signal at time t for compartment c ∈ {X, R, N} and each metabolite α ∈ {Glu, GABA} is calculated using the Bloch Equation (Bloch, 1946):
| (19) |
Where TR is the scan repetition time, T1 is the longitudinal relaxation rate, TE is the echo time, and is the compartment-specific transverse relaxation rate for each metabolite (see Table 1 for values reported at 3 Tesla). is the effective spin density for each compartment which is modelled as the corresponding compartmental fraction of the total spin density for the voxel , so that . can be thought of as the maximum signal strength for a given molecule at TE = 0 ms and infinite TR (An and Lin, 2001). Note that the factor (1 − e−TR/T1) in the above equation is constant across compartments and approximately equal to 1. This is because even though T1 is likely to be much shorter in the vesicular compartment, the almost complete signal loss due to the short T2 at TE > 35 ms renders any T1 correction negligible when we consider percentage differences from baseline.
Therefore, the total predicted MRS signal for each metabolite at time t, is given by:
| (20) |
This predicted time-resolved signal is then averaged over the recording period δt to produce the observed MRS signal for each metabolite , which gives the observation equation:
| (21) |
where 〈x〉δt denotes the time average of x over the time window, δt. For simulation purposes in the present paper we have assumed .
In practice, as the cytosolic pool is so much larger than the ECS pool, changes in the MRS signal are driven almost exclusively by changes in the former. As an illustration, if 70% of the NT is initially in the cytosol, then 99.9% of the signal contribution is from the cytosolic and ECS compartments calculated using TE = 30 ms and T2 = 5 ms for the vesicular compartment. If vesicular T2 = 10 ms, this reduces to 97.5%, and for vesicular T2 = 15 ms, to 93.6%, with cytosolic/ECS T2 values taken from the literature (see Table 1). Subsequent movement of a portion of the NT pool from vesicles to other compartments will increase the signal in direct proportion to the quantity of NT released.
3.3. Simulations
We aim to study the response of a single fMRS voxel to the different stimulation types described previously, and will therefore consider the response of a single two-population model represented in Fig. 2. The following simulations were performed in MATLAB (The Mathworks Inc., MATLAB ver. R2019b) on a Dell PC using Intel(R) Core(TM) i7-7700HQ CPU 2.80 GHz with 32 GB RAM. The model was solved numerically using the forward Euler integration method with a time step of 0.01 ms, similar to (Kobayashi and Kitano, 2016). As an illustration, each graph relating to a specific stimulus types in Fig. 7 took approximately 35 mins to run.
Fig. 7. Model predictions for pain, visual, and current stimulation.
We stimulate the model with the 3 input types: tDCS (left), Pain (middle), and Vision (right). Top panel: the percentage of total NT in the ’visible’ pool (ECS and cytosol). Lower panel: we calculate the predicted MRS signal (ST using the ’Observation Model’) as a weighted sum of NT from each compartment. ST is calculated using specific T2 values assigned to NT within each compartment with an assumed TE of 30 ms for Glu and 68 ms for GABA (see Table 1 for a list of all parameters). Results are expressed as a percentage difference from the baseline case, where . For sensory stimulation (pain and vision), we only consider input currents greater than 5 as that is the minimum input current required to elicit cell firing in this model.
3.3.1. Simulation 1 - Effect of firing rate and amplitude of firing on NT cycling dynamics
We varied the average firing rate (modelled as a series of Dirac functions) between 0 and 100 spikes s −1 and solved the differential equations governing NT cycling rates Eqs. (6) to (8) for 100 s. U was set to 0.7, as in (Tsodyks and Markram, 1997).
3.3.2. Simulation 2 - Effect of τr on vesicular refilling times
We set the average firing rate to 10 spikes s−1 and solved the differential equations governing NT cycling rates Eqs. (6) to (8)) for 100 s while varying τr between 1000 and 5000 ms to determine the time course for the vesicular pool to reach its maximum steady state value of 30% of the total cortical Glu concentration (starting from fully depleted vesicles).
3.3.3. Simulation 3 - Effect of current stimulation on NT dynamics
We allow the MFM to run for 30 s to reach a steady-state and then apply either a positive (excitatory) or negative (inhibitory) tDCS input current for the remaining duration of the simulation (see coloured bars) set at . Note that the data presented in Fig. 5 is for 10 s pre and post onset of stimulation. When presenting the temporal trace of the NT dynamics in Fig. 5, the activity is presented as an average over a sliding window of 1 s which is comparable to the time resolution of the MRS acquisitions (usually in the order of 1 to 5 seconds).
Fig. 5. Temporal dynamics of NT concentrations in response to polarity-specific current stimulation.
We assess the effect of applying an input current on the NT dynamics within each pool and describe the expected effect on the resulting MRS signal assuming that the vesicular compartment is MR-invisible. Left panels: the network is allowed to run for 30 seconds so as to reach steady-state and then the excitatory stimulus was applied for the remaining duration of the simulation (see coloured bars). In the case of the excitatory population (orange), we observe a shift of Glu from the vesicles to the cytosolic pool indicating an increased Glu MRS signal. In the case of the inhibitory population (blue), we observe the opposite effect in that GABA accumulates in the vesicles and is reduced in the cytosolic compartment. This would be reflected as a reduction in the GABA MRS signal in this condition. Note only 10 s of pre-stimulus activity is shown here. Right panels: an inhibitory current is applied in the same way , causing the percentage of Glu and GABA in the vesicular pools to increase with a corresponding decrease in the cytosolic pool. The effect of this would be a reduction in both the Glu and GABA MRS signals.
3.3.4. Simulation 4 - Effect of current stimulation on time-averaged NT dynamics
We applied a tDCS input current that was varied between -5 to +5 mA to the MFM. Initially, the model was allowed to run for 30 s to achieve a steady-state and then the input was applied for a further 30 s. In Fig. 6, the mean proportion of each of NT, GABA and Glu are presented for each of the pools, averaged over the duration of the simulation where the input current was applied.
Fig. 6. Effect of polarity-specific current stimulation on mean NT concentrations in each pool.
We evaluate the proportion of Glu (red) and GABA (blue) in each of the three pools in response to current stimulation averaged over the 30 s of the simulation for a range of positive and negative currents. We note that the x-axis refers to the excitatory input current . Inhibitory (negative) current reduces GABA and Glu in the cytosolic pool, and increases them in the vesicles. Excitatory (positive) current reduces GABA and increases Glu in cytosolic pools, and has the opposite effect in the vesicles. The direction and magnitude of the change in the cytosol coincide with the direction and magnitude of change of the empirically measured GABA and Glu-MRS: inhibitory current reduces both neurotransmitters, while excitatory current decreases GABA and increases Glu. We conclude that the observed MRS concentrations and changes reflect the dynamics of the neurotransmitters within the cytosol and ECS, while their passage through the vesicles remains invisible to MR. Concentrations in the ECS appear negligible due to their rapid clearance rate. Vertical dashed lines indicate the specific current values of Fig. 5 .
3.3.5. Simulation 5 - Model predictions for pain, visual, and current stimulation
We applied an input current (modelled as defined for each case in ’Input Types’) for varied between -5 to +5 mA (for the tDCS case, as before), and 0 to 10 mA (for vision and pain) to the MFM. In Fig. 7 initially, the model was allowed to run for 30 s to achieve a steady-state and then the input was applied for a further 30 s. The mean proportion of each NT, (GABA or Glu) within the ECS and cytosolic pools, averaged over the duration of the simulation where the input current was applied, are presented as a percentage of the total.
3.3.6. Simulation 6 - Calculation of change in MRS signal
We assigned different values for T2 relaxation constants for GABA and Glu based on whether the NT was found in the vesicles (invisible) or the ECS/cytosol (visible). For each of the input types described previously, we calculated a predicted MRS signal using the Observation model described previously (Eq. (21)). The total signal is calculated as a weighted sum of NT from each compartment with T2 values assumed as per Table 1, and using a typical echo time from empirical data. We plot this as a percentage difference from baseline (where ), see Fig. 7.
3.3.7. Simulation 7 - Effect of vesicular T2 and TE on model predictions
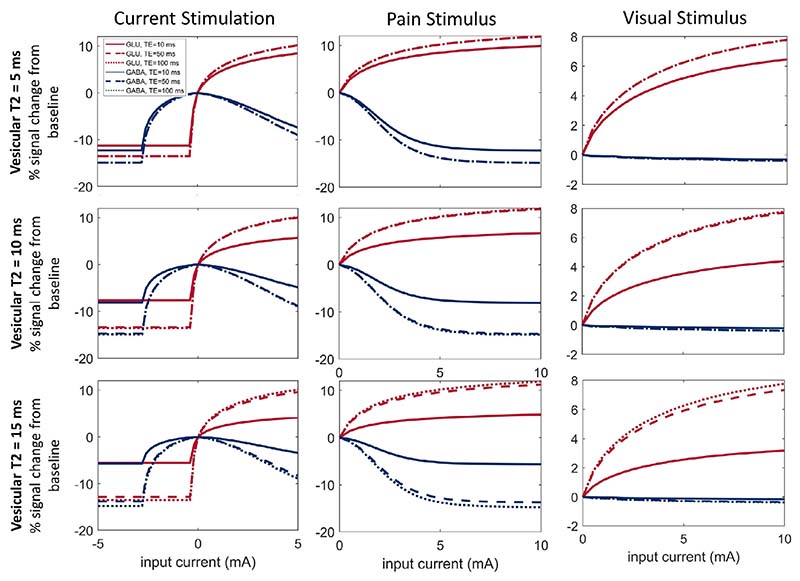
To assess the effect of the assumed value for vesicular T2 and TE on the model predictions, Simulation 6 was repeated for different combinations of these two parameters (TE = 10, 50, 100 ms; vesicular T2 = 5, 10, 15 ms), see Fig. 8.
Fig. 8. Effect of vesicular T2 and TE.
We recreate Fig. 7 (lower panel) with different values for TE and assumed values for vesicular T2. Each column relates to the stimulation type, described as before: left, tDCS; middle, pain; right, visual. The top row assumes vesicular T2 to be 5 ms, the middle row 10 ms, and the lower row 15 ms. Echo times used are 10 ms (solid lines) and 50 (dashed lines), and 100 ms (dotted lines indistinguishable from TE = 50 ms for vesicular T2 less than 15 ms).
3.4. Parameter values
All parameters have been set to values within their physiologically measurable ranges, where such values exist. Values in the model that are arbitrary or have been estimated include the connection strengths used in all simulations, and the TE/T2 values used in Simulation 6. For an analysis of the effects of these variables on model behaviour please see Results and Supplementary Information.
4. Results
In the present study, we investigated the effect of stimulation on neural activity and, in turn, on GABA and Glu dynamics. For this, we used the MFM described previously composed of 2 local networks, one excitatory and one inhibitory interconnected via AMPA and GABA receptor mediated synapses (see Fig. 2).
4.1. Effect of firing rate and amplitude of firing on NT cycling dynamics
In Fig. 3 the percentages of NT found in the R pool (vesicular, left), the X (ECS, middle), and the N pool (cytosolic, right) were averaged over the duration of the simulation and are presented as a function of firing rate. Additionally, the amplitude of the input signal was varied, which can be considered as a local measure of neural synchronisation in a MFM (Daffertshofer and van Wijk, 2011).
Fig. 3. Effect of firing rate and amplitude of firing on NT cycling dynamics.
The proportion of neurotransmitter (averaged over 100 s of simulation) found in the vesicular pool (left, R), the ECS (middle, X), and the cytosolic pool (right, N) is presented as a function of firing rate and neural synchrony (amplitude). As the firing rate increases, the NT concentration shifts from the vesicles to the ECS and cytosolic compartments. If vesicular NT is invisible to MRS then this would be reflected as an increase in the MRS signal. Additionally, the amplitude of the input signal was varied between 0.5 (light blue), 1 (dark blue) and 2 (purple); we found that increasing the amplitude enhanced the shift of NT from the vesicular to the ECS and cytosolic pools for the same firing rate whereas reducing the amplitude inhibited this effect.
When firing rates are zero, the vesicular component is at its maximum (30% of the total) and as firing rates increase, this percentage reduces. Variations in amplitude either enhance or inhibit this effect. We find that the reduction in vesicular NT is accompanied by an increased proportion of NT in the ECS (as a result of increased firing) or in the cytosol. The accumulation of NT in the cytosol is due to the mismatch between the rate that vesicles are depleted and the rate at which they are refilled, as observed in empirical data (Stevens and Tsujimoto, 1995). We observe that, in general, an increase in firing (or amplitude of firing) leads to a shift of NT from the vesicular pool to the ECS and cytosolic pools, whereas a decrease in firing (or amplitude) drives a shift of NT into the vesicles as predicted (also see Fig. 1).
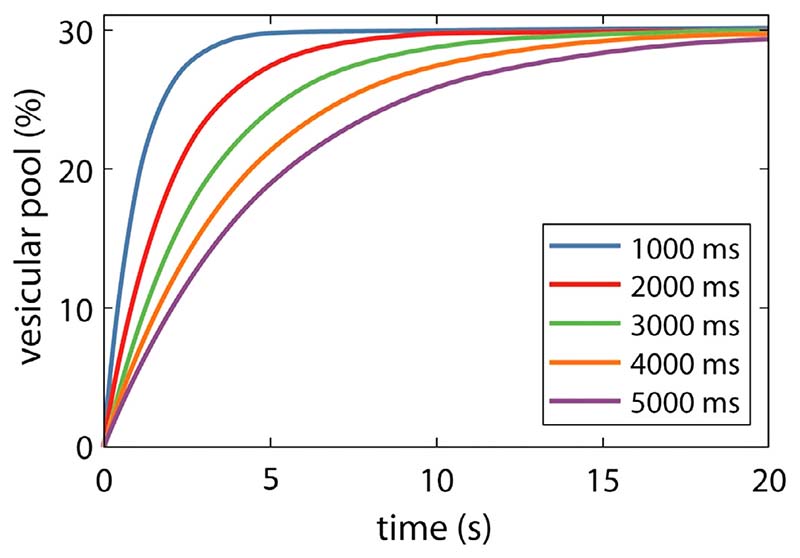
4.2. Effect of τr on vesicular refilling times
Next, we examined the effect of τron the refilling time of the vesicular pool to ensure that the model behaviour is physiologically plausible (see Fig. 4). τr governs the rate at which NT is recovered from the cytosolic pool and packaged into vesicles ready for release. Here, τr is varied between 1000 and 5000 ms and the time course for the vesicular pool to reach its maximum steady state value of 30% of the total cortical Glu concentration (starting from fully depleted vesicles) is shown. We fix the value of τr to be 1800 ms for all simulations that follow as this value allows refilling of the vesicular pool in approximately 10 seconds which is in line with experimental data (Stevens and Tsujimoto, 1995) using a firing rate of 10 spikes s−1. We note that that the time taken to reduce this pool to a new lower steady-state value is in the order of 5 seconds, which is also in line with experimental data (Stevens and Tsujimoto, 1995), see Fig. 5.
Fig. 4. Effect of τr on vesicle refilling times.
The effect of τr on the refilling time of the vesicular pool. Here τr is varied between 1000 and 5000 ms and the time course of the vesicular pool to reach its steady state value (from empty) is shown. We fix the value of τr to be 1800 ms for the following simulations which results in refilling of the pool in approximately 10 seconds in line with (Stevens and Tsujimoto, 1995) using a firing rate of 10 spikes s−1.
4.3. Effect of current stimulation on NT dynamics
We interrogate the model with an current stimulation, analogous to tDCS, to make predictions about how the MFM activity affects NT dynamics. The temporal trace of the NT dynamics in each of the 3 pools (vesicular, ECS, cytosolic) is given for the E-population (orange, left column) and the I-population (blue, right), see Fig. 5.
For excitatory current input, in the case of the excitatory population, we observe a shift of Glu from the vesicles to the cytosolic pool. Under the assumption that NT in the vesicular pool does not contribute to the MRS signal, this would be reflected as an increased Glu MRS signal. In the case of the inhibitory population, we observe the opposite effect in that GABA starts to accumulate in the vesicles and is similarly reduced in the cytosolic compartment. This change would be reflected as a reduction in the GABA MRS signal.
Next, we applied an inhibitory current to the model after allowing the system to reach steady-state as described previously Fig. 5 (right panel). In this instance, we observe similar behaviour in both of the excitatory and inhibitory populations, specifically a shift of neurotransmitter from the cytosolic and ECS compartments to the vesicles. The effect of this in the spectroscopic data would be a reduction in both the Glu and GABA MRS signals.
Next, the model was used to systematically test the effects of current stimulation of varying polarity and magnitude on GABA and Glu dynamics. For excitatory input currents, we generally observe a shift of Glu from the vesicular to the cytosolic pools accompanied by a shift of GABA from the cytosolic to the vesicular pool. Under our assumption that NT in the vesicular pool does not contribute to the MRS signal, the model predicts that we would observe a decrease in the GABA signal and an increase in the Glu MRS signal in experimental scenarios using excitatory current stimuli (anodal tDCS). For inhibitory currents, we observe a reduction in GABA and Glu in the ECS and cytosolic pools accompanied by an increase of NT in the vesicular pool compared to the baseline case . Therefore, the model predicts that we would observe a reduction in the MRS signal for both GABA and Glu in experimental scenarios using inhibitory current stimuli (cathodal tDCS). Highlighted with dashed lines is the case where which corresponds to the diagrams shown in Fig. 5.
4.4. Model predictions for pain, visual, and current stimulation
We present the model predictions for 3 stimulus types: pain, visual, and current stimulation of varying intensities. In Fig. 7 top panel, we present the proportion of Glu (red) and GABA (blue) that is considered to be ’visible’, i.e., the sum of the cytosolic and ECS compartments in response to the stimulation as a percentage of the total concentration. Pain and vision only allow for excitatory input currents and we observe that as the stimulus intensity increases, the proportion of visible Glu grows in both cases. We observe a greater reduction in GABA for the painful stimulus than for vision and this is due to the fact that the pain stimulus is modelled as targeting the inhibitory population directly whereas in the case of vision, the activity of the GABergic cells is modulated indirectly via their connection to the excitatory population. In Fig. 7 lower panel, we calculate the predicted MRS signal intensity for each condition using the ’Observation Model’ described previously and present this as a percentage difference from the baseline (when ). We have assigned T2 values to NT within each compartment and assumed standard echo times from the literature (see Table 1). We observe that for approximately a 10% change in the proportion of visible Glu or GABA, we achieve a 12% signal increase. Please see Supplementary Information for a detailed exploration of the effect of assumed T2 values on these results.
4.5. Effect of vesicular T2 and TE
We present the variations in the model predictions for a range of assumed vesicular T2 (5, 10, and 15 ms) and TE (10, 50, and 100 ms) values for each of the stimulation types, essentially recreating Fig. 7 (lower panel). We find that for shorter echo times or longer assumed values for vesicular T2, the effect of compartmental redistribution on the MRS signal is diminished.
5. Discussion
In this study, we present a mathematical model that bridges between the physiological changes at the micro-scale of the cell and synapse and fMRS measurements of the neurotransmitters GABA and Glu at the macroscale. The results presented in this paper indicate that echo-time is an important timing parameter that can be leveraged to maximise fMRS experimental outcomes.
5.1. Comparison with empirical data
In the following section, we assess the model performance against empirical data in the literature. We focus on studies measuring changes in the concentration of GABA, Glu, or Glx using fMRS in healthy participants in response to either painful, visual, or tDCS stimuli. Within each section there is considerable variation in the findings reported. However, analysing emerging patterns from the findings is an important first step.
The original aim of the paper was to test how much of the signal could be explained by shifting of NT between compartments over short timescales of less than 1 min. Unfortunately, most studies use acquisition times longer than a minute and this is due to known issues with SNR in MRS measurements. The model provides predictions at a much faster spatial scale; a new steady-state is reached within 5 seconds in response to a change in activity levels. Further modelling, including kinetic modelling, will be required to explain longer-term changes in NT concentrations following stimulation, but here we provide a framework which offers a supplementary perspective to the purely metabolic one. With this in mind, we present a range of fMRS studies to compare with the model outputs.
5.1.1. Current stimulation - Empirical studies
Although tDCS studies are generally conducted over longer timescales than considered by the model, they are included here due to the fact that tDCS allows explicit negative/inhibitory stimulation to both neural populations simultaneously. We point out, however, that animal data indicates this to be a limitation of the measurement technologies, not the biology as neural changes occur rapidly, for example (Sánchez-León et al., 2021). This allows us to show that the same model responds differentially to stimulation and presents a more general and therefore more robust test to the origins of the fMRS signal.
MRS studies looking at the effect of current stimulation are summarised in Table 2. In response to anodal stimulation of between 1 and 2 mA, empirical studies indicated an increase in Glu of between 0 and 11% (model prediction 9% increase using 3 mA stimulus), and a decrease in GABA of between 0 and 19% (model prediction 5% reduction using 3 mA stimulus). Whereas, in response to cathodal stimulation of the same intensity, empirical studies indicated a decrease of Glu of between 0 and 19% (model prediction 14% reduction using 3 mA stimulus), and a decrease in GABA of between 0 and 13% (model prediction 15% reduction using 3 mA stimulus). We refer to a 3 mA input for comparison as this appears to match more closely the empirical results using 1–2 mA. Empirically measured changes are generally of greater magnitude than the model predictions, especially for GABA. This could be due to the fact that the duration of the experiments is much longer than the simulated data which represents 1 min of activity, meaning that contributions to the signal from other sources become more likely. tDCS is thought to modulate the excitability of targeted neural populations by altering membrane potential in a polarity specific way (Molaee-Ardekani et al., 2021). Anodal tDCS has generally been found to increase cortical excitability and cathodal tDCS to reduce it with these effects validated via TMS motor evoked potential amplitudes (Liebetanz et al., 2002). Excitatory current stimulation is thought to drive a reduction in the MRS GABA signal due to reduced activity of GAD-67 (Floyer-Lea et al., 2006; Stagg et al., 2009), which is an enzyme involved in GABA synthesis that reduces with increased excitatory firing (Hendry and Jones, 1988; Levy et al., 2002). The inclusion of these processes is beyond the scope of this work, although we note that even without these details, the model predictions are in line with empirical observations.
Table 2. A summary of tDCS studies discussed in this section.
| System | Current | Glu/Glx change (%) | GABA change (%) | TE | Event-related/Block | Temporal Resolution | |
|---|---|---|---|---|---|---|---|
| Anodal Stimulation | |||||||
| (Bachtiar et al., 2015) | Motor | 1 mA | not reported | reduction | 68 ms (MEGA-PRESS) | Block | 20 mins |
| (Clark et al., 2011) | Parietal lobe | 2 mA | 11% | not reported | 40 ms | Block | 30 mins |
| (Dwyer et al., 2019) | pSTG | 2 mA | 0% | 0% | 68 ms (MEGA-PRESS) | Block | 10 mins |
| (Hunter et al., 2015) | Parietal lobe | 2 mA | increase | not reported | 40 ms | Block | 30 mins |
| (Jalali et al. (2018)) | Cerebellum | 1.8 mA | 0% | 0% | 68 ms (MEGA-PRESS) | Block | 25 mins |
| (Kim S et al., 2014) | Motor | 1.5 mA | 0% | -19.77% | 16 ms | Block | 15 mins |
| (Stagg et al., 2009) | Motor | 1 mA | 0% | -9.2% | 68 ms (MEGA-PRESS) | Block | 10 mins |
| (Stagg et al., 2011) | Motor | 1 mA | 0% | -11.5% | 68 ms (MEGA-PRESS) | Block | 10 mins |
| Cathodal Stimulation | |||||||
| (Kim S et al., 2014) | Motor | 1.5 mA | 0% | 0% | 16 ms | Block | 15 mins |
| (Patel et al., 2019) | Motor | 1 mA | not reported | -13.6% | 68 ms (MEGA-PRESS) | Block | 10 mins |
| (Stagg et al., 2009) | Motor | 1 mA | -19.1% | -11.1% | 68 ms (MEGA-PRESS) | Block | 10 mins |
In the case of negative current stimulation, it has been suggested that Glu is reduced as a direct consequence of decreased neuronal firing (Stagg et al., 2009), as Glu/Gln cycling is tightly linked to glucose oxidation and therefore, neural activity (Petroff et al., 2002; Rothman et al., 1999; Sibson et al., 1997, 1998). It has also been suggested that the reductions in GABA found during cathodal stimulation are explained due to the maintenance of the physiological balance between Glu, Gln, and GABA (see Martin and Tobin, 2000; Petroff, 2002; Sonnewald et al., 1993). In the model, this change is explained due to the reduction in inhibitory population firing activity although, in reality, this process is likely to be more complex. For example, in a recent study in the cat visual cortex, Zhao et al. found anodal (cathodal) tDCS enhanced (suppressed) the amplitude of visually evoked field potentials, these effects were not found in a sham condition (Zhao et al., 2020). The authors found anodal tDCS caused GABA to decrease with no change in Glu and cathodal tDCS to cause a reduction in Glu, but not GABA. Furthermore, the mechanism driving these changes was that the polarity of the tDCS selectively suppressed the expression of GABA- and glutamate-synthesizing enzymes.
5.1.2. Vision - Empirical studies
fMRS studies using visual stimulation are summarised in Table 3. In response to visual stimulation and using block designs, most empirical studies reported an increase in Glu of between 0 and 4% (model prediction up to 8% increase), with no change in GABA apart from a single study reporting a decrease of 5% (model prediction up to 1% decrease). A single event-related repetition suppression study saw modulation of Glu from -11% to +12%, and we note that this study used the longest echo time which would sensitise measurements to shifts of Glu between compartments. The model predictions are in line with these reports; the minimal inhibitory response of the model is because the effect of stimulation on inhibitory populations is an indirect effect of their connection to the activated excitatory population rather than via the stimulation itself. Essentially, we present the results from a ’block design’ in our model with NT activity averaged over 30 s in response to a flickering stimulus. An ’event-related’ design would yield larger changes as seen in the empirical studies (see the following section for a discussion of this).
Table 3. A summary of the visual fMRS studies discussed in this section. Where there exists more than a single entry under ’temporal resolution’, this indicates that data was presented at the higher temporal resolution but stats were calculated using averaged data over the longer timescale.
| Authors | Glu/Glx change (%) | GABA change (%) | TE | Event-related/Block | Temporal Resolution |
|---|---|---|---|---|---|
| (Apšvalka et al., 2015) | +12/-11% | 0% | 105 ms | Event-related | 36 s |
| (Bednařík et al., 2015) | 3.3% | 0% | 26 ms | Block | 2.7 mins/ 20 s |
| (Bednařík et al., 2017) | 3.1-3.9% | 0% | 26 ms | Block | 2.7 mins |
| (Boillat et al., 2020) | 1.65% | 0% | 16 ms | Block | 3 mins/ 1 min |
| (Ip et al., 2017) | 2% | 0% | 36 ms | Block | 64 s/ 16 s |
| (Lin et al., 2012) | 2.5% | 0% | 6 ms | Block | 6.6 mins |
| (Mangia et al., 2006) | 3% | not reported | 6 ms | Block | 2 mins 40 s/ 20 s |
| (Mekle et al., 2017) | 0% | -5% | 6 ms | Block | 10 mins 40 s/ 40 s |
| (Schaller et al., 2013) | 4% | 0% | 6 ms | Block | 3.3 mins/ 30 s |
5.1.3. Pain - Empirical studies
fMRS studies focussed on pain generally report the largest changes in metabolite concentrations and are presented in Table 4. In response to painful stimulation, empirical studies indicated an increase in Glu of between 0 and 22% (model prediction up to 12% increase), and a general decrease in GABA of between 0 and 15% (model prediction up to 15% decrease). The model predictions are aligned with the general observation that increased pain correlates with increased Glu and reduced GABA. We note here that we implement a simplified model of acute pain in a single voxel which does not take into consideration top-down and bottom-up inputs as well as feedback loops which may account for disparities between the model predictions and empirical results, such as in (Kupers et al., 2009).
Table 4. A summary of the pain fMRS studies discussed in this section.
| Authors | Glu/Glx change (%) | GABA change (%) | TE | Event-related/Block | Temporal Resolution |
|---|---|---|---|---|---|
| (Cleve et al., 2015) | 21.5% | -15.1% | 68 ms (MEGA-PRESS) | Event-related | 3 s |
| (Cleve et al., 2015) | 15.7% | -12.7% | 68 ms (MEGA-PRESS) | Event-related | 3 s |
| (Cleve et al., 2017) | 0% | 0% | 68 ms (MEGA-PRESS) | Event-related | 16 s |
| (de Matos et al., 2017) | 0% | -10.8% | 43 ms | Event-related | 12 s |
| (Gussew et al., 2010) | 18.1% | not reported | 30 ms | Event-related | 5 s |
| (Gutzeit et al., 2011) | 16.4% | not reported | 30 ms | Block | 9 mins |
| (Gutzeit et al., 2013) | 9% | not reported | 30 ms | Block | 3.48 mins |
| (Hansen et al., 2014) | 0% | not reported | 30 ms | Block | 5 mins |
| (Kupers et al., 2009) | 0% | 15% | 20 ms | Block | 4 mins |
| (Mullins et al., 2005) | 9.3% | not reported | 20 ms | Block | 10 mins |
5.2. Block vs event-related study design
In its current form, the model predicts a greater change in NT dynamics for an event-related design rather than for a block design which aligns with empirical results. Event-related designs generally have a much finer temporal resolution than block designs and the signal is acquired very close to the stimulus onset. The model indicates that in just a few seconds the maximal change in NT is attained and therefore an event-related design will capture thefull magnitude of the signal change as the data is only collected close to the stimulus onset. In a block design, it is usual that the stimulus is applied intermittently (flashing light, for example). In this case, the model returns to baseline during the interstimulus interval and the total signal is an average of the stimulus on and off periods which will dilute the magnitude of the signal change. The reason for this rapid return to baseline is that the model does not account for adaptation and plasticity mechanisms and understanding how these contribute to the NT signal change is an important area for future work.
5.3. Controversy in the fMRS literature
The model clearly predicts changes in NT for a wide variety of stimulus inputs and intensities, however, in reality, the outcomes are variable making it difficult to compare results. An important factor in this controversy is in the study design itself. For example, methodological differences such as sample size, stimulation parameters, variability in stimulating probe position, duration of stimulation, acquisition protocol, echo-time, MRS analysis method, reference metabolite, and brain region, all contribute to the variability in the empirical data. Choice of echo time is particularly important as at short TE, MRS will be less sensitive to compartmental shifts of NT however, further work is required to determine the effect of this acquisition parameter on the fMRS signal. Ultimately, optimal scan acquisition will require balancing TE with constraints imposed by imaging system, brain region, SNR, and experimental paradigm.
5.4. Empirical support for model assumptions
In the model, we assume that there is no net increase in either Glu or GABA in the timescales shown here as it is assumed that flux through the Glu-Gln-GABA or TCA cycle would have minimal impact (Jelen et al., 2018; Mullins, 2018). However, we note that an alternative interpretation favours changes in metabolic flux as an explanation for stimulus-related Glu changes (Martínez-Maestro et al., 2019), based on calculations that the available pool of vesicular Glu is too small to account for the signal changes if this pool is released. We point out that this estimation is based on the assumption of 1 vesicle release per synapse at a single point in time (Barbour and Häusser, 1997). The model accounts for the sustained release of vesicular NT due to activation over many seconds driving the vesicular component closer to zero, or at least to a new lower steady-state value as firing rates increase. This has been found to be the case in as little as 5 seconds in animal studies using a preparation designed to mimic high frequency stimulation (Stevens and Tsujimoto, 1995). We suggest that in reality both of these processes contribute to the change in fMRS signal to different degrees depending on the temporal resolution of the experiment. This means that although the model was initially designed to explain short-term changes in physiology in response to stimulation, it may be that the same mechanisms presented here i.e., a mismatch between the rates of synthesis, repackaging, and exocytosis, also contribute to longer-term in vivo measurements in addition to changes in absolute concentrations brought about via de novo synthesis and degradation of GABA and Glu.
The key determinant of the shift of NT between the pools of differing MR visibility defined here, is the mismatch between the release and refilling rates of vesicles in response to an altered firing rate. Upon sustained stimulation, the number of vesicles released per second has been found to reduce until a lower steady-state is reached (Stevens and Tsujimoto, 1995). The release rate is predicted to decline according to the equation where KX is the rate of exocytosis, and KD is the vesicular refilling rate (Stevens and Tsujimoto, 1995). In the same paper, the authors estimated KX to be almost seven times greater than KD. We chose τr to allow a vesicle refilling rate of approx 10 seconds as in (Stevens and Tsujimoto, 1995). Other authors have found this rate to be longer (23 seconds) (Hori and Takahashi, 2012). Similarly, the model was tuned to reach a new steady-state in response to stimulation after approx 5 seconds, as observed in animal data (Stevens and Tsujimoto, 1995). Further work is required to ascertain the direct effect of these rates on NT dynamics.
Animal work has shown that the average sustainable release capacity for a central synapse is approximately two vesicles per μm3 per second (Danbolt, 2001). Assuming 5000 Glu molecules per vesicle (which is at the upper end of current estimations) (Danbolt, 2001), this equates to approximately 1 mMol min−1 which is equivalent to the 10% changes we observe in the model, assuming an average cortical Glu concentration of 10 mM (Danbolt, 2001; Schousboe, 1981). This rate would be further increased (allowing for even larger changes in shorter time scales) if not all cytosolic Glu were MRS-visible, as we have assumed here. This is higher than both the rate of flux through the Glu-Gln cycle (Shen et al., 1999) and the estimated rates of astrocytic uptake for Glu (Kanamori et al., 2002). We suggest that in the short term it is not a requirement for Glu production to keep up with metabolic demand as there is a surplus of Glu in the cytosol which can be recycled into vesicles. Astrocytic uptake rates must also be considered as a limiting factor; however, it has been argued that Glu uptake is relevant to the ”slow component of glutamate removal [from the cleft]... ”(Diamond and Jahr, 1997; Danbolt, 2001; Otis et al., 1996) and that immobilisation by binding is a much faster method of inactivating Glu, allowing some time for astrocytic uptake to take place. Therefore, in the short-term, these limiting factors may not apply.
5.5. Model limitations and future work
The metabolic pathway involving each of the neurotransmitters modelled here is highly complex; this holds in the case of Glu particularly. For example, within the neuron, cytosolic Glu may be utilised for new amino-acid synthesis, entry into the TCA cycle, or conversion into glutathione or GABA amongst many other possibilities (Mangia et al., 2012). Here we make the simplified assumption that all cytosolic Glu in the model is available for repackaging into vesicles for neurotransmission. For the purpose of the present work, we have assumed that cycling rates (time constants) of GABA and Glu are the same in the first approximation. Rigorously speaking, the molecular processes that underlie the metabolism of these NTs are distinct, which might lead to differences in their cycling rates. The current model does not account for processes involving Gln. Glu released at the synapse is almost entirely taken up by the surrounding glial cells and accumulates in the cytosol with a small fraction of released GABA. Approximately, 80% of astrocytic Glu is converted to Gln and is returned to the Glu-Gln(-GABA) cycle with the rest being degraded via the TCA cycle (Hertz and Rothman, 2017). The conversion rate of Gln from Glu appears to approximately match rates of conversion in the opposite direction (Hertz and Rothman, 2017). And so although there may be short-term transients, there are unlikely to be significant changes over the longer term. However, we note that various complexities such as the inhibition of this cycle due to large extracellular Glu/Gln concentrations (Hertz and Rothman, 2017), which may be the case after a period of activity, must also be accounted for. Future work will endeavour to consider all of these complexities.
We acknowledge that when considering concentration changes on minute time scales, rebalancing of steady-state TCA intermediates following metabolic stimulation and a degree of increased anaplerosis may go some way to explaining neurotransmitter concentration changes. However, the goal of this paper was to explain much faster changes in a quantitative manner. Further work includes modelling of the anaplerotic pathway, including the malate-aspartate shuttle and the lactate astrocyte-neuron shuttle to examine the effect that these might have on MRS measurements over longer time scales (Mangia et al., 2009 ; Mason, 2017). Though metabolic consequences/effectors of activation do need to be considered, we also point out that, following (Sonnewald, 2014), ’as the TCA cycle cannot act as a carbon sink, anaplerosis must be coupled with cataplerosis’, implying that net increases in Glu are unlikely to account for the increases found in fMRS studies.
Further work is required to substantiate the hypothesis that the vesicular pool of NT is not visible to MRS since there are no studies which we are aware of that have investigated MRS in vesicular preparations. There are studies of synaptosomes, which are nerve terminal preparations prepared by sub-cellular fractionation that contain membrane-sealed cytosol as well as synapses and vesicles (Petroff et al., 1992; Sonnewald and McKenna, 2002). However, the MRS was carried out on acid extracts of the preparations, thus destroying the integrity of vesicles. Furthermore, our assumption of an MR-invisible GABA pool is based on our knowledge of Glu, but as far as we are aware, this has not been established empirically.
The mean-field approximation used in this work, describes the evolution of the first-order moments of the system states (i.e. the means), and discarded higher order terms (Marreiros et al., 2009). A consequence of this first order approximation is that the model is unable to capture dependencies between the moments within or between the ensembles. As an example, the mean membrane potential of one population may be affected by the variance of the depolarisation of another or the same population (Deco et al., 2008). A possible future extension of this work might be to consider a second order approximation as in the dynamic mean-field framework, described in (Hasegawa, 2003).
This model is intended to replicate a generic patch of cortical sheet (or a standard MRS voxel) to understand how changes in neural activity (excitatory and inhibitory) might relate to observed changes in the fMRS signal. Future work should account for the anatomical diversity of different brain regions as well as the various types of interneurons and their cytoarchitecture. Tailoring the model to a specific neural region or circuit is an area for future work, as is the addition of plasticity mechanisms and adaptation as a major application of fMRS is in the study of plasticity. Another exciting avenue for future research will be to understand how the fMRS and BOLD signals are related in order to explain results found in simultaneous MRS-BOLD studies. To achieve this, the current model will be coupled to a haemodynamic response function which will allow the model to generate predictions for both imaging modalities.
6. Conclusions
In this paper, we bridge the gap between spatial scales by developing a mean-field model of macro measurements in fMRS, to test the validity of the hypothesis that fMRS reflects a shift of NT between pools. We have developed a mean-field model to link human in vivo quantification of task-related neurotransmitter changes via MRS to synaptic activity. We have shown that, using a biologically realistic model, it is possible to predict changes in GABA and Glu concentrations which are in agreement with experimentally observed values. We hope that this work highlights the issue of echo-time choice in fMRS experiments and how this important timing parameter can be leveraged to maximise experimental outcomes.
Supplementary Material
Acknowledgements
The authors would like to thank Prof. Peter Robinson for his careful reading and insightful comments on an early version of this manuscript, Daniel Wand for his assistance with graphics, and the anonymous reviewers for their invaluable insights which have improved the paper vastly. CLC is funded by the Medical Research Council (MRC) Grant MR/PO14445/1. WeD acknowledges ANID, Chile (projects FONDE-CYT 1201822, ANILLO ACT210053 and Basal FB0008), ValgrAI and the Generalitat Valenciana, Spain. NTB is funded by EPSRC Grant EP/N006771/1. CJS holds a Senior Research Fellowship, funded by the Wellcome Trust (224430/Z/21/Z). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).
Abbreviations
- AMPA
α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid
- ECS
extracellular space
- E
excitatory
- fMRS
functional magnetic resonance spectroscopy
- GABA
γ-aminobutyric acid
- GAD
glutamic acid decarboxylase
- Gln
glutamine
- Glu
glutamate
- Glx
the sum of glutamine plus glutamate
- HH
Hodgkin-Huxley
- I
inhibitory
- MFM
mean-field model
- mM
millimolar
- MRI
magnetic resonance imaging
- MRS
magnetic resonance spectroscopy
- NAA
N-acetylaspartate
- NMDA
N-methyl-D-aspartate
- NT
neurotransmitters
- PAG
phosphate activated glutaminase
- SD
standard deviation
- SE
standard error
- SNR
signal-to-noise ratio
- TCA
tricarboxylic acid cycle
- tCr
total creatine, the sum of creatine plus phosphocreatine
- tDCS
transcranial direct current stimulation
Footnotes
Credit authorship contribution statement
Caroline A. Lea-Carnall: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. Wael El-Deredy: Conceptualization, Investigation, Methodology, Supervision, Validation, Visualization, Writing –original draft, Writing –review & editing. Charlotte J. Stagg: Conceptualization, Investigation, Methodology, Supervision, Validation, Visualization, Writing – original draft, Writing –review & editing. Stephen R. Williams: Conceptualization, Investigation, Methodology, Supervision, Validation, Visualization, Writing – original draft, Writing –review & editing. Nelson J. Trujillo-Barreto: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Supervision, Validation, Visualization, Writing – original draft, Writing –review & editing.
Data availability
Data will be made available on request.
References
- Abbott LF, Chance FS. Drivers and modulators from push-pull and balanced synaptic input. Prog Brain Res. 1995;149:147–155. doi: 10.1016/S0079-6123(05)49011-1. [DOI] [PubMed] [Google Scholar]
- An H, Lin W. Spin Density, T1, T2, T2 ∗ Relaxation and Bloch Equations. Current Protocols in Magnetic Resonance Imaging. 2001;00:B3.1.1–B3.1.10. doi: 10.1002/0471142719.mib0301s00. [DOI] [Google Scholar]
- Apšvalka D, Gadie A, Clemence M, Mullins PG. Event-related dynamics of glutamate and BOLD effects measured using functional magnetic resonance spectroscopy (fMRS) at 3T in a repetition suppression paradigm. Neuroimage. 2015;118:292–300. doi: 10.1016/j.neuroimage.2015.06.015. [DOI] [PubMed] [Google Scholar]
- Bachtiar V, Near J, Johansen-Berg H, Stagg CJ. Modulation of GABA and resting state functional connectivity by transcranial direct current stimulation. eLife. 2015;4:e08789. doi: 10.7554/eLife.08789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbour B, Häusser M. Intersynaptic diffusion of neurotransmitter. Trends in Neurosciences. 1997 Sep;20(9):377–384. doi: 10.1016/s0166-2236(96)20050-5. [DOI] [PubMed] [Google Scholar]
- Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat Rev Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- Bednařík P, Tkác I, Giove F, DiNuzzo M, Deelchand DK, Emir UE, Eberly LE, Mangia S. Neurochemical and BOLD responses during neuronal activation measured in the human visual cortex at 7 Tesla. J Cereb Blood Flow Metab. 2015;35(4):601–610. doi: 10.1038/jcbfm.2014.233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednařík P, Tkác I, Giove F, Eberly LE, Deelchand DK, Barreto FR, Mangia S. Neurochemical responses to chromatic and achromatic stimuli in the human visual cortex. J Cereb Blood Flow Metab. 2017;38(2):347–359. doi: 10.1177/0271678X17695291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berzhanskaya J, Chernyy N, Gluckman B, Schiff S, Ascoli G. Modulation of hippocampal rhythms by subthreshold electric fields and network topology. J. Comput. Neurosci. 2013;34(3):369–389. doi: 10.1007/s10827-012-0426-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloch F. Nuclear induction. Phys Rev. 1946;70:460–474. doi: 10.1103/PhysRev.70.460. [DOI] [Google Scholar]
- Boillat Y, Xin L, van der Zwaag W, Gruetter R. Metabolite concentration changes associated with positive and negative BOLD responses in the human visual cortex: a functional MRS study at 7 Tesla. J. Cereb. Blood Flow Metab. 2020;40(3):488–500. doi: 10.1177/0271678X19831022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonaiuto J, Bestmann S. Chapter 4 - understanding the nonlinear physiological and behavioral effects of tDCS through computational neurostimulation. Prog Brain Res. 2015;222:75–103. doi: 10.1016/bs.pbr.2015.06.013. [DOI] [PubMed] [Google Scholar]
- Bustillo J, Rowland L, Mullins P, Jung R, Chen H, Qualls C, Hammond R, Brooks W, Lauriello J. 1H-MRS At 4 Tesla in minimally treated early schizophrenia. Mol Psychiatry. 2010;15(6):629–636. doi: 10.1038/mp.2009.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark VP, Coffman BA, Trumbo MC, Gasparovic C. Transcranial direct current stimulation (tDCS) produces localized and specific alterations in neurochemistry: a 1H magnetic resonance spectroscopy study. Neurosci Lett. 2011;500(1):67–71. doi: 10.1016/j.neulet.2011.05.244. [DOI] [PubMed] [Google Scholar]
- Cleve M, Gussew A, Reichenbach JR. In vivo detection of acute pain-induced changes of GABA+ and Glx in the human brain by using functional 1H MEGA-PRESS MR spectroscopy. Neuroimage. 2015;105:67–75. doi: 10.1016/j.neuroimage.2014.10.042. [DOI] [PubMed] [Google Scholar]
- Cleve M, Gussew A, Wagner G, Bär KJ, Reichenbach JR. Assessment of intra- and inter-regional interrelations between GABA+, Glx and BOLD during pain perception in the human brain - A combined 1 H fMRS and fMRI study. Neuroscience. 2017;365:125–136. doi: 10.1016/j.neuroscience.2017.09.037. [DOI] [PubMed] [Google Scholar]
- Czeiger D, White EL. Synapses of extrinsic and intrinsic origin made by callosal projection neurons in mouse visual cortex. J Comp Neurol. 1993;330(4):502–513. doi: 10.1002/cne.903300406. [DOI] [PubMed] [Google Scholar]
- Daffertshofer A, van Wijk BC. On the influence of amplitude on the connectivity between phases. Front Neuroinform. 2011;5:6. doi: 10.3389/fninf.2011.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danbolt NC. Glutamate uptake. Prog Neurobiol. 2001;65(1):1–105. doi: 10.1016/s0301-0082(00)00067-8. [DOI] [PubMed] [Google Scholar]
- de Matos NMP, Hock A, Wyss M, Ettlin DA, Brügger M. Neurochemical dynamics of acute orofacial pain in the human trigeminal brainstem nuclear complex. Neuroimage. 2017;162:162–172. doi: 10.1016/j.neuroimage.2017.08.078. [DOI] [PubMed] [Google Scholar]
- Deco G, Jirsa VK, Robinson PA, Breakspear M, Friston K. The Dynamic Brain: From Spiking Neurons to Neural Masses and Cortical Fields. PLoS Comput Biol. 2008;4(8):e1000092. doi: 10.1371/journal.pcbi.1000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G, Ponce-Alvarez A, Hagmann P, Romani GL, Mantini D, Corbetta M. How local excitation inhibition ratio impacts the whole brain dynamics. J Neurosci. 2014;34(23):7886–7898. doi: 10.1523/JNEUROSCI.5068-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Paré D. Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J Neurophysiol. 1999;81(4):1531–1547. doi: 10.1152/jn.1999.81.4.1531. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Mainen ZF, Sejnowski TJ. Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. J. Comp. Neurosci. 1994;1(3):195–230. doi: 10.1007/BF00961734. [DOI] [PubMed] [Google Scholar]
- Destexhe A. In: Methods in Neuronal Modeling. 2nd edition. Koch C, Segev I, Mainen ZF, Senowski TJ, editors. MIT Press; Cambridge MA: 1997. Kinetic Models of Synaptic Transmission. [Google Scholar]
- Diamond J, Jahr C. Transporters buffer synaptically released glutamate on a submillisecond time scale. The J neurosci. 1997;17:4672–4687. doi: 10.1523/JNEU-ROSCI.17-12-04672.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwyer GE, Craven AR, Hirnstein M, Kompus K, Assmus J, Ersland L, Hugdahl K, Grüner R. No effects of anodal tDCS on local GABA and Glx levels in the left posterior superior temporal gyrus. Front Neurol. 2019;9 doi: 10.3389/fneur.2018.01145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edden RAE, Intrapiromkul J, Zhu H, Cheng Y, Barker PB. Measuring T2 in vivo with J-difference editing: application to GABA at 3 Tesla. J Magn Reson Imaging. 2011;35(1):229–234. doi: 10.1002/jmri.22865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elhanany E, White EL. Intrinsic circuitry: synapses involving the local axon collaterals of corticocortical projection neurons in the mouse primary somatosensory cortex. J. Comp. Neurol. 1990;291(1):43–54. doi: 10.1002/cne.902910105. [DOI] [PubMed] [Google Scholar]
- Floyer-Lea A, Wylezinska M, Kincses T, Matthews PM. Rapid modulation of GABA concentration in human sensorimotor cortex during motor learning. J Neurophysiol. 2006;95(3):1639–1644. doi: 10.1152/jn.00346.2005. [DOI] [PubMed] [Google Scholar]
- Freund TF, Katona I. Perisomatic inhibition. Neuron. 2007;56(1):33–42. doi: 10.1016/j.neuron.2007.09.012. [DOI] [PubMed] [Google Scholar]
- Ganji SK, Banerjee A, Patel AM, Zhao YD, Dimitrov IE, Browning JD, Brown ES, Maher EA, Choi C. T2 Measurement of J-coupled metabolites in the human brain at 3T. NMR Biomed. 2012;25(4):523–529. doi: 10.1002/nbm.1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gussew A, Rzanny R, Erdtel M, Scholle HC, Kaiser WA, Mentzel HJ, Reichenbach JR. Time-resolved functional 1H MR spectroscopic detection of glutamate concentration changes in the brain during acute heat pain stimulation. Neuroimage. 2010;49(2):1895–1902. doi: 10.1016/j.neuroimage.2009.09.007. [DOI] [PubMed] [Google Scholar]
- Gutzeit A, Meier D, Meier ML, von Weymarn C, Ettlin DA, Graf N, Froehlich JM, Binkert CA, Brügger M. Insula-specific responses induced by dental pain. A proton magnetic resonance spectroscopy study. Eur Radiol. 2011;21(4):807–815. doi: 10.1007/s00330-010-1971-8. [DOI] [PubMed] [Google Scholar]
- Gutzeit A, Meier D, Froehlich JM, Hergan K, Kos S, Weymarn CV, Lutz K, Ettlin D, Binkert CA, Mutschler J, Sartoretti-Schefer S, et al. Differential NMR spectroscopy reactions of anterior/posterior and right/left insular subdivisions due to acute dental pain. Eur Radiol. 2013;23(2):450–460. doi: 10.1007/s00330-012-2621-0. [DOI] [PubMed] [Google Scholar]
- Hansen TM, Olesen AE, Simonsen CW, Drewes AM, Frøkjær JB. Cingulate metabolites during pain and morphine treatment as assessed by magnetic resonance spectroscopy. J Pain Res. 2014;7:269–276. doi: 10.2147/JPR.S61193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasegawa H. Dynamical mean-field theory of noisy spiking neuron ensembles: application to the hodgkin-huxley model. Phys Rev E. 2003;68(4 Pt 1):041909. doi: 10.1103/PhysRevE.68.041909. [DOI] [PubMed] [Google Scholar]
- Hendry SH, Jones EG. Activity-dependent regulation of GABA expression in the visual cortex of adult monkeys. Neuron. 1988;1(8):701–712. doi: 10.1016/0896-6273(88)90169-9. [DOI] [PubMed] [Google Scholar]
- Hertz L, Rothman DL. Glutamine-glutamate cycle flux is similar in cultured astrocytes and brain and both glutamate production and oxidation are mainly catalyzed by aspartate aminotransferase. Biology (Basel) 2017;6(1):17. doi: 10.3390/biology6010017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hori T, Takahashi T. Kinetics of synaptic vesicle refilling with neurotransmitter glutamate. Neuron. 2012;76(3):511–517. doi: 10.1016/j.neuron.2012.08.013. [DOI] [PubMed] [Google Scholar]
- Hunter MA, Coffman BA, Gasparovic C, Calhoun VD, Trumbo MC, Clark VP. Baseline effects of transcranial direct current stimulation on glutamatergic neurotransmission and large-scale network connectivity. Brain Res. 2015;1594:92–107. doi: 10.1016/j.brainres.2014.09.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyder F, Herman P, Bailey CJ, Møller A, Globinsky R, Fulbright RK, Rothman DL, Gjedde A. Uniform distributions of glucose oxidation and oxygen extraction in gray matter of normal human brain: no evidence of regional differences of aerobic glycolysis. J Cereb Blood Flow Metab. 2016;36:903–916. doi: 10.1177/0271678X15625349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ip IB, Berrington A, Hess AT, Parker AJ, Emir UE, Bridge H. Combined fMRI-MRS acquires simultaneous glutamate and BOLD-FMRI signals in the human brain. Neuroimage. 2017;155:113–119. doi: 10.1016/j.neuroimage.2017.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalali R, Chowdhury A, Wilson M, Miall R, Galea J. Neural changes associated with cerebellar tDCS studied using MR spectroscopy. Exp Brain Res. 2018;236(4):997–1006. doi: 10.1007/s00221-018-5170-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelen LA, King S, Mullins PG, Stone JM. Beyond static measures: a review of functional magnetic resonance spectroscopy and its potential to investigate dynamic glutamatergic abnormalities in schizophrenia. J Psychopharm. 2018;32(5):497–508. doi: 10.1177/0269881117747579. [DOI] [PubMed] [Google Scholar]
- Johnson RR, Burkhalter A. Microcircuitry of forward and feedback connections within rat visual cortex. J Comp Neurol. 1996;368(3):383–398. doi: 10.1002/(SICI)1096-9861(19960506)368:3<383::AID-CNE5>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- Kanamori K, Ross BD, Kondrat RW. Glial uptake of neurotransmitter glutamate from the extracellular fluid studied in vivo by microdialysis and (13)CNMR. J Neurochem. 2002;83(3):682–695. doi: 10.1046/j.1471-4159.2002.01161.x. [DOI] [PubMed] [Google Scholar]
- Kauppinen RA, Williams SR. Nondestructive detection of glutamate by 1H NMR spectroscopy in cortical brain slices from the guinea pig: evidence for changes in detectability during severe anoxic insults. J Neurochem. 1991;57(4):1136–1144. doi: 10.1111/j.1471-4159.1991.tb08271.x. [DOI] [PubMed] [Google Scholar]
- Kauppinen RA, Pirttilä TRM, Auriola SOK, Williams SR. Compartmentation of cerebral glutamate in situ as detected by 1H/13C NMR. Biochem J. 1994;298:121–127. doi: 10.1042/bj2980121. (Pt1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, Stephenson MC, Morris PG, Jackson SR. tDCS-induced alterations in GABA concentration within primary motor cortex predict motor learning and motor memory: a 7 T magnetic resonance spectroscopy study. Neuroimage. 2014;99(100):237–243. doi: 10.1016/j.neuroimage.2014.05.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi R, Kitano K. Impact of slow K+ currents on spike generation can be described by an adaptive threshold model. J Comp Neurosci. 2016;40:347–362. doi: 10.1007/s10827-016-0601-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupers R, Danielsen ER, Kehlet H, Christensen R, Thomsen C. Painful tonic heat stimulation induces GABA accumulation in the prefrontal cortex in man. Pain. 2009;142(1–2):89–93. doi: 10.1016/j.pain.2008.12.008. [DOI] [PubMed] [Google Scholar]
- Levy LM, Ziemann U, Chen R, Cohen LG. Rapid modulation of GABA in sensorimotor cortex induced by acute deafferentation. Ann Neurol. 2002;52(6):755–761. doi: 10.1002/ana.10372. [DOI] [PubMed] [Google Scholar]
- Li D, Zhu Y, Huang H. Spike activity regulates vesicle filling at a glutamatergic synapse. J Neurosci. 2020;40(26):4972–4980. doi: 10.1523/JNEUROSCI.2945-19.2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liebetanz D, Nitsche MA, Tergau F, Paulus W. Pharmacological approach to the mechanisms of transcranial DC-stimulation-induced after-effects of human motor cortex excitability. Brain. 2002;125(Pt 10):2238–2247. doi: 10.1093/brain/awf238. [DOI] [PubMed] [Google Scholar]
- Lin Y, Stephenson MC, Xin L, Napolitano A, Morris PG. Investigating the metabolic changes due to visual stimulation using functional proton magnetic resonance spectroscopy at 7 T. J Cereb Blood Flow Metab. 2012;32(8):1484–1495. doi: 10.1038/jcbfm.2012.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malerba P, Straudi S, Fregni F, Bazhenov M, Basaglia N. Using biophysical models to understand the effect of tdcs on neurorehabilitation: searching for optimal covariates to enhance poststroke recovery. Front Neurol. 2017;8(58):1–13. doi: 10.3389/fneur.2017.00058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangia S, Tkác I, Gruetter R, Van de Moortele PF, Maraviglia B, Ugurbil K. Sustained neuronal activation raises oxidative metabolism to a new steady-state level: evidence from 1H NMR spectroscopy in the human visual cortex. J Cereb Blood Flow Metab. 2006;27(5):1055–1063. doi: 10.1038/sj.jcbfm.9600401. [DOI] [PubMed] [Google Scholar]
- Mangia S, Giove F, Tkác I, Logothetis NK, Henry PG, Olman CA, Maraviglia B, Di Salle F, Uurbil K. Metabolic and hemodynamic events after changes in neuronal activity: current hypotheses, theoretical predictions and in vivo NMR experimental findings. J Cereb Blood Flow Metab. 2009;29(3):441–463. doi: 10.1038/jcbfm.2008.134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangia S, Giove F, DiNuzzo M. Metabolic pathways and activity-dependent modulation of glutamate concentration in the human brain. Neurochem Res. 2012;37(11):2554–2561. doi: 10.1007/s11064-012-0848-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marreiros AC, Daunizeau J, Kiebel SJ, Friston KJ. Population dynamics: variance and the sigmoid activation function. Neuroimage. 2008;42(1):147–157. doi: 10.1016/j.neuroimage.2008.04.239. [DOI] [PubMed] [Google Scholar]
- Marreiros A, Kiebel SJ, Daunizeau J, Harrison LM, Friston KJ. Population dynamics under the laplace assumption. Neuroimage. 2009;44(3):701–714. doi: 10.1016/j.neuroimage.2008.10.008. [DOI] [PubMed] [Google Scholar]
- Martínez-Maestro M, Labadie C, Möller HE. Dynamic metabolic changes in human visual cortex in regions with positive and negative blood oxygenation level-dependent response. J Cereb. Blood Flow Metab. 2019;39(11):2295–2307. doi: 10.1177/0271678X18795426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin D, Tobin A. In: Martin D, Olsen R, editors. LWW; 2000. Mechanisms controlling GABA synthesis and degradation in the brain In GABA in the nervous system: the view at fifty years; pp. 25–41. [Google Scholar]
- Mason S. Lactate shuttles in neuroenergetics - homeostasis, allostasis and beyond. Front Neurosci. 2017;11:43. doi: 10.3389/fnins.2017.00043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mekle R, Kühn S, Pfeiffer H, Aydin S, Schubert F, Ittermann B. Detection of metabolite changes in response to a varying visual stimulation paradigm using short-TE 1H. MRS at 7 T. NMR Biomed. 2017;30(2) doi: 10.1002/nbm.3672. [DOI] [PubMed] [Google Scholar]
- Mody I, De Koninck Y, Otis TS, Soltesz I. Bridging the cleft at GABA synapses in the brain. Trends Neurosci. 1994;17(12):517–525. doi: 10.1016/0166-2236(94)90155-4. [DOI] [PubMed] [Google Scholar]
- Molaee-Ardekani B, Benquet P, Bartolomei F, Wendling F. Computational modeling of high-frequency oscillations at the onset of neocortical partial seizures: from ’altered structure’ to ’dysfunction. Neuroimage. 2010;52(3):1109–1122. doi: 10.1016/j.neuroimage.2009.12.049. [DOI] [PubMed] [Google Scholar]
- Molaee-Ardekani B, Márquez-Ruiz J, Merlet I, Leal-Campanario R, Gruart A, Sánchez-Campusano R, Birot G, Ruffini G, Delgado-García JM, Wendling F. Effects of transcranial Direct Current Stimulation (tDCS) on cortical activity: a computational modeling study. Brain Stimul. 2021;6(1):25–39. doi: 10.1016/j.brs.2011.12.006. [DOI] [PubMed] [Google Scholar]
- Mountcastle VB. The columnar organization of the neocortex. Brain. 1997;120:701–722. doi: 10.1093/brain/120.4.701. [DOI] [PubMed] [Google Scholar]
- Mullins PG, Rowland LM, Jung RE, Sibbitt WL., Jr A novel technique to study the brain’s response to pain: proton magnetic resonance spectroscopy. Neuroimage. 2005;26(2):642–646. doi: 10.1016/j.neuroimage.2005.02.001. [DOI] [PubMed] [Google Scholar]
- Mullins PG. Towards a theory of functional magnetic resonance spectroscopy (fMRS): a meta-analysis and discussion of using mrs to measure changes in neuro-transmitters in real time. Scand J Psychol. 2018;59:91–103. doi: 10.1111/sjop.12411. [DOI] [PubMed] [Google Scholar]
- Olsen RW, DeLorey TM. In: 6th edition. Siegel GJ, Agranoff BW, Albers RW, et al., editors. Philadelphia: Lippincott-Raven; 1999. Chapter 16. GABA and Glycine in: Basic neurochemistry: Molecular, cellular and medical aspects. [Google Scholar]
- Otis TS, Wu YC, Trussell LO. Delayed clearance of transmitter and the role of glutamate transporters at synapses with multiple release sites. J Neurosci. 1996;16(5):1634–1644. doi: 10.1523/JNEUROSCI.16-05-01634.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel HJ, Romanzetti S, Pellicano A, Nitsche MA, Reetz K, Binkofski F. Proton magnetic resonance spectroscopy of the motor cortex reveals long term GABA change following anodal transcranial direct current stimulation. Sci Rep. 2019;9(1):2807. doi: 10.1038/s41598-019-39262-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petroff OAC, Burlina AP, Black J, Prichard JW. Quantitative analysis of rat synaptosomes and cerebrum using high-resolution 1h magnetic resonance spectroscopy. Clin Chim Acta. 1992;206(1–2):137–146. doi: 10.1016/0009-8981(92)90014-H. [DOI] [PubMed] [Google Scholar]
- Petroff OA, Errante LD, Rothman DL, Kim JH, Spencer DD. Glutamate-glutamine cycling in the epileptic human hippocampus. Epilepsia. 2002;43(7):703–710. doi: 10.1046/j.1528-1157.2002.38901.x. [DOI] [PubMed] [Google Scholar]
- Petroff OAC. GABA And glutamate in the human brain. Neuroscientist. 2002;8(6):562–573. doi: 10.1177/1073858402238515. [DOI] [PubMed] [Google Scholar]
- Pirttilä TR, Hakumäki JM, Kauppinen RA. 1H nuclear magnetic resonance spectroscopy study of cerebral glutamate in an ex vivo brain preparation of guinea pig. J Neurochem. 1993;60(4):1274–1282. doi: 10.1111/j.1471-4159.1993.tb03287.x. [DOI] [PubMed] [Google Scholar]
- Pospischil P, Toledo-Rodriguez M, Monier C, Piwkowska Z, Bal T, Frégnac Y, Markram H, Destexhe A. Minimal hodgkin bhuxley type models for different classes of cortical and thalamic neurons. Biol Cybern. 2008;99:427–441. doi: 10.1007/s00422-008-0263-8. [DOI] [PubMed] [Google Scholar]
- Rae CD. A guide to the metabolic pathways and function of metabolites observed in human brain 1H magnetic resonance spectra. Neurochem Res. 2014;39(1):1–36. doi: 10.1007/s11064-013-1199-5. [DOI] [PubMed] [Google Scholar]
- Rahman A, Lafon B, Bikson M. Multilevel computational models for predicting the cellular effects of noninvasive brain stimulation. Prog Brain Res. 2015;222:25–40. doi: 10.1016/bs.pbr.2015.09.003. [DOI] [PubMed] [Google Scholar]
- Ramadan S, Lin A, Stanwell P. Glutamate and glutamine: a review of in vivo MRS in the human brain. NMR Biomed. 2013;26(!2):1630–1646. doi: 10.1002/nbm.3045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez R, Tuckwell HC. Statistical properties of stochastic nonlinear dynamical models of single spiking neurons and neural networks. Phys Rev E. 1996;54:5585. doi: 10.1103/PhysRevE.54.5585. [DOI] [PubMed] [Google Scholar]
- Rodriguez R, Tuckwell HC. Noisy spiking neurons and networks: useful approximations for firing probabilities and global behavior. BioSystems. 1998;48(1–3):187–194. doi: 10.1016/S0303-2647(98)00065-3. [DOI] [PubMed] [Google Scholar]
- Rothman DL, Sibson NR, Hyder F, Shen J, Behar KL, Shulman RG. In vivo nuclear magnetic resonance spectroscopy studies of the relationship between the glutamate-glutamine neurotransmitter cycle and functional neuroenergetics. Philos Trans R Soc Lond B Biol Sci. 1999;354:1165–1177. doi: 10.1098/rstb.1999.0472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman DL, Behar KL, Hyder F, Shulman RG. In vivo NMR studies of the glutamate neurotransmitter flux and neuroenergetics: implications for brain function. Ann Rev Physiol. 2003;65(1):401–427. doi: 10.1146/annurev.physiol.65.092101.142131. [DOI] [PubMed] [Google Scholar]
- Sánchez-León CA, Cordones I, Ammann C, Ausín JM, Gómez-Climent MA, Carretero-Guillén A, Sánchez-Garrido Campos G, Gruart A, Delgado-García JM, Cheron G, Medina JF, et al. Immediate and after effects of transcranial direct-current stimulation in the mouse primary somatosensory cortex. Sci Rep. 2021;11(3123) doi: 10.1038/s41598-021-82364-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Südhof TC. In: Basic Neurochemistry: Molecular, Cellular and Medical Aspects. 6th edition. Siegel GJ, Agranoff BW, Albers RW, et al., editors. Philadelphia: Lippincott-Raven; 1999. Composition of Synaptic Vesicles. [Google Scholar]
- Schaller B, Mekle R, Xin L, Kunz N, Gruetter R. Net increase of lactate and glutamate concentration in activated human visual cortex detected with magnetic resonance spectroscopy at 7 Tesla. J Neurosci Res. 2013;91(8):1076–1083. doi: 10.1002/jnr.23194. [DOI] [PubMed] [Google Scholar]
- Schousboe A. Transport and metabolism of glutamate and gaba in neurons and glial cells. Intl Rev Neurobiol. 1981;22:1–45. doi: 10.1016/s0074-7742(08)60289-5. [DOI] [PubMed] [Google Scholar]
- Shen J, Petersen KF, Behar KL, Brown P, Nixon TW, Mason GF, Petroff O, Shulman GI, Shulman RG, Rothman DL. Determination of the rate of the glutamate/glutamine cycle in the human brain by in vivo 13C NMR. Proc Natl Acad Sci USA. 1999;96(14):8235–8240. doi: 10.1073/pnas.96.14.8235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sibson NR, Dhankhar A, Mason GF, Behar KL, Rothman DL, Shulman RG. In vivo 13C NMR measurements of cerebral glutamine synthesis as evidence for glutamate glutamine cycling. Proc Natl Acad Sci USA. 1997;94(6):2699–2704. doi: 10.1073/pnas.94.6.269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sibson NR, Dhankhar A, Mason GF, Rothman DL, Behar KL, Shulman RG. Stoichiometric coupling of brain glucose metabolism and glutamatergic neuronal activity. Proc Natl Acad Sci USA. 1998;95:316–321. doi: 10.1073/pnas.95.1.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Somogyi P, Tamas G, Lujan R, Buhl EH. Salient features of synaptic organisation in the cerebral cortex. Brain Res Revs. 1998;26(2–3):113–115. doi: 10.1016/s0165-0173(97)00061-1. [DOI] [PubMed] [Google Scholar]
- Song Y, Yao M, Kemprecos H, Byrne A, Xiao Z, Zhang Q, Singh A, Wang J, Chen Z. Predictive coding models for pain perception. J Comp Neurosci. 2021;49:107–127. doi: 10.1007/s10827-021-00780-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonnewald U, McKenna M. Metabolic compartmentation in cortical synaptosomes: influence of glucose and preferential incorporation of endogenous glutamate into GABA. Neurochem Res. 2002;27(1):43–50. doi: 10.1023/A:1014846404492. [DOI] [PubMed] [Google Scholar]
- Sonnewald U, Westergaard N, Schousboe A, Svendsen JS, Unsgård G, Petersen SB. Direct demonstration by [13C]NMR spectroscopy that glutamine from astrocytes is a precursor for GABA synthesis in neurons. Neurochem Int. 1993;22(1):19–29. doi: 10.1016/0197-0186(93)90064-c. [DOI] [PubMed] [Google Scholar]
- Sonnewald U. Glutamate synthesis has to be matched by its degradation where do all the carbons go? J Neurochem. 2014;131(4):399–406. doi: 10.1111/jnc.12812. [DOI] [PubMed] [Google Scholar]
- Stagg CJ, Best JG, Stephenson MC, O’Shea J, Wylezinska M, Kincses T, Morris PG, Matthews PM, Johansen-Berg H. Polarity-sensitive modulation of cortical neurotransmitters by transcranial stimulation. J Neurosci. 2009;29(16):5202–5206. doi: 10.1523/JNEUROSCI.4432-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stagg CJ, Bachtiar V, Johansen-Berg H. The role of GABA in human motor learning. Curr Biol. 2011;21(6):480–484. doi: 10.1016/j.cub.2011.01.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens CF, Tsujimoto T. Estimates for the pool size of releasable quanta at a single central synapse and for the time required to refill the pool. Proc Natl Acad Sci USA. 1995;92(3):846–849. doi: 10.1073/pnas.92.3.846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szentágothai J. The modular architectonic principle of neural centers. Rev Phys Biochem Pharmacol. 1983;98:11–61. doi: 10.1007/BFb0033866. [DOI] [PubMed] [Google Scholar]
- Taylor R, Neufeld R, Schaefer B, Densmore M, Rajakumar N, Osuch E, Williamson P, Théberge J. Functional magnetic resonance spectroscopy of glutamate in schizophrenia and major depressive disorder: anterior cingulate activity during a color-word stroop task. NPJ Schizophr. 2015;1:15028. doi: 10.1038/npjschz.2015.28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Théberge J, Bartha R, Drost D, Menon R, Malla A, Takhar J, Neufeld R, Rogers J, Pavlosky W, Schaefer B, Densmore M, Al-Semaan Y, Williamson P. Glutamate and glutamine measured with 4.0 T proton MRS in never-treated patients with schizophrenia and healthy volunteers. Am J Psychiatry. 2002;159(11):1944–1946. doi: 10.1176/appi.ajp.159.11.1944. [DOI] [PubMed] [Google Scholar]
- Thompson SM. Modulation of inhibitory synaptic transmission in the hippocampus. Progr Neurobiol. 1994;42(5):575–609. doi: 10.1016/0301-0082(94)90044-2. [DOI] [PubMed] [Google Scholar]
- Tranchina D, Nicholson C. A model for the polarization of neurons by extrinsically applied electric fields. Biophys J. 1986;50(6):1139–1156. doi: 10.1016/S0006-3495(86)83558-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks M, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci USA. 1997;94(2):719–723. doi: 10.1073/pnas.94.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks M, Pawelzik K, Markram H. Neural networks with dynamic synapses. Neural Comput. 1998;10(4):821–835. doi: 10.1162/089976698300017502. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12(1):1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik. 1973;13:55–80. doi: 10.1007/BF00288786. [DOI] [PubMed] [Google Scholar]
- Wilson HR. Computational evidence for a rivalry hierarchy in vision. Proc Natl Acad Sci USA. 2003;100(24):14499–14503. doi: 10.1073/pnas.2333622100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandt BJ, Visser S, van Putten M, ten Haken B. A neural mass model based on single cell dynamics to model pathophysiology. J Comp Neurosci. 2014;37:549–568. doi: 10.1007/s10827-014-0517-5. [DOI] [PubMed] [Google Scholar]
- Zhao X, Ding J, Pan H, Zhang S, Pan D, Yu H, Ye Z, Hua T. Anodal and cathodal tDCS modulate neural activity and selectively affect GABA and glutamate syntheses in the visual cortex of cats. J Physiol. 2020;598:3727–3745. doi: 10.1113/JP279340. [DOI] [PubMed] [Google Scholar]
- Zou Q, Destexhe A. Kinetic models of spike-timing dependent plasticity and their functional consequences in detecting correlations. Biol Cybern. 2007;97(1):81–97. doi: 10.1007/s00422-007-0155-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.