A synergistic core for human brain evolution and cognition

Abstract

How does the organisation of neural information-processing enable humans’ sophisticated cognition? Here we decompose functional interactions between brain regions into synergistic and redundant components, revealing their distinct information-processing roles. Combining functional and structural neuroimaging with meta-analytic results, we demonstrate that redundant interactions are predominantly associated with structurally-coupled, modular sensorimotor processing. Synergistic interactions instead support integrative processes and complex cognition across higher-order brain networks. The human brain leverages synergistic information to a greater extent than non-human primates, with high-synergy association cortices exhibiting the highest degree of evolutionary cortical expansion. Synaptic density mapping from Positron Emission Tomography and convergent molecular and metabolic evidence demonstrate that synergistic interactions are supported by receptor diversity and human-accelerated genes underpinning synaptic function. This information-resolved approach provides analytic tools to disentangle information integration from coupling, enabling richer, more accurate interpretations of functional connectivity, and illuminating how the human neurocognitive architecture navigates the trade-off between robustness and integration.

Introduction

In theoretical and cognitive neuroscience, considering the human brain as a distributed information-processing system has emerged as a powerful framework to understand the neural basis of cognition ¹. However, information is not all the same: rather, several fundamentally distinct kinds of information can be discerned, each providing specific advantages ^2–4. Therefore, in order to properly understand any information-processing architecture - including the human brain - it is necessary to provide an account of what kind of information is being processed.

As an example, consider humans’ two main sources of information about the world: the eyes. Each eye provides some information about the periphery of the visual field, which the other eye cannot see. This is each eye’s “unique information”. In contrast, the information that we still have when we close either eye is known as “redundant” (or “shared”) information — because it is information that is provided equally by multiple sources (for instance, information about colour is largely redundant between the two eyes). Redundancy provides the system with robustness ⁵: we can still see with one eye closed, because the same information is largely available from the other eye. However, closing one eye also deprives us of stereoscopic information about depth. This information does not come from either eye alone: one needs both eyes working together, in order to perceive the third dimension through stereopsis. This is known as “synergistic” (or “complementary”) information between two sources: the extra advantage obtained from combining and integrating them, reflecting their complementary nature ^2,6.

Thus, beyond their own unique information, different sources can also provide redundant information (equally available from either source) or synergistic information (only available by combining both sources). This is a fundamental distinction because a system will not be able to perform cognitively useful computation, just by having several copies of the same information: computation and cognition demand that information should eventually be combined.

Crucially, synergy and redundancy are fundamental concepts that apply to any specific content that is being encoded, be it about an apple or a predator ⁷: they are fundamentally different kinds of information encoding. Thus, every information-processing system, including the human brain, needs to strike a balance between these distinct kinds of information and the specific advantages they provide: robustness and integration, respectively ^3,8–10. Therefore, understanding how the human brain navigates the trade-off between these different kinds of information could provide fundamental insights about its information-processing architecture.

However, synergistic and redundant information cannot be adequately captured by traditional measures of “functional connectivity” (FC) in the human brain, which simply quantify the similarity between regional activity ^6,11,12; nor by approaches focused on capturing the direction of information transfer from one region to another ^13,14. Hence, it is currently unknown to what extent the human brain differentially relies on synergistic versus redundant information for processing, and to what extent the involvement of these different kinds of information varies across distinct macroscale neural systems and cognitive domains.

Here, we address these fundamental questions in neuroscience by providing an “information-resolved” framework to decompose the intrinsic information flow within the brain’s BOLD signals ^6,9,15,16, in order to quantify synergistic and redundant interactions based on the recently developed Integrated Information Decomposition ⁶. This approach regards the brain as a dynamical system, whose temporal evolution is influenced by the current state of its constituent parts (brain regions) and their interactions. This means that the brain’s current state intrinsically carries information about its own future - information that we can decompose into synergistic and redundant contributions. Specifically, we quantify redundancy as information about the system’s future that is equally available from the current state of each of the parts (brain regions). In contrast, synergy is quantified as the additional information arising from the interactions between regions ⁶. Crucially, this mathematical definition indicates that synergy provides a rigorous quantification of how brain regions mutually influence each other’s activity over time: that is, the integration of information between those regions.

Therefore, our information-resolved approach to functional interactions in the brain contributes to reducing the gap between a fundamental concept of interest in neuroscience - integration of information - and neuroscientists’ practical ability to quantify it at the macroscale. Although appealing for its conceptual simplicity, traditional FC essentially reflects the similarity between regions’ temporal fluctuations, and therefore it is further removed from the phenomenon of theoretical interest: integration of information. It is helpful to compare our approach to dynamic functional connectivity analysis. Dynamic functional connectivity goes beyond traditional “static” FC, by demonstrating that static FC in fact comprises distinct time-resolved patterns, with distinct roles for cognition ^17–20. Analogously, Integrated Information Decomposition provides insights over and above those offered by traditional FC, because it reveals distinct information-resolved connectivity patterns that could not be discerned from traditional FC. More specifically, synergy corresponds to information that only becomes available when the activity of different regions is considered together (reflecting the value of integration), and redundancy to information that is available from multiple brain regions (providing robustness) ⁶.

By providing both a richer conceptual framework and widely applicable computational tools to disentangle different kinds of interactions, our information-resolved approach simultaneously highlights and overcomes some of the fundamental limitations of traditional FC analysis. Its richer perspective on neural information dynamics offers the opportunity to investigate the information-processing principles that govern how cognitive functions arise from the brain’s neural architecture. In this work, we investigate how synergistic and redundant information are organised with respect to the human neurocognitive architecture. Specifically, we seek to establish whether the extent of their involvement varies consistently with the functional roles of well-known macroscale neural systems, and whether studying brain function in terms of synergistic and redundant information provides a fertile new perspective complementing our current understanding of the functional organisation of the brain. Combining multimodal neuroimaging (functional, structural and diffusion MRI, PET) with cytoarchitectonics, in vitro autoradiography, and genetic evidence, here we reveal the organisation and neurobiological underpinnings of synergy and redundancy. Comparing the brains of humans and non-human primates, we further demonstrate the involvement of synergy in humans’ sophisticated cognitive abilities and also in the evolution of the human brain.

Results

Information decomposition

We developed an information-resolved approach for the analysis of macroscale functional interactions in brain dynamics, to investigate how synergistic and redundant information are organised in the human brain, their functional significance, and the neurobiology that supports them. Shannon’s mutual information quantifies the interdependence between two random variables X and Y. Put simply, the mutual information I(X;Y) quantifies the information that source variable X provides about target variable Y ²¹. Partial Information Decomposition (PID) extends Shannon’s theory, showing that the information that two source variables X and Y give about a third target variable Z, I(X,Y; Z), can be decomposed into three conceptually distinct kinds of information: information provided by one source but not the other (unique information), or by both sources separately (redundant information), or jointly by their combination (synergistic information) ². Integrated Information Decomposition ⁶ provides a further extension, but in time. Consider a system X comprised of two parts evolving jointly over time, $X_t=\{X_t^1,X_t^2\}$ — in our case, this corresponds to the timeseries of the BOLD activity of two brain regions. The amount of information flowing from the system’s past to its future is known as the time-delayed mutual information (TDMI) ⁶ and given by $I(X_{t-\tau }^1,X_{t-\tau }^2;X_t^1,X_t^2).$ The fundamental advancement offered by Integrated Information Decomposition ⁶ is to decompose TDMI into redundant, unique, and synergistic information shared with respect to both past and present state of both variables (Methods). Here, we focus on the temporally persistent redundancy and synergy. As interdependencies between the past and present states of both X_t and Y_t, synergy and redundancy capture phenomena that are not assessed by approaches focused on the transfer of information from the past of one to the present of the other; therefore, they are distinct from (and complementary to) alternative information-theoretic measures such as transfer entropy ^13,14.

Distinct neuroanatomical profiles for synergy and redundancy

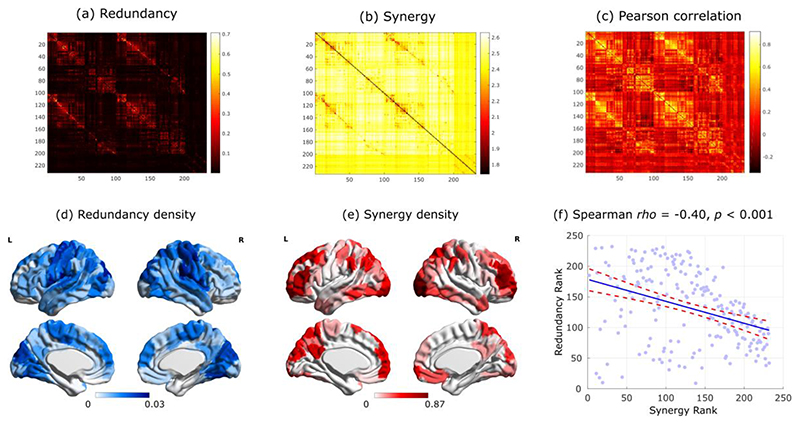
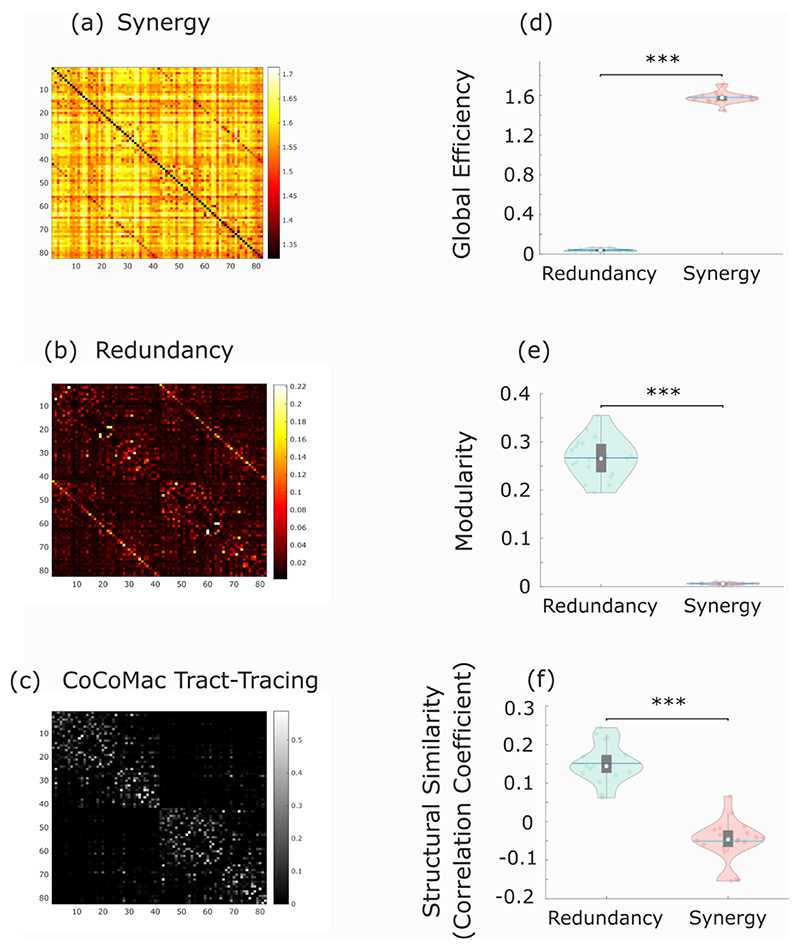
Here, we applied Integrated Information Decomposition to resting-state functional MRI data from 100 Human Connectome Project subjects, allowing us to quantify how much information about the brain’s future trajectory is carried redundantly by distinct brain regions, and how much of it is carried by the synergy between regions. Distinguishing synergistic and redundant interactions between the BOLD timeseries of each pair of 232 cortical and subcortical brain regions, we reveal that synergy and redundancy are distributed following distinct patterns across the human brain (Fig. 1a,b). In particular, we show that the organisation of redundancy between pairs of brain regions is significantly more similar to traditional functional connectivity (Pearson correlation) than synergy: pairs of regions with more correlated time-courses are more likely to provide redundant information, and less likely to provide synergistic information (Fig. 1c and Extended Data Fig. 1). Note that synergy and redundancy do not need to be anticorrelated, at a theoretical level, and models can be constructed where e.g. both increase, or where one changes while the other remains constant ²²

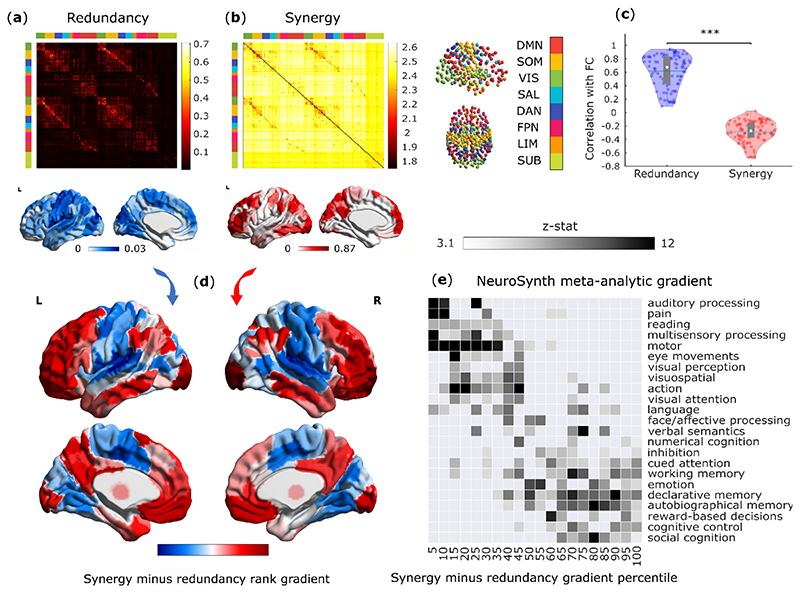
Fig. 1. Synergistic and redundant networks exhibit distinct anatomical and cognitive profiles.

(a,b) Group-average matrices display the redundant (a) and synergistic (b) interactions between each pair of brain regions (note that colorbars do not include entries on the diagonal). Brain plots show the cortical distribution of the strongest redundant (blue) and synergistic (red) connections (thresholded to retain the top 5% of connections, for display purposes only). (c) Subject-specific Pearson correlation values of synergy and redundancy matrices with the matrix of traditional functional connectivity (Redundancy: M=0.62, SD=0.24; Synergy: M=-0.29, SD=0.16; t(99)=24.06, p<0.001, Hedges’s g=4.39, effect size CI: [3.88, 5.11], from paired-sample non-parametric permutation t-test (two-sided); n=100 unrelated HCP subjects). Note that the relationships of redundancy and synergy with traditional FC are not equal: the absolute value of the correlation is significantly stronger for redundancy than for synergy (Redundancy: M=0.62, SD=0.24; Synergy: M=0.29, SD=0.16; t(99)=20.35, p<0.001, Hedges’s g=1.65, effect size CI: [1.36, 1.92], from paired-sample non-parametric permutation t-test (two-sided); n=100 unrelated HCP subjects). Violin plots: each colored circle represents one subject; white circle: median; blue line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001. (d) Brain surface projections of regional redundancy-to-synergy gradient scores, based on the respective ranks. These ranks exhibit an inverse correlation (Spearman’s p = -0.40, p < 0.001; Extended Data Fig. 1). (e) NeuroSynth term-based meta-analysis, relating the distribution of redundancy-to-synergy gradient across the brain to a cognitive gradient of cognitive domains, from lower-level sensorimotor processing to higher-level cognitive tasks. These results are robust to the use of different parcellations (cortical-only, having lower or higher number of nodes, and obtained from anatomical rather than functional considerations; Extended Data Fig. 2a,b). Likewise, although these results were obtained after deconvolving the hemodynamic response function from the BOLD signals to account for regional variations (Methods), analogous results are also obtained when this step is omitted, or if synergy and redundancy are computed from discretised rather than continuous data (Extended Data Fig. 2c,d).

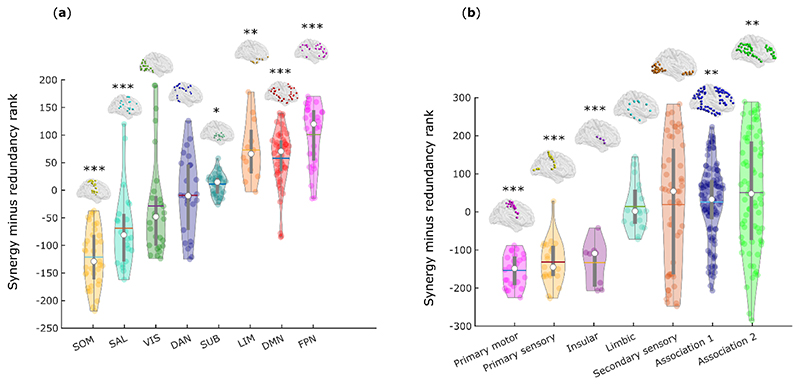
We ranked each brain region separately in terms of how synergistic and redundant its interactions with other brain regions are; the difference between these ranks (synergy minus redundancy) determines the relative relevance of a given region for synergistic versus redundant processing, thereby defining a redundancy-to-synergy gradient across brain regions (Fig. 1d). The results of our information-resolved analysis reveal that redundant interactions are especially prominent in the brain’s somatomotor and salience subnetworks, and most visual regions (Fig. 2a), corresponding to primary sensory, primary motor and insular cortices, in terms of Von Economo’s cytoarchitectonic classification ²³ (Fig. 2b). In contrast, regions with higher relative importance for synergy predominate in higher-order association cortices, and are affiliated with the default mode (DMN), fronto-parietal executive control (FPN) and “limbic” (orbitofrontal cortex and temporal poles) subnetworks ²⁴ (Fig. 2a,b).

Fig. 2. Distinct cytoarchitectonic and resting-state network profiles for synergy-dominated and redundancy-dominated regions.

(a) Regional redundancy-to-synergy gradient values for each canonical resting-state network, based on the definition of Yeo et al. (2011) ²². DMN, default mode network. SOM, somatomotor network. VIS, visual network. SAL, salience/ventral attention network; DAN, dorsal attention network. FPN, fronto-parietal executive control network. LIM, limbic network. SUB, subcortical network. (b) Regional redundancy-to-synergy gradient values for each of seven cytoarchitectonic classes (the five canonical classes identified by Von Economo, plus limbic and insular cortices), for 308 cortical ROIs of equal size (500 mm2), obtained from subdivisions of the Desikan-Killiany cortical parcellation ²¹. For both panels, each colored circle represents one brain region; panel (a), n=232 regions divided into 8 resting-state networks; panel (b), n=308 regions divided into 7 cytoarchitectonic classes. Each violin plot shows the distribution of brain regions assigned to the subnetwork or cytoarchitectonic class indicated on the x-axis (for each panel, each region is assigned exactly once). White circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; * p < 0.05; ** p < 0.01; *** p < 0.001 from one-sample non-parametric permutation t-test (two-sided), corrected for multiple comparisons using the False Discovery Rate. Full statistical results are shown in Supplementary Table 1 (Yeo RSN) and Supplementary Table 2 (Von Economo).

The distinct subnetwork affiliations and cytoarchitectonic profiles further suggest that redundant and synergistic interactions may be involved with radically different cognitive domains. To empirically validate this hypothesis, we performed a term-based meta-analysis using NeuroSynth, which is widely used to characterise macroscale brain patterns in terms of cognitive relevance ^25–28. NeuroSynth enables automated probabilistic mappings between broad cognitive domains and neural patterns, by synthesizing thousands of published fMRI studies ²⁸. We employed 24 topic terms used by previous studies 26,28, which range from lower sensorimotor functions (e.g. eye movement, motion, visual and auditory perception) to higher cognitive functions (e.g. attention, working memory, social and numerical cognition). The redundancy-to-synergy gradient identified in terms of regional rank differences was then related to these 24 terms ^25,27.

Supporting the inference from neuroanatomy to cognition, our results reveal that the regional gradient from redundancy to synergy corresponds to a gradient from lower sensorimotor functions to higher cognitive ones, requiring the integration of complex information. Specifically, high-redundancy regions loaded strongly onto auditory, visual and multisensory processing and motion. In contrast, high-synergy regions had the strongest loadings onto social cognition, memory and cognitive control (Fig. 1e).

Distinct graph-theoretic profiles for synergy and redundancy

From a theoretical standpoint, sensorimotor and higher-order cognitive functions impose distinct and opposite demands on cognitive architectures: sensory processing benefits from segregation of the whole network into segregated modules, whereas integration of information demands a highly interconnected network organisation ^9,29.

The set of all synergistic (respectively, redundant) interactions between pairs of brain regions can be viewed as a whole-brain network, whereby each node is a region, and each edge represents the synergistic (respectively, redundant) information between two regions. This makes it possible to combine the advantages of our information-resolved analysis with the powerful mathematics of graph theory ³⁰, to obtain insights into the network organisations of synergistic and redundant interactions in the human brain. Indeed, combining Integrated Information Decomposition with subsequent graph-theoretical analysis of the resulting synergistic and redundant whole-brain networks, reveals how the human brain resolves the tension between specialised processing and global integration.

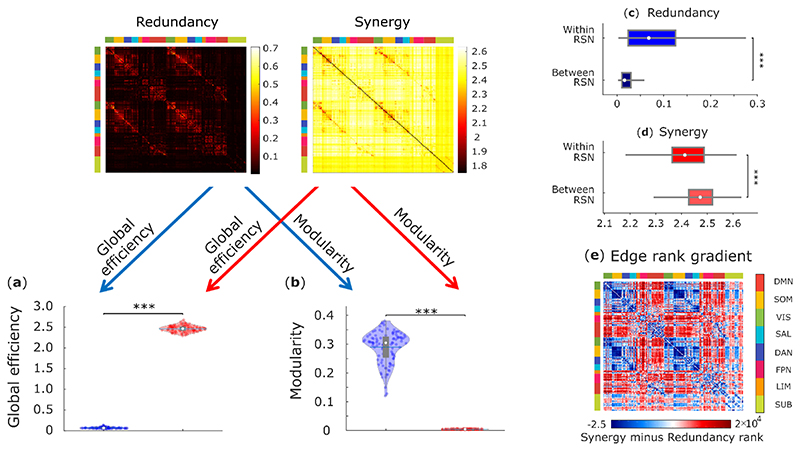
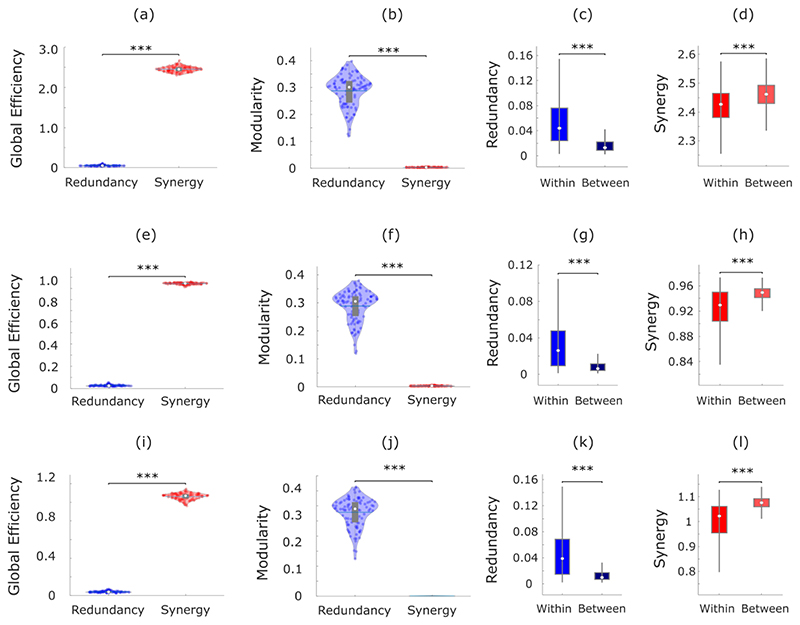
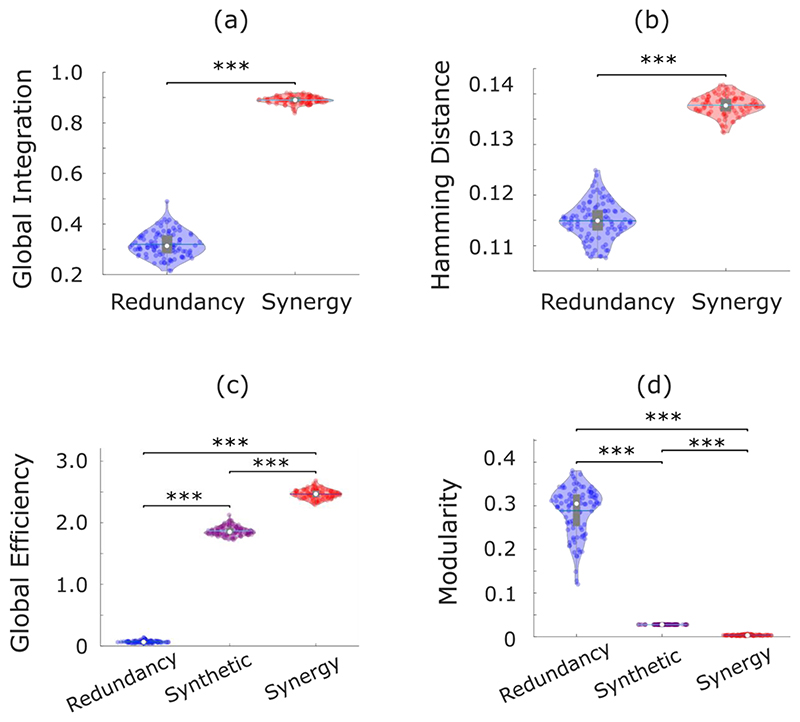
Across individuals, the whole-brain network of synergistic interactions is more highly interconnected and globally efficient than the corresponding whole-brain network defined by the redundancy between brain regions, owing to the high strength of synergistic connections (Fig. 3a). In contrast, redundant interactions delineate a network characterised by a highly modular structure, which is virtually absent in the network of synergistic interactions across the brain (Fig. 3b). Thus, when viewed through the lens of graph theory, the whole-brain networks of synergistic and redundant interactions exhibit distinct graph-theoretical properties, favouring global and segregated processing, respectively – as demanded by the cognitive functions they support.

Fig. 3. Network analysis indicates global and segregated processing for synergy and redundancy, respectively.

(a) The whole-brain network organization of synergistic interactions exhibits significantly higher global efficiency than the whole-brain network of redundant interactions (Synergy: M=2.47, SD=0.08; Redundancy: M=0.07, SD=0.02; t(99)=-285.75, p<0.001, Hedges’s g=-43.58, effect size CI: [-50.46, -38.75], from paired-sample non-parametric permutation t-test (two-sided); n = 100 unrelated HCP subjects). (b) The whole-brain network of redundant interactions exhibits significantly higher segregation (modularity) than the network of synergistic interactions (Synergy: M=0.003, SD=0.001; Redundancy: M=0.29, SD=0.05; t(99)=52.12, p<0.001, Hedges’s g=7.28, effect size CI: [6.22, 8.85], from paired-sample non-parametric permutation t-test (two-sided); n = 100 unrelated HCP subjects). For the violin plots in both (a) and (b), each colored circle represents one subject; white circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001. (c) Redundant connections are significantly stronger within functional resting-state subnetworks than between them (Within-RSN: M=0.087, SD=0.078, n=7178 within-RSN connections; Between-RSN: M=0.026, SD=0.027, n=46414 between-RSN connections; t(53590)=127.45, p<0.001, Hedges’s g=1.61, effect size CI: [1.58, 1.66]; from two-sample non-parametric permutation t-test (two-sided)). (d) Synergistic connections are significantly stronger between functional resting-state subnetworks than within them (Within-RSN: M=2.41, SD=0.09, n=7178 within-RSN connections; Between-RSN: M=2.47, SD=0.06, n=46414 between-RSN connections; t(53590)= -75.31, p<0.001, Hedges’s g=-0.96, effect size CI: [-0.99, -0.92]; from two-sample non-parametric permutation t-test (two-sided)). For the box-plots in both (c) and (d): white circle represents the median; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range. (e) Matrix of redundancy-to-synergy gradient scores for each connection between brain regions, highlighting regions’ affiliation with the resting-state subnetworks of Yeo et al. (2011). Red indicates synergy > redundancy. These results are robust to the use of alternative ways of defining nodes and edges, and alternative network measures (Extended Data Fig. 3-5 and Supplementary Tables 3-4).

Complementing this graph-theoretical analysis, we show that redundant interactions tend to be stronger within resting-state subnetworks than between them (Fig. 3c), whereas the opposite is true for synergistic interactions (Fig. 3d), which are stronger across different resting-state subnetworks, especially between DMN/FPN and other subnetworks (Fig. 3e). These results indicate that brain regions can rely on redundant information to interact within their own segregated subnetwork, while simultaneously supporting integrated processing across subnetworks through synergistic interactions.

Distinct structural support for synergy and redundancy

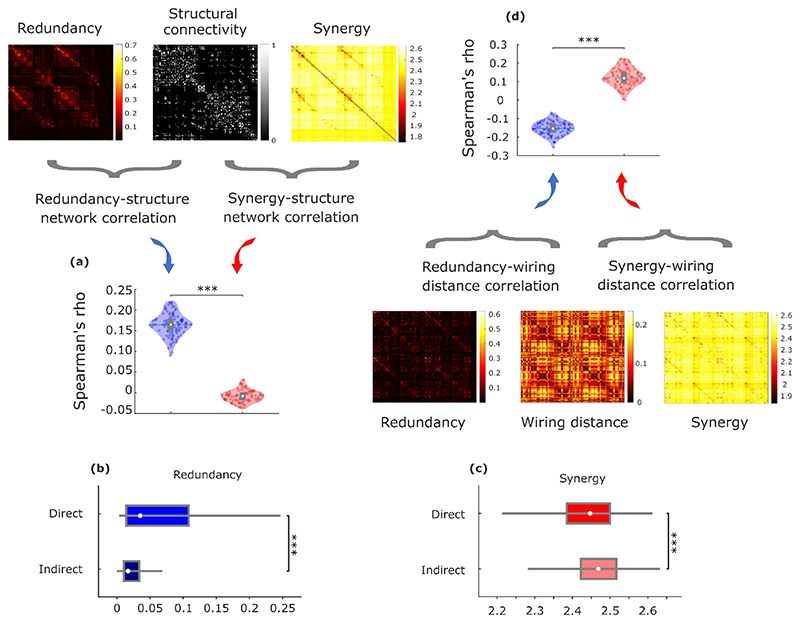
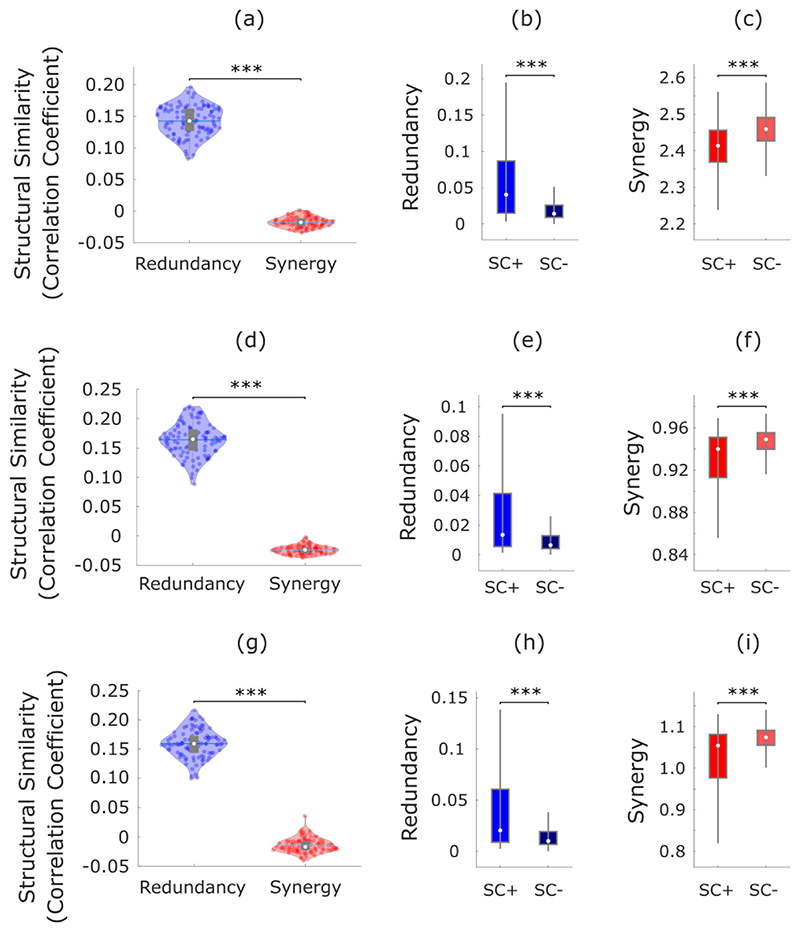
Since only a subset of brain regions are directly connected by white matter tracts ²⁹, we reasoned that the more an organism’s survival depends on interactions between regions A and B, the more we may expect A and B to be directly physically connected, rather than relying on intermediate polysynaptic connections. Thus, direct anatomical connections may be understood as revealing where the brain’s need for robust communication is highest. Consequently, if redundant interdependencies provide robustness to the system (since they correspond to information that is not contingent on any single brain region), they should be co-located with underlying direct structural connections. Our results support this hypothesis: across subjects, the number of white matter streamlines (quantified using diffusion-weighted imaging) was significantly more correlated with redundant than synergistic interactions between regions (Fig. 4a).

Fig. 4. Redundant interactions are supported by anatomical connections, synergistic interactions connect regions with distinct structural wiring profiles.

(a) Whole-brain networks of redundant interactions are significantly more correlated (average Spearman’s ρ) with underlying structural connectivity than synergistic interactions (Redundancy: M=0.16, SD=0.028; synergy: M=-0.008, SD=0.014; t(99)=48.67, p<0.001, Hedges’s g=7.79, effect size CI: [6.98, 8.92] from paired-sample non-parametric permutation t-test (two-sided); n=100 unrelated HCP subjects). (b) Redundant connections are significantly stronger in the presence of an underlying direct structural connection (Direct: M=0.074, SD=0.083, n=5276 direct connections; Indirect: M=0.029, SD=0.034, n=48548 indirect connections; t(53822)=73.38, p<0.001, Hedges’s g=1.06, effect size CI: [1.02, 1.11]). (c) Synergistic connections are significantly stronger between regions that do not share a direct structural connection (Direct: M=2.43, SD=0.10, n=5276 direct connections; Indirect: M=2.46, SD=0.18; t(53822)=-10.23, p<0.001, Hedges’s g=-0.15, effect size CI: [-0.17, -0.12] from two-sided non-parametric permutation t-test). These results are robust to the use of alternative ways of defining nodes and edges, and a different measure of structure-function coupling (Hamming distance) (Extended Data Fig. 4-5 and Supplementary Table 4). (d) Whole-brain networks of synergistic connections are significantly more associated than redundant networks with cortico-cortical wiring distance, a measure of dissimilarity between anatomical wiring that combines diffusion tractography, spatial proximity and microstructural profile similarity (note that this analysis was performed on a different parcellation; see Methods) (Redundancy: M=-0.15, SD=0.04; Synergy: M=0.12, SD=0.05; t(99)=-36.82, p<0.001, Hedges’s g= -6.43, effect size CI: [-7.30, -5.82] from paired-sample non-parametric permutation t-test (two-sided); n=100 unrelated HCP subjects). For the violin plots in (a) and (d), each colored circle represents one subject; white circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001. For the box-plots in (b) and (c): white circle represents the median; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001.

Having established that synergy and redundancy differ in their association with the underlying network of anatomical connections, we sought to obtain more fine-grained insights into their respective relationships with structural connectivity. To this end, we compared the values of redundancy (respectively, synergy) between regions that do (“Direct”) or do not (“Indirect”) have direct anatomical connections between them, as indicated by the presence of a white-matter tract between them, based on diffusion tractography. As expected from our previous analysis, we found that redundancy is relatively stronger in the presence of a direct anatomical connection (Fig. 4b). In contrast, we found that synergy is relatively stronger between regions that do not share a direct physical connection (Fig. 4c). These results are in line with recent evidence that regions that share a direct anatomical connection tend to be more similar in terms of the profile of dynamics they exhibit ³¹, corroborating our expectation of greater redundancy between them. Conversely, indirect (polysynaptic) connections offer greater opportunity for different information streams to become integrated along the way from region A to B, and become influenced by diverse modulatory factors - which should correspond to higher opportunity for synergy to occur.

More broadly, beyond the presence or absence of a direct connection between two regions, we reasoned that there will be greater scope for synergy between the activity of two brain regions if they are exposed to diverse inputs from the rest of the brain. On the other hand, similarity of inputs should favour the presence of redundant information. To test these hypotheses, we capitalised on a recently developed measure of multi-scale wiring distance between pairs of cortical regions, which combines diffusion tractography with geodesic distance (spatial proximity) and microstructural similarity ³². This measure of wiring distance quantifies the difference between regional profiles of structural connectivity, accounting for both long-range white matter pathways and short-range intracortical connections ³².

Corroborating our hypotheses, comparing the matrices of synergy and redundancy with cortico-cortical wiring distance shows that greater difference between the structural connectivity profiles of two regions diminishes the extent to which they hold the same information, but increases the potential for synergy between them (Fig. 4d).

Overall, redundant interactions demarcate a modular structural-functional backbone in the human brain, ensuring robust sensorimotor input-output channels, whereas synergistic interactions are poised to facilitate high-level cognition through globally efficient connections across different subnetworks, benefiting from diverse patterns of structural connections. Our approach reveals how the brain balances modular and global information processing in the service of different aspects of cognitive function.

Evolutionary potentiation of high-synergy brain regions

The association between synergistic information processing and higher cognitive functions, raises the intriguing possibility that the human brain may enable humans’ uniquely sophisticated cognitive capacities specifically in virtue of its highly synergistic nature. We pursued this hypothesis through three convergent approaches.

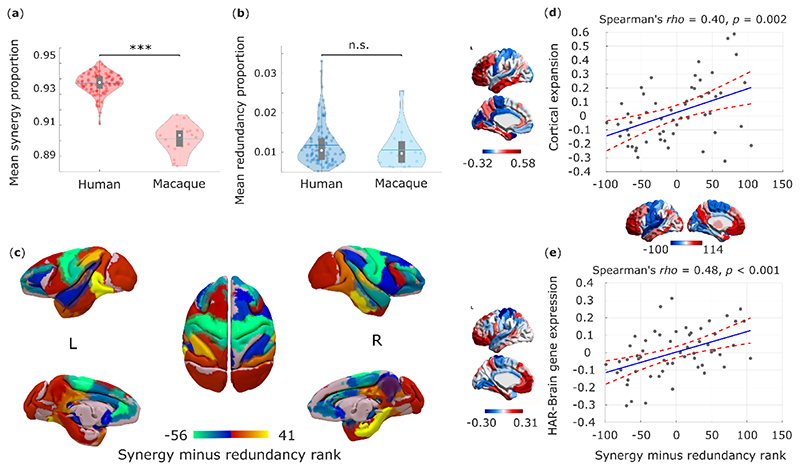
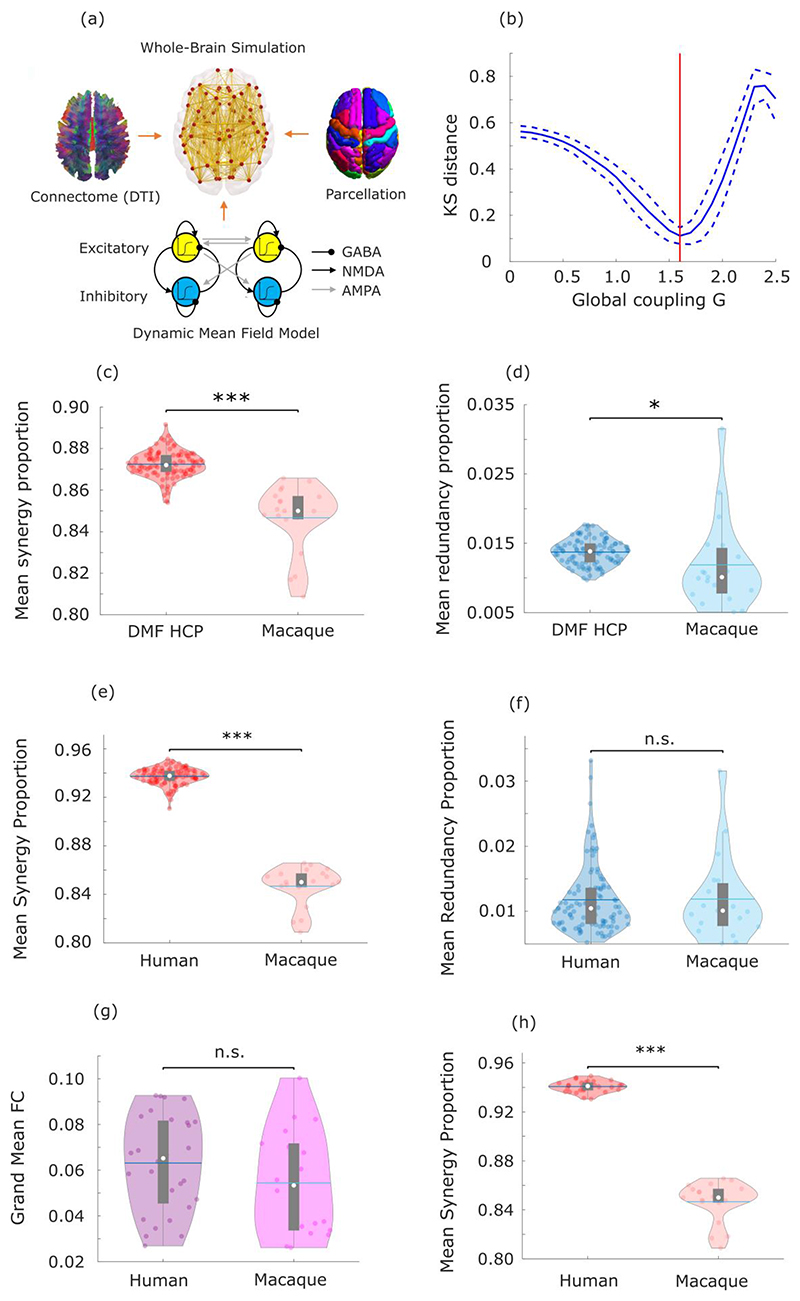
First, we show that the human brain is especially successful at leveraging synergistic information, compared with the brains of non-human primates. Synergistic interactions account for a higher proportion of total information flow in the human brain than in the macaque (Macaca mulatta) (Fig. 5a), whereas the two species’ brains are equal in terms of proportion of total information accounted for by redundancy (Fig. 5b). Further corroborating the key role of synergy, we show that the difference between humans and macaques in terms of synergy is significantly greater than the difference in total strength (grand mean of FC matrix) of functional connectivity, or in the global efficiency or modularity of FC networks (Supplementary Table 6). These results are also robust to the use of alternative analytic approaches (Supplementary Tables 7-9).

Fig. 5. Human brain evolution favoured high synergy.

(a) The proportion of synergistic interactions across the brain is significantly higher in humans (Homo sapiens) than macaques (Macaca mulatta) (Human M=0.937, SD=0.007; Macaque M=0.901, SD=0.009; t(117)=19.86, p<0.001, Hedges’s g=4.94, effect size CI: [4.12, 6.10], from two-sample non-parametric permutation t-test (two-sided). Human data: n=100 unrelated HCP subjects. Macaque data: n=19 distinct sessions from 10 individual macaques). (b) The proportion of redundant interactions across the brain is equivalent in humans and macaques (Redundancy: Human M=0.012, SD=0.005; Macaque M=0.011, SD=0.005; t(117)=0.90, p=0.372, Hedges’s g=0.22, effect size CI: [-0.28, 0.66], from two-sample non-parametric permutation t-test (two-sided). Human data: n=100 unrelated HCP subjects. Macaque data: n=19 distinct sessions from 10 individual macaques). White circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range. ***, p < 0.001; n.s., p > 0.05. Note that the proportion of synergy can differ even if the proportion of redundancy remains the same: as mentioned in the Introduction, synergy and redundancy are not the only constituent elements of total information flow in the system: each source (here, brain region) also brings a unique contribution ^2,6. The results presented here cannot be solely attributed to either the choice of bandpass filter, or the difference in TR between datasets (Extended Data Fig. 6). The proportion of synergistic information is significantly higher in humans than macaques even when the comparison is restricted only to those humans whose total FC strength is in the range of macaques values (Extended Data Fig. 6). (c) Surface projection of regional redundancy-to-synergy gradient scores for the macaque brain. Corresponding matrices of synergy and redundancy are shown in Extended Data Fig. 7. (d) Significant Spearman correlation (two-sided CI: [0.16, 0.59]) between human regional redundancy-to-synergy gradient scores and regional cortical expansion from chimpanzee (Pan troglodytes) to human (n=57 regions of the left hemisphere of the DK-114 atlas). This result is not due to spatial autocorrelation, as assessed using spin-based permutation testing; p_spin = 0.010. (e) Significant Spearman correlation (two-sided CI: [0.25, 0.66]) between human regional redundancy-to-synergy gradient scores and regional expression of brain-related human-accelerated (HAR-Brain) genes (n=57 regions of the left hemisphere of the DK-114 atlas). This result is not due to spatial autocorrelation, as assessed using spin-based permutation testing; p_spin = 0.002. These results are also robust to the use of unadjusted scores (Extended Data Fig. 8).

The patterns of synergy and redundancy in the macaque brain broadly resemble those observed in humans (Extended Data Fig. 7 and Supplementary Table 5), demonstrating their evolutionary stability – including the expected high redundancy in sensorimotor regions (Fig. 5c). However, redundancy is more prevalent than synergy in macaque prefrontal cortex (PFC), despite PFC being among the most synergy-dominated cortices in humans (Fig. 5c). Intriguingly, prefrontal cortex underwent substantial cortical expansion in the course of human evolution ³³.

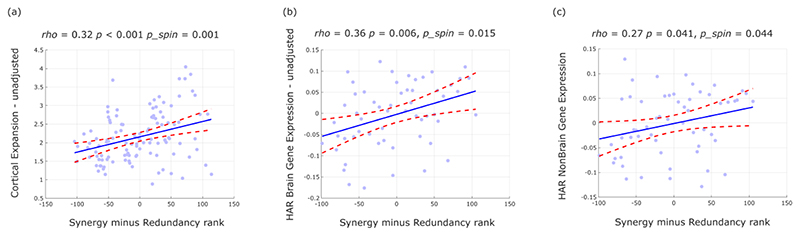
These findings suggest that the high synergy observed in human brains may be specifically related to evolutionary cortical expansion. To explore this hypothesis, we analysed cortical morphometry data from in vivo structural MRI, comparing humans and one of the closest evolutionary relatives of Homo sapiens: chimpanzees (Pan troglodytes) ³⁴. Supporting our hypothesis, we identified a significant positive correlation between relative cortical expansion in humans versus chimpanzees, and the gradient of regional prevalence of synergy previously derived from functional MRI (Fig. 5d). These findings suggest that the additional cortical tissue may be primarily dedicated to synergy, rather than redundancy.

To provide further support for the evolutionary relevance of synergistic interactions, we capitalised on human adult brain microarray datasets across 57 regions of the left cortical mantle, made available by the Allen Institute for Brain Science (AIBS) ³⁴. We demonstrate that regional predominance of synergy correlates with regional expression of genes that are both (i) related to brain development and function, including intelligence and synaptic transmission ³⁴; and (ii) selectively accelerated in humans versus non-human primates ³⁴ (“HAR-Brain genes”; Fig. 5e). Thus, the more prominent a brain region is in terms of synergy, the more likely it is to express brain genes that are uniquely human.

Taken together, these findings provide converging evidence that human brain evolution may have resulted in the increased prominence of synergistic interactions, in terms of dedicated genes, (Fig. 5e) dedicated cortical real estate (Fig. 5d), and the end result: higher prevalence of synergy in human brains than in the brains of non-human primates (Fig. 5a,b).

Convergent synaptic underpinnings of synergy in the brain

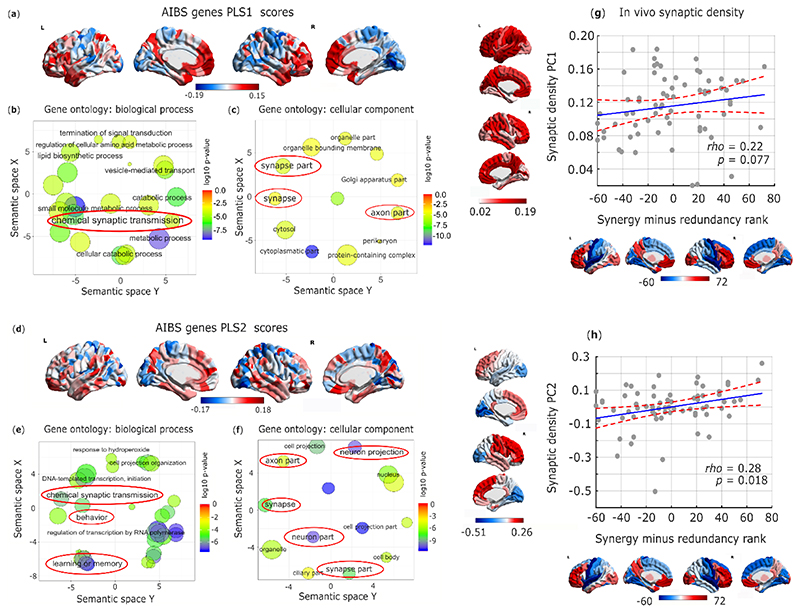
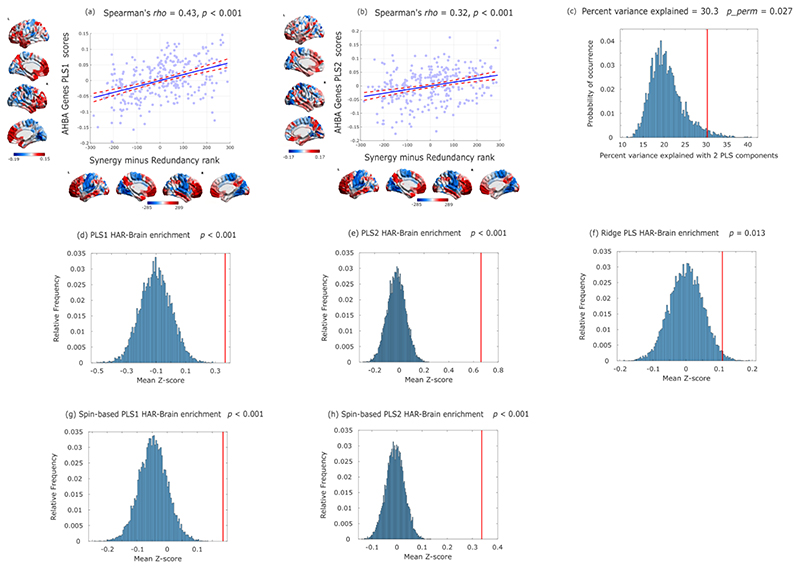
These observations raise the question of how such high synergy in the human brain could have been attained. To address this question from a neurobiological perspective, we explored the association between the redundancy-to-synergy gradient and regional expression profiles of 20,674 genes from AIBS microarray data ^23,35. Using partial least squares (PLS) regression, we show that the first two PLS components explained 30% of the variance in the regional synergy-redundancy values: significantly more than could be expected by chance (permutation test, p=0.004) even when accounting for spatial autocorrelation (p_spin=0.027). Both components were significantly enriched for HAR-Brain genes, corroborating the hypothesis-driven results presented above (PLS1: p<0.001; PLS2: p<0.001; Extended Data Fig. 9). We next sought to identify the role played by overexpressed genes related to brain synergy, for each PLS component. Analysis of gene ontology revealed that the transcriptional signature of our PLS components were significantly enriched in genes involved in learning/memory (consistently with our NeuroSynth meta-analysis), as well as synapses, synapse components and synaptic transmission (Fig. 6a-f; all p<10^-4 for significant enrichment.).

Fig. 6. Synaptic underpinnings of synergy in the human brain.

(a) First principal component of PLS (PLS1) relating the redundancy-to-synergy regional gradient to n=20,647 genes from the Allen Institute for Brain Science. (b,c) Dimensionality-reduced gene ontology terms pertaining to biological processes (b) or cellular components (c) that are significantly enriched in PLS1, obtained from GOrilla using the “P-value threshold 10-4” setting in order to best approximate FDR correction with α = 0.05 ³⁵, and summarized with REVIGO (added red ovals highlight psychologically- or neurobiologically-relevant terms). Semantic space axes indicate the relative distance between terms in multi-dimensional space, but have no intrinsic meaning. (d) Second principal component of PLS (PLS2) relating the redundancy-to-synergy regional gradient to n=20,647 genes from the Allen Institute for Brain Science. (e,f) Dimensionality-reduced gene ontology terms pertaining to biological processes (e) or cellular components (f) that are significantly enriched in PLS2, obtained from GOrilla using the “P-value threshold 10-4” setting in order to best approximate FDR correction with α = 0.05 ³⁵, and summarized with REVIGO (added red ovals highlight psychologically- or neurobiologically-relevant terms). These results were robust to the use of alternative approaches (ridge-regularised PLS regression on the synergy-redundancy cortical pattern; and controlling for spatial autocorrelation using spin-based permutations ⁵³; Extended Data Fig. 9). The significant enrichment for synaptic transmission and organisation was also preserved when using recently developed advanced null models based on random phenotype ensembles (Supplementary Table 10). (g) Spearman correlation between regional redundancy-to-synergy gradient scores and the first principal component of in-vivo synaptic density from [¹¹C]UCB-J PET (Spearman ρ = 0.22, p = 0.077; two-sided CI: [-0.019, 0.436]; p_spin = 0.053; n=68 cortical regions). Color-bars correspond to scatter-plot axes. (h) Spearman correlation between regional redundancy-to-synergy gradient scores and the second (anterior-posterior) principal component of in-vivo synaptic density from [¹¹C]UCB-J PET (Spearman ρ = 0.28, p = 0.018; two-sided CI [0.044, 0.486]; p_spin = 0.059; n=68 cortical regions). Color-bars correspond to scatter-plot axes.

Synapses are the key structures by which neurons exchange information; therefore, they constitute a prime candidate for the neurobiological underpinning of synergistic interactions in the human brain, as suggested by our genetic analysis. To provide a more direct link between synaptic density and regional prevalence of synergy, we used positron emission tomography (PET) to estimate regional synaptic density in vivo, based on the binding potential of the synapse-specific radioligand [¹¹C]UCB-J, which has high affinity for the synaptic vesicle glycoprotein 2A, ubiquitously expressed in all synapses throughout the brain ^36,37. Therefore, [¹¹C]UCB-J binding potential enables in vivo estimation of synaptic density at a regional level ^36,37. Across N=15 healthy volunteers, we obtained regional values of [¹¹C]UCB-J PET binding potential ³⁷, which we then decomposed into two principal components reflecting gradients of synaptic density across cortical regions.

Supporting the notion that regional brain synergy is related to underlying synaptic density, we found that an anterior-posterior principal component of regional synaptic density derived from [¹¹C]UCB-J PET correlates with the regional gradient from redundancy to synergy, with a clear trend to significance persisting even after accounting for spatial autocorrelation (Fig. 6d,e). Thus, regional synaptic density predicts regional prevalence of synergy over redundancy across the cortex.

Metabolic and molecular underpinnings of synergy

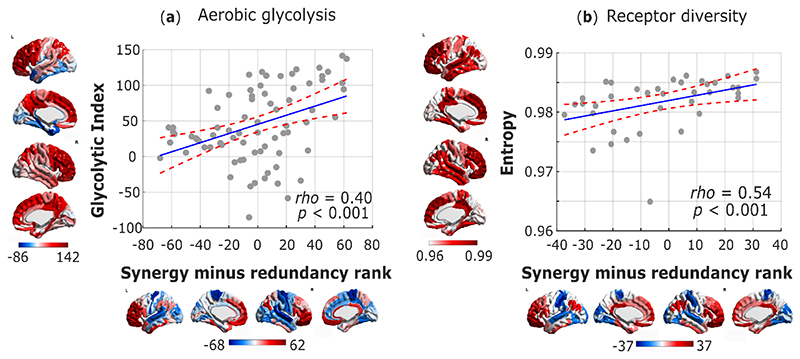
Although genetic and in vivo data indicate the relevance of synapses for brain synergy, synapses themselves are not fixed, but rather they develop over the human lifespan. In both space and time, synaptic growth has well-established metabolic underpinnings, specifically pertaining to aerobic glycolysis (AG). Temporally, meta-analytic results indicate that in the course of human development AG peaks during peak synaptic growth; spatially, the regional distribution of AG in the adult brain coincides with regional expression of genes promoting synaptic growth – suggesting that even during adulthood, AG may support continuous synapse formation ³⁸.

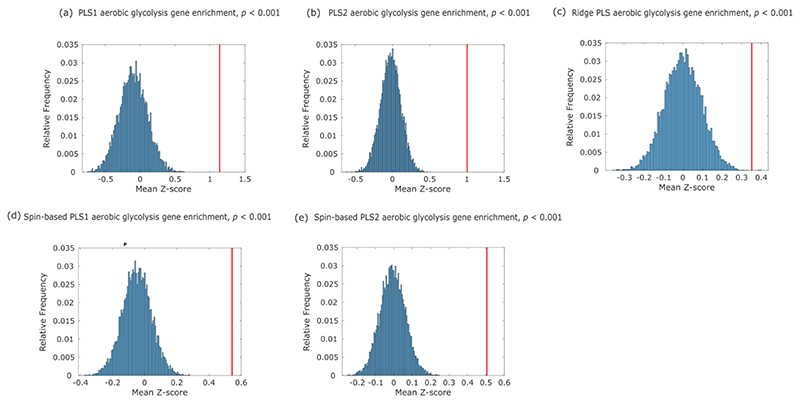
In line with this body of literature and our previous findings, we show that a significant correlation exists between the redundancy-to-synergy gradient, and the cortical distribution of Glycolytic Index, a measure of AG obtained from PET measurements of cerebral metabolic rates for oxygen and glucose ³⁹ (Spearman ρ = 0.40, p < 0.001, p_spin = 0.013; Fig. 7a). Additionally, the same genes promoting synaptic development that were previously related to regional AG distribution ³⁸, are also significantly enriched in both PLS components of gene expression related to the synergy-redundancy gradient identified here (Extended Data Fig. 10). Therefore, genetic and PET evidence converge to indicate that the same metabolic process that supports synaptic growth may also underpin synergistic interactions in the human brain.

Fig. 7. Metabolic and molecular underpinnings of synergy in the human brain.

(a) Significant Spearman correlation (two-sided CI: [0.195, 0.572]) between regional redundancy-to-synergy gradient scores, and the mean regional estimate of aerobic glycolysis based on PET measurements of cerebral metabolic rates for oxygen and glucose (Glycolytic Index); n=78 cortical regions. (b) Significant Spearman correlation (two-sided CI: [0.270, 0.731]) between cortical redundancy-to-synergy gradient scores, and the diversity (entropy) of neurotransmitter receptor expression from in vitro quantitative autoradiography across n=39 regions of human visual, somatosensory, auditory and multimodal association cortices. Color-bars correspond to scatter-plot axes.

Although a high density of synapses reflects high potential for integrating multiple inputs, the actual interactions between neurons rely on multiple distinct neurotransmitters acting on a variety of different receptors. Importantly, the distribution of neurotransmitter receptors in the human brain is not uniform, but rather it varies both across cortical regions and across different layers (supragranular, granular, and infragranular) of the same region ^40,41. In particular, cortical regions differ systematically in terms of the diversity of neurotransmitter receptors they exhibit ⁴⁰. This provides an opportunity to identify potential neurochemical underpinnings of synergy in the human brain: we reasoned that diverse receptor expression across receptor types and layers should endow a region with greater flexibility, so that its activity will be able to reflect the integration of distinct inputs and neuromodulatory influences from a variety of regions and systems.

Supporting the hypothesis of an association between molecular diversity and synergy, we demonstrate that the redundancy-to-synergy gradient corresponds to increasing diversity of receptor densities across supragranular, granular and infragranular layers for 15 different receptor types, obtained from in vitro quantitative receptor autoradiography ⁴⁰ (Spearman ρ = 0.54, p < 0.001). This result suggests that a more diverse receptor profile corresponds to a larger range of information that a region can respond to and integrate, as reflected in higher predominance of synergy for that region.

Overall, hypothesis-driven and data-driven genetic, metabolic, and molecular evidence converge to indicate synapses, synaptic formation, synaptic transmission and the diversity of neurotransmitters as key neurobiological underpinnings of synergy in the brain – in line with the notion that synergy quantifies information integration, and its role in supporting higher cognition.

Validation of results against surrogates

Finally, we validated our results pertaining to the association between the redundancy-to-synergy gradient and macroscale features of cortical organisation by showing that they cannot be recovered if the synergy ranks are obtained from surrogate data. We do this in three different ways: (i) randomising the matrix of inter-regional synergistic connections; (ii) replacing the true synergy ranks with a random vector with the same (negative) correlation with the redundancy ranks; and (iii) computing both synergy and redundancy after phase-randomising each timeseries (thereby removing inter-regional correlations from the signal (Methods)). The results of these analyses are summarised in Table 1.

Table 1. Comparison of macroscale associations for the redundancy-to-synergy gradient, its randomly-generated counterparts from surrogates, and traditional FC (node strength).

	Original gradient	Surrogate gradient (randomised synergy)	Surrogate gradient (random anticorrelated)	Surrogate gradient (phase-randomised)	Traditional FC
Expansion	Spearman ρ = 0.40, p-spin = 0.010	Spearman ρ = 0.07, p-spin = 0.331	Spearman ρ = -0.18, p-spin = 0.109	Spearman ρ = 0.09, p-spin = 0.277	Spearman ρ = -0.18, p-spin = 0.132
HAR-Brain	Spearman ρ = 0.48, p-spin = 0.002	Spearman ρ = 0.18, p-spin = 0.130	Spearman ρ = 0.22, p-spin = 0.066	Spearman ρ = 0.01, p-spin = 0.492	Spearman ρ = -0.38, p-spin = 0.007
PET Synaptic density PC1	Spearman ρ = 0.22, p-spin = 0.053	Spearman ρ = 0.08, p-spin = 0.228	Spearman ρ = 0.02, p-spin = 0.505	Spearman ρ = 0.17, p-spin = 0.114	Spearman ρ = -0.17, p-spin = 0.118
PET Synaptic density PC2	Spearman ρ = 0.28, p-spin = 0.059	Spearman ρ = 0.32, p-spin = 0.020	Spearman ρ = 0.24, p-spin = 0.037	Spearman ρ = 0.21, p-spin = 0.129	Spearman ρ = -0.13, p-spin = 0.179
Glycolytic Index	Spearman ρ = 0.40, p-spin = 0.013	Spearman ρ = 0.14, p-spin = 0.283	Spearman ρ = 0.14, p-spin = 0.216	Spearman ρ = 0.26, p-spin = 0.028	Spearman ρ = -0.11, p-spin = 0.320
Receptor diversity	Spearman ρ = 0.54, p < 0.001	Spearman ρ = 0.19, p = 0.246	Spearman ρ = 0.54, p < 0.001	Spearman ρ = -0.16, p = 0.328	Spearman ρ = -0.52, p = 0.001

Correlation coefficients are derived from Spearman’s rank-based correlation; p_spin indicates the p-value estimated from a spatial permutation test comparing the empirical correlation against 10,000 randomly rotated brain maps with preserved spatial covariance; no correction for multiple comparisons applied.

Discussion

Our multi-modal, multi-species investigation of information-resolved brain dynamics illuminates how the human brain has evolved to address the inherent trade-off between robustness and integration. Leveraging Integrated Information Decomposition to decompose the intrinsic dynamics of human BOLD signals, we quantified how much information about the brain’s dynamics is carried redundantly by the present state of distinct brain regions, reflecting their robustness, and how much of it is carried synergistically between regions, reflecting their integration.

We provided converging evidence that synergistic interactions play a crucial role in the human neurocognitive architecture, and further identified their neurobiological underpinnings across scales by combining genetic, molecular, cytoarchitectonic, metabolic, structural and neuroanatomical evidence. Our findings reveal that basic sensorimotor functions are supported by a modular structure-function backbone of redundant interactions. As the brain’s input-output systems, reliable sensorimotor channels are vital for survival, warranting the additional robustness provided by redundant interactions and supported by direct anatomical connections — as indicated by our structural-functional analysis.

In contrast, meta-analytic and graph-theoretical results indicate that synergistic interactions form a globally efficient network throughout the brain, with synergistic interactions bridging across different brain modules to support higher cognitive functions. Intriguingly, high-synergy regions also exhibit high rates of aerobic glycolysis: in addition to providing a fast and flexible supply of energy, AG is theorized to provide the substrate for biosynthetic processes supporting ongoing synapse formation and turnover ^15,42. Indeed, we show that the neuroanatomical organization of high-synergy regions coincides with synapse-rich association cortices. We also show that high-synergy cortical regions exhibit the most diverse profiles of neurotransmitter receptor expression, enabling flexible neuromodulation. Thus, network organisation and neurobiology across scales provide converging evidence that synergistic interactions are ideally poised to act as a “global workspace” in the human brain ⁴³, enabling the integration of complementary information from across the brain in the service of higher cognitive functions.

It is noteworthy that synergy, which quantifies the extra information gained by integrating multiple sources ^6,44, is especially prevalent in regions of the default mode and fronto-parietal (sub)networks. Functionally, these regions are recruited by complex tasks that rely on multimodal information, decoupled from immediate sensorimotor contingencies ^25,45,46; anatomically, they receive multimodal inputs from across the brain ⁴⁷. Therefore, it has been conjectured that these networks are devoted to the integration of information ^25,47. Our original findings about regional prevalence of synergy in DMN and FPN provide formal information-theoretic evidence to confirm this long-standing hypothesis.

Taken together, our results delineate a neural architecture whereby direct anatomical connections predominantly contribute to ensuring that the same information is available to regions within the same specialised module - especially in sensory and motor subnetworks. Conversely, indirect polysynaptic connections are better poised to favour the integration of information between different modules, converging to association cortices in default and fronto-parietal subnetworks that are associated with anatomical and cognitive integration of information.

Indeed, high-order association cortices of the DMN and FPN may be able to support human higher cognition precisely thanks to their extensive involvement with synergistic processing: we discovered that synergistic (as opposed to redundant) interactions are specifically enhanced in humans over other primates, with dedicated cortical real estate and dedicated genes, including those promoting synaptic transmission and formation. This process resulted in a neural architecture that is capable of leveraging synergistic information to a greater extent than other primates.

At the same time, the DMN and FPN exhibit distinct patterns of activity in tasks and at rest ^48–50, and play different roles in controlling brain dynamics ⁵¹. Thus, it will be crucial for future work to delineate their respective roles within the brain’s synergistic core – for instance by examining how the prevalence and regional distributions of synergy and redundancy vary during cognitive tasks ⁵² or pathological conditions, where our framework for information-resolved analysis could also find fruitful application. Additionally, future work may seek a convergence between the information-resolved and time-resolved approaches to brain function ^17–20, as possible complementary strategies to balance the brain’s competing needs for integration and robustness.

Disentangling synergistic and redundant contributions to the interactions between two regions makes it possible to distinguish cases of “integration of information” (synergy) versus simply “having the same information” (redundancy). The quantification of synergistic information provides a rigorous approach to capture the integration between the activity of different brain regions in terms of their mutual influence, going beyond measures of traditional functional connectivity (e.g. Pearson correlation) that are unable to account for high-order statistical phenomena. Specifically, our results suggest that traditional FC is significantly more similar to redundancy than to synergy. These observations suggest that care should be taken when interpreting the results of traditional FC analyses in terms of “integration”. Such an interpretation may well be appropriate if what is meant is simply the similarity between regional time-courses – which is conceptually close to redundancy. However, if the intention is to quantify information being brought together and combined, then traditional FC may be insufficient, and the more sophisticated machinery of our information-resolved approach would be called for in order to provide the full picture in terms of synergy. Indeed, recent complementary work has also emphasised that focusing on time-locked fluctuations alone will miss out on important aspects of interactions between regions ³¹.

Our information-resolved approach does not just highlight these limitations of traditional FC, however: it also provides the means to overcome them. Thus, we believe that the richer understanding of macroscale interactions provided by Integrated Information Decomposition will help researchers to interpret their FC results more appropriately; generate more specific hypotheses; and choose more appropriate analytic tools, if what they actually wish to quantify is integration rather than simple coupling (similarity of time-courses).

Finally, a key strength of our approach for information-resolved analysis of brain dynamics is its broad range of possible applications: being grounded in information theory, Integrated Information Decomposition can be applied to neural data across scales, from fMRI to neuron cultures. Thus, our framework holds the promise of critical new insights into a wide array of questions across the breadth of neuroscience, from healthy and pathological development to cognition and its disorders. Overall, this work offers the potential to reveal the information-processing principles that govern how mental phenomena emerge from neurobiology.

Methods

Human Connectome Project: Dataset description

The dataset of human MRI data used in this work came from the Human Connectome Project (HCP, http://www.humanconnectome.org/), Release Q3. Per HCP protocol, all subjects gave written informed consent to the HCP consortium. These data contained fMRI and diffusion weighted imaging (DWI) acquisitions from the widely-used 100 unrelated subjects (54 females and 46 males, mean age = 29.1 ± 3.7 years) of the HCP 900 data release ⁵⁴. We did not use statistical methods to pre-determine sample size, but this 100-subject dataset has been extensively studied, so that our sample size is similar to those reported in previous publications ^25,27,55,56,; no data-points were excluded. Data collection and analysis were not performed blind to the conditions of the experiments. All HCP scanning protocols were approved by the local Institutional Review Board at Washington University in St. Louis.

HCP: Functional data acquisition

The following sequences were used: Structural MRI: 3D MPRAGE T1-weighted, TR= 2400 ms, TE = 2.14 ms, TI = 1000 ms, flip angle = 8°, FOV= 224 × 224, voxel size = 0.7 mm isotropic. Two sessions of 15 min resting-state fMRI: gradient-echo EPI, TR= 720 ms, TE= 33.1 ms, flip angle = 52°, FOV= 208 × 180, voxel size = 2 mm isotropic. Here, we only used functional data from the first scanning session, in LR direction. HCP-minimally preprocessed images were used for all acquisitions ⁵⁷.

Functional MRI preprocessing and denoising

We used the minimally preprocessed fMRI data from the HCP, which includes bias field correction, functional realignment, motion correction, and spatial normalisation to Montreal Neurological Institute (MNI-152) standard space with 2mm isotropic resampling resolution ⁵⁷. We also removed the first 10 volumes, to allow magnetisation to reach steady state. Additional denoising steps were performed using the CONN toolbox (http://www.nitrc.org/projects/conn), version 17f ⁵⁸. To reduce noise due to cardiac and motion artifacts, we applied the anatomical CompCor method of denoising the functional data. The anatomical CompCor method (also implemented within the CONN toolbox) involves regressing out of the functional data the following confounding effects: the first five principal components attributable to each individual’s white matter signal, and the first five components attributable to individual cerebrospinal fluid (CSF) signal; six subject-specific realignment parameters (three translations and three rotations) as well as their first-order temporal derivatives ⁵⁹. Linear detrending was also applied, and the subject-specific denoised BOLD signal timeseries were band-pass filtered to eliminate both low-frequency drift effects and high-frequency noise, thus retaining frequencies between 0.008 and 0.09 Hz.

HRF deconvolution

Following previous work on the use of information-theoretic measures in the context of functional MRI data, we used state-of-the-art techniques ⁵⁵ to deconvolve the hemodynamic response function from our regional BOLD signal timeseries. The only exceptions were the computation of traditional functional connectivity (Pearson correlation – see below), for which the un-deconvolved BOLD signal timeseries were instead used, in line with common practice; and the comparison with macaque fMRI: since no HRF deconvolution was performed for macaque data, they were compared with non-deconvolved human data.

HCP: Diffusion weighted data

We used DWI data from the 100 unrelated subjects of the HCP 900 subjects data release ⁵¹. The diffusion weighted (DW) acquisition protocol is covered in detail elsewhere ⁵². The diffusion MRI scan was conducted on a Siemens 3T Skyra scanner using a 2D spin-echo single-shot multiband EPI sequence with a multi-band factor of 3 and monopolar gradient pulse. The spatial resolution was 1.25 mm isotropic. TR = 5500 ms, TE = 89.50 ms. The b-values were 1000, 2000, and 3000 s/mm2. The total number of diffusion sampling directions was 90, 90, and 90 for each of the shells in addition to 6 b0 images. We used the version of the data made available in DSI Studio-compatible format at https://pitt.app.box.com/v/HCP1065.

DWI reconstruction and fiber tracking

The minimally-preprocessed DWI data ⁵² were corrected for eddy current and susceptibility artifact. DWI data were then reconstructed using q-space diffeomorphic reconstruction (QSDR), as implemented in DSI Studio (www.dsi-studio.labsolver.org) ⁶⁰, following previous work ⁵⁵. QSDR is a model-free method that calculates the orientational distribution of the density of diffusing water in a standard space, to conserve the diffusible spins and preserve the continuity of fiber geometry for fiber tracking. QSDR first reconstructs diffusion-weighted images in native space and computes the quantitative anisotropy (QA) in each voxel. These QA values are used to warp the brain to a template QA volume in Montreal Neurological Institute (MNI) space using the statistical parametric mapping (SPM) nonlinear registration algorithm. A diffusion sampling length ratio of 2.5 was used, and the output resolution was 1 mm. A modified FACT algorithm ⁶¹ was then used to perform deterministic fiber tracking on the reconstructed data, with the same parameters used in previous work ⁵⁵. Angular cutoff of 55°, step size of 1.0 mm, minimum length of 10 mm, maximum length of 400mm, spin density function smoothing of 0.0, and a QA threshold determined by DWI signal in the cerebro-spinal fluid. Each of the streamlines generated was automatically screened for its termination location. A whole-brain white matter mask was created by applying DSI Studio’s default anisotropy threshold (0.6 Otsu’s threshold) to the SDF’s anisotropy values. The mask was used to eliminate streamlines with premature termination in the white matter region. Deterministic fiber tracking was performed until 1,000,000 streamlines were reconstructed for each individual.

Macaque data from PRIME-DE Initiative

The non-human primate MRI data were made available as part of the Primate neuroimaging Data-Exchange (PRIME-DE) monkey MRI data sharing initiative, a recently introduced open resource for non-human primate imaging ⁶².

Macaque dataset description

We used fMRI data from rhesus macaques (Macaca mulatta) scanned at Newcastle University. This samples includes 14 exemplars (12 male, 2 female); Age distribution: 3.9-13.14 years; Weight distribution: 7.2-18 kg (full sample description available online: http://fcon_1000.projects.nitrc.org/indi/PRIME/files/newcastle.csv and http://fcon_1000.projects.nitrc.org/indi/PRIME/newcastle.html).

To ensure comparability with the human data, we excluded a priori any functional MRI data acquired from anaesthetized animals. Out of the 14 total animals present in the Newcastle sample, 10 had available awake resting-state fMRI data; of these 10, all except the first animal had two scanning sessions available: to maximise our statistical power, these repeated sessions were included in the analysis. Thus, the total was 19 distinct sessions across 10 individual macaques.

Ethics approval

All of the animal procedures performed were approved by the UK Home Office and comply with the Animal Scientific Procedures Act (1986) on the care and use of animals in research and with the European Directive on the protection of animals used in research (2010/63/EU). We support the Animal Research Reporting of In Vivo Experiments (ARRIVE) principles on reporting animal research. All persons involved in this project were Home Office certified and the work was strictly regulated by the U.K. Home Office. Local Animal Welfare Review Body (AWERB) approval was obtained. The 3Rs principles compliance and assessment was conducted by National Centre for 3Rs (NC3Rs). Animal in Sciences Committee (UK) approval was obtained as part of the Home Office Project License approval.

Animal care and housing

All animals were housed and cared for in a group-housed colony, and animals performed behavioural training on various tasks for auditory and visual neuroscience. No training took place prior to MRI scanning.

Macaque MRI acquisition

Animals were scanned in a vertical Bruker 4.7T primate dedicated scanner, with single channel or 4-8 channel parallel imaging coils used. No contrast agent was used. Optimization of the magnetic field prior to data acquisition was performed by means of 2^nd order shim, Bruker and custom scanning sequence optimization. Animals were scanned upright, with MRI compatible head-post or non-invasive head immobilisation, and working on tasks or at rest (here, only resting-state scans were included). Eye tracking, video and audio monitoring were employed during scanning.

Resting-state scanning was performed for 21.6 minutes, with a TR of 2600ms, 17ms TE, Effective Echo Spacing of 0.63ms, voxels size 1.22 x 1.22 x 1.24. Phase Encoding Direction: Encoded in columns. Structural scans comprised a T1 structural, MDEFT sequence with the following parameters: TE: 6ms; TR: 750 ms; Inversion delay: 700ms; Number of slices: 22; In-plane field of view: 12.8 x 9.6cm2 on a grid of 256 x 192 voxels; Voxel resolution: 0.5 x 0.5 x 2mm; Number of segments: 8.

Macaque functional MRI preprocessing and denoising

The macaque MRI data were preprocessed using the recently developed pipeline for non-human primate MRI analysis, Pypreclin, which addresses several specificities of monkey research. The pipeline is described in detail in the associated publication ⁶³. Briefly, it includes the following steps: (i) Slice-timing correction. (ii) Correction for the motion-induced, time-dependent B0 inhomogeneities. (iii) Reorientation from acquisition position to template; here, we used the recently developed National Institute of Mental Health Macaque Template (NMT): a high-resolution template of the average macaque brain generated from in vivo MRI of 31 rhesus macaques (Macaca mulatta) ⁶⁴. (iv) Realignment to the middle volume using FSL MCFLIRT function. (v) Normalisation and masking using Joe’s Image Program (JIP-align) routine (http://www.nmr.mgh.harvard.edu/~jbm/jip/, Joe Mandeville, Massachusetts General Hospital, Harvard University, MA, USA), which is specifically designed for preclinical studies: the normalization step aligns (affine) and warps (non-linear alignment using distortion field) the anatomical data into a generic template space. (vi) B1 field correction for low-frequency intensity non-uniformities present in the data. (vii) Coregistration of functional and anatomical images, using JIP-align to register the mean functional image (moving image) to the anatomical image (fixed image) by applying a rigid transformation. The anatomical brain mask was obtained by warping the template brain mask using the deformation field previously computed during the normalization step. Then, the functional images were aligned with the template space by composing the normalization and coregistration spatial transformations.

Denoising

The aCompCor denoising method implemented in the CONN toolbox was used to denoise the macaque functional MRI data, to ensure consistency with the human data analysis pipeline. White matter and CSF masks were obtained from the corresponding probabilistic tissue maps of the high-resolution NMT template (eroded by 1 voxel); their first five principal components were regressed out of the functional data, as well as linear trends and 6 motion parameters (3 translations and 3 rotations) and their first derivatives.

Following previous work on macaque functional MRI ⁶⁵, data were bandpass-filtered in the range of 0.0025-0.05 Hz. When comparing directly between human and macaque data, results were also robust to the use of the same bandpass filter of 0.008-0.09 Hz used for human data.

Brain parcellations

Human brains were parcellated into 232 cortical and subcortical regions of interest (ROIs). The 200 cortical ROIs were obtained from the scale-200 version of the recent local-global functional parcellation of Schaefer et al. (2018) ⁶⁶. Since this parcellation only includes cortical regions, it was augmented with 32 subcortical ROIs from a recent subcortical functional parcellation ⁶⁷. We refer to this 232-ROI parcellation as the augmented “Schaefer-232” parcellation. A recent study indicates that this parcellation results in networks whose topology is more generalizable than networks obtained from the same data but with alternative node definition schemes ⁵⁵.

The data pertaining to regional PET-derived synaptic density, HAR gene expression, human cortical expansion, Von Economo cytoarchitectonics and cortico-cortical wiring distance were each only available according to specific parcellations: the Desikan-Killiany anatomical atlas ⁶⁸ with 68 cortical regions (DK-68) for PET data; a 114-ROI subparcellation of the Desikan-Killiany atlas for HAR genes and cortical expansion (DK-114); and a different subparcellation of the Desikan-Killiany atlas with 308 equally-sized ROIs of 500 mm2 each (DK-308 ⁶⁹), for the Von Economo cytoarchitectonic classes; and the 360-ROI HCP Multi-Modal Parcellation (HCP-MMP) ⁷⁰ for the cortico-cortical wiring distance. Therefore, we show that our results are robust to the use of these alternative parcellations.

Macaque functional data were parcellated according to the whole-cortex 82-ROI “Regional Mapping” (RM) atlas of Kotter and Wanke ⁷¹, nonlinearly registered to the NMT template used for preprocessing.

BOLD timeseries extraction

To construct matrices of functional connectivity, the timecourses of denoised BOLD signals were averaged between all voxels belonging to a given atlas-derived ROI, using the CONN toolbox. The resulting region-specific timecourses of each subject were then extracted for further analysis in MATLAB version 2019a.

Traditional functional connectivity

For each pair of brain regions i and j, their traditional functional connectivity FC_ij was computed as the Pearson correlation between their denoised BOLD signal timeseries.

Structural connectome construction

To construct matrices of structural connectivity, the edge weights a_ij of the structural connectivity matrix A were defined as the number of streamlines connecting end-to-end each of the regions in the atlas, normalised to lie between zero and one. Note that deterministic tractography produces naturally sparse matrices, so that no thresholding is required.

Partial Information Decomposition

Shannon’s Mutual information (MI) quantifies the interdependence between two random variables X and Y. It is calculated as

$$\text{I}(X;Y)=\text{H}(X)-\text{H}(X|Y)=\text{H}(X)+\text{H}(Y)-\text{H}(X,Y),$$ (1)

where H(X) stands for the Shannon entropy of a variable X. Above, the first equality states that the mutual information is equal to the reduction in entropy (i.e. uncertainty) about X after Y becomes accessible. Put simply, the mutual information quantifies the information that one variable provides about another ²¹.

Crucially, Williams and Beer ² observed that the information that two source variables X and Y give about a third target variable Z, I(X,Y; Z), should be decomposable in terms of different kinds of information: information provided by one source but not the other (unique information), or by both sources separately (redundant information), or jointly by their combination (synergistic information). Following this intuition, they developed the Partial Information Decomposition (PID ²) framework, which leads to the following fundamental decomposition:

$$\text{I}(X,Y;Z)=\text{Red}(X,Y;Z)+\text{Un}(X;Z|Y)+\text{Un}(Y;Z|X)+\text{Syn}(X,Y;Z)$$ (2)

Above, Un corresponds to the unique information one source has but the other doesn’t, Red is the redundancy between both sources, and Syn is their synergy: information that neither X nor Y alone can provide, but that can be obtained by considering X and Y together.

The simplest example of a purely synergistic system is one in which X and Y are independent fair coins, and Z is determined by the exclusive-OR function Z = XOR(X,Y): i.e., Z=0 whenever X and Y have the same value, and Z=1 otherwise. It can be shown that X and Y are both statistically independent of Z, which implies that neither of them provide – by themselves – information about Z. However, X and Y together fully determine Z: hence, the relationship between Z with X and Y is purely synergistic. Although here we base our analysis on the PID framework, it is worth remarking that alternative formulations of measures related to synergy and redundancy have been developed in other contexts (see Timme et al., (2014) ³ for a discussion).

While PID provides a formal framework to decompose information, it does not enforce how the corresponding parts ought to be calculated (e.g. what counts as “the same information” for the purpose of measuring redundancy). While there is ongoing research on the advantages of different decompositions for discrete data, most decompositions converge into the same simple form for the case of continuous Gaussian variables ²². Known as minimum mutual information PID (MMI-PID), this decomposition quantifies redundancy in terms of the minimum mutual information of each individual source with the target; synergy, then, becomes identified with the additional information provided by the weaker source once the stronger source is known.

Since linear-Gaussian models are adequate descriptors of functional MRI timeseries (and more complex, non-linear models do not seem to offer additional explanatory power ^72,73) here we adopt the MMI-PID decomposition, following previous applications of PID to neuroscientific data ⁷⁴. However, we also demonstrate that our results do not crucially rely on the assumption of gaussianity, by showing that they are robust to the use of discretised data (see below). That being said, information decomposition is an active field of investigation ⁷⁵, and further advances may shed new light on improved ways to compute and interpret these quantities.

Synergy and redundancy: Integrated Information Decomposition

Let us consider now a stochastic process X comprised of two random variables evolving jointly over time, $X_t=\{X_t^1,X_t^2\}$ – in our case, this corresponds to the timeseries of the BOLD activity of two brain regions, although in other applications it could be any form of multivariate timeseries data. One can first consider the amount of information flowing from the system’s past to its future, known as time-delayed mutual information (TDMI) ⁷⁶ and given by $I(X_{t-\tau }^1,X_{t-\tau }^2;X_t^1,X_t^2).$

The fundamental advancement offered by Integrated Information Decomposition ⁶ is to decompose TDMI into redundant, unique, and synergistic information shared with respect to both past and present state of both variables. In practice, this involves setting up a linear system of 15 equations with 16 unknowns relating the standard (Shannon) mutual information with the redundant, unique, and synergistic components of TDMI ⁶. The system can be solved by specifying the redundancy between X_t−τ and X_t, which, following the discussion in the previous section, we compute using MMI as

$$Red(X_{t-\tau };X_t)=mi{n}_{ij}I(X_{t-\tau }^i;X_t^j).$$ (3)

This allows us to solve the linear system of equations and obtain all components of the Integrated Information Decomposition of X. Of these, we focus on the temporally persistent redundancy and synergy (denoted by $I_{\partial }^{\left\{1\right\}\left\{2\right\}\to \left\{1\right\}\left\{2\right\}}$ and $I_{\partial }^{\left\{12\right\}\to \left\{12\right\}}$ in standard PID notation ²). It is worth noting that the Integrated Information Decomposition framework scrutinizes the interdependencies between the past and present states of both X_t and Y_t, and therefore captures phenomena that are not assessed by approaches focused on the transfer of information from the past of one to the present of the other. Indeed, the metrics of redundancy and synergy studied here reveal a view on brain dynamics that is fundamentally different – and ultimately complementary – to the one provided by directed information-theoretic measures such as directed information and transfer entropy ^13,14,77,78. The reader is referred to the original article for details ⁶.

For all the analyses in the paper we use the Gaussian solver implemented in the JIDT toolbox ⁷⁹ to compute all information-theoretic quantities for each pair of brain regions, based on their HRF-deconvolved BOLD signal timeseries. In addition, we also show that our analyses are not critically dependent on the Gaussianity assumption by computing synergy and redundancy from discrete (binary) timeseries. We implemented this by estimating the corresponding information-theoretic quantities on mean-binarised signals with the well-known plug-in estimator. Finally, given the recent formulation of Integrated Information Decomposition, it is worth keeping in mind that these metrics and their implementations for both continuous and discrete signals may be refined in future research, including extensions beyond the current pair-wise approach ^80,81.

Gradient of redundancy-to-synergy relative importance

After building networks of synergistic and redundant interactions between each pair of regions of interest (ROIs), we determined the role of each ROI in terms of its relative engagement in synergistic or redundant interactions. We first calculated the nodal strength of each brain region as the sum of all its connections in the group-averaged matrix. Then, we ranked all 232 regions based on their nodal strength (with higher-strength regions having higher ranks). This procedure was done separately for networks of synergy and redundancy. Subtracting each region’s redundancy rank from its synergy rank yielded a gradient from negative (i.e. ranking higher in terms of redundancy than synergy) to positive (i.e. having a synergy rank higher than the corresponding redundancy rank); note that the sign is arbitrary.

It is important to note that the gradient is based on relative – rather than absolute – differences between regional synergy and redundancy. Consequently, a positive rank difference does not necessarily mean that the region’s synergy is greater than its redundancy; rather, it indicates that the balance between its synergy and redundancy relative to the rest of the brain is in favour of synergy – and vice versa for a negative gradient.

The same procedure was also repeated for network edges (instead of nodes), using their weights to rank them separately in terms of synergy and redundancy and then calculating their difference. This produced a single connectivity matrix where each edge’s weight represents its relative importance, being higher for synergy (positive edges) or redundancy (negative edges).

NeuroSynth term-based meta-analysis

The regional redundancy-to-synergy gradient identified in terms of nodal rank differences was related to specific words using NeuroSynth, an online platform for large-scale, automated synthesis of fMRI data [https://neurosynth.org/]. For our analyses we employ 24 topic terms used by previous studies ^23,25, which range from lower sensorimotor functions (such as eye movement, motion, visual and auditory perception) to higher cognitive functions (e.g. attention, working memory, social and numerical cognition).

A meta-analysis analogous to the one implemented by previous studies ^25,27, was conducted to identify topic terms associated with the redundancy-to-synergy gradient. Twenty binary brain masks were obtained by splitting the values of the redundancy-to-synergy gradient into five-percentile increments. These brain masks served as input for the meta-analysis, based on the chosen 24 topic terms. For visualisation, terms were ordered according to the weighted mean of the resulting Z-statistics. Note that the term “visual semantics” was excluded from visualisation, because it failed to reach the significance threshold of Z > 3.1, leaving 23 terms (Fig. 1). The analyses were carried out using modified code made freely available at [https://www.github.com/gpreti/GSP_StructuralDecouplingIndex].

Von Economo cytoarchitectonic classes

Whitaker and Vertes (2016) ³⁵ assigned each regions in the DK-308 cortical parcellation to one of the cytoarchitectural types delineated by von Economo. This atlas subdivided the cortex into five types according to the laminar structure of the cortex: the primary motor cortex/precentral gyrus; two types association cortices; secondary and primary sensory areas. Two additional subtypes were added ⁸²: limbic cortex (which included the entorhinal, retrosplenial, presubicular and cingulate cortices, and thus primarily constitutes allocortex); and the insular cortex.

Subsequently, synergy and redundancy were obtained for the DK-308 parcellation as described above, as well as the redundancy-to-synergy gradient based on rank differences. The regional values of this gradient were then averaged across all ROIs belonging to each of the seven cytoarchitectonic classes. For each cytoarchitectonic class, a positive overall score indicates that cortical regions belonging to that class have overall higher importance for synergy than for redundancy – and vice-versa for negative scores.

Canonical resting-state subnetworks

We used the canonical subdivision of the brain into 7 cortical subnetworks of Yeo ²²: default mode (DMN), somatomotor (SOM), visual (VIS), salience/ventral attention (SAL), dorsal attention (DAN), fronto-parietal executive control (FPN) and limbic (LIM). Schaefer et al (2018) ⁶³ assigned each ROI in their cortical parcellation to one of these canonical subnetworks. The 32 subcortical regions were all assigned to an 8^th subcortical subnetwork (SUB).

Quantifying network efficiency and segregation

By considering each brain region as a node in a network, it is possible to obtain two distinct whole-brain networks: one whose edges correspond to the synergistic interactions between each pair of brain regions, and one whose edges correspond to the redundant interactions. The whole-brain networks of synergistic and redundant interactions can then be compared in terms of graph-theoretical properties: our analysis focused on properties quantifying the ease of communication through the network (efficiency) and its level of segregation.

We quantified the ease of communication in the whole-brain networks of synergistic and redundant connections in terms of the network’s global efficiency, a well-known measure of the ease of parallel information transfer in the network. More precisely, the global efficiency of a network corresponds to the average of the inverse of the shortest path length between each pair of nodes ⁷⁹:

$$Ge=\frac{1}{n}{\displaystyle \sum _i^n\frac{{\displaystyle {\sum }_{j\ne i}^n{(d_{ij})}^{-1}}}{n-1}}$$

Following Cruzat et al (2018) ⁸⁰, segregation of brain networks was quantified by means of network modularity. Put simply, the modularity function quantifies the extent to which a network can be partitioned such that the number of within-group edges is maximised and the density of between-group edges is minimised. We employed an implementation of Newman’s spectral modularity algorithm ⁸¹ available in the Brain Connectivity Toolbox (BCT ^79,82).

Structural-functional similarity

Matrices of synergy and redundancy were thresholded proportionally using the same network density as the structural connectivity matrix of the same subject. This procedure was selected in order to ensure that the same number of edges would be present in both matrices, so that the two matrices can be compared. Then, the upper triangular portion of each connectivity matrix (structural and synergy/redundancy) was flattened into a vector, and the Spearman correlation coefficient between these two vectors was computed ⁸³. We use this correlation as a measure of similarity between synergy or redundancy and structural connectivity. The same procedure was also adopted to compare synergy and redundancy matrices with the matrices of traditional functional connectivity and cortico-cortical wiring distance (described below). Since these matrices are dense (all-to-all) matrices, for such analyses the thresholding step was omitted.

Alternative network measures

As an alternative quantification of how well-connected a network is, we also employed the measure of global integrative capacity developed by Cruzat and colleagues ⁸⁴. This measure is calculated by taking the un-thresholded connectivity as input, and rescaling it to the range of 0 to 1 by dividing it by its largest element (note that both synergy and redundancy are guaranteed to be non-negative, and therefore we did not need to take the absolute value). Then, the matrix is progressively thresholded with an increasing threshold ρ in 1% increments. At each threshold value, the size of the largest connected component of the resulting network is evaluated (normalised by the total number of nodes to lie between 0 and 1). The final measure is the integral of the curve of largest connected component sizes over all thresholds:

$$I_{GC}={\displaystyle {\int }_{\rho =0.01}^{0.99}GC(A_{\rho })}$$

where GC(A_ρ) indicates the size (number of nodes) of the largest connected component of the network whose adjacency matrix A has been thresholded at threshold ρ, and N is the total number of nodes in the network. This procedure was applied for both redundancy and synergy whole-brain networks of each subject.

As an alternative method to quantify the similarity of synergistic and redundant connections to the underlying structural connectome, we computed the Hamming distance between the connectivity patterns of each ROI in the functional and anatomical connectivity matrices ⁸⁵. The Hamming distance between binary vectors a and b is computed as the number of symbol substitutions required to turn one vector into the other (normalised by their length).

The matrices were therefore binarised by setting all supra-threshold entries to unity, and all others to zero. In the present application, the Hamming distance measures the proportion of connections that need to be changed before the two connectivity patterns become the same. This analysis was performed for each ROI in our augmented Schaefer-232 atlas; by averaging over all ROI values, we obtained a value of structural-functional connectivity distance. Both correlation and Hamming distance analysis were performed separately for the matrices of synergy and redundancy between each pair of brain regions.

Network null models for graph-theoretical analysis

We compared the modularity and global efficiency of the networks of synergistic and redundant interactions against synthetic null models. The considered null models are based on the fact that, within a given individual, both the synergy and the redundancy between regions i and j are upper-bounded by the TDMI between i and j and lower-bounded by 0, and there is no a priori reason dictating which one should be greater. Therefore, we constructed our null models as follows. For each individual we obtained a random network whereby the weight of the edge between each pair of regions i and j is randomly sampled from the range between 0 and the TDMI between i and j – thereby being in the same theoretical range as both synergy and redundancy. We then computed the global efficiency and modularity of this synthetic network, and repeated the procedure 100 times, comparing the global efficiency and modularity averaged across 100 simulations, with the corresponding measures obtained from the empirical networks of synergy and redundancy, for each individual.

Cortico-cortical wiring distance

Paquola and colleagues ³² developed a measure of cortico-cortical wiring distance. They used diffusion map embedding, a nonlinear dimensionality reduction approach, to combine diffusion tractography with cortico-cortical spatial proximity (geodesic distance) and microstructural profile similarity between regions, to obtain a multi-scale measure of difference between cortico-cortical wiring profiles, termed wiring distance. For our analysis, we used the matrix of wiring distance provided in terms of the multimodal cortical parcellation of Glasser and colleagues ⁷⁰ with 360 cortical regions.

Structural-functional similarity in macaque brains

Individual structural connectomes were not available for the macaques included in this study. Anatomical connectivity for the macaque brain was instead obtained from the fully-weighted, whole-cortex macaque connectome recently developed by Shen and colleagues ^86,87. This connectome was generated by combining information from two different axonal tract-tracing studies from the CoCoMac database [http://cocomac.g-node.org/main/index.php?] with diffusion-based tractography obtained from 9 adult macaques (Macaca mulatta and Macaca fascicularis). The resulting connectome provides a matrix of weighted and directed anatomical connectivity between each of the 82 cortical ROIs of the RM atlas. Since synergy and redundancy are undirected measures of connectivity, the matrix of directed anatomical connections was made undirected by averaging the strength of connections in the two directions.

As for humans, networks of synergistic and redundant interactions were thresholded proportionally using the same density as the anatomical connectivity matrix, to ensure that the same number of edges would be present in the two matrices being compared. Then, Spearman correlation was used as the measure of structural-functional similarity.

Human-macaque comparison of synergy and redundancy

Separately for humans and macaques, each subject’s matrices of synergistic and redundant interactions were each divided by the corresponding subject’s matrix of TDMI. The global mean of the resulting matrices (across rows and columns) therefore represents the proportion of total information across the brain that is provided by synergistic (v. redundant) interactions. The human data were parcellated for this analysis according to the 83-ROI Lausanne parcellation (corresponding to the original Desikan-Killiany atlas, plus subcortical regions ⁸⁸), thereby ensuring a similar number of ROIs in human (83 ROIs) and macaque brains (82 ROIs).

Since macaque brains were not HRF-deconvolved, for this analysis we also used synergy and redundancy obtained from non-deconvolved human fMRI. As shown above, the use of HRF deconvolution had negligible effects on synergy and redundancy calculations, arguably thanks to the high temporal resolution of HCP data. To ensure that the observed differences in the proportion of synergistic information could not be attributed to differences in bandpass-filter, we also repeated this analysis with macaque data filtered in the range 0.008-0.09Hz (i.e. same range as the HCP human data). These data were also used to compare the effect size between humans and macaques in terms of total proportion of synergistic information versus total mean functional connectivity (overall mean of the FC matrix), or the modularity or global efficiency of functional connectivity networks, computed as described above (after removing negative connections by taking the absolute value). The procedure for comparing effect sizes is described below in the section on Statistical analysis.

Validation with dynamic mean field

Model construction

To determine whether the differences in the proportion of synergy between humans and macaques could be driven by the different TR (0.72s for HCP data, and 2.6s for macaque data), we simulated human functional MRI data with the same TR as the macaque data, using a dynamic neuronal mean-field model derived from the collective behavior of empirically validated integrate-and-fire (80% excitatory and 20% inhibitory) neurons ⁸⁷. The model combines macroscale information about neuroanatomy and structural connectivity (from DTI) with excitatory and inhibitory neuronal populations interconnected by AMPA, NMDA and GABA synapses, providing a neurobiologically plausible account of regional neuronal firing rate. We set all model parameters to be the same as those used by previous publications ^87–89, except for the global coupling parameter G, which we fit (see below). Code for the DMF model is freely available at http://www.gitlab.com/concog/fastdmf ⁸⁹.

The structural connectivity for the model was obtained by following the procedure of Wang et al (2019) ⁹⁰, which derives a consensus structural connectivity matrix A from the individual SC matrices of the 100 HCP subjects included in the present study. Hence, for each individual, the structural connectivity was obtained from deterministic tractography (as described above) performed with the Lausanne-83 parcellation. Subsequently, for each pair of regions i and j, if more than half of subjects had non-zero connection i and j, A_ij was set to the average across all subjects with non-zero connections between i and j. Otherwise, A_ij was set to zero.

A Balloon-Windkessel hemodynamic model was then used to turn simulated regional neuronal activity into simulated regional BOLD signal. The Balloon-Windkessel model considers the BOLD signal as a static nonlinear function of the normalized total deoxyhemoglobin voxel content, normalized venous volume, resting net oxygen extraction fraction by the capillary bed, and resting blood volume fraction. The BOLD-signal estimation for each brain area is computed from the level of neuronal activity in that particular area. Finally, simulated regional BOLD signal was bandpass filtered in the same range as the empirical data (0.008-0.09Hz).

Model fitting

The model has only one free parameter G, which scales the global coupling strength. To find the value of G that generates the most realistic data, we first generated 100 simulations with a TR of 0.72s (i.e. the same as the empirical HCP data) for each value of G between 0.1 and 2.5, using increments of 0.1. Following previous work ^90–92, we selected the value of G that minimised the Kolmogorov-Smirnov distance between the empirical and simulated functional connectivity dynamics (FCD), which has been shown to provide a better fit than simply using the global functional connectivity. The KS distance between empirical and simulated FCD was minimised for a value of G=1.6 (Extended Data Fig. 6).

Simulated human fMRI data

To determine whether the observed difference in proportion of synergy between human and macaque brains could be explained exclusively by the difference in TR, we then generated another set of 100 simulations, using the empirically determined best-fitting G parameter of 1.6, but now with a TR of 2.6s, i.e. the same as the macaque data. The simulated data were filtered between 0.008-0.09Hz and their mean normalised synergy across all pairs of regions (i.e., the proportion of total information accounted for by synergy) was compared with the normalised synergy empirically observed in macaque brains (Extended Data Fig. 6).

HAR-BRAIN genes

The maps of regional expression of human-accelerated genes for the DK-114 atlas were made available by Wei et al (2019) ³⁴, where the reader can find detailed information about how these data were generated. Briefly, genes located in a total of 2737 human accelerated regions (HARs) of the genome were taken as presented by comparative genome analysis representing genomic loci with accelerated divergence in humans ⁹³. Out of 2143 HAR-associated genes identified from this procedure, 1711 were described in the Allen Human Brain Atlas (AHBA) microarray dataset (human.brain-map.org) ⁹⁴ and were used in the analyses by Wei and colleagues, referred to as HAR genes.

HAR genes were subsequently subdivided into HAR-BRAIN and HAR-NonBRAIN genes. BRAIN genes were selected as the set of genes commonly expressed in human brain tissue using the Genotype-Tissue Expression (GTEx) database (data source: GTEx Analysis Release V6p; https://www.gtexportal.org/), which includes 56,238 gene expression profiles in 53 body sites collected from 7333 postmortem samples in 449 individuals. From these 56,238 genes, a total number of 2823 genes were identified as BRAIN genes showing significantly higher expressions in brain sites than non-brain sites (one-sided t-test and an FDR corrected q < 0.05 were used). HAR-BRAIN genes were identified as the 405 genes that overlapped between the 2823 BRAIN genes and the 1711 HAR genes, whereas the remaining HAR genes were labelled as HAR-NonBRAIN genes. Finally, the HAR gene expression data were mapped to the 114-region subdivision of the Desikan-Killiany atlas [DK-114]. Since only two of the six AHBA donors have data for the right hemisphere, Wei et al (2019) only considered HAR gene expression patterns for the left hemisphere.

Cortical expansion

The maps of evolutionary cortical expansion were made available by Wei et al (2019) ³⁴, who describe in detail how these data were generated. Briefly, Wei and colleagues analysed in-vivo MRI data from 29 adult chimpanzees, as well as 30 adult human subjects from the Human Connectome Project. Pial surface reconstructions of chimpanzee and human T1-weighted MRI scans (processed with FreeSurefer v5.3.0; https://surfer.nmr.mgh.harvard.edu/) were used for both vertex-to-vertex mapping across chimpanzee and humans and also for subsequent computation of region-wise expansion for cortical morphometry. A regional-level cortical surface area (Si) was computed by summing up face areas within each cortical region, for all regions of the DK-114 atlas. Normalized cortical area was obtained by dividing the regional area by the area of the whole cortex. Cortical expansion between every pair of chimpanzee and human subjects was calculated based on both the raw (“unadjusted”) and normalized (“adjusted”) cortical surface area by

$$E_{i,j}=\frac{S_{human,i}-S_{chimp,j}}{S_{chimp,j}}$$

with E_i,j denoting the expansion from chimpanzee j to human i. A group-level region-wise cortical expansion map was calculated by taking averages over the 870 chimpanzee-to-human comparisons.

Regional Glycolytic Index data

The maps of average regional Glycolytic Index (GI) for 41 regions (left and right) of the Brodmann atlas were made available by Vaishnavi et al (2010) ³⁹ based on PET scans of 33 healthy adults (scanned at rest and with eyes closed). We mapped 78 of these values onto an MNI-space parcellation of the Brodmann atlas, which we used to parcellate our fMRI data. The GI is a measure of regional aerobic glycolysis, since it quantifies the extent to which empirically measured glucose consumption exceeds or falls short of the glucose consumption that would be predicted based on oxygen metabolism. Specifically, GI is obtained by linear regression of regional cerebral metabolic rate of glucose (measured using [18F]-labeled fluorodeoxyglucose) on regional cerebral metabolic rate of oxygen, measured by combining three PET scans administering [150-]labeled H₂0, CO and O₂ 40.

Genes related to aerobic glycolysis

Goyal et al., (2014) ³⁸ performed data-driven analysis using AHBA microarray data and an independent transcriptomic database (BrainSpan Study [BSS], http://brainspan.org ⁹⁵), to identify genes whose regional distribution was significantly associated with the regional distribution of aerobic glycolysis values (Glycolytic Index) previously obtained by Vaishnavi and colleagues ³⁹. They identified and made available a list of 116 genes that consistently occurred among the top 1,000 out of 17,205 genes whose expression is associated (after correction for multiple comparisons) with the regional distribution of GI in the human brain, both in the AHBA dataset and in five matched BSS adult brains.

AIBS data-driven gene expression analysis

Regional gene expression levels for 20,647 human genes were obtained from transcriptomic measurements in six post-mortem brains from adult human donors with no history of psychiatric or neuropathological disorders (age: 24-57 years), made available by the Allen Institute for Brain Science (human.brain-map.org) ⁹⁴. We used code made freely available by Morgan et al (2019) ²³ to obtain a 308 x 20,647 regional transcription matrix, matching gene expression data to each cortical region of the DK-308 atlas ^23,35,82,96. Each tissue sample was assigned to a cortical region using the AIBS MRI data for each donor, pooling samples between bilaterally homologous regions ^23,82.

Partial least squares

To explore the association between the redundancy-to-synergy regional gradient and all 20,647 genes measured in the AHBA microarrays, at each of 308 regions, we used partial least squares (PLS) as a dimensionality reduction technique ^23,82,97. PLS finds components from the predictor variables (308 × 20,647 matrix of regional gene expression scores) that have maximum covariance with the response variables (308 × 1 matrix of regional redundancy-to-synergy gradient). The PLS components (i.e., linear combinations of the weighted gene expression scores) are ranked by covariance between predictor and response variables, so that the first few PLS components provide a low-dimensional representation of the covariance between the higher dimensional data matrices.

Goodness of fit of low-dimensional PLS components was tested non-parametrically by repeating the analysis 1000 times after shuffling the regional labels. The error on the PLS weights associated with each gene were tested by resampling with replacement of 308 ROIs (bootstrapping); the ratio of the weight of each gene to its bootstrap standard error was used to Z-score the genes and rank their contributions to each PLS component ^23,82.

Gene ontology and enrichment analysis

We used Gorilla for enrichment analysis of the first two PLS components ^35,98. Gorilla identifies enriched gene ontology (GO) terms in ranked gene list, leveraging a large online database of gene annotations corresponding to ‘biological processes’ and ‘cellular components’ ⁹⁸. We identified GO terms that were over-represented among the genes with the strongest positive weightings on each PLS component (i.e. those most strongly associated with dominance of synergy over redundancy). For our analyses on the online Gorilla platform (http://cbl-gorilla.cs.technion.ac.il) we unchecked the “Run Gorilla in fast mode” option and used the “P-value threshold 10-4” setting in order to best approximate FDR correction with α = 0.05 ³⁵.

We then used the online tool REViGO (http://revigo.irb.hr) to summarize the list of significant GO terms and visualize the results of whole-genome enrichment analysis. First, REViGO employs measures of semantic similarity between terms ⁹⁹ to identify representative clusters of genes. Then, REViGO plots significant GO terms in semantic space, where semantically similar GO terms are represented clustered near one another and labelled in a representative manner.

We note that this analysis does not take into account within-category gene-gene correlations; therefore, we also employed a more sophisticated null model that was recently developed to estimate gene enrichment relative to an ensemble of null phenotypes (rather than an ensemble of random genes) ¹⁰⁰, using a freely available toolbox: https://github.com/benfulcher/GeneCategoryEnrichmentAnalysis/wiki/Ensemble-enrichment.

For our hypothesis-driven analysis, testing for enrichment of HAR-Brain genes, we also used non-parametric permutation testing. Specifically, we randomly drew 1000 samples of the same number of genes and estimated their PLS weighting, and compared the PLS weights of the HAR-Brain genes to this permutation distribution. This provided an estimate of the probability of HAR-Brain gene enrichment of each PLS component under the null hypothesis 24,36. The same procedure was used to test for significant enrichment of genes related to regional aerobic glycolysis.

Robustness of gene enrichment results

Our data-driven analysis of regional gene expression also indicated significant enrichment when performed using an alternative approach: ridge-regularised PLS regression implemented in the R package plsgenomics (https://CRAN.R-project.org/package=plsgenomics). As this package requires binary target variables, we therefore turned the regional gradient from synergy to redundancy into a binary vector characterizing each region in terms of the predominance of synergy or redundancy (as indicated by the sign of the gradient), regardless of magnitude. Therefore, this analysis seeks to find regularized coefficients to predict each region’s binary status as synergy-rich vs redundancy-rich, based on regional gene expression. We obtained regression coefficients for each AHBA gene using a ridge (L2) penalty norm determined by 10-fold cross-validation. These coefficients were then turned into z-scores and enrichment for HAR-Brain genes and genes related to aerobic glycolysis was computed using permutation testing as described above.

The second alternative approach was designed to account for the potential confound of spatial autocorrelation. To this end, we obtained a z-score for each AHBA gene, by dividing its empirical Spearman correlation with the redundancy-to-synergy cortical map, with the standard deviation of the distribution of correlations obtained from 5000 randomly rotated cortical maps having preserved spatial autocorrelation ^53,101. Enrichment for HAR-Brain genes and genes related to aerobic glycolysis was then computed using permutation testing as described above, by comparing the weights of the genes of interest with the weights of 1000 random selections of the same number of genes.

Synaptic density from positron emission tomography

In-vivo estimates of regional synaptic density in the human brain were obtained from positron emission tomography (PET) with the radioligand [¹¹C]UCB-J ((R)-1-((3-(methyl-¹¹C)pyridin-4-yl)methyl)-4-(3,4,5-trifluorophenyl)pyr-rolidin-2-one) 38. This ligand quantifies synaptic density ³³ based on its affinity for the presynaptic vesicle glycoprotein 2A (SV2A) ¹⁰² which is ubiquitously expressed in all brain synapses ¹⁰³.

PET/MR imaging protocol

The research protocol was approved by an NHS Research Ethics Committee (REC: 18/EE/0059) and the Administration of Radioactive Substances Advisory Committee (ARSAC), and all participants provided written informed consent in accordance with the Declaration of Helsinki.

Participant recruitment and exclusion criteria are described in detail in the original publication 38. Briefly, 14 patients with PSP-Richardson’s syndrome and 15 patients with CBS were recruited from a tertiary specialist clinic for PSP/CBS at the Cambridge University Centre for Parkinson-Plus (Cambridge, UK). Additionally, 15 age-/sex-/education-matched healthy volunteers were recruited from the UK National Institute for Health Research Join Dementia Research register between June 2019 and June 2020. Both healthy controls and patient volunteers were pre-screened by telephone; participants were excluded based on any of the following: history of cancer within the last 5 years; concurrent use of the medication levetiracetam; any severe physical illness or co-morbidity that limited ability to fully participate in the study; any contraindications to performing MRI. Participants were also excluded based on history of ischaemic or haemorrhagic stroke evident on MRI available from the clinic. Here, we only included data from the healthy volunteers (N=15, 8 females; age: 68 ± 7 years).

The radioligand [¹¹C]UCB-J was synthesized at the Radiopharmacy Unit, Wolfson Brain Imaging Centre, Cambridge University ¹⁰². All participants underwent simultaneous 3T MRI and [11C]UCB-J PET on a GE SIGNA PET/MR (GE Healthcare, Waukesha, USA). Participants were under continuous visual observation from the adjacent control room, and there was an open microphone channel in case a participant needed to be in contact with the radiographers. The radiographer was present throughout with medical cover on site in case of need (such a need did not arise).

Dynamic PET data acquisition was performed for 90 minutes starting immediately after [11C]UCB-J injection (median (range) injected activity: 408 (192-523) MBq, injected UCB-J mass ≤ 10 μg). Attenuation correction included the use of a multi-subject atlas method ¹⁰⁴ and improvements to the MRI brain coil component ¹⁰⁵. Each emission image series was aligned using SPM12 (www.fil.ion.ucl.ac.uk/spm/software/spm12/) then rigidly registered to a T1-weighted MRI acquired during PET data acquisition (TR = 3.6 msec, TE = 9.2 msec, 192 sagittal slices, in plane resolution 0.55 x 0.55 mm (subsequently interpolated to 1.0 x 1.0 mm); slice thickness 1.0 mm). Regional time-activity curves were extracted following the application of geometric transfer matrix partial volume correction ¹⁰⁵ to each of the dynamic PET images. To quantify SV2A density (and therefore synaptic density), regional [¹¹C]UCB-J non-displaceable binding potential (BP_ND) was determined for a 68-ROI subdivision of the Desikan-Killiany cortical atlas (DK-68), using a basis function implementation of the simplified reference tissue model ¹⁰⁶, with the reference tissue defined in the centrum semiovale ^107,108.

Principal components of synaptic density

Principal Components Analysis (PCA) was subsequently employed to derive the principal components that explain most of the variance in regional [¹¹C]UCB-J BP_ND across volunteers. Components were selected if their associated eigenvalue was greater than unity; two principal components satisfied this criterion, explaining 45% and 16% of the variance, respectively.

Molecular diversity from quantitative autoradiography

Following the recent work of Goulas and colleagues 41, we analysed quantitative data about the density of neurotransmitter receptors obtained from in vitro quntitative autoradiography. Data were obtained for 15 different types of receptors: glutamate (AMPA, NMDA, kainate), GABA (GABA_A, GABA_A/BZ, GABA_B), acetylcholine (muscarinic M₁, M₂, M₃, nicotinic a₄b₂), noradrenaline (a₁, a₂), serotonin (5-HT_1A, 5-HT₂), and dopamine (D₁). Thus, both excitatory and inhibitory receptors were considered, and both ionotropic and metabotropic receptors.

The receptor autoradiography data collection and processing are described in detail in the original publication ⁴¹. Briefly, in vitro autoradiography was performed on four postmortem cerebral hemispheres obtained from three human donors with no known history of neurological or psychiatric diseases (one female; age 75 ± 3 years) with their previous written consent. All procedures were in accordance with the ethical requirements of the body donor program of the Department of Anatomy, University of Dusseldorf (Dusseldorf, Germany). The causes of death were reported as cardiac arrest, lung edema, and myocardial infarction; postmortem delay was 12 ± 5 hours (neurotransmitter binding-site densities are stable up to 70-80 hours postmortem). For additional details, see 42. Laminar data were collected for 44 visual, somatosensory, auditory and multimodal association regions of the human cerebral cortex, and summarised into receptor densities for infra-, supra-, and granular layers for each region. The same regions were also used to obtain a redundancy-to-synergy gradient (albeit without full cortical coverage) as described above; for this, areas V2v and V2d were combined together, as were areas 37B, 37L and 37M, and areas 10L and 10M; data from both hemispheres were combined to obtain one value per region, and the corresponding receptor density values were averaged separately for each layer. Following previous work ⁴⁰, area 24 was not included in the present analysis due to its lack of a granular layer; thus, a total of 39 areas were considered.

Molecular diversity was then estimated as described by Goulas and colleagues ⁴⁰. Briefly, a vector N was obtained for each area, encoding its normalised receptor profile so that each entry denotes the density of a specific receptor, divided by the maximum density value observed for this receptor across all areas. Diversity of each area was then quantified as the Shannon entropy H of the normalised receptor profile N, computed as

$$\text{H}=-\text{sum}(\text{N}\ast \text{log}(\text{N}))/\text{log}(\text{M}).$$

Here, M denotes the length of the vector N, i.e., 45 elements (15 receptors times three layers), and log is the natural logarithm (so that entropy was normalised to lie between 0 and 1) ⁴⁰.

Validation with surrogate data methods

We generated pseudo-gradients of redundancy-to-synergy patterns in three different ways. The first way was to generate surrogate pseudo-synergy matrices by randomly rewiring the matrix of inter-regional synergy prior to obtaining the (pseudo-)synergy ranks for the gradient, while using the original redundancy ranks, to test whether our results could be obtained if synergy were randomly distributed across regions. The second approach was to obtain a random vector that has the same (negative) correlation with redundancy, and then using it to obtain pseudo-synergy ranks to compute the redundancy-to-synergy gradient (again with the redundancy ranks being the true ones), to test whether the observed anticorrelation would suffice to produce our results. The third approach was to generate phase-randomised surrogate timeseries for each subject by taking the Fourier transform of each region’s activity, replacing the Fourier phase with a random (antisymmetric) complex vector, and taking the inverse Fourier transform. Then, matrices of redundancy and synergy were computed from these phase-randomised timeseries for each subject, and used to build a redundancy-to-synergy gradient, to test whether our results could arise from signals with the same autocorrelation, but no correlation with each other.

Statistical analysis

One-sample non-parametric t-tests with 10,000 permutations were used to determine whether the synergy-redundancy scores were significantly different from zero for each of the Yeo resting-state subnetworks and for each cytoarchitectonic class of Von Economo; FDR correction for multiple comparisons was adopted according to the Benjamini-Hochberg procedure ¹⁰⁹.

The statistical significance of within-group differences was determined with non-parametric permutation t-tests (paired-sample), with 10,000 permutations. Two-sample non-parametric t-tests (also with 10,000 permutations) were instead used to test the statistical significance of human-macaque comparisons, and of comparisons between different subsets of connections in the brain. The use of non-parametric tests alleviated the need to assume normality of data distributions (which was not formally tested). All tests were two-sided, with an alpha value of 0.05. The effect sizes were estimated using Hedges’s measure of the standardised mean difference, g. To statistically assess the difference between effect sizes obtained from comparing humans and macaques using different measures, we used a Z-test as described by Borenstein et al. (2009) ¹¹⁰.

To ensure robustness to possible outliers, all correlations were quantified using Spearman’s rank-based non-parametric correlation coefficient. To further ensure the robustness of our results to the potential confounding effect of spatial autocorrelation and contralateral symmetry ^53,111, we also estimated p-values from a spatial permutation test which generates a null distribution of 10,000 randomly rotated brain maps with preserved spatial covariance (“spin test”) ^53,101. This analysis is only applicable for parcellations with full cortical coverage; when data were only available for the left cortical hemisphere, they were mirrored to the corresponding regions of the right hemisphere in order to perform the spatial rotations, since this test explicitly controls for contralateral symmetry, and then we only considered this hemisphere for computing the empirical and permuted correlations ⁵³.

Extended Data

Extended Data Fig. 1. Synergistic and redundant interactions in the brain.

(a-c) Group average matrices of pairwise functional interactions between brain regions of the Schaefer-232 atlas, quantified by (a) redundancy; (b) synergy; (c) traditional functional connectivity (Pearson correlation). (d) Mean regional density of redundant interactions, after thresholding the group-average redundancy matrix to retain the 5% strongest edges, for display purposes. (e) Mean regional density of synergistic interactions, after thresholding the group-average synergy matrix to retain the 5% strongest edges, for display purposes. (f) Spearman correlation (two-sided CI: [-0.51, -0.28]) between synergy vs. redundancy ranks across cortical regions.

Extended Data Fig. 2.

Synergy-redundancy identification and NeuroSynth meta-analysis are robust to the use of alternative methods. Left: Group-average matrices of redundant and synergistic interactions; Middle: Redundancy-to-synergy gradient scores (synergy rank minus redundancy rank) displayed on medial and lateral brain surfaces (left hemisphere); Right: Results of the NeuroSynth term-based meta-analysis, relating the distribution of redundancy-to-synergy gradient across the brain to a gradient of cognitive domains, from lower-level sensorimotor processing to higher-level cognitive tasks (note that one term, “visual semantics”, was excluded from visualisation because it failed to reach the threshold of Z > 3.1, leaving 23 terms). (a) DK-308 parcellation with equally-sized cortical areas (500 mm2), obtained as subdivisions of the Desikan-Killiany cortical atlas. (b) Lausanne-129 parcellation, comprising the DK-114 cortical ROIs, supplemented with 15 subcortical regions. (c) Synergy and redundancy computed without deconvolution of the hemodynamic response function (HRF) from the BOLD signal timeseries. (d) Synergy and redundancy computed from discretised (binary) BOLD signal timeseries.

Extended Data Fig. 3. Robustness of synergy and redundancy network results (efficiency, modularity, and within- vs between-resting state subnetwork comparison) to alternative node and edge definitions.

(a-d) Robustness of network results to the use of the 308-ROI cortical parcellation. (e-h) Robustness of network results to using synergy and redundancy normalised by TDMI. (i-l) Robustness of network results to using synergy and redundancy obtained from discretised signals. For all violin plots: each colored circle represents one subject; white circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001 from paired-sample non-parametric permutation t-test (two-sided); n = 100 unrelated HCP subjects. For all box-plots: white circle, median; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001 from two-sample non-parametric permutation t-test (two-sided). For (c-d) and (k-l), Within-RSN n=7178 connections; Between-RSN n=46414 connections. For (g) and (h), Within-RSN n=14784 connections; Between-RSN n=79772 connections.

Extended Data Fig. 4. Robustness of synergy and redundancy structural results to alternative node and edge definitions.

(a-c) Robustness of network results to the use of the 308-ROI cortical parcellation. (d-f) Robustness of network results to using synergy and redundancy normalised by TDMI. (g-i) Robustness of network results to using synergy and redundancy obtained from discretised signals. For all violin plots: each colored circle represents one subject; white circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001 from paired-sample non-parametric permutation t-test (two-sided); n = 100 unrelated HCP subjects. For all box-plots: white circle: median; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; *** p < 0.001 from two-sample non-parametric permutation t-test (two-sided). For (b-c), SC+, n=6864 direct connections; SC-, n=88000 connections. For (e-f) and (h-i), SC+, n=5276 direct connections; SC-, n=48548 indirect connections.

Extended Data Fig. 5. Additional validation of synergy and redundancy network results.

(a) Alternative measure of global integration (area under the curve of the size of the largest connected component across thresholds). (b) Alternative structural-functional dissimilarity (mean Hamming distance). For both (a) and (b): *** p < 0.001 from paired-sample non-parametric permutation t-test (two-sided), n=100 unrelated HCP subjects. (c) Comparison of global efficiency of synergy and redundancy networks of each subject with the average global efficiency of 100 synthetic null networks with edges randomly drawn from the distribution between 0 and the empirical TDMI. (d) Comparison of modularity of synergy and redundancy networks of each subject with the average modularity of 100 synthetic null networks with edges randomly drawn from the distribution between 0 and the empirical TDMI. For (c) and (d), *** p < 0.001 (FDR-corrected) from two-sample non-parametric permutation t-test (two-sided); n = 100 unrelated HCP subjects and n=100 synthetic null networks. For all violin plots: each colored circle represents one subject; white circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range.

Extended Data Fig. 6. Validation analysis for human-macaque comparison of synergy and redundancy.

(a-d) Simulation of human fMRI data with same TR as the macaque data shows that human-macaque differences in synergy cannot be attributed solely to TR differences between datasets. (a) The dynamic mean field (DMF) model used to simulate human fMRI data combines macroscale information about neuroanatomy and structural connectivity (from DTI) with excitatory and inhibitory neuronal populations interconnected by AMPA, NMDA and GABA synapses, providing a neurobiologically plausible account of regional neuronal firing rate, which is turned into simulated BOLD signal by means of the Balloon-Windkessel hemodynamic model. (b) Using a TR of 0.72s (the same as the empirical HCP data), the model is fitted to the empirical HCP data by finding the value of the global coupling parameter G that minimises the Kolmogorov-Smirnov distance between the distributions of empirical and simulated functional connectivity dynamics (FCD). The KS distance is minimised for G=1.6, which is the value of G used for subsequent simulations with TR=2.6s (the same TR as the macaque data). (c) The proportion of synergistic information exchange across the brain is significantly higher in simulated human data than in empirical macaque data with the same TR=2.6s (p<0.001). (d) The proportion of redundant information exchange across the brain is also significantly higher in simulated human data than empirical macaque data (p=0.036). Statistical significance assessed with two-sample non-parametric permutation t-test (two-sided); DMF HCP data: n=100 simulations; macaque data: n=19 distinct sessions from 10 individual macaques. (e-f) The human-macaque comparison of synergy and redundancy proportion is robust to bandpass filtering both human and macaque functional MRI data between 0.008-0.09Hz. The proportion of synergistic information exchange across the brain is significantly higher in humans (p<0.001) (e) whereas the proportion of redundant information exchange across the brain is equivalent in humans and macaques (p=0.943) (f). Statistical significance assessed with two-sample non-parametric permutation t-test (two-sided). Human data: n=100 unrelated HCP subjects. Macaque data: n=19 distinct sessions from 10 individual macaques. (g-h) The proportion of total synergy is significantly higher in humans than macaques (p<0.001) (h), even when only considering humans whose total FC is in the range of values exhibited by macaques (excluding one outlier with extreme value), such that there is no significant difference in total FC between the two groups (p=0.196), shown in (g). Statistical significance assessed with two-sample non-parametric permutation t-test (two-sided). Human data: n=28 unrelated HCP subjects with FC values in the range of the macaque FC values. Macaque data: n=19 distinct sessions from 10 individual macaques (one outlier excluded in (g)). For all violin plots: each colored circle indicates one data-point; white circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range; n.s., p > 0.05; * p < 0.05; *** p < 0.001.

Extended Data Fig. 7. Characterisation of synergistic and redundant network profiles in macaque brains are similar to humans.

(a) Synergistic interactions between regions of the macaque brain. (b) Redundant interactions between regions of the macaque brain. (c) Anatomical connectivity was estimated from axonal tracing and diffusion MRI (Shen et al., 2019), and Spearman correlation coefficient was used to assess the similarity of redundancy and synergy matrices with structural connectivity, after thresholding to ensure equal numbers of connections. (d) The network organisation of synergistic interactions exhibits significantly higher global efficiency than redundant interactions (p < 0.001). (e) The network organisation of redundant interactions exhibits significantly higher segregation (modularity) than synergistic interactions(p < 0.001). (f) Networks of redundant interactions are significantly more correlated with underlying anatomical connectivity than synergistic interactions (p < 0.001). For all tests: *** p < 0.001 from paired-sample non-parametric permutation t-test (two-sided); n=19 distinct sessions from 10 individual macaques (Supplementary Table 7). For all violin plots: each colored circle indicates one data-point; white circle: median; central line: mean; box limits, upper and lower quartiles; whiskers, 1.5x inter-quartile range.

Extended Data Fig. 8. Synergy-redundancy gradient correlates with unadjusted cortical expansion and gene expression.

(a) Significant Spearman correlation (two-sided CI: [0.145, 0.476]) between regional redundancy-to-synergy gradient scores and unadjusted regional cortical expansion from chimpanzee (Pan troglodytes) to human (both on DK-114 cortical atlas, both hemispheres; n =114 cortical regions). (b) Significant Spearman correlation (two-sided CI: [0.109, 0.567]) between regional redundancy-to-synergy gradient scores and unadjusted regional expression of brain-related human-accelerated (HAR) genes (both on left hemisphere of DK-114 atlas: n=57 left-hemisphere regions). (c) Significant Spearman correlation (two-sided CI: [0.010, 0.496]) between regional redundancy-to-synergy gradient scores and unadjusted regional expression of non-brain-related human-accelerated (HAR) genes (both on left hemisphere of DK-114 atlas; n=57 left-hemisphere regions). p_spin indicates the p-value estimated from a spatial permutation test comparing the empirical correlation against 10,000 randomly rotated brain maps with preserved spatial covariance.

Extended Data Fig. 9. Characterisation of PLS components of 20,647 genes from the Allen Institute for Brain Science, for the 308-ROI subdivision of the Desikan-Killiany cortical parcellation.

(a) Spearman correlation (two-sided CI: [0.334, 0.517]; n=308 regions) between the redundancy-to-synergy regional pattern, and the first principal component of PLS (PLS1). (b) Spearman correlation (two-sided CI: [0.216, 0.417]; n=308 regions) between the redundancy-to-synergy regional pattern, and the second principal component of PLS (PLS2). For both (a) and (b), color-bars correspond to scatter-plot axes. (c) The variance explained by the first 2 PLS components is significantly higher than would be expected based on random patterns with preserved spatial autocorrelation, assessed using spin-based permutations (Methods). (d-e) Significant enrichment of HAR-Brain genes in PLS1 and PLS2. (f) Significant HAR-Brain gene enrichment is also observed using an alternative approach: ridge-regularised PLS regression on the binarised cortical pattern of synergy vs redundancy prevalence. (g-h) HAR-Brain gene enrichment in PLS1 and PLS2 is also observed when controlling for spatial autocorrelation using spin-based permutations. (c-h) Statistical significance is assessed via bootstrap resampling of Z-scores; histograms indicate the relative frequency (over 1,000 bootstraps) of the mean Z-score of a random sample of genes of equal size as the HAR-Brain genes. Red vertical line: empirical mean Z-score of HAR-Brain genes.

Extended Data Fig. 10. Enrichment analysis for genes pertaining to synaptic formation, whose regional distribution corresponds to the distribution of aerobic glycolysis in the human brain, as reported by Goyal et al. (2014) (“aerobic glycolysis genes”).

(a-b) PLS1 and PLS2 are significantly enriched for aerobic glycolysis genes. (c) Enrichment for genes related to aerobic glycolysis is also observed using an alternative approach: ridge-regularised PLS regression on the binarised cortical pattern of synergy vs redundancy prevalence. (d-e) Significant enrichment for genes related to aerobic glycolysis in PLS1 and PLS2 is also observed when controlling for spatial autocorrelation using spin-based permutations. (a-e) Statistical significance is assessed via bootstrap resampling of Z-scores; histograms indicate the relative frequency (over 1,000 bootstraps) of the mean Z-score of a random sample of genes of equal size as the aerobic glycolysis genes. Red vertical line: empirical mean Z-score of aerobic glycolysis genes.

Data availability

The HCP DWI data in SRC format are available online (http://brain.labsolver.org/diffusion-mri-data/hcp-dmri-data). The HCP fMRI data are available online (https://www.humanconnectome.org/study/hcp-young-adult/data-releases). Macaque MRI data are available from the PRIMatE Data Exchange (PRIME-DE) through the Neuroimaging Informatics Tools and Resources Clearinghouse (NITRC; http://fcon_1000.projects.nitrc.org/indi/indiPRIME.html). The PET data that support the findings of this study are available from author James Rowe (James.Rowe@mrc-cbu.cam.ac.uk) upon reasonable request for academic (non-commercial) purposes, subject to restrictions required to preserve participant confidentiality. The macaque connectome is available online on Zenodo: DOI: 10.5281/zenodo.1471588. The CoCoMac database on which it is based, is also available online: http://cocomac.g-node.org/main/index.php?. The Genotype-Tissue Expression (GTEx) database (data source: GTEx Analysis Release V6p) is available at https://www.gtexportal.org/. The BrainSpan Study [BSS] database is available at http://brainspan.org. Cortical gene expression patterns were taken from the transcriptomic data of the Allen Human Brain Atlas (AHBA, http://human.brain-map.org/static/download). Region-wise maps of chimpanzee-to-human cortical expansion and HAR gene expression are available as Supplementary Materials from Wei et al. (2019) ³⁴; DOI: https://doi.org/10.1038/s41467-019-12764-8. The NMT anatomical volume and associated probabilistic tissue segmentation maps (GM, WM and CSF) are freely available online: https://afni.nimh.nih.gov/pub/dist/atlases/macaque/nmt and http://github.com/jms290/NMT. The maps of average regional Glycolytic Index (GI) are available as Supplementary Materials from Vaishnavi et al. (2010) ³⁹; DOI: https://doi.org/10.1073/pnas.1010459107. The genes whose expression is associated with the regional distribution of GI in the human brain are available as Supplementary Materials from Goyal et al. (2014) ³⁸; DOI: 10.1016/j.cmet.2013.11.020. Anonymized receptor autoradiography data from Goulas et al. (2021) ⁴⁰ are available online: https://github.com/AlGoulas/receptor_principles. The measure of cortical wiring distance is available as Supplementary Information from Paquola et al. (2020) ³²; DOI: https://doi.org/10.1371/journal.pbio.3000979.

Code availability

Data analysis was carried out in MATLAB version 2019a.

The Java Information Dynamics Toolbox v1.5 is freely available online: (https://github.com/jlizier/jidt). An updated version with MATLAB/Octave code to compute synergy and redundancy from Integrated Information Decomposition of timeseries with the Gaussian MMI solver is available as Supplementary Information. The CONN toolbox version 17f is freely available online (http://www.nitrc.org/projects/conn). DSI Studio is freely available online (https://dsi-studio.labsolver.org/). The Brain Connectivity Toolbox code used for graph-theoretical analyses is freely available online (https://sites.google.com/site/bctnet/). The code used for NeuroSynth meta-analysis is freely available online: (https://www.github.com/gpreti/GSP_StructuralDecouplingIndex). The HRF deconvolution toolbox v2.2 is freely available online: (https://www.nitrc.org/projects/rshrf). The Pypreclin pipeline code v1.0.1 is freely available at GitHub (https://github.com/neurospin/pypreclin). The code for PLS analysis of gene expression profiles is freely available online: https://github.com/SarahMorgan/Morphometric_Similarity_SZ. The R package plsgenomics v1.5 is freely available online: https://CRAN.R-project.org/package=plsgenomics. The GOrilla platform is available online at http://cbl-gorilla.cs.technion.ac.il. The REVIGO platform is available online at http://revigo.irb.hr. The code for the dynamic mean-field model is freely available at http://www.gitlab.com/concog/fastdmf. The code for spin-based permutation testing of cortical correlations is freely available online at https://github.com/frantisekvasa/rotate_parcellation. The code for gene enrichment relative to an ensemble of null phenotypes is freely available online at https://github.com/benfulcher/GeneCategoryEnrichmentAnalysis/wiki/Ensemble-enrichment.

FreeSurefer v5.3.0 is available at https://surfer.nmr.mgh.harvard.edu/.

SPM12 is available at www.fil.ion.ucl.ac.uk/spm/software/spm12/.