Missing data: A statistical framework for practice

Abstract

Missing data are ubiquitous in medical research, yet there is still uncertainty over when restricting to the complete records is likely to be acceptable, when more complex methods (e.g. maximum likelihood, multiple imputation and Bayesian methods) should be used, how they relate to each other and the role of sensitivity analysis. This article seeks to address both applied practitioners and researchers interested in a more formal explanation of some of the results. For practitioners, the framework, illustrative examples and code should equip them with a practical approach to address the issues raised by missing data (particularly using multiple imputation), alongside an overview of how the various approaches in the literature relate. In particular, we describe how multiple imputation can be readily used for sensitivity analyses, which are still infrequently performed. For those interested in more formal derivations, we give outline arguments for key results, use simple examples to show how methods relate, and references for full details. The ideas are illustrated with a cohort study, a multi-centre case control study and a randomised clinical trial.

1. Introduction

Missing data are inevitable and ubiquitous in medical and social research. They often complicate the analysis and cause consternation in the study team. Yet there have been substantial methodological developments in the analysis of partially observed datasets, and there are now many available approaches. Nevertheless, routine practice often falls short and fails to frame the issues raised by missing data appropriately in the context of the substantive study analysis.

For example, Wood et al. (2004) reviewed 71 papers published in the British Medical Journal (BMJ), Journal of the American Medical Association (JAMA), Lancet and the New England Journal of Medicine (NEJM). They found 89% had partly missing outcome data, and in 37 trials with repeated outcome measures, 46% restricted analysis to those with complete records; only 21% reported sensitivity analysis to the missing data assumptions underpinning their primary analysis. Bell et al. (2014) updated this review and found that while the use of multiple imputation (MI) was now considerably more popular, there had been little progress with sensitivity analysis. This is consistent with Sterne et al. (2009), who searched four major medical journals (BMJ, Lancet, NEJM, JAMA) from 2002–2007 for articles involving original research in which MI was used (see also Klebanoff & Cole, 2008), reporting

“Although multiple imputation is increasingly regarded as a ‘standard’ method, many aspects of its implementation can vary and very few of the papers that were identified provided full details of the approach that was used, the underlying assumptions that were made, or the extent to which the results could confidently be regarded as more reliable than any other approach to handling the missing data (such as, in particular, restricting analyses to complete cases).”

Indeed, while the CONSORT guidelines (Schulz et al., 2010) state that the number of patients with missing data should be reported by treatment/exposure group, Chan & Altman (2005) estimated that 65% of studies in PubMed journals do not even report the handling of missing data.

The aim of this article is to set out an accessible framework for addressing the issues raised by missing data and illustrate its application with data from trials and observational studies. In many cases, we believe that it is unfamiliarity, rather than technical hurdles, that hinders adoption of an improved approach. Towards the end, we highlight areas where there have been recent methodological developments, and where more methodological work is needed.

The article is structured as follows. We begin in Section 2 with a practical review of Rubin’s missing data mechanisms, leading to consideration of when an analysis restricted to the complete data is sufficient in Section 3. Armed with this, in Section 4 we give with a framework for handling the issues raised when data are missing, outlining how to structure the analysis. Then, we give more detail about how the steps recommended in the framework are implemented, specifically analysis under Missing At Random (MAR) – principally MI and inverse probability weighting (IPW) – in Section 5. As the framework argues for increased use of sensitivity analysis, we discuss methods for performing these in Section 6. Section 7 reviews software for MI, and Section 8 highlights some active research topics. We conclude with a discussion in Section 9.

2. Missing Data Mechanisms

We begin with a practical review of Rubin’s missing data mechanisms (Rubin, 1976). Suppose we have three variables (more generally sets of variables), (Y,X,Z), with Y and Z fully observed. Table 1 shows the three possible scenarios for the probability of X being missing, that is the missingness mechanism.

Table 1. Definition of Rubin’s missingness mechanisms.

Probability of X being missing depends on	Missingness mechanism
Neither X, Y or Z	Missing Completely At Random
Y and/or Z, but given (Y, Z) not on X	Missing At Random
X, Y and/or Z	Missing Not At Random

In applications, if data are Missing Completely at Random (MCAR) this means that the reasons for the missing data are unrelated to the questions we seek to answer from the analysis. In this setting, we may have variables that predict when X is missing (e.g. for administrative reasons unrelated to the scientific question), but they tell us nothing about the missing values (so they cannot be used to predict the actual missing values). Therefore, using all the available data for each analysis will give us unbiased inferences, but these will be less precise than if we had observed all the data.

We now define a new variable R to be 1 if X is observed and 0 otherwise. Then if data are MCAR it is necessary that neither Y nor Z is predictive of R. The plausibility of this can be explored empirically with a logistic regression. However, note that this is not sufficient for MCAR: for example X may be predictive of X being missing, but we cannot observe this!

If X is MAR, this means that simple summary statistics estimated from the observed X will be biased, because when we consider X alone, the reason for missing values depends on the unseen values themselves. The key point about MAR is that this association can be broken given the observed variables. Thus R depends on fully observed Y and Z, but given these R(i.e. the probability that X is missing) does not depend on X. Again, this can be explored using a logistic regression, but note it is not sufficient for MAR, because we cannot check for any residual dependence of R on X.

MAR has a very important consequence. This is that (see Appendix A.1 for details) the distribution of X given Y, Z is the same whether or not X is observed. Therefore, under MAR, we can estimate the distribution of X given Y, Z in the observed data and use this (implicitly or explicitly) to impute the missing values of X. As we expand on below, this is the key insight that is used explicitly by MI, and implicitly in other approaches to missing data, such as IPW. Note that these points also hold under MCAR.

In the third scenario in Table 1, if X is neither MCAR nor MAR, then we say it is Missing Not at Random (MNAR). This means that, even given Y,Z, the probability of observing X depends on the actual value of X. When X is MNAR, this in turn means that Appendix equation (A.1) does not hold, so that the distribution of X given Y, Z is different between units (individuals) for whom X is observed and for whom X is missing.

This discussion implies that handling missing data would be relatively straightforward if we knew for sure the missing data mechanism. Unfortunately, as we have highlighted in the previous paragraphs, it is not possible to determine this definitively from the data itself – although the logistic regression with the missing data indicator R can give us important clues. In particular, we can never definitively distinguish between MAR and MNAR. Therefore, sensitivity analyses – where we explore the robustness of our inferences to different contextually plausible assumptions about the missing data mechanism – have a key role to play in applications.

First, though, we discuss when an analysis restricted to the subset of complete records is valid.

3. Complete Records Analysis

When variables have missing values, the default in all statistical software is to use only those with complete records. If we are simply calculating the mean of a variable, this corresponds to taking average of all the observed values of that variable. If we assume data are MCAR this will give valid results; otherwise – as discussed in the previous section – it will be biased.

In regression models, a complete records analysis only includes those individuals with no missing data on any of the variables in the regression model. Besides possible bias, this can quickly lead to a substantial reduction in the sample size and consequent statistical information. Moreover, all the effort involved in collecting data on an individual is discarded if just one of their variables is missing.

For these reasons, while complete records analysis is a natural and useful starting point, except in special circumstances it will not be not valid, or efficient. We now investigate these circumstances; the results of this exploration are summarised in Box 1.

Box 1. When is a complete records analysis valid and efficient?

When is fitting a model using complete records valid?

• -when, regardless of which variables in the model have missing data, it is plausible that the probability of each individual's record being complete depends on the covariates only, and not the outcome.

When is it efficient?

• -when either (i) all the missing values are in the outcome or (ii) each individual with missing covariate(s) also has a missing outcome

3.1. When is a complete records analysis valid?

By valid, we mean that (i) estimators of population parameters are consistent (i.e. that as the sample size increases any bias goes to zero and their variance also goes to zero) and (ii) that inferences (e.g. p-values, confidence intervals) are correct: for example the 95% confidence interval calculated from a complete records analysis includes the population value in 95% of replications.

Fortunately, it is relatively straightforward to see when a complete records analysis is approximately valid. Suppose our scientifically substantive model is a generalised linear model of Y_i on variables X_i (individual (or unit) i = 1,…, n) and assume that the regression model is correctly specified. Let R_i = 1 if (Y_i, X_i) are all observed, that is data are complete for unit i, and R_i = 0 otherwise. We focus not on which values are missing, but simply on which of the variables (Y, X) are driving the probability of a complete record.

Denote the ith unit’s contribution to the regression, given a complete record, by f(Y_i|X_i, R_i = 1), where for notational simplicity we omit the parameters (θ_Y|X,θ_R) of the regression of Y on X and the model for R. Using standard conditional probability arguments,

$$f\left(Y_i\mid X_l,R_i=1\right)=\frac{f\left(Y_l,X_i,R_i=1\right)}{f\left(X_i,R_i=1\right)}=\frac{f\left(R_i=1\mid Y_i,X_l\right)f\left(Y_i,X_l\right)}{f\left(R_i=1\mid X_l\right)f\left(X_l\right)}$$ (1)

$$=f\left(Y_i\mid X_i\right)\text{when}f\left(R_l\mid Y_i,X_i\right)=f\left(R_i=1\mid X_i\right).$$ (2)

In words, if the probability of a complete record, given the covariates does not depend on the outcome variable, Y, then a complete records analysis is valid. This is because the regression in the complete records (left-hand side of (1)) is the same as the regression in the population (right-hand side of (2)).

In the special case of the logistic regression of Y on X₁ and X₂, we can further relax this criteria, as summarised in Table 2 (see Appendix A.2 for a justification). This is simply a version of the same argument that justifies the use of logistic regression for case-control studies; there selection depends on case/control status (Y), but not on exposure (X), and so the estimate of the odds ratio relating exposure to outcome is valid. The validity of complete records in logistic regression is explored in more detail by Bartlett et al. (2015a), using simulations and an example.

Table 2.

Variables involved in missing data mechanisms and the consequent expected bias (compared to the true population values) of coefficient estimates from using the complete records to fit a linear regression and logistic regression of Y on X₁, X₂

Mechanism depends on	Biased estimation of parameters using complete records
	Typical regression				Logistic regression
	Constant	Coefficient of X1	Coefficient of X2		Constant	Coefficient of X1	Coefficient of X2
Y	Yes	Yes	Yes		Yes	No	No
X 1	No	No	No		No	No	No
X 2	No	No	No		No	No	No
X1, X2	No	No	No		No	No	No
Y, X1	Yes	Yes	Yes		Yes	Yes	No
Y, X2	Yes	Yes	Yes		Yes	No	Yes
Y, X1, X2	Yes	Yes	Yes		Yes	Yes	Yes

3.2. When is a complete records analysis efficient?

An efficient statistical analysis gets the most precise estimates of model parameters given the available data. This means a complete records analysis is potentially inefficient because any unit, or individual, who has even one missing value is excluded from the analysis. Therefore, all the time and effort spent on collecting their data is wasted. This consideration usually means an analysis of the complete data is insufficient.

A natural question is whether it is worth performing a complete records analysis, or whether it is better to move straight to more sophisticated methods? Following Sterne et al. (2009), we always begin by using logistic regression to explore predictors of complete records, and performing a complete records analysis, since (as the examples below illustrate) this builds intuition for what should be expected from more sophisticated methods, and how to interpret their results.

3.3. Two examples of complete records analysis

Example 1: Risk of sudden unexplained infant death with bed-sharing

Carpenter et al. (2013b) report a case-control study to investigate whether bed-sharing is a risk factor for sudden infant death syndrome. This is an individual-patient-data meta-analysis of data from five case-control studies, with in total 1472 cases and 4679 controls.

The authors wished to adjust for a number of known risk factors for sudden infant death, including alcohol and drug use. However, unfortunately, data on alcohol and drug use were unavailable in three of the five studies (about 60% of the data).

In this example, we do not need to look at whether other variables in the dataset predict alcohol and drug use; the reason they are missing is because, at the design stage, a decision was taken not to collect these data. The substantive model adjusted for study as a covariate; therefore, given the covariates, the probability of a complete record does not depend on the outcome, which in this example is the case-control status. Therefore, as discussed in the supplementary material for the original paper, we expect that the complete records analysis that adjusts for alcohol and drug use will be valid, but potentially inefficient.

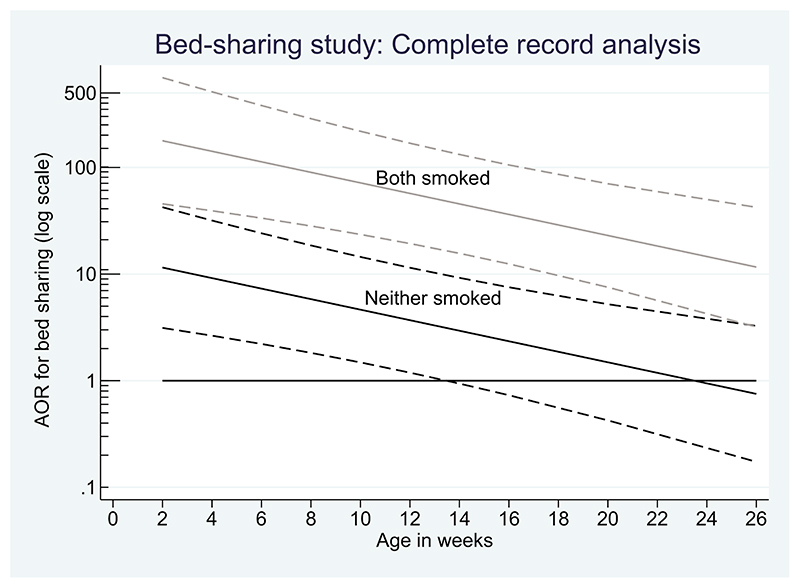
Figure 1 shows the results of the complete records analysis. Even for children of non-smokers, we see evidence of an increased risk of sudden, unexplained infant death when bed-sharing with children under 12 weeks old.

Figure 1.

Complete records analysis of the bed-sharing study: adjusted odds ratio (AOR) showing how the risk of bed-sharing for sudden infant death changes with the baby’s age. Grey lines: risk when mother smokes; black lines: risk for non-smokers. Dashed lines: 95% confidence interval

Despite the missing data, because the reason for missing data is unlikely to involve the outcome (case/control status), it is reasonable to believe this complete records analysis result is valid. However, a lot of carefully collected data have been omitted. Therefore, we expect an analysis under a MAR – that makes full use of the partially observed data – to recover information (giving narrower confidence intervals) but not alter the principal conclusion. We keep this expectation in mind when we discuss the results of using multiple imputation (MI) for this example below.

Example 2: UK 1958 National Childhood Development Study (NCDS)

The NCDS is a continuing longitudinal study that seeks to follow the lives of all those living in Great Britain who were born in one particular week in 1958. The aim of the study is to improve understanding of the factors affecting human development over the whole lifespan (see, e.g. https://ukdataservice.ac.uk/).

We will explore this example in some detail and focus on how early life factors affect educational achievement aged 23. Table 3 shows the variables that we will consider. Our illustrative substantive model seeks to understand contextually important questions about the effect of a child’s early life on their subsequent educational achievement (Carpenter & Plewis, 2011). In particular we focus on (i) whether there is a non-linear effect of mother’s age on the probability of the child obtaining educational qualifications by age 23 and (ii) whether this effect is different for families in social housing. To explore this, we use the following regression:

$$\text{logit}\{\text{Pr}(\text{child}\text{has}\text{no}\text{educational}\text{qualifications}\text{at}23\text{years})\}={\beta }_0+{\beta }_1\text{care}+{\beta }_2\text{soch}7+{\beta }_3\text{invbwt}+{\beta }_4\text{mo\_age}+{\beta }_5\text{mo\_agesq}+{\beta }_6\text{agehous}+{\beta }_7\text{agesqhous}.$$ (3)

Table 3. Description of NCDS variables used in the analysis.

chrtid	Unique child (individual) identifier
fammove	Number of family moves since child’s birth (from 0 to 9)
readtest	Childhood reading test score at 7 years (from 0 to 35, high is good)
bsag	Behavioural score (from 0 to 70, high indicates more behavioural problems at 7 years)
sex	Child’s sex (0 – boy; 1 – girl)
care	In care before 7 years old (0 – no; 1 – yes)
soch7	In social housing before 7 years old (0 – no; 1 – yes)
invbwt mo_age	inverse of birthweight (ounces) Mother’s age at child’s birth (centred at 28 years)
mo_agesq noqual2	Square of mo_age Binary variable, child has no qualifications at 23 years of age (0 – at least 1 qualification; 1 – no qualifications)
agehous agesqhous	Interaction: mo_age× soch7 Interaction: mo_agesq× soch7

For the five underlying variables in the substantive model (noqual2, care, soch7, invbwt, mo_age), the pattern of missing data is shown in Table 4.

Table 4. Pattern of missing values in the NCDS data: √=observed, · = missing; noqual2 is the dependent variable in the substantive model.

Pattern	mo_age	invbwt	care	soch7	noqual2	Number	Percentage of total
1	√	√	√	√	√	10,279	58
2	√	√	√	√	·	3,324	19
3	√	√	·	·	·	1,886	11
4	√	√	·	·	√	1,153	7
5	Other patterns					989	5

The principal pattern is that noqual2 is missing, either alone (19%) or in conjunction with other variables (11%). This is unsurprising in a longitudinal study of this kind and reflects the inevitable attrition and loss to follow-up.

Next, we consider whether a complete records analysis is likely to be valid, and how this may be expected to compare with the results of an analysis assuming MAR.

For a complete records analysis to be valid, the probability of a complete record, given covariates, needs to be independent of the dependent variable (noqual2, the probability of no educational qualifications age 23). Logistic regression of the probability of a complete case on noqual2 and each of the covariates in turn shows that (i) noqual2 is predictive of a record being complete (i.e. having no missing values), but (ii) after additionally adjusting for care it is no longer close to statistical significance. This suggests that, given a covariate (care) in the substantive model, the probability of a complete record does not strongly involve the dependent variable in the substantive model, noqual2. Therefore, from (2), a complete records analysis could be approximately valid.

Turning to the MAR assumption, we now consider where the missing data are. Around 30% are in the dependent variable, noqual2. Moreover, the logistic regressions in the previous paragraph suggest that it is reasonable that noqual2 is MAR given the covariates in the substantive model.

These two paragraphs suggest we should not be surprised if the complete records and analysis under MAR give similar results in this example, although the latter may be slightly more efficient. Nevertheless, this does not mean either are necessarily correct, since we cannot definitively verify their assumptions from the data at hand.

Since noqual2 is missing for ≈ 30% of cases, assuming MAR means that given the covariates, the probability of no educational qualifications age 23 is the same, whether or not it is observed. As we have already noted, this is one way of interpreting the MAR assumption. Further, analysis of the complete records shows that all the covariates in (3) are predictive of noqual2, and that care, mo_age and mo_agesq are independent predictors of noqual2 being observed. Thus, the MAR assumption is plausible for the initial analysis, and under this assumption the complete records analysis is likely to be valid.

3.4. When can an MAR analysis gain information over complete records?

As the bed-sharing study illustrates, it makes sense to consider whether an analysis under the MAR assumption, for example using MI, could recover substantial additional information by bringing back into the analysis records with one or more missing values. This brings us to the bottom part of Box 1. While an analysis under MAR will typically gain information relative to a complete records analysis, there are two exceptions: (i) when missing values are in the outcome only, and we assume MAR; and (ii) when each individual with missing covariate(s) also has missing outcome. In both these special cases, individuals with missing data have no information about the regression parameters.

To see why, suppose, as before, the substantive model is a regression of Y on X and Z. The likelihood of the observed data is always obtained by integrating, or summing, the likelihood of the full data over the missing values. Thus, for each individual i with missing Y_i, their contribution to the likelihood is

$$L_i(\theta )={\displaystyle \int f(Y_i|X_i,Z_i,\theta )d{Y}_i=1,}$$ (4)

regardless of whether X_i or Z_i, are observed. Therefore, unless we have the option of including additional information, in the form of what are termed auxiliary variables, which are both: (i) observed when Y_i is missing, and (ii) are good predictors of missing Y_i values, then MI (or equivalent procedures) will recover no information for units with Y_i missing.

Therefore, in the NCDS analysis, unless we have good auxiliary variables, MI will recover no additional information for individuals with missing data patterns (2) and (3) in Table 4.

4. Framework for Analyses When Data are Missing

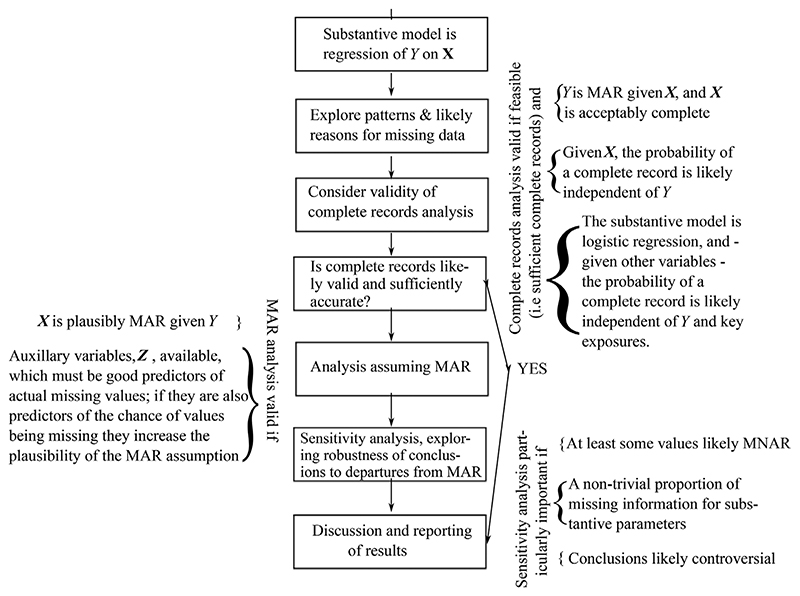
Having discussed the Rubin’s missing data mechanisms and when a complete records analysis is valid, we can present our proposed framework for handling missing data in an analysis in Figure 2. It is hard to give a general definition of ‘acceptably complete’: analysts need to consider whether the information in the complete records is likely sufficient to answer the key scientific questions, and the proportion of the remaining incomplete cases that have missing outcomes – since in the absence of auxiliary variables, they have no information about the model parameters (see (4)).

Figure 2.

Framework for addressing issues raised by missing data, when (i) the scientifically substantive model is a generalised linear model of dependent variable Y_i on covariates X_i (i = 1,…, n) and (ii) we may also have auxiliary variables, Z_i, which are associated with (Y_i, X_i), but which are not in the substantive model

As we touched on above, as part of exploring the reasons for missing data, a number of exploratory regressions are typically useful:

1. define an indicator for all the variables in the substantive model being observed (a complete record) and use logistic regression to identify its key predictors, using both variables that are within the substantive model, and other auxiliary variables, Z, in the dataset.

2. define indicators for the principal patterns of missing values and repeat step (1), and

3. focusing on the variables with the most missing values, use regression to identify key predictors of the missing values.

Because these analyses are exploratory, as illustrated in the examples above, while we should take note of statistical significance, we should not be looking for the ‘best’ model; the aim is to understand plausible causes of and predictors for missing values. When, for reasons discussed and illustrated in the previous section, exploratory analyses suggest a complete records analysis is insufficient, the framework suggests an analysis assuming MAR. This is because, as discussed in Section 2 and Appendix A.1, MAR is the most general assumption about the missing data distribution we can make without recourse to bringing in external information (which is needed in one form or another for analyses assuming MNAR). Therefore, methods analysing data under the MAR assumption are the focus of Section 5.

However, because we cannot definitively identify the missingness mechanism, missing data introduce an element of ambiguity into the conclusions, qualitatively different from the familiar sampling imprecision, and both our analysis and reporting should reflect this. Therefore, having reflected on any differences between the complete records and MAR analysis, and come to some preliminary conclusions, we should explore the robustness of these conclusions to plausible MNAR mechanisms, as suggested in Figure 2. We consider practical methods for this in Section 6.

5. Principled Analysis Methods Assuming Mar

In this section, we discuss analyses assuming data are MAR. There is a very sizeable statistical literature on this, whose evolution and connections are explored in Carpenter & Kenward (2015b). Here we touch on the principal approaches, how they relate to each other, and their practicality. We begin with maximum likelihood, then the Expectation-Maximization (EM) algorithm (which is a method for finding maximum likelihood estimates), MI and IPW.

5.1. Direct likelihood

From a theoretical viewpoint, this is perhaps the most natural way to obtain estimates when data are MAR. We consider two cases, and as usual our substantive model is a regression. In the first case, the dependent variable has missing values but the covariates are fully observed, and in the second the situation is reversed. In all cases, the general approach is the same: we (i) write down the likelihood of the data we intended to observe, (ii) sum or integrate over the missing values to obtain the likelihood of the observed data then (iii) maximise this to obtain the maximum likelihood estimates.

Specifically, suppose that we are interested in the regression of Y on X and Z, where Y values are missing at random. Then the contribution of unit i to the likelihood is

$$L_i(\theta )={{\displaystyle \int }}^{\text{}}f\left(Y_i\mid X_i,Z_i;\theta \right)d{Y}_i=1.$$ (5)

Therefore, under MAR, units where Y_i is missing contain no information about the parameter(s), θ, and can be excluded. This is also the case when, in addition to missing Y_i, one or more of the covariate values are also missing; the first step is again to integrate over Y_i (as in (5)), which shows there is again no information on θ.

Now suppose that the dependent variable is multivariate, say Y_i = (Y_i,1, Y_i,2)^T, and again suppose that the covariates are observed. There are three cases:

$$\begin{array}{rr}\hfill \text{both}{Y}_{i,1}\text{and}{Y}_{i,2}\text{missing}{L}_i& =\underset{Y_1}{{\displaystyle \int }}\underset{Y_2}{{\displaystyle \int }}f\left(Y_{i,1},f_{Y_i,2}\mid X_i,Z_i;\theta \right)d{Y}_{1}d{Y}_2=1\hfill \\ \hfill Y_{i,1}\text{missing}{L}_i& =\underset{Y_1}{{\displaystyle \int }}f\left(Y_{i,1},f_{Y_i,2}\mid X_i,Z_i;\theta \right)d{Y}_1=f\left(Y_{i,2}\mid X_i,Z_i;\theta \right)\hfill \\ \hfill Y_{i,2}\text{missing}{L}_i& =\underset{Y_2}{{\displaystyle \int }}f\left(Y_{i,1},f_{Y_i,2}\mid X_i,Z_i;\theta \right)d{Y}_2=f\left(Y_{i,1}\mid X_l,Z_i;\theta \right).\hfill \end{array}$$ (6)

We see that if one or other of the dependent variables is missing, the contribution to the likelihood is the marginal distribution of the remaining values.

In longitudinal, or multilevel analyses, the marginal likelihood is readily derived and is applied automatically by the computer software. Therefore, assuming MAR, in such settings we obtain valid inference by fitting the model to the observed data. This is often the simplest approach and avoids the need for MI (although MI may still be a natural approach to explore departures to MNAR). Clinical trials, in particular, tend to have reasonably complete baseline data but over the course of longitudinal follow-up missing outcomes are almost inevitable. Assuming MAR, maximum likelihood provides a natural approach to inference. This is especially the case when the protocol-specified primary substantive analysis can be embedded in the longitudinal model for all the follow-up data.

In this setting, a complete records analysis would discard all patients who were not present at the final follow-up visit. This is likely to be biased, as the probability of being present at the final visit is inevitably linked to treatment response. It also discards all the information we obtained from patients who began the study but were not followed through to the end. We now illustrate with an example.

Example 3: Asthma trial

We consider data from a five-arm asthma clinical trial to assess the efficacy and safety of budesonide, a second- generation glucocorticosteroid, on patients with chronic asthma. Four hundred and seventy-three patients with chronic asthma were enrolled in the 12-week randomised, double-blind, multi-centre parallel-group trial, which compared the effect of a daily dose of 200, 400, 800 or 1600 mcg of budesonide with placebo. Further details about the conduct of the trial, its conclusions and the variables collected can be found elsewhere (Busse et al., 1998).

Here, we restrict our attention to the placebo and lowest active dose arm, and focus on the forced expiratory volume, FEV₁, (the volume of air, in litres, the patient with fully inflated lungs can breathe out in 1 s), which was measured at baseline, and 2, 4, 8 and 12 weeks after randomisation.

The intention was to compare FEV₁ across treatment arms at 12 weeks. However, as Table 5 shows (excluding three patients whose participation in the study was intermittent) only 37 out of 90 patients in the placebo arm, and 71 out of 90 patients in the lowest active dose arm, still remained in the trial at 12 weeks.

Table 5. Placebo and lowest active dose arms: mean FEV₁ (litres) at each visit, by deviation pattern and intervention arm.

Dropout pattern	Placebo arm
	Mean FEV1 (L) measured at week					Number	Percent
	0	2	4	8	12
1	2.11	2.14	2.07	2.01	2.06	37	40
2	2.31	2.18	1.95	2.13	–	15	16
3	1.96	1.73	1.84	–	–	22	24
4	1.84	1.72	–	–	–	16	17
All patients (mean)	2.06	1.97	1.98	2.04	2.06	90	100
All patients (standard deviation)	0.59	0.67	0.56	0.58	0.55
	Lowest active arm
1	2.03	2.22	2.23	2.24	2.23	71	78
2	1.93	1.91	2.01	2.14	–	8	9
3	2.28	2.10	2.29	–	–	8	9
4	2.24	1.84	–	–	–	3	3
All patients (mean)	2.05	2.17	2.22	2.23	2.23	90	100
All patients (standard deviation)	0.65	0.75	0.80	0.85	0.81

Table 5 shows that dropout is strongly linked to poor lung function (particularly in the early part of follow-up). Therefore, fitting the substantive model to the 108 patients with complete records is likely to be biased.

However, rather than employing MI, with the data observed at 2, 4 and 8 weeks as auxiliary variables, we can use a longitudinal model which embeds the substantive model. Let i = 1,…, 180 denote patient and j index week. Let Y_i,j denote the baseline (j = 0) and 2, 4, 8, and 12 week data on patient i. Let T_i indicate that patient i was randomised to the active treatment. The substantive regression of 12 week on baseline and treatment is embedded within the following model:

$$\left(\begin{array}{l}{Y}_{i,1}\hfill \\ Y_{i,2}\hfill \\ Y_{i,3}\hfill \\ Y_{i,4}\hfill \end{array}\right)\sim N\left\{\left(\begin{array}{l}{\beta }_{1,0}+{\beta }_{1,1}{Y}_{i,0}+{\beta }_{1,2}{T}_i\hfill \\ {\beta }_{2,0}+{\beta }_{2,1}{Y}_{i,0}+{\beta }_{2,2}{T}_i\hfill \\ {\beta }_{3,0}+{\beta }_{3,1}{Y}_{i,0}+{\beta }_{3,2}{T}_i\hfill \\ {\beta }_{4,0}+{\beta }_{4,1}{Y}_{i,0}+{\beta }_{4,2}{T}_i\hfill \end{array}\right),\text{Ω}\right\},$$ (7)

that is a model where we have a separate effect of baseline and treatment at each follow-up visit, and an unstructured 4 × 4 covariance matrix Ω.

If there were no missing data, then inference for the 12-week treatment effect, β_4,2, would be the same as from the linear regression of just the 12-week data on baseline and treatment alone. However, with missing data, fitting the joint model (7) allows inference under the much more plausible assumption that the distribution of values later in the follow-up, given values early in the follow-up, is the same whether or not those later values are observed.

In other words, through a mixed model we can incorporate all the information provided by the patients, giving substantially more plausible inferences that obtained by restricting the analysis to patients with complete data. However, because the data are missing outcomes, we can do this without using the more general methodology, such as MI.

The covariance matrix plays a key role here, as it controls the way information from patients who withdraw contribute to the final treatment estimate. Therefore, it is important that it is unstructured, so that data can drive the association. We can readily do this because we have a limited number of scheduled follow-up times (four in the asthma study) so the covariance matrix is (4 × 4) with no restrictions. Carpenter & Kenward (2008, Ch. 3) show (see p. 53) this has a negligible effect on the power. Given this, it is often better to allow a different covariance matrix in (7) for each arm, since treatment often effects both the evolution of the mean and the variance structure over the course of the follow-up. Table 5 suggests this is the case for the asthma study.

Table 6 compares the results of the primary substantive model fitted to data from the 108 patients who complete, with estimates of the corresponding 12-week treatment estimate β_4,2 obtained from fitting (7) using all the observed data, with (i) a common covariance matrix across both treatment arms and (ii) a separate covariance matrix for each treatment arm. We see that (7) gives a larger treatment effect, similar standard error, and hence substantial increase in the statistical significance of the treatment effect. This is particularly the case when we allow for a separate covariance matrix for each treatment group. This is because, particularly in the placebo group, patients’ lung function declines quite steeply prior to withdrawal. Carrying this information forward through a treatment-arm specific covariance matrix leads to a notably lower estimate of the 12-week lung function for the placebo group, and hence a larger treatment effect. Table 6 also shows the results of MI, which we return to below.

Table 6. Estimated 12 week treatment effect on FEV₁ (litres), from ANCOVA, mixed models and MI using 100 imputations.

Analysis	Treatment estimate (L)	Standard error	p-value
ANCOVA (n = 108 completers), joint variance	0.247	0.101	0.016
Model (7), n = 180, common covariance matrix	0.283	0.094	0.003
Model (7), n = 180, treatment arm-specific covariance matrices	0.345	0.102	0.001
Multiple imputation, n = 180	0.334	0.106	0.002

To conclude with direct likelihood, we consider the setting when the dependent variable, Y in the substantive model is fully observed, but a covariate is missing. For simplicity, let the partially observed covariate X be binary. In this setting, though the substantive model conditions on X, because X is missing we need to complete the likelihood by specifying a distribution for partially observed X. Thus the likelihood for unit i is

$$f\left(Y_i\mid Z_i;\theta \right)=\underset{x=0,1}{{{\displaystyle \sum }}^{\text{}}}\left\{f\left(Y_i\mid X_i=x,Z_i;\theta \right)f\left(X_i=x\mid Z_i;\varphi \right)\right\},$$ (8)

where θ are the parameters of the regression of Y on X,Z and f(X_i = x,Z_i;ϕ;) is our choice of marginal distribution for X_i, which will generally depend on Z_i.

In this setting, it is straightforward to do the sum in (8) for all units i with missing data. These terms are then combined with likelihood contributions for those without missing data, to give the observed data likelihood which is then maximised to give the parameter estimates.

Unfortunately, this approach is not going to be straightforward in general. This is because we will typically have a range of covariate types and complex missingness pattern, making the necessary integrals intractable analytically and challenging computationally. Then, for the standard errors, we need to estimate the information matrix at the maximum. Therefore, we do not pursue direct likelihood further here. However, for particular classes of models, it is possible to write code to carry out (at least approximately) the calculations required. Thus this approach has been quite widely used in structural equation modelling (e.g. Rabe-Hesketh et al., 2004, Ch. 4) and is implemented in the software Mplus (https://www.statmodel.com/).

5.2. Bayesian approach

Another option – again centred on the likelihood - for handling missing data is the Bayesian approach, which we now briefly discuss; indeed one approach to MI is to view it as a two-stage Bayesian procedure with good frequentist properties. Considering a regresion of Y on partially observed covariates X, the Bayesian approach is to either calculate, or sample from, the posterior distribution of the parameters given data and prior. The missing values are additional parameters in the Bayesian framework. Writing partially observed X = (X₁,…,X_n), and partitioning it into (X_obs, X_miss) the posterior distribution is

$$f\left(\theta ,X_{\text{miss}}\mid Y,X_{\text{obs}}\right)=\frac{\left[\left\{{\displaystyle {\prod }_{i=1}^{n}f\left(Y_i\mid X_i;\theta \right)}\right\}\left\{{\displaystyle {\prod }_{i=1}^{n}f\left(X_i;\varphi \right)}\right\}f(\theta ),f(\varphi )\right]}{{{\displaystyle \int }}^{\text{}}\left[\left\{{\displaystyle {\prod }_{t=1}^{n}f\left(Y_i\mid X_i;\theta \right)}\right\}\left\{{\displaystyle {\prod }_{t=1}^{n}f\left(X_i;\varphi \right)}\right\}f(\theta ),f(\varphi )\right]d{X}_{\text{miss}}d\theta }$$ (9)

and we are interested in posterior summaries such as the posterior mean and variance of θ from (9).

Such calculations are typically not analytically tractable. However, we can always use either Gibbs sampling or Metropolis Hastings sampling to draw from (9) (see, e.g. Carpenter & Kenward, 2013, Appendix A). This is most easily done by using one of the increasing number of Bayesian software packages (e.g. WinBUGS, OpenBUGS, JAGS and in R, STAN). From the analysts perspective, the attraction is that almost any level of complexity of substantive model can be handled. However, lower level coding, and greater technical facility, is typically required than when using MI. To address this, many software packages have model templates available. A notable development in this area is the STATJR software (www.cmm.bristol.ac.uk), which will create templates and fit models to users’ data.

5.3. The expectation-maximisation algorithm

Looking at (8), for unit i the RHS is taking the expectation of the substantive model likelihood f(Y_i|X_i,Z_i;θ) over the distribution of the missing binary variable, X_i. This suggests an alternative, iterative approach; intuitively:

1. estimate the missing data given current parameter values;

2. use the observed data and current estimates of the missing data to update the parameter estimates;

3. iterate steps 1, 2 till convergence.

This broad approach goes back at least to McKendrick (1926); the literature has a number of similar algorithms which are essentially special cases of the EM algorithm, whose general applicability was shown by Orchard & Woodbury (1972) and fully formalised by Dempster et al. (1977). Continuing our example of regression of Y on Z and partially observed X, the full data log-likelihood can be written

$$\ell (\eta ;Y,X,Z)={\displaystyle \sum _{i=1}^n\{\log \left\{f\left(Y_i\mid X_i,Z_i;\theta \right)f\left(X_i\mid Z_i;\varphi \right)\right\}}$$

where η = (θ, ϕ). The expectation-maximisation algorithm proceeds as follows:

1. Initialise the algorithm with parameter values η⁰.

2. At iteration fc = 1,2, … :

   • (a)
     at the current parameter values, derive the distribution of the missing given observed data, f(X_miss|X_obs, Y, Z; η^k-1)
   • (b)
     calculate the expectation of the log-likelihood

     $$Q\left(\eta \mid Y,X_{\text{obs}},Z,{\eta }^{k-1}\right)=E_{f\left(X_{\text{miss}}\mid X_{\text{obs}},Y,Z;{\eta }^{k-1}\right)}\{\ell (\eta ;Y,X,Z)\}$$
   • (c)
     set

     $${\eta }^k={\max }_{\eta }Q\left(\eta \mid Y,X_{\text{obs}},Z,{\eta }^{k-1}\right)$$

Little & Rubin (2019) give an accessible overview of the EM algorithm with examples. While the general form given above may look intimidating, in many cases the calculations are simple expectations of sufficient statistics. Nevertheless, in complex examples both the expectation and maximisation step can be computationally awkward and Little & Rubin (2002) review a number of developments which seek to address this. In addition to this, the EM algorithm does not provide an estimate of the standard errors as a by-product. The bootstrap may be used (but this is computationally intensive). An elegant, often practical, approach was proposed by Louis (1982).

Despite its elegance, the EM algorithm generally requires a higher degree of technical proficiency from analysts. Because implementing it requires model-specific calculations (in contrast to MI) it does not lend itself to generic code. Rather, tailored code for the EM algorithm is typically embedded in specific modelling software, where it is used to obtain maximum likelihood estimates. This, and the relative difficulty of obtaining standard errors, are the reasons so we do not pursue it further here.

5.4. Mean-score estimation

In this approach, we average the score statistic over the distribution of the missing data given the observed data, and then maximise it to obtain the parameter estimates. Continuing the regression example, it can be shown (see, e.g. Clayton et al., 1998) that if unit i is missing X, then its contribution to the overall score-statistic for the data (i.e. the first derivative of the log-likelihood, which is solved to find the maximum likelihood estimates) is

$$s\left(\theta ;Y_i,Z_i\right)={{\displaystyle \int }}^{\text{}}s\left(Y_i\mid X_i,Z_i;\theta \right)f\left(X_i\mid Y_i,Z_i,\eta \right)d{X}_i.$$ (10)

To operationalise this, we again need to fit a model to X_Obs|Y, Z to estimate its parameters η and hence calculate the expectation of the right-hand-side of (10).

Calculation of this expectation may be awkward. However, we can use simulation: if we can estimate η and draw

$$X_{\text{miss},i}^1,X_{\text{miss},i}^2,\dots ,X_{\text{miss},i}^K\stackrel{ild}{\sim }f\left(X_i\mid Y_i,Z_i,\widehat{\eta }\right)$$

then

$$s\left(\theta ;Y_i,Z_l\right)\approx \frac{1}{K}{\displaystyle \sum _{k=1}^{K}s\left(Y_i\mid X_{\text{miss},l}^k,Z_i;\theta \right)}.$$

Once we have estimated all the score statistics, we sum them and solve for the maximum likelihood estimate of θ.

This approach can be viewed as (i) draw from the distribution of the missing given observed data (ii) calculate an expectation and (iii) solve for the parameter estimates. But what happens if we reverse the last two steps? Then we (i) draw from the distribution of the missing given observed data, (ii) estimate the parameters and then (iii) take expectations. This is the heart of the MI algorithm; its key attraction is that in step (ii) we can use the standard statistical software to fit our substantive model. For most analysts, this approach gives MI an decisive practical advantage over other approaches.

5.5. Multiple imputation

We have already seen that the MAR assumption can be intuitively interpreted as implying that the distribution of partially observed variables, given fully observed variables, is the same for both observed and unobserved values of the partially observed variables. MI exploits this in order to impute the missing values, giving multiple ‘complete’ datasets. Simply speaking, we estimate (using the observed data) the distribution of the partially observed variables given the fully observed variables, and then use this to impute the missing data. The reason for the ‘multiple’ imputation is that the imputed data can never have the same status as the observed data; rather they are drawn from the estimated distribution of the missing given the observed data under MAR. This distribution is reflected by the multiple imputed datasets. MI is useful in a wide variety of settings, summarised in Box 2 and makes use of all the available information.

Box 2. When is MI most likely to help?

When data are plausibly close to MAR and either or both:

• -the outcome is mostly observed, and missing data are in the covariates.
• -Auxiliary variables are available, which are good predictors of missing values, and which are observed when those values are missing (note, predictors of missing values alone should be avoided).

5.5.1. Informal rationale for MI

Suppose as before that we are interested in the regression of Y on partially observed X with parameters θ and denote the observed and missing portions of X by X_obs, X_miss. Recalling that in the Bayesian perspective missing data are parameters, the posterior distribution is

$$f\left(\theta ,X_{\text{miss}}\mid Y,X_{\text{obs}}\right)=f\left(\theta \mid Y,X_{\text{obs}},X_{\text{miss}}\right)f\left(X_{\text{miss}}\mid Y,X_{\text{obs}}\right).$$

We want the mean of the posterior distribution of the regression parameters, θ, given the observed data. We have that

$$\begin{array}{lll}f\left(\theta \mid \text{Y},{\text{X}}_{\text{obs}}\right)\hfill & =\hfill & {{\displaystyle \int }}^{\text{}}f\left(\theta ,X_{\text{miss}}\mid Y,X_{\text{obs}}\right)d{X}_{\text{miss}}\hfill \\ \hfill & =\hfill & {{\displaystyle \int }}^{\text{}}f\left(\theta \mid Y,X_{\text{obs}},X_{\text{miss}}\right)f\left(X_{\text{miss}}\mid Y,X_{\text{obs}}\right)d{X}_{\text{miss}}\hfill \\ \hfill & =\hfill & E_{f\left(X_{\text{miss}}\mid Y,X_{\text{obs}}\right)}\left[f\left(\theta \mid Y,X_{\text{obs}},X_{\text{miss}}\right)\right],\hfill \\ \text{so that}\text{E}\left[f\left(\theta \mid Y,X_{\text{obs}}\right)\right]\hfill & =\hfill & E_{f\left(X_{\text{miss}}\mid Y,X_{\text{obs}}\right)}\left[E_{\theta }\left[f\left(\theta \mid Y,X_{\text{obs}},X_{\text{miss}}\right)\right]\right].\hfill \end{array}$$

We now notice two things. First, given values of X_miss, we have a ‘completed’ dataset. We can fit our regression model to this in the usual way – using standard software – giving $\widehat{\theta }$. Provided we have an uninformative prior, this will be an excellent estimate of E_θ [f (θ | Y, X_obs, X_miss)]. Second, we can replace the analytic calculation of the expectation over f (X_miss | Y, X_obs) by a Monte Carlo approximation. Putting both these together, we get the following:

1. Take k = 1,…,K independent identically distributed draws, denoted $X_{\text{miss}}^k$, from f(X_miss|Y, X_obs).

2. For each, fit the regression model to the ‘completed’ dataset, giving the maximum likelihood estimate of the parameters, ${\widehat{\theta }}^k$.

3. The MI estimator is

   $${\widehat{\theta }}_{\text{MI}}=\frac{1}{K}\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{\theta }}^k\approx \text{E}\left[f\left(\theta \mid Y,X_{\text{obs}}\right)\right].$$

We return to how to draw $X_{\text{miss}}^k$, below. First, we stress one of several attractive aspects of MI: having imputed ‘complete’ datasets, we simply fit our substantive scientific model to each imputed dataset using the same approach we would have used if missing data were not an issue. However, we need to derive a variance estimate and rules for confidence intervals and tests.

To estimate the variance, focus on a scalar parameter in the vector regression parameters, say θ₁, and recall the conditional variance formula:

$$V\left({\theta }_1\mid Y,X_{\text{obs}}\right)=E_{f\left(X_{\text{miss}}\mid Y,X_{\text{obs}}\right)}\left[V\left[{\theta }_1\mid Y,X_{\text{obs}},X_{\text{miss}}\right]\right]+V_{f\left(X_{\text{miss}}\mid Y,X_{\text{obs}}\right)}\left[E\left[{\theta }_1\mid Y,X_{\text{obs}},X_{\text{miss}}\right]\right].$$ (11)

Given our draws $X_{\text{miss}}^k$, recall that when we use standard software to fit our substantive model to each imputed, ‘complete’ dataset, we get a point estimate, ${\widehat{\theta }}_1^k$, alongside the corresponding standard error, which we can square to give a variance estimate, ${\widehat{\sigma }}^{2,k}$. Given these, we can estimate the RHS of (11), giving:

$$\begin{array}{ll}V\left({\theta }_1\mid Y,X_{\text{obs}}\right)\hfill & =\frac{1}{K}\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\widehat{\sigma }}^{2,k}+\frac{1}{K-1}\underset{k=1}{\overset{K}{{{\displaystyle \sum }}^{\text{}}}}{\left({\widehat{\theta }}_1^k-{\widehat{\theta }}_{\text{MI}}\right)}^2\text{,}\hfill \\ \hfill & ={\widehat{\sigma }}_W^2+{\widehat{\sigma }}_B^2,\hfill \end{array}$$ (12)

where ${\widehat{\sigma }}_W^2$ is termed the within imputation variance and ${\widehat{\sigma }}_B^2$ the between imputation variance.

A potential drawback of the approach is that a large number of imputations, K, may be required. However, Rubin (1987) showed that by conditioning on the number of imputations, K, we can get correct inference if we take:

$$\begin{array}{c}{V}_{\text{MI}}\left({\widehat{\theta }}_1\right)={\widehat{\sigma }}_W^2+\left(1+\frac{1}{K}\right){\widehat{\sigma }}_B^2,\\ \text{with}\left(\frac{{\widehat{\theta }}_{1,\text{MI}}-{\theta }_1}{\sqrt{V_{\text{MI}}\left({\widehat{\theta }}_1\right)}}\right)\sim t_{\nu },\text{where}\nu =(K-1){\left[1+\frac{{\widehat{\sigma }}_W^2}{1+(1/K){\widehat{\sigma }}_b^2}\right]}^2.\end{array}$$ (13)

Equations (13) are known as Rubin’s MI rules. They are valid if (i) without missing data, the parameter estimate is approximately normally distributed; (ii) the imputations are statistically valid, or proper, draws from the correct Bayesian predictive distribution of the missing data given the observed data and (iii) this Bayesian predictive distribution conditions on all the observed data in the substantive model (including the dependent variable). While we have outlined Rubin’s rules for a scalar parameter, corresponding formulae exist for vectors of parameters (Li et al., 1999b), likelihood ratio tests (Meng & Rubin, 1992), p-values (Li et al., 1991a) and small samples (Reiter, 2007); for a more general discussion, see Reiter & Raghunathan (2007).

Looking at (13), we see that a key attraction of Rubin’s rules is their generality, since they are the same whatever the substantive model. Moreover, the restriction for the estimator to be normally distributed does not limit their applicability, since for generalised linear models and survival models we can apply them on the linear predictor scale. Combined with the attraction of directly fitting the substantive model to each imputed dataset, these rules cement the attraction of MI, giving it a marked practical advantage over the EM, mean-score and related approaches. Although all MI analysis can be done in one-step using a Bayesian procedure, again MI has the advantage because (i) we can use standard software, rather than a Bayesian program, to fit the substantive model and (ii) it turns out (see below) that in standard cases sufficiently good imputations can be obtained with standard software.

Given these points, critics of MI have focused their attention on Rubin’s rules. First, often in applications we will have additional, auxiliary variables which we would like to include in the imputation model because they contain valuable information about the missing values. However, for one reason or another we cannot include them in our substantive model (often because they are on the causal pathway). As Spratt et al. (2010) show, using such auxiliary variables is very desirable in applications, and the ability to do so readily is a key practical advantage over MI. In this case, Rubin’s rules may give a slightly biased, typically small overestimate, of the variance. Meng (1994) considers this and concludes this is unlikely to be an issue in practice (especially if we check for marked imputation model mis-specification). Second, in situations where the imputation and analysis are done separately, if the imputer has a simpler model (e.g. omitting sex) than the analyst (who wants estimates for each sex) again Rubin’s rules will be conservative. Related issues arise if the substantive model is weighted, but the weights are not included in the analysis (Kim et al., 2006). In practice, these errors are not large. Further, increasingly these days, the analyst and imputer are the same. When this is the case, the issue can be avoided by putting the structure of the substantive model (e.g. sex effects) in the imputation model. Likewise, if the weights (or the variables derived from them) are appropriately included in the imputation model, this issue does not arise (Seaman et al., 2012a; Quartagno et al., 2019a). Lastly, if the imputation model is mis-specified (e.g. does not reflect non-constant variance or skewness) Rubin’s rules may be conservative. This can, though, be checked by exploring the fit of the imputation model and has to be quite extreme to be of practical concern (Hughes et al., 2012). Carpenter and Kenward (2013, Ch. 2) reflect on these issues and conclude that, provided due care is taken, they are of negligible concern in practice.

5.5.2. Basic algorithm for imputing data

The remaining challenge is imputing the missing data. We are assuming MAR, and given this we have already seen (e.g. in the asthma study example) that the regression of partially observed on fully observed variables can be validly estimated from all the observed data. Therefore, one option is to create such a model and use it to impute the data. If a number of variables have missing values, then this will need to be a multivariate response model. A multivariate normal model is a natural starting point, and this approach is developed by Schafer (1997). Discrete variables can be treated as categorical for imputation and then rounded; however, a latent normal model provides a more attractive alternative (Goldstein et al., 2009; Quartagno & Carpenter, 2019). In order for the imputations to be properly Bayesian (vital for Rubin’s rules to work), such models are typically formulated as Bayesian models and fitted using Gibbs sampling and/or Markov Chain Monte Carlo (MCMC). The key issue is that we do not condition on a single (say maximum likelihood) estimate of the parameters of the imputation model when imputing. Rather, for each imputed dataset, we draw from the distribution of the imputation model parameters and then draw the missing data. Carpenter and Kenward (2013, pp. 41–43) give a simple illustration of what this means.

As an alternative to the joint modelling approach, a number of authors (Kennickel, 1991; van Buuren, 2007, 2018; van Buuren et al., 1999; Raghunathan et al., 2001) proposed and developed the full conditional specification (FCS) approach, sometimes known as ‘chained equations’. To illustrate, suppose as before we have variables X, Y, Z, but now suppose they all have some missing values. FCS imputation proceeds as follows:

Step 0. Replace all missing values in each variable by starting values, typically sampled from observed values of the variable.

Step 1. Regress X_obs on ‘complete’ Y and Z; properly impute X_miss and carry them forward.

Step 2. Regress Y_obs on ‘complete’ X and Z; properly impute Y_miss and carry them forward. Step 3. Regress Z_obs on ‘complete’ X and Y; properly impute Z_miss and carry them forward.

Steps 1–3 form a ‘cycle’ (Step 0 is only needed to get started: after the first cycle we have drawn preliminary values for all the missing data). Typically, we perform 10–20 cycles of the algorithm, then keep the imputed/observed data as the first imputed dataset, perform 10–20 further cycles then keep the imputed/observed data as the second imputed dataset and so on.

The key advantage of this approach is that it can be programmed in standard software using pre-existing regression commands; all that is needed is some ‘housekeeping’ of the data and (ii) care to ensure the imputations are proper. For this, the Bayesian approach can be sufficiently well approximated by at each step (a) taking a draw of the regression parameters from their estimated large sample distribution and (b) using these to impute the missing values. A further advantage is that the ‘regression’ models need not be linear regression; they can be changed to logistic, Poisson etc., reflecting the type of variable. It is more challenging to formally show the FCS algorithm converges. However, Hughes et al. (2014) showed that it is equivalent to a well-defined joint model for multivariate normal data and count data, and that in other settings, even in finite samples, the discrepancies are of no practical importance.

In summary, MI provides the most practical approach to analysis under the MAR assumption; it is particularly useful for the settings highlighted in Box 2. We therefore illustrate its use with an extended example below. We will see that, while the FCS algorithm is sufficient for many analyses, more complex data structures (with interactions, hierarchies, weights) require more subtle imputation algorithms; usually when MI analyses are misleading, such issues have been overlooked (Box 3 and Box 4) (Morris et al., 2014).

Box 3. What are the likely pitfalls of MI?

• -Our model has interactions or non-linear effects and these are omitted from the imputation model.
• -Our model has hierarchical (multilevel) structure, and this is omitted from the imputation model.
• -Theassumption of Missing At Random is markedly violated.

Box 4. Strategy for imputation with interactions and non-linear effects.

• -If the interaction variable is categorical, and (near) fully observed, impute separately in each category and append the imputed data sets. Then fit the sub-stantive model and apply Rubin’s rules.
• -If the variables involved in the non-linear relationship are fully observed, be sure to include this non-linear structure in each FCS imputation model.
• -Otherwise, use substantive model compatible imputation (software available for both single and multlevel data).

5.6. Inverse probability weighting

The last approach we consider for analysis under the MAR assumption is perhaps the oldest and technically simplest, namely IPW; for an early discussion, see Horvitz & Thompson (1952). The key idea is illustrated in Table 7. The mean of the full data (i.e. the actual values of the nine observations we sought) is 2; however, the mean of what we actually observe is 13/6, which is biased, because the chance of data being missing depends on its value. However, now consider the group variable; if we assume that data are MAR given group (an assumption we know is true as here we can check with the full data), then the estimated probability of observing the data is shown in the third row of Table 7.

Table 7. Simple example of IPW.

Group	A			B			C
Full data	1	1	1	2	2	2	3	3	3
Observed data	1	?	?	2	2	2	?	3	3
Probability of observation given group:	1/3	·	·	1	1	1	·	2/3	2/3

We make use of this by replacing the mean with a weighted mean, where the weights are the reciprocal of the probability of observation. Thus, the first observation in group A is given weight 3, to represent the three observations in group A. The weighted mean is then:

$$\frac{1\times \frac{3}{1}+(2+2+2)\times 1+(3+3)\times \frac{3}{2}}{\frac{3}{1}+1+1+1+\frac{3}{2}+\frac{3}{2}}=2.$$

We see that weighting has eliminated the bias; more generally, it will not always eliminate the bias, but it will generally reduce it, unless missingness does not depend on the outcome in the substantive model.

In order to show how this generalises, let Y_i, i = 1,…, 9, be the nine observations in Table 7; R_i = 1 if Y_i is observed, and π_i = Pr(R_j = 1). Thus Y₁ = 1,R₁ = 1,π₁ = 1/3 and so on. Then the estimates of the mean from the full, observed and weighted data are the values of θ that solve the following three equations:

$$\underset{i=1}{\overset{9}{{{\displaystyle \sum }}^{\text{}}}}\left(Y_l-\theta \right)=0;\underset{i=1}{\overset{9}{{{\displaystyle \sum }}^{\text{}}}}{R}_i\left(Y_i-\theta \right)=0;\underset{i=1}{\overset{9}{{{\displaystyle \sum }}^{\text{}}}}\frac{R_i}{{\pi }_i}\left(Y_i-\theta \right)=0.$$ (14)

Recall that maximum likelihood estimates are found by (i) calculating the first derivative of the log-likelihood, s_i(θ) for each individual and (ii) solving ∑ s_i(θ) = 0. We see that if we replace (Y_i – θ) with s_i(θ) in (14) we get consistent estimates if π_i is the true probability of observing s_i (i.e. the probability the record is complete). In applications, of course, we need to estimate π_i, and we can only do this if data are MAR. Having estimated π_i, the analysis is straightforward: we simply weight the regression command. While the resulting standard errors are slightly conservative (because we have ignored estimation of the weights), this is not often practically important.

Example 2: NCDS analysis (continued)

We now explore IPW for our substantive model, (3). In particular, our focus is how the probability of a child in the NCDS cohort having no qualifications when they are 23 years old varies by their mother’s age when they were born, and whether they lived in social housing. As in (3), we further adjust for being in care and inverse birthweight.

Table 4 shows the pattern of missing values; 30% have noqual2 missing. However, mother’s age and inverse birthweight have fewest missing values and are therefore the obvious candidates to put into the weight model, as both are also strongly predictive of the outcome. Therefore, we create an indicator for a complete record and fit a logistic regression of this on mo_age and invbwt. After including these, neither care or soch7 are statistically significant. We then calculate the fitted probabilities from this model and the weights as their reciprocal. Before fitting the re-weighted model, a check on the weights showed that the 99%-ile was 3.06, but that a small number of individuals had very high weights. In such cases, it is sensible to fit the weighted substantive model with and without the very high weights and compare the results; generally, omitting the high weights is desirable. In this example, the results were little changed, but we report results omitting the 1% of records with weights > 3.06. The remaining weights have mean 1.6 and a unimodal slightly positively skewed distribution.

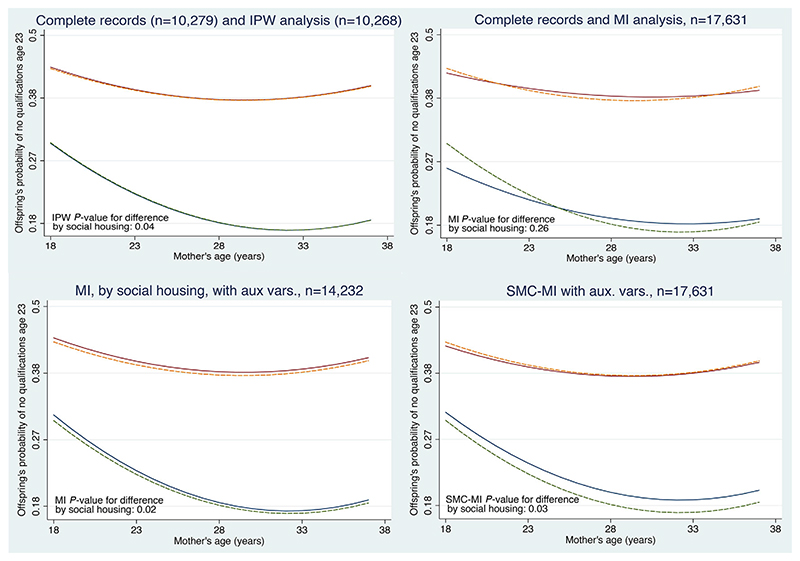
The top-left panel of Figure 3 compares the complete records analysis with IPW. We see that the results are virtually identical. For those not in social housing, the probability of no qualifications curves downwards with increasing age (this is statistically significant at the 5% level); for those in social housing, the probability of no qualifications is higher, and the decline with increasing mother’s age is slight. The test for a difference in the relationship with mothers age by social housing (on 2 degrees of freedom) gives p = 0.03 in the complete records and p = 0.04 with IPW.

Figure 3.

NCDS data: panels show how the probability of no qualifications age 23 varies with mother’s age at birth and social housing. In each panel, for children not in care and with a birth weight of 111 ounces, the upper lines are for children who were in social housing and the lower lines for those who were not. Each panel compares the complete records analysis (dashed lines) with those from IPW (top left, largely overlaps complete records); standard MI (top right, 100 imputations); MI separately by social housing, with auxiliary variables (bottom left, 100 imputations); and substantive model compatible MI with auxiliary variables (bottom right, 100 imputations)

The results with IPW are essentially the same as complete records. This is inevitable for this example, because most missing values are in the dependent variable, noqual2, and the complete records analysis gives valid, efficient inference if these are MAR. The IPW analysis can only be valid under MAR (because the weights are estimated from the observed data); since the weights do not include noqual2, the results will be similar. However, we could estimate the weights using data observed between early life and age 23: there are three principal candidates – school behavioural score, school reading test and the number of family moves. The most predictive of these is the behavioural score, but this is missing for 1106 of the complete records; including it in the weight model therefore reduces the number of records in the analysis, and in this example gives similar results.

The above example highlights some general issues with IPW. First, only the complete records are re-weighted; all records with one or more missing values remain excluded from the analysis. Thus, IPW will not recover this information or gain efficiency relative to a complete records analysis. Second, the results will not differ markedly from the complete records unless the covariates are MAR given the dependent variable (so the CR (complete records) analysis is not valid). In this case, the dependent variable will need to be in the weight model. Third, often variables we wish to include in the weight model have missing values, complicating the estimation of the weights. Fourth, the results can be sensitive to large weights and the choice of weight model, but is often unclear how to make appropriate decisions about these issues.

To improve the efficiency, Robins and colleagues (e.g. Robins et al., 1995; Scharfstein et al., 1999) proposed bringing in information from partially observed individuals by augmenting the IPW estimating equation (e.g. the right-hand-side equation in (14)) with a term whose expectation is zero and which can be calculated from the observed data. Adding a term of expectation zero does not affect the consistency of the point estimate, but if appropriately chosen may add efficiency.

It turns out that, if the unweighted estimating equation is ∑ s(θ; Y_i) = 0, then the most efficient choice for this additional term is the expectation of ∑s(θ; Y_i) over the missing data. This gives so-called augmented inverse probability weighting estimating equation,

$$\underset{i=1}{\overset{n}{{{\displaystyle \sum }}^{\text{}}}}\left\{\frac{R_i}{{\pi }_i}s\left(\theta ;Y_i\right)+\left(1-\frac{R_i}{{\pi }_i}\right)E_{Y_{i,\text{miss}}\mid Y_{i,\text{obs}}}\left[s\left(\theta ;Y_i\right)\right]\right\}=0,$$ (15)

which it turns out is efficient if the conditional distribution of Y_i,miss| Y_i,obs is specified correctly.

The intriguing property that equation (15) has is that if either the weight model is wrong, or the conditional expectation model is wrong, the estimate of θ is still consistent. This is because, in either case, the expectation of the estimating equation is still 0 at θ = θ_true. To see this, suppose first that the weight model, that is π_i = Pr(R_i = 1) is correct. First take expectations over R_i (so the second term vanishes) and then take expectations over Y at θ = θ_true. This is zero regardless of whether the conditional expectation is correct.

However, if the conditional expectation model is right, then we can first take expectations over Y_miss|Y_obs which leaves

$$\underset{i=1}{\overset{n}{{{\displaystyle \sum }}^{\text{}}}}E{Y}_{i,\text{miss}}\mid Y_{i,\text{obs}}\left[s\left(\theta ;Y_i\right)\right].$$

If we now take expectations over Y_obs (again, at θ = θ_true) we again get zero. We see this is true regardless of whether the weight model is correct.

So, if either the weight model or the model for Y_miss|Y_obs is correct, we obtain a consistent estimate of θ. Noting that getting Y_miss|Y_obs correct is necessary for correct inference from MI, we see that solutions of (15) are consistent if (a) our weight model is right but imputation model wrong or (b) our imputation model is right but weight model wrong. Thus, they are known as doubly robust estimators.

Vansteelandt et al. (2009) give an accessible introduction to these developments, and Carpenter et al. (2006) explore the comparison with MI. Although the protection afforded by double robustness is attractive, in general calculating the expectations may be awkward, and no general software exists. One option, explored by Daniel & Kenward (2012), is to embed the approach in MI. However, results may be still be sensitive to mis-specification of the weight model and Rubin’s variance formula is not doubly robust. In the NCDS example, since the dependent variable has the most missing data, as noted above the corresponding likelihood terms are 1, so their derivative is zero. In this example, therefore, the large majority of the ‘additional’ terms on the RHS in (15) will be zero, so doubly robust estimation will give virtually identical results to IPW.

5.7. MI for the NCDS educational qualifications analysis

We now explore the application of MI for fitting model (3) to the NCDS data, assuming the missing values are MAR.

5.7.1. Standard application of MI

A standard application of MI takes the five variables in (3) (noqual2, care, soch7, mo_age, invbwt) and performs MI using the FCS algorithm described above. In other words, each variable is regressed – in turn – on all the others and missing values properly imputed. Linear regression is used for mo_age, invbwt and logistic regression for noqual2, care, soch7. After imputing the data, the square of mother’s age, mo_agesq, and the two interaction variables with soch7 are calculated. The substantive model is then fitted to each imputed dataset and the results combined using Rubin’s rules.

The top-right panel of Figure 3 shows the results. Compared with the complete records analysis (dashed lines) we see that the curved reduction in the probability of the offspring having no qualifications age 23 with mother’s age (at birth) is much reduced, and that the p-value for this difference by social housing is 0.26, far from statistical significance. Since the principal missing data pattern is the dependent variable (noqual2), and both the complete records analysis and this MI analysis assume data are MAR, this difference should give pause for thought. The reason is not hard to find: standard MI imputes missing values assuming only linear dependence of each variable on the others. Therefore, all the imputed values have no non-linear relationship with mothers age and no interaction with social housing; this explains the results. Application of standard MI is therefore misleading (cf Box 3).

5.7.2. Imputing separately in groups of soch7, with auxiliary variables

In order to preserve the interaction with soch7 in the imputed data, a natural approach is to impute separately for the two soch7 groups. This inevitably means some loss of power, because the 3399 individuals with soch7 missing are excluded from the analysis. However, a logistic regression shows that given care, the probability of missing soch7 does not depend on noqual2, so this is not expected to bias the results.

Next, we need to explore whether there are any auxiliary variables, predictive of noqual2 but not in our substantive model, that can be included in the imputation model to recover information. Two potential auxiliary variables are the school behavioural score and the number of family moves. These are excluded from the substantive model because they are on the causal pathway between ‘early life’ and educational qualifications age 23. However, they are strong predictors of noqual2. Unfortunately, there is a snag: first, of the 5587 missing values on noqual2, only 3458 have one or both of the auxiliary variables observed; second for those with soch7 observed, these numbers reduce to 3485 and 2925, respectively.

We also need to attempt to retain the non-linear relationship with mother’s age in the imputation model. A natural proposal for this is to include mo_agesq in the FCS imputation process as if it is just another variable. When doing this, we have to remember to exclude mo_age from the predictors in the conditional imputation model for mo_agesq and exclude mo_agesq from the predictors in the conditional imputation model for mo_age.

We now put these three strategies into action using FCS. We use ordinal regression for the grouped family move variable (1,2,3 and > 4) and the square root of the behavioural score, as this is nearly normally distributed. The results, again with 100 imputations, are shown in the bottom left panel of Figure 3. We see the results are very similar to the complete records analysis, right down to the p-value for the test for the interaction with soch7. Any gain in information using the auxiliary variables appears outweighed by the exclusion of all those with soch7 missing.

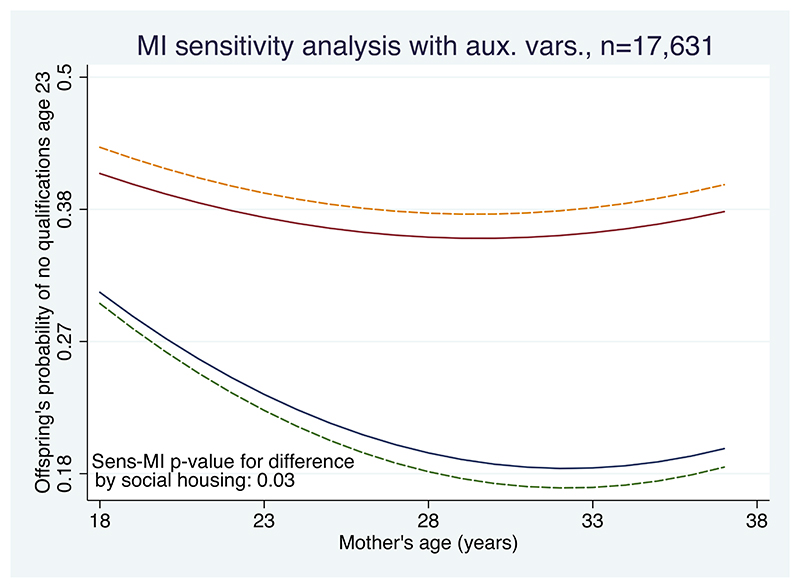
5.7.3. Substantive model compatible MI, with auxiliary variables

In order to improve on this, we need to impute consistent with both the non-linear effect and the interaction. First, we note (Seaman et al., 2012b) that the just-another-variable approach to non-linear effects (Von Hippel, 2009) can perform poorly when the substantive model is not a linear regression and the data are not approximately MCAR. Second, although one way to handle interactions is to include the appropriate interaction component in each of the conditional imputation models (Tilling et al., 2016), this is complicated in our setting by the non-linear effect.

In order to address these issues, Goldstein et al. (2014) and Bartlett et al. (2015b) proposed incorporating the substantive model explicitly into the imputation process, to preserve any non-linear/interaction effects in the imputed data; they termed this substantive model compatible MI. Within the FCS framework, it turns out this is fairly straightforward to implement. We apply FCS imputation to the covariates in the substantive model (plus any auxiliary variables we wish to include); however, for each proposed imputed value we perform an acceptance step. To derive the acceptance probability, at the start of FCS imputation cycle k we fit the substantive model to the current imputed/observed data, imputing any missing values of the dependent variable and obtaining substantive model parameter estimates ${\widehat{\theta }}_k$. Then, in the course of cycle k of the FCS algorithm on the covariates, a proposed imputed value for one of the covariates X_i,1 in X_i = (X_i,1, X_{i,1 (-1)}) is accepted with probability

$$\frac{f\left(Y_i\mid X_{i,1},X_{i,(-1)};{\widehat{\theta }}^k\right)}{{\max }_{X_{i,1}}f\left(Y_i\mid X_{i,1},X_{i,(-1)};{\widehat{\theta }}^k\right)}$$

For logistic regression, the denominator is 1 so the calculation is particularly easy. Substantive model compatible imputation has been implemented in Stata and R (Bartlett & Morris, 2015) and extended to impute consistent with survival data including competing risks models (Bartlett & Taylor, 2016); handling time-varying covariates is discussed by Keogh & Morris (2018). Further, the multilevel imputation package jomo (Quartagno et al., 2019b) has recently been extended to include substantive model compatible imputation. Given this software, our recommended approach for handling interactions and non-linear effects is summarised in Box 4.

We now apply SCM (substantive model compatible) MI to the NCDS data, with the auxiliary variables mentioned above and 100 imputations. This gives the results shown in the bottom right panel of Figure 3. Compared with complete records, we see the imputations have (i) preserved the non-linear relationship and its interaction with social housing, (ii) reduced the absolute difference in the effect of social housing, yet (iii) recovered some information about the missing values (particularly missing noqual2) so that the interaction test now yields a p-value of 0.03. Because it both uses auxiliary variables and imputes consistent with non-linear effects and interactions, this is our preferred analysis under MAR.

6. Beyond Mar: Sensitivity Analysis

Continuing with our framework, Figure 2, the next step is to explore whether the conclusions from the analysis under MAR are robust to plausible departures from this inherently untestable assumption. It is important that such departures are both couched in terms that are accessible as possible to the scientific team and contextually plausible. When a nontrivial proportion of data are missing, the conclusions can often be shown to be sensitive to implausible departures from MAR; but this is of little practical value.

When performing sensitivity analysis, it is important to focus on variables with the most missing data, and typically to take these variables one at a time. When these variables are binary or categorical, sometimes it is sufficient to perform a sensitivity analysis when all the missing values take a ‘0’ or ‘1’. While this is unlikely to be true, if the results from the analysis assuming MAR are robust to this relatively extreme assumption we can be confident of our conclusions.

Example 1: Risk of sudden infant death with bed-sharing (continued)

We now return to the analysis of the bed-sharing study. Following through the framework, the next step is analysis under MAR. This was performed using MI. Cases and controls were imputed separately, and in line with the approach discussed by Tilling et al. (2016), the imputation model contained the appropriate interactions. Further details are given in Carpenter et al. (2013b) and further technical details in Smuk (2015).

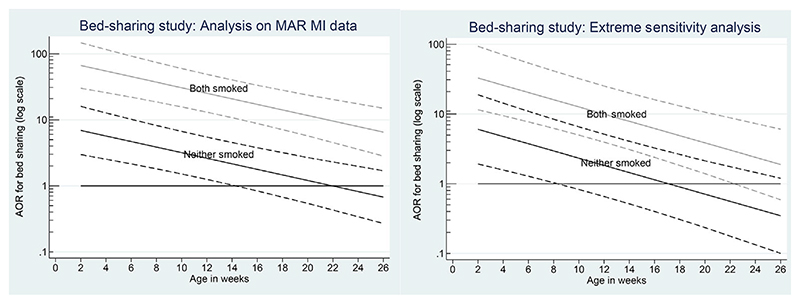
The left panel of Figure 4 shows the results. As discussed above, because the reason for the missing data is unrelated to case-control status, we expect MI to give similar point estimates to the CR analysis, but recover a substantial amount of information. Comparing the left panel of Figures 4 and 1 shows that this is the case. Although the estimated adjusted odds ratio for infants with a non-smoking mother is slightly reduced, the confidence interval is now markedly narrower, suggesting the risk is statistically significant at the 5% level for infants younger than 14 weeks.

Figure 4.

Adjusted odds ratio (AOR) for risk of bed-sharing. Left panel: after imputation of missing alcohol and drug data under MAR; right panel: sensitivity analysis. Both panels: solid lines show estimated adjusted odds with non-smoking (solid) and smoking (grey) mother; dashed lines: 95% confidence intervals

However, this finding proved contentious (see, e.g. online reaction to Carpenter et al., 2013b). Therefore, Smuk (2015) explored various sensitivity analyses. As suggested above, sensitivity to missing values in each of the variables with non-trivial proportions of missing values was explored in turn. The right panel of Figure 4 shows the results when, after imputing the missing values assuming MAR, all missing alcohol values in the cases were set to ‘drinking = 1’ (in each imputed dataset) and all missing alcohol data in the controls were set to ‘not drinking = 0’. This is simple, but extreme sensitivity analysis. Comparing with the left panel, we see that the 95% confidence interval for the adjusted odds-ratio (AOR) of bed-sharing now only clears the null value (i.e. 1) at 8 weeks; the broad conclusion remains unchanged however.

For this bed-sharing example, this completes working through the missing data framework; we conclude bed-sharing for young infants is a readily avoidable risk factor.

The previous example shows the use of best/worst case sensitivity analysis after MI under MAR. More generally, there are three broad approaches we can adopt: selection modelling, latent variable modelling and pattern mixture modelling. These approaches, and their pros and cons, are discussed in Carpenter & Kenward (2015a) and also Carpenter (2019), where the pattern mixture approach emerges as both accessible and widely applicable via MI. We therefore focus on this. Recall from the discussion earlier that MAR can be interpreted as assuming that the missing and observed values in the partially observed variables – given fully observed variables – have the same conditional distribution.

Pattern mixture sensitivity analysis builds on this, by exploring the impact on the scientific conclusions of changing this distribution. Continuing with our generic substantive model of the regression of Y on exposure X and covariates Z, suppose the focus is on sensitivity analysis for missing Z values, and let R_i = 1 if Z_i is observed, and 0 otherwise. Once data are MNAR, the distribution f(Z_i | Y_i, X_i, R_i = 1) ≠ f(Z_i |Y_i,X_i, R_i = 0). This complicates the analysis considerably, because

• (a)these differences can take any form, for example mean, variance, skewness etc. and
• (b)there is no information in the observed data about these differences!

Given this, a practical way forward using MI is to

• (I)start with the imputed values under MAR then
• (II)alter them in (i) the simplest way possible to represent plausible departures from MAR that (ii) are likely to impact on inferences and (iii) are accessible to subject experts.

Points II(i), II(ii) and II(iii) are important. By making the changes as simple as possible, we limit the number of unknown parameters describing the changes, which are known as sensitivity parameters. By focusing on changes that are likely to impact inferences, we focus our efforts where it matters. Finally, by being accessible to subject experts, we make the results interpretable.

6.1. Generic algorithm

Our generic substantive model is a regression of outcome vector Y on exposure vector X adjusting for confounders Z, and there is a non-trivial proportion of missing data in Z. We assume we have multiply imputed k = 1,.,.,K datasets under MAR. Then, within each imputed dataset we proceed as follows:

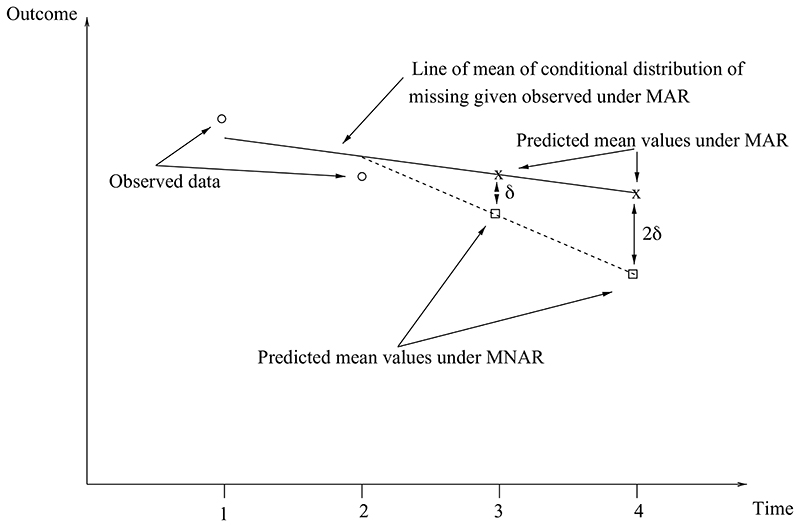
1. Use an appropriate generalised linear model to regress Z on Y, X, obtaining coefficients ${\widehat{\gamma }}_0,\dots ,{\widehat{\gamma }}_2$.

2. Change the parameters to ${\gamma }_j^{\star }=\left({\delta }_j+{\widehat{\gamma }}_j\right),j=0,1,2$ where the user specifies the δ_j, which represent the difference between the distribution of the observed and missing Z values, conditional on the other variables. The easiest sensitivity analysis is to focus on δ₀ and leave the other parameters unchanged (i.e. δ₁ = δ₂ = 0).

3. Leave the imputed values of other variables unchanged, but re-impute (using the ${\gamma }_j^{\star }$) the missing Z values.

This gives us K imputed datasets under MNAR. Fit the substantive model to each imputed dataset, and combine the results using Rubin’s rules. Before implementing this approach, it may be useful to centre Y, X, Z, so that the parameters δ_j are more interpretable.

Note that because Steps 1–3 are applied to each imputed dataset in turn, this preserves the between imputation variation and we do not need to sample from the distribution of the parameters $\widehat{\gamma }$ before imputing the missing Z values in Step 3.

We illustrate this approach below. However, while it is very practical, in general it is only approximate; intuitively, it may be slightly conservative. This is because if there are a non-trivial number of missing values in other variables, and we change the imputation distribution for Z, then this will in turn affect the values imputed for those other variables. If the MI has been carried out using the FCS algorithm, it can be modified to address this (Tompsett et al., 2018).

Example 2: NCDS analysis (continued)

Continuing with the NCDS example, we now use the pattern mixture approach to explore the robustness of our findings to noqual2 being MNAR. Specifically, we explore what happens when the MAR-imputed association between the log-odds of no qualification and the social housing/mother’s age interaction (adjusted for the other variables) is reduced by 25%.

To do this, we implement the algorithm above, taking our substantive model compatible imputations as the starting point. For each of these imputations, we fit the substantive model (3). Then, we multiply the coefficients of soch7, agehous, agesqhous by 0.75 and re-impute noqual2. Note that we could have additionally adjusted for reading score and family move; but this has no material effect on the results. Having done this for each imputation, we fit the substantive model to each imputed dataset and apply Rubin’s rules.

Figure 5 shows the results. As expected, there is no change to the lower (not in social housing) group. However, the upper curve, for those in social housing, is now reduced. Nevertheless, although the 25% reduction in the odds of no qualifications from the MAR values is non-trivial, there is little change in the interaction test p-value (which is slightly less than for the substantive model compatible analysis, reflecting our intuition that this method is slightly conservative). It remains close to the p-value of 0.03 obtained in the complete records analysis.

Figure 5. NCDS analysis: Comparison of CR (dashed) and MI under MNAR (solid) lines; upper lines: in social housing; lower lines: not in social housing; 100 imputations.

This completes the application of the missing data framework to the NCDS analysis. We conclude that there is a statistically significant difference in the odds of no qualifications age 23 for children in those families who were, and were not in, social housing. Further, for those not in social housing, there is a marked decrease in the probability of no qualifications with increasing mother’s age; however, this is not seen for those in social housing. These results are robust to plausible departures from the missing at random assumption.

6.2. Further developments with MI sensitivity analysis

The above sensitivity analyses are all examples of what is termed controlled imputation, because the analyst intervenes in the MAR imputation process to introduce controlled departures from the MAR assumption. This approach has been applied quite widely in clinical trials. Here the focus is on imputing missing outcome variables under MNAR, and the effect this might have on the treatment difference between the arms.

We briefly discuss two approaches which may be used with longitudinal follow-up. The first is to impute under MAR, and then, for each patient who withdraws, change their first imputed value by δ, the second by 2δ and so on. This is described schematically in Figure 6.

Figure 6. Schematic illustration of ‘δ-method’ controlled sensitivity analysis.

This approach is often sufficient; if appropriate, δ can be increased till the conclusions change, a so-called ‘tipping-point’ analysis. However, in general we may wish to have different values of δ for different arms at different times. If we do this, a further complication is that the standard error of our treatment effect often is markedly affected by the covariance of these parameters. This led Carpenter et al. (2013a) to develop a work of Little & Yau (1996) into a version of controlled imputation termed reference-based sensitivity analysis. Here, instead of choosing a number of sensitivity parameters and their covariances, we instead make qualitative statements about post-dropout behaviour. Examples include (i) ‘copy reference’, where an individual’s missing values are imputed as if they were randomised to a reference, typically control, treatment, and (ii) ‘Jump-to-reference’, where a patient’s post-withdrawal data are imputed assuming they jumped to a reference, typically control, treatment at withdrawal.

One concern about such sensitivity analyses, particularly in the context of drug evaluation, is whether – relative to the primary analysis under MAR – they increase or reduce the statistical information about the treatment effect. Cro et al. (2019) examine this and show that using MI to implement both the ‘δ-method’ and a broad class of reference-based sensitivity methods has the desirable property that the results of primary and sensitivity analyses are information anchored: they neither increase, nor decrease, the information lost due to missing data about the treatment effect. For an accessible discussion of this approach, see Carpenter (2019).

Example 3: Asthma trial (continued)

We now complete application of our framework to the asthma trial by implementing two sensitivity analyses via MI.

Table 8 compares the results of the previous MAR analysis with three sensitivity analyses. The first uses the δ-method and reduces the imputed lung function from MAR by 0.1 L for the first post-withdrawal value, 0.2 L for the second and so on. This strengthens the treatment effect, because the majority of dropout early on is in the placebo arm, so the δ-method increases the difference between the arms over the 12-week follow-up.

Table 8. Estimated 12 week treatment effect on FEV₁ (litres) under MAR and three information-anchored sensitivity scenarios.

MAR Analysis	Treatment estimate (L)	Standard Error	p -value
Model (7), n = 180, common covariance matrix	0.283	0.094	0.003
MNAR Analysis
MNAR, δ-method, δ = 0.1 (L)	0.416	0.109	<0.001
MNAR, jump-to-reference (active)	0.127	0.109	0.249
MNAR, jump-to-reference (placebo)	0.232	0.107	0.032

The second analysis imputes missing data in the active arm under MAR, but has patients who withdraw from the placebo arm ‘jumping-to-active’. This corresponds to a pragmatic interpretation of the trial, where we explore the effect of placebo patients obtaining an active treatment following withdrawal. The consequence is that the 12-week treatment effect is much reduced, and no longer statistically significant. We complement this with the alternative assumption: patients on the placebo arm are imputed under MAR, but following withdrawal, patients on the active arm ‘jump-to-placebo’ (equivalently have no active treatment). Again, this reduces the 12-week treatment effect, but it remains significant at the 5% level.

This concludes our application of the framework to the asthma study. Analysis under MAR finds a stronger, and markedly more significant benefit of treatment, which is robust to departures from MAR that assume post-withdrawal lung function is worse than predicted by MAR.

7. Software

There is now a wide range of software available for MI. While earlier packages were standalone (e.g. NORM for multivariate normal data: (https://www.methodology.psu.edu/training/missing-data/), and REALCOM (http://www.bristol.ac.uk/cmm/software/realcom/) for multilevel data) most researchers use MI tools within R, SAS, SPSS or Stata. Table 9 summarises what is available.

Table 9. Summary of standalone and MI programmes available in some of the leading statistical software packages.

Software for MI: methods derived from multivariate normal
Data types →	Normal		Mixed response
Data structure →	Independent	Multi-level	Multi-level
Software ↓
Standalone:	NORM†	PAN†	REALCOM⋆, PAN†
MLwiN	MCMC approach emulates REALCOM		+ 1–2 binary variables
R§	NORM-port	PAN-port	jomo
SAS	PROC MI	–	–
Stata	mi impute mvn	–	–
Software for MI using full conditional specification:
Software:	functions/packages	Comments
R§	mi, mice	Available from CRAN; mice based on van Buuren (2018)
Standalone:	IVEware+	Can be accessed from R, SAS, SPSS, Stata
SAS	PROC MI	More limited FCS imputation than IVEware
SPSS	MULTIPLE IMPUTATION	Comes with core package
Stata	mi impute chained	Comes with the core package

^†see Schafer (2001);

^⋆see Carpenter et al. (2011), uses latent normal model for categorical data;

⁺see https://www.src.isr.umich.edu/software/;

^§R has many MI packages; a more complete list is given in the text.

All the software in Table 9 will handle a general pattern of missing data; a monotone missingness pattern is not required. The methods derived from the multivariate normal use a MCMC or data augmentation algorithm (see Carpenter & Kenward, 2013, Appendix B). Shafer also has a standalone package, mix, which handles a mix of continuous and categorical variables using the general location model (Schafer, 1997). Schafer’s packages have been ported to R. By contrast, REALCOM and jomo (Quartagno et al., 2019b) use a latent normal model for categorical data (Quartagno & Carpenter, 2019). The jomo package supports multilevel imputation and in particular allows the level-1 covariance matrix to be random (Yucel, 2011), which can be very useful for imputing data from individual patient meta-analysis and similar structures (Quartagno & Carpenter, 2015).

R has multiple packages for MI, some ofwhich call each other: mice, mi, VIM, aregImpute in Hmisc, BaBooN, hot.deck for FCS, the NORM- and PAN-ports, Amelia and jomo for multilevel data. Probably the most widely used is mice, whose functionality is described in van Buuren (2018).

PROC MI in SAS supports imputation using the multivariate normal model, and also using FCS. However, the SAS macros iveWARE are a more f exible way to impute using FCS in SAS, with good support for survey data.

SPSS has a MI function that imputes using FCS; like the other FCS packages it allows users to control the variables in the imputation models, allowing inclusion of auxiliary variables.

Stata supports MI using either FCS or multivariate normal imputation and has perhaps the most flexible approach to handling practical complexities such as interval censored data, skips in questionnaires, and perfect prediction issues (White et al., 2010).

Interactions need to be included appropriately in the imputation model if the effects are not to be attenuated. SPSS has an option to automatically include all two way interactions of categorical variables (see Tilling et al., 2016), while the more general ‘substantive model compatible full conditional specification’ smcfcs software is available in Stata and R (Bartlett et al., 2015b); there is also a beta-version of smcJOMO.

8. Active Research Topics

In this penultimate section, we briefly discuss some active missing data research topics.

8.1. Sub-sample ignorability

Little & Zhang (2011) describe the idea of sub-sample ignorable likelihood. Suppose we have four (sets of) variables, and the pattern of missing data is shown in Table 10. We now make the sub-sample ignorability assumption, that is,

1. within pattern 2, missing values of X and Y are MAR and

2. within pattern 3, W is MNAR, with a mechanism that does not depend on Y.

Table 10. Missing data patterns for sub-sample ignorable likelihood. A ‘√’ denotes observed, ‘·’ missing and ‘√/·’ denotes some observed and some missing.

Pattern	Variables
	Z	W	X	Y
1	√	√	√	√
2	√	√	√/·	√/·
3	√	·	√/·	√/·

Consider a regression of Y on X, W, Z. Following from the discussion of MAR above, we see a complete records analysis will be invalid, because for observations in pattern 2 the missingness mechanism includes the response. Also, an analysis assuming MAR using observations from all three patterns will be invalid, because data are MNAR in pattern 3. However, using only data from patterns 1 and 2, the missingness mechanism is MAR; therefore, an appropriate analysis (e.g. using MI) in this setting gives valid inference. In essence, this is a partial likelihood analysis, where the MNAR component is set aside.

Thus, by careful consideration of the reasons for missing data, we may be able to get valid inference via MI without recourse to a full MNAR analysis, even if a portion of the data are MNAR. A more formal justification of this approach is given by Little & Zhang (2011), who also present some simulations confirming the validity of inference when the sub-sample ignorability assumption holds, together with an example.

8.2. Sensitivity analysis using prior information from external sources

The key challenge of sensitivity analysis is specifying values (and uncertainty) for the parameters that describe the differences between the distribution of the observed and missing data. A natural approach to this is to try and elicit information from experts. The idea is to capture quantitatively the way that experts interpret the analysis of studies with missing values. Smuk et al. (2017) develop this approach in the context of analysing cancer registry data, and Mason et al. (2017a) develop it in the context of the IMPROVE clinical trial comparing two treatments for patients with a clinical diagnosis of ruptured abdominal aortic aneurysm, providing a link to an R-shiny app to elicit views from experts. While the approach was promising, Heitjan (2017) challenged whether the experts really understood the questions they were answering, which is key for clinical validity of the results. Mason et al. (2017b) provided some reassurance, and Mason et al. (2020) set out a general framework, but further work is needed to develop, build confidence in, and empirically evaluate this approach.

8.3. Using MI with propensity score models

Analysis of observational studies increasingly makes use of propensity score methods to handle confounding. The propensity score is a model for the probability of exposure. Conditional on it, the distribution of observed covariates is balanced in the exposed and unexposed groups, and using it in the analysis provides an effective approach to tackle confounding. Unfortunately, particularly when using large electronic databases, many of the natural candidate variables for the propensity score have missing values. MI provides a natural approach here, but there has been controversy over how it should be applied. Leyrat et al. (2019) resolve this, showing that (i) the imputation model for variables in the propensity score model should include the outcome in the substantive model and (ii) Rubin’s rules should be applied to the K exposure effect estimates and standard errors obtained from fitting the substantive model to each of the K imputed datasets in turn. More generally, Leyrat et al. (2020) explore how MI compares with other methods for marginal structural models.

8.4. Multilevel MI

We have already mentioned the importance of the imputation model being consistent with the substantive model. In particular, if the substantive model is multilevel, the imputation model should be too. Schafer (1997, 2001) outlines how this may be done, and this approach has been further developed using a latent normal model to handle categorial variables by Quartagno & Carpenter (2015) and Quartagno et al. (2019b). In particular, when data on level-1 units are clustered in level-2 units, they build on an approach proposed by Yucel (2011), which allows the level-2 unit covariance matrices to be randomly distributed (generalising the idea of random intercepts and slopes). This provides a natural approach for imputing systematically missing variables in individual patient data meta-analysis. Quartagno et al. (2019a) show that it also provides an attractive method when the substantive model is a weighted analysis. In such situations, imputation is complicated because the relationship between the variables may vary with the weights. They show that this may be successfully handled by grouping the weights and then using these groups to define the second level in a multilevel imputation model. This procedure approximately satisfies the criteria for valid imputation with weights (see Carpenter & Kenward, 2013, Ch. 11 and references therein). This approach may also provide a measure of double robustness.

8.5. Imputation with large datasets

For large datasets, direct application of standard imputation can be problematic; for example, within the FCS procedure, correlations between variables cause instability when there are tens of covariates in the regression models. In the context of joint-modelling imputation, Schafer (1997) proposed a ridge regression prior to stabilise the covariance matrix; this is a promising approach but relatively little used. Within FCS, one approach is to be more selective in the choice of covariates for each of the conditional models; however, this needs to be done carefully as there is risk that they may be incompatible with each other.

Another option explored, for example, by Shah et al. (2014) is to replace conditional regressions with tree-based classifiers or related machine learning methods. This has potential for handling co-linearity and over-specification issues, but the challenge is to produce (approximately) proper Bayesian imputations, which are necessary for Rubin’s rules to give valid inference.

When data are longitudinal (or have a similar natural structure), another approach to limit the complexity of the imputation model is to impute within a time-window, which is repeatedly moved through the dataset. This approach, proposed by Nevalainen et al. (2009), and developed and evaluated by Welch et al. (2014), has been shown to perform well in many settings, though longitudinal correlations may not always be well preserved (Oya et al., 2015).

8.6. ICH-E9 addendum on estimands

Appropriate handling of missing data in clinical trials has been a recurring theme in the literature and was the subject of a report by the U.S. National Research Council in 2010 (National Research Council, 2010). A number of the report’s recommendations put the spotlight on the estimand: that is the patient population for which a treatment estimate is sought. This has led to renewed concern about precisely what is being assumed when missing trial outcome data are assumed MAR and imputed (or analysed by equivalent approaches). This concern has been reflected in the recent ICH E9 guideline on clinical trials (International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use, 2019).

A particular focus is on how to account for treatment deviations and non-randomised interventions in trial follow-up (termed inter-current events). Such events either cause data for an estimand to be missing or are not directly applicable. MI is a natural approach for assessing the robustness of treatment inferences to different assumptions about such data; together with related causal approaches (e.g. Imbens & Rubin, 1997; Frangakis & Rubin, 2002) make this an active ongoing research area.

9. Summary and Discussion

While initially it may prove surprising, the conceptual issues raised by missing data are common across a range of analyses of experimental and observational data. In this article, we have therefore proposed a systematic framework for thinking through and addressing these issues and illustrated its application.

In Section 3, we considered when complete records analysis is likely to be valid, showing that in regression analyses a key criterion is that the probability of a complete record (regardless of which data are missing) does not depend on the outcome (or dependent) variable. While – as with all missing data assumptions – this cannot be formally tested, in many settings (such as Example 1, the sudden infant death study) it is contextually plausible and provides practical guidance on what we might expect from a more sophisticated analysis (e.g. using MI).

Then, having argued that Rubin’s MAR assumption is typically a natural starting point if we wish to move beyond a complete records analysis, in Section 5 we reviewed a range of available methods for doing this. When there are only missing data in the outcome (which may be cross sectional or longitudinal), Subsection 5.1 showed that maximising the likelihood of the observed data gives valid inference (provided we choose an appropriate covariance structure). With missing values in both dependent and independent variables, we reviewed a range of approaches in Subsections 5.2–5.4, concluding that MI (Subsection 5.5) was the most flexible and practical approach, with wide choice of well-documented software (Section 7). A key practical advantage is the ability to include auxiliary variables in the imputation model (i.e. additional variables from our dataset that are not in the scientific model). Where these are good predictors of the missing values, they add useful information; when they additionally predict that data are likely to be missing, they make the MAR assumption more plausible and will remove bias. However, when they merely predict the probability that data are missing, they should not be included. For illustration and a practical strategy, see Spratt et al. (2010); Collins et al. (2001) is also worth reading carefully, noting the different findings for including auxiliary variables depending on whether outcome, exposure or confounders are primarily being imputed.

We then illustrated the application of our framework to a cohort study, multi-centre case-control study and randomised clinical trial. In each case, use of the framework shows how careful preliminary analysis can reveal the likely gains of MI and how to avoid the key pitfall, which is use of an imputation model that is inconsistent (e.g. by omitting interactions) with the scientific model.

The final key component is sensitivity analysis (Section 6). We showed that while in some settings (e.g. the Sudden Infant Death study), a simple approach will be sufficient, in other settings a more sophisticated approach is needed. A practical approach is to focus on one or more key variables and explore the effect of moving away from MAR. We described a generic algorithm for doing this (see also Carpenter, 2019) and illustrated its application to the NCDS analysis.

The challenge with sensitivity analysis is that they may entail choosing values for a large number of sensitivity parameters. To avoid this, we suggest reference-based sensitivity analysis, which describes the missing not at random distribution by reference to observed data distributions. This accessible approach continues to attract interest and applications, has been extended to survival data (Atkinson et al., 2019) and is the subject of a tutorial (Cro et al., 2020).

Finally, Section 8 shows that missing data remains an active research topic: this is fuelled both by its increasingly wide application and the increasing complexity of the scientific models it is being used for.

In conclusion, the size of the literature on missing data, together with the range of software tools available, can be bewildering even for experienced statisticians. We hope that this article has succeeded in its aim of providing a framework which can be used to both chart a practical way forward through the literature and guide those analysing partially observed data. Interested readers are encouraged to visit the STRATOS initiative (https://stratos-initiative.org) and in particular the missing data topic group which has recently posted a manuscript describing the ‘Treatment and Reporting of Missing Data in Observational Studies’ (TARMOS) framework (Lee et al., 2020), which gives further practical guidance on planning and reporting analyses, together with a worked example.