Towards personalized computer simulation of breast cancer treatment: a multi-scale pharmacokinetic and pharmacodynamic model informed by multi-type patient data

Abstract

The usefulness of mechanistic models to disentangle complex multi-scale cancer processes such as treatment response has been widely acknowledged. However, a major barrier for multi-scale models to predict treatment outcomes in individual patients lies in their initialization and parametrization which need to reflect individual cancer characteristics accurately. In this study we use multi-type measurements acquired routinely on a single breast tumor, including histopathology, magnetic resonance imaging, and molecular profiling, to personalize parts of a complex multi-scale model of breast cancer treated with chemotherapeutic and anti-angiogenic agents. The model accounts for drug pharmacokinetics and pharmacodynamics. We developed an open-source computer program that simulates cross-sections of tumors under 12-week therapy regimens and use it to individually reproduce and elucidate treatment outcomes of four patients. Two of the tumors did not respond to therapy, and model simulations were used to suggest alternative regimens with improved outcomes dependent on the tumor’s individual characteristics. It was determined that more frequent and lower doses of chemotherapy reduce tumor burden in a low proliferative tumor while lower doses of anti-angiogenic agents improve drug penetration in a poorly perfused tumor. Furthermore, using this model we were able to predict correctly the outcome in another patient after 12 weeks of treatment. In summary, our model bridges multi-type clinical data to shed light on individual treatment outcomes.

Introduction

Current personalized cancer treatment is based on a few biomarkers which allow assigning each patient to a subtype of the disease, for which treatment has been established [1]. In breast cancer, multigene tests like Mammaprint or PAM50 give prognostic information to guide clinical decisions [2, 3]. Such stratified patient treatments represent a first important step away from one-size-fits-all treatment. However, the accuracy of disease classification comes short in the granularity of the personalization: it assigns patients to one of a few classes, within which heterogeneity in response to therapy is still large [4]. In each of these classes, randomized clinical trials (RCT) can be run, to compare a few treatment regimens and to identify the best on-average one. As there is a combinatorial explosive quantity of combinations of cancer drugs, doses and regimens, only very few can be explored by RCTs. The concept of ‘one disease in each patient’ challenges diagnosis and therapy.

Mechanistic mathematical modeling and simulation have emerged as a powerful approach to investigate the influence of biological factors on tumor progression and therapy response [5–7]. Current models are able to account for complex interactions at the cellular and molecular level, and are capable of bridging multiple spatial and temporal scales in ways that would be impossible using experimentation [8, 9]. Successful multi-scale models can describe with acceptable approximation the dynamics of tumors under the effect of a specific therapy. The present computing capacity allows exploration of a large number of treatment regimens by running multiple model simulations in parallel. Yet, considerable challenges hinder the use of computational modeling to guide patient’s treatment in clinical practice [7, 10]. The choice of the level of biological detail represented in the mathematical model can always be questioned and a judicious balance between biological and model complexity has to be found. An essential question is whether at all mathematical models can be personalized to predict the effect of therapies in each specific patient [7, 11]. This requires individualized initialization and parameterization of such a model which are typically difficult to perform.

For this paper, our team of oncologists, pathologists, molecular biologists, medical imaging physicists, statisticians and mathematicians examined whether a computational modeling approach can effectively simulate individual outcomes of a group of patients with invasive breast cancer receiving different treatment regimens (described later). Is it possible to design a mathematical model that integrates individual patient’s data collected in routine clinical practice to reproduce patients’ outcome? Can such a model be flexible enough to simulate a wide range of possible responses by capturing fundamental biological processes at an acceptable level of approximation? Are the available data sufficient to personalize such a mathematical model? This paper answers positively the first two questions: we developed a model which allows in-silico simulation of the treatment outcome. Regarding the third question, we show the need to measure more precisely certain individual drug and tumor characteristics, in order to estimate certain parameters which modulate the dynamics.

Barbolosi et al. [7] underline the importance of capturing in a mathematical model pharmacokinetics (the fate of drugs in biological tissues) and pharmacodynamics (their mechanisms of action and effect). Both are present in our model. Furthermore, reference [7] distinguishes between phenomenological (descriptive) models and mechanistic (explicative) ones. Phenomenological models are parametric models of the time evolution of the tumor that do not rest on explicit biological mechanisms. Mechanistic models instead, account for specific biological details and dynamics. We present here a mechanistic model that captures nonlinear, multi-scale dynamics in space and time. We consider discrete individual cells and blood vessels together with continuous quantities like oxygen and drug concentrations; such models are termed ‘hybrid’. Gallo and Birtwistle [12] use the term ‘enhanced pharmacodynamics’ for models that merge multi-scale dynamics with pharmacokinetics, as is in our case. An important distinction is between models informed by individual patient data and those who are not, and therefore cannot be used for personalized treatment optimization. While there are many studies in the literature which propose models in some of these dimensions (for instance [13–25]), our study is possibly the first one towards personalized computer simulation of breast cancer treatment incorporating relevant biologically-specific mechanisms and multi-type individual patient data in a mechanistic and multi-scale manner.

We inform our model with data from five breast tumors collected in a recent neoadjuvant clinical phase II trial [26]. Patients included in this study were randomized in two arms to receive chemotherapy with or without bevacizumab. Histological, magnetic resonance imaging (MRI) and molecular data were collected before, during and at the end of neoadjuvant treatment. We develop precise pipelines for clinical data preprocessing, model initialization and personalization. Besides individual histological and MRI data, our model also makes use of some genomic patient data. By means of extensive numerical simulations, we show, as a proof-of-concept, that patient-specific and multi-scale modeling allows us to reproduce treatment outcomes of the four patients. We also predicted correctly the outcome after 12 weeks treatments of one further patient. In addition, we investigate if and how alternative treatment protocols would have produced different outcomes. This is a first step towards virtual treatment comparison. Finally, we suggest which additional data and experimentation with tumor material is needed to improve the accuracy of the simulation, towards precise outcome prediction. Our study shows that simulation-based personal treatment optimization is feasible and powerful and should be developed further as a promising avenue of personalized treatment.

Materials and methods

Patients and treatment

We selected five patients with HER-2 negative mammary carcinomas from the NeoAva cohort [26], a randomized, phase II clinical trial that evaluated the effect of bevacizumab in combination with neoadjuvant treatment regimens for 24 weeks. Written informed consent was obtained from all patients prior to inclusion. The study was approved by the Institutional Protocol Review Board, the regional ethics committee, the Norwegian Medicines Agency, and carried out in accordance with the Declaration of Helsinki, International Conference on Harmony/Good Clinical practice. The study is registered in the http://www.ClinicalTrials.gov/ database with the identifier NCT00773695. See section S2.1 in Supplementary Material (SM) for more details about the trial inclusion criteria.

For simplicity, we analyze only the first 12 weeks, where patients were treated with chemotherapy (FEC100, 4 courses) and randomized 1:1 to receive bevacizumab (15 mg/kg every third week given concurrently with chemotherapy) or not. The five patients were selected to belong to both arms of the trial and to have either a complete or no response by clinical examination and caliper measurements at 12 weeks of treatment. Additionally, MRI were used to facilitate precise validation of simulated outcomes in small tumor portions. An overview of baseline characteristics, treatment and response for the five patients is shown in table 1. Further details on clinical data can be found in table S1 and fig. S1–S10 of the SM.

Table 1.

Patient overview. Baseline characteristics are shown together with assigned clinical trial arms and tumor volumes measured from DW-MRI segmentation at weeks 0, 1 and 12 after initiation of the treatment. By clinical examination and caliper measurement, at week 12, patients 1 and 3 were classified as non-responders (NR) while patients 2 and 4 were classified as complete responders (CR). Volumes marked with asterisks were unavailable due to problems such as fat suppression and instead computed from Dynamic Contrast Enhanced (DCE) segmentation. As patient 1 was treated with bevacizumab which typically reduces DCE-MRI signal, maximum tumor diameters were used (30mm at week 0 and 31mm at week 12).

Patient ID		1	2	3	4	5
Age		48	31	40	41	53
Histological tumor type		IDC†	IDC	IDC	IDC	IDC
Histological tumor grade		2	3	3	2 - 3	3
Hormone Receptor status	ER	positive (100%)	positive (1%)	negative	negative	negative
	PR	positive	negative	negative	positive	negative
Lymph Node (LN) status	Week 0	positive	negative	positive	negative‡	positive
PAM50 subtype		luminal B	basal	HER2	basal	basal
Clinical Trial Arm		FEC100 + bevacizumab	FEC100 + bevacizumab	FEC100 only	FEC100 only	FEC100 + bevacizumab
	Week 0	3987	14940	11449.5*	1934	3327*
Tumor volume (mm3)	Week 1	3392	-	11460	1279	2115*
	Week 12	1662*	89	11780	0	0
Response at week 12		NR	CR	NR	CR	CR

^†Invasive Ductal Carcinoma

^‡A few possibly malignant cells not further classified were seen in lymph node aspirate before treatment start.

Histopathology

The histopathological analysis was performed on needle biopsies taken from the breast tumors at week 0. See details and used images in section S2.2 of SM. Fiji and its cell counter plugin [27] were used for manual identification of cancer and stroma cells in each image.

Magnetic resonance imaging

Patients were examined on a 1.5 T MRI scanner (ESPREE, Siemens, Erlangen, Germany) at weeks 0, 1 and 12 of the neoadjuvant treatment. See section S2.3 in SM for a description of the imaging protocol and data, including dynamic contrast-enhanced (DCE-MRI) and diffusion weighted (DW-MRI) imaging. For DCE-MRI analysis, an extended Tofts model was used, which included the determination of the contrast-enhancement curve of the contrast agent in each individual voxel (volume 1mm × 1mm × 1.5mm). DW-MRI data were analyzed using a simplified IVIM model-based analysis as described in [28].

Molecular data

To estimate parameters representing subcellular processes, we assessed several molecular features for each tumor. mRNA levels of VEGFA and TP53 in the tumor samples were determined using one color SurePrint G3 HumanGE 8 60 k Microarrays (Agilent Technologies) as described in [26], available in the ArrayExpress database, accession number E-MTAB-4439. The PAM50 subtyping [29] was used to assign a subtype to each sample in the NeoAva cohort and proliferation score was derived for each tumor by computing mean expression values of the 11 proliferation-related PAM50 genes [26, 29]. TP53 mutation status was determined by sequencing the entire coding region (exons 2-11), including splice junctions as described in [26]. Furthermore, pathway deregulation score (PDS) [30] of the Hypoxia-inducible factor 1-alpha (HIF1A) pathway was calculated for all five patients at screening and at week 12 and normalized against 50 tumor-free samples.

Mathematical model

To model the response of a cross section of tumor tissue to a combination of chemotherapeutic and antiangiogenic drugs, we use a multi-scale hybrid cellular automaton model. We combine cellular, extracellular and intracellular dynamics and inform them by multi-type, individual patient data. The model is detailed in section S1 and illustrated in fig. S11 of the SM. Briefly, we describe individual cells and cross sections of functional blood vessels in a 2D section of tumor tissue as discrete agents on a regular grid. Cell division and death as well as blood vessel formation and removal, are controlled in the cellular automata by intracellular and environmental factors, described by ordinary and partial differential equations. For instance, the concentration of each drug in the blood and in the tumor tissue is described by ordinary (pharmacokinetics) and partial (reaction-diffusion) differential equations respectively. As FEC chemotherapeutic agents can only kill cycling cells, we consider a simple cell cycle model for each cell and model the effect of low oxygen tension as delaying cell division. We account in each cell for the effect of hypoxia to TP53 and VEGF expression using a system of ordinary differential equations. This allows us to model the amount of VEGF produced by each cell and the inhibition of VEGF molecules by the antiangiogenic drug. To model the effect of VEGF on the tumor vasculature, we use a stochastic model where the probability of formation or removal of vessels is influenced by the local VEGF concentration.

Tumor simulation and validation workflow

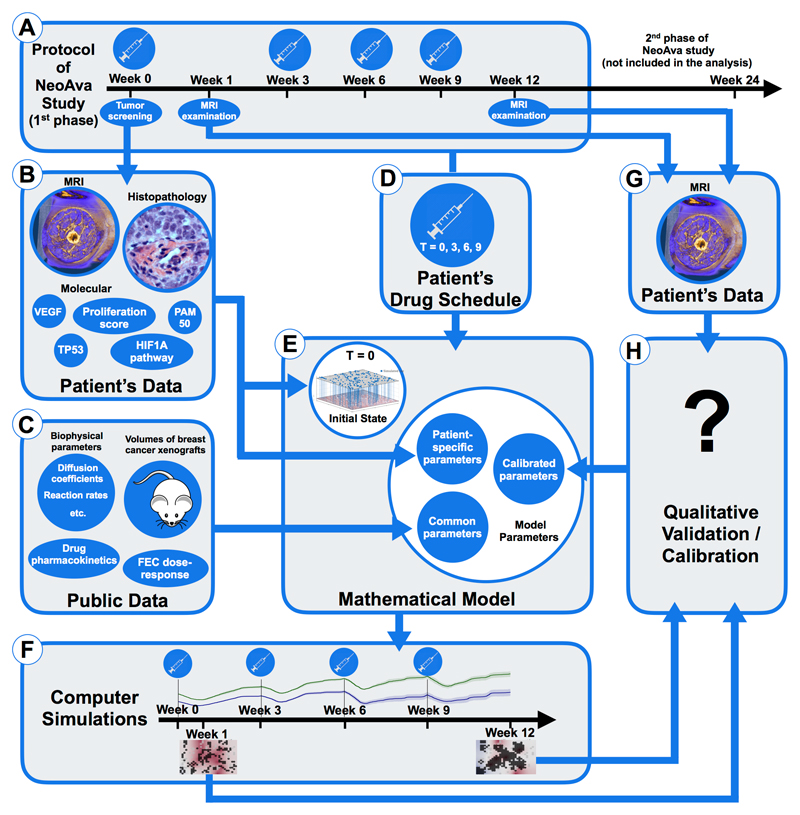
The workflow to run personalized simulations of drug response of a breast tumor portion is outlined in fig. 1. Box A sketches the timeline of treatment application and tumor screening during the first phase of the NeoAva protocol. Tumor screening data at week 0, including MRI, histopathology and molecular data (box B), are used to initialize and parametrize the mathematical model (box E). Model initialization and parametrization is explained in detail in section S3 and illustrated in fig. S12 in the SM: (i) Patient-derived parameters are obtained directly from her clinical data (see box B in fig. 1 and table S2 in the SM); (ii) Common parameters to all studied patients are obtained from public data (see box C in fig. 1 and table S3 in the SM); (iii) Finally, there are model parameters that are calibrated because they cannot be inferred from the clinical data directly, nor relevant quantities were found in the literature. Calibration is done by finding ranges of parameter values where the simulated and patient outcome qualitatively agree (see table S4 and fig. S13–S18 in the SM for parameter exploration of effects on treatment outcomes). Specifically, the exact drug schedule used in the clinical trial for each patient (box D) is simulated by increasing the amount of the corresponding drugs (FEC100 +/- bevacizumab) in the blood at the time points of administration according to the dosage. Each computer simulation then runs a complete cycle of 12 weeks of the spatio-temporal dynamics of the considered tumor portion under the effect of the applied drugs. Computational details and a link to the open-source computer code can be found in section S4 of SM. Simulated outcomes include the spatial distribution of cells, blood vessels and all considered molecules at any time between the start of the therapy and week 12 and in particular at the end of the study period (box F). To calibrate the three model parameters, we compare the simulated outcomes with the actual ones (box H). For that we use clinical tumor volumes and apparent diffusion coefficients (ADC) [26] calculated from DW-MR imaging at week 1 and 12 (box G). As we are simulating only very small portions of the tumor bulk, we selected only patients who were complete responders (number of tumor cells in all simulated tumor portions at week 12 should be around zero) or complete non-responders at week 12 (approximately the same number of tumor cells in week 12 as in week 0). Moreover, changes in ADC histograms of the segmented tumor volume at weeks 0, 1 and 12, which relate to changes in the tumor cellularity [20], should qualitatively agree with the number of tumor cells in our simulations.

Figure 1.

Simulation and validation workflow, outlined through panels A to H

Results

Comparison of patient characteristics and treatment responses

We consider four patients (1 to 4), see table 1 and section S2 in SM. Patients 1 and 2 received FEC100 plus bevacizumab with the same dose and schedule. Patient 1 did not respond to the therapy after 12 weeks, while patient 2 responded well. At baseline, patient 2 had a higher tumor cell density than patient 1, as shown by histological images and DW-MRI. This coincided with higher PDS of HIF1A pathway. Their tumors were also classified differently as Basal-like and Luminal B, respectively, and the estimated proliferative capacity of patient 2 was much higher (see parameter T_min in section S3.5.1 of the SM), in agreement with the estimated PAM50 proliferation scores [31] of both patients. Other molecular and MRI-deduced parameters used in this study, did not differ significantly. Specifically, expression levels of VEGF and TP53 were almost identical, and both tumors were TP53 wild-type. The typical values of perfusion parameters k_trans and v_p estimated from DCE-MRI, were similar too.

Patients 3 and 4 received only FEC100 with the same dose and schedule. Patient 3 did not respond to the therapy after 12 weeks, while patient 4 responded completely. The tumors were classified as HER2 enriched and Basal-like respectively, but they had similar proliferative capacity as shown by their estimated PAM50 proliferation scores. They differed in tumor morphology, vessel perfusion and TP53 status and expression. Comparing histological slices and DW-MRI, the tissue of patient 3 was densely packed with cells, while patient 4 showed more heterogeneity. DW-MRI of patient 4 also showed heterogeneity. At week 0, by DCE-MRI the tumor in patient 3 had a very poorly perfused core while it was highly perfused on the outer edge, resulting in cross sections with ring-like patterns. Interestingly, DW-MRI analysis suggests that the tumor core is not necrotic. The tumor from patient 3 was TP53 wild-type while the tumor from patient 4 was TP53-mutated. Expression levels of TP53 were higher in patient 4 while VEGF expression was comparable and very high in both patients. Patient 3 had much higher HIF1A PDS at week 0, exhibiting signs of a denser and more hypoxic tumor.

Model simulations reproduce treatment outcomes

For each of the four patients we run personalized simulations of tumor portions under the treatment received in the clinical trial as outlined in fig. 1 and described in the SM.

Low vs. highly proliferative tumor in bevacizumab arm

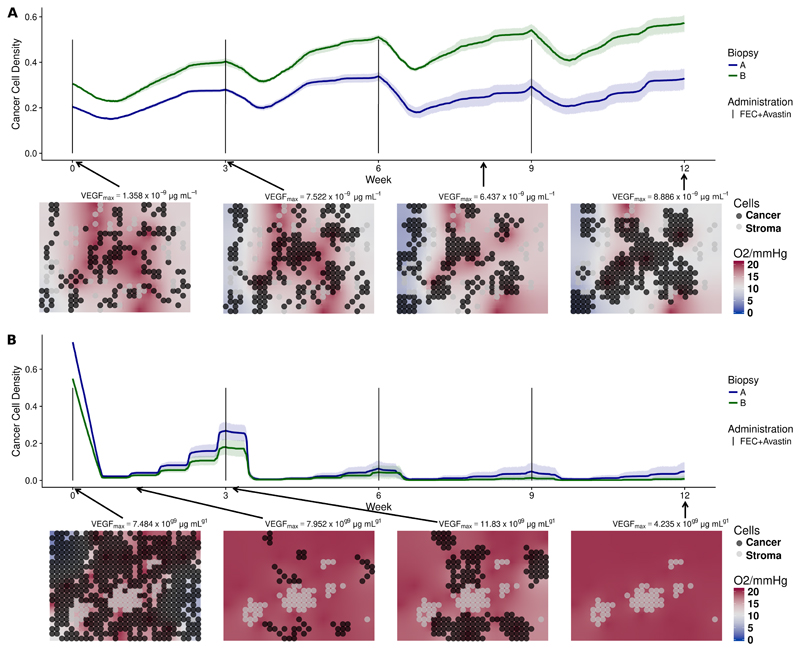
Model simulations of the outcomes of patient 1 and patient 2 are shown in fig. 2. We used two biopsy portions for each patient (biopsy A and B). For each portion, we ran ten independent stochastic simulations of the 12-week treatment using the same parameterization, but different random events such as births and deaths of vessels. We plot the time evolution of the cancer cell density, defined as the proportion of grid points occupied by cancer cells at any given time, for the ten simulations. Simulated cell densities for patient 1, shown in fig. 2a, decrease moderately after drug administration and grow in the period between consecutive administrations. The four grid snapshots show, at different time points, the spatial distribution of cancer and stroma cells together with the oxygen level in one representative simulation. All twenty simulated experiments presented moderate degrees of hypoxia, as seen by the white and light blue background displayed in the snapshots of fig. 2a. This is in agreement with the observed hypoxic pathway activity and VEGF expression, shown in fig. S10b and fig. S10d in the SM. In fact, despite of production of VEGF by hypoxic cells, the applied dose of bevacizumab reduces VEGF concentration in the tumor tissue to very low levels, as recorded above each snapshot in fig. 2a. In our model blood vessels disappear with a certain probability under low VEGF concentration. For patient 1, if this probability is high enough, the tumor can persist, because bevacizumab reduces tumor perfusion and the chemotherapeutic agents cannot reach the tumor tissue. We can reproduce the outcome at week 12 using any value for the probability for vessels to become dysfunctional under low VEGF and an intermediate value of the chemosensitivity parameter, as shown in fig. S13 and fig. S16 in the SM. In fig. 2a, even when using a very low probability of vessel death (p_death = 0.0001), the killing of cancer cells after each dose administration does not prevent cancer cells to proliferate again, resulting in a net balance between killing and proliferation in 20 out of 20 simulations. This is in agreement with the available ADC data of patient 1 at week 0 and 1, showing little difference in tumor density (fig. S9a in the SM). By the end of the simulations, the cancer cell density is approximately the same as it was at the beginning.

Figure 2.

(a) Simulations of NeoAva drug schedule in patient 1. (b) Simulations of NeoAva drug schedule in patient 2. Simulated time evolution of the cancer cell density starting from two different cell configurations at week 0 corresponding to biopsy portions A and B. Each line represents the average cancer cell density of 10 independent stochastic simulations. The corresponding color band indicates the 95% bootstrap confidence interval. Lower panel of each figure shows the spatial distribution of cancer and stroma cells for a representative simulation of the biopsy portion B for each patient. Background color represents oxygen pressure in mmHg.

Patient 2 is a responder. Many blood vessels remain in the tissue to allow chemotherapeutic drugs to be distributed and thus kill most of the tumor cells. To reproduce the available ADC data, where virtually no tumor remained at week 12 (fig. S9b in the SM), the following is required: First, a low probability of vessel disappearing (p_death < 0.01), so that part of the tumor vasculature is resistant to the VEGF inhibitor; second, a chemosensitivity high enough (β > 6000), so that few cells escape the therapy, see fig. S13 and fig. S16 in the SM. In the simulations of patient 2 shown in (fig. 2b), all tumor cells were killed after 12 weeks in 19 out of 20 experiments. Due to higher cell densities at week 0, hypoxia is more severe than for patient 1, in agreement with the HIF pathway (fig. S10d in the SM) and ADC data (fig. S9b in the SM).

Heterogeneous perfusion condition without bevacizumab

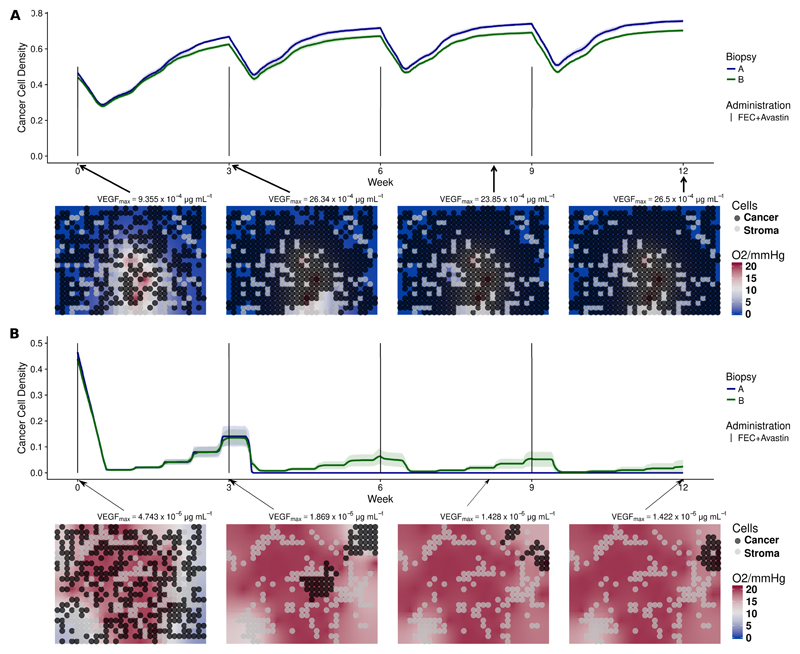
Patient 3 is a non-responder. As revealed by MRI data (fig. S7 in the SM), the core of the tumor is poorly perfused with much higher perfusion at the tumor edge. Since the location of our biopsy was not identifiable, we show in fig. 3 simulations for both perfusion profiles. k_trans = 0.0067min⁻¹ and v_p = 1.73% were estimated from the core to reflect its poorly perfused condition (fig. 3a). Since the number of vessels is small and their permeability is low, the simulated drug concentration arriving in the tissue is very low. Therefore, free spaces in the simulation grid were occupied by the cancer cells, see fig. 3a. This is in agreement with DW-MRI data (fig. S9c in the SM) and HIF1A PDS which explain patient 3 being a non-responder. At the highly-perfused tumor edge, k_trans and v_p were estimated to be 0.2145min⁻¹ and 15.35% respectively, and drugs arrive in the tissue more efficiently. Provided cell chemosensitivity is high enough, simulated cancer cell densities can be reduced, as shown in fig. 3b. Although cells in the edge could be killed, this area could have been repopulated by the highly-proliferative cells from the core.

Figure 3.

(a) Simulations of NeoAva drug schedule in patient 3 under poorly-perfused condition. (b) Simulations of NeoAva drug schedule in patient 3 under well-perfused condition. Time evolution of cancer cell density for two different cell configurations, biopsy portions A and B, and drug schedules under two different perfusion profiles. Each line represents the average cancer cell density of 10 independent stochastic simulations. The corresponding color band indicates the 95% bootstrap confidence interval. Figure 3a represents the core of the tumor of patient 3, while lower panel of fig. 3b shows the peripheral spatial distribution of cancer and stroma cells for a representative simulation of the biopsy portion B for each patient. Background color represents oxygen pressure in mmHg.

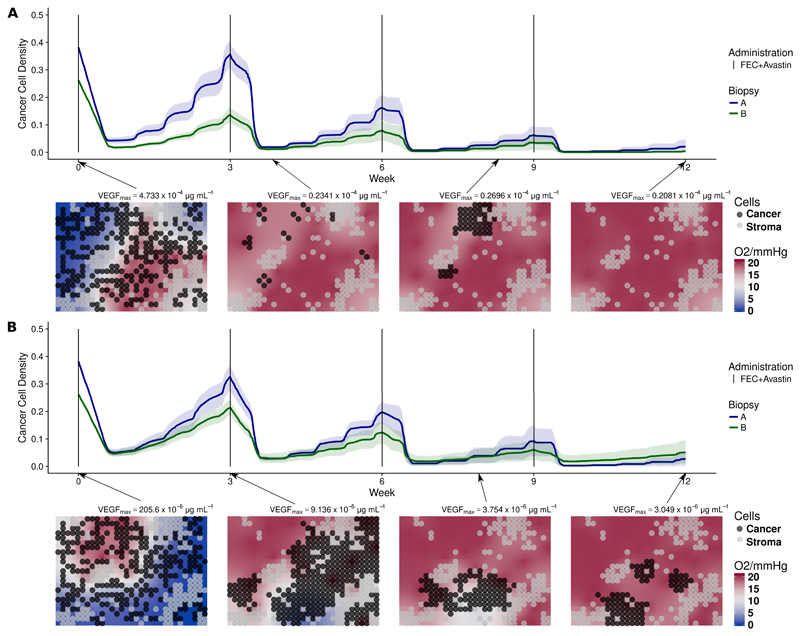
Patient 4 is a responder with also a heterogeneous perfusion profile as seen by DCE-MRI. Contrary to patient 3, a scattered pattern with two representative perfusion profiles is observed, one highly perfused with low permeability, the second with lower perfusion but high permeability. We show simulations of the first perfusion profile in fig. 4a, with the estimated parameters v_p = 6.0% and k_trans = 0.0067min⁻¹. Simulations of the second profile are in fig. 4b, where we estimated v_p = 3.99% and k_trans = 0.1107min⁻¹. To reproduce the DWMRI data in both cases, where we see that the tumor was drastically reduced at week 1 and almost disappeared by week 12 (fig. S9d in the SM), a higher rate of vessel creation compared to the other three patients is required (fig. S15b and fig. S14 in the SM). This was achieved by increasing p_birth and High_V, see table S4. This allowed to transport the drug efficiently to the tissue, even when the permeability was very small. The simulated reduction of severe hypoxia to normoxia shown in the snapshots of fig. 4 is also in agreement with the observed significant decrease in HIF1A PDS comparing week 0 to week 12 (fig. S10d in the SM).

Figure 4.

(a) Simulations of NeoAva drug schedule in patient 4 under perfusion profile 1. (b) Simulations of NeoAva drug schedule in patient 4 under perfusion profile 2. Time evolution of cancer cell density for two different cell configurations, biopsy portions A and B, and drug schedules under two different perfusion profiles. Each line represents the average cancer cell density of 10 independent stochastic simulations. The corresponding color band indicates the 95% bootstrap confidence interval. Lower panel of figs. 4a and 4b show the spatial distribution of cancer and stroma cells for a representative simulation of the biopsy portion B for the patient. Background color represents oxygen pressure in mmHg.

Simulating alternative drug regimens

In addition to the regimens used in the clinical study, we simulated alternative drug regimens (schedules and doses) for the two non-responders.

Low dosage frequent chemotherapy dosing for slowly proliferative tumor

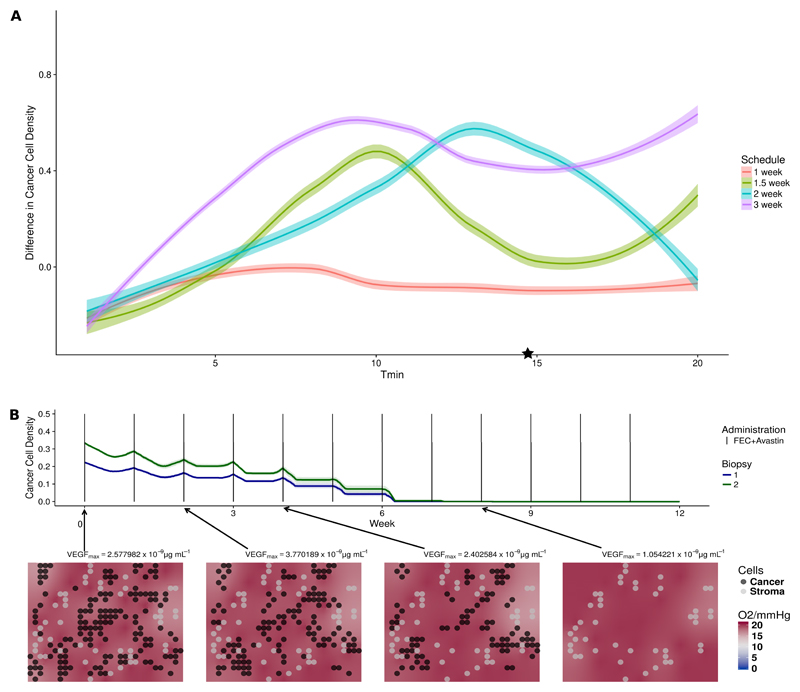
The simulations of patient 1 in fig. 2a suggest that a main reason behind the survival of cancer cells after each drug administration was their low proliferation rate. As the interplay of treatment frequency and cell proliferation rate can contribute to the outcome, we hypothesized that administrating a smaller dose more frequently, while keeping the overall amount would be beneficial. We therefore simulated four chemotherapy regimens: every week with one third of the original dose, every one and a half week with half of the original dose, every two weeks with two thirds of the original dose and the original three-week schedule used in the clinical trial. In fig. 5a we compare the outcomes after 12 weeks of treatment in terms of change in cell density. We used the same initialization and parameters of the personalized simulations of patient 1. To see the effect of cell proliferation rate, we repeated the same simulations while changing the cell cycle length parameter over a wide range. Simulation results show that the interplay between cell cycle length and schedule is complex and can exhibit non-monotonic behaviors. Interestingly, we see that drug administrations every week or every week and a half can improve the treatment outcome of patient 1 (marked with a star in fig. 5a). In fig. 5b, we show simulations of the most successful schedule for patient 1, where we reduced FEC100 and bevacizumab to a third of their original dose, but administrated every week instead of every 3 weeks. The tissue was free of cancer cells after approximately 6 weeks.

Figure 5.

(a) Effects of different chemotherapy schedules on Patient 1 and effect of cell proliferation. (b) Simulations of an alternative schedule in patient 1. In fig. 5a, each colored dot represents the difference in cancer cell density between start and end of therapy under a specific drug schedule and minimal cell cycle length. T_min of daughter cells is randomized to introduce variability in cell cycle duration. Colored lines represent the locally weighted smoothed curve smoothing fitting of the simulations of different cell cycle length under the same drug schedule. The simulations of patient 1 corresponding to the value T_min = 14.69 are labeled with a star. fig. 5b illustrates the temporal dynamics of the alternative drug schedule providing better outcome. Solid lines represent the average cell density (n=10) of the alternative therapy obtained by reducing FEC100 and bevacizumab to a third of its original dose, and administrating them every week instead of every third week.

Low dosage bevacizumab for poorly perfusive tumor

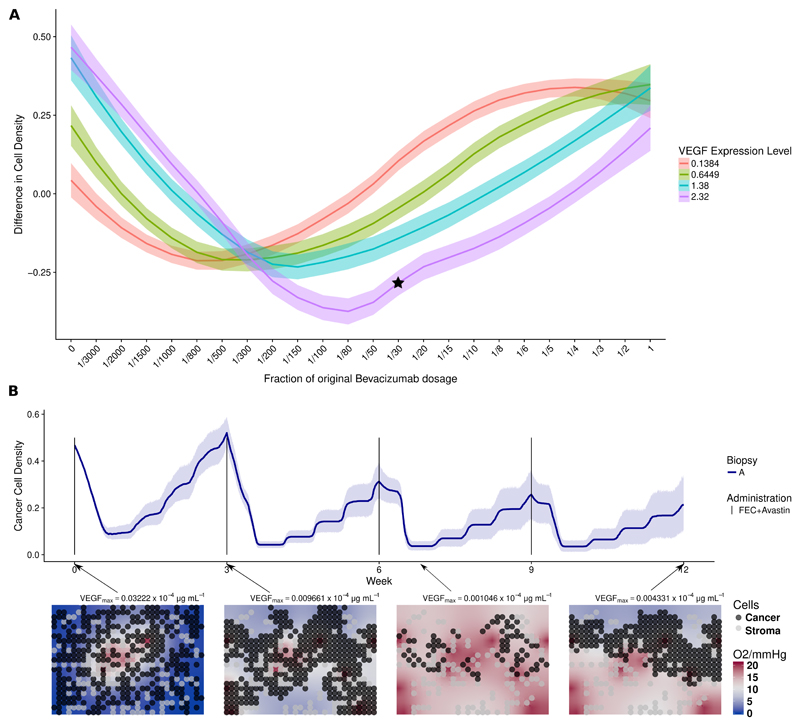
Patient 3 is a non-responder in the trial arm with chemotherapy only. Our analysis suggests that the main reason for the negative outcome was that drugs did not penetrate enough in the tumor core. We hypothesized that by administrating an appropriate amount of bevacizumab, VEGF levels could be reduced appropriately, and tumor perfusion could be improved with the creation of new functional vessels in the core [32, 33]. Thereafter chemotherapy could be delivered efficiently. We added different bevacizumab regimens to the personalized simulations of patient 3, using the same initialization and parameters. Moreover, to see the effect of VEGF expression on the outcome, we repeated the same simulations while changing the parameters modulating VEGF expression levels from low to high (fig. 6a). Since bevacizumab has a long half-life, the same schedule was used like for the chemotherapy (every three weeks) while scaling the amount with respect to what originally administered in the other arm of the trial. We see in fig. 6a, applying full amount of bevacizumab led to no improvement comparing to chemotherapy only and the simulated outcomes strongly depend on the applied bevacizumab regime and the VEGF expression. For patient 3 (VEGF Level = 2.32), tumor burden is reduced with doses lower than a fourth of the full bevacizumab dose. In fig. 6b, we show simulations using the optimal bevacizumab regime for patient 3. Comparing this simulation to its actual clinical outcome, the new therapy appears to improve the outcome by inhibiting the growth of the tumor, reducing the density of the tumor by 50% on average.

Figure 6.

(a) Effects of different bevacizumab schedule on Patient 3 with different estimated VEGF expression. (b) Simulation of an alternative drug schedule for Patient 3. In fig. 6a, the y-axis represents the simulated difference in cancer cell density between week 0 and week 12 under a 3-week administration interval. The x-axis indicates the hypothetical quantity of bevacizumab administered to the patient as fractions with respect to the full dose, corresponding to 15 mg/kg. Each colored band summarizes 10 independent simulations for patient 3 with VEGF expression from low to high given in the legend. These four expression levels correspond to those observed in our four patients. However, all other parameters are fixed as for Patient 3. In fig. 6b, we showed temporal dynamics of an alternative drug schedule providing better outcome. Solid lines represent the average cell density (n=10) of the alternative therapy obtained by administrating a reduced bevacizumab dosage of 0.5mg per kg body weight, equivalent of 3.33% of the dosage in the experimental arm alongside of chemotherapy following a 3-week interval. The corresponding simulation is labeled with a star in fig. 6a.

Other alternative treatments

We tested several regimens removing fluorouracil from the treatment. We found no difference in patient’s outcome comparing to the FEC100 regime administered every 3 and every 2 weeks. Interestingly, this is in agreement with findings in clinical study [34], see fig. S19 in the SM.

We investigated the effect of prolonging the 12-wk FEC regimens, by continuing to administer the same chemotherapy and bevacizumab for another 12 weeks for patient 1. We saw no benefit in terms of patient’s treatment outcome. This confirmed the appropriateness of the actual clinical decision of switching to taxane-based chemotherapy after week 12 (fig. S20 in the SM).

Predicting treatment outcome

Here we predict the response to treatment of a new patient using our model. We chose a patient, patient 5, with the same subtype and in the same trial arm as one of the other four patients, namely patient 2. Screening data was then collected as we did for the other patients and as described in section S3. The simulations were initialized with parameters estimated from the same patient 5 or from the literature, but we did not calibrate any parameter. Instead we use exactly the same chemosensitivity, probability of vessel birth and death and the VEGF thresholds as for patient 2. At week 0, patient 5 has a moderately sized tumor with necrotic region shown on DCE and DWI MR images. Both biopsies showed a high cancer cell density. As a result of this, HIF pathway score was high, comparable to patient 2, indicating hypoxia.

For each of the two digitally captured biopsy images, we ran twenty stochastic simulations and obtain a bootstrap confidence interval for the cell density at the end of week 12. At the end of week 12, the simulated tumor disappeared, and HIF PDS was close to 0. The two-sided 95% bootstrapped confidence interval for biopsies A and B were (0,0.0154) and (0,0.0049) respectively. This agrees with the truth, as patient 5 experienced a clinical complete response.

Discussion

This paper is a new step towards the simulation of individualized tumor response to therapy. We have shown that it is possible to design a multi-scale mathematical model, which integrates different types of individual patient’s data collected in clinical practice and simulates the observed patient outcome. Our model is flexible enough to simulate different outcomes based on individual data, by capturing fundamental biological processes at an acceptable level of approximation. Importantly, our model suggests possible mechanistic explanations of individual treatment outcomes and allows virtual testing of alternative treatment plans. For example, the administrated amount of bevacizumab did not benefit patients. Simulations show that moderate amounts of bevacizumab can improve the outcome of patients with extreme hypoxia. As for FEC, we found that for highly proliferative tumors, cell-cycle specific drugs are very effective, while for low proliferative tumors, a more frequent but lower dosing of FEC can be advantageous.

We are well equipped to recognize limitations of our approach that need to be addressed in the future. First, we have only simulated a few tumor sections of 200 × 300 microns, which might not be representative of the whole tumor bulk. Although the current computational power allows multi-scale model simulations of larger tumor portions, the approach is still limited by the availability of clinical data to inform them. For instance, clinical information at the cellular level, such as the number, position and type of cells, is currently possible only for biopsies. We are extending our algorithms to run cross-sections of full biopsies. A second limitation of our model relates to tumor heterogeneity. Some cell clones can be more proliferative than others, produce more VEGF or be more resistant to therapy. Vessels can be different in size, have unequal functionality and permeability, contain different oxygen and drug concentrations. Due to the current impossibility of characterizing cells and vessels heterogeneity from the available clinical data, our simulations assume all cells and vessels to be of the same type. Extending our model to multiple clones, competing for resources would rely on a deeper picture of the patients’ tumor than routinely available today.

Third, we have assumed that model parameters are constant during the simulated treatment. For instance, we use constant drug chemosensitivity, which is a simplification and neglects the possible evolution of resistant phenotypes. To incorporate such details in the present approach, monitoring of tumor evolution is needed.

We incorporated some degree of heterogeneity in our studies by running simulations with different cell configurations (observed in the biopsies), and different perfusion and permeabilities (observed in MR images of the whole tumor). We account for spatio-temporal heterogeneity in the simulated tissue section where cell and vessel numbers, as well as oxygen, VEGF and drug concentrations change in space and time.

Fourth, VEGF is the only angiogenic factor present in our model and does not explicitly reflect the redundancy of angiogenic stimulants and inhibitors known to be present in a tumor. The mode of action of the VEGF depletion treatment was assumed to be a reduction in the number of functional capillaries, resulting in local reduced supply of oxygen and treatment. However, the effect may be more complex, related to the perfusion and leakage of the tumor influenced by the VEGF, as in [26, 35]. See also [22] for a different susceptibility of VEGF withdrawal dependent on the immune activation in the tumor. Future version of the model should incorporate first principles of such mechanisms.

An important contribution of our paper is the identification of three parameters which cannot be estimated precisely enough from the present clinical data: the chemosensitivity of tumor cells and the sensitivity of vessels to the local VEGF concentration. In our feasibility study, we calibrated these parameters, within a range of realistic values, by choosing the ones which allow simulating a trajectory compatible with the true patient endpoint. A systematic sensitivity analysis is beyond the scope of this paper. We intend to address it in the future. We were able to predict the treatment outcome for one patient without calibration. More tests are needed.

There are several ideas on how the three parameters could be estimated in the future. Drug chemosensitivities can be measured using ex-vivo patient material; sensitivity of vessels can be perhaps estimated using in-vivo experiments on mice xenografts [35, 36]. Another possibility is to use Approximate Bayesian Computation [37] to estimate individual parameters from observing the first cycle of treatment. Preliminary results in this direction are promising.

We highlight the importance of rich longitudinal data to improve the accuracy of the simulated therapies. Repeated MR images at different time points matched to each other [11] would allow to relate tumor features such as volume, perfusion and cell density along therapy. Additionally, matching biopsies and MRI data would be crucial to locate the exact location of the extracted biopsy in the MR images, allowing more accurate estimation of parameters such as the vessel permeability. Furthermore, instead of using average drug pharmacokinetic models, individual longitudinal measurements of drug concentrations in the blood could be easily performed allowing further personalization [7].

In this paper we use some genomic data but much more should be done. It is known that mutations, gene expression and copy number variations portrait properties of tumor cells some of which may have implication on treatment success. For example, the PAM50 gene expression signature [29] allows classification of breast cancers tumors into five distinct classes. As these genomic features modulate the efficacy of therapy, our study suggests that the key parameters in our model, proliferative capacity and chemosensitivity of tumor cells, should depend on such genomic features of the patient.

This paper opens the possibility to build models that allow the simulation of other solid tumors. This would require extensive work on the mathematical modeling and inferential side, and the identification of informative clinical data. In conclusion, our work shows realistic possibilities for simulation guided personalized therapy and indicates where further research should focus to make this possible.