Abstract
A computational model was developed to better understand the impact of elevated skin temperatures on transdermal drug delivery and dermal clearance. A simultaneous heat and mass transport model with emphasis on transdermal delivery system (TDS) applications was developed to address transient and steady-state temperature effects on dermal absorption. The model was tested using representative data from nicotine TDS applied to human skin either in vitro or in vivo. The approximately 2-fold increase of nicotine absorption with a 10°C increase in skin surface temperature was consistent with a 50–65 kJ/mol activation energy for diffusion in the stratum corneum, with this layer serving as the primary barrier for nicotine absorption. Incorporation of a dermal clearance component into the model revealed efficient removal of nicotine via the dermal capillaries at both normal and elevated temperatures. Two-compartment pharmacokinetic simulations yielded systemic drug concentrations consistent with the human pharmacokinetic data. Both in vitro skin permeation and in vivo pharmacokinetics of nicotine delivered from a marketed TDS under normal and elevated temperatures can be satisfactorily described by a simultaneous heat and mass transfer computational model incorporating realistic skin barrier properties and dermal clearance components.
Keywords: nicotine transdermal, heat-enhanced, heat and mass transport, mathematical model, human skin
INTRODUCTION
The effect of temperature on skin permeability and flux has been experimentally investigated in ex vivo human skin over the last several decades, e.g., (1–6). These permeation studies and analyses thereof have shown the potential for substantially increased percutaneous absorption of compounds applied on the skin at elevated skin temperatures, notably so for lipophilic compounds (5). A recent analysis based on Gaussian process regression (7) confirms that factoring in experimental temperature improves the quality of fit for QSPR models to steady-state skin permeability data. Drug delivery from transdermal and topical delivery systems (TDS) both in vitro (8,9) and in vivo (9–16) has also been shown to be affected by temperature. Most studies have shown that elevated temperatures increase the drug flux from these TDS in vitro as well as the maximum plasma concentration (Cmax) and total drug amount delivered (AUC) to the systemic circulation in vivo.
A variety of mechanisms have been proposed to explain the increased delivery rates at higher skin temperatures, including changes in skin lipid organization and fluidity (6,17), increased drug solubility (8), altered thermodynamic behavior of the drug in the skin (3–6,8,12,18,19), and increased blood flow to the skin (8,11,15,20). It is clear that temperature effects on skin lipids are involved, but the relative contributions of the other mechanisms are not well understood. The model presented here provides a tool for sorting out these factors.
Local application of heat increases skin perfusion (21) by either capillary recruitment (22) or vasodilation (23) via neuropeptide or nitric oxide control (24,25). Vasodilation is maximal at a skin surface temperature of 42°C (26). The increased transdermal nitroglycerin flux with in vivo skin exposures to infrared heat (20) and increased nicotine drug absorption after heat exposure (11,15) were attributed by both these groups to increased microcirculation. Both compartmental (27–31) and diffusion-based (32–35) models of the impact of skin blood flow (SkBF) on capillary clearance are available. Some of these models include a dispersive mechanism by which topically applied solutes are carried deeply into the underlying fat, muscle, and fascia (27,28,33,34). Dispersion is key to understanding the feasibility of local enhanced transdermal delivery, a concept which has been around since the early 1990s (36). Dispersion has been closely tied to protein binding in the dermal interstitial fluid (33). It is noteworthy that in Dancik et al.’s study (33), it was found that nicotine distribution in skin was minimally impacted by dispersion relative to the highly protein bound solute, diclofenac. Nicotine was found by this group to have a fraction unbound of 0.90 ± 0.02 in 4% BSA solution and 0.72 ± 0.02 in dermis, consistent with literature findings of 0.92–0.95 in plasma.
This paper presents, for the first time, a multilayered diffusion with elimination model of drug transport through skin coupled with heat transfer equation to describe transient and steady-state temperature in the skin. We analyze the temperature effect not only in the SC, but in deeper skin layers. The model parameters are based on an in-depth analysis of literature and applied to human in vivo and in vitro data for nicotine. The diffusion component of the model is based on the three-layer skin transport model described by Dancik et al. (37), herein called UB/UC. The UB/UC model has been extended by the incorporation of temperature effects, the addition of a TDS layer and the substitution of a diffusive/convective dermal clearance component (35,38) for the original dermis model (32). It is coupled with a systemic pharmacokinetic (PK) model so that Cmax and AUC for an arbitrary drug can be calculated. A more thorough discussion of temperature effects on nicotine absorption in vitro and the modeling thereof will be reported elsewhere (39).
METHODS
Mass Transport
The mass transport model (UB/UC) was that described by Dancik et al. (37) and references therein with modifications as described below. UB/UC is a three-layer skin diffusion model with effective transport (Di) and partition (Ki/j) parameters based on underlying microscopic models for each skin layer. The geometry and governing equations are shown in Fig. 1.
Fig. 1.
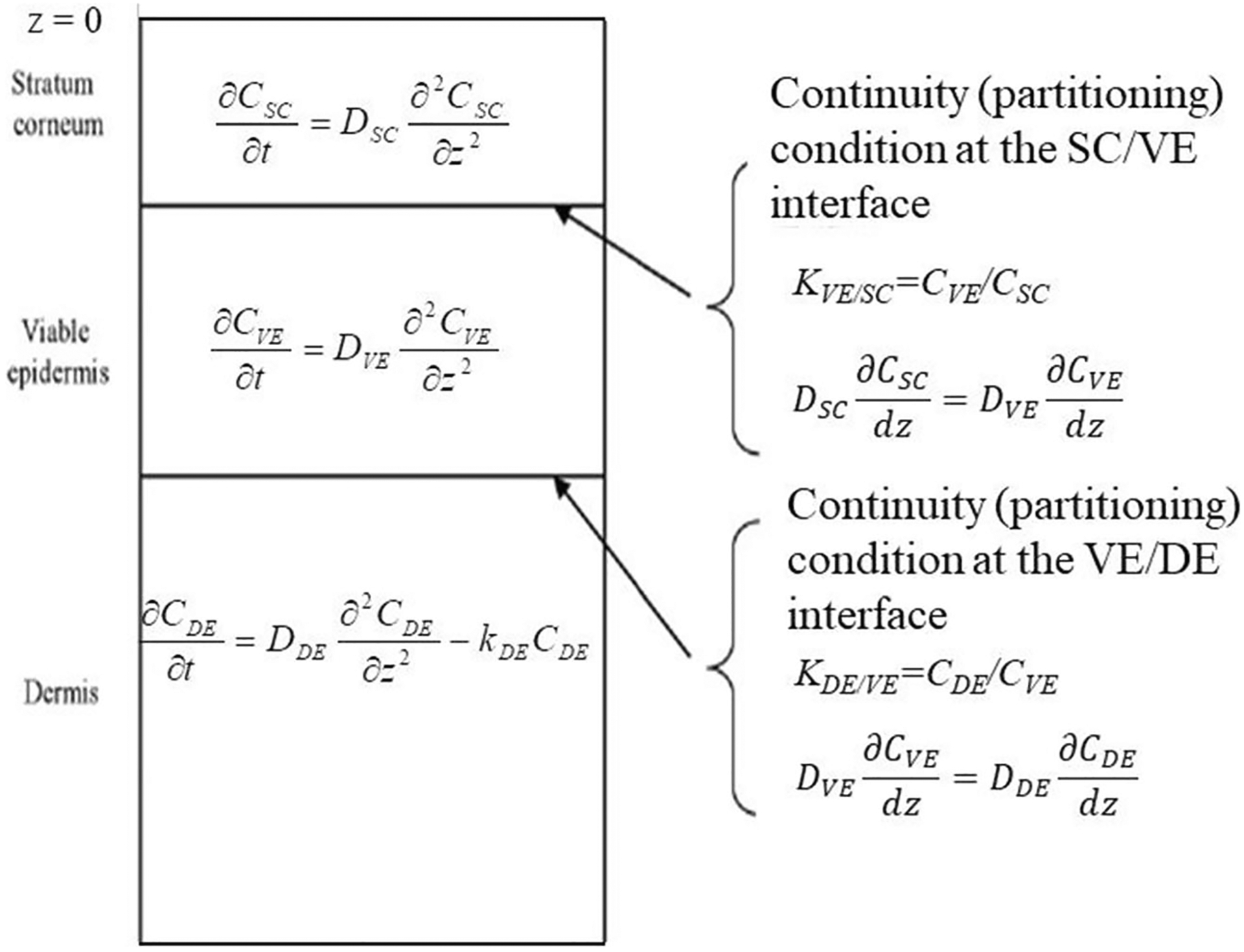
Schematic diagram of UB/UC model. Corresponding governing equations are included for each layer and interface. The constant kDE in the dermis layer represents a distributed dermal clearance by blood and lymphatic capillaries. Figure adapted from (37)
To simulate release from a matrix-type TDS with an impermeable backing, an additional slab layer was constructed above the stratum corneum, with a no-flux condition imposed at the top and flux and continuity conditions enforced at the TDS/SC interface. Effective parameters for this layer were DTDS, KTDS/SC, and hTDS.
The dermis clearance constant kDE was calculated as in Ibrahim et al. (35) as amended by Kapoor et al. (38). The value of kDE is calculated as the sum of blood capillary clearance, and lymphatic clearance, . For small molecules, dominates this sum. It is calculated from a combination of the effective permeability-surface area product of the dermal capillaries, (PS)eff, and skin blood flow, Q, according to
| (1) |
| (2) |
| (3) |
In Eqs. 1 and 2, all variables have units of s−1, e.g., Q is expressed as (cm3 blood s−1/cm3 tissue) = s−1. “Free” and “bound” refer to freely diffusing solute and solute bound to albumin or other soluble proteins in the dermis. Equation 1 was originally introduced by Dedrick et al. (40) and subsequently employed by Gupta et al. (41) and others. In Eq. 3, fu is the unbound fraction of solute in the dermal interstitial fluid and CF is a “concentration factor” designed to distinguish freely diffusing solute from that partitioned into dermal lipids (35). The calculation of (PS)eff follows closely the two-pore model of Rippe and Haraldsson (42), except that pores are represented by slits rather than cylinders. The exchanging capillary surface area S was taken to 70 cm2/cm3 as in (35) and Q was calculated as described in the next section. For more details, the reader is referred to Ibrahim et al. (35).
It is well known that a significant fraction of the normal blood flow in human skin occurs through non-exchanging capillaries, technically known as arterio-venous anastomoses (43–45). This results from the fact that effective thermoregulation requires more blood flow than does maintenance of dermal and epidermal metabolism. At high skin or core temperatures, more non-exchanging capillaries are recruited; thus, blood flow Q increases without the corresponding increase in clearance predicted by Eqs. 1–3. The analysis presented here does not take this phenomenon into account. Thus, solute clearance at elevated blood flows, and resulting blood levels in vivo, may be somewhat overestimated. However, for largely unbound solutes such as nicotine, the impact of this inaccuracy is small because clearance is already very efficient at normal blood flows, as will be shown. This matter should be reconsidered for highly protein bound solutes.
The influence of temperature on permeant diffusivity within each layer was handled via the Arrhenius relationship:
| (4) |
where is the diffusivity in layer i (cm2·s−1) at the baseline temperature (305.15 K or 32°C), T is the absolute temperature (K), is the activation energy for the corresponding layer (J·mol−1), and R is the molar gas constant (8.314 J·mol−1·K−1). The value of Ea was taken to be 18.8 kJ·mol−1 for the viable epidermis and dermis layers, which represents the temperature dependence for solute diffusivities in water between 22 and 42°C according to the Stokes-Einstein equation, using the known temperature dependence of water viscosity (data not shown). For the stratum corneum, we recommend using measured human SC permeabilities ex vivo at 32°C and 42°C to determine . However, as a starting point, Eq. 5 may be used to estimate the expected value:
| (5) |
Here, Koct is the solute octanol-water partition coefficient. Equation 5 represents a fit to the 43 values of human SC activation energies reported by Mitragotri (5). When only human SC data are considered, we find no evidence for the size dependence of for lipophilic compounds reported by Mitragotri.
Heat Transport
For modeling heat transfer through biological tissues, the resulting energy balance includes terms for the accumulation of heat in a slab of tissue as well as the combined effects of blood convection, tissue conduction, and metabolic heat generation. A common model, known as the bioheat or Pennes equation is (46):
| (6) |
where ρ is the density (kg·m−3), cP the specific heat (J·kg−1·K−1), k the thermal conductivity (W·m−1·K−1), ω the mass skin blood flow rate (kg·m−3·s−1), q the metabolic heat generation (W·m−3), z the tissue depth (m), and Ta and T the arterial and tissue temperatures (K), respectively. Those parameters with the superscript “b” pertain to blood; those without a superscript pertain to the specific tissue layer. The mass blood flow rate ω is related to the commonly reported volumetric blood flow rate Q (cf. Eqs. 1 and 2) according to
| (7) |
Equation 6 reverts to the general heat equation when ω and q are zero, as in the case of a TDS layer. It is the basis of numerous analyses of heat flow in skin over six decades, e.g., (46–49).
In the steady state, Eq. 6 and simplifications thereof can be solved analytically in a multiple layer system (49). A solution for the 5-layer system (SC, VE, DE, fat, muscle) with fixed temperatures at the outer boundaries is given in the Appendix. Time lags for achievement of steady-state temperatures after a step change are also estimated. This solution combined with appropriate blood flow estimates was used to calculate tissue temperature profiles under sustained normothermic or hyperthermic conditions.
Based on regression of literature data (18,50–52), specific heat for the SC and VE layers was assigned a weak temperature dependence:
| (8) |
| (9) |
The selected values of additional thermal parameters are shown in Table I. The values of the metabolic heat (q) deserve comment. The SC has only slow hydrolytic metabolism; thus, q is close to zero. For the dermis, we chose the value q = 200 W·m−3 reported by Wilson and Spence (49), which traces to a 1970 study by Mitchell et al. (53). A credible alternative value of 610 W·m−3 was estimated by Elia (54) for “residual tissues” (which include skin, intestines, bones, and lungs) as discussed by Wang et al. (55) and an intermediate value of 460 W·m−3 was estimated by Werner and Buse (56). These values may be compared with the commonly quoted whole body average of 1000 W·m−3, an adipose tissue value of 200 W·m−3 (55) and the much higher values of highly active organs, e.g., 22,000–23,000 W·m−3 in heart and kidney (55).
Table I.
Thermal Parameters and Thicknesses Used in Simulations for the TDS, Tissue Layers, and Blood
| Parameter | Units | Model domain | Blood | |||||
|---|---|---|---|---|---|---|---|---|
| TDS | SC | VE | DE | Fata | Musclea | |||
| ρ | kg m−3 | ρwater(T)b | 1220c 1080d |
1060e | 1116f | 850 | 1270 | 1060g |
| CP | J kg−1 K−1 | cPwater(T)b | Eq. 7 | Eq. 7 | 3800h | 2300 | 3800 | 3800g |
| k | W m−1 K−1 | 0.2967i | Eq. 8 | Eq. 8 | 0.53h | 0.16 | 0.53 | – |
| qmet | W m−3 | 0 | 0 | 2000j | 200h | 5 | 800 | – |
| ωk | kg m−3 s−1 | – | – | – | Table II | 0.60 | 0.50 | |
| α × 107l | m2 s−1 | 0.709 | 0.456c 0.456d |
0.629 | 1.25 | 8.18E-08 | 1.10E-07 | – |
| h × 103m | m | 0.10 | 0.0134c 0.0434d |
0.080 | 1.50 | 2.00 | 6.80 | – |
| h2/αn | s | 0.14 | 0.04c 0.04d |
0.10 | 18.00 | 48.88 | 421.05 | – |
All fat and muscle values taken from (49)
Default water values as a function of temperature supplied by COMSOL
Partially hydrated SC (0.34 g water/g dry tissue) assuming ρSC(dry) = 1300 kg m−3 (37)
Fully hydrated SC (2.87 g water/g dry tissue) assuming ρSC(dry) = 1300 kg m−3 (37)
Authors’ estimate based on hydrated SC value
Value for full thickness guinea pig skin obtained by Morales et al. (57)
(49)
Calculated for an Alza nicotine TDS of thickness 0.027 cm and thermal resistance 9.1 × 10−4 m2 K W−1 (59)
Estimated from the ratio of protein synthesis in epidermis and dermis under unstressed conditions (60)
Blood flow in SI units. ω is related to the commonly reported value Q [mL blood/(mL tissue·s)] according to Eq. 7
Thermal diffusivity at 32°C, calculated as k / ρcp
Layer thickness
Thermal time constant
For the viable epidermis, the value q = 0 W·m−3 widely employed in engineering analyses (48,49) is almost certainly incorrect. The epidermis is a rapidly proliferating, cellular tissue with high levels of protein and lipid synthesis. In the absence of an experimental value, we have estimated a value of 2000 W·m−3 under unstressed conditions based on the 10:1 ratio of protein synthesis in the epidermis and dermis reported by Zhang et al. (60). However, epidermal metabolism nearly ceases as the skin temperature is raised to 42°C (61), so the value of q under heat stress may approach zero. Regardless of these details, the engineers’ conclusion that the exact value of q for epidermis and dermis does not have much impact on the skin temperature profile is almost certainly correct. The epidermis is a very thin tissue and heat generation in the dermis is dominated by the term in Eq.6 (49).
Skin blood flow estimates were drawn from the physiology and thermoregulation literature (Table II). There is substantial agreement that skin blood flow is maximal when the skin surface temperature reaches 42°C or the core temperature rises by much less. According to Arens and Zhang (62), “The [hypothalamus temperature] mechanism is precise: the setpoint for vasodilatation and sweating is only two tenths of a degree higher than the 37°C set point for vasoconstriction, and the setpoint for shivering is just below 36°C.” Resting whole body skin blood flow rises from about 250 mL/min under normothermic conditions to 6–8 L/min under severe hyperthermia (62). These values translate into about 1.33 and 32–42 mL blood/(mL tissue·s), respectively, according to Charkoudian’s analysis (23). Other workers have made different estimates, especially for resting blood flow, cf. Table II. We have selected Charkoudian’s values for illustrative purposes in this report.
Table II.
Dermis Blood Flow Values (Q) Considered in the Model Analysis
| Skin surface temperature, °C | Q × 1000 (s−1) | Reference |
|---|---|---|
| 32 | 0.4a | (48) |
| 1.32–9.47 | (78) | |
| 1.33b | (23) | |
| 1.8 | (49) | |
| 2.2 (rat) | (32) | |
| 3.8–5.5c | (79) | |
| 1.33 | Selected value | |
| 42 | 30–40d | (79) |
| 32–43d | (23) | |
| 43 | Selected value |
Corresponds to 2.4 × 10−2 mL blood/(mL tissue·min). Note that both the exponent and the units are misprinted in (48)
Corresponds to 8 mL/(100 mL·min) or a whole body skin blood flow of 250 mL/min
Corresponds to a forearm blood flow (skin + muscle) of 4–5 mL/ (min × 100 mL)
Corresponds to whole body skin blood flow of 6–8 L/min (~ 60% of cardiac output)
To estimate skin blood flow within the temperature range encompassed by Table II, we assumed a log sigmoidal form centered at 37°C. A fit to the endpoints assuming a unit slope for the logistic function yielded:
| (10) |
Equation 10 should not be used to extrapolate Q outside of the stated temperature range as it does not account for diminished blood flow under hypothermic conditions or severe burns at temperatures higher than 42°C.
Pharmacokinetic Analysis
Both one- and two-compartment analyses were investigated to relate the capillary nicotine flux resulting from dermal nicotine exposure to systemic drug concentrations. Model calculations were compared with plasma concentration profiles arising from two studies of transdermal nicotine under conditions of heat stress (9,11). The two-compartment approach yielded better results and will be described here. Blood concentration profiles were calculated from the integrated form of the governing mass balance equation(s) that describe the rate of drug distribution into and out of each compartment. For a two-compartment open model, the relationships are as follows (63):
| (11) |
| (12) |
Here, Cb and Ct are the nicotine concentration in the blood and tissue compartments, respectively (generally expressed in ng/mL), Vb and Vt are the blood and tissue volumes, respectively (L), dM/dt is the delivery rate (equal to flux × corresponding area) of the drug into the blood compartment (μg·s−1), k12 and k21 are the kinetic transfer rates between the central (blood, denoted by the subscript 1) and peripheral (tissue, denoted by the subscript 2) compartments (s−1), and kel is the elimination rate of the drug from the body (s−1) where kel × Vb equals to systemic drug clearance.
Nicotine Physicochemical Properties and Pharmacokinetic Parameters
Nicotine was chosen as the model skin permeant as it was a focus of the project and we had both in vitro and in vivo data available for comparison. Nicotine is a small, moderately lipophilic compound (MW = 162.2 Da, log Koct = 1.17, pKa = 8.02) (64). It is 19% ionized at physiological pH and is largely unbound in albumin solution, plasma, or dermis as described in the “INTRODUCTION” section. The experimental (log) human skin permeability coefficient from aqueous solutions at 37°C, taken as the mean ± SD of five determinations reported in refs. (65) and (66) (one outlying low value was discarded), is log kp(cm/s) = − 5.54 ± 0.31, yielding kp = 2.91 × 10−6 cm/s or 1.05 × 10−2 cm/h. This value is higher than those calculated from either the Potts-Guy model (67) or the UB/ UC model (37) by factors of 8.4 and 8.9, respectively. For nicotine under these conditions, the stratum corneum (SC) accounts for ~ 99% of the skin’s diffusive resistance (37). Consequently, the aqueous permeability may be approximately interpreted as
| (13) |
Using the experimental value of kp and the model values for hydrated skin KSC/w = 3.76 and hSC = 43.4 × 10−4 cm (37), one finds DSC = 3.39 × 10−9 cm2s−1 to be the effective SC diffusion coefficient for nicotine in skin exposed to a dilute aqueous solution of nicotine at 37°C.
The activation energy for nicotine diffusion in the SC () was taken to be 65 kJ·mol−1 based on analysis of the extensive experimental IVPT data reported in (39). This value may be compared with the value 63 kJ·mol−1 estimated from Eq. 5. This value is subject to refinement as more data become available.
Model simulations were conducted for several scenarios including (a) infinite dose from dilute aqueous solutions, (b) TDS (finite) dosing, and (c) varying skin blood flow levels. Example in vivo transdermal nicotine exposure data were obtained from the literature (9,11). Example in vitro permeation test (IVPT) data for a nicotine TDS were obtained from a parallel study in our laboratory (39). Fits of the developed model to these representative data are presented; for a more thorough analysis, see ref. (39).
Nicotine pharmacokinetic parameters for the two-compartment model were derived from intravenous bolus serum concentration data available in the literature (68,69). Specifically, the values of k12, k21, and kel were calculated from regression analyses of semi-log plots of blood concentration as a function of time. The volume of the central compartment (Vb) and steady-state distribution volume () were also calculated from the data. The derived values were k12 = 1.23 × 10−3 s−1, k21 = 1.60 × 10−3 s−1, kel = 3.35 × 10−4 s−1, Vb = 0.065 m3, and . An analysis using WinNonlin software (Certara USA Inc., Princeton, NJ) confirmed that the nicotine intravenous bolus serum concentration data were better described by a two-compartment model than a one-compartment model.
COMSOL® Computational Details
Time-dependent simulations were performed using COMSOL® multiphysics finite element analysis platform (Burlington, MA). Diffusive transport in the three skin layers was solved in one dimension (Fig. 1). Where applicable, a fourth layer was included on top of the skin for TDS modeling. Estimated transport parameters for nicotine as a test solute are given in Table III.
Table III.
Nicotine Transport and Partition Parameters Used in COMSOL Model Calculations. Parameters Were Estimated as in Dancik et al. (37) Unless Otherwise Noted
| Parameter | Definition | Units | TDS | SCa | VE | DE |
|---|---|---|---|---|---|---|
| Di @ 32°C | Diffusivity | cm2 s−1 | 6 × 10−7 | 22.5 × 10−10 | 3.18 × 10−6 | 3.18 × 10−6 |
| 0.90 × 10−10 | ||||||
| Di @ 42°C | Diffusivity | cm2 s−1 | 6 × 10−7 | 50.6 × 10−10 | 3.84× 10−6 | 3.84 × 10−6 |
| 2.01 × 10−10 | ||||||
| Ki/w | Partition coefficient w/ respect to water | – | 2.25 | 3.76 | 3.19 | 3.19 |
| 2.22 | 9.11 |
First parameter listed applies to fully hydrated skin; second to partially hydrated skin (70)
The initial condition for concentration in the TDS was determined from the relationship
| (14) |
where Load is the mass of nicotine per unit area (mg·cm−2), hv is the thickness of the drug-containing layer (cm), and is the average concentration in this layer at time 0. Thermodynamic activity of drug in the TDS, av, was estimated as
| (15) |
where Sv is the solubility of the drug in the vehicle layer. A similar relationship was assumed for the activity of the drug in the SC (37), aSC, and partitioning at the TDS-SC interface was calculated from the relationship av = aSC at z = 0. For highly soluble drugs applied at high concentrations, e.g., nicotine in a TDS, Eq. 15 was replaced by a practical limit as described later. Initial concentrations in the three skin layers were assumed to be zero. Additional boundary conditions for concentration included no flux at the top surface of the TDS and Cde = 0 at the base of the dermis. Initial conditions for temperature were T = 32°C in the TDS, SC, and VE and T = 37°C in the dermis. Boundary conditions included T = 32°C or 42°C at the air/TDS interface and T = 37°C at the base of the dermis. Concentrations evolved according to the equation system shown in Fig. 1, and temperatures evolved according to Eq. 6.
COMSOL automatically implemented the best solver for the model stipulations chosen. The direct simulations used the PARDISO direct default solver. The optimization simulations employed a Levenberg-Markquardt least squares approach and combined with the PARDISO solver for parameter estimation. Absolute tolerance was set to 1E-08 while the relative tolerance (default) specification was 0.01. An extremely fine mesh was employed in all simulations.
Excel® Model
A simplified version of the COMSOL model was created in Microsoft Excel® to facilitate calculations conducted under steady-state temperature conditions. The Excel model considered transient mass transport, but included temperature-dependent mass transport coefficients as defined in Eqs. 4 and 10. The vehicle (or TDS) was considered well-stirred, and the temperature within each skin layer was taken to be the average temperature predicted from steady-state calculations. With more effort towards programming, this model could simulate temperature changes at the skin surface during exposure via a pseudo steady-state approximation.
RESULTS AND DISCUSSION
Steady-State Skin Temperature Profiles and Thermal Time Lag
Figure 2 shows steady-state temperature profiles in skin calculated according to the method described in the Appendix, which presents the steady-state solution to Eqs. 6 and 7. Significant departures from core temperature occur well into the subcutaneous layers, in agreement with the findings of Wilson and Spence (49). The non-linear temperature profile in the dermis under heat stress is a consequence of the high dermis blood flow under these conditions (Table II). Nevertheless, the temperature only drops by 1.5°C in the dermis despite the high blood flow, according to the model.
Fig. 2.
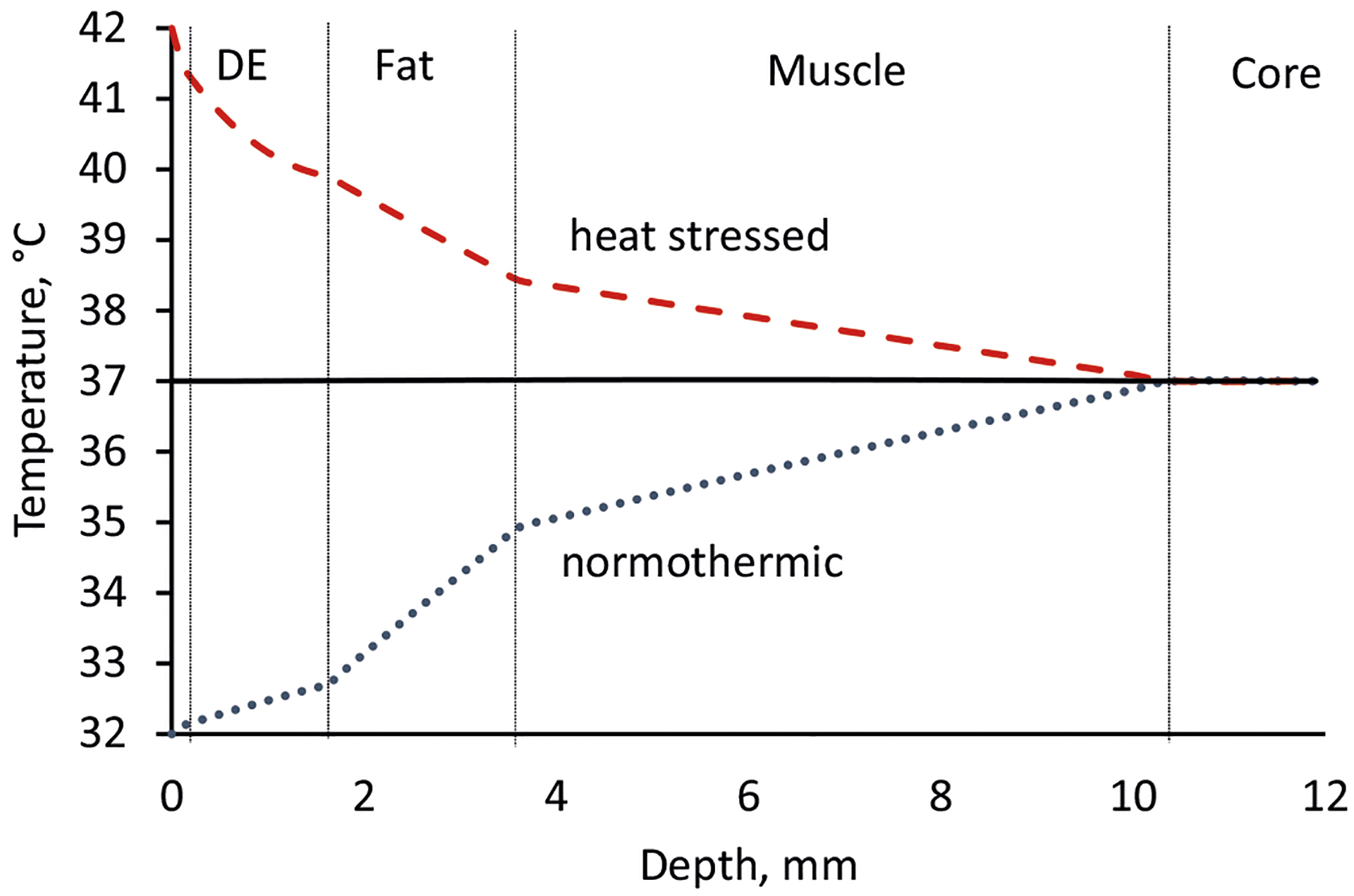
Steady-state temperatures in skin and subcutaneous tissues calculated from Eqs. 16–19 using the thermal, dimensional, and blood flow parameters in Tables I and II. In the calculation, the core temperature was held at 37°C and the skin surface at either 32°C (dotted blue line), 37°C (black line), or 42°C (dashed red line). Dermis blood flow was varied with skin surface temperature as shown in Table II, whereas blood flow in the fat and muscle layers was taken to be constant (Table I)
The time to achieve a steady-state temperature profile following a step change in skin surface temperature is, in general, a complex function of the thermal diffusivity of the tissue layers and the rate at which blood flow to the affected site is adjusted by the body. An upper limit can be placed on this value by considering multilaminate time lag calculations based on diffusive transport only (71). A trilaminate slab calculation for dermis, fat and muscle layers (not shown) employing the properties in Table I yields a thermal time lag of just under 180 s or about 3 min. Considering that it takes about three time lags to reach steady-state temperature profiles, the maximum thermal response time is 9 min. While this time frame is somewhat less than that associated with significant mass transport, it does provide justification for including time-dependent heat flow into the transient heat and mass transport model.
Infinite Aqueous Dose with Dermal Clearance
Figure 3 shows the calculated effect of skin surface temperature on the total flux (defined as total flux exiting the dermis or the sum of the blood capillary flux, the lymphatic flux and the lower dermal boundary flux) of nicotine delivered to the skin from a large volume of dilute aqueous solution. Based on the skin blood flow values selected (cf. Table II and Eq. 10), total flux values at 42°C and 37°C were graphically indistinguishable from blood capillary flux; at 32°C, blood capillary flux represented 94% of total flux at steady state and an even larger fraction at shorter times. In other words, diffusion of nicotine through the SC rather than capillary uptake was rate-limiting at all times and temperatures.
Fig. 3.
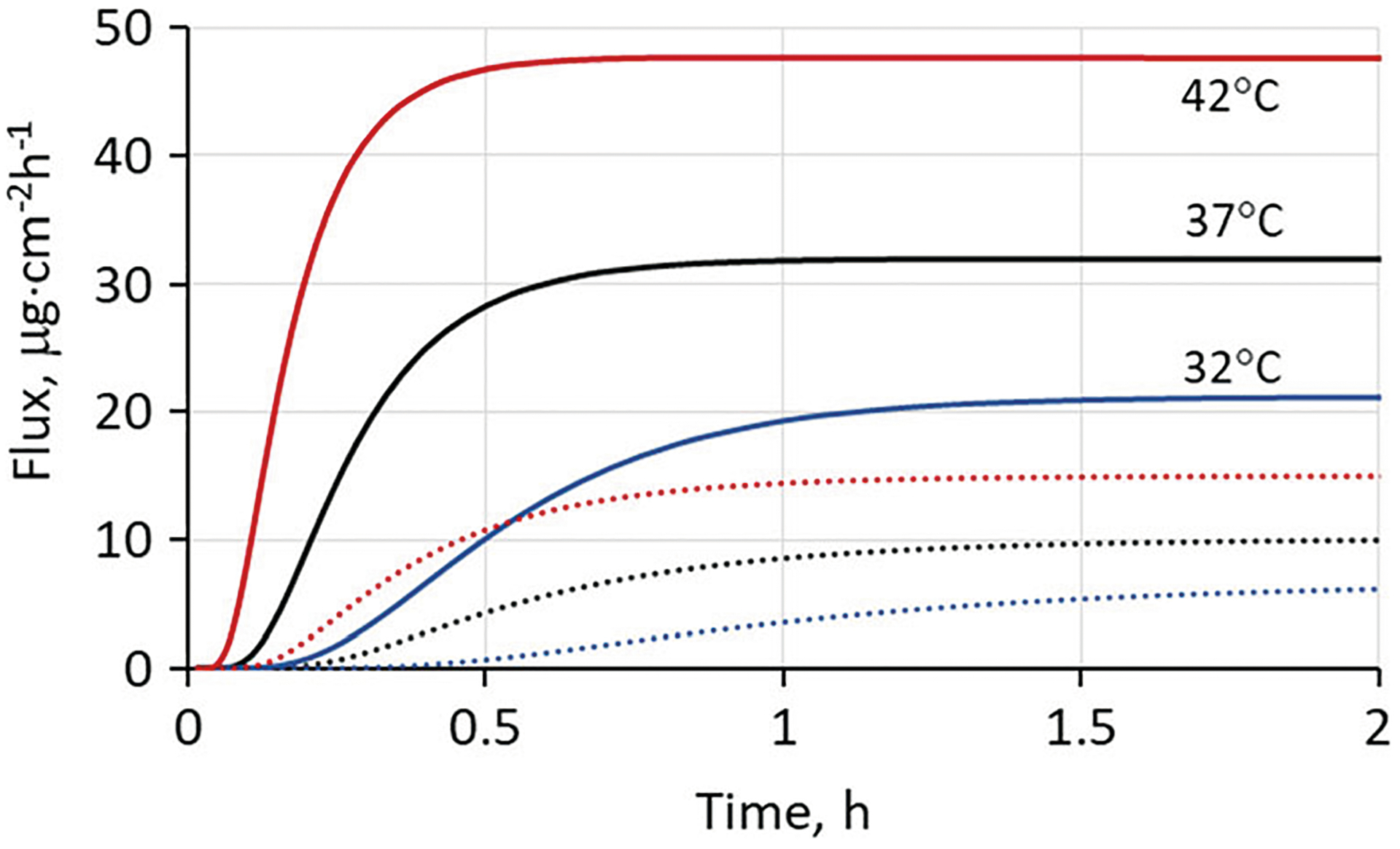
Solid curves show calculated transdermal flux profiles of nicotine delivered to human skin in vivo from a dilute (3 mg mL−1) aqueous solution in the non-ionized form (pH 10). Calculations were based on the experimental permeability coefficient of 1.05 × 10−2 cm·h−1 in fully hydrated skin at 37°C (see “METHODS” section). Temperature-dependent diffusivities were calculated from Eq. 4 with kJ mol−1 and skin blood flow was calculated from Eq. 10. The dashed curves show calculated flux from a non-hydrating formulation having comparable nicotine activity, so that the stratum corneum is only partially hydrated (37). The calculation does not account for possible irritation or skin damage resulting from the high pH exposure
To show how skin blood flow (Q) plays into the model, the 42°C (hydrated) simulation was repeated with lower values of Q. The results are shown in Fig. 4. Total nicotine flux exiting the dermis was not significantly impacted by reduced blood flow until the reduction exceeded a factor of 100 (cf. curves labeled 43 and 0.43). However, a 10-fold reduction in blood flow introduced an additional time delay of about 6 min and a 100-fold reduction about 50 min for attainment of a flux equal to 90% of the steady-state value of 43.5 μg cm−2 h−1.
Fig. 4.
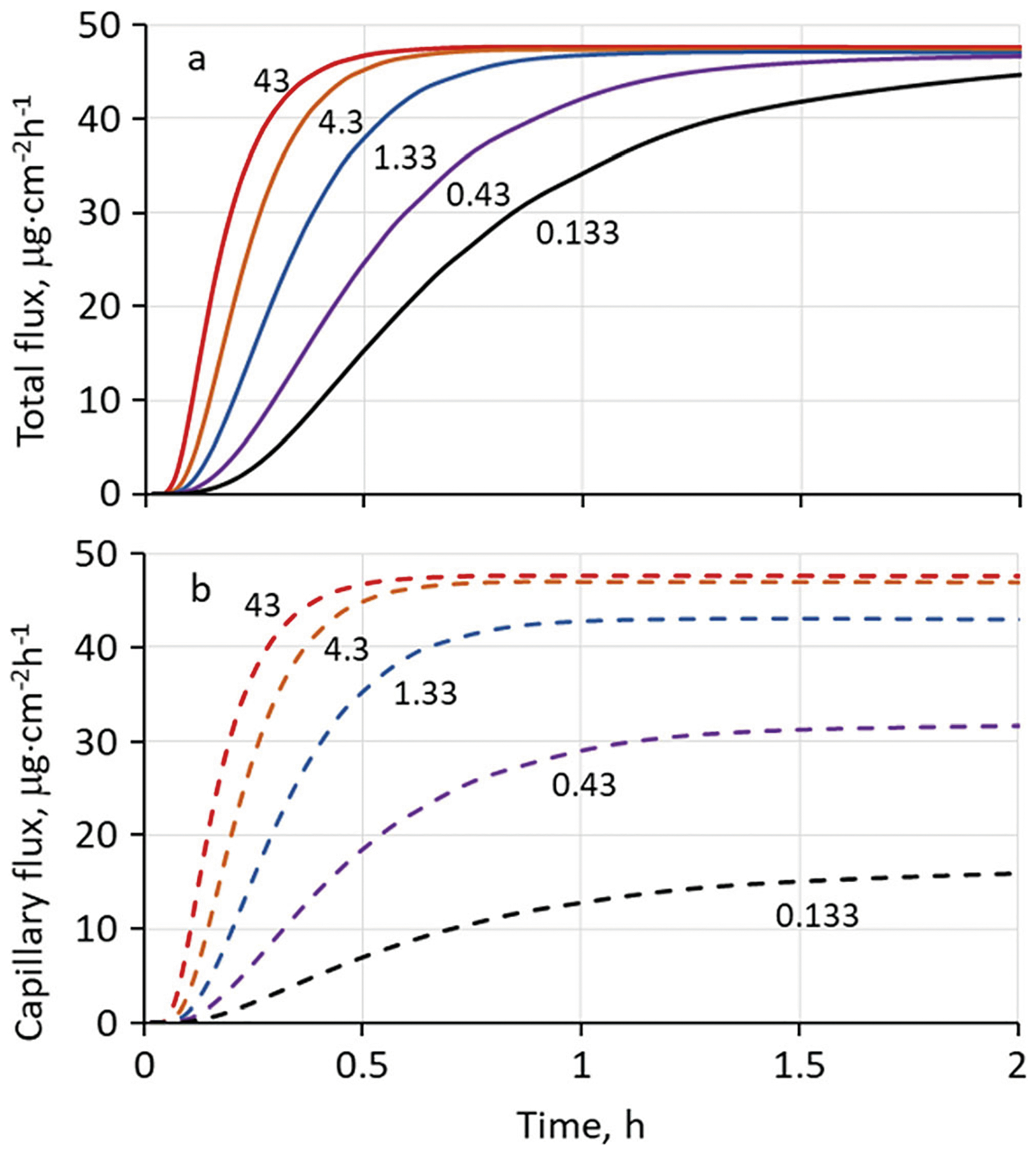
Calculated transdermal (a) and blood capillary (b) flux profiles for nicotine delivered from a dilute aqueous solution at 42°C at varying values of skin blood flow, Q (s−1). Labels on the curves represent Q × 103 as in Table II. All other parameters were the same as Fig. 3. The curve labeled 43 employs the default blood flow for this temperature; the 1.33 curve employs the blood flow associated with a 32°C skin surface temperature. Blood flows labeled 0.43 and 0.133 would only occur under conditions of hypothermia
It should be noted that time delays for flux entering the bloodstream are expected to be larger than those exiting the dermis at low skin blood flow. Solute not cleared by the blood or lymphatic capillaries permeates into the subcutaneous fat and thence into muscle, cf. Fig. 2, which is significant to local delivery but not as much to transdermal delivery. In each layer, it accumulates according to its solubility and partitioning characteristics. Subsequently, it is either metabolized or slowly removed by the blood. According to the values in Table I, the relevant values of blood flow in the fat and muscle layers, expressed in the units in Fig. 4, are Q × 1000 = 106 ω /ρb = 0.57 s−1 and 0.47 s−1, respectively. To complete a calculation of the subcutaneous clearance rate from these layers, one would have to incorporate them into the model and estimate appropriate diffusion coefficients, partition coefficients and capillary permeability-surface area products, (PS)eff, for each tissue, cf. Fig. 1 and Eqs. 1–3. Because the estimated amounts of nicotine reaching subcutaneous layers are low, we have chosen to not pursue this calculation in the present report.
Finite Dose from a Simulated TDS with Dermal Clearance
Figure 5 shows calculations analogous to those in Fig. 3, but carried out for a simulated nicotine TDS. The simulation considered a 15.75 cm2 TDS designed to deliver 14 mg/day of nicotine with a skin surface temperature of 32°C, yielding a target mean flux of 37 μg cm−2 h−1 for a 24 h application. These are characteristics associated with the Nicoderm CQ® TDS studied recently by Shin et al. (9,72). The calculation assumed a nicotine content (or load) equal to twice the targeted 24-h delivery to be dissolved in a 100-μm layer of pressure sensitive adhesive plus excipients in which it was highly soluble. This choice does not imply that the Nicoderm CQ® product is constructed in such a manner; it is simply one of many scenarios that can lead to the desired delivery rate.
Fig. 5.
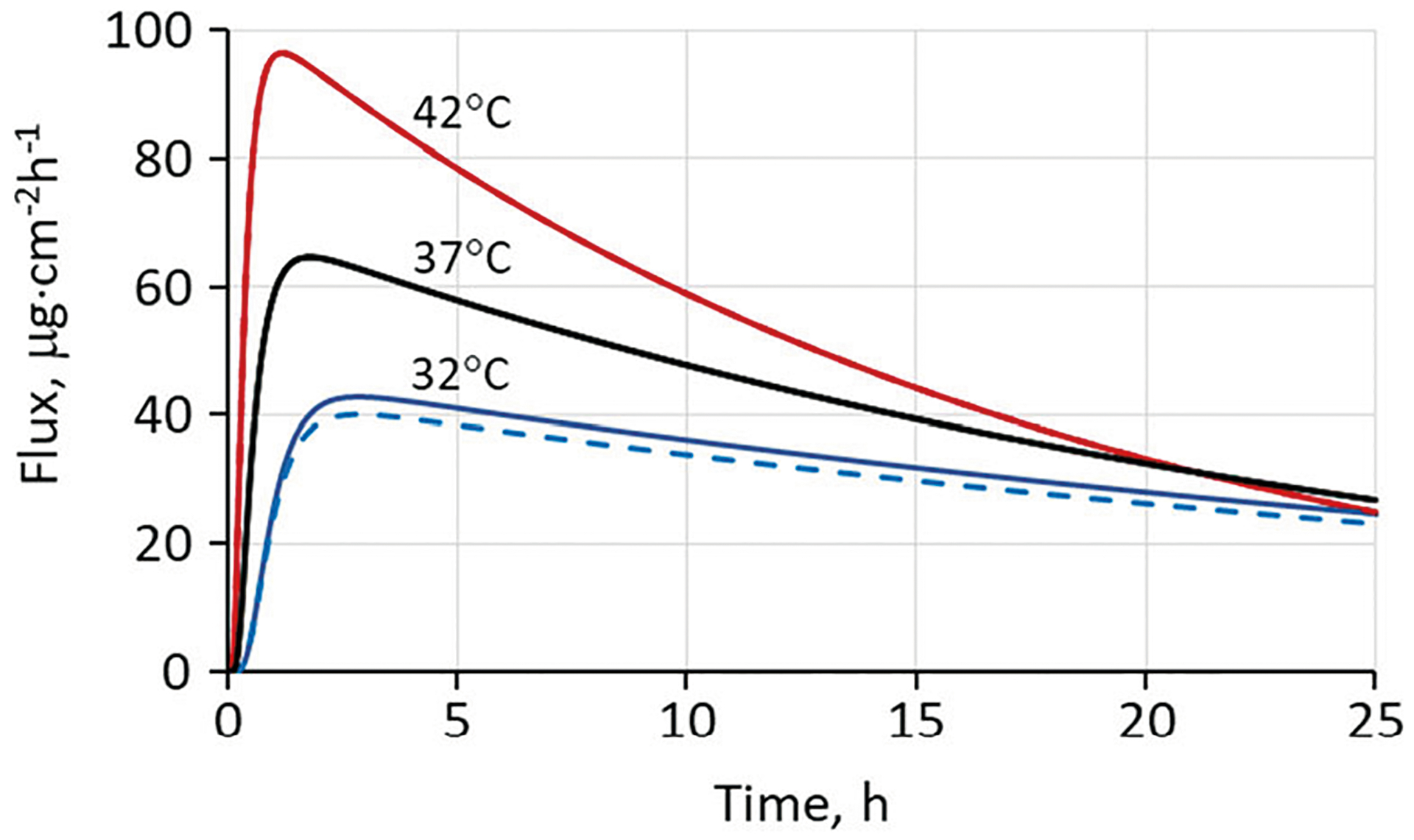
The total flux (solid lines) and capillary blood flux (dashed lines) of nicotine exiting the dermis as a function of skin surface temperature for a simulated nicotine TDS. The two curves coincide at 37°C and 42°C. A partially hydrated skin model was used with nicotine diffusion and partition coefficients in the SC modified as discussed in the text. Temperature-dependent diffusivities were calculated from Eq. 4 with kJ mol−1 and skin blood flow was calculated from Eq. 10. The values Load = 1.78 mg·cm−2, hv = 0.0100 cm, Sv = 950 mg·cm−3, KSC/TDS = 1.06 and DSC= 1.39 × 10−10 cm2·s−1 at 37°C were used in the simulations
Estimation of diffusion and partition coefficients in the SC for highly soluble compounds like nicotine applied to skin at high concentrations using the UB/UC model (37) presents technical issues. The formula used for KSC/w and the assumed relationship KSC/v = KSC/w/Kv/w are both dilute solution approximations. Extrapolation of these relationships to high concentrations of test solute in the vehicle leads to implausibly high concentrations of solute in the upper layers of the SC. To circumvent this issue, an approximation we have employed for some time is to limit the solute concentration in the SC to a plausible value (often the solute density or a fraction thereof at saturation) and to recalculate DSC and KSC/v according to this limit, while holding their product constant. We employed this device for the calculations shown in Fig. 5. Model-calculated values of DSC = 1.53 × 10−11 and KSC/w = 9.11 were adjusted to DSC = 1.39 × 10−10 and KSC/w = 1.00 by this method. The change clearly has a strong impact on the rise time of the permeation curves, but it is more in accord with experimental rise times as will be shown in the next section.
Calculations similar to those in Fig. 4 to demonstrate the influence of skin blood flow (Q) on peak flux (Jmax) and time-to-peak (tmax) were conducted. At 42°C, a 10-fold reduction in Q resulted in no reduction of Jmax and an 8-min increase in tmax. A 100-fold reduction in Q yielded a 2% decrease in Jmax and a 41-min increase in tmax. The impact of Q was even less at lower temperatures because the flux was more strongly controlled by the SC diffusion barrier.
Application to IVPT Data for a Marketed Nicotine TDS
Figure 6 shows experimental in vitro permeation test (IVPT) data and associated model simulations for a circular punch-out section (0.58 cm2) of a Nicotine Transdermal System, 21 mg/24 h, manufactured by Aveva Drug Delivery Systems (Miramar, FL). The data were part of a larger study (39). The measured area of the TDS was 30.2 cm2, so the nicotine delivery rate is equivalent to 0.70 mg cm−2 day−1 or 29 μg cm−2 h−1. The TDS content (or load) was determined experimentally to be 1.08 mg cm−2 (39). The model parameters were optimized using the partially hydrated skin model with concentration limitations in the SC and an adhesive layer thickness hv = 0.0100 cm (as in Fig. 5) by varying solubility of the permeant in the adhesive layer (Sv) to achieve the fit. The result of this simulation was a TDS that in 24 h delivered 80.5% of its content at 32°C and 95.5% of its content at 42°C. These apparently high efficiencies reflect the substantial depletion of nicotine in the TDS evident in the experimental flux values in Fig. 6. We defer a discussion of these results to ref. (39), in which a much larger body of data was evaluated.
Fig. 6.
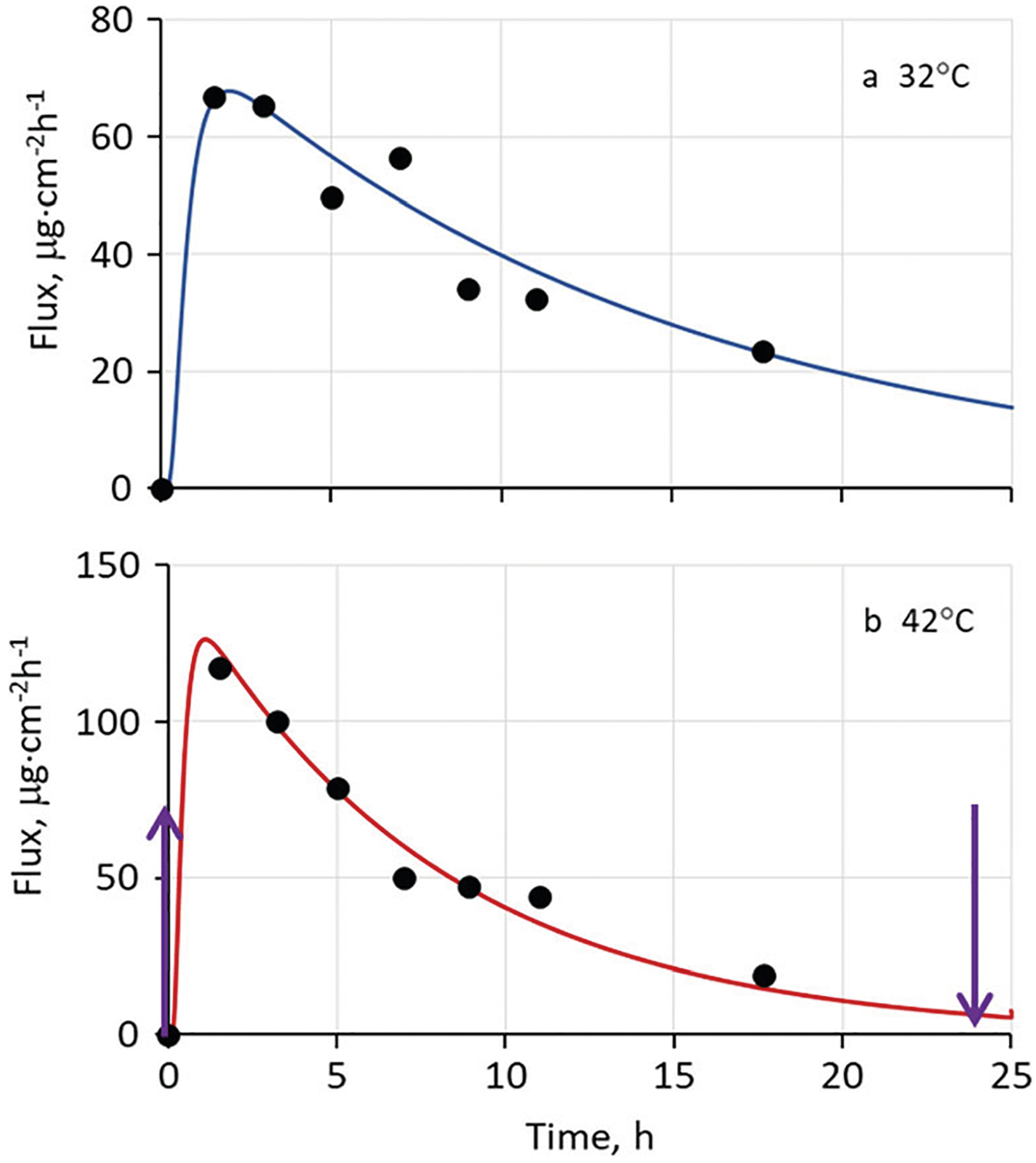
Representative experimental in vitro permeation data for an Aveva nicotine TDS selected from the more extensive study described in ref. (39), along with simulated permeation curves calculated according to the present model with no skin blood flow (Q = 0). A partially hydrated skin model was employed. Temperature-dependent diffusivities were calculated from Eq. 4 with kJ mol−1. The values Load = 1.08 mg cm−2, hv = 0.0100 cm, Sv = 350 mg cm−3, KSC/TDS = 2.88 and DSC = 1.39 × 10−10 cm2 s−1 at 37°C were used in the simulations. The dermis thickness hde was reduced to 0.0300 cm for this simulation since data were obtained using split-thickness human skin. Arrows in panel b indicate initial and final times of heat application
We note that the simulated delivery rate of 80.5% of a nicotine load of 1.08 mg cm−2 in 24 h at 32°C corresponds to an average delivery rate 38.6 μg cm−2 h−1, a value 33% higher than the 29 μg cm−2 h−1 value calculated from the TDS labeling and dimensions. The difference in the simulated and observed delivery rate highlights the fact that the nominal delivery rate listed in the TDS product labeling is usually an average of the amount of drug delivered over the period of wear of the drug product determined using either a pharmacokinetic based approach or a residual drug-based approach. The nominal value may not accurately reflect the increase in drug delivery rate following application of the drug product followed by an “approximately” steady drug delivery rate during the period of product wear.
Pharmacokinetic Analysis for TDS Application
Figure 7 shows experimental and simulated nicotine serum concentrations associated with transdermal nicotine absorption for the “early heat” protocol employed by Shin et al. (9). This simulation was based on nicotine diffusion and partition parameters determined in an independent, in vitro permeation study conducted in our laboratory (39). The only parameter that was fitted to the Shin et al. data was the initial concentration in the TDS (C0). Following removal of the TDS at 9 h, simulated serum concentration followed an exponential decay. The value of Cmax was ~ 1.8-fold higher than baseline value for the 4–5 h exposure to elevated skin temperature of 42°C. The two-compartment approach yielded a rapid attainment of Cmax and a correspondingly rapid decline in serum concentration to near-baseline levels following the heat exposure. This rapid increase and decline could not be reproduced by a one-compartment model. Specifically, the two-compartment model provided a smaller central blood compartment, effectively leading to more rapid changes in blood concentration when external heat was applied or removed.
Fig. 7.
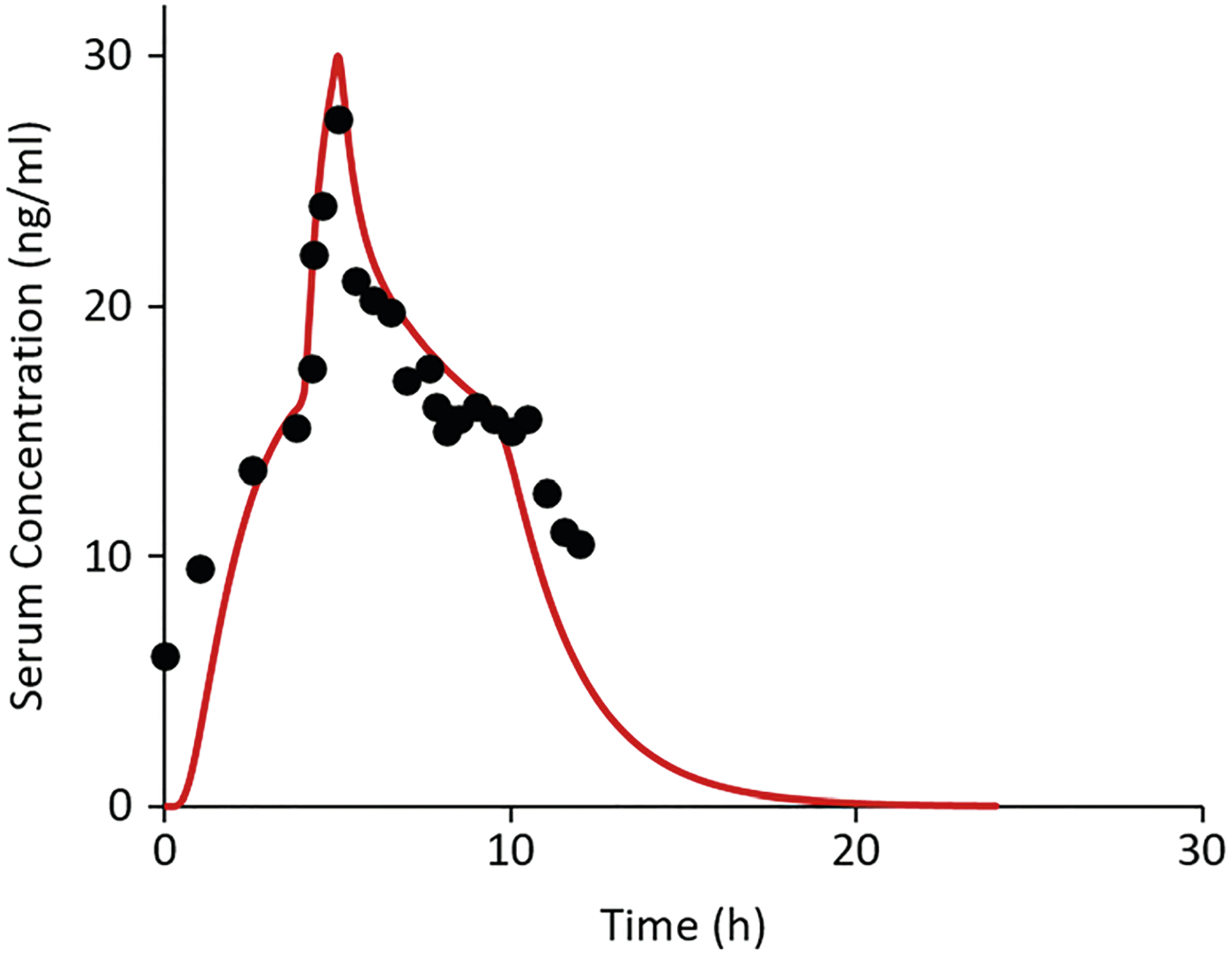
Experimental nicotine serum concentration data from Shin et al. (9) following application of a Nicoderm CQ TDS in vivo and simulation thereof using the present heat effects simulation model. The experimental data involved a 1-h exposure to external heat supplied by a heating pad from 4 to 5 h post-dose leading to a skin surface temperature of 42°C at the application site. The TDS was removed at 9 h post-dose. Parameter values for the simulations were those calculated from our in vitro nicotine investigation (C0 = 244 mg/mL, Load = 1.33 mg·cm−2, hv = 0.024 cm, KSC/TDS = 1.05, DSC = 7.15 × 10−10 cm2·s−1 at 32°C, and kJ/mol) (39)
Figure 8 shows baseline and heat-enhanced serum concentration data for the transdermal nicotine study of Vanakoski et al. (11) along with model simulations. This study employed a Nicorette TDS. As in Fig. 7, the model calculations were based on DSC and KSC/TDS values derived from our in vitro permeation study of Alza and Aveva transdermal systems (39); the only fitted parameter was C0. Significant increases in serum plasma Cmax (~ 1.6-fold) and AUC due to heat exposure were observed in the experimental study and reproduced (with a small time delay) by the simulation. This analysis provides further support for the predictive power of the heat effects model based on IVPT data and the availability of systemic nicotine PK data.
Fig. 8.
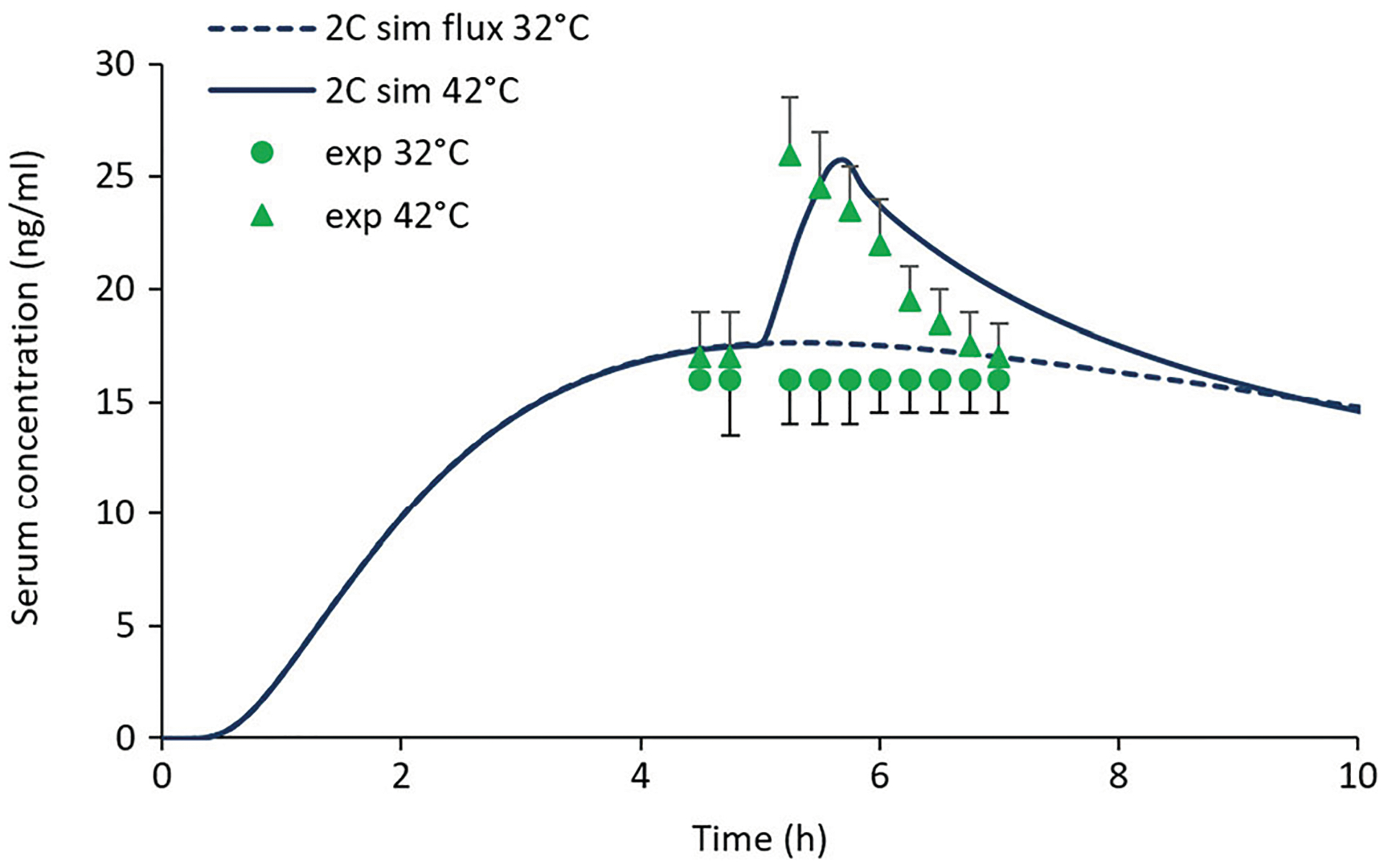
Experimental and predicted serum concentrations for the transdermal nicotine heat effects study described by Vanakoski et al. (11). The heat exposure in this study involved three consecutive 10-min stays in a sauna bath (mean temperature 82°C), starting at 5 h post-dose. The stays in the sauna were separated by two 5-min breaks in a cooling room maintained at 25–27°C. Baseline (32°C) experimental (circles) and simulated (dashed curve) data are shown for reference. Parameter values for the simulations were those calculated from our in vitro nicotine investigation (Load = 0.83 mg cm−2, hv = 0.024 cm, KSC/TDS = 1.05, DSC = 7.15 × 10−10 cm2 s−1 at 32°C, and kJ/mol) (39) with the exception of C0, which was 127 mg/mL. The pharmacokinetic parameter values are given in the “METHODS” section
Differentiation from Earlier Work
Three key aspects of transdermal delivery at elevated skin temperatures are brought together in the present model: increased stratum corneum permeability, increased skin blood flow and the impact of the latter on dermal clearance. Many experimental studies of the first two factors, and associated models thereof, are available. We have drawn freely from this rich literature. The dermal clearance aspect is less characterized. The correspondence between clearance and skin blood flow is not 1:1, as an increase in the latter does not increase clearance if it is already efficient (40,41) or if the additional blood flow is largely through non-exchanging capillaries (43,45), cf. Eqs. 1–3. Furthermore, protein binding (Eq. 2) and potential dispersion of highly protein bound solutes (33,34) complicate the picture in ways that are not fully understood. The new model is physiologically based and thereby provides a framework for addressing these questions in a manner that is more than phenomenological. For nicotine, the present analysis suggests that dermal clearance is not highly impacted by a change in skin temperature from 32 to 42°C (because it is already efficient at the lower temperature), but it might be substantially reduced by a change from 32 to 22°C, such as might be experienced during hypothermia, cf. Figure 4. These projections arise uniquely from the present model structure and parameterization and are not (in our estimation) easily drawn from earlier work. In fact, some previous investigators of heat effects in nicotine TDS had come to the opposite conclusion (15). The new projections are both experimentally testable and extendable to solutes with different physicochemical properties.
The developed model also incorporates a systemic pharmacokinetic component and parameter optimization capabilities through the COMSOL platform. While these capabilities are not new to PK modeling, they do represent an upgrade from the Microsoft Excel® platform employed in our earlier models, e.g., (37,73). For nicotine, we employed a two-compartment open model (Eqs. 11 and 12); however, any appropriate systemic PK model could be readily inserted to handle compounds with different distribution and elimination properties. With more effort, the present equation-based model could be used as a dermal input function for a physiologically based pharmacokinetic (PBPK) model in which other organ systems are given explicit roles in the body’s handling of exogenous chemical agents.
We note that the present model represents a very different approach than that taken in a recent QSPR analysis of skin permeability (7). We offer here a mechanistic model in which enables specific predictions of drug delivery from a TDS subjected to external heat exposure for a finite period of time, based on in vitro skin permeation data (cf. Fig. 7). The key parameters for predicting heat effects are the activation energy for transport through the stratum corneum () and the release properties of the TDS, which can be determined by in vitro testing or estimated from previous experience, e.g., Eq. 5 for . The approach taken by Ashrafi et al. (7) could contribute to this process by improving upon estimates for for individual compounds based on multivariate analysis of a large database.
Model Capabilities and Limitations
To our knowledge, this is the first model to predict heat effects in transdermal delivery in vivo by combining SC permeability, dermal clearance, and systemic PK components. The model has been tested in our laboratory for selected nicotine (39) and fentanyl (74) TDS, and it can be validated for other transdermal drug products when in vitro IVPT and in vivo human TDS data become available. The heat effects model has the advantages of flexibility to represent a wide array of test conditions and the ability to impart insight into the drug release and transport processes. The model can potentially describe other scenarios, such as when skin blood flow is affected by vasoconstrictors or by physical exertion. The model provides a tool to distinguish the impact of changes in stratum corneum permeability from changes in dermal clearance when interpreting the effect of elevated temperatures on transdermal drug delivery from marketed products.
The key parameters for simulating delivery of a moderately lipophilic drug from a TDS are the load, i.e., the total drug content per unit area in the TDS, the thermodynamic activity of the drug in the TDS, the diffusivity of the drug in the stratum corneum (DSC), and the partition coefficient of the drug between the TDS and the SC (KSC/v). It is not possible to accurately estimate all four parameters from a modest set of experimental IVPT data. Starting estimates for DSC and KSC/v are available from existing models, but these estimates derive from dilute solution approximations that may not be valid for a TDS. In order to arrive at the best mechanistic description of drug delivery from these systems, we recommend that the load and the thermodynamic activity (av) of the drug in the TDS be separately determined. The latter is often approximated by the ratio of the dissolved concentration to solubility, cf. Eq. 15. With this information in hand, reliable estimates of DSC and KSC/v can be obtained from IVPT data.
Limitations of the current model include the following: (a) The model framework is based on the 2013 UB/UC model (37), which does not extend to large hydrophilic permeants. This group has recently extended their model to remove this limitation (73). This extension should be incorporated prior to using the model to predict delivery of such compounds; (b) The capillary permeability-surface area product (PS)eff was constrained to a constant value in the dermal clearance calculations, with all blood flow Q passing through these exchanging capillaries. Recruitment of non-exchanging capillaries during thermoregulation will limit the impact of increased Q on dermal clearance, thereby mitigating the influence of increased skin or core temperature (43–45); (c) Clearance of highly protein bound permeants that are not readily removed by blood capillaries is not explicitly considered; (d) Treating the TDS as a homogeneous reservoir of uniform drug concentration may be overly simplistic. Many marketed products have more complex designs. Information regarding the engineering design of specific TDS could readily be added to the current model, a modification which could improve the predictive ability for these systems.
Further elaboration of the details of dermal capillary clearance is certainly possible. Detailed microstructural models of capillary loops in the papillary dermis are available (75,76), as is a projection of the depth profile for capillary density (77). The present model describes this complexity in terms of a single distributed clearance constant kDE, which has blood and lymphatic capillary components (see “METHODS” section and Eqs. 1–3). The more complex models, as presented in refs. (75–77), do not explicitly describe the effects of changing blood flow or temperature, nor do they explicitly account for dispersion of protein bound solutes. Further development may be warranted. However, we believe that new experimental studies focused on specific components of the clearance mechanism must be conducted in order to make such an effort worthwhile. Motivation for such studies might come from transdermal drug development efforts involving microporated or otherwise permeabilized skin, for which the dermal clearance aspects will be the key determinants of drug delivery.
CONCLUSIONS
A computational model for diffusion and capillary clearance in skin, interfaced with a systemic compartmental PK model, has been developed to account for the influence of externally-applied heat on dermal absorption. For the test compound nicotine, model simulations demonstrated (a) an approximately 2-fold increase in skin permeation rate with an increase in skin surface temperature from 32 to 42°C, (b) the important role played by blood capillary clearance in transdermal absorption in vivo, with the blood capillary flux accounting for ≥ 94% of the total flux exiting the dermis for skin surface temperatures in the range 32–42°C, and (c) transient increases in skin absorption for a variety of heat exposure conditions. Results showed that the major impact of elevated temperature on transdermal delivery rate of a moderately lipophilic, unbound permeant is increased permeability of the stratum corneum lipids rather than increased dermal clearance. The simulated heat-induced increases in nicotine serum concentration during in vivo exposures were well described by a two-compartment pharmacokinetic model. The developed model may be used in the design phase of transdermal delivery systems; however, it is particularly useful for estimating heat effects on systemic drug levels of compounds for which experimental IVPT data and systemic pharmacokinetic data are available.
ACKNOWLEDGMENTS
Funding for this project was made possible, in part, by the US Food and Drug Administration (FDA) through a cooperative agreement (Research Award U01FD004942). In response to funding opportunity announcement RFA-FD-13-015, separate research projects were awarded in parallel to the University of Cincinnati and the University of Maryland, and each institution was requested by the FDA to perform independent research with the same drug products under comparable study conditions in a manner coordinated by the FDA. The views expressed in this paper do not reflect the official policies of the Department of Health and Human Services; nor does any mention of trade names, commercial practices, or organization imply endorsement by the United States Government.
APPENDIX.
STEADY-STATE TEMPERATURE PROFILE IN THE SKIN AND SUBCUTANEOUS TISSUES
Following the analysis of Wilson and Spence (49), steady-state temperatures in the tissue and TDS layers can be calculated by solving Eq. 6 and simplifications thereof with appropriate boundary conditions and blood flows in the various layers. The solution for the case in which the upper boundary of the SC (z = 0) is held at temperature T0 and the lower boundary of the muscle layer (z = z5) is assumed to be equal to the core temperature Tc is given below.
Stratum corneum (q = 0, ω = 0; i = 1):
| (16) |
Viable epidermis (ω = 0; i = 2):
| (17) |
Dermis, subcutaneous fat and muscle (i = 3, 4, 5):
| (18) |
| (19) |
There are 10 constants of integration, Ai, two for each layer. The boundary conditions at z = 0 and z = z5 give A1 = T0 and . The other 8 constants are determined by the continuity conditions on temperature and heat flux at the four internal interfaces. The non-linear system of 8 equations and 8 unknowns can be solved by standard methods. We found that the Solver add-in to Microsoft Excel™, set to the GRG non-linear option, worked very well. Note that this method of solution differs from the sequential optimization routine described by Wilson and Spence (49).
REFERENCES
- 1.Scheuplein RJ. Analysis for permeability data for the case of parallel diffusion pathways. Biophys J. 1966;6:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Blank IH, Scheuplein RJ, MacFarlane DJ. Mechanism of percutaneous absorption III. The effect of temperature on the transport of non-electrolytes across the skin. J Invest Dermatol. 1967;49(6):582–9. [PubMed] [Google Scholar]
- 3.Peck KD, Ghanem A-H, Higuchi WI. The effect of temperature upon the permeation of polar and ionic solutes through human epidermal membrane. J Pharm Sci. 1995;84(8):975–82. [DOI] [PubMed] [Google Scholar]
- 4.Akomeah F, Nazir T, Martin GP, Brown MB. Effect of heat on the percutaneous absorption and skin retention of three model penetrants. Eur J Pharm Sci. 2004;21:337–45. [DOI] [PubMed] [Google Scholar]
- 5.Mitragotri S Temperature dependence of skin permeability to hydrophilic and hydrophobic solutes. J Pharm Sci. 2007;96(7):1832–9. [DOI] [PubMed] [Google Scholar]
- 6.Wood DG, Brown MB, Jones SA. Understanding heat-facilitated drug transport across human epidermis. Eur J Pharm Biopharm. 2012;81:642–9. [DOI] [PubMed] [Google Scholar]
- 7.Ashrafi P, Sun Y, Davey N, Wilkinson SC, Moss GP. The influence of diffusion cell type and experimental temperature on machine learning models of skin permeability. J Pharm Pharmacol. 2020;72:197–208. [DOI] [PubMed] [Google Scholar]
- 8.Prodduturi S, Sadrieh N, Wokovich AM, Doub WH, Westenberger BJ, Buhse L. Transdermal delivery of fentanyl from matrix and reservoir systems: effect of heat and compromised skin. J Pharm Sci. 2010;99:2357–66. [DOI] [PubMed] [Google Scholar]
- 9.Shin SH, Thomas S, Raney SG, Ghosh P, Hammell DC, El-Kamary SS, et al. In vitro-in vivo correlations for nicotine transdermal delivery systems evaluated by both in vitro skin permeation (IVPT) and in vivo serum phramacokinetics under the influence of transient heat application. J Control Release. 2018;270:76–88. [DOI] [PubMed] [Google Scholar]
- 10.Gupta SK, Southam M, Hwang SS. System functionality and physicochemical model of fentanyl transdermal system. J Pain Symptom Manag. 1992;7:S17–26. [DOI] [PubMed] [Google Scholar]
- 11.Vanakoski J, Seppala T, Sievi E, Lunell E. Exposure to high ambient temperature increases absorption and plasma concentrations of transdermal nicotine. Clin Pharmacol Ther. 1996;60:308–15. [DOI] [PubMed] [Google Scholar]
- 12.Shomaker TS, Zhang J, Ashburn MA. Assessing the impact of heat on the systemic delivery of fentanyl through the transdermal fentanyl delivery system. Pain Med. 2000;1:225–30. [DOI] [PubMed] [Google Scholar]
- 13.Gourlay GK. Treatment of cancer pain with transdermal fentanyl. Lancet Onol. 2001;2:165–72. [DOI] [PubMed] [Google Scholar]
- 14.Ashburn MA, Ogden LL, Zhang J, Love G, Basta SV. The pharmacokinetics of transdermal fentanyl delivered with and without controlled heat. J Pain. 2003;4(6):291–7. [DOI] [PubMed] [Google Scholar]
- 15.Petersen KK, Rousing ML, Jensen C, Arendt-Nielsen L, Gazerani P. Effect of local controlled heat on transdermal delivery of nicotine. Int J Physiol Pathophysiol Pharmacol. 2011;3:236–42. [PMC free article] [PubMed] [Google Scholar]
- 16.Moore KJ, Sathyan G, Richarz U, Natarajan J, Vandenbossche J. Randomized 5-treatment crossover study to assess the effects of external heat on serum fentanyl concentrations during treatment with transdermal fentanyl systems. J Clin Pharmacol. 2012;52:1174–85. [DOI] [PubMed] [Google Scholar]
- 17.Clarys P, Alewaeters K, Jadoul N, Barel A, Manadas RO, Preat V. In vitro percutaneous penetration through hairless rat skin: influence of temperature, vehicle, and penetration enhancers. Eur J Pharm Biopharm 1998;46:279–283. [DOI] [PubMed] [Google Scholar]
- 18.Oliveira G, Leverett JC, Emamzadeh M, Lane ME. The effect of heat on skin barrier function and in vivo dermal absorption. Int J Pharm. 2014;464:145–51. [DOI] [PubMed] [Google Scholar]
- 19.Park J-H, Lee J-W, Kim Y-C, Prausnitz MR. The effect of heat on skin permeability. Int J Pharm. 2008;359:94–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Klemsdal TO, Gjesdal K, Bredesen J-E. Heating and cooling of the nitroglycerin patch application area modify the plasma level of nitroglycerin. Eur J Clin Pharmacol. 1992;43:625–8. [DOI] [PubMed] [Google Scholar]
- 21.Gazerani P, Arendt-Nielsen L. Cutaneous vasomotor reactions in response to controlled heat applied in various body regions of healthy humans: evaluation of time course and application parameters. Int J Physiol Pathophysiol Pharmacol. 2011;3:202–9. [PMC free article] [PubMed] [Google Scholar]
- 22.Widmer RJ, Stewart RH, Young MF, Laurinec JE, Laine GA, Quick CM. Application of local heat induces capillary recruitment in the pallid bat wing. Am J Phys Regul Integr Comp Phys. 2007;292:R2312–7. [DOI] [PubMed] [Google Scholar]
- 23.Charkoudian N Skin blood flow in human thermoregulation: how it works, when it does not, and why. Mayo Clin Proc. 2003;78:603–12. [DOI] [PubMed] [Google Scholar]
- 24.Boron WF, Boulpaep EL. Medical physiology: a cellular and molecular approach. Philadelphia: Saunders; 2012. [Google Scholar]
- 25.Kellogg DL, Liu Y, Kosiba IF, O’Donnell D. The role of nitric oxide in the vascular effects of local warming of the skin in humans. J Appl Physiol. 1999;86:1185–90. [DOI] [PubMed] [Google Scholar]
- 26.Pergola PE, Kellogg DL, Johnson JM, Kosiba WA, Solomon DE. Role of sympathetic nerves in the vascular effects of local temperature in human forearm skin. Am J Physiol (Heart). 1993;265:H785–92. [DOI] [PubMed] [Google Scholar]
- 27.Singh P, Robert MS. Blood flow measurements in skin and underlying tissues by microsphere method-application to dermal pharmacokinetics of polar nonelectrolytes. J Pharm Sci. 1993;82:873–9. [DOI] [PubMed] [Google Scholar]
- 28.Singh P, Roberts MS. Effects of vasoconstriction on dermal pharmacokinetics and local tissue distribution of compounds. J Pharm Sci. 1994;83:783–91. [DOI] [PubMed] [Google Scholar]
- 29.Clough GF, Boutsiouki P, Church MK, Michel CC. Effects of blood flow on the in vivo recovery of a small diffusible molecule by microdialysis in human skin. J Pharmacol Exp Ther. 2002;302:681–6. [DOI] [PubMed] [Google Scholar]
- 30.Higaki K, Nakayama K, Suyama T, Amnuaikit C, Ogawara K, Kimura T. Enhancement of topical delivery of drugs via direct penetration by reducing blood flow rate in skin. Int J Pharm. 2005;288:227–33. [DOI] [PubMed] [Google Scholar]
- 31.Cross SE, Roberts MS. Dermal blood flow, lymphatics, and binding as determinates of topical absorption, clearance and distribution In: Riviere JE, editor. Dermal absorption models in toxicology and pharmacology. Boca Raton: CRC Press; 2006. p. 251–82. [Google Scholar]
- 32.Kretsos K, Miller MA, Zamora-Estrada G, Kasting GB. Partitioning, diffusivity and clearance of skin permeants in mammalian dermis. Int J Pharm. 2008;346(1–2):64–79. [DOI] [PubMed] [Google Scholar]
- 33.Dancik Y, Anissimov YG, Jepps OG, Roberts MS. Convective transport of highly plasma protein bounds drug facilitates direct penetration into deep tissues after topical application. Brit J Clin Pharmacol. 2011;73:564–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Anissimov YG, Roberts MS. Modelling dermal drug distribution after topical application in human. Pharm Res. 2011;28:2119–29. [DOI] [PubMed] [Google Scholar]
- 35.Ibrahim R, Nitsche JM, Kasting GB. Dermal clearance model for epidermal bioavailability calculations. J Pharm Sci. 2012;101:2094–108. [DOI] [PubMed] [Google Scholar]
- 36.McNeill S, Potts RO, Francoeur ML. Local enhanced topical delivery (LETD) of drugs: does it truly exist? Pharm Res. 1992;9:1422–7. [DOI] [PubMed] [Google Scholar]
- 37.Dancik Y, Miller M, Jaworska J, Kasting GB. Design and performance of a spreadsheet-based model for estimating bioavailability of chemicals from dermal exposures. Adv Drug Deliv Rev. 2013;65:221–36. [DOI] [PubMed] [Google Scholar]
- 38.Kapoor Y, Milewski M, Mitra A, Kasting GB. Clarifications: dermal clearance model for epidermal bioavailability calculations. J Pharm Sci. 2016;105:1341–4. [DOI] [PubMed] [Google Scholar]
- 39.La Count TD, Zhang Q, Murawsky M, Hao J, Ghosh P, Dave K, Raney SG, Talattof A, Kasting GB, Li SK. Evaluation of heat effects on transdermal nictoine delivery in vitro and in silico using heat-enhanced transport model analysis; AAPS J, 2020;22:82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dedrick RL, Flessner MF, Collins JM, Schultz JS. Is the peritoneum a membrane? ASAIO J. 1982;5:1–8. [Google Scholar]
- 41.Gupta E, Wientjes MG, Au JL-S. Penetration kinetics of 2′,3′-dideoxyinosine in dermis is described by the distributed model. Pharm Res. 1995;12:108–12. [DOI] [PubMed] [Google Scholar]
- 42.Rippe B, Haraldsson B. Transport of macromolecules across microvascular walls: the two-pore theory. Physiol Rev. 1994;74:163–219. [DOI] [PubMed] [Google Scholar]
- 43.Riviere JE. Pharmacokinetic implications of changing blood flow in skin. J Pharm Sci. 1992;81:601–2. [DOI] [PubMed] [Google Scholar]
- 44.Ryan TJ. Cutaneous circulation In: Goldsmith LA, editor. Biochemistry and physiology of the skin. New York: Oxford University Press; 1983. p. 817–77. [Google Scholar]
- 45.Braverman IM. The cutaneous microcirculation: ultrastructure and microanatomical organization. Microcirc. 1997;4(3):329–40. [DOI] [PubMed] [Google Scholar]
- 46.Pennes HH. Analysis of tissue and arterial blood temperatures in resting human forearm. J Appl Physiol. 1948;1:93–122. [DOI] [PubMed] [Google Scholar]
- 47.Çetingül MP, Herman C. A heat transfer model of skin tissue for the detection of lesions: sensitivity analysis. Phys Med Biol. 2010;55:5933–51. [DOI] [PubMed] [Google Scholar]
- 48.Diller KR, Hayes LJ. A finite element model of burn injury in blood-perfused skin. ASME Trans. 1983;105:300–7. [DOI] [PubMed] [Google Scholar]
- 49.Wilson SB, Spence VA. A tissue heat transfer model for relating dynamic skin temperature changes to physiological parameters. Phys Med Biol. 1988;33:895–912. [DOI] [PubMed] [Google Scholar]
- 50.Becker SM, Kuznetsov AV. Local temperature rises influence in vivo electroporation pore development: a numerical stratum corneum lipid phase transition model. J Biomech Eng. 2007;129:712–21. [DOI] [PubMed] [Google Scholar]
- 51.Becker SM, Kuznetsov AV. Numerical assessment of thermal response associated with in vivo skin electroporation: the importance of the composite skin model. J Biomech Eng. 2007;129:330–40. [DOI] [PubMed] [Google Scholar]
- 52.Pavselj N, Miklavcic D. Resistive heating and electropermeabilization of skin tissue during in vivo electroporation: a coupled nonlinear finite element model. Int J Heat Mass Transf. 2011;54:2294–302. [Google Scholar]
- 53.Mitchell JW, Galvez TL, Hengle J, Myers GE, Siebecker KL. Thermal response of human legs during cooling. J Appl Physiol. 1970;29:859–65. [DOI] [PubMed] [Google Scholar]
- 54.Elia M Organ and tissue contribution to metabolic rate In: Kinney J, Tucker H, editors. Energy metabolism: tissue determinants and cellular corollaries. New York, NY: Raven Press; 1992. p. 61–80. [Google Scholar]
- 55.Wang Z, Ying Z, Bosy-Westphal A, Zhang J, Schautz B, Later W, et al. Specific metabolic rates of major organs and tissues across adulthood: evaluation by mechanistic model of resting energy expenditure. Am J Clin Nutr. 2010;92:1369–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Werner J, Buse M. Temperature profiles with respect to inhomogeneity and geometry of human body. J Appl Physiol. 1988;65:1110–8. [DOI] [PubMed] [Google Scholar]
- 57.Morales M, Rathbun E, Smith R, Pace N. Studies on body composition: II. Theoretical considerations regarding the major tissue components, with suggestions for application to man. J Biol Chem. 1945;158:677–84. [Google Scholar]
- 58.Duck FA. Physical properties of tissue: a comprehensive reference book. London: Academic Press; 1990. [Google Scholar]
- 59.Zhang Q, Murawsky M, LaCount TD, Hao J, Kasting GB, Newman B, et al. Characterization of temperature profiles in skin and transdermal delivery system when exposed to temperature gradients in vivo and in vitro. Pharm Res. 2017;34:1491–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Zhang X, Chinkes D, Wolfe R. Measurement of protein metabolism in epidermis and dermis. Am J Physiol Endocrinol Metab. 2003;284:E1191–201. [DOI] [PubMed] [Google Scholar]
- 61.Duncan RF, Hershey JWB. Protein synthesis and protein phosphorylation during heat stress, recovery and adaptation. J Cell Biol. 1989;109:1467–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Arens EA, Zhang H. The skin’s role in human thermoregulation and comfort In. Indoor Environmental Quality (IEQ). Berkeley, CA: University of California Berkeley; 2006. pp. 560–602. [Google Scholar]
- 63.Wagner JG. Fundamentals of clinical pharmacokinetics. Hamilton, IL: Drug Intelligence Publications; 1975. [Google Scholar]
- 64.EPA. Estimation Program Interface (EPI) Suite v 4.11. U.S. Environmental Protection Agency; Available from: http://www.epa.gov/oppt/exposure/pubs/episuite. [Google Scholar]
- 65.Chen L, Lian G, Han L. Modeling transdermal permeation. Part I. Predicting skin permeability of both hydrophobic and hydrophilic solutes. AICHE J. 2010;56:1136–46. [Google Scholar]
- 66.Baba H, Ueno Y, Hashida M, Yamashita F. Quantitative prediction of ionization effect on human skin permeability. Int J Pharm. 2017;522:222–33. [DOI] [PubMed] [Google Scholar]
- 67.Potts RO, Guy RH. Predicting skin permeability. Pharm Res. 1992;9:663–9. [DOI] [PubMed] [Google Scholar]
- 68.Compton R, Sandborn W, Lawson G, Sheets A, Mays D, Zins B, et al. A dose-ranging pharmacokinetic study of nicotine tartrate following single-dose delayed-release oral and intravenous administration. Aliment Pharmacol Ther. 1997;11:865–74. [DOI] [PubMed] [Google Scholar]
- 69.Mello NK, Peltier MR, Duncanson H. Nicotine levels after IV nicotine and cigarette smoking in men. Exp Clin Psychopharmacol. 2013;21:188–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wang T-F, Kasting GB, Nitsche JM. A multiphase microscopic model for stratum corneum permeability. II. Estimation of physicochemical parameters and application to a large permeability database. J Pharm Sci. 2007;96:3024–51. [DOI] [PubMed] [Google Scholar]
- 71.Ash R, Barrer RM, Palmer DG. Diffusion in multiple laminates. Brit J Appl Phys. 1965;16:873–84. [Google Scholar]
- 72.Shin SH, Ghosh P, Newman B, Hammell DC, Raney SG, Hassan HE, et al. On the road to development of an in vitro permeation test (IVPT) model to compare heat effects on transdermal delivery systems: exploratory studies with nicotine and fentanyl. Pharm Res. 2017;34:1817–30. [DOI] [PubMed] [Google Scholar]
- 73.Kasting GB, Miller MA, LaCount TD, Jaworska J. A composite model for the transport of hydrophilic and lipophilic compounds across the skin. J Pharm Sci. 2019;108:337–49. [DOI] [PubMed] [Google Scholar]
- 74.Zhang Q, Murawsky M, LaCount TD, Hao J, Ghosh P, Raney SG, Kasting GB, Li SK. Evaluation of heat effects on fentanyl transdermal delivery systems using in vitro permeation and in vitro release methods, unpublished data. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Kretsos K, Kasting GB. A geometrical model of dermal capillary clearance. Math Biosci. 2007;208:430–53. [DOI] [PubMed] [Google Scholar]
- 76.Calcutt JJ, Anissimov YG. Physiologically based mathematical modeling of solute transport in the epidermis and dermis. Int J Pharm. 2019;569:118547. [DOI] [PubMed] [Google Scholar]
- 77.Cevc G, Vierl U. Spatial distribution of cutaneous microvasculature and local drugclearance after drug application on the skin. J Control Release. 2007;118:18–26. [DOI] [PubMed] [Google Scholar]
- 78.Charny CK, Hagmann MJ, Levin RL. A whole body thermal model of man during hyperthermia. IEEE Trans Biomed Eng. 1987;34:375–87. [DOI] [PubMed] [Google Scholar]
- 79.Johnson JM, Brengelmann GL, Hales JRS, Vanhoutte PM, Wenger CB. Regulation of cutaneous circulation. Fed Proc. 1986;45:2841–50. [PubMed] [Google Scholar]


