The Oscillation Amplitude, Not the Frequency of Cytosolic Calcium, Regulates Apoptosis Induction

Summary

Although a rising concentration of cytosolic Ca²⁺ has long been recognized as an essential signal for apoptosis, the dynamical mechanisms by which Ca²⁺ regulates apoptosis are not clear yet. To address this, we constructed a computational model that integrates known biochemical reactions and can reproduce the dynamical behaviors of Ca²⁺-induced apoptosis as observed in experiments. Model analysis shows that oscillating Ca²⁺ signals first convert into gradual signals and eventually transform into a switch-like apoptotic response. Via the two processes, the apoptotic signaling pathway filters the frequency of Ca²⁺ oscillations effectively but instead responds acutely to their amplitude. Collectively, our results suggest that Ca²⁺ regulates apoptosis mainly via oscillation amplitude, rather than frequency, modulation. This study not only provides a comprehensive understanding of how oscillatory Ca²⁺ dynamically regulates the complex apoptotic signaling network but also presents a typical example of how Ca²⁺ controls cellular responses through amplitude modulation.

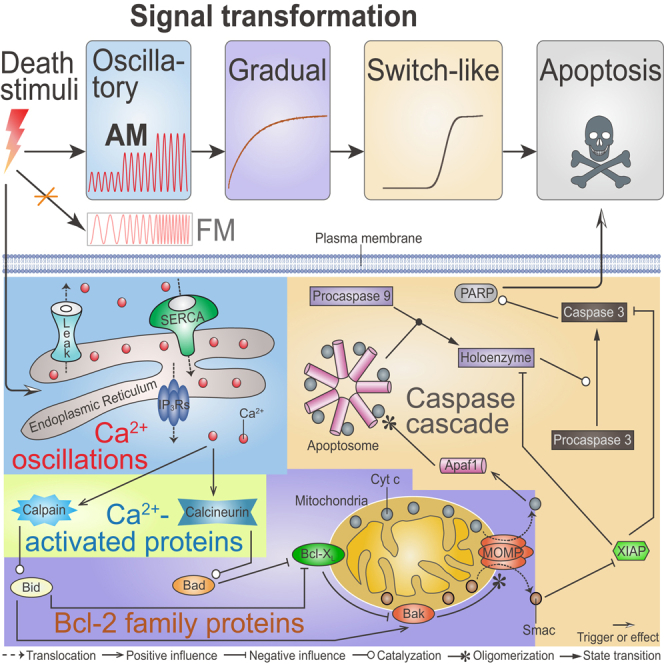
Graphical Abstract

Highlights

• •A signaling network of cytosolic Ca²⁺-induced apoptosis is constructed
• •The network is converted into a mathematical model composed of four modules
• •Oscillatory signals first transform into gradual ones and then into switch-like ones
• •Ca²⁺ regulates apoptosis mainly via amplitude, rather than frequency, modulation

Biological Sciences; Cell Biology; Mathematical Biosciences

Introduction

Calcium ion (Ca²⁺) is one of the most versatile and universal signaling agents to translate extra- and intracellular information into specific cellular outcomes (Berridge et al., 1998; Giorgi et al., 2018a). Upon stimulation, Ca²⁺ is released from the endoplasmic reticulum (ER) into the cytosol through inositol 1,4,5-trisphosphate receptor (IP₃R) channels. Changes in cytosolic Ca²⁺ concentration ([Ca²⁺]) of a moderate level can govern a myriad of vital cell functions, including fertilization, proliferation, and differentiation, and are essential for cell survival (Berridge et al., 2003). However, excessive elevations of [Ca²⁺] typically result in cell death, including apoptosis (Orrenius et al., 2003).

A cytosolic Ca²⁺ overload initiates the mitochondrial apoptotic pathway as follows. Ca²⁺ can activate calpain and calcineurin, causing the activation of BH3-only proteins (Chen et al., 2001; Wang et al., 1999). This results in the sequestering of anti-apoptotic Bcl-2 proteins and the activation of the pro-apoptotic effectors Bax and Bak (Czabotar et al., 2014; Youle and Strasser, 2008). These interaction patterns among Bcl-2 protein family culminate in Bax and Bak oligomerization and mitochondrial outer membrane permeabilization (MOMP) (Tait and Green, 2010). Subsequently, several apoptogenic factors are released from the mitochondrial intermembrane space, particularly cytochrome c (Cyt c) (Ow et al., 2008). In the cytosol, Cyt c engages Apaf1 and forms the apoptosome, which recruits caspase 9 and promotes caspase 3 activation. Active caspase 3 cleaves several hundred proteins, resulting in apoptosis (Shi, 2004). In addition, mitochondria retain cytosolic Ca²⁺ and this massive mitochondrial Ca²⁺ accumulation causes the opening of mitochondrial permeability transition pore, which leads to the Cyt c release and cell death (Qi and Shuai, 2016). Despite this detailed characterization of the molecular sequence of events, we still lack a comprehensive understanding of how Ca²⁺ dynamics control this complex apoptosis signaling network.

Differential equation modeling can simulate the dynamic output of individual proteins and can identify critical players in a signaling network, thus often providing novel insights to our understanding of cellular dynamics (Spencer and Sorger, 2011; Yao et al., 2016). Such modeling efforts have been devoted to understand intracellular Ca²⁺ dynamics (Dupont and Sneyd, 2017; Goldbeter et al., 1990; Li and Rinzel, 1994; Qi et al., 2015; Shuai and Jung, 2003; Sneyd et al., 2017) and the mechanistic details of the apoptotic pathway (Albeck et al., 2008; Anderson et al., 2019; Legewie et al., 2006; Qi et al., 2018; Rehm et al., 2006; Santos et al., 2019; Spencer and Sorger, 2011; Yin et al., 2017; Zhao et al., 2015). However, so far, Ca²⁺ signaling has not been mathematically integrated into models of apoptosis yet.

Two major types of Ca²⁺ temporal profiles have been reported in apoptotic cells, including a high plateau and oscillations (Boehning et al., 2003, Lee et al., 2010; Garcia et al., 2017). Oscillations of [Ca²⁺] in individual cells often occur as repetitive spikes or sinusoid-like oscillations (Berridge, 1990; Oancea and Meyer, 1998). In our study, we focused on investigating how cytosolic Ca²⁺ oscillations, especially sinusoidal oscillations, regulate apoptosis from a network dynamics perspective.

Typically, Ca²⁺ oscillations occur with periods from seconds to minutes (Uhlén and Fritz, 2010), whereas the apoptotic program normally takes between a few and several tens of hours (Garcia et al., 2017; Márquez-Jurado et al., 2018). Owing to technical limitations in producing distinct long-term Ca²⁺ oscillations in experimental setups of apoptotic processes, the switch from a fast oscillatory Ca²⁺ signal to a switch-like apoptotic response with a long latency remains unclear.

Ca²⁺ oscillations contain information in their amplitude and frequency, thus providing two ways to selectively activate downstream signaling pathways (Berridge, 1997; Parekh, 2011). It has been shown that some gene expression events (Li et al., 1998) and the activations of CaMKII (De Koninck and Schulman, 1998), PKC (Oancea and Meyer, 1998), and Ras (Kupzig et al., 2005), as well as ATP production (Hajnóczky et al., 1995), are regulated by the frequency of Ca²⁺ oscillations. These experimental observations, together with a well-known engineering principle that frequency modulation (FM) signaling is more precise than amplitude modulation (AM) signaling, have led to the prevailing view that Ca²⁺ controls cellular functions typically by an FM mode (Dupont and Combettes, 2016; Dupont and Sneyd, 2017; Goldbeter et al., 1990; Smedler and Uhlén, 2014). We have decided to investigate whether this is also the case during Ca²⁺-induced apoptosis.

To solve these two basic issues, we constructed a four-module network model, including Ca²⁺ oscillations, Ca²⁺-activated proteins, Bcl-2 family proteins, and Cyt c-induced caspase cascade. We transformed the biochemical reactions of the network into a set of ordinary differential equations (ODEs). The simulation results reveal that oscillatory Ca²⁺ signals will be first converted into gradual signals, i.e., the slowly and monotonically changed signals, and then be transformed into a switch-like apoptotic response. Furthermore, our results show that, with such converting processes, Ca²⁺ regulates apoptosis mainly through an AM mode, rather than through an FM mode. Our work provides crucial insight in the understanding of the modulatory role of Ca²⁺ signals on the apoptotic process.

Results

Model Construction

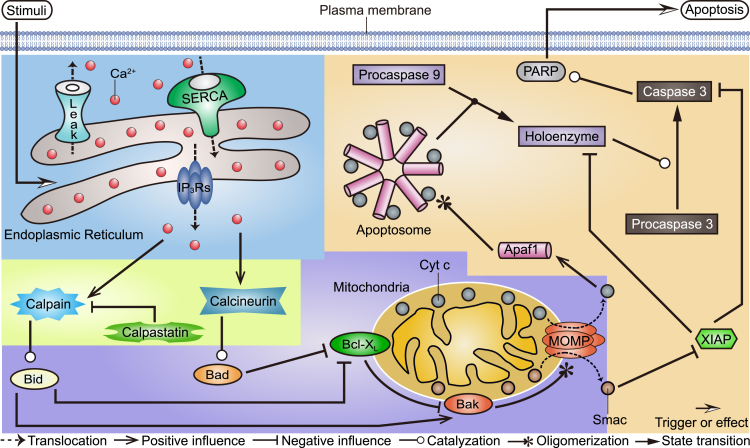
A complete picture of the role of Ca²⁺ as a mechanistic trigger of apoptosis is still missing. Based on previous works (Albeck et al., 2008; Rehm et al., 2006) and our recent studies (Qi et al., 2018; Qi and Shuai, 2016; Yin et al., 2017), we developed an integrative signaling network comprising four modules (Figure 1): (1) ER-involved Ca²⁺ oscillations, (2) Ca²⁺-activated proteins, (3) MOMP controlled by Bcl-2 family proteins on mitochondria, and (4) Cyt c-induced caspase cascade. The brief descriptions of each module are presented below (see details in Supplemental Information).

Figure 1.

Model Topology Scheme

The four modules are highlighted by different background colors. The blue region is for the module of Ca²⁺ oscillations, the green for the module of Ca²⁺-activated proteins, the purple for the module of MOMP controlled by Bcl-2 family proteins, and the yellow for the module of the Cyt c-induced caspase cascade. More details can be found in the main text.

Extracellular stimuli result in the formation of IP₃ (inositol 1,4,5-trisphosphate), which binds to the IP₃ receptors (IP₃Rs) to release Ca²⁺ from the ER. Cytosolic Ca²⁺ oscillations derive from three mechanisms of ions exchange between the ER and the cytoplasm: IP₃Rs-mediated Ca²⁺ release from the ER into the cytosol, SERCA (sarco/ER Ca²⁺-ATPase)-dependent Ca²⁺ uptake from the cytosol into the ER, and Ca²⁺ leakage from the ER into the cytosol (Shuai and Jung, 2003). An important machinery linking cytosolic Ca²⁺ signal and apoptosis is the activation of two Ca²⁺-regulated enzymes, i.e., calpain and calcineurin. In the presence of high [Ca²⁺], calcineurin dephosphorylates Bad, thus allowing Bad to inhibit the anti-apoptotic Bcl-X_L (Wang et al., 1999). Calpain, which is normally inhibited by calpastatin (Hanna et al., 2008), cleaves Bid to form truncated Bid (tBid), which in turn can directly activate Bak or inhibit Bcl-X_L that then indirectly activates Bak (Chen et al., 2001). Active Bak monomers form oligomers to trigger MOMP. Following MOMP, Smac and Cyt c are released from the mitochondria into the cytosol. In the cytosol, Cyt c binds Apaf1 to form the heptameric apoptosome, which interacts with procaspase 9 to induce the formation of holoenzyme, thereby triggering caspase 3 activation (Li et al., 2017). Caspase 3 can cleave a series of substrates (a process represented in the model by cleavage of PARP to form cPARP [Albeck et al., 2008]) and orchestrate the demolition of the cell. Smac assists this function by neutralizing the caspase inhibitor XIAP.

Using well-established kinetics approaches (Anderson et al., 2019; Qiao et al., 2019; Zhang et al., 2011), we translated these biochemical processes into a set of ODEs. Every variable represents the amount or concentration of a molecular species, which is dynamically controlled by the combination of all processes that increase and decrease the level of that particular molecular species. Each process is described by chemical kinetics, i.e., the mass action law or Hill function. The ODEs are numerically solved and the total simulation time was set to 18 h, the typical length of cell cycle (Spiller et al., 2010), reflecting the fact that a cell ultimately adopts one of two fates, either to survive by cell division or to die by apoptosis at the end of 18 h. In our model we assumed that the cell fate depends on the concentration of cleaved PARP ([cPARP]) within 18 h. A detailed description of all biochemical reactions, ODEs, and parameters is provided in Transparent Methods.

Dynamics of Ca²⁺ and cPARP

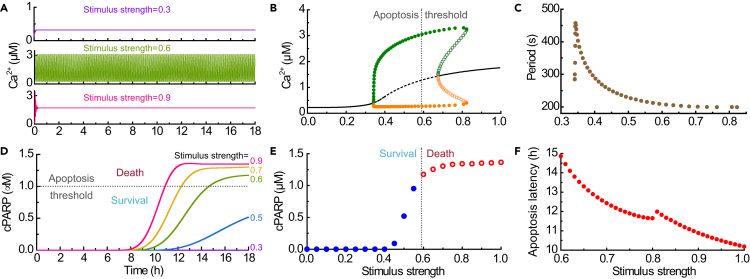
The simulation results we obtained are qualitatively consistent with the reported dynamics of Ca²⁺ (Dupont and Goldbeter, 1993; Gerasimenko et al., 2002; Jacob et al., 1988; Scorrano et al., 2003) and cPARP (Albeck et al., 2008; Rehm et al., 2006; Spencer and Sorger, 2011) upon incubation with apoptotic triggers. In many cell types, Ca²⁺ oscillations occur within an appropriate range of stimulus levels (Dupont and Goldbeter, 1993; Jacob et al., 1988). The time course plot (Figure 2A) and bifurcation diagram, i.e., the maximal and minimal value of Ca²⁺ oscillations (Figure 2B) show that, as the stimulus strength increases, the cytosolic Ca²⁺ changes from a stationary to an oscillatory behavior, before returning to a stationary state. The oscillation period is about 200 s (Figure 2C), as seen both in healthy and apoptotic cells (Gerasimenko et al., 2002; Scorrano et al., 2003). To define the apoptotic cell from the healthy cell, we proposed that apoptosis occurs when [cPARP] is above the apoptosis threshold of 1.02 μM, a value that corresponds to 60% substrate cleavage (dotted line in Figure 2D). This result agrees with the experimental result that apoptosis is triggered only when the level of substrate cleavage exceeds a high value (Rehm et al., 2006). Accordingly, when the multiple maximal concentration of sustained Ca²⁺ oscillations exceeds a critical threshold of about 3 μM (Figure 2B), apoptosis is initiated, which is compatible with the experimental observation for [Ca²⁺] under resting conditions and after stimulation (Giorgi et al., 2018b). Figure 2D also shows that the latency from the exposure to the apoptotic stimulus to the actual initiation of apoptosis is about 10 h, but the cleavage of PARP is sudden and switch-like, again in agreement with experimental observation (Albeck et al., 2008; Spencer and Sorger, 2011). The reasons for the selection of critical threshold of [Ca²⁺] and [cPARP] are detailed in Supplemental Information.

Figure 2.

The Dynamical Behavior of Ca²⁺ and cPARP at Different Stimulus Strengths

(A) Different kinetic behaviors of Ca²⁺ in response to different stimuli lasting for 18 h.

(B) Bifurcation diagram of Ca²⁺ in response to different stimuli. Solid/dashed lines represent stable/unstable fixed point; filled/empty circles represent minimal (orange) and maximal (green) [Ca²⁺] during a stable/unstable oscillation.

(C) Periods of Ca²⁺ oscillations within the stable oscillation range.

(D) The kinetic behavior of cPARP responding to different stimuli.

(E and F) The final [cPARP] (E) and the apoptosis latency (F) at different stimulus strengths.

The dotted lines in (B), (D), and (E) depict the apoptosis threshold.

It should be pointed out that, in order to provide a global view of the dynamical behavior of the system, the bifurcation diagram of Ca²⁺ is obtained mathematically with the steady states of the system (Figure 2B). However, considering the biological fact that a cell ultimately commits to apoptosis or to division at a limited time duration, we simply limited the discussion of the cell fate within 18 h for all the simulation results.

Two Indexes for Apoptosis

The relationship between the stimulus strength and the corresponding final [cPARP] yields an ultrasensitive signal-response curve (Figure 2E). Here [cPARP] at 18 h is defined as the final [cPARP], which is used as an index for cell fate. In detail, the fate of a cell is survival if the final [cPARP]<1.02 μM; otherwise, the apoptosis process is initiated. This result is insensitive to the variations in the cell cycle, i.e., total simulation time (Figure S2C). If apoptosis is triggered, another index, i.e., the apoptosis latency is introduced to evaluate how quickly apoptosis can be induced. In other words, it measures the interval between the time when the stimulus is applied and the time when the increasing [cPARP] crosses the apoptosis threshold of 1.02 μM. As shown in Figure 2F, the stronger the stimulus intensity is, the shorter the apoptosis latency becomes.

Signal Transduction

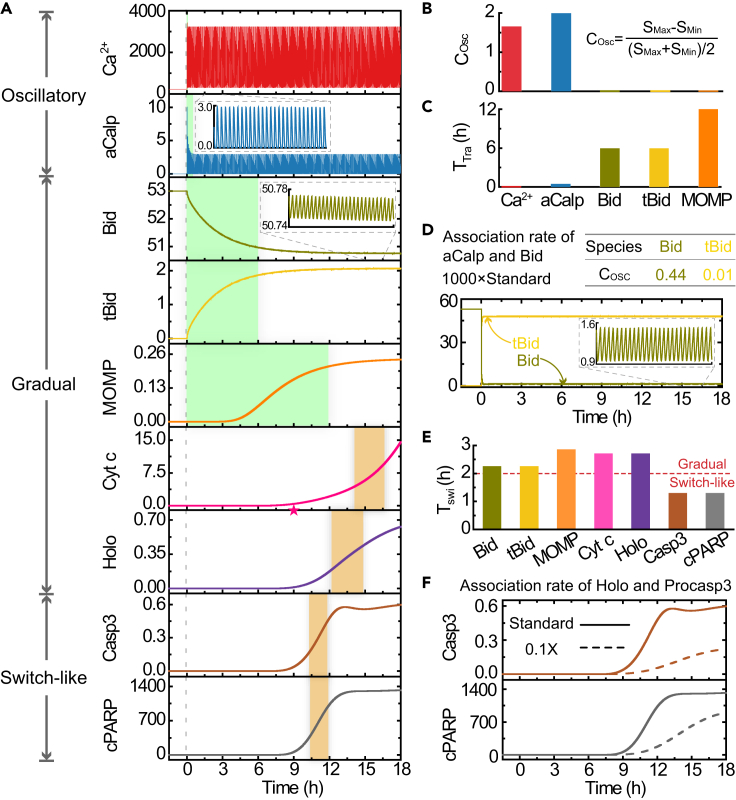
Given the different dynamics of Ca²⁺ and cPARP (Figures 2A and 2D), it is curious how the fast oscillatory Ca²⁺ signal is converted into a slow but switch-like apoptotic signal. To address this question, we analyzed the time series of the main reaction species along the reaction pathway (Figure 3A). These species include Ca²⁺, aCalp (activated calpain), Bid, tBid, MOMP, Cyt c, holoenzyme, caspase 3, and cPARP. According to the kinetic patterns of these species, we observed that the oscillatory patterns starting with Ca²⁺ signal first become gradual for proteins such as Bid, and then become switch-like for proteins such as caspase 3.

Figure 3.

Transition from Oscillatory to Switch-like Kinetics

(A) Time courses of the main species in the signaling network. The vertical dashed line indicates the time at which the stimulus (strength = 0.73) is introduced. The green and orange shaded regions denote the transient time and the switch time, respectively. The time at which mitochondrial Cyt c begins to release into the cytosol is marked by an asterisk.

(B and C) (B) Oscillation coefficient (C_Osc) and (C) transient time (T_Tra) of five upstream species. S_Max and S_Min are the maximal and minimal concentrations of a certain species at the steady state, respectively.

(D) Time series and C_Osc of Bid and tBid with the association rate of aCalp and Bid increased by 1,000-fold.

(E) Switch time (T_Swi) of gradual and switch-like signals. The horizontal dashed line at 2 h is applied to distinguish the switch-like signals from the gradual ones.

(F) Time series of Casp3 and cPARP when the association rate of holoenzyme and procaspase 3 is decreased by 10% (broken lines). The results obtained under standard parameter are the same as in (A) and are shown to facilitate comparison. The insets in (A) and (D) show representative time courses of 1.5 h. The units of y axes in (A), (D), and (F) are nM. Abbreviation: aCalp, activated calpain; Holo, holoenzyme; Casp3, caspase 3.

As shown in Figure 3A, the transition from oscillatory to gradual pattern involves two changes. First, the oscillation amplitudes of the upstream species become successively smaller. In detail, it is about 3,000 nM for Ca²⁺, nearly 3 nM for aCalp, only 0.03 nM for Bid and tBid, and barely perceptible for MOMP. To compare the oscillation strength among different species with a uniform standard, an oscillation coefficient, which is the ratio of oscillation amplitude to mean (looks like the deterministic version of the coefficient of variation), is calculated (Figure 3B). As a consequence, the oscillation coefficients of Ca²⁺ and aCalp are far larger than those of Bid, tBid, and MOMP. Here we define a signal as oscillatory if the oscillation coefficient of a species is larger than 0.1. Accordingly, the signals of Bid, tBid, and MOMP are not considered oscillatory. Second, upon stimulation, the system transitions from a resting steady state to a new equilibrium state, generating a transient time, which is defined as the time required for oscillatory species to reach steady oscillation or for other species to reach 90% of their peaks. As a result, the transient times for Ca²⁺, aCalp, Bid, tBid, and MOMP are about 0.1, 0.5, 6, 6, and 12 h, respectively (Figure 3C), becoming successively longer. Compared with the length of cell cycle (18 h), a transient time longer than 6 h is a duration that is not negligible. Therefore, we suggest that such a non-oscillatory signal with long transient time should be labeled as gradual. According to the oscillation coefficient and transient time, we therefore classify Ca²⁺ and aCalp as oscillatory signals and Bid, tBid, and MOMP as gradual signals.

Obviously the most dramatic change in the kinetics from Ca²⁺ to MOMP occurs upon the truncation of Bid by aCalp. The result of parameter sensitivity analysis also shows that this step indeed exerts a substantial influence on the output of the system (Figure S2B). Interestingly, the kinetics of Bid owns two distinct timescales. On the one hand, Bid oscillates at a fast timescale of around 200 s. On the other hand, a gradually decreasing trend occurs for Bid in a slower timescale of about 6 h as a transient process (Figure 3A). Meanwhile, the oscillation amplitude is far smaller than the mean value of its steady oscillations. This is mainly due to the slow truncation reaction of Bid by aCalp, which directly results in a long transient time and also generates a small oscillation amplitude for Bid by averaging aCalp over a long duration with slow association rate of aCalp with Bid (5 × 10⁻⁶ nM⁻¹s⁻¹). If this rate is increased 1,000-fold, Bid will achieve its new equilibrium very quickly and its oscillation coefficient will be 0.44 (Figure 3D), thus becoming an oscillatory signal. The slow truncation of Bid by aCalp, therefore, plays a significant role to convert the oscillatory signals to gradual signals in this pathway.

The kinetics from Bid to cPARP (Figure 3A) shows a transition from a gradual pattern to a switch-like pattern. Here, we distinguish a switch-like signal from gradual signal according to their switch time, which is defined as the time it takes to progress from a 30% to a 70% final concentration of any reaction species. If its switch time is longer than 2 h, it is labeled a gradual signal; otherwise, it is labeled a switch-like signal. According to this classification, Bid, tBid, MOMP, Cyt c, and holoenzyme are gradual signals, whereas caspase 3 and cPARP are switch-like signals (Figure 3E). If the switch time is defined as the time for a signal to increase from 20% to 80% of its final value, similar results are obtained, albeit with a longer switch time.

As a gradual signal, the MOMP-released Cyt c leads to a gradual accumulation of the apoptosome and thus the holoenzyme. In detail, before MOMP accumulates to reach a threshold, Cyt c cannot be released, thus maintaining Cyt c and downstream signals in an “off” state. After MOMP reaches the threshold at about 9 h (marked by asterisk in Figure 3A), the Cyt c-induced holoenzyme assembly ensures the downstream signals switch to an “on” state.

The conversion from gradual to switch-like signals is regulated by multiple reactions, including the mechanics of MOMP assembly, mitochondria-to-cytosol translocation of Smac and Cyt c (Albeck et al., 2008), the direct repression of holoenzyme and caspase 3 by XIAP (Figure S3), and holoenzyme-mediated activation of caspase 3. As seen in Figure 3A, holoenzyme activation results in a sudden and rapid cleavage of caspase 3 and thus the processing of PARP into cPARP, suggesting that the conversion from gradual to switch-like signals is strongly influenced by the interaction between holoenzyme and procaspase 3. If the association rate of holoenzyme and procaspase 3 (1.0 μM⁻¹s⁻¹) is decreased to 10%, the original switch-like signals, i.e., caspase 3 and cPARP, will become gradual signals (Figure 3F). Thus, the holoenzyme-mediated activation of caspase 3 has a crucial influence on the conversion from gradual into switch-like signals.

Three Ideal Ca²⁺ Inputs

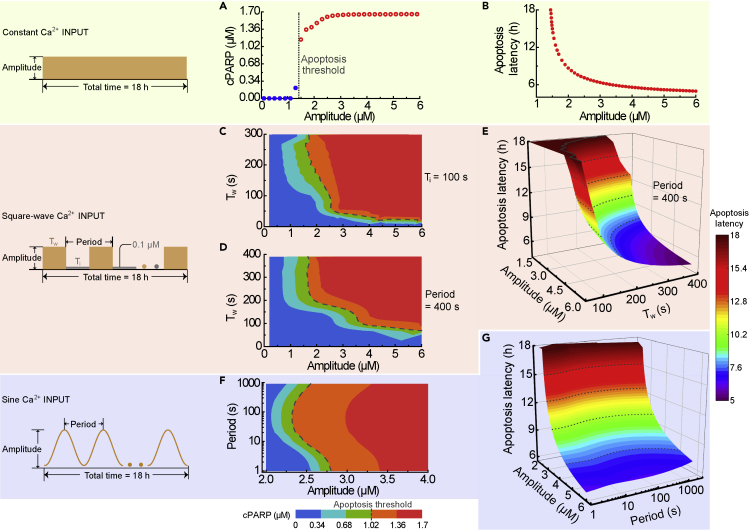
Since both the amplitude and frequency of the ER-involved Ca²⁺ oscillations largely increase with stimulus strength (Figures 2B and 2C), it is hard to dissect the individual contributions of amplitude and frequency to apoptosis. To explore whether amplitude or frequency of Ca²⁺ oscillations is the critical determinant for Ca²⁺-induced apoptosis, three ideal Ca²⁺ waveforms and their effects on the two indexes for evaluating apoptosis are presented in Figure 4.

Figure 4.

Three Ideal Ca²⁺ Inputs and Their Impact on Apoptosis

(A and B) The final [cPARP] (A) and apoptosis latency (B) as a function of the amplitude of constant Ca²⁺ input. (C) The final [cPARP] in response to the amplitude and period (varying T_w with the unchanged T_i) of square-wave Ca²⁺ input. (D and E) The final [cPARP] (D) and apoptosis latency (E) in response to the amplitude and T_w with the fixed period of square-wave Ca²⁺ input. (F and G) The dependence of the final [cPARP] (F) and apoptosis latency (G) on the amplitude and period of sinusoidal Ca²⁺ input. (C), (D), and (F) have the same color bar at the bottom, whereas (E) and (G) share the same color bar on the right.

First a constant Ca²⁺ input is imposed to assess its efficacy in triggering apoptosis. Figure 4A shows that, as the amplitude of the constant Ca²⁺ increases, the final [cPARP] exhibits an almost all-or-none pattern. When the amplitude increases beyond an apoptotic threshold, the apoptosis latency decreases first rapidly and then slowly approaches 5 h (Figure 4B). Different from the high amplitude threshold of 3 μM [Ca²⁺] for apoptosis with an oscillatory Ca²⁺ signal, a small [Ca²⁺] threshold of 1.5 μM is obtained with constant Ca²⁺ input for apoptosis. These results suggest that Ca²⁺ amplitude alone is sufficient to cause a low or high final [cPARP], corresponding to survival or apoptosis of cells.

Second, we used a square-wave Ca²⁺ input to investigate the roles of its amplitude and frequency in regulating apoptosis. For such a pulsating Ca²⁺ signal, besides the amplitude, we can define the wave width (T_w) and inter-wave interval (T_i), which can be varied separately, as well as the period (T_w + T_i). Such type of signal has been used experimentally (De Koninck and Schulman, 1998) and in mathematical models (Marhl et al., 2006; Salazar et al., 2008). In the case of varied wave width but fixed inter-wave interval, the contour map in Figure 4C shows that the final [cPARP] mainly depends on the Ca²⁺ amplitude but not on the wave width and of course not on its period. Figure 4D shows the dependence of final [cPARP] on the Ca²⁺ amplitude and wave width, while keeping the period constant. From the apoptosis threshold (dashed line) shown in Figure 4D, one can see that the final [cPARP] is high when the Ca²⁺ amplitude is large (>1.5 μM) and the wave width is long (>75 s). Thus, the Ca²⁺ amplitude is the dominant pro-apoptotic factor.

The comparison of the results in Figures 4C and 4D reveals that the final [cPARP] depends less on oscillation period than on its wave width. Next, we examined the influence of the Ca²⁺ amplitude and wave width on apoptosis latency. The result plotted in Figure 4E indicates that apoptosis latency is less sensitive to wave width than to wave amplitude. A similar but more obvious trend for apoptosis latency can be found when comparing Ca²⁺ amplitude and period (Figure S4). Together, the results obtained in Figures 4C–4E and S4 indicate that apoptosis is mainly modulated by amplitude, rather than frequency of a square-wave Ca²⁺ input.

Third we used sinusoidal Ca²⁺ input to further strengthen the conclusion that apoptosis depends more on amplitude than on frequency. The sinusoidal input mimics more closely biological Ca²⁺ oscillations, and its oscillation amplitude and period can be varied separately. Figure 4F shows that the final [cPARP] exhibits only a modest response to the change of Ca²⁺ oscillation period but a pronounced sensitivity to the change of oscillation amplitude. Notably, a cell remains alive when its Ca²⁺ amplitude is small but undergoes apoptosis when the amplitude is large, regardless of the oscillation period. This result holds true when the top two most sensitive parameters are varied in a limited range (Figures S5). In addition, the change in Ca²⁺ amplitude significantly influences apoptosis latency, whereas its period does not (Figure 4G). These results reveal that AM is the dominant mechanism for Ca²⁺-regulated apoptosis.

In summary, by virtue of three ideal Ca²⁺ waveforms, we demonstrated that cytosolic Ca²⁺ regulates apoptosis mainly via AM but not via FM. Although the Ca²⁺ amount or average Ca²⁺ and action time of Ca²⁺ input also have impacts on apoptosis (Figures S6 and S7), these factors appear insignificant.

Signal Transduction of Sinusoidal Ca²⁺ Input

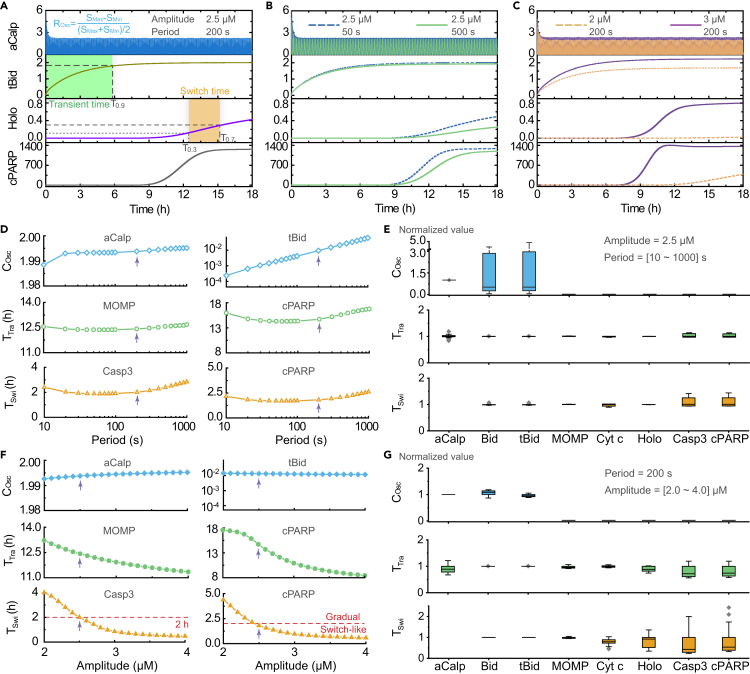
Given that sinusoidal Ca²⁺ oscillations can mimic one of the two biologically oscillatory patterns (the sinusoid-like oscillations and the repetitive spikes) in vivo (Berridge, 1990; Putney and Bird, 1993), we explored the roles of amplitude and frequency of sinusoidal Ca²⁺ oscillations in the apoptotic signal transduction pathway. Figure 5A presents the temporal evolution of four key species in the signal transduction process where the Ca²⁺ amplitude is 2.5 μM and its period is 200 s. Here, aCalp is an oscillatory signal, tBid and holoenzyme are gradual signals, and cPARP is a switch-like signal, which are almost the same as those induced by the ER-involved Ca²⁺ oscillations (Figure 3A).

Figure 5.

Effects of Amplitude and Period of Sinusoidal Ca²⁺ Input on Signal Transduction

(A-C) Time series of representative species such as aCalp, tBid, Holo, and cPARP (A) at amplitude = 2.5 μM and period = 200 s, (B) at amplitude = 2.5 μM and period = 50 s or 200 s, and (C) at period = 200 s and amplitude = 2 μM or 3 μM. The units of y axes are nM.

(D) Oscillation coefficient (C_Osc) of aCalp and tBid, transient time (T_Tra) of MOMP and cPARP, and switch time (T_Swi) of Casp3 and cPARP, keeping the amplitude constant at 2.5 μM and changing the period.

(E) C_Osc, T_Tra, and T_Swi of the main species are normalized to the corresponding value at amplitude = 2.5 μM and period = 200 s, as indicated by the arrows in (D).

(F and G) (F) and (G) are the counterparts of (D) and (E), respectively, but at fixed period of 200 s and varying amplitude. In the box plot, the middle line denotes the median; the top and bottom of the box denote 75th and 25th percentiles, respectively; whiskers denote 1.5×interquartile range; and diamonds denote outliers. Abbreviation: aCalp, activated calpain; Holo, holoenzyme; Casp3, caspase 3.

If the period of sinusoidal Ca²⁺ input becomes significantly shorter or longer, i.e., 50 s or 500 s, the kinetics of the four species change slightly (Figure 5B). The frequency information carried in Ca²⁺ oscillations becomes largely suppressed within the gradual signal of tBid. In contrast, if the amplitude of sinusoidal Ca²⁺ input becomes smaller or bigger, i.e., 2 or 3 μM, the kinetics of the four species change significantly, especially for the holoenzyme and cPARP (Figure 5C). A decreased amplitude causes the original switch-like cPARP signal to become a gradual signal, and the eventual cell fate changes from apoptosis to survival. An increased amplitude transforms the original gradual holoenzyme signal into a switch-like signal, and the apoptosis latency becomes dramatically shorter. The time course study suggests that the signal transduction from Ca²⁺ to tBid acts as a frequency filter of the Ca²⁺ oscillation information. Moreover, the information of the Ca²⁺ amplitude is important to determine the final intensity of the gradual signals, which is in turn crucial to determine the curve pattern of cPARP.

To gain further insights into these mechanisms, we analyzed how the changes in the period and amplitude of a sinusoidal Ca²⁺ input affect the oscillation coefficient, transient time, and switch time of the key species.

First, we considered the situation where the sinusoidal Ca²⁺ period changes from 10 to 1,000 s, while keeping the amplitude constant at 2.5 μM. Figure 5D depicts the change of the oscillation coefficients of aCalp and tBid, the transient times of MOMP and cPARP, and the switch times of caspase 3 and cPARP against the sinusoidal Ca²⁺ period. In order to clearly describe the process of information transformation, Figure S8A shows the distribution of the values of the three characteristic times of all key species. To accommodate the wide range of values, these values are normalized with respect to the corresponding value at period = 200 s, and each box plot in Figure 5E exhibits the distribution of the normalized values. Then, we considered the situation where the sinusoidal Ca²⁺ amplitude varies from 2 to 4 μM, while keeping the period constant at 200 s. Figures 5F, 5G, and S8B are the counterparts of Figures 5D, 5E, and S8A, respectively.

Figures 5D and 5F show that the oscillation coefficient of aCalp is far larger than that of tBid, which indicates that the frequency attribute of Ca²⁺ oscillations is only well retained in the aCalp signal, whereas it is largely lost in the gradual signals. When comparing Figures 5E and 5G, it is evident that the change in the period of a sinusoidal Ca²⁺ input only significantly affects the oscillation coefficients of the two upstream gradual signals, i.e., Bid and tBid, whereas the change in the Ca²⁺ amplitude dramatically modulates both the transient times and switch times of the downstream species, especially for the switch-like signals, i.e., caspase 3 and cPARP. Together, these results imply that the Ca²⁺-regulated apoptotic transduction pathway is capable of efficiently filtering the frequency attribute during the transformation from oscillatory signals to gradual signals but capable of sensitively responding to the amplitude attribute of the Ca²⁺ oscillations. Hence, the results here reveal the underlying mechanism that Ca²⁺ signal regulates apoptosis mainly via the Ca²⁺ oscillation amplitude, rather than via its frequency.

Discussion

Given the difficulties of experimentally tracking long-term Ca²⁺ signaling dynamics simultaneously with apoptotic protein processing, it is currently unknown how a fast and oscillatory Ca²⁺ signal transforms into a slow but switch-like apoptotic response. How Ca²⁺ signaling regulates apoptosis has also remained elusive because the amplitude and period of Ca²⁺ oscillations cannot be manipulated independently within a biological system. We address these two fundamental questions with a mathematical model for deciphering the mechanism underlying Ca²⁺-induced apoptosis.

Our results indicate that the conversion of an oscillatory Ca²⁺ signal into a switch-like apoptotic signal requires two steps. In the first step, oscillatory signals transform into gradual signals during which the oscillation amplitudes of the upstream species in signal cascade decrease successively, meanwhile their transient times to the new equilibrium increase successively. During this transformation, the slow truncation of Bid by aCalp plays a significant role. In the second step, gradual signals are converted into switch-like signals, during which the switch times of the downstream species in the apoptotic signaling pathway decrease dramatically. This process critically depends on the fast activation of caspase 3 by the holoenzyme.

Cellular information can be encoded in the amplitude and frequency of Ca²⁺ oscillations, and that information can then be decoded by distinct downstream effectors to achieve different cellular outcomes (Berridge, 1997; Monteith et al., 2017). The predominant view is that the cellular function is determined by the frequency of Ca²⁺ oscillations (Dupont and Combettes, 2016; Dupont and Sneyd, 2017; Goldbeter et al., 1990; Smedler and Uhlén, 2014). In contrast, our results show that the amplitude of Ca²⁺ oscillations is primarily used to modulate apoptosis in three different systems, that is, in the constant, square-wave, and sinusoidal Ca²⁺ input systems. Of note, the elucidation in the last system is compelling not only because sinusoidal Ca²⁺ input has separable amplitude and period but also because it can largely mimic the biologically oscillatory pattern observed in cells. Strikingly, by employing sinusoidal Ca²⁺ input, we revealed that the frequency property of Ca²⁺ oscillations is filtered but the amplitude property is retained during the apoptotic signal transduction process. During the process to translate these oscillatory signals into gradual signals, the oscillatory Ca²⁺ signal is converted into a non-oscillatory signal by filtering out the frequency information. Thus, the amplitude, other than the frequency, of Ca²⁺ oscillations, functions as the more important attribute for apoptosis induction.

The mechanisms by which cells encode the dynamic properties of oscillatory signaling (e.g., amplitude and/or frequency) into their decision-making processes are the subject of very intense investigation (Benzinger and Khammash, 2018; Cai et al., 2008; Hannanta-anan and Chow, 2016; Hansen and O'Shea, 2015). For a Ca²⁺ signal, it is generally believed that AM is less reliable than FM, owing to the difficulty of distinguishing small Ca²⁺ changes from the background noise level (Berridge et al., 1998). However, the fidelity of apoptotic Ca²⁺ signal can by guaranteed through AM mode because the apoptotic Ca²⁺ levels are much higher than those produced by spontaneous fluctuation. Indeed, a recent experiment revealed that individual cells exhibit high amplitude Ca²⁺ release events but significant heterogeneity in the frequency of these events after treatment with apoptosis-inducing drugs (Garcia et al., 2017). In addition, Monteith et al. recently proposed that it is the amplitude of Ca²⁺ oscillations that controls cell fate (e.g., proliferation or cell death), whereas it is their frequency that controls gene transcription (Monteith et al., 2017). Our finding demonstrates that Ca²⁺-regulated apoptosis is a typical example of AM fashion, which is a key perspective in the field of Ca²⁺ signaling.

Limitations of the Study

Although Ca²⁺ oscillations are intrinsically stochastic because of stochastic IP₃R channel dynamics (Powell et al., 2020; Thul, 2014; Thurley et al., 2012), the Ca²⁺ oscillations at the cellular level can be effectively treated as deterministic (Cao et al., 2014; Sneyd et al., 2017; Voorsluijs et al., 2019). As a result, we only used the two-variable Li-Rinzel model as the simplest but useful model to produce Ca²⁺ oscillations. The focus of this work is on cytosolic Ca²⁺-induced apoptosis, and for simplicity, we did not take mitochondrial Ca²⁺ into account. In addition, the prediction of AM given in the paper largely depends on a sinusoidal type of Ca²⁺ oscillations. Thus, whether our prediction can be generalized to other types of Ca²⁺ oscillations such as repetitive spikes remains an open question for future study. Furthermore, the test of this prediction will rely on the experimental design that can compare directly the effects of the amplitude and period of cytosolic Ca²⁺ oscillations on the apoptosis.

Resource Availability

Lead Contact

Jianwei Shuai

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplemental Information. The code related to this paper may be requested from the authors.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: November 20, 2020