Abstract
Dosimetric measurement error is known to potentially bias the magnitude of the dose response, and can also affect the shape of dose response. In this report, generalized relative and absolute rate models are fitted to the latest Japanese atomic bomb survivor solid cancer, leukemia and circulatory disease mortality data (followed from 1950 through 2003), with the latest (DS02R1) dosimetry, using Bayesian techniques to adjust for errors in dose estimates and assessing other model uncertainties. Linear-quadratic models are fitted and used to assess lifetime mortality risks for contemporary UK, USA, French, Russian, Japanese and Chinese populations. For a test dose of 0.1 Gy absorbed dose weighted by neutron relative biological effectiveness, solid cancer, leukemia and circulatory disease mortality risks for a UK population using a generalized linear-quadratic relative rate model were estimated to be 3.88% Gy−1 [95% Bayesian credible interval (BCI): 1.17, 6.97], 0.35% Gy−1 (95% BCI: −0.03, 0.78) and 2.24% Gy−1 (95% BCI: −0.17, 13.76), respectively. Using a generalized absolute rate linear-quadratic model at 0.1 Gy, the lifetime risks for these three end points were estimated to be 3.56% Gy−1 (95% BCI: 0.54, 6.78), 0.41% Gy−1 (95% BCI: 0.01, 0.86) and 1.56% Gy−1 (95% BCI: −1.10, 7.21), respectively. There was substantial evidence of curvature for solid cancer (in particular, the group of solid cancers excluding lung, breast and stomach cancers) and leukemia, so that for solid cancer and leukemia, estimates of excess risk per unit dose were nearly doubled by increasing the dose from 0.01 to 1.0 Gy, with most of the increase occurring in the interval from 0.1 to 1.0 Gy. For circulatory disease, the dose-response curvature was inverse, so that risk per unit dose was nearly halved by going from 0.01 to 1.0 Gy weighted absorbed dose, although there were substantial uncertainties. In general, there were higher radiation risks for females compared to males. This was true for solid cancer and circulatory disease overall, as well as for lung, breast, stomach and the group of other solid cancers, and was the case whether relative or absolute rate projection models were employed; however, for leukemia this pattern was reversed. Risk estimates varied somewhat between populations, with lower cancer risks in aggregate for China and Russia, but higher circulatory disease risks for Russia, particularly using the relative rate model. There was more pronounced variation for certain cancer sites and certain types of projection models, so that breast cancer risk was markedly lower in China and Japan using a relative rate model, but the opposite was the case for stomach cancer. There was less variation between countries using the absolute rate models for stomach cancer and breast cancer, but this was not the case for lung cancer and the group of other solid cancers, or for circulatory disease.
INTRODUCTION
Epidemiological studies of cancer rates associated with external and internal exposure to ionizing radiation have been subject to extensive reviews by various scientific bodies (1-3). In particular, the United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) 2006 Report assessed cancer incidence (4) and mortality data (5) relating to the Japanese atomic bomb survivor Life Span Study (LSS) cohort using the (then current) Dosimetry System 2002 (DS02) dose estimates, as well as many other studies of persons exposed occupationally, environmentally and medically (therapeutically or diagnostically) (2).
It has long been assumed that radiation-induced cancer rates at low doses or low dose rates are associated with lower rates (per unit dose) than those at higher doses and dose rates (1, 2). Based on a combination of experimental and epidemiologic evidence the International Commission on Radiological Protection (ICRP) recommended the use of a dose and dose-rate effectiveness factor (DDREF) of 2 to reduce solid cancer rates obtained from moderate-to-high acute dose studies (e.g., those mostly derived from the Japanese atomic bomb survivors) when applied to low-dose or low-dose-rate exposures (1). Recently, the ICRP Task Group 91 (TG 91) has re-examined the evidence for such ameliorating effects of lower dose or lower dose-rate radiation exposures.
It has been known for some time that circulatory disease is associated with high acute doses (6, 7). There is emerging evidence that circulatory disease may also be associated with lower levels of radiation exposure, in particular at occupational dose levels (8-10). A meta-analysis and systematic review of various moderate- and low-dose-exposed groups (with mean dose <0.5 Gy) suggested that lifetime population risks associated with circulatory disease could be comparable to those for cancer (8).
Measurement error can substantially alter the shape of the dose-response relationship and thus the derived population risk estimates. The problem of dosimetric error in the LSS cancer data has been investigated by several researchers with a view towards removing measurement-error bias in rate estimates. The method of dose adjustment usually employed is the so-called “regression calibration” method (11), which entails substitution of the DS02 dose estimate by the expected true dose given the estimated dose. Although this approach leads to reasonable adjusted point estimates of rate parameters for linear dose-response models, it is an approximate method with non-linear dose-effect relationships and does not fully take account of the variability induced by the measurement errors. Bayesian approaches to the measurement error problem have been extensively developed over the last 30 years, which distinguish and link models for disease, measurement error and exposure (12-14); dosimetric uncertainty is reflected in the variability of the model parameters. In principle, the Bayesian approach allows for more of the uncertainties, in particular relating to the dose-error distribution, to be taken into account and will produce a wider uncertainty envelope. There is an important practical advantage arising from use of the Bayesian Markov chain Monte Carlo (MCMC) approach to calculate population risk in that it easily facilitates estimation of propagated uncertainties from the sampled posterior distribution of model parameters to the population risks. In this work, assessment is made of uncertainties in population risk, which is a function of the model parameters.
We apply these approaches to grouped data on cancer and circulatory disease mortality in the LSS cohort using the recently published mortality dataset of Ozasa et al. (15) and compare resulting risk estimates to those based on the regression calibration method. A variety of fitted models, specifically modeling both relative and absolute rates, will be used to estimate lifetime population cancer and circulatory disease mortality risks for a number of major world populations. We are particularly interested in assessing evidence for curvature in the dose response. This work was undertaken as part of work done for ICRP TG91 by the first and last authors.
METHODS
Poisson disease models were used for all fitting to the LSS mortality data, closely following the structure of the existing publicly available dataset of Ozasa et al. (15). The models that were used in this work are fundamentally functions of the (unobserved) “true” mean organ/tissue dose, , averaged over the survivors in the stratum. Two specific forms of rate model, namely generalized relative rate and generalized absolute rate models, were used for all malignant and circulatory disease end points, where the expected number of cancer or circulatory disease deaths in the stratum, with city c, sex s, attained age a, age at exposure e, other stratifying variables v (calendar period of follow-up, ground distance category, Adult Health Study status) and “true” average organ/tissue dose, , for the generalized excess relative rate model (ERR) is:
| (1) |
where PY is the number of person-years of follow-up in the stratum. The dose is measured in Gy, weighted by a neutron relative biological effectiveness (RBE) value of 10 (1), as employed in most previously published LSS analyses (5, 16, 17). The appropriate RBE-10 weighted organ/tissue dose (colon, lung, stomach, breast, red bone marrow) was used for the relevant analyses of each cancer site; for all solid cancers combined, colon dose was used. For circulatory disease lung dose was employed. The corresponding generalized excess absolute rate (EAR) is:
| (2) |
The functions and describe the radiation-induced ERR and EAR, respectively, and were assumed to be zero for zero average organ/tissue dose; h0(a,e,c,s,v) describes the “baseline” (zero dose) cancer or circulatory disease mortality rate.
Previous dose-response relationships considered for these and other similar datasets include linear and quadratic models, and certain more general forms (8, 18-24). In modeling all end points except leukemia, the following expression for was used:
| (3) |
where y = a – e is time since exposure. For leukemia, a slightly different form of temporal adjustment was used, identical to that previously used elsewhere (2, 25):
| (4) |
This yields an ERR that is linear-quadratic in dose, and with adjustment to the ERR for age at exposure, e, and attained age, a. Similar expressions were used to model EAR. Slight variants of these models, using adjustments to the ERR or EAR similar to those employed by Ozasa et al. (15) were also fitted; further details of these models are given in the Supplementary Information (https://doi.org/10.1667/RR15571.1.S1).
It should be emphasized that the “true” stratum-average organ/tissue dose, , is not known; the only recorded dosimetric quantity in any stratum is the “nominal” stratum-average DS02 revision 1 (DS02R1) organ/tissue dose, . The DS02R1 organ doses are those employed by Grant et al. (26) in recent analyses of the LSS cancer incidence data, and slightly modify the previous DS02 system.
Model Fitting
Classical (likelihood-based) analysis using regression calibration.
Following the example of Pierce et al. (18), in this work the distribution of the nominal dose d conditional on the true dose D was assumed to be log-normal. At an individual level, the “true” dose distribution in each of the two cities (Hiroshima, Nagasaki) was modeled by a generalized Weibull distribution, in which the probability density of the “true” dose D in city c and sex s was given by:
| (5) |
This superposition of an extended Weibull density function [similar to that used previously (27, 28)], with an additional uniform density on the true dose interval [0.0, 0.01], was previously used (25).
The methods used for adjusting for dosimetric error were reasonably similar to those employed by Little et al. (25). In general, the mean true dose in stratum i was not known; the only observable dosimetric quantity in the stratum is the nominal (or estimated) DS02R1 dose . It can be shown (11) that approximately unbiased parameter estimates are obtained by replacing or with or , respectively, in the model fitting. This approach to measurement error correction is an example of “regression calibration” (11).
For computational simplicity, in the LSS mortality data and , were evaluated, and substituted into or . Therefore, for example, Eq. (3) was replaced with:
| (6) |
Models were fitted by Poisson maximum likelihood (29).
Measurement error at individual level.
The natural modeling of measurement error in Bayesian MCMC methods is at the individual level. The stratification creates groups of subjects, and so requires transfer of the modeling of measurement error on the individual dose to the measurement error on the mean dose over the stratum. At an individual level, the “true” dose distribution in each of the two cities (Hiroshima, Nagasaki) is modeled as above by a generalized Weibull distribution, as given by Eq. (5), and this yields in a natural way a distribution of mean dose at the stratum level, and as above, a “classical” measurement error model was employed.
Bayesian modeling at the strata level.
As in the earlier published work of Little et al. (22, 23, 25) a two-stage method was used for modeling the stratum-specific dosimetric uncertainties, described in more detail there and in the Supplementary Information (https://doi.org/10.1667/RR15571.1.S1). In the first-stage Monte Carlo sampling, the parameters of the generalized Weibull distributions are simulated via a Metropolis-Hastings algorithm. This first-stage Markov Chain sampling also computes the distribution of the dose means for each dose group. The uncertainty in the Weibull distribution parameters is considered in the prior parameters for the mean μij, and variance , which determine the distribution of the in the first-stage sampling (as described in step f in the section “Bayesian modelling at the strata level” in the Supplementary Information. The means μij and variances of these stratum level dose means are then used to determine the parameters for normal or gamma priors for the means, which form the priors for the dose means in the second stage of model fitting, using Gibbs sampling; 35% log-normal dose errors are assumed, consistent with the magnitude of error assumed previously by various researchers (18, 22, 25).
This procedure was necessitated by the grouped nature of the data, in particular by the fact that individual “nominal” doses are not available. However, it has certain decisive advantages in relationship to computational speed and convergence. In the second stage, the derived distribution of all the was then used together with the disease model Eqs. (1)-(4), to derive the posterior distribution of the parameters of these models. The second-stage Bayesian sampling was performed using OpenBUGS (30). The deviance information criterion (DIC) was used as a method of model choice, as outlined by Spiegelhalter et al. (31). All Fortran code for the first-stage sampling and OpenBUGS code for the second-stage sampling is available from upon request from the corresponding author (MPL)
Sampling from the full posterior distribution of the various model parameters in the Bayesian method was achieved using MCMC simulation (13, 14) since no analytic expression for the posterior distribution is available. Generally vague prior distributions were assumed for most model parameters. Care was taken to check stability and convergence of the posterior MCMC samples, using Brooks-Gelman-Rubin (BGR) statistics (32, 33) and other graphical techniques; in all cases BGR statistics were less than 1.05, and with one exception (the leukemia relative rate model coefficients) were less than 1.01.
Lifetime Risk Projection
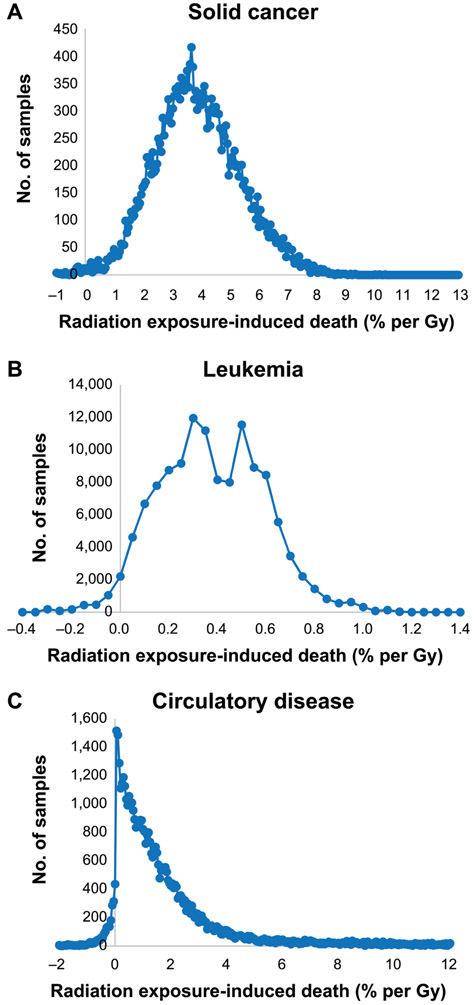
All high-dose-rate lifetime population cancer mortality risks were evaluated from model Eqs. (3) and (4) fitted to the Japanese data by regression calibration/maximum likelihood, or by Bayesian MCMC, as discussed above. Four commonly used measures of lifetime risk were calculated in this work, namely excess deaths per unit dose, risk of radiation exposure-induced death (REID) per unit dose, years of life lost per unit dose and years of life lost per radiation-induced death. All four measures of risk are discussed in more detail elsewhere (23, 25) and in the Supplementary Information (https://doi.org/10.1667/RR15571.1.S1), and have been employed by a number of national and international scientific committees (1-3, 34). In calculating all these risk measures, for most purposes (Tables 2-5; Supplementary Tables S5 and S9) the age- and sex-specific mortality rates of the current (2017) UK population (35) and the various other national populations (France, USA, Russia, Japan, China) (36) were used as the background rates. All projections assumed a two-year minimum latent period for leukemia, and a five-year minimum latent period for solid cancers and circulatory disease. These values of latent period have been assumed in many previous analyses of the cancer and circulatory disease data (2, 8, 9). Population risks are evaluated up to age infinity, although in practice the contribution for age >120 years was negligible. Each set of model parameter values from the MCMC sample was used to calculate each of the above four measures of population cancer risk for these current populations. This sample of parameter values was therefore associated with a sample of population cancer and circulatory disease mortality risks for these populations. The distribution of REID is shown graphically in Fig. 2. The cause-specific risks were evaluated singly, assuming that each specific cause of death was the only one being affected by radiation. In this way it mirrors exactly what was done in the UNSCEAR 2006 report (2), and also in previously published studies (23, 25). Slightly different calculations could be envisaged in which all radiogenic causes of death were assumed to operate together, jointly decrementing the survival probability, such as that which was performed by the ICRP (1, 37); jointly calculated risks would therefore be expected to be slightly lower. We prefer the individual estimates of risk because end point-specific estimates of years of life lost are thereby more easily derived. Nevertheless, the results of employing this alternative method of evaluating risk are given in Supplementary Table S10 (https://doi.org/10.1667/RR15571.1.S1).
TABLE 2.
Population Mortality Risks (Using 2017 Mortality Rates for England and Wales) Predicted by Optimal Excess Relative and Excess Absolute Rate Models, Unadjusted Weighted Colon Dose ≤3 Gya
| Cancer/circulatory disease mortality end point |
Model | Test dose (Gy) | Radiation exposure-induced deaths/Gy (×102) (95% BCI) |
Years life lost/Gy (95% BCI) |
|---|---|---|---|---|
| All solid cancer | Relative rate | 0.01 | 3.57 (0.70, 6.81) | 0.50 (0.10, 0.94) |
| 0.1 | 3.88 (1.17, 6.97) | 0.55 (0.17, 0.96) | ||
| 1 | 6.59 (4.82, 8.46) | 0.96 (0.76, 1.18) | ||
| Absolute rate | 0.01 | 3.11 (−0.13, 6.51) | 0.43 (−0.02, 0.87) | |
| 0.1 | 3.56 (0.54, 6.78) | 0.49 (0.08, 0.91) | ||
| 1 | 7.51 (5.61, 9.50) | 1.08 (0.85, 1.32) | ||
| Lung cancer | Relative rate | 0.01 | 2.57 (0.40, 5.09) | 0.32 (0.05, 0.62) |
| 0.1 | 2.61 (0.55, 5.02) | 0.33 (0.07, 0.61) | ||
| 1 | 2.99 (1.66, 4.53) | 0.38 (0.23, 0.55) | ||
| Absolute rate | 0.01 | 1.58 (−0.36, 4.07) | 0.15 (−0.04, 0.36) | |
| 0.1 | 1.65 (−0.17, 4.03) | 0.16 (−0.02, 0.36) | ||
| 1 | 2.25 (0.86, 4.14) | 0.22 (0.09, 0.37) | ||
| Stomach cancer | Relative rate | 0.01 | 0.09 (−0.02, 0.26) | 0.01 (0.00, 0.03) |
| 0.1 | 0.09 (−0.01, 0.26) | 0.01 (0.00, 0.03) | ||
| 1 | 0.11 (0.03, 0.26) | 0.01 (0.01, 0.03) | ||
| Absolute rate | 0.01 | 0.54 (−0.33, 1.47) | 0.09 (−0.05, 0.23) | |
| 0.1 | 0.58 (−0.23, 1.45) | 0.10 (−0.04, 0.23) | ||
| 1 | 0.90 (0.38, 1.58) | 0.15 (0.07, 0.24) | ||
| Breast cancer | Relative rate | 0.01 | 2.03 (0.49, 4.94) | 0.31 (0.09, 0.62) |
| 0.1 | 2.01 (0.53, 4.80) | 0.31 (0.10, 0.61) | ||
| 1 | 1.87 (0.72, 3.82) | 0.30 (0.16, 0.50) | ||
| Absolute rate | 0.01 | 0.91 (0.30, 1.76) | 0.14 (0.05, 0.24) | |
| 0.1 | 0.90 (0.32, 1.73) | 0.14 (0.06, 0.23) | ||
| 1 | 0.87 (0.46, 1.50) | 0.14 (0.09, 0.20) | ||
| All solid cancer excluding lung, stomach, breast | Relative rate | 0.01 | 0.22 (−1.56, 2.23) | 0.03 (−0.25, 0.34) |
| 0.1 | 0.48 (−1.17, 2.38) | 0.08 (−0.19, 0.36) | ||
| 1 | 2.93 (1.76, 4.38) | 0.48 (0.32, 0.64) | ||
| Absolute rate | 0.01 | −0.52 (−2.75, 1.94) | −0.08 (−0.39, 0.27) | |
| 0.1 | −0.13 (−2.21, 2.21) | −0.02 (−0.32, 0.30) | ||
| 1 | 3.57 (2.15, 5.22) | 0.53 (0.36, 0.71) | ||
| Leukemia | Relative rate | 0.01 | 0.27 (−0.13, 0.71) | 0.06 (−0.02, 0.20) |
| 0.1 | 0.35 (−0.03, 0.78) | 0.07 (0.00, 0.22) | ||
| 1 | 1.14 (0.75, 1.56) | 0.21 (0.13, 0.47) | ||
| Absolute rate | 0.01 | 0.34 (−0.09, 0.82) | 0.11 (−0.03, 0.26) | |
| 0.1 | 0.41 (0.01, 0.86) | 0.13 (0.00, 0.27) | ||
| 1 | 1.11 (0.83, 1.41) | 0.35 (0.25, 0.46) | ||
| All circulatory disease | Relative rate | 0.01 | 2.84 (−0.22, 17.90) | 0.21 (−0.02, 1.22) |
| 0.1 | 2.24 (−0.17, 13.76) | 0.18 (−0.02, 1.01) | ||
| 1 | 1.28 (0.01, 5.07) | 0.11 (0.00, 0.46) | ||
| Absolute rate | 0.01 | 1.76 (−1.26, 8.01) | 0.17 (−0.13, 0.62) | |
| 0.1 | 1.56 (−1.10, 7.21) | 0.16 (−0.11, 0.57) | ||
| 1 | 1.15 (−0.06, 4.12) | 0.12 (−0.01, 0.35) |
For all end points a burn-in of one-half the total Monte Carlo samples were used; for most end points a total of 50,000 Monte Carlo samples were taken, with the exception of leukemia (250,000 for the relative rate model, 200,000 for the absolute rate model), lung cancer (75,000 for the relative rate model), breast cancer (150,000 for the relative rate model) and circulatory disease (100,000 for the relative rate model, 150,000 for the absolute rate model). The dose used is: (a) weighted colon dose for all solid cancer and all solid cancers apart from lung, stomach and breast; (b) weighted lung dose for lung cancers and circulatory disease; (c) weighted stomach dose for stomach cancer; (d) weighted breast dose for breast cancer; and (e) weighted red bone marrow dose for leukemia.
TABLE 5.
Population Mortality Risks (Using 2017 Mortality Rates for England and Wales) for Solid Cancer, Leukemia and All Circulatory Disease Predicted by Optimal Excess Relative Rate Models, Unadjusted and Untruncated Weighted Colon Dose ≤2 Gy, ≤3 Gy or ≤4 Gy, Both Sexesa
| Cancer/circulatory disease mortality end point |
Unadjusted, untruncated colon dose limit used for analysis |
Test dose (Gy) |
Excess deaths/Gy (×102) (95% BCI) |
Radiation-induced deaths/Gy (×102) (95% BCI) |
Years life lost/Gy (95% BCI) |
Years life lost/radiation induced death (years) (95% BCI) |
|---|---|---|---|---|---|---|
| All solid cancer | ≤2 Gy | 0.01 | 2.62 (−0.19, 5.68) | 3.17 (−0.24, 6.85) | 0.44 (−0.04, 0.93) | 14.18 (12.34, 16.23) |
| 0.1 | 2.95 (0.33, 5.82) | 3.57 (0.41, 7.01) | 0.50 (0.06, 0.95) | 14.20 (12.37, 16.24) | ||
| 1 | 5.80 (4.13, 7.68) | 7.03 (5.03, 9.28) | 1.02 (0.79, 1.27) | 14.67 (12.97, 16.62) | ||
| ≤3 Gy | 0.01 | 2.95 (0.58, 5.66) | 3.57 (0.70, 6.81) | 0.50 (0.10, 0.94) | 14.25 (12.63, 16.15) | |
| 0.1 | 3.21 (0.97, 5.79) | 3.88 (1.17, 6.97) | 0.55 (0.17, 0.96) | 14.28 (12.66, 16.16) | ||
| 1 | 5.44 (3.96, 7.01) | 6.59 (4.82, 8.46) | 0.96 (0.76, 1.18) | 14.69 (13.18, 16.51) | ||
| ≤4 Gy | 0.01 | 5.08 (2.63, 7.90) | 6.14 (3.19, 9.52) | 0.86 (0.46, 1.28) | 14.07 (12.48, 15.92) | |
| 0.1 | 5.13 (2.82, 7.79) | 6.20 (3.41, 9.40) | 0.87 (0.50, 1.26) | 14.10 (12.53, 15.94) | ||
| 1 | 5.54 (4.07, 7.15) | 6.72 (4.96, 8.64) | 0.97 (0.77, 1.19) | 14.52 (13.04, 16.30) | ||
| Leukemia | ≤2 Gy | 0.01 | 0.07 (−0.28, 0.45) | 0.07 (−0.28, 0.45) | 0.02 (−0.04, 0.10) | 19.42 (12.90, 35.16) |
| 0.1 | 0.17 (−0.15, 0.54) | 0.17 (−0.15, 0.55) | 0.03 (−0.02, 0.12) | 19.38 (12.90, 35.47) | ||
| 1 | 1.12 (0.70, 1.78) | 1.12 (0.70, 1.79) | 0.21 (0.13, 0.40) | 19.54 (13.01, 35.14) | ||
| ≤3 Gy | 0.01 | 0.27 (−0.13, 0.71) | 0.27 (−0.13, 0.71) | 0.06 (−0.02, 0.20) | 18.81 (12.50, 37.60) | |
| 0.1 | 0.35 (−0.03, 0.77) | 0.35 (−0.03, 0.78) | 0.07 (0.00, 0.22) | 18.81 (12.50, 38.13) | ||
| 1 | 1.13 (0.75, 1.56) | 1.14 (0.75, 1.56) | 0.21 (0.13, 0.47) | 18.84 (12.55, 37.65) | ||
| ≤4 Gy | 0.01 | 0.44 (0.03, 0.97) | 0.44 (0.03, 0.98) | 0.09 (0.00, 0.22) | 20.00 (13.15, 37.47) | |
| 0.1 | 0.50 (0.09, 1.01) | 0.50 (0.09, 1.02) | 0.10 (0.02, 0.24) | 20.00 (13.15, 37.46) | ||
| 1 | 1.04 (0.68, 1.50) | 1.04 (0.69, 1.50) | 0.21 (0.12, 0.39) | 20.00 (13.21, 37.08) | ||
| All circulatory disease | ≤2 Gy | 0.01 | 2.79 (−0.61, 23.56) | 3.79 (−0.83, 32.12) | 0.28 (−0.07, 2.19) | 10.82 (6.34, 28.62) |
| 0.1 | 2.00 (−0.51, 15.73) | 2.71 (−0.69, 21.44) | 0.22 (−0.06, 1.62) | 10.90 (6.57, 28.62) | ||
| 1 | 0.92 (−0.02, 4.01) | 1.25 (−0.03, 5.46) | 0.11 (−0.01, 0.49) | 11.09 (6.79, 28.27) | ||
| ≤3 Gy | 0.01 | 2.09 (−0.16, 13.19) | 2.84 (−0.22, 17.90) | 0.21 (−0.02, 1.22) | 10.38 (6.24, 24.89) | |
| 0.1 | 1.66 (−0.12, 10.12) | 2.24 (−0.17, 13.76) | 0.18 (−0.02, 1.01) | 10.43 (6.47, 24.89) | ||
| 1 | 0.94 (0.01, 3.74) | 1.28 (0.01, 5.07) | 0.11 (0.00, 0.46) | 10.65 (6.72, 24.89) | ||
| ≤4 Gy | 0.01 | 1.16 (−0.42, 5.99) | 1.57 (−0.56, 8.11) | 0.12 (−0.05, 0.56) | 9.47 (6.35, 17.04) | |
| 0.1 | 1.00 (−0.35, 5.26) | 1.36 (−0.48, 7.11) | 0.11 (−0.04, 0.52) | 9.49 (6.45, 17.04) | ||
| 1 | 0.83 (0.02, 2.71) | 1.12 (0.03, 3.68) | 0.10 (0.00, 0.30) | 9.63 (6.65, 17.08) |
For all end points a burn-in of one half the total Monte Carlo samples were used; for most end points a total of 50,000 Monte Carlo samples were taken, with the exception of leukemia (150,000 for ≤2 Gy, 250,000 for ≤3 Gy, 200,000 for ≤4 Gy), and circulatory disease (150,000 for ≤2 Gy, 100,000 for ≤3 Gy, 80,000 for ≤4 Gy). The dose used is: (a) weighted colon dose for all solid cancer; (b) weighted lung dose for circulatory disease; and (c) weighted red bone marrow dose for leukemia.
FIG. 2.
Distribution of radiation exposure-induced death (REID) (% per Gy) evaluated at a test dose of 0.1 Gy and using relative rate models for a population with 2017 UK mortality rates for solid cancer (panel A), leukemia excluding CLL (panel B) and circulatory disease (panel C). Number of Monte Carlo samples from the 25,000, 125,000 and 50,000 sampled for these end points, respectively, after chain burn-in in intervals of REID in histogram with increment = 0.0005 per Gy.
RESULTS
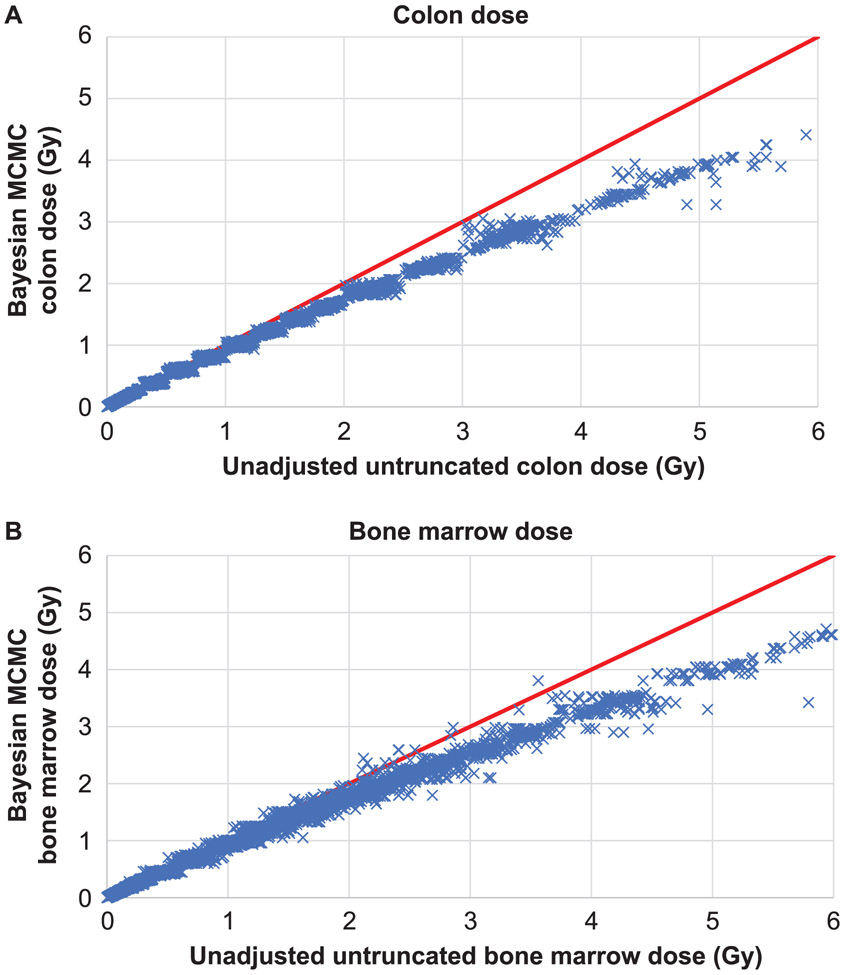
Figure 1 shows the MCMC mean colon dose compared with the unadjusted colon dose, and the analogous plot for red bone marrow dose. As can be seen, there is some scatter above approximately 3 Gy colon dose, and increased scatter above approximately 2 Gy red bone marrow dose. Supplementary Fig. S2 (https://doi.org/10.1667/RR15571.1.S1) shows the same plots, but by city (Hiroshima compared with Nagasaki), while also showing the comparison with the regression calibration adjustment estimated by Pierce et al. (18). As is evident here, the regression calibration adjustment of Pierce et al. (18) is generally consistent with the adjustment implied by our models, for each city. The means of the MCMC model coefficients (Table 1) are generally close to the model coefficients fitted to the regression-calibration adjusted doses (Supplementary Table S4). Table 2 suggests that for a test dose of 0.1 Gy, solid cancer, leukemia and circulatory disease mortality risk for a UK population using generalized linear-quadratic relative rate models were estimated as 3.88% Gy−1 [95% Bayesian credible interval (BCI): 1.17, 6.97)], 0.35% Gy−1 (95% BCI: −0.03, 0.78) and 2.24% Gy−1 (95% BCI: −0.17, 13.76), respectively. Using a generalized absolute rate linear-quadratic model at 0.1 Gy, the risks for these three end points were estimated as 3.56% Gy−1 (95% BCI: 0.54, 6.78), 0.41% Gy−1 (95% BCI: 0.01, 0.86) and 1.56% Gy−1 (95% BCI: −1.10, 7.21), respectively. The years of life lost at this test dose using the relative rate model for these three end points are, respectively, 0.55 years Gy−1 (95% BCI: 0.17, 0.96), 0.07 years Gy−1 (95% BCI: 0.00, 0.22), and 0.18 years Gy−1 (95% BCI: −0.02, 1.01) (Table 2). The years of life lost at this test dose using the absolute rate model for these three end points are 0.49 years Gy−1 (95% BCI: 0.08, 0.91), 0.13 years Gy−1 (95% BCI: 0.00, 0.27) and 0.12 years Gy−1 (95% BCI: −0.01, 0.35), respectively (Table 2). Very similar risks are predicted by maximum-likelihood fitted models using either the unadjusted, Radiation Effects Research Foundation (RERF) adjusted-truncated, regression-calibration adjusted or the stage-1 MCMC dose means, but the adjusted-truncated doses generally yield somewhat lower risks (Table 3). For example, for a test dose of 0.1 Gy, the central estimate of population risk for solid cancers is lower for the Bayesian MCMC model than for the unadjusted model fits or the regression calibration fits, 3.88 Gy−1 vs. 4.49 Gy−1 vs. 4.19 Gy−1, respectively, and likewise for circulatory disease 2.24 Gy−1 vs. 2.52 Gy−1 vs. 2.61 Gy−1. However, for leukemia the regression-calibration risk is 0.33 Gy−1, and so is slightly lower than the central estimate using MCMC, 0.35 Gy−1, and the unadjusted risk model, 0.43 Gy−1 (Tables 2 and 3). As with the Bayesian model fits (Table 2), increasing the test dose from 0.01 Gy to 1 Gy yielded a near doubling in risk per unit dose for solid cancer, leukemia and the miscellaneous group of solid cancers excluding lung, stomach and breast, whether using the relative or absolute rate models, but for lung, stomach and breast cancers, the risk per unit dose did not change much, and for circulatory disease there was some reduction in risk per unit dose with increasing dose (Table 3). Using the alternative adjustments to the ERR and EAR models suggested by Ozasa et al. (15) did not markedly change the pattern of variation of risk with test dose (Supplementary Table S9; https://doi.org/10.1667/RR15571.1.S1). The results of jointly estimating population risks across all mortality end points rather than singly estimating risks are given in Supplementary Table S10. In general, the two sets of risks are close (almost always within 5%) when test doses of 0.01 or 0.1 Gy are used, although the discrepancy is slightly larger, up to 15%, when a test dose of 1 Gy is employed.
FIG. 1.
Untruncated unadjusted weighted colon and bone marrow dose vs. posterior mean of Markov chain Monte Carlo weighted colon (panel A) and bone marrow (panel B) doses from first-stage sampling. The solid red line is the diagonal (x = y).
TABLE 1.
Model Coefficients (Mean and 95% BCI) for Optimal Excess Relative and Excess Absolute Rate Models, Restricted to Unadjusted Weighted Colon Dose ≤ 3 Gya
| Cancer/ circulatory disease mortality end point |
Relative rate model | ||
|---|---|---|---|
| κ1 [Sex]b (95% BCI) |
κ2 [age at exposure/10] (95% BCI) |
κ3 [time since exposure/10] (95% BCI) |
|
| Solid cancer | −0.90 (−1.35, −0.49) | −0.53 (−0.71, −0.36) | −0.20 (−0.35, −0.04) |
| Lung cancer | −1.30 (−2.50, −0.36) | −0.16 (−0.53, 0.18) | −0.12 (−0.46, 0.25) |
| Stomach cancer | −25.42 (−70.64, −2.04) | −0.58 (−1.06, −0.15) | −0.15 (−0.53, 0.20) |
| Breast cancer | −21.42 (−68.75, 3.69) | −0.70 (−1.34, −0.20) | −0.12 (−0.61, 0.31) |
| All solid cancer apart from lung, stomach, breast | −0.56 (−1.14, −0.01) | −0.72 (−1.02, −0.45) | −0.38 (−0.61, −0.15) |
| Circulatory disease | −24.75 (−70.64, −0.56) | −0.59 (−1.99, 0.24) | −0.20 (−1.20, 0.59) |
| Absolute rate model | |||
|
κ1 [Sex]b (95% BCI) |
κ2 [age at exposure/10] (95% BCI) |
κ3 [time since exposure/10] (95% BCI) |
|
| Solid cancer | −0.38 (−0.89, 0.07) | 0.35 (0.19, 0.49) | 0.63 (0.50, 0.76) |
| Lung cancer | −5.00 (−47.62, 0.75) | 0.70 (0.42, 0.96) | 0.97 (0.67, 1.30) |
| Stomach cancer | −24.68 (−71.24, −1.00) | 0.37 (−0.05, 0.73) | 0.32 (0.03, 0.61) |
| Breast cancer | −21.46 (−67.82, −2.13) | −0.15 (−0.50, 0.15) | 0.58 (0.34, 0.86) |
| All solid cancer apart from lung, stomach, breast | −0.09 (−0.71, 0.47) | 0.25 (0.03, 0.46) | 0.59 (0.41, 0.78) |
| Circulatory disease | −23.22 (−70.76, 0.40) | 0.40 (−1.07, 1.42) | 0.54 (−0.56, 1.49) |
| Relative rate model | |||
|
κ1 [ln[age at exposure/20] (95% BCI) |
κ2 [ln[attained age/50]] (95% BCI) |
||
| Leukemia | −0.05 (−0.49, 0.51) | −1.67 (−2.66, −0.72) | |
| Absolute rate model | |||
|
κ1 [Sex]c (95% BCI) |
κ2 [ln[time since exposure/30]] (95% BCI) |
||
| Leukemia | 0.52 (0.05, 1.04) | −0.45 (−0.85, −0.87) | |
| Relative rate model | |||
|
D [dose (Gy)] (95% BCI) |
D2 [dose2 (Gy2)] (95% BCI) |
Quadratic/linear coefficient ratio (Gy) (95% BCI) |
|
| 0.57 (0.10, 1.06) | 0.60 (0.22, 1.00) | 1.04c (0.17, 6.14) | |
| 1.26 (0.19, 2.82) | 0.28 (−0.42, 1.25) | 0.20c (−0.22, 2.97) | |
| 0.72 (−0.17, 1.78) | 0.24 (−0.41, 0.95) | 0.25c (−6.71, 7.52) | |
| 2.06 (0.60, 4.05) | 0.04 (−0.78, 0.90) | 0.01c (−0.23, 1.11) | |
| 0.05 (−0.53, 0.65) | 0.93 (0.42, 1.52) | 1.19c (−47.13, 52.38) | |
| 0.18 (−0.04, 0.55) | −0.04 (−0.23, 0.11) | −0.28c (−2.26, 2.41) | |
| Absolute rate model | |||
|
D [dose (PY × 104 Gy)] (95% BCI) |
D2 [dose2 (PY × 104 Gy2)] (95% BCI) |
Quadratic/linear coefficient ratio (Gy) (95% BCI) |
|
| 3.64 (−0.26, 7.57) | 6.33 (0.14, 9.43) | 1.60c (−10.24, 20.39) | |
| 0.61 (−0.14, 1.53) | 0.29 (−0.20, 0.93) | 0.38c (−5.98, 7.01) | |
| 1.38 (−0.77, 3.62) | 0.88 (−0.68, 2.68) | 0.35c (−12.55, 13.08) | |
| 1.68 (0.53, 3.00) | 0.00 (−0.61, 0.73) | −0.02c (−74.37, 0.68) | |
| −0.70 (−3.34, 2.07) | 5.03 (1.12, 7.42) | −3.14c (−45.63, 43.83) | |
| 1.00 (−0.73, 3.55) | −0.18 (−1.42, 1.06) | −0.31c (−3.20, 2.98) | |
| Relative rate model | |||
|
D [dose (Gy)] (95% BCI) |
D2 [dose2 (Gy2)] (95% BCI) |
Quadratic/linear coefficient ratio (Gy) (95% BCI) |
|
| 0.87 (−0.45, 2.36) | 2.87 (1.75, 3.87) | 2.45c (−42.43, 56.60) | |
| Absolute rate model | |||
|
D [dose (PY × 104 Gy)] (95% BCI) |
D2 [dose2 (PY × 104 Gy2)] (95% BCI) |
Quadratic/linear coefficient ratio (Gy) (95% BCI) |
|
| 0.48 (−0.14, 1.22) | 1.14 (0.49, 1.90) | 1.88c (−31.30, 31.16) | |
For all mortality end points a burn-in of one-half the total Monte Carlo samples was used; for most end points a total of 50,000 Monte Carlo samples were taken, with the exception of leukemia (250,000 for the relative rate model, 200,000 for the absolute rate model), lung cancer (75,000 for the relative rate model), breast cancer (150,000 for the relative rate model) and circulatory disease (100,000 for the relative rate model, 150,000 for the absolute rate model).
Adjustment for males relative to females.
Median.
TABLE 3.
Population REID [Radiation-Induced Deaths/Gy (×102)] for a Population Having the Mortality Rates of the 2017 UK Population Based on Model Coefficients Derived from Maximum Likelihood Fits Using Either (a) Unadjusted Doses, (b) Adjusted Truncated. Doses, (c) Regression Calibration adjusted Doses or (d) MCMC Mean Doses (from the Stage 1 Models)
| Mortality end point | Test dose (Gy) |
||||||
|---|---|---|---|---|---|---|---|
| Relative rate models |
Absolute rate models |
||||||
| 0.01 | 0.1 | 1 | 0.01 | 0.1 | 1 | ||
| Solid cancer | Unadjusted dose | 4.31 | 4.49 | 6.06 | 3.80 | 4.11 | 6.83 |
| Adjusted, truncated dosea | 3.70 | 4.01 | 6.68 | 2.84 | 3.33 | 7.66 | |
| Regression calibration adjusted | 3.96 | 4.19 | 6.16 | 3.22 | 3.59 | 6.90 | |
| MCMC dose means | 3.83 | 4.13 | 6.81 | 2.97 | 3.46 | 7.80 | |
| Lung cancer | Unadjusted dose | 2.81 | 2.82 | 2.93 | 1.93 | 1.98 | 2.41 |
| Adjusted, truncated dosea | 2.81 | 2.85 | 3.15 | 1.79 | 1.87 | 2.61 | |
| Regression calibration adjusted | 2.87 | 2.88 | 3.06 | 1.84 | 1.90 | 2.44 | |
| MCMC dose means | 2.89 | 2.92 | 3.23 | 1.83 | 1.92 | 2.67 | |
| Stomach cancer | Unadjusted dose | 0.10 | 0.10 | 0.11 | 0.82 | 0.84 | 1.01 |
| Adjusted, truncated dosea | 0.10 | 0.10 | 0.12 | 0.76 | 0.79 | 1.12 | |
| Regression calibration adjusted | 0.10 | 0.10 | 0.11 | 0.76 | 0.78 | 1.05 | |
| MCMC dose means | 0.10 | 0.10 | 0.12 | 0.73 | 0.77 | 1.19 | |
| Breast cancer | Unadjusted dose | 2.16 | 2.13 | 1.85 | 0.97 | 0.96 | 0.86 |
| Adjusted, truncated dosea | 2.20 | 2.17 | 1.92 | 0.99 | 0.98 | 0.89 | |
| Regression calibration adjusted | 2.20 | 2.17 | 1.91 | 0.99 | 0.98 | 0.88 | |
| MCMC dose means | 2.18 | 2.15 | 1.93 | 0.98 | 0.97 | 0.90 | |
| All solid cancer apart from lung, stomach breast | Unadjusted dose | 0.58 | 0.76 | 2.51 | −0.07 | 0.22 | 2.99 |
| Adjusted, truncated dosea | 0.07 | 0.34 | 2.90 | −0.09 | 0.20 | 3.02 | |
| Regression calibration adjusted | 0.28 | 0.49 | 2.47 | −0.10 | 0.19 | 2.99 | |
| MCMC dose means | 0.15 | 0.42 | 2.97 | −0.10 | 0.19 | 3.04 | |
| Leukemia excluding CLL | Unadjusted dose | 0.38 | 0.43 | 0.91 | 0.42 | 0.46 | 0.93 |
| Adjusted, truncated dosea | 0.24 | 0.31 | 1.03 | 0.29 | 0.36 | 1.06 | |
| Regression calibration adjusted | 0.27 | 0.33 | 0.90 | 0.33 | 0.38 | 0.93 | |
| MCMC dose means | 0.24 | 0.32 | 1.05 | 0.30 | 0.37 | 1.07 | |
| Circulatory disease | Unadjusted dose | 2.56 | 2.52 | 2.05 | 5.38 | 4.88 | 2.62 |
| Adjusted, truncated dosea | 2.66 | 2.60 | 2.12 | 5.78 | 5.20 | 2.67 | |
| Regression calibration adjusted | 2.66 | 2.61 | 2.15 | 5.45 | 4.95 | 2.72 | |
| MCMC dose means | 2.49 | 2.45 | 2.11 | 5.82 | 5.24 | 2.68 | |
Adjusted, truncated dose as supplied by RERF with the collapsed person-year table.
In general, there were higher radiation risks for females compared to males (Supplementary Table S5; https://doi.org/10.1667/RR15571.1.S1). This was true both for solid cancer and circulatory disease overall, as well as for lung, breast, stomach and the group of other solid cancers, and was the case whether relative or absolute rate projection models were employed (Supplementary Table S5). However, for leukemia this pattern was reversed (Supplementary Table S5).
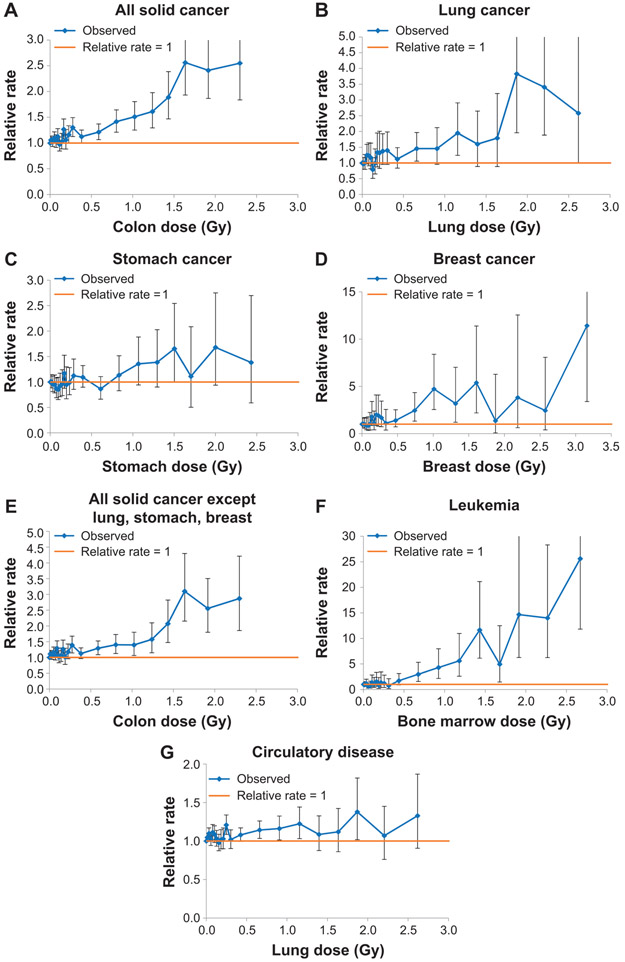
Supplementary Fig. S1 (https://doi.org/10.1667/RR15571.1.S1) suggests that there is a substantial downturn in the dose response at high doses for most cancers and circulatory disease, in particular for the two highest unadjusted colon dose groups (3–4 Gy, 4–6 Gy). For this reason, most results are presented using those survivors with unadjusted, untruncated weighted colon dose ≤3 Gy. This is comparable to the most recently published analyses in the LSS where the subjects with shielded kerma >4 Gy were treated separately, either using an indicator of high dose or excluding those subjects (26); only 9 subjects with shielded kerma >4 Gy remained in the group of survivors with unadjusted weighted colon dose ≤3 Gy. However, we present sensitivity analysis using survivors restricted to colon dose ≤2 Gy or ≤4 Gy (Table 5). Even at lower doses there is considerable evidence of dose-response curvature, generally positive for cancer end points (and in particular, all solid cancer, lung cancer, all solid cancers apart from lung, stomach and breast, and leukemia), and generally negative for circulatory disease, as indicated by the size of the quadratic dose coefficients and their BCI in all models (Table 1), and as also shown in Fig. 3. Another indication of this is that for solid cancer and leukemia, risk estimates (per unit dose) are approximately doubled when going from a test dose of 0.01 to 1.0 Gy (Tables 2 and 3). This evidence of upward curvature is not much changed if only those survivors with unadjusted colon dose ≤2 Gy are considered, but the evidence of variation in risk per unit dose with test dose is much weaker if those survivors with unadjusted colon dose ≤4 Gy are considered (Table 5). Lifetime mortality risk estimates varied somewhat between populations, with lower cancer risks in aggregate for China and Russia, but higher circulatory disease risks for Russia, particularly using the relative rate model (Table 4). There is more pronounced variation for certain cancer sites and certain types of projection models, so that breast cancer risk is markedly lower in China and Japan using a relative rate model, but the opposite is the case for stomach cancer (Table 4). There is less variation between countries using the absolute rate models for stomach cancer and breast cancer, but not for lung cancer, aggregate solid cancer risk, the remainder category of solid cancer excluding lung, stomach and breast cancer, or for circulatory disease (Table 4).
FIG. 3.
Panels A–G: Dose response (and 95% CI) over 0–3 Gy unadjusted absorbed colon dose for mortality from (panel A) solid cancer, (panel B) lung cancer, (panel C) stomach cancer, (panel D) breast cancer, (panel E) all solid cancer apart from lung, stomach, breast, (panel F) leukemia, (panel G) circulatory disease. Log-linear models using a factor dose variable are fitted by maximum likelihood with stratification by city, sex, ground distance (<3 km, >3 km from hypocenters), age at exposure, attained age, calendar period of follow-up. The CI are estimated from the profile likelihood. The mean dose used is the posterior mean from the stage 1 Bayesian MCMC models.
TABLE 4.
REID [Radiation-Induced Deaths/Gy (×102)] (95% BCI) at Test Dose of 0.1 Gy Weighted Dose for Various Populations and Risk Transfer Methods (Excess Relative Rate, Excess Absolute Rate), Both Sexesa
| Mortality end point | Country (and year) | REID/Gy (×102) (95% BCI) relative rate models |
REID/Gy (×102) (95% BCI) absolute rate models |
|---|---|---|---|
| All solid cancer | UK (2017) | 3.88 (1.17, 6.97) | 3.56 (0.54, 6.78) |
| France (2014) | 3.65 (1.11, 6.58) | 4.43 (0.67, 8.55) | |
| USA (2015) | 3.84 (1.18, 6.77) | 2.89 (0.45, 5.43) | |
| Russia (2013) | 3.01 (0.92, 5.26) | 2.61 (0.41, 4.86) | |
| Japan (2015) | 3.51 (1.04, 6.40) | 4.26 (0.65, 8.18) | |
| China (2000) | 3.25 (0.98, 5.72) | 2.72 (0.42, 5.12) | |
| Lung cancer | UK (2017) | 2.61 (0.55, 5.02) | 1.65 (−0.17, 4.03) |
| France (2014) | 1.90 (0.40, 3.68) | 2.66 (−0.26, 6.85) | |
| USA (2015) | 3.10 (0.68, 5.86) | 1.22 (−0.13, 2.84) | |
| Russia (2013) | 1.03 (0.21, 2.05) | 1.09 (−0.11, 2.51) | |
| Japan (2015) | 2.08 (0.40, 4.22) | 2.25 (−0.23, 5.51) | |
| China (2000) | 2.17 (0.47, 4.10) | 1.13 (−0.12, 2.68) | |
| Stomach cancer | UK (2017) | 0.09 (−0.01, 0.26) | 0.58 (−0.23, 1.45) |
| France (2014) | 0.10 (−0.01, 0.31) | 0.71 (−0.29, 1.88) | |
| USA (2015) | 0.07 (−0.01, 0.19) | 0.51 (−0.20, 1.27) | |
| Russia (2013) | 0.31 (−0.03, 0.84) | 0.50 (−0.20, 1.22) | |
| Japan (2015) | 0.41 (−0.04, 1.26) | 0.70 (−0.29, 1.82) | |
| China (2000) | 0.44 (−0.04, 1.17) | 0.47 (−0.19, 1.16) | |
| Breast cancer | UK (2017) | 2.01 (0.53, 4.80) | 0.90 (0.32, 1.73) |
| France (2014) | 2.31 (0.56, 5.74) | 1.17 (0.39, 2.50) | |
| USA (2015) | 1.98 (0.56, 4.33) | 0.79 (0.29, 1.47) | |
| Russia (2013) | 1.60 (0.49, 3.28) | 0.77 (0.28, 1.40) | |
| Japan (2015) | 1.03 (0.30, 2.27) | 1.14 (0.39, 2.33) | |
| China (2000) | 0.53 (0.17, 1.06) | 0.72 (0.27, 1.30) | |
| All solid cancer excluding lung, stomach, breast | UK (2017) | 0.48 (−1.17, 2.38) | −0.13 (−2.21, 2.21) |
| France (2014) | 0.46 (−1.12, 2.28) | −0.15 (−2.69, 2.74) | |
| USA (2015) | 0.46 (−1.13, 2.25) | −0.11 (−1.76, 1.76) | |
| Russia (2013) | 0.40 (−1.00, 1.96) | −0.10 (−1.58, 1.56) | |
| Japan (2015) | 0.40 (−0.99, 2.01) | −0.15 (−2.58, 2.62) | |
| China (2000) | 0.39 (−0.97, 1.90) | −0.10 (−1.69, 1.68) | |
| Leukemia excluding CLL | UK (2017) | 0.35 (−0.03, 0.78) | 0.41 (0.01, 0.86) |
| France (2014) | 0.46 (−0.04, 0.99) | 0.41 (0.01, 0.87) | |
| USA (2015) | 0.44 (−0.03, 0.97) | 0.39 (0.01, 0.82) | |
| Russia (2013) | 0.32 (−0.02, 0.87) | 0.37 (0.01, 0.78) | |
| Japan (2015) | 0.32 (−0.02, 0.70) | 0.41 (0.01, 0.87) | |
| China (2000) | 0.36 (−0.02, 1.18) | 0.39 (0.01, 0.83) | |
| Circulatory disease | UK (2017) | 2.24 (−0.17, 13.76) | 1.56 (−1.10, 7.21) |
| France (2014) | 2.65 (−0.18, 16.63) | 2.73 (−1.93, 15.45) | |
| USA (2015) | 2.84 (−0.25, 15.91) | 1.26 (−0.92, 5.71) | |
| Russia (2013) | 5.16 (−0.53, 25.29) | 1.16 (−0.86, 5.20) | |
| Japan (2015) | 2.69 (−0.19, 16.75) | 2.34 (−1.66, 12.17) | |
| China (2000) | 3.48 (−0.34, 18.29) | 1.10 (−0.80, 4.89) |
For all end points a burn-in of one half the total Monte Carlo samples was used; for most end points a total of 50,000 Monte Carlo samples was used, with the exception of leukemia (250,000 for the relative rate model, 200,000 for the absolute rate model), lung cancer (75,000 for the relative rate model), breast cancer (150,000 for the relative rate model) and circulatory disease (100,000 for the relative rate model, 150,000 for the absolute rate model).
Supplementary Table S6 (https://doi.org/10.1667/RR15571.1.S1) shows that while for most end points the absolute and relative rate models yield roughly equal DIC, for all solid cancer, lung cancer, solid cancer except lung, stomach and breast, and leukemia the relative rate models have substantially lower DIC than the absolute rate models (32,920.0 vs. 32,930.0, 9,193.0 vs. 9,198.0, 22,750.0 vs. 22,760.0, 3,246.0 vs. 3,379.0, respectively). For breast cancer the absolute rate model has lower DIC than the relative rate model (2,765.0 vs. 2,772.0). The DIC for the models with alternative adjustments to the ERR and EAR suggested by Ozasa et al. (15) were close to those of the corresponding standard model (Supplementary Table S7), and in particular for all solid cancers, the relative rate models had lower DIC than the absolute rate models (32,920.0 vs. 32,930.0).
DISCUSSION
In this paper a class of linear-quadratic excess relative and absolute rate models, allowing for modifications in rates by time since exposure and age at exposure, have been fitted to the latest Japanese atomic bomb survivor mortality data. The uncertainty distributions in the model parameters, which were taken from the posterior distribution of the Bayesian models, were used to derive uncertainties in lifetime population mortality risks for several contemporary national populations.
A notable feature of our model fits is the curvature in the dose response for all end points, in particular solid cancer, leukemia and circulatory disease (Tables 1 and 2, Fig. 3). There has been considerable interest engendered by a recently published analysis of the LSS incidence data, which showed evidence of upward curvature for solid cancer among males but not females (26). However, recent reanalysis of the incidence data taking account of heterogeneity in cancer-specific background rates found that the curvature in the male dose response, and the difference from the female dose response, was somewhat reduced (38). The estimates of the curvature parameter (the ratio of the quadratic to linear coefficients) for males obtained by excluding certain influential groups of cancer end points, or stratifying by end point, with values ranging from −0.058 Gy−1 to 0.71 Gy−1 (38), overlap with ours (for both sexes, Table 1); given the width of the Bayesian credible intervals in the final column of Table 1, the two datasets are clearly statistically consistent. Ozasa et al. (15) analyzed the solid cancer mortality data over the 0–2 Gy dose range and documented curvature over the full follow-up of 0.81 Gy−1 (95% CI: 0.08, 8.6), a value entirely consistent with those given here (Table 1). Ozasa et al. (15) also showed that the curvature increased over the follow-up. Cullings et al. (39) re-analyzed the LSS mortality data of Ozasa et al. (15) using the original DS02 dosimetry and the revised DS02R1 dosimetry that is employed here, and showed that the effect of the change in dosimetry was to increase curvature for males, from 0.05 Gy−1 for DS02 to 0.12 Gy−1 for DS02R1, but there was no change in the curvature for females, which was 0.13 Gy−1 for both DS02 and DS02R1. Over the 0–2 Gy dose range the changes in curvature were more complex, going from 3.2 Gy−1 for males and 0.50 Gy−1 for females using DS02 to 1.14 Gy−1 for males and 1.01 Gy−1 for females using DS02R1 (39). These curvature values over the 0–2 Gy dose range are entirely consistent with what we found over the 0–3 Gy dose range in the current study (Table 1). The curvature that can be seen in the higher dose groups may reflect dose errors, which could be more substantial in these groups of survivors. It may also reflect the effect of selection, since these higher doses are close to the human LD50 for acute gamma radiation doses, thought to be 3–5 Gy for healthy adults (40).
The Bayesian MCMC methodology that is employed in fitting the rate models is somewhat similar to that previously applied by Little et al. (25), and used also in the UNSCEAR 2006 report (2). As in the previous analysis (25), there are only modest differences in the central estimates of population risk derived from the Bayesian MCMC models and the regression calibration adjusted rate models, or indeed from models without adjustment for dose error (Tables 2 and 3). However, in the earlier studies (2, 25) risks were only derived for solid cancer and leukemia, as these were the only mortality end points available with the then current DS02 doses (41). Since then there has been extended follow-up, from the end of 2000 (5) to the end of 2003 (15), and a further change in the dosimetry, to DS02R1, resulting from updates to map location data and improved modeling of terrain shielding; in the group exposed to <3 Gy, the extra 3 years of follow-up results in another 803 (on top of 10,083) solid cancer deaths, another 22 (on top of 285) leukemia deaths and another 943 (on top of 18,058) circulatory disease deaths.
Another advantage of the Bayesian MCMC method in comparison with the regression-calibration method is that the adjustments for random dosimetric error take account of the information provided by cancer outcome, as a result of the conditional sampling in the second-stage sampling (as described in step g in the section “Bayesian modelling at the strata level” in the Supplementary Information (https://doi.org/10.1667/RR15571.1.S1). In particular, it should be noted that the mean doses are also updated as part of the conditional updating of doses and all other parameters. The uncertainty in the Weibull distribution parameters is taken into account in the prior parameters for the mean μij and variance that determine the distribution of the in the first-stage sampling (as described in step f in the section “Bayesian modelling at the strata level” in the Supplementary Information), although the Weibull distribution parameters are not part of the second-stage sampling.
We model seven mortality end points, which include circulatory disease as well as six malignant end points encompassing the main types of radiogenic cancer. In the earlier published studies (2, 25) a simpler Weibull model was used for the stage 1 Bayesian MCMC model fits, with constraints on the parameters ω1 = 1 and ω4 = 0; this corresponds to the standard Weibull distribution. However, the regression calibration model fitted in the earlier work (25) used the same dose model as that given here. There were substantial differences in the rate models fitted, which in the earlier work were generally of linear-quadratic-exponential form, with adjustments using log-linear functions of sex, ln[age], ln[age at exposure] and ln[time since exposure], in contrast to the linear-quadratic functions used here, with adjustments for sex, age at exposure and time since exposure; however, the form of the adjustments to the leukemia relative and absolute rate models for age at exposure and time since exposure was identical to that previously employed (25). The simpler linear-quadratic models were chosen here in part because of the difficulties in identifying parameters in the linear-quadratic-exponential model, discussed in the previous study (25), which could inflate variance unnecessarily. Fits of the linear-quadratic-exponential models were attempted, generally unsuccessfully, because of lack of convergence of the Markov chains. There were problems of convergence also in parallel maximum-likelihood-based fits of linear-quadratic-exponential models, analogous to the model fits described in Supplementary Table S4 (https://doi.org/10.1667/RR15571.1.S1). There have been many other analyses modeling dose error in the LSS, usually by means of regression calibration (18, 19, 21, 25, 42), but simulation-extrapolation (SIMEX) methods (43) have also been employed (44, 45). As would be expected, the resulting central estimates of model parameters that the Bayesian methodology gives are similar to those obtained using likelihood-based methods using regression-calibration adjustment (see Table 1 and Supplementary Table S4) and the associated central estimates of population risk implied by the two types of model are also similar (Tables 2 and 3). However, the uncertainties in population risk that the Bayesian method gives cannot be readily compared with results from regression calibration fits; while in principle uncertainties could be estimated from regression calibration fits, this is rarely done.
Statistically, the optimal models (those with the lowest DIC) are the ERR models, but for most end points there is not much to choose in goodness of fit (Supplementary Table S6; https://doi.org/10.1667/RR15571.1.S1). However, this is not simply a statistical question. As discussed by Little and Wakeford (46) there are grounds for thinking that certain cancer sites, specifically breast cancer and lung cancer, are better modeled by absolute rate models, and that other sites, specifically stomach cancer and leukemia, are better modeled by relative rate models.
Comparison of Risks with Those Previously Estimated
The solid cancer mortality risks derived here are generally similar to those others have calculated, as shown in Table 6. In general, the uncertainties derived here are comparable with those predicted in the other studies. For example, at a test dose of 1.0 Gy for a UK population, the risk of REID is 6.59% Gy−1 (95% BCI: 4.82, 8.46), whereas the risks calculated by Little et al. (25) [and in the UNSCEAR 2006 report (2)] at the same dose were 6.66% Gy−1 (90% BCI: 5.29, 8.09). The UNSCEAR 2000 report (47) calculated risks that range between 7.9% and 14.4% Gy−1; two methods were employed to transfer of risk between the Japanese atomic bomb survivors and the current UK population, i.e., relative and absolute rate transfer. As shown in Table 2, models with absolute transfer of rates produce somewhat higher risks, 7.51% (95% BCI: 5.61, 9.50) Gy−1, compared with relative rate models, 6.59% (95% BCI: 4.82, 8.46) Gy−1. This contrasts with the UNSCEAR 2000 report models, in which models with absolute transfer of rates produce risks in the range 7.9%–12.6% Gy−1, compared to the relative rate model range of 10.1%–14.4% Gy−1. The UNSCEAR 2000 report also uses two different risk projection models, one in which relative rate varies with age at exposure, the other in which it varies proportional to a power of attained age. The age-at-exposure model generally produces higher risks. These should be contrasted with the more flexible variation of relative or absolute rate employed here, allowing for variations in excess (relative or absolute) rate as a function of age at exposure and time since exposure.
TABLE 6.
Comparison of Risk Estimates for Mortality due to Solid Cancers and to Leukemia Derived in this Report with Those from Various Other Studies
| Cancer type |
Ref(s). | Population | Test dose, Dt (Gy) |
Excess cancer deaths Gy−1 (×100) |
Radiation-induced cancer deaths Gy−1 (×100) |
Years life lost Gy−1 |
Years life lost/radiation-induced cancer death |
|---|---|---|---|---|---|---|---|
| Solid | Current study | UK | 0.1 | 3.21 (0.97–5.79)a,d | 3.88 (1.17–6.97)a,d | 0.55 (0.17–0.96)a,d | 14.28 (12.63–16.15)a,d |
| UK | 1.0 | 5.44 (3.96–7.01)a,d | 6.59 (4.82–8.46)a,d | 0.96 (0.76–1.18)a,d | 14.69 (13.18–16.51)a,d | ||
| (25, 2) | UK | 0.1 | 4.53 (2.54–6.65)a,b | 5.45 (3.06–7.99)a,b | 0.76 (0.44–1.09)a,b | 14.0 (12.7–15.5)a,b | |
| UK | 1.0 | 5.52 (4.38–6.72)a,b | 6.66 (5.29–8.09)a,b | 0.95 (0.78–1.12)a,b | 14.3 (13.1–15.8)a,b | ||
| (23)c | UK | 0.001 | 10.18 (7.99–12.65)d | 12.10 (9.46–15.05)d | 1.53 (1.20–1.91)d | 12.6 (12.2–13.0)d | |
| UK | 1.0 | 8.67 (7.06–10.36)d | 10.36 (8.41–12.42)d | 1.38 (1.11–1.68)d | 13.3 (12.8–13.9)d | ||
| (34) | USA | 0.1 | 6.95 (5.45–9.34)b | – | – | – | |
| (3) | USA | 0.1 | – | 4.8 (2.4–9.8)d,e,j | – | – | |
| (66) | UK | 1.0 | – | 8.95f, 12.07g | – | – | |
| (67) | Japanese | 0.2 | – | 12.0h, 8.0i | 1.34h, 1.09i | 11.2h, 13.6i | |
| Japanese | 1.0 | – | 10.9h, 7.5i | 1.26h, 1.00i | 11.6h, 13.3i | ||
| (47) | Japanese | 1.0 | 7.6j,k, 4.9j,l | 11.2k, 7.4l | 1.05j,k, 0.79j,l | 11.1j,k, 12.8j,l | |
| USA | 1.0 | – | 12.5k,c, 9.9k,m, 9.3l,c, 6.5l,m | – | – | ||
| UK | 1.0 | – | 14.4k,c, 12.6k,m, 10.1l,c, 7.9l,m | – | – | ||
| (48) | EU/USA | 1.0 | – | 9.29 | – | – | |
| (68) | UK | 0.001 | – | 6.93–13.79n | 1.04–1.71n | 12.4–15.0n | |
| Leukemia | Current study | UK | 0.1 | 0.35 (−0.03–0.77)a,d | 0.35 (−0.03–0.78)a,d | 0.07 (0.00–0.22)a,d | 18.81 (12.50–38.13)a,d |
| UK | 1.0 | 1.13 (0.75–1.56)a,d | 1.14 (0.75–1.56)a,d | 0.21 (0.13–0.47)a,d | 18.84 (12.55–37.65)a,d | ||
| (25, 2) | UK | 0.1 | 0.50 (0.11–0.97)a,b | 0.50 (0.11–0.97)a,b | 0.12 (0.02–0.25)a,b | 22.4 (15.2–36.0)a,b | |
| UK | 1.0 | 1.02 (0.70–1.41)a,b | 1.02 (0.70–1.42)a,b | 0.23 (0.14–0.41)a,b | 22.4 (15.2–35.8)a,b | ||
| (23)c | UK | 0.001 | 0.84 (0.02–2.04)d | 0.84 (0.02–2.04)d | 0.19 (0.00–0.53)d | 22.3 (16.4–32.2)d | |
| UK | 1.0 | 1.93 (1.14–3.37)d | 1.93 (1.14–3.38)d | 0.44 (0.22–0.94)d | 22.5 (16.5–32.7)d | ||
| (34) | USA | 0.1 | 0.95 (0.56–1.96)b | – | – | – | |
| (3) | USA | 0.1 | – | 0.69 (0.22–2.20)d,e,j | – | – | |
| (66) | UK | 1.0 | – | 0.75f, 0.83g | – | – | |
| (67) | Japanese | 0.2 | – | 0.70 | 0.22 | 31 | |
| Japanese | 1.0 | – | 1.1 | 0.34 | 31 | ||
| (47) | Japanese | 1.0 | 1.0j | 0.92 | 0.3 j | 30.6j | |
| USA | 1.0 | – | 1.19 | – | – | ||
| UK | 1.0 | – | 0.95 | – | – | ||
| (48) | EU/USA | 1.0 | – | 0.91 (0.03–2.33)b | – | – |
Based on Bayesian Markov chain Monte Carlo fit (ERR linear-quadratic fit).
90% CI/BCI.
Model with multiplicative transport of rate, as described in Section IV.B.1 of Annex I of UNSCEAR (47).
95% CI/BCI.
Combined 95% subjective uncertainty interval based on weighted EAR and ERR model, taking account of the dose and dose-rate effectiveness factor (DDREF).
NIH projection model.
Multiplicative projection model.
Constant relative rate.
Constant relative rate for first 45 years after exposure, risk declining to 0 at attained age 90.
Males only.
Model with excess relative rate (ERR) declining as an exponential function of age at exposure, as described in Section IV.B.1 of Annex I of UNSCEAR (47).
Model with ERR declining as a power of attained age, as described in Section IV.B.1 of Annex I of UNSCEAR (47).
Model with additive transport of rate, as described in Section IV.B.1 of Annex I of UNSCEAR (47).
Range of risks for models with: (a) power adjustment to ERR for age and time since exposure; (b) exponential adjustment to ERR for age; (c) exponential adjustment to ERR for age at exposure, and for years since exposure for those with age at exposure <15; and 4. Exponential adjustment to ERR for age at exposure.
The leukemia risks predicted using the Bayesian MCMC method are also reasonably consistent with those derived by various other bodies, as shown in Table 6. There are generally smaller discrepancies between the risks given here for leukemia and those calculated by others than for solid cancers. In general, the risk uncertainty range in the current study is similar to that predicted by Little et al. (25) [and in the UNSCEAR 2006 report (2)], who used a similar Bayesian methodology, but based on a slightly older version of the LSS cancer mortality data. For the most part, uncertainties derived here are at least as large as those predicted by others, the only significant exception being the study of Little et al. (48). As shown in Table 6, the 95% uncertainty range in REID calculated here at the test dose of 1.0 Gy, 0.75–1.56% Gy−1, is encompassed by the larger uncertainty range derived from Little et al. (48), 0.03–2.33% Gy−1. Alone among the studies presented in Table 6, the risks in the study of Little et al. (48) are not directly based on models fitted to the Japanese atomic bomb survivors; Little et al. (48) assessed risks and uncertainties using a novel expert-elicitation methodology within a Bayesian framework that involves elicitation of uncertainties in cancer risk from a panel of experts. This approach should be contrasted with that adopted in a recent NCRP report (49), as well as in the NCI-CDC revised radio-epidemiological tables (50), in both of which a committee assessed various sources of uncertainty (e.g., sampling uncertainty, model uncertainty, dosimetric error) in cancer rate models. These were used to propagate uncertainties in population risk (49) and probability of causation (50). However, unlike Little et al. (48), the resulting uncertainty distributions are a consensus; no attempt was made to elicit uncertainties from each individual on the committee, and it could be argued that uncertainties may be underestimated in consequence.
One factor that results in variation in absolute rate model projections between countries is life expectancy, a function of the overall mortality rates. For solid cancer and circulatory disease this likely accounts for the generally low absolute rate model-based projections for Russia, and the relatively large risks for France (Table 4). For the relative rate models this consideration also applies, but for these end points there is an offsetting effect of the very much higher baseline end point-specific mortality rates in Russia compared to France.
Other Considerations
One of the consistent features of mortality risks that we observed, as have many others (2), is the generally higher radiation risk for females compared to males (Supplementary Table S5; https://doi.org/10.1667/RR15571.1.S1). This was true both for solid cancer and circulatory disease overall, as well as other individual solid cancer sites, and was the case whether relative or absolute rate projection models were employed (Supplementary Table S5). Only for leukemia was this not the case (Supplementary Table S5).
In principle, the modeling conducted in this work could be extended to take account of model uncertainties, and in particular other sorts of errors in the DS02R1 dosimetry from those considered here. It might also be possible to take account of uncertainties in the magnitude of the dose errors, but this would require access to individual data; the two-step model formulation adopted here (see Methods), because of the grouped nature of the publicly available data, makes this difficult or impossible. It might also be possible to construct more sophisticated models that account for the likely differential magnitude of the errors for survivors with different types of shielding. It is very likely that the survivor dose errors are not purely classical in form. For example, there will certainly be a Berkson-type error component because of the rounding of reported map coordinates and the rather limited number of canonical shielding situations considered in the dosimetry system. Pierce and Kellerer (51) have discussed how such a mixed Berkson-classical error model could be fitted, but implementing it would be difficult or impossible given the grouped data we have access to. The fact that survivors will in general contribute to more than one cell in the person-year table will induce some correlations between the posterior doses in these cells. This would be expected to result in a slight widening of confidence intervals (52). However, simulations performed elsewhere (45) suggest that the effect of these induced correlations on regressions using the person-year table are likely to be negligible. The two-step approach that is used here is adopted in part because of the substantial reduction in computational burden in comparison with analysis based on individual doses. The reason for this is that in the current approach we are only making inference on unknown doses in a few thousand cells in the person-year table, whereas we would be doing so for approximately 80,000 cells for an individual-based analysis.
There are additional uncertainties in the atomic-bomb survivor doses used here, not reflected in what we present. It is likely that the RBE for cancer of the neutron component of dose will slightly decrease with increasing distance from the hypocenters in Hiroshima and Nagasaki, because of the hardening of the neutron energy spectrum with increasing distance in both cities (53). However, even when neutron absorbed doses are weighted by the RBE of 10 used here, they comprise only about 9% and 3% of the total weighted absorbed dose in Hiroshima and Nagasaki approximately 1,000 m from the respective hypocenters, a fraction that decreases with increasing distance from the hypocenters (5). Possibly of greater significance is the hardening of the gamma energy spectrum with distance from the two hypocenters (54), which is likely to induce some decrease in the biological effectiveness of the photon component of dose (55).
One could envisage construction of a model in which information was shared among cancer sites, so that, for example, some of the rate parameters (e.g., main slope parameter, parameter for age-at-exposure modifier) could be assumed to come from the same prior distribution for a subset of specific cancer sites. Additionally, one might assume an informative prior distribution for the site-specific ratios of quadratic to linear components [i.e., a prior distribution for site-specific low dose extrapolation factor (LDEF)]. However, this would take us beyond the scope of the current study.
In general, the marked estimates of dose-response curvature for most malignant end points (Tables 1 and 2) suggest that there is a substantial ameliorating effect of low-dose compared to high-dose exposure for these end points, implying that the LDEF is greater than 1. There is much (quite old) experimental data yielding information on LDEF, and the somewhat related idea of dose-rate extrapolation factor (DREF), the factor by which one divides risk at high dose rate to obtain risk at low dose rate, accounting for the ameliorating effect of low dose rate (56). Our findings are consistent with this older body of data (56), although moderately inconsistent with results of a recently published re-analysis of the JANUS experimental animal data, which suggested only modest LDEF, of approximately 1.2 for all solid tumors and generally no more than 2 (57). However, the LDEF we find for most malignant end points is consistent with the DDREF of 2 adopted by ICRP (1). The ICRP DDREF (1) also incorporates adjustment for DREF, for which the calculations in this work provide no information. The JANUS re-analysis suggests a DREF, independent of LDEF, in the range of 1.2–2.3 (57). Set against that, recent analyses of nuclear workers exposed at predominantly low dose rate do not suggest radiation risks markedly different from those in comparable (age/sex matched) subsets of the LSS (58, 59). While this may suggest a DREF (and indeed DDREF) of close to 1, this inference may be faulty. The radiation received by nuclear workers is mostly in the 100 keV–3 MeV range, and therefore likely to be more effective (per unit dose) by approximately a factor of 2 than the radiation received by the atomic bomb survivors, with energy predominantly in the 2–5 MeV range (60), so that the risks in the nuclear workers and the LSS are still consistent with a DDREF of 2 (61). Furthermore, uncertainties in occupational doses and their effect on the dose response should be considered (62). The JANUS data suggest an LDEF for circulatory disease of about 1, with substantial uncertainties (57). A meta-analysis of epidemiologic circulatory disease data suggests 2.1-2.8 fold higher risk per unit dose associated with low or fractionated doses (9). Both these findings are consistent with our observations for this endpoint.
The Bayesian MCMC methodology that has been employed in model fitting here and in previously reported analyses of the Japanese incidence and mortality data (22, 23, 25) is unusual, at least as applied to the LSS dataset, in that it explicitly takes account of random errors such as those in the DS02R1 dose estimates, as well as uncertainties in the model parameters determining the shape of the dose response and the variation of rate as a function of time since exposure and age at exposure. As previously discussed elsewhere (22, 23, 25), despite the novelty of this technique, the results that it gives are similar to those obtained by regression-calibration methods used by other researchers (18, 19, 21, 25, 42), as shown in Table 6. The reasons for this are not surprising. When vague priors are assumed, the difference between the Bayesian MCMC approach and the first-order regression-calibration approach is between using the exact likelihood and using the regression-calibration approximation, obtained by substituting in the likelihood for the true dose D the conditional expectation, E[D∣d], of the true dose given the nominal dose d. It is well known that when dosimetric errors are not too large, as is the case here, the first-order regression-calibration parameter estimates are a good approximation to the full likelihood-based estimates (11, 63, 64).
A theoretical advantage of the Bayesian approach is its lack of reliance on the asymptotic normality assumptions that are fundamental to much frequentist inference (65). This will matter most when small datasets are being analyzed. However, when, as here, the numbers of events (deaths) are mostly large, asymptotic normality of frequentist statistics will be valid, so that differences between a Bayesian and frequentist approach should not be large.
However, there is an important practical advantage arising from use of the Bayesian MCMC approach to calculate population risks. In this work, assessment is made of uncertainties in a non-linear population risk function REID(s,a,Dt) = REID(s,a,Dt,θ) (among others) of the model parameters, θ. The Bayesian MCMC approach produces an arbitrarily large collection of realizations (θj)j sampled from the posterior parameter distribution. The uncertainty in the function REID(s,a,Dt,θ) can be directly evaluated by describing the distribution of values [REID(s,a,Dt,θj)]j.
CONCLUSIONS
We have fitted linear-quadratic ERR and EAR models to the latest Japanese atomic bomb survivor mortality data using classical (regression-calibration) and Bayesian methods. In general, we find quite substantial dose-response curvature for most end points, in particular solid cancer, leukemia and circulatory disease, although the direction of curvature is positive (upward curving) for the malignant disease end points, and negative (downward curving) for circulatory disease. This suggests that the LDEF for cancer may be approximately 2, and lower than 1 for circulatory disease, although with substantial uncertainties (Table 2). Risks that we derive, for a variety of contemporary populations (UK, USA, France, Russia, Japan, China) are generally similar to those obtained by others, and there is little difference between the classical and Bayesian central estimates. Risk estimates varied somewhat between populations, with lower cancer risks in aggregate for China and Russia, but higher circulatory disease risks for Russia using the relative rate model, although not using the absolute rate model. There was more pronounced variation for certain cancer sites and certain types of projection models, so that breast cancer risk was markedly lower in China and Japan using a relative rate model, while the opposite was the case for stomach cancer. There was less variation between countries using the absolute rate models for stomach cancer and breast cancer, but this was not the case for other types of solid cancer, or for circulatory disease. Apart from leukemia, risks were generally higher for females than for males, irrespective of the rate model used.
Supplementary Material
Table S1. Models used for baseline rates.
Table S2. Markov Chain Monte Carlo fits of generalized Weibull density function in true dose D: f(D) = exp[ω1]/(1 + exp[ω1]) exp[−ω2Dω3 – ω4D] (ω2ω3Dω3 – 1 + ω4) + 100 1D < 0.01/(1 + exp[ω1]).
Table S3. Maximum likelihood fits of generalized Weibull density function in true dose D: f(D) = exp[ω1]/(1 + exp[ω1]) exp[−ω2Dω3 – ω4D] (ω2ω3Dω3 – 1 + ω4) + 100 1D < 0.01/(1 + exp[ω1]).
Table S4. Model coefficients (and Wald-based 95% CI) derived from maximum likelihood fits using either: (a) unadjusted doses, (b) adjusted truncated doses, (c) regression calibration adjusted doses, or (d) MCMC mean doses (from the stage 1 models). Model fits are restricted to survivors with unadjusted, untruncated weighted colon dose ≤3 Gy.
Table S5. Population risks (using 2017 mortality rates for England and Wales) predicted by optimal excess relative and excess absolute rate models, unadjusted weighted colon dose ≤3 Gy.
Table S6. Deviance information criteria for various models.
Table S7. Deviance information criteria for fits of standard models and comparable models with adjustments to the excess relative rate or excess absolute rate employed by Ozasa et al. (15).
Table S8. Akaike information criteria (AIC) for fits of models via maximum likelihood, and comparable models with adjustments to the excess relative rate or excess absolute rate employed by Ozasa et al. (15).
Table S9. Population risks (radiation exposure-induced deaths/Gy (×102) and 95% BCI) (using 2017 mortality rates for England and Wales) predicted by optimal excess relative and excess absolute rate models using the standard form of adjustments, and those of Ozasa et al. (15), unadjusted weighted colon dose ≤3 Gy.
Table S10. Population REID (radiation exposure-induced deaths/Gy (×102)) for a population having the mortality rates of the 2017 UK population based on model coefficients derived from maximum likelihood fits using MCMC mean doses (from the stage 1 models), with risks either calculated singly (by end point) or jointly (across all end points), using excess relative rate and excess absolute rate models.
Fig. S1. Part 1: Dose response (+95% CI) over 0–6 Gy unadjusted weighted colon dose for: solid cancer; lung cancer; stomach cancer; and breast cancer. Part 2: Dose response over 0–6 Gy unadjusted weighted colon dose for: all solid cancer apart from lung, stomach breast cancers; leukemia; all circulatory disease.
Fig. S2. Untruncated unadjusted weighted colon and bone marrow dose vs. posterior mean of Markov chain Monte Carlo weighted colon and bone marrow doses from first stage sampling, by city.
ACKNOWLEDGMENTS
We are grateful for the detailed and helpful comments of Dr. Werner Rühm, the four referees and the associate editor. The Intramural Research Program of the National Institutes of Health, the National Cancer Institute, Division of Cancer Epidemiology and Genetics supported the work of MPL, who was also supported by the International Commission on Radiological Protection Task Group 91, of which he was a member. This work makes use of data obtained from the Radiation Effects Research Foundation (RERF), Hiroshima and Nagasaki, Japan. RERF is a public interest foundation funded by the Japanese Ministry of Health, Labour and Welfare (MHLW) and the U.S. Department of Energy (DOE). The research was also funded in part through DOE award no. DE-HS0000031 to the National Academy of Sciences. This work was supported by RERF Research Protocol RP-S1-17. The views of the authors do not necessarily reflect those of the two governments.
Footnotes
SUPPLEMENTARY INFORMATION
Detailed statistical methods and supplementary results.
REFERENCES
- 1.International Commission on Radiological Protection (ICRP). The 2007 Recommendations of the International Commission on Radiological Protection. ICRP publication 103. Ann ICRP; 2007; 37(2–4):1–332. [DOI] [PubMed] [Google Scholar]
- 2.UNSCEAR 2006 Report. Annex A. Epidemiological studies of radiation and cancer. Report No. 978-92-1-142263-4. New York: United Nations; 2008. [Google Scholar]
- 3.Committee to Assess Health Risks from Exposure to Low Levels of Ionizing Radiation NRC Health risks from exposure to low levels of ionizing radiation: BEIR VII - Phase 2. pp. 1–406. Washington, DC: National Academy Press; 2006. [PubMed] [Google Scholar]
- 4.Preston DL, Ron E, Tokuoka S, Funamoto S, Nishi N, Soda M, et al. Solid cancer incidence in atomic bomb survivors: 1958–1998. Radiat Res 2007; 168:1–64. [DOI] [PubMed] [Google Scholar]
- 5.Preston DL, Pierce DA, Shimizu Y, Cullings HM, Fujita S, Funamoto S, et al. Effect of recent changes in atomic bomb survivor dosimetry on cancer mortality risk estimates. Radiat Res 2004; 162:377–89. [DOI] [PubMed] [Google Scholar]
- 6.Little MP, Tawn EJ, Tzoulaki I, Wakeford R, Hildebrandt G, Paris F, et al. A systematic review of epidemiological associations between low and moderate doses of ionizing radiation and late cardiovascular effects, and their possible mechanisms. Radiat Res 2008; 169:99–109. [DOI] [PubMed] [Google Scholar]
- 7.McGale P, Darby SC. Low doses of ionizing radiation and circulatory diseases: a systematic review of the published epidemiological evidence. Radiat Res 2005; 163:247–57. [DOI] [PubMed] [Google Scholar]
- 8.Little MP, Azizova TV, Bazyka D, Bouffler SD, Cardis E, Chekin S, et al. Systematic review and meta-analysis of circulatory disease from exposure to low-level ionizing radiation and estimates of potential population mortality risks. Environ Health Perspect 2012; 120:1503–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Little MP, Radiation and circulatory disease. Mutat Res Revw 2016; 770:299–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gillies M, Richardson DB, Cardis E, Daniels RD, O’Hagan JA, Haylock R, et al. Mortality from circulatory diseases and other non-cancer outcomes among nuclear workers in France, the United Kingdom and the United States (INWORKS). Radiat Res 2017; 188:276–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu CM. Measurement error in nonlinear models A modern perspective. pp. 1–526. Boca Raton, FL: Chapman and Hall/CRC; 2006. [Google Scholar]
- 12.Clayton D The analysis of event history data - a review of progress and outstanding problems. Statist Med 1988; 7:819–41. [DOI] [PubMed] [Google Scholar]
- 13.Richardson S, Gilks WR. Conditional independence models for epidemiological studies with covariate measurement error. Statist Med 1993; 12:1703–22. [DOI] [PubMed] [Google Scholar]
- 14.Richardson S, Gilks WR. A Bayesian approach to measurement error problems in epidemiology using conditional independence models. Am J Epidemiol 1993; 138:430–42. [DOI] [PubMed] [Google Scholar]
- 15.Ozasa K, Shimizu Y, Suyama A, Kasagi F, Soda M, Grant EJ, et al. Studies of the mortality of atomic bomb survivors, report 14, 1950–2003: an overview of cancer and noncancer diseases. Radiat Res 2012; 177:229–43. [DOI] [PubMed] [Google Scholar]
- 16.Preston DL, Kusumi S, Tomonaga M, Izumi S, Ron E, Kuramoto A, et al. Cancer incidence in atomic bomb survivors. Part III. Leukemia, lymphoma and multiple myeloma, 1950–1987. Radiat Res 1994; 137:S68–S97. [PubMed] [Google Scholar]
- 17.Thompson DE, Mabuchi K, Ron E, Soda M, Tokunaga M, Ochikubo S, et al. , Cancer incidence in atomic bomb survivors. Part II: Solid tumors, 1958–1987. Radiat Res 1994; 137:S17–S67. [PubMed] [Google Scholar]
- 18.Pierce DA, Stram DO, Vaeth M. Allowing for random errors in radiation dose estimates for the atomic bomb survivor data. Radiat Res 1990; 123:275–84. [PubMed] [Google Scholar]
- 19.Little MP, Muirhead CR. Evidence for curvilinearity in the cancer incidence dose-response in the Japanese atomic bomb survivors. Int J Radiat Biol 1996; 70:83–94. [DOI] [PubMed] [Google Scholar]
- 20.Little MP, Muirhead CR. Curvilinearity in the dose-response curve for cancer in Japanese atomic bomb survivors. Environ Health Perspect 1997; 105:S1505–09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Little MP, Muirhead CR. Curvature in the cancer mortality dose response in Japanese atomic bomb survivors: absence of evidence of threshold. Int J Radiat Biol 1998; 74:471–80. [DOI] [PubMed] [Google Scholar]
- 22.Bennett J, Little MP, Richardson S. Flexible dose-response models for Japanese atomic bomb survivor data: Bayesian estimation and prediction of cancer risk. Radiat Environ Biophys 2004; 43:233–45. [DOI] [PubMed] [Google Scholar]
- 23.Little MP, Deltour I, Richardson S. Projection of cancer risks from the Japanese atomic bomb survivors to the England and Wales population taking into account uncertainty in risk parameters. Radiat Environ Biophys 2000; 39:241–52. [DOI] [PubMed] [Google Scholar]
- 24.Little MP, Kleinerman RA, Stovall M, Smith SA, Mabuchi K. Analysis of dose response for circulatory disease after radiotherapy for benign disease. Int J Radiat Oncol Biol Phys 2012; 84:1101–09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Little MP, Hoel DG, Molitor J, Boice JD Jr., Wakeford R, Muirhead CR. New models for evaluation of radiation-induced lifetime cancer risk and its uncertainty employed in the UNSCEAR 2006 report. Radiat Res 2008; 169:660–76. [DOI] [PubMed] [Google Scholar]
- 26.Grant EJ, Brenner A, Sugiyama H, Sakata R, Sadakane A, Utada M, et al. Solid cancer incidence among the Life Span Study of Atomic Bomb Survivors: 1958–2009. Radiat Res 2017; 187:513–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Little MP. Absence of evidence for differences in the dose-response for cancer and non-cancer endpoints by acute injury status in the Japanese atomic-bomb survivors. Int J Radiat Biol 2002; 78:1001–10. [DOI] [PubMed] [Google Scholar]
- 28.Little MP. Threshold and other departures from linear-quadratic curvature in the non-cancer mortality dose-response curve in the Japanese atomic bomb survivors. Radiat Environ Biophys 2004; 43:67–75. [DOI] [PubMed] [Google Scholar]
- 29.McCullagh P, Nelder JA. Generalized linear models. 2nd edition. Boca Raton, FL: Chapman and Hall/CRC; 1989. [Google Scholar]
- 30.Lunn D, Spiegelhalter D, Thomas A, Best N. OpenBUGS version 3.2.3. 2016. (http://www.openbugs.net/w/Downloads) [Google Scholar]
- 31.Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. J Royal Statist Soc Series B - Statistical Methodology 2002; 64:583–639. [Google Scholar]
- 32.Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statist Science 1992; 7:457–72. [Google Scholar]
- 33.Brooks SP, Gelman A. General methods for monitoring convergence of iterative simulations. J Computat Graph Statist 1998; 7:434–55. [Google Scholar]
- 34.Committee on the Biological Effects of Ionizing Radiations. Health effects of exposure to low levels of ionizing radiation BEIR V. pp. 1–421. Washington, DC: National Academy Press; 1990. [Google Scholar]
- 35.Mortality statistics - underlying cause, sex and age. London, UK: Office for National Statistics; 2019. (https://bit.ly/2TXqBAs). [Google Scholar]
- 36.WHO Health statistics and information systems. World Health Organization (WHO); 2019. (https://bit.ly/36Sk5jV). [Google Scholar]
- 37.Zhang W, Laurier D, Cléro E, Hamada N, Preston D, Vaillant L, et al. Sensitivity analysis of parameters and methodological choices used in calculation of radiation detriment for solid cancer. Int J Radiat Biol 2020; 96:596–605. [DOI] [PubMed] [Google Scholar]
- 38.Cologne J, Kim J, Sugiyama H, French B, Cullings HM, Preston DL, et al. Effect of heterogeneity in background incidence on inference about the solid-cancer radiation dose response in atomic bomb survivors. Radiat Res 2019; 192:388–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cullings HM, Grant EJ, Egbert SD, Watanabe T, Oda T, Nakamura F, et al. DS02R1: improvements to atomic bomb survivors’ input data and implementation of Dosimetry System 2002 (DS02) and resulting changes in estimated doses. Health Phys 2017; 112:56–97. [DOI] [PubMed] [Google Scholar]
- 40.Mole RH. The LD50 for uniform low LET irradiation of man. Br J Radiol 1984; 57:355–69. [DOI] [PubMed] [Google Scholar]
- 41.Reassessment of the atomic bomb radiation dosimetry for Hiroshima and Nagasaki. Dosimetry System 2002 Report of the Joint US-Japan Working Group. Report No. B001J1TD3Y. pp. 1–998. Hiroshima, Japan: Radiation Effects Research Foundation (RERF); 2005. [Google Scholar]
- 42.Pierce DA, Stram DO, Vaeth M, Schafer DW. The errors-in-variables problem: considerations provided by radiation dose-response analyses of the A-bomb survivor data. J Am Statist Assoc 1992; 87:351–9. [Google Scholar]
- 43.Cook JR, Stefanski LA. Simulation-extrapolation estimation in parametric measurement error models. J Am Statist Assoc 1994; 89:1314–28. [Google Scholar]
- 44.Allodji RS, Schwartz B, Diallo I, Agbovon C, Laurier D, de Vathaire F. Simulation-extrapolation method to address errors in atomic bomb survivor dosimetry on solid cancer and leukaemia mortality risk estimates, 1950–2003. Radiat Environ Biophys 2015; 54:273–83. [DOI] [PubMed] [Google Scholar]
- 45.Misumi M, Furukawa K, Cologne JB, Cullings HM. Simulation-extrapolation for bias correction with exposure uncertainty in radiation risk analysis utilizing grouped data. J R Stat Soc Ser C Appl Stat 2018; 67:275–89. [Google Scholar]
- 46.Little MP, Wakeford R. How is the risk of radiation-induced cancer influenced by background risk factors? Invited commentary on “A method for determining weights for excess relative risk and excess absolute risk when applied in the calculation of lifetime risk of cancer from radiation exposure” by Walsh and Schneider (2012). Radiat Environ Biophys 2013; 52:147–50. [DOI] [PubMed] [Google Scholar]
- 47.Sources and effects of ionizing radiation. UNSCEAR 2000 report to the General Assembly, with scientific annexes. Volume II: Effects. Report No. E.oo.IX.4. pp. 1–566. New York: United Nations; 2000. [Google Scholar]
- 48.Little MP, Muirhead CR, Goossens LHJ, Kraan BCP, Cooke RM, Harper FT, et al. Probabilistic accident consequence uncertainty analysis. Late health effects uncertainty assessment. Main report. pp. 1–62. Brussels: European Commission; 1997. [Google Scholar]
- 49.Uncertainties in fatal cancer risk estimates used in radiation protection. NCRP Report No. 126. pp. 1–112. Bethesda, MD: National Council on Radiation Protection and Measurements; 1997. [Google Scholar]
- 50.Land C, Gilbert E, Smith JM, Hoffman FO, Apostoaei I, Thomas B, et al. Report of the NCI-CDC Working Group to revise the 1985 NIH Radioepidemiological Tables. pp. 1–118. Washington, DC: U.S. Department of Health and Human Services; 2003. [Google Scholar]
- 51.Pierce DA, Kellerer AM. Adjusting for covariate errors with nonparametric assessment of the true covariate distribution. Biometrika 2004; 91:863–76. [Google Scholar]
- 52.Zhang Z, Preston DL, Sokolnikov M, Napier BA, Degteva M, Moroz B, et al. Correction of confidence intervals in excess relative risk models using Monte Carlo dosimetry systems with shared errors. PloS One 2017; 12(4):e0174641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Rühm W, Walsh L. Current risk estimates based on the A-bomb survivors data - a discussion in terms of the ICRP recommendations on the neutron weighting factor. Radiat Prot Dosimetry 2007; 126:423–31. [DOI] [PubMed] [Google Scholar]
- 54.Egbert SD, Kerr GD, Cullings HM. DS02 fluence spectra for neutrons and gamma rays at Hiroshima and Nagasaki with fluence-to-kerma coefficients and transmission factors for sample measurements. Radiat Environ Biophys 2007; 46:311–25. [DOI] [PubMed] [Google Scholar]
- 55.Evaluation of the relative effectiveness of low-energy photons and electrons in inducing cancer in humans. NCRP Report No. 181. pp. 1–103. Bethesda, MD: National Council on Radiation Protection and Measurements; 2018. [Google Scholar]
- 56.Rühm W, Woloschak GE, Shore RE, Azizova TV, Grosche B, Niwa O, et al. Dose and dose-rate effects of ionizing radiation: a discussion in the light of radiological protection. Radiat Environ Biophys 2015; 54:379–401. [DOI] [PubMed] [Google Scholar]
- 57.Tran V, Little MP. Dose and dose rate extrapolation factors for malignant and non-malignant health endpoints after exposure to gamma and neutron radiation. Radiat Environ Biophys 2017; 56:299–328. [DOI] [PubMed] [Google Scholar]
- 58.Richardson DB, Cardis E, Daniels RD, Gillies M, O’Hagan JA, Hamra GB, et al. Risk of cancer from occupational exposure to ionising radiation: retrospective cohort study of workers in France, the United Kingdom, and the United States (INWORKS). BMJ 2015; 351:h5359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Leuraud K, Richardson DB, Cardis E, Daniels RD, Gillies M, O’Hagan JA, et al. Ionising radiation and risk of death from leukaemia and lymphoma in radiation-monitored workers (IN-WORKS): an international cohort study. Lancet Haematol 2015; 2:e276–e81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.The relative biological effectiveness of radiations of different quality. Report No. 104. pp. 1–218. Bethesda, MD: National Council on Radiation Protection and Measurements; 1990. [Google Scholar]
- 61.Little MP. Ionising radiation in the workplace. BMJ 2015; 351:h5405. [DOI] [PubMed] [Google Scholar]
- 62.Wakeford R The growing importance of radiation worker studies. Br J Cancer 2018; 119:527–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rosner B, Willett WC, Spiegelman D. Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error. Statist Med 1989; 8:1051–69. [DOI] [PubMed] [Google Scholar]
- 64.Kuha J Corrections for exposure measurement error in logistic regression models with an application to nutritional data. Statist Med 1994; 13:1135–48. [DOI] [PubMed] [Google Scholar]
- 65.Schervish MJ. Theory of statistics. pp. 1–218. New York, NY: Springer Verlag; 1995. [Google Scholar]
- 66.International Commission on Radiological Protection (ICRP). 1990 Recommendations of the International Commission on Radiological Protection. Ann ICRP; 1991; 21(1–3):1–201. [PubMed] [Google Scholar]
- 67.Sources and effects of ionizing radiation. UNSCEAR 1994 report to the General Assembly, with scientific annexes. Report no. E.94.IX.11. pp. 1–272. New York: United Nations; 1994. [Google Scholar]
- 68.Little MP, de Vathaire F, Charles MW, Hawkins MM, Muirhead CR. Variations with time and age in the relative risks of solid cancer incidence after radiation exposure. J Radiol Prot 1997; 17:159–77. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1. Models used for baseline rates.
Table S2. Markov Chain Monte Carlo fits of generalized Weibull density function in true dose D: f(D) = exp[ω1]/(1 + exp[ω1]) exp[−ω2Dω3 – ω4D] (ω2ω3Dω3 – 1 + ω4) + 100 1D < 0.01/(1 + exp[ω1]).
Table S3. Maximum likelihood fits of generalized Weibull density function in true dose D: f(D) = exp[ω1]/(1 + exp[ω1]) exp[−ω2Dω3 – ω4D] (ω2ω3Dω3 – 1 + ω4) + 100 1D < 0.01/(1 + exp[ω1]).
Table S4. Model coefficients (and Wald-based 95% CI) derived from maximum likelihood fits using either: (a) unadjusted doses, (b) adjusted truncated doses, (c) regression calibration adjusted doses, or (d) MCMC mean doses (from the stage 1 models). Model fits are restricted to survivors with unadjusted, untruncated weighted colon dose ≤3 Gy.
Table S5. Population risks (using 2017 mortality rates for England and Wales) predicted by optimal excess relative and excess absolute rate models, unadjusted weighted colon dose ≤3 Gy.
Table S6. Deviance information criteria for various models.
Table S7. Deviance information criteria for fits of standard models and comparable models with adjustments to the excess relative rate or excess absolute rate employed by Ozasa et al. (15).
Table S8. Akaike information criteria (AIC) for fits of models via maximum likelihood, and comparable models with adjustments to the excess relative rate or excess absolute rate employed by Ozasa et al. (15).
Table S9. Population risks (radiation exposure-induced deaths/Gy (×102) and 95% BCI) (using 2017 mortality rates for England and Wales) predicted by optimal excess relative and excess absolute rate models using the standard form of adjustments, and those of Ozasa et al. (15), unadjusted weighted colon dose ≤3 Gy.
Table S10. Population REID (radiation exposure-induced deaths/Gy (×102)) for a population having the mortality rates of the 2017 UK population based on model coefficients derived from maximum likelihood fits using MCMC mean doses (from the stage 1 models), with risks either calculated singly (by end point) or jointly (across all end points), using excess relative rate and excess absolute rate models.
Fig. S1. Part 1: Dose response (+95% CI) over 0–6 Gy unadjusted weighted colon dose for: solid cancer; lung cancer; stomach cancer; and breast cancer. Part 2: Dose response over 0–6 Gy unadjusted weighted colon dose for: all solid cancer apart from lung, stomach breast cancers; leukemia; all circulatory disease.
Fig. S2. Untruncated unadjusted weighted colon and bone marrow dose vs. posterior mean of Markov chain Monte Carlo weighted colon and bone marrow doses from first stage sampling, by city.