Systems biology approach suggests new miRNAs as phenotypic stability factors in the epithelial–mesenchymal transition

Abstract

The epithelial–mesenchymal transition (EMT) is a cellular programme on which epithelial cells undergo a phenotypic transition to mesenchymal ones acquiring metastatic properties such as mobility and invasion. TGF-β signalling can promote the EMT process. However, the dynamics of the concentration response of TGF-β-induced EMT is not well explained. In this work, we propose a logical model of TGF-β dose dependence of EMT in MCF10A breast cells. The model outcomes agree with experimentally observed phenotypes for the wild-type and perturbed/mutated cases. As important findings of the model, it predicts the coexistence of more than one hybrid state and that the circuit between TWIST1 and miR-129 is involved in their stabilization. Thus, miR-129 should be considered as a phenotypic stability factor. The circuit TWIST1/miR-129 associates with ZEB1-mediated circuits involving miRNAs 200, 1199, 340, and the protein GRHL2 to stabilize the hybrid state. Additionally, we found a possible new autocrine mechanism composed of the circuit involving TGF-β, miR-200, and SNAIL1 that contributes to the stabilization of the mesenchymal state. Therefore, our work can extend our comprehension of TGF-β-induced EMT in MCF10A cells to potentially improve the strategies for breast cancer treatment.

1. Introduction

The epithelial–mesenchymal transition (EMT) is a cellular programme in which epithelial cells transition to a mesenchymal phenotype occurring in various pathological processes, mainly cancer progression [1]. The loss of adhesive properties and the gain of migratory abilities are the main EMT features characterizing phenotypic changes from epithelial (E) to mesenchymal (M). Additionally, some studies demonstrated the stabilization of a hybrid (H) state having both E and M features [2–4]. Cells in this state present adhesive and invasive abilities, which confers high-grade malignancy on individual carcinoma cells [4]. This phenomenon directly depends on the signals received by cells in the tissue environment affecting the intracellular gene circuitry dynamics.

The malignant progression is dependent on activation of the EMT and the development of metastasis [5]. This mechanism is a multistep process in which the EMT is important for the migration of cancer cells until the metastatic colonization in distant organs [6]. The initiation of EMT is triggered by the tumour microenvironment. The secretion of various cytokines and chemokines by stromal cells can act as initiation factors inducing EMT in epithelial cancer cells [7]. Transforming growth factor-β (TGF-β) is a commonly secreted molecule in the tumour microenvironment and its corresponding pathway has been extensively studied in the EMT context. By activation of the corresponding surface receptors of the cell membrane, TGF-β triggers the induction of the transcription factors (TFs), the Snail family transcriptional repressor 1 (SNAIL1) and the Zinc finger E-box binding homeobox 1 (ZEB1) which, in turn, repress an important feature of the epithelial phenotype, the calcium-dependent cell–cell adhesion glycoprotein cadherin-1 encoded by the CDH1 gene [8]. Thus, activation of SNAIL1 and ZEB1 is fundamental for TGF-β-induced EMT.

The well-known controllers of SNAIL1 and ZEB1 expressions are the family of microRNAs 34 (miR-34) and 200 (miR-200), respectively. Their interactive correlation occurs via reciprocal inhibitions forming double-negative feedback loops (or circuits) between SNAIL1 and miR-34 [9] and ZEB1 and miR-200 [10]. The activation of these circuits is reported as essential for EMT [8]. With the advances in EMT research, other molecules were found to regulate ZEB1 expression affecting the EMT programme. For instance, two new microRNAs, miR-340 and miR-1199, were shown to form double negative circuits with ZEB1 [11,12]. Regarding SNAIL1 regulators, the Twist family bHLH transcription factor 1 (TWIST1), another potent EMT inducer, was reported to form a positive feedback circuit with SNAIL1 during TGFB signalling [13]. The study showed that this positive circuit can downregulate the miR-129-5p forming a double-negative feedback circuit with TWIST1. In addition, TWIST1 is also a negative regulator of CDH1, favouring the EMT process. Understanding the functional role of the negative regulators of SNAIL1 and ZEB1 during EMT can help the development of new strategies to target these regulators in order to control EMT.

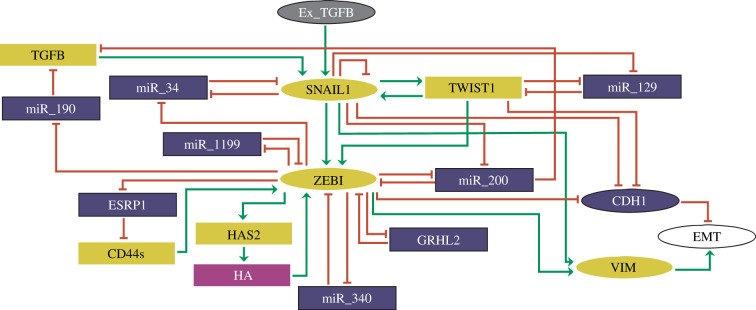
Recently, we published a model about the dynamics of the regulatory cores of SNAIL1 and ZEB1 during TGF-β-induced EMT using a logical computational approach [14] based on the experimental work by Zhang et al. [8]. The logical method is recognized as a valuable tool to study biological regulatory processes [15–24]. Our analysis indicated testable predictions that could help improve strategies for breast cancer treatment. In our approach, we focused only on the coexistence region of the E, H and M states, which correspond to a specific dose of TGF-β used in the work by Zhang et al. [8]. However, different concentrations of TGF-β can lead to distinct dynamics in the EMT process [8]. So, to study a more realistic dose-dependent dynamics of EMT, here we present a more general model (figure 1) contemplating different levels of activity of TGF-β-induced EMT and also the additional molecules, TWIST1 and miR-129, that play important roles on the regulatory core of EMT.

Figure 1.

Proposed regulatory network of TGF-β-driven EMT. Elliptic and rectangular nodes represent multi-valued and Boolean components, respectively. Nodes in grey and white denote the input (Ex_TGFB) and the output (EMT) of the network, respectively. Epithelial markers in the network are represented by blue, while mesenchymal markers are in yellow. Green arrows represent activatory interactions and hammer-head arcs denote inhibitory ones. The rectangular node in purple represents hyaluronic acid (HA). This figure was generated using GINsim 3.0.0b.

2. Methods

2.1. The logical formalism and GINsim

The logical formalism aims to explain qualitatively the dynamical systems [15,25]. For molecular systems, the molecules in a regulatory graph are represented as nodes and their interactions as directed edges (representing activatory or inhibitory interactions). In a logical model, nodes can have two states (active or inactive, also known as Boolean variables) or more than two (also known as multi-valued variables) which considers intermediate levels between active and inactive states. This definition depends on the activity level of the molecule in the biological process. In other words, if the node states depend on concentration levels that are well characterized by only active or inactive states, then modelling via Boolean variables is considered, otherwise multi-valued nodes are used. The regulatory interactions reported in the experimental literature are translated into logical functions that control the state of each node in terms of its regulators through combinations of the logical operators AND, OR and NOT. The operator OR represents an individual effect of a regulator on a specific node independent of other regulators, whereas the operator AND denotes a joint requirement to perform an effect. The operator NOT represents inhibitory actions.

The update of the model components can be performed by asynchronous or synchronous methods. In the first one, the components are updated randomly, whereas in the second one all nodes are updated at the same time and the evolution is completely deterministic. In the present study, we performed the simulations using only the asynchronous updating scheme due to its potential to present stochastic behaviour [25].

The network evolution in its state space is determined by its attractors and initial states. Each state in this space is represented by a vector encompassing the current levels of activity of all network nodes. The transitions among the network states are determined by the logical functions controlling each network node. In the asynchronous updating scheme, nodes are selected randomly for updating. When the update scheme reaches an unchanging state, we call it a stable attractor (also known as stable state or steady state). Otherwise, it can be trapped in a subset of network states characterizing a cyclic attractor (also known as complex attractor). The network evolution can be represented in the form of a state transition graph (STG), whose nodes are network states and whose edges represent the transitions between these states.

The presence of functional circuits (or feedback loops) characterizes in more detail the origin of attractors [26]. The existence of a negative circuit can trigger sustained oscillations, while a positive one is a necessary condition for multistationarity. A closed circuit in the network with an odd/even number of inhibitions is defined as negative/positive.

The logical approach allows in silico perturbations of nodes to analyse the effect of such circuits on the dynamics of the network [27]. Logic-based perturbations represent modifications in the dynamics of the model that account for a perturbation affecting the states of the nodes. Knock-out of a gene encoding a specific component is represented by a loss of function (LoF) of the corresponding node by fixing its value at 0. On the other hand, overexpression or ectopic expression of the gene is translated into the model as its gain of function (GoF) by forcing it to remain in a value greater than zero. To identify important circuits, we performed node perturbations to evaluate their role in the model dynamics.

In the present study, we used the GINsim 3.0.0b tool for the simulation and logical analysis of the model. This tool is a Java software suite, freely available for download from the GINsim website (http://ginsim.org/downloads) [28]. This software can compute the dynamical behaviour of the model for any initial state as well as the functional circuits of the network. Moreover, in silico perturbations can be tested with GINsim.

It is possible to compute the dynamical behaviour of the model for any initial state. The state of each model component is iteratively updated according to the logical formulae. The resulting dynamics is represented in terms of STG. The number of states in STG, i.e. the graph connecting all network states visited in the evolution, increases exponentially with the number of network nodes. Then, to deal with this complexity, we used the hierarchical transition graph (HTG) algorithm in GINsim. A node in the HTG represents a cluster of states that share the same set of successor states. The clustered nodes represent irreversible sequences of states or cycles. A transient cyclic component denotes a set of states composed by cyclic trajectories that present outgoing transitions to other clusters in the HTG. Whereas the irreversible ones containing outgoing transitions are not composed of cyclic trajectories. The attractors (cyclic or stable) have no outgoing transitions to other components in the HTG. For instance, the presence of cycles in the dynamics elucidate the role of negative circuits in the system. For a deeper description of HTGs see [29]. Cytospace 3.6.1 was used to generate the HTGs in the present study [30].

3. Results

3.1. Proposed signalling network driving the EMT

The proposed signalling network is based on our previously published model for EMT [14], which contemplated the recent biochemical data on the EMT regulatory core composed by the positive circuits SNAIL1/miR-34 and ZEB1/miR-200 and endogenous TGF-β [8]. New experimentally validated circuits were considered in the proposed network such as ZEB1-mediated positive circuits with ESRP1 and CD44s [31], miR-1199 [12], miR-340 [11] and GRHL2 [21]. HA and HAS2 were also included in the network as performed by Jolly et al. [32]. MiR-190 and CD24 were also considered due to their influence on TGF-β signalling during EMT [21,33]. CDH1 and VIM are considered important epithelial and mesenchymal markers, respectively, [34] then they were also included. However, in the present study, we propose a much more general model considering five different levels for the input representing the concentration of extracellular TGF-β: absent (0), low (1), intermediate (2), high (3) and very high (4). This allows us to model the influence on the EMT dynamics of extracellular TGF-β concentration, as performed in the detailed experiment by Zhang et al. [8]. The experiment analysed epithelial breast cells (MCF10A) exposed to different concentrations of human recombinant TGF-β1 (hTGF-β1). Cells without treatment with hTGF-β1 remained in the E state, whereas with 0.5 ng/ml of hTGF-β1 close fractions of E and H cells were produced. For a concentration of 1.0 ng/ml, E, H and M states were populated, but a smaller fraction of cells remained in the E state. The high 2.0 ng/ml produced only H and M cells, whereas the highest one (4.0 ng/ml) induced mostly the M state. In addition, we also contemplate in the model the observation by Yu and colleagues that TWIST1 can cooperate with SNAIL1 to induce EMT in MCF10A cells [13]. Such cooperation occurs via a double-positive circuit between these molecules controlled by miR-129.

Then, these experimental observations motivated us to propose this new model for the EMT dynamics.

3.2. Translating the proposed network into a logical model

In order to analyse the dynamics of the proposed regulatory network, we translated it into a computational logical model. Each node representing a molecule of the network is defined as Boolean or multi-valued (see §2 Methods). Based on the work of Zhang et al. [8], CDH1 and VIM require three levels of activity to characterize the EMT states [8]. Exposure of cells to different concentrations of hTGF-β1 leads to three expression patterns of CDH1 (E-cadherin) and VIM [8]: high CDH1 and low VIM; intermediate CDH1 and intermediate VIM; low CDH1 and high VIM. This prompted us to consider three levels of activity for both molecules in the model. High and low levels of CDH1 and VIM, respectively, correspond to the E state, whereas the inverse pattern is associated with the M state. When both present intermediate concentrations, the H state is featured. The same approach was applied to the input, exogenous TGF-β, in order to model the different concentrations used in the study by Zhang and colleagues [8]. Concentrations of 0 (absence), 0.5 (low), 1 (intermediate), 2 (high) and 4 (very high) ng/ml of TGF-β were assigned to levels 0, 1, 2, 3 and 4, respectively (see previous section). Similarly, the network output (EMT) was defined with three levels: 0, 1 and 2, corresponding to E, H, and M states, respectively. For SNAIL1 and ZEB1 were also assigned three levels denoting low, intermediate and high levels. According to Zhang and colleagues [8], SNAIL1 and ZEB1 present mainly two expression patterns: low/high SNAIL1 and low ZEB1 (indicating the E or H states), and high SNAIL1 and high ZEB1 (indicating the M state). In addition, we included another level characterizing very high concentrations of SNAIL1 and ZEB1. This was proposed because the relative protein abundances of SNAIL1 and ZEB1 in response to 4 ng/ml of TGF-β present higher levels than 2 ng/ml. To the regulators of SNAIL1 and ZEB1, MiRNAs 34 and 200, respectively, were assigned two levels. ZEB1/miR-200 and SNAIL1/miR-34 circuits were observed to present two distinct stable states [8]: high SNAIL1 and low miR-34, and low SNAIL1 and high miR-34; high ZEB1 and low miR-200, and low ZEB1 and high miR-200. This prompted us to consider two states for both miRNAs. The remaining components of the proposed network were defined as Boolean variables due to the lack of quantitative information. Specification of the logical rule controlling each component and the corresponding published experimental validation are provided in electronic supplementary material, table S1 (PubMed links included). A summary of the modelling assumptions is presented in the electronic supplementary material. The model file is provided in electronic supplementary material, file S1.

3.3. Wild-type case of the model

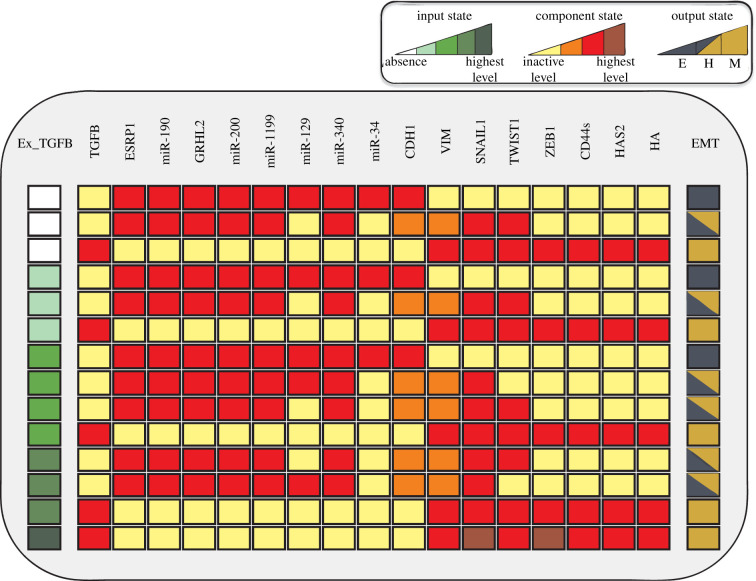
To analyse the dynamics of the different levels of the input exogenous TGF-β (referred to as Ex_TGFB in the model), we determined the wild-type (WT) case of the model by considering all possible initial conditions in the simulation (figure 2). The phenotypic characterization of each state was performed according to phenotype markers [8–13,21,31,35]: activation of miR-200, 34, 1199, 340, CDH1, GRHL2, CD24 and ESRP1 and inactivation of the remaining components was assigned to the epithelial phenotype. Activation of SNAIL1, TGFB, ZEB1, VIM, CD44s, HAS2 and inactivation of the remaining components was assigned to the M phenotype. The hybrid state was assigned to the case when VIM and CHD1 remain in their intermediate states [8]. The WT shows strong multistable (stochastic) behaviour, i.e. the coexistence of different phenotypes (stable states or attractors) for a given input value. Detailed information on the states of the model can be found in table 1.

Figure 2.

Wild-type results of the model. Each line represents a steady state of the model. Yellow, orange, and red cells represent inactive, intermediate, and active states of the components, respectively. White, light green, green, dark green, and very dark green denote levels of the input Ex_TGFB corresponding to absence, low, intermediate, high, and very high concentration, respectively. The model phenotypes are interpreted according to the output state (EMT): inactive, intermediate, and high values of the EMT node represent epithelial (dark blue), hybrid (half coloured cells) and mesenchimal (dark yellow) phenotypes, respectively.

Table 1.

Definition of the model attractors and related phenotypes. References supporting the definitions are listed.

model state	considered phenotype	references
active: miR-190, miR-34, miR-340, miR-1199, miR-129, miR-200, CDH1 (highest level), GRHL2, ESRP1	epithelial	[8–13,21,31,35]
inactive: TGFB, SNAIL1, TWIST1, ZEB1, CD44s, HAS2, HA, VIM
active: miR-190, miR-340, miR-1199, miR-129, miR-200, CDH1 (intermediate level), GRHL2, ESRP1, VIM (intermediate level), SNAIL1 (high level)	hybrid	[8–13,21,31,35]
inactive: miR-34, TGFB, TWIST1, ZEB1, CD44s, HAS2, HA
active: miR-190, miR-340, miR-1199, TWIST1, miR-200, CDH1 (intermediate level), GRHL2, ESRP1, VIM (intermediate level), SNAIL1 (high level)	hybrid	[8–13,21,31,35]
inactive: miR-34, TGFB, miR-129, ZEB1, CD44s, HAS2, HA
active: TGFB, ZEB1 (high/highest levels), CD44s, HAS2, HA, TWIST1, VIM (highest level), SNAIL1 (high/highest levels)	mesenchymal	[8–13,21,31,35]
inactive: miR-34, miR-190, miR-340, miR-1199, miR-200, CDH1, GRHL2, ESRP1, miR-129

For absence and low Ex_TGFB levels, three phenotypes (attractors) were observed: the E, H and M states. Regarding the intermediate level, Ex_TGFB induced four attractors (a quadri-stability) corresponding to the E, H and M states. Its high level destabilized the E state, maintaining the stability of H and M states. The highest level of Ex_TGFB triggers a deterministic behaviour, inducing only the M phenotype.

In the WT model, our approach identified 10 functional circuits, i.e. circuits that influence the dynamics (table 2). Nine of which have already been validated by experimental studies, which supports the model, and a predicted one. We further analysed the functionality context of circuits according to input levels. In this way, we observed that most circuits are functional for all activity levels (0, 1, 2, 3 and 4), except the circuits TGFB/SNAIL1/miR-200, SNAIL1/miR-34 and SNAIL1 self-inhibition (table 2). The functional role of these circuits depends on specific activity levels of the input. The sorting of circuit functionality according to the input level is important to analyse the WT dynamics, results are shown in (table 2). Once the functionality of a circuit is characterized for one input level, its role for other input levels is identical.

Table 2.

Functional circuits of the wild-type dynamics of the model and the corresponding input levels required for their functionalities. Experimental reference for each circuit is presented.

positive circuits	input level context	references
GRHL2 /ZEB1	any	[21]
ZEB1/ miR_340	any	[11]
ZEB1 /miR_1199	any	[12]
TWIST1 / miR-129	any	[13]
TGFB /SNAIL1 /miR_200	0	prediction
SNAIL1 /miR_34	range (0–1), 2	[9]
ZEB1/ HAS2/ HA	any	[35]
ZEB1/ miR_200	any	[10]
ZEB1 /ESRP1/ CD44s	any	[31]
negative circuit
SNAIL1	1	[36]

In a previous work limited to describe only the coexistence of the phenotypes in EMT, we studied the functional role of eight of these circuits [14]. In summary, the SNAIL1/miR-34 circuit is responsible for the E to H transition, whereas the ZEB1-mediated circuits involving miR-340, miR-1199, miR-200 and GRHL2 are associated with the H to M transition. The circuits ZEB1/HA/HAS2 and ZEB1/ESRP1/CD44s contribute to stabilize the M state via sustained activation of ZEB1, the main regulator of the M state.

3.4. Model dynamics

To characterize the system dynamics, we investigated the qualitative behaviour of the trajectories in the state space. However, the number of states in the state transition graph (i.e. the graph connecting all network states visited in the evolution) increases exponentially with the number of network nodes. Then, to deal with this complexity, we used the HTG algorithm to visualize the transitions. The method produces a more compact representation of the trajectories. For more details, see the last paragraph of §2 Methods and references therein.

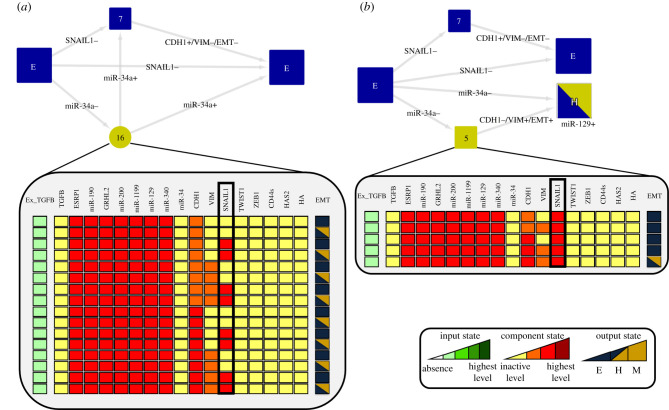
We found that SNAIL1 self-inhibition is involved in the stability of the E phenotype for the low level of the input Ex₋TGFB = 1. To do that, we started from a state of the network that was neighbour to state E, a neighbour state is defined as an initial network state where all nodes are in the E state but one which is set to the M state. Then, we let the system evolve examining which circuits were actively involved and the trajectory performed in the space state (figure 3). That was repeated for each node. We found that unperturbed SNAIL1 circuit triggered trajectories that ended only at the E state (figure 3a). The removal of the self-inhibition of SNAIL1 creates a bistable state between E and H (figure 3b), implying that this negative circuit is responsible for the stability of the E state for low dose. Upon perturbations of the circuit miR-34/SNAIL1, the bistability of E and H is removed suggesting that this circuit is involved in the stability of state H (see electronic supplementary material, file S2).

Figure 3.

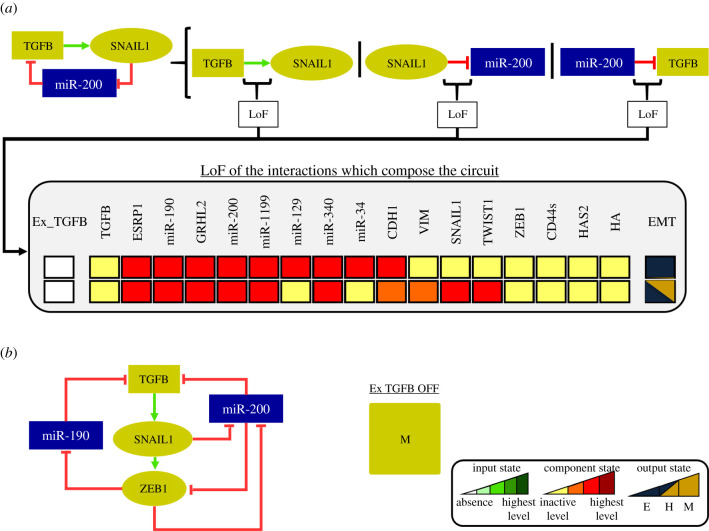
Analysis of lower input active level. In HTG, most-left states represent initial states of the simulation, whereas most-right ones denote final states. Arrows representing transitions between the states are labelled with the updated components. Plus and minus signs indicate that the component is increasing or decreasing its activity level, respectively. Blue and yellow transient states denote that incoming transitions are related to E and M phenotypes, respectively. The number of states that compose each transient is shown. (a) We observed that the unperturbed SNAIL1 circuit generated trajectories where the final state was only the E state. The HTG shows that SNAIL1 transient oscillations can also contribute to stabilize the E state. The depicted 16 states show that the system can oscillate between E and H states until it finally remains at the E state. (b) LoF of SNAIL1 self-inhibition triggers the transition to the H state destabilizing the E state.

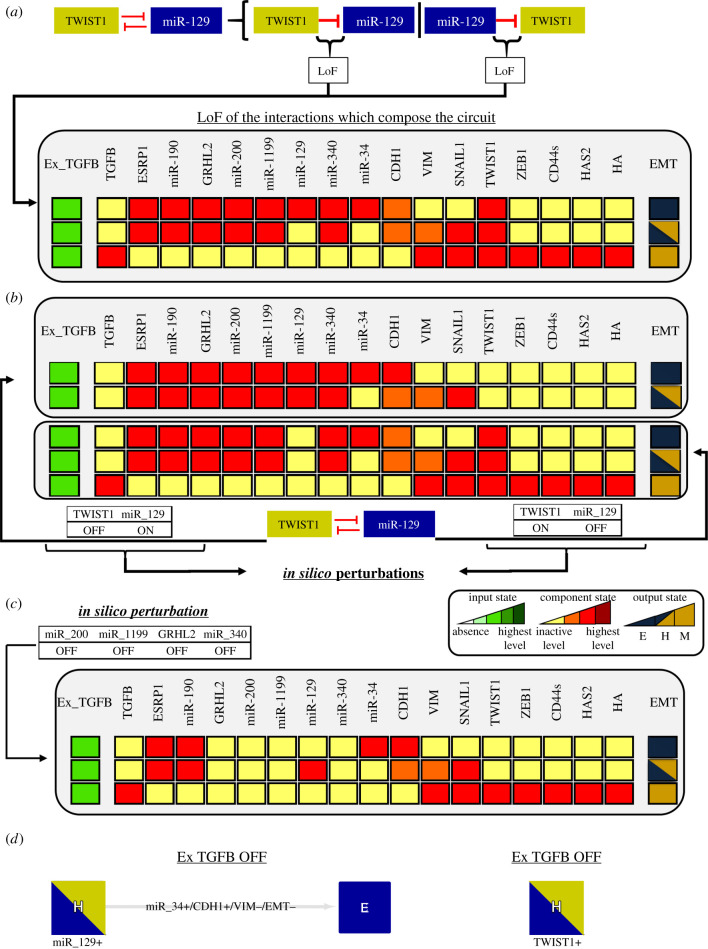
For the intermediate level (Ex₋TGFB = 2), the SNAIL1/miR-34 circuit contributes to stabilize the E state as shown in our previous work [14]. Interestingly, two distinct H states appear and their difference is only the activation of TWIST1. The H state with inactive TWIST1 becomes stable as an effect of the circuit TWIST1/miR-129 and the higher level of the input Ex₋TGFB=2. As we did for the low input, we determined that the circuit TWIST1/miR-129 contributes to the bistability of the H states because the LoF of the circuit interactions destroys this behaviour (figure 4a). By performing individual perturbations on the circuit interactions, we observed that the inhibitory interaction of miR-129 on TWIST1 is responsible for the stabilization of the H state. In this way, the stability of this specific H state is directly related to the ability of miR-129 to inhibit TWIST1 expression during TGF-β signalling. Hence, miR-129 should be considered as a phenotypic stability factor (PSF) of the H phenotype.

Figure 4.

Perturbation analysis of TWIST1/miR-129 circuit for intermediate level with active input. Dark red, red, orange and yellow colours denote the model component levels highest, high, intermediary and inactivation, respectively. (a) LoF of the interactions which compose the TWIST1/miR-129 circuit. The results show the loss of the H state with the absence of TWIST1. (b) The perturbations of the TWIST1/miR-129 circuit show that the bistable switches TWIST1 OFF/miR-200 ON and TWIST1 ON/miR-129 OFF control the bistability between the H states found in figure 2 for the intermediate level of Ex_TGFB. (c) LoF of miR-200, miR-1199, GRHL2, and miR-340 destabilize the H state in the presence of activated TWIST1. (d) Under Ex_TGFB OFF and using H as the initial state with activated miR-129, the system transits to the E state, whereas using the H state with activated TWIST1 the system does not transit to the E state.

In addition to this analysis, we perturbed the components of the circuit. We observed that a bistable switch (TWIST1 ON/miR-129 OFF and TWIST1 OFF/miR-129 ON) controls the stability of the H states (figure 4b). Then, we concluded that this circuit should be added to the set of circuits involved in the stability of the H state that includes ZEB1/GHRL2, ZEB1/miR-1199, ZEB1/miR-340 and ZEB1/miR-200 (see §3.3). Perturbations of the latter circuits (figure 4c) abrogate the H state with activated TWIST1. GHRL2 and miRNAs 1199, 340 and 200 negatively regulate the expression of ZEB1 in the model. Their LoF favour the ZEB1 upregulation which, in turn, destabilizes the H state with upregulated TWIST1. The remaining H state is stable due to activation of miR-129, as previously discussed. We also evaluated whether the transition between the E and the H states is reversible or irreversible (figure 4d). Starting from the H state with miR-129 activated, the system transits to the E state under Ex_TGFB OFF, whereas for the H state with TWIST1 activated the effect is not observed (figure 4d). These results suggest that the bistable switches associated with TWIST1/miR-129 circuit can control the reversibility of the transition.

Regarding the circuit TGFB/SNAIL1/miR-200, not studied in the experimental literature for MCF10A cells, it is only functional for Ex₋TGFB = 0 (table 2). The perturbations show that this circuit is involved in the stabilization of the M state (figure 5a). Node perturbations of the circuit TFGB/SNAIL1/miR-200 were not performed because they affect other functional circuits that share components such as ZEB1/miR-200 and SNAIL1/miR-34, and so, we cannot evaluate its specific role in the model dynamics. Specifically, the inhibitory interaction of SNAIL1 on miR-200 is responsible for the stabilization of the M state. LoF of this interaction favours the miR-200 upregulation which, in turn, inhibits ZEB1 expression destabilizing the M state. As performed for the TWIST1/miR-129 circuit, we evaluated the reversibility of the transition from the M state (figure 5b). In this way, we set the M state as an initial condition of the simulation for Ex_TGFB OFF. Thus, we observed that the system does not transit back. These results suggest that the TGFB/SNAIL1/miR-200 circuit is also involved in the irreversibility of EMT. As ZEB1 is the main regulator of the M state in the model (see the last paragraph of §3.3), the functionality of the TGFB/SNAIL1/miR-200 circuit is associated with the ZEB1 regulation. Once ZEB1 is activated, it inhibits miR-200 and miR-190, allowing the activation of TGFB (figure 5b; most-left subnetwork). This mechanism induces again ZEB1 activation due to TGFB-induced SNAIL1. Thus, the circuit regulates sustained ZEB1 activation and, thus, maintaining the stability of the M state.

Figure 5.

Perturbation analysis of TGFB/SNAIL1/miR-200 circuit with off input. The colours yellow, orange, and red denote the model component levels: off, intermediary, and high, respectively. (a) LoF of the circuit interactions leads to the loss of stability of the M state. (b) According to the network, TGFB can only be activated through ZEB1 activation that, in turn, inhibits miR-200 and miR-190, inducing the circuit functionality. Once TGFB is activated, it sustains the ZEB1 activation via SNAIL1 inducing the M state even with Ex_TGFB OFF.

Both circuits, TGFB/SNAIL1/miR-200 and TWIST1/miR-129, are able to produce an irreversibility effect on the transition. The activation of TGFB and TWIST1 in the respective circuits leads to the stabilization of the M and H states, respectively, explaining the stability of these phenotypes for the input levels OFF and low (due to preservation of the E state caused by SNAIL1 self-inhibition; figure 3) in figure 2. Since all possible initial states were considered in the simulation in figure 2, those which presented TWIST1 and/or TGFB in active states led to stabilization of the H and/or M states, respectively.

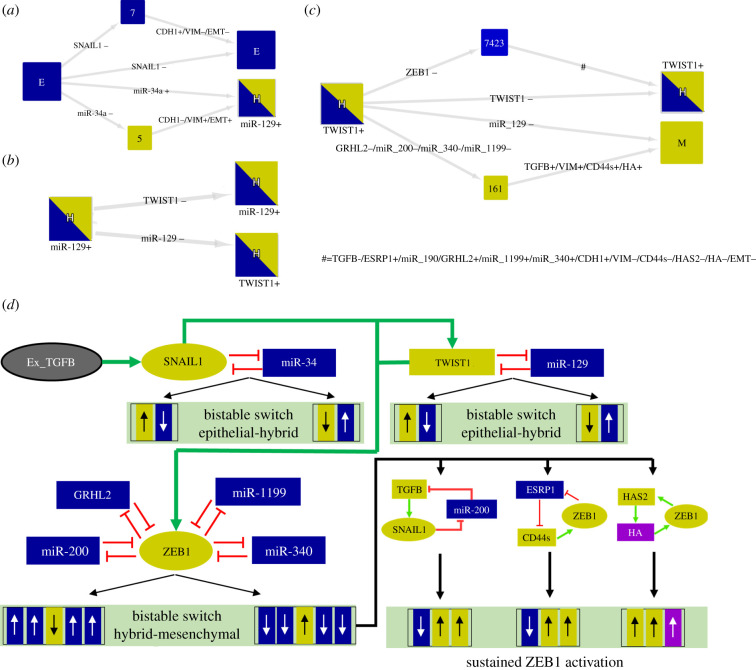
As mentioned in §3.3, the obtained stable states agree with known markers of the E, H, and M states. In terms of the transition processes, the simulations demonstrated a sequential stepwise dynamics of EMT (figure 6). First, the E state transits to the H state, which is controlled by the SNAIL1/miR-34 circuit (figure 6a). This result is consistent with our previous study [14]. In addition to this finding, our previous work showed that once the system reaches the H state, transition to the M state is possible. However, the presence of the circuit TWIST1/miR-129 in this proposed network triggered the stabilization of another H state (figure 6b). From the activation of TWIST1, the system can transit to the M state via the LoF of GRHL2, miR-200, miR-1199 and miR-340 (figure 6c). Collectively, these results show that the model reproduces a stepwise dynamics of EMT consistent with the literature [8]. A schematic figure showing a summary of these results is shown in figure 6d.

Figure 6.

Stepwise process of the model dynamics via activation of multiple circuits. HTGs are displayed as in figure 3. The simulations were performed for $E{x}_{\mathrm{TGFB}}=2$. (a) The initial state E (considering active SNAIL1) induces a bistability between the E and H (with the presence of miR-129) states. (b) Subsequently, the initial state H (considering active TWIST1) triggers another bistability between the H states. (c) Considering the H state with the presence of TWIST1 and additional activation of ZEB1 as the initial condition, the simulation showed another multistability between H and M states. (d) Up and down arrows represent up and downregulation, respectively. Yellow and blue colours denote E and M markers. The induction of SNAIL1/miR-34 circuit by Ex_TGFB triggers bistable switches that control the transition E to H. The activation of SNAIL1 induces the functionality of TWIST1/miR-129 circuit. The switch TWIST1 OFF/miR-129 ON stabilizes one of the H states, whereas its counterpart (TWIST1 ON/miR-129 OFF) triggers the transition to another H state which is stable due to miR-200-miR-1199-GRHL2-miR-340-ZEB1 circuits. Active TWIST1 can induce ZEB1 and subsequently inactivate miR-200, GRHL2, miR-1199 and miR-340 and inducing the transition to the M state which is sustained by TGFB/miR-200/SNAIL1, ESRP1/CD44s/ZEB1 and HAS2/HA/ZEB1 circuits.

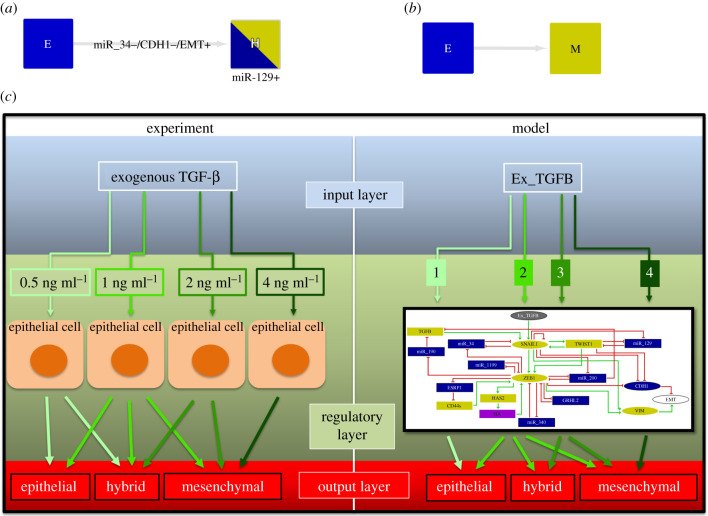
The aim of the present study was to expand the model including different levels of activity for the input component Ex_TGFB. This approach was motivated by the study of Zhang et al. [8] as mentioned in §3.1. Our work showed that SNAIL1 self-inhibition might present an important role at low level of the input maintaining the stability of the E state (see figure 3). Also, we demonstrated that in the intermediate level of the input, the TWIST1/miR-129 circuit can stabilize two H states producing a quadri-stability. At its two highest levels, the input triggered two different behaviours. The high level is tristable with the E state absent, while the very high level induces only the M state. Indeed, by using the E state with activated SNAIL1 as the initial condition, we observed a transition to the H state with activated miR-129 (figure 7a), while the very high level induces a direct transition to the M state (figure 7b). Taken together, our results agree with the experimental observations by Zhang et al. [8], which show the stepwise process of EMT induced by different concentrations of TGF-β (figure 7c).

Figure 7.

Schematic comparison between model and experimental observations. (a) The high level of Ex_TGFB induces a transition from the E to the H state with activated miR-129. (b) The very high level of Ex_TGFB induces a direct transition from the E to the M state. (c) The model reproduces the experimental approach by Zhang et al. [8] where epithelial cells are treated with concentrations of 0.5, 1 and 2 ng/ml of exogenous TGF-β. Following the treatment, the stable phenotypes agree with the stable states found in the model dynamics. The disagreement related to the lower level of Ex_TGFB is explained in the Discussion of the paper.

We further performed a perturbation analysis in order to investigate the correspondence between the resulting stable states of the model and observed experimental phenotypes. In table 3, we present the agreement between the node perturbations and experimental observations. The stable states resulting from the model perturbation can be found in the electronic supplementary material, file S2. In addition to the perturbation analysis, we summarize the remaining predictions and experimental support of modelling results table 5. Collectively, these results suggest an excellent agreement between the model and experimental results.

Table 3.

List of node perturbations and the corresponding abrogated states. The corresponding experimental validation with the MCF-10A cell line for each perturbation is listed.

stimulus/perturbation	abrogated phenotypes	references
miR-34 GoF	H, M	[9]
miR-34 LoF	E	[9]
miR-1199 GoF	M	[12]
miR-200 GoF	M	[37]
miR-340 GoF	M	[11]
GRHL2 GoF	M	[38]
miR-129 GoF	H, M	[13]
TWIST1 LoF	H, M	[39]
SNAIL1 GoF (level 2)	E, H	[40]
SNAIL1 GoF (level 1)	E	[40]
SNAIL1 LoF	H, M	[40]
ZEB1 GoF (level 2)	E, H	[41]
ZEB1 GoF (level 1)	E	[41]
ZEB1 LoF	M	[41]

Table 5.

Summary of findings of the present study and experimental and theoretical support found in the literature.

findings	references
the EMT occurs through a stepwise process controlled by multiple circuits	[8]
the H state is characterized by the simultaneous presence of E and M phenotypic makers	[8]
TGF-β initiates the EMT via activation of SNAIL1 inducing the H states, while subsequent induction of ZEB1 maintains the M state	[8,42]
the SNAIL1 negative circuit can preserve the E state	[8,36,43]
the SNAIL1/miR-34 circuit controls the E-to-H transition via two bistable switches	[8,14,42]
the TWIST1/miR-129 circuit is involved in the induction of an H state through an irreversible bistable switch	prediction
miR-129 is a phenotypic stability factor of the H state	prediction
the ZEB1-mediated circuits involving miR-340, miR-1199, GRHL2 and miR-200 account for the stabilization of one of the H states	[8,14,42,44]
the TWIST1 ON and miR-129 OFF bistable switch results from the functionality of ZEB1/miR-340, ZEB1/miR-1199, ZEB1/miR-200 and ZEB1/GRHL2 circuits	prediction
the TGFB/SNAIL1/miR-200 circuit is involved in the maintenance of the M state	prediction
the ZEB1/HAS2/HA and ZEB1/ESRP1/CD44s circuits induce sustained ZEB1 activation maintaining the stability of the M state	[14,31,35]

3.5. Analysis of robustness of the results

In order to perform a systematic evaluation of the model's robustness, we checked the network response when the model is confronted with topology failures. A failure is simulated by the removal of a single interaction from the network in figure 1 and quantified by the number of states and circuit functionality changes produced when compared to the WT. However, the removal of a node can be seen as a stronger interference in the network than deleting an interaction, as the former simulates the simultaneous removal of all interactions pointing at that nodes. Accordingly, deleting nodes implies some stronger variation from the original result. Table 4 shows the LoF of each incoming interaction to a given node and the changes produced in WT model states and circuit functionality. For example, the first row of the table corresponds to the LoF of each incoming interaction to the SNAIL1 node. This perturbation produces nine changes in the initial model states of the WT. We obtained an average value of 1.55 errors for introduced failure. Table 4 shows that miR-129 has a strong influence on the network dynamics. For more details about the robustness of the model, see electronic supplementary material, table S2.

Table 4.

Robustness analysis of the model. The deletion of each incoming interaction of a node was simulated and the number of node states and circuit functionality affected were computed.

deletion of each incoming interaction to the node	number of errors
SNAIL1	9
TWIST1	2
miR-129	16
miR-34	4
TGFB	0
miR-190	0
miR-1199	4
ZEB1	5
miR-200	8
ESRP1	0
CDH1	0
CD44s	0
HAS2	0
GRHL2	4
HA	0
VIM	0
miR-340	4

3.6. Proposed experimental design based on the model

The theoretical analysis of the present study can provide guidance for experimental studies based on the model provided that the experimental data are obtained at the equilibrium concentration of the molecules, see table 5. From this perspective, we suggest a systematic measurement of the changes in abundance of proteins, mRNAs and microRNAs of the model components under TGF-β stimulus in MCF10A cells. Flow cytometry can be performed to test the bistable switch of the TWIST1/miR-129 circuit as performed by Zhang and colleagues [8] to analyse the SNAIL1/miR-34 and ZEB1/miR-200 circuits. The possible outcome of this experiment would be subpopulations of cells with high and low amounts of TWIST1 and miR-129. Such different amounts might suggest the functionality of TWIST1/miR-129 during the transition. Subpopulations with high and low amounts of TWIST1 and miR-129, respectively, can unravel the role of miR-1199, miR-200, miR-340 and, GRHL2 as predicted by the present study. Whether these molecules are active in these subpopulations, their role in the stabilization might be verified. Regarding the TGFB/SNAIL1/miR-200 circuit, the measurement of ZEB1 expression resulting from the TGFB/SNAIL1/miR-200 axis might be a good strategy to verify the maintenance of the M state due to the activity of the molecules in MCF10A cells. The possible outcome of this experiment would be sustained ZEB1 expression caused by the miR-200 downregulation-induced autocrine TGFB activation.

3.7. Discussion

The presence of EMT-inducing molecules in the tumour microenvironment favours cancer metastatization. Cells stabilized in H and M states are able to migrate into circulatory systems originating metastasis in the host’s body. Consequently, a complete understanding of the EMT process is indispensable to treat such a complex disease. A large number of studies reported that TGF-β, one of the main EMT inducers, is frequently dysregulated in cancer [45–47]. Such dysregulation can trigger the initiation of EMT in epithelial cancer cells inducing metastasis. The TGF-β pathway is characterized by its regulatory core composed by ZEB1 and SNAIL1 [8], and the control of the activity of these molecules is fundamental for the regulation of the mechanistic process of EMT. A recent paper published by our group suggested that new molecules could work as phenotypic stability factors [14]. However, the current model presents a more complex dynamics via consideration of different levels of exogenous TGF-β. The modelling was mainly based on SNAIL1, the only target of the input in the proposed network. The proposal of its controlling logical equation took into consideration the effect of its regulators for each level of the response to exogenous TGF-β. For instance, the influence of miR-34 and SNAIL1 self-inhibition on the logical equation was considered for the low dose (Ex_TGFB = 1) due to their ability to preserve the epithelial state, which is predominately observed in E cells treated with concentrations of 0.5 ng/ml of TGF-β [8]. The same idea was performed for the remaining levels of the input related to the logical equation controlling SNAIL1. The proposed logical equations were validated through comparison between the steady states produced by the model with experimental data. The only disagreement is related to the low dose of the input. The presence of both E and H states were observed experimentally [8], whereas the model only presented the E state. This result is associated with the direct influence of SNAIL1 self-inhibition as observed in figure 3. Indeed, Lu and colleagues [43], via quantitative modelling, showed that the SNAIL1 negative circuit reduces the variation of the SNAIL1 level, triggering a monostable dynamics in the SNAIL1/miR-34 circuit corresponding to the E state. However, Zhang and colleagues [8] revealed that SNAIL1/miR-34 is bistable (characterizing the E and H states) even when the effect of SNAIL1 self-inhibition is considered. The authors revised a previously published model of EMT [42] due to its agreement with experimental data in order to include the SNAIL1 self-inhibition and other relevant biochemical information. In this way, our model is limited to show only the E state for the low dose of the input; however, this does not exclude the importance of our findings on the SNAIL1 negative circuit. Taken together, the results suggest that our model is a useful tool to study the different phenotypes induced by TGF-β during EMT. The WT simulations showed stability of the E state only for the low dose and controlled by the SNAIL1 self-inhibitory circuit. LoF of this self-inhibitory interaction led to the transition to the H state. This result supports the idea of a threshold related to sustained activation of SNAIL1, as suggested by Peiro and colleagues [36].

In the present study, we used a discrete modelling approach to simulate the EMT process. Our results describe a dynamics consistent with the study of Zhang et al. [8]. Moreover, our model is coherent with other computational studies of EMT. Tian et al. [42] proposed a continuous model which predicts the stability of three stable states associated with E, H and M states. In addition, this work showed that the mechanistic process of EMT occurs via two coupled bistable switches. The first reversible switch is associated with the SNAIL1/miR-34 circuit regulating the initiation of EMT, whereas the second irreversible one is based on the ZEB1/miR-200 circuit controlling the transition to the M state. The switches have the same behaviour as those described in the present work for the SNAIL1/miR-34 and ZEB1/miR-200 circuits. The SNAIL1/miR-34 switch controls the E-to-H transition, whereas ZEB1/miR-200 regulates the transition to the M state. It was further demonstrated that EMT proceeds through a stepwise process in which the E cell first transits to the H state and then to the M state [42]. This is observed in our model. The authors also reported that autocrine TGF-β and miR-200 can contribute to the irreversibility observed in the second switch controlled by the miR-200/ZEB1 circuit. According to Tian et al. [42], the irreversibility is relative to the capacity of miR-200 to inhibit TGF-β. That is, the second switch is irreversible if TGF-β activation or miR-200 inhibition is large enough [42]. Our results show that the inhibitory effect of SNAIL1 on miR-200 is responsible for the stabilization of the M state, which is coherent with the study of Tian and colleagues [42].

It has been widely studied theoretically and experimentally that cells can undergo either partial (hybrid) or complete EMT. Although our study shows the presence of two hybrid states during TGF-β-induced EMT, this does not exclude the possibility of the existence of additional hybrid states. Font-Clos and colleagues reported the existence of multiple hybrid states during the EMT process [48]. The authors used a Boolean modelling approach, however the initial conditions differ from those used in the present study. Their network contemplated the crosstalk of several inducer pathways of EMT. In this way, the existence of multiple hybrid phenotypes related to this network may be associated with this crosstalk. Another computational study by Huang and colleagues [49] showed the presence of two hybrid states and a proposed network with 22 components including CDH1, ZEB1, VIM and SNAIL1. These H states have correspondence with those observed in our study. Both H states were characterized with the intermediate expression of CDH1 and VIM, and active SNAIL1. However, one of these states presents active ZEB1, which is not observed in our study.

The circuit analysis identified a new circuit, TGFB/SNAIL1/miR-200, which is not characterized in the literature in terms of its functionality. This circuit is associated with autocrine mechanisms in which the cell itself induces the expression of TGF-β favouring the EMT induction. These mechanisms present an important role during EMT [50–52]. In the present study, the results showed that the new circuit contributes to the stability of the M state. The study of Gregory and colleagues reported an autocrine mechanism composed of endogenous TGF-β and the ZEB1/miR-200 circuit [53]. The authors showed that TGF-β is able to drive sustained ZEB1 expression via SNAIL1 activation favouring the stabilization of the M state. Our results describe this exact function, the activation of TGFB and SNAIL1 leads to the induction of ZEB1 and the inhibition of miR-200 activity, stabilizing the M state. Thus, our findings are consistent with published biochemical information. Unraveling the functionality of the new circuit might help to extend the knowledge of the mechanistic process of EMT. Hence, the control of such a functionality through the inhibition of the circuit components or the induction of the circuit controllers such as miR-190 might prevent cells acquiring a complete M phenotype.

The TWIST1/miR-129 double-negative circuit seems to present an important role during EMT. According to figure 4, the circuit can control the transition between the two H states via a bistable switch. The negative correlation between TWIST1 and miR-129 observed in this switch is consistent with experimental data using MCF10A cells [13] showing that miR-129 is negatively correlated with TWIST1 and SNAIL1 expression [13]. Also, this work showed that miR-129 expression was not reduced in TWIST1 or SNAIL-depleted MCF10A cells treated with TGF-β, indicating that both are required to inhibit the expression of miR-129. Indeed, we observed in figure 4 that when TWIST1 and SNAIL1 are active, miR-129 is not present. Additional experimental evidence that supports our finding on the bistable switch of TWIST1/miR-129 circuit is related to the cooperation of SNAIL1 and TWIST1 during EMT. According to Tran and colleagues [54], SNAIL1 is uniquely required to initiate the TGF-β-induced EMT, whereas TWIST1 is able to maintain the later phase of EMT characterized by the down and upregulation of CDH1 and VIM, respectively. The bistable switch of the TWIST1/miR-129 circuit might be associated with the mechanism studied by Tran and colleagues [54]. One state of the bistable switch is characterized by the presence of SNAIL1, whereas in the other state both TWIST1 and SNAIL1 are active. Moreover, Yu and colleagues showed that miR-129 downregulation-induced TWIST1 activation in the maintenance of the EMT in breast epithelial cells [13]. In this way, the irreversibility of the transition associated with the presence of TWIST1 observed in our study also seems to be experimentally reliable. Regarding miR-129, its ability to stabilize the H state is an important finding of our study. This feature characterizes miR-129 as a PSF of the H phenotype. The identification of PSFs of the H state can expand the knowledge of the EMT-related hybrid phenotype. In this context, Jolly and colleagues identified two PSFs during EMT process via mathematical modelling: GRHL2 and miR-145. The authors further observed that the knockdown of GRHL2 in H1975 cells leads to a full EMT, which emphasizes the importance of GRHL2 in the stabilization of the H state [44]. In this context, Watanabe and colleagues showed that cells can be maintained in a hybrid phenotype by the transcription factor OVOL, which characterizes this transcription factor as another PSF of the H state [55]. With the possible experimental validation of this prediction, this could help new strategies to treat the metastatic process. Drugs that inhibit the expression of miR-129 might decrease the number of cells in the H phenotype in the carcinoma, since cells of this phenotype present up to 50 times higher metastatic potential than cells in the M state [4]. The possible lower number of cells in the H state triggered by miR-129 depletion might help to reduce the migration of breast cancer cells to other tissues via metastasis.

EMT is known to be reversible via the mesenchymal–epithelial transition (MET) process. However, many studies have suggested that, under specific conditions, EMT can become irreversible [56,57]. Such conditions are based on E cells with continuous exposure to TGF-β for a sufficiently long period of time. Jia and colleagues have reported that prolonged TGF-β exposure (12–15 days) can give rise to irreversible M cells [56]. The authors also reported that MCF10A cells underwent a stronger EMT process, characterizing the loss of E-cadherin (CDH1) and the upregulation of ZEB1 expression. Moreover, Watanabe et al. [57] have shown that ZEB1 is essential to control the reversibility of EMT in MCF10A cells. In addition, the authors demonstrated that once the cells have reached the M state, EMT is irreversible, which is consistent with the mathematical model published by Tian and colleagues [42] and experimentally observed by Zhang et al. [8]. The E and M states of our model characterize a complete phenotypic transition. As seen in figure 5b, the M state does not transit back to the E state, which is consistent with previously discussed results from the literature. Besides, our findings on the TGFB/SNAIL1/miR-200 circuit-related reversibility predicts that this circuit might sustain ZEB1 activation which controls the irreversibility. In this way, our model also describes ZEB1 as an important player of the reversibility. Regarding TWIST1, also predicted as responsible for irreversibility in the model, there is a lack of experimental results on MCF10A cells. Nevertheless, Dragoi and colleagues reported that TWIST1 induces irreversible changes in the mesenchymal state of mammary epithelial cells (HMLE), resulting in the loss of dependency on TGF-β [58]. This supports our findings on TWIST1 as an important player in the irreversibility.

Synthetic biological networks are able to feature various dynamical behaviours such as multistability and oscillations through functional circuits. The model shows nine functional positive circuits responsible for multistability and a negative one. Some circuits are responsible for the stabilization of specific transitions such as the SNAIL1/miR-34 (E-to-H transition) and TWIST1/miR-129 (H-to-H transition) circuits. The ZEB1-mediated circuits involving the protein GRHL2, and the miRNAs 1199, 200 and 340 control the H-to-M transition. The remaining positive circuits of the model sustain the stabilization of the M state. Our results show that loss of functionality of the positive circuits can affect the multistability of the model. For instance, LoFs of miR-34 and ZEB1 abrogate the E and M states, respectively. These perturbations lead to loss of functionality of their respective circuits affecting the multistability of the model. This suggests that the multistability is correlated with the number of positive circuits in the network, which is supported by the study of Hari et al. [59]. By considering all input levels, the multistability of the model triggered six H states, while the number of E and M states is lower. This is a signature of a frustrated dynamics for the H case according to the literature [60]. Indeed, Font-Clos and colleagues reported that the E and M states are less frustrated than the H state by using a Boolean modelling approach to study the EMT dynamics [48]. In summary, our findings provide new insights into the complex dynamics of TGF-β-induced EMT via consideration of different concentrations of this molecule. The circuit analysis demonstrated new important features about EMT dynamics such as functionalities of SNAIL1, TGFB/miR-200/SNAIL1, and TWIST1/miR-129 circuits during the transition. Further investigations of these features will extend our comprehension of TGF-β-induced EMT in MCF10A breast cells, which might help improve strategies for breast cancer treatment.

Data accessibility

This article has no additional data.

Authors' contributions

D.A.S., S.G., and J.C.M.M. conceived the experiment(s); D.A.S. and S.G. conducted the experiment(s); D.A.S., S.G., and J.C.M.M. analysed the results. All authors reviewed the manuscript.

Competing interests

The authors declare no conflict of interest.

Funding

This work was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Coordenação de Aperfeiçoamento de Pessoal de Nóvel Superior (CAPES).