Abstract
A challenging and outstanding problem in interdisciplinary research is to understand the interplay between transients and stochasticity in high-dimensional dynamical systems. Focusing on the tipping-point dynamics in complex mutualistic networks in ecology constructed from empirical data, we investigate the phenomena of noise-induced collapse and noise-induced recovery. Two types of noise are studied: environmental (Gaussian white) noise and state-dependent demographic noise. The dynamical mechanism responsible for both phenomena is a transition from one stable steady state to another driven by stochastic forcing, mediated by an unstable steady state. Exploiting a generic and effective two-dimensional reduced model for real-world mutualistic networks, we find that the average transient lifetime scales algebraically with the noise amplitude, for both environmental and demographic noise. We develop a physical understanding of the scaling laws through an analysis of the mean first passage time from one steady state to another. The phenomena of noise-induced collapse and recovery and the associated scaling laws have implications for managing high-dimensional ecological systems.
Keywords: transients, stochasticity, tipping point, mutualistic networks, nonlinear dynamics, complex networks
1. Introduction
In ecology, to predict the state of the system in the future is critical to sustainable ecosystem management [1]. Long-term prediction is also of paramount importance to fields such as epidemiology and climate science. In the real world, the ability to predict the future of the system is often hindered by a number of factors, among which transients, stochasticity and high dimensionality stand out as some of the most daunting challenges. To understand the complex interplay among the three factors is of fundamental importance to ecology and related fields, but this has remained an outstanding problem in interdisciplinary research. The purpose of this paper is to present a case study to gain significant insights into the interplay among transients, stochasticity and high dimensionality. In particular, using complex, high-dimensional ecological networks as a paradigmatic model, we investigate the phenomenon of noise-induced transients associated with tipping-point dynamics and uncover the scaling laws characterizing the dependence of the average transient lifetime on the noise amplitude.
1.1. Transients in ecological systems
Transient behaviours are ubiquitous in chaotic systems [2,3], and their importance to ecology has been increasingly recognized [4–10]. In ecological systems, the phenomenon of ‘regime shift’, where a qualitative change in the dynamical state occurs suddenly with no warning [11–13], is particularly devastating because, (i) any understanding of the system based on observations made before the regime shift would become irrelevant, (ii) its time of occurrence is highly unpredictable, and (iii) it often results in population collapse and species extinction. On the dynamical origin of regime shift, the traditional view is that it is due to parameter drifting, but it has been proposed that regime shift can be the consequence of transient dynamics without requiring any parameter change [9,10].
1.2. Stochasticity in ecological systems
In the real-world ecological environment, the population dynamics are under inevitable and constant influences of random disturbances. It has been known for a long time that stochasticity can affect species abundance in terms of its size, dynamics and resilience [9,14–28]. As different species in an ecosystem interact with each other through a complicated pattern, the extinction of one species as caused by stochasticity can lead to the extinction of other species that are linked to it. Likewise, external perturbations leading to improved environmental conditions can make certain species recover their abundance from near zero values which, in turn, can lead to the recovery of mutually interacting species [29].
There are two main types of stochastic perturbations in ecological systems: those due to changes in the environmental conditions (external) and those caused by variations in the populations themselves (internal). Environmental stochasticity has a direct impact on the birth rate and mortality of the species and can be modelled as additive Gaussian white noise [30,31], while internal stochasticity is due to the inherent uncertainties related to individual reproduction, growth, death, competition and migration within the species and is thus demographic [21,32–34], representing correlated or ‘coloured’ noises. Mathematically, a demographic stochastic process can be modelled as a type of multiplicative noise with strength proportional to the square root of the fluctuating abundance. In the present work, both types of stochasticity are studied.
1.3. High dimensionality of ecological systems
Ecosystems are typically high-dimensional and complex. To be concrete, we shall focus on mutualistic interaction networks [29,35–44]. In general, mutualism is referred to as a close, interdependent, mutually beneficial relationship between two species. Mutualistic interactions are one of the most important interspecific relationships in ecosystems. For instance, the corals and the single-celled zooxanthellae that form huge coral reefs are in a mutualistic relationship, where the zooxanthellae provide nutrients to their host and in return receive essential nourishment in a process associated with reef-building corals. On land, mutualistic interactions are fundamental to species diversity, such as the network of pollinators and plants. Because of the typically large number of species involved in the mutualistic interactions, the underlying networked system is a high-dimensional nonlinear dynamical system.
1.4. Methods and results of this paper
In this paper, employing complex mutualistic networks subject to environmental and demographic noises, we set out to unveil and decipher the interplay among transients, stochasticity and high dimensionality. While this setting naturally has the elements of high dimensionality and stochasticity, where do transients come from? To generate transient dynamics, we focus on the parameter regime where the networked system exhibits a tipping point [13,38,42,43,45–57]. Especially, as a bifurcation parameter changes, the system can exhibit a transition from a survival state to an extinction state, or vice versa. To be concrete, we choose the normalized species decay rate κ as the bifurcation parameter. For a collapse leading to species extinction, e.g. caused by continuous deterioration of the environment so that the value of κ keeps increasing (the forward direction), the system remains in the survival state for and becomes extinct for , where is the critical point. Similarly, for the recovery process triggered by continuously improving the environment so that the value of κ keeps decreasing (the backward direction), the system is in an extinction state for but the species abundances are recovered for , where is the critical point. Note that the critical points and are often different, due to the emergence of a hysteresis loop. Stochasticity can change this deterministic picture: in the forward direction, even for , a transition from the survival state to extinction can occur, whereas in the backward direction, the system can transition to a survival state from an extinction state even for . These noise-induced transitions, of course, do not occur instantaneously but rather requires some time to complete, leading to transients. The setting of our study is thus adequately suited for addressing the intricate interplay among transients, stochasticity and high dimensionality in ecological systems.
Our main results are as follows. Firstly, using the full, high-dimensional empirical mutualistic networks constructed from data from four geographical regions subject to stochastic influences as modelled by environmental and demographic noises, we demonstrate the phenomena of noise-induced collapse and recovery. Secondly, we search for any possible scaling relation between the average transient time and the noise amplitude. To render the task computationally feasible, we take advantage of an effective 2D model that was previously derived and demonstrated to capture the essential dynamical behaviours associated with tipping point transitions in mutualistic networks [42]. Extensive numerical simulations indicate that the scaling relation is algebraic for both types of noise. Thirdly, exploiting the basic, saddle-node bifurcation based nonlinear dynamical picture underlying the two noise-induced transition phenomena, we argue that the average transient lifetime is essentially the mean first passage time from one steady state to another driven by noise. We obtain formulae for this time and demonstrate that the formulae give the algebraic scaling as observed from direct numerical simulations.
The uncovered phenomena of noise-induced collapse and recovery and the associated algebraic scaling law of the average transient lifetime with the noise amplitude represent a quantitative characterization of the interplay between stochasticity and transients in high-dimensional ecological systems. In addition, our analysis reveals that demographic noise plays a dominant role in causing a system to collapse, while environmental noise is key to species recovery. These results have implications to managing high-dimensional ecosystems. For example, in order to prevent a healthy system from collapsing to extinction, reducing demographic noise would be effective. On the contrary, if the system is already in extinction, supplying an appropriate level of environmental noise could facilitate recovery.
2. Model of stochastic mutualistic networks
We extend the deterministic model [38–42] for complex mutualistic networks of plant and pollinator species to include environmental white and demographic noises [29]:
| 2.1 |
and
| 2.2 |
where Xi and Yi are the abundances of the ith pollinator and ith plant, respectively, and are the intrinsic growth rates in the absence of intraspecific competition and any mutualistic effect, βii and βij (i ≠ j) are parameters quantifying intraspecific and interspecific competitions, respectively, and the parameters and characterize species migration. For the pollinator–plant system, intraspecific competition is typically stronger than interspecific competition [38,39]: βii ≫ βij. The saturation effect is taken into account by the constant h, which is the half-saturation density of the Holling type-II functional response [58]. The beneficial effect of the interactions on the population growth saturates when the mutualistic partners have high abundance. The parameters and are the strengths of the mutualistic interactions, which depend on the degree of the node as
| 2.3 |
where γ is the normalized strength and aij’s are the elements of the network adjacency matrix: aij = 1 if there is an interaction between pollinator i and plant j; otherwise aij = 0. The parameter ki is the number of mutualistic links associated with species i, and ρ determines the strength of the trade-off between the interaction strength and the number of interactions. If there is no trade-off (i.e. ρ = 0), the network topology has no effect on the strength of the mutualistic interactions. In contrast, a full trade-off (ρ = 1) means that the interaction strength is weighed by the nodal degree so the network topology affects the species gain from the interactions. To make a numerical study of the collapse and recovery processes in the presence of different types of stochastic processes feasible, we choose , the pollinator decay rate, as the bifurcation parameter while fixing the values of the other parameters as reported in the literature [38–42].
We consider three cases of stochastic influences: environmental noise (EN) only, demographic noise (DN) only and simultaneous presence of both types of noise (EDN). The process dBi(t) in equations (2.1) and (2.2) is a Brownian motion obeying the normal distribution with zero mean and variance dt. For EN, the noise strength terms are constants:
| 2.4 |
with σ being the noise amplitude. DN is modelled as [21,34,59]
| 2.5 |
with noise amplitude ζ. For EDN, we have
| 2.6 |
We simulate the stochastic dynamics of four empirical pollinator–plant mutualistic networks (available from the Web of Life database (http://www.web-of-life.es)). Network A is from Hicking, Norfolk, UK (SX = 61 and SY = 17 with the number of mutualistic links L = 146), where SX and SY are the numbers of pollinator and plant species, respectively. Network B is from Tenerife, Canary Islands (SX = 38, SY = 11 and L = 106). Network C is from North Carolina, USA (SX = 44, SY = 13 and L = 143). Network D is from Hestehaven, Denmark (SX = 42, SY = 8 and L = 79). A graphic representation of the adjacency matrices for the four networks provides a better visualization of the structure of the mutualistic interactions [42], including nestedness that is often associated with the intrinsic ability of pollinators to overcome harsh conditions.
3. Numerical results
3.1. Noise-induced collapse and recovery processes
An increase in the pollinator decay rate κ, the bifurcation parameter, can be viewed as a consequence of the deterioration of the environment. Due to the mutualistic interactions, plants are affected by the decay of pollinators, albeit indirectly. We present the simulation results from network A here, while leaving those with networks B–D in the electronic supplementary material. For EN, the stochastic system is integrated using a standard second-order method [60]. When DN is present, we use a previously developed integration method for multiplicative noises [59,61].
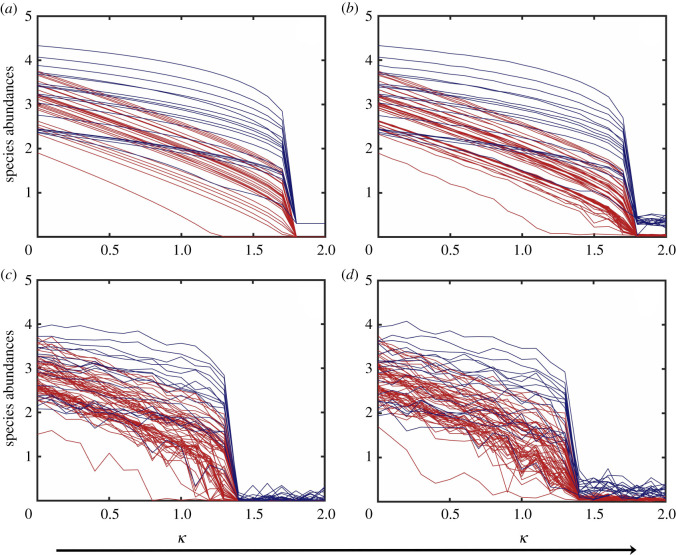
A tipping point transition of the collapse type occurs when the system switches from a high to a low-abundance steady state as κ increases through a critical point, and noise can affect this transition by advancing its occurrence. Figure 1a shows such a transition in the absence of noise, where the transition point is κc ≈ 1.8. For κ < κc, the system is in the high-abundance steady state. For κ > κc, the system approaches asymptotically an extinction state in which most species abundances are near zero. Similar transitions occur when noise is present, as shown in figure 1b–d for EN, DN and EDN, respectively. The value of the critical transition point for the EN case is κc ≈ 1.7, while that for the DN or EDN case is κc ≈ 1.4, indicating that environmental noise has caused the transition to occur at a slightly smaller value of the bifurcation parameter as compared with the deterministic case, but demographic noise has a more devastating effect, as it causes the transition to occur at a markedly smaller value of κ. Qualitatively, this can be understood by noting that when the system is in the high abundance state, the corresponding stochastic perturbation is stronger due to the dependence of the noise term on the abundance.
Figure 1.
Noise-induced collapse through a tipping point transition. (a–d) Species abundances versus the normalized decay rate κ for networks A in the absence of noise, with EN, DN and EDN, respectively. The red and blue curves represent the pollinator and plant abundances. The collapse tipping points for the four cases in (a–d) are approximately κc ≈ 1.8, 1.7, 1.4 and 1.4, respectively. Other parameter values are , , γ = 1, h = 0.2, ρ = 0.5, μX = 10−4 and μY = 10−4. In (b,d), the environmental noise amplitude is σ = 0.1. In (c,d), the demographic noise amplitude is ζ = 0.25. The time duration of each simulation run is T = 400, which is long enough to allow the species abundances to switch to the lower stable state after a transient. The initial conditions are randomly chosen from the basin of the high-abundance steady state.
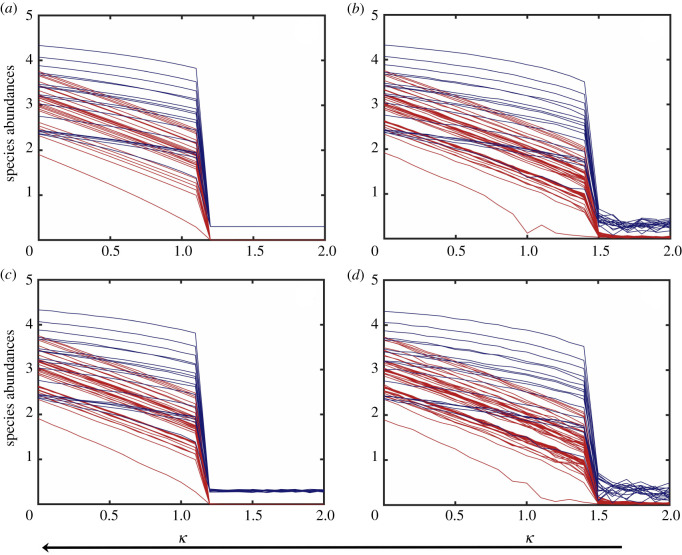
When the system is in an extinction state where the species abundance is near zero, noise can induce an ‘early’ recovery of the species, a phenomenon that was reported recently [29] but mainly for the case of EN. Dynamically, this occurs when noise induces a state transition of the system from a low to a high abundance state—a process that is opposite to noise-induced collapse. Representative results are shown in figure 2, where the panels (a–d) correspond to the deterministic case and the three cases with EN, DN and EDN, respectively. In terms of the bifurcation parameter, the recovery point for cases (a) and (c) is κc ≈ 1.2 while that for cases (b,d) is κc ≈ 1.5. Since case (c) involves DN only and cases (b,d) have EN, we see that DN has little effect on the recovery point. This is reasonable because, prior to the recovery, the system is in the low steady state with near zero abundance, so the stochastic perturbation due to DN is insignificant. The results in figure 2 indicate that EN can be beneficial to species recovery, as it prompts the transition to occur ‘earlier’ as the bifurcation parameter decreases from a value in the extinction regime [29].
Figure 2.
Noise-induced recovery process. (a–d) Species abundances versus the bifurcation parameter as its value continuously decreases from that in the extinction state for the four cases of absence of noise, EN, DN and EDN, respectively. The red and blue curves represent the pollinator and plant abundances, respectively. The recovery points for the four cases are approximately 1.2, 1.5, 1.2 and 1.5, respectively. Other parameter values are , , γ = 1, h = 0.2, ρ = 0.5, μX = 10−4 and μY = 10−4. In (b,d), the environmental noise amplitude is σ = 0.1. In (c,d), the demographic noise amplitude is ζ = 0.025. The time duration of each simulation run is T = 400, which is sufficient for the transition from a low to a high abundance state to complete. The initial conditions are randomly chosen from the basin of the low abundance steady state.
Comparing the results in figures 1 and 2, we see that the value of the species recovery point is generally smaller than that for the collapse tipping point. This indicates that, once the system is in extinction, the environment needs to be more suited for the species than that at the collapse for recovery to occur [43].
3.2. Noise-induced transients and scaling
The phenomena of noise-induced collapse and recovery both involve the transition from one steady state to another, which takes time to complete, leading to a transient behaviour. The average transient time τ depends on the type of noise and its amplitude.
To make it feasible to numerically calculate and mathematically derive the noise scaling law of the average transient time, we exploit the effective 2D reduced model that has been demonstrated [42] to generate the dynamical behaviours associated with the tipping point transition in the full mutualistic networked system. The 2D model not only captures the essential behaviour of empirical mutualistic networks from different regions and climate across the Earth, but it also predicts correctly the onset of the tipping point in all 59 available network data from pollinator–plant habitats, even in presence of noise. Being much less complicated than the full network model, the reduced system can be used as a paradigm to gain insights into mutualism.
Under noise, the 2D model is written as
| 3.1 |
and
| 3.2 |
where x and y are the effective or average abundances of pollinators and plants, respectively, α is the effective growth rate in the reduced model, β stands for the combined effects of intraspecific and interspecific competitions, κ is the bifurcation parameter that accounts for the decay rate of the pollinator and μ represents the migration effect of the species. The two effective mutualistic interaction parameters, 〈γx〉 and 〈γy〉, are obtained [42] through properly weighed averages of the quantities and based on the empirical complex networks, equations (2.1) and (2.2). The terms in equations (3.1) and (3.2) that involve the Brownian motion dynamics dB(t) represent the stochastic perturbations. For EN, we have v(x) = σ2 and u(y) = σ2. For DN, we have v(x) = ζ2x and u(y) = ζ2y. For EDN, we have v(x) = σ2 + ζ2x and u(y) = σ2 + ζ2y.
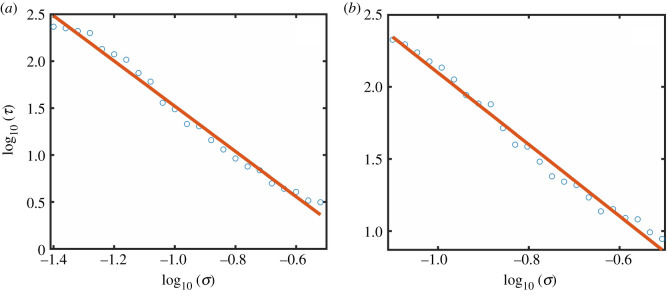
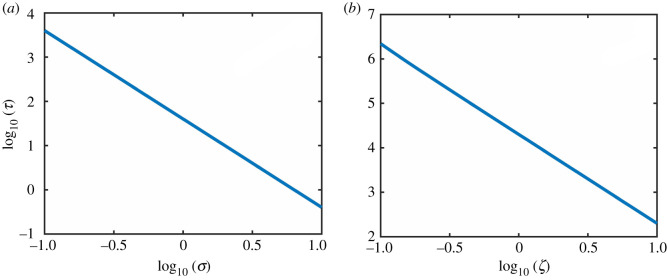
Suppose the system is in the high abundance state, i.e., the value of κ is smaller than that associated with the deterministic tipping point of collapse. The presence of noise can induce a transition to the low abundance state. Figure 3a shows, for EN, the average transient time τ required for the collapse transition to complete versus the noise amplitude σ on a logarithmic scale. As σ increases, τ decreases, and the scaling relation is algebraic:
| 3.3 |
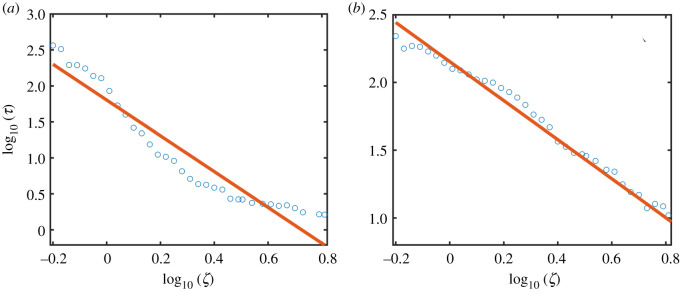
with the scaling exponent p ≈ 2.45. Likewise, when the system is in the low abundance state, noise can induce a transition to the high abundance state and the scaling of the average transient time with the noise amplitude is also algebraic, as exemplified in figure 3b, where p ≈ 2.40. Similar algebraic scaling relations have been obtained with DN:
| 3.4 |
as shown in figure 4a and 4b for the processes of noise-induced collapse and recovery, respectively.
Figure 3.
Algebraic scaling between the average transient time τ and the environmental noise amplitude σ. (a,b) Dependence of τ on σ on a logarithmic scale for the collapse and recovery processes, respectively. The values of κ are 1.65 for the collapse process and 1.5 for the recovery process. Other parameter values are α = 0.3, β = 1, h = 0.2, γ = 1 and ρ = 0.5. For each value of σ, simulations are carried out for a long time interval (T = 1000), which guarantees that the system has approached the desired stable steady state by then. For each σ value, 100 random initial conditions are chosen from the basin of the stable steady state that the systems leaves.
Figure 4.
Algebraic scaling between the average transient time τ and the demographic noise amplitude ζ. (a,b) Dependence of τ on ζ on a logarithmic scale for the collapse and recovery processes, respectively. The values of κ are 1.0 for the collapse process and 1.5 for the recovery process. Other parameter values are α = 0.3, β = 1, h = 0.2, γ = 1 and ρ = 0.5. The simulation setting is the same as that in figure 3.
3.3. Loss of mutualism induced by demographic noise
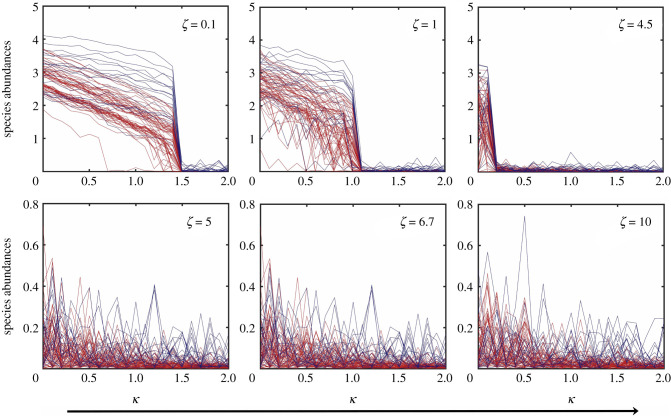
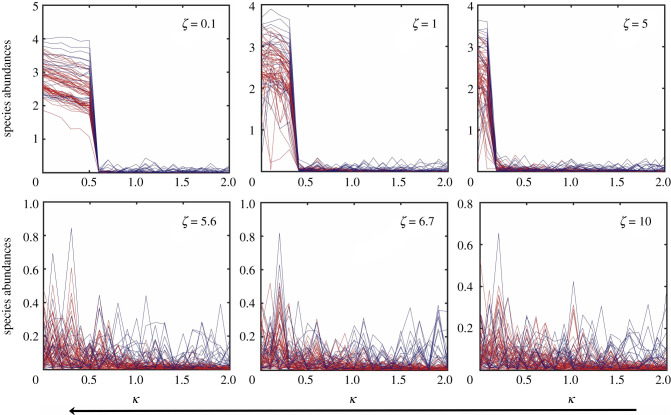
If the amplitude of stochastic processes of the DN type are sufficiently large, they can have a devastating effect on the system: loss of mutualism. Dynamically, this occurs when the basins of the high and low abundance steady states overlap so significantly that these states can no longer be distinguished from each other. A consequence is that the movements of the individual species populations are effectively independent stochastic processes, as the mutualistic interactions are completely overwhelmed by the noise. An example is shown in figure 5, where the variations in the species abundances as the bifurcation parameter κ increases are displayed for six values of ζ, the amplitude of DN. It can be seen that, for ζ < ζc, where , there is still mutualism but it is completely lost for ζ > ζc. This phenomenon of loss of mutualism also occurs during the species recovery process, i.e. as κ decreases continuously from a relatively high value for which the deterministic system is in the low abundance steady state, as shown in figure 6 for six values of ζ. The critical value ζc obtained from the recovery (‘backward’) process is approximately the same as that from the collapse (‘forward’) process in figure 5.
Figure 5.
Loss of mutualism in the forward (collapse) direction. Shown are the steady state species abundances of network A versus the bifurcation parameter κ as it increases from zero for six values of ζ, the amplitude of DN. Mutualism is lost for ζ > ζc, where 4.5 < ζc < 5.0. The network parameter values are , , γ = 1, h = 0.2, ρ = 0.5, μX = 10−4 and μY = 10−4. The initial conditions are randomly chosen from the basin of the high abundance steady state.
Figure 6.
Loss of mutualism in the backward (recovery) direction for network A. Shown are, for six values of ζ, the steady state species abundances versus κ as it decreases from high value for which the deterministic network system is in the extinction state. The value of the critical noise amplitude ζc is approximately the same as that obtained from the forward process in figure 5. The initial conditions are chosen randomly from the basin of the low abundance steady state. Other parameter values are the same as those in figure 5.
Large environmental noise, analogous to demographic noise, can cause the survival and extinction basins of attraction to overlap, resulting in the loss of mutualism. The mathematical reason is that the environmental and demographic noise amplitudes enter the system equations on an equal footing. Extraordinarily strong environmental noise in which the stochastic terms are much larger than the others, including the mutualistic interaction terms, may be unrealistic. The situation with demographic noise is somewhat different because its amplitude is inversely proportional to the habitat size, so effectively large fluctuations can arise in small habitats, implying that such a system is more vulnerable to collapse. By the same token, from the point of view of recovery, small population clusters corresponding to larger noise strength are advantageous for the population to cross over the unstable equilibrium to recover.
4. Physical theory for the scaling law of average transient time
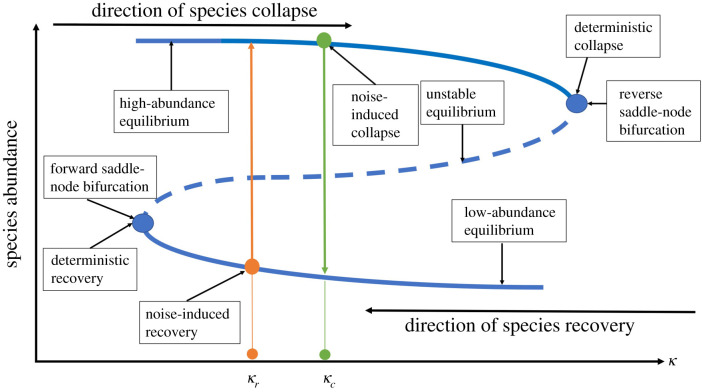
We develop a physical theory to understand the algebraic scaling law of the average transient time for the phenomena of noise-induced collapse and recovery. We base our analysis of the stochastic tipping point dynamics on the effective 2D reduced model [42] for mutualistic networks. Figure 7 schematically illustrates the deterministic as well as the noise-induced collapse and recovery processes. In the deterministic case, these processes are the result of saddle-node bifurcations, where the collapse tipping point is due to a reverse saddle-node bifurcation and recovery is the result of a forward saddle-node bifurcation. For κ to the left of the forward saddle-node bifurcation point, the system possesses only one stable equilibrium corresponding to the high abundance steady state. For κ to the right of the reverse saddle node bifurcation point, there is only the low abundance equilibrium, corresponding to extinction. However, for κ in-between the two saddle-node bifurcation points, the system exhibits multistability [62–65] with three equilibria: two stable equilibria and one unstable equilibrium between them. The two stable equilibria are two attractors with their own basins of attraction, while the stable manifold of the unstable equilibrium is the basin boundary [3,66]. Under the influence of noise, the dynamical trajectory of the system can cross the basin boundary [63,67,68]. In particular, as the value of κ increases, the system can have a transition from the high- to the low-abundance equilibrium at κc, as indicated by the green arrow in figure 7. This is the phenomenon of noise-induced collapse. Conversely, when the system is already in the extinction state, noise can trigger a transition from the low- to the high-abundance state at κr, as illustrated by the orange arrow in figure 7. This is the phenomenon of noise-induced species recovery.
Figure 7.
A schematic illustration of the dynamical mechanisms of the noise-induced collapse and recovery processes. The species abundance is plotted versus the environmental deterioration parameter κ (the bifurcation parameter). The deterministic tipping point corresponds to the birth of a reverse saddle-node bifurcation, while the recovery process in the backward direction is the result of a forward saddle-node bifurcation. When the system is initially in the high abundance state, noise-induced collapse occurs at κc, before the system reaches the reverse saddle-node bifurcation point. When the system is in the low abundance state, noise-induced recovery can occur at κr as κ decreases, before the systems reaches the forward saddle-node bifurcation point.
For both the noise-induced collapse and recovery phenomena, the dynamical mechanism is a noise-induced transition between two stable equilibria (attractors). There is a competition between the attractiveness of the dynamics in the neighbourhood of the stable equilibria, which is controlled by the negative eigenvalues of the Jacobian matrix, and the stochastic random jumps that take the trajectory out of the open neighbourhood possibly into the other attractor [63,67,69,70]. To enable a transition, the noisy ‘kicking’ must be sufficiently large to bring the system trajectory across the unstable equilibrium. Our analysis of the 2D model reveals that, for the collapse process, the Euclidean distance between the upper stable equilibrium and the unstable equilibrium varies in the interval (2.7, 3.4) for κ ∈ [1.0, 2.0]. For the recovery process, the Euclidean distance between the lower stable equilibrium and the unstable equilibrium is in (0.5, 1.0) for κ ∈ [1.0, 2.0]. The sizable difference in the distance range implies that, for the same noise, recovery can occur more readily, where a noise of relatively small amplitude is able to drive the system to overcome the distance to the basin boundary, allowing the trajectory to enter the basin of the upper equilibrium. For an ensemble of trajectories, the transient time required for the transition is exponentially distributed [64,71] with the mean transient lifetime τ that depends on the noise amplitude.
In terms of the underlying stochastic process, the average transient time τ is nothing but the first passage time [72] for the transition, which decreases with the noise amplitude. To derive the algebraic scaling relations (3.3) and (3.4), we note that, for population stochastic processes, the equilibrium distribution is typically stationary [73,74]. We thus assume that the distributions of the pollinators and plants have the following respective stationary probability density functions [75,76]:
| 4.1 |
and
| 4.2 |
where C is a normalization constant. The integral in the exponent is an antiderivative, and the constants produced by the integration are grouped into C. The functions
and
are from equations (3.1) and (3.2), respectively, of the 2D model. In principle, for a population that goes extinct, we should consider a quasi-stationary distribution characterized by a transient, typically fluctuating about a stable equilibrium before becoming extinct [77]. In this case, we would deal with a truncated portion of a stationary distribution, which would be appropriate for our problem. However, since our goal is to obtain the scaling dependence of the first passage time on the noise amplitude, we exploit stationary distributions for both the pollinator and plant species.
We first treat demographic noise. Substituting v(x) = ζ2x2, u(y) = ζ2y2, d(x) and d(y) into equations (4.1) and (4.2) yields,
| 4.3 |
and
| 4.4 |
where
| 4.5 |
and
| 4.6 |
For an ergodic variable x with a stationary distribution, the mean first passage time is given by [75]
| 4.7 |
where x < n and n is the final abundance. The mean first passage time τ for the pollinator species is
| 4.8 |
where the area under p(x) between x0 and xf gives the fraction of time that the process x spends in the interval (x0, xf), x0 is the initial value and xf is the final value. Substituting equation (4.3) into equation (4.8), we get
| 4.9 |
where is the error function. Carrying out the integration, we get
| 4.10 |
Equation (4.10) gives dependence of τ on the noise amplitude ζ. While the dependence appears complicated, numerical testing of equation (4.10) in figure 8b reveals the scaling relation (3.4).
Figure 8.
Numerical test of equation (4.10) and equation (4.16). (a,b) are the numerical simulation of the formulae of scaling law for environmental noise and demographic noise, respectively. The constant C is set as 1.
We next consider environmental noise. With v(x) = σ2 and v(y) = σ2, we can rewrite the probability density function as
| 4.11 |
and
| 4.12 |
where
| 4.13 |
and
| 4.14 |
For initial condition x0 and final state xf, the mean first passage time τ for pollinators is
| 4.15 |
Substituting equation (4.11) into equation (4.15), we get
| 4.16 |
where is the error function. Numerical testing of equation (4.16) shown in figure 8a attests to the scaling law (3.3).
A remark about the generality of the scaling laws is in order. Our calculation of the equilibria and derivation of the scaling laws of noise-induced transients rely on the reduced 2D model that is mathematically amenable to analysis. The 2D model was developed based on data from 59 empirical real world networks and was shown to capture the essential behaviour of the real networks from a wide geographical range across continents and climate zones [42]. The 2D model can accurately predict the occurrence of the tipping point, even in presence of stochastic disturbances. These features of the 2D model suggest that it can serve as a general paradigm to study the dynamics of complex stochastic mutualistic networks and, consequently, the scaling results obtained here are expected to be general as well.
5. Discussion
Transients, stochasticity and high dimensionality represent the three main obstacles to long-term forecasting of ecological systems. To understand the interplay among the three is thus of paramount importance and broad interest. In this paper, we take a step forward to addressing this challenging issue by investigating the transient dynamics associated with species collapse and recovery in a generic class of mutualistic networked systems subject to stochastic influences. Such a networked system is high-dimensional [29,35–44], whose dynamics are described by the interactions of two groups of species, e.g. pollinators and plants, in a mutualistic manner.
How do transients manifest themselves in a mutualistic networked system? According to current understanding, the deterministic dynamical picture of a mutualistic network is dominated by a tipping point transition [43]. In particular, as a parameter characterizing the ecological conditions varies in the direction of environmental deterioration, at a critical point (tipping point), the populations of all species can collapse. As the environment is gradually improved so as to cause the parameter to vary in the opposite direction, at another critical point the species populations begin to recover. The values of the two critical points typically differ, leading to a hysteresis loop with the implication that the environment needs to be significantly more improved for the recovery to take place [43]. In the presence of stochasticity, this deterministic picture is replaced by the phenomena of noise-induced collapse and recovery. For example, at a parameter value prior to the deterministic tipping point where the system would be in a survival state with healthy populations, noise can induce a collapse. Likewise, in the parameter regime where the deterministic system is in an extinction state, noise can induce recovery of the species populations. For both noise-induced phenomena, the basic dynamical mechanism is a transition between two stable steady states: one corresponding to survival and another to extinction, and it takes time for the transition to complete. This naturally brings transients into the picture and provides a paradigmatic setting for gaining insights into the complex interplay of transients, stochasticity and high dimensionality.
Our approach is to use the full high-dimensional networked system to demonstrate the phenomena of noise-induced collapse and recovery. Simulations reveal the ubiquity of transient behaviours for both environmental (Gaussian white) noise and demographic (state-dependent, coloured) noise. However, to obtain a quantitative understanding of the transients, the full high-dimensional system becomes infeasible both computationally and theoretically. We thus take advantage of the 2D reduced model that was previously demonstrated to be effective at capturing the essential tipping point dynamics [42] to numerically obtain the scaling laws quantifying the two noise-induced phenomena. The 2D model also enables a theoretical analysis of the underlying transient behaviours in terms of the mean first passage time. In particular, the tipping point transition occurs between the steady states created by saddle-node bifurcations, where the low- and high-abundance steady states correspond to extinction and survival, respectively, and the unstable state determines the boundary that separates the basins of the two steady states. Depending on the initial and final states, the transition can be a collapse process (a reverse saddle-node bifurcation) or a recovery process (a forward saddle-node bifurcation). The phenomena of noise-induced collapse and recovery occur in the parameter regime in between the two saddle-node bifurcations, which also depend on the nature of the noise. In particular, environmental noise has an additive influence on the transition behaviours, but the effect of demographic noise depends on the species abundance. If the initial state of the system is in the high-abundance steady state, demographic noise is strong, making it the dominant stochastic source to induce a system collapse. In contrast, the strength of the demographic noise becomes small when the initial state is in the basin of the low-abundance steady state, so it has little effect on the dynamics, leaving room for environmental noise to play a dominant role in affecting the recovery dynamics. For both types of noise, the associated average transient time is found to scale with the amplitude algebraically, which is established numerically with support from a physical theory based on the mean first passage time of the underlying stochastic dynamical system.
In nonlinear dynamical systems in general, transients can have a deterministic origin or they can be induced by noise. In the high-dimensional ecological networks studied in this paper, both types of transients can occur. In particular, if the bifurcation parameter κ is below the tipping point, the noiseless deterministic dynamics are governed by stable survival and extinction states. For a fixed value of κ (and other system parameters too) in this regime, neither a collapse from the survival state nor a recovery from the extinction state can occur. The two transitions are possible only if either or both environmental and demographic noises are present. Dynamically, we have then, what we call, noise-induced transients, whose duration is exponentially distributed and the average transient time follows an algebraic scaling with the noise amplitude. However, if κ is beyond the deterministic tipping point, transient dynamics can occur before the system finally collapses into the extinction state. A tipping point transition or a regime shift can occur after a period of relative stasis without noise, even in the absence of further deterioration of the environment. The timing of the eventual collapse is difficult to predict because of the random nature of the transient time. Taken together, in the pre-tipping point regime, transients are induced by noise but, in the post-tipping point regime, deterministic transients arise.
In the present work, we have used mutualistic networks as a gateway to studying high-dimensional ecological networks. Because of the mutualistic interactions, when a group of pollinators or plants becomes extinct, the abundances of other species that are in mutualistic relationships with the extinct species are also greatly affected. Under external drivers such as improved environmental conditions and incubation of pollinators, the extinct species may gradually recover their abundances and the corresponding species with the mutualistic relationship are also recovered. This kind of dynamics is at the core of our work, and its general principles, ideas and methods can be extended to complex networks in other disciplines to address critical issues such as resilience and sustainability.
Our results suggest possible management strategies for high-dimensional ecological systems under stochastic influences. For example, in view of the detrimental effect of demographic noise in causing an ecosystem to collapse, as analysed in this paper, it is of critical importance to devise methods to reduce the level of demographic noise to keep the system in the survival state. In contrary, when the system is already in extinction, a suitable amount of environmental noise may facilitate recovery [29]. The algebraic scaling law of the average transient lifetime uncovered here suggests that the recovery process can be expedited with stronger noise.
There has been large-scale extinction of many species of pollinators, such as wild bees, while other species are in trouble as well. The collapse of pollinators has unimaginable consequences for biodiversity and food production. Their protection is vital for our survival. The pollinator ecosystems are affected by a host of perturbations, such as climate change caused by global warming, the excessive use of pesticides, diseases and bacterial infections, and loss of habitats due to pollution, fragmentation and destruction. A reliable understanding of the tipping point dynamics in ecological networks has profound implications for addressing critical issues, such as resilience and sustainability, for nature conservation and ecosystem management.
Supplementary Material
Supplementary Material
Data accessibility
All data and computer codes are available from the authors upon request. All data are available as electronic supplementary material.
Authors' contributions
C.G. and Y.-C.L. conceived the project. Y.M. performed computations and analysis. All analysed data. All wrote the paper.
Competing interests
The authors declare that they have no competing interests.
Funding
Y.M. was partially supported by the University of Aberdeen Elphinstone Fellowship. Y.-C.L. would like to acknowledge support from the Vannevar Bush Faculty Fellowship Program sponsored by the Basic Research Office of the Assistant Secretary of Defense for Research and Engineering and funded by the Office of Naval Research through grant no. N00014-16-1-2828.
References
- 1.Dietze MC. 2017. Prediction in ecology: a first-principles framework. Ecol. Appl. 27, 2048–2060. ( 10.1002/eap.1589) [DOI] [PubMed] [Google Scholar]
- 2.Grebogi C, Ott E, Yorke JA. 1983. Crises, sudden changes in chaotic attractors and chaotic transients. Physica D 7, 181–200. ( 10.1016/0167-2789(83)90126-4) [DOI] [Google Scholar]
- 3.Lai Y-C, Tél T. 2011. Transient chaos—complex dynamics on finite time scales. New York, NY: Springer. [Google Scholar]
- 4.Hastings A, Higgins K. 1994. Persistence of transients in spatially structured ecological models. Science 263, 1133–1136. ( 10.1126/science.263.5150.1133) [DOI] [PubMed] [Google Scholar]
- 5.Hastings A. 2001. Transient dynamics and persistence of ecological systems. Ecol. Lett. 4, 215–220. ( 10.1046/j.1461-0248.2001.00220.x) [DOI] [Google Scholar]
- 6.Dhamala M, Lai Y-C, Holt RD. 2001. How often are chaotic transients in spatially extended ecological systems? Phys. Lett. A 280, 297–302. ( 10.1016/S0375-9601(01)00069-X) [DOI] [Google Scholar]
- 7.Hastings A. 2004. Transients: the key to long-term ecological understanding? Trends Ecol. Evol. 19, 39–45. ( 10.1016/j.tree.2003.09.007) [DOI] [PubMed] [Google Scholar]
- 8.Hastings A. 2016. Timescales and the management of ecological systems. Proc. Natl Acad. Sci. USA 113, 14 568–14 573. ( 10.1073/pnas.1604974113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hastings A. et al. 2018. Transient phenomena in ecology. Science 361, eaat6412 ( 10.1126/science.aat6412) [DOI] [PubMed] [Google Scholar]
- 10.Morozov A. et al. 2020. Long transients in ecology: theory and applications. Phys. Life Rev. 32, 1–40. ( 10.1016/j.plrev.2019.09.004) [DOI] [PubMed] [Google Scholar]
- 11.Scheffer M, Straile D, van Nes EH, Hosper H. 2001. Climatic warming causes regime shifts in lake food webs. Limnol. Oceanogr. 46, 1780–1783. ( 10.4319/lo.2001.46.7.1780) [DOI] [Google Scholar]
- 12.Carpenter SR. et al. 2011. Early warnings of regime shifts: a whole-ecosystem experiment. Science 332, 1079–1082. ( 10.1126/science.1203672) [DOI] [PubMed] [Google Scholar]
- 13.Boettiger C, Hastings A. 2012. Quantifying limits to detection of early warning for critical transitions. J. R. Soc. Interface 9, 2527–2539. ( 10.1098/rsif.2012.0125) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Roughgarden J. 1975. A simple model for population dynamics in stochastic environments. Am. Nat. 109, 713–736. ( 10.1086/283039) [DOI] [Google Scholar]
- 15.Lande R. 1993. Risks of population extinction from demographic and environmental stochasticity and random catastrophes. Am. Nat. 142, 911–927. ( 10.1086/285580) [DOI] [PubMed] [Google Scholar]
- 16.Yao Q, Tong H. 1994. On prediction and chaos in stochastic systems. Phil. Trans. R. Soc. Lond. A 348, 357–369. ( 10.1098/rsta.1994.0096) [DOI] [Google Scholar]
- 17.Ludwig D. 1996. The distribution of population survival times. Am. Nat. 147, 506–526. ( 10.1086/285863) [DOI] [Google Scholar]
- 18.Ripa J, Lundberg P, Kaitala V. 1998. A general theory of environmental noise in ecological food webs. Am. Nat. 151, 256–263. ( 10.1086/286116) [DOI] [PubMed] [Google Scholar]
- 19.Lande R. 1998. Demographic stochasticity and Allee effect on a scale with isotropic noise. Oikos 83, 353–358. ( 10.2307/3546849) [DOI] [Google Scholar]
- 20.Dennis B. 2002. Allee effects in stochastic populations. Oikos 96, 389–401. ( 10.1034/j.1600-0706.2002.960301.x) [DOI] [Google Scholar]
- 21.Bonsall MB, Hastings A. 2004. Demographic and environmental stochasticity in predator–prey metapopulation dynamics. J. Anim. Ecol. 73, 1043–1055. ( 10.1111/j.0021-8790.2004.00874.x) [DOI] [Google Scholar]
- 22.Ellner SP, Turchin P. 2005. When can noise induce chaos and why does it matter: a critique. Oikos 111, 620–631. ( 10.1111/j.1600-0706.2005.14129.x) [DOI] [Google Scholar]
- 23.Lai Y-C, Liu Y-R. 2005. Noise promotes species diversity in nature. Phys. Rev. Lett. 94, 038102 ( 10.1103/PhysRevLett.94.038102) [DOI] [PubMed] [Google Scholar]
- 24.Lai Y-C. 2005. Beneficial role of noise in promoting species diversity through stochastic resonance. Phys. Rev. E 72, 042901 ( 10.1103/PhysRevE.72.042901) [DOI] [PubMed] [Google Scholar]
- 25.Guttal V, Jayaprakash C. 2007. Impact of noise on bistable ecological systems. Ecol. Model. 201, 420–428. ( 10.1016/j.ecolmodel.2006.10.005) [DOI] [Google Scholar]
- 26.Doney SC, Sailley SF. 2013. When an ecological regime shift is really just stochastic noise. Proc. Natl Acad. Sci. USA 110, 2438–2439. ( 10.1073/pnas.1222736110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bjornstad ON. 2015. Nonlinearity and chaos in ecological dynamics revisited. Proc. Natl Acad. Sci. USA 112, 6252–6253. ( 10.1073/pnas.1507708112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.O’Regan SM. 2018. How noise and coupling influence leading indicators of population extinction in a spatially extended ecological system. J. Biol. Dyn. 12, 211–241. ( 10.1080/17513758.2017.1339834) [DOI] [PubMed] [Google Scholar]
- 29.Meng Y, Jiang J, Grebogi C, Lai Y-C. 2020. Noise-enabled species recovery in the aftermath of a tipping point. Phys. Rev. E 101, 012206 ( 10.1103/PhysRevE.101.012206) [DOI] [PubMed] [Google Scholar]
- 30.Heino M. 1998. Noise colour, synchrony and extinctions in spatially structured populations. Oikos 83, 368–375. ( 10.2307/3546851) [DOI] [Google Scholar]
- 31.Benton TG, Lapsley C, Beckerman AP. 2002. The population response to environmental noise: population size, variance and correlation in an experimental system. J. Anim. Ecol. 71, 320–332. ( 10.1046/j.1365-2656.2002.00601.x) [DOI] [Google Scholar]
- 32.Grenfell BT, Bjornstad ON, Finkenstädt BF. 2002. Dynamics of measles epidemics: scaling noise, determinism, and predictability with the TSIR model. Ecol. Monogr. 72, 185–202. ( 10.1890/0012-9615(2002)072[0185:DOMESN]2.0.CO;2) [DOI] [Google Scholar]
- 33.Martín PV, Bonachela JA, Levin SA, Muñoz MA. 2015. Eluding catastrophic shifts. Proc. Natl Acad. Sci. USA 112, E1828–E1836. ( 10.1073/pnas.1414708112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Constable GWA, Rogers T, McKane AJ, Tarnita CE. 2016. Demographic noise can reverse the direction of deterministic selection. Proc. Natl Acad. Sci. USA 113, E4745–E4754. ( 10.1073/pnas.1603693113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bascompte J, Jordano P, Melián CJ, Olesen JM. 2003. The nested assembly of plant–animal mutualistic networks. Proc. Natl Acad. Sci. USA 100, 9383–9387. ( 10.1073/pnas.1633576100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Guimaraes PR, Jordano P, Thompson JN. 2011. Evolution and coevolution in mutualistic networks. Ecol. Lett. 14, 877–885. ( 10.1111/j.1461-0248.2011.01649.x) [DOI] [PubMed] [Google Scholar]
- 37.Nuismer SL, Jordano P, Bascompte J. 2013. Coevolution and the architecture of mutualistic networks. Evolution 67, 338–354. ( 10.1111/j.1558-5646.2012.01801.x) [DOI] [PubMed] [Google Scholar]
- 38.Lever JJ, Nes EH, Scheffer M, Bascompte J. 2014. The sudden collapse of pollinator communities. Ecol. Lett. 17, 350–359. ( 10.1111/ele.12236) [DOI] [PubMed] [Google Scholar]
- 39.Rohr RP, Saavedra S, Bascompte J. 2014. On the structural stability of mutualistic systems. Science 345, 1253497 ( 10.1126/science.1253497) [DOI] [PubMed] [Google Scholar]
- 40.Dakos V, Bascompte J. 2014. Critical slowing down as early warning for the onset of collapse in mutualistic communities. Proc. Natl Acad. Sci. USA 111, 17 546–17 551. ( 10.1073/pnas.1406326111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Guimaraes PR, Pires MM, Jordano P, Bascompte J, Thompson JN. 2017. Indirect effects drive coevolution in mutualistic networks. Nature 550, 511–514. ( 10.1038/nature24273) [DOI] [PubMed] [Google Scholar]
- 42.Jiang J. et al. 2018. Predicting tipping points in mutualistic networks through dimension reduction. Proc. Natl Acad. Sci. USA 115, E639–E647. ( 10.1073/pnas.1714958115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jiang J, Hastings A, Lai Y-C. 2019. Harnessing tipping points in complex ecological networks. J. R. Soc. Interface 16, 20190345 ( 10.1098/rsif.2019.0345) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ohgushi T, Schmitz O, Holt RD. 2012. Trait-mediated indirect interactions: ecological and evolutionary perspectives. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 45.Scheffer M. 2004. Ecology of shallow lakes. Amsterdam, The Netherlands: Springer Science & Business Media. [Google Scholar]
- 46.Scheffer M. et al. 2009. Early-warning signals for critical transitions. Nature 461, 53–59. ( 10.1038/nature08227) [DOI] [PubMed] [Google Scholar]
- 47.Scheffer M. 2010. Complex systems: foreseeing tipping points. Nature 467, 411–412. ( 10.1038/467411a) [DOI] [PubMed] [Google Scholar]
- 48.Wysham DB, Hastings A. 2010. Regime shifts in ecological systems can occur with no warning. Ecol. Lett. 13, 464–472. ( 10.1111/j.1461-0248.2010.01439.x) [DOI] [PubMed] [Google Scholar]
- 49.Drake JM, Griffen BD. 2010. Early warning signals of extinction in deteriorating environments. Nature 467, 456–459. ( 10.1038/nature09389) [DOI] [PubMed] [Google Scholar]
- 50.Dai L, Vorselen D, Korolev KS, Gore J. 2012. Generic indicators for loss of resilience before a tipping point leading to population collapse. Science 336, 1175–1177. ( 10.1126/science.1219805) [DOI] [PubMed] [Google Scholar]
- 51.Ashwin P, Wieczorek S, Vitolo R, Cox P. 2012. Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system. Phil. Trans. R. Soc. A 370, 1166–1184. ( 10.1098/rsta.2011.0306) [DOI] [PubMed] [Google Scholar]
- 52.Lenton TM, Livina VN, Dakos V, van Nes EH, Scheffer M. 2012. Early warning of climate tipping points from critical slowing down: comparing methods to improve robustness. Phil. Trans. R. Soc. A 370, 1185–1204. ( 10.1098/rsta.2011.0304) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Barnosky AD. et al. 2012. Approaching a state shift in Earth’s biosphere. Nature 486, 52–58. ( 10.1038/nature11018) [DOI] [PubMed] [Google Scholar]
- 54.Boettiger C, Hastings A. 2013. Tipping points: from patterns to predictions. Nature 493, 157–158. ( 10.1038/493157a) [DOI] [PubMed] [Google Scholar]
- 55.Tylianakis JM, Coux C. 2014. Tipping points in ecological networks. Trends Plant Sci. 19, 281–283. ( 10.1016/j.tplants.2014.03.006) [DOI] [PubMed] [Google Scholar]
- 56.Lontzek TS, Cai Y-Y, Judd KL, Lenton TM. 2015. Stochastic integrated assessment of climate tipping points indicates the need for strict climate policy. Nat. Clim. Change 5, 441–444. ( 10.1038/nclimate2570) [DOI] [Google Scholar]
- 57.Gualdia S, Tarziaa M, Zamponic F, Bouchaudd J-P. 2015. Tipping points in macroeconomic agent-based models. J. Econ. Dyn. Control 50, 29–61. ( 10.1016/j.jedc.2014.08.003) [DOI] [Google Scholar]
- 58.Holling CS. 1959. Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398. ( 10.4039/Ent91385-7) [DOI] [Google Scholar]
- 59.Weissmann H, Shnerb NM, Kessler DA. 2018. Simulation of spatial systems with demographic noise. Phys. Rev. E 98, 022131 ( 10.1103/PhysRevE.98.022131) [DOI] [PubMed] [Google Scholar]
- 60.Van den Broeck C, Parrondo JMR, Toral R, Kawai R. 1997. Nonequilibrium phase transitions induced by multiplicative noise. Phys. Rev. E 55, 4084–4094. ( 10.1103/PhysRevE.55.4084) [DOI] [Google Scholar]
- 61.Pechenik L, Levine H. 1999. Interfacial velocity corrections due to multiplicative noise. Phys. Rev. E 59, 3893 ( 10.1103/PhysRevE.59.3893) [DOI] [Google Scholar]
- 62.Feudel U, Grebogi C. 1997. Multistability and the control of complexity. Chaos 7, 597–604. ( 10.1063/1.166259) [DOI] [PubMed] [Google Scholar]
- 63.Kraut S, Feudel U, Grebogi C. 1999. Preference of attractors in noisy multistable systems. Phys. Rev. E 59, 5253–5260. ( 10.1103/PhysRevE.59.5253) [DOI] [PubMed] [Google Scholar]
- 64.Sommerer JC, Ott E, Grebogi C. 1991. Scaling law for characteristic times of noise-induced crises. Phys. Rev. A 43, 1754 ( 10.1103/PhysRevA.43.1754) [DOI] [PubMed] [Google Scholar]
- 65.Lai Y-C, Grebogi C. 2017. Quasiperiodicity and suppression of multistability in nonlinear dynamical systems. Eur. Phys. J. Spec. Top. 226, 1703–1719. ( 10.1140/epjst/e2017-70062-0) [DOI] [Google Scholar]
- 66.McDonald SW, Grebogi C, Ott E, Yorke JA. 1985. Fractal basin boundaries. Physica D 17, 125–153. ( 10.1016/0167-2789(85)90001-6) [DOI] [Google Scholar]
- 67.Liu Z, Lai Y-C, Billings L, Schwartz IB. 2002. Transition to chaos in continuous-time random dynamical systems. Phys. Rev. Lett. 88, 124101 ( 10.1103/PhysRevLett.88.124101) [DOI] [PubMed] [Google Scholar]
- 68.Lai Y-C, Liu Z, Billings L, Schwartz IB. 2003. Noise-induced unstable dimension variability and transition to chaos in random dynamical systems. Phys. Rev. E 67, 026210 ( 10.1103/PhysRevE.67.026210) [DOI] [PubMed] [Google Scholar]
- 69.Poon L, Grebogi C. 1995. Controlling complexity. Phys. Rev. Lett. 75, 4023–4026. ( 10.1103/PhysRevLett.75.4023) [DOI] [PubMed] [Google Scholar]
- 70.Lai Y-C. 1996. Driving trajectories to a desirable attractor by using small control. Phys. Lett. A 221, 375–383. ( 10.1016/0375-9601(96)00609-3) [DOI] [Google Scholar]
- 71.Grebogi C, Ott E, Romeiras F, Yorke JA. 1987. Critical exponents for crisis-induced intermittency. Phys. Rev. A 36, 5365–5380. ( 10.1103/PhysRevA.36.5365) [DOI] [PubMed] [Google Scholar]
- 72.Talkner P. 1987. Mean first passage time and the lifetime of a metastable state. Z. Physik B Condensed Matter 68, 201–207. ( 10.1007/BF01304226) [DOI] [Google Scholar]
- 73.Dennis B, Patil GP. 1984. The gamma distribution and weighted multimodal gamma distributions as models of population abundance. Math. Biosci. 68, 187–212. ( 10.1016/0025-5564(84)90031-2) [DOI] [Google Scholar]
- 74.Dennis B, Costantino RF. 1988. Analysis of steady-state populations with the gamma abundance model: application to Tribolium. Ecology 69, 1200–1213. ( 10.2307/1941275) [DOI] [Google Scholar]
- 75.Dennis B, Assas L, Elaydi S, Kwessi E, Livadiotis G. 2016. Allee effects and resilience in stochastic populations. Theor. Ecol. 9, 323–335. ( 10.1007/s12080-015-0288-2) [DOI] [Google Scholar]
- 76.Karlin S, Taylor HE. 1981. A second course in stochastic processes. New York, NY: Elsevier. [Google Scholar]
- 77.Allen LJ. 2010. An introduction to stochastic processes with applications to biology. New York, NY: CRC Press. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data and computer codes are available from the authors upon request. All data are available as electronic supplementary material.