Distance-based analysis of variance for brain connectivity

Abstract

The field of neuroimaging dedicated to mapping connections in the brain is increasingly being recognized as key for understanding neurodevelopment and pathology. Networks of these connections are quantitatively represented using complex structures, including matrices, functions, and graphs, which require specialized statistical techniques for estimation and inference about developmental and disorder-related changes. Unfortunately, classical statistical testing procedures are not well suited to high-dimensional testing problems. In the context of global or regional tests for differences in neuroimaging data, traditional analysis of variance (ANOVA) is not directly applicable without first summarizing the data into univariate or low-dimensional features, a process that might mask the salient features of high-dimensional distributions. In this work, we consider a general framework for two-sample testing of complex structures by studying generalized within-group and between-group variances based on distances between complex and potentially high-dimensional observations. We derive an asymptotic approximation to the null distribution of the ANOVA test statistic, and conduct simulation studies with scalar and graph outcomes to study finite sample properties of the test. Finally, we apply our test to our motivating study of structural connectivity in autism spectrum disorder.

1 |. INTRODUCTION

Connectomics, the field of neuroimaging dedicated to mapping connections in the brain, is increasingly being recognized as key for understanding neurodevelopment. Structural networks exist as physically connected regions of the brain, and functional networks are groups of regions that tend to function together. The study of these complex networks is crucial for developing cognitive and pharmaceutical therapies for treating psychiatric, neuro-logical, and developmental disorders. Quantitatively, these networks are often represented using complex structures, including matrices, functions, and graphs, and require specialized statistical techniques for estimation and inference about developmental and disorder-related changes.

Principled statistical methods are necessary for analyzing these structures. Due to the scale of their dimensionality, common approaches currently include simplistic connection-wise methods whose power is hindered by the need for multiple comparison correction. Unfortunately, classical statistical testing procedures are not well suited to high-dimensional testing problems. An alternative approach, which is also common in the context of neuroimaging analysis, is to test for global differences in summary measures and then visualize or use exploratory techniques to investigate where group differences exist in structure or function. Common techniques for this include averaging across volumetric or surface-based images, or extraction of salient network features such as modularity (Newman, 2006); however, this current state of the art fails to leverage the full structure of the observed data for comparisons.

In the context of global or regional tests for differences in neuroimaging data, traditional analysis of variance (ANOVA) is not directly applicable without first summarizing the data into univariate or low-dimensional features, a process that might mask the salient features of high-dimensional distributions. Direct statistical inference on the imaging objects is fundamentally hindered by the lack of a precise definition of variance in high-dimensional data, which in turn hampers the comparison of within-group to between-group variability. In this paper, we propose a general framework for ANOVA testing of complex structures by studying generalized within-group and between-group variances based on distances between high-dimensional observations.

The methods we propose are closely related to the fields of distance statistics and kernel testing, which have been shown to be equivalent in many cases (Sejdinovic et al., 2013). Similar to our proposed methodology, the literature in both of these fields centers around the reduction of the observed data using a distance (or kernel) to describe the dissimilarity between subjects. Kernel tests have been used extensively in statistical genetics, and were pioneered in association studies by Kwee et al. (2008). These score-based tests, which use the high-dimensional genetic data as predictors and scalar outcomes, have been used in the context of common and rare variant analyses (Wu et al., 2011; Ionita-Laza et al., 2013), and are recognized as an important tool for the analysis of sequencing data. The limiting distribution of kernel test statistics is well understood (Zhang and Lin, 2003). Another approach in genetic analyses involves sum tests (Wang and Elston, 2007; Pan, 2009), which are based on the assumption that all genetic predictors have the same association with the outcome, and sum tests study this common association parameter using weighted sums of the predictors. More recently, much work has focused on developing versions of these tests that adaptively choose these weights and combine kernels to optimize power (Lee et al., 2012; Ionita-Laza et al., 2013; Pan et al., 2014; Zhao et al., 2015; Van de kar et al., 2018) to detect both sparse and dense alternatives. While both kernel and sum tests benefit from the convenience of linear model specification for the sake of adjusting for confounding variables, their performance under model misspecification is not well understood. Finally, distance correlation (Székely et al., 2007; Székely and Rizzo, 2009) is an alternate measure of multivariate dependence for high-dimensional random vectors. Leveraging a distance measure to generalize Pearson correlation, distance correlation provides a means for assessing complex nonlinear correlations and testing independence. Distance correlation, which was proposed for the Euclidean random vector observation case, has also been shown to be related to the kernel-based maximum mean discrepancy tests popular in machine learning literature (Sejdinovic et al., 2013). More recently, other manifold-based testing procedures that leverage distance between the spaces in which the observed data reside have been proposed. These have based inference on the bootstrap (Pan et al., 2017) or asymptotic approximations for particular ball-based divergences (Pan et al., 2018).

For testing in higher dimensions, distance-based ANOVA considers the partitioning of sums of squared distances between subjects. Although pioneered in the ecology literature (McArdle and Anderson, 2001), distance-based ANOVA is increasingly being used in genomics (Minas et al., 2011) and neuroimaging (Reiss et al., 2010). This approach uses a pseudo-F statistic that assesses the ratio of the within-group distances to the between-group distances. The framework is similar to the kernel-based testing proposed by Gretton et al. (2012) based on the maximum mean discrepancy, but the form of the test statistic differs. Unfortunately, the null distribution of the distance-based ANOVA test statistic is not easily approximated and thus inference to date has been based solely on Monte Carlo approximations of the permutation distribution (PERMANOVA). This is computationally intensive and suboptimal in terms of statistical power. The potential inefficiency of permutation-based testing stems from the flexible estimation strategy for the null distribution. A recent work by Minas and Montana (2014) developed an analytical approximation to the permutation null distribution, which promises much improved computational time with similar power. Fast versions of kernel tests and distance correlation statistics based on matching moments to the permutation distribution have also been proposed by Zhan et al. (2017). While PERMANOVA tests are closely related to distance correlation under specific choices of distance functions in the case of random vectors, their extension to the case of more complex outcome structures has not yet been formalized.

In the remainder of this paper, we propose an analytical approach for testing for differences in the distribution of complex structures leveraging the PERMANOVA framework. In the next section, we describe this test in detail and derive its limiting distribution. We then consider a motivating study of structural connectivity in the brains of subjects with autism spectrum disorders. In Section 4, we conduct simulation analyses in four different settings: a scalar outcome, a graphical outcome, a functional outcome, and a real data-based connectomic outcome. We conclude with a discussion in Section 5.

2 |. PROPOSED METHODOLOGY

For a prototypical subject, the data unit is X ≔ (M, D), where M is an object in some space $\mathcal{M}$ and D ∈ {0, 1, …, K − 1} is a disease group indicator. We denote by P₀ the true distribution of X. Suppose that $r:\mathcal{M}\times \mathcal{M}\to [0,+\infty )$ is a semimetric, symmetric discrepancy function that quantifies in some scientific context-dependent manner how dissimilar two given objects in $\mathcal{M}$ are. Suppose that we observe n independent draws X₁ ≔ (M₁, D₁), X₂ ≔ (M₂, D₂), …, X_n ≔ (M_n, D_n) from P₀—each of these corresponds to measurements taken on a different subject.

Our goal is to use the available data to determine whether the distribution of M is the same across all subpopulations defined by D. For each d ∈ {0, 1, …, K − 1}, we denote by P_0d the conditional distribution of M given D = d implied by P₀. Our null hypothesis is then

$${\mathcal{H}}_0:P_{00}=P_{01}=\cdots =P_{0(K-1)}.$$

This corresponds to the null hypothesis wherein M and D are independent under P₀. To test this hypothesis, we will use the classical partitioning of variation approach from the classical ANOVA setting. A central quantity in the developments to follow, which we refer to as the r-variance of a population of objects $M\in \mathcal{M}$ with distribution P, is defined as ${\sigma }^2(P):=E_{P\times P}\left\{r\left(M_1,M_2\right)\right\}=\iint r\left(m_1,m_2\right)dP\left(m_1\right)dP\left(m_2\right)$. This definition for the variance of an object is particularly convenient because it generalizes the usual notion of variance in an interpretable fashion. Also, the natural U-statistic estimator

$${\sigma }_n^2:={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}r\left(M_i,M_j\right)$$

of the r-variance σ² (P_0*) based on the marginal distribution P_0* of M implied by P₀ lends itself to relatively simple theoretical analysis. We note that although the computation of the above sum may be burdensome in large samples, a Monte Carlo approximation based on randomly sampling pairs of subjects can easily be used. We wish to construct an ANOVA-like test statistic using r-variance. Denoting by π_s the marginal probability that D = s under P₀, we observe that the ANOVA discrepancy

$$T\left(P_0\right):=\frac{{\sigma }^2\left(P_{0*}\right)-{\sum }_{s=0}^{K-1}{\pi }_s{\sigma }^2\left(P_{0s}\right)}{{\sum }_{s=0}^{K-1}{\pi }_s{\sigma }^2\left(P_{0s}\right)}$$

is identically zero under ${\mathcal{H}}_0$. A sample version of this discrepancy based on U-statistics can be used as the test statistic. To construct this statistic, we define the within-group analog of the sum of squared distances as

$$\begin{gathered} SS{E}_n:=\sum _{s=0}^{K-1}\left(n_s-1\right){\left(\begin{array}{c}{n}_s\\ 2\end{array}\right)}^{-1}\sum _{i<j}r\left(M_i,M_j\right)I(D_i=D_j \\ =s) \end{gathered}$$

and the total sum of squared distances as $S{S}_n:=(n-1){\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}r\left(M_i,M_j\right)$, where we set $n_s:={\sum }_{i}I\left(D_i=s\right)$. The scaled quantities SSE_n∕n and SS_n∕n are nonparametric estimators of ${\sum }_{s=0}^{K-1}{\pi }_s{\sigma }^2\left(P_{0s}\right)$ and σ² (P_0*), respectively. The difference SST_n ≔ SS_n − SSE_n corresponds to an analog of the between-group sum of squares. An empirical estimator of T(P ₀) is thus given by

$$T_n:=\frac{1}{n}\left\{\frac{SS{T}_n/(K-1)}{SS{E}_n/(n-K)}\right\},$$

which can be seen as a scaled F-like test statistic. The unscaled counterpart of this statistic, Q_n ≔ nT_n, is known as the distance-based pseudo-F statistic. Large positive values of the test statistic Q_n are incompatible with the null hypothesis ${\mathcal{H}}_0$ of independence between M and D. This approach was first proposed by Anderson (1963), who noted that it reduces to the classical ANOVA F statistic in the scalar Euclidean case. However, in the general case the test statistic does not follow an F distribution, and Anderson (1963) suggested randomly permuting the group labels (D₁, D₂, …, D_n) to approximate sampling from the null distribution. Minas et al. (2011) suggested a similar statistic with different degrees of freedom in the numerator and denominator. Recently, Minas and Montana (2014) developed a Pearson type III approximation for the permutation distribution of the F statistic, which significantly reduces the computational burden of testing. These methods all potentially suffer from a loss of power from the permutation-based approximation, which we investigate in Section 4. The proposed test statistic T_n is also closely related to work by Gretton et al. (2012), who studied a quantity similar to SST_n from the perspective of maximum mean discrepancy. When M is a random vector in ${ℝ}^p$ and r is the Euclidean norm, the numerator of the proposed pseudo-F statistic is closely related to the empirical distance covariance (Székely and Rizzo, 2009) between M and D observations, which is a weighted combination of the average within-group and between-group distances. However, for more complex structures, such as those of interest in connectomics, the ability to use more general distance functions and to accommodate complex data objects is crucial.

To determine appropriate test cutoffs to use for Q_n without relying on permutations, we require a better understanding of the distribution of Q_n under ${\mathcal{H}}_0$. The U-statistic form of the sample r-variance can be leveraged to obtain a distributional approximation to the various building blocks of the pseudo-F statistic under ${\mathcal{H}}_0$. We begin by studying the large-sample behavior of both SSE_n and SST_n.

Theorem 1.

1. Under ${\mathcal{H}}_0$, the denominator SSE_n∕(n − K) of Q_n tends to σ² (P_0*) in probability.

2. Provided σ² (P_0*) ∈ (0, +∞) and π_s ∈ (0, 1) for some s ∈ {0, 1, …, K − 1}, the numerator of Q_n can be written as

   $$\begin{gathered} SS{T}_n/(K-1)={\sigma }^2\left(P_{0*}\right)+n/(K-1) \\ \times {\left(\begin{array}{l}n\hfill \\ 2\hfill \end{array}\right)}^{-1}\sum _{i<j}u\left(M_i,M_j\right)+o_P(1) \end{gathered}$$

   under ${\mathcal{H}}_0$ for some first-order nondegenerate kernel u, whose form is given in the Supporting Information. As such, in large samples, the distribution of SST_n is approximated by that of the infinite series

   $$(K-1)\cdot {\sigma }^2\left(P_{0*}\right)+\sum _{j=1}^{\infty }{\lambda }_j\left(Z_j^2-1\right),$$

   where Z₁, Z₂, … are independent standard normal variates and λ₁, λ₂, … are eigenvalues of the operator that maps any given function g into $m\mapsto \int u\left(m,m_2\right)g\left(m_2\right)d{P}_{00}\left(m_2\right)$.

The proof of this theorem leverages a representation of the statistic as a first-order degenerate U-statistic. To demonstrate this, in appendix, we outline the decomposition of SST_n into three parts. We state and prove a lemma that shows that the product the estimation errors of two asymptotically linear estimators is asymptotically equivalent to a U-statistic. Together with the Hájek projection, this in turn shows that SST_n admits the claimed representation. The result then follows directly from the theory of U-statistics. Using this description of the behavior of the key building blocks of our test statistic Q_n, we are able to describe its large-sample properties.

Corollary 1.

Suppose that σ² (P_0*) ∈ (0, +∞) and π_s ∈ (0, 1) for some s ∈ {0, 1, …, K − 1}. Under ${\mathcal{H}}_0$, Q_n tends in distribution to

$$Z^{*}:=1+{(K-1)}^{-1}\cdot \sigma {\left(P_{0*}\right)}^{-2}\sum _{j=1}^{\infty }{\lambda }_j(Z_j^2-1),$$ (1)

where Z₁, Z₂, … are independent standard normal variates and λ₁, λ₂, … are eigenvalues described in the above theorem.

We note that this result provides an asymptotic approximation to the null distribution of Q_n without any restriction on the complexity of the structure of M except for the symmetry of the discrepancy r. Furthermore, estimates of the eigenvalues λ₁, λ₂, … can be computed in a relatively straightforward fashion by calculating the eigenvalues of the kernel matrix H_n defined to have (i, j)th element $H_{n,ij}:=u\left(X_i,X_j\right)/n$ (Rosasco et al., 2010). While somewhat complicated, the exact form of u(X_i, X_j) is provided in appendix. Once estimates λ_1,n, λ_2,n, … of the eigenvalues λ₁, λ₂, … have been obtained, the quantiles of the distribution of Z* are estimable via Monte Carlo simulation, thereby enabling the construction of asymptotically valid test cutoffs.

For concreteness, we outline the sequence of steps involved in the implementation of our proposed test:

1. Compute the test statistic Q_n and the estimator SS_n/n of σ² (P_0*)

2. Calculate the matrix H_n and its first J eigenvalues ${\lambda }_{1,n},{\lambda }_{2,n},\dots ,{\lambda }_{J,n}$.

3. Sample B realizations $Z_1^{*},Z_2^{*},\dots ,Z_B^{*}$ from the null distribution of Q_n by setting

   $$Z_b^{*}:=1+\frac{n}{(K-1)S{S}_n}\sum _{j=1}^J{\lambda }_{j,n}(Z_{j,b}^2-1)$$

   for a large array {Z_{j, b}}_j,b of draws from independent standard normal variates.

4. Estimate the P-value by (1/B) ${\sum }_{b=1}^{B}I\left(Z_b^{*}>Q_n\right)$.

The approximation parameters B and J are chosen to be sufficiently large so that the P-value estimates are precise; more details are provided in Section 4. The selection of J may be based on the proportion of variation in the distributional approximation $Z_b^{*}$. The proposed test consists of rejecting the null hypothesis whenever the statistic Q_n is above the (1 − α)th quantile of the distribution of Z* and failing to reject otherwise. The probability of rejection is thus given by P₀ (Q_n > q_α). Under a weak condition, the test has good operating characteristics, as described in the theorem below.

Theorem 2.

Under the null hypothesis, the rejection probability of the test based on Q_n is asymptotically no larger than α. Suppose that the discrepancy r is sensitive to group differences, in the sense that

$$\begin{gathered} \iint r\left(m_1,m_2\right)d{P}_{0s_1}\left(m_1\right)d{P}_{0s_2}\left(m_2\right) \\ >\iint r\left(m_1,m_2\right)d{P}_{0d}\left(m_1\right)d{P}_{0d}\left(m_2\right) \end{gathered}$$

for some s₁ ≠ s₂ ∈ {0, 1, …, K − 1} for each d ∈ {0, 1, …, K − 1}. Then, the power of T_n tends to one as n → +∞.

This result indicates that with any discrepancy r we can conduct testing on data observed in complex forms. Furthermore, with an appropriate choice of r, our proposed test is expected to have enough power to detect group differences with a sample of sufficient size. An appropriate distance function takes into account salient features of the data structure, and the power of the test depends on the sensitivity of the selected distance function to group differences that exist in the sample. In the context of vector outcomes, possible distance functions include the Euclidean distance or absolute distance; in the context of vectors of correlations, other metrics such as those proposed by Reiss et al. (2010) and Shehzad et al. (2014) have been argued to better capture variation. However, as the dimension of the observed data increases, the potential for the accumulation of noise that can drown out signal is also of concern (Fan and Fan, 2008; Hall et al., 2008; Fan et al., 2014). The use of distances that weight specific subsets of variables based on biological understanding can mitigate this by emphasizing variables in which differences are expected and down-weighting noisy variables that may contribute less to group differences (e.g., Wang and Elston, 2007; Madsen and Browning, 2009; Han and Pan, 2010). In the context of data in which group differences are expected to manifest in variables which are adjacent with respect to an ordering, distance functions which involve smoothing across adjacent or nearby variables can also provide improved power. For more complex data structures such as matrices, which are commonly used to represent networks via potentially weighted adjacency matrices, as is the case for our motivating connectomic study, there are a variety of potential distance functions that can be applied. Settings involving lower dimensional matrix observations are amenable to the metric induced by Frobenius norm or the square thereof for sensitivity to group-level differences (Reiss et al., 2010). In cases of higher dimensional observed data matrices, the trace distance induced by the nuclear norm is a metric that may also be helpful for determining differences between populations of matrices. Functional data are also amenable to distance-based testing, and distances between functions that have been advocated for include the integrated square error and the L² distance (Cuevas et al., 2004), the Kolmogorov-Smirnov distance, as well as the squared Hellinger distance, which has desirable numerical properties (Shinohara et al., 2014). Careful selection of r is critical for assuring optimal power of distance-based testing. Below, we investigate the performance of our test in the context of our motivating structural connectomic study. Software implementing these analyses in R is available on Github (link provided in the Supporting Information section).

3 |. RESULTS FROM A DIFFUSION TENSOR IMAGING STUDY OF CONNECTOMICS IN AUTISM

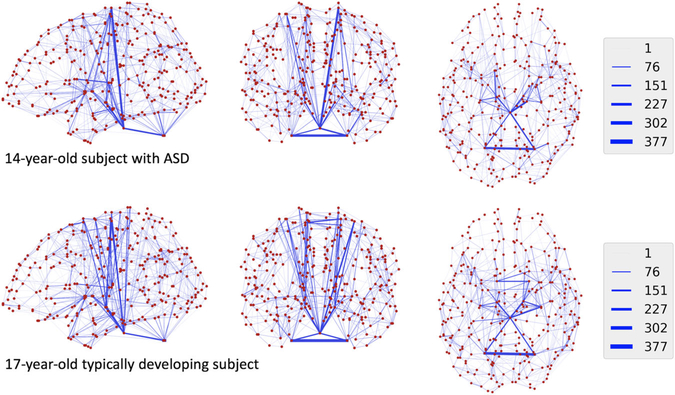
Autism is a neurodevelopmental disorder that results in challenges with social behaviors, communication, and repetitive behaviors. Normal and abnormal neurodevelopment has been the focus of a significant amount of literature in neuroscience, and recent large investments in studies involving neuroimaging (Van Essen et al., 2013; Satterthwaite et al., 2014; Jernigan et al., 2016; Volkow et al., 2017) have provided brain researchers with data resources for studying mechanisms of behavioral phenotypes through structural connectomic analyses. To examine the utility of the proposed distance-based test in such studies, we used a diffusion tensor imaging (DTI) dataset including 264 subjects aged 6 to 19 consisting of 144 subjects with autism spectrum disorders (ASD) and 120 typically developing controls (TDC). Diagnoses were confirmed by expert consensus of two independent psychologists following the guidelines set by Collaborative Programs of Excellence in Autism. ASD and TDC subjects had similar age distributions by design (t-test P = .83). Thirty-direction DTI was acquired and quality assured after denoising and brain extraction, and a tensor model was fit to identify the direction of water diffusion across the brain. The brain was segmented into 301 regions using a coregistered T1-weighted image, and FSL probtrackx (Behrens et al., 2003) was used to estimate the degree of structural connectivity between each of the 301 regions accounting for the volume of each region. The observed data for each subject were thus symmetric 301 by 301 connectivity matrices, with (i, j)th entry being a measure of the strength of connection between regions i and j. Figure 1 shows network representations of connectivity matrices, with nodes representing regions and edges being weighted by connection strength for two subjects for illustration. We used the sum of squared differences in a number of connections represented by edges as our distance function for all hypothesis testing.

FIGURE 1.

Observed data for two selected subjects, consisting of volume-normalized counts of streamline connections between each pair of regions. Regions are represented spatially in sagittal, coronal, and axial views as red dots, and blue lines are connections. Darker and wider blue lines indicate stronger connections between regions

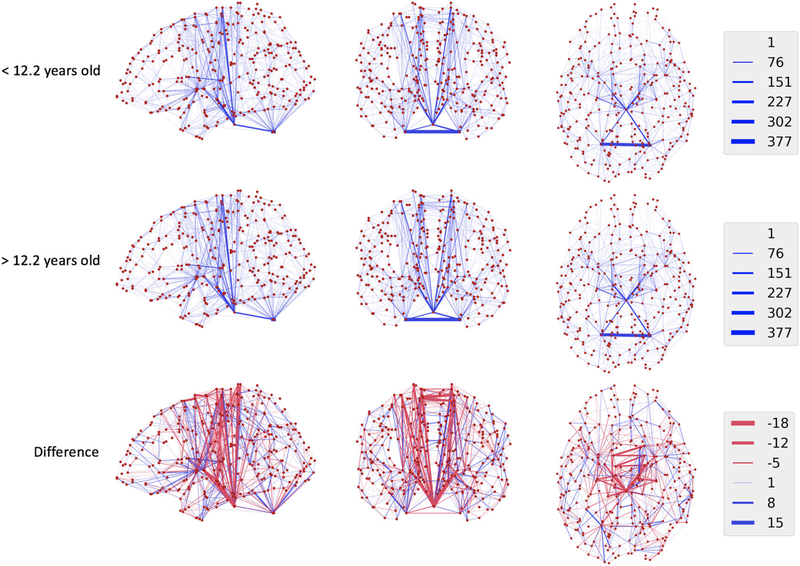
Our experiment included two comparisons which we accomplished using both the proposed test and traditional permutational ANOVA. First, to examine the power of the proposed test in the context of large effect sizes, we tested for differences associated with age-related development by dichotomizing age by its median across all subjects (12.2 years). Average connectivity matrices in the younger and older groups, respectively, are shown in the top two rows of Figure 2 for illustration. Both the proposed test (P = .01) and the PERMANOVA (P = .004) indicated a significant difference in structural connectivity associated with age, as expected. The proposed method was, as also expected, an order of magnitude faster computationally (10s) compared with the permutation-based approach (141s). We also compared connectivity across quintiles of age, and the proposed test (P = .06) and the PERMANOVA (P = .05) indicated similar age-associations. Across deciles of age, neither the proposed test (P = .37) nor the permutation-based analysis (P = .26) found differences across age groups in structural connectivity. This shows promise for the faster proposed method for detecting structural changes in the connectome despite the high dimensionality and complexity of the connectomic representation.

FIGURE 2.

Mean networks (first and second rows) for subjects younger than the median age (12.2 years) compared to older subjects. Regions are represented as red dots, and connections are shown as blue lines. Thicker lines indicate stronger connections on average between regions, and the legend indicates the number of streamline connections estimated. In the third row, the differences between the maps are shown with blue lines indicating stronger connections in older subjects, and red lines indicating weaker connections in these groups

Next, we tested for differences between the ASD and TDC groups. As based on previous literature (for an excellent review, see Travers et al., 2012) we expect differences in the structural connectome between ASD and TDC subjects to be subtle, and effect sizes to be relatively small. Neither the proposed test (P = .36) nor PERMANOVA (P = .15) rejected the null of no difference between groups, likely due to the small effect size and relatively small sample size. The global nature of the discrepancy measure selected may also have been suboptimal for detecting differences associated with ASD. Future work will focus on biologically informed distance functions to better elucidate group differences, including those that emphasize established findings concerning structure and function abnormalities in ASD (Figure 3).

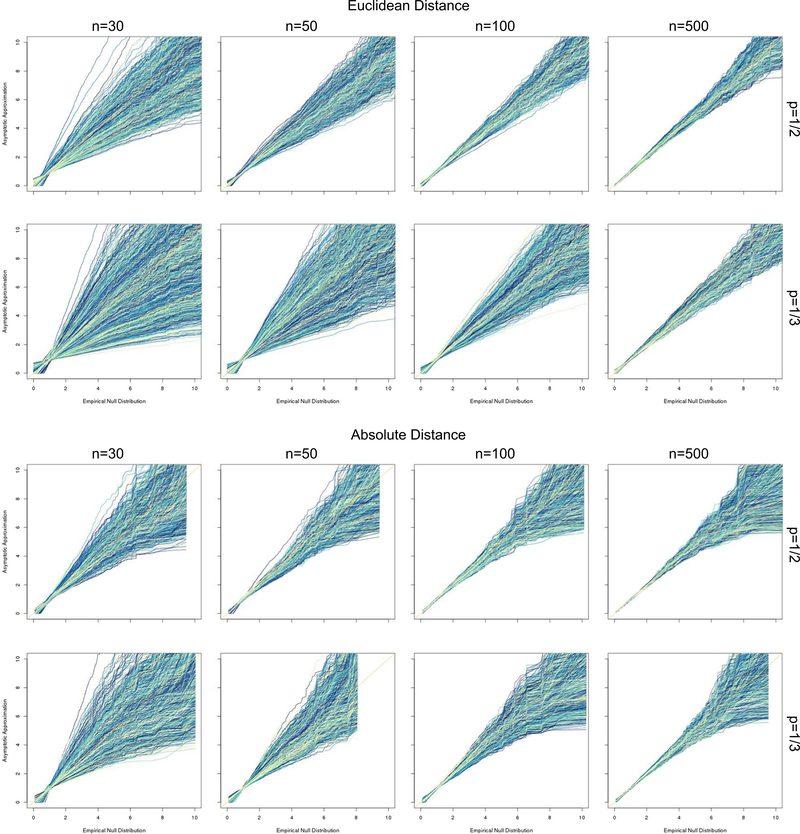
FIGURE 3.

Q-Q plots comparing the proposed approximation to the empirical null distribution of the squared Euclidean (top) and absolute (bottom) distance-based ANOVA test statistic Q_n in the scalar case. ANOVA, analysis of variance; Q-Q, quantile-quantile

4 |. SIMULATION STUDIES

To assess the performance of our proposed test in a variety of controlled settings, we considered four simulation scenarios: (1) a simple scalar ANOVA case with a normally distributed outcome; (2) a small graphical case with five nodes (see Figure 4); (3) a functional data case; and (4) simulations based on the DTI data from Section 3. In this section, we will outline each of these simulation scenarios as well as the results for these experiments. For all simulation settings, we estimated the number of eigenvalues to be used in the proposed approximation of the null distribution to ensure that the proportion of variation explained was 95% or greater. Next, to determine a reasonable value for the number of Monte Carlo samples to be used to calculate P values, we estimated the number of samples necessary using the graphical case in scenario 2 to achieve P-value root-mean-square error (RMSE) rates of less than 10⁻³ by comparison with cases of very large values of B. We found that B = 2.5 × 10⁵ was sufficient. Similarly, we estimated the necessary number of permutations to ensure similar RMSE rates using the state-of-the-art PERMANOVA approach. We used the adonis function in the vegan package (Oksanen et al., 2015) in R (R Core Team, 2015), and found that 2.5 × 10⁵ permutations were necessary. Details of this analysis are shown in Figure S1.

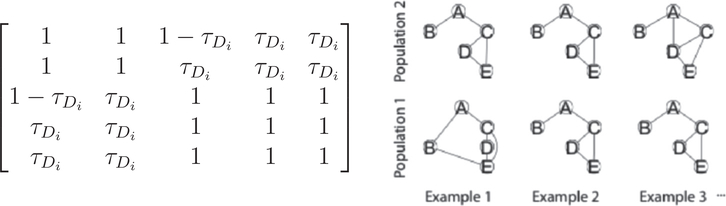
FIGURE 4.

Graph-outcome simulation design. On the left, the adjacency matrix for the simulated graphs is shown, and on the right three example subjects are shown with τ₀ =5% for the first population and τ₁ =10% for the second

4.1 |. Scenario 1: Scalar case

We first conducted a simulation study with two groups of subjects whose outcomes were randomly generated from a normal distribution. That is, we repeatedly (B = 1000 times) sampled subjects i = 1, …, n with group indicator D_i~Bern(π₀) and outcome $M_i\sim N\left({\mu }_{D_i},{\sigma }^2\right)$ for n ∈ {30, 50, 100, 500}, π₀ ∈ {1/2, 1/3}, and σ ∈ {1, 2, 3}. We then conducted a traditional ANOVA, which compares the classical F statistic calculated from the observed data to the F-distribution with the appropriate number of degrees of freedom. Finally, we conducted the proposed distance-based ANOVA using two distance functions: the squared Euclidean distance r₁(m₁, m₂) = (1/2)(m₁ − m₂)² and the absolute distance r₂(m₁, m₂) = (1/2)∣m₁ − m₂ ∣.

We first assessed the appropriateness of the asymptotic approximation to the test statistic null distribution by simulating data under the null for each noise level and sample size setting. We investigated the convergence of the null distribution of the test statistic Q_n with the proposed approximation, selecting σ² = 1, and the results are shown in quantile-quantile (Q-Q) plots in Figure 3. Each line shown compares the quantiles of one of 10⁴ simulations with 5000 samples from the approximate distribution using J = 10 with the observed distribution across simulations. As expected, the approximation is closer to the true distribution for larger sample sizes. The approximation also performs better in cases with similar group sizes (π₀ = 1/2). At larger sample sizes, the approximation appears to be slightly more accurate for the Euclidean distance compared with the absolute discrepancy; however, both approximations appear excellent. For some plots (in particular, the absolute distance for n = 50 and π₀ = 1/3), we found the empirical null to have a slightly shorter range compared with that of the approximation, which yields a Q-Q plot with white space on the right of the subfigure.

We then investigated the performance of the approximation for hypothesis testing in terms of three key aspects: the maintenance of the nominal type I error rate, power for detecting alternatives of various effect sizes, and computation time. We averaged over 10⁴ simulated datasets to evaluate each of these criteria. For the type I error simulations, we assumed σ² = 1 and μ₀ = μ₁ = 0. For all simulated scenarios, the type 1 error rates were around the nominal 5% level and are shown in the first and third rows of Figure S2. We examined type 1 error rates for sample sizes as small as n ∈ {30, 50} to determine the performance of our test when the asymptotic approximation to the null distribution is likely to be far from the true distributions. While these results for n ∈ {30, 50} are reassuring in their conservatism, for small sample sizes a permutation-based test is recommended.

Next, we studied the power of the distance-based ANOVAs by setting μ₀ = 0 and μ₁ = 1, and varying the level of noise σ². These results are shown in the second and fourth rows of Figure S2. As expected, the power rises quickly as the sample size increases, with all tests achieving nearly 100% power for all noise settings at n = 500. Similarly, increased noise levels were associated with decreased power for all three methods. We found the power of the proposed tests to be quite similar but slightly lower than the standard ANOVA, with the Euclidean distance-based ANOVA showing very similar power to the classical test. The absolute distance-based test showed the lowest power, with a loss of up to 10%. Finally, in Figure S3, we compare the computation time necessary for each of the simulation studies presented. Note that computation time does rise with sample size but is similar across group proportions and across the two selected discrepancy measures, and takes at most approximately 4.5 seconds.

To determine J, the number of eigenvalues λ_{j n,} used in the approximation, we adopted a strategy of selecting J based on the data for all type I error and power simulations. We selected J to be the minimum number of terms necessary for explaining 95% of the variation in Z*. We found that the number of terms varied across distances, and in the case of the absolute distance differed across sample sizes (see top rows of Table 1 for these results for the type I error case with π₀ = 1/2 as an illustration).

TABLE 1.

Average number of terms J used in asymptotic approximation for the scalar type I error (top) and graph power (bottom) simulation studies with π₀ = 1/2

Scalar case	n = 30	n = 50	n = 100	n = 500
Euclidean distance	1.00	1.00	1.00	1.00
Absolute distance	7.85	9.87	12.23	15.40
Graph case	n = 30	n = 50	n = 100	n = 250
τ1 = 0.1	3.92	4.40	4.87	5.00
τ1 = 0.15	4.17	4.63	4.96	5.00
τ1 = 0.2	4.28	4.75	4.99	5.00

Note: The parameter J was estimated using the data to ensure greater than 95% of the variation was explained.

4.2 |. Scenario 2: Graphical case

We next considered a simple graph-outcome case with five common nodes, labeled A through E, in each subject and variation in the presence or absence of edges between the nodes as illustrated in Figure 4. For this computationally more complex case, we averaged over 10³ simulations for each set of parameters. We used the Frobenius norm of the difference in the adjacency matrices as our distance function, which counts the number of edge disagreements. To compare this with the state-of-the-art PERMANOVA approach, we used the adonis function in the vegan package (Oksanen et al., 2015) in R (R Core Team, 2015). The adonis function first generates the null distribution of the pseudo-F statistic by permuting the group labels of the simulated data, and compares this with the calculated pseudo-F statistic for the observed data.

To assess type I error rates, we fixed τ = τ₀ = τ₁ ∈ {10%, 15%, 20%} and simulated datasets for n ∈ {30, 50, 100, 250} and π₀ ∈ {1/2, 1/3}. The results from these experiments are shown in the first and third rows of Figure S4. Both methods had approximately nominal rates, with the proposed approximation showing slight conservatism in the smallest sample size (n = 30) cases. Next, we fixed τ₀ = 5% and simulated datasets for τ₁ ∈ {5%, 10%, 15%, 20%} to assess the statistical power of the two approaches for various effect sizes. The results from this analysis are shown in the second and fourth rows of Figure S4. Surprisingly, the permutation test showed low power in most cases; indeed, for the smaller effect sizes of τ₁ ∈ {0.1, 0.15}, the permutation-based analysis showed no power to detect the simulated group differences, and only moderate power with the largest effect size of τ₁ = 0.2. The proposed distance-based test showed high power for the n = 500 sample size across all effect sizes. Indeed, for τ₁ ∈ {0.15, 0.2}, our test showed excellent power for sample sizes as small as n = 100 whereas the permutation-based test showed markedly lower power. The number of terms J used varied across alternatives and sample sizes, and averages of J across simulations are shown in Table 1.

The computation times from this analysis are presented in Figure S5. Notably, the computing time required by the two methods is remarkably different, with the proposed test requiring only a small fraction (less than 30 seconds) of the time required for the permutation test (up to 17 minutes).

4.3 |. Scenario 3: Functional case

We next investigated whether the proposed test might be useful for comparing samples of functions. In particular, we generated data according to a specified parametric form:

$$t\mapsto M(t)=\tau \left[\frac{\exp \{10(t-0.5)\}}{1+\exp \{10(t-0.5)\}}\right]+t{Z}_1+Z_2,$$

where Z₁ and Z₂ are independent mean-zero normal variates with variance σ². We defined the discrepancy between two curves m₁ and m₂ as the integrated squared error $r\left(m_1,m_2\right)={\int }_t{\left\{m_1(t)-m_2(t)\right\}}^{2}dt$, and simulated 10³ samples of curves for each set of parameters and sample size n ∈ {30, 50, 100, 250}. To assess the type I error rate of our proposed test as well as the permutation test, we simulated data with three noise levels: σ ∈ {0.1, 0.3, 0.5}. The results of this analysis are shown in Figure S6 and demonstrate that all methods provided nominal type I error rates. Next, we estimated the power of each method by simulating data for which τ = 0 for the D = 0 group, but for which we varied τ for the D =1 group (shown in subfigure titles in second and fourth rows of Figure S6). Note that for the smallest effect size of τ = 0.1, neither method showed power. However, for the medium effect size case of τ = 0.3, both methods showed moderate to high power for samples larger than n = 100, and the proposed method showed higher power than the permutation test, as in the scalar and graph cases. Furthermore, all tests had high power for the large effect size case when n = 50 or larger. Comparisons of computing time yielded similar results to the graphical case, with the proposed method approximately two orders of magnitude faster—the results are shown in Figure S7.

4.4 |. Scenario 4: Connectome case

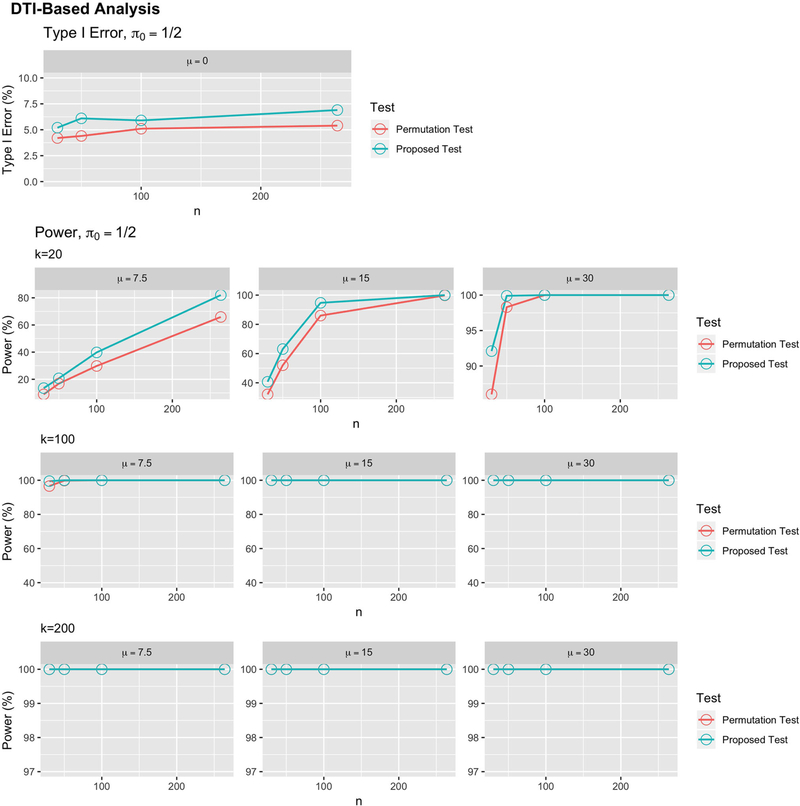
Finally, to study the performance of our test in the context of the structural connectomic study described in Section 3, we developed a simulation study based on these data. We resampled from the observed networks without replacement and randomly sampled a fictitious phenotype D_i~Bern(π₀) for n ∈ {30, 50, 100, 264}. Using the same squared difference discrepancy measure as in the data analysis, we estimated the type I error rate by simulating 10³ samples under the null distribution. We then assessed the power of the two tests by simulating signal in the observed data. For each sample, we began by again simulating a fictitious phenotype. We then induced a shift, μ ∈ {7.5, 15, 30}, in a number of connections, k ∈ {20, 100, 200}, where the strongest associations between ASD and the edge weights existed in the observed data based on t-tests. This allowed us to induce varying levels of signal in the biologically most plausible regions.

The results from these analyses are shown in Figure 5, with rows indicating the number of connections where signal was added and columns showing the strength of the signal. Estimates of power are shown in the second through fourth rows, and the first row shows type I error rates. Both the proposed and permutation tests had nominal type I error rates. As expected, when k = 200, all methods showed high power for sample sizes larger than n = 30. For k = 100, the larger effect sizes showed high power for both methods, but for μ = 7.5, the methods were only powered when the sample size was larger than n = 100. For the most sparse signal (k = 20), only cases with large sample sizes or large effect sizes showed differences. In the n = 264 cases with k = 20, the proposed method showed higher power than the permutation test when μ ∈ {7.5, 15}. When the signal was strongest (μ = 30), the two tests performed remarkably similarly. Finally, the computation time results were similar to those from the graph and functional cases and are shown in Figure S8.

FIGURE 5.

Figures showing the type I error rates and power for various settings with network outcomes in scenario 4. The top row shows type I error rates for several noise levels and power under several alternatives for the case of π₀ = 1/2, and the bottom rows show results for the case of imbalanced group sizes

To assess the proposed test’s performance in the case where K > 2, we randomly sampled a fictitious phenotype D_i from a discrete uniform distribution on {0, …, 4} for n ∈ {30, 50, 100, 264}. Using the approach as the above K = 2 example, we estimated the type I error rate. We then assessed the power of the two tests by simulating signal in the observed data by inducing a shift, but to different degrees in the different groups dμ (where d ∈ {0, …, 4} denotes group) in k ∈ {20, 100, 200} connections. We found the results to be similar to the K = 2 case (see Figures S9 and S10).

5 |. DISCUSSION AND CONCLUSION

In this paper, we propose a distance-based ANOVA technique that allows for fast two-sample testing of connectomes represented by graphs and more complex structures using a subject-to-subject distance or discrepancy measure. We leverage the U-statistic form of the generalized variance to find the limiting behavior of the pseudo-F statistic. Our test shows improved power in simulations while maintaining nominal type I error rates. We expect that this test will also be useful in large genomic studies and other biomedical big data settings, in which permutational ANOVA testing is increasingly popular. Our test also generalizes directly to the case of more than two groups by appropriate scaling of the test statistic, as in the case of the classical F-test.

We demonstrate the utility of this methodology in a modern connectivity study. As ASD is an elusive disease in which only certain networks are affected, a global test using structural connectivity measures alone may neither be most informative nor powerful. Future investigations of ASD using connectivity measures for certain functional systems and targeted comparisons in prespecified brain networks will likely be more fruitful for understanding disorder-related dysconnectivity. The proposed testing methodology may be useful for such scenarios, in combination with other approaches that include appropriate dimension reduction. In addition, to study global connectivity differences such as those attributable to age, the proposed test is promising for examining group differences. We demonstrated this by stratifying age by the sample median, as well as into quintiles and deciles. In future studies, we propose to investigate analytical approximations to the cases where the predictor is continuous or there are multiple predictors (Reiss et al., 2010).

A key modeling choice left to the analyst when using distance-based testing, including that proposed here, involves the selection of an appropriate distance function. The flexibility of the choice of distance function is a key advantage of the distance-based testing approach, and allows for comparisons of observations of complex and composite form based on a biological understanding of the scientific problem of interest. However, selection of a suboptimal distance function without regard for the structure of the observations, especially in the context of high-dimensional data, can lead to poor statistical power. Thus, we advise careful consideration of the construction of the distance function based on previous knowledge about the measurement structure as well as the scientific problem under study.