The field of values of Jones matrices: classification and special cases

Abstract

The concept of field of values (FoV), also known as the numerical range, is applied to the 2 × 2 Jones matrices used in polarization optics. We discover the relevant interplay between the geometric properties of the FoV, the algebraic properties of the Jones matrices and the representation of polarization states on the Poincaré sphere. The properties of the FoV reveal hidden symmetries in the relationships between the eigenvectors and eigenvalues of the Jones matrices. We determine the main mathematical properties of the FoV, discuss the special cases that are relevant to polarization optics, and describe its application to calculate the Pancharatnam-Berry phase introduced by an optical system to the input state.

1. Introduction

The Jones calculus introduced by R. C. Jones in 1941 [1,2] is a powerful tool used in polarization optics to describe the transformation of totally polarized coherent optical fields by non-depolarizing elements [3,4]. In the Jones formalism, polarized light is represented by a 2 × 1 complex column Jones vector, and linear optical elements by 2 × 2 complex Jones matrices. The Jones matrices have the advantage that they can describe the absolute optical phase change, which is crucial, for example, in interferometry, and coherent optical communications. Nowadays, Jones calculus is typically studied in university courses on polarization optics and its properties and applications can be checked out in many classic textbooks [3–6].

In linear algebra, an important property of a square matrix is its field of values (FoV), also known as the numerical range, which in general is defined as follows [7–9]:

Definition 1.1. —

For an n × n matrix $\mathbb{J}$ with complex entries, the FoV $\mathcal{F}(\cdot )$ is the region (subset) on the complex plane defined by

$$\mathcal{F}(\mathbb{J},|s⟩)\equiv \frac{⟨s|\mathbb{J}|s⟩}{⟨s|s⟩}:|s⟩\in {\mathbb{C}}^n,⟨s|s⟩=S_0>0,$$ 1.1

where |s〉 is a column vector with n entries, and 〈s| is its (adjoint) conjugate transpose.

The FoV is a convex and compact finite region on the complex plane $\mathbb{C}.$ It can be considered as a picture of the matrix that provides useful information about it. For example, another source of information of $\mathbb{J}$ is its spectrum $\lambda (\mathbb{J})$ (or set of eigenvalues) which is a discrete set of points on the complex plane. A relevant result is that all eigenvalues of $\mathbb{J}$ lie in its FoV, i.e. $\lambda (\mathbb{J})\subset \mathcal{F}(\mathbb{J},|s⟩).$ In general, the FoV provides information on the matrices that the spectrum does not give alone. Special cases are particularly relevant, for example, the FoV of a Hermitian matrix is a line segment on the real axis, whereas for a normal matrix is a polygon of n vertices. The FoV is not just a mathematical curiosity, but it has interesting applications in the numerical solution of partial differential equations and the stability analysis of dynamical systems [7].

The notion of FoV is well known in matrix algebra [7–9], but does not seem to have been fully applied before in optical problems. In a recent article [10], we have marginally applied the concept of FoV in the calculation of the optical phase introduced by inhomogeneous matrices to an input polarization state. However, we believe that the FoV is much richer in mathematical properties and has additional potential applications in other areas of optics.

In this work, we apply the concept of FoV to describe the characteristics of the Jones matrices used in polarization optics. The main contributions of this work are: (i) the analysis of the interplay between the geometric properties of the FoV, the algebraic properties of the Jones matrices, and the representation of polarization states on the Poincaré sphere, see §3a,b. (ii) The description of the elliptic FoV on the complex plane and its connection with parameters of the Jones matrices, §3b,c. (iii) The discussion of the special cases of the FoV, §3d. (iv) The solution path of the inverse problem, i.e. designing a Jones matrix given its FoV.

In obtaining these contributions and establishing the notation, we have included in §2 some known definitions and results from linear algebra and Pauli matrices [11–13]. This allows us to make the paper relatively self-contained. In §3, we introduce the geometric representation of FoV on the complex plane and analysed in detail its relation with the Poincaré sphere. The special cases of the FoV and some its applications are discussed in §4.

It should be mentioned that some of the concepts discussed in this article were anticipated in previous papers [10,14–18]. This new article complements these works in the sense that it establishes a complete, unified and consistent description of the Jones matrices (including all the special cases) applying the concept of the FoV. The theory described in this paper can be directly applied to physical systems where linear transformations are described by 2 × 2 complex matrices, e.g. two-level spinor systems [19].

2. Classification and parametrization of Jones matrices

Consider an optical system characterized by a Jones matrix

$$\mathbb{J}=\left[\begin{array}{cc}{j}_1& j_2\\ j_3& j_4\end{array}\right]\in {\mathbb{C}}^{2\times 2},$$ 2.1

with eigenvalues μ_a, μ_b and eigenvectors (i.e. polarization eigenstates)

$$|a⟩=\left[\begin{array}{c}{a}_x\\ a_y\end{array}\right]\in {\mathbb{C}}^2\text{and}|b⟩=\left[\begin{array}{c}{b}_x\\ b_y\end{array}\right]\in {\mathbb{C}}^2.$$ 2.2

In order to establish notation and necessary concepts, it is very convenient to review briefly the classification of 2 × 2 matrices in terms of their Jordan decomposition.

(a). Canonical Jordan forms of the Jones matrices

The Jordan decomposition is one of the most important and powerful theorems is matrix theory [11–13]. For the special case of 2 × 2 matrices it states:

Theorem 2.1. —

Let $\mathbb{J}$ be a complex 2 × 2 matrix. Then there always exist an invertible 2 × 2 matrix $\mathbb{T}$ such that

$$\mathbb{J}=\mathbb{T}\mathbb{Q}{\mathbb{T}}^{-1},$$ 2.3

where $\mathbb{Q}$ has one of the following forms:

$${\mathbb{Q}}_1=\left[\begin{array}{cc}{\mu }_a& 0\\ 0& {\mu }_b\end{array}\right]and{\mathbb{Q}}_2=\left[\begin{array}{cc}\mu & 1\\ 0& \mu \end{array}\right].$$ 2.4

The matrices ${\mathbb{Q}}_1$ and ${\mathbb{Q}}_2$ are the Jordan canonical forms of $\mathbb{J}$ and their diagonal elements are its eigenvalues. All 2 × 2 complex matrices, without exception, belong to one form or the other [11,12]. In equation (2.3), the matrices $\mathbb{Q}$ and $\mathbb{J}$ are similar, in the sense that represents the same linear transformation with respect to different basis defined by the matrix $\mathbb{T}$. Let us describe each case with a little more detail.

1. Diagonalizable Jones matrices. The Jordan canonical form ${\mathbb{Q}}_1$ corresponds to matrices $\mathbb{J}$ that are diagonalizable, have two linearly independent eigenvectors |a〉, |b〉, and two eigenvalues ${\mu }_a,\hspace{0.17em}{\mu }_b$ (possibly degenerate). $\mathbb{T}$ is a matrix whose columns are the eigenvectors |a〉, |b〉, with |a〉 ≠ |b〉. Geometrically, ${\mathbb{Q}}_1$ represents a complex scaling (stretch) transformation of an input state |s〉 expressed in the basis of states |a〉, |b〉.

The vast majority of Jones matrices that one finds in optical applications belong to the diagonalizable ${\mathbb{Q}}_1$ form. In the optics literature [3,4,14], a Jones matrix $\mathbb{J}$ is said to be homogeneous if the eigenvectors are orthogonal, 〈b|a〉 = 0, otherwise it is said to be inhomogeneous, 〈b|a〉 ≠ 0. Mathematically, homogeneous matrices coincide with normal matrices, i.e. matrices that commute with their transpose conjugate ($\mathbb{J}{\mathbb{J}}^{†}={\mathbb{J}}^{†}\mathbb{J}$). Hermitian (${\mathbb{J}}^{†}=\mathbb{J}$), skew-Hermitian (${\mathbb{J}}^{†}=-\mathbb{J}$) and unitary (${\mathbb{J}}^{†}\mathbb{J}=\mathbb{I}$) matrices belong to the class of normal (homogeneous) matrices . The properties of homogeneous matrices have been widely studied because most of the basic polarization elements, such as polarizers, retarders, rotators, belong to this category of matrices [3–6].

The case when one of the eigenvalues of the Jones matrix is equal to zero, e.g. μ_b = 0, leads to singular matrices with zero determinant. These singular matrices model perfect polarizers that transform any input state |s〉 into the eigenstate |a〉. Singular matrices can be either homogeneous or inhomogeneous [14].

2. Non-diagonalizable Jones matrices. The Jordan canonical form ${\mathbb{Q}}_2$ corresponds to defective matrices $\mathbb{J}$ that are not diagonalizable [11–13]. They have only one eigenvector |a〉 with eigenvalue μ, that is, $(\mathbb{J}-\mu \mathbb{I})|a⟩=0.$ Actually, the shifted matrix $\mathbb{K}\equiv \mathbb{J}-\mu \mathbb{I}$ operating over any arbitrary normalized vector $|s⟩\in {\mathbb{C}}^2$ yields always a resulting vector proportional to the eigenvector |a〉, i.e.

$$\mathbb{K}|s⟩=(\mathbb{J}-\mu \mathbb{I})|s⟩=c|a⟩,$$ 2.5

where c is the complex constant of proportionality. The special vector |s〉 → |g〉 for which c = 1 is called generalized eigenvector of $\mathbb{J}$ and satisfies the equation $(\mathbb{J}-\mu \mathbb{I})|g⟩=|a⟩.$

When $\mathbb{Q}$ in equation (2.3) corresponds to the Jordan form ${\mathbb{Q}}_2$, the columns of $\mathbb{T}$ are the eigenvector |a〉 and the generalized eigenvector |g〉. It can be verified that |c| is maximum when |s〉 is the vector orthogonal to |a〉, and takes the value |c|_max = |j₂| + |j₃|. Geometrically, ${\mathbb{Q}}_2$ represents a skew (shear) transformation along the axes defined by the vectors |a〉, |g〉.

Equations (2.3) and (2.4) provide a way to set up a Jones matrix given their eigenvalues and eigenvectors. To relate the Jordan canonical forms with the global parameters of the Jones matrix we recall that the eigenvalues of a matrix $\mathbb{J}$ are given by

$${\mu }_{a,b}=\frac{\mathrm{tr}\mathbb{J}}{2}\pm \sqrt{{\left(\frac{\mathrm{tr}\mathbb{J}}{2}\right)}^2-det\mathbb{J}},$$ 2.6

where $\mathrm{tr}\mathbb{J}$ and $det\mathbb{J}$ are the trace and determinant of $\mathbb{J}$, respectively. We identify two situations

• (i)If ${(\mathrm{tr}\mathbb{J}/2)}^2\ne det\mathbb{J},$ the eigenvalues are distinct, and then the matrix $\mathbb{J}$ is diagonalizable with Jordan form ${\mathbb{Q}}_1.$
• (ii)
  If ${(\mathrm{tr}\mathbb{J}/2)}^2=det\mathbb{J},$ there is a unique eigenvalue, $\mu =\mathrm{tr}\mathbb{J}/2,$ and there are two subcases

  • (a)
    $\mathbb{J}$ is already diagonal, i.e. $\mathbb{J}=\mu \mathbb{I}$, which corresponds to a Jordan form ${\mathbb{Q}}_1$ with degenerate eigenvalues μ_a = μ_b = μ.
  • (b)
    $\mathbb{J}$ is not diagonal, belonging to the Jordan form ${\mathbb{Q}}_2.$

An advantage of the Jordan factorization in equation (2.3) is that it decomposes the matrix $\mathbb{J}$ into matrix factors that depend on the eigenvectors and eigenvalues separately. The classification of Jones matrices using their canonical Jordan forms will be useful in the following sections when we discuss the special cases of the FoV of the Jones matrices.

(b). Parametrization of Jones matrices: Pauli formalism

A useful parametrization of Jones matrices is via the Pauli matrices [5,6,20–23]

$$\mathbb{I}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],{\sigma }_1=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right],{\sigma }_2=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\text{and}{\sigma }_3=\left[\begin{array}{cc}0& -\mathrm{i}\\ \mathrm{i}& 0\end{array}\right],$$ 2.7

which form an orthonormal basis for all 2 × 2 complex matrices. This means that $\mathbb{J}$ can be written as a linear combination of the four Pauli matrices as follows:

$$\mathbb{J}(z_0,z_1,z_2,z_3)=\{\begin{array}{l}{z}_0\mathbb{I}+z_1{\sigma }_1+z_2{\sigma }_2+z_3{\sigma }_3,\\ z_0\mathbb{I}+\mathbf{\text{Z}}\cdot \overrightarrow{\mathit{\sigma }},\\ \left[\begin{array}{cc}{z}_0+z_1& z_2-\mathrm{i}{z}_3\\ z_2+\mathrm{i}{z}_3& z_0-z_1\end{array}\right],\end{array}$$ 2.8

where z_m (m = 0, 1, 2, 3) are the complex Pauli coefficients related to the matrix elements j_k (m = 1, 2, 3, 4) by

$$z_0=\frac{j_1+j_4}{2},\hspace{0.17em}{z}_1=\frac{j_1-j_4}{2},\hspace{0.17em}{z}_2=\frac{j_2+j_3}{2}\text{and}{z}_3=\mathrm{i}\frac{j_2-j_3}{2},$$ 2.9

the symbol ( · ) stands for the usual dot product, $\overrightarrow{\mathit{\sigma }}={[{\sigma }_1,{\sigma }_2,{\sigma }_3]}^{\text{T}}$ is the vector of Pauli matrices, and

$$\mathbf{\text{Z}}\equiv \left[\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right]=Z\widehat{\mathbf{\text{Z}}}\in {\mathbb{C}}^3$$ 2.10a

is the column vector of Pauli coefficients with norm

$$Z=|\mathbf{\text{Z}}|=\sqrt{{\mathbf{\text{Z}}}^{†}\mathbf{\text{Z}}}=\sqrt{|z_1{|}^2+|z_2{|}^2+|z_3{|}^2}.$$ 2.10b

Eigenvalues μ_a, μ_b and (non-normalized) eigenvectors |a〉, |b〉 of the matrix $\mathbb{J}$ are expressed in terms of the Pauli coefficients as follows [5,6]:

$${\mu }_a=z_0+f,|a⟩\propto \left[\begin{array}{c}{z}_1+f\\ z_2+\mathrm{i}{z}_3\end{array}\right]$$ 2.11a

and

$${\mu }_b=z_0-f,|b⟩\propto \left[\begin{array}{c}{z}_1-f\\ z_2+\mathrm{i}{z}_3\end{array}\right],$$ 2.11b

where

$$f\equiv \sqrt{{\mathbf{\text{Z}}}^T\mathbf{\text{Z}}}=\sqrt{z_1^2+z_2^2+z_3^2}$$ 2.12

a parameter that depends only on Z and is equal to the half-difference of the eigenvalues, i.e. f = (μ_a − μ_b)/2.

The global parameters of the Jones matrix $\mathbb{J}$ are given by

$$\frac{\mathrm{tr}\mathbb{J}}{2}=\frac{j_1+j_4}{2}=\frac{{\mu }_a+{\mu }_b}{2}=z_0$$ 2.13

and

$$det\mathbb{J}=z_0^2-(z_1^2+z_2^2+z_3^2)=z_0^2-f^2=(z_0+f)(z_0-f)={\mu }_a{\mu }_b.$$ 2.14

Once reviewed the Pauli description of the Jones matrices, we are in position to describe their FoV.

3. Field of values of the Jones matrices

The general definition of the FoV of a square matrix is given by equation (1.1). For the case of a 2 × 2 Jones matrix, it reduces to [7]

$$\mathcal{F}(\mathbb{J},|s⟩)\equiv \frac{⟨s|\mathbb{J}|s⟩}{⟨s|s⟩},|s⟩\in {\mathbb{C}}^2,$$ 3.1

where |s〉 is an arbitrary polarization state described by the Jones vector

$$|s⟩=\left[\begin{array}{c}{s}_x\\ s_y\end{array}\right],\begin{array}{l}{s}_x,s_y\in \mathbb{C},\\ ⟨s|s⟩=S_0\in \mathbb{R}\ge 0,\end{array}$$ 3.2

or, equivalently, by its normalized Stokes vector on the Poincaré sphere

$$\widehat{\mathbf{\text{S}}}=\left[\begin{array}{c}{S}_1\\ S_2\\ S_3\end{array}\right]=\frac{1}{S_0}\left[\begin{array}{c}⟨s|{\sigma }_1|s⟩\\ ⟨s|{\sigma }_2|s⟩\\ ⟨s|{\sigma }_3|s⟩\end{array}\right]=\frac{1}{S_0}\left[\begin{array}{c}|s_x{|}^2-|s_y{|}^2\\ 2\mathrm{Re}(s_x^{\ast }{s}_y)\\ 2\mathrm{Im}(s_x^{\ast }{s}_y)\end{array}\right],$$ 3.3

where the hat symbol means unit vector. In the same way, let us denote by $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}}$ the Stokes vectors corresponding to the eigenvectors |a〉 and |b〉 of the Jones matrix, respectively.

The FoV (3.1) is a function of the Jones vector |s〉, but we can express it conveniently in terms of the Stokes vector $\widehat{\mathbf{\text{S}}}.$ To this end, we substitute the Jones matrix $\mathbb{J}$ in terms of Pauli coefficients (2.8), then apply equation (3.3), and after factorizing the Stokes parameters, we get

$$\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}})\equiv \frac{⟨s|\mathbb{J}|s⟩}{⟨s|s⟩}=z_0+\mathbf{\text{Z}}\cdot \widehat{\mathbf{\text{S}}}.$$ 3.4

Equation (3.4) is an algebraic and very useful expression for the FoV of a Jones matrix. The set of polarization states is defined by the Stokes vector $\widehat{\mathbf{\text{S}}}$ which spans the Poincaré sphere. The linear relation (3.4) is a surjective mapping of the unit sphere in ${\mathbb{R}}^3$ onto a finite region on the complex plane. We will use it to derive the properties and special cases discussed in the following sections.

(a). Geometric representation of the FoV on the complex plane

The FoV of the matrix $\mathbb{J}$ (equation (3.4)) is the complete set of all possible resulting values of $\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}})$ after we have substituted the complete set of possible values of $\widehat{\mathbf{\text{S}}}$. From the theory of linear algebra [7,8], it is known that the FoV of any 2 × 2 matrix is a closed and bounded elliptical disc on the complex plane, see figure 1a. All possible values of $\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}})$ lie inside the elliptic region or its contour. Equation (3.4) shows that the term $\mathbf{\text{Z}}\cdot \widehat{\mathbf{\text{S}}}$ is the generator of the elliptic disc in the complex plane.

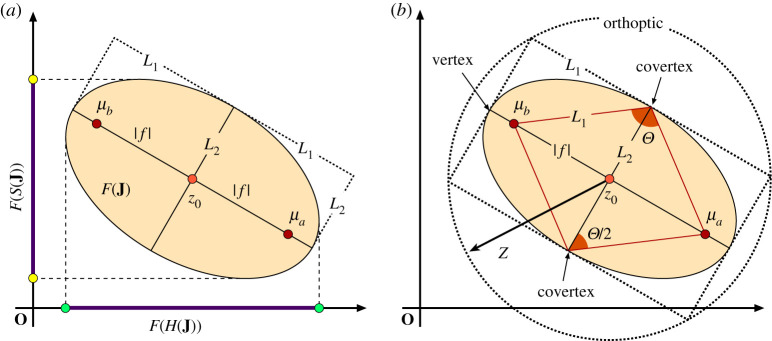
Figure 1.

The FoV of a Jones matrix is a closed and bounded elliptic disc in the complex plane with foci at the eigenvalues of $\mathbb{J}$. (a) Relevant parameters of the elliptic FoV. The projections of the FoV to the real and imaginary planes are the FoV of the Hermitian and skew-Hermitian components of the matrix $\mathbb{J}$, respectively. (b) The orthoptic of the FoV is the circle that circumscribes the minimum bounding box of the ellipse. (Online version in colour.)

The geometric parameters of the elliptic disc are shown in figure 1, we have

• —
  The centre of the ellipse is located at

  $$z_0=\frac{\mathrm{tr}\mathbb{J}}{2}=\frac{({\mu }_a+{\mu }_b)}{2}.$$ 3.5
• —The foci of the ellipse are the eigenvalues μ_a and μ_b of the matrix $\mathbb{J}$.
• —
  Size: The major L₁ and minor L₂ semi-axes of the ellipse can be expressed either in terms of the shifted matrix $\mathbb{K}\equiv \mathbb{J}-z_0\mathbb{I}$ or the Pauli coefficients as follows:

  $$L_{1,2}=\frac{1}{2}\sqrt{\mathrm{tr}({\mathbb{K}}^{†}\mathbb{K})\pm 2|det\mathbb{K}|}=\frac{1}{\sqrt{2}}\sqrt{Z^2\pm |f{|}^2},$$ 3.6

  where Z and f are defined in equations (2.10) and (2.12), respectively.
• —
  Semifocal distance: The distance of the foci from the centre of the ellipse is

  $$|f|=|det\mathbb{K}{|}^{1/2}=\frac{|{\mu }_a-{\mu }_b|}{2}.$$ 3.7
• —Inclination: The major axis lies on a line passing through the eigenvalues of $\mathbb{J}$, then its angle respect to the real axis is $\arg \hspace{0.17em}({\mu }_a-{\mu }_b).$
• —
  Orthoptic: The orthoptic (i.e. director circle) of an ellipse is the circle that circumscribes the minimum bounding box of the ellipse, as shown in figure 1b. From equation (3.6), we can conclude that the radius of the orthoptic is given by the norm of the vector Z, that is

  $$R_{\text{orthoptic}}=\sqrt{L_1^2+L_2^2}=Z.$$ 3.8
• —
  Covertex angle: The covertex angle Θ of the ellipse is the angle subtended by the two straight lines getting out of the covertex to the focal points, see figure 1b. The angle Θ is related to the inner product of the eigenvectors |a〉, |b〉 of the matrix $\mathbb{J}$ through the relation

  $$\eta \equiv |⟨b|a⟩|=\cos \left(\frac{\mathrm{\Theta }}{2}\right)=\frac{L_2}{L_1}\in [0,1],$$ 3.9

  where Θ ∈ [0, π] is also equal to the angle subtended between the Stokes eigenvectors $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}}$ on the Poincaré sphere, see figure 2a. The parameter η = |〈b|a〉| is a measure of the orthogonality of the eigenvectors and has been proposed to characterize the degree of inhomogeneity of a Jones matrix [14].

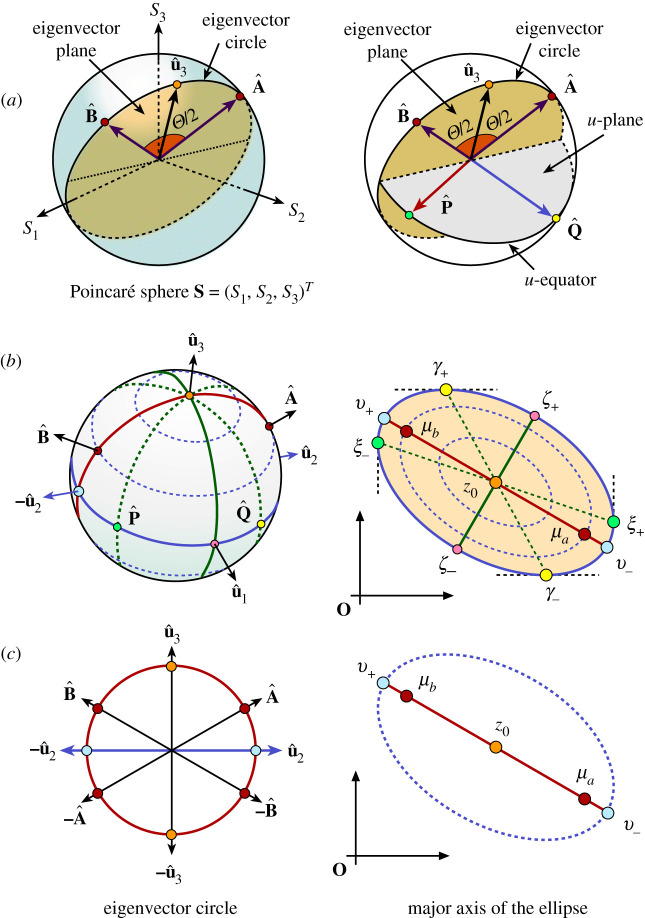
Figure 2.

(a) Characteristic planes in the Poincaré sphere associated with the Jones matrix. The Stokes eigenvectors $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}}$ define the eigenvector plane. The u-plane formed by the vectors $\widehat{\mathbf{\text{P}}}$ and $\widehat{\mathbf{\text{Q}}}$ is normal to the vector ${\widehat{\mathbf{\text{u}}}}_3$. (b) Surjective mapping of polarization states on the Poincaré sphere onto the elliptic FoV. (c) The eigenvector circular meridian maps onto the major axis of the FoV covering it twice. (Online version in colour.)

(b). Relation of the FoV with the Poincaré sphere

As suggested by equation (3.4), the FoV of a Jones matrix has a deep and nice connection with the representation of polarization states on the Poincaré sphere. This relationship is not usually studied in the context of linear algebra [7,8,12,13], but in the context of polarization optics it plays a special role since it allows to visualize graphically many properties and symmetries at a glance.

Consider the Poincaré sphere S = [S₁, S₂, S₃]^T:|S| = 1, depicted in figure 2a. The Stokes eigenvectors of $\mathbb{J}$ are represented by the unit vectors $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}},$ with eigenvalues μ_a and μ_b, respectively. Let us call the plane formed by the eigenvectors $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}}$ as eigenvector plane and the great circle that passes through the eigenvectors as eigenvector circle.

It is convenient to introduce a new rotated orthonormal system $({\widehat{\mathbf{\text{u}}}}_1,{\widehat{\mathbf{\text{u}}}}_2,{\widehat{\mathbf{\text{u}}}}_3)$ defined by (figure 2b)

$${\widehat{\mathbf{\text{u}}}}_1\equiv \frac{\widehat{\mathbf{\text{A}}}\times \widehat{\mathbf{\text{B}}}}{|\widehat{\mathbf{\text{A}}}\times \widehat{\mathbf{\text{B}}}|},{\widehat{\mathbf{\text{u}}}}_2=\frac{\widehat{\mathbf{\text{A}}}-\widehat{\mathbf{\text{B}}}}{|\widehat{\mathbf{\text{A}}}-\widehat{\mathbf{\text{B}}}|}\text{and}{\widehat{\mathbf{\text{u}}}}_3\equiv \frac{\widehat{\mathbf{\text{A}}}+\widehat{\mathbf{\text{B}}}}{|\widehat{\mathbf{\text{A}}}+\widehat{\mathbf{\text{B}}}|},$$ 3.10

where ${\widehat{\mathbf{\text{u}}}}_3$ is the middle unit vector between $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}},$ and ${\widehat{\mathbf{\text{u}}}}_3={\widehat{\mathbf{\text{u}}}}_1\times {\widehat{\mathbf{\text{u}}}}_2.$ Taking the point ${\widehat{\mathbf{\text{u}}}}_3$ like a north pole, the plane spanned by the vectors $({\widehat{\mathbf{\text{u}}}}_1,{\widehat{\mathbf{\text{u}}}}_2)$ is like an equatorial plane and thus it will be referred to as u-plane and its circular perimeter to as u-equator, see figure 2a,b. Do not confuse the equator of the Poincaré sphere (i.e. S₃ = 0) with the u-equator of the rotated system $({\widehat{\mathbf{\text{u}}}}_1,{\widehat{\mathbf{\text{u}}}}_2,{\widehat{\mathbf{\text{u}}}}_3).$

$\mathcal{F}(\mathbb{J},|s⟩)$ may be thought of as the image of the surface of the Euclidean unit sphere in ${\mathbb{C}}^2$ under the continuous transformation $|s⟩\to ⟨s|\mathbb{J}|s⟩.$ In the Pauli formalism, this corresponds to a surjective linear transformation relating each complex point in $\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}})$ with two points on the Poincaré unit sphere in ${\mathbb{R}}^3$ through the linear mapping $\mathcal{F}=z_0+\mathbf{\text{Z}}\cdot \widehat{\mathbf{\text{S}}}.$

The mapping between the FoV and the points on the Poincaré sphere is illustrated graphically in figure 2b,c. We identify the following properties:

• —
  The eigenvector circle maps onto the major axis of the ellipse. Special points on the circle are (figure 2c):

  • (a)
    Stokes eigenvectors $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}}$ and their antipodal vectors map onto the foci of the ellipse, i.e.

    $${\mu }_a=\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{A}}})=\mathcal{F}(\mathbb{J},-\widehat{\mathbf{\text{B}}})$$ 3.11a

    and

    $${\mu }_b=\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{B}}})=\mathcal{F}(\mathbb{J},-\widehat{\mathbf{\text{A}}}).$$ 3.11b
  • (b)
    The Stokes vector ${\widehat{\mathbf{\text{u}}}}_3$ and its antipodal vector are the vectors that satisfy $\mathbf{\text{Z}}\cdot {\widehat{\mathbf{\text{u}}}}_3=0$ in equation (3.4), then map onto the centre of the ellipse

    $$z_0=\mathcal{F}(\mathbb{J},\pm {\widehat{\mathbf{\text{u}}}}_3).$$ 3.12
  • (c)
    The Stokes vector ${\widehat{\mathbf{\text{u}}}}_2$ and its antipodal vector map onto the vertices of the ellipse, i.e. the endpoints of the major axis

    $${\upsilon }_{\pm }=\mathcal{F}(\mathbb{J},\pm {\widehat{\mathbf{\text{u}}}}_2).$$ 3.13
• (ii)
  The u-equator maps onto the elliptic contour of the FoV, see figure 2b.

  • (a)
    The Stokes vector ${\widehat{\mathbf{\text{u}}}}_1$ and its antipodal vector map onto the covertices of the ellipse, i.e. the endpoints of the minor axis

    $${\zeta }_{\pm }=\mathcal{F}(\mathbb{J},\pm {\widehat{\mathbf{\text{u}}}}_1).$$ 3.14
  • (b)
    The extreme points ξ_± of the ellipse along the horizontal direction are

    $${\xi }_{\pm }=\mathcal{F}(\mathbb{J},\pm \widehat{\mathbf{\text{P}}}),\text{where}\hspace{0.17em}\mathbf{\text{P}}\equiv \mathrm{Re}\mathbf{\text{Z}}.$$ 3.15
  • (c)
    The extreme points γ_± of the ellipse along the vertical direction are

    $${\gamma }_{\pm }=\mathcal{F}(\mathbb{J},\pm \widehat{\mathbf{\text{Q}}}),\text{where}\hspace{0.17em}\mathbf{\text{Q}}\equiv \mathrm{Im}\mathbf{\text{Z}}.$$ 3.16
  • (d)
    The real vectors $\widehat{\mathbf{\text{P}}}$ and $\widehat{\mathbf{\text{Q}}}$ always lie on the u-plane; therefore, they can be expressed as a linear superposition of the vectors $({\widehat{\mathbf{\text{u}}}}_1,{\widehat{\mathbf{\text{u}}}}_2)$. The middle vector ${\widehat{\mathbf{\text{u}}}}_3$ may be defined in terms of the vectors $\widehat{\mathbf{\text{P}}}$ and $\widehat{\mathbf{\text{Q}}}$ as follows:

    $${\widehat{\mathbf{\text{u}}}}_3=\frac{\widehat{\mathbf{\text{P}}}\times \widehat{\mathbf{\text{Q}}}}{|\widehat{\mathbf{\text{P}}}\times \widehat{\mathbf{\text{Q}}}|}.$$ 3.17
  • —
    As shown in figure 2b, the meridians and parallels of the system $({\widehat{\mathbf{\text{u}}}}_1,{\widehat{\mathbf{\text{u}}}}_2,{\widehat{\mathbf{\text{u}}}}_3)$ on the Poincaré sphere transform onto radial straight lines and concentric ellipses on the FoV, respectively.

The values inside the elliptic FoV are double degenerate, which means that each value can be obtained with two different polarization states $\widehat{\mathbf{\text{S}}}$ located symmetrically about the equatorial u-plane of the Poincaré sphere.

(c). Mathematical properties

The FoV has several useful functional properties [7–9]. Here, we mention briefly some of them for reference and later use.

• —
  (P1) Linearity (scaling + translation): For all ${\mathbb{J}\in \mathbb{C}}^{2\times 2}$ and $\alpha ,\beta \in \mathbb{C},$

  $$\mathcal{F}(\alpha \mathbb{J}+\beta \mathbb{I})=\alpha \mathcal{F}(\mathbb{J})+\beta ,$$ 3.18

  where we have omitted the second argument in the notation of $\mathcal{F}(\mathbb{J},\cdot )$ for simplicity.
• —(P2) Projection: Let $H(\mathbb{J})\equiv (\mathbb{J}+{\mathbb{J}}^{†})/2$ be the Hermitian part of $\mathbb{J}$, and $S(\mathbb{J})\equiv (\mathbb{J}-{\mathbb{J}}^{†})/2$ the skew-Hermitian part of $\mathbb{J}$.
  Hermitian projection: The Hermitian part of $\mathbb{J}$ projects its FoV onto the real axis, see figure 1a, i.e.

  $$\mathcal{F}(H(\mathbb{J}))=\mathrm{Re}\mathcal{F}(\mathbb{J}).$$ 3.19

  The extreme points of the line $\mathcal{F}(H(\mathbb{J}))$ are the eigenvalues of the Hermitian matrix $H(\mathbb{J}),$ and correspond to the real parts of ξ_± in equation (3.15).
  Skew-Hermitian projection: The skew-Hermitian part of $\mathbb{J}$ projects its FoV onto the imaginary axis, i.e.

  $$\mathcal{F}(S(\mathbb{J}))=\mathrm{i}\mathrm{Im}\mathcal{F}(\mathbb{J}).$$ 3.20

  The extreme points of the line $\mathcal{F}(S(\mathbb{J}))$ are the eigenvalues of the skew-Hermitian matrix $S(\mathbb{J}),$ and correspond to the imaginary parts of γ_± in equation (3.16).
• —
  (P3) Unitary similarity invariance. For all ${\mathbb{J}\in \mathbb{C}}^{2\times 2},$ and $\mathbb{U}$ unitary (i.e. ${\mathbb{U}}^{†}\mathbb{U}=I$),

  $$\mathcal{F}({\mathbb{U}}^{†}\mathbb{J}U)=\mathcal{F}(\mathbb{J}).$$ 3.21

  Therefore, the FoV of a Jones matrix is invariant under unitary transformations.
• —
  (P4) Spectral containment: For all ${\mathbb{J}\in \mathbb{C}}^{2\times 2}$, its eigenvalues $\lambda (\mathbb{J})=\{{\mu }_a,{\mu }_b\}$ lie inside the FoV,

  $$\lambda (\mathbb{J})\subset \mathcal{F}(\mathbb{J}).$$ 3.22

  As mentioned above, the eigenvalues are the foci of the elliptic FoV.
• —
  (P5) Subadditivity. For all $\mathbb{J},{\mathbb{M}\in \mathbb{C}}^{2\times 2}$

  $$\mathcal{F}(\mathbb{J}+M)\subset \mathcal{F}(\mathbb{J})+\mathcal{F}(\mathbb{M}).$$ 3.23

  Thus, the FoV of a sum of matrices in a subset of the sum of the respective FoV.

Combining the properties (P4) and (P5) yields the inclusions

$$\lambda (\mathbb{J}+M)\subset \mathcal{F}(\mathbb{J}+M)\subset \mathcal{F}(\mathbb{J})+\mathcal{F}(\mathbb{M}),$$ 3.24

so if $\mathcal{F}(\mathbb{J})$ and $\mathcal{F}(\mathbb{M})$ are known, something can be concluded about the spectrum of the sum. For example, let $\mathbb{J}=[0,j;0,0]$ and $\mathbb{M}=[0,0;m,0]$. Then $\lambda (\mathbb{J})=\lambda (\mathbb{M})=\{0\},$ and $\lambda (\mathbb{J}+M)=\{\pm \sqrt{jm}\}\subset \mathcal{F}(\mathbb{J}+M),$ which is the elliptic disc with foci $\pm \sqrt{jm}$ and minor axis equal to ||j| − |m||.

Here, we presented the properties of the FoV that are useful in understanding the behaviour of 2 × 2 complex matrices. We refer the reader to a specialized reference for a more extended treatment of the general case with n × n matrices [7–9].

4. Special cases of the field of values and applications

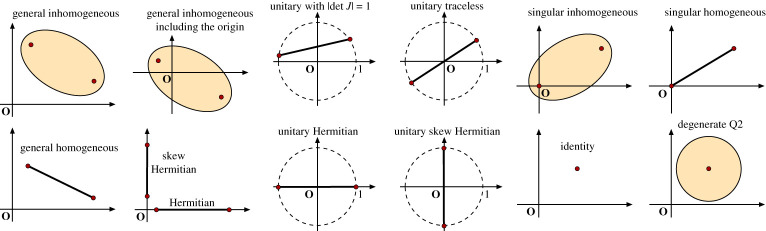
The properties of the FoV are useful to characterize the meaningful special cases that we usually find in optical applications. To obtain a graphic visualization of the relevant cases, see figure 3.

• —
  Homogeneous (normal) matrices. If $\mathbb{J}$ becomes normal ($\mathbb{J}{\mathbb{J}}^{†}={\mathbb{J}}^{†}\mathbb{J}$), i.e. homogeneous with orthogonal eigenstates (having antipodal eigenvectors $\widehat{\mathbf{\text{A}}},$ and $\widehat{\mathbf{\text{B}}}=-\widehat{\mathbf{\text{A}}}$ in the Poincaré sphere), then the elliptic FoV equation (3.4) reduces to the straight line connecting the eigenvalues, i.e.

  $$\mathcal{F}({\mathbb{J}}_{\text{homo}},\widehat{\mathbf{\text{S}}})=z_0+\widehat{\mathbf{\text{A}}}\cdot \widehat{\mathbf{\text{S}}}.$$ 4.1

  This result is very striking. Once the eigenvalues have been defined, all Jones matrices with orthogonal eigenvectors have the same FoV. If $\mathbb{J}$ is an homogeneous matrix, the shifted matrix $\mathbb{K}\equiv \mathbb{J}-z_0\mathbb{I}$ satisfies ${\mathbb{K}}^{†}\mathbb{K}=k\mathbb{I}$, for some constant k ≥ 0. We have the following meaningful subcases:

  • (a)
    Hermitian matrices (${\mathbb{J}}^{†}=\mathbb{J}$): Their FoV is a line segment on the real axis, with endpoints being the eigenvalues of $\mathbb{J}.$ Example: let $\mathbb{J}=(\begin{array}{cc}2& \mathrm{i}\\ -\mathrm{i}& 0\end{array})$. Then $\mathcal{F}(\mathbb{J})\in [1-\sqrt{2},1+\sqrt{2}].$ Optical devices described by Hermitian matrices are non-singular absorbers and partial polarizers, either linear and circular.
  • (b)
    Skew-Hermitian (${\mathbb{J}}^{†}=-\mathbb{J}$): Their FoV is a line segment on the imaginary axis, with endpoints being the eigenvalues of $\mathbb{J}.$ Skew-Hermitian optical devices could be implemented with a partial polarizer and a λ/4 phase retarder in cascade.
  • (c)
    Unitary matrices (${\mathbb{J}}^{†}\mathbb{J}=\mathbb{I}$): Since the eigenvalues of unitary matrices have modulus one, i.e. ${\text{e}}^{\mathrm{i}\alpha },$ it can be concluded that their FoV is a line segment with endpoints lying on a unit circle centred at the origin. An unitary matrix can be scaled such its determinant is not unitary, i.e. ${\mathbb{J}}^{†}\mathbb{J}=\alpha \mathbb{I}$; in this case, the endpoints of its FoV lie on the circle with radius |α|^1/2. Example: let $\mathbb{J}=(\begin{array}{cc}0.6& -0.8\\ 0.8& 0.6\end{array})$. Then $\mathcal{F}(\mathbb{J})$ is the vertical line connecting the points (0.6 − i0.8) and (0.6 + i0.8). The typical optical devices described by unitary matrices are the lossless phase retarders, either linear and circular.
  • —
    Singular matrices: If $\mathbb{J}$ is singular ($det\mathbb{J}=0$), then one of the focal points of its FoV coincides with the origin $\mathcal{F}=0.$ Singular matrices can be inhomogeneous (elliptic FoV) or homogeneous (line FoV). Example: Let $\mathbb{J}=(\begin{array}{cc}1& 0\\ 0& 0\end{array})$. Then $\mathcal{F}(\mathbb{J})\in [0,1].$ The standard optical devices characterized by singular matrices are the perfect polarizers, where the transmission of one of the eigenstates is equal to zero.
  • —
    Degenerate matrices: If both eigenvalues are equal, they collapse at the point μ on the complex plane. Here, we have the two subcases discussed in §2a.
  • (a)
    If $\mathbb{J}$ is diagonal, $\mathbb{J}=\mu \mathbb{I}$, then the FoV reduces to a single point located at z₀ = μ.
  • (b)
    If $\mathbb{J}$ is not diagonalizable, it belongs to the Jordan form ${\mathbb{Q}}_2,$ then the FoV becomes a circle centred at μ with radius

    $$R_{\mathbb{Q}2}=L_1=L_2=\frac{|c{|}_{max}}{2}=\frac{|j_2|+|j_3|}{2}.$$ 4.2

    Example: Let $\mathbb{J}=(\begin{array}{cc}0& 2\\ 0& 0\end{array})$. Then $\mathcal{F}(\mathbb{J})$ is the closed unit disc centred at the origin, i.e. $\mathbf{\text{D}}=\{\alpha \in \mathbb{C}:|\alpha |\le 1\}.$ The defective optical systems are optical realizations of degenerate matrices [18].

Figure 3.

FoV of special cases of Jones matrices. Small circles represent the eigenvalues of the matrix. (Online version in colour.)

The FoV of any linear transformation of $\mathbb{J}$ of the special cases discussed above can be derived easily with the linearity property (P1).

(a). Considerations of the inverse problem

Geometrically speaking, an arbitrary ellipse on the plane needs five independent real parameters to be fully specified. On the other hand, a 2 × 2 Jones matrix with complex entries has eight real parameters. Therefore, there are three free parameters to adjust the properties of the Jones matrix for a given FoV and, in fact, it is possible to get different Jones matrices with the same elliptical FoV.

For instance, with the parametrization used in equations (3.5)–(3.8), the two complex eigenvalues μ_a, μ_b define the foci of the ellipse and provide four real parameters; the fifth parameter could be the magnitude Z. It is clear that, as long as Z remains constant, the coefficients z₁, z₂, z₃ of Z can be modified freely without changing the FoV. A natural question arise here: What is the effect of varying the values z_m on the Jones matrix and on the FoV? In this case, the effect is to change the eigenvectors of $\mathbb{J}$ but keeping constant the angular aperture between them on the Poincaré sphere.

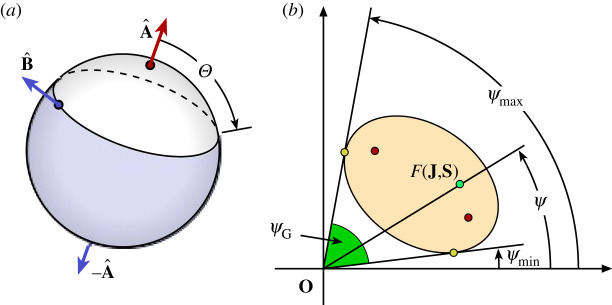
Consider that we want to determine a Jones matrix $\mathbb{J}$ given its FoV. The ellipse can be specified using a variety of parameters, but as mentioned earlier, we need five independent parameters. For example, suppose we give the two coordinates of the centre, the length of the 2 axes and the inclination of the major axis. With this information, we can calculate the position of the foci of the ellipse, which defines the eigenvalues of $\mathbb{J}$. Once the foci are known, we can determine the covertex angle Θ, which corresponds to the angle between the two Stokes eigenvectors in the Poincaré sphere, see figure 4a. Now, we have three extra parameters to define the matrix $\mathbb{J}$ and set up its eigenvectors. First, we freely propose a Stokes eigenvector, say $\widehat{\mathbf{\text{A}}}$, on the Poincaré sphere. This requires two parameters. Because the angle between the Stokes eigenvectors must be Θ, then the eigenvector $\widehat{\mathbf{\text{B}}}$ must lie at any point on a circular parallel Θ taking $\widehat{\mathbf{\text{A}}}$ to be a north pole, see figure 4a. The location of $\widehat{\mathbf{\text{B}}}$ on the circle defines the third parameter. Finally, once we have determined the Stokes eigenvectors $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}}$, we can find the corresponding Jones eigenvectors |a〉 and |b〉, and together with the eigenvalues, we can calculate the matrix $\mathbb{J}$ using the Jordan decomposition equation (2.3).

Figure 4.

(a) The angle between the Stokes eigenvectors $\widehat{\mathbf{\text{A}}}$ and $\widehat{\mathbf{\text{B}}}$ is equal to the covertex angle of the elliptic FoV. (b) The geometric Pancharatnam-Berry phase introduced by the Jones matrix is the angular opening of the smallest angular sector of the complex plane anchored at the origin by the ellipse, i.e. ψ_G = ψ_max − ψ_min. (Online version in colour.)

(b). An application of the FoV to determine the Pancharatnam-Berry phase

From a mathematical point of view, the FoV can be applied in a variety of situations. For example in the numerical solution of partial differential equations and in the stability analysis of dynamical systems arising in mathematical biology, where an estimation of eigenvalues of the associated matrices can be obtained using the FoV [7]. In this subsection, we describe briefly an application of the FoV in polarization optics. For a more detailed explanation of this application, we refer the reader to [10].

When a light polarization state |s〉 passes through the system $\mathbb{J}$, the output field is $|h⟩=\mathbb{J}|s⟩$. As proposed by Pancharatnam [24–28], the phase difference ψ between two normalized states |s〉 and |h〉 is the argument of its inner product, i.e.

$$\psi =\arg ⟨s|h⟩=\arg ⟨s|\mathbb{J}|s⟩.$$ 4.3

Assuming the time convention exp ( − iωt), the state |s〉 is in phase with state |h〉exp ( − iψ), or equivalently, the superposition |s〉 + |h〉exp ( − iψ) yields maximum intensity. It is clear that ψ is directly related with the FoV defined in equation (3.1). As shown in figure 4b, for a given input state with Stokes vector $\widehat{\mathbf{\text{S}}},$ the phase difference with its corresponding output state is the phase of the complex number $\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}})$, that is, $\psi =\arg \mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}})$. Now, the number $\mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}})$ must lie inside the elliptic FoV or its contour. Therefore, the minimum and maximum values of ψ are determined with the angles of the tangent lines to the ellipse that go through the origin, as shown in figure 4b. In this way, the geometric Pancharatnam-Berry phase introduced by the Jones matrix is the angular opening of the smallest angular sector of the complex plane anchored at the origin by the ellipse, i.e. ψ_G = ψ_max − ψ_min.

If the ellipse contains the origin, $0\in \mathcal{F}(\mathbb{J},\widehat{\mathbf{\text{S}}}),$ the phase ψ span the full range ( − π, π], and there are not definite extrema. This case leads to the possibility of having two ortho-transmission states, i.e. input polarization states whose output states are orthogonal, i.e. $⟨s|h⟩=⟨s|\mathbb{J}|s⟩=0$. A detailed discussion of the ortho-transmission states and the properties of the FoV applied to the description of the optical phase can be found in [10]. Additional applications of the concept of FoV in the characterization of optical systems are described in [29].

5. Conclusion

We have applied the concept of the FoV of a square matrix to the case of 2 × 2 Jones matrices used in polarization optics. The FoV proved to be a very useful tool for analysing the Jones matrices through the geometric properties and connections between their eigenvalues and eigenvectors. For the particular case of matrices of dimension 2, the FoV is an ellipse on the complex plane. Much matrix information can be extracted simply by analysing the geometry of the ellipse. The special cases of the ellipse (circles, lines and points) serve to classify the matrices typically found in optical polarization applications. We believe that the concept of FoV contributes to the understanding and characterization of optical systems that can be described with Jones matrices.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interest.

Funding

Consejo Nacional de Ciencia y Tecnologia, Mexico (grant no. PN2016-3140).