Abstract
Predicting the effects of seasonality and climate change on the emergence and spread of infectious disease remains difficult, in part because of poorly understood connections between warming and the mechanisms driving disease. Trait-based mechanistic models combined with thermal performance curves arising from the metabolic theory of ecology (MTE) have been highlighted as a promising approach going forward; however, this framework has not been tested under controlled experimental conditions that isolate the role of gradual temporal warming on disease dynamics and emergence. Here, we provide experimental evidence that a slowly warming host–parasite system can be pushed through a critical transition into an epidemic state. We then show that a trait-based mechanistic model with MTE functional forms can predict the critical temperature for disease emergence, subsequent disease dynamics through time and final infection prevalence in an experimentally warmed system of Daphnia and a microsporidian parasite. Our results serve as a proof of principle that trait-based mechanistic models using MTE subfunctions can predict warming-induced disease emergence in data-rich systems—a critical step towards generalizing the approach to other systems.
Keywords: temperature, thermal ecology, parasite, metabolic theory of ecology, Daphnia magna, Ordospora colligata
1. Introduction
The emergence and dynamics of infectious disease epidemics often depends on temperature, including for diseases of humans [1–4], livestock and crops [5,6], and wildlife populations [7–10]. The impacts of climate change on host–parasite systems remain difficult to predict, however, as the emergence, severity and duration of epidemics depend on the interaction of many factors [11], such as host density [12], the infectivity of a parasite [13] and the balance between transmission and host exploitation that underlies virulence [14]. Each of these characteristics can have distinct temperature dependencies, possibly differing in strength and direction, and it is their interactions that ultimately determine the net effect of temperature on the course of an epidemic [4,15,16].
Trait-based mechanistic models that explicitly incorporate the effects of temperature can provide an effective approach for predicting how these different interactions shape an epidemic [17]. In this approach, the thermal dependencies of host and parasite traits are described either discretely or, more often, continuously using thermal performance curves [18]. These thermal performance curves are then nested within a mechanistic model of disease spread, allowing predictions of how temperature affects various metrics of interest for the host–parasite system. This method has predicted temperature's effects on several host–parasite systems [4,15,16,19–22], but the equations used to relate trait performance to temperature are often described by fitting system-specific phenomenological functions, such as quadratic or Briere functions, to data-rich experiments (but see [19,23] which use monotonic Arrhenius functions to model temperature-dependence in Daphnia–fungal parasite populations). This suggests that our ability to understand and predict impacts of climate change on disease dynamics will be restricted to systems for which data are available and can be fit using thermal performance curves. As most host–parasite systems are data poor, this impedes our ability to apply trait-based modelling in many disease systems [24].
The metabolic theory of ecology (MTE) is one area of ecological theory that holds promise for predicting the response of infectious diseases to climate change or seasonality when little data are available [25–28]. The MTE is a general framework that characterizes from first (metabolic) principles how temperature affects physiological rates, how temperature sensitivities may vary among taxa based on macroecological commonalities as well as how these thermal dependencies propagate across biological levels of organization [26]. MTE functions that have their bases in biological reaction rates, such as the Arrhenius or Sharpe–Schoolfield functions, have been shown to capture thermal scaling of disease-related traits such as the mortality and development rates of parasite larvae [27], the parasite equilibrium abundance within a host [29] and the contact rate of hosts with parasites [30]. However, to date, most studies using the MTE to predict infectious disease dynamics have focused on individual hosts rather than disease at the population level (but see [19,23]).
Taken together, trait-based mechanistic models provide a promising approach to predicting how warming will influence disease emergence, and the MTE offers a potential way forward for filling in the thermal performance data requirements in these models. Using this combination of methods, we identified two key research gaps that must be addressed in order to predict warming-induced disease emergence and spread at the host population level. First, while predicted by theory, we still lack experimental evidence that a slowly warming system can be pushed from a disease-free or low-disease state (where R0 < 1) into an epidemic state (where R0 > 1). Second, though trait-based models have been shown to capture observed patterns of disease across different thermal conditions (e.g. [4,19,20]), they have not been tested under controlled experimental conditions that isolate the role of gradual temporal warming on disease dynamics and emergence.
Here, using a combination of models and experiments, we address these gaps by testing whether it is possible to predict warming-induced outbreaks of an infectious disease by using MTE functions to thermally scale the parameters in a susceptible–infected (SI) type trait-based model for environmentally transmitted disease. The model predicted that the basic reproduction number R0 for the disease crosses the R0 = 1 boundary just below 12°C, indicating that epidemics should only be able to establish once environmental temperatures reach and exceed 12°C. Experimentally, we drove populations of the host–parasite system Daphnia magna–Ordospora colligata (a microsporidian parasite) with constant, low immigration of infected individuals through slowly warming conditions (10–13.5°C over 120 days) and compared the course of the resultant epidemics to constant-temperature controls. In agreement with the independently parametrized model, experimental epidemics established in the warming populations once temperatures reached 12°C, but were never established in populations that remained at 10°C.
2. Material and methods
(a). Host–parasite system
Ordospora colligata is an environmentally transmitted microsporidian parasite of D. magna, a small freshwater invertebrate. The parasite infects the epithelial cells of its host's gut after being inadvertently ingested by the host during filter feeding [31]. The parasite replicates intracellularly, eventually lysing the cell and releasing spores that spread to nearby gut cells or are released into the water column where they can go on to infect other individuals. All Daphnia individuals in this experiment (and in the previous experiments used to parametrize our model; [29,30]) are from a single Finnish clone (FI-OER-3-3), from which the parasite strain (OC3) we used was originally isolated.
(b). Model
Our mechanistic trait-based model (equations (2.1)–(2.4)) contains 13 parameters (table 1), six of which are temperature dependent [29,30]. We incorporated the thermal dependency of these parameters using relationships from the MTE that were previously determined from experimental data on individual hosts (see [29,30]; figure 1); equations (2.1)–(2.4) describe how susceptibles (S; (equation (2.1))) transition to infecteds (I; equation (2.2)), which then transition to dead infecteds (D; equation (2.3)) that can still shed the parasite into the environment while they decay (E (environmental spores); equation (2.4)) (see model parametrization and assumptions in the electronic supplementary material for a more detailed description of the model and figure 1 for thermal functions). We note that our model is aimed at tracking disease dynamics across large, female adult Daphnia in each population, as we did not inspect juvenile or male Daphnia for infections (see Experimental methods for more detail and justification):
| 2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
Table 1.
Parameters for equations (2.1)–(2.5). (Our mechanistic susceptible–infected model (equations (2.1)–(2.4)) and corresponding expression for the basic reproduction number (R0; equation (2.5)) contains 13 parameters, of which six are temperature-dependent arising from four thermal functions (figure 1). We incorporated the thermal dependency of the temperature-dependent parameters using the MTE relationships that were previously determined from experimental data on individual hosts in Kirk et al. [29,30].)
| temperature-independent parameters |
||||
|---|---|---|---|---|
| parameter | description | source | value | |
| ϕS | input of susceptibles | methods used in this study | 3.535 day−1 | |
| ϕI | input of infecteds | methods used in this study | 0.465 day−1 | |
| K | adult density-dependent recruitment constraint | abundance measured in this study | 170 | |
| ψ | maximum per capita recruitment | assumed (such that abundance remains constant near K) | 1.33 day−1 | |
| h | harvesting | methods used in this study | 0.0235 day−1 | |
| γ | environmental spore mortality | experimental medium removal rate used in this study | 0.0286 day−1 | |
| θ | corpse degradation | average from degradation experiment | 0.1 day−1 | |
| temperature-dependent parameters | ||||
| parameter | description | source | function | unit |
| μ(T) | natural mortality rate | [29] | Sharpe–Schoolfielda,b | day−1 |
| χ(T) | contact rate | [30] | Sharpe–Schoolfielda | day−1 |
| σ(T) | probability of infection | [30] | Sharpe–Schoolfielda,b | |
| λ(T) | parasite shedding rate | [29] | Sharpe–Schoolfielda,c | day−1 |
| α(T) | parasite-induced mortality rate | [29] | Sharpe–Schoolfielda,c | day−1 |
| ω(T) | parasite intensity at host death | [29] | Sharpe–Schoolfielda,c | |
aSee figure 1 for functional forms.
bNatural mortality rate and probability of infection were determined by underlying expressions which use Sharpe–Schoolfield functions (see the electronic supplementary material for more details).
cThe model parameters shedding rate, parasite-induced mortality rate and parasite intensity at death were each modelled as proportional to within-host infection intensity, which is modelled using a Sharpe–Schoolfield function.
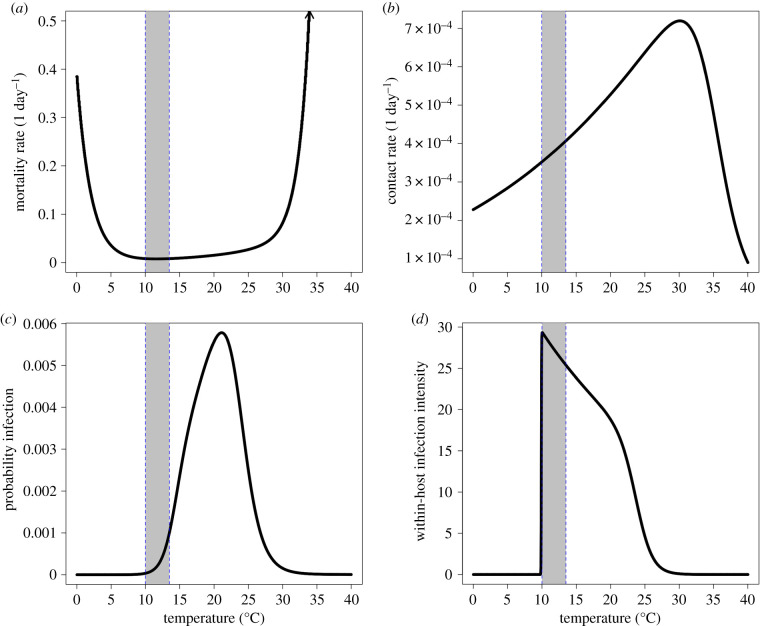
Figure 1.
Temperature-dependence of (a) host natural mortality rate, (b) contact rate with environmental parasites, (c) probability of infection after contact and (d) average within-host infection intensity from Kirk et al. [29,30]. While contact rate and within-host infection intensity were each modelled as MTE functions directly, natural mortality rate and probability of infection were determined here by underlying expressions which use MTE functions (see the electronic supplementary material for more details). The model parameters shedding rate, parasite-induced mortality rate and parasite intensity at death were each modelled as proportional to within-host infection intensity (d). The contact rate is the proportion of the entire water volume filtered per day by an individual. The grey shaded region between the dashed blue lines represents the temperature range over which the experimental warming treatments warmed (10–13.5°C), while the constant temperature treatments were kept at 10°C. (Online version in colour.)
In equations (2.1)–(2.4), susceptible adult individuals are continuously added to each population as per our experimental methods (ϕS) or by natural density-dependent recruitment (determined by intrinsic recruitment rate (ψ), adult density and carrying capacity (K)), and are lost via natural mortality (μ), by being harvested out of the experiment (h) or by becoming infected at rate χσSE. The product of contact rate (χ) and the probability of infection after contact (σ) is the transmission coefficient that is classically represented by the parameter β, but separated here to allow for modelling via the MTE [30]. Infected adult individuals are added via transmission and by immigration of infected animals (ϕI) and are lost via natural mortality (μ), parasite-induced mortality (α) and harvesting (h). Infected individuals that die transition to the D class and are eventually lost via degradation (θ). Spores are released into the environment via continuous shedding by live infected individuals (λ) and also released from dead infected individuals at rate ωθ, where ω is the number of spores in the host when they die. Spores are lost via experimentally induced mortality rate (γ) when medium is removed.
The basic reproduction number (R0) of the parasite is formulated from equations (2.1)–(2.4), and is equal to
| 2.5 |
where all parameters except h, γ and Seq (density of susceptible adult hosts) depend on temperature, T. Harvesting (h) is temperature-independent because it is experimentally induced; we also assume that our experimentally induced spore mortality rate (γ) overwhelms any natural spore mortality rate that may be temperature-dependent. Our data did not show a signal of temperature-dependent Seq over our experimental temperature range (electronic supplementary material, figure S1), although we consider potential effects of temperature-dependent host density in the Discussion. When parametrized, equation (2.5) predicts the host densities and thermal regimes the disease can (R0 > 1) and cannot (R0 < 1) invade under (figure 2).
Figure 2.
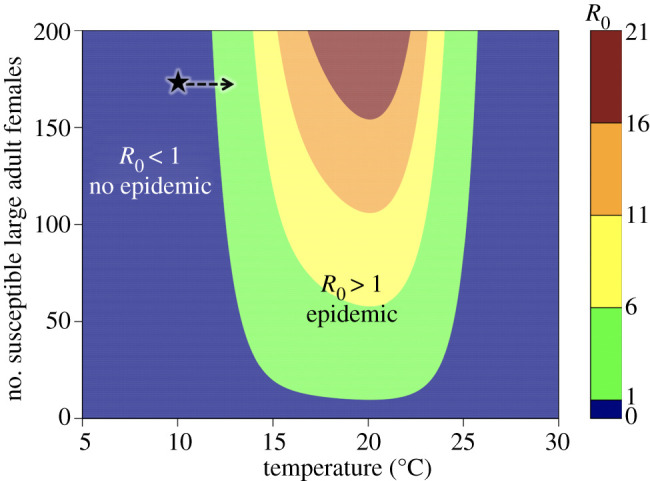
The basic reproduction number (R0) as a function of temperature (x-axis) and susceptible large, adult female host density (y-axis) as predicted from equation (2.5). Blue represents conditions in which R0 < 1 and the disease cannot spread. The star denotes the approximate initial conditions of our experiment and the arrow denotes the trajectory of the warming populations. The arrow is moving horizontally across the plane, because we did not see any clear evidence of a temperature effect on Daphnia population abundances (electronic supplementary material, figure S1). The constant 10°C populations remained at the starred conditions for the duration of the experiment, while the warming populations moved to conditions where epidemics should occur. (Online version in colour.)
Our R0 formulation makes two key assumptions. First, we assume that spores that are ingested but do not infect the host are expelled, re-enter the water column and remain viable. While there has not yet been an experimental test of this assumption in this system, evidence from a similar host–parasite system (D. magna–Pasteuria ramosa) showed that the parasite was not killed if it failed to infect the host [32] and there are several reasons to believe the same holds for our system (electronic supplementary material). Second, we assume that the rate of spore loss from the water column owing to ingestion and subsequent infection is very small compared to spore loss via media removal (i.e. << ) and can, therefore, be ignored, which is supported in this system as σ is very small [30]. The electronic supplementary material contains additional details on the R0 formulation.
The temperature-dependent parameters of the model were described using thermal relationships arising from the MTE (table 1). Specifically, we used the Sharpe–Schoolfield equation ([33]; equation (2.6)) and its variants [27,29] to capture: (i) the Boltzmann–Arrhenius relationship that describes the thermal dependence of a process' rate within intermediate temperature ranges based on the process’ activation energy and Boltzmann's constant [26]; and (ii) how reaction rates are altered at high or low temperatures (T) when biological processes are impeded
| 2.6 |
The Sharpe–Schoolfield equation can be described by equation (2.6), where x0 is the rate of a given process x at the reference temperature T0, is the activation energy, k is Boltzmann's constant (k = 8.62 × 10−5 eV K−1) and EIx and EHx are the inactivation energies at the low (TLx) and high (THx) temperature thresholds, respectively. All temperatures are recorded in degrees Kelvin. For unimodal curves where x decreases past the temperature thresholds, z is equal to −1, whereas z is equal to +1 if x increases past the temperature thresholds (e.g. if x is mortality rate; [27,29]). In some processes x may only have low- or high-temperature thresholds rather than both.
Previous work has shown that these metabolic models can accurately capture the thermal dependencies of many host and parasite traits in the Daphnia–Ordospora system at the scale of individual hosts [29,30], and we used these previously published MTE functions to represent the parameters in equations (2.1)–(2.4) that were temperature-dependent (table 1 and figure 1). In other words, the temperature-dependence of our model was parametrized using experiments that were completely independent from the one reported here. While we refer readers to the previous studies for details on parameter experiments and model fitting, briefly: contact rate (χ) was modelled using a Sharpe–Schoolfield function with only an upper-temperature threshold (figure 1b; [30]); within-host infection intensity was modelled using a Sharpe–Schoolfield function with upper and lower temperature thresholds and a negative activation energy, causing infection intensity to decrease across the intermediate temperature range (figure 1d; [29]). Natural mortality rate (μ; figure 1a) and probability of infection (σ; figure 1c) were each composite functions of other terms (e.g. ageing rate, infection rate) that were represented by the Sharpe–Schoolfield functions ([29,30]; see the electronic supplementary material for more details). Additionally, contact rate (χ) increases with, and the probability of infection (σ) decreases with, Daphnia size [30]. We, therefore, assumed that large, female adult Daphnia size was constant in both treatments at 2700 µm and found that our model predictions were not strongly impacted by this and other parameter assumptions (electronic supplementary material, figure S2). The model parameters shedding rate (λ), parasite-induced mortality (α) and parasite intensity at death (ω) were each modelled as proportional to within-host infection intensity.
Finally, to assess the role of demographic stochasticity in our experiment and model predictions, we conducted 250 stochastic simulations of the model, both under warming and under constant-temperature conditions, using the GillespieSSA package [34] in R (R 2018). We refer the reader to the electronic supplementary material for further discussion of model parametrization and assumptions.
(c). Experimental methods
We evaluated our model predictions using eight experimental host–parasite populations. The experiment was initiated with eight 35 l tanks that housed populations of uninfected Daphnia. Prior to the experiment, these populations were maintained at laboratory conditions (20°C) for 15 days before they were moved into four environmental growth chambers set to 10°C. They remained at 10°C for another 15 days to allow for acclimatization, and population abundances stabilized between 150 and 240 large (approx. 2.7 mm in length) individuals in each population before the experiment began (electronic supplementary material, figure S1).
To initiate the experiment, we introduced three large adult individuals that had previously been exposed to the parasite into each of the eight experimental populations. Exposed animals were randomly selected from infected stock cultures that were kept in multiple 2 l mesocosms. Prevalence in these infected stock cultures was determined on day 100 by randomly selecting 314 individuals across all stocks and was found to be 46.5%. This prevalence is similar to that found in a less thorough sampling event prior to the experiment (55 out of 100 infected), so we assume that stock prevalence was constant at 46.5% throughout the experiment (i.e. on average, we introduced 1.4 infected animals into each experimental population every 3 days).
The infected stock cultures were maintained at 20°C, such that the individuals introduced from these populations were not acclimatized to 10°C. We did this to ensure that parasites were introduced as intended, rather than risk animals losing their infection during the acclimatization period and prior to their introduction (within-host parasite abundances are extremely low at 10°C and infections have rarely been reported at this temperature; [29,30]). An additional experiment revealed no signs of increased mortality in the first 24 h after a group of 20 individuals was transferred from 20 to 10°C (animals alive after the temperature shift: 19.6 ± 0.6, animals alive in the control: 19.3 ± 0.6, 3 replicates per treatment; data not shown). Other rates such as filtration may not be immediately acclimatized to 10°C, though the acclimatization process for this is generally quite rapid (less than 48 h; [30]).
On day 3 and subsequently every 3 days for the duration of the 120 day experiment, we randomly collected 12 large females from each experimental population. In the model and experiment, we focused on large adult females (rather than males or juveniles) for three reasons. First, large adult females should be the primary contributors to the force of infection in the population, as they have significantly higher parasite loads compared to males [35] and have much higher parasite loads compared to juveniles (i.e. infection has less time to develop in juveniles) [29]. Second, Daphnia populations are often female biased (as asexual reproduction is the predominant reproductive mode), further reducing the role males play in disease transmission. And third, it is methodologically fraught to quantify O. colligata abundance in juvenile D. magna owing to their small body size that renders dissections unreliable and makes it difficult to characterize the typically low parasite abundances in juveniles, resulting in increased false negatives in juveniles. Our measures of prevalence and host density should thus be considered as the prevalence of infection in adult female Daphnia and the density of adult female Daphnia, respectively.
Sampled individuals were destructively inspected using phase contrast microscopy to assess (i) whether they were infected and (ii) their infection intensity, which is defined here as the number of parasite spore clusters per individual [29]. To replace the 12 destructively sampled individuals, we introduced 12 new individuals—three randomly selected from infected stock populations at 20°C plus nine from uninfected stock populations that were acclimatized to their new temperature for 15 days. In summary, every 3 days, we removed 12 individuals and introduced 12 new individuals, of which on average 1.4 were infected (i.e. three individuals from infected stocks × 0.465 infection prevalence in these stocks), with a minimum of zero and a maximum of three infected. Each sampling day, we also removed 3 l of Daphnia growth medium (ADaM; [36]) and replaced it with 3 l of new ADaM. Assuming that Ordospora spores are randomly distributed throughout the medium, our experimental process of removing 3 l of the 35 l every 3 days invoked a mortality rate of γ = 0.0286 days−1. Finally, each population was fed 350 million batch cultured algae (Monoraphidium minutum) each sampling day.
After the first 15 days (i.e. five sampling events), we raised the temperature in two of the environmental growth chambers that were randomly selected on day 0 to be the ‘warming treatment’ (i.e. experimental populations 5–8). The temperature was raised in these chambers by 0.5 to 10.5°C, while the other two chambers (i.e. experimental populations 1–4) remained at 10°C. This process of warming 0.5°C every 15 days continued for a total of 120 days, resulting in 40 sampling days (480 samples per population). At the conclusion of the experiment, 15 days after the last temperature increase to 13.5°C, we sampled an additional 36 individuals per population (for a total of 48 individuals per population on day 120) to provide a more accurate estimate of final disease prevalence. We used a generalized linear model with random effects (glmer function from the R package lme4; [37]) with family = binomial and link = logit to test for significant differences in the final number of infected individuals in the warming versus constant treatments where the random effect was replicate population. To test for increases in infection prevalence over time, we used a similar generalized linear model with random effects where the response was prevalence, the fixed predictors were treatment, day scaled to be centred on zero, and an interaction between these two predictors, and the random effect was the replicate population.
On days 0, 15, 30, 45, 60, 75, 90, 105 and 120, we estimated the number of large adults in each population via visual inspection (i.e. individuals large enough to be considered for random sampling of infection status on sampling days). We repeated each estimate three times to obtain an estimate of our variation in counts. Juvenile D. magna were not included in abundance counts because they were too small and numerous for visual counting and would also not have been sampled for infection status. Although at times, especially earlier in the experiment, there was large variation in the host population sizes, we did not observe any clear differences in population abundances in warming versus constant 10°C experimental populations (electronic supplementary material, figure S1). The mean population size across all populations throughout the experiment was 169.5, so we set the density-dependent constraint on adult recruitment (K) to be 170 in our model, and set maximum per capita recruitment to the adult class (ψ) at a relatively high value of 1.33 to keep population-size constant over time at approximately 169 individuals. We note that here the choice of K and ψ are inconsequential to the analysis focused on disease invasion so long as the chosen parameters generate a host abundance equilibrium that matches the experimental mean.
3. Results
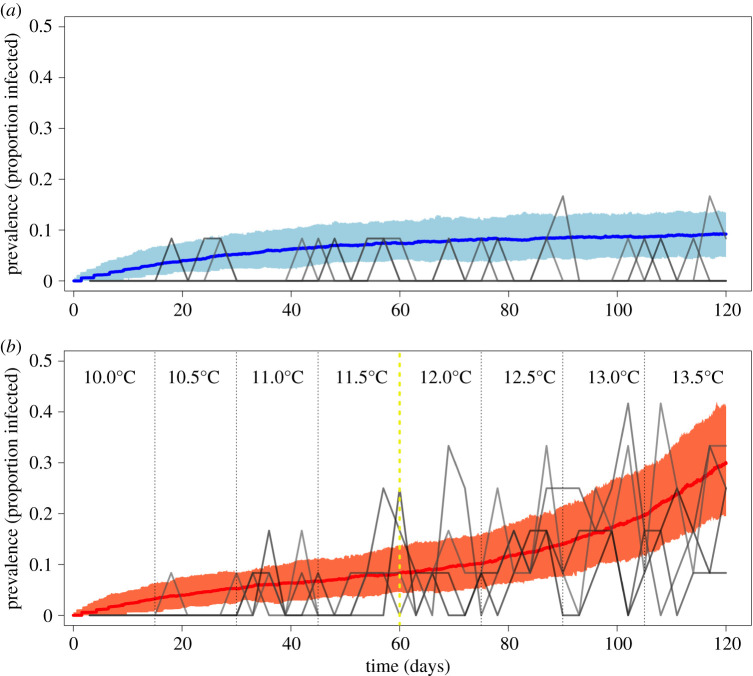
The experiment carried four host–parasite populations through a 3.5°C warming over 120 days from the predicted low-disease conditions at 10°C, across the predicted R0 = 1 boundary near 12°C and into disease invasion conditions up to 13.5°C (figure 2), while four control populations were held at 10°C where the disease was not expected to establish. Observations from experimental populations and model predictions were concordant. At very low host densities, the model predicted that the disease would be unable to spread regardless of temperature (figure 2). At sufficiently high adult host density, however, temperature becomes the primary determinant of whether an epidemic can occur (figure 2). Early in the experiment, disease prevalence was very low across all populations (figure 3a,b), though a low immigration rate of infected individuals allowed the disease to persist under unfavourable thermal conditions. As the experiment neared its mid-point (day 60) and warming populations reached 12°C, the frequency and number of infected individuals increased in the warming populations (figure 3b). This trend of increased disease prevalence continued as temperature increased in warming populations, whereas the control populations that remained at 10°C never experienced a large increase in disease incidence (i.e. there was a significant interaction between treatment and day in the glmer model: p = 0.002; figure 3a). The trait-based mechanistic model predicted both that disease prevalence rose quickly once temperatures reached 12°C (figure 3b; prevalence increased from approx. 10% to approx. 30% over 60 days) and that the disease was maintained at less than 10% prevalence when temperatures remained constant at 10°C (figure 3a). The observed versus model predicted prevalence values for the warming populations are shown in the electronic supplementary material, figure S4, with R2 values ranging from 0.297 to 0.533.
Figure 3.
Experimental data from four replicate control (constant 10.0°C) populations (a; grey lines) and four replicate warming populations (b; grey lines). Blue (a) and red (b) lines represent the median of 250 stochastic simulations of our temperature-dependent model (equations (2.1)–(2.4)) being forced through constant (a) or warming (b) conditions. Light blue and light red shaded areas represent 95% confidence intervals from simulations which incorporate demographic stochasticity but not parameter uncertainty (see the electronic supplementary material, figure S3 for predictions with parameter uncertainty). Note that owing to the continuous input of infected individuals into the experiment, the disease is predicted to be present at low prevalence even when R0 < 1 (a; constant 10.0°C). The vertical yellow dashed line represents the temperature/time-point at which the trait-based model predicts R0 > 1. Prevalence is modelled for and calculated from the experimental data from large, adult female Daphnia. (Online version in colour.)
On the final day of the experiment, we assessed an additional 36 individuals per population (12 + 36 = 48 total; approx. 30% of the total population) to obtain a better estimate of the disease prevalence in the population. We found that the warming population prevalence (mean ± s.e. = 0.229 ± 0.043) had significantly higher disease prevalence (p < 0.0001; figure 4) at the conclusion of the experiment relative to the constant 10°C populations (mean ± s.e. = 0.031 ± 0.010).
Figure 4.
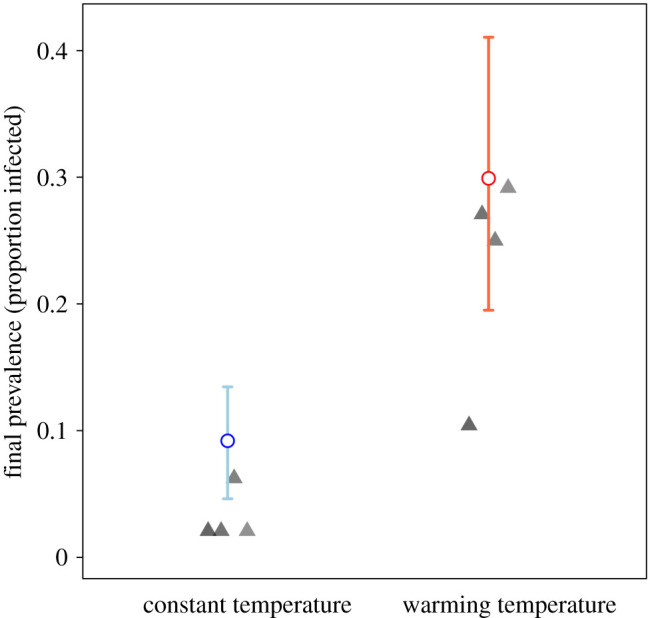
Observed final prevalence based on 48 individuals (approx. 30% of population; solid triangles) compared to predicted final prevalence from the stochastic MTE model (hollow circles). Error bars represent 95% confidence intervals on the final prevalence values observed in 250 stochastic simulations. Experimental warming population prevalence (mean ± s.e. = 0.229 ± 0.043) had significantly higher disease prevalence (p < 0.0001; generalized linear model with logit link) at the conclusion of the experiment relative to the constant 10°C populations (mean ± s.e. = 0.031 ± 0.010). The prevalence and size of population are measured in terms of large, adult female Daphnia. (Online version in colour.)
4. Discussion
We provide experimental evidence that gradually increasing temperatures over time can push a disease system through the critical transition (R0 = 1) into an epidemic state, and that this process can be predicted using trait-based mechanistic models in which thermal performance curves are specified by MTE functional forms. These MTE models were parametrized by previous experiments, and our results serve as a proof of principle that this framework can predict warming-induced disease emergence. This is a critical step towards generalizing this approach for predicting local disease emergence in other host–parasite systems.
Our trait-based modelling framework, which employed temperature-sensitive model parameters in a mechanistic disease model, produced predictions concordant with experimental observations. Indeed, the model predictions are in qualitative and quantitative agreement with the experimental data, in terms of the predicted temperature at which disease outbreaks occur (figure 2), disease dynamics through time (figure 3; electronic supplementary material, figure S4) and final disease prevalence (figure 4). Although previous studies have shown that rising temperatures can exacerbate [19] or mitigate disease [20], controlled experiments of infectious disease spread under slowly rising temperatures have rarely been conducted. Our study not only experimentally shows that warming owing to climate change may alter disease dynamics, but also provides a framework by which these changes could be anticipated. This may assist in mitigating damage done by disease to ecosystem services [38], biodiversity [39] and human health [40].
Integrating thermal performance curves within trait-based mechanistic disease models can be used to predict disease emergence, but it is a data-intensive approach. We show here that a well-parametrized trait-based mechanistic model which isolates the roles and contributions of different characteristics of a host–parasite system (e.g. adult host density, infection rate) to the dynamics of an epidemic can be capable of predicting disease emergence. However, the formulation of such models requires a good understanding of the system as well as data for parametrizing and testing the thermal functions. The MTE thermal performance curves used here were parametrized via several large experiments [29,30] that will not be feasible in most systems. Indeed, if experiments need to be conducted for each host–parasite system to fit temperature-dependent MTE functions to data, its purported advantage (using little to no data) would be negated. The MTE was originally proposed as a means for overcoming such data gaps [27,28], but to make that vision reality, we first require an experimental proof of principle that MTE functions, when parametrized in data-rich systems, can reasonably predict warming-induced disease dynamics. This work addresses this knowledge gap by showing that a combination of trait-based mechanistic modelling and the MTE can predict warming-induced disease emergence at a population level.
Moving forward, using the MTE in a trait-based mechanistic model for data-poor systems will require parameter values to be input into the MTE functions a priori. A potential starting point could be to use parameter values near the broad averages found in other systems (e.g. activation energies in the 0.60–0.70 eV range; [25,26]), but this approach is unlikely to have performed well at predicting R0 in this study, as several traits in this system differ significantly in their activation energies and temperature thresholds from one another [29,30]. This highlights that until further meta-analyses, such as the ones that have shown how activation energy varies among free-living species with covariates such as taxon, trait function or habitat [41], are performed for disease systems, accurately parametrizing the MTE functions a priori will be difficult. However, as we learn more about the generalities of activation energies, inactivation energies and temperature thresholds, we should eventually be able to make predictions about how these MTE parameters may deviate from means based on the characteristics of the system or the trait in question [24]. This would allow for the possibility of parametrizing models for data-poor disease systems.
In addition to predicting a warming-induced epidemic, the trait-based mechanistic framework may be useful for predicting range shifts of infectious disease as well as disease fade-out arising from climate warming. For example, the model predicts that if we had started the experiment near 23°C, epidemics would have initially occurred in both the constant temperature and warming treatments, and that warming would subsequently drive disease elimination. For a given system, knowledge of host density, environmental temperature and magnitude of warming would enable the application of our modelling framework and allow for predictions related to whether warming could lead to epidemics or disease elimination.
Whether increases in the mean temperature will generally lead to more or fewer epidemics will depend on the balance between the number of host–parasite systems that will be pushed into R0 > 1 space (i.e. the arrow in figure 2) and those that will be pushed from epidemics into R0 < 1 space [27,42]. At the same time, warming may alter the ability of parasites to disperse into new regions that were previously unsuitable [43]. This suggests that for some systems, it may be insufficient to predict warming's effects on epidemics based solely on changes to R0, and that factors such as dispersal and colonization may need to be incorporated [43]. The breadth of the MTE, covering thermal relationships from the individual to the ecosystems level, could provide a means for incorporating the temperature sensitivities of such phenomena, as has, for example, been demonstrated in previous work that linked dispersal, temperature and metabolic rate in free-living marine species [44].
Although the model was able to capture the thermal dependence of disease emergence, it overestimated disease prevalence in the constant 10°C treatment (figures 3 and 4). This might be because the model may overestimate within-host parasite equilibrium abundance at this temperature, as there is uncertainty at which precise temperature the parasite equilibrium abundance decreases to zero, though it is estimated to occur between 9.5 and 11.8°C [29]. Beyond reducing uncertainty in the MTE parameter estimates, there are additional thermal responses that could be incorporated into this model or models for other host–parasite systems. For example, we did not have information to parametrize the temperature-dependence of environmental spore mortality and microparasite shedding. While these additional MTE submodels could improve the quantitative match between predicted and observed dynamics, our results were generally insensitive to a range of parameter values for these traits (electronic supplementary material, figure S2 and table S1). Additionally, our model neglects the contribution to transmission from juveniles in the population and focuses on large, adult female Daphnia only, both because the latter are the predominant contributors to the force of infection and because infections in juveniles are hard to detect. If infections were able to be detected reliably in juveniles, a more complicated stage- or age-structured model that explicitly tracks infections across juveniles and adults may provide more information on the overall disease dynamics in the population, but this is unlikely to alter model predictions for R0 owing to the small contribution of juveniles to the transmission dynamics. Finally, our analyses disregard shorter-term temperature fluctuations that are probably important in natural host–parasite systems [9,45–50] and are predicted by climate models to increase in many regions [51]; however, the effects of temperature variability on rates may be incorporated in future efforts via methods such as nonlinear averaging [52]. When considering temperature fluctuations and the speed of temperature change in a system, it may also be worthwhile to account for how long-lived the particular host species is, as different systems can experience temperature change over a range of temporal scales.
Our results inform on the seasonality of disease dynamics, as our slowly warming experimental system mimics the onset of spring. Indeed, many populations living in temperate and polar climates encounter seasonal variation in temperature that far exceeds our experimental change of 3.5°C over 120 days. For instance, the water temperature of temperate lakes can increase from 4°C during the winter to greater than 25°C during the summer months [53]. In these systems, disease is typically regulated by temperature, and ecological variables that are correlated with temperature [28]. Warming can alter the seasonality of epidemics, potentially causing epidemics to occur earlier in the season [19], leading to larger transmission peaks in the autumn, or even splitting one annual transmission period into two distinct seasonal transmission periods [27]. Understanding the likelihood of these events is critical to predicting and mitigating future epidemics. Using mechanistic models of disease transmission with temperature-dependent parameters is proving an excellent way forward for describing the seasonality of infectious diseases [19,20,27,54]. Similarly, it may also prove useful in predicting the effects of pulse heat stress events on host–parasite systems, a task of emerging importance [50].
Beyond causing changes in key epidemiological parameters such as contact rate, temperature may also indirectly or directly affect host population density [55]—typically another key variable in determining R0. For example, changing temperatures may alter the amount of available habitat for a population [56], indirectly leading to reduced or increased competition and larger or smaller population densities, respectively. The MTE suggests that increased temperatures will result in lower population carrying capacities for ectothermic hosts owing to the increased per capita metabolic demands of individuals [57], though this effect may be counteracted by potential changes in resource availability with temperature [58]. We did not see any evidence of a temperature effect on adult female Daphnia abundances over our relatively small temperature range (10–13.5°C; electronic supplementary material, figure S1), suggesting that differences in population size were not the driver of higher disease prevalence in the warming treatments versus in the constant 10°C treatments. Because of this, we did not allow population densities to vary with temperature in our model. However, densities will be influenced by temperature in many other systems, as well as potentially in this one if a wider temperature range were considered, and these changes can again be captured by the MTE, as demonstrated in phytoplankton [59]. In general, the effects of warming temperatures on disease risk via host density effects could be positive or negative.
In summary, a general predictive framework for climate effects on infectious disease is required to advance our understanding of how climate change will affect disease emergence, and a trait-based approach using the MTE has been highlighted as a promising way forward [24,27,28,60]. Accumulating evidence has shown that MTE models can capture the thermal dependence of many host–parasite traits [27,29,30] and we have shown here that these models can be scaled up to predict population-level disease dynamics in a warming or constant environment. Our results do not make specific predictions for how warming will affect different host–parasite systems; however, this case study can serve as a much-needed experimental verification of warming-induced disease emergence and its predictability using trait-based mechanistic models with MTE thermal performance curves.
Supplementary Material
Acknowledgements
We thank Jessica Philips, Andrijana Stanić and Stephanie Peacock for assistance with parameter estimates and Dieter Ebert and Jürgen Hottinger for the provision of host and parasite material. We also thank Spencer Hall, Dak de Kerckhove, Nicole Mideo and Ben Gilbert for comments on the manuscript.
Ethics
No ethics approval was required for this research.
Data accessibility
The data supporting the results are archived at the Dryad Digital Repository and accessible at https://dx.doi.org/10.5061/dryad.tb2rbnzxq [61]. Code used in this study is accessible at https://github.com/devingkirk/warming_disease_emergence.
Authors' contributions
D.K., P.L., N.J., L.K., C.P., P.M. and M.K. conceived the study. D.K., L.K. and C.P. conducted the experiment. D.K. and M.K. developed the model, and D.K. conducted the simulations. D.K. and P.L. wrote the first draft, and all authors contributed to revisions.
Competing interests
The authors declare no competing interests.
Funding
This work was supported by an Ontario Graduate Scholarship to D.K., a Canada Research Chair and Discovery and Accelerate grants from the Natural Sciences and Engineering Research Council of Canada to M.K. and an Institutional Strategic Fund from the Wellcome Trust to Trinity College Dublin to P.L. P.M. is grateful for support from a Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant (RGPIN-2016-06301), the Canada Foundation for Innovation (CFI) John R. Evans Leaders Fund (grant no. 35341) and the Ministry of Research, Innovation and Sciences (MRIS) Ontario Research Fund.
References
- 1.Randolph SE, Green RM, Peacey MF, Rogers DJ. 2000. Seasonal synchrony: the key to tick-borne encephalitis foci identified by satellite data. Parasitology 121, 15–23. ( 10.1017/S0031182099006083) [DOI] [PubMed] [Google Scholar]
- 2.Pascual M, Bouma MJ, Dobson AP. 2002. Cholera and climate: revisiting the quantitative evidence. Microbes Infect. 4, 237–245. ( 10.1016/S1286-4579(01)01533-7) [DOI] [PubMed] [Google Scholar]
- 3.Zhou G, Minakawa N, Githeko AK, Yan G. 2004. Association between climate variability and malaria epidemics in the East African highlands. Proc. Natl Acad. Sci. USA 101, 2375–2380. ( 10.1073/pnas.0308714100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mordecai EA, et al. 2013. Optimal temperature for malaria transmission is dramatically lower than previously predicted. Ecol. Lett. 16, 22–30. ( 10.1111/ele.12015) [DOI] [PubMed] [Google Scholar]
- 5.Hoberg EP, Polley L, Jenkins EJ, Kutz SJ. 2008. Pathogens of domestic and free-ranging ungulates: global climate change in temperate to boreal latitudes across North America. Rev. Sci. Tech. Off. Int. Epiz. 27, 511–528. ( 10.20506/rst.27.2.1818) [DOI] [PubMed] [Google Scholar]
- 6.Kumar R, Mina U, Gogoi R, Bhatia A, Harit RC. 2016. Effect of elevated temperature and carbon dioxide levels on maydis leaf blight disease tolerance attributes in maize. Agric. Ecosyst. Environ. 231, 98–104. ( 10.1016/j.agee.2016.06.029) [DOI] [Google Scholar]
- 7.Pounds JA, et al. 2006. Widespread amphibian extinctions from epidemic disease driven by global warming. Nature 439, 161–167. ( 10.1038/nature04246) [DOI] [PubMed] [Google Scholar]
- 8.Cohen JM, Venesky MD, Sauer EL, Civitello DJ, McMahon TA, Roznik EA, Rohr JR. 2017. The thermal mismatch hypothesis explains host susceptibility to an emerging infectious disease. Ecol. Lett. 20, 184–193. ( 10.1111/ele.12720) [DOI] [PubMed] [Google Scholar]
- 9.Cohen JM, Civitello DJ, Venesky MD, McMahon TA, Rohr JM. 2019. An interaction between climate change and infectious disease drove widespread amphibian declines. Glob. Change Biol. 25, 927–937. ( 10.1111/gcb.14489) [DOI] [PubMed] [Google Scholar]
- 10.Harvell CD, et al. 2019. Disease epidemic and a marine heat wave are associated with the continental-scale collapse of a pivotal predator (Pycnopodia helianthoides). Sci. Adv. 5, eaau7042 ( 10.1126/sciadv.aau7042) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lafferty KD, Mordecai EA. 2016. The rise and fall of infectious disease in a warmer world. F1000 Res. 5, 1–8. ( 10.12688/f1000research.8766.1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lloyd-Smith JO, Cross PC, Briggs CJ, Daugherty M, Getz WM, Latto J, Sanchez MS, Smith AB, Swei A. 2005. Should we expect population thresholds for wildlife disease? Trends Ecol. Evol. 20, 511–519. ( 10.1016/j.tree.2005.07.004) [DOI] [PubMed] [Google Scholar]
- 13.Duffy MA, Sivars-Becker L. 2007. Rapid evolution and ecological host-parasite dynamics. Ecol. Lett. 10, 44–53. ( 10.1111/j.1461-0248.2006.00995.x) [DOI] [PubMed] [Google Scholar]
- 14.Galvani AP. 2003. Epidemiology meets evolutionary ecology. Trends Ecol. Evol. 18, 132–139. ( 10.1016/S0169-5347(02)00050-2) [DOI] [Google Scholar]
- 15.Mordecai EA, et al. 2017. Detecting the impact of temperature on transmission of Zika, dengue, and chikungunya using mechanistic models. PLOS Negl. Trop. Dis. 11, e0005568 ( 10.1371/journal.pntd.0005568) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shapiro LLM, Whitehead SA, Thomas MB. 2017. Quantifying the effects of temperature on mosquito and parasite traits that determine the transmission potential of human malaria. PLoS Biol. 15, e2003489 ( 10.1371/journal.pbio.2003489) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mangal TD, Paterson S, Fenton A. 2008. Predicting the impact of long-term temperature changes on the epidemiology and control of schistosomiasis: a mechanistic model. PLoS ONE 3, e1438 ( 10.1371/journal.pone.0001438) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Angilletta MJ. 2006. Estimating and comparing thermal performance curves. J. Therm. Biol. 31, 541–545. ( 10.1016/j.jtherbio.2006.06.002) [DOI] [Google Scholar]
- 19.Shocket MS, et al. 2018. Temperature drives epidemics in a zooplankton-fungus disease system: a trait driven approach points to transmission via host foraging. Am. Nat. 191, 435–451. ( 10.1086/696096) [DOI] [PubMed] [Google Scholar]
- 20.Gehman AM, Hall RJ, Byers JE. 2018. Host and parasite thermal ecology jointly determine the effect of climate warming on epidemic dynamics. Proc. Natl Acad. Sci. USA 115, 744–749. ( 10.1073/pnas.1705067115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huber JH, Childs ML, Caldwell JM, Mordecai EA. 2018. Seasonal temperature variation influences climate suitability for dengue, chikungunya, and Zika transmission. PLoS Negl. Trop. Dis. 12, e0006451 ( 10.1371/journal.pntd.0006451) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tesla B, Demakovsky LR, Mordecai EA, Ryan SJ, Bonds MH, Ngonghala CN, Brindley MA, Murdock CC. 2018. Temperature drives Zika transmission: evidence from empirical and mathematical models. Proc. R. Soc. B 285, 20180795 ( 10.1098/rspb.2018.0795) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hall SR, Tessier AJ, Duffy MA, Huebner M, Cáceres CE. 2006. Warmer does not have to mean sicker: temperature and predators can jointly drive timing of epidemics. Ecology 87, 1684–1695. ( 10.1890/0012-9658(2006)87[1684:WDNHTM]2.0.CO;2) [DOI] [PubMed] [Google Scholar]
- 24.Molnár PK, Sckrabulis JP, Altman KA, Raffel TR. 2017. Thermal performance curves and the metabolic theory of ecology: a practical guide to models and experiments for parasitologists. J. Parasitol. 103, 423–439. ( 10.1645/16-148) [DOI] [PubMed] [Google Scholar]
- 25.Gillooly JF, Brown JH, West GB, Savage VM, Charnov EL. 2001. Effects of size and temperature on metabolic rate. Science 293, 2248–2251. ( 10.1126/science.1061967) [DOI] [PubMed] [Google Scholar]
- 26.Brown JH, Gillooly JF, Allen AP, Savage VM, West GB. 2004. Toward a metabolic theory of ecology. Ecology 85, 1771–1789. ( 10.1890/03-9000) [DOI] [Google Scholar]
- 27.Molnár PK, Kutz SJ, Hoar BM, Dobson AP. 2013. Metabolic approaches to understanding climate change impacts on seasonal host-macroparasite dynamics. Ecol. Lett. 16, 9–21. ( 10.1111/ele.12022) [DOI] [PubMed] [Google Scholar]
- 28.Altizer S, Ostfeld RS, Johnson PTJ, Kutz S, Harvell CD. 2013. Climate change and infectious diseases: from evidence to a predictive framework. Science 341, 514–519. ( 10.1126/science.1239401) [DOI] [PubMed] [Google Scholar]
- 29.Kirk D, et al. 2018. Empirical evidence that metabolic theory describes the temperature dependency of within-host parasite dynamics. PLoS Biol. 16, e2004608 ( 10.1371/journal.pbio.2004608) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kirk D, Luijckx P, Stanic A, Krkosek M. 2019. Predicting the thermal and allometric dependencies of disease transmission via the metabolic theory of ecology. Am. Nat. 193, 661–676. ( 10.1086/702846) [DOI] [PubMed] [Google Scholar]
- 31.Ebert D. 2005. Ecology, epidemiology, and evolution of parasitism in Daphnia. Bethesda, MD: National Library of Medicine (US), National Center for Biotechnology Information; See http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=Books. [Google Scholar]
- 32.King KC, Auld SKJR, Wilson PJ, James J, Little TJ. 2013. The bacterial parasite Pasteuria ramosa is not killed if it fails to infect: implications for coevolution. Ecol. Evol. 3, 197–203. ( 10.1002/ece3.438) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schoolfield RM, Sharpe PJH, Magnuson CE. 1981. Non-linear regression of biological temperature-dependent rate models based on absolute reaction-rate theory. J. Theor. Biol. 88, 719–731. ( 10.1016/0022-5193(81)90246-0) [DOI] [PubMed] [Google Scholar]
- 34.Pineda-Krch M. 2012. GillespieSSA: Gillespie's stochastic simulation algorithm (SSA). R package version 0.5-4 See https://CRAN.R-project.org/package=GillespieSSA.
- 35.Zukowski N, Kirk D, Wadhawan K, Shea D, Start D, Krkosek M. 2020. Predators can influence the host–parasite dynamics of their prey via nonconsumptive effects. Ecol. Evol. 10, 6714–6722. ( 10.1002/ece3.6401) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Klüttgen B, Dülmer U, Engels M, Ratte HT. 1994. AdaM, an artificial freshwater for the culture of zooplankton. Water Res. 28, 743–746. ( 10.1016/0043-1354(94)90157-0) [DOI] [Google Scholar]
- 37.Bates D, Maechler M, Bolker B, Walker S. 2015. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48. ( 10.18637/jss.v067.i01) [DOI] [Google Scholar]
- 38.Vanbergen AJ, et al. 2013. Threats to an ecosystem service: pressure on pollinators. Front. Ecol. Environ. 11, 251–259. ( 10.1890/120126) [DOI] [Google Scholar]
- 39.De Castro F, Bolker B. 2005. Mechanisms of disease-induced extinction. Ecol. Lett. 8, 117–126. ( 10.1111/j.1461-0248.2004.00693.x) [DOI] [Google Scholar]
- 40.Patz JA, Campbell-Lendrum D, Holloway T, Foley JA. 2005. Impact of regional climate change on human health. Nature 438, 310–317. ( 10.1038/nature04188) [DOI] [PubMed] [Google Scholar]
- 41.Dell AI, Pawar S, Savage VM. 2011. Systematic variation in the temperature dependence of physiological and ecological traits. Proc. Natl Acad. Sci. USA 108, 10 591–10 596. ( 10.1073/pnas.1015178108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dobson A, Molnár PK, Kutz S. 2015. Climate change and Arctic parasites. Trends Parasitol. 31, 181–188. ( 10.1016/j.pt.2015.03.006) [DOI] [PubMed] [Google Scholar]
- 43.Hurford A, Cobbold CA, Molnár P. 2019. Skewed temperature dependence affects range and abundance in a warming world. Proc. R. Soc. B 286, 20191157 ( 10.1098/rspb.2019.1157) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.O'Connor MI, Bruno JF, Gaines SD, Halpern BS, Lester SE, Kinlan BP, Weiss JM. 2007. Temperature control of larval dispersal and the implications for marine ecology, evolution, and conservation. Proc. Natl Acad. Sci. USA 104, 1266–1271. ( 10.1073/pnas.0603422104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rohr JR, Raffel TR. 2010. Linking global climate and temperature variability to widespread amphibian declines putatively caused by disease. Proc. Natl Acad. Sci. USA 107, 8269–8274. ( 10.1073/pnas.0912883107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Raffel TR, Romansic JM, Halstead NT, McMahon TA, Venesky MD, Rohr JR. 2012. Disease and thermal acclimation in a more variable and unpredictable climate. Nat. Clim. Change 3, 146–151. ( 10.1038/nclimate1659) [DOI] [Google Scholar]
- 47.Raffel TR, Halstead NT, McMahon TA, Davis AK, Rohr JR. 2015. Temperature variability and moisture synergistically interact to exacerbate an epizootic disease. Proc. R. Soc. B 282, 20142039 ( 10.1098/rspb.2014.2039) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Paiijmans KP, Blanford S, Bell AS, Blanford JI, Read AF, Thomas MB, Denlinger DL. 2010. Influence of climate on malaria transmission depends on daily temperature variation. Proc. Natl Acad. Sci. USA 107, 15 135–15 139. ( 10.1073/pnas.1006422107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lambrechts L, Paaijmans K, Fansiri T, Carrington LB, Kramer LD, Thomas MB, Scott TW. 2011. Impact of daily temperature fluctuations on dengue virus transmission by Aedes aegypti. Proc. Natl Acad. Sci. USA 108, 7460–7465. ( 10.1073/pnas.1101377108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Claar DC, Wood CL. 2020. Pulse heat stress and parasitism in a warming world. Trends Ecol. Evol. 35, 704–715. [DOI] [PubMed] [Google Scholar]
- 51.Bathiany S, Dakos V, Scheffer M, Lenton TM. 2018. Climate models predict increasing temperature variability in poor countries. Sci. Adv. 4, eaar5809 ( 10.1126/sciadv.aar5809) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bernhardt JR, Sunday JM, Thompson PL, O'Connor MI. 2018. Nonlinear averaging of thermal experience predicts population growth rates in a thermally variable environment. Proc. R. Soc. B 285, 20181076 ( 10.1098/rspb.2018.1076) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.O'Reilly CM, et al. 2015. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 42, 10 733–10 781. [Google Scholar]
- 54.Shocket MS, et al. 2018. Parasite rearing and infection temperatures jointly influence disease transmission and shape seasonality of epidemics. Ecology 99, 1975–1987. ( 10.1002/ecy.2430) [DOI] [PubMed] [Google Scholar]
- 55.Myers RA. 2001. Stock and recruitment: generalizations about maximum reproductive rate, density dependence, and variability using meta-analytic approaches. ICES J. Mar. Sci. 58, 937–951. ( 10.1006/jmsc.2001.1109) [DOI] [Google Scholar]
- 56.Cline TJ, Bennington V, Kitchell JF. 2013. Climate change expands the spatial extent and duration of preferred thermal habitat for Lake Superior fishes. PLoS ONE 8, e62279 ( 10.1371/journal.pone.0062279) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Savage VM, Gillooly JF, Brown JH, West GB, Charnov EL. 2004. Effects of body size and temperature on population growth. Am. Nat. 163, 429–441. ( 10.1086/381872) [DOI] [PubMed] [Google Scholar]
- 58.Kerkhoff AJ, Enquist BJ, Elser JJ, Fagan WF. 2005. Plant allometry, stoichiometry and the temperature-dependence of primary productivity. Global Ecol. Biogeogr. 14, 585–598. ( 10.1111/j.1466-822X.2005.00187.x) [DOI] [Google Scholar]
- 59.Bernhardt JR, Sunday JM, O'Connor MI. 2018. Metabolic theory and the temperature-size rule explain the temperature dependence of population carrying capacity. Am. Nat. 192, 687–697. ( 10.1086/700114) [DOI] [PubMed] [Google Scholar]
- 60.Rohr JR, et al. 2011. Frontiers in climate change-disease research. Trends Ecol. Evol. 26, 270–277. ( 10.1016/j.tree.2011.03.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kirk D, Luijckx P, Jones N, Krichel L, Pencer C, Molnár P, Krkošek M. 2020. Data from: Experimental evidence of warming-induced disease emergence and its prediction by a trait-based mechanistic model Dryad Digital Repository. ( 10.5061/dryad.tb2rbnzxq) [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Kirk D, Luijckx P, Jones N, Krichel L, Pencer C, Molnár P, Krkošek M. 2020. Data from: Experimental evidence of warming-induced disease emergence and its prediction by a trait-based mechanistic model Dryad Digital Repository. ( 10.5061/dryad.tb2rbnzxq) [DOI] [PMC free article] [PubMed]
Supplementary Materials
Data Availability Statement
The data supporting the results are archived at the Dryad Digital Repository and accessible at https://dx.doi.org/10.5061/dryad.tb2rbnzxq [61]. Code used in this study is accessible at https://github.com/devingkirk/warming_disease_emergence.