Abstract
In theoretical modeling of a physical system, a crucial step consists of the identification of those degrees of freedom that enable a synthetic yet informative representation of it. While in some cases this selection can be carried out on the basis of intuition and experience, straightforward discrimination of the important features from the negligible ones is difficult for many complex systems, most notably heteropolymers and large biomolecules. We here present a thermodynamics-based theoretical framework to gauge the effectiveness of a given simplified representation by measuring its information content. We employ this method to identify those reduced descriptions of proteins, in terms of a subset of their atoms, that retain the largest amount of information from the original model; we show that these highly informative representations share common features that are intrinsically related to the biological properties of the proteins under examination, thereby establishing a bridge between protein structure, energetics, and function.
1. Introduction
The quantitative investigation of a physical system relies on the formulation of a model of it, that is, an abstract representation of its constituents and the interactions among them in terms of mathematical constructs. In the realization of the simplest model that entails all of the relevant features of the system under investigation, one of the most crucial aspects is the determination of its level of detail. The latter can vary depending on the properties and processes of interest: the quantum-mechanical nature of matter is explicitly incorporated in ab initio methods,1 while effective classical interactions are commonly employed in the all-atom (AA) force fields used in AA molecular dynamics (MD) simulations.2,3 Representations of a molecular system whose resolution level is lower than the atomistic one are commonly dubbed coarse-grained (CG) models:4−8 in this case, the fundamental degrees of freedom, or effective interaction centroids, are representatives of groups of atoms, and the interactions among these CG sites are parametrized so as to reproduce equilibrium properties of the reference system.
An important distinction should be made between reproducing a given property and describing it. For example, it is evident that the explicit incorporation of the electronic degrees of freedom in the model of a molecule is necessary to reproduce its vibrational spectrum with qualitative and quantitative accuracy; on the other hand, the latter can be measured and described from the knowledge of the nuclear coordinates alone, i.e., from the inspection of a subset of the system’s degrees of freedom. This is a general feature, in that the understanding of a complex system’s properties and behavior can typically be achieved in terms of a reduced set of variables: statistical mechanics provides some of the most recognizable examples of this, such as the description of systems composed of an Avogadro’s number of atoms or molecules in terms of a handful of thermodynamical parameters.
In computer-aided studies, and particularly in the fields of computational biophysics and biochemistry, recent technological advancements—most notably massive parallelization,9 GPU computing,10 and tailor-made machines such as ANTON11—have extended the range of applicability of atomistic simulations to molecular complexes composed of millions of atoms;12−14 even in the absence of such impressive resources, it is now common practice to perform microseconds-long simulations of relatively large systems, up to hundred thousands of atoms. However, a process of filtering, dimensionality reduction, or feature selection is required in order to distill the physically and biologically relevant information from the immense amount of data in which it is buried.
The problem is thus to identify the most synthetic picture of the system that entails all and only its important properties: an optimal balance is sought between parsimony and informativeness. This objective can be pursued by making use of the language and techniques of bottom-up coarse-grained modeling;5,15 in this context, in fact, one defines a mapping operatorM that performs a transformation from a high-resolution configuration ri (i = 1, ..., n) of the system described in great detail to a simpler, coarser configuration RI (I = 1, ..., N < n) at lower resolution:
| 1 |
where n and N are the number of atoms in the system and the number of CG sites chosen, respectively. The linear coefficients cIi in eq 1 are constant, positive, and subject to the normalization condition ∑icIi = 1 to preserve translational invariance. Furthermore, coefficients are generally taken to be specific to each site,15 that is, an atom i taking part in the definition of CG site I will not be involved in the construction of another site J (cJi = 0 ∀ J ≠ I).
Once the mappingM is chosen, the interactions among CG sites must be determined. In this respect, several methodologies have been devised in the past decades to parametrize such CG potentials.4−8 Some approaches aim at reproducing as accurately as possible the exact effective potential obtained through the integration of the microscopic degrees of freedom of the system, that is, the multibody potential of mean force (MB-PMF); this is achieved in practice by tuning the CG interactions so as to reproduce specific low-resolution structural properties of the reference systems.16,17 Recently, other methods have been proposed that target not only the structure but also the energetics.18,19
In this work, we do not tackle the issue of parametrizing approximate CG potentials but rather focus on the consequences of the simplification of the system’s description even if the underlying physics is the same, i.e., configurations are sampled with the reference AA probability. In other words, we focus purely on the effect of projecting the AA conformational ensemble onto a CG configurational space using the mapping as a filter.
Inevitably, in fact, a CG representation loses information about the high-resolution reference,5,20 and the amount of information lost depends only on the number and selection of the retained degrees of freedom. In CG modeling, the mapping is commonly chosen on the basis of general and intuitive criteria: for example, it is rather natural to represent a protein in terms of one single centroid per amino acid (usually the choice falls on the α-carbon of the backbone).21 However, it is by no means assured that a given representation that is natural and intuitive to the human eye is also the one that allows the CG model to retain the largest amount of information about the original higher-resolution system.22,23 A quantitative criterion to assess how much detail is lost upon structural coarsening is thus needed in order to make a sensible choice.
In the past few years, various methods have been developed that target the problem of the automated construction of a simplified representation of a protein at a resolution level lower than atomistic. In a pioneering work, Gohlke and Thorpe proposed to partition a protein into a few sizewise diverse blocks, distributing the amino acids among the different domains so as to minimize the degree of internal flexibility of the latter.24 This picture of a protein subdivided into quasi-rigid domains, which has been further developed by several other authors,25−31 is founded on the notion of a simplified model where groups of atoms are assigned to coarse-grained sites not according to their chemistry (e.g., one residue ↔ one site) but rather on the basis of the local properties of the specific molecule under examination. These partitioning methods, however, employ only structural information, in that they aim to minimize each block’s internal strain, while the energetics of the system is neglected.
Some approaches systematically reduce the number of atoms in a system’s representation by grouping them according to graph-theoretical procedures. For example, the method reported by De Pablo and co-workers maps the static structure on a graph and hierarchically decimates it by clustering together the “leaves”;32 alternative methods lump residues in effective sites on the basis of a spectral analysis of the graph Laplacian.33 More recently, Li et al.34 developed a graph neural network-based method to match a data set of manually annotated CG mappings.
Alternatively, it was proposed to retain only those atoms that guarantee the set of new interactions to quantitatively reproduce the MB-PMF.22,35 However, these methods are based on linearized elastic network models36−41 that have the remarkable advantage of being exactly solvable, thus allowing a direct comparison between the CG potential and MB-PMF, but cannot be taken as significant representations of the system’s highly nonlinear interactions.
It follows that all of these pioneering approaches rely either on purely geometrical/topological information obtained from a single static structure; on an ensemble of structures, neglecting energetics and thermodynamics; or on extremely simplified representations of both structure and interactions that do not guarantee general applicability to systems of great complexity.
Here we tackle the issue of the automated, unsupervised construction of the most informative simplified representation of biological macromolecules in purely statistical-mechanical terms, that is, in the language that is most naturally employed to investigate such systems. Specifically, we search for the mapping operator that, for a given number of atoms retained from the original AA model, provides a description whose information content is as close as possible to that of the reference. In this context, then, the term “coarse-grained representation” should not be interpreted as a system with effective interactions whose scope is to reproduce a certain property, phenomenon, or behavior; rather, the representations we discuss here are simpler pictures of the reference system evolving according to the reference microscopic Hamiltonian but viewed in terms of fewer degrees of freedom. Our objective is thus the identification of the most informative simplified picture among those possible.
To this end, we make use of the concept of mapping entropy, Smap,17,42−44 a quantity that measures the quality of a CG representation in terms of the “distance” between probability distributions—the Boltzmann distribution of the reference AA system and the equivalent distribution when the AA probabilities are projected into the CG coordinate space. The mapping entropy is ignorant of the parametrization of the effective interactions of the simplified model: Smap effectively compares the reference system, described through all of its degrees of freedom, to the same system in which configurations are viewed through “coarse-graining lenses”. The difference between these two representations lies only in the resolution, not in the microscopic physics.
Recently, the introduction of a mapping-entropy-related metric proved to be a powerful instrument for determining the optimal coarse-graining resolution level for a biological system.44 Applied to a set of model proteins, this method was capable of identifying the number of sites that needed to be employed in the simplified CG picture to preserve the maximum amount of thermodynamic information about the microscopic reference. However, such analysis was carried out at a fixed CG resolution distribution, with a homogeneous placement of sites along the protein sequence. Moreover, calculations were performed using an exactly solvable yet very crude approximation to the system’s microscopic interactions, namely, a Gaussian network model.
Motivated by these results, in the following we develop a computationally effective protocol that enables the approximate calculation of the mapping entropy for an arbitrarily complex system. We employ this novel scheme to explore the space of the system’s possible CG representations, varying the resolution level as well as the distribution, with the objective of identifying the ones featuring the lowest mapping entropy—that is, allowing for the smallest amount of information loss upon resolution reduction. The method is applied to three proteins of substantially different size, conformational variability, and biological activity. We show that the choice of retained degrees of freedom, guided by the objective of preserving the largest amount of information while reducing the complexity of the system, highlights biologically meaningful and a priori unknown structural features of the proteins under examination, whose identification would otherwise require computationally more intensive calculations or even wet lab experiments.
2. Results
In this section we report the main findings of our work. Specifically, (i) we outline the theoretical and computational framework that constitutes the basis for the calculation of the mapping entropy; (ii) we illustrate the biological systems on which we apply the method; and (iii) we describe the results of the mapping entropy minimization for these systems and the properties of the associated mappings.
2.1. Theory
The concept of mapping entropy as a measure of the loss of information inherently generated by performing a coarse-graining procedure on a system was first introduced by one of us in the framework of the relative entropy method17 and subsequently expanded in refs (42−44). For the sake of brevity, we here omit the formal derivation connecting the relative entropy Srel and the mapping entropy as well as a discussion of the former. A brief summary of the relevant theoretical results presented in refs (17) and (42−44) is provided in Appendix A.
In the following we restrict our analysis to the case of decimation mappings M in which a subset of N < n atoms of the original system are retained while the remaining ones are integrated out, so that
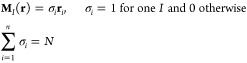 |
2 |
In this case, as shown in Appendix A, the mapping entropy Smap reads as42
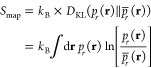 |
3 |
where DKL(pr(r) ∥ p̅r(r)) is the Kullback–Leibler (KL) divergence45 between pr(r), the probability distribution of the high-resolution system, and p̅r(r), the distribution obtained by observing the latter through “coarse-graining glasses”. Following the notation of ref (42), p̅r(r) is defined as
| 4 |
where pR(R) is the probability of the CG macrostate R, given by
| 5 |
in which β = 1/kBT, u(r) is the microscopic potential energy of the system, and Z = ∫dr e–βu(r) is its canonical partition function, while Ω1(R) is defined as
| 6 |
which is the degeneracy of the macrostate—how many microstates map onto the CG configuration R.
The calculation of Smap in eq 3 thus amounts to determining the distance (in the KL sense) between two, although both microscopic, conceptually very different distributions. In contrast to pr(r), eq 4 shows that p̅r(r) assigns the same probability to all configurations that map onto the same CG macrostate R; this probability is given by the average of the original probabilities of these microstates. Importantly, p̅r(r) represents the high-resolution description of the system that would be accessible only starting from its low-resolution description—i.e., pR(R). Grouping together configurations into a CG macrostate has the effect of flattening the detail of their original probabilistic weights. An attempt to revert the coarse-graining procedure and restore atomistic resolution by reintroducing the mapping operator M in pR(R) can only result in microscopic configurations that are uniformly distributed within each macrostate.
Because of the smearing of probabilities, the coarse-graining transformations constitute a semigroup.46 This irreversible character highlights a fundamental consequence of coarse-graining strategies: a loss of information about the system. The definition based on the KL divergence (eq 3) is useful for practical purposes. A more direct understanding of this information loss and how it is encoded in the mapping entropy, however, can be obtained by considering the nonideal configurational entropies of the original and CG representations,
| 7 |
| 8 |
which respectively quantify the information contained in the associated probability distributions pr(r) and pR(R):47 the higher the entropy, the more uniform the distribution, which we associate with a lower information content. By virtue of Gibbs’ inequality, from eq 3 one has Smap ≥ 0. Furthermore, as shown in Appendix A,
| 9 |
so that the entropy of the CG representation is always higher than that of the reference microscopic representation, implying that a loss of information occurs in decreasing the level of resolution.42,44 Critically, the difference between the two information contents is precisely the mapping entropy.
The information that is lost in the coarse-graining process as quantified by Smap depends only on the mapping operator M—in our case, on the choice of the retained sites. This paves the way for the possibility of assessing the quality of a CG mapping on the basis of the amount of information about the original system that it is able to retain, a qualitative advancement with respect to the more common a priori selection of CG representations.21 Unfortunately, eqs 3 and 9 do not allow—except for very simple microscopic models (see ref (44))—a straightforward computational estimate of Smap for a system arising from a choice of its CG mapping, as the observables to be averaged involve logarithms of high-dimensional probability distributions and ultimately configuration-dependent free energies. However, having introduced the loss of information per macrostate Smap(R), defined by the relation42,44
| 10 |
in Appendix B we show that this problem can be overcome by further subdividing microscopic configurations that map to a given macrostate according to their potential energy. Let us define Pβ(U|R) as the conditional probability that a system thermalized at inverse temperature β has energy U provided that is in macrostate R:
| 11 |
Then Smap(R) can be exactly rewritten as follows (see Appendix B):
| 12 |
where ⟨U⟩β|R is the average of the potential energy restricted to the CG macrostate R, given by
| 13 |
This derivation enables a direct estimate of the mapping entropy Smap from configurations sampled according to the microscopic probability distribution pr(r). For a given mapping, the histogram of these configurations with respect to CG coordinates R and energy U approximates the conditional probability Pβ(U|R) and, consequently, Smap(R) (see eq 12); the total mapping entropy can thus be obtained as a weighted sum of the latter over all CG macrostates (eq 10).
The only remaining difficulty consists of obtaining accurate estimates of the exponential average in eq 12, which are prone to numerical errors. As is often done in these cases (see, e.g., free energy calculations through Jarzynski’s equality or the free energy perturbation method48,49), it is possible to rely on a cumulant expansion of eq 12, which when truncated at second order provides
| 14 |
Inserting eq 14 into eq 10 results in a total mapping entropy given by
| 15 |
For a CG representation to exhibit a mapping entropy of exactly zero, it is required that all microstates r that map onto a given macrostate R = M(r) have the same energy in the reference system. Indeed, in this case one has Pβ(U|R) = δ(U – u̅R) in eq 12, where u̅R is the potential energy common to all microstates within macrostate R, and consequently, Smap(R) = 0. Equation 14 highlights that deviations from this condition result in a loss of information associated with a particular CG macrostate that is proportional to the variance of the potential energy of all the atomistic configurations that map to R. The overall mapping entropy is an average of these energy variances over all macrostates, each one weighted with the corresponding probability.
In the numerical implementation we thus seek to identify those mappings that cluster together atomistic configurations having the same energy, or at least very close energies, in order to minimize the information loss arising from coarse-graining. With respect to eq 15, we further approximate Smap as its discretized counterpart S̃map (see Methods):
| 16 |
where we identify Ncl discrete CG macrostates Ri, each of which contributes to S̃map with its own probability pR(Ri), taken as the relative population of the cluster. We then employ an algorithmic procedure to estimate and efficiently minimize, over the possible mappings, a cost function (see eq 25 in Methods)
| 17 |
defined as an average of values of S̃map computed over different CG configuration sets, each of which is associated with a given number of conformational clusters Ncl.
Finally, it is interesting to note that the mapping entropy in the form presented in eq 15 appears in the dual-potential approach recently developed by Lebold and Noid.18,19 In those works, the authors obtained an approximate CG energy function E(R) that is able to accurately reproduce the exact energetics of the low-resolution system—i.e., the average energy ⟨U ⟩β|R in macrostate R (see eq 13). This was achieved by minimizing the functional
| 18 |
with respect to the force field parameters contained in E, where the average in eq 18 is performed over the microscopic model. Expressing ⟨U ⟩β|R as a function of r through the mapping M allows χ2[E] to be decomposed as18,19
| 19 |
Minimizing χ2[E] on E(R) for a given mapping as in refs (18) and (19) is tantamount to minimizing the second term in eq 19 with the objective of reducing the error introduced by approximating ⟨U ⟩β|R through E(R).
However, a comparison of eqs 15 and 19 shows that Smap coincides, up to a multiplicative factor, with the first term of eq 19. Critically, the latter depends only on the mapping M and would be nonzero also in the case of an exact parametrization of E, i.e., for E(R) ≡ ⟨U⟩β|R. The approach illustrated in the present work goes in a direction complementary to that of refs (18) and (19), as we concentrate on identifying those mappings that minimize the one contribution to χ2[E] that is due to, and depends only on, the CG representation M.
2.2. Biological Structures
It is worth stressing that the results of the previous section are completely general and independent of the specific features of the underlying system. Of course, characteristics of the input such as the force field quality, the simulation duration, the number of conformational basins explored, etc. will impact the outcome of the analysis, as is necessarily the case in any computer-aided investigation; nonetheless, the applicability of the method is not prevented or limited by these features or other system properties, e.g., the specific molecule under examination, its complexity, its size, or its underlying all-atom modeling.
To illustrate the method in its generality, here we focus our attention on three proteins that we chose to constitute a small yet representative set of case studies. These molecules cover a size range spanning from ∼30 to ∼400 residues and a similarly broad spectrum of conformational variability and biological function, and they can be taken as examples of several classes of enzymatic and non-enzymatic proteins.
Each protein is simulated for 200 ns in the NVT ensemble with physiological ion concentration. Out of 200 ns, snapshots are extracted from each trajectory every 20 ps, for a total of 104 AA configurations per protein employed throughout the analysis. Details about the simulation parameters, quantitative inspection of MD trajectories, characteristic features of each protein’s results, and the validation of the latter with respect to the duration of the MD trajectory employed can be found in the Supporting Information. Hereafter we provide a description of each molecule along with a brief summary of its behavior as observed along MD simulations.
The first protein is a recently released50 31-residue tamapin mutant (TAM, PDB code 6D93). Tamapin is the toxin produced by the Indian red scorpion. It features a remarkable selectivity toward a peculiar calcium-activated potassium channel (SK2), whose potential use in the pharmaceutical context has made it a preferred object of study during the past decade.51,52 Throughout our simulation, almost every residue is highly solvent-exposed. Side chains fluctuate substantially, thus giving rise to extreme structural variability.
The second protein is adenylate kinase (AKE, PDB code 4AKE), which is a 214 residue phosphotransferase enzyme that catalyzes the interconversion between adenine diphosphate (ADP) and adenine monophosphate (AMP) on the one hand, and the energy-rich complex adenine triphosphate (ATP) on the other hand.53 It can be subdivided in three structural domains: CORE, LID, and NMP.54 The CORE domain is stable, while the other two undergo large conformational changes.55 Its central biochemical role in the regulation of the energy balance of the cell and its relatively small size, combined with the possibility to observe conformational transitions over time scales easily accessible by plain MD,56 make it an ideal candidate to test and validate novel computational methods.22,57,58 In our MD simulation, the protein displays many rearrangements in the two motile domains, which happen to be quite close at many points. Nevertheless, the protein does not undergo a full open ⇄ closed conformational transition.
The third protein is α-1-antitrypsin (AAT, PDB code 1QLP). With 5934 atoms (372 residues), this protein is almost 2 times bigger than AKE. AAT is a globular biomolecule, and it is well-known to exhibit a conformational rearrangement over the time scales of minutes.59−61 During our simulated trajectory, the molecule experiences fluctuations particularly localized in regions corresponding to the most solvent-exposed residues. The protein bulk appears to be very rigid, and there is no sign of a conformational rearrangement.
2.3. Minimization of the Mapping Entropy and Characterization of the Solution Space
The algorithmic procedure described in Methods and Appendix B enables one to quantify the information loss experienced by a system as a consequence of a specific decimation of its degrees of freedom. This quantification, which is achieved through the approximate calculation of the associated mapping entropy, opens the possibility of minimizing such a measure in the space of CG representations in order to identify the mapping that, for a given number of CG sites N, is able to preserve as much information as possible about the AA reference.
In the following we allow CG sites to be located only on heavy atoms, thus reducing the maximum number of possible sites to Nheavy. We then investigate the properties of various kinds of CG mappings having different numbers of retained sites N. Specifically, we consider three chemically intuitive values of N for each biomolecule: (i) Nα, the number of Cα atoms in the structure (equal to the number of amino acids); (ii) Nαβ, the number of Cα and Cβ atoms; and (iii) Nbkb, the number of heavy atoms belonging to the main chain of the protein. The values of N for mappings (i)–(iii) in the cases of TAM, AKE, and AAT are listed in Table 1 together with the corresponding values of Nheavy.
Table 1. Values of Nα, Nαβ, Nbkb, and Nheavy (See the Text) for Each Analyzed Protein.
| protein | Nα | Nαβ | Nbkb | Nheavy |
|---|---|---|---|---|
| TAM | 31 | 59 | 124 | 230 |
| AKE | 214 | 408 | 856 | 1656 |
| AAT | 372 | 723 | 1488 | 2956 |
Even with N restricted to Nα, Nαβ, and Nbkb, the combinatorial dependence of the number of possible decimation mappings on the number of retained sites and Nheavy makes their exhaustive exploration unfeasible in practice (see Methods). To identify the CG representations that minimize the information loss, we thus rely on a Monte Carlo simulated annealing (SA) approach (Methods).62,63 For each analyzed protein and value of N, we perform 48 independent optimization runs, i.e., minimizations of the mapping entropy with respect to the CG site selection; we then store the CG representation characterized by the lowest value of Σ in each run, thus resulting in a pool of optimized solutions. In order to assess their statistical significance and properties, we also generate a set of random mappings and calculate the associated Σ values, which constitute our reference values.
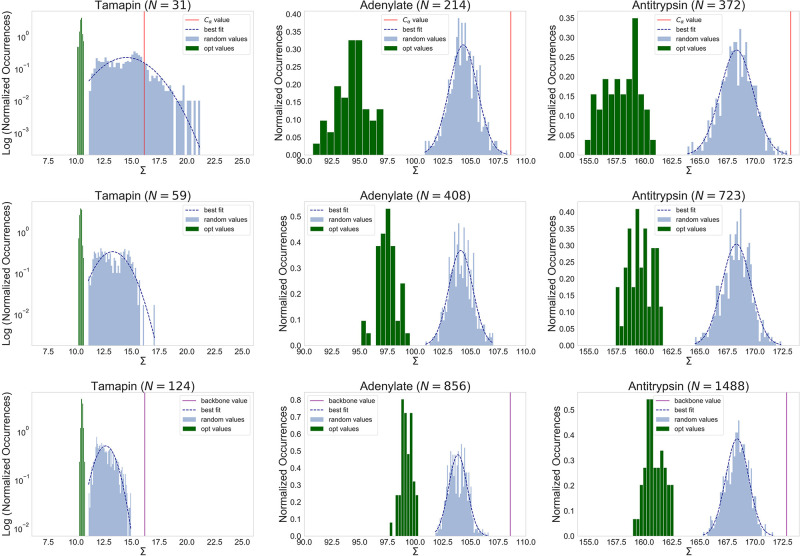
Figure 1 displays, for each value of N considered, the distributions of mapping entropies obtained from random choices of the CG representations of TAM, AKE, and AAT together with each protein’s optimized counterpart. For N = Nbkb and N = Nα in Figure 1 we also report the values of Σ associated with physically intuitive choices of the CG mapping that are commonly employed in the literature: the backbone mapping (N = Nbkb), which neglects all atoms belonging to the side chains; and the Cα mapping (N = Nα), in which we retain only the Cα atoms of the structures. The first is representative of united-atom CG models, while the second is a ubiquitous and rather intuitive choice to represent a protein in terms of a single bead per amino acid.21
Figure 1.
Distributions of the values of the mapping entropy Σ [in kJ mol–1 K–1] in eq 17 for random mappings (light-blue histograms) and optimized solutions (green histograms). Dark-blue dashed lines show the best fit with normal distributions over the random cases. Each column corresponds to an analyzed protein and each row to a given number N of retained atoms. In the first and last rows, corresponding to numbers of CG sites equal to the numbers of Cα atoms and backbone atoms (Nα and Nbkb, respectively), the values of the mapping entropy associated with the physically intuitive choice of the CG sites (see the text) are indicated by vertical lines (red for N = Nα, purple for N = Nbkb). It should be noted that the σ ranges have the same width in all of the plots.
The optimality of a given mapping with respect to a random choice of the CG sites can be quantified in terms of the Z score,
| 20 |
where μ and σ represent the mean and standard deviation, respectively, of the distribution of Σ over randomly sampled mappings. Table 2 summarizes the values of Z found for each N for the proteins under examination, including Z[backbone] and Z[Cα], which were computed with respect to the random distributions generated with N = Nbkb and N = Nα respectively.
Table 2. Z Scores for Each Analyzed Proteina.
| TAM | AKE | AAT | |
|---|---|---|---|
| Z̅[Nα] | –2.22 ± 0.06 | –7.85 ± 1.14 | –6.96 ± 1.03 |
| Z[Nαβ] | –2.38 ± 0.08 | –6.09 ± 0.79 | –6.64 ± 0.84 |
| Z̅[Nbkb] | –2.65 ± 0.09 | –5.55 ± 0.62 | –7.24 ± 0.85 |
| Z[backbone] | 4.37 | 5.65 | 4.31 |
| Z[Cα] | 0.87 | 3.36 | 3.28 |
We report the means (Z̅) and standard deviations of the distributions of Z values of the optimized solutions for all values of N investigated. Results for the standard mappings (Z[backbone] for backbone atoms only and Z[Cα] for Cα atoms only) are also included.
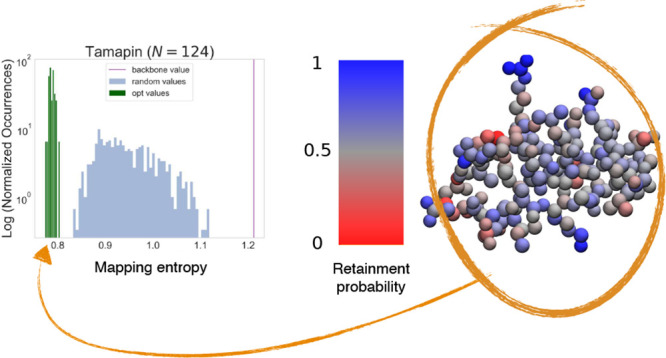
For the physically intuitive CG representations, Figure 1 shows that the value of Σ associated with the backbone mapping is very high for all structures. For TAM in particular, the amount of information retained is so low that the mapping entropy is 4.37 standard deviations higher than the average of the reference distribution of random mappings (see Table 2). This suggests that neglecting the side chains in a CG representation of a protein is detrimental, at least as far as the structural resolution is concerned. In fact, the backbone of the protein undergoes relatively minor structural rearrangements when exploring the neighborhood of the native conformation, thereby inducing negligible energetic fluctuations; for side chains, on the other hand, the opposite is true, with comparatively larger structural variability and a similarly broader energy range associated with it. Removing side chains from the mapping induces the clustering of atomistically different structures with different energies onto the same coarse-grained configuration, the latter being solely determined by the backbone. The corresponding mapping entropy is thus large—worse than a random choice of the retained atoms—since it is related to the variance of the energy in the macrostate.
Calculations employing the Cα mapping for the three structures show that this provides Σ values that are very close to the ones we find with the backbone mapping, thus suggesting that Cα atoms retain about the same amount of information that is encoded in the backbone. This is reasonable given the rather limited conformational variability of the atoms along the peptide chain. However, a comparison of the random case distributions for Nα and Nbkb as the number of retained atoms in Figure 1 reveals that the former generally has a broader spread than the latter because of the lower number of CG sites; consequently, the value of Σ for the Cα atom mapping is closer to the bulk of the distribution of the random case than that of the backbone mapping.
We now discuss the case of optimized mappings, that is, CG representations retaining the maximum amount of information about the AA reference. Each of the 48 minimization runs, which were carried out for each protein in the set and value of N considered, provided an optimal solution—a deep local minimum in the space of CG mappings; the corresponding Σ values are spread over a compact range of values that are systematically lower than, and do not overlap with, those of the random case distributions (Figure 1).
The optimal solutions for AKE and AAT span wide intervals of Σ values; for N = Nα in particular, the support of this set and of the corresponding random reference have comparable sizes. A quantitative measure of this broadness is displayed in the distributions of Z scores for the optimal solutions presented in Table 2. In both proteins, we observe that the Σ values associated with the optimal mappings increase with the degree of coarse-graining, N; this is a consequence of keeping the number of CG configurations of each system (conformational clusters; see section 4.2) constant across different resolutions. As N increases, the available CG conformational clusters are populated by more energetically diverse conformations, thereby incrementing the associated energy fluctuations. On the other hand, TAM shows narrowly peaked distributions of optimal values of Σ whose position does not vary with the number of retained sites. Both effects can be ascribed to the fact that most of the energy fluctuations in TAM—and consequently the mapping entropy—are due to a subset of atoms that are almost always maintained in each optimal mapping (see section 2.4), in contrast to a random choice of the CG representation. At the same time, the associated Z scores are lower than the ones for the bigger proteins for all values of N under examination, as TAM conformations generally feature a lower variability in energy than the other molecules.
For all of the investigated proteins, the absence of an overlap between the distributions of Σ associated with the random and optimized mappings raises some relevant questions. First, one might wonder what kind of structure the solution space has, that is, whether the identified solutions lie at the bottom of a rather flat vessel or, on the contrary, each of them is located in a narrow well, neatly separated from the others. Second, it is reasonable to ask whether some degree of similarity exists between these quasi-degenerate solutions of the optimization problem and, if so, what significance this has.
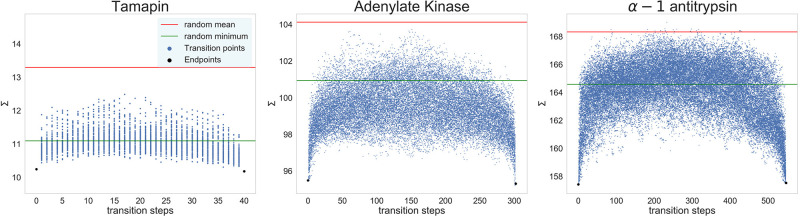
In order to answer these questions, for each structure we select four pairs of mapping operators Mopt that result in the lowest values of Σ. We then perform 100 independent transitions between these solutions, constructing intermediate mappings by randomly swapping two non-overlapping atoms from the two solutions at each step and calculating the associated mapping entropies. Figure 2 shows the results of this analysis for the pair of mappings with the lowest Σ; all of the other transitions are reported in Figure S2. It is interesting to notice that the end points (that is, the optimized mappings) correspond to the lowest values of Σ along each transition path; as the size of the protein increases, the values of Σ for intermediate mappings get closer to the average of Σrandom. By this analysis we cannot rule out the absence of lower minima over all of the possible paths, although it seems quite unlikely given the available sampling.
Figure 2.
Values of the mapping entropy Σ [in kJ mol–1 K–1] for mappings connecting two optimal solutions. In each plot, one per protein under examination, the two lowest-Σ mappings are taken as initial and final end points (black dots) for paths constructed by swapping pairs of atoms between them (blue dots). For each protein, 100 independent paths at the given N = Nαβ were constructed, and the mapping entropy of each intermediate point was computed. In each plot, horizontal lines represent the mean (red) and minimum (green) values of Smap obtained from the corresponding distributions of random mappings presented in Figure 1.
Finally, it is interesting to observe the pairwise correlations of the site conservation probability within a pool of solutions, as it is informative about the existence of atom pairs that are, in general, simultaneously present, simultaneously absent, or mutually exclusive. As reported in detail in Figures S6 and S7, no clear evidence is available that conserving a given atom can increase or decrease in a statistically relevant manner the conservation probability of another: this behavior supports the idea that the organization internal to a given optimal mapping is determined in a nontrivial manner by the intrinsically multibody nature of the problem at hand.
These analyses thus address the first question by showing that at least the deepest solutions of the optimization procedure are distinct from each other. It is not possible to (quasi)continuously transform an optimal mapping into another through a series of steps while keeping the value of the mapping entropy low. Each of the inspected solutions is a small town surrounded by high mountains in each direction, isolated from the others with no valleys connecting them.
The second question, namely, what similarity (if any) exists among these disconnected solutions, is tackled in the following section.
2.4. Biological Significance
The degree of similarity between the optimal mappings can be assessed by a simple average, returning the frequency with which a given atom is retained in the 48 solutions of the optimization problem.
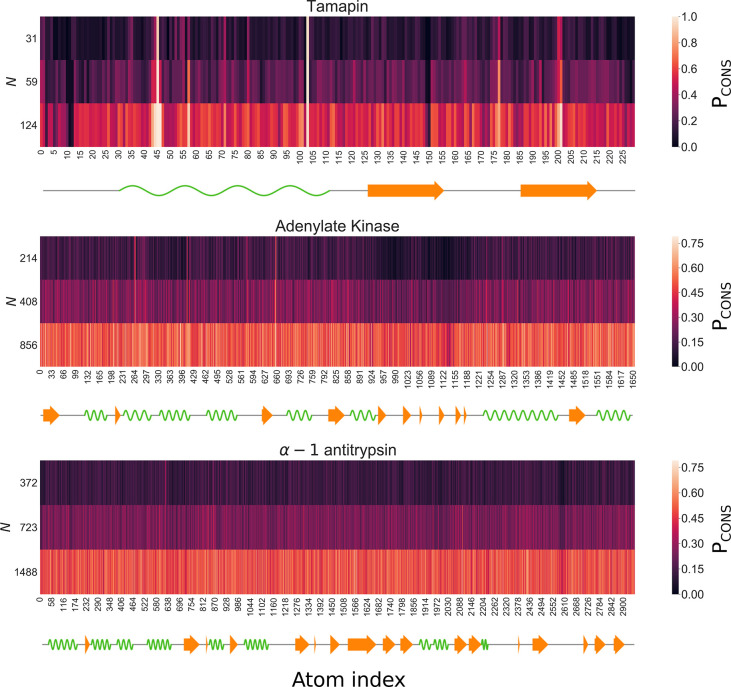
Figure 3 shows the values of Pcons, the probability of conserving each heavy atom, for each analyzed protein and degree of coarse-graining N investigated, computed as the fraction of times it appears in the corresponding pool of optimized solutions. One can notice the presence of regions that appear to be more or less conserved. Quantitative differences between the three cases under examination can be observed: while the heat map of TAM shows narrow and pronounced peaks of conservation probability, the optimal solutions for AKE feature a more uniform distribution, where the maxima and minima of Pcons extend over secondary structure fragments rather than small sets of atoms. The distribution gets even more blurred for AAT.
Figure 3.
Probability Pcons that a given atom is retained in the optimal mapping at various numbers N of CG sites and for each analyzed protein, expressed as a function of the atom index. Atoms are ordered according to their numbers in the PDB file. The secondary structure of the proteins is depicted using Biotite:64 green waves represent α-helices, and orange arrows correspond to β-strands.
As index proximity does not imply spatial proximity in a protein structure, we mapped the aforementioned probabilities to the three-dimensional configurations. Results for TAM are shown in Figure 4, while the corresponding ones for AKE and AAT are provided in Figure S3. From the distributions of Pcons for different numbers of retained sites N it is possible to infer some relevant properties of optimal mappings.
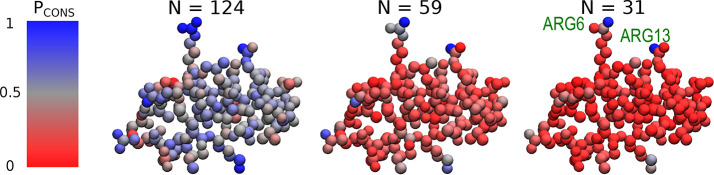
Figure 4.
Structure of tamapin (one bead per atom) colored according to Pcons, the probability for each atom to be retained in the pool of optimal mappings. Each structure corresponds to a different number N of retained CG sites. Residues presenting the highest retainment probability across N (ARG6 and ARG13) are highlighted.
With regard to TAM (Figure 4), it seems that at the highest degree of CG (N = Nα), only two sites are always conserved, namely, two nitrogen atoms belonging to the ARG6 and ARG13 residues (Pcons(NH1, ARG6) = 0.92; Pcons(NH2, ARG13) = 0.96). The atoms that constitute the only other arginine residue, ARG7, are well-conserved but with lower probability. By increasing the resolution, i.e., employing more CG sites (N = Nαβ), we see that the atoms in the side chain of LYS27 appear to be retained more than average together with atoms of GLU24 (Pcons(NZ, LYS27) = 0.65; Pcons(OE2, GLU24) = 0.75). At N = 124, the distribution becomes more uniform but is still sharply peaked around terminal atoms of ARG6 and ARG13.
Interestingly, ARG6 and ARG13 have been identified to be the main actors involved in the TAM–SK2 channel interaction.65−67 Andreotti et al.65 suggested that these two residues strongly interact with the channel through electrostatics and hydrogen bonding. Furthermore, Ramírez-Cordero et al.67 showed that mutating one of the three arginines of TAM dramatically decreases its selectivity toward the SK2 channel.
It thus appears that the mapping entropy minimization protocol was capable of singling out the two residues that are crucial for a complex biological process. The rationale for this can be found in the fact that such atoms strongly interact with the remainder of the protein, so that small variations of their relative coordinates have a large impact on the value of the overall system’s energy. Retaining these atoms and fixing their positions in the coarse-grained conformation thus enable the model to discriminate effectively one macrostate from another.
We note that this result was achieved solely by relying on data obtained in standard MD simulations. This aspect is particularly relevant, as the simulations were performed in absence of the channel, whose size is substantially larger than that of TAM. Consequently, we stress that valuable biological information, otherwise obtained via large-scale, multicomplex simulations, bioinformatic approaches, or experiments, can be retrieved by means of straightforward simulations of the molecule of interest in the absence of its substrate.
For AKE (Figure S3), we find that for N = Nα the external, solvent-exposed part of the LID domain is heavily coarse-grained, while its internal region is more conserved. The CORE region of the protein is always largely retained, without noteworthy peaks in probability. Such peaks, on the contrary, appear in correspondence to the terminal nitrogens of ARG36, LYS57, and ARG88 (Pcons(NH2, ARG36) = 0.52; Pcons(NZ, LYS57) = 0.48; Pcons(NH2, ARG88) = 0.58). The two arginines are located in the internal region of the NMP arm, at the interface with the LID domain. ARG88 is known to be the most important residue for catalytic activity,68,69 being central in the process of phosphoryl transfer.70 Phenylglyoxal,71 a drug that mutates ARG88 to a glycine, has been shown to substantially hamper the catalytic capacity of the enzyme.70 ARG36 is also bound to phosphate atoms.69 Finally, LYS57 is on the external part of NMP and has been identified to play a pivotal role in collaboration with ARG88 to block the release of adenine from the hydrophobic pocket of the protein.72 More generally, this amino acid is crucial for stabilizing the closed conformation of the kinase,73,74 which was never observed throughout the simulation. The overall probability pattern persists as N increases, even though it is less pronounced.
For AAT, Figure S3 shows that the associated optimizations heavily coarse-grain the reactive center loop of the protein. On the other hand, two of the most conserved residues in the pool of optimized mappings, MET358 and ARG101, are central to the biological role of this serpin. MET358 (Pcons(CE, MET358) = 0.31) constitutes the reactive site of the protein.75 Being extremely inhibitor-specific, mutation or oxidation of this amino acid leads to severe diseases. In particular, heavy oxidation of MET358 is one of the main causes of emphysema.76 The AAT Pittsburgh variant shows MET358–ARG mutation, which leads to diminished antielastase activity but markedly increased antithrombin activity.59,75,77 In turn, ARG101 (Pcons(CZ, ARG101) = Pcons(NH1, ARG101) = Pcons(NH2, ARG101) = 0.35) has a crucial role due to its connection to mutations that lead to severe AAT deficiency.60,61
In summary, we observe that in all of the proteins investigated, the presented approach identifies biologically relevant residues. Most notably, these residues, which are known to be biologically active in the presence of other compounds, are singled out from substrate-free MD simulations. With the exception of MET358 of AAT, the most probably retained atoms belong to amino acids that are charged and highly solvent-exposed. To quantify the statistical significance of the selection operated by the algorithm, we note that the latter detects those fragments out of pools of 8, 69, and 100 charged residues for TAM, AKE, and AAT, respectively. If we account for solvent exposure, these numbers are reduced to 7, 32, and 40 when amino acids with solvent-accessible surface area (SASA) higher than 1 nm2 are considered.
Another aspect worth mentioning is the fact that several atoms pinpointed as highly conserved in optimal mappings are located in the side chains of relatively large residues, such as arginine, lysine, and methionine. It is thus legitimate to wonder whether a correlation might exist between the size of an amino acid and the probability that one or more of its atoms will be present in a low-Smap reduced representation. An inspection of the root-mean-square fluctuation values of the three proteins’ atoms versus their conservation probability (see Figure S4) shows no significant correlation for low or intermediate values of Pcons; highly conserved atoms, on the other hand, tend to be located on highly mobile residues because a relatively large conformational variability is a prerequisite for an atom to be determinant in the mapping. In conclusion, highly mobile residues are not necessarily highly conserved, while the opposite is more likely.
3. Discussion and Conclusions
In this work, we have addressed the question of identifying the subset of atoms of a macromolecule, specifically a protein, that retains the largest amount of information about its conformational distribution while employing a reduced number of degrees of freedom with respect to the reference. The motivation behind this objective is to provide a synthetic yet informative representation of a complex system that is simulated in high resolution but observed in low resolution, thus rationalizing its properties and behavior in terms of relatively few important variables, namely, the positions of the retained atoms.
This goal was pursued by making use of tools and concepts largely borrowed from the field of coarse-grained modeling, in particular bottom-up coarse-graining. The latter term identifies a class of theoretical and computational strategies employed to construct a simplified model of a system that would be too onerous to simulate if it were treated in terms of a high-resolution description. Coarse-graining methods make use of the configurational landscape of the reference high-resolution model to construct a simplified representation that retains its large-scale properties. The interactions among effective sites are parametrized by directly integrating out (in an exact or approximate manner) the higher-resolution degrees of freedom and imposing the equality of the probability distributions of the coarse-grained degrees of freedom in the two representations.5
These approaches have a long and successful history in the fields of statistical mechanics and condensed matter, the most prominent, pioneering example probably being Kadanoff’s spin block transformations of ferromagnetic systems.78 This process, which lies at the heart of real-space renormalization group (RG) theory, allows the relevant variables of the system to naturally emerge out of a (potentially infinite) pool of fundamental interactions, thus linking microscopic physics to macroscopic behavior.79,80
The generality of the concepts of the renormalization group and coarse-graining has naturally taken them outside of their native environment,81−83 with the whole field of coarse-grained modeling of soft matter being one of the most fruitful offsprings of this cross-fertilization.5 However, a straightforward application of RG methods in this latter context is severely restricted by fundamental differences between the objects of study. Most notably, the crucial assumptions of self-similarity and scale invariance, which justify the whole process of renormalization at the critical point, clearly do not apply to, say, a protein in that the latter certainly does not resemble itself upon resolution reduction. Furthermore, scaling laws cannot be applied to a system such as a biomolecule that is intrinsically finite, for which the thermodynamic limit is not defined.
Additionally, one of the key consequences of self-similarity at the critical point is that the filtering process put forward by the renormalization group turns out to be largely independent of the specific coarse-graining prescription: the set of relevant macroscopic variables emerges as such for almost whatever choice of mapping operator is taken to bridge the system across different length scales.84 In the case of biological matter, where the organization of degrees of freedom is not fractal but rather hierarchical—from atoms to residues to secondary structure elements and so on—the mapping operator acquires instead a central role in the “renormalization” process. The choice of a particular transformation rule, projecting an atomistic conformation of a molecule to its coarse-grained counterpart, more severely implies an external—i.e., not emergent—selection of which variables are relevant in the description of the system and which others are redundant. In this way, what should be the main outcome of a genuine coarse-graining procedure is demeaned to be one of its ingredients.
It is only recently that the central importance of the resolution distribution, i.e., the definition of the CG representation, has gradually percolated into the field of biomolecular modeling.22,44 Moving away from a priori selection of the effective interaction sites,21 a few different strategies have been developed that rather aim at the automatic identification of CG mappings. These techniques rely on specific properties of the system under examination: examples include quasi-rigid domain decomposition24−31 or graph-theory-based model construction methods that attempt to create CG representations of chemical compounds based only on their static graph structure;32,33,85 other approaches aim at selecting those representations that closely match the high-resolution model’s energetics.22,35 Finally, more recent strategies rooted in the field of machine learning generate discrete CG variables by means of variational autoencoders.86 All of these methods take into account the system structure, or its conformational variability, or its energy, but none of them integrates these complementary properties in a consistent framework embracing topology, structure, dynamics, and thermodynamics.
In this context, information-theoretical measures, such as the mapping entropy,17,42−44 can bring novel and potentially very fruitful features.87 In fact, this quantity associates structural and thermodynamic properties, so that both the conformational variability of the system and its energetics are accurately taken into account. Making use of the advantages offered by the mapping entropy, we have developed a protocol to identify, in an automated, unsupervised manner, the low-resolution representation of a molecular system that maximally preserves the amount of thermodynamic information contained in the corresponding higher-resolution model.
The results presented here suggest that the method may be capable of identifying not only thermodynamically consistent but also biologically informative mappings. Indeed, a central result reported here is that those atoms consistently retained with high probability across various lowest-Smap mappings for different numbers of CG sites tend to be located in amino acids that play a relevant role in the function of the three proteins under examination. Most importantly, these key residues, whose biological activity consists of binding with other molecules, have been singled out on the basis of plain MD simulations of the substrate-free molecules in explicit solvent. In general, the vast majority of available techniques for the identification of putative binding or allosteric sites in proteins explicitly or implicitly rely on the analysis of the interaction between the molecule of interest and its partner—be that a small ligand, another protein, or something else.88−93 This is the case, for example, of binding site prediction servers,94,95 which perform a structural comparison between the target protein and those archived in a precompiled, annotated database; other bioinformatic tools make use of machine learning methods96−99—with all of the pros and cons that come with training over a possibly vast but certainly finite data set of known cases.100 To the best of our knowledge, the remaining alternative methods perform a structural analysis of the protein in search of binding pockets based on purely geometrical criteria.101,102 The results obtained in the present work, on the contrary, suggest that a significant fraction of biologically relevant residues, whose function is intrinsically related to interactions with other molecules, might be identified as such from the analysis of simulations in absence of the substrate. This observation would imply that a substantial amount of information about functional residues, even those that exploit their activity through the interaction with a partner molecule, is entailed in the protein’s own structure and energetics. In the past few decades, the successful application of extremely simplified representations of proteins such as elastic network models has shown that the key features of a protein’s large-scale dynamics are encoded in its native structure;27,36−41,103−107 in analogy with this, we hypothesize that the mapping entropy minimization protocol is capable of bringing to light those relational properties of proteins—namely the interaction with a substrate—from the thermodynamics of the single molecule in the absence of its partner.
The mapping entropy minimization protocol establishes a quantitative bridge between a molecule’s representation—and hence its information content—on the one side and the structure–dynamics–function relationship on the other. This method might represent a novel and useful tool in various fields of applications, e.g., for the identification of important regions of proteins, such as druggable sites and allosteric pockets, relying on simple, substrate-free MD simulations and efficient analysis tools. In this study, a first exploration of the method’s capabilities, limitations, and potential developments has been carried out, and several perspectives lie ahead that deserve further exploration. Among the most pressing and interesting ones, we mention the investigation of how the optimized mappings depend on the conformational space sampling; the relation of mapping entropy minimization to more established schemes such as the maximum entropy method; and the viability of a machine-learning-based implementation of the protocol, e.g., making use of deep learning tools that have proven to be strictly related to coarse-graining, dimensionality reduction, and feature extraction. All of these avenues are objects of ongoing study.
In conclusion, it is our opinion that the proposed automated selection of coarse-grained sites has great potential for further development, being at the nexus between molecular mechanics, statistical mechanics, information theory, and biology.
4. Methods
In this section we describe the technical preliminaries and the details of the algorithm we employ to obtain the CG representation M (see eq 2) that minimizes the loss of information inherently generated by a coarse-graining procedure—that is, the mapping entropy.
Equation 15 provides us with a way of measuring the mapping entropy of a biomolecular system associated with any particular choice of decimation of its atomistic degrees of freedom. One can visualize a decimation mapping (eq 2) as an array of bits, where 0 and 1 correspond to not retained and retained atoms, respectively. Order matters: swapping two bits produces a different mapping operator. Applying this procedure, one finds that the total number of possible CG representations of a biomolecule, irrespective of how many atoms N are selected out of n, is
| 21 |
which is astronomical even for the smallest proteins. In this work, we restrict the set of possibly retained sites to the Nheavy heavy atoms of the compound—excluding hydrogens—thus significantly reducing the cardinality of the space of mappings. Nonetheless, finding the global minimum of eq 15 for a reasonably large molecule would be computationally intractable whenever N is different from 1, 2, Nheavy – 1, and Nheavy – 2. As an example, there are 2.4 × 1038 CG representations of tamapin with 31 sites (N = Nα) and 9.6 × 10887 representations for antitrypsin with 1488 sites (N = Nbkb).
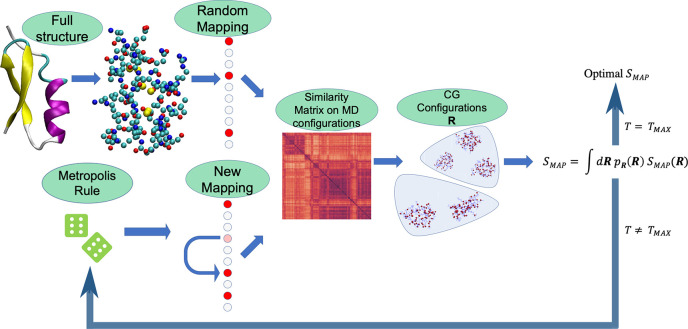
Hence, it is necessary to perform the minimization of the mapping entropy through a Monte Carlo-based optimization procedure, and we specifically rely on the simulated annealing protocol.62,63 As it is typically the case with this method, the computational bottleneck consists of the calculation of the observable (the mapping entropy) at each SA step.
We develop an approximate method that is able to obtain the mapping entropy of a biomolecule by analyzing an MD trajectory that can contain up to tens of thousands of frames. At each SA step, that is, for each putative mapping, the algorithm calculates a similarity matrix among all of the generated configurations. The entries of this matrix are given by the root-mean-square deviation (RMSD) between structure pairs, the latter being defined only in terms of the retained sites associated with the CG mapping, and aligned accordingly; we then identify CG macrostates by clustering frames on the basis of the distance matrix, making use of bottom-up hierarchical clustering (UPGMA108). Finally, we determine the observable of interest from the variances of the atomistic intramolecular potential energy of the protein corresponding to the frames that map onto the same CG conformational cluster (see eq 16).
The protocol is initiated with the generation of a mapping such that the overall number of retained sites is equal to N. Then, in each SA step, the following operations are performed:
-
1.
swap a retained site (σi = 1) and a removed site (σj = 0) in the mapping;
-
2.
compute a similarity matrix among CG configurations using the RMSD;
-
3.
apply a clustering algorithm on the RMSD matrix in order to identify the CG macrostates R;
- 4.
Once the new value of S̃map is obtained, the move is accepted/rejected using a Metropolis-like rule. The overall workflow of the algorithm is illustrated schematically in Figure 5.
Figure 5.
Schematic representation of the algorithmic procedure described in the text that we employ to minimize the mapping entropy, the latter being calculated by means of eq 25. The full similarity matrix is computed once every TK steps, while in the intermediate steps we resort to the approximation given by eq 23. TK depends on both the protein and N. TMAX is the number of simulated annealing steps (here TMAX = 2 × 104).
For the sake of the accuracy of the optimization, more exhaustive sampling is better, and hence, the number of sampled atomistic configurations should be at least on the order of tens of thousands. However, in that case step 2 would require the alignment of a huge number of structure pairs for each proposed CG mapping, which in turn would dramatically slow down the entire process. This problem is circumvented performing a reasonable approximation in the calculation of the CG RMSD matrix.
4.1. RMSD Matrix Calculation
The RMSD between two superimposed structures x and y is given by
| 22 |
where n is the number of sites in the system, be they atomistic or CG, and xi and yi represent the Cartesian coordinates of the ith elements in the two sets. According to Kabsch,109,110 it is possible to find the superimposition that minimizes this quantity, namely, the rotation matrix U that has to be applied to x for a given y in order to reach the minimum of the RMSD.
The aforementioned procedure is not computationally heavy per se; in our case, however, we would have to repeat this alignment for all configuration pairs in the MD trajectory every time a new CG mapping is proposed along the Monte Carlo process, thus making the overall workflow inctractable in terms of computational investment.
The simplest solution to this problem is to discard the differences in the Kabsch alignment between two CG structures differing by a pair of swapped atoms. This assumption is particularly appealing from the point of view of speed and memory, since the expensive and relatively slow alignment procedure produces a result (a rotation matrix) that can be stored with negligible use of resources. In order to take advantage of this simplification without losing accuracy, for each structure and degree of coarse-graining we select an interval of SA steps TK in which we consider the rotation matrices constant. After these steps, the full Kabsch alignment is applied again.
This approximation results in a substantial reduction in the number of operations that we have to execute at each Monte Carlo step. At first, given the initial random mapping operator M, we build the sets of coordinates that have been conserved by the mapping operator Γ(M) = M(r). Then we compute RMSD(Γα(M), Γβ(M)), the overall RMSD matrix between every pair of aligned structures Γα and Γβ, where α and β run over the MD configurations. For all moves M → M′ within a block of TK Monte Carlo steps, where M and M′ differing only in a pair of swapped atoms, this quantity is then updated with the simple rule
| 23 |
where s and a are the removed (substituted) and added atoms, respectively, and MSD is the mean-square deviation.
This approach clearly represents an approximation to the correct procedure; it has to be emphasized, however, that the impact of this approximation is increasingly perturbative as the size of the system grows. Furthermore, the computational gain that the described procedure enables is sufficient to counterbalance the fact that the exact protocol would be so inefficient to make the optimization impossible. For example, with TK = 1000 for AAT with N = Nbkb, our approximation gives a speed-up factor of the order of 103.
4.2. Hierarchical Clustering of Coarse-Grained Configurations
Several clustering algorithms exist that have been applied to group molecular structures based on RMSD similarity matrices.111,112 Many such algorithms have been developed and incorporated in the most common libraries for data science. Among the various available methods, we choose to employ the agglomerative bottom-up hierarchical clustering with average linkage (UPGMA) algorithm.108 Here we briefly recapitulate the basics underpinnings of this procedure:
-
1.
In the first step, the minimum of the similarity matrix is found, and the two corresponding entries x, y (leaves) are merged together in a new cluster k.
-
2.
k is placed in the middle of its two constituents. The distance matrix is updated to take into account the presence of the new cluster in place of the two close structures: d(k, z) = (d(x, z) + d(y, z))/2.
-
3.Steps 1 and 2 are iterated until one root is found. The distance among clusters k and w is generalized as follows:
where |k| and |w| are the populations of the clusters and k[i] and w[j] are their elements.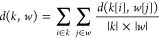
24 -
4.
The actual division into clusters can be performed by cutting the tree (dendrogram) using a threshold value on the intercluster distance or taking the first value of the distance that gives rise to a certain number of clusters Ncl. In both cases it is necessary to introduce a hyperparameter. In our case, the latter is a more viable choice to reduce the impact of roundoff errors. Indeed, the first criterion would push the optimization to create as many clusters as possible in order to minimize the energy variance inside them (a cluster with one sample has zero variance in energy).
This algorithm, whose implementation113,114 is available in Python Scipy,115 is simple, relatively fast (O(n2 log n)), and completely deterministic: given the distance matrix, the output dendrogram is unique.
Although this algorithm scales well with the size of the data set, it may not be robust with respect to small variations along the optimization trajectory. In fact, even the slightest modifications of the dendrogram may lead to abrupt changes in S̃map. This is perfectly understandable from an algorithmic point of view, but it is deleterious for the stability of the optimization procedure. Furthermore, the aforementioned choice of Ncl is somehow arbitrary. Hence, we perform the following analysis in order to enhance the robustness of S̃map at each Monte Carlo (MC) move and to provide a quantitative criterion to set the hyperparameter:
-
1.
compute the RMSD similarity matrix between all of the heavy atoms of the biological system under consideration;
-
2.
apply the UPGMA algorithm to this object, retrieving the all-atom dendrogram;
-
3.
impose lower and upper bounds on the intercluster distance depending on the conformational variability of the structure (see Table 3);
-
4.
visualize the cut dendrogram to identify the numbers of different clusters available at each of the two threshold values (Ncl+ and Ncl; Table 3);
-
5.
build a list CL of five integers, selecting three (intermediate) values between Ncl– and Ncl;
- 6.
Table 3. Bounds on Intercluster Distances and Corresponding Numbers of Clusters.
| protein | upper bound (nm) | lower bound (nm) | Ncl+ | Ncl– |
|---|---|---|---|---|
| TAM | 0.20 | 0.18 | 91 | 34 |
| AKE | 0.25 | 0.20 | 147 | 29 |
| AAT | 0.20 | 0.15 | 96 | 7 |
The overall procedure amounts to identifying many different sets of CG macrostates R on which S̃map can be computed, assuming that the average of this quantity can be used effectively as the driving observable inside the optimization. This trivial assumption increases the robustness of the SA optimization and allows all of the values of S̃map calculated at different distances from the root of the dendrogram to be kept in memory.
4.3. Simulated Annealing
We use Monte Carlo simulated annealing to stochastically explore the space of the possible decimation mappings associated with each degree of coarse-graining. We here briefly describe the main features of our implementation of the SA algorithm, referring the reader to a few excellent reviews for a comprehensive description of the techniques that can be employed in the choice of temperature decay and parameter estimation.116,117
We run the optimization for 2 × 103 MC epochs, each of which is composed of 10 steps. This amounts to keeping the temperature constant for 10 steps and then decreasing it according to an exponential law. For the ith epoch, we have T(i) = T0e–i/ν. The hyperparameters T0 and ν are crucial for a well-behaved MC optimization. We choose ν = 300 so that the temperature at i = 2000 is approximately T0/1000. In order to feed our algorithm with reasonable values of T0, for each of 100 random mappings we perform 10 MC stochastic moves and measure ΔΣ, the difference between the observables computed in two consecutive steps. Then we estimate T0 so that a move that leads to an increment of the observable equal to the average of ΔΣ would possess an acceptance probability of 0.75 at the first step.
4.4. Data Available
For each analyzed protein, the raw data for all of the CG representations investigated in this work, including random, optimized, and transition mappings, together with the associated mapping entropies are freely available on the Zenodo repository (https://zenodo.org/record/3776293). We further provide all of the scripts we employed to analyze such data and construct all of the figures presented in this work.
Acknowledgments
The authors thank Attilio Vargiu for critical reading of the manuscript and useful comments. This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme (Grant Agreement 758588). M.S.S. acknowledges funding from the U.S. National Science Foundation through Award CHEM-1800344.
Appendix A: Relative Entropy and Mapping Entropy
Bottom-up coarse-graining approaches aim at constructing effective low-resolution representations of a system that reproduce as accurately as possible the equilibrium statistical-mechanical properties of the underlying high-resolution reference. In particular, this problem is phrased in terms of the parametrization of a CG potential that approximates the reference system’s multibody potential of mean force (MB-PMF) U0,
| 26 |
where pR(R) is the probability that the atomistic model will sample a specific CG configuration R. In the canonical ensemble, one has
| 27 |
where β = 1/kBT, u(r) is the microscopic potential energy of the system, pr(r) ∝ exp(−βu(r)) is the Boltzmann distribution, and Z is the associated configurational partition function.
From eqs 26 and 27 it follows that a computer simulation of the low-resolution system performed with the potential U0 (more precisely, a free energy) would allow the CG sites to sample their configurational space with the same probability as they would in the reference system. Unfortunately, the intrinsically multibody nature of U0 is such that its exact determination is largely unfeasible in practice.118 Considerable effort has thus been devoted to devise increasingly accurate methods to approximate the MB-PMF with a CG potential U;16,17,119,120 however, the latter is in general defined in terms of a necessarily incomplete set of basis functions.4−7 It is thus natural to look for quantitative measures of a CG model’s quality with respect to U0.
In this respect, one of the most notable examples of such metrics is the relative entropy,17,42−44
| 28 |
where DKL(p1∥p2) denotes the Kullback–Leibler divergence between two probability distributions p1 and p2,45 with Srel ≥ 0 by virtue of Gibbs’ inequality. In eq 28, pr(r) is the atomistic probability distribution of the system, while Pr(r|U) is defined as a product of probabilities over the CG and AA configurational spaces:42,44
| 29 |
The term PR(R|U) ∝ exp(−βU(R)) in eq 29 runs over CG configurations and describes the probability that a CG model with approximate potential U(R) samples the CG configuration R. Then, to obtain Pr(r|U) it is sufficient to multiply PR(R|U) by the atomistic probability pr(r) of sampling r normalized by the Boltzmann weight pR(R) of the CG configuration R (see eq 27).
KL divergences quantify the information loss between probability distributions; specifically, DKL(s(r)∥t(r)) represents the information that is lost by representing a system originally described by a probability distribution s(r) using another distribution t(r).45 Given a CG mapping M, the relative entropy Srel in eq 28 implicitly measures the loss that arises as a consequence of approximating the exact CG PMF U0 for a system by an effective potential U, that is, the error introduced by using an incomplete interaction basis to describe the low-resolution system. By substituting eq 29 into eq 28 and introducing 1 = ∫dR δ(M(r) – R), one indeed obtains
| 30 |
that is, a KL divergence DKL(pR(R)∥PR(R|U)) between the exact and approximate probability distributions in the CG configuration space with no explicit connection to the underlying microscopic reference. As such, Srel is a measure of an approximate CG model’s quality. However, it is possible to expand Srel as a difference between two information losses (the one due to U and the one due to U0) calculated with respect to the atomistic system,
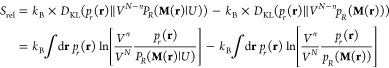 |
31 |
where n and N denote the numbers of atomistic and CG sites, respectively.
Both KL divergences in eq 31 are positive defined because of Gibbs’ inequality, with DKL(pr(r)∥VN–nPR(M(r)|U)) ≥ DKL(pr(r)∥VN–npR(M(r))) because Srel ≥ 0; the second one is called the mapping entropy, Smap:17,42,44,121
| 32 |
It is noteworthy that Smap does not depend on the approximate CG force field U but only on the mapping operator M.
In multiscale modeling applications, one seeks to minimize the relative entropy with respect to the coefficients in terms of which the coarse-grained potential U(R) is parametrized for a given mapping.17,42−44 The aim is to generate CG configurations that sample the atomistic conformational space with the same microscopic probability pr(r) (see eq 28). However, since the model can generate only configurations in the CG space, minimizing eq 28 is tantamount to minimizing eq 30, that is, the “error” introduced by approximating U0 with U; furthermore, in the minimization with respect to U the contribution of the mapping entropy vanishes because the latter does not depend on the coarse-grained potential. In this context, then, Smap represents only a constant shift of the KL distance between the AA and the CG models, and a minimization of the first term of eq 31 is equivalent to a minimization of eq 28.
When taken per se, on the other hand, the mapping entropy provides substantial information about the modeling of the system. In fact, this quantity represents the loss of information that would be inherently generated by reducing the resolution of a system even in the case of an exact coarse-graining procedure, in which U = U0 and Srel = 0.42 In the calculation of Smap, the reference AA density is compared with a distribution in which probabilities are smeared out and redistributed equally to all of the microscopic configurations r inside each CG macrostate.
Starting from eq 32, Rudzinski and Noid further divide Smap into a sum of two terms,42
| 33 |
where the first one is purely geometrical, while the second one accounts for the smearing of the probabilities generated by the coarse-graining procedure. In eq 33, Ω1(M(r)) = ∫dr δ(M(r) – R) is the degeneracy of the CG macrostate R—i.e., how many microstates map onto a given CG configuration—and
| 34 |
is the average probability of all microstates that map to the macrostate R = M(r).
The geometric term in eq 33 does not vanish in general.42 However, if the mapping takes the form of a decimation (see eq 2), one has
| 35 |
and the first logarithm in eq 33 is identically zero, so that
| 36 |
In the case of decimation mappings, moreover, a direct relation holds between the mapping entropy Smap as expressed in eq 36 and the nonideal configurational entropies of the original and CG systems:42,44
| 37 |
| 38 |
Indeed, introducing eq 27 in eq 38 allows sR to be rewritten as
| 39 |
Subtracting eq 37 from eq 39 results in
| 40 |
and by virtue of eqs 34 and 35, one finally obtains
| 41 |
further highlighting that the mapping entropy represents the difference in information content between the distribution obtained by reducing the level of resolution at which the system is observed, pR(R), and the original microscopic reference, pr(r).
Appendix B: Explicit Calculation of the Mapping Entropy
We here provide full details of our derivation of the mapping entropy, as in eqs 10–12, and its cumulant expansion approximation, eq 15, starting from eq 36.
In the case of CG representations obtained by decimating the number of original degrees of freedom of the system, the mapping entropy Smap in eq 36 vanishes if the probabilities of the microscopic configurations that map onto the same CG one are the same.42,44 In the canonical ensemble, the requirement is that those configurations must possess the same energy. This can be directly inferred by writing the negative of the average in eq 36 as
| 42 |
so that if u(r′) = u(r) ∀ r′ such that M(r′) = M(r), the argument of the logarithm is unity and the right-hand side of eq 42 vanishes.
Importantly, this implies that no information on the system is lost along the coarse-graining procedure if CG macrostates are generated by grouping together microscopic configurations characterized by having the same energy. In our case, this translates into the search for isoenergetic mappings.
By introducing 1 = ∫dR δ(M(r) – R) into eq 42, one obtains
| 43 |
| 44 |
so that the overall mapping entropy is decomposed as a weighted average over the CG configuration space of the mapping entropy Smap(R) of a single CG macrostate,
| 45 |
Equation 45 shows that determining Smap(R) for a given macrostate R involves a comparison of the energies of all pairs of microscopic configurations that map onto it. A further identity 1 = ∫dU′ δ(u(r′) – U′) that fixes the energy of configuration r′ can be inserted into the logarithm in eq 45 to switch from a configurational integral to an energy integral. This provides:
| 46 |
where
| 47 |
is the microcanonical (unweighted) conditional probability of possessing energy U′ given that the CG macrostate is R. It is possible to write it as Ω1(U′, R)/Ω1(R), that is, the multiplicity of AA configurations such that M(r) = R and u(r′) = U′ normalized by the multiplicity of configurations that map to R.
A second identity 1 = ∫dU δ(u(r) – U) on the energies provides the following expression for Smap(R):
 |
48 |
The last integral in eq 48, which we dub Pβ(U|R),
| 49 |
is now the canonical—i.e., Boltzmann-weighted—conditional probability of possessing energy U provided that M(r) = R, namely, pR(U, R)/pR(R). One thus obtains
 |
50 |
where
| 51 |
is the canonical average of the microscopic potential energy over the CG macrostate R.
A direct calculation of Smap(R) starting from the last line of eq 50 requires the average over the microcanonical distribution P(U′|R), which is not straightforwardly accessible in NVT simulations. However, there is a connection between P(U|R) in eq 47 and Pβ(U|R) in eq 49: if one writes pR(R) as ∫dU′ exp[−β(U′)]Ω1(U′, R) and pR(U, R) as exp[−β(U)]Ω1(U, R), standard reweighting provides
| 52 |
Equation 52 enables one to convert the microcanonical average in eq 50 to a canonical one, so that
| 53 |
Finally, by means of a second-order cumulant expansion of eq 12, one obtains
| 54 |
Insertion of eq 54 into eq 44 results in a total mapping entropy given by eq 15.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00676.
Quantitative analysis of the all-atom MD simulations of the three proteins investigated in this work; additional figures about the CG representations that minimize the mapping entropy; analysis of the relation between the size and mobility of residues and the conservation probability of their atoms; analysis of the pair correlations between atoms belonging to the pool of optimized mappings; assessment of the results’ stability with respect to the duration of the MD trajectory (PDF)
The authors declare no competing financial interest.
Notes
The raw data for all of the CG representations investigated in this work (including random, optimized, and transition mappings) and the associated mapping entropies for each analyzed protein along with the scripts used to analyze the data and construct the figures presented in this work are freely available at https://zenodo.org/record/3776293.
Supplementary Material
References
- Car R.; Parrinello M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. 10.1103/PhysRevLett.55.2471. [DOI] [PubMed] [Google Scholar]
- Alder B. J.; Wainwright T. E. Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 1959, 31, 459–466. 10.1063/1.1730376. [DOI] [Google Scholar]
- Karplus M. Molecular Dynamics Simulations of Biomolecules. Acc. Chem. Res. 2002, 35, 321–323. 10.1021/ar020082r. [DOI] [PubMed] [Google Scholar]
- Takada S. Coarse-grained molecular simulations of large biomolecules. Curr. Opin. Struct. Biol. 2012, 22, 130–137. 10.1016/j.sbi.2012.01.010. [DOI] [PubMed] [Google Scholar]
- Noid W. G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139, 090901. 10.1063/1.4818908. [DOI] [PubMed] [Google Scholar]
- Saunders M. G.; Voth G. A. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013, 42, 73–93. 10.1146/annurev-biophys-083012-130348. [DOI] [PubMed] [Google Scholar]
- Potestio R.; Peter C.; Kremer K. Computer Simulations of Soft Matter: Linking the Scales. Entropy 2014, 16, 4199–4245. 10.3390/e16084199. [DOI] [Google Scholar]
- D’Adamo G.; Menichetti R.; Pelissetto A.; Pierleoni C. Coarse-graining polymer solutions: A critical appraisal of single-and multi-site models. Eur. Phys. J.: Spec. Top. 2015, 224, 2239–2267. 10.1140/epjst/e2015-02410-3. [DOI] [Google Scholar]
- https://foldingathome.org.
- http://www.gpugrid.net.
- Shaw D. E.; Dror R. O.; Salmon J. K.; Grossman J. P.; Mackenzie K. M.; Bank J. A.; Young C.; Deneroff M. M.; Batson B.; Bowers K. J.; Chow E.; Eastwood M. P.; Ierardi D. J.; Klepeis J. L.; Kuskin J. S.; Larson R. H.; Lindorff-Larsen K.; Maragakis P.; Moraes M. A.; Piana S.; Shan Y.; Towles B.. Millisecond-scale Molecular Dynamics Simulations on Anton. In SC ’09: Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, Portland, OR, November 2009; ACM: New York, 2009; Article 39.
- Freddolino P. L.; Arkhipov A. S.; Larson S. B.; McPherson A.; Schulten K. Molecular dynamics simulations of the complete satellite tobacco mosaic virus. Structure 2006, 14, 437–449. 10.1016/j.str.2005.11.014. [DOI] [PubMed] [Google Scholar]
- Bock L. V.; Blau C.; Schröder G. F.; Davydov I. I.; Fischer N.; Stark H.; Rodnina M. V.; Vaiana A. C.; Grubmüller H. Energy barriers and driving forces in tRNA translocation through the ribosome. Nat. Struct. Mol. Biol. 2013, 20, 1390–1396. 10.1038/nsmb.2690. [DOI] [PubMed] [Google Scholar]
- Singharoy A.; Maffeo C.; Delgado-Magnero K. H.; Swainsbury D. J.; Sener M.; Kleinekathöfer U.; Vant J. W.; Nguyen J.; Hitchcock A.; Isralewitz B.; et al. Atoms to Phenotypes: Molecular Design Principles of Cellular Energy Metabolism. Cell 2019, 179, 1098–1111. 10.1016/j.cell.2019.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noid W. G.Biomolecular Simulations; Springer, 2013; pp 487–531. [Google Scholar]
- Noid W. G.; Chu J.-W.; Ayton G. S.; Krishna V.; Izvekov S.; Voth G. A.; Das A.; Andersen H. C. The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models. J. Chem. Phys. 2008, 128, 244114. 10.1063/1.2938860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shell M. S. The relative entropy is fundamental to multiscale and inverse thermodynamic problems. J. Chem. Phys. 2008, 129, 144108. 10.1063/1.2992060. [DOI] [PubMed] [Google Scholar]
- Lebold K. M.; Noid W. G. Dual approach for effective potentials that accurately model structure and energetics. J. Chem. Phys. 2019, 150, 234107. 10.1063/1.5094330. [DOI] [PubMed] [Google Scholar]
- Lebold K. M.; Noid W. Dual-potential approach for coarse-grained implicit solvent models with accurate, internally consistent energetics and predictive transferability. J. Chem. Phys. 2019, 151, 164113. 10.1063/1.5125246. [DOI] [PubMed] [Google Scholar]
- Jin J.; Pak A. J.; Voth G. A. Understanding Missing Entropy in Coarse-Grained Systems: Addressing Issues of Representability and Transferability. J. Phys. Chem. Lett. 2019, 10, 4549–4557. 10.1021/acs.jpclett.9b01228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kmiecik S.; Gront D.; Kolinski M.; Wieteska L.; Dawid A. E.; Kolinski A. Coarse-grained protein models and their applications. Chem. Rev. 2016, 116, 7898–7936. 10.1021/acs.chemrev.6b00163. [DOI] [PubMed] [Google Scholar]
- Diggins IV P.; Liu C.; Deserno M.; Potestio R. Optimal coarse-grained site selection in elastic network models of biomolecules. J. Chem. Theory Comput. 2019, 15, 648–664. 10.1021/acs.jctc.8b00654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khot A.; Shiring S. B.; Savoie B. M. Evidence of information limitations in coarse-grained models. J. Chem. Phys. 2019, 151, 244105. 10.1063/1.5129398. [DOI] [PubMed] [Google Scholar]
- Gohlke H.; Thorpe M. F. A natural coarse graining for simulating large biomolecular motion. Biophys. J. 2006, 91, 2115–2120. 10.1529/biophysj.106.083568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z.; Lu L.; Noid W. G.; Krishna V.; Pfaendtner J.; Voth G. A. A Systematic Methodology for Defining Coarse-Grained Sites in Large Biomolecules. Biophys. J. 2008, 95, 5073–5083. 10.1529/biophysj.108.139626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z.; Pfaendtner J.; Grafmüller A.; Voth G. A. Defining Coarse-Grained Representations of Large Biomolecules and Biomolecular Complexes from Elastic Network Models. Biophys. J. 2009, 97, 2327–2337. 10.1016/j.bpj.2009.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potestio R.; Pontiggia F.; Micheletti C. Coarse-grained description of proteins’ internal dynamics: an optimal strategy for decomposing proteins in rigid subunits. Biophys. J. 2009, 96, 4993–5002. 10.1016/j.bpj.2009.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aleksiev T.; Potestio R.; Pontiggia F.; Cozzini S.; Micheletti C. PiSQRD: a web server for decomposing proteins into quasi-rigid dynamical domains. Bioinformatics 2009, 25, 2743–2744. 10.1093/bioinformatics/btp512. [DOI] [PubMed] [Google Scholar]
- Zhang Z.; Voth G. A. Coarse-Grained Representations of Large Biomolecular Complexes from Low-Resolution Structural Data. J. Chem. Theory Comput. 2010, 6, 2990–3002. 10.1021/ct100374a. [DOI] [PubMed] [Google Scholar]
- Sinitskiy A. V.; Saunders M. G.; Voth G. A. Optimal number of coarse-grained sites in different components of large biomolecular complexes. J. Phys. Chem. B 2012, 116, 8363–8374. 10.1021/jp2108895. [DOI] [PubMed] [Google Scholar]
- Polles G.; Indelicato G.; Potestio R.; Cermelli P.; Twarock R.; Micheletti C. Mechanical and assembly units of viral capsids identified via quasi-rigid domain decomposition. PLoS Comput. Biol. 2013, 9, e1003331. 10.1371/journal.pcbi.1003331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webb M. A.; Delannoy J.-Y.; de Pablo J. J. Graph-Based Approach to Systematic Molecular Coarse-Graining. J. Chem. Theory Comput. 2019, 15, 1199–1208. 10.1021/acs.jctc.8b00920. [DOI] [PubMed] [Google Scholar]
- Ponzoni L.; Polles G.; Carnevale V.; Micheletti C. SPECTRUS: A Dimensionality Reduction Approach for Identifying Dynamical Domains in Protein Complexes from Limited Structural Datasets. Structure 2015, 23, 1516–1525. 10.1016/j.str.2015.05.022. [DOI] [PubMed] [Google Scholar]
- Li Z.; Wellawatte G. P.; Chakraborty M.; Gandhi H. A.; Xu C.; White A. D. Graph neural network based coarse-grained mapping prediction. Chem. Sci. 2020, 11, 9524–9531. 10.1039/D0SC02458A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehl P.; Poitevin F.; Navaza R.; Delarue M. The renormalization group and its applications to generating coarse-grained models of large biological molecular systems. J. Chem. Theory Comput. 2017, 13, 1424–1438. 10.1021/acs.jctc.6b01136. [DOI] [PubMed] [Google Scholar]
- Tirion M. M. Large Amplitude Elastic Motions in Proteins from a Single-Paramter Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- Bahar I.; Atilgan A. R.; Erman B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Folding Des. 1997, 2, 173–181. 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- Hinsen K. Analysis of domain motions by approximate normal mode calculations. Proteins: Struct., Funct., Genet. 1998, 33, 417–429. . [DOI] [PubMed] [Google Scholar]
- Atilgan A. R.; Durell S. R.; Jernigan R. L.; Demirel M. C.; Keskin O.; Bahar I. Anistropy of Fluctuation Dynamics of Proteins with an Elastic Network Model. Biophys. J. 2001, 80, 505–515. 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delarue M.; Sanejouand Y. H. Simplified normal mode analysis of conformational transitions in DNA-dependent polymerases: the elastic network model. J. Mol. Biol. 2002, 320, 1011–1024. 10.1016/S0022-2836(02)00562-4. [DOI] [PubMed] [Google Scholar]
- Micheletti C.; Carloni P.; Maritan A. Accurate and efficient description of protein vibrational dynamics: comparing molecular dynamics and Gaussian models. Proteins: Struct., Funct., Genet. 2004, 55, 635–645. 10.1002/prot.20049. [DOI] [PubMed] [Google Scholar]
- Rudzinski J. F.; Noid W. G. Coarse-graining entropy, forces, and structures. J. Chem. Phys. 2011, 135, 214101. 10.1063/1.3663709. [DOI] [PubMed] [Google Scholar]
- Shell M. S. Systematic coarse-graining of potential energy landscapes and dynamics in liquids. J. Chem. Phys. 2012, 137, 084503. 10.1063/1.4746391. [DOI] [PubMed] [Google Scholar]
- Foley T. T.; Shell M. S.; Noid W. G. The impact of resolution upon entropy and information in coarse-grained models. J. Chem. Phys. 2015, 143, 243104. 10.1063/1.4929836. [DOI] [PubMed] [Google Scholar]
- Kullback S.; Leibler R. A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. 10.1214/aoms/1177729694. [DOI] [Google Scholar]
- Fisher M. E. Renormalization group theory: Its basis and formulation in statistical physics. Rev. Mod. Phys. 1998, 70, 653. 10.1103/RevModPhys.70.653. [DOI] [Google Scholar]
- Shannon C. E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. 10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- Park S.; Khalili-Araghi F.; Tajkhorshid E.; Schulten K. Free energy calculation from steered molecular dynamics simulations using Jarzynski’s equality. J. Chem. Phys. 2003, 119, 3559–3566. 10.1063/1.1590311. [DOI] [Google Scholar]
- Chipot C.; Pohorille A.. Free Energy Calculations; Springer, 2007. [Google Scholar]
- Mayorga-Flores M.; Chantôme A.; Melchor-Meneses C. M.; Domingo I.; Titaux-Delgado G. A.; Galindo-Murillo R.; Vandier C.; del Río-Portilla F. Novel blocker of onco SK3 channels derived from scorpion toxin tamapin and active against migration of cancer cells. ACS Med. Chem. Lett. 2020, 11, 1627–1633. 10.1021/acsmedchemlett.0c00300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedarzani P.; D’hoedt D.; Doorty K. B.; Wadsworth J. D. F.; Joseph J. S.; Jeyaseelan K.; Kini R. M.; Gadre S. V.; Sapatnekar S. M.; Stocker M.; Strong P. N. Tamapin, a Venom Peptide from the Indian Red Scorpion (Mesobuthus tamulus) That Targets Small Conductance Ca2+-activated K+ Channels and Afterhyperpolarization Currents in Central Neurons. J. Biol. Chem. 2002, 277, 46101–46109. 10.1074/jbc.M206465200. [DOI] [PubMed] [Google Scholar]
- Gati C. D.; Mortari M. R.; Schwartz E. F. Towards therapeutic applications of arthropod venom K+-channel blockers in CNS neurologic diseases involving memory acquisition and storage. J. Toxicol. 2012, 2012, 756358. 10.1155/2012/756358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller C. W.; Schlauderer G. J.; Reinstein J.; Schulz G. E. Adenylate kinase motions during catalysis: an energetic counterweight balancing substrate binding. Structure 1996, 4, 147–56. 10.1016/S0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- Shapiro Y. E.; Kahana E.; Meirovitch E. Domain mobility in proteins from NMR/SRLS. J. Phys. Chem. B 2009, 113, 12050–12060. 10.1021/jp901522c. [DOI] [PubMed] [Google Scholar]
- Formoso E.; Limongelli V.; Parrinello M. Energetics and Structural Characterization of the large-scale Functional Motion of Adenylate Kinase. Sci. Rep. 2015, 5, 8425. 10.1038/srep08425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitford P. C.; Miyashita O.; Levy Y.; Onuchic J. N. Conformational transitions of adenylate kinase: switching by cracking. J. Mol. Biol. 2007, 366, 1661–1671. 10.1016/j.jmb.2006.11.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Peng C.; Yu Y.; Chen Z.; Xu Z.; Cai T.; Shao Q.; Shi J.; Zhu W. Exploring Conformational Change of Adenylate Kinase by Replica Exchange Molecular Dynamic Simulation. Biophys. J. 2020, 118, 1009–1018. 10.1016/j.bpj.2020.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seyler S. L.; Beckstein O. Sampling large conformational transitions: adenylate kinase as a testing ground. Mol. Simul. 2014, 40, 855–877. 10.1080/08927022.2014.919497. [DOI] [Google Scholar]
- Scott C. F.; Carrell R. W.; Glaser C. B.; Kueppers F.; Lewis J. H.; Colman R. W. Alpha-1-antitrypsin-Pittsburgh. A potent inhibitor of human plasma factor XIa, kallikrein, and factor XIIf. J. Clin. Invest. 1986, 77, 631–634. 10.1172/JCI112346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nukiwa T.; Brantly M. L.; Ogushi F.; Fells G. A.; Crystal R. G. Characterization of the gene and protein of the common alpha 1-antitrypsin normal M2 allele. Am. J. Hum. Genet. 1988, 43, 322–330. [PMC free article] [PubMed] [Google Scholar]
- Luisetti M.; Seersholm N. α1-antitrypsin deficiency · 1: Epidemiology of α1-antitrypsin deficiency. Thorax 2004, 59, 164–169. 10.1136/thorax.2003.006494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick S.; Gelatt C. D.; Vecchi M. P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Černỳ V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. 10.1007/BF00940812. [DOI] [Google Scholar]
- Kunzmann P.; Hamacher K. Biotite: a unifying open source computational biology framework in Python. BMC Bioinf. 2018, 19, 346. 10.1186/s12859-018-2367-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andreotti N.; di Luccio E.; Sampieri F.; De Waard M.; Sabatier J.-M. Molecular modeling and docking simulations of scorpion toxins and related analogs on human SKCa2 and SKCa3 channels. Peptides 2005, 26, 1095–1108. 10.1016/j.peptides.2005.01.022. [DOI] [PubMed] [Google Scholar]
- Quintero-Hernández V.; Jiménez-Vargas J.; Gurrola G.; Valdivia H.; Possani L. Scorpion venom components that affect ion-channels function. Toxicon 2013, 76, 328–342. 10.1016/j.toxicon.2013.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramírez-Cordero B.; Toledano Y.; Cano-Sánchez P.; Hernández-López R.; Flores-Solis D.; Saucedo-Yáñez A. L.; Chávez-Uribe I.; Brieba L. G.; del Río-Portilla F. Cytotoxicity of Recombinant Tamapin and Related Toxin-Like Peptides on Model Cell Lines. Chem. Res. Toxicol. 2014, 27, 960–967. 10.1021/tx4004193. [DOI] [PubMed] [Google Scholar]
- Thach T. T.; Luong T. T.; Lee S.; Rhee D.-K. Adenylate kinase from Streptococcus pneumoniae is essential for growth through its catalytic activity. FEBS Open Bio 2014, 4, 672–682. 10.1016/j.fob.2014.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellinzoni M.; Haouz A.; Graña M.; Munier-Lehmann H.; Shepard W.; Alzari P. M. The crystal structure of Mycobacterium tuberculosis adenylate kinase in complex with two molecules of ADP and Mg2+ supports an associative mechanism for phosphoryl transfer. Protein Sci. 2006, 15, 1489–1493. 10.1110/ps.062163406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinstein J.; Gilles A.-M.; Rose T.; Wittinghofer A.; Saint Girons I.; Bârzu O.; Surewicz W. K.; Mantsch H. H. Structural and catalytic role of arginine 88 in Escherichia coli adenylate kinase as evidenced by chemical modification and site-directed mutagenesis. J. Biol. Chem. 1989, 264, 8107–8112. [PubMed] [Google Scholar]
- Akbari A. Phenylglyoxal. Synlett 2012, 23, 951–952. 10.1055/s-0031-1290293. [DOI] [Google Scholar]
- Matsunaga Y.; Fujisaki H.; Terada T.; Furuta T.; Moritsugu K.; Kidera A. Minimum Free Energy Path of Ligand-Induced Transition in Adenylate Kinase. PLoS Comput. Biol. 2012, 8, e1002555. 10.1371/journal.pcbi.1002555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gur M.; Madura J. D.; Bahar I. Global transitions of proteins explored by a multiscale hybrid methodology: application to adenylate kinase. Biophys. J. 2013, 105, 1643–1652. 10.1016/j.bpj.2013.07.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halder R.; Manna R. N.; Chakraborty S.; Jana B. Modulation of the Conformational Dynamics of Apo-Adenylate Kinase through a π–Cation Interaction. J. Phys. Chem. B 2017, 121, 5699–5708. 10.1021/acs.jpcb.7b01736. [DOI] [PubMed] [Google Scholar]
- Schapira M.; Ramus M.-A.; Jallat S.; Carvallo D.; Courtney M. Recombinant alpha 1-antitrypsin Pittsburgh (Met 358—Arg) is a potent inhibitor of plasma kallikrein and activated factor XII fragment. J. Clin. Invest. 1986, 77, 635–637. 10.1172/JCI112347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taggart C.; Cervantes-Laurean D.; Kim G.; McElvaney N. G.; Wehr N.; Moss J.; Levine R. L. Oxidation of either Methionine 351 or Methionine 358 in α1-Antitrypsin Causes Loss of Anti-neutrophil Elastase Activity. J. Biol. Chem. 2000, 275, 27258–27265. 10.1074/jbc.M004850200. [DOI] [PubMed] [Google Scholar]
- Owen M. C.; Brennan S. O.; Lewis J. H.; Carrell R. W. Mutation of Antitrypsin to Antithrombin. N. Engl. J. Med. 1983, 309, 694–698. 10.1056/NEJM198309223091203. [DOI] [PubMed] [Google Scholar]
- Kadanoff L. P. Scaling laws for Ising models near Tc. Physics 1966, 2, 263. 10.1103/PhysicsPhysiqueFizika.2.263. [DOI] [Google Scholar]
- Ma S.-K.Modern Theory of Critical Phenomena; Routledge, 2018. [Google Scholar]
- Zinn-Justin J.Phase Transitions and Renormalization Group; Oxford University Press, 2007. [Google Scholar]
- Schäfer L.Excluded Volume Effects in Polymer Solutions As Explained by the Renormalization Group; Springer Science & Business Media, 2012. [Google Scholar]
- Cavagna A.; Di Carlo L.; Giardina I.; Grandinetti L.; Grigera T. S.; Pisegna G. Dynamical Renormalization Group Approach to the Collective Behavior of Swarms. Phys. Rev. Lett. 2019, 123, 268001. 10.1103/PhysRevLett.123.268001. [DOI] [PubMed] [Google Scholar]
- Antonov N. V.; Kakin P. I. Scaling in landscape erosion: Renormalization group analysis of a model with infinitely many couplings. Theor. Math. Phys. 2017, 190, 193–203. 10.1134/S0040577917020027. [DOI] [Google Scholar]
- Van Enter A. C.; Fernández R.; Sokal A. D. Regularity properties and pathologies of position-space renormalization-group transformations: Scope and limitations of Gibbsian theory. J. Stat. Phys. 1993, 72, 879–1167. 10.1007/BF01048183. [DOI] [Google Scholar]
- Chakraborty M.; Xu C.; White A. D. Encoding and selecting coarse-grain mapping operators with hierarchical graphs. J. Chem. Phys. 2018, 149, 134106. 10.1063/1.5040114. [DOI] [PubMed] [Google Scholar]
- Wang W.; Gómez-Bombarelli R. Coarse-graining auto-encoders for molecular dynamics. npj Comput. Mater. 2019, 5, 125. 10.1038/s41524-019-0261-5. [DOI] [Google Scholar]
- Lenggenhager P. M.; Gökmen D. E.; Ringel Z.; Huber S. D.; Koch-Janusz M. Optimal Renormalization Group Transformation from Information Theory. Phys. Rev. X 2020, 10, 011037. 10.1103/PhysRevX.10.011037. [DOI] [Google Scholar]
- Ghersi D.; Sanchez R. EasyMIFS and SiteHound: a toolkit for the identification of ligand-binding sites in protein structures. Bioinformatics 2009, 25, 3185–3186. 10.1093/bioinformatics/btp562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngan C.-H.; Hall D. R.; Zerbe B.; Grove L. E.; Kozakov D.; Vajda S. FTSite: high accuracy detection of ligand binding sites on unbound protein structures. Bioinformatics 2012, 28, 286–287. 10.1093/bioinformatics/btr651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmanic A.; Bowman G. R.; Juarez-Jimenez J.; Michel J.; Gervasio F. L. Investigating Cryptic Binding Sites by Molecular Dynamics Simulations. Acc. Chem. Res. 2020, 53, 654–661. 10.1021/acs.accounts.9b00613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady G. P.; Stouten P. F. Fast prediction and visualization of protein binding pockets with PASS. J. Comput.-Aided Mol. Des. 2000, 14, 383–401. 10.1023/A:1008124202956. [DOI] [PubMed] [Google Scholar]
- Laurie A. T.; Jackson R. M. Q-SiteFinder: an energy-based method for the prediction of protein–ligand binding sites. Bioinformatics 2005, 21, 1908–1916. 10.1093/bioinformatics/bti315. [DOI] [PubMed] [Google Scholar]
- Hendlich M.; Rippmann F.; Barnickel G. LIGSITE: automatic and efficient detection of potential small molecule-binding sites in proteins. J. Mol. Graphics Modell. 1997, 15, 359–363. 10.1016/S1093-3263(98)00002-3. [DOI] [PubMed] [Google Scholar]
- Yang J.; Roy A.; Zhang Y. BioLiP: a semi-manually curated database for biologically relevant ligand-protein interactions. Nucleic Acids Res. 2012, 41, D1096–D1103. 10.1093/nar/gks966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J.; Roy A.; Zhang Y. Protein-ligand binding site recognition using complementary binding-specific substructure comparison and sequence profile alignment. Bioinformatics 2013, 29, 2588–2595. 10.1093/bioinformatics/btt447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiménez J.; Doerr S.; Martínez-Rosell G.; Rose A. S.; De Fabritiis G. DeepSite: protein-binding site predictor using 3D-convolutional neural networks. Bioinformatics 2017, 33, 3036–3042. 10.1093/bioinformatics/btx350. [DOI] [PubMed] [Google Scholar]
- Song K.; Liu X.; Huang W.; Lu S.; Shen Q.; Zhang L.; Zhang J. Improved Method for the Identification and Validation of Allosteric Sites. J. Chem. Inf. Model. 2017, 57, 2358–2363. 10.1021/acs.jcim.7b00014. [DOI] [PubMed] [Google Scholar]
- Krivák R.; Hoksza D. P2Rank: machine learning based tool for rapid and accurate prediction of ligand binding sites from protein structure. J. Cheminf. 2018, 10, 39. 10.1186/s13321-018-0285-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jendele L.; Krivak R.; Skoda P.; Novotny M.; Hoksza D. PrankWeb: a web server for ligand binding site prediction and visualization. Nucleic Acids Res. 2019, 47, W345–W349. 10.1093/nar/gkz424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J.; Shen C.; Huang N. Predicting or pretending: artificial intelligence for protein-ligand interactions lack of sufficiently large and unbiased datasets. Front. Pharmacol. 2020, 11, 69. 10.3389/fphar.2020.00069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Guilloux V.; Schmidtke P.; Tuffery P. Fpocket: an open source platform for ligand pocket detection. BMC Bioinf. 2009, 10, 168. 10.1186/1471-2105-10-168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu H.; Pisabarro M. T. MSPocket: an orientation-independent algorithm for the detection of ligand binding pockets. Bioinformatics 2011, 27, 351–358. 10.1093/bioinformatics/btq672. [DOI] [PubMed] [Google Scholar]
- Amadei A.; Linssen A. B. M.; Berendsen H. J. C. Essential dynamics of proteins. Proteins: Struct., Funct., Genet. 1993, 17, 412–425. 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- Pontiggia F.; Colombo G.; Micheletti C.; Orland H. Anharmonicity and self-similarity of the free energy landscape of protein G. Phys. Rev. Lett. 2007, 98, 048102–048102. 10.1103/PhysRevLett.98.048102. [DOI] [PubMed] [Google Scholar]
- Hensen U.; Meyer T.; Haas J.; Rex R.; Vriend G.; Grubmüller H. Exploring Protein Dynamics Space: The Dynasome as the Missing Link between Protein Structure and Function. PLoS One 2012, 7, e33931. 10.1371/journal.pone.0033931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nussinov R.; Wolynes P. G. A second molecular biology revolution? The energy landscapes of biomolecular function. Phys. Chem. Chem. Phys. 2014, 16, 6321–6322. 10.1039/c4cp90027h. [DOI] [PubMed] [Google Scholar]
- Wei G.; Xi W.; Nussinov R.; Ma B. Protein Ensembles: How Does Nature Harness Thermodynamic Fluctuations for Life? The Diverse Functional Roles of Conformational Ensembles in the Cell. Chem. Rev. 2016, 116, 6516–6551. 10.1021/acs.chemrev.5b00562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal R. R.; Michener C. D. A statistical method for evaluating systematic relationships. Univ. Kans. Sci. Bull. 1958, 28, 1409–1438. [Google Scholar]
- Kabsch W. A solution for the best rotation to relate two sets of vectors. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1976, 32, 922–923. 10.1107/S0567739476001873. [DOI] [Google Scholar]
- Kabsch W. A discussion of the solution for the best rotation to relate two sets of vectors. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1978, 34, 827–828. 10.1107/S0567739478001680. [DOI] [Google Scholar]
- Kim H.; Jang C.; Yadav D. K.; Kim M.-h. The comparison of automated clustering algorithms for resampling representative conformer ensembles with RMSD matrix. J. Cheminf. 2017, 9, 21. 10.1186/s13321-017-0208-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraccalvieri D.; Pandini A.; Stella F.; Bonati L. Conformational and functional analysis of molecular dynamics trajectories by Self-Organising Maps. BMC Bioinf. 2011, 12, 158. 10.1186/1471-2105-12-158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müllner D.Modern hierarchical, agglomerative clustering algorithms. arXiv (Statistics.Machine Learning), September 12, 2011, 1109.2378, ver. 1. https://arxiv.org/abs/1109.2378.
- Bar-Joseph Z.; Gifford D. K.; Jaakkola T. S. Fast optimal leaf ordering for hierarchical clustering. Bioinformatics 2001, 17, S22–S29. 10.1093/bioinformatics/17.suppl_1.S22. [DOI] [PubMed] [Google Scholar]
- Jones E.; Oliphant T.; Peterson P.. SciPy: Open source scientific tools for Python, 2001. –. http://www.scipy.org/.
- Park M.-W.; Kim Y.-D. A systematic procedure for setting parameters in simulated annealing algorithms. Comput. Oper. Res. 1998, 25, 207–217. 10.1016/S0305-0548(97)00054-3. [DOI] [Google Scholar]
- Connolly D. An Improved Annealing Scheme for the QAP. European Journal of Operational Research 1990, 46, 93–100. 10.1016/0377-2217(90)90301-Q. [DOI] [Google Scholar]
- Dijkstra M.; van Roij R.; Evans R. Phase diagram of highly asymmetric binary hard-sphere mixtures. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1999, 59, 5744. 10.1103/PhysRevE.59.5744. [DOI] [PubMed] [Google Scholar]
- Rudzinski J. F.; Noid W. G. A generalized-Yvon-Born-Green method for coarse-grained modeling. Eur. Phys. J.: Spec. Top. 2015, 224, 2193–2216. 10.1140/epjst/e2015-02408-9. [DOI] [Google Scholar]
- Menichetti R.; Pelissetto A.; Randisi F. Thermodynamics of star polymer solutions: A coarse-grained study. J. Chem. Phys. 2017, 146, 244908. 10.1063/1.4989476. [DOI] [PubMed] [Google Scholar]
- In this work, we employ a different sign convention for the mapping entropy Smap with respect to refs (42) and (44) and consistent with the one in ref (17). On one hand, this enables the mapping entropy to be directly related to a loss of information in the KL sense: a positive KL divergence implies a loss of information. On the other hand, it allows the relative entropy Srel in refs (42) and (44) to be considered a difference of information losses—those of U and U0 (see eq 31)—calculated with respect to the atomistic system, so that the vanishing of Srel for U = U0 in refs (42) and (44) effectively amounts to a recalibration of the zero of the relative entropy as originally defined in ref (17).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.