Intelligent Electromagnetic Sensing with Learnable Data Acquisition and Processing

Summary

Electromagnetic (EM) sensing is a widespread contactless examination technique with applications in areas such as health care and the internet of things. Most conventional sensing systems lack intelligence, which not only results in expensive hardware and complicated computational algorithms but also poses important challenges for real-time in situ sensing. To address this shortcoming, we propose the concept of intelligent sensing by designing a programmable metasurface for data-driven learnable data acquisition and integrating it into a data-driven learnable data-processing pipeline. Thereby, a measurement strategy can be learned jointly with a matching data post-processing scheme, optimally tailored to the specific sensing hardware, task, and scene, allowing us to perform high-quality imaging and high-accuracy recognition with a remarkably reduced number of measurements. We report the first experimental demonstration of “learned sensing” applied to microwave imaging and gesture recognition. Our results pave the way for learned EM sensing with low latency and computational burden.

Graphical Abstract

Highlights

• •First demonstration of “learned sensing” in electromagnetics
• •Low-latency imaging and gesture recognition with learned illumination patterns
• •Data acquisition and processing integrated into unique machine-learning pipeline
• •Selection of task-relevant information already during measurements

The Bigger Picture

Many futuristic “intelligent” concepts that will affect our society, from ambient-assisted health care via autonomous vehicles to touchless human-computer interaction, necessitate sensors that can monitor a device's surroundings fast and without extensive computational effort. To date, sensors indiscriminately acquire all information and only select relevant details during data processing, thereby wasting time, energy, and computational resources. We demonstrate intelligent electromagnetic sensing that uses learned illumination patterns to already select relevant details during the measurement process. Our experiments use a home-made programmable metasurface to generate the learned microwave patterns that enable a remarkable reduction in the number of necessary measurements. Our demonstration addresses a widespread need for high-quality contactless electromagnetic sensing under strict time, energy, and computation constraints.

“Smart” devices must “see” and “recognize” objects and gestures in their surroundings as quickly as possible. We consider a contactless sensor that illuminates its surroundings with microwave illumination shaped by a programmable metasurface. By integrating the measurement process directly into the machine-learning pipeline that processes the data, we learn optimal illumination patterns that efficiently extract task-relevant information. Our experimental demonstration of low-latency intelligent electromagnetic sensing will influence human-computer interaction, health care, automotive radar, and security screening.

Introduction

Electromagnetic (EM) sensing is a widely used contactless examination technique because it relies on harmless nonionizing radiation that can penetrate optically opaque materials. Consequently, EM sensing has emerged as promising tool in various applications ranging from health care1, 2, 3, 4 via security screening5, 6, 7 up to planetary explorations.8, 9, 10 However, to fully exploit the application potential of EM sensing, cost efficiency and speed remain two major challenges. Traditional EM hardware relies on mechanically or electronically scanned beams, suffering from slow acquisition or high cost, respectively. Recently, novel hardware solutions to shift the cost from the hardware to the software level were proposed: rather than acquiring the information in the spatial domain, the information can be multiplexed across independent frequencies or configurations of a complex system such as a chaotic cavity or a metasurface aperture.11, 12, 13, 14 The computationally intensive challenge is then to recover the spatial information from the multiplexed measurements. Given the typical scene sparsity, compressive sensing schemes are usually employed to recover the information from an underdetermined set of measurements.¹⁵ Especially when analytical models are lacking, machine-learning (ML) techniques have recently been proposed to solve the electromagnetic inverse scattering problem.16, 17, 18

However, these EM sensing schemes based on generic (random) scene illuminations still lack “intelligence”: they indiscriminately acquire all information, ignoring available knowledge about scene, sensing task, and hardware constraints. Yet using this available a priori knowledge is critical to limit data acquisition to relevant information—the crucial conceptual improvement necessary to reduce latency and computational burden. A first step to add intelligence consisted in adapting the scene illuminations to the knowledge of what scene is expected via a principal component analysis (PCA) of the expected scene.^19,20 Albeit yielding significant performance improvements, this technique still considers acquisition and processing separately, and hence fails to use task-specific measurement settings that highlight salient features for the processing layer.

To fully reap the benefits of ML techniques in EM sensing, acquisition and processing must be jointly learned in a unique pipeline. Recently, inspired by pioneering work in optical microscopy,²¹ the idea of learned EM sensing with programmable metasurface hardware was introduced.²² Thereby, a model of the programmable measurement process is directly integrated into the ML pipeline used to process the data, enabling the joint learning of optimal measurement and processing settings for the given hardware, task, and expected scene. We note that there is a number of related works in optics23, 24, 25, 26, 27 and a similar concept has recently also been studied in the context of ultrasonic imaging.²⁸ It is important to realize that most of the time in EM sensing, the specific task can be executed without first reconstructing a visual image of the scene. While current EM sensing systems are designed to first generate high-resolution images as a checkpoint for subsequent ML-aided recognition tasks, the resulting acquisition of irrelevant information and the huge flux of data to be processed cause significant inefficiencies. Hence, for tasks such as object recognition it is most efficient to skip the intermediate imaging step and directly process the raw data, as done in previous studies.^20,22

Here, we report the first experimental demonstration of learned EM sensing. We consider the tasks of (1) imaging and (2) gesture recognition, two examples with immediate real-life application in security screening and human-machine interaction. Our intelligent hardware layer relies on a programmable metasurface29, 30, 31 to shape the waves illuminating the scene. Unlike del Hougne et al.,²² we do not use an analytical description of the measurement process but train a three-port deep artificial neural network (ANN), called the measurement ANN (m-ANN), to capture the link between scene, metasurface coding pattern, and microwave measurement. Being sharply different from the study by Li et al.,³² where only the data processing is treated with the ANN, here we jointly optimize the control coding patterns of the metasurface together with the weights of another ANN, called the reconstruction ANN (r-ANN), which is used to extract the desired information from the raw measurements. To this end, we interpret measurement and reconstruction as, respectively, encoding and decoding the relevant scene information (an image or a gesture classification) in/from a measurement space. Thus, we can employ a variational autoencoder (VAE) framework33, 34, 35 to jointly learn optimal measurement and processing settings with a standard supervised-learning procedure. This strategy drastically reduces the number of necessary measurements, helping us to remarkably improve many critical metrics such as speed, processing burden, and energy consumption.

Results

Operation Principle

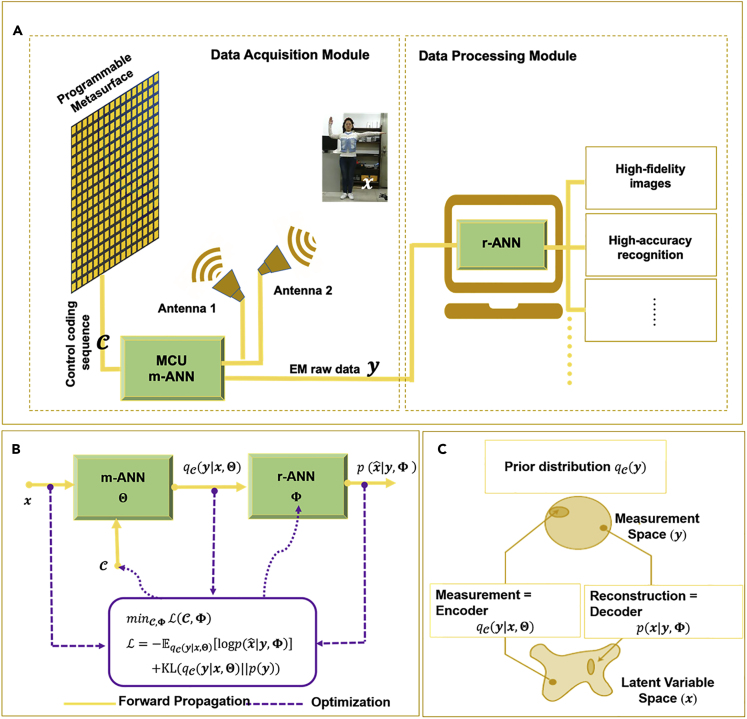
Learned sensing requires the integration of a model of the reconfigurable measurement process into the pipeline used for data processing, in order to jointly optimize the learnable physical and digital weights, as illustrated in Figure 1. Given the difficulty of accurately modeling the measurement process in an analytical manner, for instance, due to inaccuracies in the metasurface fabrication or multipath effects in the indoor environment, here we propose the use of a data-driven model of the measurement process instead. We introduce a three-port-deep ANN, the measurement ANN (m-ANN), that links two inputs (the scene $\mathit{x}$ and the metasurface configuration $\mathcal{C}$) to one output (the raw microwave measurements $\mathit{y}$). First, we learn the trainable weights $\mathbf{\Theta }$ of the m-ANN from an $\left(\mathit{x},\mathcal{C},\mathit{y}\right)$-triple labeled training dataset with a standard supervised-learning procedure, as detailed in Experimental Procedures and Note S4.

Figure 1.

Setup and Working Principle of the Learned EM Sensing System

(A) The intelligent sensing system consists of two data-driven learnable modules: the m-ANN-driven data acquisition module and the r-ANN-driven data processing module. m-ANN models the measurement process involving a pair of horn antennas and a coding metasurface programmed with a micro-control unit. Antenna 1 emits plane microwave fronts, which are shaped by the programmable metasurface and then incident upon the scene. The waves scattered by the subject of interest are received by Antenna 2. The received raw microwave data are directly processed by the r-ANN, producing the desired imaging or recognition results.

(B) The m-ANN-based model of data acquisition as a trainable physical network is fully integrated with the r-ANN-driven data-processing pipeline into a unique sensing chain. The m-ANN has three ports: the scene of interest $\mathit{x}$ and the metasurface coding pattern $\mathcal{C}$ that shapes the scene illumination are its inputs, and the raw EM data $\mathit{y}$ is its output. First, the weights $\mathbf{\Theta }$ of m-ANN are fixed using a data-driven supervised-learning protocol. Second, optimal values of the physical and digital parameters of the sensing chain, $\mathcal{C}$ and Φ, respectively, are jointly learned using a standard supervised-learning procedure (error back-propagation) in a VAE framework. These optimal settings ensure that already on the hardware level only task-relevant information is captured and that a matching processing layer extracts the relevant information from the measurements.

(C) Our interpretation of the entire sensing process in the VAE framework: the latent variable space, $\mathit{x}$, is encoded by the analog measurements in a measurement space, $\mathit{y}$; the digital reconstruction decodes the measurements to return to the latent variable space.

Once the weights $\mathbf{\Theta }$ of m-ANN are fixed, we can proceed with the integration of m-ANN into the unique sensing pipeline. Following Vedula et al.,²⁸ we view the entire sensing process (data acquisition and processing) as a user-controlled end-to-end process. Given a scene $\mathit{x}$ (an image or a gesture class), a set of complex-valued measurements $\mathit{y}$ is generated by sampling from the $\mathcal{C}$-controllable conditional distribution $\mathit{y}\sim q_{\mathcal{C}}\left(\mathit{y}|\mathit{x},\mathbf{\Theta }\right)$. In other words, the latent scene variable of interest, $\mathit{x}$, is encoded in a measurement space $\mathit{y}$ via a distribution controlled by the metasurface configuration $\mathcal{C}$. The goal of the processing is then to find an estimator that retrieves the relevant scene information $\mathit{x}$ from the measurements $\mathit{y}$. This estimator inverts the action of the measurement process—in other words, it decodes the information of interest to return from the measurement space to the latent variable space. Using the VAE33, 34, 35 framework, the digital decoder can be modeled as sampling the measurement space with a conditional distribution$\mathit{x}\sim p_{\mathbf{\Phi }}\left(\mathit{x}|\mathit{y}\right)$, controlled by its digital weights $\mathbf{\Phi }$, to generate estimates of the latent variable of interest. The decoding is implemented with a deep ANN, called r-ANN, whose trainable weights can hence be identified as $\mathbf{\Phi }$.

To jointly learn optimal analog and digital weights, i.e., the metasurface control coding pattern $\mathcal{C}$ and the r-ANN weights $\mathbf{\Phi }$, respectively, we minimize the following objective function:³⁵

$$\mathcal{L}\left(\mathcal{C},\mathbf{\Phi }\right)=-{\mathbb{E}}_{q_{\mathcal{C}}\left(\mathit{y}|\mathit{x},\mathbf{\Theta }\right)}\left[\log p_{\mathbf{\Phi }}\left(\mathit{x}|\mathit{y}\right)\right]+\text{KL}\left(q_{\mathcal{C}}\left(\mathit{y}|\mathit{x},\mathbf{\Theta }\right)|p\left(\mathit{y}\right)\right)\text{.}$$ (Equation 1)

The first term in Equation 1, $-{\mathbb{E}}_{q_{\mathcal{C}}\left(\mathit{y}|\mathit{x},\mathbf{\Theta }\right)}\left[\log p_{\mathbf{\Phi }}\left(\mathit{x}|\mathit{y}\right)\right]$, can be interpreted as the “reconstruction error” of our VAE: it is the log likelihood of the true latent data given the inferred latent data. The second term, $\text{KL}\left(q_{\mathcal{C}}(\mathit{y}|\mathit{x},\mathbf{\Theta })|p\left(\mathit{y}\right)\right)$, acts as a regularizer and encourages the distribution of the decoder to be close to a chosen prior distribution $p\left(\mathit{y}\right)$. In our work, both analog encoder $q_{\mathcal{C}}\left(\mathit{y}|\mathit{x},\mathbf{\Theta }\right)$ and digital decoder $p_{\mathbf{\Phi }}\left(\mathit{x}|\mathit{y}\right)$ are treated with deep ANNs, namely m-ANN and r-ANN, as detailed in Experimental Procedures and Notes S1 and S4.

To determine the optimal settings of $\mathcal{C}$ and$\mathbf{\Phi }$, we apply a so-called alternatively iterative approach. Starting with some initializations of $\mathcal{C}$ and $\mathbf{\Phi }$, we calculate $\mathcal{C}$ ($\text{resp}.\mathbf{\Phi }$) for $\mathbf{\Phi }$ ($\text{resp}.\mathcal{C}$) updated in the last iteration step, followed by calculating $\mathbf{\Phi }$ ($\text{resp}.\mathcal{C}$) based on the obtained $\mathcal{C}$ ($\text{resp}.\mathbf{\Phi }$). This procedure is repeated until a stopping criterion is fulfilled. Such an optimization can be implemented using error-backpropagation³⁶ routines for continuous variables such as $\mathbf{\Phi }$ and $\mathbf{\Theta }$. However, we have a binary constraint (0 or 1) on the entries of $\mathcal{C}$, resulting in an NP-hard problem. While del Hougne et al.²² addressed this binary constraint with a temperature parameter trick,²³ in this work we use a randomized simultaneous perturbation stochastic approximation (r-SPSA) algorithm. The latter was originally developed for treating the problem of optimal well placement and control in the area of petroleum engineering.³⁷ More details about Equation 1 and the implementation of the optimization algorithm are provided in Figures S2 and S3 and Note S2.

In Situ Imaging of the Human Body

First, we apply our learned EM sensing system to the task of in situ high-resolution imaging of a human body in our laboratory environment. As outlined previously, we integrate m-ANN for data acquisition and r-ANN for smart data processing into a unique data-driven learnable sensing chain. To this end, we need to jointly optimize the coding patterns $\mathcal{C}$ of the m-ANN together with the weights $\mathbf{\Phi }$ of r-ANN for the specific task of human body imaging. The integrated ANN, containing a multitude of nonlinear ML layers, can be trained with a standard supervised-learning procedure in TensorFlow. Following Vedula et al.,²⁸ to illustrate the significant improvement of the proposed learned sensing strategy on the image quality over conventional learning-based sensing methods, we consider a two-stage training procedure. During the first stage, the coding patterns of the m-ANN and the digital weights of the r-ANN are optimized separately, as in Li et al.²⁰ The coding patterns of m-ANN are assigned following the two most common state-of-the-art approaches that correspond to using random or PCA-based scene illuminations. During the second stage, m-ANN and r-ANN are jointly trained to achieve the overall optimal sensing performance. In this two-stage training, the benefit reaped by the proposed sensing strategy over the conventional methods can be clearly demonstrated. In our study we use several people, called training persons in short, to train our intelligent microwave sensing system, and use a different person, called test persons, to test it. In addition, we use 1,000 random codes and 1,000 PCA-based codes (200 standard PCA-based codes and their 800 perturbations) as raining samples for training $\mathbf{\Theta }$. The details of the training persons are provided by Li et al.³² The ground truth is defined using binarized optical images of the scene.

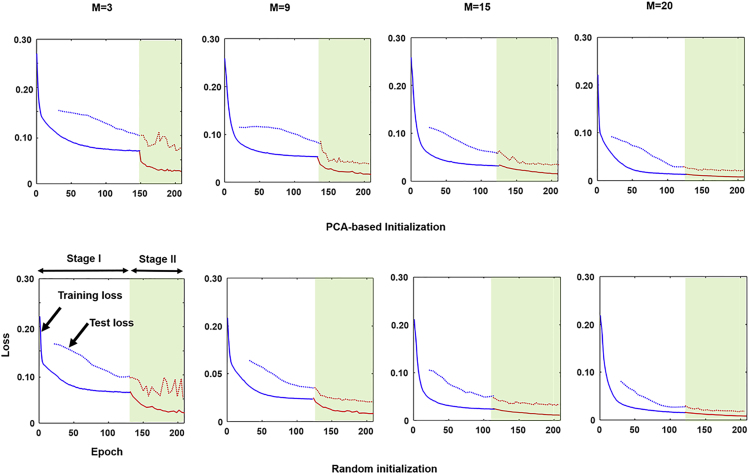
In general, depending on the difficulty of the sensing task and the signal-to-noise ratio,³⁸ a measurement with a single coding pattern cannot be expected to obtain sufficient relevant information. Figure 2 displays the cross-validation errors over the course of the training iterations for different numbers M of coding patterns of the metasurface (3, 9, 15, and 20). The two stages of the aforementioned training protocol can be clearly distinguished. To assess the image quality quantitatively, the so-called structure similarity index metric (SSIM) is considered, which is calculated using the MATLAB library function, i.e., ssim. Figure S4 displays SSIM histograms for different values of M and different sensing methods. Since the trainable physical ($\mathcal{C}$) and digital ($\mathbf{\Phi }$) parameters are initialized randomly before training, except PCA-based $\mathcal{C}$, we have conducted 500 realizations to remove any sensitivity to the choices of random initializations made for m-ANN and r-ANN. Examples of the corresponding optimized coding patterns of the metasurface are displayed in Figure S5.

Figure 2.

Training Dynamics for Learned EM Sensing Applied to an Imaging Task

The dependence of the training and test loss functions on the progress of iterative epochs is shown for different numbers of coding patterns M, i.e., M = 3, 9, 15, and 20. The continuous lines indicate the training loss and the dashed lines indicate the test loss. The control coding patterns of the metasurface are initialized randomly (top) or PCA-based (bottom). During stage I, only the digital decoder weights $\mathbf{\Phi }$ are optimized. Then, during stage II, both the physical weights $\mathcal{C}$ and the digital weights $\mathbf{\Phi }$ are jointly optimized. The presented results show a remarkable improvement of the image quality achieved by using the joint optimization of $\mathcal{C}$ and $\mathbf{\Phi }$ during stage II, compared with that based on solely optimizing $\mathbf{\Phi }$ (i.e., the end of stage I). The effect is especially striking when the number of measurements is very limited.

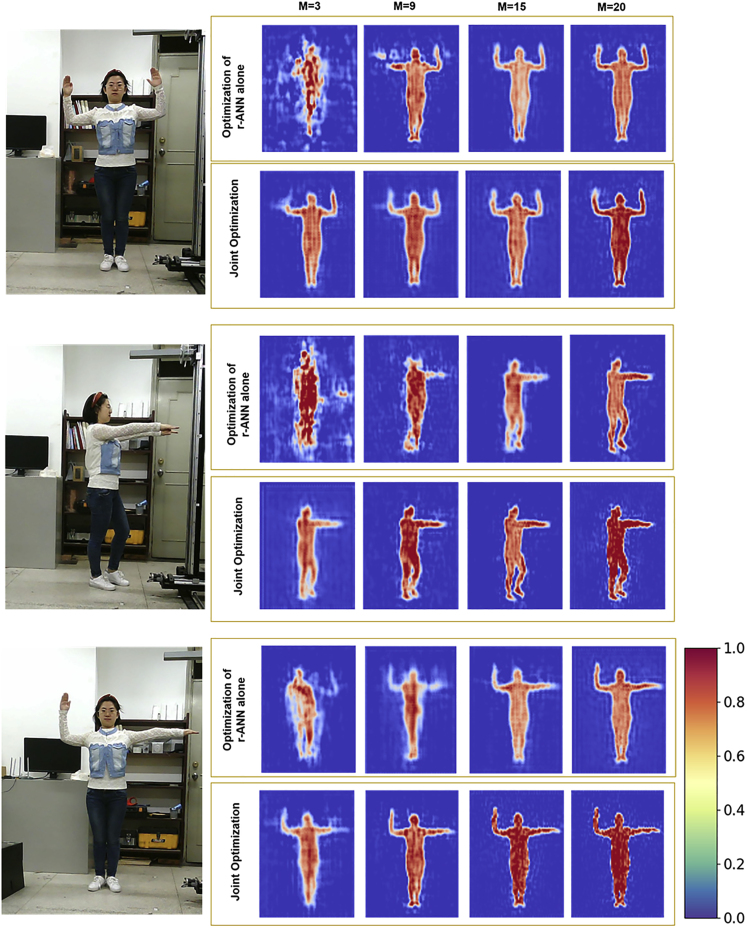
Figure 3 reports several selected image reconstruction results of the test person with different body gestures using the aforementioned sensing methods. The corresponding coding patterns of the metasurface are displayed in Figure S5. In line with del Hougne et al.,²² we observe that the sensing quality (here image quality) achieved by jointly optimizing physical ($\mathcal{C}$) and digital ($\mathbf{\Phi }$) parameters is significantly better than if only $\mathbf{\Phi }$ is optimized. This may be intuitively expected, since more trainable parameters are available and all a priori knowledge is used in the learned sensing scheme. Unlike Vedula et al.,²⁸ we do not observe a significant performance dependence on the initialization of the m-ANN (PCA-based or random) in this work.

Figure 3.

Experimental Results for Learned EM Sensing Applied to an Imaging Task

For three different poses, we display the images reconstructed with different numbers of coding patterns of the metasurface, M, for the case of only optimizing $\mathbf{\Phi }$ (first row) or jointly optimizing $\mathcal{C}$ and $\mathbf{\Phi }$ (second row). Remarkable improvements of the image quality are achieved by using the joint optimization of $\mathcal{C}$ and $\mathbf{\Phi }$, compared with the case of only optimizing $\mathbf{\Phi }$, when the number of coding patterns of metasurface is less than 9. In this set of experiments, the random initialization is used.

Our experimental results demonstrate, in line with del Hougne et al.,²² that simultaneous learning of measurement and reconstruction settings is remarkably superior to the conventional sensing strategies whereby measurement and/or reconstruction are optimized separately (if optimized at all). The benefits of learned sensing are especially strong when the number of measurements is highly limited such that learned sensing enables a remarkable dimensionality reduction. Ultimately, these superior characteristics are enabled by training a unique integrated sensing chain, making use of all available a priori knowledge about the probed scene, task, and constraints on measurement setting and processing pipeline.

In Situ Recognition of Body Gestures

Finally, we consider the task of recognizing body gestures from raw measurement data, i.e., without an intermediate imaging step. Similar to before, m-ANN and r-ANN are merged into a unique sensing chain, which is simultaneously trained using a standard supervised-learning technique, this time to maximize the entire system's gesture classification accuracy. We use the same training and test dataset of four different body gestures as well as the same two-stage training procedure as before. $\mathcal{C}$ is initialized randomly.

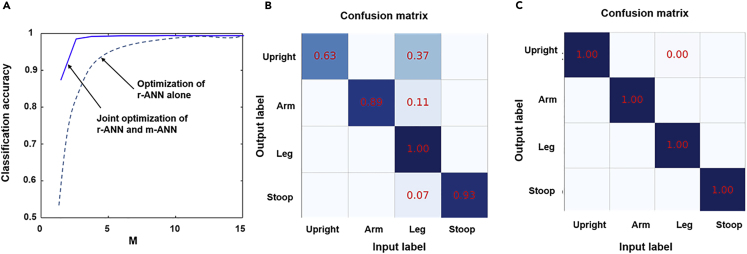
Figure 4A reports the average classification accuracy as a function of the number of measurements M. The presented results have been obtained over four different body gestures, and each gesture with 100 test samples. Additionally, the corresponding classification matrices for different sensing methods are reported in Figures 4B and 4C. A classification matrix shows how often a given body gesture is mistakenly classified as one of the other gesture classes. Note that the strong diagonal elements (corresponding to correctly identified body gestures) reflect the achieved recognition accuracy of almost 100% on average by using the learned sensing method. The performance using the learned sensing scheme saturates around M = 5 at 98%, meaning that we extract all task-relevant information with only three coding patterns of the metasurface. For M ≤ 5, our scheme yields gains in accuracy of the order of 5%–35%, a substantial improvement in the context of classification tasks. The reduction in the number of necessary measurements thanks to the learned sensing scheme will reduce the time needed to acquire and process data, as well as the sensor's energy consumption.

Figure 4.

Experimental Results for Learned EM Sensing Applied to a Gesture-Recognition Task

Rather than imaging the scene, we now directly process the raw data with the r-ANN in order to classify the gesture displayed in the scene. The metasurface coding patterns $\mathcal{C}$ are initialized randomly.

(A) Dependence of the classification accuracy on the number of coding patterns of the programmable metasurface.

(B) The classification confusion matrix for M = 3 if only $\mathbf{\Phi }$ is optimized.

(C) The classification confusion matrix for M = 3 for jointly optimized $\mathcal{C}$ and $\mathbf{\Phi }$.

Discussion

We have reported an experimental implementation of the recently proposed learned EM sensing paradigm applied to two real-life tasks: imaging and gesture recognition. We leveraged a programmable metasurface on the physical layer to shape scene illuminations. Our integrated sensing chain is composed of two dedicated deep ANNs, the m-ANN for smart data acquisition and the r-ANN for instant data processing. Using a VAE formalism, we jointly trained the learnable weights of the measurement process and those of the processing layer to learn an optimal sensing strategy. Thereby, we make use of all available a priori knowledge about the probed scene, the specific sensing task, and the constraints on the measurement setting and processing pipeline. As a result, the learned sensing strategy with simultaneous learning of measurement and reconstruction procedures yields a superior performance compared with conventional sensing strategies that optimize measurement and processing separately (or not at all). The performance improvements are particularly large when the number of measurements is very limited, as we have experimentally demonstrated. To summarize, we have reported experimental results with immediate practical impact showing how to merge artificial materials and artificial intelligence in the design of a learned EM sensing architecture. Our work paves the path to low-latency microwave sensing for security screening, human-computer interaction, health care, and automotive radar.

Experimental Procedures

Design of Programmable Coding Metasurface

The programmable metasurface29, 30, 31 is an ultrathin planar array of electronically reconfigurable meta-atoms. Thanks to its unique capabilities to manipulate EM wave fields in a reprogrammable manner, it has elicited many exciting physical phenomena^39,40 and versatile functional devices,⁴¹ such as computational imagers and sensors,11, 12, 13^,20,22,32,42 programmable holography,⁴³ wireless communication in programmable environments,^44,45 and even analog wave-based computing.⁴⁶

The designed programmable metasurface consists of 32 × 24 meta-atoms operating around 2.4 GHz, as shown in Figure S1, in which the meta-atom with size of 54 × 54 mm is detailed. The designed meta-atom is composed of two substrate layers: the top layer is F4B with a relative permittivity of 2.55 and loss tangent of 0.0019; the bottom layer is FR4 with dimensions of 0.54 × 0.54 mm². The top square metal patch of size 0.37 × 0.37 mm² contains a PIN diode (SMP1345-079LF) to control the EM reflection phase of the meta-atom. In addition, a Murata LQW04AN10NH00 inductor with inductance of 33 nH is used to achieve good isolation between the radiofrequency and direct current signals. In our design, the entire programmable metasurface is composed of 3 × 3 metasurface panels, and each panel is composed of 8 × 8 electronically controllable digital meta-atoms. Each metasurface panel is equipped with eight 8-bit shift registers (SN74LV595APW), and eight PIN diodes are sequentially controlled. The adopted clock (CLK) rate is 50 MHz, and the ideal switching time of the PIN diodes is 10 μs. In our specific implementation, the switching time of the coding pattern of the metasurface is set to 20 μs; thus, the time of data acquisition is on the order of M × 20 μs, where M is the total number of the coding patterns.

Model of the m-ANN

Rather than attempting to write down an analytical forward model of the measurement process as done by del Hougne et al.,²² we opt for learning a forward model, m-ANN, that automatically accounts for metasurface fabrication inaccuracies and stray reflections. Note that this approach could also readily be applied to alternative hardware capable of generating programmable scene illuminations such as dynamic metasurface antennas⁴⁷ or even traditional antenna arrays.⁴⁸ Unlike conventional end-to-end deep ANNs that have two ports, our m-ANN has three ports: one inputs the latent variable $\mathit{x}$ of the probed scene (in our work an image or a gesture class), one inputs the metasurface coding pattern $\mathcal{C}$, and the third one outputs the raw measurement $\mathit{y}$ (in our work the raw microwave data), as illustrated in Figure 1. From a deterministic standpoint, we can describe the three-port m-ANN with a pair of coupled nonlinear equations:

$$\mathit{y}=\mathit{f}\left(\mathit{x};{\mathcal{W}}_{\mathcal{C}}\right)+\mathit{n}$$ (Equation 2)

$$\text{and}{\mathcal{W}}_{\mathcal{C}}=\mathit{g}\left(\mathcal{C};\mathbf{\Theta }\right)+\mathit{N}$$ (Equation 3)

The variables $\mathit{n}$ and $\mathit{N}$ in Equations 2 and 3 represent the modeling errors, and their entries are considered to be independent identically distributed complex-valued Gaussian random numbers. In Equation 2, ${\mathcal{W}}_{\mathcal{C}}$ encapsulates all learnable weights of an end-to-end ANN relating the input $\mathit{x}$ to the desired measurement $\mathit{y}$. ${\mathcal{W}}_{\mathcal{C}}$ imposed with the subscript $\mathcal{C}$ highlights the fundamental fact that these trainable network weights depend on the coding patterns of metasurface $\mathcal{C}$ through Equation 3. In our implementation, these two nonlinear equations, i.e., $\mathit{f}$ and $\mathit{g}$, are modeled with a deep convolutional neural network (CNN) with trainable weights ${\mathcal{W}}_{\mathcal{C}}$ and $\mathbf{\Theta }$, respectively. In this work, we explore the deep residual CNN architectures developed by Li et al.³⁷ but with eight layers for $\mathit{f}$ and three layers for $\mathit{g}$. Both ${\mathcal{W}}_{\mathcal{C}}$ and $\mathbf{\Theta }$ can be readily learned with a standard supervised-learning procedure from triplet training samples $\left\{{\mathit{x}}^{\left(i\right)},{\mathcal{C}}^{\left(i\right)},{\mathit{y}}^{\left(i\right)},i=\mathrm{1,2},\dots \right\}$, where the superscript denotes the index of training samples. More details can be found in Note S4.

Training of m-ANN and r-ANN

The training of the complex-valued weights of m-ANN and r-ANN is performed using the ADAM optimization method.⁴⁹ In addition, we take the deep residual CNN architectures developed by Li et al.³² for the r-ANN. The complex-valued weights are initialized by random weights with a zero-mean Gaussian distribution of standard deviation 10⁻³. The training is performed on a workstation with an Intel Xeon E5-1620v2 central processing unit, NVIDIA GeForce GTX 1080Ti, and 128 GB access memory. The ML platform Tensor Flow⁵⁰ is used to design and train the networks in the learned EM sensing system. It will take about 267 h to train the whole learnable sensing pipeline including the m-ANN and r-ANN. Once the r-ANN is well trained, its calculation costs less than 0.6 ms.

Configuration of Proof-of-Concept Sensing System

The experimental setup, sketched in Figure 1A, consists of a transmitting (TX) horn antenna, a receiving (RX) horn antenna, a large-aperture programmable metasurface, and a vector network analyzer (VNA; Agilent E5071C). The two horn antennas are connected to two ports of the VNA via two 4-m-long 50-Ω coaxial cables, and the VNA is used to acquire the response data by measuring transmission coefficients (S₂₁). To suppress the measurement noise level, the average number and filtering bandwidth of the VNA are set to 10 and 10 kHz, respectively. More details can be found in Note S1.

Published: April 10, 2020