Intrinsically disordered regions of the DNA-binding domain of human FoxP1 facilitate domain swapping

Abstract

Forkhead box P (FoxP) proteins are unique transcription factors that spatiotemporally regulate gene expression by tethering two chromosome loci together via functional domain-swapped dimers formed through their DNA-binding domains. Further, the differential kinetics on this dimerization mechanism underlie an intricate gene regulation network at physiological conditions. Nonetheless, poor understanding of the structural dynamics and steps of the association process impedes to link the functional domain swapping to human-associated diseases. Here, we have characterized the DNA-binding domain of human FoxP1 by integrating single-molecule Förster Resonance Energy Transfer (FRET) and Hydrogen-Deuterium Exchange coupled with Mass Spectrometry (HDXMS) data with Molecular Dynamics (MD) simulations. Our results confirm the formation of a previously postulated domain-swapped (DS) FoxP1 dimer in solution and reveal the presence of highly populated, heterogeneous, and locally disordered dimeric intermediates along the dimer dissociation pathway. The unique features of FoxP1 provide a glimpse of how intrinsically disordered regions can facilitate domain swapping oligomerization and other tightly regulated association mechanisms relevant in biological processes.

Introduction

Regulation of gene expression is a paramount pleiotropic process in life, where transcriptional factors are essential in maintaining cellular homeostasis. In humans, the forkhead box (Fox) family of transcription factors play crucial regulatory roles in embryogenesis, development, and cancer, and their biological relevance have been studied in great detail^1-3.

It has been observed that several FoxP mutations that lead to disease alter the dimerization of their DNA-binding (forkhead) domain via three-dimensional domain swapping (3D-DS)⁴ process, rather than altering protein-DNA interactions directly. This mechanism, a protein-protein association process that is unique to FoxP members^5-7, involves the exchange of identical structural segments between two monomers to form an intertwined dimer (Figure 1a).

Figure 1. Structure and mechanism of domain swapping in FoxP proteins.

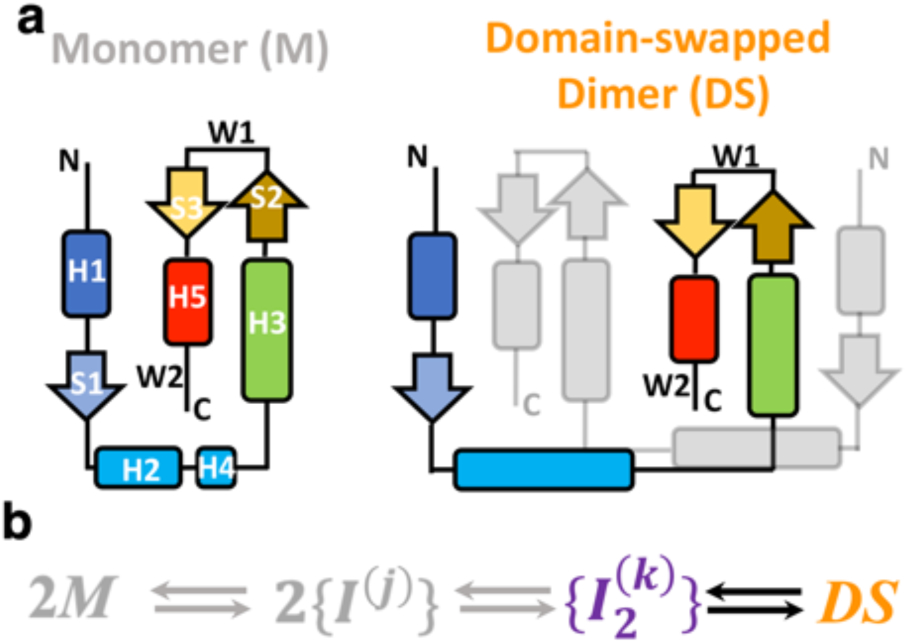
a) Topology of the monomer and domain-swapped dimer (DS) of FoxP proteins. Secondary structure elements are represented with different colors in order to clarify the topological changes between monomer and dimer. Helices H2 and H4 in the dimer are fused in the dimer. b) Kinetic scheme highlighting the inferred association/dissociation steps. According to previous studies, the dimerization of FoxP proteins from native monomers (M) proceeds toward the formation of monomeric intermediates ({I^(j)) that must adopt different conformations, constituting observed ensembles of states. In this scenario, the adoption of the DS could be promoted by the formation of dimeric and heterogeneous intermediate ensembles ({I₂^(k)}).

In contrast to most proteins that associate via 3D-DS, dimerization of FoxP is favored under physiological conditions^5-8 and does not require complete protein unfolding⁸. Using the forkhead domain of human FoxP1 (hereafter FoxP1), we previously showed a native-like monomeric intermediate state during its equilibrium unfolding (Figure 1b). In contrast, a monomeric FoxP1 mutant (A39P) showed no changes in secondary structure content or solvent-accessibility in the same conditions⁸. Although the biological relevance of FoxP1 has been experimentally demonstrated by enabling long-range DNA-DNA interactions within single or multiple chromosomes⁹, the molecular mechanism behind its regulatory function is mostly unknown. Hence, we investigate how functional 3D-DS dimers are formed from stable monomers in physiological conditions, and which events facilitate the 3D-DS-dependent gene regulation mechanism.

Although the sequence and structural factors enabling FoxP proteins to undergo 3D-DS have been described before^5-8, a consensus understanding of the association mechanism has not been achieved. This is primarily due to the experimental challenge of characterizing the local flexibility changes and dynamics responsible for 3D-DS (Figure 1b), with the timescales involved only accessible under high-resolution approaches^10-13. These spatiotemporal restrictions obscure the visualization of possible local unfolding events or even the presence of heterogeneous disordered ensembles ({I₂^(k)}) that could promote 3D-DS of FoxP1 in physiological conditions.

Building upon this evidence, the present work describes a detailed sequence of local unfolding events coupled to the intrinsic structural dynamics of FoxP1 that ultimately enable 3D-DS. We use a hybrid approach with high spatial and temporal resolution by combining single-molecule multiparameter fluorescence detection (smMFD), hydrogen-deuterium exchange mass spectrometry (HDXMS), and molecular dynamics (MD) simulations (Figure S1). We identify partially disordered intermediates of the dimeric FoxP1 in native conditions that are the result of intrinsic flexibility differences in the secondary structure elements. Moreover, we found that the local flexibility in the highly conserved helix H3 imposes an energetic barrier of ~1 kcal·mol⁻¹ in the adoption of the intermediate state; thus, stressing the relevance of local structural dynamics in the 3D-DS process. The partially-disordered intermediates described herein may be crucial in the highly diverse role of FoxP1 in homo and heterodimerization with members of the FoxP subfamily, and in accelerating the physical bridging of two DNA sequences using the “monkey bar” mechanism¹⁴.

Our findings represent the first description of critical structural features that explain the dimerization mechanism of FoxP and contribute to a general understanding of how domain swapping can be promoted under cellular conditions to perform their biological functions.

Results and Discussion

FoxP1 is a domain-swapped dimer with disordered regions

Previous equilibrium unfolding and HDXMS with FoxP1, under both native and mild-denaturing conditions, described a native-like monomeric intermediate whose local structural changes may facilitate association via 3D-DS⁸. Nevertheless, all characterized FoxP members undergo 3D-DS under physiological conditions^5-8; thus, suggesting that FoxP dimers must be conformationally heterogeneous to enable 3D-DS under these conditions. Given the lack of experimental evidence of the local structural dynamics of FoxP at high resolution, we analyzed the dimer of FoxP1 using single-molecule multiparameter fluorescence detection (smMFD)¹⁵.

Four different single-cysteine mutants of FoxP1 (L18C, N32C, S57C, and V78C; hereafter referred to as L, N, S, and V) were designed based on the differences in deuteron incorporation observed in our previous HDXMS measurements⁸ to probe local dynamics of different protein regions (Figure S2). To perform single-molecule experiments, we label each monomer containing a single cysteine substitution with Alexa488 (donor) or Alexa647 (acceptor). Then, we combined them to obtain ten different donor-acceptor pseudohomodimers (LL, NN, SS, VV, LN, LS, NS, SV, VN, and VL; Figure 2a) observable by Förster Resonance Energy Transfer (FRET) measurements¹⁶. Equilibrium anisotropy measurements in which each Alexa488-labelled mutant was titrated with wild-type FoxP1 indicated that none of these mutations altered the dimer dissociation constant when compared to the wild-type protein (Figure S3). Based on the determined K_D values (ranging from 0.2-0.6 μM), we used 0.5 μM of unlabeled FoxP1 in all our smMFD measurements under native conditions to maintain high dimeric populations in these experiments (40-80%).

Figure 2. Strategy to study dynamics of dimeric FoxP1 at the single-molecule level.

a) Cartoon representation summarizing the ten pseudohomodimers generated with single-cysteine mutants, showing the positions of the fluorescence acceptors (red) and donors (green). It is worth noting that acceptors and donors are located in different polypeptide chains. The secondary structure elements across the amino acid chain are shown to clarify the orientation of the single-cysteine mutants. b) Time-resolved fluorescence for pseudohomodimers of FoxP1 at single–molecule level was used to identify the limiting states. For all samples, two models, one or two lifetimes in addition to No FRET signal, was fitted. Residuals for the first and the second model are shown in olive and orange, respectively (Materials and Methods). c) MFD plots showing the distribution of events with specified ⟨τ_D(A)⟩_f and F_D/F_A for dimers SS and VV. The black and red lines indicate the static and dynamic FRET lines, respectively. Orange and purple lines indicate the DS and the dimeric intermediate ensemble ({I₂^(k)}) states described using the lifetime measurements. F_D/F_A values above the gray line represents states beyond the distance range practically resolvable by FRET. d) The relative population of each FRET state for each pseudohomodimer derived with PDA analysis. e) Correlation plot comparing modeled DS interdye distances with the FRET derived distances obtained by smMFD. f) Kinetic model generated from time-resolved decays and PDA analysis, where the expected DS is in equilibrium with a heterogenous dimeric intermediate ensemble ({I₂^(k)}). The presence of static -the unsolved and fast kinetic exchange- (represented as circular arrows) and the characterized dynamic exchange in the model represents the complexity of the reaction.

Dimers containing one donor and one acceptor fluorophores were exclusively selected via Pulsed Interleaved Excitation (PIE)¹⁷ (Materials and Methods). Additionally, we determined the number of limiting FRET distances and the population heterogeneity for all pseudohomodimers based on their corresponding donor fluorescence lifetime by performing time-resolved fluorescence analysis (Figure 2b and S4). Our results indicated that all samples require two distinct fluorescence lifetimes, τ₁ and τ₂ (Table S1) in addition to a No FRET (Donor Only) lifetime, to properly fit the fluorescence decays. This behavior indicates the presence of two limiting FRET states under physiological conditions.

Using a DS homology model of FoxP1 based on the crystal structure of FoxP2 as the template⁵, we determined the expected donor-acceptor distances by considering the predicted mean positions of the fluorophores tethered to the molecule. Next, we matched them against the limiting distances derived from fluorescence lifetime analysis (Table S1). With exception of the pseudohomodimers SS and LN, the expected distances for the DS dimer match with the limiting distance in the high FRET state. For SS and LN dimers, the matching distances correspond to the low FRET state (Table S1). Considering the states found by time-resolved fluorescence analysis and the PIE selection of dimer molecules, the simplest exchange model is between two different states: the DS and a dimeric intermediate, excluding the No FRET signal.

From our smMFD measurements, a typical multidimensional frequency histograms is built based on two FRET indicators: the burstwise fluorescence of donor over acceptor (F_D/F_A) and the burstwise average donor fluorescence lifetime in the presence of acceptor (⟨τ_D(A)⟩_f) (Materials and Methods). For dimeric FoxP1, ten different smMFD plots were obtained corresponding to the generated pseudohomodimers (Figure 2c and Figure S5). These FRET indicators reflect the changes in the inter-fluorophore distances and provide qualitative indication of dynamic averaging of FRET states due to dynamics occurring faster than the ms timescale (timescale passage through confocal volume). Further, use of both indicators provides robustness against experimental artifacts as they are sensitive to different subsets of potential artifacts^18,19 (Materials and Methods). For all pseudohomodimers, we identified a broad and highly populated low FRET burst distribution with F_D/F_A values between ~5-10 and ⟨τ_D(A)⟩_f between 3.5-4 ns. With the exception of LL, VL and VV dimers, this low FRET population connects to a less pronounced, high FRET population with F_D/F_A between ~0.2-1.5 and ⟨τ_D(A)⟩_f around 1-1.5 ns (Figure 2c and Figure S5). Moreover, these histograms are centered to the right of the static FRET line (black line in Figure 2c and S5, Table S2) where non-exchanging, static FRET populations would be centered, indicating possible dynamic exchange between conformational states with different FRET efficiencies¹⁸.

From our fluorophore lifetime determinations, we calculated dynamic FRET lines (red line in Figure 2c and S5, Table S3), corresponding to the populations undergoing transitions between the limiting FRET distances in the smMFD experiments during the observation time (1-5 milliseconds) (red line, Figure 1c and Figure S5). We observed different distribution patterns depending on the regions that were probed according to the fluorophore locations (Figure S2, Figure 1c, and Figure S5), reflecting differential dynamics according to specific segments mapped by single-cysteine mutations. Though all dimers show two limiting FRET states, the monodisperse distribution of the LF states for dimers LL, VV, and VL (Figure 2c and Figure S5) strongly suggests that the dynamic exchange between these states is biased towards the LF state.

Next, we used photon distribution analysis (PDA)²⁰ to determine the average donor-acceptor distance ⟨R_DA⟩_E for each sample, taking into account their full burstwise distributions. Using the time window analysis of the permanence of fluorescence in the confocal volume during the smMFD measurements, PDA allowed us to identify and quantify two FRET states in all pseudohomodimers despite the monodisperse population observed for LL, VV and VL in the MFD plots (Figure S6) and the high fraction of molecules showing no FRET signal (16-51% of total counts, Table S4), which could be attributed to inter-dye distances beyond 70 Å or molecules with temporarily inactive acceptor²¹ (Materials and Methods). Using the assumption of an equilibrium between high and low FRET states, PDA finds a low population (4-37% of total counts) with ⟨R_DA1⟩ varying between 32-52 Å, and a highly populated state (22-80% of total counts) with ⟨R_DA2⟩ between 53-70 Å (Figure 2d and Table S4). Also, we found that most ⟨R_DA1⟩ distances matched those determined from our DS homology model of FoxP1, showing a correlation of 0.70 (Figure 2e). Later, we improved the structural model by employing all-atom native-centric MD simulations, performed to obtain an atomic description of the dynamical behavior of dimeric FoxP1 within the timescales of the smMFD experiments (see Materials and Methods). We extracted a representative structure of the most populated ensemble under native conditions, obtaining a correlation of 0.91 for the simulation representative and experimental distances (Figure 2e).

Although we successfully found a kinetic model that best fits the distribution considering the exchange between the high and low FRET states (Figure 1c and Table S4), the results obtained from PDA also suggests a high degree of temporal and structural heterogeneity in all samples. Of all pseudohomodimers inspected by smMFD, SS retains most of the DS state (37% of total counts), in stark contrast to VV, whose DS fraction is only 4% (Table S4). However, the DS configuration is differentially conserved in all pseudohomodimers (Figure 2d), indicating large variations in flexibility among the protein regions labelled for each dimer. Additionally, both time-resolved fluorescence (Table S1) and PDA found a large “No FRET” population that could correspond to an even more extended configuration that cannot be adequately probed by the FRET pair used in this work. Moreover, PDA was satisfactorily fitted only when assuming that a fraction of the limiting states populations shows “static” behavior or where the exchange rates are significantly faster than milliseconds. This behavior complements the dynamics characterized via PDA (Materials and Methods), showing transitions at similar scales to the observation time window (Table S4). Although we were only able to quantify overall transition rates for these slower exchanges^18-20, the presence of a large population of No FRET, and the structural and temporal differences between all these protein elements, indicate that the previously mentioned intermediate is likely a heterogenous ensemble instead of a single, specific configuration (Figure 2f; Materials and Methods: Kinetic models).

Finally, we calculated the average hydrodynamic radius (R_h) of dimeric FoxP1 to obtain an average behavior of FoxP1 despite the heterogeneity of the intermediate ensemble and the low population of the DS state. This was calculated in the assayed conditions via fluorescence correlation spectroscopy (FCS), obtaining an average R_h of ~24 Å (Figure S7) that is in agreement with previous ensemble measurements⁸. Altogether, these results validate that the dimeric FoxP1 is effectively DS, but also, it dynamically exchanges with an extended and dimeric ensemble ({I₂^(k)}) that, in spite of presenting localized order-disorder transitions and high heterogeneity, exhibits a hydrodynamic radius of a well-folded native dimer.

Linking the timescales of order-disorder transitions and domain swapping in FoxP1

The reaction rate constants of the interconversion between the DS dimer and the heterogeneous ensemble as determined via PDA were estimated in a range of ~0.07 ms⁻¹ (slow) to ~2.7 ms⁻¹ (fast) (Table S4). Additionally, previously identified flexible regions of FoxP1⁸ show a higher ratio between the reaction rate constants from the DS to the {I₂^(k)} (k_DS→I) and vice versa (k_I→DS), corroborating the differences in structural flexibility throughout the dimer and accounting for the higher population of the observed intermediate ensemble. However, the static/dynamic limiting states equilibrium approach strongly suggests that additional fast time scales are needed to satisfy the complexity of the dynamics of dimeric FoxP1.

To conciliate the timescales of the 3D-DS process of FoxP1²² with the order-disorder transitions ascertained by smMFD, we performed a kinetic analysis across timescales ranging from nanoseconds to minutes using both single-molecule FRET-FCS (smFRET-FCS)²³ and ensemble HDXMS²⁴. In smFRET-FCS, the correlation of a fluorescence signal can be analyzed across a broad timescale from ns to ms from the sequential sampling of individual molecules, instead of traditional FCS in which multiple molecules are always present in the observation volume. smFRET-FCS uses the data stream of individual molecules whose fluctuations in FRET indicate changes in conformation in these timescales^23,25. In the case of HDXMS, local conformational dynamics within the second to minutes timescale for a given protein ensemble are ascertained by deuteron incorporation kinetics of peptides derived from pepsin digestion²⁴.

For smFRET-FCS measurements, we focused our investigation on the cross-correlation signal between the donor (green channel) and the acceptor fluorescence (red channel) under donor excitation, although a global fit of the auto- and cross-correlation was performed. The characteristic timescales over which the correlation between these signals decay correspond to the various processes which lead to fluctuations in the fluorescence signal. We first obtained the dye-dependent photophysical contribution terms (<10⁻² ms), such as transitions to non-fluorescent dark states, by analysis of the red and green autocorrelations. Next, we analyzed the cross-correlation information for all our pseudohomodimers (Materials and Methods). The analysis shows that most samples contain prominent cross-correlation terms in the μs range, as well as another term at much longer timescales (>1 ms) (Table S5, Figure S8). Considering both smMFD and smFRET-FCS results together (as the analyses are performed with the same raw data), the presence of two or more distinct transition rates spread across different orders of magnitude corroborates a complex model suggesting a kinetic scheme with at least three different FRET states or ensembles (Materials and Methods: Kinetic models).

To determine if we observe this highly dynamic behavior in ensemble conditions at longer time scales, we performed HDXMS to determine deuteron incorporation extents and kinetics over local regions of FoxP1. Once the exchange reactions under conditions that favor the native DS dimer or monomer were completed (Materials and Methods), all peptides generated by pepsin digestion of FoxP1 (Figure S9) were analyzed. Deuteron exchange reactions were allowed between 0.5-6 min to observe flexible amides, and the resulting deuteron incorporations were fitted to single or double exponential models to describe the exchange rates (k_HDX)^26,27 (Table S6). While the average deuteron incorporation of the whole protein is ~35%, peptides containing β strands S2-3 and helix H5 show the highest extents of deuteration (50-60%). In contrast, helices H2 and H3 show the lowest extents (0-20%, Figure S10). These results suggest extensive structural flexibility for the S2-S3 and H5 and reduced flexibility for H2-H3. These observations are consistent with the differences in kinetic rates observed between these regions by smFRET-FCS (Table S6).

Kinetic information about deuteron incorporation showed that amides from most peptides exhibit a single exponential behavior, with exchanging rates that fall in the range of 1.5-8.5 min⁻¹. In contrast, peptides covering regions comprising helix H1 and β strand S1 (H1-S1, residues 13-33) show an additional phase with amides having slower exchange rates between 0.06-0.5 min⁻¹ (Table S6). Also, in this aspect, we do not observe significant differences between dimer and monomer, besides the faster deuteration of amides in peptides covering helices H4-H3 in the monomer (Table S6), which is explained by the rearrangement of H2-H4 into a single elongated helix with an extra turn in the DS dimer^5,6. Thus, the biphasic behavior observed for H1-S1 region suggests that this region could be prone to major conformational changes upon dimerization or unfolding. Compared with unfolded elements (k_HDX > 100 min⁻¹)²⁸ and amides typically located in stable regions of secondary elements (k_HDX <1·10⁻⁵ min⁻¹)^29-31, all regions of FoxP1 can be described as having high or intermediate flexibility^29-31, strongly suggesting the presence of locally-fluctuating elements under native conditions.

Altogether, these results are informative about the dynamic behavior and timescales of different regions of the FoxP1 dimer and suggest that the local order-disorder transitions ascertained by smMFD and smFRET-FCS underlie the behavior observed for the domain-swapped dimer of FoxP1 in ensemble conditions.

Low energetical barriers characterize the local unfolding of dimeric FoxP1

To this point, we have described the local structural dynamics of dimeric FoxP1 at the ensemble and single-molecule level, observing a complex order-disorder behavior between the known DS and an extended dimeric intermediate ensemble. Based on its slow transition rates towards the {I₂^(k)} (k_DS→I 0.07 ms⁻¹; Table S4), its highly populated DS state (37%; Table S4), and its low deuteration extent and kinetics (20% deuteration, k_HDX ~1 min⁻¹; Table S6), helix H3 (probed by the corresponding pseudohomodimer SS in smMFD experiments) is one of the most stable regions in the FoxP1 dimer, and should indicate the largest energy barrier to the local unfolding.

To further quantify energetical differences between more flexible and more stable regions of FoxP1 along the dissociation of the DS dimer, we study the SS (helix H3) pseudohomodimer under conditions that favor its dissociation up to 2 M of the denaturant GdmCl⁸. For comparison, we used the VV pseudohomodimer, in which both fluorophores are attached to a highly flexible element according to both smMFD and HDXMS (Table S4 and S6).

Although 2 M of the denaturant GdmCl favors the monomeric intermediate⁸, we use PIE selection to capture only dimeric molecules despite their expected low abundance under these conditions (Figure S11, Materials and Methods). From these measurements, we again used PDA to determine the GdmCl-dependent changes in the population of DS and {I₂^(k)}, in the “dynamic population”, in the k_DS→I rate and in the free energy difference of this transition (Figure 3). We also used FCS to determine the change in R_h in comparison with ensemble measurements⁸.

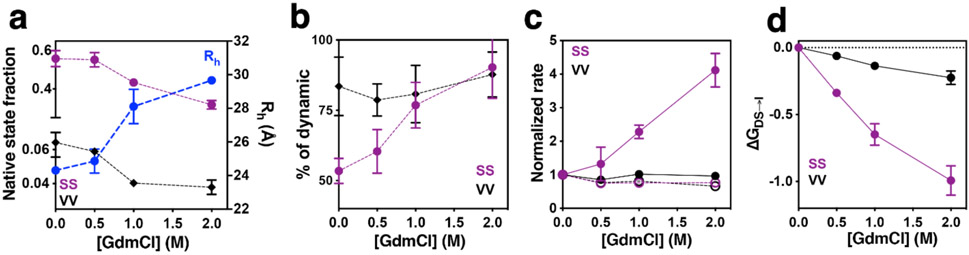
Figure 3. Analysis of dimers SS and VV in the presence of different GdmCl concentrations.

a) Changes in the DS dimer in SS (purple) and VV (black) dimers, and changes in averaged R_h as a function of the denaturant concentration (blue). The native fraction was normalized by excluding No FRET counts. b) Quantification of the dynamic population of the SS (purple) and VV (black) dimers as a function of the denaturant concentration. c) Quantification of rates from DS to intermediate (k_DS→I, continuous lines) and vice versa (k_I→DS, dashed lines) for SS (purple) and VV (black) dimers. Values were normalized using rates obtained in native conditions to highlight the changes. d) Differences in free energy change of the DS to intermediate transition using native conditions as reference values. Free energy values are calculated as kcal·mol⁻¹.

As seen in Figure 3, both SS and VV dimers, although starting from strongly different native state fractions, alter their behavior in a GdmCl-dependent fashion, showing a ~50% (SS) and ~40% (VV) decrease in the DS population upon increasing denaturant concentrations respect their initial values (Figure 3a). Also, the average R_h increases from 24 to 29 Å at 2 M GdmCl, a significant expansion of the protein due to the chemical perturbation that is consistent with previous ensemble measurements (R_h ~32 Å)⁸. Additionally, we analyzed the relative “static” and “dynamic” populations that we identified by PDA (Figure 3b), showing that dynamic behavior of the protein increases mostly in SS dimer, reaching a dynamic fraction of ~90% at 2 M of denaturant, similar to the VV dimer. This result may suggest that (i) specific regions of the protein with high stability are maintained in order to impede complete dissociation; (ii) there is an increase of the population exhibiting fast kinetic exchange unsolved via PDA, or (iii) a combination of these previous suggestions. Interestingly, only the k_DS→I rate increased as a function of the GdmCl concentration, while the kinetics of the reverse transition were unaffected (Figure 3c). Using the rate constants to calculate the difference in free energy of this conformational transition (ΔΔG_DS⇌I) as a function of denaturant concentration, we determined that the transition from the DS to the {I₂^(k)} is favored by ~1 kcal·mol⁻¹ at 2 M GdmCl. Although this transition exhibits a relatively low energetical barrier, it is five times higher than the corresponding value obtained for the VV dimer (Figure 3d). These results show that the denaturant accelerates reaching of the locally unfolded dimeric ensemble ({I₂^(k)}), lowering the energy barrier for more stable elements in the protein.

To further understand how these local order-disorder transitions enable dimer dissociation, we performed HDXMS experiments under conditions that favor the accumulation of the monomeric native-like intermediate. While there were no significant changes in the exchange rates of exchangeable amides (Table S6) when comparing 2M of GdmCl with native monomer or dimer. We observed a significant increase in the number of exchangeable amides with intermediate rates of exchange throughout the whole protein (Table S6), with the most considerable effects posited on regions H1-S1, H4-H3 and S2-S3 (Figure S12), but additionally, the increase in the number of fast-exchanging amides in helices H4-H3 and helix H2 when compared mostly with the dimer, indicating a structural perturbation of these 3D-DS enabling regions (Figure S12). These results indicate that a group of amides that are protected under native conditions are now available for exchange (Figure S12), which we interpret as an increase in the flexibility of these regions upon reaching the intermediate state.

Our data presented here provide quantitative and robust evidence that high flexibility of specific regions is critical in promoting dynamical transitions between the DS dimer and the dimeric intermediate ensemble of FoxP1, which in turn leads to dissociation of FoxP1 into a monomeric intermediate captured in ensemble experiments. Moreover, the low energetic barrier for this process must be responsible for the characteristic kinetics of 3D-DS in FoxP proteins under physiological conditions.

Atomistic description of the conformational ensembles in dimeric FoxP1

In order to better understand the mechanism of protein folding and dimerization of FoxP1 and to provide compelling insights into the structural conformation of the highly disordered and dimeric intermediate ensemble observed by smMFD, we performed all-atom MD simulations using structure-based models (SBM)³². These models, which rely on a simplified energy function based on the native contacts of a given protein structure and rooted in the energy landscape theory of protein folding³³, have been successfully used in the efficient exploration of large-scale conformational transitions^34,35 and folding pathways^36,37 in a variety of protein models.

We performed MD simulations at several temperatures above and below the folding temperature (T_F) of the dimer of FoxP1, sampling several folding-unfolding transitions (Figure S13). Given the concentration dependence of domain swapping²², we control the effective protein concentration of the simulation by imposing a harmonic restraint between the centers of mass of each monomer and vary the concentration by employing four different harmonic potential strengths (Figure S14). Folding changes throughout the simulations were analyzed using the hydrodynamic radius of the dimer, the native contacts, and the root-mean-square deviation (rmsd) of the monomer and the dimer. Among them, we chose the monomeric (Q_M) and dimeric (Q_D) native contacts as the preferred reaction coordinates due to their ability to better discriminate between different basins along the DS folding pathway of FoxP1 (Figure S13).

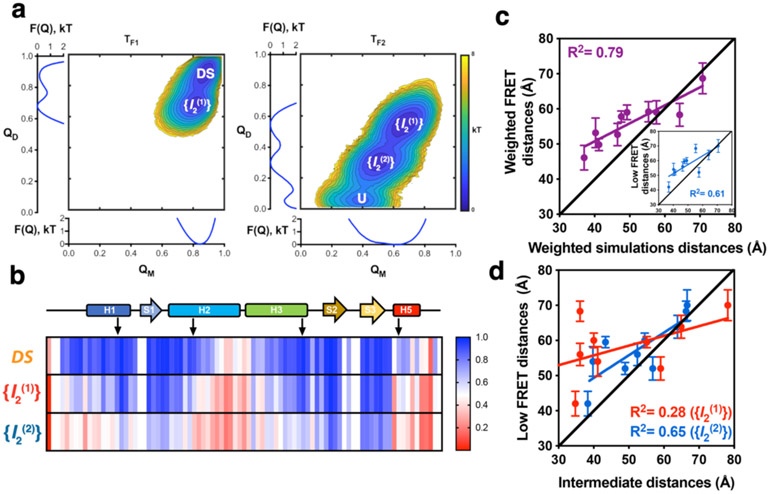
Employing the weighted histogram analysis method (WHAM)³⁸ along with the energy and structural state data from different temperatures, using the reaction coordinates Q_M and Q_D, we determined the folding landscape of dimeric FoxP1 (Figure 4a). The analysis of the changes in specific heat showed two clear transitions: the first transition at T = 1.09 (T_F1) and the second one around T = 1.18 (T_F2) (Figure S14 and Movies S1-S3). The two-dimensional landscape at T_F1 using Q_M and Q_D as reaction coordinates shows two states: the DS and a representative ensemble dimer with an extended and partially unfolded hinge ({I₂⁽¹⁾}). In contrast, the two-dimensional landscape at T_F2 shows three well-defined states: the intermediate ensemble {I₂⁽¹⁾}, an asymmetric dimeric ensemble in which only one forkhead domain stabilized by both chains is folded whereas the other one is unfolded ({I₂⁽²⁾}), and the unfolded state (U).

Figure 4. Structure-based MD simulations of FoxP1 dimer.

a) Folding free energy landscape of FoxP1 dimer, calculated from 1.6E8 timestep simulations in different temperature conditions, where T_F1 and T_F2 are the two peaks of the changes in specific heat as a function of temperature observed for FoxP1. Two clearly defined basins, DS and the intermediate state ({I₂⁽¹⁾}) can be seen at T = T_F1. In contrast, three states were observed at T = T_F2, corresponding to {I₂⁽¹⁾}, a second intermediate ensemble state ({I₂⁽²⁾}), and the unfolded state (U). b) Changes in the per-residue probabilities of intramolecular native contact formation (from 0 to 1) of FoxP1 in the DS conformation and in the described dimeric intermediate ensembles {I₂⁽¹⁾} and {I₂⁽²⁾}. c) Correlation between the weighted donor-acceptor distances determined via PDA and the weighted theoretical FRET distances estimated based on MD simulations. Inset: correlation between the low FRET distances determined by PDA and the weighted theoretical FRET distances estimated based on the MD simulations. d) Correlation between low FRET distances derived from PDA and the representative structure of {I₂⁽¹⁾} and {I₂⁽²⁾}.

Using Q_D and Q_M values together to identify the structural states sampled by FoxP1 throughout the simulations, multiple transitions between native, intermediate and unfolded populations are observed in trajectories at the previously determined T_F, showing that the transitions occur sequentially from DS⇄{I₂⁽¹⁾} followed by {I₂⁽¹⁾}⇄{I₂⁽²⁾} (Figure S13, Materials and Methods: Kinetic models). Increasing the effective protein concentration increases the population of {I₂⁽¹⁾} and {I₂⁽²⁾} and displaces T_F2 toward higher temperatures without affecting T_F1 (Figures S14 and S15). These results suggest that {I₂⁽²⁾} precludes the direct transition from {I₂⁽¹⁾} to the unfolded state upon increasing the protein concentration. Altogether, these simulations determine that the folding pathway of dimeric FoxP1 is {I₂⁽²⁾}⇄{I₂⁽¹⁾}⇄ DS.

We extracted the configurations corresponding to DS, {I₂⁽¹⁾} and {I₂⁽²⁾} from the simulations at T_F1 and T_F2, to determine the per-residue contact probability for intramolecular native interactions (Figure 4b). We also determined the R_h of the most representative structure for DS at T_F1, and for {I₂⁽¹⁾} and {I₂⁽²⁾} at T_F2, respectively, using rmsd-based clustering (Figure S16). These analyses show that most of the contacts stabilizing H5 and the C-terminal half of H2 are lost upon reaching the {I₂⁽¹⁾} ensemble, whereas H3 is only partially destabilized. Full destabilization of H3, as well as H1-S1, is achieved in the {I₂⁽²⁾} ensemble. These results are in good agreement with the scarce structural and energetical changes for the VV pseudohomodimer and the significant changes observed for the SS pseudohomodimer in smMFD experiments upon increasing concentrations of denaturant (Figure 3), which correspond to the regions H5 and H3, respectively. Moreover, the R_h of the most representative structure of the {I₂⁽²⁾} ensemble is consistent with the experimental R_h determined for FoxP1 at 2 M GdmCl (Figure S16).

To determine if the structure of the DS state and {I₂⁽¹⁾} and {I₂⁽²⁾} ensembles were compatible with the distances observed in smMFD experiments, we determine the residue-residue distances from the most representative structure for DS, {I₂⁽¹⁾} and {I₂⁽²⁾}. The structural cluster of the DS state is fully compatible with the donor-acceptor distances observed by smMFD in the high FRET state (Figure 2e). Interestingly, there is a high correlation between weighted experimental distances derived from PDA (excluding No FRET) and weighted distances from simulations (excluding the U state) (Figure 4c), although good correlation was also found between the low FRET state and the weighted distances from simulations (Figure 4c inset), suggesting that in both approaches, the non-native conformations are predominant in the dimeric FoxP1, but are not enough to explain by themselves the experimental results. Additionally, we correlated the low FRET distances derived from PDA with those determined in the intermediate basins from simulations, finding a better correlation with the {I₂⁽²⁾} ensemble (Figure 4d). These results provide a structural description of the observed low FRET intermediate ({I₂⁽²⁾}), and also suggest the presence of a dimeric intermediate with a higher number of native contacts ({I₂⁽¹⁾}) that is not directly observed by smMFD. Even though PDA was able to identify two FRET states, which match with the atomistically described DS and at least one possible intermediate structure from the MD simulations, there is also evidence from both smFRET-FCS and PDA that a more complex kinetic model, including additional dimeric intermediates, are necessary to fully satisfy all observed data. However, there are current significant limitations on the ability to unambiguously identify distinct states in a highly heterogeneous mixture from the experimental observables.

Discussion: Structural dynamics of dimeric FoxP1

We determined the structure and dynamics for the DS FoxP1 in solution by integrating experimental long-range inter-monomeric distances, local structural dynamics and computational simulations of protein folding. This hybrid approach has been successfully used to resolve fast exchanging configurations in multidomain proteins³⁹ and dynamic processes occurring in ternary complexes⁴⁰, highlighting the robustness of this technique in resolving multiple structural configurations with high accuracy. Our results demonstrate that dimeric FoxP1 maintains a domain-swapped structure but exchanges between a compact conformation and at least one open and locally disordered ensemble, which allows for unique kinetic properties than can be used for gene regulation.

The extended structure seen in smMFD is consistent with one of the two well-defined intermediate ensembles sampled through structure-based MD simulations, which exhibit high disorder on either the hinge loop ({I₂⁽¹⁾}) or on a complete subunit ({I₂⁽²⁾}) (Figure 4c). The simulation distances of the {I₂⁽²⁾} correlate better with the experimentally derived distances from the low FRET ensemble. Moreover, we characterize “slow” (ms temporal regime) exchange between the DS state and local disordered Intermediates by using PDA (Table S4) and additionally we provide evidence of “fast” (μs temporal regime) exchange. This is later corroborated by smFRET-FCS (Figure S8 and Table S5), identifying regions that are flexible and dynamic, as previously identified via HDXMS^8,12. However, HDXMS reports on the structural changes from seconds to minutes (Table S6), suggesting that broad timescales in the dynamics of this protein exist alongside the reported fast timescales.

When comparing the hydrodynamic radii using parameters derived from FCS in 0 M (native) and 2 M of denaturant (Figure S16) in which dimer dissociation is largely favored, we observe that i) the experimental R_h in native conditions could be an weighted representation of the DS and the intermediate ensemble ({I₂⁽¹⁾}, considering the complexity and temporality described with smFRET-FCS and MD simulation, and ii) the significant increase in the average R_h in the presence of denaturant reflect the increase population fraction of the ({I₂⁽²⁾}). We conclude that the mild-denaturing conditions maintain local dynamic conformational behavior and could favor the accumulation of the ({I₂⁽²⁾}) intermediate as observed in R_h changes observed in our previous report⁸.

Several biophysical studies performed with FoxO3a indicate broad disordered regions in the polypeptide chain allowing for conformational heterogeneity that impacts its biological function^41,42. Our data on FoxP1 similarly suggests the presence of regions of high disorder within a canonically well-folded forkhead domain. Although a quantitative assignment of the distances of a specific intermediate is limited for the highly heterogeneous ensemble of conformations, this hybrid single-molecule/MD simulations approach elucidates a general pathway towards the formation of the DS state through these intrinsically disordered intermediates (Figure 5a). This sequential pathway can be justified by the intrinsically low energetic barrier between native and intermediate states that was observed experimentally and computationally (Figure 5b) in the presence of varying denaturant concentrations (or temperature increase, in the case of MD simulations). However, our experimental limitations obscure the presence of other intermediates that may also participate in this pathway, suggesting that in the 3D-DS the landscape of FoxP1 is in fact more complex.

Figure 5. Integrative structural dynamic characterization of the native and locally disordered intermediate ensembles in the domain swapping pathway of FoxP1.

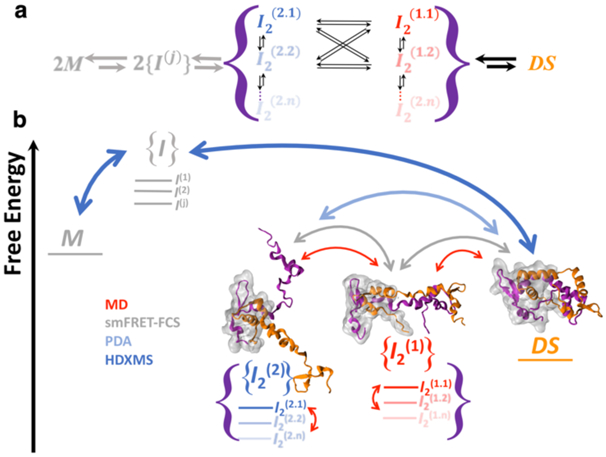
a) Cartoon schematic of the domain swapping pathway of FoxP1, showing the connectivity of the different sub-ensemble conformations that account for the {I₂⁽¹⁾} and {I₂⁽²⁾} described in this work. b) Integrative information from the approaches used in this work to describe the energy landscape of the two dimeric intermediate ensembles. Our results highlight the linearity in the transition from the DS structure to the {I₂⁽²⁾}, although we cannot describe the sub-ensemble connectivity. In the structures, one subunit is highlighted in gray to differentiate the changes in each subunit.

The local disorder to order transitions described in this work suggest a functional versatility of FoxP1 and possibly of all FoxP family members, which could be functionally relevant in the adoption of previously described FoxP heterodimers in vivo^43,44. Such a mechanism would explain the complex regulatory network in this subfamily and also the binding of different DNA sequences by different locally disordered intermediates. The sequence conservation among FoxP members (76-92%), which is not detrimental for the formation of domain-swapping contacts in other study models⁴⁵, implies that similar DS dimers may constitute a combinatorial approach to altering gene regulation through the formation of homo and heterodimers amongst FoxP family members.

The accumulation of an extended intermediate could also decrease the probability of aggregation and misfolding by promoting a dimeric pseudo-swapped dimer during the folding and association pathway. In line with this hypothesis, studies performed with α-synuclein^46,47, SOD1⁴⁸ and γ-crystallin⁴⁹ show the intimate relationship between the presence of stable and structurally heterogeneous conformations and the promotion of oligomeric species in the folding pathway, suggesting that topological constraints of this intermediate favor the transition to the proper conformation. Interestingly, this description highlights the strong relationship between this "disordered" pseudo-swapped dimer and the macroscopic kinetics and thermodynamic properties of FoxP proteins as observed previously^7,8,22; hence, corroborating –with high temporal and spatial resolution– that the 3D-DS mechanism of FoxP obeys local unfolding. Such a mechanism could be critical for screening distant chromosome domains and in parallel provide a path towards a stable DS structure (i.e. by the “monkey bar” mechanism) upon identification of targeted regions^14,50,51. Furthermore, the interplay between the effects of DNA binding on the local flexibility and protein dynamics suggest that protein-ligand interactions may stabilize the DS structure^14,50. This stabilization seems especially relevant when considering the low energetic barrier between the native and disordered intermediates of FoxP1, from which we can infer that locally-disordered elements in the dimeric intermediates may offer a more dynamic regulation mechanism of FoxP1 folding and function.

Materials and Methods

Protein expression and purification

A codon-optimized DNA sequence encoding the forkhead domain of human FoxP1 (positions 462 to 547 of the full-length protein) and its mutants were cloned into a modified pET-28a vector, containing a His₆-tag, a TEV cleavage site, and an S-tag sequence in the 5’ end of the gene. Amino acid residues are numbered according to the sequence numbering in the used structure of the forkhead domain of FoxP1 (PDB ID 2KIU). Plasmids containing the DNA sequence of FoxP1 were used to obtain the different mutants used in this work through PCR mutagenesis using the QuickChange Site-directed mutagenesis kit (Stratagene, La Jolla, CA, USA). Proteins were purified as described by Medina et al⁸ and dialyzed into a standard buffer (20 mM HEPES pH 7.8, 150 mM NaCl, 2mM β-mercaptoethanol) prior to each experiment, unless other buffers are specified.

Size exclusion chromatography (SEC)

We separated the monomeric and dimeric fractions of FoxP1 on a Water Breeze HPLC system (Waters Corporation, Milford, MA, USA) using a Superdex 75 10/30 column (GE Healthcare Biosciences, Pittsburgh, PA, USA) as described^7,8. Briefly, the column was equilibrated with 45 ml of mobile phase (standard buffer) at 25 °C before isolating the monomer or dimer. Each fraction was stored at ~1 °C on ice prior to the different experiments.

Hydrogen-deuterium exchange mass spectrometry (HDXMS)

HDXMS was performed using a Waters Synapt G2Si system with H/DX technology (Waters Corporation), as previously described^8,55. Briefly, 5 μL of protein solution (monomer or dimer), at an initial concentration of 11 μM, was allowed to exchange at 25 °C for 0-5 min in 55 μL of either deuterated standard buffer alone for native state conditions or supplemented with 2M of Guanidium chloride (GdmCl) for characterizing the domain-swapping intermediate states. Then, reactions were quenched for 2 min at 1 °C using an equal volume of a solution containing 2 M GdmCl, 1% formic acid, pH 2.66. The quenched samples were injected onto a custom-built column containing pepsin-agarose (Thermo Fischer Scientific, Rockford, IL), and the resulting peptic peptides were separated by analytical chromatography at ~1 °C within a mobile phase containing 0.1% formic acid using a gradient of 7-95% acetonitrile in 7 min. The analytes were electrosprayed into a Synapt G2-Si quadrupole time-of-flight (TOF) mass spectrometer (Waters Corporation). The mass spectrometer was set to Mobility-MS^E-ESI+ mode for initial peptide identification and to Mobility-TOF-ESI+ mode to collect H/DX data. The mass range was set to 200 - 2,000 (m/z), scanning every 0.4 s. Infusion and scanning every 30.0 s of leu-enkephalin (m/z = 556.277) was used for continuous lock mass correction. Peptides were identified, and MSMS fragments were scored using the PLGS 3.0 software (Waters Corporation). Peptides with a score ≥7 were selected for analysis if their mass accuracy was at least 3 ppm and were present in at least two independent runs. Deuterium uptake was determined by calculating the shift in the centroids of the mass envelopes for each peptide compared with the undeuterated controls, using the DynamX 3.0 software (Waters Corporation). The amount of deuteration was corrected for back-exchange (~34%) based on a full-deuteration control, using a peptide covering the unstructured, fully solvent-accessible S-tag region as a reporter.

The extent of hydrogen-deuterium exchange for each peptide was calculated according to equation 1:

$$\%\mathrm{D}=({\mathrm{D}}_{\mathrm{i}}∕{\mathrm{D}}_{\max })\times \cdot 100$$ (1)

Where D_i is the extent of deuterons incorporated, and D_max is the theoretical extent of deuterons incorporated for a full peptide. To calculate the exchange rate (k_HDX), we fitted the extent of exchange as a function of time of exposure to an exponential model that follows (eq. 2)

$$\%\mathrm{D}(t)={\sum }_i^n{\mathrm{A}}_{\mathrm{i}}\cdot (1-e^{-k\cdot t})$$ (2)

Where %D(t) is the maximum extent of exchange upon t time, A_i is the amplitude of the change in terms of % of deuterons incorporated. Deuterium exchange curves were fitted to a mono- or bi-exponential model, to describe the fast and intermediate exchange of amides.

Production of dye-labeled FoxP1 for ensemble and single-molecule fluorescence studies

We prepared FoxP1 constructs in which the native cysteine (Cys) residue (at position 61) was replaced by serine (C61S), and four single-cysteine mutants (L18C, N32C, S57C, and V78C) were synthesized to allow specific labeling with fluorescent dyes. Before labeling the proteins, all buffers were sterile filtered and degassed. FoxP1 was concentrated to 80-100 μM in buffer A (20 mM HEPES pH 7.8, 150 mM NaCl, 2 M GdmCl) with 0.5 mM of Tris (2-carboxyethyl) phosphine hydrochloride (TCEP). 2.5 mL of concentrated protein was loaded onto a PD10 column, and the protein was eluted with freshly degassed 3.5 ml of buffer A without TCEP. The eluted protein was labeled with the acceptor Alexa Fluor 647 maleimide fluorophore or donor Alexa Fluor 488 maleimide fluorophore (Invitrogen). In all cases, the labeling was performed with a 1:5 (protein: fluorophore) ratio. Finally, excess fluorophore was removed by gel-filtration chromatography. Labeled proteins were unfolded using 5 M GdmCl, and different combinations of donor-acceptor between mutants were made with 40 μM of each monomer and dialyzed against buffer A without GdmCl for 16 hrs at 4 °C. All dimers were incubated at 37 °C for 3 h in order to reach a monomer-dimer equilibrium prior to single-molecule analysis.

Anisotropy measurements

Anisotropy changes in the single-cysteine mutants were measured in a Jasco FP-8300 spectrofluorometer with polarized filters. Alexa 488-labeled proteins were separately assayed at a concentration of 100 nM, and increasing concentrations of unlabeled wild-type (wt) FoxP1 (0-3 μM) were added to obtain the dimeric complexes; L18C-wt, N32C-wt, S57C-wt, and V78C-wt. Proteins were incubated for 2 h at 37°C until no changes in final anisotropy were observed. The G factor was measured with Alexa 488 in buffer at 2 μM to calculate the correct anisotropy values. Binding curves were analyzed using a general saturation equation of protein-ligand experiments.

Single-molecule Multiparameter Fluorescence Detection (MFD)

MFD for confocal high-precision Förster Resonance Energy Transfer (hpFRET) studies of single-molecules was done using a 485 nm diode laser (LDH-D-C 485 PicoQuant, Germany, operating at 40 MHz, power at objective 110 μW) exciting freely diffusing labeled molecules that passed through a detection volume of the 60X, 1.2 NA collar (0.17) corrected Olympus objective. The emitted fluorescence signal was collected through the same objective and spatially filtered using a 70 μm pinhole to define the confocal detection volume. We used a new detection and data registration scheme to measure dead time-free species cross-correlation functions. The signal was divided into parallel and perpendicular components at two different colors ("green" and "red") through bandpass filters, HQ 520/35, and HQ 720/150, for green and red, respectively. A total of four photon-detectors are used, two for green (PMA 40 Hybrid, PicoQuant, Germany) and two for red channels (PMA 50 Hybrid, PicoQuant). A time-correlated single-photon counting (TCSPC) module 5 (HydraHarp 400, PicoQuant, Germany) with Time-Tagged Time-Resolved (TTTR) mode and 4 synchronized input channels were used for data registration. Single-molecule fluorescence was acquired as described in Ma et al. (2017)⁵⁶ and Yanez-Orozco et al. (2018)³⁹.

For smMFD measurement, samples were diluted in buffer (20 mM HEPES, pH 7.8, 150 mM NaCl, 2 mM DTT) to pM concentration in the presence of 500 nM of unlabeled protein, assuring ~ 1 burst per second. For long measurements, we used an oil immersion liquid with the refraction index of water (Immersol, Carl Zeiss Inc., Germany). NUNC chambers (Lab-Tek, Thermo Scientific, Germany) were used with 500 μL sample volume. Standard controls consisted of measuring water to determine the instrument response function (IRF), buffer for background subtraction, and the nM concentration of green and red standard dyes (Rhodamine110 and Rhodamine101) in water solutions for calibration of green and red channels, respectively. To calibrate the detection efficiencies, we used a mixed solution of double-labeled DNA oligonucleotides with known distance separation between donor and acceptor dyes and standard procedures previously benchmarked¹⁶.

Identification of individual bursts is done by comparing the inter-photon arrival time against background with a 2σ confidence with duration that, on average, approximates to the mean t_diff obtained via fluorescence correlation spectroscopy. Photons within identified bursts are shown as histograms and fit to obtain the florescence lifetime per burst (⟨τ_{D(A)}⟩_f) using a maximum likelihood estimator⁵⁷. Photon counts are corrected for proper quantification of intensity-based FRET indicators as the ratio of the corrected donor over acceptor fluorescence (F_D/F_A) (Eq. 3).

$$F_D=\frac{F_G}{g_G}=\frac{S_G-\langle B_G\rangle }{g_G}\text{and}{F}_A=\frac{F_R}{g_R}=\frac{S_R-\alpha F_G-\langle B_R\rangle }{g_R}$$ (3)

Here, S_G and S_R are the recorded counts in the green and red channel, respectively; g_G and g_R are the corresponding detection efficiencies for each detection channel; and ⟨B_G⟩ and ⟨B_R⟩ are the background counts. Burst are then filtered for selection of dimers that contain one monomer labeled with donor and the other labeled with an acceptor using the PIE stoichiometry of values between 0.3 < S_PIE < 0.7 ¹⁷. S_PIE considers the ratio of total fluorescence of donor and acceptor when excited via the donor excitation source, to the total fluorescence of both donor and acceptor by donor excitation, after the interleave direct acceptor excitation. This normalization assures that molecules that contain only donor fluorophores have S_PIE = 1, while molecules that contain only acceptor fluorophores will show an S_PIE = 0, and bursts containing one donor and one acceptor would be centered at S_PIE = 0.5. However, a molecule with proper 1:1 donor to acceptor stoichiometry may still fail to exhibit FRET due to several factors: i) the inter dye distance goes beyond what is detectable ⟨R_DA⟩_E > ~80 Å, and ii) acceptor blinking. In the latter case, the acceptor has not de-excited from a non-emitting state and thus cannot be excited through FRET, but it is present in the molecule appearing as a No-FRET molecule. In addition, we make sure that burst duration observed by the signal of the green channels during donor excitation (T_G∣D) and the signal in the red channels during acceptor excitation pulses (T_R∣A) are similar by the selection (−1 < T_G∣D − T_R∣A < 1) to reduce events that are marked by photophysical effects.

F_D/F_A, like FRET efficiency, reports on the process of energy transfer but without the need of other correction parameters that depend on the experimental settings, and thus is used for visualization purposes. In addition, a smMFD histogram including F_D/F_A provides a semi-quantitative understanding of FRET. Several guidelines are followed for interpreting this data, as follows: I) The No FRET population typically is found when ⟨τ_{D(A)}⟩_f ~ 4 ns and $\frac{F_D}{F_A}$ > 20, typically corresponding to long distances with high uncertainty, with ⟨R_DA⟩_E > 80 Å. II) High FRET populations are found when ⟨τ_{D(A)}⟩_f → 0 and $\frac{F_D}{F_A}$ → 0.III) For guidance, we use the static FRET line (black lines in all smMFD histograms), representing the ideal scenario of a rigid molecule for which no conformational exchange occurs and hence the FRET population lies along the static line. IV) Dynamic lines (shown in red in smMFD histograms) correspond to the path that a population in the two-dimensional histogram would follow if there was dynamic exchange between two states; thus, connecting two populations. The location and shape of the distribution (i.e. elongation) along the dynamic line depends on the equilibrium constant and time of exchange. Elongated populations along this line correspond to slower transition times between limiting states that approach the time of diffusion (t_R = $\frac{1}{k_f+k_r}\sim 1$ ms, where k_f and k_r are the forward and reverse reaction rate constants between two states). Therefore, bursts along the dynamic line are expected to have undergone a transition between two or more states and are not to be interpreted as maintaining a single state corresponding to the burst parameter. No significant bursts are expected between the static and dynamic lines unless an additional limiting state transition is required. V) Events that appear on the smMFD histograms correspond to either long lived states (t_R ≥ t_diff) or dynamically averaged states if exchange is faster that the diffusion time t_R ≤ t_diff.

Fluorescence analysis of smMFD experiments

smMFD experiments were analyzed using the suite of programs developed at Seidel’s laboratory¹⁵. To identify the number of configurations or FRET states within the observed population distributions in the smMFD histograms, we first generated sub-ensemble TCSPC¹⁵ histograms (fluorescence decay histograms) of the photons within selected FRET bursts and fit with single and multi-exponential decays having the general form of

$$F_{norm}(t)={\sum }_i^n{x}_i\text{exp}(t∕{\tau }_{DA}^{(i)}),$$ (4)

where x_i is i-th population fraction of the normalized fluorescence decay (F_norm(t)) and ${\tau }_{DA}^{(i)}$ are the identified fluorescence lifetimes of the DA sample for each i-th population. Based on the statistical analysis (see “statistical uncertainties and error analysis” section) two exponentials plus a population that shows No FRET were enough to model the fluorescence decays (Figure S3) as evaluated by the improvement in the figure of merit ${\chi }_r^2$ and visual inspection of the residuals and their correlations. Next, we used Probability Distribution Analysis (PDA)^19,58 to model the F_D/F_A distributions and identify mean FRET distances (⟨R_DA⟩_E) of the limiting states and their corresponding uncertainties. To properly account for the heterogeneity in the duration of bursts, bursts are split into equal time windows per burst with multiple time window sizes (Δt = 1, 3, and 6 ms)^58,59, and the FRET indicator F_D/F_A histogram is obtained for each time window size. We globally fit all time windows with different models that vary in increasing level of complexity and the best model is selected based on the global figure of merit ${\chi }_r^2$ and statistical uncertainties (see “statistical uncertainties and error analysis” section). A static model considering one and two states was not enough to fully describe the F_D/F_A histograms at these time windows (Figure S5). The selected models consider a population that showed No FRET. For details on the kinetic models used in each data analysis see “kinetic models” section. The distances derived from PDA are consistent with those identified using seTCPSC (Table S1).

With time window analysis, we were able to identify if a single static or two dynamic states better represented the experimental observables (Fig. S5). In-house written software used to perform the analysis can be downloaded from http://www.mpc.hhu.de/software.html and https://github.com/Fluorescence-Tools.

Single-molecule Fluorescence Correlation Spectroscopy (smFCS)

Single-molecule Fluorescence Correlation spectroscopy was accomplished by selecting the single-molecule bursts to differentiate the fluorescence photons from the DA-labeled pseudoheterodimer from background photons. Then this fluorescence species was auto and cross-correlated based on the detection spectral windows (Green, G, and Red R) to generate three Correlation curves ($G_{GG}^{(DA)}(t_c)$, $G_{RR}^{(DA)}(t_c)$, $G_{GR}^{(DA)}(t_c)$), where the subscripts correspond to the correlated spectral windows, and the superscript in parenthesis is the labeled species that is observed. These correspond to the color auto- and cross-correlation function of the FRET labeled samples at single-molecule resolution (smMFD-FCS). Additionally, the signal from the direct excitation of the acceptor, named AOnly, is shown as a reference. Details on the procedure can be found elsewhere²⁵.

To determine the R_h, all ten $G_{GG}^{(DA)}$(t_c) were globally fitted with the model function (eq. 5) that considers a 3-dimensional Gaussian confocal volume to identify the characteristic time of diffusion t_diff.

$$G(t_c)=\frac{1}{N}\left(\frac{1}{1+\frac{t}{t_{diff}}}\right)\sqrt{\left(\frac{1}{1+(\frac{\omega }{z}{)}^{{}^2}\frac{t}{t_{diff}\cdot z}}\right)}\left(1-\mid d\mid +\mid d\mid \text{exp}\left(-\frac{t}{t_{pho}}\right)\right)+B$$ (5)

Where N is the average number of particles in the confocal volume, ω and z are the axes for the geometrical volume, and $t_{diff}={}^{{\omega }^2}∕_{4D}$, where D is the characteristic diffusion constant. The diffusion constant can be related to the R_h following the Stokes-Einstein relationship ($D={}^{k_{B}T}∕_{6\eta \pi R_h}$). The ω² was obtained using our experimental t_diff and the determined D (4.7·10⁻⁶ cm²·s⁻¹) from Rhodamine 110 as a standard tracer. The t_pho term with amplitude ∣d∣ is meant to account for the contribution of dye photophysical effects to the correlation and was allowed to vary for individual curves. B is a standard offset baseline for the calculated correlations, typically taken as 1 but here allowed to vary near 1 to account for slight shifts in the baseline of the correlation curve.

The cross-correlated green(G)-red(R) signal [$G_{GR}^{(DA)}(t_c)$] was fitted to eq. 6

$$\begin{gathered} G_{GR}^{(DA)}(t_c)=\frac{1}{N}\left(\frac{1}{1+\frac{t}{t_{diff}}}\right)\sqrt{\left(\frac{1}{1+(\frac{\omega }{z}{)}^{{}^2}\frac{t}{t_{diff}\cdot z}}\right)}\left(1-\mid d\mid +\mid d\mid \text{exp}\left(-\frac{t}{t_{pho,D}}\right)\right)(1-\mid a\mid +\phantom{)} \\ \mid a\mid \text{exp}\phantom{(}\left(-\frac{t}{t_{pho,A}}\right))\left(1-\mid C\mid \sum \mid c_i\mid \text{exp}\left(-\frac{t}{t_{k,i}}\right)\right)+\mathrm{B} \end{gathered}$$ (6)

where the t_k,i terms are anticorrelation contributions due to exchange processes which affect the fluorescence signal, namely changes in the FRET efficiency. Here, N takes on a more general meaning as a function of molecular brightness and the number of molecules in the confocal volume. Photophysical terms for both donor and acceptor are included with decay times set to those from the corresponding donor and acceptor autocorrelation curves to ensure that any kinetic terms present are distinct from photophysical effects. C is a scaling factor determining the total contribution of the kinetic terms to the correlation and allowed to vary between 0 and 2, while the amplitudes of the kinetic terms are normalized to 1. Fitting of correlation curves was performed using Chisurf software⁶⁰.

Statistical uncertainties and error analysis

To determine the statistical uncertainties of the different model functions and resulted fit parameters for PDA, seTCSPC, and smFCS, we employ a search algorithm over the figure of merit ${\chi }_r^2$ against all varying parameters considering the number of degrees of freedom (v) and the number of free parameter for each model. We use the statistical test of the F-distribution with a 95% (P = 2σ) confidence interval to define the upper and lower limits for each parameter with respect to the ${\chi }_r^2$ surface, such that the maximum allowed ${\chi }_{r,max}^2$(P) is defined

$${\chi }_{r,max}^2(P)={\chi }_{r,min}^2\left(1+\frac{n}{v}\cdot {\text{cdf}}^{-1}(F(n,v,P)\right),$$ (7)

with cdf⁻¹ (F(n,v,P) as the inverse of the cumulative distribution function of the F-distribution and. ${\chi }_{r,min}^2$ is the optimized ${\chi }_r^2$ ⁶¹. The general algorithm for each parameter is as follows: I) The final fit is obtained through a minimization of ${\chi }_r^2$. II) Each parameter is varied about the final fit value and for each variation the fit curve, residuals, and new ${\chi }_r^2$ are calculated to obtain a ${\chi }_r^2$ surface. III) The ratios of final to varied ${\chi }_r^2$ values are used to identify the 95% confidence interval bounds above and below the final fit value via the F-test cdf as a function of the ratio of ${\chi }_r^2$ values. An example of this procedure can be observed in Figure S17.

MD simulations

All-atom structure-based models (SBM)³² were employed for all MD simulations. In these models, all non-hydrogen atoms are included as a bead of unit mass, and all bonded interactions (bonds, angles, and dihedrals) are maintained through harmonic potentials. Non-bonded atom pairs that are in contact in the native state (i.e., their distance is < 6 Å and are not shadowed by another atom in between them⁶²) and at least three residues apart in the sequence are given Gaussian interactions⁶², whereas all other non-interacting atom pairs are given repulsive interactions. These models effectively reduce the complexity of molecular interactions and enable exploration of protein folding processes. The functional form of the potential is described in detail elsewhere^32,33,62.

The input structure and forcefield files for domain-swapped FoxP1 were generated using the SMOG server (http://smog-server.org)⁶³. Given that no crystal structure of domain-swapped FoxP1 has been determined, a comparative model was generated based on the structure of the domain-swapped dimer of FoxP2⁵ using MODELLER v9.18⁶⁴. In order to avoid undesirable effects on the protein folding landscape due to uneven distributions of native contacts for each monomer in the domain-swapped dimer⁶⁵, these interactions were symmetrized similarly to previous work⁶⁶. Briefly, the intrachain and interchain native contacts from monomer A were replicated for monomer B, such that both monomers have the same interacting atom pairs and number of native contacts (433 total contacts per monomer and 584 dimer contacts). The same symmetry modification was performed for all bonded interactions.

All MD simulations were performed using a modified version of GROMACS 4.5.4⁶⁷ that includes Gaussian interactions⁶². In these simulations using SBM models, reduced units are used. Simulations were performed using the leapfrog stochastic dynamics integrator and a time step of 0.002 τ (in reduced units) for 1.6E8 simulation steps at several temperatures (ranging 1.05-1.25 reduced temperature units) close to the folding temperature (T_F) of FoxP1, such that multiple reversible transitions towards the unfolded state (>100) were observed. Structures and energies were saved every 2,000 steps.

Folding Free Energy Profiles and Ensemble Clustering

Folding free energy profiles were calculated through the weighted histogram analysis method (WHAM)³⁸. For the free energy profiles, native intrachain (Q_M) and interchain (Q_D) residue pair interactions, as well as the radius of gyration of the dimer of FoxP1 (Rg), were used as reaction coordinates to monitor the changes in its structure. For each simulation snapshot, two residues are considered in contact if any native atom-atom interactions between the interacting residue pairs are within 1.2 times their native distance. Q_M and Q_D vary from 0 (unfolded) to 1 (folded) and is obtained by dividing the number of observed contacts per frame by the total number of contacts in the native state.

Clustering analysis of each ensemble basin identified in the folding landscape of domain-swapped FoxP1 was performed using the g_cluster tool from GROMACS v4.5.4⁶⁷ using the linkage method and a structural similarity cutoff of 1 nm over the root mean square deviation (rmsd) of the Cα trace. One cluster was identified for basin DS, three clusters for basin {I₂⁽¹⁾} (with the selected cluster representing 95% of the structures in this ensemble), and one for basin {I₂⁽²⁾}. The structure with the smallest average distance to all other structures in the cluster was chosen as the most representative structure for each ensemble for determination of R_h and comparisons against FRET observables.

Comparing Structural Models to FRET observables

In order to compare structural models resulting from MD simulations against FRET observables, we used FRET Positioning and Screening (FPS)⁶⁸. FPS screens structural models by computing the predicted or modeled FRET distances using in silico labeling and coarse graining of the fluorescent labels. The volume for distance sampling is computed using a Monte Carlo sampling method to compute the Accessible Volume (AV) that each fluorescent label can occupy as grids of points in xyz format. Each of those positions are then used to compute a FRET distance as the mean distance between the centers of mass of the AVs, which then can be compared against experimental observables.

We employed the representative structures obtained by rmsd-based clustering analysis for each identified ensemble in the MD simulations (DS, {I₂⁽¹⁾}, {I₂⁽²⁾}) along with the known labeling positions and geometric and linker parameters for the fluorophores to calculate the AVs for each combination of FRET pairs for all structures. Later, the FPS-calculated FRET distances for the representative structures from MD clusters are correlated with those from the experiments to check the agreement between experimental and in silico results, as shown in Fig. 4. To compute the AV simulations, we used FPS⁶⁸ and AVTraj programs available from http://www.mpc.hhu.de/software.html and the Fluorescence Toolbox at https://github.com/Fluorescence-Tools, respectively.

Kinetic models

To better understand the mechanism of formation of the domain-swapped dimer, we first considered the general kinetic scheme describing the transition from 2 monomers (M + M → 2M) to the 3D-DS folding of FoxP1. First, the DNA-binding domain must partially unfold in order to sample monomeric intermediate configurations ({I^(j)}, superscript indicates “degeneracy” of ensemble) that allow transition to the DS state. The interacting monomers then transition to the dimeric intermediate ensemble ($\{I_2^{(k)}\}$, subscript indicates dimer formation and superscript is as in the monomeric ensemble), followed by final transition to the folded DS state. The reversible scheme is represented as

$$2M\rightleftharpoons 2\left\{I^{\{j)}\right\}\rightleftharpoons \left\{I_2^{(k)}\right\}\rightleftharpoons DS.$$ (8)

This linear scheme is an oversimplification in which the intermediate ensembles allow for a complex network of possible exchange processes. Therefore, to reach a kinetic scheme that is compatible with experimental and computational observations, we reduce this complex scheme to the presented simple ensemble representation to account for experimental observables. Following is a description of the scheme as it corresponds to each experiment.

First, visual inspection of the MFD histograms indicates either mono or bimodal distributions. However, to be quantitative we constructed seTCSPC fluorescence decays and determined that the best fit was a bi exponential decay in addition to a decay that represents a No FRET state or a state with fluorescence decay equal to the donor only decay. This model can be written as

$$\text{No FRET}+\left\{\{I_2^{(k)}\}\rightleftharpoons DS\right\}$$ (9)

and suggests a dynamic exchange between a conformation that resembles the DS state and a dimeric intermediate ensemble.

Next, we used PDA to model the FRET indicator (F_D/F_A) histogram distributions and reach a model that globally fits multiple time windows as

$$\text{No FRET}+\left\{\circlearrowright \{I_2^{(k)}\}\rightleftharpoons DS\circlearrowleft \right\}$$ (10)

in which, in order to fully fit the F_D/F_A distributions, we needed a millisecond-scale dynamic exchange between a DS state and a dimeric intermediate ensemble. The addition of two static sates with the same FRET limiting distances was also required to adequately fit the histograms. In other words, the dynamic exchange between two sates is not enough to reproduce the experimental observations, but rather it requires a more complex kinetic scheme in which “internal conversion” occurs within the limiting states, indicating heterogeneous limiting ensembles in which states are indistinguishable by FRET. Graphically this model is represented by overlaying the FRET lines (static and dynamic) over the MFD histograms where the exchange occurs between the DS state and the dimeric intermediate ensemble.

Next, using smFRET-FCS we identified that most FRET samples, except SS, requires two relaxation times when fitting the cross-correlation function. Based on equilibrium kinetics, the number of states that exchange is the number of relaxation times plus one, or

$$\text{No FRET}+\left\{\{I_2^{(2)}\}\rightleftharpoons \{I_2^{(1)}\}\right\}\rightleftharpoons DS$$ (11)

MD simulations help us identify a kinetic model that follows the linear kinetic scheme along the reaction coordinate system (Q_M or Q_D)

$$2\left\{I^{\{j)}\right\}\rightleftharpoons \left\{I_2^{(k)}\right\}\rightleftharpoons DS$$ (12.a)

$$2\left\{I^{\{j)}\right\}\rightleftharpoons \left\{\{I_2^{(2)}\}\rightleftharpoons \{I_2^{(1)}\}\right\}\rightleftharpoons DS$$ (12.b)

where the dimeric ensemble $\{I_2^{(k)}\}$ could be split into two in pathway different dimeric ensembles $\{I_2^{(1)}\}$ and $\{I_2^{(2)}\}$ with different level of contacts (Q_M or Q_D ).

Finally, when combining all observable and kinetic models we can generalize the kinetic scheme first presented in eqn. 13, as

$$2M\rightleftharpoons 2\{I^{\{j)}\}\rightleftharpoons \left\{\begin{array}{ccc}\hfill I_2^{(1.1)}\hfill & \hfill \rightleftharpoons \hfill & \hfill I_2^{(2.1)}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill I_2^{(1.n)}\hfill & \hfill \rightleftharpoons \hfill & \hfill I_2^{(2.n)}\hfill \end{array}\right\}\rightleftharpoons DS,$$ (13)

where the DS state could exit though a complex ensemble of dimeric intermediate states in a rough energy landscape leading to the monomeric disordered intermediates {I^{j}}. Given the resolution of our experiments and the overlap of the integrative approach, the simplified model eqn. 12.b is the most consistent with all our observations.

Data Availability

The authors declare that all data supporting the findings of this study are available within the paper and its supplementary information file, and available from the corresponding authors upon reasonable request.