Statistical Laws of Protein Motion in Neuronal Dendritic Trees

Summary

Across their dendritic trees, neurons distribute thousands of protein species that are necessary for maintaining synaptic function and plasticity and that need to be produced continuously and trafficked to their final destination. As each dendritic branchpoint splits the protein flow, increasing branchpoints decreases the total protein number downstream. Consequently, a neuron needs to produce more proteins to maintain a minimal protein number at distal synapses. Combining in vitro experiments and a theoretical framework, we show that proteins that diffuse within the cell plasma membrane are, on average, 35% more effective at reaching downstream locations than proteins that diffuse in the cytoplasm. This advantage emerges from a bias for forward motion at branchpoints when proteins diffuse within the plasma membrane. Using 3D electron microscopy (EM) data, we show that pyramidal branching statistics and the diffusion lengths of common proteins fall into a region that minimizes the overall protein need.

Graphical Abstract

Highlights

• •Surface proteins are more efficient at reaching distal sites than soluble proteins
• •Daughter radius optimization reduces the number of proteins needed to populate dendrites
• •Ratios of daughter radii at branchpoints are cell type specific
• •Highly diffusive proteins incur a smaller extra cost for non-optimized radii

Sartori et al. show that surface diffusion is more effective at providing proteins for distal dendritic sites than cytoplasmic diffusion. Daughter radius distribution at branchpoints can be optimized for long-range protein transport and reduce the total protein count necessary to populate distal synapses by orders of magnitude.

Introduction

Neurons have highly complex dendritic trees that can span thousands of micrometers. Dendrites propagate the electrochemical stimulation received from other neurons at synapses to the neuronal cell body to eventually elicit action potentials in the axon hillock. To achieve this signal integration, neurons must supply synaptic compartments with a diverse set of proteins ranging from neurotransmitter receptors to intracellular signaling molecules (Craciun et al., 2005; Smith and Simmons, 2001; Ziv, 2018). In addition, neurons can tune the efficiency or relevance of synaptic signal detection by modulating the copy numbers of synaptic proteins at individual synapses (Nusser et al., 1997; Nair et al., 2013; Choquet, 2018). For example, each excitatory synapse contains, on average, 60 AMPA receptors (Nair et al., 2013), and this number is increased or decreased within minutes (Zhang et al., 2008) during long-term potentiation and depression.

The most energy efficient means to traffic proteins is via passive, non-directed diffusion, and experiments show that many dendritic proteins undergo passive diffusion while moving in the cytoplasm or at the cell surface (Hirokawa and Takemura, 2005; Dieterich et al., 2010). For example, diffusion of AMPA receptors at a neuron’s surface is a key step for its synaptic incorporation (Opazo and Choquet, 2011). After exocytosis, AMPA receptors move via lateral diffusion within the cell plasma membrane, with average synaptic dwell times of only 3–7 s (Ehlers et al., 2007). For cytosolic proteins, passive diffusion can be very fast (several $\mu m^2/s$) and competes with active mechanisms promoting protein subcellular targeting (Fonkeu et al., 2019). As proteins travel across the branching dendritic tree, they can encounter tens of different branchpoints, each of which splits the flow of proteins. To serve distal compartments, a neuron could compensate for the number of downstream branchpoints by allocating more proteins to longer dendrites and those that branch more. How does this branch-based protein allocation work?

Theory-based attempts to understand dendritic protein distribution often consider a non-branching linear dendrite (Bressloff and Newby, 2013; Bressloff and Earnshaw, 2007; Fonkeu et al., 2019) or assume that the flow of proteins splits in half at each branchpoint (Williams et al., 2016). On the other hand, growing experimental and theoretical evidence suggests that protein trafficking cannot be understood by using such simplified approaches. First, even the simplest branching rule, introduced by Rall (1964), implies that the radii of daughter branches may not be half of those of the mother dendrite; recent analysis of reconstructed dendritic trees indicates that the daughter radius ratio is highly variable (Otopalik et al., 2017), and it may even depend on the length of the downstream branch (Bird and Cuntz, 2016). Second, some recent theoretical studies focusing on electrical flow in dendritic trees indicate that the daughter radius ratio at branchpoints can limit backpropagation of APs (Vetter et al., 2001) and alter the synaptic plasticity response of a whole branch (Ebner et al., 2019). These studies raise the possibility that branchpoints might also regulate protein copy numbers at synapses. However, a full understanding of the effect of dendritic arbor architecture on protein distribution in entire cells requires new computational perspectives.

Here we present a data-driven model framework that incorporates dendrite statistics of 3D electron microscopy (EM)-reconstructed mouse cortical pyramidal neurons and the annotated morphological database NeuroMorpho.org (Ascoli et al., 2007). Using this framework, we explored the consequences of branching morphologies on the protein supply and made three key discoveries. First, we predict a greater forward bias for the motion of surface proteins compared with cytoplasmic proteins. We validated the existence and amplitude of this forward bias experimentally using in situ fluorescent labeling of cytoplasmic and surface proteins. By measuring the relative abundance of surface and cytoplasmic proteins before and after the branchpoint, we obtained a $35\text{\%}$ average forward bias for surface proteins. Second, we show that our experimental measurements of dendritic radius ratios and branch lengths in pyramidal neurons, together with the diffusion lengths of common proteins, fall into a region that minimizes overall protein need. Proteins with diffusion lengths favored by the pyramidal branchpoint geometry distribution include prominent synaptic proteins such as CamkII and the GABA-A receptor. Third, we show that daughter radius optimization not only supports protein transport of dendritic proteins but also has the potential to reduce the total protein count needed to populate the dendritic arbors by four orders of magnitude.

Overall, our results indicate that neuronal dendritic morphologies have a key role in shaping neuronal function and reflect optimization strategies and constraints imposed by protein trafficking.

Results

To understand how proteins are supplied to synapses across the dendritic tree, we propose a mathematical framework that describes protein flow in the branching dendritic tree with consideration of the radii at individual branchpoints. We start by addressing the motion of proteins along straight dendritic segments and branchpoints. We then generalize this to complex branching geometries.

The dendritic protein density along linear dendritic stretches is captured by the diffusion equation

$$\frac{\mathrm{\partial }\mathit{\rho }\left(x,t\right)}{\partial t}=D\frac{{\partial }^2\rho \left(x,t\right)}{\partial x^2}-\phi \rho \left(x,t\right),$$ (Equation 1)

where $\rho \left(x,t\right)$ is the protein density per unit of length, D is the diffusion coefficient, and $\phi =\text{log}\left(2\right)/T_{1/2}$ is the degradation rate, which is inversely proportional to the half-life of the protein, $T_{1/2}$. Here we considered proteins that emerge from a source located at $x=0$ and populate the dendrite of length L.

The solution of Equation 1 is a combination of exponentials that combine into a fraction of hyperbolic functions:

$$\rho \left(x\right)=N\cdot \frac{\text{cosh}\left(\frac{L-x}{\lambda }\right)}{\text{sinh}\left(\frac{L}{\lambda }\right)\lambda }.$$ (Equation 2)

We obtained Equation 2 by considering the algebraic steps detailed in the STAR Methods. Here, L is the length of the considered dendrite and λ the diffusion length, which characterizes the spatial width of the protein density:

$$\lambda =\sqrt{\left(D{T}_{1/2}\right)/\text{log}\left(2\right)}.$$ (Equation 3)

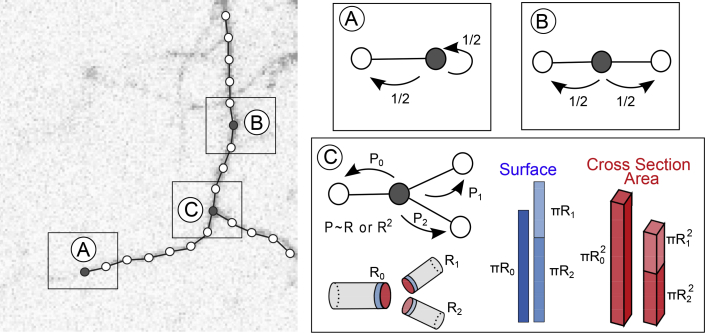
Next we generalized Equation 1 to include biologically realistic morphologies. To this end, we define boundary conditions for each dendritic segment that capture how proteins move close to bifurcations or dendritic tips. In Figure 1, we consider three types of dendritic segments: continuations, branchpoints, and terminations (representing the end of a dendritic branch). At the continuations, protein motion is described by Equation 1. At the terminations, the protein density fulfills the no-flux condition (see Equation 10, which states that the protein flux at the dendritic tips is zero).

Figure 1.

Protein Motion in a Branching Dendrite and the Associated Probabilities

A reconstructed dendritic arbor can be divided into compartments of equal length. The dendritic image was recorded using methods described in the STAR Methods section Image Acquisition. Each compartment can have one (A), two (B), or three (C) neighboring compartments. If a compartment has one neighboring compartment (A), the protein can jump back or stay, which is equivalent to a no-flux boundary condition. For two connected compartments (B), the probability of moving in either direction is equal. For a bifurcation (C), the probability of moving in either direction is determined by the cross-section or the circumference of the branches. These two options lead to fundamentally different outcomes: daughter branches are predicted to accumulate more protein relative to the mother dendrites (larger surface area than cross-section area) when the proteins move along the surface rather than in the dendrite.

In the next sections, we derived mathematical relations and analyzed neuronal reconstructions and in vitro protein distributions to describe the behavior of proteins in the vicinity of branchpoints and across the dendritic tree.

Rall Exponents and Their Consequences for Downstream Protein Distribution

At a dendritic branchpoint, the probability of a protein to take a particular route depends on the available space in the route of interest. Conversely, surface proteins diffusing within the plasma membrane can explore the circumference of a dendrite, where the probability of choosing a particular route is proportional to the radius of the dendrite in that direction (surface area $\propto 2\pi R_i$, $i=\mathrm{0,1,2}$). On the other hand, proteins moving within the cytoplasm can explore the volume within the dendrite, where the probability of choosing a particular route is proportional to the radius squared (cross-section area $\propto \pi R_i^2$). We considered a situation where the intracellular conditions shaping the movement of proteins (e.g., viscosity, molecule crowding, access to degradation machinery, etc.) were homogeneous in the vicinity of the branchpoint. To parametrize the dependency of the radii of the three afferent dendrites, we considered a generalization of Rall’s $3/2$ branching rule (Rall, 1964):

$$R_0^{\alpha }=R_1^{\alpha }+R_2^{\alpha },$$ (Equation 4)

where the mother branch radius is $R_0$, and the radii of the two daughter branches are $R_1$ and $R_2$ (see Figure 1, C). Pioneering studies by Rall describing passive neuron models found that if $\alpha =3/2$, then the flow of electrical current along the branching dendritic tree is equivalent to that along a long cylinder (Rall, 1964).

Although the relation does not hold exactly for many neuronal families (Otopalik et al., 2017; Kernell and Zwaagstra, 1989; Mainen et al., 1996; Desmond and Levy, 1984), its underlying idea is used as a baseline for many dendritic models (Kubota et al., 2011; Bird and Cuntz, 2016). It is conceivable that the typical Rall exponent, α, is cell type specific. In the next section, we address the statistics of the Rall exponents in cortical pyramidal neurons, hippocampal pyramidal neurons, and stomatogastric ganglion (STG) neurons.

To accurately capture the effect of branchpoints on the flow of proteins, it is necessary to understand how the radii of the mother dendrite and the daughter dendrites relate to one another. The relation between the daughter and the mother radii determines the number of proteins that can pass through the branchpoint and is an important predictor of the protein number downstream. We approximated each branchpoint as a point where mother and daughter cylinders terminate with perfect circle cross-sections. However, dendritic branchpoint geometries in vivo could deviate from this symmetry and exhibit variable length of tapering cylinders, variable diameter of the branchpoint trunk, etc. (Ferrante et al., 2013). Although we did not include this branchpoint variability in the model, it can be captured in future work by considering local tapering effects and including a local drift around branchpoints using the methods introduced in the supplement in Fonkeu et al. (2019). This more complex branchpoint geometry does not significantly alter our model predictions regarding the global steady-state protein distributions because the number of proteins leaving a branchpoint, after the tapering, will depend on the radii of the daughter branches after tapering. However, the branchpoint heterogeneity could modify the time it takes to establish the steady state described by our model.

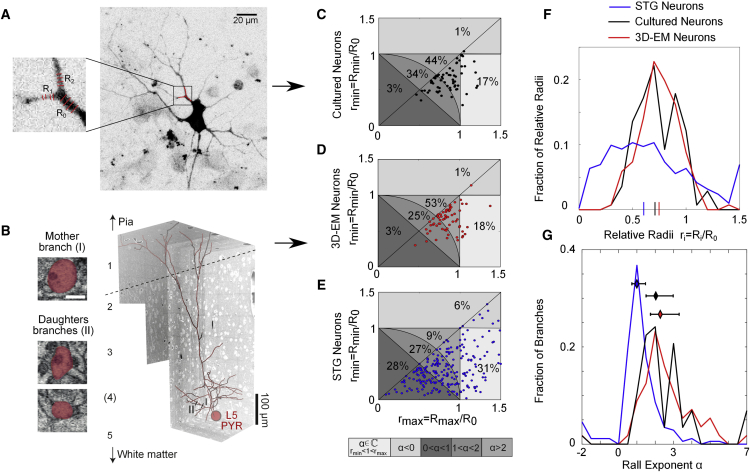
We proceed by considering Figure 1, C, and the definition of the Rall exponent in Equation 4. We evaluated the mother and daughter radii around branchpoints in cultured pyramidal neurons (Figures 2A and 2C) and in pyramidal neurons reconstructed in the posterior parietal cortex (PPC) and imaged using 3D EM (Figures 2B and 2D; Karimi et al., 2020; Boergens et al., 2017). To examine whether the branchpoint radius statistics vary across neural types, we used an additional, published dataset on STG neurons (Otopalik et al., 2017; Figure 2E). For all branchpoints, we calculated the Rall exponent using Equation 4; their resulting distribution is shown in Figure 2E.

Figure 2.

The Distribution of Daughter Radii at Branchpoints Is Cell Type Specific

(A) A selected branchpoint in a cultured pyramidal neuron is displayed as used in our analysis. The dendritic image was recorded using methods described in the STAR Methods section Image Acquisition.

(B) A selected branchpoint of a neuron in a 3D reconstructed PPC pyramidal neuron as used in our analysis.

(C and D) Normalized smaller daughter radii $\left(r_{\text{min}}=R_{\text{min}}/R_0\right)$ are displayed versus the normalized larger radii $\left(r_{\text{max}}=R_{\text{max}}/R_0\right)$ in pyramidal neurons reconstructed in the posterior parietal cortex (PPC) and imaged using 3D electron microscopy (EM). Experimental 3D EM methods can be found in the STAR Methods section Dendrite Diameter Measurement in Three-Dimensional Electron Microscopy.

(E) For comparison, published data on stomatogastric ganglion (STG) neurons from Otopalik et al. (2017) are shown.

(C–E) Bottom: the contour lines and the corresponding gray color scale denote different parameter regimens in: Rall exponent $\alpha <0$, $0<\alpha <1$, $1<\alpha <2$, $\alpha >2$, and $\alpha \in \mathrm{C}1$.

(F) Distribution of normalized radii from (C)–(E).

(G) Distribution of Rall exponents in pyramidal (red and black lines) and STG (blue) neurons. For PPC pyramidal neurons, the median value of the Rall exponent is $\alpha =2.28$, and its 50% confidence interval is $\left(1.76,3.3\right)$. For cultured hippocampal neurons, $\alpha =2.03$ with a 50% confidence interval of $\left(1.50,2.99\right)$. For neurons in the STG, $\alpha =1.00$ with a 50% confidence interval of $\left(0.72,1.47\right)$. The mean values of α are $\alpha =2.56\pm 1.78$, $\alpha =2.44\pm 3.86$, and $0.88\pm 2.26$, respectively.

Next we analyzed how the two daughter radii are related to one another (Figures 2A–2E). $R_{max}$ denotes the larger of the two radii and $R_{min}$ the smaller. The corresponding normalized radii are $r_{max}=R_{max}/R_0$ and $r_{min}=R_{min}/R_0$, where $R_0$ is the radius of the mother dendrite as measured in the vicinity of the branchpoint (STAR Methods). To understand the consequences of the measured radii, we divided them into five classes based on the corresponding Rall exponent α; different shades of gray denote branchpoint radii with $0<\alpha <1$ in darkest gray, $1<\alpha <2$ in gray, $\alpha >2$ in lighter gray, $\alpha <0$ in light gray, and $\alpha \in \mathrm{C}$ in lightest gray (Figures 2C–2E).

Analyzing the distribution of Rall exponents in Figure 2G, we found that the Rall exponent distributions are skewed toward the right. We therefore used the median values rather than the means to derive characteristic Rall exponents. We obtained the following median Rall exponents: $\alpha =2.28$ for PPC pyramidal neurons, $\alpha =2.03$ for cultured pyramidal neurons, and $\alpha =1.00$ for STG neurons (Figures 2F and 2G). The difference between surface and cytoplasmic proteins at branchpoints, which we present in the following sections, can be derived from Rall exponents or directly from the ratio of the daughter radii. In the next paragraph, we will use the Rall exponents to derive whether the expected numbers of surface and cytoplasmic proteins after a branchpoint are higher or lower than the numbers in the corresponding mother dendrite, and we will use the normalized radius, $r_{min},r_{max}$, to explicitly calculate the surface-to-cytoplasm bias for individual branchpoints.

Daughter Radii at Branchpoints Determine the Downstream Protein Count

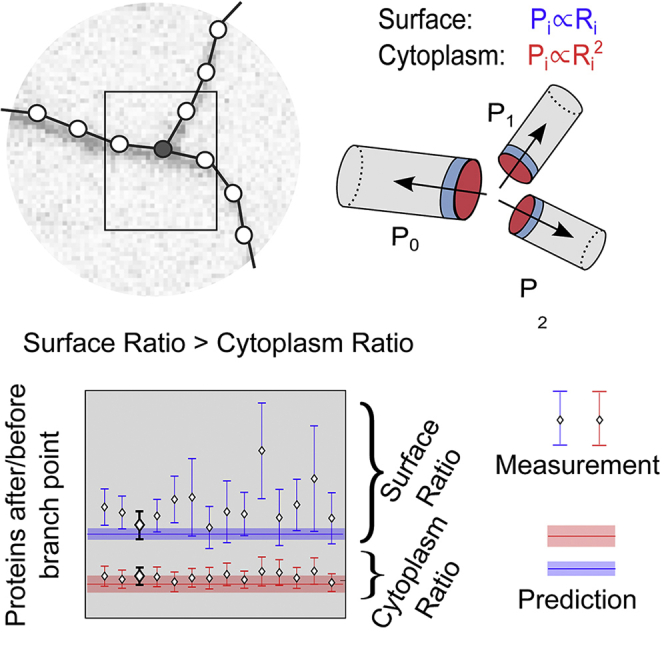
Next we used the Rall exponents derived in the previous section to predict how the dendritic branchpoints affect the protein distribution downstream. For a protein, the probability of diffusing into either branch depends on the daughter and mother radii because these determine how much space is available for protein movement (Figure 3A). The probability of moving into one of the three possible directions at a branchpoint is

$$P_i^{\left(\gamma \right)}=\frac{R_i^{\gamma }}{R_0^{\gamma }+R_1^{\gamma }+R_2^{\gamma }},\gamma =\{\begin{array}{cc}1,& \text{surface}\\ 2,& \text{cytoplasm}.\end{array}$$ (Equation 5)

In the following, $i=0$ denotes the mother dendrite and $i=\mathrm{1,2}$ the two daughter dendrites, respectively. Evaluating this relation in Figure 3B, we found that the probability of a protein to diffuse into the daughter dendrites or to go back to the mother dendrite is cell type specific and depends on the diffusion medium. In Figure 3B, top, we show that, for a typical pyramidal neuron with Rall exponent $\alpha =2.28$, the fraction of proteins immediately after the branchpoint is higher than the fraction of protein before it; that is true for surface proteins (solid red line) and for cytoplasm proteins (dashed red line). We repeated the same plot for a typical STG neuron, $\alpha =1.03$, and in Figure 3B, bottom, we observed that the fraction of surface protein after the branchpoint is almost independent of the radius of the first dendrite and slightly bigger than $1/2$ (solid blue line), whereas the fraction of cytoplasm protein after the branch is constantly lower than $1/2$ (dashed red line). In both cases, the fraction of surface protein after the branchpoint is consistently higher than the fraction of cytoplasmic protein before the branchpoint.

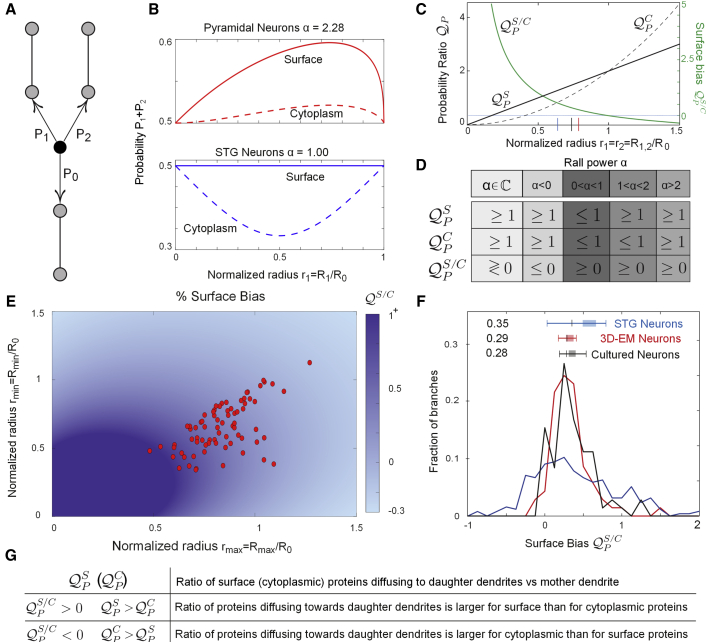
Figure 3.

Protein Diffusion toward Distal Dendrites Is Greater for Surface Proteins Than Soluble Proteins

(A) Diffusing proteins that reached a branchpoint move back toward the mother dendrite with a probability $P_0$ and toward either distal site with probability $P_1$ and $P_2$.

(B) The probability for a surface or cytoplasmic protein to move into the daughter branches, $P_1+P_2$, depends on the normalized radius of one of the daughter dendrites (e.g., $r_1$) and on the Rall exponent α. Using the Rall exponents from Figure 2E, we calculated the probability of moving into the daughter dendrites as a function of the normalized radii. The probability of forward motion $\left(P_1+P_2\right)$ is larger for surface proteins than for soluble proteins (solid versus dashed lines).

(C) The probability ratio, under the assumption that the two daughter dendrites have the same radius as a function of their normalized radius $r_i$. For each value $r_i\le 1$ ($\alpha >0)$, the probability ratio of surface proteins (solid line) is higher than the probability ratio for cytoplasmic proteins (dashed line), and the relative bias (solid green line) is bigger than zero. Vertical ticks represent the median normalized radius of STG neurons (blue), PPC pyramidal neurons (red), and cultured pyramidal neurons (black).

(D) Relations between the probability ratios (Equation 6) as function of the Rall exponent.

(E) The color code represents the predicted relative bias, ${\mathcal{Q}}_P^{S/C}$, as a function of the relative radii of the daughter dendrites, and the red circles represent the location of the measured PPC pyramidal branches.

(F) The fraction of branches with a specific relative bias ${\mathcal{Q}}_P^{S/C}$, PPC pyramidal neurons (red) with $\text{median }{\mathcal{Q}}_P^{S/C}=0.29$ with a $50\text{\%}$ confidence interval $\left(0.18,0.41\right)$, STG neurons (blue) with $\text{median}{\mathcal{Q}}_P^{S/C}=0.35$ with a $50\text{\%}$ confidence interval $\left(0.02,0.79\right)$, and cultured pyramidal neurons (black) with $\text{median}{\mathcal{Q}}_P^{S/C}=0.28$ with a $50\text{\%}$ confidence interval $\left(0.19,0.54\right)$. The shaded area represents the mean and SE of the surface bias for the three neuronal classes. The mean and SE of the theoretically predicted relative bias in cultured pyramidal neurons is 0.36, SE $=0.11$.

(G) Table summarizing the meaning of ${\mathcal{Q}}_P^S$,${\mathcal{Q}}_P^C$, and ${\mathcal{Q}}_P^{S/C}$.

Experimental methods and sample sizes underlying the data points in (E) and (F) can be found in the STAR Methods sections Dendrite Diameter Measurement in Three-Dimensional Electron Microscopy, Hippocampal Neuron Preparation, Neuron Transfection, and Image Acquisition.

Next we used these probabilities to make quantitative predictions for the distribution of proteins around a branchpoint. We defined the expected protein number ratio ${\mathcal{Q}}_P^{\gamma }$ as the ratio between the number of proteins immediately after and before the branchpoint. Here, $\gamma =C$ for cytoplasmic proteins, and $\gamma =S$ for surface proteins. In the STAR Methods, we show that the number of proteins in a compartment adjacent to the branchpoint is proportional to the probability of moving from the branchpoint toward that compartment. We can therefore link the probability ratio to the expected protein numbers in the immediate vicinity of a branchpoint:

$${\mathcal{Q}}_P^{\gamma }=\frac{P_1+P_2}{P_0}=\{\begin{array}{c}{\mathcal{Q}}_P^S=r_1+r_2\\ {\mathcal{Q}}_P^C=r_1^2+r_2^2\end{array}\text{where}{r}_i=R_i/R_0.$$ (Equation 6)

Next we studied how the expected protein number ratio ${\mathcal{Q}}_P^{\gamma }$ depends on the radii at the branchpoint, the mode of protein transport (surface versus cytoplasm), and the Rall exponent α (Figures 3C and 3D). A probability ratio ${\mathcal{Q}}_P^{\gamma }>1$ indicates that the proteins move preferentially forward into the daughter branches, and a number ratio ${\mathcal{Q}}_P^{\gamma }<1$ indicates that a backward motion toward the mother dendrite is preferred. We found that all Rall exponents that are larger than zero favor transport of surface proteins to daughter dendrites. Therefore, the relative bias,

$${\mathcal{Q}}_P^{S/C}={\mathcal{Q}}_P^S/{\mathcal{Q}}_P^C-1,$$ (Equation 7)

is always positive for Rall exponents that are larger than zero (Figure 3 D).

In Figures 2C–2G, the areas spanned by the two daughter radii that correspond to a specific relation between the predicted number ratios ${\mathcal{Q}}_P^S$ and ${\mathcal{Q}}_P^C$ are color coded to interpret the predicted number ratio for individual branchpoints. The measured branchpoints located in the dark gray area follow $0\le {\mathcal{Q}}_P^C<{\mathcal{Q}}_P^S\le 1$, branchpoints in the gray area follow ${\mathcal{Q}}_P^C\le 1\le {\mathcal{Q}}_P^S\le \sqrt{2}$, branchpoints in the light gray area follow $1\le {\mathcal{Q}}_P^C\le {\mathcal{Q}}_P^S\le 2$, and those in the lightest gray area follow $2\le {\mathcal{Q}}_P^S\le {\mathcal{Q}}_P^C$. The values of ${\mathcal{Q}}_P^S,{\mathcal{Q}}_P^C\text{ and }{\mathcal{Q}}_P^{S/C}$ are shown in Figure 3C for the limiting case $r_1=r_2$. The experimental values of ${\mathcal{Q}}_P^{S/C}$ for PPC pyramidal neurons are shown in Figure 3F; and its distribution for the three classes of neurons is analyzed in Figure 3G. Next we analyzed the $\left(r_1,r_2\right)$ distribution to calculate the expected ${\mathcal{Q}}_P^S$ and ${\mathcal{Q}}_P^C$ of cultured neurons; the mean and standard error are ${\mathcal{Q}}_P^S=1.48,$ SE $=0.03$, and ${\mathcal{Q}}_P^C=1.17$, SE $=0.05$.

Experimental Validation In Vitro

Our theory predicted that the typical pyramidal neuron dendritic branch, with an experimentally measured median normalized radius $r=0.71$, would favor the forward motion of surface proteins over cytoplasmic proteins. We tested this prediction by measuring the distribution of fluorescent cytoplasmic or surface protein in the vicinity of branchpoints in cultured hippocampal neurons. We analyzed the fluorescence intensities in the vicinity of branchpoints for a soluble cytoplasmic green fluorescent protein (GFP) and a GFP coupled to a surface-expressed transmembrane protein, Neuroligin-1 (GFP::Nlg-1) (Figure 4A), integrating the fluorescence in the neighborhood of the branchpoint (Figures 4A and 4B; STAR Methods). Assuming that the ratio between the protein fluorescence signals is equal to the copy number ratio of proteins, we calculated the fluorescence ratio analogous to Equation 6. Confirming our prediction, we found that the fluorescence ratio of surface proteins is higher than the fluorescence ratio of cytoplasmic proteins, ${\mathcal{Q}}_F^S>{\mathcal{Q}}_F^C$. In Figure 4C, we show the distribution of ${\mathcal{Q}}_F^S$ and of ${\mathcal{Q}}_F^C$ for a particular choice of the neighborhood size, and in Figure 4D, we show the mean and SE for varying neighborhood sizes. This difference is summarized by the surface bias in Figure 4E. Previous studies have shown that, in the absence of untranslated targeting sequences, transfected mRNAs coding for GFP and GFP::Nlg-1 are confined to the soma region (Tushev et al., 2018). This indicates that our proteins of interest are synthesized in the soma and, from there, populate the entire dendritic arbor. Thus, there is likely little contribution of local protein synthesis to these measurements. The fluorescence intensities of both expressed proteins are continuous along the dendritic arbor. The expected value of the protein ratios for surface and cytoplasmic proteins obtained in Figure 3C are reported in Figure 4D (blue and red horizontal lines denote the respective theoretical predictions) and the corresponding surface bias in Figure 4E. We quantified the surface bias by calculating the mean value of the fluorescence ratio for the surface protein and dividing it by the mean value of the fluorescence ratio for the cytoplasmic protein. We found a forward bias of $35\text{\%}$, SE $=10\text{\%}$, which is in line with our theoretical prediction of $35\text{\%}$, SE $=3\text{\%}$ (Figures 4D and 4E).

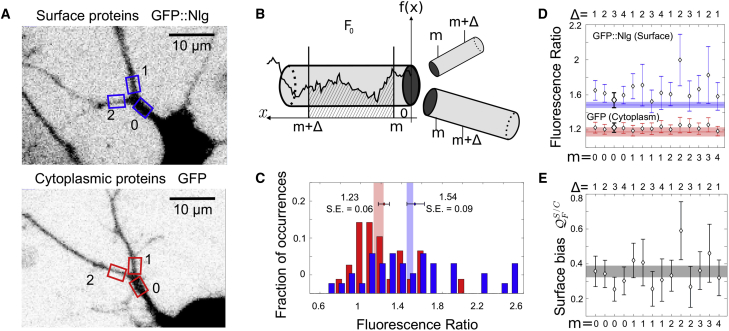
Figure 4.

In Vitro Experiments Confirm that Surface Proteins Are Favored over Cytoplasmic Proteins at Branchpoints

(A) Representative images of a surface protein, GFP::Nlg-1 (top), and cytoplasm protein, GFP (bottom), in cultured pyramidal neurons, along with the regions of interest for the mother and daughter dendrites.

(B) A sketch of the parameter definitions used in the data analysis in (C)–(E). The fluorescent signal (black line) is integrated between m and $m+\text{Δ}m$. The integrated fluorescence is denoted by $F_i$, where $i=0$ represents the mother dendrite and $i=\mathrm{1,2}$ the daughter dendrites.

(C) Distribution of the fluorescence ratios ${\mathcal{Q}}_F$ for GFP (red) and GFP::Nlg-1 (blue). The error bars represent the mean and SE for the two proteins. Vertical shaded areas represent the predicted value of the fluorescence ratio, obtained in Figure 3 for cytoplasmic (red) and surface (blue) proteins. Here we chose $m=0\mu m$ and $\text{Δ}=3\mu m$.

(D and E) The bootstrapped mean and SE of the fluorescence ratio ${\mathcal{Q}}_F$ for GFP and GFP::Nlg-1 proteins (D; red and blue, respectively) and of the relative bias (E, black) in cultured pyramidal neurons for different values of $m=\mathrm{0,1,2,3,4}$ and $\text{Δ}=\mathrm{1,2,3,4}$. The solid lines represent the mean values obtained in Figure 3F and the shaded area their SE. The bold error bars summarize (C).

Experimental methods and sample sizes underlying the images and data can be found in the STAR Methods sections Hippocampal Neuron Preparation, Neuron Transfection, and Image Acquisition.

In Figure 4D, we see a small upward shift in the data values compared with the model prediction. Considering two supplemental statistics for mean and median (Figure S1), we see that the deviation between the predicted mean and measured mean for surface and cytoplasmic proteins is not significant.

Can a Neuron Optimize Branchpoints for Protein Trafficking?

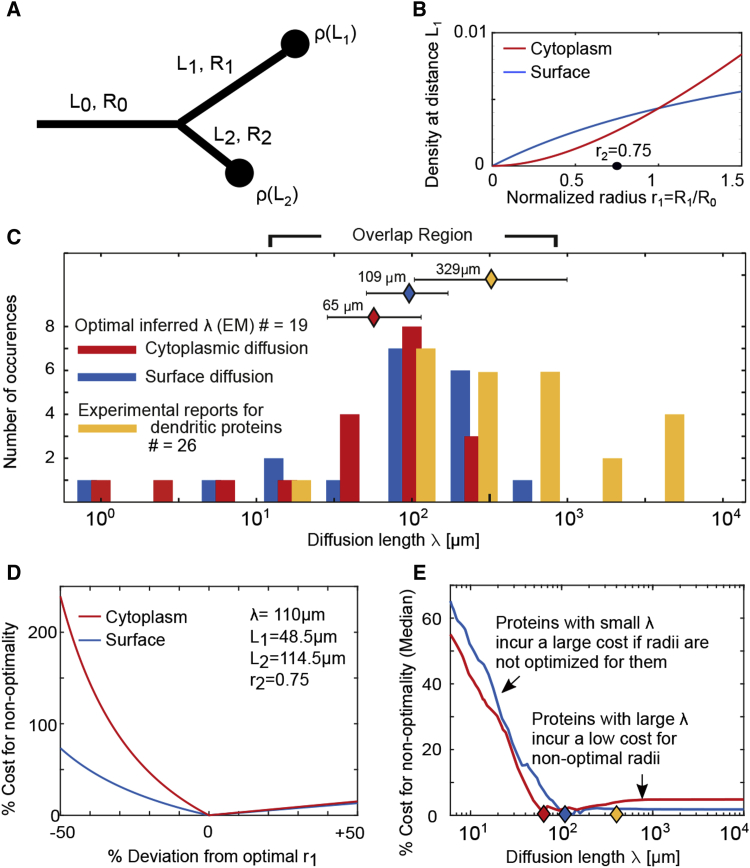
Our results so far suggest that the ratio of the daughter radii is an important determinant of downstream protein concentration (Figure 5A). Therefore, we next investigated whether an optimal daughter radius ratio exists that can maximize the flow of proteins to longer dendrites without increasing the total protein count. The energy needed to translate a single protein is approximately 5–13 ATP per amino acid (Schimmel, 1993) (e.g., $\sim 7947$ ATPs for a single GluA2 protein), and a neuron has to produce $\sim \mathrm{12,000}$ different proteins (Sharma et al., 2015), each of which lives only for a few days (Dörrbaum et al., 2018). This imposes a large energy demand and suggests that the total copy number of synaptic proteins should be kept as low as possible to minimize the overall energy expenditure of the neuron (Harris et al., 2012). If an optimal radius ratio exists that can help lower the energy cost of maintaining synaptic protein counts at longer dendrites, then what is the energy cost of not meeting this optimality criterion?

Figure 5.

Daughter Radii in Pyramidal Neurons Are Optimized for Protein Diffusion Lengths that Overlap with the Experimentally Reported Distribution of Dendritic Proteins

(A) A sketch of a dendritic branch and its corresponding radii, lengths, and density of proteins at the tips of the daughter dendrites.

(B) Predicted protein density at the tips of the daughter dendrites as a function of the daughter radius $\left(r_1\right)$. The second daughter radius is set to the median radius for PPC pyramidal neurons $r_2=0.75$, $L_1=50\mu m$, $L_2=25\mu m$ and diffusion length $\lambda =110\mu m$.

(C) Distribution showing the number of branches optimized for a particular diffusion length for cytoplasmic (red) and surface (blue) proteins. Shown in yellow are diffusion lengths for 26 dendritic proteins with experimentally reported diffusion coefficients and half-lives (STAR Methods). The median values of the distributions are $\lambda =65\mu m$, $\lambda =110\mu m$, and $\lambda =329\mu m$, respectively.

(D) For a given set of λ, $L_1$, and $L_2$, there is only one value of the normalized radius $r_1$ (here, $r_2=0.75$) that minimizes the total amount of proteins needed to ensure at least $N_{\text{target}}$ proteins are localized to the tips of both daughter branches. A normalized radius $r_1$ of less than the optimal $r_1$ leads to a substantial increase in the number of proteins (cost) needed to populate the dendritic arbor, whereas a higher $r_1$ value does not significantly increase the cost.

(E) Proteins with small diffusion lengths (short-diffusivity proteins) incur a larger cost for non-optimal daughter radii than those with large diffusion lengths.

Experimental methods underlying the data can be found in the STAR Methods sections Dendrite Diameter Measurement in Three-Dimensional Electron Microscopy, Hippocampal Neuron Preparation, Neuron Transfection, and Image Acquisition.

Let us consider two daughter branches that have different lengths downstream of a branchpoint; we assume that they are assigned the same protein number (equal daughter radii). The shorter dendritic branch would now receive an overabundance of proteins, whereas the longer is deprived of them. In such a scenario, the neuron would need to increase overall production of proteins to ensure that the protein concentration in the deprived dendrite is above the minimal threshold for synaptic function. In an optimal branching tree, the protein density ρ at the tips of the branches would be the same, and the shorter dendritic branches would be assigned smaller dendritic radii because they have a lower protein demand than longer branches. When examining the terminal branch points of a dendrite, we noted that each protein type has its optimal radius ratio, given its diffusion length and the length of daughter dendrites:

$$\frac{\text{cosh}\left(L_1/\lambda \right)}{\text{cosh}\left(L_2/\lambda \right)}=\frac{R_1^{\gamma }}{R_2^{\gamma }},$$ (Equation 8)

where λ is the diffusion length (Equation 3). Next we considered 28 EM-reconstructed pyramidal branchpoints with known daughter lengths $L_1,L_2$ and known mother and daughter radii $R_0$, $R_1$, and $R_2$. For 19 measured branchpoints, we computed the diffusion length λ, for which the measured daughter radius ratio is optimal. We did this by inserting $L_1,L_2$ and $R_1,R_2$, for each measured branchpoint into Equation 8 and identifying λ, which fulfills this relation. Proteins whose diffusion length corresponds to such λs will minimize the total protein count needed to achieve equal protein density at both dendritic tips.

The resulting distribution of diffusion lengths is shown in Figure 5C for cytoplasmic proteins (red) and surface proteins (blue). For comparison, the distribution of diffusion lengths for dendritic proteins $\left(n=26\right)$ is shown in yellow. We found that the protein diffusion lengths for which the dendritic branchpoints are optimized have significant overlap with the experimentally reported diffusion lengths of dendritic proteins (Figure 5C). The overlap region corresponds to diffusion lengths ranging from 50–500 $\mu m$. This range includes important synaptic proteins, such as receptor subunit GluA1, a subunit of AMPA-type glutamate receptors, and the ${\alpha }_1$ subunit of GABA-A receptors (Table S1). Experimental methods to obtain diffusion coefficients in these studies are based on the mean square displacement along straight dendritic segments; methods to obtain the protein half-life are based on mass spectrometry and cycloheximide chase assay experiments. Overall, dendritic proteins are a diverse set and can exhibit different diffusion properties and have different diffusion lengths. Therefore, any branchpoint radii and dendritic lengths that may be optimal for one protein type may not be optimal for another.

If the daughter radii deviate from the optimal ratio, then the number of proteins needed to maintain equal protein concentration at the dendritic tips would increase. To measure this cost, we studied the amount of extra proteins needed to maintain equal protein concentrations at the tips of the two daughter branches (Figure 5A) and expressed it as a percentage of the total protein count under optimal conditions. We calculated this percentage cost for daughter radius deviations ($R_1/R_0$ relative to its optimal value) and for deviations in λ (Figures 5D and 5E). We found that radii smaller than the optimal value incur a higher cost than those that are larger (Figure 5). Finally, we analyzed the non-optimality cost for different diffusion lengths. We found that proteins with smaller diffusion lengths incur a larger cost for non-optimal radii compared with proteins whose diffusion lengths are larger than the optimal value. Intuitively, this can be understood by considering that proteins with larger diffusion lengths travel longer distances and, thus, reach both dendritic tips in larger numbers, making their concentration less dependent on any particular branching radius ratio. Conversely, proteins with shorter diffusion lengths reach the dendritic tips less readily, and their concentration is dependent on dendritic radii. Next we generalized our model calculations to consider the anatomy of spines that branch off a dendrite and found (see STAR Methods section Spine-Dendrite Coupling and Figure S3) that the dendritic radius and spine head size have a larger role in protein availability in spines compared with the radius of the spine neck or its length.

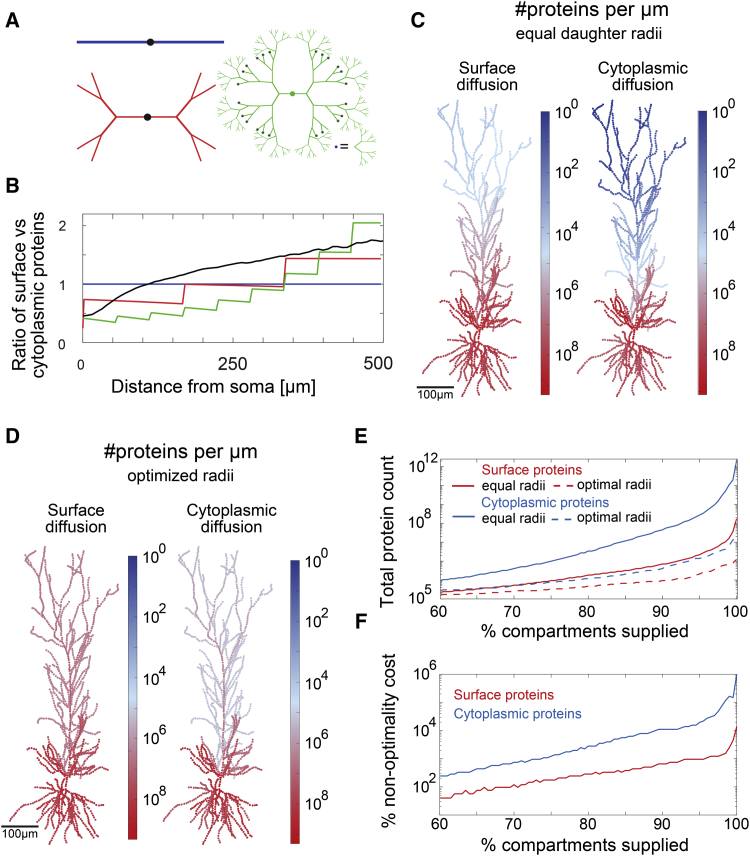
Consequences for Protein Distributions in Reconstructed and Artificial Morphologies

Our next goal was to move from individual branchpoints to whole dendritic trees. How do the number of branchpoints and lengths of dendritic segments determine the downstream protein copy number? To answer this question, we considered two types of dendritic trees: synthetic dendritic trees with a controlled number of branchpoints and reconstructed hippocampal pyramidal neurons from Ascoli et al. (2007). First we considered dendritic trees with symmetrical branching, where the radius of the daughter dendrites is equal to the average value obtained for pyramidal neurons ($R_1=R_2=0.75\cdot R_0$; Figure 2F). We applied these considerations to artificial morphologies (Figure 6A) and 65 reconstructed pyramidal neurons. We found that, as the number of branchpoints increases toward the dendritic tips, the fraction of surface/cytoplasmic proteins away from the soma increases, too. As expected, this effect accumulates with each branchpoint (Figure 6B), which explains the step-like increase in the distribution in synthetic morphologies. Because of the high number of branchpoints in the reconstructed pyramidal neurons and their random positions, we found a smooth increase in the surface-to-cytoplasm ratio in the $0-500\mu m$ range.

Figure 6.

Influence of Dendritic Morphology and Radius Optimization on the Distribution of Proteins

(A) Synthetic dendritic morphologies with zero, two, and eight consecutive branches.

(B) Protein number ratio between surface and cytoplasmic proteins versus distance calculated for proteins with the same diffusion coefficient and half-life. Red, blue, and green correspond to synthetic morphologies in (A). The solid black line corresponds to an average of 65 reconstructed pyramidal morphologies obtained from the NeuroMorpho database (Ascoli et al., 2007).

(C) Predicted number of proteins per micrometer in a pyramidal neuron (morphology taken from Dalrymple-Alford et al., 2015). The color code represents the predicted number of proteins per micrometer. The number of proteins in the distal parts is larger for surface proteins than for cytoplasmic proteins. Here we considered symmetrical daughter branches where the radius of a daughter dendrite is $R_1=R_2=0.75R_0$.

(D) Predicted number of proteins per micrometer for optimized radii.

(E) Dendritic trees with optimized radii need smaller protein counts to supply dendritic compartments with at least one protein per compartment.

(F) Percent cost $\left(\left(N-N_{opt}\right)/N_{opt}100\text{\%}\right)$ versus fraction of compartments supplied. The diffusion coefficient and half-life are kept constant throughout: $D=0.36\mu m^2/s$ and $T_{1/2}=5.0$ days, respectively, leading to a diffusion length of $472\mu m$ corresponding to GABA-A subunit $\alpha 2$ (Table S1).

Our previous results indicated that daughter radii in pyramidal neuron are not necessarily equal and that their ratio can reflect an optimization strategy for downstream protein numbers. To find out how effectively this optimization strategy is able to raise protein copy numbers at the distal sites, we simulated it in pyramidal morphologies. We compared protein distributions for symmetrical and optimized daughter radii in the same dendritic morphology of a representative pyramidal neuron. We set the total protein count to $N=2.1\cdot {10}^{12}$ to ensure that at least one protein is allocated to all dendritic compartments. As predicted, surface proteins had a higher protein copy number at distal sites compared with cytoplasmic proteins with equal diffusion coefficients and half-lives (Figure 6C). The same proteins and the same morphology resulted in significantly higher distal protein counts when radii were optimized using the strategy in Equation 8 (Figure 6D). We found that daughter radius optimization could reduce 1,000-fold the total protein necessary to supply all compartments of a dendritic tree with at least one protein. In our example, we found that $1.7\cdot {10}^9$ surface proteins (this is an average of 65 morphologies) and $N=2.1\cdot {10}^{12}$ cytoplasmic proteins were necessary to supply a dendritic tree with symmetrical daughter radii. Daughter radius optimization reduced this number 100- to 10,000-fold to $1.2\cdot {10}^7$ and $2.1\cdot {10}^8$, respectively.

We chose the GABA-A receptor as an example because its diffusion length is close to the median diffusion length of the experimentally characterized proteins in Table S1 and Figure 5C. In Figure S4, we show the predicted protein distributions for an alternative diffusion length $\lambda =109\mu$m, which corresponds to the median of the EM-inferred diffusion lengths (Figure 5C, blue).

Next we asked whether the optimization strategy is still beneficial when only a part of the dendritic tree is supplied with proteins. If 90% of compartments require this type of proteins, does radius optimization still matter? Here we found that this reduced the total protein count to $7.1\cdot {10}^6$ for surface proteins and $4.5\cdot {10}^8$ for cytoplasmic proteins in dendritic trees with symmetrical radii. However, daughter radius optimization reduced this number 10–100 times to $9.5\cdot {10}^5$ and $4.0\cdot {10}^6$, respectively.

These results indicate that daughter radius optimization and membrane-bound protein transport can be powerful strategies that help supply proteins to distal dendrites while minimizing the total neuronal energy expenditure for protein synthesis. Combining these optimization strategies with dendritic mRNA localization or active protein transport could help to further lower the necessary total protein counts and provide neurons with a powerful arsenal of candidate mechanisms to maintain synaptic copy numbers. What could be the consequences of these optimization strategies for synaptic plasticity?

Synaptic plasticity alters the local demand for proteins on short and long timescales. To maintain synaptic potentiation over a long period of time, the local proteome at individual synapses (and, thus, protein supply) needs to be altered persistently (Schanzenbächer et al., 2016; Dörrbaum et al., 2018). This means that global proteostasis following the induction of long-term plasticity needs to be adjusted to this new demand by producing an altered constellation of proteins. The question is how to serve such global protein demand change long term in a way that is energetically favorable for the neuron. Our results indicate that a neuron can minimize the energy needed for translation of proteins in the maintenance phase by harnessing the optimality of dendritic branching radii (Figure 5; Figure S2) and can tune the amount of proteins diffusing in a spine (Bloodgood and Sabatini, 2005) by varying spine geometry (see STAR Methods section Spine-Dendrite Coupling and Figure S3).

Discussion

Dendritic morphology is highly diverse across cell types and has a critical role in synaptic plasticity (Ebner et al., 2019) and computation (Vetter et al., 2001; Bird and Cuntz, 2016). To keep synapses functional, it is important to maintain protein supply across the dendritic tree (Nusser et al., 1997; Cottrell et al., 2000). The short half-life of proteins, only 5–7 days on average (Dörrbaum et al., 2018; Cohen and Ziv, 2019), together with the highly branched structure of the dendritic and axonal arbor, poses a severe trafficking challenge because every second, more than $\mathrm{50,000}$ proteins need to be synthesized, trafficked, and replaced. How this is accomplished across the complex, branching dendritic trees is still a puzzle. Existing models describing the protein dynamics in a dendritic tree often assume that the flow of proteins is independent of the daughter radius ratio at a branchpoint (Williams et al., 2016) and often simplify the complex morphology by a linear dendrite (Bressloff and Earnshaw, 2007; Fonkeu et al., 2019). This limits the ability to understand the functional consequences of dendritic morphology because many key features, such as dendritic radius ratios at branchpoints or lengths of dendritic segments, are not captured accurately. Here we present a model of passive dendritic protein dynamics that is based on experimentally measured dendritic morphologies and dendritic radius distributions. We derived mathematical predictions for the distribution of proteins by incorporating experimental data on protein degradation and synthesis, protein diffusion, dendritic radii, and dendritic morphology. We validated our model predictions using in situ protein distributions in cultured pyramidal neurons for two types of proteins: surface proteins moving within the plasma membrane and cytosolic proteins that diffuse in the cytoplasm of a dendrite. Our model and our experimental results offer insights into how proteins are supplied across the dendritic tree.

First we showed that the classic dendritic Rall exponent of 3/2 does not hold for all cell types. Instead, we found that the median Rall exponent is approximately $\alpha =2.28$ in EM-reconstructed PPC pyramidal cells ($\alpha =2.03$ for cultured pyramidal cells) and $\alpha =1.00$ in STG neurons (Otopalik et al., 2017). This indicates that the Rall exponent is not universal but a cell-type-specific feature, and it even varies within cells. While studying the consequences of dendritic branchpoints on protein flow in dendrites, we predicted that the ratio of dendritic radii determines the amount of proteins moving downstream toward the distal tips or upstream toward the soma. Specifically, we found that all Rall exponents larger than unity, as is the case for the median Rall exponent in STG and pyramidal neurons, facilitate motion of surface proteins toward distal sites to a greater degree than of cytoplasmic proteins. We confirmed the presence and amplitude of the expected forward bias, providing a visual display of the distribution of a cytoplasmic and surface protein in cultured hippocampal neurons. By measuring the relative fluorescence of surface and cytoplasmic proteins before and after branchpoints, we obtained a $35\text{\%}$ higher average forward bias for surface proteins, as predicted by our theory.

Second, we have shown, using EM-reconstructed branchpoints of pyramidal neurons, that the combination of daughter radii and the corresponding lengths of each daughter dendrite can facilitate protein transport for dendritic proteins. The protein diffusion lengths for which the dendritic branchpoints are optimized $\left(\lambda \sim 100\mu m\right)$ have significant overlap with the experimentally reported diffusion lengths of dendritic proteins.

Last, our results show that such daughter radius optimization has the capacity to reduce the total protein count needed to populate the dendritic arbor with proteins by up to four orders of magnitude relative to symmetrical daughter branches. These results underscore the surprising capacity of dendritic morphology to facilitate protein transport and reconcile it with other competing demands, including fast transmission of backpropagating APs (Stuart and Sakmann, 1994; Vetter et al., 2001) and electrical current transfer between somata and dendrites (Bird and Cuntz, 2016). Our results provide data-driven insights into how dendritic morphology is interwoven not only with electric signaling but also with protein dynamics. The data and mathematical framework we present here fill a crucial gap in the current understanding of the regulation of protein numbers in dendritic trees and the role of different molecular transport modes.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Papain	Sigma-Aldrich	P-3125
Neurobasal-A	Life Technologies	10888022
B27	GIBCO	17504044
GlutaMax	GIBCO	35050038
Effectene Transfection Reagent	QIAGEN	301425
Experimental Models: Cell Lines
Rat hippocampal cultured neurons from $P0-1$	Charles River Laboratories	RRID: RGD_734476
Experimental Models: Organisms/Strains
Rattus norvegicus, Sprague-Dawley	Charles River Laboratories	RRID: RGD_734476
Recombinant DNA
Plasmid: GFP::Nlg-1	Dean and Scheiffele, 2009	https://doi.org/10.1101/pdb.prot5315
Plasmid: pEGFP-N1	Clontech	6085-1
Software and Algorithms
Fiji	Schindelin et al., 2012	https://imagej.net/Welcome
MATLAB	MathWorks	https://www.mathworks.com/
Code and original data	This paper	http://www.tchumatchenko.de/SartoriEtAl.zip
Other
LSM880	Zeiss	https://blogs.zeiss.com/microscopy/news/de/zeiss-prasentiert-schnellen-bildaufnahmemodus-fur-lsm-880-mit-airyscan/?doing_wp_cron=1603981117.8288860321044921875000
Deposited Data
Dendritic data and code	Zenodo repository	Zenodo https://doi.org/10.5281/zenodo.4242977

Resource Availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Tatjana Tchumatchenko (tatjana.tchumatchenko@brain.mpg.de).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

Original source code and data for all figures in the paper have been deposited to gitLab https://gitlab.mpcdf.mpg.de/mpibr/tchu/branchingrules and zenodo (accession number: https://doi.org/10.5281/zenodo.4242977).

Experimental Model and Subject Details

Primary rat hippocampal culture

For protein distribution measurements we dissected hippocampi from postnatal day 0 to 1 rat pups of either sex (Sprague-Dawley strain; Charles River Laboratories). All experiments complied with national animal care guidelines and the guidelines issued by the Max Planck Society, and were approved by local authorities.

Mouse cortex

For the measure of dendrite diameter in adult pyramidal neuron we used posterior parietal cortex tissue from male adult (postnatal day 57) C57BL/6J mouse (see Karimi et al., 2020 for experimental details). All experimental procedures were performed according to the law of animal experimentation issued by the German Federal Government under the supervision of local ethics committees and according to the guidelines of the Max Planck Society. The experimental procedures were approved by Regierungspräsidium Darmstadt, under protocol ID V54 - 19c20/15 F126/1015 (LPtA, PPC-2) or V54 - 19 c 20/15 - F126/1002 (V2, PPC, ACC). The S1 sample was prepared following experimental procedures approved by Regierung von Oberbayern, 55.2-1-54-2532.3-103-12.

Method Details

Linear dendrite

The diffusion dynamics in Equation 1 along a linear dendrite of length L, at position x, has the following equilibrium distribution

$$\rho \left(x\right)=A{e}^{-x/\lambda }+B{e}^{+x/\lambda },$$ (Equation 9)

where A and B are determined by the no-flux boundary condition at the end of the dendrite (length L) and the total number of proteins, N, in the dendrite

$${\frac{\partial \rho \left(x\right)}{\partial x}|}_L=0\text{and}$$ (Equation 10)

$${\int }_0^L\rho \left(x\right)dx=N.$$ (Equation 11)

A and B are therefore equal to:

$$A=N\frac{1+\text{coth}\left(L/\lambda \right)}{2\lambda }\text{and}$$ (Equation 12)

$$B=A{e}^{-\frac{2L}{\lambda }},$$ (Equation 13)

leading to Equation 2. At equilibrium, the number of newly synthesized proteins and the number of proteins degraded along the

Bifurcations

The density distributions ${\rho }_i$ (proteins per unit length) for three branches $i=\mathrm{0,1,2}$ connected to a bifurcation need to satisfy three boundary conditions. For proteins diffusing within the cytoplasm, the volume densities, ${\rho }_i^C={\rho }_i/\pi R_i^2$, need to be continuous at the branch point, i.e., the volume densities of all branches need to be the same in this point. Analogously, for proteins diffusing on the surface, ${\rho }_i^S={\rho }_i/2\pi R_i$, the surface density needs to be equal. This leads to the first two boundary conditions:

$$R_0^{-\gamma }{\rho }_0\left(b\right)=R_1^{-\gamma }{\rho }_1\left(b\right)=R_2^{-\gamma }{\rho }_2\left(b\right)=\text{const},$$ (Equation 14)

where b indicates the branch point, and $\gamma =S,C$ for surface and cytoplasmic proteins, respectively. Additionally, the in- and out-fluxes at the branch point need to balance. If the coordinate x points away from the bifurcation, the influxes are given by $D\left(\partial \rho /\partial x\right)$, and therefore the third boundary condition is:

$${\sum _i\frac{\partial {\rho }_i}{\partial x}|}_b=0.$$ (Equation 15)

Discretization procedure

To simulate protein movement along a dendritic segment, we discretized Equation 1 using a finite difference method in space and the Euler-forward discretization in time to obtain the steady state. Numerical stability of the diffusion equation requires (Jaluria, 2002) $\text{Δ}t\le \text{Δ}{x}^2/\left(2D\right)$. For numerical convenience, we chose the limiting case $\text{Δ}t=\text{Δ}{x}^2/\left(2D\right)$.

Protein-based interpretation

The diffusion equation (Equation 1) with boundary conditions (Equations 14 and 15) describes the average dynamics of proteins performing a random walk in the cytoplasm or at the surface. Here we show which laws each individual protein follows. Along a dendrite, the probability of a protein moving in either direction is equal, see Figure 1, B.

At a bifurcation, see Figure 1, C, the proteins can move into one of the three possible directions, $i=\mathrm{0,1}$ or 2. The proteins at the branch point are re-distributed according to the cross-sectional areas and the circumference lengths of the branches for volume and surface diffusing proteins, respectively. Let us consider a pool of proteins, $N_b$, which is re-distributed within the branch point in each time step. This pool is equal to

$$N_b=\frac{p}{2}\sum _i{\rho }_i\left(\text{Δ}x\right),$$ (Equation 16)

where $p=2D\left(\text{Δ}t/\text{Δ}{x}^2\right)$ is the fraction of mobile proteins, and ${\rho }_i\left(\text{Δ}x\right)$ is the density per unit length in branch i, evaluated at the compartment at distance $\text{Δ}x$ from the branch point.

The probability $P_i^{\left(\gamma \right)}$ that a protein moves in direction i from the branch point is then proportional to the circumference or cross-section of the respective branch:

$$P_i^{\left(\gamma \right)}=\frac{R_i^{\gamma }}{R_0^{\gamma }+R_1^{\gamma }+R_2^{\gamma }}.$$ (Equation 17)

Here, $\gamma =S$ for surface proteins that diffuse in the plasma membrane, and $\gamma =S$ for cytoplasmic diffusion. The incoming flux per time step into branch i is then set equal to $p{P}_i^{\left(\gamma \right)}{N}_b$. For $\text{Δ}x,\text{Δ}t\to 0$, this is equivalent to the conditions in Equations 14 and 15.

Generalized Rall Rule

A generalized Rall’s Rule, Equation 4, is used to connect the radii of the mother and of the two daughter dendrites:

$$1=r_1^{\alpha }+r_2^{\alpha },$$ (Equation 18)

where $r_i=R_i/R_0$ is the normalized radius of the dendrite i. A non-negative value of α means that both daughter dendrites are smaller than the mother dendrite, and therefore $r_i\le 1$.

A negative value of α means that both daughter dendrites are bigger than the mother dendrites, and therefore $r_i\ge 1$. A complex value of α means that one of the two daughter dendrites is smaller than the mother dendrite and the other is bigger: $r_1>1>r_2$. In Figures 2A–2E, we show the scatterplot of experimentally measured values of the normalized maximum radius versus the normalized minimum radius. The three background colors reflect the three possible regimes of Rall exponents.

Radii measurements in cultured neurons

To calculate the Rall exponent distribution for cultured neurons and compare it to its EM-reconstructed counterpart, we manually measured the mother and daughter diameters at branch points of cultured pyramidal neurons (n = 68). To this end, we analyzed the fluorescence signal of GFP or GFP::Neuroligin-1a in these neurons around the branch points (Figure 2G). In an area of $2-5\mu m$ around the branch point we manually measured the mother and daughter diameters in dendrites whose thickness was greater than 3 pixels, four times, and calculated the average diameter.

Spine-Dendrite coupling

Our result in Equation 14 can be generalized to understand spine-dendrite coupling. If the size of a synapse is considerably smaller than the diffusion length of a protein, which can justified by the following consideration $R_{neck},R_{spine}\approx 1\mu$m $\ll \lambda \approx 100\mu$m, the local density of protein in the spine and dendrite are equal. In this case, the number of proteins inside the spine and in the local dendritic segment is equal and proportional to the volume or surface of these structured. To calculate the protein number in the spine relative to the local dendritic segment, we use a simplified geometric model (Figure S3), where a spine has a cylindrical neck of length $L_{\text{neck}}$, radius $R_{\text{neck}}$ and a spherical spine head with radius $R_{\text{spine}}$. The protein density in the spine and in the dendrite is equal in this scenario, but the protein number is determined by the spine versus dendrite space. We consider the ratio of protein numbers inside the spine and in an interval of dendrite around the spine and calculate the ratio of the two:

$$N_{spine}=N_{dend}\{\begin{array}{cc}\frac{S_{spine}}{S_{dend}},& \text{surface}\\ \frac{V_{spine}}{V_{dend}},& \text{cytoplasm}\end{array}=N_{dend}\{\begin{array}{cc}\frac{2\pi r_{\text{neck}}{L}_{\text{neck}}+4\pi R_{\text{spine}}^2}{2\pi R_{\text{dend}}\text{Δ}L},& \text{surface}\\ \frac{\pi r_{\text{neck}}^2{L}_{\text{neck}}+\frac{4}{3}\pi R_{\text{spine}}^3}{\pi R_{\text{dend}}^2\text{Δ}L},& \text{cytoplasm},\end{array}$$ (Equation 19)

where $\text{Δ}L$ is a small dendritic segment around the spine, $\text{Δ}L=1\mu m$ in the Figure S3 to mimic the typical distance of spines in a pyramidal neuron. In the Figures S3B–S3E, we show the fraction of proteins in the spine relative to the local dendritic segment, $N_{spine}/\left(N_{spine}+N_{dendrite}\right)$, while varying the spine neck radius and length, spine head radius and the dendritic radius.

Detailed calculations of optimal branch radii and optimal diffusion lengths

We considered a branch point where the daughter dendrites had different lengths, $L_1$ and $L_2$ (Figure 5A). We assumed that the same dendritic density of proteins was needed at the tip of each daughter branch to maintain the synaptic copy numbers at the dendritic tips. Therefore, the daughter radii after the branch point needed to be such that more proteins diffused toward the longer branch.

Then, we calculated the optimal daughter radii ratio resulting in equal protein density values at the tips of the daughter branches. We started by considering the density of proteins in the mother dendrite and the two daughter dendrites as given by Equation 2. We were interested in a solution where ${\rho }_1\left(L_1\right)={\rho }_2\left(L_2\right)$. This occurs when

$$\frac{N_1}{\text{sinh}\left(L_1/\lambda \right)}=\frac{N_2}{\text{sinh}\left(L_2/\lambda \right)}$$ (Equation 20)

whereby $N_1$ and $N_2$ denote the total number of proteins in the dendritic segments of length $L_1$ and $L_2$, respectively. Considering that the number of proteins at the branch point must fulfill the branching conditions (Equation 14,) we obtained

$$\frac{{\rho }_1\left(0\right)}{r_1^{\gamma }}=\frac{{\rho }_2\left(0\right)}{r_2^{\gamma }}.$$ (Equation 21)

Combining Equations 20 and 21 we obtained

$$\frac{r_2}{r_1}={\left(\frac{\text{cosh}\left(L_2/\lambda \right)}{\text{cosh}\left(L_1/\lambda \right)}\right)}^{1/\gamma },$$ (Equation 22)

where $\gamma =1$ denotes diffusion of surface proteins and $\gamma =2$ the diffusion of cytoplasmic proteins. If the thicker branch is not the longer branch, then Equation 22 does not have a real solution, which occurred for 9 of the 28 analyzed branches.

We used this relation to obtain the optimal λ for EM-reconstructed branch points in which $L_1,L_2$ and $r_1,r_2$ had been measured using methods described in the STAR Methods section “Dendrite diameter measurement in three-dimensional electron microscopy.” We used this procedure to obtain optimal inferred λ in Figure 5C (blue and red histograms). Out of the 65 measured branch points, 28 were terminal branches. To these we could directly apply Equation 22. Our inversion procedure converged for 19 branch points and led to a finite value for the optimal λ.

The result is summarized in Figure 5C in blue and red bars. As expected, the optimal λ for diffusion of surface proteins is bigger than the corresponding value for cytoplasmic proteins.

The median optimal λ for diffusion on the surface is $109\mu m$ and its $50\text{\%}$ confidence interval is $\left(\mathrm{58,197}\right)\mu m$; while the median value of λ for proteins diffusing in the cytoplasm is $65\mu m$ and its $50\text{\%}$ confidence interval is $\left(\mathrm{32,132}\right)\mu m$. As a comparison to experimental reports of dendritic proteins, we present the same statistics for the diffusion lengths of 26 dendritic proteins in the Table S1.

Cost for non-optimal daughter radii

We denote the total number of proteins needed to ensure at least one protein is at the end of each dendritic branch by $N=N\left(r_1,r_2\left(r_1\right),L_1,L_2,\lambda \right)$. For each choice of $r_1$, the minimum values of N is obtained when $r_1/r_2$ satisfied Equation 22. We refer to it as the optimal number. It is equal to the inverse of the density of proteins at either dendritic tip:

$$N^{\text{opt}}\left(\lambda ,r_1\right)=\frac{1}{{\rho }_1\left(L_1,r_1,r_2^{\text{opt}}\left(r_1\right),\lambda \right)}=\frac{1}{{\rho }_2\left(L_2,r_1,r_2^{\text{opt}}\left(r_1\right),\lambda \right)}.$$ (Equation 23)

If the radii ratio differs from the optimal ratio, then the minimum number of proteins N, needed to guarantee at least one protein at the end of both daughter dendrites is higher and equal to the inverse of the minimum density of proteins at the dendritic tips:

$$N^{\text{non}-\text{opt}}\left(\lambda ,r_1\right)=\frac{1}{\text{min}\left({\rho }_1\left(L_1,r_1,r_2\left(r_1\right),\lambda \right),{\rho }_2\left(L_2,r_1,r_2\left(r_1\right),\lambda \right)\right)}.$$ (Equation 24)

The percentage cost for non-optimality is therefore defined as the rescaled ratio of Equations 24 and 23:

$$\text{\%}C=\left(\frac{N^{\text{non}-\text{opt}}}{N^{\text{opt}}}-1\right)\cdot 100$$ (Equation 25)

Note that a given ratio $r_1/r_2$ alone is not sufficient to determine the optimal N, it is also necessary to know $r_2$. In Figure 5D we set $r_2$ to be the median measured value of r in 3D-EM pyramidal neuron (Figures 2B and 2D). We then varied the dendritic radius $r_1$, and we further assumed $\lambda =110\mu m$. We set the dendritic lengths $L_1$ and $L_2$ such that they represented the minimal experimentally measured $L_1/L_2$ ratio: $L_1=48.5\mu m$ and $L_2=114.5\mu m$.

Cost for non-optimal diffusion lengths

Considering the diversity of the protein diffusion coefficients and half-lives, one could expect a variety of diffusion lengths (Figure 5C). To this end, we aimed to quantify the cost associated with non-optimal diffusion length. For each branch point k, and diffusion length λ, we calculated $N_k^{\text{opt}}\left(\lambda \right)$ and $N_k^{\text{non}-\text{opt}}\left(\lambda \right)$ as in Equations 23 and 24. For $N_k^{\text{opt}}\left(\lambda \right)$ we assumed $r_2$ to be equal to the median value of the relative radius, as in the previous section and $r_1$ we obtained from Equation 22. For $N_k^{\text{non}-\text{opt}}\left(\lambda \right)$ we used the measured values of $r_1$ and $r_2$. We defined the percentage cost for non-optimal diffusion length analogously to Equation 25, averaged over branches:

$$\text{\%}C=\left(\begin{array}{c}\text{median}\\ k\end{array}\left[\frac{N^{\text{non}-\text{opt}}}{N^{\text{opt}}}\right]-1\right)\cdot 100$$ (Equation 26)

and used this quantity in Figure 5E.

Synthetic dendritic trees

We considered synthetic dendritic trees in order to control the number and the location of branch points. Each tree was constructed as follows. First, the soma was connected to primary dendrites of length $L=500\mu m$, $L=167\mu m$ or $56\mu m$. Next, at each termination point in the red and the green graphs two additional dendrites of the same length were added. This procedure was repeated twice for the red graph, and eight times for the green graph. In each tree, we chose symmetrical daughter radii where the normalized ratio is equal to the median value of the normalized radii, from Figure 2F, $R_1=R_2=0.75R_0$.

To simulate the distribution of proteins along each synthetic tree, we injected N proteins at the soma at $t=0$ and measured the distribution at the equilibrium, to obtain the protein density we divided the number of proteins by N. We integrated the protein numbers at distance d across all dendrites both for surface and for cytoplasm diffusion, and calculate their ratio (Figure 6B):

$$\text{Ratio}\text{S}/\text{C}=\frac{{\sum }_{x:\left|x-0\right|=d}{\rho }^S\left(x\right)}{{\sum }_{x:\left|x-0\right|=d}{\rho }^C\left(x\right)}$$ (Equation 27)

Optimization algorithm

Equation 8 determines the optimal ratio of the daughter radii for terminal branches. However, it cannot be used for non-terminal branches. We therefore extended the optimality concept to comprise non-terminal branches and to collapse each branch into an equivalent linear dendrite of effective length $L_{\text{eff}}$. To find the value of the effective length, first we optimize the radii of the terminal branch, and then we calculate the decay in density in the original branch from the root of the mother dendrite to the tip of one of the two daughters. And, finally, we impose this ratio to be equal to the ratio of an effective dendrite, ${\rho }_{\text{eff}}\left(x\right)$, without branches, of length $L_{\text{eff}}$:

$$\frac{{\rho }_i\left(L_i\right)}{{\rho }_0\left(0\right)}=\frac{{\rho }_{\text{eff}}\left(L_{\text{eff}}\right)}{{\rho }_{\text{eff}}\left(0\right)}.o$$ (Equation 28)

$L_{\text{eff}}$ can be obtain analytically from Equation 28, and its value depends on the lengths of the dendritic segments, $L_0$, $L_1$, $L_2$, on the diffusion length λ, the Rall exponent α, and the value of γ ($\gamma =1$ for surface diffusion and $\gamma =2$ for cytoplasmic diffusion).

This procedure allowed us to calculate the effective length for the whole dendritic arbor as ${\text{N}}^{\text{th}}$-to-terminal branches are progressively collapsed into a linear dendrite of growing $L_{\text{eff}}$, which became the daughter dendrite of the next branch.

Numerical convergence

We considered in Figure 6 the limiting case of surface and cytoplasmic proteins with the same diffusion coefficient and half-life: $D=0.36\mu m^2/s$, and ${\tau }_{1/2}=5.0$ days. We calculated the protein distributions by iterating the dynamical equations forward until the difference between two consecutive time points was smaller than $\mathit{\epsilon }={10}^{-10}$:

$$\mathit{\epsilon }>\underset{x}{\text{max}}\left(\left|1-\frac{\text{min}\left({\rho }_{\text{new}}\left(x\right),{\rho }_{\text{old}}\left(x\right)\right)}{\text{max}\left({\rho }_{\text{new}}\left(x\right),{\rho }_{\text{old}}\left(x\right)\right)}\right|\right).$$ (Equation 29)

Hippocampal neuron preparation

Dissociated rat hippocampal neuron cultures were prepared and maintained essentially as described previously (Aakalu et al., 2001; Banker and Goslin, 1990). Briefly, we dissected hippocampi from postnatal day 0 to 1 rat pups of either sex (Sprague-Dawley strain; Charles River Laboratories), dissociated them with papain (Sigma) and plated them at a density of 40–30 $\times$ 10³ cells/cm² onto poly(d-lysine)-coated (BD Biosciences) glass-bottom Petri dishes (MatTek). Hippocampal neurons were maintained, fed weekly with a neuronal growth medium and allowed to mature in a humidified atmosphere at 37° C and 5% CO₂ in a growth medium (Neurobasal-A supplemented with B27 and GlutaMAX-I, Life Technologies) for 8 days in vitro.

Neuron transfection

Glass-bottom dishes with cultured hippocampal neurons were transfected after 7 days in vitro with plasmids coding for either GFP (cytoplasmic protein) or GFP::Neuroligin-1 (GFP::Nlg-1, which is a surface protein expressed at the dendritic surface). Transfections were performed using Effectene (QIAGEN) according to the supplier recommendations with 0.5 μg DNA per MatTek (18 mm diameter). Cells were fixed 13 hours after transfection in vitro in paraformaldehyde 4% in a lysine phosphate buffer (pH = 7.4) containing 2.5% of sucrose for 30 min at room temperature. Nuclei were stained for 1 min in PBS with DAPI (Sigma-Aldrich, 1:1000). Cells were kept at 4° C in PBS until imaging, up to 4 days following fixation.

Image acquisition

Hippocampal neurons were imaged using a Zeiss LSM780 confocal microscope using a 40X oil objective (NA 1.4). Z stacks spanning the entire volume of neurons were acquired.

Full dendritic reconstructions of pyramidal neurons

To calculate the average protein distribution in pyramidal neurons (black line in Figure 6B) we simulated the protein distribution in 65 hippocampal pyramidal morphologies and obtained their average. To this end, we started with 5813 reconstructed hippocampal C1 pyramidal neurons from the NeuroMorpho database (Ascoli et al., 2007) and imposed the following criteria to obtain a homogeneous population of 65 hippocampal pyramidal neurons. From the initial pool of morphologies, we excluded those containing branch points with three daughter dendrites, we required that each morphology had at least 75 branch points at 900 μ from the soma, that at least the $15\text{\%}$ of the total dendritic length belonged to the apical dendrite and that the total dendritic length was at least 15000 $\mu m$. To ensure that the distal dendrites were densely reconstructed, we selected morphologies where at least $1\text{\%}$ of the total dendritic length was located in the most distal region, corresponding to $90\text{\%}$ or more of the maximum distance from the soma. Of the 65 reconstructions that met these criteria, we extracted the dendritic tree (without axon) from each and replaced the soma by a point source. All reconstructed dendritic trees contained information about the location of branch points and the lengths of dendritic segments. We considered two branching rules for the radii: either symmetric, using the equal daughter radii, $r_1=r_2=0.75$, or optimized radii for the Rall exponent $\alpha =2.28$. We then inserted at the soma N proteins, where N is the minimum number such that each micrometer of dendrite contains at least 1 protein: $N=1/\text{min}\left[\rho \left(x\right)\right]=2\cdot {10}^{12}$.

Quantification and Statistical Analysis

Dendrite diameter measurement in three-dimensional electron microscopy

To measure the diameter of dendrites around branch points, we used a three-dimensional electron microscopy volume acquired using serial block-face imaging (Denk and Horstmann, 2004) from adult mouse posterior parietal cortex (PPC-2 dataset, see Karimi et al., 2020 for experimental details). The dataset contained L1-5 of cortex and allowed for reconstruction of dendrites from layer 2-5 pyramidal neurons. The three-dimensional skeleton of 35 apical dendrites were reconstructed using webKnossos (Boergens et al., 2017). Next, we selected a random subset of branch points for measuring the diameter of the mother and two daughter branches (n = 39 branch points). Since dendrites taper in diameter, we used a distance of at least $3-4\mu m$ from the branch point, where the dendriteâ€s diameter was stable. The data slice that was most orthogonal to the dendritic path was used for diameter annotation to avoid overestimation. Furthermore, the dendrite diameter was measured along two axes to estimate the elliptical shape of the cross-section. In addition, we searched for terminal branches, where the exact length and diameter of each daughter branch were measured (n = 29 branches). The diameter annotations were retrieved as an NML file (XML-based file format) and exported to MATLAB (MathWorks, USA, 2019a) for diameter length extraction.

Image analysis

The fluorescence signals from GFP and GFP::Neuroligin 1a (GFP::Nlg-1) were each obtained using the open-source image processing package Fiji, while the data analysis was performed in MATLAB R2017b (MathWorks). In our analysis, we used 31 branch points for the GFP-expressing neurons and 39 for GFP::Nlg-expressing neurons. First, we tracked all dendritic branches where the signals of the mother and of the daughter dendrites were unambiguous and not overlapping with other dendrites. For each branch point, we manually selected triplets consisting of two daughter and one mother Regions Of Interest (ROIs). For each of these ROIs, we quantified the spatial dependent fluorescence signal $f_i\left(x\right)$ and considered the integrated fluorescence.

$$F_i={\int }_m^{m+\text{Δ}}{f}_i\left(x\right)dx,$$ (Equation 30)

where m is the minimum distance from the branch point and $\text{Δ}$ is the length of the considered integral (Figure 6B). Assuming that the intensity of the fluorescence is proportional to the number of molecules present in that area, we were able to link the integrated fluorescence Equation 30 to the number of proteins in this region of dendrite:

$$F_i={\int }_m^{m+\text{Δ}}{f}_i\left(x\right)dx=k{\int }_m^{m+\text{Δ}}{\rho }_i\left(x\right)dx=k{N}_i$$ (Equation 31)

Next, we expressed the daughters-to-mother ratio for GFP and GFP::Nlg-1 using the respective fluorescence intensities:

$${\mathcal{Q}}_F^{S\text{or}C}=\frac{F_1+F_2}{F_0}.$$ (Equation 32)

For each couple of $m=0-4$ and $\text{Δ}=1-4$, we showed the bootstrapped mean of ${\mathcal{Q}}_F^{S\text{ or }C}$ in Figure 4D, and the value of ${\mathcal{Q}}_F^{S/C}={\mathcal{Q}}_F^S/{\mathcal{Q}}_F^C-1$ in Figure 4E.

Published: November 17, 2020