Summary
In this article, we develop a graphical modeling framework for the inference of networks across multiple sample groups and data types. In medical studies, this setting arises whenever a set of subjects, which may be heterogeneous due to differing disease stage or subtype, is profiled across multiple platforms, such as metabolomics, proteomics, or transcriptomics data. Our proposed Bayesian hierarchical model first links the network structures within each platform using a Markov random field prior to relate edge selection across sample groups, and then links the network similarity parameters across platforms. This enables joint estimation in a flexible manner, as we make no assumptions on the directionality of influence across the data types or the extent of network similarity across the sample groups and platforms. In addition, our model formulation allows the number of variables and number of subjects to differ across the data types, and only requires that we have data for the same set of groups. We illustrate the proposed approach through both simulation studies and an application to gene expression levels and metabolite abundances on subjects with varying severity levels of chronic obstructive pulmonary disease. Bayesian inference; Chronic obstructive pulmonary disease (COPD); Data integration; Gaussian graphical model; Markov random field prior; Spike and slab prior.
Keywords: Bayesian inference, Chronic obstructive pulmonary disease (COPD), Data integration, Gaussian graphical model, Markov random field prior, Spike and slab prior
1. Introduction
Gaussian graphical models, which describe the dependence relations among a set of random variables, have been widely applied to estimate biological networks on the basis of high-throughput data. When all samples are collected under similar conditions or reflect a single type of disease, methods such as the graphical lasso (Meinshausen and Bühlmann, 2006; Yuan and Lin, 2007; Friedman and others, 2008) or Bayesian network inference approaches (Roverato, 2002; Wang and Li, 2012) can be applied to infer a sparse network. In many studies, however, such as the COPDGene study (Regan and others, 2010) of this article, described below, samples are obtained for different subtypes or disease, varying experimental settings, or other heterogeneous conditions. In this setting, applying standard graphical model inference approaches to the pooled data across conditions will lead to spurious findings, while separate estimation for each subgroup reduces statistical power. The challenge becomes even more formidable when multiple data types (or platforms) are under consideration, specifically gene expression levels and metabolite abundances in the COPDGene study, measured on multiple subjects. In this case, pooling the data is not appropriate, as it ignores the fact that direct connections between variables of different data types may not be sensible. Nonetheless, analyzing data from each platform separately ignores potential commonalities, for example, that subjects with more advanced disease may have more extensive disruption of functional mechanisms across data types. The need for statistical methods to address these questions is particularly pressing given the increasing number of studies investing in comprehensive profiling of subjects across multiple data platforms. Our proposed statistical method enables joint inference of networks across sample groups and data types, providing accurate characterization of complex disease mechanisms which can be used to develop targeted treatment approaches.
Recently, methods have been proposed to estimate multiple networks on a common set of variables. Early work includes approaches that encourage either common edge selection or precision matrix similarity by penalizing cross-group differences (Guo and others, 2011; Danaher and others, 2014; Zhu and others, 2014; Cai and others, 2016). These methods use a single penalty parameter to control network similarity across all groups. Hao and others (2018) have extended the approach to simultaneously infer graph clustering via an additional penalty on the estimated cluster mean. In contrast, more recent proposals encourage network similarity in a more tailored manner, assuming that the networks for each sample group are related within a tree structure (Oates and Mukherjee, 2014), or, more generally, within an undirected weighted graph (Saegusa and Shojaie, 2016; Ma and Michailidis, 2016). These methods require that the cross-group relations are known a priori or inferred in a preliminary step. More flexible approaches that employ Bayesian frameworks to simultaneously learn the networks for each group and their similarity have been proposed in Peterson and others (2015) and Shaddox and others (2018).
In this work, we develop a graphical modeling framework which enables the joint inference of network structures when there is heterogeneity among both sets of subjects (i.e., at different stages of a disease) and sets of variables (i.e., types of data or platforms). Our proposed Bayesian hierarchical model first links the network structures within each platform using a Markov random field (MRF) prior to relate edge selection across the sample subgroups, and then links the measures of cross-group similarity across platforms. This is a flexible modeling approach, which allows the number of variables and number of subjects to differ across the data types, and only requires that we have data for the same set of subgroups. Consider for example, the gene expression and metabolite abundances measured on healthy controls and on moderate and severe COPD subjects of our case study. These two platforms measure different aspects of the same biological pathway. Small compounds and metabolites are measured by the LC/MS platform, while gene expression levels of enzymes and proteins are measured by the microarray platform. Also, alterations in the pathway affect different components (metabolites or enzymes) of the pathway. In this type of scenario, we can expect data between the two platforms to be related. Our modeling framework is concerned with two types of network similarity-within and between platforms. Within each platform, we assess how similar subgroups are in terms of their graph structure. This results in a super-graph for each platform expressing whether two subgroups are similar, i.e., connected, within each platform. We then assess whether or not these super graphs are similar between platforms. This approach enables the joint estimation of the biological networks in a flexible manner, as we make no assumptions on the directionality of influence across the data types, nor on the extent of network similarity across the sample groups and platforms. In this regards, our approach differs from many of the existing methods for integrative analysis, that typically model the association between different types of observed random variables assuming a direction of influence among the data types, see for example Wang and others (2013) and Cassese and others (2014) for the use of multi-component hierarchical models, Chen and others (2015) for mixed graphical models, and Lin and others (2016) for a multi-layered Gaussian graphical model where directed edges are allowed across layers of each data type. Instead, we infer measures of relative similarity based on the data, which provide valuable insight into the extent of network relatedness across sample groups and data types.
The article is organized as follows. We present the motivating chronic obstructive pulmonary disease (COPD) case study in Section 2. In Section 3, we describe the proposed Bayesian model and procedures for posterior inference. We return to the COPD data set in Section 4, where we apply our proposed method to infer metabolic and gene co-expression networks for varying disease stages. Section 5 provides simulations studies illustrating the performance of the proposed method against competing approaches. Finally, we conclude with a discussion in Section 6.
2. The COPDGene study
Our work has been motivated, in particular, by a collaborative study aimed at understanding
how cellular metabolic and gene expression networks are disrupted by COPD, the 3rd leading
cause of death in the United States (National Center for
Health Statistics, 2016), and one of the top causes of hospitalization. While
smoking is the primary risk factor for COPD, only 20% of smokers will ever develop the
disease. There is a poor understanding of risk factors accounting for disease
susceptibility, as well as the underlying pathogenic mechanisms resulting in airway
inflammation and emphysema. Understanding the genetic, clinical, and molecular factors that
determine why some smokers develop COPD is the primary motivation of the NIH funded
multicenter observational study, COPDGene, which has over 10 000 participants and includes
extensive molecular profiling using transcriptomics, metabolomics, and proteomics. For this
study, subjects 45–80 years old with at least a 10 pack-year history of smoking were
recruited and biomarker measurements were attained from blood (Regan and others, 2010). There is a high degree of
heterogeneity in the patient population, which includes subjects from various clinical
stages, defined using the global initiative for chronic obstructive lung disease (GOLD)
staging criteria. We apportioned subjects according to GOLD COPD stages and model resulting
networks for a control group (GOLD stage = 0), a mild or moderate group (GOLD stage = 1 or
2), and a severe group (GOLD stage = 3 or 4). Here, we focus in particular on a subset of
subjects for whom gene expression levels or metabolite abundances are available. For the
gene platform, this apportionment resulted in a control group (GOLD stage = 0) of 42
subjects, a mild or moderate group (GOLD stage = 1 or 2) of 42 subjects, and a severe group
(GOLD stage = 3 or 4) of 42 subjects. For the metabolite platform, the control group again
had 42 subjects, whereas the moderate and severe group had 45 and 44 subjects, respectively.
Ten subjects had GOLD stage 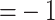 , indicating that although they had
abnormal lung function, they did not satisfy the clinical criteria for COPD. Therefore,
these subjects were excluded from the analysis. This data set illustrates the need for our
proposed method, which can be used to analyze the multi-platform data across the
heterogenous patient groups in a coherent and integrative fashion. In summary, this article
is concerned with the analysis of data measured on two platforms, genes and metabolites, for
three subgroups of subjects classified by COPD GOLD stage.
, indicating that although they had
abnormal lung function, they did not satisfy the clinical criteria for COPD. Therefore,
these subjects were excluded from the analysis. This data set illustrates the need for our
proposed method, which can be used to analyze the multi-platform data across the
heterogenous patient groups in a coherent and integrative fashion. In summary, this article
is concerned with the analysis of data measured on two platforms, genes and metabolites, for
three subgroups of subjects classified by COPD GOLD stage.
3. Proposed method
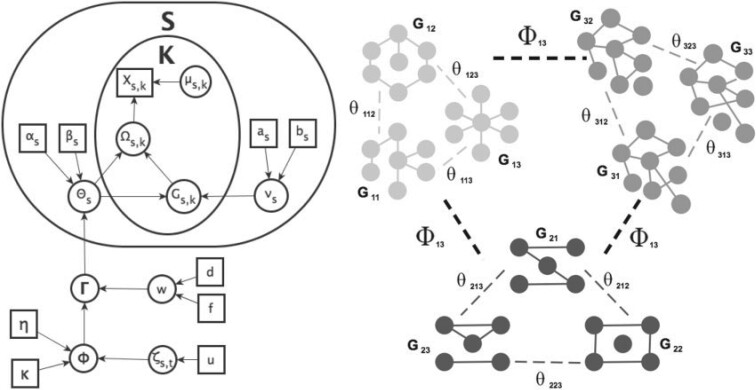
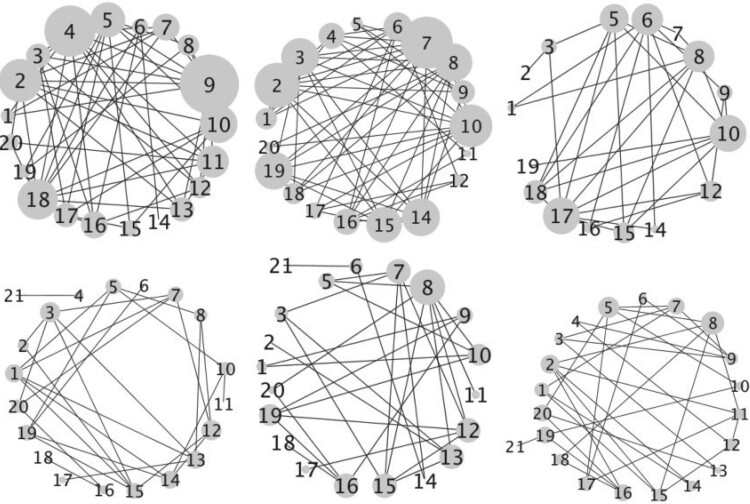
In this section, we provide details on the proposed method, including the likelihood, prior formulation, and procedures for posterior inference. Graphical representations are provided in Figure 1.
Fig. 1.
Left: Graphical model representation of the proposed model,
illustrating variables, parameters, and hyper parameters for each of the
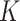 groups and
groups and 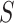 platforms.
Right: A graphical illustration with
platforms.
Right: A graphical illustration with 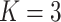 subgroups
and
subgroups
and 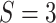 platforms.
platforms.
3.1. Likelihood
Suppose, we observe data on 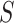 data types and
data types and 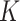 subgroups. In
our COPDGene case study, we have
subgroups. In
our COPDGene case study, we have 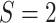 and
and 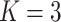 . For each
subgroup and each platform, let
. For each
subgroup and each platform, let 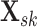 be the
be the
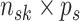 data matrix, with
data matrix, with
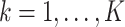 indexing the subgroup,
indexing the subgroup,
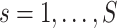 indexing the platform type,
indexing the platform type,
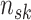 the sample size for subgroup
the sample size for subgroup
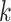 from platform
from platform 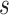 , and
, and
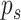 the total number of observed variables
for platform
the total number of observed variables
for platform 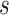 . Assuming that the samples are
independent and identically distributed within each of the
. Assuming that the samples are
independent and identically distributed within each of the 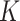 subgroups and
subgroups and
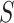 platforms, we can write the likelihood for
subject
platforms, we can write the likelihood for
subject 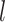 in subgroup
in subgroup 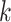 and platform
and platform
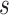 as the multivariate normal distribution
as the multivariate normal distribution
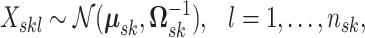 |
(3.1) |
where the mean vector 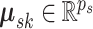 and precision matrix
and precision matrix 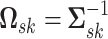 are specific to subgroup
are specific to subgroup 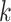 and platform
and platform 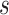 . For
simplicity, we column center the data for each subgroup, and therefore, assume
. For
simplicity, we column center the data for each subgroup, and therefore, assume
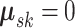 . We note that
. We note that
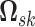 is constrained to the
space
is constrained to the
space 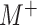 of
of 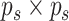 positive-definite symmetric matrices. We denote the entry in the
positive-definite symmetric matrices. We denote the entry in the 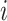 th row and
th row and
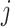 th column of
th column of 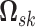 as
as
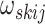 .
.
3.2. Prior formulation
The patterns of zeros in the precision matrices 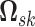 correspond to undirected graphs among the variables. Specifically,
correspond to undirected graphs among the variables. Specifically,
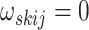 if and only if the
corresponding edge
if and only if the
corresponding edge 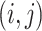 is missing in the conditional
dependence graph for subgroup
is missing in the conditional
dependence graph for subgroup 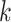 from platform
from platform 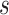 . The goal of
our modeling formulation is to infer a sparse version the precision matrices
. The goal of
our modeling formulation is to infer a sparse version the precision matrices
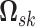 in a manner that links
inference across platforms.
in a manner that links
inference across platforms.
The graph for each platform 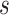 and subgroup
and subgroup 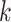 can be defined
by a set of vertices
can be defined
by a set of vertices 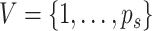 and edges
and edges
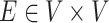 , and may be expressed as a
symmetric binary matrix
, and may be expressed as a
symmetric binary matrix 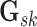 , where each off-diagonal
element
, where each off-diagonal
element 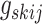 denotes the inclusion of edge
denotes the inclusion of edge
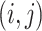 . Our proposed model first links the
edge inclusion indicators across sample subgroups within each platform, and then links
platforms based on the dependences across subgroups within each platform. We now describe
in detail the components of our prior.
. Our proposed model first links the
edge inclusion indicators across sample subgroups within each platform, and then links
platforms based on the dependences across subgroups within each platform. We now describe
in detail the components of our prior.
3.2.1. Mixture prior on precision matrix elements.
We rely on the mixture prior proposed in Wang
(2015) to infer a sparse version of 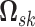 .
This prior is attractive as it allows direct modeling of the latent graph
.
This prior is attractive as it allows direct modeling of the latent graph
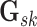 and is computationally
scalable. Mathematically, it can be expressed as a product of
and is computationally
scalable. Mathematically, it can be expressed as a product of 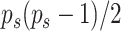 normal mixture densities on the off-diagonal elements, and
normal mixture densities on the off-diagonal elements, and 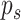 exponential densities on the diagonal elements, normalized to have total probability of
one. This is equivalent to a hierarchical model
exponential densities on the diagonal elements, normalized to have total probability of
one. This is equivalent to a hierarchical model
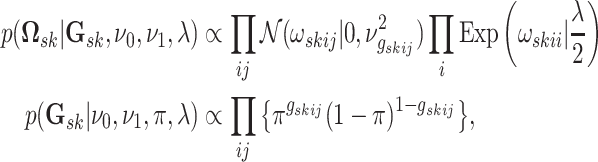 |
(3.2) |
where 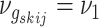 if edge
if edge
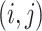 is present in graph
is present in graph
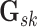 and
and
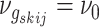 otherwise, with
otherwise, with
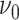 (
(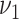 ) being set to a
small number. The two component normal mixture model has been shown to be a successful
prior in the context of variable selection, which in our case is equivalent to edge
selection, and the choice of hyperparameters
) being set to a
small number. The two component normal mixture model has been shown to be a successful
prior in the context of variable selection, which in our case is equivalent to edge
selection, and the choice of hyperparameters 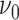 and
and
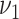 has been closely studied by George and McCulloch (1993). If for example,
has been closely studied by George and McCulloch (1993). If for example,
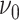 is chosen to be small, the event
is chosen to be small, the event
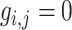 indicates that the edge
indicates that the edge
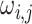 comes from the
comes from the
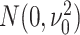 or diffuse component of the
mixture, and consequently
or diffuse component of the
mixture, and consequently 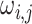 is closer to zero and can be
estimated as zero. In contrast, if
is closer to zero and can be
estimated as zero. In contrast, if 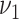 is chosen to be large, the event
is chosen to be large, the event
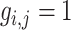 means
means 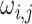 comes from the other component
comes from the other component 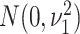 and
and
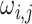 can then be thought of as
substantially different from zero.
can then be thought of as
substantially different from zero.
3.2.2. MRF priors for linked network inference.
MRF priors (Besag, 1974) have been successfully employed to capture network structure among the variables in Bayesian variable selection modeling frameworks (Li and Zhang, 2010; Stingo and others, 2011) and more recently to link the selection of edges across multiple networks (Peterson and others, 2015; Shaddox and others, 2018). Here, we build upon this line of work and utilize MRF priors both to link edge selection across networks within a platform, and to link the network similarity parameters across platforms.
Prior linking networks within each platform: Let
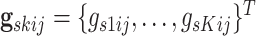 represent the vector of binary inclusion indicators of edge
represent the vector of binary inclusion indicators of edge 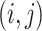 across
the
across
the 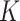 graphs for platform
graphs for platform
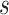 . We define a MRF prior on this vector of
binary inclusion indicators, linking edge selection across networks within a platform as
. We define a MRF prior on this vector of
binary inclusion indicators, linking edge selection across networks within a platform as
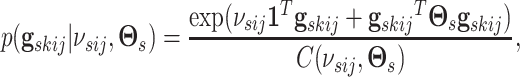 |
(3.3) |
with 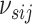 a sparsity parameter and
a sparsity parameter and
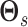 a
a
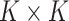 symmetric matrix characterizing
pairwise relatedness across sample subgroups. The diagonal elements of
symmetric matrix characterizing
pairwise relatedness across sample subgroups. The diagonal elements of
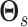 are constrained to be
0, while the off-diagonal elements
are constrained to be
0, while the off-diagonal elements  drive the within
platform similarity and link the edge selection between sample subgroups
drive the within
platform similarity and link the edge selection between sample subgroups
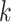 and
and 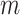 , such that a larger
magnitude represents increased preference for shared similar structure between those two
subgroups. In our experience, these entries can be interpreted on a relative rather than
an absolute scale, as magnitude can vary depending on hyperparameter settings, although
ordering is generally preserved. Additionally, the vector of binary inclusion indicators
allows easy interpretation of the off-diagonal elements of
, such that a larger
magnitude represents increased preference for shared similar structure between those two
subgroups. In our experience, these entries can be interpreted on a relative rather than
an absolute scale, as magnitude can vary depending on hyperparameter settings, although
ordering is generally preserved. Additionally, the vector of binary inclusion indicators
allows easy interpretation of the off-diagonal elements of 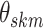 as regression coefficients of a probit model. If we introduce the notation
as regression coefficients of a probit model. If we introduce the notation
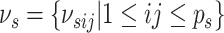 ,
then we can write the joint prior across graphs
,
then we can write the joint prior across graphs 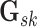 for
platform
for
platform 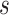 as the product of the densities for
each edge as
as the product of the densities for
each edge as
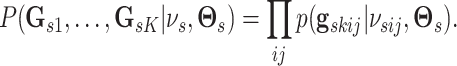 |
(3.4) |
Imposing sparsity on the matrix 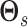 results in a
“super-graph” describing relatedness of the networks across the sample subgroups, with
zero entries indicating that the networks are sufficiently different that edge selection
should not be shared. This is achieved assuming a spike-and-slab prior on the
off-diagonal entries of
results in a
“super-graph” describing relatedness of the networks across the sample subgroups, with
zero entries indicating that the networks are sufficiently different that edge selection
should not be shared. This is achieved assuming a spike-and-slab prior on the
off-diagonal entries of 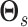 , with a Gamma as the
slab, since only positive values for
, with a Gamma as the
slab, since only positive values for 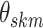 are
sensible,
are
sensible,
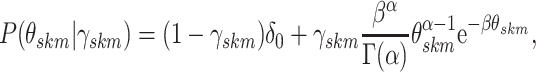 |
(3.5) |
where 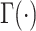 represents the gamma
function,
represents the gamma
function, 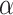 and
and 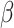 are
fixed hyperparameters, and the latent indicator variable
are
fixed hyperparameters, and the latent indicator variable 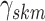 indicates the event that the network for subgroup
indicates the event that the network for subgroup 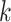 is related to subgroup
is related to subgroup
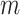 on platform
on platform  . The joint
prior on the off-diagonal entries is the product of the marginal densities
. The joint
prior on the off-diagonal entries is the product of the marginal densities
 |
(3.6) |
This prior construction allows sharing of information between subgroups when
appropriate, without forcing similarity in cases where the networks are actually
different. Additionally, we specify a prior on the sparsity parameter
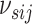 as
as
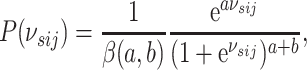 |
(3.7) |
where  denotes the Beta function,
and
denotes the Beta function,
and 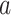 and
and 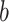 are fixed
hyperparameters. Platform specific hyperparameters may be chosen in cases where sparsity
is known to be different from one platform to another.
are fixed
hyperparameters. Platform specific hyperparameters may be chosen in cases where sparsity
is known to be different from one platform to another.
Prior linking cross-group relations across platforms: To link networks
at the platform level, we model the overall relationship between each pair of platforms
based on the dependencies across subgroups within each platform. This is a flexible
approach which allows the number of variables and number of subjects to differ across
the platforms, and only requires that we have data for the same set of subgroups.
Specifically, we construct an MRF prior on the vector of binary indicators for network
relatedness between subgroups 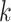 and
and 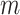 across all
platforms,
across all
platforms, 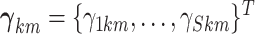 ,
as
,
as
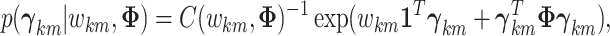 |
(3.8) |
with 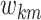 capturing the sparsity of the
vector
capturing the sparsity of the
vector 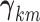 and
and
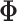 a
a  symmetric matrix denoting pairwise similarity across platforms, in a similar manner to
the matrices
symmetric matrix denoting pairwise similarity across platforms, in a similar manner to
the matrices 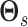 described previously.
The off-diagonal elements of
described previously.
The off-diagonal elements of  drive the between
platform similarity, a non-zero
drive the between
platform similarity, a non-zero 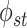 indicates
platforms
indicates
platforms 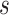 and
and 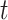 have similar
super graphs
have similar
super graphs 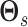 and
and
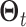 . As above, we place a
spike-and-slab prior on the entries of
. As above, we place a
spike-and-slab prior on the entries of 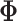 ,
,
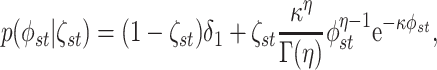 |
(3.9) |
with 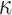 and
and 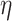 fixed
hyperparameters, and
fixed
hyperparameters, and 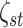 a latent binary variable which
indicates that platforms
a latent binary variable which
indicates that platforms  and
and 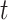 have related
cross-group dependencies. Off-diagonal entries
have related
cross-group dependencies. Off-diagonal entries 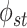 in the
symmetric
in the
symmetric 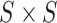 matrix signify the magnitude of
pairwise relatedness across platforms, modeling the relations across different platforms
as learned from the data in an innovative and versatile manner. We then place
independent Bernoulli
matrix signify the magnitude of
pairwise relatedness across platforms, modeling the relations across different platforms
as learned from the data in an innovative and versatile manner. We then place
independent Bernoulli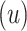 priors on the latent indicators
priors on the latent indicators
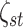 , with
, with
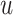 a fixed hyperparameter
a fixed hyperparameter
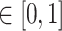 , and specify a prior on
, and specify a prior on
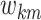 similarly to (3.7) with hyperparameters
similarly to (3.7) with hyperparameters
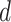 and
and  to complete the
model.
to complete the
model.
3.3. Posterior inference
Let 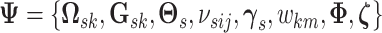 denotes the set of all parameters and
denotes the set of all parameters and 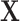 denotes the
observed data for all sample subgroups and all platforms. We can write the joint posterior
as
denotes the
observed data for all sample subgroups and all platforms. We can write the joint posterior
as
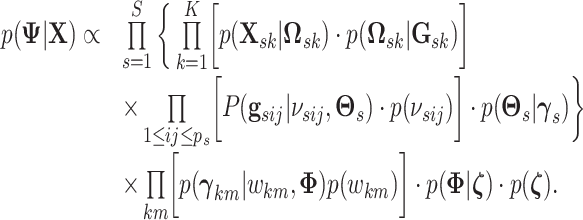 |
(3.10) |
As this distribution is analytically intractable, we construct a Markov chain Monte Carlo (MCMC) sampler to obtain a posterior sample of the parameters of interest.
3.3.1. MCMC sampling scheme.
Our MCMC scheme includes a block Gibbs sampler to sample the precision matrix
 and graph
and graph
 for each platform
for each platform
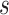 and subgroup
and subgroup 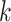 . Then, we
sample the graph similarity parameters
. Then, we
sample the graph similarity parameters 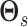 and
and
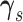 for each platform
using a Metropolis–Hastings method that is equivalent to a reversible jump and
incorporates between-model and within-model moves. Next, we use Metropolis-Hastings
steps to sample the edge-specific sparsity parameters
for each platform
using a Metropolis–Hastings method that is equivalent to a reversible jump and
incorporates between-model and within-model moves. Next, we use Metropolis-Hastings
steps to sample the edge-specific sparsity parameters  and
the cross-subgroup relation sparsity parameters
and
the cross-subgroup relation sparsity parameters 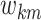 from their
respective posterior conditional distributions. Lastly, we update the cross-platform
parameters
from their
respective posterior conditional distributions. Lastly, we update the cross-platform
parameters  and
and
 using a
Metropolis–Hastings method similarly to the one used to update
using a
Metropolis–Hastings method similarly to the one used to update 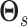 and
and
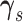 . A detailed
description of the MCMC algorithm is provided in the supplementary material available
at Biostatistics online.
. A detailed
description of the MCMC algorithm is provided in the supplementary material available
at Biostatistics online.
3.3.2. Model selection.
There are various approaches for making inference on the graph structures based on the
MCMC output. One approach is to use the maximum a posteriori (MAP) estimate, which
represents the mode of the posterior distribution for each graph. However, this approach
is generally not preferred in the context of large networks since the space of possible
graphs is large, and we may only visit a particular graph a few times during the MCMC.
We then rely on a more practical approach for model selection, and estimate the marginal
posterior probability (MPP) of inclusion for each edge  ,
which we calculate as the proportion of MCMC iterations, after burn-in, where edge
,
which we calculate as the proportion of MCMC iterations, after burn-in, where edge
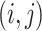 was included in graph
was included in graph
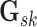 . Final inference is
performed by selecting edges according to the median model (i.e., with MPP
. Final inference is
performed by selecting edges according to the median model (i.e., with MPP
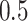 ) for inclusion in our posterior
selected graphs (Barbieri and Berger, 2004).
) for inclusion in our posterior
selected graphs (Barbieri and Berger, 2004).
4. Case study on COPD severity
We are interested in studying the reshaping of gene and metabolite networks as disease stage worsens. Our ultimate goal is to be able to map the underlying molecular causes of disease progression and to determine whether biological platforms describe the same mechanisms.
Gene expression levels were measured from peripheral blood mononuclear cells using the Affymetrix Human Genome U133 Plus 2.0 Array (Bahr and others, 2013), and plasma metabolite abundances were generated from liquid chromotography/mass spectrometry (Bowler and others, 2014). Candidate pathways were selected as follows. Differently expressed genes and differently abundant metabolites were identified for airflow obstruction (forced expiratory volume in 1 s percent predicted) correcting for age, sex, body mass index, and current smoking status. KEGG Pathways (Kanehisa and others, 2014) that showed enrichment of the significant genes and metabolites were then prioritized. Top candidate pathways may play a role in the response to cigarette smoke exposure and are interesting candidates for more detailed exploration in emphysema.
Below, we report results on one of the top candidate pathways we analyzed, Regulation of
autophagy (RegAuto). Results on a second candidate pathway, Fc R-mediated
phagocytosis (Fc
R-mediated
phagocytosis (Fc R), can be found in the supplementary material available at
Biostatistics online. Expression levels were measured for 28 (RegAuto)
and 104 (Fc
R), can be found in the supplementary material available at
Biostatistics online. Expression levels were measured for 28 (RegAuto)
and 104 (Fc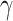 R) probesets. These were collapsed to
20 (RegAuto), and 58 (Fc
R) probesets. These were collapsed to
20 (RegAuto), and 58 (Fc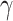 R) unique genes by selecting, for each
gene, the probeset with the strongest association to emphysema. Metabolite data were matched
to lipid and aqueous annotation files in order to extract KEGG IDs for each sample. After
subsetting to the RegAuto and Fc
R) unique genes by selecting, for each
gene, the probeset with the strongest association to emphysema. Metabolite data were matched
to lipid and aqueous annotation files in order to extract KEGG IDs for each sample. After
subsetting to the RegAuto and Fc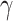 R pathways, we were left with 117
(RegAuto) and 60 (Fc
R pathways, we were left with 117
(RegAuto) and 60 (Fc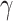 R) measurements, but numerous instances
of duplicate KEGG IDs. To reduce redundancy and exclude highly correlated covariates, we
carried out an iterative principal component analysis procedure to select a subset of less
correlated variables for analysis. This procedure is outlined in the supplementary material available at
Biostatistics online and an example code is provided online. After this
procedure, 21 (RegAuto) and 23 (Fcy
R) measurements, but numerous instances
of duplicate KEGG IDs. To reduce redundancy and exclude highly correlated covariates, we
carried out an iterative principal component analysis procedure to select a subset of less
correlated variables for analysis. This procedure is outlined in the supplementary material available at
Biostatistics online and an example code is provided online. After this
procedure, 21 (RegAuto) and 23 (Fcy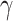 R) metabolites were left for
analysis.
R) metabolites were left for
analysis.
4.1. Hyperparameter settings
The application of our model requires the specification of several hyperparameters. Here
we describe the specification we used to obtain the results reported below and refer to
the simulation study for more insights and sensitivity analyses. For prior (3.2) on the precision matrix elements,
hyperparameters were specified as 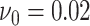 and
and 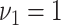 according to published guidelines given in Wang
(2015). As for the prior (3.5) on the off-diagonal entries of
according to published guidelines given in Wang
(2015). As for the prior (3.5) on the off-diagonal entries of 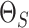 linking sample
subgroups within a platform, we specified the slab portion of the mixture prior as a
Gamma
linking sample
subgroups within a platform, we specified the slab portion of the mixture prior as a
Gamma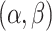 with
with
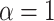 and
and 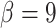 for
both platforms. This resulted in a prior with mean approximately equal to 0.1 and
for
both platforms. This resulted in a prior with mean approximately equal to 0.1 and
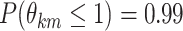 , which avoids
assigning high values to the off diagonal entries of
, which avoids
assigning high values to the off diagonal entries of 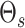 . For the prior
(3.7) on the sparsity parameter
. For the prior
(3.7) on the sparsity parameter
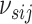 of the MRF prior linking networks
within each platform, we specified
of the MRF prior linking networks
within each platform, we specified 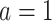 and
and 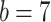 resulting
in a prior probability of edge inclusion around 0.125. The similarly specified prior on
sparsity parameter
resulting
in a prior probability of edge inclusion around 0.125. The similarly specified prior on
sparsity parameter  in the MRF prior (3.8) linking cross-subgroup relations
across platforms was specified as
in the MRF prior (3.8) linking cross-subgroup relations
across platforms was specified as 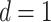 and
and  , for all
subgroup pairs
, for all
subgroup pairs 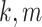 , resulting in approximately
, resulting in approximately
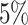 prior probability of subgroup
relatedness. The mixture prior (3.9)
on the off-diagonal entries of
prior probability of subgroup
relatedness. The mixture prior (3.9)
on the off-diagonal entries of 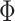 was specified as
Gamma
was specified as
Gamma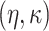 with
with
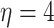 and
and 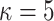 ,
resulting in a prior mean of
,
resulting in a prior mean of 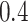 and
and 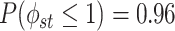 , avoiding
assigning high values to the off diagonal entries of
, avoiding
assigning high values to the off diagonal entries of 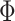 . Lastly, the
hyperparameter
. Lastly, the
hyperparameter  in the Bernoulli prior on the indicators
of platform similarity
in the Bernoulli prior on the indicators
of platform similarity 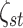 was specified as
was specified as
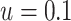 . Sensitivity analyses reported in the
supplementary material
available at Biostatistics online show that hyperparameter settings have
minimal impact on graph learning performance as the inferred network remains fairly
stable. With certain settings, large changes may occur in the magnitude of relative
similarity measures
. Sensitivity analyses reported in the
supplementary material
available at Biostatistics online show that hyperparameter settings have
minimal impact on graph learning performance as the inferred network remains fairly
stable. With certain settings, large changes may occur in the magnitude of relative
similarity measures 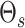 and
and 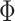 , however,
ordering is generally preserved. Results, we report here and in the supplementary material available at
Biostatistics online were obtained by running two MCMC samplers for 10
000 burn-in iterations followed by 30 000 iterations used for inference, with different
starting points. To verify convergence of the chains, we compared correlations of
resulting MPPs from the two chains. Those were in the range
, however,
ordering is generally preserved. Results, we report here and in the supplementary material available at
Biostatistics online were obtained by running two MCMC samplers for 10
000 burn-in iterations followed by 30 000 iterations used for inference, with different
starting points. To verify convergence of the chains, we compared correlations of
resulting MPPs from the two chains. Those were in the range 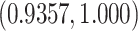 ,
for Pearson correlations. Final results were obtained by pooling together the output of
the two chains.
,
for Pearson correlations. Final results were obtained by pooling together the output of
the two chains.
4.2. Results
Estimated graphs for control, moderate, and severe subgroups, for the RegAuto pathway,
obtained by selecting edges with MPPs greater than 0.5, are shown in Figure 2, and those for the Fc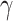 R pathway are
reported in the supplementary
material available at Biostatistics online. In these plots,
obtained using the software cytoscape (Shannon and others, 2003), the size of a node is drawn
proportionally to the number of edges connecting that node to others in the same graph
(i.e., the “degree” of the node). For the RegAuto pathway, relative network similarities
across subgroups were estimated as
R pathway are
reported in the supplementary
material available at Biostatistics online. In these plots,
obtained using the software cytoscape (Shannon and others, 2003), the size of a node is drawn
proportionally to the number of edges connecting that node to others in the same graph
(i.e., the “degree” of the node). For the RegAuto pathway, relative network similarities
across subgroups were estimated as
Fig. 2.
RegAuto pathway, gene (top), and metabolite (bottom) platforms: estimated graphs for control (left), moderate (middle), and severe (right) subgroups, obtained by selecting edges with MPPs greater than 0.5. The size of the nodes is proportional to their degree.
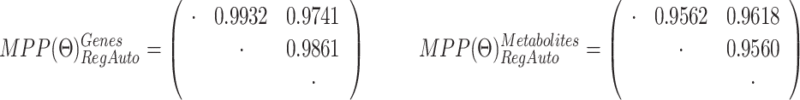 |
with relative similarity across platforms estimated as
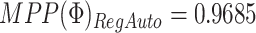 . These values
indicate a preference for shared structure across platforms and sample subgroups.
Histograms of posterior distributions of non-zero values of
. These values
indicate a preference for shared structure across platforms and sample subgroups.
Histograms of posterior distributions of non-zero values of  and
and
 are shown in the supplementary material available at
Biostatistics online.
are shown in the supplementary material available at
Biostatistics online.
Table 1 indicates the total number of inferred pair
interactions across the two pathways, together with the counts of pairs that exhibit
evidence of disrupted interactions due to disease severity. In the table, for each
pathway, the three disease subgroups ordered from least to most severe are coded with 0’s
and 1’s, with 1 indicating a high MPP (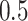 ) of edge inclusion
in the subgroup network. For instance, 110 would indicate that the edge is present in the
control and moderate subgroup, yet not in the severe subgroup. That is, in the severe
subgroup the MPP of edge inclusion falls below the threshold of 0.50. Group codings of 100
and 110 indicate greater interaction in the control and group codings 011 and 001 indicate
greater interaction in disease. For the gene platform, counts for known protein–protein
interactions are included in parentheses for the gene platform. Biological General
Repository for Interaction Datasets (BioGrids) v. 3.4.156 (Chatr-Aryamontri and others, 2017) was used to obtain
protein–protein interactions and disease annotation information was gathered from Stelzer and others (2011). We observe
50–60% disruption in total pairs of genes and metabolites, and different patterns of
disruption for metabolites and gene interactions. For both metabolites and genes, there
are a large number of connections in control subjects that are then disrupted in
moderate/severe subjects. But for metabolites, there is also a relatively large number of
metabolite connections in severe subjects that are not present in the moderate/control
subjects, suggesting that parts of the metabolite pathway are activated as disease
severity increases. These results also illustrate that while our method takes advantages
of commonalities between the platforms, it can also highlight platform specific
differences.
) of edge inclusion
in the subgroup network. For instance, 110 would indicate that the edge is present in the
control and moderate subgroup, yet not in the severe subgroup. That is, in the severe
subgroup the MPP of edge inclusion falls below the threshold of 0.50. Group codings of 100
and 110 indicate greater interaction in the control and group codings 011 and 001 indicate
greater interaction in disease. For the gene platform, counts for known protein–protein
interactions are included in parentheses for the gene platform. Biological General
Repository for Interaction Datasets (BioGrids) v. 3.4.156 (Chatr-Aryamontri and others, 2017) was used to obtain
protein–protein interactions and disease annotation information was gathered from Stelzer and others (2011). We observe
50–60% disruption in total pairs of genes and metabolites, and different patterns of
disruption for metabolites and gene interactions. For both metabolites and genes, there
are a large number of connections in control subjects that are then disrupted in
moderate/severe subjects. But for metabolites, there is also a relatively large number of
metabolite connections in severe subjects that are not present in the moderate/control
subjects, suggesting that parts of the metabolite pathway are activated as disease
severity increases. These results also illustrate that while our method takes advantages
of commonalities between the platforms, it can also highlight platform specific
differences.
Table 1.
Case study on COPD: numbers of total pairs of unique gene interactions and numbers of disease disrupted pairs based on disease severity. Numbers in parentheses reflect the number of pairs with known protein protein interactions
| Pathway | Platform | Total pairs | 100 | 110 | 011 | 001 | Total disrupted |
|---|---|---|---|---|---|---|---|
Fc R R |
Metabolites | 73 | 17 | 5 | 3 | 18 | 43 |
Fc R R |
Genes | 656 (49) | 151 (8) | 63 (7) | 74 (3) | 63 (4) | 351 (22) |
| Reg Auto | Metabolites | 66 | 14 | 4 | 5 | 17 | 40 |
| Reg Auto | Genes | 101 (6) | 23 (2) | 13 | 7 | 8 | 51 (2) |
In order to gain further intuition on the properties of the estimated graphs, we calculated a number of graph metrics across all subgroups and pathways. Results on number of edges, global clustering coefficient, averaged betweenness centrality, and count of hub nodes are reported in Table 2. The global clustering coefficient of a graph is based on node triplets, i.e., three connected nodes, and is defined as the number of closed triplets divided by the total number of connected triplets. It measures the degree to which nodes in a graph tend to cluster together, with values closer to one if the graph is more modular i.e., it can be divided into clusters of highly connected nodes. Betweenness centrality quantifies the number of times a node acts as a bridge along the shortest path between two other nodes, as a measure of how important the node is in serving as a connector between other nodes in the graph.
Table 2.
Case study on COPD: graph measures results, including number of edges, global
clustering, betweenness centrality, and count of hub nodes, for each subgroup. Hub
nodes are defined as nodes with a degree 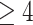 , or at least
four connections
, or at least
four connections
Fc R pathway R pathway
| ||||||
|---|---|---|---|---|---|---|
| Metabolites | Genes | |||||
| Group 1 | Group 2 | Group 3 | Group 1 | Group 2 | Group 3 | |
| 59 | 57 | 58 | Number of edges | 405 | 444 | 332 |
| 0.1665 | 0.2430 | 0.1683 | Global clustering | 0.4268 | 0.4495 | 0.4442 |
| 0.2122 | 0.2783 | 0.3348 | Betweenness centrality | 0.0771 | 0.0483 | 0.0995 |
| 12 | 5 | 10 | Count of hub nodes | 50 | 53 | 46 |
| Reg Auto pathway | ||||||
| 49 | 51 | 54 | Number of edges | 71 | 76 | 49 |
| 0.0881 | 0.2143 | 0.1003 | Global clustering | 0.4649 | 0.5175 | 0.4123 |
| 0.1524 | 0.21117 | 0.1862 | Betweenness centrality | 0.1800 | 0.1205 | 0.1435 |
| 9 | 8 | 6 | Count of hub nodes | 14 | 15 | 8 |
Specific hub nodes and extended degree results can be found in the supplementary material available at Biostatistics online.
A close inspection of the estimated networks and our results suggests that, in general, estimated gene networks exhibited a trend of decreased connectivity or a large drop in connections as disease severity increased, while metabolite networks do not show such a trend. There may be several reasons why the network patterns are different between the genes and metabolites. One possible reason is that the same metabolites are present in other biological pathways that may be compensating for the changes due to disease. Another reason is that the plasma metabolomics may be reflecting activity in multiple organs, while the gene level data is primarily reflecting changes in gene expression more specifically in the blood. Additionally, results in Table 2 generally indicate higher global clustering coefficients and degree centrality measures for gene platforms than for metabolite platforms. This suggests that gene networks are generally more clustered into denser subnetworks characterized by high connectivity within each pathway when compared to metabolite networks. Additionally, interpreting degree centrality measures in the context of information flow within networks suggests that when disrupted, highly connected genes may impact network communication more than disrupted metabolite interactions.
4.3. Hub node analysis
Further analysis of the results was carried out on hub nodes, for both platforms, to
validate findings with known protein–protein interactions and to examine disease related
gene annotation. Hub listings were generated for each pathway and each platform to allow
analysis of node connectivity and variations in connectivity as disease increased in
severity. A summary of results is given in Table 2,
where hub node count for our application setting signifies the number of nodes per group
with a degree 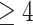 , or at least four connections. As an
example, for genes in the FC
, or at least four connections. As an
example, for genes in the FC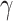 R pathway, we find that there are
less connections per node, less hub nodes, and less connections in the Severe subjects
compared to the Moderate/Control subjects suggesting that there is overall disruption for
this pathway at the gene expression level. In the supplementary material available at Biostatistics
online, we provide biological background on specific genes, metabolites, and connections
in the estimated networks for the two pathways.
R pathway, we find that there are
less connections per node, less hub nodes, and less connections in the Severe subjects
compared to the Moderate/Control subjects suggesting that there is overall disruption for
this pathway at the gene expression level. In the supplementary material available at Biostatistics
online, we provide biological background on specific genes, metabolites, and connections
in the estimated networks for the two pathways.
5. Simulation studies
In this section, we compare our proposed method with three recently proposed graphical model learning methods: Fused Graphical Lasso, Group Graphical Lasso, and Hub Graphical Lasso. The first two methods are designed to learn the network structure of related subgroups (Danaher and others, 2014): The Fused Graphical Lasso encourages both shared structure and shared edge values, the Group Graphical Lasso encourages shared graph structures but not shared edge values. The Hub Graphical Lasso (Mohan and others, 2014) encourages similarity across networks based on the presence or absence of highly connected hub nodes. None of the competing methods encourages similarity across platforms.
5.1. Comparison study
We investigate whether alternative methods can produce satisfactory results, in terms of
network accuracy, in settings that mimic our COPD data (two platforms and three sampling
subgroups). We consider two set-ups for generating 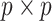 adjacency and
precision matrices, for each sampling group
adjacency and
precision matrices, for each sampling group 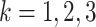 :
:
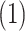 Scale free networks: the probability that a given node has
Scale free networks: the probability that a given node has
 edges is proportional to
edges is proportional to
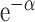 . We kept
. We kept
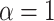 , the default setting as stated in
the igraph package (Csardi and
Nepusz, 2006), and simulated networks of the same size of pathways analyzed in
the COPD case study (
, the default setting as stated in
the igraph package (Csardi and
Nepusz, 2006), and simulated networks of the same size of pathways analyzed in
the COPD case study ( nodes).
nodes).
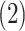 AR(2) networks: the entries of the
AR(2) networks: the entries of the 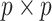 precision matrix
are defined as
precision matrix
are defined as 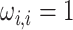 for
for
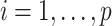 ,
, 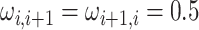 for
for
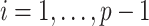 and
and
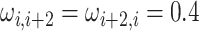 for
for
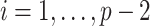 . We simulated networks of
larger size than pathways analyzed in the COPD case study (
. We simulated networks of
larger size than pathways analyzed in the COPD case study (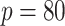 nodes).
nodes).
As our model learns similarity between networks and does not enforce similarity unless
supported by the data, current modeling allows for all patterns of similarity. In
particular, from the preliminary adjacency matrices above, in our simulations we
considered two settings of pairwise similarity across sampling groups for each platform:
In setting one, for platform 1, Groups 1 and 2 were set up to be “similar” while Group 3
was set up to be different. We generated “similar” networks across all three groups for
the second platform. Here, two groups are defined as “similar” if the precision matrix of
one group shares approximately 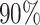 of edges with the precision matrix of
the other group. In setting 2, both platforms were set up to have different networks
across all three subgroups.
of edges with the precision matrix of
the other group. In setting 2, both platforms were set up to have different networks
across all three subgroups.
For scale free networks, to ensure that each generated precision matrix was positive
definite, we used a similar approach to that of Danaher
and others (2014) where each off-diagonal element is divided
by the sum of the off-diagonal elements in its row, and then the matrix is averaged with
its transpose. Consequently, precision matrices generated via the scale free network
method have lower signal, in terms of magnitude of the non-zero elements of the precision
matrices, than the AR(2) networks; we simulated scale free networks of size
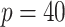 and AR(2) networks of size
and AR(2) networks of size
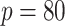 to ensure a minimal signal strength.
After all precision matrices were determined, data matrices
to ensure a minimal signal strength.
After all precision matrices were determined, data matrices 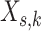 of size
of size
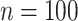 for
for 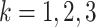 and
and
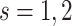 , were generated from normal
distributions
, were generated from normal
distributions 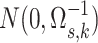 and variables were
standardized to have a standard deviation of one. We used the same hyperparameter setting
used in the analysis of the COPD data, and ran our MCMC samplers for 10 000 burnin
iterations followed by 30 000 iterations used for inference. Additional sensitivity
analyses may be found in the supplementary material available at Biostatistics online. Using
a 2-core 1.7 GHz Intel core i7 processor with 8 GB memory, our code takes approximately 40
min to run 5000 iterations for a two platform scenario with 40 variables per platform.
Alternative methods, such as the fused and group graphical lasso, are computationally more
efficient, although grid searches and trials to determine optimized penalty parameters can
be quite time consuming.
and variables were
standardized to have a standard deviation of one. We used the same hyperparameter setting
used in the analysis of the COPD data, and ran our MCMC samplers for 10 000 burnin
iterations followed by 30 000 iterations used for inference. Additional sensitivity
analyses may be found in the supplementary material available at Biostatistics online. Using
a 2-core 1.7 GHz Intel core i7 processor with 8 GB memory, our code takes approximately 40
min to run 5000 iterations for a two platform scenario with 40 variables per platform.
Alternative methods, such as the fused and group graphical lasso, are computationally more
efficient, although grid searches and trials to determine optimized penalty parameters can
be quite time consuming.
In Table 3, we report network accuracy metrics averaged over 25 replicates; we considered the true positive rate (TPR), the false positive rate (FPR), the Matthews correlation coefficient (MCC), and area under the curve (AUC). Overall the proposed method performs comparatively well, and it is the only approach that controls the false positive rate across all scenarios. The differences in performances in favor of the proposed approach are particularly large in Setting Two. This is not surprising since the proposed approach is the only joint graph inference approach that learns from the data whether groups are related and, consequently, does not always enforce similarity across groups. Additionally, in the supplementary material available at Biostatistics online, we show a comparison of TPRs attained across methods for fixed FDRs, providing some evidence that our proposed method improves power with respect to methods that employ separate estimations for each subgroup.
Table 3.
Simulation study: in setting one, one group on one of the two platforms is dissimilar
from the others. In setting two, both platforms have dissimilar groups. Network
accuracy metrics are reported as Mean (Standard Error) over 25 replicates for
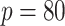 scenarios and 50 replicates for
scenarios and 50 replicates for
 scenarios.
scenarios.
| Methods | TPR | FPR | MCC | AUC |
|---|---|---|---|---|
Setting one, 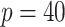
| ||||

|
0.743 (0.0031) | 0.028 (0.0004) | 0.639 (0.0028) | 0.936 (0.0020) |
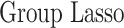
|
0.785 (0.0031) | 0.060 (0.0005) | 0.536 (0.0023) | 0.912 (0.0022) |

|
0.123 (0.0049) | 0.005 (0.0004) | 0.263 (0.0062) | 0.899 (0.0022) |
|
0.611 (0.0063) | 0.022 (0.0005) | 0.579 (0.0055) | 0.895 (0.0036) |
Setting two, 
| ||||
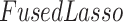
|
0.907 (0.0016) | 0.157 (0.0006) | 0.439 (0.0012) | 0.963 (0.0003) |
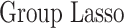
|
0.930 (0.0015) | 0.167 (0.0005) | 0.436 (0.0010) | 0.954 (0.0004) |

|
1.000 (0.0000) | 0.467 (0.0048) | 0.232 (0.0021) | 0.945 (0.0004) |

|
1.000 (0.0001) | 0.028 (0.0004) | 0.794 (0.0020) | 1.000 (0.0001) |
Setting one, 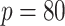
| ||||

|
0.657 (0.0037) | 0.035 (0.0005) | 0.546 (0.0029) | 0.919 (0.0023) |
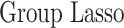
|
0.777 (0.0031) | 0.069 (0.0005) | 0.506 (0.0022) | 0.916 (0.0023) |
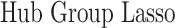
|
0.263 (0.0064) | 0.005 (0.0003) | 0.427 (0.0050) | 0.905 (0.0023) |
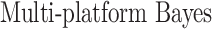
|
0.636 (0.0063) | 0.023 (0.0005) | 0.597 (0.0053) | 0.941 (0.0037) |
Setting two, 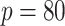
| ||||
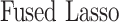
|
0.735 (0.0017) | 0.080 (0.0004) | 0.451 (0.0015) | 0.957 (0.0009) |
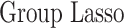
|
0.998 (0.0002) | 0.270 (0.0006) | 0.343 (0.0005) | 0.938 (0.0229) |
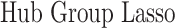
|
1.000 (0.0000) | 0.464 (0.0044) | 0.233 (0.0019) | 0.945 (0.0004) |
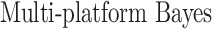
|
1.000 (0.0001) | 0.026 (0.0004) | 0.808 (0.0021) | 1.000 (0.0001) |
6. Conclusion
Motivated by a collaborative study on COPD progression, we have proposed a novel approach for joint multiple platform network analysis (here, genes and metabolites). Our Bayesian approach uses computationally efficient priors on precision matrices and hierarchical MRF priors to link similarities across subgroups and platforms. Even though less scalable than alternative methods, a Bayesian framework makes use of all information in the data, sharing it across subgroups when appropriate, and enabling joint estimation in a very flexible manner, as we make no assumptions on the directionality of influence across the data types or on the extent of network similarity. In addition, our model formulation allows the numbers of variables and subjects to differ across data types. We have demonstrated improved performance over alternative approaches for multiple networks using simulated data. On the COPDGene data, we have jointly inferred metabolite and gene networks across subgroups of disease stage, identifying notable interactions that illustrate disease progression and suggesting pathway compensation as a consequence to disease. These interactions pinpoint molecular targets for further study and provide potential therapy options.
Supplementary Material
Supplementary Data
Acknowledgments
The authors also acknowledge support from NSF/RTG 1547433 and thank Dessy Akinfenwa and Ami Sheth for help with the simulation study. Conflict of Interest: None declared.
7. Software
MATLAB code is available at https://github.com/elinshaddox/MultiplePlatformBayesianNetworks.
Funding
NSF/DMS 1811568/1811445 (to M.V. and C.P.) NHLBI (U01HL089897, U01HL089856, and P20HL113445) and Butcher Foundation. NLM Training Program (T15 LM007093 to E.S.); NIH/NCI (P30CA016672 to C.B.P.). COPDGene study (NCT00608764) supported by the COPD Foundation through contributions to an Industry Advisory Committee comprised of AstraZeneca, Boehringer-Ingelheim, GlaxoSmithKline, Novartis, Pfizer, Siemens, and Sunovion.
References
- Bahr T. M., Hughes G. J., Armstrong M., Reisdorph R., Coldren C. D., Edwards M. G., Schnell C., Kedi R., LaFlamme D. J., Reisdorph N., Keckris K. J. and others. (2013). Peripheral blood mononuclear cell gene expression in chronic obstructive pulmonary disease. American Journal of Respiratory Cell and Molecular Biology 49, 316–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri M. M. and Berger J. O. (2004). Optimal predictive model selection. The Annals of Statistics 32, 870–897. [Google Scholar]
- Besag J. (1974). Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society, Series B 36, 192–236. [Google Scholar]
- Bowler R. P., Jacobson S., Cruickshank C., Hughes G. J., Siska C., Ory D. S., Petrache I., Schaffer J. E., Reisdorph N. and Kechris K. (2014). Plasma sphingolipids associated with copd phenotypes. American Journal of Respiratory and Critical Care Medicine 191, 275–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai T. T., Li H., Liu W. and Xie J. (2016). Joint estimation of multiple high dimensional precision matrices. Statistica Sinica 26(2), 445–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassese A., Guindani M., Tadesse M. G., Falciani F. and Vannucci M. (2014). A hierarchical Bayesian model for inference of copy number variants and their association to gene expression. Annals of Applied Statistics 8, 148–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatr-Aryamontri A., Oughtred R., Boucher L., Rust J., Chang C., Kolas N. K., O’Donnell L., Oster S., Theesfeld C., Sellam A., Stark C., Britkreutz B., Dolinski K. and others. (2017). The biogrid interaction database: 2017 update. Nucleic Acids Research 45, D369–D379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S., Witten D. M. and Shojaie A. (2015). Selection and estimation for mixed graphical models. Biometrika 102, 47–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csardi G. and Nepusz T. (2006). The igraph software package for complex network research. InterJournal Complex Systems, 1695. [Google Scholar]
- Danaher P., Wang P. and Witten D. (2014). The joint graphical lasso for inverse covariance estimation across multiple classes. Journal of the Royal Statistical Society, Series B 76, 373–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., Hastie T. and Tibshirani R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George E. and McCulloch R. (1993). Variable selection via gibbs sampling. Journal of the American Statistical Association 88, 881–889. [Google Scholar]
- Guo J., Levina E., Michailidis G. and Zhu J. (2011). Joint estimation of multiple graphical models. Biometrika 98, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao B., Sun W., Liu Y. and Cheng G. (2018). Simultaneous clustering and estimation of heterogeneous graphical models. Journal of Machine Learning Research 217, 1–58. [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M., Goto S., Sato Y., Kawashima M., Furumichi M. and Tanabe M. (2014). Data, information, knowledge and principle: back to metabolism in kegg. Nucleic Acids Research 42, 199–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F. and Zhang N. (2010). Bayesian variable selection in structured high-dimensional covariate spaces with applications in genomics. Journal of the American Statistical Association 105, 1202–1214. [Google Scholar]
- Lin J., Basu S., Banerjee M. and Michailidis G. (2016). Penalized maximum likelihood estimation of multi-layered Gaussian graphical models. Journal of Machine Learning Research 17, 1–51. [Google Scholar]
- Ma J. and Michailidis G. (2016). Joint structural estimation of multiple graphical models. Journal of Machine Learning Research 17, 1–48. [Google Scholar]
- Meinshausen N. and Bühlmann P. (2006). High-dimensional graphs and variable selection with the lasso. The Annals of Statistics 34, 1436–1462. [Google Scholar]
- Mohan K., London P., Fazel M., Witten D. and Lee S. (2014). Node-based learning of multiple Gaussian graphical models. Journal of Machine Learning Research 15, 445–488. [PMC free article] [PubMed] [Google Scholar]
- National Center for Health Statistics. (2016). Health, United States, 2015: With Special Feature on Racial and Ethnic Health Disparities. [PubMed]
- Oates C. and Mukherjee S. (2014). Joint structure learning of multiple non-exchangeable networks. Proceedings of the 17th International Conference on Artificial Intelligence and Statistics 33, 687–695. [Google Scholar]
- Peterson C., Stingo F. and Vannucci M. (2015). Bayesian inference of multiple Gaussian graphical models. Journal of the American Statistical Association 110, 159–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regan E. A., Hokanson J. E., Murphy J. R., Make B., Lynch D. A., Beaty T. H., Curran-Everett D., Silverman E. K. and Crapo J. D. (2010). Genetic epidemiology of copd (copdgene) study design. COPD 7, 32–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roverato A. (2002). Hyper inverse Wishart distribution for non-decomposable graphs and its application to Bayesian inference for Gaussian graphical models. Scandinavian Journal of Statistics 29, 391–411. [Google Scholar]
- Saegusa T. and Shojaie A. (2016). Joint estimation of precision matrices in heterogeneous populations. Electronic Journal of Statistics 10, 1341–1392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaddox E., Stingo F., Peterson C. B., Jacobson S., Cruickshank-Quinn C., Kechris K., Bowler R. and Vannucci M. (2018). A Bayesian approach for learning gene networks underlying disease severity in COPD. Statistics in Biosciences 10, 59–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon P., Markiel A., Ozier O., Baliga N. S., Wang J. T., Ramage D., Amin N., Schwikowski B. and Ideker T. (2003). Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Research 13, 2498–2504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelzer G., Dalah I., Stein T., Satanower Y., Rosen N., Nativ N., Oz-Levi D., Olender T., Belinky F., Bahir I., Krug H., Perco P., Mayer B., Kolker E., Safran M. and others. (2011). In-silico human genomics with genecards. Human Genomics 5, 709–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stingo F. C., Chen Y. A., Tadesse M. G. and Vannucci M. (2011). Incorporating biological information into linear models: A Bayesian approach to the selection of pathways and genes. The Annals of Applied Statistics 5, 1978–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H. (2015). Scaling it up: stochastic search structure learning in graphical models. Bayesian Analysis 10, 351–377. [Google Scholar]
-
Wang H. and
Li
S. (2012).
Efficient Gaussian graphical model determination under
 -Wishart prior
distributions. Electronic Journal of Statistics
6, 168–198. [Google Scholar]
-Wishart prior
distributions. Electronic Journal of Statistics
6, 168–198. [Google Scholar] - Wang W., Baladandayuthapani V., Morris J. S., Broom B. M., Manyam G. and Do K. A. (2013). iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics 29, 149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M. and Lin Y. (2007). Model selection and estimation in the Gaussian graphical model. Biometrika 94, 19–35. [Google Scholar]
- Zhu Y., Shen X. and Pan. W. (2014). Structural pursuit over multiple undirected graphs. Journal of the American Statistical Association 109, 1683–1696. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Data