Abstract
Perceptual sensitivity varies from moment to moment. One potential source of variability is spontaneous fluctuations in cortical activity that can travel as a wave1. Spontaneous traveling waves have been reported during anesthesia2–7, but it is not known whether spontaneous traveling waves play a role during waking perception. Using newly developed analytic techniques to characterize the moment-to-moment dynamics of noisy multielectrode data, we find spontaneous waves of activity in extrastriate visual cortex of awake, behaving marmosets (Callithrix jacchus). In monkeys trained to detect faint visual targets, the timing and position of spontaneous traveling waves, prior to target onset, predict the magnitude of target-evoked activity and the likelihood of target detection. In contrast, spatially disorganized fluctuations of neural activity are much less predictive. These results reveal an important role for spontaneous traveling waves in sensory processing through modulating neural and perceptual sensitivity.
Our perceptual experience can be highly variable. A faint stimulus presented at perceptual threshold may be detected in one instance but go undetected at another time. What occurs within the nervous system to account for this difference? Cortical neurons emit variable spike patterns in response to repeated presentations of an identical stimulus8,9. This variability is due, in part, to ongoing spontaneous fluctuations in the local network state that regularly show periods of high or low excitability10–12 and are reflected in the local field potential (LFP)13,14. Spontaneous fluctuations have been observed under anesthesia to propagate like waves in visual2,4,5,7, auditory6, and somatosensory3 cortex, but only in slow-wave fluctuations associated with sleep or arousal. Therefore, there is controversy over whether waking spontaneous fluctuations travel as waves and, if they do, whether they contribute meaningfully to waking cortical function15. Here, we report that moment-by-moment fluctuations of neural activity recorded in behaving, non-human primates propagate as waves across the extrastriate middle temporal (MT) visual area, and they strongly influence spontaneous spike rates. Critically, these waves are generated endogenously, without requiring an external event to trigger them. They are thus an internally generated brain state, distinct from sensory- and behavior-evoked waves5,16–19. Further, we find that spontaneous waves strongly regulate visual perception. In particular, in the excitable phase of a traveling wave, target-evoked neuronal responses and perceptual sensitivity are both elevated in monkeys performing a challenging visual detection task.
We chronically implanted multi-electrode arrays (Utah Arrays, Blackrock Microsystems) into motion selective visual area MT of two marmosets, whose lissencephalic cortical structure and small size enabled us to record simultaneously from the majority of the cortical area (Fig. 1a). We measured receptive fields of well isolated neurons and multi-unit activity in monkeys as they maintained fixation (Extended Data 1). We also examined LFPs, which are driven by synaptic currents in the vicinity of the electrode, and reflect the activity within the local network10,13,14. From the perspective of a single electrode, the raw LFP spontaneously fluctuated with broad spectral energy20. However, these fluctuations were not synchronous across the cortical area. Rather, the peak of a fluctuation often moved coherently with the spatiotemporal profile of a traveling wave (Fig. 1b, Video S1). Peaks and troughs in the LFP have been found to correspond to epochs of relatively low and high excitability in the local network14. We hypothesized that, when organized as waves, these excitability states might gate the flow of spiking activity through cortical circuits, depending on their alignment (Fig. 1c).
Fig. 1. Spontaneous LFP fluctuations often travel as waves across the cortex.
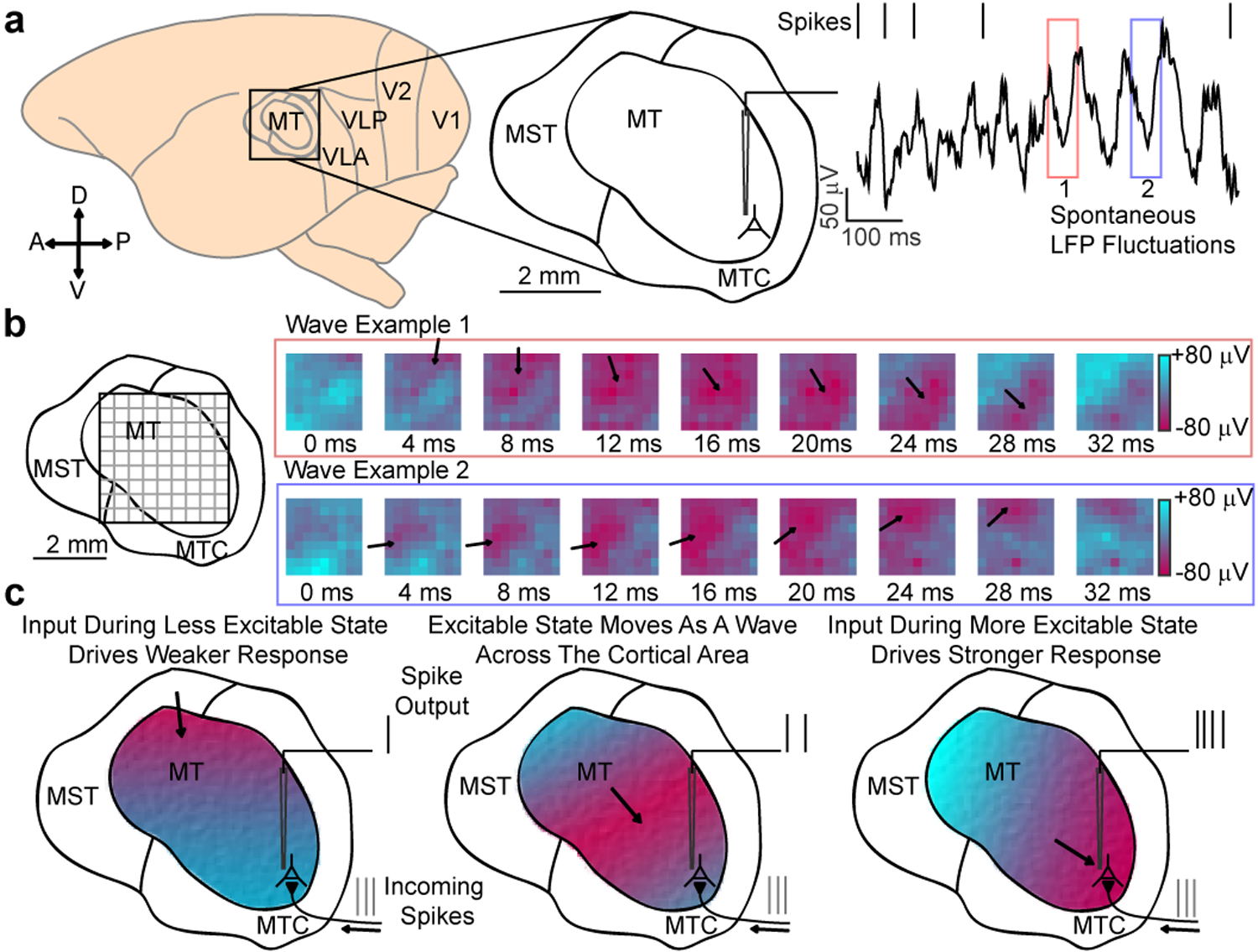
(a) Recordings were made from area MT of the common marmoset. The raw (1–100 Hz) local field potential (LFP) recorded from a single electrode is spectrally complex, with large, dynamic spontaneous fluctuations (red and blue boxes). (b) When viewed simultaneously across a multielectrode array, spontaneous fluctuations in the wideband (5–40 Hz) LFP often travel as a wave (example waves from red and blue boxes). The peaks and troughs of the wave correspond to spatially distinct regions of cortex that are in more (red) or less (blue) excitable states. (c) Our mechanistic hypothesis: as waves traverse cortex, they alter excitability states, modulating the relative spiking output based on their alignment, with the more excitable (red) and less excitable (blue) phases momentarily potentiating and, respectively, reducing sensitivity to incoming spikes.
Reliably detecting spontaneous waves in noisy multichannel data is challenging. Many wave detection techniques rely on spike-triggered averaging5, spatial smoothing4, or narrowband temporal filtering16,19,21, which can distort phase estimations of the underlying veridical fluctuation, giving false positives or unreliable measures of wave dynamics. Further, unlike during anesthesia, waking cortical dynamics are more complex, dominated by higher frequency, lower amplitude fluctuations that are more variable across the cortex22,23. To address this, we adapted a recently introduced statistical method for detecting traveling waves in noisy multichannel data24 that is better suited to studying the dynamics of awake cortex (Extended Data 2). This method used LFP phase to detect coherent flows of activity; however, while phase is conventionally analyzed only for narrowband oscillations, such as the theta (4–8 Hz) and alpha (8–13 Hz) frequency bands25–27, the network fluctuations we observed were not stable, sustained narrowband oscillations20 (Fig. 2b). Rather, they were broad in frequency content, which shifted from moment to moment.
Fig. 2. Spontaneous traveling waves modulate ongoing spiking probability.

(a) Illustration of the Generalized Phase (GP) measure. The GP (coded by color) describes the phase of the dominant fluctuation in the wideband (5–40 Hz, colored line) LFP at each moment, and matches well to the raw LFP (5–200 Hz, black line). (b) Power spectral density for the raw, unfiltered LFP in a, (black line) and 20 additional single trials in gray. (5–40 Hz marked by black dashed lines). (c) Blue bars indicate the relative frequency of spikes across GPs, peaking near ±π radians (N spikes > 1.5 × 105; Rayleigh test, p < 1 × 10−5, example from monkey W). There is no phase relationship when the LFP is averaged across electrodes (red dots). (d) Scatter plot showing phase offsets with distance from the putative source of a detected spontaneous wave (black dots). The slope of the linear fit (red line) gives the wave’s speed. The gray lines show the fits for multiple spatial shuffles. (e) Spontaneous fluctuations have varying degrees of wave organization (ρΦ,d, black line). Similarly filtered randomly generated noise does not exhibit wave organization (gray line; 99% cutoff of noise distribution, dashed line; example wave correlation value, red line).
In order to track these fluctuating patterns, we developed a technique for computing the Generalized Phase (GP) of the wideband filtered (5–40 Hz) LFP (Fig. 2a). The wide frequency band captured the dominant fluctuating components of the LFP while excluding 1) the lowest frequencies that are thought to reflect slow global changes such as arousal23,28 and 2) higher frequencies so as to avoid contamination of the LFP by spike artifacts29. Consistent with the identification of wave peaks and troughs as reflecting less and more excitable states, spontaneous spiking was strongly dependent on GP, with spike probability at the more excitable state (±π radians) approximately twice that of the less excitable state (0 radians; monkey W, N > 1.5 × 105 spikes across 20 recording sessions, p < 1 × 10−5, Rayleigh test for circular uniformity; Fig. 2c). The wideband filter captured the waveform of the LFP better than alpha and theta narrowband filters (681 ms example LFP trace; Pearson’s correlation: wideband r = 0.91, significantly different from alpha r = 0.38 and theta r = 0.23, ɑ = 1 × 10−5 confidence interval (CI) test; Extended Data 3a) and spontaneous spiking activity was more coupled to GP than the phase of theta or alpha (Extended Data 3b, c). The strong spike-GP coupling was spatially specific13,30, as phases from adjacent electrodes were significantly less coupled to spike timing (monkey W, p < 1 × 10−4; monkey T, N = 18 sessions, p < 1 × 10−3; two-sided Wilcoxon signed-rank test; Extended Data 4).
Use of a wideband filter avoids phase distortions that could artificially produce waves or distort estimates of wave properties. Importantly, our wave detection algorithm was applied to spatially unsmoothed data, thus preserving as much of the veridical relationship between phase and spatial position as possible. The strength of wave-like spatiotemporal organization across electrodes was quantified by the circular-linear correlation of GP with distance (ρΦ,d) from putative sources on the recording array (Fig. 2d). ρΦ,d spans from 0 (perfectly uncorrelated random noise) to 1 (perfect radial wave organization). During spontaneous fluctuations on the Utah array, the distribution of this measure spans up to 0.8, while for a matched number of trials of filtered Gaussian random noise, the 99th percentile is approximately 0.3 (Fig. 2e). We then took this value as a threshold for wave-like states.
We found spontaneous waves occur frequently (monkey W, 11.98 ± 4.38 mean ± s.d. times per second, mean ± s.d.; monkey T, 9.18 ± 4.18 times per second). Spontaneous waves traveled at speeds consistent with the conduction velocity of spikes traveling along unmyelinated horizontal projection axons (0.1–0.6 m/s; Extended Data 2), suggesting waves propagate via the horizontal fibers that populate the superficial and deep layers of cortex31–33. The average power spectrum for detected wave epochs exhibited reduced low-frequency power (< 12 Hz; monkey W, N = 215 fixation epochs with waves and 524 epochs without waves, p < 1 × 10−4; monkey T, N = 113 epochs with wave and 938 epochs without waves, p < 1 × 10−5 two-sided Wilcoxon rank-sum test; Extended Data 2) and power distributed over a broad range from 10 to 30 Hz, suggesting spontaneous waves reflect a distinct cortical state. It was not the case that larger fluctuations were more likely to be waves as there was no difference in the amplitude distribution between wave and non-wave fluctuations (monkey W, N = 798 wave and 216 non-wave fluctuations, p = 0.85; monkey T, N = 696 wave and 565 non-wave fluctuations, p = 0.79; two-sample F test for equal variances; Extended Data 2). Further, though previous work found high contrast visual stimulation attenuates waves with a spike-triggered average (STA) analysis5, our method found traveling waves while the monkeys freely viewed high contrast naturalistic images (with −50 to +100 ms perisaccadic activity excluded; Extended Data 5), indicating traveling waves are present during natural vision.
Do spontaneous waves play a role in perception? To test this, we trained two marmosets to perform a simple detection task. During the task, the monkeys were required to maintain fixation while awaiting the appearance of a low contrast (< 2% Michelson contrast) 200ms drifting Gabor target that appeared at an unpredictable time at one of two equally eccentric locations, coinciding with retinotopic locations of channels on the array (Fig. 3a). Juice reward was provided if the monkey made a saccade to the location of a target within 500ms of target onset. For each monkey, target contrast was set to a value that was detected approximately 50 percent of the time (Extended Data 7a).
Fig. 3. Waves facilitate detection when aligned with the retinotopic location of visual targets.
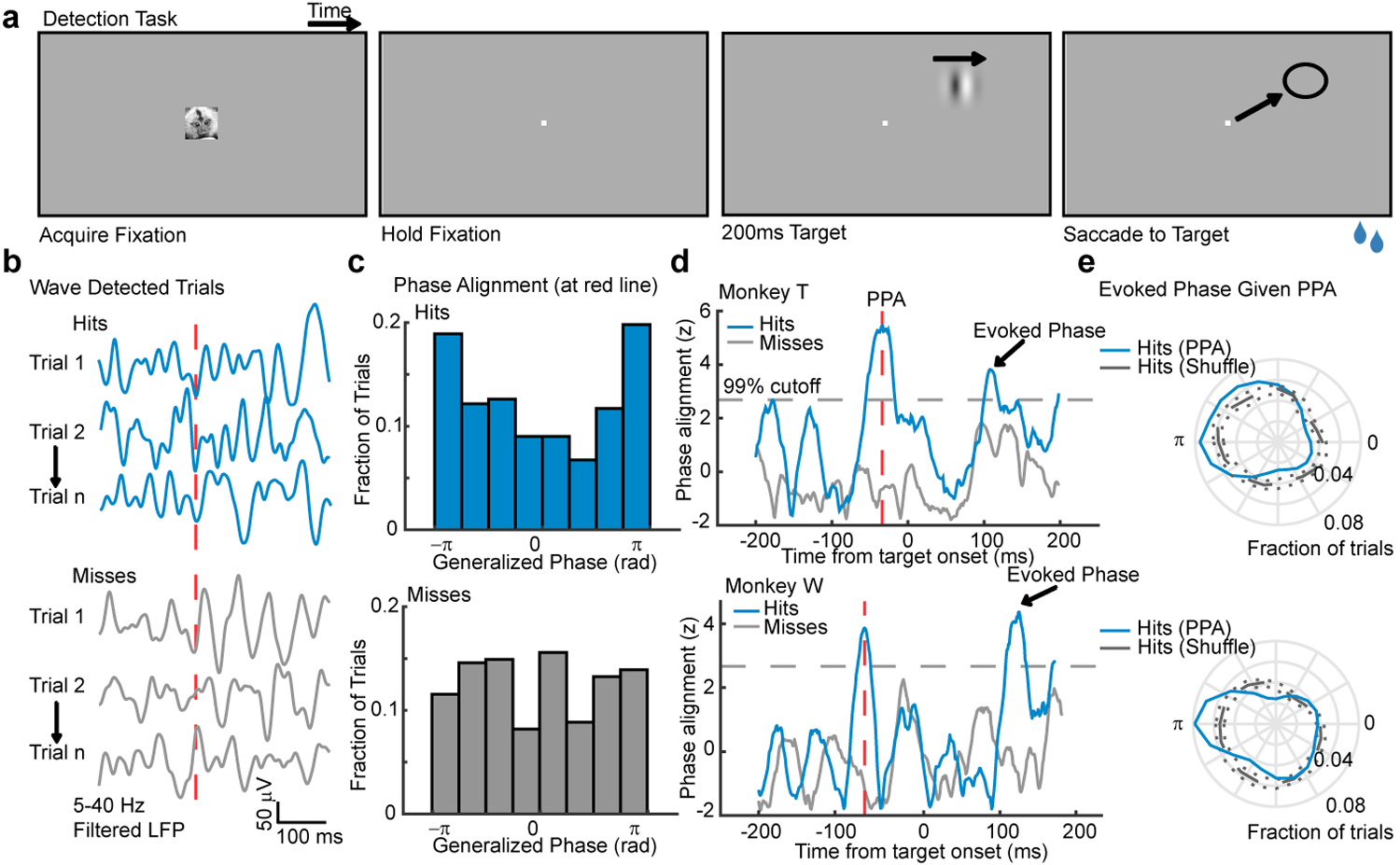
(a) Target detection task. A marmoset face appeared, and when foveated it was replaced with a fixation point. Marmosets held fixation until a target (200ms drifting Gabor) appeared at one of two possible locations after a random delay. The marmoset was rewarded with juice for making a saccade to the target location. (b) Example wideband LFP traces from a target-aligned electrode (hits, top; misses, bottom) where waves were detected on the array at the time indicated by the red-dashed line. (c) Distributions of phase across hit (blue, top, N = 223 trials) and miss trials (gray, bottom, N = 298 trials) at the time in (b). Data are from monkey T. (d) The cross-trial phase alignment in (c) plotted for each moment in time around the onset of the target for monkey T (top) and monkey W (bottom, N = 348 hits, 412 misses). Each phase distribution was z-scored relative to shuffled phase distributions (gray dashed line: 99% cutoff from permutation control). The time of peak phase alignment (red dashed line) is shown for each monkey (−33 ms, monkey T; −60 ms, monkey W). (e) Polar plots showing that the network was in a more excitable state (±π rad) at the time of target-evoked phase alignment (arrowheads) if the aligned phase occurred at peak PPA (blue line; gray line is a distribution of shuffled hits).
We hypothesized that target detection should be facilitated when spontaneous waves align a more excitable state with target locations. To test this, we collected trials on which waves were detected (monkey W, 80.05% of trials; monkey T, 57.37%; collapsed across both target locations) and asked if detection probability varied with the state of the wave, measured at the retinotopically aligned electrode (Fig. 3b, c). We only included trials where fixation had been maintained for at least 300 ms prior to target onset to avoid including waves triggered by the saccade to fixation that initiated each trial19. To avoid any confounding effect due to the activation by the target itself, we leveraged the observation that similar wave phases tend to recur over 1–2 sequential cycles34, and examined wave alignments before the presentation of the target that predicted detection performance. Detected targets (hits) tended to be preceded by the alignment of a particular wave phase (peak −60 ms relative to target onset monkey W, p < 1 × 10–3; −33 ms monkey T, p < 1 × 10–5; Rayleigh test; Fig. 3d–g). We refer to this as the Pre-target Phase Alignment (PPA). No significant phase alignment was observed in non-wave trials (not shown).
How might the alignment of waves, before the target appeared, affect detection performance? We hypothesized that this aligned phase was predictive because it led to a more excitable state during the target-evoked response that favored detection. To test this, we selected trials with detected waves whose phase at the peak of PPA was within ±π/6 of the aligned phase. For these trials, we then computed the LFP phase during the target-evoked response. Consistent with our prediction, the target-evoked LFP was more likely to be in the more excitable state (±π; blue trace, Fig. 3e) than expected from randomly selected hit trials (gray trace, Fig. 3e; permutation test, ɑ = 0.01). This indicates that the PPA reflects waves that lead directly to a more excitable network state during the target-evoked response.
Next we asked whether the wave alignment predictive of hits reflects a shift in sensitivity for faint targets, or an increase in response bias to the target location. We therefore tested whether waves were predictive of false alarms, defined as a saccade to a potential target location when no target was presented. We found no evidence that more excitable wave states were predictive of false alarms (Extended Data 6). We therefore conclude that the alignment of spontaneous waves modulates the monkeys’ sensitivity to the appearance of a faint target.
If true, the wave state should modulate the magnitude of evoked responses caused by the appearance of the target. Consistent with the observation that stronger target-evoked responses are correlated with better detection performance35, we found that firing rates during the target-evoked response (80–200ms from target onset) were higher for hits than misses for both monkeys (monkey W, N = 25 single- and 83 multi-units, p = 0.0015; monkey T, N = 27 single and 110 multi-units, p < 1 × 10−5; two-sided Wilcoxon signed-rank test; Extended Data 7d, e). We hypothesized the more excitable states following PPA increased the magnitude of evoked activity, producing the stronger evoked responses correlated with improved detection. To test this, we calculated average multi-unit firing rates collapsed across target-aligned electrodes for trials where waves were of the aligned phase, or in the opposite phase at PPA (Fig. 4a, c). Consistent with our hypothesis, the evoked firing rate was larger across units for trials where a wave occurred and aligned the more excitable state to the target location rather than an oppositely aligned wave (± π/3 rad, N = 43 multi-units across both monkeys; p < 1×10−6; two-tailed Wilcoxon sign-rank test). We performed the same analysis on trials that did not meet our statistical criterion for waves (non-wave) and found the phase did not modulate firing rates (N = 143 multi-units; p = 0.074; Fig. 4b, c).
Fig. 4. Wave state predicts target-evoked response magnitude and perceptual sensitivity.
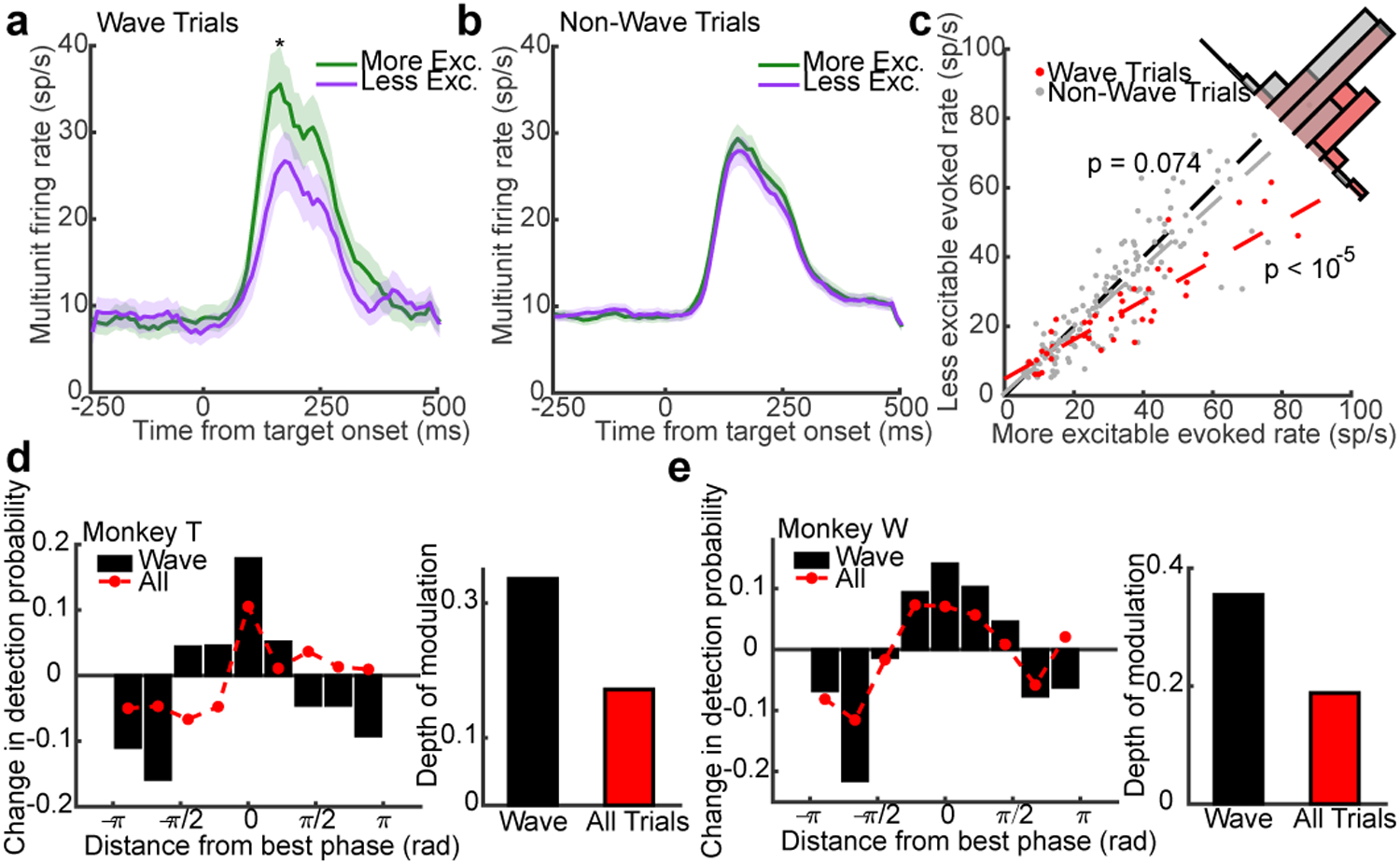
(a) Average target-evoked responses following wave alignment to the more excitable state (green line; N = 43 multi-units across both monkeys) are significantly greater than less excitable wave states (purple line; p < 10−5, two-sided Wilcoxon rank-sum test; shaded regions ± SEM). (b) The same analysis for non-wave fluctuations showed no difference. (N = 147 multi-units; p = 0.074). (c) Scatter plot of target-evoked responses across multi-units for trials in the more excitable (x-axis) or less excitable state (y-axis) at the time of PPA for wave (red dots; linear fit, red dashed line) or non-wave trials (gray dots; linear fit, gray dashed line). (d, e) Bar plots show the change in detection probability centered on the aligned phase at peak PPA in each monkey (rotated to 0 radians) for detected waves. Red dots show weaker phase-dependent changes in detection probability when all trials (wave, non-wave) are combined. The depth of modulation in detection probability given wave state is roughly double the depth for all trials (insets; monkey T, 33% to 17%, N = 464 wave and 494 non-wave trials; monkey W, 35% to 19%, N = 479 wave and 485 non-wave trials).
Finally, because the pre-target wave state predicts the magnitude of target-evoked spiking, we wished to quantify how well one could predict the monkey’s likelihood of detecting the faint target based solely on the knowledge of wave state at the time of PPA. We calculated the monkey’s conditional probability of target detection as a function of phase distance from the optimally aligned wave in each monkey (rotated to 0 radians). In both monkeys, the conditional probability of detection reached a maximum for the optimal phases and a minimum for opposite phases (Fig. 4d, e), with a depth of modulation of 33% (monkey T) and 35% (monkey W) from peak to trough. If we take the perspective of a single electrode, with no knowledge about the state of the wave, there remains a strong, but significantly lower phase-dependent probability of detection (17% monkey T, 19% monkey W; CI test, α = 0.05).
How does wave state compare relative to other indicators of network state that have previously been found to be predictive of perceptual performance? To quantify this we constructed a Generalized Linear Model (GLM) regressing perceptual performance (hit, miss) against target-evoked spike rate35,36, pre-target baseline activity, a measure of attentional state37, pupillary diameter, a measure of arousal28,38,39, and pre-target alpha power40 (logit link function, binomial error distribution, N = 1277 trials; Extended Data 8). On trials where waves were detected, generalized phase at the time of PPA was the strongest predictor of perceptual performance (βGP = 0.25, p < 0.0001) as compared with arousal (βPUP = 0.15, p < 0.05) and target-evoked spiking activity (βFR = 0.13, p < 0.05). Pre-target alpha power and spontaneous pre-target firing rate were not significant measures (p = 0.69 and p = 0.80 respectively).
Taken together, these results demonstrate that spontaneous traveling waves do occur in the neocortex of the awake monkey, they modulate sensory-evoked responses, and they gate perception. The waves travel at speeds consistent with the conduction velocity of unmyelinated horizontal axons that populate the superficial and deep layers of cortex, suggesting they emerge from the activation of cortical populations by spikes traveling along topographic connections that fall off with distance. These waves are distinct from the large, slow-wave deflections reported during anesthesia or quiet wakefulness41,42. Rather, they are present during active vision, and their alignment preceding the presentation of a target predicts detection performance. Importantly, these wave effects are only apparent due to our measurement of the Generalized Phase, and cannot be explained by latent narrowband oscillations embedded in the wideband signal. Narrowband filtering in alpha or beta bands fails to reveal any phase alignment predictive of perception (Extended Data 9).
The importance of waves to perception is further underscored by the fact that they are more predictive of perceptual sensitivity than previous reports of pre-target alpha oscillation phase in visual detection43–45 or theta oscillation phase in frontal-parietal networks during the deployment of attention46,47. We speculate, given that we observe weaker predictive effects when we mix wave and non-wave trials, that the alpha and theta effects previously observed were in fact due to the undetected presence of traveling waves. This is supported by the recent discovery that alpha and theta oscillations travel as propagating waves across awake human cortex21. If these two phenomena are related, this raises the intriguing possibility that spontaneous waves may also be coordinated across brain areas. Such coordination might explain how waves in MT are so strongly predictive of detection for stimuli that presumably activate other visual areas such as V1. These results have important implications for the neural organization of sensory processing demonstrating that, when viewed across the spatial extent of the cortex, fluctuations of cortical activity are neither purely synchronous nor spatially disorganized noise processes. Rather, neocortex exhibits propagating waves of activity that dynamically regulate neuronal responses and perceptual sensitivity.
Methods
Surgeries
Two marmosets (Callithrix jacchus), one male (monkey W) and one female (monkey T) participated in this study. The sample size was chosen to minimize animal use while providing for reproducibility of results. No blinding or randomization was applied. Each marmoset was fitted with a headpost for head stabilization and eye tracking. The headpost contained a hollow chamber housing an Omnetics connector for a Utah array, which was chronically implanted in a subsequent surgery. For that surgery, a 7×10mm craniotomy was made over area MT (stereotaxic coordinates 2mm anterior, 12mm dorsal). An 8×8 (64 channel, monkey W) and 9×9 with alternating channels removed (40 channel, monkey T) Utah array was chronically implanted over area MT using a pneumatic inserter wand. The electrodes spacing was 400μM with a pitch depth of 1.5mm. The craniotomy was closed with Duraseal (Integra Life Sciences, monkey W) or Duragen (Integra Life Sciences, monkey T), and covered with a titanium mesh embedded in dental acrylic. All surgical procedures were performed with the monkeys under general anesthesia in an aseptic environment in compliance with NIH guidelines. All experimental methods were approved by the Institutional Animal Care and Use Committee (IACUC) of the Salk Institute for Biological Studies and conformed to NIH guidelines.
Data Acquisition
Marmosets were trained to enter a custom-built marmoset chair that was placed inside a faraday box with an LCD monitor (ASUS VG248QE) at a distance of 40 cm. The monitor was set to a refresh rate of 100Hz and gamma corrected with a mean gray luminance of 75 candelas/m2. Electrode voltages were recorded from the Utah arrays using two Intan RHD2132 amplifiers connected to an Intan RHD2000 USB interface board. Data were sampled at 30 kHz from all channels. The marmosets were headfixed by a headpost for all recordings. Eye position was measured with an IScan CCD infrared camera sampling eye position at 500 Hz. Stimulus presentation and behavioral control was managed through MonkeyLogic in Matlab. Digital and analog signals were coordinated through National Instrument DAQ cards (NI PCI6621) and BNC breakout boxes (NI BNC2090A). Neural data was broken into two streams for offline processing of spikes (single-unit and multi-unit activity) and LFPs. Spike data was high-pass filtered at 500 Hz and candidate spike waveforms were defined as exceeding 4 standard deviations of a sliding 1 second window of ongoing voltage fluctuations. Artifacts were rejected if appearing synchronously (within 0.5 ms) on over a quarter of all recorded channels. Segments of data (1.5 ms) around the time of candidate spikes were selected for spike sorting using principal component analysis through the open source spike sorting software MClust in Matlab (A. David Redish, University of Minnesota). Sorted units were classified as single- or multi-units and single units were validated by the presence of a clear refractory period in the autocorrelogram. LFP data was low-pass filtered at 300 Hz and down-sampled to 1000 Hz.
Generalized Phase
The analytic signal paradigm was originally developed by Denis Gabor in 194648, defining the concept of “instantaneous frequency” and “instantaneous phase” for non-stationary signals; however, due to several technical limitations, the analytic signal representation is commonly used strictly in the context of signals pre-treated with a tight narrowband filter49. Here, we sought to address the technical limitations in the analytic signal to generalize its application beyond signals where tight narrowband filtering is appropriate. For this reason, we call our updated approach for non-stationary, wideband signals Generalized Phase (GP).
Consider a real-valued signal xn ∈ ℝ for n ∈ [1,2,…,Ns], where Ns is the number of samples in one recorded trial obtained at a sampling frequency Fs. Given xn, its analytic signal representation (Xn) is:
where i is the imaginary unit and H[yn] is the Hilbert transform (HT) of the signal yn. This representation can be obtained by implementing the HT operator as an FIR filter in time domain50, or by using a single-sided Fourier transform approach51,52. Sinusoidal cycles appear in this representation as circular contours in the complex plane, while non-sinusoidal fluctuations appear as closed, quasi-circular contours. In this complex plane representation, phase is calculated numerically by the four-quadrant arctangent function.
The technical limitations in the analytic signal framework occur for two principal reasons. First, low-frequency intrusions effectively shift the representation by a complex constant, which has the critical effect of highly distorting phase angles estimated by the arctangent. As an initial step in the GP representation, then, we filter the signal within a wide bandpass (5–40 Hz; 8th-order zero-phase Butterworth filter), excluding low-frequency content. Note that this important step is distinct from narrow bandpass filtering (e.g. 8–13 Hz), as this approach preserves a significant portion of the signal spectrum, thereby minimizing waveform distortion and potential artifacts due to narrowband filtering of broadband noise (Fig. 2a and Supplementary Figure S3a). We then use the single-sided Fourier transform approach51,52 on the wideband signal and compute phase derivatives as finite differences, which are calculated by multiplications in the complex plane18,24,53. Second, high-frequency intrusions appear in the analytic signal representation as complex riding cycles53, which manifest as periods of negative frequencies in the analytic signal representation. As a secondary step in the GP representation, then, we numerically detect these complex riding cycles -- namely, Nc points of negative frequency in the phase sequence Arg[Xn] -- and utilize shape-preserving piecewise cubic interpolation on the next 2Nc points of Arg[Xn] following the detected negative frequency epoch. The resulting representation captures the phase of the largest fluctuation on the recording electrode at any moment in time (Fig. 2a), without the distortions due to the large, low-frequency intrusions or the smaller, high-frequency intrusions characteristic of the 1/f-type fluctuations in cortical LFP54–56. The GP represents a coherent numerical approach to the original analytic signal framework of Denis Gabor48, suitable for implementation in modern digital signal processing applications.
Wave Detection
We employed a recently introduced statistical approach to detect spontaneous traveling waves in noisy multichannel recordings18,24, adapted to utilize GP. The advantage of GP is to capture the dominant fluctuation on each electrode at each point in time; further, it does not distort the signal waveform, as would occur with a narrowband filter. When these fluctuations are shared across electrodes and exhibit consistent phase offsets, the algorithm detects these patterns as traveling waves, as described below and illustrated in Figure S2.
Spontaneous waves were detected during epochs of fixation, excluding 50 ms before, and 100 ms after eye movements, identified from the eye tracking signals. The wave detection technique occurs in three steps. First, the algorithm finds the time point nearest to each positive LFP peak on the array. This defines a flexible window in which we test for a spontaneous wave, where the phases are valid in a neighborhood around that time point. Secondly, the algorithm finds the most likely starting point for the wave, by finding the point that maximizes the divergence of the phase gradient in a smoothed version of the scalar phase field. This captures the point from which neural activity flows outward at each moment. Thirdly, with the putative source point found, the algorithm then quantifies how clearly activity is organized about this point, by calculating the circular-linear correlation with distance (ρφ,d ∈ [−1,1]57) across the whole electrode array, consistent with our observation that the wavelengths were long relative to the spatial extent of the array. Importantly, this step is done on the tested scalar phase field without spatial smoothing, which prevents smoothing artifacts from contaminating the results. Finally, a null distribution was constructed for ρφ,d by randomly shuffling phase values on the electrode array. Unless stated otherwise, a scalar threshold of 0.3 was used to detect waves throughout, which represented a conservative threshold on all constructed null distributions.
Data Inclusion Criteria
Only visually responsive units (defined by having a mean evoked firing rate 80–200 ms after target onset that was at least 2 times the mean baseline firing rate, computed from −200 to 0 ms) were included. Units were excluded if they had fewer than 6 trials on which the preferred-orientation target appeared in the unit’s receptive field on the trial type being considered (hits vs. misses; wave vs. non-wave). For the analysis of PSD in Fig. 2f, wave trials were only included if they exhibited at least four detected waves over a 300 ms fixation epoch. For the analysis in Fig. 3e, trials were only included if a wave was detected prior to target onset on hit trials, and phase at the target-aligned electrode was within ±π/6 of the aligned phase.
Receptive Field Mapping
Receptive fields were mapped through reverse correlation. The marmoset was trained to hold fixation on an image (marmoset face, 1 degree of visual angle (DVA) square) presented to the center of the LCD monitor. A drifting Gabor (2 degrees diameter, spatial frequency: 0.5 cycles per degree, temporal frequency 10 cycles per second) was presented at a random position on the monitor between 0–18 degrees in azimuth and −15 to 15 degrees in elevation, drifting in one of 8 possible directions for 200ms, after which it disappeared. After a random delay drawn from an exponential distribution (mean 40ms), a new probe appeared and the pattern repeated until the marmoset broke fixation (defined as an excursion of 1.5 degrees from fixation) or viewed 16 probes. The marmoset was given a juice reward proportional to the number of probes presented. The receptive field for each unit recorded on the array was estimated by calculating the spike-triggered average (STA) stimulus that evoked the maximal response:
The STA is the sum of probe location xi weighted by the spike count yi within the time bin 40 to 200ms after probe onset, normalized by the number of all recorded spikes N. From the location of estimated receptive fields on each spiking channel, and the known topography of area MT in the marmoset58, we estimated the relative position of each recording array in marmoset cortex (Fig. 1a). We excluded from the analysis the upper half of monkey W’s array as the recordings did not appear to be in area MT.
Target Detection Task
Marmosets initiated each trial by fixating a marmoset face (a stimulus that naturally attracts marmoset gaze) that, upon fixation, transformed into a fixation point (0.15 DVA). They were trained to hold fixation on the fixation point (1.5 degree tolerance) awaiting the appearance of a drifting Gabor (4 DVA diameter which reliably produced evoked responses on 1–2 electrodes; spatial frequency, 0.5 cycles per degree; temporal frequency, 10 cycles per second, drifting in one of up to 8 possible directions). After establishing fixation, the marmoset was required to hold fixation for a minimum duration (400 ms monkey W, 300 ms monkey T) to avoid contamination from waves caused by the saccade to the fixation point19. Early fixation breaks (defined by the excursion of the eye position from the fixation window) were excluded from analysis. The target only appeared if fixation was held for an additional random duration drawn from an exponential distribution (mean 200ms) to generate a flat hazard function. The target could appear at one of two locations selected based on receptive field mapping at equal eccentricity (7 degrees monkey W, 8 degrees monkey T). The target was presented for 200ms, after which the monkey had 300ms (for a total of 500ms) to saccade to within 2.5 degrees of the target center for a juice reward. On 10 percent of trials no target was presented, and the monkey was rewarded for holding fixation to the trial end. If a saccade reached the target in less than 100 ms from target onset, the trial was rejected from analysis. The trial was classified as a miss if the marmoset broke fixation to a non-target location after the target had appeared, or if the marmoset held fixation until after the response window closed. The trial was classified as a false alarm if the monkey broke fixation to a target location after achieving a minimum fixation duration (500 ms) but when no target had been shown to any location. This minimum duration was to help avoid classifying early fixation breaks as false alarms. Only trials from the preferred directions of motion (DSI greater than 0.2) presented within the receptive field of a single- or multi-unit were analyzed for that unit. Target contrasts were selected to generate a correct detection rate of 50 percent based (mean 1.4 percent Michelson contrast for both monkeys). High contrast (10 percent Michelson contrast) targets were presented on 10 percent of trials. If performance for these targets was below 70 percent, the session was rejected from analysis.
Free Viewing Natural Images
Marmosets were headfixed and their gaze monitored as in the previous tasks. Grayscale versions of naturalistic images (spanning 20–30 DVA) were randomly interleaved and presented to the monkey. The monkey was free to look at the images, and after 10 seconds was given a juice reward. Saccades were identified from the absolute value of the first numerical derivative of the smoothed vertical and horizontal eye traces (5 ms sliding Gaussian). Saccades were defined as velocity peaks exceeding 25 degrees per second. We analyzed periods between saccades, excluding 50 ms before and 100 ms after each detected saccade.
Cross-Trial Phase Alignment
To quantify alignment of the GP across trials, we utilized the standard formulation for the Kuramoto order parameter:
where Nt is the number of trials in each condition (hit or miss), i is the complex unit, and φj is the GP at the tested time point. The order parameter ranges between 0 (uniform distribution of phase values) and 1 (identical phase values for each trial). To compare meaningfully between two sets of observations (hit and miss) with slightly different number of trials while accounting for the expected mean and variances of the order parameter at finite scales59, all phase alignment values were put in z-score units of a null distribution computed from 10,000 iterations of the value from randomly selected trials, with the same number of observations.
Conditional probability estimate
In order to understand how waves modulate the probability of target detection, we calculated the conditional probability of detection at each phase:
where h ∈ {0,1} is an indicator variable for target detection and Φi represents GP in bin i ∈ [1,Nb], where Nb is the number of bins (nine throughout). To balance trial counts between wave and non-wave conditions, in this analysis we used the median of the ρφ,d distributions as the wave detection threshold. We then fit a sinusoid by least-squares estimate to the binned conditional probabilities in wave and non-wave states. Finally, significance of the difference in modulation amplitude between the two states was assessed in each monkey by comparing confidence intervals for each fit at the α = 0.05 level.
Generalized linear model (GLM) analysis
To determine the relative predictive power of the state of spontaneous traveling waves compared to other measures of network state on the detection task, we fitted a GLM to the trial-by-trial responses of the monkeys. Predictors included (1) target-evoked firing rate, measured from +80 to +200 ms after target onset, (2) the attentive state, estimated by the spontaneous spike rate measured during a window preceding the appearance of the target (−120 to 0 ms), (3) the pre-target alpha (8–13 Hz) power 50 ms prior to target onset, measured as the instantaneous power (Hilbert transform modulus) after narrowband filtering and normalized by the broadband power spectrum (5–200 Hz), (4) arousal state, estimated by the pupil diameter at the time of target onset, and (5) GP at the time of maximal PPA (Fig. 3f). For the measure of normalized alpha-band power, transformation by the logarithm function was utilized for the purpose of variance stabilization. The fit was performed using 1277 trials on which waves were detected in both monkeys. Predictor distributions were standardized by z-scoring prior to fitting so that resulting model weights (βFR, βSP, βα, βPUP, βGP) could be compared to assess relative importance60,61. The GLM was fitted using a logit link function to relate changes in the continuous predictor variables to the binary response variable (hit or miss in the detection task). Individual predictors were evaluated by calculating the t-statistic associated with the estimated weight (H0: β = 0, H1: β ≠ 0), with significance determined at the α = 0.05 level.
Data Availability:
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code Availability:
An open-source code repository for all methods is available on BitBucket: http://bitbucket.org/lylemuller/wave-matlab.
Extended Data
Extended Data 1. Retinotopic mapping and motion direction tuning is consistent with the anatomical organization and tuning preferences of marmoset MT.

(a) Receptive fields for recorded units were measured by reverse correlation. Monkeys held fixation on a marmoset face while visual probes (drifting Gabors) appeared at random locations in the visual hemifield contralateral to the recording array. Each probe would appear, drift for 200ms, and disappear after which a new probe would appear in a new random location and the process would repeat until the monkey broke fixation. (b) The estimated position and orientation of Utah arrays in area MT based on retinotopy and histological examination for monkey W (blue) and monkey T (red). (c) Example receptive fields and their preference for motion direction are consistent with previous reports of marmoset MT58.
Extended Data 2. Detection of spontaneous traveling waves.

(a) The method for detecting spontaneous waves from the Generalized Phase. First, the detection algorithm finds the most likely starting point for a putative wave as the point that maximizes the divergence of the phase gradient (step 1). (b) With this source point found, the algorithm then quantifies the spatiotemporal organization about this point from the circular-linear correlation of phase with distance across the whole array (step 2). With this approach, the algorithm can robustly detect arbitrarily shaped wavefronts in the array data. (c) The average power spectrum for waves (N = 215) has significantly less power in low frequencies (<12Hz) as compared to non-wave fluctuations (N = 524). Dotted bounds represent SEM. Asterisk: p < 1 × 10−5, two-tailed Wilcoxon rank-sum test. (d) Detected waves in both monkeys predominantly travel at speeds consistent with the conduction velocity of unmyelinated horizontal axons (0.1–0.6 m/s, red dashed lines; monkey W, 5571 waves, blue line; monkey T, 9285 waves, red line). (e) There is no difference in the amplitude of fluctuations that are detected as waves (blue line; N = 696 waves) or rejected (non-wave, gray line; N = 565 non-wave fluctuations; example monkey T session).
Extended Data 3. Wideband Generalized Phase is better coupled to spike timing than narrowband alpha or theta filters.

(a) The phase and amplitude of the raw (5–100 Hz) LFP is poorly captured by narrow-band theta (4–8 Hz, blue dotted line) or alpha (8–13 Hz, red dotted line) filters. (b) Scatter plot showing spontaneous spike-phase coupling is greater for GP (5–40 Hz) than alpha or theta narrowband filtered phases. Coupling averaged across electrodes for individual recording sessions is plotted as black dots and each red dot represents the average value across sessions. (c) Spontaneous spike-phase coupling remains stronger for GP than the narrow frequency bands even when the spontaneous LFP epochs are restricted to periods where there is large alpha (12.06% of recorded time) or theta (7.24%) LFP power during fixation (5 dB SNR, narrow- to broad-band power ratio). Results are presented from monkey W.
Extended Data 4. Spike coupling to Generalized Phase (GP) is spatially dependent.
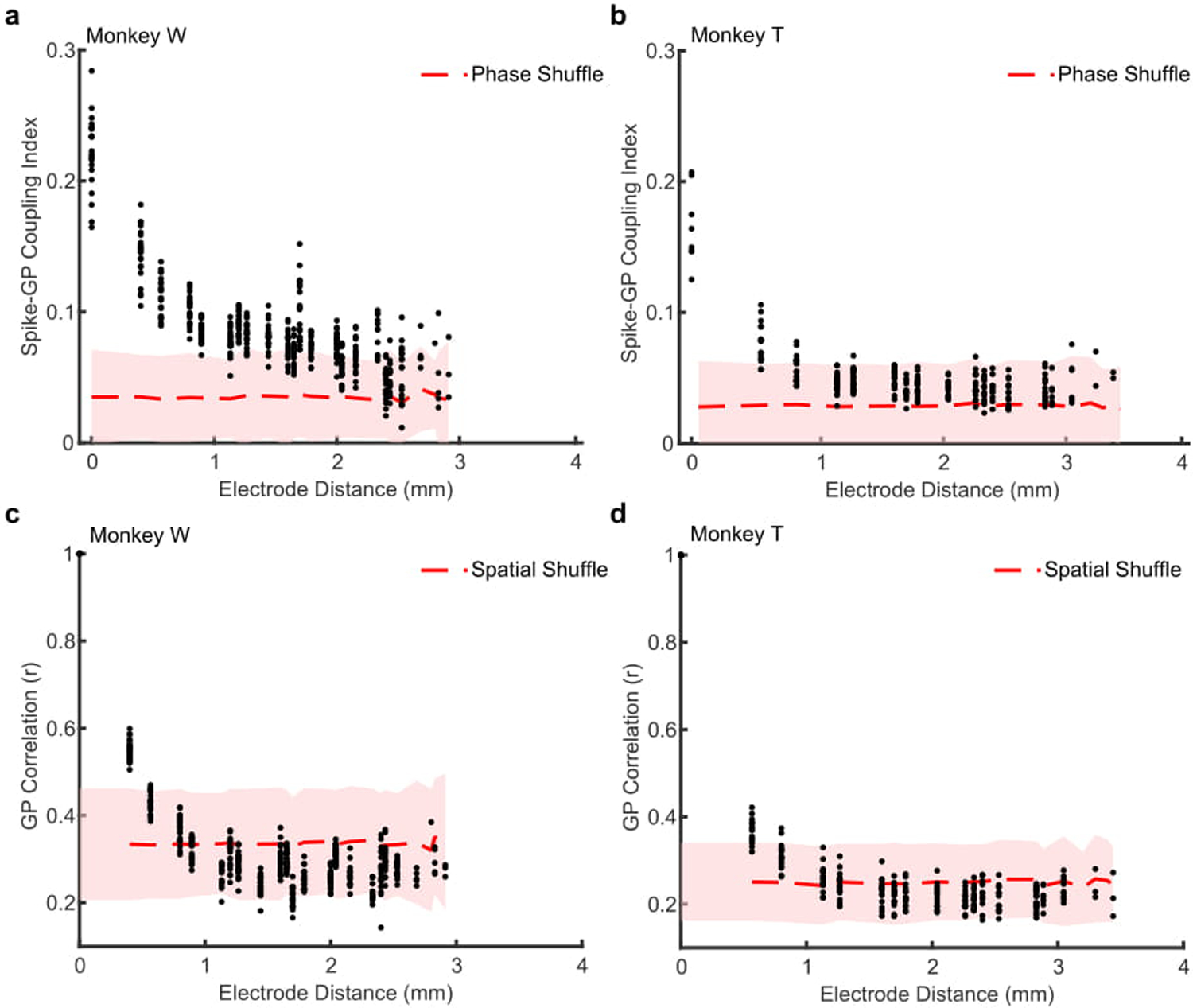
(a) Scatter plot showing the average spike-GP coupling across the distances of the array. Each point is averaged across a given spike-phase distance for a single recording session (N = 22 sessions). The red dashed line shows the average null distribution for shuffled phases ± 2 S.D. (shaded region). Data shown for monkey W. (b) Scatter plot showing the cross-channel GP correlation for 200 ms of LFP during fixation across the electrode distances of the recording array. Each dot is the average circular correlation within an individual recording session across that channel distance. Shaded region represents the mean (± 2 S.D.) correlation after shuffling the spatial position of the electrodes. (c, d) Same as a and b, but for monkey T (N = 18 sessions).
Extended Data 5. Spontaneous traveling waves are present during normal viewing of naturalistic visual scenes.

Marmosets freely viewed static natural images for 10 seconds while head-fixed. (a) An example high contrast image with the gaze of the marmoset over the 10 second viewing interval shown in red. (b) An example of a spontaneous traveling wave detected during a period of fixation while monkey T was freely viewing a high contrast image. (c) Across 86 trials, 593 spontaneous traveling waves were detected during spontaneous fixations while the monkey freely viewed the images (−50 to +100 ms perisaccadic activity excluded). (c) The density of observed wave speeds was consistent with the conduction velocity of unmyelinated axons (0.1–0.6 m/s).
Extended Data 6. False alarms are not predicted by the phase of traveling waves.
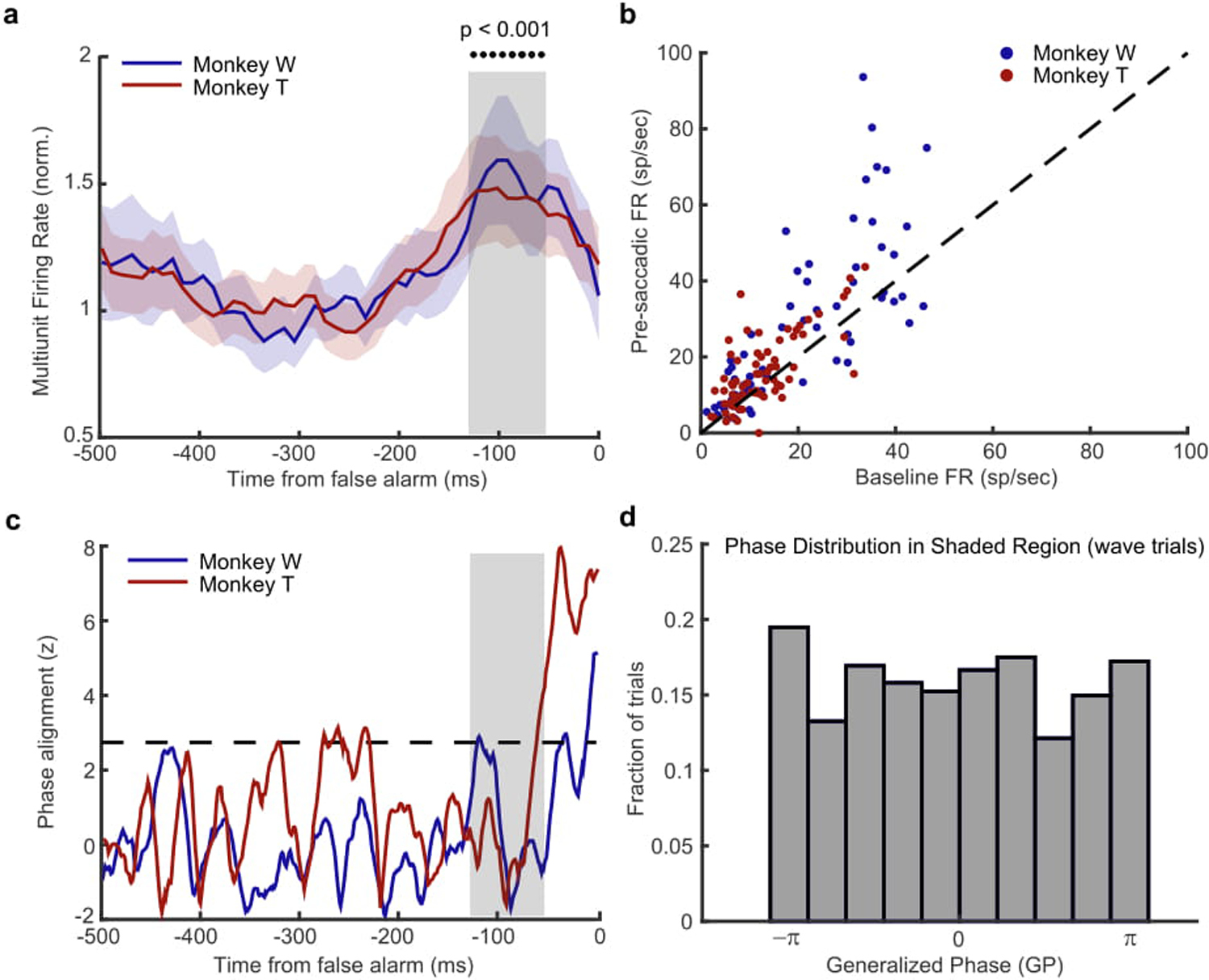
To test whether the alignment of waves with the target location produces a bias toward saccading to that location, we examined the spontaneous activity prior to false alarms, time locked to the eye movement. This is distinct from our analysis of hits, which is time locked to the onset of the target, and is a limitation in our design for comparing hits to false alarms. However, we do find a significant modulation of spontaneous spiking activity that is possibly the sensory signal generating the false alarm, giving us a window to explore their potential relationship with waves62. If waves increase the likelihood of false alarms, they should show some phase-dependent relationship similar to what we observe in hits, but time-locked to the spiking activity predictive of a false alarm. (a) Multi-unit spiking activity (normalized to the baseline, shaded regions ± SEM) for monkey W (blue) and monkey T (red) is significantly increased in the interval prior to a false alarm (gray shaded box, −120 ms to −60 ms, p < 0.001, two-sided Wilcoxon rank-sum test). (b) Scatter plot showing the average firing rate prior to the false alarm (y-axis, shaded interval in a) is significantly greater than the spontaneous background firing rate (x-axis, −400ms to −200ms) for monkey W (blue dots; N = 62 multi-units, p < 0.0001, Wilcoxon signed rank test) and monkey T (red dots; N = 70 multi-units). (c) Cross-trial phase alignments for waves aligned to the location of false alarm for the interval preceding the occurrence of a false alarm. There is no strong phase alignment during the period of significant spiking activity (shaded region) for either monkey W (blue line) or monkey T (red line) that would show a wave state is predictive of a false alarm. However, there is a strong phase alignment just prior to (monkey T −40ms) and during the eye movement (monkey W, 0ms). Given their close proximity to the onset of the eye movement we suspect the observed alignment may reflect an efference signal related to the pending saccade63. (d) The distribution of observed wave phases is uniform during the period of significantly increased spiking activity (−90 ms before false alarm), indicating there is no relationship between the phase of spontaneous waves and the spontaneous spiking fluctuation associated with false alarms. Data collapsed across both monkeys as there was no difference in their distributions.
Extended Data 7. Target-evoked response magnitude is correlated with detection performance.
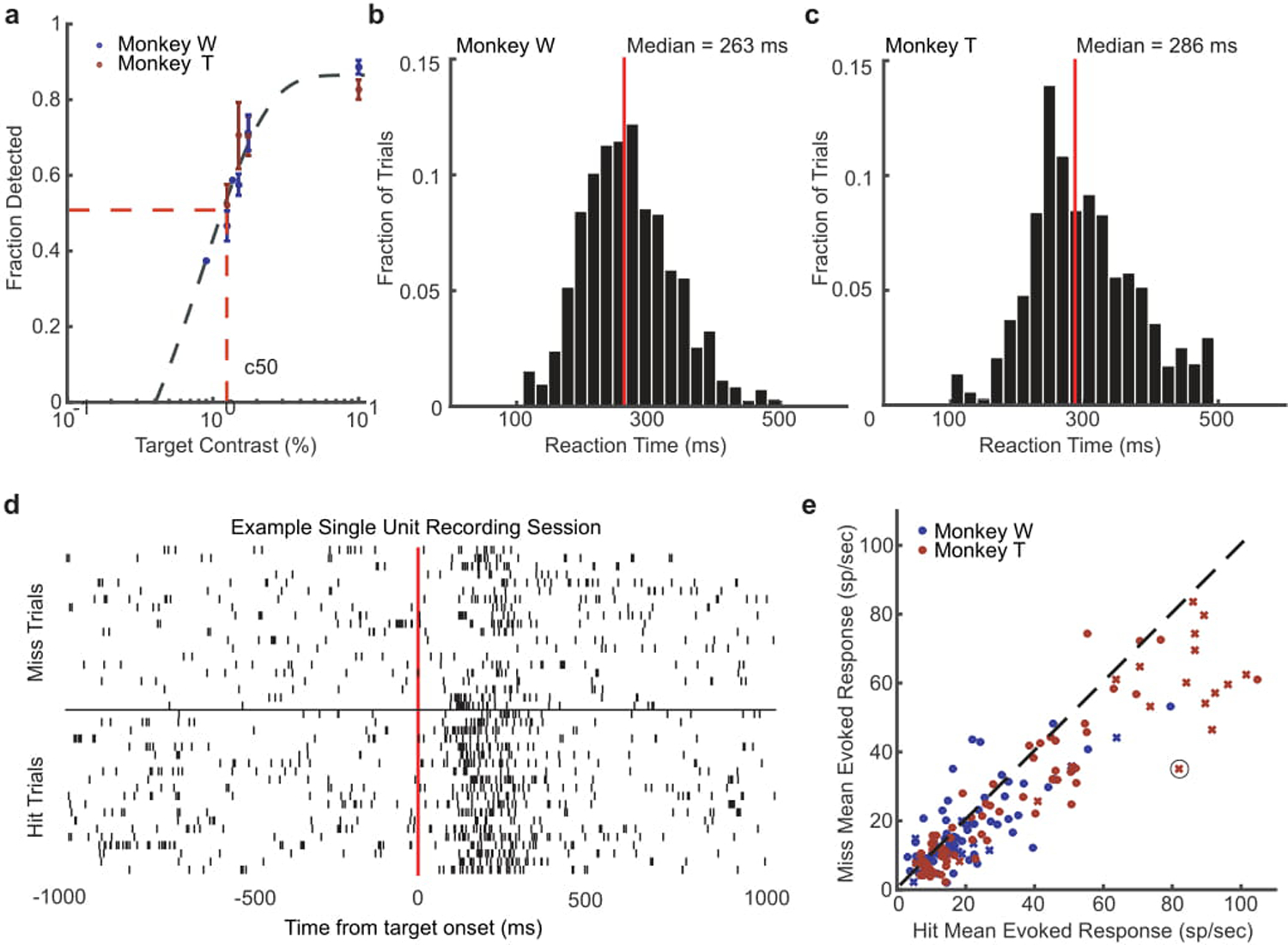
(a) Detection performance of different target contrasts for monkey W (blue) and monkey T (red) across training days where those contrasts were presented. Both monkeys had similar psychophysical thresholds, defined as the contrast where the monkey detected the target 50 percent of the time on average (c50) as estimated from a sigmoid fit (gray dashed line). (b, c) Distributions of reaction times for monkey W (b) and monkey T (c) during the detection task at their c50 value. The median reaction time for each monkey is shown by a red line. (d) Spike rasters for an example neuron with trials sorted into hits (bottom rasters) and misses (top rasters). (e) Scatter plot showing the distribution of mean hit (x-axis) and miss (y-axis) evoked responses (80–200 ms) for all single- (x) and multi-units (dot) recorded across all sessions for monkey W (blue) and monkey T (red). The circled x is the example neuron from panel d. Target-evoked responses were significantly stronger for detected targets in both monkeys. (monkey W, N = 25 single- and 83 multi-units, p < 0.01; monkey T, N = 27 single and 110 multi-units, p < 1 × 10−5; two-sided Wilcoxon signed-rank test).
Extended Data 8. Narrowband filters fail to detect any significant wave phase alignment prior to target onset.

(a) The cross-trial phase alignment computed as in Figure 3, but using a narrowband alpha (8–13 Hz) filter, does not show any significant alignment (gray dashed line) for hits (blue) or misses (gray) prior to target onset (gray region) for either monkey T (top) or monkey W (bottom). (b) The same as in (a), but for a beta (15–30 Hz) narrowband filter.
Extended Data 9. Instantaneous voltage is less predictive of spike timing and perception than Generalized Phase.
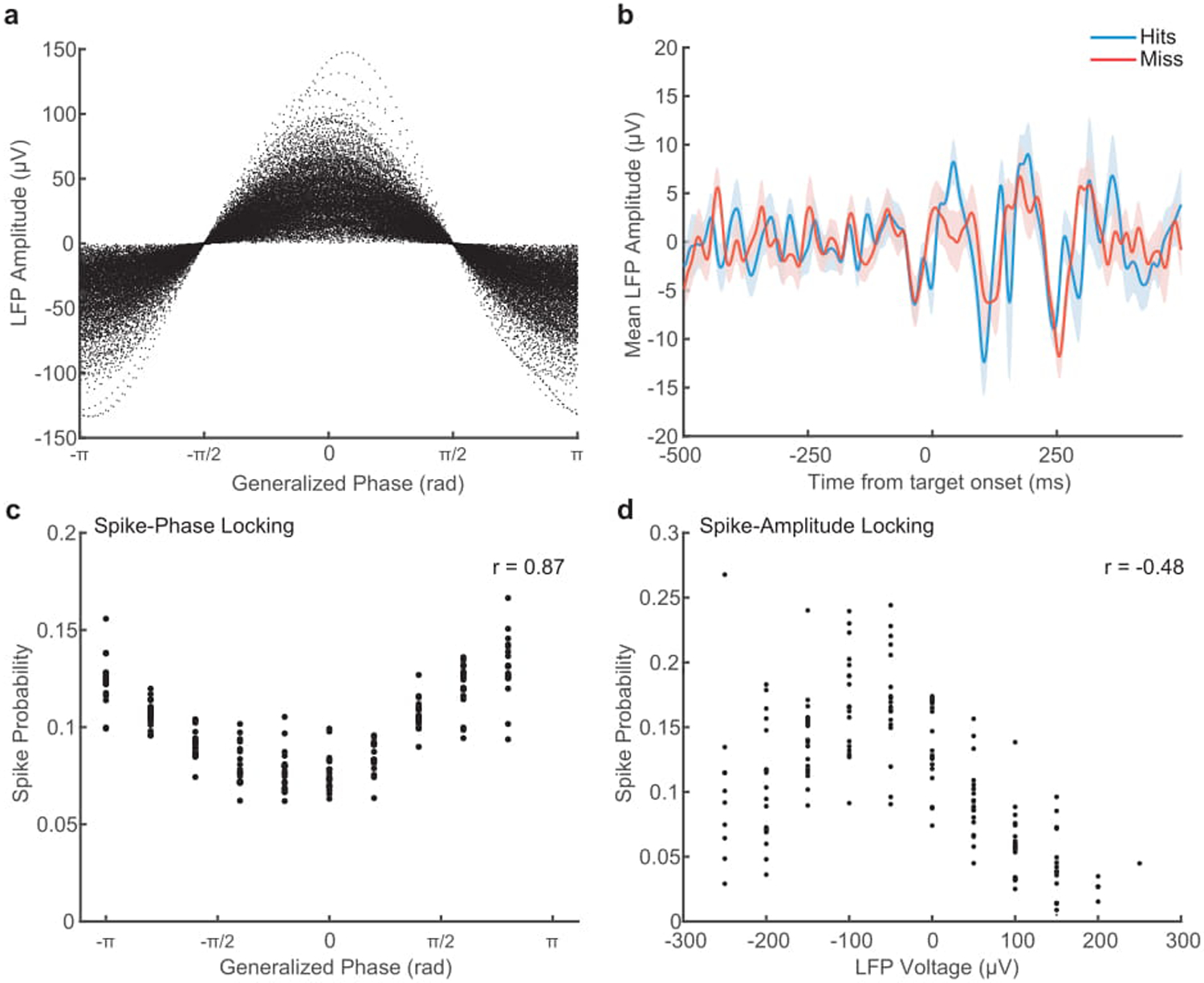
(a) Scatter plot showing the relationship between instantaneous LFP amplitude in voltage, and GP. The same voltage value can occur across a broad range of phases. (b) While we find wave phase to be predictive of detection, the average LFP voltage is not different preceding a hit (blue) or a miss (red). Shaded area indicates SEM across 18 sessions in monkey T. (c) Scatter plot showing the coupling of spike probability to GP. Each point is the probability of a spike occurring in that phase bin within a recording session (N = 18). There is a strong circular-linear correlation of GP with spike probability (r = 0.87). (d) Scatter plot showing weaker spike-amplitude coupling. Each point is the relative probability of a spike occurring in each voltage bin, normalized by the amount of time that instantaneous voltage occurs. Spike probability is less correlated with LFP amplitude (Spearman’s rank correlation, r = −0.48).
Supplementary Material
Acknowledgments:
We would like to thank Michael Avery, Katie Williams, Sean Adams, and Mat LeBlanc for their contributions to this project. We would also like to thank Tony Movshon for his feedback in the early stages of this project. Funding: The Dan and Martina Lewis Biophotonics Fellowship, Gatsby Charitable Foundation, the Fiona and Sanjay Jha Chair in Neuroscience, the Canadian Institute for Health Research, BrainsCAN at Western University (Canada First Research Excellence Fund, CFREF), the Swartz Foundation, Office of Naval Research N00014-16-1-2829, NIH grants R01-EY028723, U01-NS108683, P30-EY019005, T32 EY020503-06, and T32 MH020002-16A.
Footnotes
Competing Interests: Authors declare no competing interests.
References
- 1.Engel TA & Steinmetz NA New perspectives on dimensionality and variability from large-scale cortical dynamics. Curr. Opin. Neurobiol 58, 181–190 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Roland PE et al. Cortical feedback depolarization waves: a mechanism of top-down influence on early visual areas. Proc. Natl. Acad. Sci. U. S. A 103, 12586–12591 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ferezou I, Bolea S & Petersen CCH Visualizing the cortical representation of whisker touch: voltage-sensitive dye imaging in freely moving mice. Neuron 50, 617–629 (2006). [DOI] [PubMed] [Google Scholar]
- 4.Xu W, Huang X, Takagaki K & Wu J-Y Compression and reflection of visually evoked cortical waves. Neuron 55, 119–129 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nauhaus I, Busse L, Carandini M & Ringach DL Stimulus contrast modulates functional connectivity in visual cortex. Nat. Neurosci 12, 70–76 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Reimer A, Hubka P, Engel AK & Kral A Fast propagating waves within the rodent auditory cortex. Cereb. Cortex 21, 166–177 (2011). [DOI] [PubMed] [Google Scholar]
- 7.Townsend RG et al. Emergence of complex wave patterns in primate cerebral cortex. J. Neurosci 35, 4657–4662 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tomko GJ & Crapper DR Neuronal variability: non-stationary responses to identical visual stimuli. Brain Res. 79, 405–418 (1974). [DOI] [PubMed] [Google Scholar]
- 9.Shadlen MN & Newsome WT The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci 18, 3870–3896 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Okun M, Naim A & Lampl I The subthreshold relation between cortical local field potential and neuronal firing unveiled by intracellular recordings in awake rats. J. Neurosci 30, 4440–4448 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Luczak A, Bartho P & Harris KD Gating of sensory input by spontaneous cortical activity. J. Neurosci 33, 1684–1695 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tan AYY, Chen Y, Scholl B, Seidemann E & Priebe NJ Sensory stimulation shifts visual cortex from synchronous to asynchronous states. Nature 509, 226–229 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Katzner S et al. Local origin of field potentials in visual cortex. Neuron 61, 35–41 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Buzsáki G, Anastassiou CA & Koch C The origin of extracellular fields and currents—EEG, ECoG, LFP and spikes. Nat. Rev. Neurosci 13, 407–420 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ray S & Maunsell JHR Network rhythms influence the relationship between spike-triggered local field potential and functional connectivity. J. Neurosci 31, 12674–12682 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rubino D, Robbins KA & Hatsopoulos NG Propagating waves mediate information transfer in the motor cortex. Nat. Neurosci 9, 1549–1557 (2006). [DOI] [PubMed] [Google Scholar]
- 17.Benucci A, Frazor RA & Carandini M Standing waves and traveling waves distinguish two circuits in visual cortex. Neuron 55, 103–117 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Muller L, Reynaud A, Chavane F & Destexhe A The stimulus-evoked population response in visual cortex of awake monkey is a propagating wave. Nat. Commun 5, 3675 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zanos TP, Mineault PJ, Nasiotis KT, Guitton D & Pack CC A sensorimotor role for traveling waves in primate visual cortex. Neuron 85, 615–627 (2015). [DOI] [PubMed] [Google Scholar]
- 20.Bullock TH, Mcclune MC & Enright JT Are the electroencephalograms mainly rhythmic? Assessment of periodicity in wide-band time series. Neuroscience 121, 233–252 (2003). [DOI] [PubMed] [Google Scholar]
- 21.Zhang H, Watrous AJ, Patel A & Jacobs J Theta and Alpha Oscillations Are Traveling Waves in the Human Neocortex. Neuron 98, 1269–1281.e4 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Steriade M, Nuñez A & Amzica F A novel slow (< 1 Hz) oscillation of neocortical neurons in vivo: depolarizing and hyperpolarizing components. J. Neurosci 13, 3252–3265 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Steriade M, Timofeev I & Grenier F Natural waking and sleep states: a view from inside neocortical neurons. J. Neurophysiol 85, 1969–1985 (2001). [DOI] [PubMed] [Google Scholar]
- 24.Muller L et al. Rotating waves during human sleep spindles organize global patterns of activity that repeat precisely through the night. Elife 5, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Buzsáki G & Draguhn A Neuronal oscillations in cortical networks. Science 304, 1926–1929 (2004). [DOI] [PubMed] [Google Scholar]
- 26.Kayser C, Montemurro MA, Logothetis NK & Panzeri S Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron 61, 597–608 (2009). [DOI] [PubMed] [Google Scholar]
- 27.Lopour BA, Tavassoli A, Fried I & Ringach DL Coding of information in the phase of local field potentials within human medial temporal lobe. Neuron 79, 594–606 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McGinley MJ, David SV & McCormick DA Cortical Membrane Potential Signature of Optimal States for Sensory Signal Detection. Neuron 87, 179–192 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zanos TP, Mineault PJ & Pack CC Removal of spurious correlations between spikes and local field potentials. J. Neurophysiol 105, 474–486 (2011). [DOI] [PubMed] [Google Scholar]
- 30.Xing D, Yeh C-I & Shapley RM Spatial spread of the local field potential and its laminar variation in visual cortex. J. Neurosci 29, 11540–11549 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bringuier V, Chavane F, Glaeser L & Frégnac Y Horizontal propagation of visual activity in the synaptic integration field of area 17 neurons. Science 283, 695–699 (1999). [DOI] [PubMed] [Google Scholar]
- 32.Lewis DA Horizontal Synaptic Connections in Monkey Prefrontal Cortex. Cerebral Cortex Jan 10, 82–92 (2000). [DOI] [PubMed] [Google Scholar]
- 33.Girard P, Hupé JM & Bullier J Feedforward and feedback connections between areas V1 and V2 of the monkey have similar rapid conduction velocities. J. Neurophysiol 85, 1328–1331 (2001). [DOI] [PubMed] [Google Scholar]
- 34.Alexander DM, Ball T, Schulze-Bonhage A & van Leeuwen C Large-scale cortical travelling waves predict localized future cortical signals. PLoS Comput. Biol 15, e1007316 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.van Vugt B et al. The threshold for conscious report: Signal loss and response bias in visual and frontal cortex. Science 360, 537–542 (2018). [DOI] [PubMed] [Google Scholar]
- 36.Palmer C, Cheng S-Y & Seidemann E Linking neuronal and behavioral performance in a reaction-time visual detection task. J. Neurosci 27, 8122–8137 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Luck SJ, Chelazzi L, Hillyard SA & Desimone R Neural mechanisms of spatial selective attention in areas V1, V2, and V4 of macaque visual cortex. J. Neurophysiol 77, 24–42 (1997). [DOI] [PubMed] [Google Scholar]
- 38.Niell CM & Stryker MP Modulation of visual responses by behavioral state in mouse visual cortex. Neuron 65, 472–479 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stringer C et al. Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Brüers S & VanRullen R Alpha Power Modulates Perception Independently of Endogenous Factors. Front. Neurosci 12, 279 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Petersen CCH, Hahn TTG, Mehta M, Grinvald A & Sakmann B Interaction of sensory responses with spontaneous depolarization in layer 2/3 barrel cortex. Proc. Natl. Acad. Sci. U. S. A 100, 13638–13643 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Poulet JFA & Petersen CCH Internal brain state regulates membrane potential synchrony in barrel cortex of behaving mice. Nature 454, 881–885 (2008). [DOI] [PubMed] [Google Scholar]
- 43.Busch NA, Dubois J & VanRullen R The phase of ongoing EEG oscillations predicts visual perception. J. Neurosci 29, 7869–7876 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mathewson KE, Gratton G, Fabiani M, Beck DM & Ro T To See or Not to See: Prestimulus α Phase Predicts Visual Awareness. J. Neurosci 29, 2725–2732 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Samaha J, Gosseries O & Postle BR Distinct Oscillatory Frequencies Underlie Excitability of Human Occipital and Parietal Cortex. J. Neurosci 37, 2824–2833 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Helfrich RF et al. Neural Mechanisms of Sustained Attention Are Rhythmic. Neuron 99, 854–865.e5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fiebelkorn IC, Pinsk MA & Kastner S A Dynamic Interplay within the Frontoparietal Network Underlies Rhythmic Spatial Attention. Neuron 99, 842–853.e8 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gabor D Theory of communication. Part 1: The analysis of information. Journal of the Institution of Electrical Engineers - Part III: Radio and Communication Engineering 93, 429–441 (1946). [Google Scholar]
- 49.Le Van Quyen M et al. Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. J. Neurosci. Methods 111, 83–98 (2001). [DOI] [PubMed] [Google Scholar]
- 50.Oppenheim AV, Schafer RW & Buck JR Discrete-time Signal Processing. (Prentice Hall, 1999). [Google Scholar]
- 51.Marple L Computing the discrete-time’ analytic’ signal via FFT. IEEE Trans. Signal Process 47, 2600–2603 (1999). [Google Scholar]
- 52.Johansson M The hilbert transform Mathematics Master’s Thesis. Växjö University, Suecia: Disponible en internet: http://w3.msi.vxu.se/exarb/mj_ex.pdf, consultado el 19, (1999). [Google Scholar]
- 53.Feldman M Hilbert transform in vibration analysis. Mech. Syst. Signal Process 25, 735–802 (2011/4). [Google Scholar]
- 54.Pereda E, Gamundi A, Rial R & González J Non-linear behaviour of human EEG: fractal exponent versus correlation dimension in awake and sleep stages. Neurosci. Lett 250, 91–94 (1998). [DOI] [PubMed] [Google Scholar]
- 55.Linkenkaer-Hansen K, Nikouline VV, Palva JM & Ilmoniemi RJ Long-range temporal correlations and scaling behavior in human brain oscillations. J. Neurosci 21, 1370–1377 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Milstein J, Mormann F, Fried I & Koch C Neuronal shot noise and Brownian 1/f2 behavior in the local field potential. PLoS One 4, e4338 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rao Jammalamadaka S & Sengupta A Topics in Circular Statistics. (World Scientific, 2001). [Google Scholar]
- 58.Rosa MGP & Elston GN Visuotopic organisation and neuronal response selectivity for direction of motion in visual areas of the caudal temporal lobe of the marmoset monkey (Callithrix jacchus): middle temporal area, middle temporal crescent, and surrounding cortex. J. Comp. Neurol 393, 505–527 (1998). [PubMed] [Google Scholar]
- 59.Frank TD & Richardson MJ On a test statistic for the Kuramoto order parameter of synchronization: An illustration for group synchronization during rocking chairs. Physica D 239, 2084–2092 (2010). [Google Scholar]
- 60.Menard S Applied Logistic Regression Analysis. (SAGE, 2002). [Google Scholar]
- 61.Menard S Six Approaches to Calculating Standardized Logistic Regression Coefficients. Am. Stat 58, 218–223 (2004). [Google Scholar]
- 62.Tehovnik EJ, Slocum WM, Carvey CE & Schiller PH Phosphene induction and the generation of saccadic eye movements by striate cortex. J. Neurophysiol 93, 1–19 (2005). [DOI] [PubMed] [Google Scholar]
- 63.Bremmer F, Kubischik M, Hoffmann K-P & Krekelberg B Neural dynamics of saccadic suppression. J. Neurosci 29, 12374–12383 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.


