Evaluating patient-specific neoadjuvant regimens for breast cancer via a mathematical model constrained by quantitative magnetic resonance imaging data

Abstract

The ability to accurately predict response and then rigorously optimize a therapeutic regimen on a patient-specific basis, would transform oncology. Toward this end, we have developed an experimental-mathematical framework that integrates quantitative magnetic resonance imaging (MRI) data into a biophysical model to predict patient-specific treatment response of locally advanced breast cancer to neoadjuvant therapy. Diffusion-weighted and dynamic contrast-enhanced MRI data is collected prior to therapy, after 1 cycle of therapy, and at the completion of the first therapeutic regimen. The model is initialized and calibrated with the first 2 patient-specific MRI data sets to predict response at the third, which is then compared to patient outcomes (N = 18). The model's predictions for total cellularity, total volume, and the longest axis at the completion of the regimen are significant within expected measurement precision (P< 0.05) and strongly correlated with measured response (P < 0.01). Further, we use the model to investigate, in silico, a range of (practical) alternative treatment plans to achieve the greatest possible tumor control for each individual in a subgroup of patients (N = 13). The model identifies alternative dosing strategies predicted to achieve greater tumor control compared to the standard of care for 12 of 13 patients (P < 0.01). In summary, a predictive, mechanism-based mathematical model has demonstrated the ability to identify alternative treatment regimens that are forecasted to outperform the therapeutic regimens the patients clinically. This has important implications for clinical trial design with the opportunity to alter oncology care in the future.

Introduction

It is well-known that neoadjuvant therapy (NAT) in the standard-of-care setting is not optimized for each breast cancer patient. Currently, therapeutic regimens are based on receptor status, tumor grade, body surface area, and genetic markers (each with known shortcomings [1], [2], [3], [4], [5], [6], [7]), rather than spatially-resolved physiological characteristics describing tumor features specific to the individual. While treatment plans may be altered due to lack of response, significant side-effects, or when considering the quality of life for the patient, this is implemented in an ad hoc manner. As there is no mathematical theory in place to guide such decisions, we are left with trial and error. Moreover, with our current clinical trial system, it is impossible to experimentally evaluate all the possible combinations, timings, orderings, and dosing strategies for unique subsets within a cancer population, let alone for an individual patient. Therefore, we (and others; [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20]) propose that using mathematical models designed to predict tumor response in individual patients can also be used to determine individually-optimized therapeutic regimens based on each patient's unique tumor characteristics.

One approach to individualizing mathematical models is to leverage physiological information (acquired in 3D and at multiple time points) from noninvasive imaging data to initialize and constrain model parameters, thereby enabling patient-specific predictions [13]. Imaging-informed, biologically-derived mathematical models have been shown to provide accurate predictions for tumor development in the kidney [8], brain [14], [15], [16], lung [17,18], and pancreas [19,20]. Our own efforts in breast cancer [21], [22], [23], [24] employ diffusion-weighted magnetic resonance imaging (DW-MRI) data to estimate tumor cellularity, mechanical-coupling of the breast tissue properties with tumor growth based on each individual patient's anatomy, and estimates of drug delivery to each voxel via dynamic contrast-enhanced (DCE-) MRI [25]. In the present work, we extend our efforts by incorporating a mathematical description of the decay and efficacy of chemotherapies (calibrated from each patient's data set). We evaluate the model's predictive ability and then, for a subgroup of patients, identify alternative—individualized—dosing strategies predicted to outperform the therapeutic regimen each patient received as standard-of-care. Furthermore, the requisite imaging data is acquired at community-based radiology centers (i.e., not research-oriented academic medical centers) using widely available hardware [20]. By developing our approach in such facilities—where the majority (85%, [26]) of oncology patients receive their care—we dramatically increase the population these technologies may serve in the future.

Data and methods

Patient population

Quantitative MRI data was acquired in a cohort of 21 patients diagnosed with intermediate to high grade invasive breast cancers, who were eligible for NAT as a component of their clinical care. The patient data was collected in an institutional review board-approved and HIPAA-compliant study where patients provided informed consent to participate in a longitudinal MRI study throughout the course of their standard-of-care NAT. All participants received their care and imaging in community care settings (i.e., not academic, research-oriented medical centers). Table 1 summarizes the key clinical features of the patient population.

Table 1.

Clinicopathologic characteristics of the patient cohort.

Patient	Age	BMI	Ethnicity	Tumor Type	Receptor Status $(\text{ER},\text{PR},\text{HER}2)$	Therapy From Scan 1 to 3	RECIST by Scan 2	RECIST by Scan 3
1	74	18.18	Hispanic	IDC	(−,−,−)	DC	−	−
2	25	22.46	Hispanic	IDC	(−,−,−)	DC	SD	SD
3	42	24.80	Hispanic	IDC	(+,−,−)	DC	SD	SD
4	47	24.80	Asian	IDC	(+,−,−)	DC	SD	CR
5	54	24.36	Caucasian	ILC	(+,+,−)	DC	PD	SD
6	59	28.30	Caucasian	IDC	(−,−,−)	PC + I	SD	SD
7	63	18.95	Caucasian	IDC	(+,+,−)	DC	−	−
8	27	18.79	Caucasian	IDC	(+,+,−)	DC	SD	PR
9	32	35.8	Asian	IDC	(+,+,+)	DC* + T	SD	SD
10	52	21.10	Caucasian	IDC	(−,−,−)	PC	SD	PR
11	38	27.50	Caucasian	IDC	(−,−,−)	PC	SD	PR
12	38	31.40	Caucasian	IDC	(−,−,−)	PC + I	PR	PD
13	62	39.32	Caucasian	IDC	(−,−,−)	DC	SD	SD
14	38	36.18	African American	IDC	(+,+,+)	DC* + T	PR	PR
15	42	29.95	Caucasian	IDC	(+,+,−)	DC	SD	SD
16	53	33.94	Caucasian	IDC	(+,+,−)	DC	SD	−
17	58	31.60	Caucasian	IDC	(−,−,−)	PC + I	PR	PR
18	48	16.90	Caucasian	IDC	(+,+,−)	DC	SD	PR
19	54	26.62	Caucasian	IDC	(+,+,−)	DC	SD	SD
20	41	24.21	Hispanic	IDC	(+,+,+)	DC	PD	PR
21	26	29.26	Hispanic	IDC	(−,+,+)	DC	SD	SD

Bolded labels denote changes in the RECIST category from the scan 1 to scan 2 evaluation to the scan 1 to scan 3 evaluation. Patients 6, 9, and 14 did not receive a second regimen; therefore, for patients 6 and 9, scans 2–4 were acquired after the first through third cycles, respectively, and for patient 14, scan 2 was acquired after the first cycle, scan 3 after the fourth, and scan 4 after the fifth. Three patients (6, 12, and 17) received either the active pembrolizumab drug or the placebo in addition to chemotherapy (NCT03036488). Bolded patients are chemo subgroup patients used for the in silico therapy regimen study.

BMI = body mass index; CR = complete response; DC = doxorubicin and cyclophosphamide; DC* = docetaxel and carboplatin; ER = estrogen receptor; HER2 = human epidermal growth factor receptor 2; +I = immunotherapy regimen (pembrolizumab or placebo); IDC = invasive ductal carcinoma; ILC = invasive lobular carcinoma; P = paclitaxel; PC = paclitaxel and carboplatin; PD = progressive disease; PR = progesterone receptor; PR = partial response (RECIST); +T = targeted therapies trastuzumab and pertuzumab; SD = stable disease.

For the majority of the patients, NAT consisted of 2 regimens; for example, patient 1 received doxorubicin and cyclophosphamide (regimen 1), followed by paclitaxel (regimen 2). MRI data were acquired at 4 times throughout NAT: (1) prior to therapy, (2) after 1 cycle of the first therapeutic regimen, (3) at the completion of the first therapeutic regimen, and (4) after 1 cycle of the second therapeutic regimen. For this study, we utilize the first 3 data sets summarizing the first regimen. NAT regimens include cycles of doxorubicin and cyclophosphamide approximately every 2 weeks for 4 cycles, paclitaxel (with or without carboplatin and/or targeted therapies) weekly for 3 weeks for 4 cycles (12 total doses), and docetaxel (with carboplatin and targeted therapies) every 3 weeks for 6 cycles. There were some variations in regimens indicated by the treating physician, as is commonly done in the standard-of-care setting (variations reported in Table 1). Note that 14 patients received only cytotoxic therapies for their first NAT regimen, which we refer to as the “chemo” group; while 7 patients received additional therapies (targeted or immunotherapies), which we refer to as the “chemo+” group.

MRI data acquisition

MRI was performed at 2 community imaging facilities. The MRI technologists at each site were directly involved and responsible for positioning the patients and deploying the research imaging protocols. Thus, the image acquisition protocol is designed for practical use for routine imaging using widely available hardware and expertise. Note that the repeatability and reproducibility of quantitative MRI at these centers was previously established [27,28].

Five MRI data types were acquired at each scan session: (1) a precontrast T₁ map, (2) a precontrast, B₁ field map to correct for radiofrequency (RF) inhomogeneity [27,29], (3) DW-MRI data, (4) high-temporal resolution, T₁-weighted DCE-MRI data before, during, and after the injection of a gadolinium-based contrast agent (Gadovist, Bayer, Ontario, Canada, or Multihance, Bracco Diagnostics, New Jersey, USA), and (5) a high-resolution, T₁-weighted anatomical scan (post contrast). The Supplemental Materials provide a detailed summary of the acquisition parameters for each of these measurements.

Data analysis

We briefly summarize our data-processing methods (see Supplemental Materials for details). The first step consists of intrascan registration of the MRI data within each scan session to correct for motion via rigid registration. Tumor regions of interest (ROIs) are then identified based on postcontrast scans, and then estimations of tissue properties related to perfusion-permeability of the vasculature are quantified by analyzing the DCE-MRI data with the standard Kety-Tofts model [30]. The DW-MRI data is analyzed to return maps of the apparent diffusion coefficient (ADC) of water. The third step is the interscan registration that aligns the images and calculated maps across all of the patient's imaging sessions into a common domain. The final step calculates the specific quantities to be used within the mathematical model. These quantities include approximating the number of tumor cells from the voxel-based ADC values [24,31,32] and segmenting the fibroglandular and adipose tissues (based on enhancement in the DCE-MRI data). To approximate the drug distribution in each voxel of tissue, a normalized map of the blood volume is calculated and then scaled by the peak concentration of drug (as estimated from the Kety-Tofts model [25]; see Supplemental Materials) to define the initial drug distribution throughout the domain at the time of each dose of therapy.

The volume and longest axis of the tumors from each patient's scans are automatically calculated on the interscan registered images, and the response evaluation criteria in solid tumors (RECIST; [33]) is used to assign the response of each patient. We note that we implement this process of image segmentation and longest diameter calculation to make the RECIST evaluation as rigorous as possible so as not to place it at a systematic disadvantage for the comparisons to the mathematical modeling. We note that when computing the longest axis of a tumor, we only consider the central, bulk tumor and disregard smaller, disconnected sections. Using the RECIST evaluation, responders were patients with a complete or partial response (CR and PR, respectively), and nonresponders were patients with stable disease or progressive disease (SD and PD, respectively) comparing tumor burdens in scans 1 and 3.

Mathematical model

We have previously developed a 3D mathematical model that includes the mechanical coupling of tissue properties to tumor growth and the delivery of therapy [25]. This model was designed to be initialized with patient-specific, quantitative, MRI data to predict therapy response. The current work extends this approach to account for multiple chemotherapy regimens. The governing equation for the spatiotemporal evolution of tumor cells (N_TC) is:

$$\begin{array}{ccc}\hfill \frac{\partial N_{TC}(\overline{x},t)}{\partial t}& =& \stackrel{\text{dif}\text{fusion}}{\overbrace{\nabla ·\left(D(\overline{x},t)\nabla N_{TC}(\overline{x},t)\right)}}+\stackrel{\text{growth}}{\overbrace{k\left(\overline{x}\right)(1-N_{TC}(\overline{x},t)/\theta )N_{TC}(\overline{x},t)}}\hfill \\ & & -\stackrel{\text{therapy}}{\overbrace{C_{drug}(\overline{x},t)N_{TC}(\overline{x},t)}}\hfill \end{array}$$ (1)

where the first term on the right-hand side describes tumor cell movement (diffusion, D), the second term describes the logistic growth of the cells with carrying capacity $\theta$ and proliferation rate k per voxel, and the third term describes the effect of chemotherapy where ${\mathrm{C}}_{\text{drug}}(\overline{\mathrm{x}},\mathrm{t})$ is the concentration of the drugs in the tissue (please see the Supplemental Materials for additional modeling details). The first term on the right-hand side of Eq. (1), representing the random diffusion (movement) of the tumor cells (D$(\overline{\mathrm{x}},\mathrm{t})$), is mechanically linked to the breast tissue's material properties via the von Mises stress. Additionally, we enforce equilibrium between the tumor and its environment dependent upon changes in tumor cell number [9,[21], [22], [23],[34], [35], [36], [37], [38]. Therefore, the diffusion term encompasses tumor changes (growth or response to therapy) that can cause deformations in the surrounding healthy tissues (fibroglandular and adipose tissues), potentially increasing stress and therefore reducing the outward expansion of the tumor. The carrying capacity is defined as the maximum number of tumors cells that can physically fit within a voxel, while the proliferation rate is calibrated per voxel for each individual patient.

The therapy term describes the spatiotemporal distribution of each drug in the tissue and its effect on the cells of each voxel. Here we expand the model (from [25]) to acknowledge their differing efficacies and decay rates using the following equation:

$$C_{drug}(\overline{x},t)=\stackrel{\text{chemotherapy}1}{\overbrace{{\alpha }_1{C}_{dru{g}_1}(\overline{x},t^{*})\exp (-{\beta }_{1}t)}}+\stackrel{\text{chemotherapy}2}{\overbrace{{\alpha }_2{C}_{dru{g}_2}(\overline{x},t^{*})\exp (-{\beta }_{2}t)}}$$ (2)

where ${\alpha }_{\mathrm{i}}$ is the efficacy of each drug, ${\mathrm{C}}_{\text{dru}{\mathrm{g}}_{\mathrm{i}}}(\overline{\mathrm{x}},{\mathrm{t}}^{*})$ is the initial concentration of each drug for each dose with ${\mathrm{t}}^{*}$being time relative to the patient scan data (described in more detail below), and the exponential decay terms ($\text{exp}(-{\beta }_{\mathrm{i}}\mathrm{t})$) represent the eventual washout of the drug over time after each dose. The ${\alpha }_{\mathrm{i}}$ and ${\beta }_{\mathrm{i}}$ parameters are calibrated for each patient and each drug, where the ${\beta }_{\mathrm{i}}$ calibration is restricted using bounds defined from ranges in the literature for the terminal elimination half-lives of each drug [39], [40], [41], [42], [43], [44]. The initial concentration of drug, ${\mathrm{C}}_{\text{dru}{\mathrm{g}}_{\mathrm{i}}}(\overline{\mathrm{x}},{\mathrm{t}}^{*})$, is approximated using the DCE-MRI data as described above in Section 2.3 (see Supplemental materials). This concentration is dependent on the time ${\mathrm{t}}^{*}$, indicating that for the calibration of the model the drug distribution map may be derived from scan 1, but an updated drug distribution map from scan 2 is provided to the model to predict the tumor at the time of scan 3. Thus, the concentration of drug in the tumor tissue is spatially nonuniform and temporally varying based on the individual patient's response to therapy and NAT schedule.

Model parametrization and evaluation of predictive ability

Our approach uses the first 2 MRI data sets for each patient to calibrate the mathematical model and the third MRI data set to evaluate the ability of the mathematical model to predict tumor response to therapy. Specifically, we use the cellularity maps of each tumor from before and after the first cycle of NAT (scans 1 and 2, respectively) to calibrate model parameters (D_0, $\alpha$, and $\beta$ parameters are global; k is spatially determined). Using these calibrated, patient-specific parameters, the model is reinitialized with the tumor cellularity, tissue, and drug distribution maps from scan 2 and run forward to the time of scan 3 to predict tumor response. See Figure 1 for a graphical depiction of this strategy and the Supplemental materials for details on the numerical implementation.

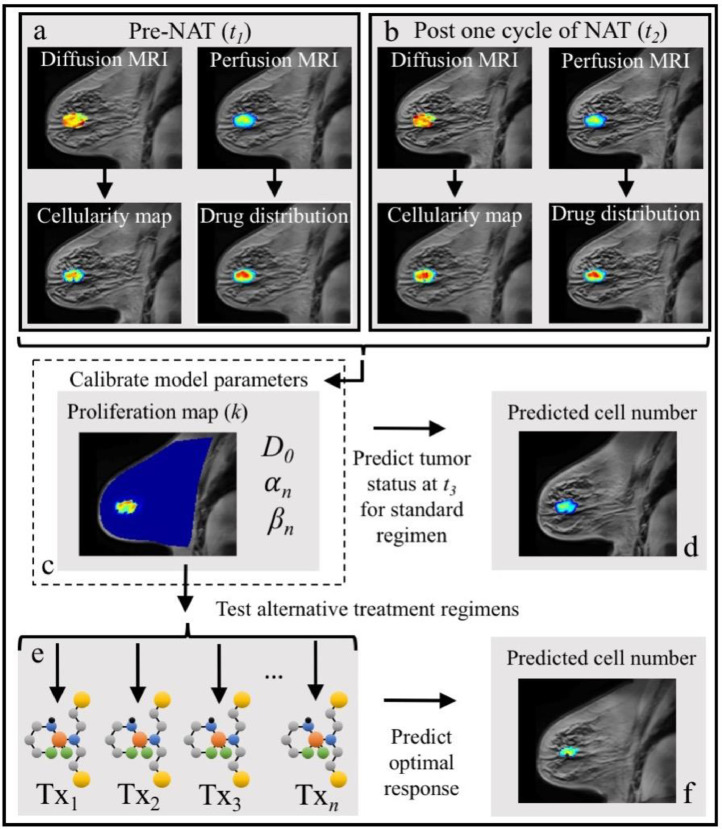
Figure 1.

Graphical depiction of the integration of breast MRI data with the mathematical model for predicting tumor response and simulating alternative treatment regimens. The data from MRI scans obtained before and after one cycle of the first NAT regimen, are used to generate spatially resolved maps of tumor cell number and drug delivery (panels a and b, respectively). The model parameters are then calibrated using this early NAT imaging data (panel c), and the model is run forward to the time of the patient's third scan (panel d). The model's predictions of total cellularity, total volume, and longest axis measures are then directly compared to each patient's actual tumor outcome as determined by their scan 3 data. The model's predictions were also compared to the RECIST designations to determine accuracy in the context of clinical measures. Using the patient-specific model parameters (panel c), alternative therapy regimens adjusting the frequency and dosage of treatments (“Tx_i”, panel e) are evaluated using the model's predictions from scan 2 to 3 for each of these regimens to determine an optimal treatment schedule for each patient (panel f).

The predictive ability of the model is evaluated by comparing 3 measures quantifying tumor response: total tumor cellularity, tumor volume, and longest axis of the tumor. Using these measures, 3 evaluations are made to assess the model's predictive ability. First, the error between the model's predictions and the patient's actual tumor values (as determined from their corresponding third scan) are calculated for the 3 measures, as is the significance of the model's predictive accuracy. Second, total cellularity, volume, and longest axis are evaluated across the cohort to determine the level of agreement between the model's predictions and the measured values from the data as a group. Third, the predicted percent change in the 3 tumor measures from scan 1 to scan 3 are compared between the 2 RECIST defined responder groups.

Simulating modified therapeutic regimens for the individual patient

Alternative regimens are proposed for the group of patients for which the model's predictions have the greatest correlation with observation (chemo group). The alternative regimens proposed use the same total dose that each individual patient received during their NAT regimen from scan 2 to scan 3, but the alternative regimens vary in the individual doses and frequency between their second and third scans. More specifically, we simulate the effects of alternative regimens that consist of doses that were one-half, one-third, or one-fourth of the dose the patients were administered but given 2 ×, 3 ×, or 4 ×, respectively, as frequently as what the patients received. We also investigated a daily dose fraction. For example, if a patient who received their chemotherapies every 2 weeks, the alternative regimens will be a one-half dose every week, a one-third dose every 4 to 5 days, a one-fourth dose every 3 to 4 days, and a one-fourteenth dose every day.

We run the model forward from scan 2 to the time of scan 3 with each patient's previously calibrated parameters and the alternative regimens implemented to evaluate the differences in tumor response across all regimens (see Figure 1). The model simulation serves as an in silico twin [45] for each patient to determine therapy response for an alternate regimen. This allows us to identify individualized, alternative therapeutic regimens that we hypothesize can lead to greater tumor control when compared to the “one-size-fits-all” approach that is the current standard.

Statistical analysis

To summarize the model's predictive performance, the absolute percent differences between the measured tumor response from the third scan data and the corresponding predicted values from the model are calculated for each patient (median and quartile ranges reported). We test the accuracy of the patient-specific predictions for total cellularity, volume, and longest axis by generating a Monte Carlo estimated P value [46] (please see Supplemental materials) to determine the significance of 10%, 15%, or 20% absolute differences between model predictions and measured outcomes (The 10%–20% range corresponds to measurement precision [27,28].). Due to the modest sample size, it is challenging to accurately evaluate the normality of the data. Thus, we calculate Kendall correlation coefficients (KCC) to determine agreement between the model-predicted tumor response and the observed values at the time of scan 3 across the cohort. However, to enable comparison to previous [25] and future efforts with larger data sets, we also report the concordance and Pearson correlation coefficients (CCC and PCC, respectively). The 2-sided Wilcoxon rank sum test is used to determine significant differences in the medians of the percent change from scan 1 to scan 3 between the responder versus nonresponder groups with P< 0.05 considered significant.

To determine which therapeutic regimen yields the greatest tumor control for each patient, we calculate the percent change from initiation of the alternate regimen (scan 2) to the predicted tumor at the time of scan 3. Comparing these percent changes across regimens for each patient, we determine the “optimal” regimen based on the greatest tumor reduction/control. We then calculate the difference between the percent changes of the standard regimen and the optimal regimen to determine the additional percent tumor reduction potentially achieved if the alternate regimen had been administered. Median and quartile ranges are reported for these values. Using the paired, 2-sided Wilcoxon signed rank test, we determine if there is a significant difference between the tumor control achieved by the group of standard regimens compared to the group of alternative regimens by comparing the percent reduction from scan 2 to scan 3 as well as the total tumor burden predicted at the time of scan 3 between the 2 groups.

Results

Three patients are excluded from the analysis. For patient 1, the tumor was invading the chest wall, which violates our assumption of a no-flux boundary condition employed in the numerical implementation (see Supplemental materials). For patient 7, a silicon breast implant caused significant artifacts in the DW-MRI data. For patient 16, the third scan was not collected due to patient scheduling conflicts. Excluding these 3 data sets reduces the total analyzed cohort to N = 18 and the chemo subgroup to N = 13.

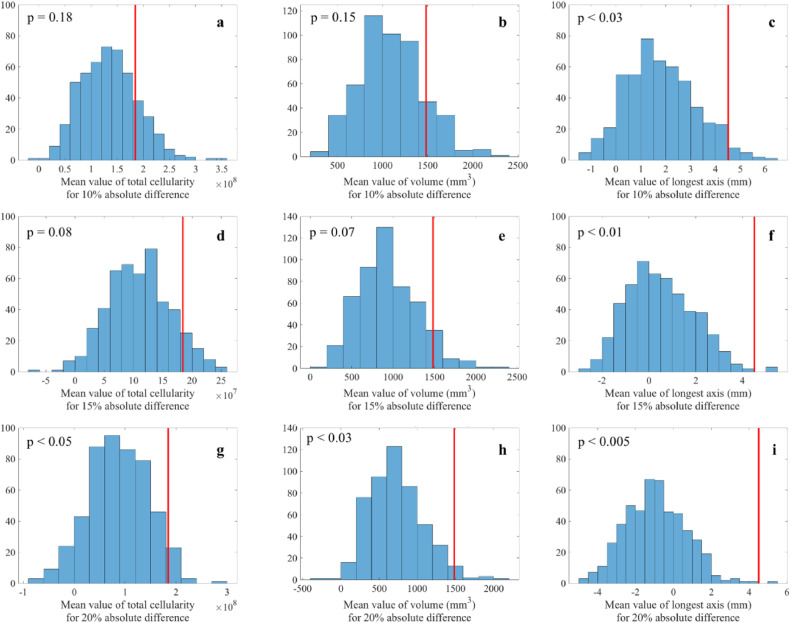
Figure 2 presents a comparison of the predicted and experimentally measured cellularity maps for a representative patient when the calibrated model is run forward to the time of scan 3 utilizing scan 1 and 2 information. The number of tumor cells predicted by the model are overlaid (in color) on a grayscale anatomical image of the breast. While areas of higher and lower cellularity may not directly match between the prediction and observation, the model is able to capture the general shape of an individual tumor, and there are small errors between the predicted and measured values for the patient's scan (listed in the figure caption). Table 2 summarizes the results for the absolute percent error in all 3 tumor measures (i.e., total cellularity, total volume, and longest axis) compared to the measured values from each patient's third scan. Figure 3 depicts distributions of the Monte Carlo generated sample averages for determining the significance of the model's prediction accuracy for 10%, 15%, and 20% absolute difference between model predictions and measured outcomes. For the cohort (N = 18), the model's prediction for longest axis is significant for all 3 thresholds (P < 0.05). The total cellularity and volume measures trend toward significance for the 10% and 15% thresholds (i.e., P < 0.1), and achieve P values <0.05 for the 20% threshold.

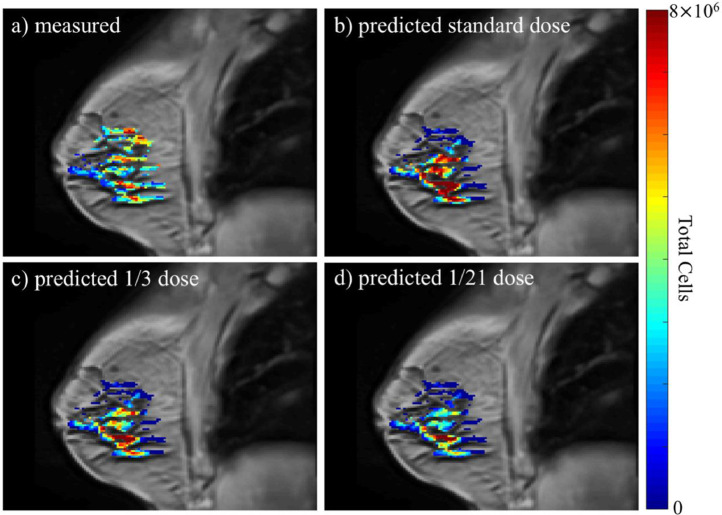
Figure 2.

Example results for the predicted response to NAT regimens for 1 patient (patient 4) whose standard-of-care regimen consisted of combination doxorubicin and cyclophosphamide every 3 weeks for 12 weeks (4 total cycles). The figure depicts anatomical images of a central slice of the breast overlaid with the total tumor cellularity in color. While there is not an exact match between the patient's actual scan 3 data (panel a) and the prediction for the standard regimen (i.e., the standard-of-care regimen the patient actually received, panel b), the percent differences between the predicted and measured tumor response for the standard-of-care regimen are 1%, 16%, and 1% for total cellularity, volume, and longest axis. The total cellularity predicted for 2 alternative regimens are also depicted: 1/3 of a dose every week (panel c), and 1/21 of a dose administered daily (panel d). (Note: each alternative regimen had the same total drug over the treatment period as the standard-of-care regimen). Across all the regimens, the model predicted the greatest tumor cell reduction when the daily dose regimen was implemented. Compared to the standard-of-care regimen, the model predicted that the daily dose regimen would result in an additional 45% reduction in total tumor cellularity.

Table 2.

Absolute percent errors of model predictions for scan 3 compared to actual measures derived from each patient's MR images. Note 1 patient had no detectable tumor in their scan 3 (N = 17, patient 4 had 0 tumor measured by the time of scan 3).

	Total cellularity	Total volume	Longest axis
Median	28	29	14
Quartile range	[8, 95]	[13, 97]	[2, 24]

Figure 3.

Distributions of sample averages between predicted and measured outcomes (i.e., total cellularity, volume, and longest axis) generated with a Monte Carlo resampling (N = 500 for each distribution) across the patient cohort. (See Supplemental Material for details on the construction of these plots.) Each panel depicts the distribution of the randomly sampled differences between each predicted and measured outcome. The red vertical lines indicate the mean difference for the cohort. (Note that the red lines do not represent mean of the sampled distributions and, therefore, are not in the center of the distributions.) For example, panel a presents the sample mean differences between the predicted and measured total cellularity assuming a 10% absolute difference between predicted and measured total cellularity. Panels b and c display similar data for volume and longest dimension, respectively. Panels d–f correspond to panels a–c, but assuming a 15% absolute difference between predicted and measured total cellularity, volume, and longest axis, respectively. Panels g-i also correspond to panels a–c but assume a 20% absolute difference between predicted and measured total cellularity, volume, and longest axis, respectively.

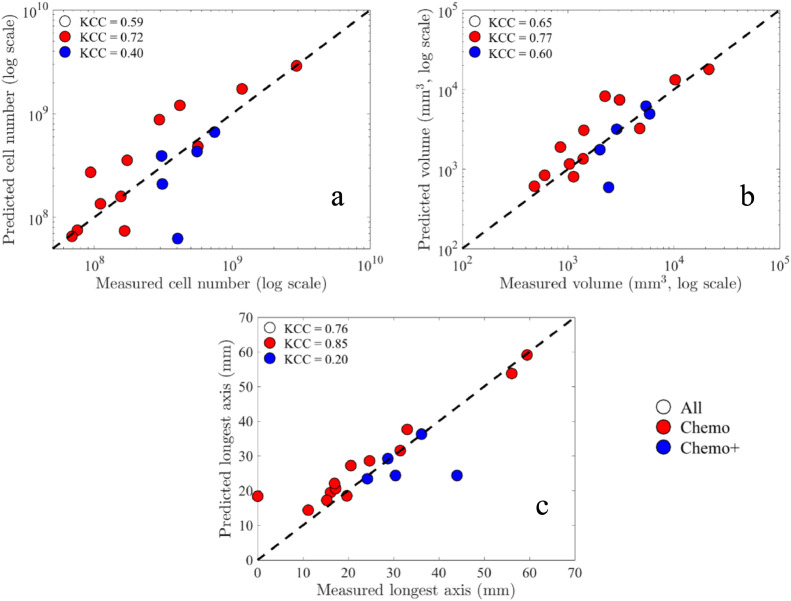
Figure 4 presents scatter plots comparing the predicted tumor response to the actual tumor response. Across all 3 measures, the model's predictions strongly correlate with actual tumor response; in particular, we find for cellularity CCC/PCC = 0.91/0.92, for volume CCC/PCC = 0.90/0.90, and for the longest axis CCC/PCC = 0.86/0.88 across the whole cohort (P < 0.01). Considering the KCC measure, the predictions are correlated with actual tumor response for these tumor measures: KCC = 0.59, 0.65, 0.76 for total cellularity, total volume, and longest axis, respectively (P < 0.01). Note that for all 3 tumor measures, there is greater correlation for the chemo subgroup compared to the chemo+. In particular, the chemo subgroup has greater CCs values than the cohort as a whole where for cellularity we find CCC/PCC = 0.92/0.94, for volume CCC/PCC = 0.90/0.91, and for the longest axis CCC/PCC = 0.92/0.96 (P < 0.01). For the KCC measures, the predictions are strongly correlated with actual tumor response for these tumor measures: KCC = 0.72, 0.77, 0.85 for total cellularity, total volume, and longest axis, respectively (P < 0.01).

Figure 4.

Scatter plots comparing the model predictions to the actual measurements of scan 3 for each patient (N = 18) along with the corresponding KCCs per group (see CCCs and PCCs in the text). The dashed line indicates the 45^o line of unity. Note that for all 3 tumor response measures, there is greater correlation for the chemo subgroup compared to the chemo+ (i.e., patients that received chemotherapy plus targeted therapy or immunotherapy). Panel (a) depicts the comparison between the predicted total cell number to the measured total cell number as estimated from the DW-MRI data. Panel (b) depicts the comparison between the predicted total tumor volume to the measured tumor volume as determined by the total number of voxels in the tumor ROI. Panel (c) depicts the comparison of the predicted longest axis of the tumors to the actual measured longest axes as determined from the tumor ROI of scan 3. Note that using the log scale for panels (a) and (b), 1 patient is not shown where zero tumor was measured at the time of scan 3 (chemo subgroup, patient 4), but corresponding KCC values include this data.

The model's predictions are also compared against the tumor response status determined by RECIST at the end of the NAT regimen. Applying RECIST to each tumor from scan 1 to scan 3 results in 8 patients labeled as responders and 10 patients as nonresponders (see Table 1). See Supplemental Table S.4 for the measured percent changes in longest axis for each of the patients (as well as percent change for total cellularity and volume) from scan 1 to scans 2 and 3. Evaluating the observed percent changes from scan 1 to scan 3, percent change in each of the 3 tumor measures results in significantly different medians between responder and nonresponder groups in total cellularity (P < 0.05), total volume (P < 0.04), and longest axis (P < 0.001). In comparison, the model predicts a significant median percent change between responders and nonresponders for the longest axis (P < 0.002), while for total cellularity and total volume, P = 0.08. See Table 3 for median and quartile ranges for measured and predicted percent change in all 3 measures. Note that comparing responder and nonresponder values for the chemo subgroup (N = 6 and N = 7, respectively), the model predicts significantly different median changes for all 3 tumor measures (P < 0.04 for total cellularity and volume, P < 0.01 for longest axis). Model predicted percent changes for this subgroup are also noted in Table 3.

Table 3.

Measured and model predicted percent changes from baseline (scan 1) to the completion of the first NAT regimen (scan 3) for responder and nonresponder groups (N = 8 and N = 10, respectively).

	Total Cellularity		Total Volume		Longest Axis
	Responders	Nonresponders	Responders	Nonresponders	Responders	Nonresponders
Measured changes
Median	−80	−50 (−62)	−79	−60 (−63)	−42	−12 (−13)
Quartile range	[−85 (−88), −56 (−63)]	[−71 (−75), −11 (−13)]	[−86 (−90), −63 (−68)]	[−69 (−74), −22 (−18)]	[−60 (−64), −37 (−36)]	[−22 (−23), −2 (−5)]
Predicted changes
Median	−69	22 (−5)	−65	−35 (−29)	−30 (−24)	−10 (−6)
Quartile range	[−81 (−82), −55]	[−70 (−63), 5 (10)]	[−81 (−80), −49 (−50)]	[−66 (−61), −20]	[−53 (−37), −17 (−15)]	[−15 (−11), 1]

Note that a positive percent change indicates tumor regrowth from the baseline. We have noted in parentheses any differing values for the chemo subgroup (N = 6 and N = 7 for responders and nonresponders, respectively.

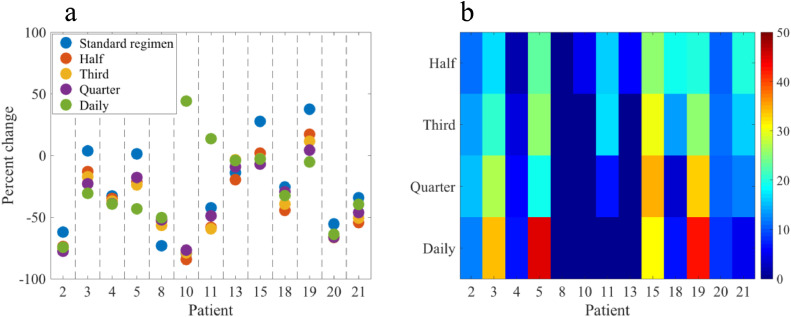
As the model's predictions show the greatest correlation with the chemo subgroup, an in silico study of alternative regimens is performed for this patient subset (see Table 1, N = 13)—we return to this important choice in the Discussion. Using each patient's parameters calibrated from scans 1 and 2, the model is simulated from scan 2 to the time of scan 3 to determine if greater or lesser control/reduction in the tumor burden can be achieved with the proposed hypothetical alternative therapy schedules (i.e., one-half, one-third, one-fourth and a daily dose fraction, given 2 ×, 3 ×, 4 × as frequently as the standard dose, and daily, respectively). For the 2 measures pertaining to the size of the tumor (volume and longest axis), comparing their percent change from scan 2 to scan 3 for the standard regimen to that of the alternative regimens tested results in a median difference of 8% for the total volume, and <1% for the longest axis. However, the differences between the standard and the alternative regimens that achieved the greatest reduction in total cellularity per individual patient range from 0% to 46% with a median difference of 17% (quartile range [6%, 35%]). The positive differences represent the additional percent reduction/control that could have been achieved if the patient received the alternative regimen. The 0% instance is the 1 patient where the standard regimen was optimal amongst all those tested; however, all other patients had additional percent reductions in total cellularity when comparing between the standard and best alternative regimens. Figure 5 summarizes the predicted percent change from initiation of the alternate regimen (scan 2) to the completion of the therapy (scan 3), as well as a heat map illustrating the differences in the alternative regimens compared to the standard-of-care regimen each patient received. When compared to the standard regimens, the model predicted optimal regimens yield a significantly greater reduction in the total tumor cell number from scan 2 to scan 3 (P < 0.001), as well as for the total number of tumor cells predicted at the time of scan 3 (P < 0.001). Notice that no single regimen is the most effective across all patients; the daily dosing regimens was best for 4 patients, while the quarter, third, half, and standard regimens were best for 2, 2, 4, and 1 patient, respectively. Figure 2 presents examples of the resulting changes in total cellularity for 2 alternative regimens for 1 patient.

Figure 5.

Comparison of the percent change in total tumor cellularity from scan 2 to the time of scan 3 achieved by the standard regimen, a one-half dose double frequency regimen, a one-third dose triple frequency regimen, a one-quarter dose quadruple frequency regimen, and an equivalent daily dose when administered daily to each patient (panel a). Across patients, differences in the percent change between the standard therapeutic regimen and the model-identified, most effective regimen have a maximum difference of 46%, a minimum difference of 0%, and a median difference of 17% (panel b). Note: a positive difference indicates a potential additional percent reduction in the total tumor cellularity achieved by the alternative regimen compared to the standard dose the patient received. The group of standard regimens was found to be statistically inferior to the group of optimal regimens selected for each patient for tumor control/reduction (P < 0.001 for percent change from scan 2 to 3 and for the predicted cell number at the time of scan 3). The most effective regimens by number of patients: standard N = 1, one-half N = 4, one-third N = 2, one-quarter N = 2, daily N = 4.

Discussion

A mathematical model accounting for patient-specific proliferation and diffusion of tumor cells, mechanical properties of breast tissue, and treatment regimens was individually calibrated with quantitative MRI data acquired in the community-based care setting. After the patient-specific calibration, the model was run forward in time to predict tumor response at the completion of the first therapeutic regimen. Analyzing various absolute differences between model predictions and measured outcomes established significance of the model's prediction accuracy (Figure 3). The model predictions are also found to be significantly correlated to the actual tumor outcome for the cohort for 3 different measures of tumor response (total cellularity, volume, and longest axis; Figure 4); in particular, the CCC values for the whole cohort are $\ge$ 0.86 when comparing all 3 tumor measurements. Further, the model predictions are significantly different for the change in the longest axis when compared between the RECIST defined responder and nonresponder groups (Table 3). It is important to note that RECIST is only an evaluation of response and is not intended to be employed for predicting response; in fact, the RECIST designation (i.e., CR, PR, SD, PD) from scan 1 and 2 changes for 8 out of the 18 patients when compared to the RECIST designation from scan 1 and 3. However, recall that the mathematical model only required the data from scans 1 and 2 (after just 1 cycle of therapy), to make predictions of response observed at the conclusion of the first regimen of NAT.

The results indicate that the model is superior at predicting tumor response for regimens consisting of only chemotherapy. For the chemotherapy only subgroup, the mathematical model's predictions had greater correlation with the measured tumor response of each patient compared to the chemo+ subgroup, and the model had significantly different predictions between responder and nonresponder patients for all 3 tumor measures. Currently, this model does not explicitly consider the effect of targeted and/or immunotherapies but only implicitly through the calibration of parameters (such as the proliferation map). Therefore, the chemo subgroup was selected for the in silico alternative regimen investigation. Future modeling efforts must account for the effects of targeted therapies to increase the generalizability of the methodology to all breast cancer subtypes.

Using the parameters derived from each individual patient of the chemo subgroup, several alternative treatment regimens were assessed where the frequency and dosage of drug differed (but the total amount of drug remained consistent) from the standard-of-care regimen each patient received. Therefore, the mathematical model served as an in silico twin for each patient, and an in silico clinical trial was performed with 4 branches—each branch testing an alternative schedule for the total standard-of-care dose and time course. The overall tumor control achieved by the group of standard regimens was found to be statistically inferior to the group of optimal regimens selected for each patient. Notably, no single regimen was optimal for all patients; this result underscores that the success of any particular treatment approach depends on all tumor characteristics of the individual patient and the importance of identifying patient-specific treatment protocols to maximize response. The only way to systematically exploit this realization for individually optimizing response is through patient-specific mathematical modeling. Furthermore, we note that the alternative regimens investigated here are a small subset of all the possible alternative regimens that could be mathematically explored to identify patient-specific therapeutic regimens that maximize efficacy.

Experimentally, a limitation of the present study is the modest cohort size (N = 18 total, N = 13 for the chemo subgroup), which consists of several different ethnicities, receptor status, body-mass-indices, and ages. This is exactly the type of population that is encountered in community-based care settings—from which our data was acquired; if any method of evaluating and/or predicting response to therapy in cancer is going to have widespread utility, this is the type of the patient population with which we must learn to work. Furthermore, the aim of this work was to provide initial motivation for using biophysical, mathematical methods for optimizing therapies on a patient specific basis—for which the cohort is sufficient. All of the above analyses presented indicated that the mathematical model's predictions are both significantly correlated with and predictive of actual response for this cohort. It is also important to note that the results of this study would be extraordinarily difficult to achieve using the methods of artificial intelligence, which typically require vast training databases to identify patterns that emerge at the population (rather than the individual) level [47].

A second experimental limitation is the small number of data points (i.e., scan times) employed in the model calibrations and this can limit the predictive ability of the approach. In particular, if the tumor changes between the calibration scans are minimal compared to the overall change observed at the conclusion of therapy, the model's ability to capture the overall dynamics may be compromised. Additional data acquired prior to and throughout therapy would enable the model calibration scheme to more accurately determine patient-specific parameter values. However, acquiring data from more scan sessions is frequently not practical due to the additional burden on the patients (and associated expenses). Additionally, there are limitations in estimating cellularity with the ADC (as we have previously discussed; see, e.g., [25,35,38]), and future efforts are needed to more precisely estimate cell number and eliminate some of the ambiguity in the standard interpretation of the ADC.

From a modeling perspective, a limitation of this current study is that the mathematical model does not yet account for an evolving vasculature and alternative drug mechanisms. Without an evolving vasculature, the drug delivery map has limited change in time, and this almost certainly affects our predictive ability. We note that the model predictions of total volume and longest axis of the tumors for the alternative regimens compared to the standard-of-care did not result in large differences. This may very well be due (in part) to the nonevolving vasculature in the model. While the model is reinitialized with each patient's data at the time of scan 2 (thereby updating the tissue map and drug dose map), the drug dose map does not evolve forward in time. Ongoing efforts are attempting to address this issue in the more well-controlled, preclinical setting [38,48]. A second limitation of the model is the characterization of the drugs themselves, as we do not explicitly account for differences in the mechanisms of each drug (only their overall efficacy and decay), do not account for drug synergy, and assume that all cancer cells will respond in the same manner. As more alternative regimens and combinations of drugs are considered for the optimization of therapy on an individual patient basis, additional differences between these drugs (and other therapeutics) need to be captured by the mathematical model. This will necessitate additional data types to properly calibrate the additional parameters required for such an extension.

The ability to predict which breast cancer patient will respond to NAT will have a fundamental and lasting impact on healthcare, but it is not the final goal. The ultimate goal is to optimize therapy given the unique characteristics of each individual patient. In the present work, we show that precise combination of advanced image analysis and rigorous—but practical—mathematical modeling can make predictions of response for the individual patient. Once there is a mathematical model that can accurately recapitulate the spatiotemporal development of a tumor, the next step is to use the model to select and optimize therapy for each individual patient. This would be accomplished by initializing the validated model with patient-specific characteristics, varying, in silico, a range of treatment plans, and then selecting via established methods (such as, optimal control theory [49]) the approach that achieves the greatest tumor control for the longest period of time. Such an achievement would represent a watershed moment in our fight against this disease.

Conclusion

The results of this study demonstrate that a biology-based, mathematical model can be predictive of tumor response using data obtained from the earliest time points—and from the individual patient—during neoadjuvant regimens. The in silico results illustrate how therapeutic regimens can be tailored, and even optimized, for each patient using a mathematical model and simulation studies. These results represent an initial effort toward personalizing patient regimens through quantitative imaging and mathematical modeling.