RADIO-IBAG: RADIOMICS-BASED INTEGRATIVE BAYESIAN ANALYSIS OF MULTIPLATFORM GENOMIC DATA

Abstract

Technological innovations have produced large multi-modal datasets that include imaging and multi-platform genomics data. Integrative analyses of such data have the potential to reveal important biological and clinical insights into complex diseases like cancer. In this paper, we present Bayesian approaches for integrative analysis of radiological imaging and multi-platform genomic data, wherein our goals are to simultaneously identify genomic and radiomic, i.e., radiology-based imaging markers, along with the latent associations between these two modalities, and to detect the overall prognostic relevance of the combined markers. For this task, we propose Radio-iBAG: Radiomics-based Integrative Bayesian Analysis of Multiplatform Genomic Data, a multi-scale Bayesian hierarchical model that involves several innovative strategies: it incorporates integrative analysis of multi-platform genomic data sets to capture fundamental biological relationships; explores the associations between radiomic markers accompanying genomic information with clinical outcomes; and detects genomic and radiomic markers associated with clinical prognosis. We also introduce the use of sparse Principal Component Analysis (sPCA) to extract a sparse set of approximately orthogonal meta-features each containing information from a set of related individual radiomic features, reducing dimensionality and combining like features. Our methods are motivated by and applied to The Cancer Genome Atlas glioblastoma multiforme data set, where-in we integrate magnetic resonance imaging-based biomarkers along with genomic, epigenomic and transcriptomic data. Our model identifies important magnetic resonance imaging features and the associated genomic platforms that are related with patient survival times.

1. Introduction.

In oncology, it is of critical importance to investigate both inter- and intra-tumor heterogeneity through an in-depth understanding of the complex interplay between genotypes and phenotypes, towards developing rational anti-cancer therapeutic strategies [Felipe De Sousa et al. (2013)]. The increased availability of complementary and matched molecular and imaging data allows for a thorough examination of tumor heterogeneity at multiple levels [Nicolasjilwan et al. (2015), Hu et al. (2017), Gutman et al. (2013)]. Investigations at the molecular level have been tremendously improved by the development of many genomic profiling technologies, including microarrays, next-generation sequencing, methylation arrays, and proteomic analyses. The Cancer Genome Atlas (TCGA) project, aiming to provide more comprehensive information of human cancer genomes by creating an “atlas” of high-throughput multiple genomic profiles across multiple cancers, was launched in 2005 as a publicly funded project [Tomczak, Czerwińska and Wiznerowicz (2015)]. The growing availability of such data has motivated the development of integrative analytical models that incorporate various genomic platforms to detect complex patterns of tumor heterogeneity that have predictive and prognostic ability [Wang et al. (2013)].

While genomic data provide information on the molecular characterization of a disease, imaging modalities such as X-ray radiography, magnetic resonance imaging (MRI), computed tomography, and positron emission tomography provide visual and broad resources for the acquisition of high-quality images and provide complementary quantitative information about the structural aspects of a disease. In the context of cancer, these imaging modalities provide a quantitative basis for detailed assessment of various features of the tumor that are associated with the development and progression of cancer. Radiomics is an emerging field with a goal of providing predictive or prognostic information by revealing quantitative mechanistic associations between radiologic images and clinical outcomes [Coroller et al. (2015), Aerts et al. (2014), Ganeshan et al. (2010), Lee et al. (2016)]. Radiomics, in general, involves the extraction and mining of various types of quantitative imaging features that are processed from high-throughput images obtained via different imaging modalities. These imaging features describe different morphological characteristics of a tumor, e.g., tumor shape features such as round or spiculated, total volume or surface area, intensity histogram features that describe the contrast intensity level, and textural features such as energy and entropy that evaluate tumor spatial heterogeneity. In particular, “texture analysis, which applies different statistical models and mathematical transforming methods to further evaluate a tumors intra-lesional heterogeneity, has become an active ongoing area of research [Castellano et al. (2004)]. In the context of glioblastoma multiforme (GBM), several studies have shown that the textural features from perfusion parametric maps provide useful information for predicting patients’ survival times [Lee et al. (2016)] and the features extracted from a gray-level co-occurrence matrix (GLCM) [Haralick, Shanmugam and Dinstein (1973), Castellano et al. (2004)] are effective in discriminating tumor volumetric phenotypes [Chaddad and Tanougast (2016)].

Radiomic and genomic features capture complementary characteristics of the underlying tumor, with radiomics capturing visual phenotypic information in the tumor and genomics capturing its underlying molecular biology. Thus, it is of interest to assess the interrelationships of these two types of features, a task termed radiogenomics, and then collectively assess how these inter-related features correlate with clinically relevant endpoints (e.g., survival, progression). From an analytical standpoint, radiogenomic analysis faces several key challenges. First, incorporating complex biological interactive mechanisms, both within and between multiple genomic platforms at the genomic (DNA), transcriptomic (mRNA) and epigenomic (methylation) levels, is understudied in the radiogenomic framework. Second, the highdimensional nature of both the quantitative features of images and genomic markers necessitates proper dimension reduction techniques and feature selection methods. Third, the analysis becomes more complicated when we wish to link clinical outcomes with genomic and radiomic outcomes in addition to modeling associations between the radiomic and genomic measurements to provide potentially biologically and clinically translatable results.

Multiple studies have addressed these challenges to various degrees. Taking advantage of multi-platform genomic data resources, additive models have been developed that treat the features from different platforms in the same models, although not explicitly modeling their interrelationships [Daemen et al. (2009), Lanckriet et al. (2004)]. Wang et al. (2013) proposed an integrative Bayesian analysis framework to integrate multi-platform genomic data using hierarchical models that capture the natural mechanistic relationships among the various molecular resolution levels. Jennings et al. (2012) generalized the method to integrate various types of genomic platforms with a single clinical outcome. These methods effectively capture the biological interaction within different molecular processes, but do not consider high dimensionality in the outcomes. Olivares et al. (2013) extended the above model with multivariate correlated imaging outcomes. This approach models image markers in separate linear models after applying a de-correlating procedure, but does not consider patient-specific clinical outcomes. Stingo et al. (2013) developed an integrative Bayesian modeling approach for imaging-genetics that incorporates the binary disease status as a clinical response, and developed a hierarchical mixture model that can select discriminatory imaging regions of interest and their relevant single-nucleotide polymorphisms simultaneously. Similarly, Batmanghelich et al. (2013) developed a joint probabilistic model of imaging and genetic features associated with disease measures, to provide insights into how imaging biomarkers can serve as intermediate phenotypes when detecting genetic and diagnostic associations. However, these approaches consider only individual platform and thus do not consider the interrelationships among the various molecular resolution levels in their analytical frameworks.

In this paper, we introduce Radio-iBAG: Radiomics-based integrative Bayesian analysis of multiplatform genomic data, an integrative multi-scale Bayesian framework to perform radiogenomic analyses. Our goal is three-fold: first, to detect explicit associations among different genomic platforms at the different molecular levels; second, to treat the radiomic-based biomarkers as an intermediate phenotype (i.e., endo-phenotype), evaluate the molecular underpinnings regulating these biomarkers and finally, evaluate the eventual associations with relevant patient-level clinical outcomes (e.g., survival times). To accomplish these tasks, we construct a multi-level regression-based modeling strategy: a first stage “genomic model” detects the complex biological mechanistic relationships among different genomic platforms, a second stage “radiogenomic model” subsequently discovers the underlying associations between gene-platform combinations and radiomic biomarkers. To assess clinical relevance, a third level model “radiogenomic clinical model” uncovers the associations between clinical outcomes and genomically-driven radiomic markers.

To address the high dimensionality in both the genomic and radiomic datasets, we utilize Bayesian shrinkage-based priors to achieve sparsity and regularization in the high-dimensional covariate space at various hierarchical levels. Specifically, we employ scale-mixture of normal representations, that allow adaptive shrinkage and borrowing strength within and across the different hierarchical levels. Our methodology is motivated by and applied to a GBM case study, wherein we discover multiple radiomic feature groups significantly associated with patients survival times along with their mechanism of action through multi-platform genomics.

In Section 2, we introduce our modeling scheme, major components, modeling methods and biomarker detection for each modeling stage. In Section 3, we illustrate our proposed model on the GBM case study with detailed description of the radiomic features and genomic profile datasets, modeling results and biological interpretations. In Section 4, we draw some conclusions and discuss some future extensions and advancements.

2. Method: Radio-iBAG Model.

2.1. Modeling stages.

As mentioned above, our core construction of the Radio-iBAG model framework consists of a multi-stage Bayesian hierarchical model. In the genomic model, we model the complex biological mechanistic relationship among genomic data from different platforms capturing information at various molecular resolution levels (e.g., gene expression, copy number and methylation). Subsequently, we carry the information garnered from the genomic model into the second stage, the radiogenomic model, to parse out the imaging-genomic correlations, which are then included as predictors in the third stage, the radiogenomic clinical model. This procedure delineates the image features that directly affect clinical outcomes, as well as those that appear to be modulated by combinations of genomic factors. This construction allows us to discover strong relationships between imaging and genomics data, among the genomic platforms, and identify which appear to be associated with clinical outcome.

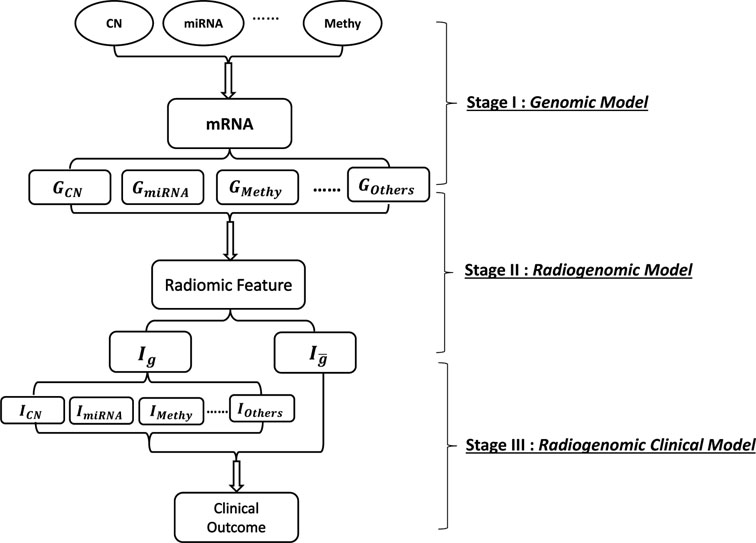
Fig 1 illustrates the general multi-stage modeling scheme. In the first stage, multiplatform genomic data sets are expressed as data matrices: X_mRNA, X_CN, X_miRNA or X_Methy, each with rows as samples and columns as genelevel summaries of the respective platforms. In stage II, we consider radiomic features (RFs) that are preprocessed and extracted from imaging data sets, forming a data frame $\mathcal{I}$ with columns as different features and rows as samples. In the final stage, we incorporate into the model the clinical outcome, denoted as Y, which is a vector with the number of elements as the sample size. The construction of each modeling stage is explained in detail in the ensuing sections.

Fig 1: Schematic representation of the multi-stage modeling process.

In stage I, for each gene, model the relationship between mRNA and different upstream genomic platforms and partition mRNA expression into multiple parts explained by different genomic platforms, CN: copy number alteration, miRNA: microRNA, Methy: methylation, Others: gene expression that is explained by other factors; In stage II, for each radiomic marker, apply Bayesian hierarchical model and partition the radiomic marker into different parts modulated by multiple mRNA factors that are explained by various gene-platform combinations and regard the residual as a non-gene-driven part denoted as $I_{\overline{g}}$; In stage III, apply Bayesian hierarchical model to investigate the relationship between segmented radiomic factors with clinical outcome.

A. Genomic Model

Our genomic model involves the integrative modeling of multiplatform genomic data sets. Modern genomics data is comprised of multiple platforms that contain measurements at various molecular resolution levels, from DNA to mRNA to proteins, and including epigenetic levels including alterations like methylation and microRNA (miRNA) that affect mRNA expression. These platforms capture complementary information at the different molecular resolution levels, and together provide a more complete picture of the underlying biology than any one platform. In this paper, we consider three genomic platforms: mRNA, DNA copy number (CN) and miRNA, but the general models we introduce can incorporate any other platforms capturing upstream genetic and epigenetic information, as well. Also, for a specific gene, we take only the genomic platforms mapped with this gene into our model, we do not consider modeling coexpression or coregulation of the neighboring genes or potential transcriptional regulators. Suppose $N_{\mathcal{G}}$=number of patients with genomic information, J=total number of genomic platforms, and $P_{\mathcal{G}}$=number of target genes. For our particular case, using copy number alteration and miRNA as our upstream platforms, the gene expression level can be modeled and expressed as

$$X_{mRN{A}_g}=\underset{\text{ upstream platform driven }}{\underbrace{f_1\left(X_{miRN{A}_g}\right)+f_2\left(X_{C{N}_g}\right)}}+\underset{\text{ explained by other factors }}{\underbrace{{\mathit{O}}_{\mathit{g}}}}$$ (1)

where each f_j(·) is a smooth nonparametric function of the corresponding predictor modeled by a penalized spline formulation that allows us to capture flexible non-linear relationships. We assessed the nonlinearity of genelevel fits and show that GAM provides better fit that GLM for most genes (see supplementary materials Section S3). Other types of splines or alternative nonparametric models could also be used. Our analysis in this stage matches the first stage of the iBAG model [Wang et al. (2013)], whereby the gene expression of a given gene is modeled as explained by upstream factors, with the effects of upstream factors modeled nonparametrically as in [Jennings et al. (2015)] via a generalized additive model (GAM) [Hastie and Tibshirani (1990)]. In principle, the model can include any number of upstream (to mRNA) platform types, including methylation, copy number, loss of heterozygosity, methylation, miRNA, and transcription factors, as long as matched data are available.

The terms in the model are described and interpreted as follows:

• $X_{mRN{A}_g}$ is the expression of gene g with dimension $N_{\mathcal{G}}\times 1$, $g=1,2,\dots ,P_{\mathcal{G}}$

• $X_{mRN{A}_g}$ is an aggregated miRNA expression value that integrates information across miRNAs that have been documented to regulate the expression of gene g. For a given gene, there exist multiple miRNAs that interact with this gene, and here we construct gene-level summaries of these miRNAs that condense their activity into a lower dimension using principal components, as described in detail in Section 3. The gene-level summaries $X_{miRNAg}$ have dimension $N_{\mathcal{G}}\times M_{miRN{A}_g}$, where $M_{miRN{A}_g}$ denotes the number of gene-level summary vectors for the g^th gene.

• $X_{C{N}_g}$ are gene-level summaries of the CN alteration for the g^th gene with dimension $N_{\mathcal{G}}\times M_{C{N}_g}$. Similarly, as there are multiple CN alteration values from different markers within the same gene, $M_{C{N}_g}$ denotes the number of gene-level summary vectors.

• O_g represents the “other” part of gene expression that is not captured by the modeled upstream factors, but instead attributed to other upstream factors not in the model, and is of dimension $N_{\mathcal{G}}\times 1$.

This model is fit separately for each gene, and effectively partitions the information contained in the mRNA measurements into an additive set of components, with each component capturing the part of mRNA expression explained by a particular upstream platform. We call these parts different genomic platform components. For gene g, the components can be estimated based on the following formula: $G_{mi{R}_g}={\widehat{f}}_1\left(X_{miRN{A}_q}\right),G_{C{N}_g}={\widehat{f}}_2\left(X_{C{N}_g}\right)and(G_{O_g}=X_{mRN{A}_g}-{\widehat{f}}_1\left(X_{miRN{A}_g}\right)-{\widehat{f}}_2\left(X_{C{N}_g}\right)$. Repeating the same procedure for all the genes, we combine the components grouped by platform, forming different genomic platform combinations: $G_{\text{mi}R}=\left\{G_{mi{R}_1},G_{mi{R}_2},\dots ,G_{mi{R}_{P_{\mathcal{G}}}}\right\},G_{\mathbf{\text{CN}}}=\left\{G_{C{N}_1},G_{C{N}_2},\dots ,G_{C{N}_{P_{\mathcal{G}}}}\right\}and(G_O=\left\{G_{O_1},G_{O_2},\dots ,G_{O_{P_{{}_{\mathcal{G}}}}}\right\}$. These combinations represent the gene expression level attributed to miRNA, CN and other factors, respectively, for all $P_{\mathcal{G}}$ target genes of interest.

At times, not all samples with genomic data have radiomic data, as in our GBM example. In that case, we denote $N_{\mathcal{G}\mathcal{I}}\left(N_{\mathcal{G}\mathcal{I}}\subseteq N_{\mathcal{G}}\right)$ as the sample size of their intersection. We carry forward the corresponding subset of the estimated gene platform combinations G_miR, G_CN, G_O, each with dimension $N_{\mathcal{G}\mathcal{I}}\times P_{\mathcal{G}}$, as predictors into the second-stage radiogenomic model.

B. Radiogenomic Model

The goal of the second stage radiogenomic model is to find gene-platform combinations that appear to be associated with radiomic markers, and to partition the radiomic markers into the parts modulated by different gene effects carried from the genomic model and those that are not modulated by the modeled genomic factors. The model can be written as

$$\begin{gathered} \mathcal{I}={\mathcal{I}}_{\mathit{g}}+{\mathcal{I}}_{\overline{\mathit{g}}} \\ =\underset{\text{ Genomically driven }}{\underbrace{{\mathit{G}}_{\mathit{\text{miR}}}{\mathit{B}}_{\mathit{\text{miR}}}+G_{\mathit{\text{CN}}}{\mathit{B}}_{\mathit{C}\mathit{N}}+{\mathit{\text{G}}}_{\mathit{\text{O}}}{\mathit{B}}_{\mathit{O}}}}+\underset{\text{ Non-genomically driven }}{\underbrace{{\mathcal{I}}_{\overline{\mathit{g}}}}} \end{gathered}$$ (2)

The terms in the model can be expressed and interpreted as follows:

• $\mathcal{I}$ denotes a $N_{\mathcal{G}\mathcal{I}}\times K$ matrix in which K is the number of general RFs (individual radiomic features or Radiomic-meta-Features (RmFs) that we constructed from high dimensional RFs that are highly correlated, described in detail in section 3.2).

• B_miR is of dimension $P_{\mathcal{G}}\times K$, with columns as the vectors of the expression effects for corresponding radiomic markers through miRNA;

• B_CN is of dimension $P_{\mathcal{G}}\times K$, with columns as the vectors of the expression effects for corresponding radiomic markers through CN;

• B_O is of dimension $P_{\mathcal{G}}\times K$, with columns as the vectors of the expression effects for the corresponding radiomic markers through “other” genomic mechanistic factors;

• G_miR, G_CN, G_O are the estimated gene expression components described in part A.

Associations are detected by examining the coefficients’ posterior probabilities based on Markov chain Monte Carlo (MCMC) samples, and estimates given by posterior means (detailed information in Section 2.3). To achieve the segmentation of the radiomic features, we can estimate each component by ${\widehat{\mathcal{I}}}_{\mathit{C}\mathit{N}}=G_{\text{CN}}{\widehat{\mathit{B}}}_{\mathit{C}\mathit{N}},{\widehat{\mathcal{I}}}_{\mathit{m}\mathit{i}\mathit{R}}=G_{\mathit{m}\mathit{i}\mathit{R}}{\widehat{\mathit{B}}}_{\mathit{m}\mathit{i}\mathit{R}},{\widehat{\mathcal{I}}}_{\mathit{O}}=G_{\mathit{\text{O}}}{\widehat{\mathit{B}}}_{\mathit{O}}$. The final nongene-driven part can be estimated by ${\widehat{\mathcal{I}}}_{\overline{\mathit{g}}}=\mathcal{I}-G_{\mathit{\text{CN}}}{\widehat{\mathit{B}}}_{\mathit{C}\mathit{N}}-G_{\mathbf{\text{miR}}}{\widehat{\mathit{B}}}_{\mathit{m}\mathit{i}\mathit{R}}-{\mathit{\text{G}}}_{\mathit{\text{O}}}{\widehat{\mathit{B}}}_{\mathit{O}}$. We then further carry the above four components into the final stage, the radiogenomic clinical model.

C. Radiogenomic Clinical Model

The third-stage model relates the various radiogenomic marker combinations from the second stage model to a clinical outcome (e.g., survival time in our context). The model can be expressed as

$$\mathit{Y}={\mathcal{I}}_{\mathit{C}\mathit{N}}{\mathit{\alpha }}_{\mathbf{1}}+{\mathcal{I}}_{\mathit{m}\mathit{i}\mathit{R}}{\mathit{\alpha }}_{\mathbf{2}}+{\mathcal{I}}_{\mathit{O}}{\mathit{\alpha }}_{\mathbf{3}}+{\mathcal{I}}_{\overline{\mathit{g}}}{\mathit{\alpha }}_{\mathbf{4}}+\mathit{ϵ}$$ (3)

where Y is the clinical outcome with dimension $N_{\mathcal{G}\mathcal{I}\mathcal{C}}\times 1$ and $N_{\mathcal{G}\mathcal{I}\mathcal{C}}(N_{\mathcal{G}\mathcal{I}\mathcal{C}}\subseteq N_{\mathcal{G}\mathcal{I}}\subseteq N_{\mathcal{G}})$ is the sample size of the intersection of the genetic, image and clinical data sets. ${\mathcal{I}}_{\mathit{C}\mathit{N}}$ is the CN modulated radiomic marker component matrix. Similarly, ${\mathcal{I}}_{\mathit{m}\mathit{i}\mathit{R}}$ denotes the microRNA modulated part; ${\mathcal{I}}_{\mathit{O}}$ is the part of radiomic features explained by a genomic factor but modulated by something other than CN or miRNA; and ${\mathcal{I}}_{\overline{\mathit{g}}}$ denotes the part of the radiomic feature not regulated by genes in the model. All four radiomic marker components have the dimension $N_{\mathcal{G}\mathcal{I}\mathcal{C}}\times K$. α₁, α₂, α₃, α₄ denote the corresponding image marker combination effects. ϵ is the error term for modeling the clinical outcome. In our GBM application, where the clinical outcome is survival time, we use an accelerated failure time (AFT) model, with Y as the log-transformed survival time [Wei (1992)]. However, for the general analytical process, our outcome Y can involve any clinical measurements with suitable regression model determined by the type of outcome (e.g., logistic models for binary outcomes or Cox proportional hazards models in the presence of censored outcomes.)

Our goal in this final stage is to identify radiomic markers associated with clinical outcome, either modulated by genomic factors or not. We identify these factors by estimation and Bayesian posterior inference of α = {α₁, α₂, α₃, α₄}, and then can characterize these effects in more detail by tracing information back through the earlier stage models. For example, if a particular radiomic feature is related to clinical outcome through a genomic effect, we can examine the corresponding second stage model to identify which genes are driving such effects, and then the first stage model for those genes to find which upstream platforms most strongly modulate the expression of those genes. In this way, the radio-iBAG model can not only detect clinically relevant radiomic features, but provide a thorough summary of the radiomic-genomic and multi-platform genomic interrelationships that appear to modulate these factors.

2.2. Radio-iBAG Model Estimation.

Our second- and third-stage models involve multiple genes and/or RFs, so it is necessary to introduce sparsity into the regression models to regularize the fitting and to obtain a relatively smaller and more interpretable set of radiogenomic factors that appear to be related to the clinical outcome. This can be done using penalized likelihood or other regularization techniques, but here we use a Bayesian approach and induce sparsity through the prior distributions on the regression parameters.

Some commonly used sparsity priors involve a discrete-mixture prior consisting of a point mass at zero for noise and a continuous density distribution for signals, for example a normal distribution and a point mass at zero [Mitchell and Beauchamp (1988)]. Other types of sparsity priors do not have a zero component, but instead are absolutely continuous distributions that accomplish sparsity via nonlinear shrinkage, which can often be accomplished using a normal scale mixture prior distribution. Examples include a normal-exponential (Bayesian lasso) [Park and Casella (2008)], Horseshoe [Carvalho, Polson and Scott (2010)], generalized double pareto [Armagan, Dunson and Lee (2013)], Dirichlet Laplace [Bhattacharya et al. (2015)], and Normal Gamma [Griffin et al. (2010)]. While the Bayesian lasso, which is a Bayesian analog to the commonly-used lasso [Tibshirani (1996)], is commonly used, it has limited flexibility given it is determined by a single hyperparameter that regulates both sparsity and the tails. We instead use the normal-gamma (NG) prior [Griffin et al. (2010)], which contains a second hyperparameter, and thus can better handle sparsity as well as flexibility to manage the tails and yield to more accurate coefficient estimates, as described and illustrated via multiple simulation settings in [Griffin et al. (2010)]. We apply this prior in both stage II radiogenomic and stage III radiogenomic clinical models. Further, we allow the sparsity hyperparameters to be indexed by platform, which enables borrowing of strength across genes in determining the desired sparsity and tail levels on a platform specific basis.

To estimate the coefficient vector, for the k^th RF, we assign the NG prior distribution to ${\mathit{\beta }}_{\mathit{k}}=\left\{{\mathit{\beta }}_{\mathit{m}\mathit{i}\mathit{R}}^{\mathit{k}},{\mathit{\beta }}_{\mathit{C}\mathit{N}}^{\mathit{k}},{\mathit{\beta }}_{\mathit{O}}^{\mathit{k}}\right\}$, each part of the coefficient vector being assigned with a particular set of the hyperparameters. In this way, we allow priors settings that incoporate multi-scale datasets. More specifically, suppose our genomic platform combination predictors can be expressed as X = {G_miR, G_CN, G_O}, then the linear regression model and its hierarchical prior setting can be expressed as

$${\mathcal{I}}_{\mathit{k}}=X{\mathit{\beta }}_{\mathit{k}}+{\mathcal{I}}_{\mathit{k}\overline{\mathit{g}}}$$

$${\mathcal{I}}_{\mathit{k}}~\mathit{\text{Normal}}\left(X{\mathit{\beta }}_{\mathit{k}},{\sigma }_k^2{\mathit{I}}_{{\mathit{N}}_{\mathcal{G}\mathcal{I}}}\right)$$

$${\mathit{\beta }}_{\mathit{k}}~Normal\left({\mathbf{0}}_{\tilde{\mathit{P}}},D_{\psi }\right)$$

$D_{\psi }=diag\left({\psi }_{1,1},{\psi }_{1,2},\dots ,{\psi }_{1,P_1},{\psi }_{2,1},{\psi }_{2,2},\dots ,{\psi }_{2,P_2},\dots ,{\psi }_{J,1},{\psi }_{J,2},\dots ,{\psi }_{J,P_J}\right)$, where $\tilde{P}=P_1+P_2+\dots +P_J$ is the total number of predictors (dimension of X), J denotes the total number of platform types (j = 1,2,3, …, J, here our J = 3), and P_j denotes the total number of genomic features (each subindexed as g) for the j^th genomic platform type. Our estimation of the scale parameters and the main coefficients (β_k) is processed by applying the NG prior ${\psi }_{j,g}~Gamma\left({\lambda }_j,1/\left(2{\gamma }_j^2\right)\right)$ for the j^th platform. Also, the hyper-prior ${\lambda }_j~exp(c)and{\gamma }_j^{-2}~Gamma\left(\tilde{a},\tilde{b}/\left(2{\lambda }_j\right)\right)$ are assigned to induce greater flexibility and completeness in shrinkage estimation. To complete our prior specification, we assume a conjugate InverseGamma(a,b) prior on ${\sigma }_k^2$. Here, we let each genomic platform combination (platform type) share the same set of hyperparameters (λ_j, ${\gamma }_j^2$), thus maintaining the grouped structure at the shrinkage level. For implementation, we utilize Markov Chain Monte Carlo (MCMC) based Bayesian sampling techniques such as Gibbs sampling and Metropolis-Hastings. The posterior means calculated from MCMC samples are used to obtain the parameter estimations, and the corresponding posterior probabilities are used to conduct signal detection. The details for the posterior distribution and MCMC sampling are shown in Appendix A.

For the radiogenomic clinical model, we utilize similar NG prior distributions, the only difference being that our group structure is determined by the RF combinations. We assign the same hyperparameters for the partitioned RFs that belong to the same combination/group. Suppose our predictor set estimated from stage II can be expressed as $\mathcal{I}=\left\{{\mathcal{I}}_{\mathit{C}\mathit{N}},{\mathcal{I}}_{\mathit{m}\mathit{i}\mathit{R}},{\mathcal{I}}_{\mathit{O}},{\mathcal{I}}_{\overline{\mathit{g}}}\right\}$, and the effect parameter α = {α₁, α₂, α₃, α₄}, then the model and prior construction can be expressed as

$$\begin{gathered} \mathit{Y}=\mathcal{I}\mathit{\alpha }+\mathit{ϵ} \\ \mathit{Y}~\mathit{\text{Normal}}\left(\mathcal{I}\mathit{\alpha },{\sigma }^2{\mathit{I}}_{{\mathit{N}}_{\mathcal{G}\mathcal{I}c}}\right) \\ \mathit{\alpha }~\mathit{\text{Normal}}\left(\mathbf{0},D_{\psi }\right) \end{gathered}$$

D_ψ = diag(ψ_1,1, ψ_1,2 ,…, ψ_1,K, ψ_2,1, ψ_2,2, …, ψ_2,K, …, ψ_J,1, ψ_J,2, …, ψ_J,K), where J denotes the total number of different RF combination types (j = 1,2,3, …, J, our J = 4), k denotes the RF index (k = 1,2,3, …, K). Further, we assign our prior and hyper-prior distributions as ${\psi }_{j,k}~Gamma\left({\lambda }_j,1/\left(2{\gamma }_j^2\right)\right)$, ${\sigma }^2~InverseGamma\left(u_1,u_2\right)$, ${\lambda }_j~exp(d)$, and $1/\left(2{\gamma }_j^2\right)~Gamma\left(\tilde{e},\tilde{f}/\left(2{\lambda }_j\right)\right)$. Note that for censored sample i, we sample Y_i from complete conditional distribution which is normal distribution with left truncation at t_i that represents the follow-up time. Finally, RF combination selection is based on the posterior probability of the MCMC samples. Details about the posterior distribution and sampling methods are provided in Appendix A.

2.3. Radiomic and Genomic Marker Selection.

For marker/feature selection we propose a thresholding procedure for the various regression models. Specifically for the radiogenomic clinical model, we choose a thresholding criteria considering both the effective size and clinical interpretability. For example, in the GBM case study, we apply the AFT model with the log-transformed survival time as the clinical outcome. In our analysis, considering that the survival times are measured in months, which is comparatively small, we choose to apply log₂-based transformation, which leads to better interpretability and a simpler calculation. Based on this setting, the region for detecting the coefficients of the image markers becomes ${\alpha }_{jk}\in \left(-\infty ,{\delta }_{-}^{*}\right)\cup \left({\delta }_{+}^{*},\infty \right)$, where we denote ${\delta }_{-}^{*}aslo{g}_2\left(1-{\delta }_2\right)$ and ${\delta }_{+}^{*}$ as log₂(1 + δ₂), particularly, α_jk is the coefficient of the k^th radiomic marker modulated by the j^th genomic platform (j = 1,2, …, J, k = 1,2, …, K). Moreover, δ₂ is determined to achieve the proper effect size and is interpreted as the percentage change in survival time, e.g., for the GBM data analysis, we choose δ₂ = 0.05, which corresponds to 5% change in survival time. More specifically, we denote $P_{+}\left({\mathcal{I}}_{jk}\right)={\Sigma }_{t=S+1}^{t=T}\mathit{I}\left({\alpha }_{jk}^{(t)}>{\delta }_{+}^{*}\right)/(T-S)$ and $P_{-}\left({\mathcal{I}}_{jk}\right)={\Sigma }_{t=S+1}^{t=T}\mathit{I}\left({\alpha }_{jk}^{(t)}<{\delta }_{-}^{*}\right)/(T-S)$ where t denotes the t^th MCMC iteration, S denotes the burn-in sample size and T represents the total number of MCMC iterations. We flag ${\mathcal{I}}_{jk}$ to be positively significant if $P_{+}\left({\mathcal{I}}_{jk}\right)>0.5$ or negatively significant if $P_{-}\left({\mathcal{I}}_{jk}\right)>0.5$ [Barbieri and Berger (2004)].

Analogously, for the radiogenomic model, considering δ-fold or larger variation in the response for a unit change in a particular predictor is defined as a standard in the significance detection, which corresponds to β_jg ∈ (−∞, −δ) ∪ (δ, ∞) and β_jg is the coefficient of the j^th platform of the g^th gene in the analysis. Once a proper threshold δ₁ is determined, the posterior probability is defined as $P\left(x_{jg}\right)={\Sigma }_{t=S+1}^{t=T}\mathit{I}\left(\left|{\beta }_{jg}^{(t)}\right|>{\delta }_1\right)/(T-S)$, where S is the burn-in sample size and T is the total number of MCMC iterations. Feature x_jg in the gene-platform combinations is highlighted to be ‘significant’ if P(x_jg) > 0.5.

Radio-iBAG modeling algorithm provides a concise summary of Radio-iBAG model implementation and genomic/radiomic marker selection.

3. Radiogenomic Mapping of Glioblastoma Multiforme.

Glioblastoma Multiforme (GBM) is an aggressive and malignant form of primary brain cancer. It is the highest grade glial tumor, with a median survival time of 14.6 months following standard treatment options and typically 3 months without treatment [Stupp et al. (2009)]. Although different treatment approaches that include radiation, surgery and chemotherapy have been developed and applied in clinical practice, the overall mortality rate still remains high, mainly due to the tumors resistance to treatment [Bleeker, Molenaar and Leenstra (2012)] and the complexity of its primary biological mechanism.

Currently, at the molecular level, TCGA provides data sets with multiple genomic platforms, including methylation, CN alteration, and gene expression. Studies based on TCGA platform have identified distinct molecular subclasses of GBM, resembling stages in neurogenesis that are relevant to prognosis [Verhaak et al. (2010)]. Also, with the availability of standardized medical image annotations from The Cancer Imaging Archive (TCIA), multiple studies currently focus on the detection of radiomic imaging variables associated with clinical outcomes [Chaddad and Tanougast (2016), Kickingereder et al. (2016)]. Relevant studies have shown that quantitative imaging features extracted from different modalities provide strong prognostic information [Nicolasjilwan et al. (2015), Lee et al. (2016)].

The availability of such large-scale data resources (TCIA and TCGA) makes it feasible to perform radiogenomic mapping in GBM to explore the complex associations between molecular features and imaging features for this particular cancer type. In this section, we apply our integrative multi-stage Bayesian hierarchical model with the data from patients with GBM and matched with TCGA and TCIA platforms, to discover radiogenomic associations characterizing these data and identify RmFs and genomic markers associated with GBM prognosis. More details of the genomic and imaging data sets are provided hereafter.

3.1. Data Description.

3.1.1. Radiomic and clinical data description.

Among 304 GBM patients with available genomic records, 78 matched patients ($N_{\mathcal{G}\mathcal{I}}$=78) also have MRI T1-weighted post contrast images and T2-weighted fluid attenuated inversion recovery (T2-weighted FLAIR) images available from TCIA for texture analysis. Image preprocessing procedures, including steps such as non-uniformity normalization (N3) correction, registration, segmentation, isotropic voxel-reslicing and image filtering, were performed prior to texture feature extraction. For this analysis, we derived textural features from the axial 2D slice that has the largest tumor area [Zhou et al. (2014)]. Our textural features were obtained from a two-step process: 1) Image filtering, 2) Haralick features¹ derivation [Haralick, Shanmugam and Dinstein (1973)] [Haralick (1979)] and summary measures calculation. These image pre-processing steps as well as the texture feature calculations are described in detail in the Supplementary Section S2.1.

For the radiomic data set, we had 972 RFs that could be categorized into 20 groups based on how they were calculated. The group names and corresponding descriptions are provided in the Supplementary S2.2. They cover the features of both T2-weighted FLAIR and T1-weighted post-contrast MRI modalities with different type of features: texture features, histogram features and regional features and with two types of ratio based normalization methods.

For clinical outcomes, we utilized overall survival times (in months) as the response in our integrative analysis. For the clinical model, we used data from $N_{\mathcal{G}\mathcal{I}\mathcal{C}}=N_{\mathcal{G}\mathcal{I}}$ = 78 GBM patients with matching multi-platform genomic, radiomic, and clinical data, and with 9 patients having censored clinical outcomes. We applied the AFT model using the log₂ transformed survival time log₂(T_i) as the response, where T_i is the survival time in months after diagnosis for patient i, and imputed the survival time for censored samples simultaneously.

3.1.2. Genomic data description.

Our gene expression data set is level 3 (summarized per gene), and was downloaded and processed by TCGA Assembler [Zhu, Qiu and Ji (2014)] with open-source software and related instructions available in public. The CN data set is level 2 (probe-level) data obtained from TCGA Portal from the HG CGH 244A platform with normalized records of CN alteration for each probe. The miRNA data set was also acquired from TCGA Portal with 534 miRNA records and 575 samples in total.

In our analysis, we focus on 49 genes that are members of signaling pathways that have previously been detected associated with GBM (RTK/PI3K, P53, and RB pathways [Network et al. (2008)] and 304 patients ($N_{\mathcal{G}}$ = 304) with records available for mRNA, CN and miRNA. The sample sizes and the specific types of the raw datasets for all genomic platform, radiomic data and clinical data are illustrated via diagram in Supplementary Fig S3 with description in Section S2.3. The genomic datasets used in the first stage are all continuous and the descriptions of the raw data structure (for 304 samples) of different genomic platforms are given in below:

• mRNA (304 × 49) contains gene expression levels for each gene and each patient.

• Copy number (304 × 491) contains the CN alteration data (columns) for each sample (rows). There exist multiple copy number markers per gene, and the columns of the data set are sorted by gene. Also, one gene, HRAS, does not have CN alteration information, thus, any variance of gene expression contributed by CN changes will be captured by the factor “others” in this analysis; in other words, for gene HRAS, the corresponding column in matrix G_CN is set as zero.

• miRNA (304 × 522) contains miRNA values for each gene (column) and patient (row) based on the miRNA-mRNA interaction membership matrix, with records coming from targetHub [Manyam et al. (2013)], which collected miRNA-mRNA interaction records based on 5 external databases, and multiMiR [Ru et al. (2014)] is based on 14 external databases, including validation databases, prediction databases and drug-associated databases. There exist multiple miRNA records corresponding to one gene, and the columns of the miRNA data set are ordered by gene.

We wish to obtain gene-level summaries for each platform based on these raw data sets. Considering that a given gene can contain multiple values from different markers for both miRNA and CN alteration records, and including all these records into the genomic model is computationally expensive and inefficient, the gene-level summaries that can be carried into the modeling stage need to be generated. There are different ways to obtain gene-level summaries, e.g., taking the average, selecting the top most correlated records, or extracting the top principal components via PCA. For the analysis of GBM data, CN alteration and miRNA, in each case, we perform PCA on the genomic platform data set mapped to a gene and keep the top principal components with cumulative variance that explain up to 90% of the total variance. In this way, we regard the remaining records as capturing most of the information of the genomic platform data. Specifically, for gene g, the gene-level summaries for each platform can be expressed as $X_{miRNAg}$ and $X_{C{N}_g}$, which have been denoted in Methods. Our genomic model is conducted based on these three data sets, $X_{mRN{A}_g}$, $X_{miRN{A}_g}$ and $X_{C{N}_g}$.

As described in Section 2.1, our genomic model uses the GAM to fit the model and estimate the partitioned mRNA that is modulated by different genomic platforms. To implement the GAM algorithm, we utilized Woods R package “mgcv” and exploited its option for the automatic smoothness selection for the penalty parameter based on generalized cross-validation [Wood (2001)]. Subsequently, for each gene, we calculated the proportion of the mRNA variance explained by each platform. We assume that if a genomic platform does not explain much variation in mRNA expression, it will not have a significant impact on image features. Thus, for G_miR, G_CN and G_O, we filtered out the genomic platform features that explain less than 10% of the total variance of gene expression, leaving the remaining features to be carried forth into the radiogenomic model.

3.2. Estimation of Radiomic-meta-Features.

One of the critical challenges in fitting the radiogenomic model is the high dimensionality and redundancy of the set of radiomic features (RFs). In our GBM case study, the preprocessed RF data set has 972 features, and contains many features within the same type of radiomic class but with different settings, e.g. filtering scales. Thus, there are extensive correlation among many RFs with high magnitudes up to 0.99, as can be seen in the correlation heatmap shown in Supplementary Fig S1. Facing these challenges, we utilize a new radiomic strategy of empirically constructing radiomic meta features (RmFs) comprised by a linear combination a sparse subset of highly correlated RFs. Each RmF defines a factor capturing one aspect of the fundamental structure in the radiomic features, and together the relatively small number of RmFs retain a vast majority of information contained in the set of 972 RFs. To our knowledge, this strategy has not been applied in the radiomics literature to date, and may be useful in other contexts. We construct the RmFs by applying sparse principal component analysis (sPCA) [Zou, Hastie and Tibshirani (2006)] which incorporates a regularization technique such as the lasso or elastic net to induce sparsity in the principal component loadings. This has the advantage of interpretability over general principal components that do not in general yield sparse loadings, in the case of our GBM application yielding RmFs that are reasonably intuitive and interpretable (see Section 3).

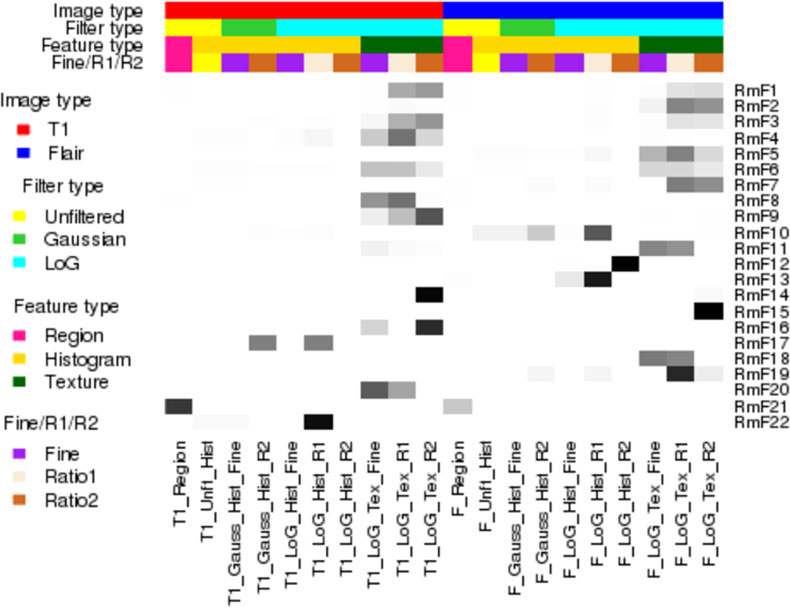
This algorithm offers a parsimonious way to obtain more comprehensive representation of radiomic features, which contain the maximum information of the original radiomic data. While not strictly orthogonal like PCs, the SPCs are approximately orthogonal so it is reasonable to model these RmFs as independent imaging features in the second stage radiogenomic model. The sparse loadings for the RmFs for our GBM application are shown in Fig 2, and by contrast, the non-sparse loadings for ordinary PCA are shown in the Supplementary Fig 2S.

Fig 2: Squared loading proportion for each RF group.

For each of the 22 radiomic-meta-features (RmFs), the sum of the squared loadings of each group is calculated, divided by the total sum of the squared loadings, which equals exactly 1. The heatmap shows this values in grey level, interpreted the RF group importance for each RmF. The grey level ranging from white to black matches the proportional values ranging from 0 to 1.

Let $\mathcal{M}$ be an $N_{\mathcal{G}\mathcal{I}}\times P$ matrix (typically with $P>>N_{\mathcal{G}\mathcal{I}}$) with the rows being the subjects and the columns the P (=972) RFs. The sparse PCA is applied as follows:

• Apply ordinary PCA to $\mathcal{M}$ and record the number of top principal components with the cumulative variance explaining up to 100(1 − α)% (eg. 90%) of the total variance. Each PC is regarded as a linear combination of the original features with its loadings can be estimated by regressing the PC on these features. Sparsity in loadings results from adding regularization terms in the regressions.

• The general sPCA algorithm and its numerical computation procedure are described by [Zou, Hastie and Tibshirani (2006)]. In most cases, the number of features is typically much bigger than the sample size; hence, the simplified version of the general sPCA described in the paper should be applied here. The mathematical formulation of sPCA is illustrated in the Supplementary file Section S2.2. To implement the algorithm, we utilized the R package “elasticnet” [Zou and Hastie (2005)], with K (the number of principal components based on the ordinary PCA) principal components and vectors of λ_j (L1 norm regularization parameter for each loading vector). The parameter λ_j can be chosen by cross validation, or various values can be tried to find one that results in the desired level of sparsity.

Suppose V is our final matrix of loadings with dimensionality P ×K, the projected imaging features matrix (PC score matrix) is then ${\mathcal{I}}_{\left(N_{\mathcal{G}\mathcal{I}}\times K\right)}={\mathcal{M}}_{\left(N_{\mathcal{G}\mathcal{I}}\times P\right)}{V}_{(P\times K)}$. We define the vectors of this matrix as RmFs, which contain the majority of the information of the original radiomic data. These features are further regarded as predictors in the analysis of the radiogenomic clinical model.

3.3. Results Using the Radio-iBAG Model.

3.3.1. Radiomic-meta-Feature Estimation.

We conducted sPCA with the regularization parameter λ = 2.5 for each principal component, leading to 22 top principal scores that explain 80.7% of the total variance. We also explored large range of λ with the corresponding loadings and the cumulative variance that are showed in Supplement Section S6. We chose λ = 2.5 given its balance in the sparsity of the loadings which leads to good interpretation and the cumulative variance that could be attained. We call these 22 principal scores Radiomic-meta-features (RmFs) as discussed in section 3.2. To summarize the RmFs, Fig 2 plots a heatmap of the squared loading proportions within the 20 broad categories of RFs to show which feature types dominate each RmF.

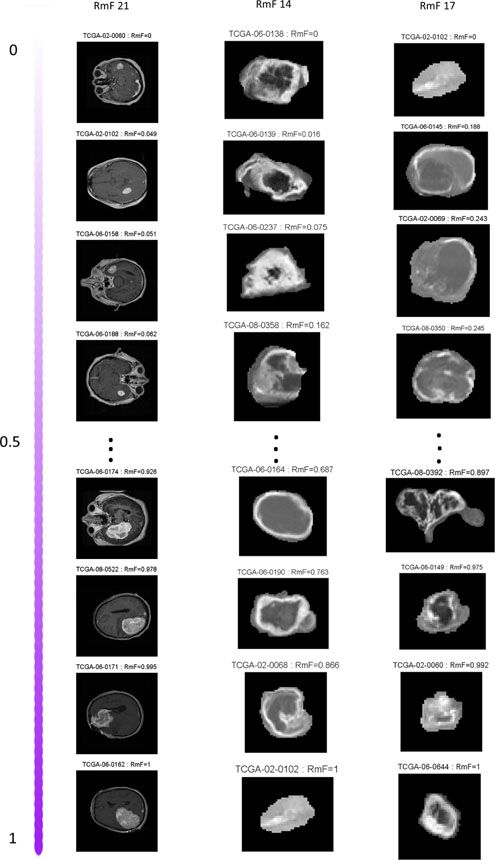
This figure reveals that many of the RMFs appear to be interpretable in the sense of summarizing certain aspects of the images, including morphological imaging features that can be directly visualized, eg. unformity, tumor area, mean intensity, etc. To further illustrate their interpretability, we pick out three example RmFs and in Fig 3 plot T1-Post Contrast images for the four tumors with highest and lowest values of the corresponding RmF scores, rescaled to [0,1]. RmF 21 has the largest loading values for feature categories indicating tumor area (T1_Region, F_Region). The first column of Fig 3 shows that samples with higher values of RmF 21 tend to have larger tumor area. RmF 14 has non-zero loadings inversely proportional to pixel intensity variance measures, and thus can be construed as representative of local pixel heterogeneity. From the second column, it is evident that larger RmF 14 (smaller variance) leads to lower local pixel heterogeneity. The third column of Fig 3 shows the sorted RmF 17, whose loadings are dominated by the imaging intensity histogram feature “uniformity”, which represents how non-uniform of the overall gray-level pixel intensities. The gray level of the magnified tumor region shows that when RmF value gets larger, the tumor surface gets more non-uniform. These RmFs quantitatively capture these fundamental features of the images.

Fig 3:

T1-Post Contrast images are shown based on the sorted results of 3 representitive RmFs: RmF 21 mainly accounts for tumor area; RmF 14 mainly represents tumor pixel heterogeneity; RmF 17 represents tumor uniformity. The RmF values are all scaled from 0 to 1.

We use these RmF as quantifications of the radiomic data in our modeling, with the radiomic model fit to Rmf matrix $\mathcal{I}$, which is of dimension 78 × 22, with RmFs as columns and subjects as rows.

3.3.2. Radio-iBAG Modeling Results.

Our model shows proper convergence and it is not sensitive to the choice of the hyperparameters based on the model checking results respectively described and shown in Supplementary file Section S4.2 and Section S7. After model fitting, the information about the prognostic radiogenomic features can be explored in the following sequence: RmFs that significantly influence the survival time, either positively or negatively, are selected using our criteria outlined in Section 2.3. For each selected RmF, the important RF groups comprising this RmF can be identified by evaluating the sPCA loading information as shown in Fig 2. To obtain significant genes and genomic platforms for the selected RmFs, we then trace back to the radiogenomic model and the genomics model, to identify which genes, if any, are associated with that RmF, and then which upstream platforms appear to be modulating the genomic effect. The specific results for each stage are described here.

Radiomic Results.

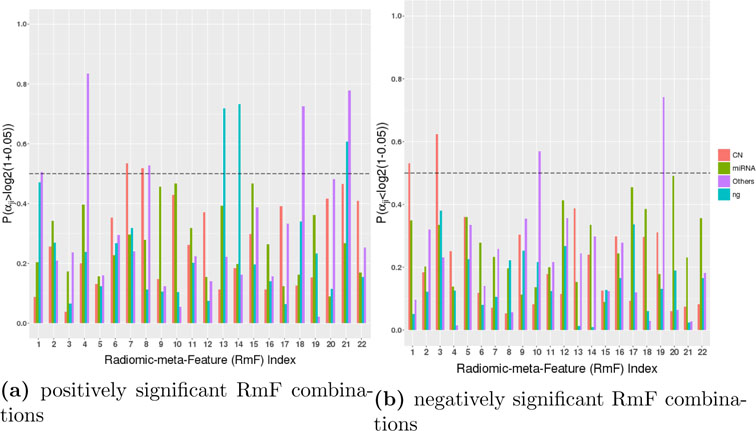
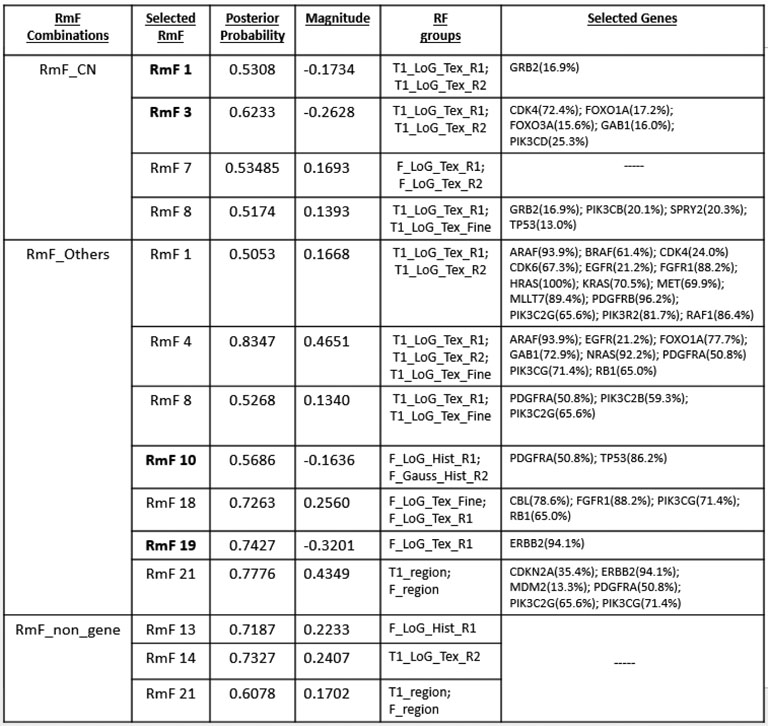
We use posterior probabilities to detect significant radiomic signals as well as genomic platform factors in both stage II and stage III based on the median probability criteria described in Section 2.3. Fig 4 shows the posterior probabilities used to select the positively and negatively significant clinical RmF combinations. The results show that more RmF are positively significant for the prognostic outcome, with 1 unit change leading to at least 5% increase in survival time (δ₂ = 0.05, the results using alternative thresholding δ₂ = 0.02 and δ₂ = 0.08 are shown in Supplementary File Section S4.3). Also negatively selected significant RmF combinations have the interpretation as 1 unit change leading to at least 5% decrease in survival time. From Fig 4(a) and Fig 4(b), we see that RmF 7 and RmF 8 have a positively significant influence on the survival time, with the parts that are modulated by genes through their copy number effects (G_CN). RmF 1 and RmF 3 are negatively associated with survival with the parts that are modulated by genes through their copy number effects (G_CN). RmF 1, RmF 4, RmF 8, RmF 18 and RmF 21 are positively related with survival via genemic effects not modulated by CN and miRNA. RmF 10 and RmF 19 are negatively associated with survival through genomic effects not modulated by miRNA nor CN. RmF 13, RmF 14 and RmF 21 are positively associated with survival apart from genetic modulated factors.

Fig 4:

Results of stage III (radiogenomic clinical model): Detecting postively and negatively significant RmF combinations. Each RmF is segmented into 4 parts, of which 3 parts are modulated by different genomic platform combinations denoted as ${\mathcal{I}}_{\mathit{C}\mathit{N}},{\mathcal{I}}_{\mathit{m}\mathit{i}\mathit{R}}$, and ${\mathcal{I}}_{\mathit{O}}$. The 4^th part is modulated by unknown/unmeasured factors represented as ${\mathcal{I}}_{\overline{\mathit{g}}}$ (“ng” in the legend). The barplot shows the posterior probabilities that the coefficient for each part ${\alpha }_{jk}>{\delta }_{+}^{*}$, where α_jk denotes the k^th RmF modulated by the j^th genomic platform. For each RmF, the probabilities of these 4 components, CN, miRNA, others, and ng, are respectively shown in red, green, purple and blue. Each probability in Fig (a) shows that 1 unit increment in the RmF component leads to at least 5% increase in survival time. Each probability in Fig (b) shows that 1 unit increment in the RmF component leads to at least 5% decrease in survival time. We consider the markers to be significant if this posterior probability is larger than 0.5.

To interpret the flagged RmFs, we turn to Fig 2 (as well as the Supplementary Material.xls file), which illustrates how much variance each RF group contributes to the corresponding RmF combinations. RmF 8 is found to be positively associated with survival through CN effects, and Fig 2 shows that RmF 8 is dominated by the the RF groups “T1_LoG_Tex_R1” and “T1_LoG_Tex_Fine”. RF names and their brief interpretations are shown in the table of Section S2.2 of the Supplementary Materials. In general, we see that texture features derived from T1-weighted post contrast images processed with R1 normalizing approach tend to be more significant, and based on the actual loading values (Supplementary Material Excel file), we found Haralick features to be important, including sum average and inverse difference moment. As another example, RmF 19 modulated by gene expression not explained by miRNA or CN changes (G_O) is detected to be negatively associated with survival, and for this RmF the dominant RF group is the Haralick features extracted from T2-weighted FLAIR images, especially with exact features named cluster shade, cluster prominence, energy and contrast. Additionally, RmF 21, which is found to be positively associated with survival both through genomic factors explained by“other” and the non-gene driven part. Further checking found that RmF 21 is associated with T1-weighted post contrast and T2- weighted FLAIR tumor areas. This indicates tumor area, as one of the major regional features, associated with the survival time and seemingly moderated by gene expression of signaling pathway genes, in part regulated by some genomic transcriptional factors other than CN or miRNA.

Radiomic Biological Significance.

In general, more radiomic features extracted from T1-weighted post contrast MRI images are selected to be clinically significant and most of them appear to be associated with genomic effects in signaling pathways. This is not unexpected given the fact that recent studies in literature showed that genomics are expected to be most related to T1-weighted post contrast images rather than T2-weighted FLAIR preprocessed ones. More specifically, RmF 14, which mostly captures the contrast margin of the enhancing MRI image, the magnitude and the loading information (included in Supplementary excel file), indicate that higher texture feature sum of average or lower texture feature sum of variance derived from the contrast of the edges leads to longer survival times. The detection of RmF 10 shows that histogram features, derived from T2-weighted FLAIR image pixel intensity and representing the global summary of the enhancement, are selected to be primarily affecting patients’ survival. It has been shown that the overall intensity is correlated with blood flow vasoconstriction. Moreover, we see associations with several key genes PDGFRA and TP53, with genomic transcriptional factors that affect the uniformity of the overall pixel intensity. In addition, RmF 21, with both genomic transcriptional factor driven part and non-gene driven part, are also selected to be significant in influencing patients’ survival time. Since the region feature, more specifically, tumor area, that captures most of the variation of RmF 21, our conclusion indicates that tumor area calculated from both T1-weighted post contrast and T2-weighted FLAIR images, are clinically important, larger area results in shorter survival times.

Genomic Results.

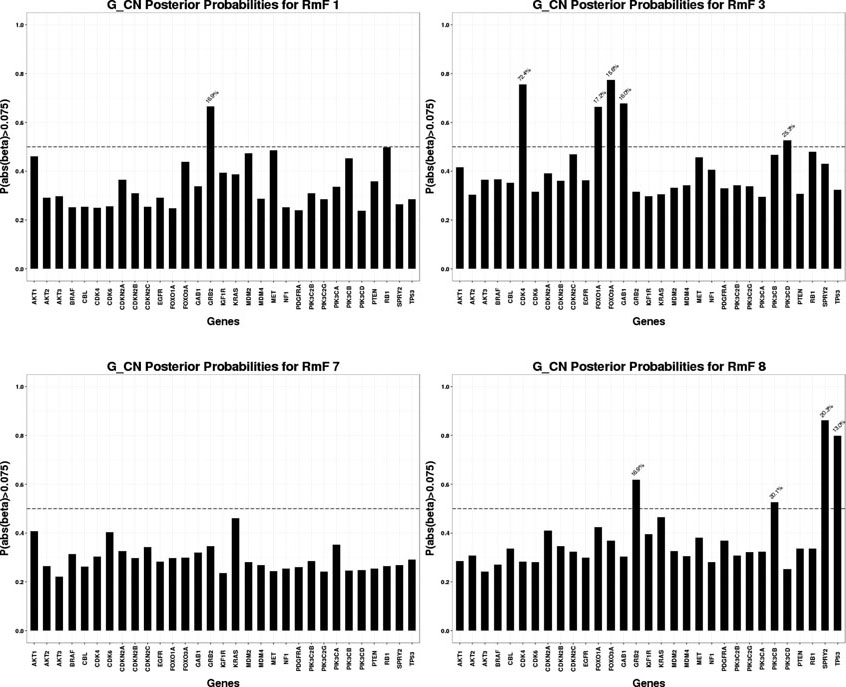
For the selected RmFs, we trace back to stage II and obtain the regulating genes that significantly affect the RmFs through specific genomic platforms (CN, miRNA or others), as shown in Fig 5, Fig 6 and Fig 7. To flag genes as associated wtih the RmFs, we compute the posterior probabilities of the magnitude exceeding a pre-specified threshold. For our analysis, we present the results with the setting δ₁ = 0.075 in this section since it gave us the best balance between the signal and sparsity (the results when setting the threshold δ₁ = 0.05, 0.075, 0.1 are shown in supplementary file Section S4.3). For the flagged genes, we traced back through the stage I model to acquire the percentage values (marked in blue) that represent the proportion of the mRNA variance that is explained by the corresponding genomic platform. For example, RmF 8 modulated by the CN combination is selected to be important, referring to the top left graph in Fig 5, genes GRB2, PIK3CB, SPRY2 and TP53 are selected as important, affecting RmF 8 through CN alteration. For gene SPRY2, 20.3% of its mRNA is explained by CN alteration. Also, genes PDGFRA and TP53 are selected as significantly influencing RmF 10 via other transcriptional factors. For TP53 in particular, the genomic factors (other than CN and miRNA) explains 86.2% of its mRNA variance.

Fig 5:

Significant genomic CN combinations

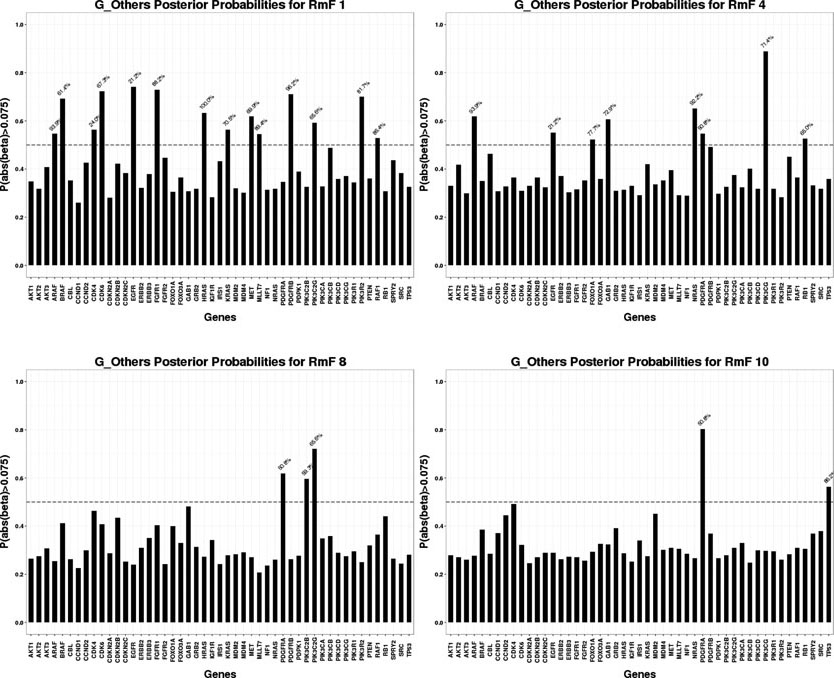
Fig 6:

Significant genomic mRNA “Other” combinations

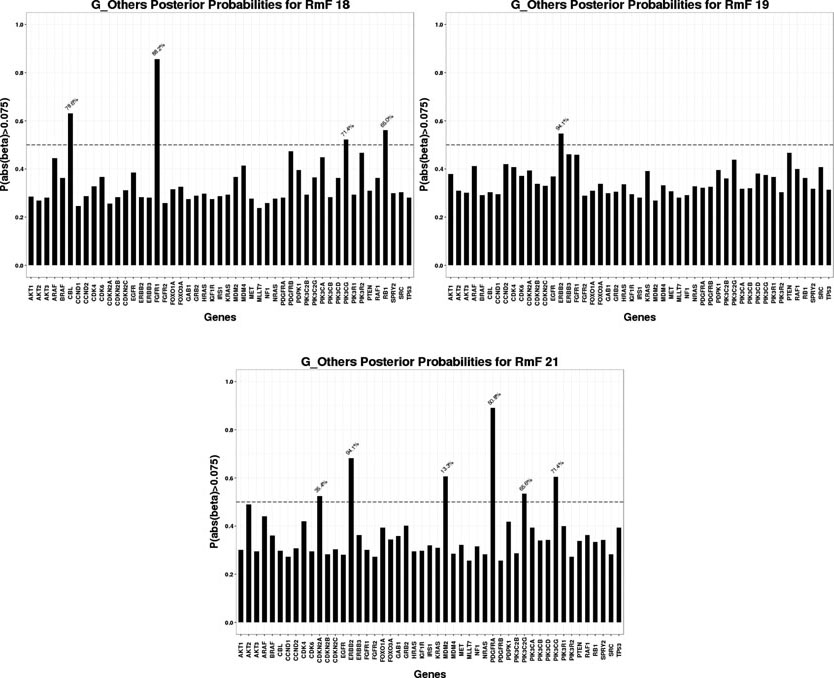
Fig 7:

Significant genomic mRNA “Other” combinations

For the results of stage I, after performing genomic modeling and filtering out the genomic platforms that did not explain much of the variance of gene expression (discussed earlier), there are 92 markers in the remaining gene-platform combinations (miRNA: 12; CN: 31; Others: 49) being carried into stage II, the radiogenomics model, as predictors. Fig 8 presents the overall genomic and radiomics results: RmF 7 and RmF 8, modulated by CN, are selected to be positively associated with survival time. Furthermore, 4 genes (GRB2, PIK3CB, SPRY2 and TP53), with their part of gene expression (mRNA) explained by CN alteration, are detected as being significantly associated with these RmFs. For the transcription modulated part, RmF 10 and RmF 19 are detected as being negatively important and associated with gene ERBB2, TP53 and PDGFRA; while RmF 21 is positively significant and associated with genes CDKN2A, ERBB2, MDM2, PDGFRA, PIK3C2G and PIK3CG. For the non-gene-driven factors, RmF 13, RmF 14 and RmF 21 are positively significant.

Fig 8: Results: Significant RmFs, genes and genomic platforms.

Four categories of RmF combinations are listed in the first column, where “non_gene” denotes “$\overline{g}$,” which is the non-gene-driven part of the RmF. For each category, several significant RmFs detected from the clinical model are listed in the second column, with unbolded indicating positive ones; bolded indicating negative ones. Posterior probability of the important radiomic markers is shown in column 3. For each selected RmF, several RF groups are selected based on RmF description heatmap (Fig 2). For each significant RmF combination, significant genes are listed with the percentage of how much the variance of mRNA is explained by the specific genomic platform.

Genomic Biological Significance.

Result table shows that gene EGFR is selected to be significant for multiple flagged RmFs. It agrees with the literature that the aberrations and gene expression of EGFR, with its full name as “epidermal growth factor receptor”, have been associated with the classical subtype of GBM among 4 major subtypes (proneural, classical, mesenchymal and neural), defined based on transcription data analysis [Verhaak et al. (2010)]. This particular subtype accounts for ~ 25%−30% of GBM cases. The amplification of the EGFR gene is the most common genomic change that leads to overexpression of the receptor variant III (EGFRvIII), and 20% or less EGFRvIII in GBM is significantly related to longer overall patient survival [Montano et al. (2011)]. Moreover, PDGFRA is another gene which has been flagged as important for multiple RmFs. It was found that for the proneural subtype, platelet-derived growth factor (PDGF) receptors (PDGFRAs) have been found to represent gene [Verhaak et al. (2010)]. Also, PDGFR has been positively correlated with patient survival time and its critical role in oncology has been well described in the context of gliomas [Nazarenko et al. (2012)]. Gene TP53 is selected to significantly influence RmF 8 via its mRNA explained by CN, and specifically, TP53 has been found to be the main hub gene that acts as tumor suppressor through comparative analyses of CN and mRNA expression in GBM tumor and xenografts Hodgson et al. (2009). The study illustrated that loss of TP53 function in GBM leads to transcriptional upregulation in gene expression network.

MDM2 is a commonly known oncogene that inhibits the tumor suppressor TP53; its overexpression and amplification have been studied through the analysis of CN alterations and gene expression profiles in previous studies [Yin et al. (2009)]. The gene CDKN2A, with other transcription factors accounting for its expression, has been found to be significantly associated with tumor area for both T1-weighted post contrast and T2-weighted FLAIR. CDKN2A belongs to the RB1 pathway, serves as a cyclin-dependent kinase inhibitor, and has been detected to be important [Solomon et al. (2008)]. It has been reported that loss of RB1 expression occurs in up to 25% of glioblastomas. Changes in RB1 expression have been associated with alterations in tumor cell proliferation and survival [Kim et al. (2011), Nakamura et al. (1997)]. Also, the assessment of RB1 promoter hypermethylation showed a clear correlation between the loss of RB1 expression and promoter hypermethylation [Nakamura et al. (2001)]. Analysis of GBM on the molecular level (TCGA data), using fluorescence in situ hybridization and immunohistochemistry, showed that alterations in RB1 occur more commonly in the proneural subtype of GBM.

4. Discussion and Conclusion.

This article presents the radio-iBAG model, a general framework for multi-scale integrative Bayesian analysis of radiogenomics data. Our hierarchical models incorporate biological mechanistic relationships among multiple genomic platforms, radiomic feature analysis and radiogenomic analysis with relevant clinical outcomes. There are three key features of this modeling strategy: (1) Multiple genomic platform profiles are incorporated in the radiogenomics framework; (2) For model fitting, high dimensionality with a pre-defined group structure in the covariates can be addressed through Bayesian shrinkage priors. In particular, we choose the normal gamma prior due to its flexibility in both shrinkage and parameter estimation; and finally (3) Investigating the relationship between clinical outcomes and radiomic features containing genomic information allows us to identify clinically significant genes, radiomic features and more importantly, the hidden associations between these two data modalities. We note that although our modeling strategy is motivated by an imaging genomics study in GBM, our methodology is general and can be applied to any other disease domain which generates quantitative imaging data with matched genomic data. This includes neurological diseases where the imaging features could be computed from structural or functional neuroimaging assays [Azadeh et al. (2016)].

We applied our methodology to the analysis of radiomic and genomic data sets of GBM. Our model analyzed the relationship between the survival times of patients and the RmFs modulated by various gene-platform combinations. Our analysis identified several RmFs that significantly impact survival times as well as identified the key radiomic features driving these factors. These results revealed that some of the most prognostically important radiomic features include tumor area, intensity histogram uniformity, and Haralick features derived from the GLCM, including energy contrast, inverse difference moment, and entropy for both T1-weighted post-contrast and T2-weighted flair images. Based on the results of modeling the relationship between RmFs and multi-platform genomic measurements, for each detected RmF, we subsequently identified which gene-platform combinations modulated that RmF. This allows us to detect prognostic RmFs modulated by upstream molecular platforms such as copy number, microRNA or other factors. Furthermore, we were able to identify which genes and platforms were driving these associations.

In summary, the advantages of applying integrative analysis of multiplatform genomic profiles in this framework are illustrated through the hierarchical back-tracking, which allows us to discover strong associations and interrelationships among the clinical, image, and genomic factors that may help elucidate the underlying biology. Most of the significant genes identified in our analysis have been shown to be biologically and clinically relevant to GBM molecular subclassifications, cancer development, or therapeutic strategies.

Several possible future extensions and generalizations could be explored based on our Radio-iBAG framework. For example, in our methodology, we applied a multi-stage modeling strategy in doing integrative analysis. A possible advancement may be using a joint model to capture all the relationships among different platforms simultaneously and maintain the detective power with interpretable results. One other possible direction may be incorporating pathway information as another hierarchy into the model structure or considering more complicated biological mechanisms at molecular level, e.g, hidden associations between a gene and other platforms of the neighboring genes, into the modeling framework, e.g. as considered in McGuffey et al. (2018). Another possible future extension may be involving histological images of different tumor tissue regions as another imaging modality into the study, which will provide more pathological based interpretable radiogenomic relationships along with relevant clinical outcomes. We leave these tasks for future work.

APPENDIX A: APPENDIX SECTION

A. Full conditi006Fnal posterior distribution.

The general posterior distribution of the coefficient parameter as well as other hyperparameters for the regression model either for the Radiogenomic Model or the Radiogenomic Clinical Model are shown below.

Consider the linear regression formula: $\mathit{Y}=X\mathit{\beta }+\mathit{ϵ}$.

In the radiogenomic model, Y denotes the specific RF, X is the matrix of the genomic platform combinations. In the radiogenomic clinical model, Y denotes the clinical outcome, X represents the RF combinations modulated by different gene expression parts explained by different genomic platforms. The full posterior distributions are

$$\begin{gathered} \mathit{\beta }|rest~Normal\left({\left(X^{T}X+{\sigma }^2{D}_{\tau }^{-1}\right)}^{-1}{X}^{T}Y,{\left(X^{T}X+{\sigma }^2{D}_{\tau }^{-1}\right)}^{-1}{\sigma }^2\right) \\ {\sigma }^2|result~IG\left(a+n/2,b+{(Y-X\beta )}^T(Y-X\beta )/2\right) \\ {\psi }_{ji}|rest~GIG\left(a={\gamma }_j^{-2},b={\beta }_{ji}^2,p={\lambda }_j-\frac{1}{2}\right) \\ {\lambda }_j|rest~{\left(1/{\lambda }_j\right)}^{\tilde{a}}exp\left\{-\tilde{b}{\gamma }_j^{-2}/\left(2{\lambda }_j\right)-c{\lambda }_j\right\}\times \prod _{i=1}^{p_j}{\psi }_{ji}^{{\lambda }_j}/\left\{{\left(\text{Γ}\left({\lambda }_j\right)\right)}^{p_j}{\left(2{\gamma }_j^2\right)}^{p_j{\lambda }_j}\right\} \\ {\gamma }_j^{-2}|rest~Gamma\left(\tilde{a}+p_j{\lambda }_j,\left(\tilde{b}/{\lambda }_j+\sum _{i=1}^{pj}{\psi }_{ji}\right)/2\right) \end{gathered}$$

If applying to the radiogenomic clinical model, j denotes the RF combination that are modulated by the gene expression that is explained by the j^th platform, and k represents the k^th RF; if applying to the radiogenomic model, j is the genomic platform type index, i is the gene index.

Specifically, λ_j is sampled through the Metropolis-Hastings method, the proposed family is $exp\left({\sigma }_{\lambda }^{2}z\right){\lambda }_j$, and z comes from the standard normal distribution. The acceptance rate is controlled between 20% and 30%.