Structure in personal networks: Constructing and comparing typologies

Abstract

A recurrent finding in personal network research is that individual and social outcomes are influenced not just by the kind of people one knows, but also by how those people are connected to each other: that is, by the structure of one’s personal network. The different ways in which a person’s social contacts know and interact with each other reflect broader variations in personal communities and social structures, and shape patterns and processes of social capital, support, and isolation. This article proposes a method to identify typologies of network structure in large collections of personal networks. The method is illustrated with an application to six datasets collected in widely different circumstances and using various survey instruments. Results are compared with those from another recently introduced method to extract structural typologies of egocentric networks. Findings show that personal network structure can be effectively summarized using just three measures describing results of the Girvan-Newman algorithm for cohesive subgroup detection. Structural typologies can then be extracted through cluster analysis on the three variables, using well-known clustering quality statistics to select the optimal typology. Both typology detection methods considered in the article capture significant variation in personal network structures, but substantial levels of disagreement and cross-classification emerge between them. I discuss differences and similarities between the methods, and potential applications of the proposed typologies to substantive research on a variety of topics, including structures and transformations of personal communities, social support, and social capital.

1. Introduction

Personal networks heavily shape individual and social life in a wide range of domains, including socioeconomic mobility, political engagement, individual identity, and physical and mental health (Crossley et al., 2015; Perry, Borgatti, & Pescosolido, 2018; McCarty, Lubbers, Vacca, & Molina, 2019). A central insight in personal network research is that individual and social outcomes are influenced not just by the kind of people one knows (the composition of a personal network), but also by how those people are connected to each other: the structure of a personal network. Personal network structure refers to the distribution of social ties among the personal contacts (alters) of a focal individual (ego), and to characteristics of this distribution such as density and fragmentation, transitivity and clustering, cohesive subgroups, centrality and centralization.¹

This article is a study of personal network structure based on six datasets collected in widely different circumstances. It has four aims. First, it introduces a relatively simple method to summarize the overall structural configuration of a personal network with three measures, and to inductively extract typologies of ego-network structures based on this summarization. This method is applied to the different datasets considered in the article. Second, I examine a different, recently proposed method to detect ego-network structural typologies (Bidart, Degenne, & Grossetti, 2018), and test it on the same datasets. Third, results from the two methods are compared, highlighting differences and similarities. Fourth, the article discusses the utility and significance of the proposed method for substantive and theoretical research on a variety of topics, including variations in personal communities and broader social structures in contemporary societies, the configuration of foci of human activity in different contexts, and the antecedents and consequences of social support, social capital and social isolation. When applied to research on these subjects, the ego-network structural typologies presented here can help explain and predict outcomes such as individual health and well-being, socioeconomic mobility, and immigrant incorporation.

The article begins with an introduction on the notion of ego-network typology (section 1.1), the significance of structure in personal networks (section 1.2), and existing attempts to identify types of ego-network structure (section 2). Section 3 presents the data and methods of analysis. Findings from the application and comparison of different typology detection methods are reported in section 4. The last two sections discuss the findings and conclude the article.

1.1. Identifying personal network typologies

Classifying egocentric networks into types or profiles has been a recurrent aim since the onset of personal network research in the 1950s (Barnes, 1954; Bott, 1957). In most applications, typology detection is based on compositional variables describing characteristics of alters and ego-alter relationships, rather than structural characteristics of tie distribution among alters. One of the most recent and insightful examples of these efforts is a study by Giannella and Fischer (2016), who analyze 1977–1978 data on residents in the area of San Francisco, California, and use a machine-learning algorithm to classify over 1,000 ego-networks into eleven types. This typology is based on dozens of compositional variables measuring counts and proportions of alters in different relationship-based and activity-based roles, types of social support, and social contexts.

Several other studies demonstrate a growing interest for typologies in personal network literature. Agneessens and colleagues (2006), for example, propose a typology of support networks based on which alter roles (partner, immediate kin, friends, etc.) provide which types of support (instrumental, emotional, companionship, etc.) to ego. Analyzing personal networks of immigrants in Europe, Lubbers et al. (2007) extract network types that incorporate both compositional and structural variables, describing profiles such as “dense family networks”, “multiple subgroups networks”, and “two worlds connected networks”. Brandes and collaborators (2010) use the same data to detect immigrant network types characterized by different sizes of, and levels of cohesion between, national and geographical classes of alters. Vacca et al. (2018) obtain types of immigrant personal networks that reveal different degrees of embeddedness into sending and receiving societies. Bidart and colleagues (2018) present the first study of ego-network typologies that is exclusively based on structural variables. Their contribution is examined in detail throughout this article.

Typologies of personal networks are appealing for several reasons, some of which are well illustrated by Giannella and Fischer (2016). First, they summarize the data by reducing the variation among hundreds or thousands of individuals in a high-dimensional space, to a variation among few types characterized by few, interpretable combinations of values in the original dimensions (i.e., the original variables). Second, typologies reveal the underlying data structure in a collection of ego-networks by identifying types, showing the distribution of types in the data, and highlighting both representative, recurrent types, and outlier types that exhibit rare characteristics. Third, typologies provide a tool for easier comparisons between different populations. The distribution of types in various datasets reveals commonalities and differences between personal networks collected in different countries, social groups, time periods, age cohorts, and so forth.

Fourth, typologies uncover patterns of association among network characteristics, which reveal central, underlying dimensions of variation among personal networks, similar to factors or components in factor analysis. While typical ego-network data allow analysts to calculate dozens of measures on many different aspects of ego’s social world, these features can often be reduced to fewer sets of correlated variables. A high number of family members in the network, for example, may consistently be associated with high network density; a low number of friends who live in the same city as ego may be associated with low counts of alters who provide support with practical, everyday problems. Rather than treating the original variables separately, a study of “packages” of correlated network characteristics (Giannella & Fischer, 2016) may yield a deeper understanding of the essential dimensions of variation in a population (Wellman & Potter, 1999). Network types emerge precisely as clusters of cases with common patterns in these “packages” of variables, allowing researchers to better “capture the holistic nature of networks” (Perry et al., 2018, p. 298).

1.2. Structure in personal networks

Personal network structure has been linked to a host of social mechanisms and outcomes in research on various topics, including social capital, social support, socioeconomic mobility, health, and immigrant incorporation. Different ego-network structures are the source of different types of social capital, generating different types of benefits and constraints for the ego. Fragmented personal networks, rich in structural holes, weak ties and links to separate social circles, are a source of bridging social capital: they facilitate exposure to diverse information, autonomy from external constraints, and control of resources on the part of the ego. This is associated with positive outcomes in such diverse domains as job search (Granovetter, 1973), career advancement (Burt, 1992), innovation (Ahuja, 2000), and health (Cornwell, 2009). On the other hand, cohesive personal networks, in which the ego is deeply embedded in tightly-knit, highly connected groups, generate closure or bonding social capital: they promote shared norms, informal controls, mutual trust and reciprocal obligations, resulting in higher levels of cooperation and support within more homogenous groups (Coleman, 1988). Yet tightly-knit personal networks can also be a source of excessive constraints on individual freedom, social control and stifling pressure to conform to norms (Portes & Sensenbrenner, 1993; Collins, 1988, p. 416), aspects of what has been called “negative social capital” (Portes, 1998).

In the social support research tradition, personal network structure has been found to influence the quantity and quality of social support, with density of ties (Haines, Hurlbert, & Beggs, 1996), alter degree centrality (Wellman & Frank, 2001), and cliquishness (Martí, Bolíbar, & Lozares, 2017) leading to higher levels of support in different domains. Structural measures of cohesion among personal network alters have also been linked to different patterns of ethnic identification and immigrant assimilation in migration studies (Lubbers et al., 2007; Vacca et al., 2018).

In one of the first studies to extensively analyze multiple structural features in ego-networks, McCarty (2002) demonstrates that measures traditionally used for sociocentric data, such as centralization, the number of components, and the number of cliques, capture meaningful aspects of structural variation in personal communities as well. In particular, McCarty’s study shows that cohesive subgroups of alters, as inductively detected from the data, correspond to different social contexts or circles that respondents (i.e., egos) are able to recognize and label, such as immediate family, in-law relatives, school friends, voluntary associations, and so forth. This suggests that cohesive subgroups of alters can be used to operationalize the central sociological notion of social context (Entwisle, Faust, Rindfuss, & Kaneda, 2007; Mollenhorst, Volker, & Flap, 2014) or interaction focus (Feld, 1981) in personal communities. The cohesive subgroup structure of a personal network is the main focus of the typology detection method proposed in the present study.

2. Toward a typology of personal network structures

Bidart, Degenne and Grossetti (2018) (hereafter BDG) recently made the first attempt to construct a typology of personal networks exclusively based on structural measures describing patterns of alter-alter ties. They analyzed 287 egocentric networks from four waves of a longitudinal survey conducted among 17- to 24-years-old students in Caen, France (1995–2004). Their typology detection method starts with “a visual recognition [of the networks] to establish an initial classification” (Bidart et al., 2018, p. 5). This qualitative inspection leads the authors to identify six structural types. In the second step, a typical or most representative ego-network is qualitatively selected for each type. Moving from this result, the goal is to assign all other networks to one of the six pre-defined types. In the third step, six network-level structural measures are derived, which are believed to best discriminate between the six types. In the final step, a discriminant analysis is conducted which, based on the six typical networks (step 2) and the six structural measures (step 3), calculates a discriminant function to assign each ego-network to a type.²

BDG’s study is the first to demonstrate that typologies of ego-network structure can be identified in real-world data and have substantive significance in applied research. The authors show that most ego-networks in their data can be assigned to a structural type, and that ego’s educational level and residential status are significantly associated with different types of ego-network structure. BDG conclude by encouraging the replication of their method to other datasets, which is one of the goals of the present study.

However, a major challenge in replicating the BDG method, and in scaling it up to more and larger datasets, lies in its first two steps: the preliminary definition of structural types and identification of representative cases based on a qualitative, visual inspection of personal network graphs. These steps are likely to be very costly, if not unfeasible, when one has to analyze many datasets or larger samples including several hundreds or thousands of networks. Furthermore, particularly with larger datasets, different analysts might derive different types and representative cases from qualitative inspection of the same networks. Validation of the identified types by multiple researchers, similar to multiple coding in qualitative text analysis, could be too costly with larger data. Therefore, to make the BDG method applicable to the datasets considered here, this study replaces discriminant analysis with a cluster analysis technique that lets the types entirely emerge from the data (see section 3.2).

A second challenge that may be encountered in the replication of the BDG method has to do with cohesive subgroups. While the six structural variables used by BDG describe important aspects of personal network structure, they do not seem to adequately capture differences between networks in terms of cohesive subgroups of alters. Variation between subgroup structures with a core-periphery pattern vis-à-vis factional structures with multiple subgroups, for example, is not effectively represented by the BDG types. By contrast, the method presented in this study constructs typologies on the basis of subgroup structure descriptors. Cohesive subgroups represent a central aspect of personal network structure for theoretical, empirical, and practical considerations. First, ego-network cohesive subgroups are essential to capture the theoretical notions of social context and interaction focus, which are consistently evoked in much personal network research (this is further discussed in section 5). Second, empirically, this study shows that the number and distribution of subgroups are a major dimension of differentiation among real-world ego-networks. Third, I find that just three measures of cohesive subgroup characteristics, when taken together, yield a parsimonious yet comprehensive description of the overall structural configuration of a personal network: a description that often reveals additional characteristics of network structure, such as centralization, diameter, and transitivity.

In this article, ego-network subgroup structure is quantified by summarizing results from community-detection algorithms (Fortunato, 2010). The three summary measures employed are relatively straightforward and easy to obtain in most network analysis software, resulting in a simple, accessible, and easily replicable method. However, subgroup structure and clustering in social networks can also be analyzed with other, possibly more sophisticated techniques. Stochastic blockmodels (Nowicki & Snijders, 2001) and latent position cluster models (Handcock, Raftery, & Tantrum, 2007), for example, provide an approach to subgroup identification based on statistical inference and modeling. Exponential Random Graph Models (Lusher, Koskinen, & Robins, 2012) offer a model-based way to precisely quantify the tendency to transitivity and clustering in a network. These methods might be preferable for in-depth analysis of one or few networks, which is typical of sociocentric designs. However, their application can be challenging or simply not feasible for large egocentric datasets, since in this case it would require conducting model estimation, goodness-of-fit evaluation, and model selection separately on each of hundreds or thousands of networks.

3. Data and methods

3.1. The six datasets

This article analyzes six personal network datasets obtained with face-to-face or Internet surveys, and collected in different countries, using various survey instruments, and as part of projects with diverse substantive foci (Table 1). The goal is to explore the applicability and replicability of the same methods to very different data. The first dataset (referred to as MBC) includes personal networks of African, Asian, and Latin American immigrants in Milan, Italy, and Barcelona, Spain. The second dataset (FRA hereafter) resulted from a personal network survey conducted in a population of oystermen in Gulf of Mexico coastal areas in Franklin county, Florida. A survey among residents of villages on the Tungurahua volcano in Ecuador produced the third dataset (ECU). The fourth dataset (PAR) comprises personal networks of Romanian Roma immigrants in Paris and other large metropolitan areas in France. The fifth dataset (TAL) was collected among residents of African American neighborhoods in Tallahassee, Florida, with high levels of residential segregation. Finally, a recent survey of a larger, representative sample of residents in the San Francisco Bay area, California, generated the sixth dataset (SFB). Table 1 reports the main characteristics of the six datasets and their respective surveys, including the questions used to elicit alters (name generators) and collect information on ties among alters (edge interpreters). The appendix provides more details about the data and the studies in which they were collected.

Table 1.

Details on the six datasets analyzed in the article. “N egos” is the number of respondents with valid personal network data included in the analysis. ¹ The survey asked edge interpreters only for 25 randomly sampled alters out of the 45 named by ego. For all respondents, the same 25 randomly extracted numbers where used to select the alters. ² Variation in number of alters per ego in the [10, 25] range was simulated by extracting random integers with preassigned probabilities (see appendix). ³ Variation in number of alters per ego in the [5, 20] range was simulated by extracting random integers with preassigned probabilities (see appendix). ⁴ See appendix for details on the name generators. ⁵ See appendix for details on the selection of alters for tie questions.

ID	Survey location (Year)	Study focus	Name generators	Edge interpreter (Response categories)	N egos		N alters per ego	N alters with tie data
MBC	Milan, Italy (2012), and Barcelona, Spain (2004–2006)	Migration	Please list the names of 45 persons whom you know and who know you, with whom you have had some contact in the past two years (face-to-face, by phone, or by the Internet), and whom you could still contact if you needed to.	How likely is it that [Alter 1] and [Alter 2] contact, meet or talk to each other independently of you? (Certainly, Maybe, Certainly not)	385		45	45
FRA	Franklin county, Florida, USA (2012)	Disasters	Please list 30 people you know outside of your own household. This includes people living anywhere in the world you know by sight or name. You must have had some contact with them in the last 2 years, and be able to contact them. Make sure you start with people you might rely on following a disaster that causes damage, such as a hurricane, or an economic disaster such as the oil spill.	What is the likelihood that [Alter 1] and [Alter 2] talk to each other independently of you? In other words, do they have a relationship independently of you? (Not at all likely, Maybe, Very likely)	293		30	30
ECU	Tungurahua and Chimborazo provinces, Ecuador (2009)	Disasters	Please name 45 people - whoever they are and wherever they are from - whom you know by name or by sight, and with whom you have had contact (or could have had contact if you needed to) in the past two years.	Do [Alter 1] and [Alter 2] have contacts with each other a lot, a little, or not at all? (Not at all, A little, A lot)	264		45	25 1
PAR	Paris and other metropolitan areas, France (2014–2015)	Migration	Please list 30 contacts, family members, friends or acquaintances, with whom you had some contact in the past two years and on whom you can rely.	Do [Alter 1] and [Alter 2] know each other? By “know each other” we mean that they might meet or talk to each other even if you are not there. (Certainly, Maybe, Certainly not)		119	30	10–25 2
TAL	Tallahassee, Florida, USA (2011)	Health, racial disparities	Name 30 people that you know and that know you, either by sight or by name, whom you could contact today if you needed to.	How likely is it that [Alter 1] and [Alter 2] speak to each other when you are not around? (Not at all likely, Not very likely, Somewhat likely, Likely, Very likely)		254	30	5–20 3
SFB	San Francisco Bay Area, USA (2015–2016)	Health, life course	Six name generators on different spheres of social activity 4	Do [Alter 1] and [Alter 2] know each other well, know each other a little (say, by first name), or do not know each other at all? (Well, A little, Do not know each other)		366	1–30	5 5

3.2. Overview of methods

I refer to the typology extraction method introduced by this article as subgroup-based method, and to the resulting ego-network typology as T₁. The method based on Bidart and colleagues’ (2018) work is called BDG method hereafter, and the resulting typology is indicated as T₂. Table 2 provides a summary list of the steps involved in the subgroup-based method (first column) and in the BDG method as originally described by Bidart and colleagues (second column) and as modified for this study (third column).

Table 2.

Summary of the typology extraction methods considered in the article.

	Subgroup-based method (T1)	BDG method	Modified BDG method (T2)
I. Description of ego-networks
	1. Apply GN community detection algorithm to each ego-network. ►Obtained partition of each ego-network’s nodes into cohesive subgroups.	1. Qualitatively identify main types in ego-network visualizations. ►6 types identified: regular dense, centered dense, centered start, segmented, pearl collar, dispersed.	1. Calculate 6 BDG measures on each ego-network: network density, betweenness centralization, modularity of Louvain subgroup partition, number of components, relative size of the main component, network diameter.
	2. Calculate 3 summary measures on GN partition of each ego-network: count of subgroups with 3 or more nodes; count of subgroups with 1 or 2 nodes; modularity of partition.	2. Qualitatively select one representative ego-network for each of the 6 types.
		3. Identify structural measures that best discriminate between types. ►6 measures identified: network density, betweenness centralization, modularity of Louvain subgroup partition, number of components, relative size of the main component, network diameter.
		4. Calculate 6 measures from Step 3 on each ego-network.
II. Extraction of typology
	3. Conduct k-medoid cluster analysis on the 3 summary measures obtained in Step 2, with k ranging from 2 to 20.	5. Conduct discriminant analysis based on ego-networks selected in Step 2 and measures calculated in step 4. ►6 assignment probabilities (one for each type) obtained for each ego-network in the data.	2. Conduct k-medoid cluster analysis on the 6 BDG measures obtained in Step 1, with k ranging from 2 to 20.
	4. Select optimal clustering partition (typology) by selecting k* based on AIC (inflection point) and silhouette (local maximum).		3. Select optimal clustering partition (typology) by selecting k* based on AIC (inflection point) and silhouette (local maximum).
III. Assignment of ego-networks to types
	5. In optimal clustering partition, each ego-network is assigned to a type (i.e., a k-medoid cluster).	6. Assign ego-network to type for which it has highest assignment probability. Ego-networks with equal probability on multiple types are assigned qualitatively or not assigned to any type.	4. In optimal clustering partition, each ego-network is assigned to a type (i.e., a k-medoid cluster).

The subgroup-based method proceeds in three main steps:

1. Subgroup identification. The Girvan-Newman (GN) algorithm for subgroup detection is applied to each personal network in the data. For each network, the algorithm returns a partition of its alters into cohesive subgroups.

2. Summarization of subgroup structure. For each network, the results of the GN algorithm are summarized using three variables: the number of detected subgroups with at least 3 nodes; the number of detected subgroups of one or two nodes; the modularity of the partition. These are referred to as subgroup variables or T₁ variables throughout the rest of the article.

3. Typology detection. K-medoid cluster analysis is conducted on the three GN subgroup variables to identify clusters of structurally similar personal networks. The optimal kmedoid clustering partition is selected using the silhouette statistic and the Akaike Information Criterion (AIC). This optimal partition is the T₁ typology: clusters of personal networks in the partition are interpreted as structural types by examining the distribution of the three subgroup variables in each cluster.

In the BDG method, typologies are detected by conducting k-medoid cluster analysis on the six BDG structural variables: network density; betweenness centralization; modularity of the subgroup partition returned by the Louvain algorithm; number of components (including isolates); relative size of the main component; network diameter. The optimal clustering partition is again selected based on silhouette and AIC, and interpreted as the T₂ typology of personal networks. The following sections provide more details about the measures used to describe egonetwork subgroup structure, the k-medoid cluster analysis, and the way T₁ and T₂ typologies are compared.

3.3. Identifying cohesive subgroups and summarizing subgroup structure

Intuitively, a cohesive subgroup is a set of network nodes that exhibit high connectedness to each other (internal cohesion), but low connectedness to the rest of the network (external separation; Wasserman & Faust, 1994, p. 249ff). One of the most popular notions in the literature on social networks, cohesive subgroups (also called clusters, communities, blocks, etc.) have been operationalized with different methods in different disciplinary traditions. Some of the most effective techniques to identify them have originated in the literature on “community detection algorithms”, one of the fastest-growing areas of research in network science (Fortunato & Hric, 2016; Dao, Bothorel, & Lenca, 2018).³

Modularity (of the GN subgroup partition) is the first summary measure I use to describe the subgroup structure of a personal network. This is a well-established measure of fit or quality of a subgroup partition in a network (Newman & Girvan, 2004), and algorithms that identify network subgroups by maximizing modularity constitute one of the most popular class of community-detection methods (Fortunato & Hric, 2016). Mostly developed in computer science and physics, modularity-optimization algorithms have been successfully applied in social science research as well (e.g., Shwed & Bearman, 2010; Wang & Soule, 2016; Vacca et al., 2018).

Given a partition of nodes into subgroups, modularity is a measure of the extent to which the network has many edges within subgroups, and only few edges between them: in other words, it is a measures of the degree to which a subgroup partition fits the network structure, entailing high internal cohesion within subgroups and external separation between them. Although modularity maximization in the space of all possible subgroup partitions for a given network is an NP-hard problem (Brandes et al., 2008), different heuristic methods have been proposed to find partitions with high values of modularity. The Girvan-Newman algorithm (Newman & Girvan, 2004) and the Louvain algorithm (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008) are two popular such methods. The modularity of the GN subgroup partition is used in the typology detection method presented here, whereas the modularity of the Louvain partition is used in the BDG method.

The count of subgroups with one or two nodes and the count of subgroups with three or more nodes (in the GN subgroup partition) are the other two summary measures used to describe personal network structure in this article. When applying the Girvan-Newman algorithm to the six datasets, a common pattern emerged which is crucial for the method presented here. Alters that are sparsely connected (but not necessarily isolates) tended to be assigned to singleton clusters or to clusters of only two nodes in the GN partitions. These are called singletons and dyads in this article, while the term “subgroup” is reserved for cohesive subgroups of at least three nodes.⁴ Singletons and dyads in the GN partition are markers of low-cohesion areas, in which alters are only loosely connected with (or entirely disconnected from) the rest of the network. On the other hand, GN subgroups of at least 3 nodes reveal high-cohesion areas in which alters are highly connected to each other.⁵ Thus, the count of GN singletons and dyads can be used as a measure of the number of alters who are only sparsely connected to each other and to the rest of the network. On the other hand, the number of GN subgroups captures the extent to which multiple, relatively large, cohesive and separate groups exist in an ego-network. Personal networks in which only one GN subgroup is found exhibit a single cohesive set of nodes that cannot be split into separate groups. These are likely to be variations of core-periphery structures (Borgatti & Everett, 2000). By contrast, a high number of subgroups in the GN partition suggests that multiple, separate yet internally cohesive “factions” of alters exist in the personal network structure.

3.4. Detecting typologies: K-medoid cluster analysis

K-medoid cluster analysis (Kaufman & Rousseeuw, 1990) divides observations (here, personal networks) into k clusters (here, structural types) such that (1) each cluster has one representative observation in the data, called medoid; and (2) the average dissimilarity between each observation and the medoid of its respective cluster is minimized. In my application the k types are clusters of ego-networks that tend to be more similar (in terms of the three subgroup variables) to the medoid of their respective type than to any other medoid of any other type.⁶

The number k of clusters to be identified is an input in the k-medoid procedure. In the following analysis the procedure was replicated varying k in the 2–20 range, and the optimal number of clusters k* was selected based on two measures of quality of a clustering partition: silhouette and the Akaike Information Criterion (AIC). Silhouette is an overall measure of how well a clustering partition fits the data (Kaufman & Rousseeuw, 1990). Intuitively, it is high if observations have low average dissimilarities from other observations in their own cluster, and high average dissimilarities from observations in other clusters; and it is low if many observations are in boundary areas between clusters, with high average dissimilarities from cases in their own cluster and low average dissimilarities from cases in other clusters.

The AIC is a penalized statistic of model fit that increases with the model’s residual deviance and the model’s number of parameters (Fox, 2008). If k-medoid clustering is regarded as an Expectation-Maximization (EM) algorithm, the AIC statistic can be used to measure the fit of different clustering partitions, with lower AIC values indicating better clustering quality. This extension of the AIC to cluster analysis has been recently used in other social network studies (Dunbar, Arnaboldi, Conti, & Passarella, 2015; Arnaboldi, Passarella, Conti, & Dunbar, 2017). The AIC decreases when the clustering partition has a lower total within-cluster sum of squares (a measure of residual deviance for the clustering) and a lower number of clusters k (a measure of number of parameters for the clustering).⁷ In cluster analysis applications, the curve of the AIC as a function of k often shows an initially steeply decreasing pattern, followed by an “elbow” or inflection point after which the curve flattens out, while still decreasing. To identify a low but meaningful number of clusters (types), it is more sensible to select k*as the AIC inflection value, rather than the (higher) global minimum value. This is the case because the inflection value k* is such that a number of clusters lower than k* implies a much poorer clustering quality (much higher AIC), while a number higher than k* determines negligible quality improvements (AIC reductions) compared to the first part of the curve, while implying more clusters (i.e., poorer and less meaningful summarization of the data).

The optimal number of types in the 2–20 range is selected as the value k* that both maximizes the silhouette (at least locally), suggesting that ego-networks are on average very similar within types and dissimilar between types; and is an inflection point for the AIC, indicating that a higher number of types, while making the typology less effective at summarizing ego-network structural variation, does not entail a substantial AIC reduction. Once the optimal clustering partition is determined, I interpret the clusters as structural types by examining boxplots and comparing average z-scores of the subgroup or BDG variables within each cluster. These interpretations can be validated by ex-post inspection of the ego-network visualizations, starting from those that the cluster analysis has identified as the medoids (representative cases) of each type.

3.5. Comparing different typologies

A major goal of this study is to compare T₁ and T₂ on the same datasets. The two typologies are simply two hard clustering partitions of the same ego-networks, therefore they can be compared using standard measures of similarity or agreement between partitions. Three wellknown measures are used in the following analyses: the Jaccard index, the Rand index, and the Adjusted Rand index. The Jaccard index (Jaccard, 1901) is defined as

$$J\left(T_1,T_2\right)=\frac{a_{11}}{a_{11}+a_{10}+a_{01}}$$

where a₁₁ is the number of pairs of ego-networks assigned to the same type in both typologies, and a₁₀ (a₁₁) is the number of ego-network pairs assigned to the same type in T₁ (T₂) but not in T₁ (T₂). Thus, J(T₁, T₂) is the number of ego-network pairs on whose similarity both typologies agree, divided by the number of ego-network pairs that either typology considers similar.

The Rand index (Rand, 1971) is defined as

$$R\left(T_1,T_2\right)=\frac{a_{11}+a_{00}}{a_{11}+a_{10}+a_{01}+a_{00}}$$

where the additional symbol, a₀₀, is the number of ego-network pairs that both typologies assign to different types. R(T₁, T₂) is the number of ego-network pairs on whose structural similarity or dissimilarity the two typologies agree (a₁₁ + a₀₀), divided by the total number of ego-network pairs in the data. The raw Rand index is often inflated by the high number of pairs that both partitions assign to different types (a₀₀). The Adjusted Rand index $\left(\widehat{R}\right)$ addresses this problem by measuring how different the observed Rand index is from the baseline Rand index that would be obtained if observations were randomly assigned to types in the two typologies (Hubert & Arabie, 1985).⁸

Since the Jaccard index is a general measure of similarity between two sets, it can also be used to measure the similarity between two types in different typologies, that is, the degree to which two types in two different classifications are in fact identifying the same personal networks. Considering type t₁ (from typology T₁) and type t₂ (from typology T₂) as two sets of personal networks (and indicating the cardinality of set A as |A|), their Jaccard similarity is the following:

$$J\left(t_1,t_2\right)=\frac{\left|t_1\bigcap t_2\right|}{\left|t_1\bigcup t_2\right|}$$

That is, the number of personal networks in both types (set intersection) as a proportion of the number of all personal networks in either type (set union). This application of the Jaccard index is used here to examine similarities and differences between structural types detected by different typology extraction methods.

4. Results

This section begins by examining the joint distributions of structural variables in the data, and what these variables reveal about the overall structural configuration of personal networks. It then presents the different typologies resulting from the subgroup variables (T₁) and the BDG variables (T₂). Finally, the two sets of typologies are compared, evaluating similarities and differences in the six datasets.

4.1. Interpreting the T₁ and T₂ structural variables

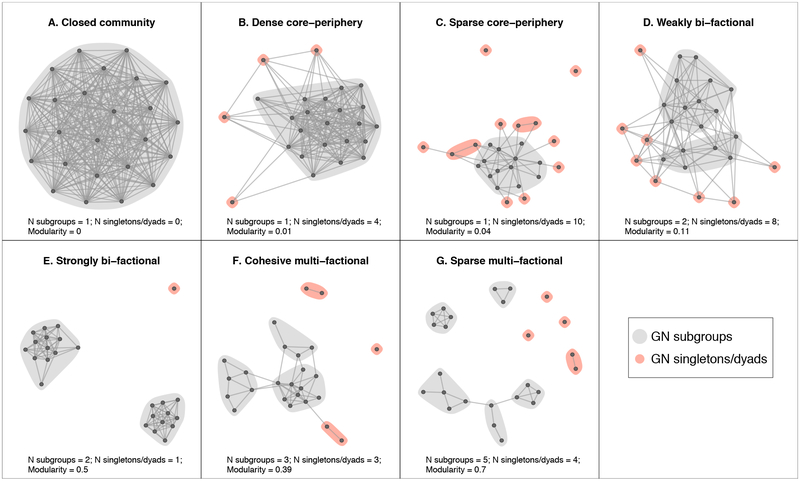
Figure 1 shows an example ego-network from each of the seven types identified by the subgroup-based method (T₁) in the ECU dataset, indicating the values of the three subgroup variables for each case. Figure 2 visualizes the joint distribution of the three T₁ variables in the ECU personal networks (Supplementary Information Figure S2 shows correlations between the variables in all datasets). The figures illustrate how the count of GN subgroups in a personal network (count of grey polygons in Figure 1, x axis in Figure 2) discriminates between more cohesive structures with central and dense cores (low count of subgroups, panels A-C in Figure 1 and left part of Figure 2); and sparser, more factional structures including multiple and separate cohesive areas (high count of subgroups, panels F-G in Figure 1 and right part of Figure 2). At the same time, the singletons and dyads in the GN partition (red polygons in Figure 1, y axis in Figure 2) reveal structural peripheries of alters that are loosely linked with, or entirely disconnected from, the rest of the network.

Fig. 1.

Representative personal networks from each of the seven types of the subgroup-based typology (T₁) in the ECU dataset.

Fig. 2.

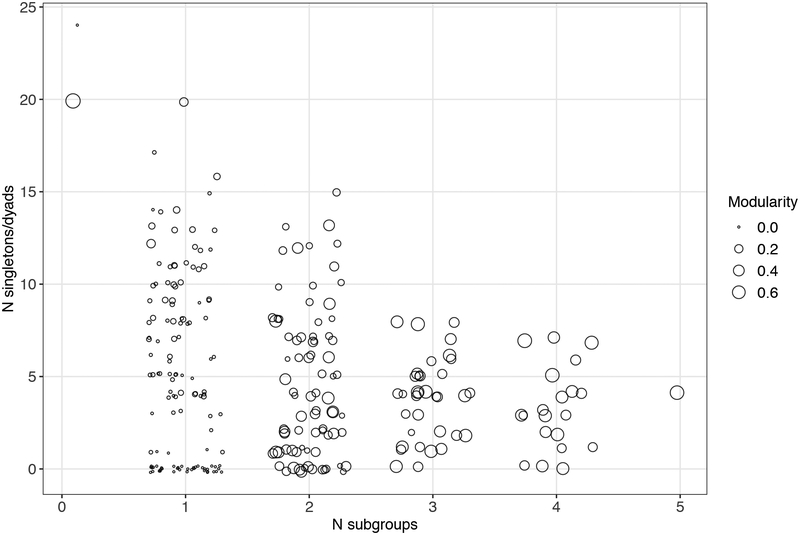
Joint distribution of the three T₁ variables in the ECU dataset. Each point is a personal network. Points are slightly jittered to reduce overplotting.

The three T₁ variables show similar patterns of association across the datasets (with the exception of the small ego-networks in SFB): higher, positive correlations between the count of subgroups and modularity; and low, slightly negative correlations between the count of subgroups and the count of singletons/dyads. A lower count of subgroups (one or two) tends to be associated with low modularity values in more tightly-knit ego-networks with higher overall cohesion (panels A-D in Figure 1). By contrast, higher modularity tends to reflect a higher number of subgroups in the network, as well as higher levels of within-subgroup cohesion and between-subgroup separation (panels E-G in Figure 1). These association patterns confirm that modularity can be interpreted as an index of the extent to which an ego-network exhibits a clearcut subgroup structure with multiple, internally cohesive and externally separate clusters (networks more similar to Figure 1E–G); rather than a core-centered, dense structure, or one with low internal cohesion and external separation between subgroups (networks closer to Figure 1A–D). With few exceptions, the generally negligible correlations between the three T₁ variables suggest that these measures tend to capture different, non-redundant aspects of personal network structure.

The BDG variables also exhibit similar correlation patterns in all the datasets (with the SFB data again often being an exception, see Supplementary Information Figure S2). Density is highly correlated with all other five BDG variables, showing highly negative correlations with betweenness centralization, Louvain modularity, the number of components, and diameter; and strongly positive correlations with the relative size of the main component. High correlation values also emerge among betweenness centralization, Louvain modularity, and diameter (positively correlated in all datasets); and between the number of components and the size of the main component (always strongly and negatively correlated). These correlations suggest that some of the six BDG variables capture the same type of information about ego-network structure. In particular, density seems to be redundant once the other five variables are included. The number of components and the relative size of the main component also gauge approximately the same structural features in the six datasets. Particularly in some of the datasets, diameter might be redundant as well once betweenness centralization and modularity are taken into account.

4.2. Typologies based on subgroup variables (T₁)

Table 3 shows the distribution of the T₁ typologies, which include between 5 and 9 types in the six datasets. Visual inspection of the medoids and a few ego-networks in each type help recognize the main structural characteristics of the different types, which are illustrated by Figure 1 for the ECU data typology. For all datasets, Figure 3 summarizes the distribution of the three subgroup variables across the types.⁹ Overall, the T₁ typologies capture variation between the subgroup structures of the personal networks in all datasets, ranging from more closely-knit, core-centered configurations (closed community, core-periphery) to more fragmented ones (multi-factional, disconnected). Each structural type is described by a unique combination of patterns in the number of subgroups, number of singletons/dyads, and modularity. The same structural types exhibit exactly the same patterns in the three subgroup variables across all the datasets (Figure 3).

Table 3.

Absolute frequencies (percentages) of subgroup-based structural types (T₁) in the six datasets.

Type	MBC	FRA	ECU	PAR	TAL	SFB
1. Closed community	27 (7)	172 (58.5)	46 (17.4)	59 (49.6)	109 (42.9)
2. Dense core-periphery	52 (13.5)	25 (8.5)	43 (16.3)	21 (17.6)
3. Sparse core-periphery	41 (10.6)	41 (13.9)	45 (17)	11 (9.2)
4. Large core-periphery					39 (15.4)
5. Small core-periphery					15 (5.9)
6. Dual core-periphery	44 (11.4)
7. Weakly bi-factional	47 (12.2)	16 (5.4)	33 (12.5)	12 (10.1)	18 (7.1)
8. Strongly bi-factional	38 (9.9)	11 (3.7)	37 (14)	13 (10.9)	33 (13)
9. Tri-factional	38 (9.9)				8 (3.1)
10. Multi-factional				3 (2.5)
11. Dense multi-factional	44 (11.4)	8 (2.7)	37 (14)
12. Sparse multi-factional	54 (14)	4 (1.4)	23 (8.7)		18 (7.1)
13. Disconnected		17 (5.8)			14 (5.5)
14. Small dense						94 (25.7)
15. Small bi-factional						31 (8.5)
16. Triad and isolates						72 (19.7)
17. Small multi-factional						37 (10.1)
18. Small disconnected						132 (36.1)
Total	385 (100)	294 (100)	264 (100)	119 (100)	254 (100)	366 (100)
N types	9	8	7	6	8	5

Fig. 3.

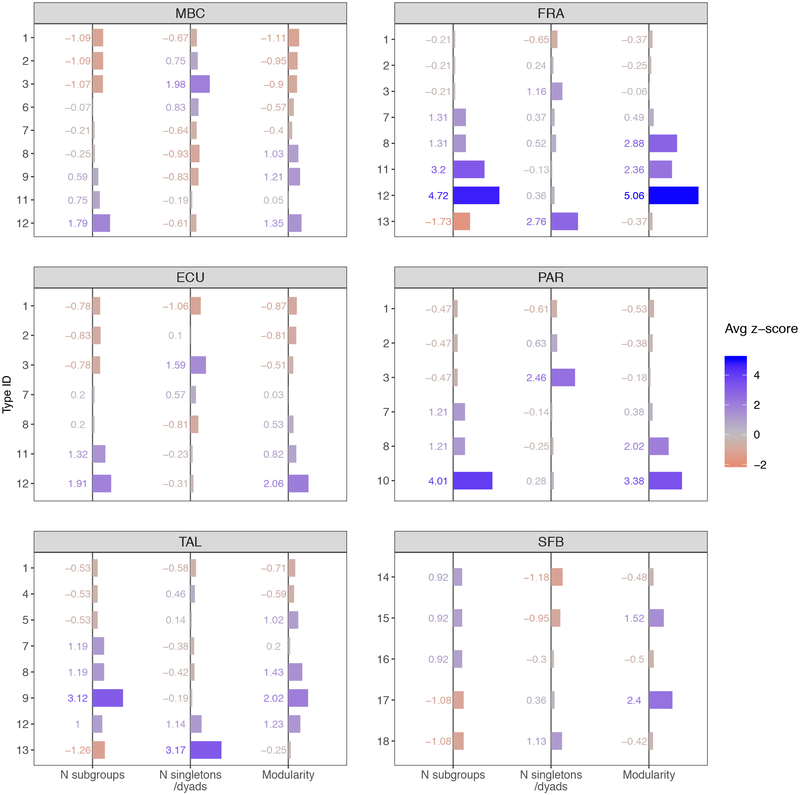
Average z-scores of the three T₁ variables in each type in the six datasets. See Table 3 for numeric IDs of T₁ types.

The closed community type (Figure 1A, type 1 in Table 3) is one in which all or most alters know each other, resulting in most nodes being assigned to a single, large and very dense subgroup (in some cases a complete subgraph). This configuration is captured by the presence of just one subgroup, zero or very few singletons/dyads, and zero modularity. Core-periphery types (Figure 1B–C, types 2–5 in Table 3) can be recognized by the presence of a single subgroup (the core), together with a higher number of singletons/dyads (the periphery) and a slightly higher modularity compared to closed-community networks. Relative to denser core-periphery structures (type 2), sparser ones (type 3) can be distinguished in four of the six datasets by a higher number of singletons/dyads and slightly higher modularity. Closed-community and coreperiphery structures are the most recurrent types of personal networks in the data, appearing in all datasets (except SFB) and including between 7% and 59% (closed community), and between 21% and 33% (core-periphery) of the networks.

Bi-factional types (Figure 1D–E, types 7–8 in Table 3) gather personal networks in which most alters are distributed between two large and separate subgroups, with few actors assigned to singletons and dyads. Different levels of modularity differentiate between weakly bi-factional types (7, with lower modularity, reflecting higher overall density and more between-group ties), and strongly bi-factional types (8, with higher modularity, reflecting higher separation between the two subgroups).

Multi-factional types (Figure 1F–G, types 9–12 in Table 3) are classes of sparser, more fragmented ego-networks in which alters are distributed among more than two separate subgroups. In certain datasets, a sparse multi-factional type emerges (12, vis-à-vis a dense multi-factional class, 11), characterized by a higher number of subgroups and singletons/dyads, as well as higher modularity. Finally, a disconnected type (13 in Table 3) is found in certain datasets, which includes small numbers of networks with almost no ties among alters, resulting in zero subgroups and an extremely high number of singletons/dyads.

The T₁ method detects similar types in all the datasets, perhaps with the exception of SFB, which is unique for the very small size of its networks. An important characteristic of the T₁ typology is the ordered distribution of its types in a spectrum ranging from more cohesive structures centered around a core, to increasingly sparse and fragmented configurations: from closed community, core-periphery and bi-factional types, to multi-factional and disconnected types (see the order of type numeric labels and rows in Table 3). This generates an ordinal variable that can be used to easily locate a personal network in the spectrum, and to compare the distributions of different network samples along the spectrum. The recurrence of similar T₁ typologies across the six datasets is a remarkable result, considering that these data originated from studies conducted in exceptionally disparate geographical and social contexts, from large European cities to Florida rural areas to Ecuadorian mountains. Section 5.3 examines the extracted typologies in more detail within the substantive context of each study.

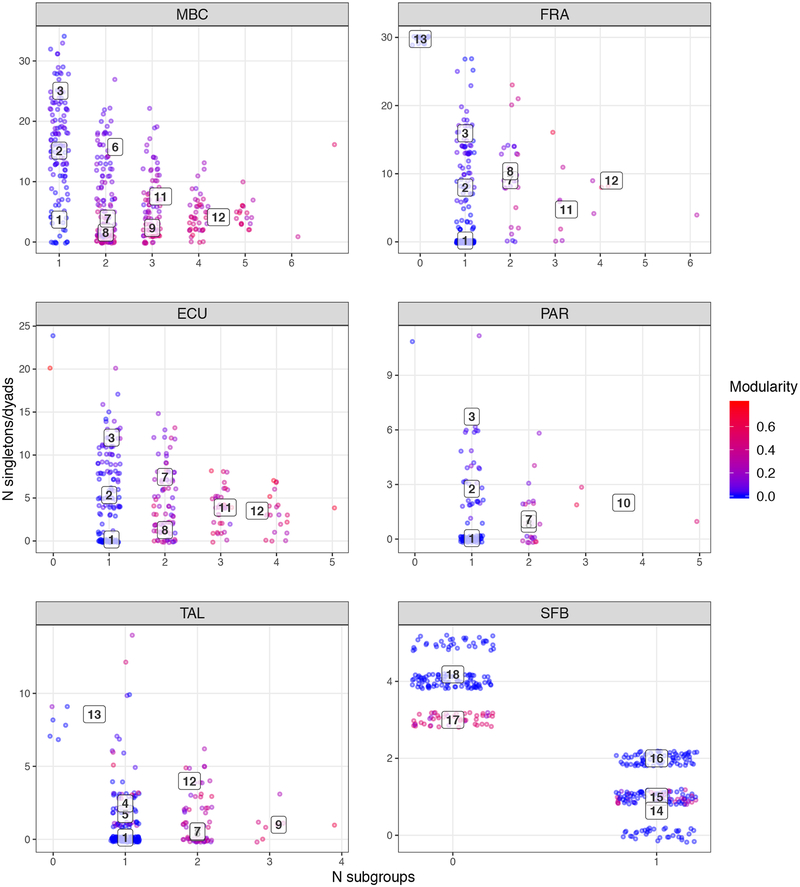
With the T₁ typologies being constructed on the basis of just three variables, the location of each ego-network in the joint distribution of these variables, and hence in the typology, can be shown in a single scatter plot (Figure 4). This can be read as a “structural map” of the data and used for a rapid assessment of the distribution of structural types in a given dataset, as well as for comparison between different datasets. The various structural types can be found in separate locations of the scatter plots, which highlights their difference in terms of count of subgroups (x axis), count of singletons/dyads (y axis) and modularity (color). The maps can be used to evaluate and compare the significance of types in different samples, and the distribution of different collections of ego-networks along the cohesive-factional structural spectrum. We can easily see, for example, that the FRA data include relatively more closed-community personal networks (type 1) compared to the MBC data; and that more factional ego-networks exist in the ECU data (types 11 and 12) compared to the PAR dataset.

Fig. 4.

Joint distribution of the three T₁ variables in the six datasets. Each point is a personal network. Black labels show the average values for structural types (see Table 3 for numeric IDs of T₁ types). Points are slightly jittered to reduce overplotting.

4.3. Typologies based on BDG variables (T₂)

Results from the T₂ typologies are interpreted here in terms of the six types defined by Bidart and colleagues (2018):

1. The regular dense type is characterized by high density and low centralization, sometimes corresponding to a core-periphery structure including a few isolates. This is relatively similar to the closed community type in the T₁ typology.

2. The centered dense type is also very cohesive (high density), but has a higher centralization compared to regular dense networks.

3. Centered star networks have high centralization but lower cohesion, as reflected by lower density and higher Louvain modularity.

4. Segmented networks have lower centralization, a higher number of disconnected, dense components of similar size (implying higher Louvain modularity), and a few isolates. This is similar to the subgroup structure called multi-factional in T₁.

5. Pearl collar networks are mainly characterized by a long diameter.

6. Dispersed networks have low density and many disconnected components (including isolates) as their major features.

The k-medoid cluster analysis on the six BDG variables finds optimal T₂ typologies with 4 to 8 types (see Supplementary Information Table S4 for the distribution of these types in the data). The types are described by considering average patterns of the six variables in each cluster (Supplementary Information Figure S5) and BDG’s interpretation of the six structural variables.

A large, regular dense type (type 1 in Table S4) and a smaller dispersed type (type 6) emerge in all datasets except SFB. The centered star type (3) described by BDG is also found in three of the six datasets. Similar to T₁ typologies, the BDG typologies detect an outlier, disconnected type (7) in half of the datasets, characterized by almost no ties among alters. On the other hand, structural types with the characteristics that BDG attribute to pearl collar (5) and centered dense (2) networks are only found in one of the six datasets (ECU and PAR, respectively). In the ECU and TAL data, a mixed type emerges (4), which combines pearl collar characteristics (high diameter) with centered star characteristics (high centralization).

Finally, in all datasets except PAR, a hybrid or residual structural type is found (15), which escapes a clear definition based on BDG’s categories as it shows average values on most variables, a mix of characteristics from several other types, and very variable subgroup structures. The emergence of this cluster, which includes between 11% and 44% of the networks in the different datasets, is consistent with BDG’s finding that discriminant analysis on their six summary variables failed to allocate 25.4% of their ego-networks to any type (Bidart et al., 2018, p. 6). One unifying characteristic of the hybrid type is the presence of a single connected component including all alters; a feature that, however, leaves room to wide structural variation among networks in this type. Thus, the inclusion of the number of components as a defining variable for the BDG typology might generate noise in the cluster (or discriminant) analysis and be the reason why this hard-to-define, hybrid type appears.

4.4. Comparison between T₁ and T₂ typologies

The subgroup-based typology and the BDG typology have different levels of agreement in the six datasets (Table 4). In general, however, they seem to classify personal networks in substantially different ways. With the exception of the FRA data, the network pairs on whose similarity both typologies agree are between only 16% and 45% of all the network pairs considered similar by any typology (Jaccard index); and the Rand index’s increase from its random baseline is only between 12% and 54% of the maximum possible increase (Adjusted Rand index).

Table 4.

Jaccard index, Rand index, and Adjusted Rand index of similarity between subgroup-based typology (T₁) and BDG typology (T₂) in each dataset.

Dataset	Jaccard	Rand	Adjusted Rand
MBC	0.16	0.67	0.12
FRA	0.73	0.87	0.73
ECU	0.23	0.76	0.23
PAR	0.33	0.70	0.28
TAL	0.23	0.73	0.20
SFB	0.45	0.85	0.54

The agreement is lowest in the dataset with the largest ego-networks, MBC (J= 0.15 and $\widehat{R}$ = 0.12). This finding is likely due to the larger network sizes and the higher frequencies of complex, factional subgroup structures in MBC, which generate wider structural variation and create more opportunities for divergence between the T₁ and T₂ classification methods. By contrast, smaller networks (e.g., in the SFB data) exhibit less structural variation and are easier to classify in similar ways in the two typologies. Yet the Tallahassee data (TAL), which have the second smallest network size on average, also exhibit low agreement between the two typologies (J= 0.23 and $\widehat{R}$ = 0.20). In this case, the variable network size may produce additional structural variation that compensates for the low average size, creating dissimilarity between typologies. In the FRA dataset, whose larger average network size would be expected to create more room for disagreement between typologies, the relatively high similarity level (J = $\widehat{R}$ = 0.73) is driven by the very high proportion of closely-knit, dense ego-networks that T₁ and T₂ put in the same class (58% and 64% of the ego-networks assigned to the closed community and regular dense types, respectively, which largely coincide).

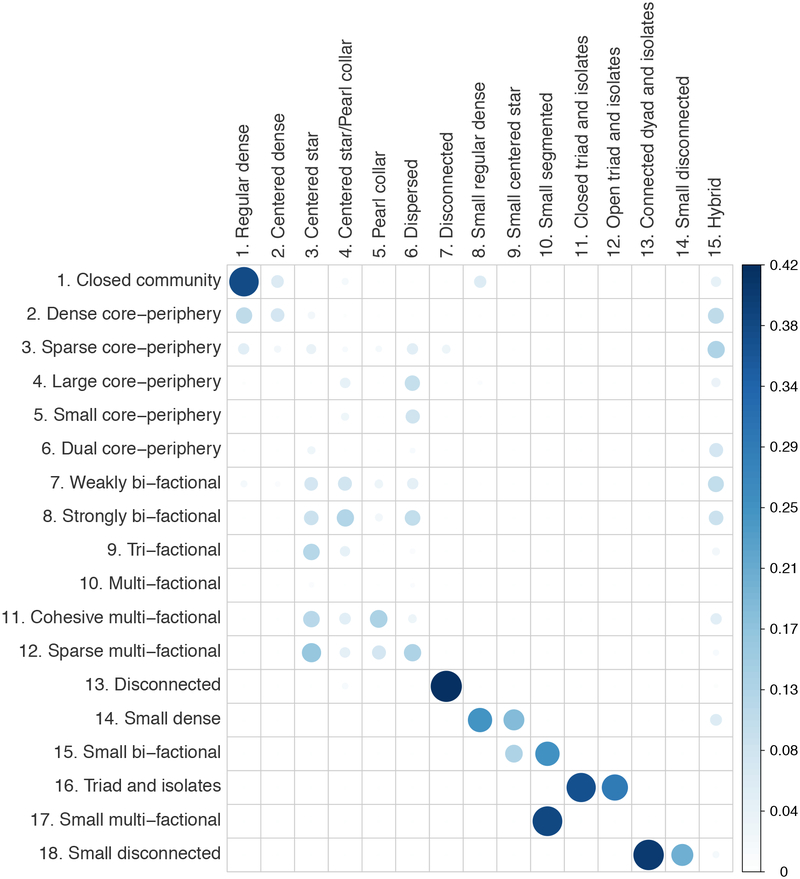
Figure 5 pools the six datasets together to examine the level of match between types in different typologies, as measured by the Jaccard index. Higher levels of type coincidence are observed between the closed community and regular dense types; and between the disconnected types from the two typologies. In both cases, approximately 42% of all personal networks in the two types are the same networks (J ≈ 0.42), indicating that the T₁ and T₂ typologies are classifying closed-community and disconnected ego-networks in a very similar way. Generally high overlap levels are also observed among all the SFB types (bottom-right part of Figure 5), highlighting that the subgroup-based and the BDG methods are producing approximately the same classification in a dataset consisting of small, five-alter ego-networks with more limited structural variation.

Fig. 5.

Jaccard index between T₁ types (rows) and T₂ types (columns) (all datasets pooled).

Except for these few cases, the levels of coincidence between types from the two typologies are generally low, with Jaccard indexes ranging between 0 and 15–20%. This suggests a high degree of cross-classification between T₁ and T₂: ego-networks in one T₁ type are assigned to multiple types by T₂, and vice versa, indicating that the two methods classify the same personal networks in different ways, on the basis of different structural characteristics. For example, ego-networks in the dense core-periphery type of T₁ are assigned to several different types by T₂. This is even more the case for the multi-factional T₁ types, which are scattered among several different T₂ clusters. Similarly, T₂ types such as centered star and dispersed gather networks that belong to various types in T₁.

5. Discussion

Three summary measures describing the Girvan-Newman subgroup partition of an egocentric network, when taken together, effectively capture variation in ego-network subgroup structure and provide a parsimonious yet insightful description of an ego-network’s overall structural configuration. These are relatively simple measures that can be easily interpreted and calculated with standard network analysis software. The resulting ego-network typologies (T₁) create a classification of networks along a spectrum from more cohesive, core-centered structures to sparser, more factional and disconnected ones.

The method proposed in this paper regards cohesive subgroups as a fundamental feature of personal networks. Personal network subgroups capture the different social circles and interaction foci that exist in a person’s social world, providing unique insights into the characteristics of a personal community and the patterns of social capital and social support they generate. The next sections discuss potential applications of the subgroup-based personal network typology to theoretical and substantive research in the social sciences.

5.1. Typologies of personal communities and social structures

The subgroup-based typology of ego-network structures, and its spectrum from core-centered to factional ego-networks, are closely aligned with other typologies proposed in recent sociological literature, including the distinction between traditional personal communities and “networked individualism” documented by Rainie and Wellman (2012); the classification of concentric, intersecting, and spoke ideal types of social structure presented by Pescosolido and Rubin (2000); and Portes and Vickstrom’s (2011) description of communitarianism and organic solidarity as opposite forms of social cohesion.

The literature on networked individualism (Rainie & Wellman, 2012; Hampton & Wellman, 2018) has documented the deep transformation in personal communities produced by the “triple revolution” of social networks, the Internet, and mobile information and communication technologies: the transition from small, closely-knit and overlapping communities based on traditional social groups (such as the family, work unit or village), to far-flung, diverse and fragmented personal networks revolving around autonomous individuals. The traditional, group-based personal communities described by Wellman and colleagues, based on strong ties, multiplex relationships, regular contact, limited spatial mobility, and high density of relations, are likely to engender egocentric networks similar to the core-centered structures identified by T₁ typologies (see Figure 1A–C). In terms of the focus theory of social network formation (Feld, 1981), personal networks of this type are more likely to derive from fewer, highly constraining foci of activity (such as family and work); and from multiplex relationships within compatible and overlapping foci (e.g., when family members are also co-workers in a family business).

By contrast, ego-networks in the factional types of T₁ (see Figure 1D–G) are more likely to be formed by “networked individuals”: more spatially and socially mobile people, who are only partially committed to different, non-overlapping social circles (such as family at home, colleagues at work, friends in voluntary associations), and able to autonomously navigate and maneuver multiple, far-flung, and sparser networks. In terms of focus theory, individuals in these types of personal communities exist at the intersection of many, distant and less constraining foci of activity.

The spectrum from core-centered to factional ego-networks also closely corresponds with the ideal types of social structure proposed by Pescosolido and Rubin (2000) and Perry and colleagues (2018, pp. 297ff). In the premodern, concentric type, the individual is embedded in concentric circles of dense, overlapping, redundant social networks with a common cultural orientation. This configuration (cf. Figure 1 in Pescosolido and Rubin, 2000) is more likely to produce core-centered personal network types (compare with Figure 1A–C in this article). By contrast, the modern, intersecting type of social structure is characterized by distinct but intersecting social circles, with the individual being able to choose among memberships in a diverse array of less constraining, yet typically long-term, groups (e.g., family, work, religious and voluntary associations). Finally, in the contemporary, spoke structure individuals are connected to distinct and distant social circles, with only limited intersections and durability. In this form of social structure, ties to diverse circles are multiple and temporary, often contingent (e.g., multiple, transient workplaces and families). The intersecting form and, even more so, the spoke form of social structure (cf. Figure 3 in Pescosolido and Rubin, 2000) are likely to produce factional and disconnected personal network structures (compare with Figure 1E–G in this article).

A third, parallel distinction contrasts communitarianism and organic solidarity as two ideal-typical, opposite sources of social cohesion and organization (Portes & Vickstrom, 2011): the former based on closely-knit, dense networks of mutual knowledge, trust, and loyalty (such as families and tribes); the latter based on ethnic and social diversity, division of labor, and strong coordinating institutions. Communitarian societies are likely characterized by a prevalence of the dense, core-centered personal networks at the first end of the T₁ spectrum; while fragmented and factional personal networks, at the other end of the spectrum, are more likely to exist in societies based on organic solidarity, diversity and division of labor.

These parallels suggest that, following recent calls to use egocentric network analysis for a “return to typologies” in the study of social life and social structures (Perry et al., 2018, p. 298ff), the ego-network typologies introduced in this article can be used to operationalize other, theoretical sociological typologies for the study of geographical and temporal variation in personal communities, social structures, and forms of social cohesion. At the same time, theoretical typologies proposed in sociological literature can be used as a framework to explain the prevalence and distribution of different types of ego-network structure in different empirical contexts.

5.2. Sources and patterns of social capital, support, and isolation

Different forms of personal communities and social structures, and the corresponding types of egocentric networks, have important consequences in terms of social capital, social support, and social isolation. This variation, which is captured by the T₁ typological spectrum, may lead to different outcomes in terms of individual health (Thoits, 2011; Kawachi & Berkman, 2014), socioeconomic mobility (Lin, 1999), and immigrant incorporation (Portes & Sensenbrenner, 1993; Hagan, 1998; Vacca et al., 2018), among other things.

With the shift from traditional personal communities to networked individualism comes a trade-off between security and support on the one hand, freedom and diversity on the other (Hampton & Wellman, 2018). Concentric social structures, group-based personal communities, and core-centered personal networks generate the advantages of closure social capital: a high level of security and social support, generalized reciprocity and solidarity, and informal controls. However, they also require more individual loyalty, commitment, and conformity, leading to greater social pressure, repression of deviance, and limits to individual freedom.

By contrast, the intersecting and spoke social structures, networked individualism, and fragmented, factional personal networks produce the benefits of weak ties, structural holes, and bridging social capital: higher individual autonomy and ability to access and maneuver diverse, non-redundant, and specialized resources in a social network. On the other hand, they entail a weaker safety net, potential exposure to dissonant values, norms and demands, the need to bridge “cultural holes” (Pachucki & Breiger, 2010), and consequent psychological tensions for the ego (Pescosolido & Rubin, 2000). In contemporary societies, the unprecedented multiplication of dissonant, non-overlapping, and temporary social circles in a personal network can lead to higher cognitive costs of maintaining social ties, less meaningful relationships, and new forms of subjective social isolation (Parigi & Henson II, 2014), with adverse consequences for individual health and well-being.

5.3. Substantive insights from the six datasets

A typological analysis of ego-network structures provides substantive insights into the nature of personal communities, social support and social capital in the six populations in which the data used in this study were collected. One clear finding is that core-centered ego-network structures are predominant in three of the datasets, with the closed-community type showing the highest relative frequencies in the FRA (58.5%), PAR (49.6%), and TAL (42.9%) data (see Table 3).

In the FRA data, the prevalence of the closed-community type is consistent with important social and spatial characteristics of the study population: one of oystermen living in relatively isolated, rural towns with similar jobs in the same industry, few and largely overlapping foci of activity, extended family ties, and multiplex family/work relationships. In the PAR data, the high proportion of closed-community structures reflects the frequency of tightlyknit, homogeneous communities of family, neighbors and coethnic contacts among Romanian Roma immigrants in Europe, a highly marginalized and segregated minority in which coethnic and homophilous support networks play a crucial role in migration and incorporation trajectories (Pantea, 2013; Sordé, Serradell, Puigvert, & Munté, 2014). The TAL data were collected in segregated, low-income African American neighborhoods of Tallahassee, Florida, a city with notoriously high levels of residential segregation along racial and socioeconomic lines (Florida & Mellander, 2015; Orfield & Ee, 2017): the high frequency of closed community structures in these data may derive from the prevalence of closely-knit networks of strong, multiplex, local ties with family, neighbors and church co-members, which other research has documented in African American neighborhoods with high segregation levels and limited spatial and social mobility (Oliver, 1988). In all these contexts, core-periphery structures (about 23% in FRA, 27% in PAR, and 21% in TAL) could reveal a periphery of contacts outside of the main social circle in which the ego is embedded, e.g., outside of the coastal town, oyster industry, Roma camp, or urban neighborhood where the core of the personal network originates.

The relatively higher frequencies of factional structures in the MBC data result from the highly transnational social lives of certain immigrant populations in Europe (Vacca et al., 2018; Lubbers, Verdery, & Molina, 2018). The personal networks in these data include native-born Spaniards and Italians, coethnic immigrants living in the same or different countries as the ego, and a substantial number of transnational contacts in sending communities. These different groups of alters tend to correspond to multiple and separate foci of interactions (e.g., work, church in receiving country, political or business association in sending country), generating separate structural subgroups in personal networks. Transnational migrants, who routinely use advanced information and communication technologies to maintain relationships with different social circles in multiple countries (Baldassar, Nedelcu, Merla, & Wilding, 2016), may be the closest to the networked individualism type among the six populations considered here, leading to the factional and fragmented personal networks found in the MBC data.

The higher diversity of structural types found in the ECU data is the intended result of a design that collected personal networks in distinct villages with different histories of exposure to natural hazards (see appendix). These include villages exposed to hazard but never evacuated, villages whose population had been evacuated but then returned to the original site, and entirely new resettlement communities. The different types of hazard exposures and consequences created diverse patterns of social tie disruption, maintenance and formation in the villages, leading to a high variability of ego-network structures (Tobin, Whiteford, Murphy, Jones, & McCarty, 2014).

A substantial variability of structural types also characterizes the SFB data, a striking finding considering the small, fixed size of these ego-networks. This result attests to the diversity of social network configurations and forms of personal community in the general population of the San Francisco Bay area, one of the largest, most urbanized and most diverse regions of the world. With five structural types representing each a substantial share of the population, the spectrum from dense to bi-factional, multi-factional and disconnected ego-networks reveals the existence of very different forms of social capital and social support in this context.

6. Conclusions

This article proposed a method to detect structural typologies of personal networks, applied it to six widely different datasets, and compared results with those from a typology detection method recently introduced by Bidart et al. (2018). It then discussed the applicability of subgroup-based ego-network typologies to research on variations in personal communities and broader social structures, patterns of social capital, support and isolation, and related outcomes such as socioeconomic mobility, individual health, and immigrant incorporation.

When applied to the six datasets in this study, the T₁ and T₂ methods capture variation in different aspects of personal network structure, leading to disagreement and cross-classification between their typologies. In particular, while T₁ typologies effectively capture variation in subgroup structure, T₂ typologies appear to better summarize variation in centralization and diameter. The choice between the different structural measures and methods considered here should be guided by theoretical considerations and substantive research applications. If social circles, interaction foci, and their implications for social capital, support and isolation, are an important focus of the research, then subgroup-based typologies may be more suitable. On the other hand, a study might be more interested in characterizing the extent to which an individual’s social world is centered around, or dependent upon, one alter (e.g., a romantic partner) or few alters (e.g., a small clique of friends): an aspect better measured by centralization. In this case, a typology similar to T₂ might be more appropriate.¹⁰

In the less hierarchical, less bounded, and less homogeneous world of networked individualism and spoke social structures, personal networks take on a wider structural variability than was the case in the past. Typologies of personal network structure will become increasingly important to classify and make sense of this variability, and to understand the new constraints and opportunities it creates for individuals. Methodologically, more research will be needed to identify dominant and recurrent dimensions of ego-network structural variation, and to evaluate different typology construction methods as applied to data from various populations, name generators, and data collection tools. Theoretically, a major challenge in the field will be to link theories and hypotheses to specific characteristics and types of ego-network structure, to identify the typology extraction methods that best operationalize central theoretical concepts, and to test their ability to explain and predict relevant outcomes in applied research.

Appendix: Additional information about the datasets and surveys

Table 1 reports basic information about the six datasets, including the name generators and alter-tie questions (edge interpreters) used to collect them. This appendix provides more details about the studies in which these data were collected.

The MBC data were collected with two surveys using identical name generators and edge interpreters. These were conducted in 2004–2006 (Barcelona, Spain) and 2012 (Milan, Italy) to study the cultural and economic integration of non-European immigrants in Spain and Italy. Respondents were immigrants from African, Asian, and Latin American countries, recruited using a combination of venue-based and link-tracing sampling (Vacca et al., 2018; Lubbers et al., 2007). The 385 ego-networks in this dataset have a fixed size of 45 alters, including any type of family, friend or acquaintance with whom ego has had contacts in the past two years (and whom ego could still contact). The name generator aimed to capture respondents’ total personal networks (McCarty, Bernard, Killworth, Shelley, & Johnsen, 1997).

The FRA dataset was obtained in 2012 as part of a study on community resilience following the 2010 Deepwater Horizon oil spill in the Gulf of Mexico, and the ensuing collapse of oyster fishery in the Florida Apalachicola Bay area (Puetz & Mayer, 2018). A survey was administered to 303 residents of Franklin county, in the Florida’s Gulf coast, to gain information on their personal relationships that could provide support in case of disaster. Following community-based participatory research principles, respondents were recruited by community organizations and complete personal network data were obtained for 293 individuals.

The ECU data include 264 personal networks with a fixed size of 25 alters. As part of a research on community resilience in case of natural disaster, a personal network survey was administered in 2009 to a random sample of residents of five Ecuadorian villages exposed to natural hazards on the stratovolcano Tungurahua (Jones et al., 2013). Similar to those in the MBC data, the resulting egocentric networks include any family, friends and acquaintances with whom ego has had recent contact.

The PAR data were collected in 2014–2015 in Paris and other large metropolitan areas of France for a study on Romanian Roma migration and incorporation in the French society. The 119 respondents were Romanian Roma immigrants in France, and they were asked to name 30 family members, friends or acquaintances “on whom they could rely”. While tie data were collected for all the 30 alters, I used this dataset to extract realistic personal networks of variable size between 10 and 25 alters. The goal was to simulate the common situation in which the data include ego-networks of different sizes within a given minimum and maximum number of alters. The data were simulated by extracting one random integer number (n_i) in the [10, 25] range for each respondent, and retaining only the subgraph of the first n_i alters nominated by the respondent. When a survey asks to list a free number of alters between a minimum and a maximum value, respondent fatigue leads to lower numbers of alters being more likely. To simulate this characteristic of the data, the random integers were extracted assigning decreasing probabilities to the integers between 10 and 25. Figure S1 in the Supplementary Information shows the resulting distribution of network size.

The TAL dataset is the result of a 2011 epidemiological and social survey conducted in Tallahassee, Florida. This was part of a research on racial health disparities with a focus on cardio-vascular diseases among African Americans (Boston, Mitchell, Collum, & Gravlee, 2015). Respondents were selected from African American households based on a multistage probability sampling design, which started with the identification of neighborhoods with higher proportions of African American residents, and then chose random block groups within neighborhoods and random residential addresses within block groups. A network of 30 alters was elicited from each respondent using a generic name generator based on acquaintance and contact. Similar to the PAR data, edge interpreters were asked for all the 30 alters, but these data were used to simulate a dataset with variable network size (in this case in the smaller network size range of 5 to 20 alters).

The final dataset, SFB, is a subset of the first-wave data from the UC Berkeley Social Networks Study (UCNets), a research on personal network change and health among young and older adults (Offer & Fischer, 2018). In its first wave (2015–2016) the survey was completed by 1,159 residents of the San Francisco Bay Area, aged 21–30 or 50–70 years. Respondents were selected using random address-based sampling and were randomly assigned to face-to-face or Internet survey modes. Personal networks were elicited using six role and activity-based name generators focused on social activities (going out to concerts, plays, clubs, sports, etc.); confiding about personal matters; advice to make important decisions (e.g., about taking a job or family issues); practical help in everyday life (e.g., with moving furniture, looking after a child, getting a ride, etc.); help in case of serious injury or sickness; and people whom the respondent provides support to. The total number of named alters ranged between 1 and 30 contacts. Up to five nominated contacts were then selected during the survey to ask alter tie questions. The algorithm used to select these contacts is described at http://ucnets.berkeley.edu. For this article, the data were subset to personal networks with tie information on five alters. These are 366 personal networks, of which 64% were obtained in face-to-face interviews and 36% through Internet surveys.

Network size is an important dimension of variation across the six datasets. The data were deliberately selected to represent different designs in terms of network size, including large, fixed-size personal networks (MBC, FRA, ECU), variable network size in different ranges (PAR and TAL), and small networks (SFB) similar to those analyzed in studies of core discussion partners (e.g., Small, 2017) or elicited by large-scale ego-network surveys such as the US General Social Survey (Burt, 1984).

Alter tie data are collected in the six surveys using slightly different edge interpreters about acquaintance between alters (see Table 1). While the surveys include different response categories to alter tie questions, this article analyzed binary ego-networks by retaining alter-alter ties whose value is at least equal to a certain threshold. Lower or higher thresholds were set in different datasets, corresponding to weaker or stricter definitions of alter-alter tie, to reproduce different possible scenarios in personal network analysis.