Random-effects meta-analysis of combined outcomes based on reconstructions of individual patient data

Abstract

Meta-analyses of clinical trials typically focus on one outcome at a time. However, treatment decision-making depends on an overall assessment of outcomes balancing benefit in various domains and potential risks. This calls for meta-analysis methods for combined outcomes that encompass information from different domains. When individual patient data (IPD) are available from all studies, combined outcomes can be calculated for each individual and standard meta-analysis methods would apply. However, IPD are usually difficult to obtain. We propose a method to estimate the overall treatment effect for combined outcomes based on first reconstructing pseudo IPD from available summary statistics and then pooling estimates from multiple reconstructed datasets. We focus on combined outcomes constructed from two continuous original outcomes. The reconstruction step requires the specification of the joint distribution of these two original outcomes, including the correlation which is often unknown. For outcomes that are combined in a linear fashion, misspecifications of this correlation affect efficiency, but not consistency, of the resulting treatment effect estimator. For other combined outcomes, an accurate estimate of the correlation is necessary to ensure the consistency of treatment effect estimates. To this end, we propose several ways to estimate this correlation under different data availability scenarios. We evaluate the performance of the proposed methods through simulation studies and apply these to two examples: (1) a meta-analysis of dipeptidyl peptidase-4 inhibitors versus control on treating type 2 diabetes; (2) a meta-analysis of positive airway pressure therapy versus control on lowering blood pressure among patients with obstructive sleep apnea.

1. Introduction

Meta-analysis is widely used in evidence-based clinical research for intervention evaluations. In clinical practice, treatment decision-making depends on an overall assessment of the patient-level outcomes balancing benefit in various domains and potential risks. Oftentimes a variety of outcome measures are reported in randomized clinical trials (RCTs), which naturally elicits the question of how to synthesize treatment effects across studies on multiple outcomes simultaneously. This motivates us to consider a single measure that is carefully constructed to reflect the effectiveness of an intervention across different outcomes. We henceforth refer to this type of measures as combined outcomes, and the reported outcomes that contribute to it as original outcomes.

Use of combined outcomes is commonplace in clinical assessment, such as the Apgar Score,¹ the Glasgow Coma Scale,² the Elixhauser Comorbidity Index,³ etc. These three examples are all constructed by summing up the component scores, which is a conventional way of constructing combined outcomes. However, the construction of combined outcomes can take on more complex forms than summation and can pool information from outcomes of different types. For instance, Evans et al⁴ proposed a way for the evaluation of antibiotic use strategies that was based on the desirability of outcome ranking (DOOR) as a unified measure of both an overall clinical outcome (an ordinal variable with 5 mutually exclusive levels of desirability based on clinical benefit and adverse effects (AE) ranging from clinical benefit without AE to death) and the duration of antibiotic use (a continuous variable). As the name suggests, the construction of DOOR involves ranking all trial participants with respect to the desirability of their clinical outcomes. When two participants have the same clinical outcome, the one with a shorter duration of antibiotic use receives a higher rank. We differentiate the term combined outcome from composite outcome. The latter is commonly seen in the survival analysis literature, where it refers to a collection of different outcomes and the interest lies in the time to any one of these outcomes, for example, time to major adverse cardiac events or death.⁵ In contrast, a combined outcome is designed to represent a clinically meaningful synthesis of multiple outcomes and can be a function of variables of different types including continuous, binary, or ordinal.

When IPD are available, combined outcomes can be easily obtained for each individual, and standard meta-analysis methods apply. However, in practice IPD are rarely available to meta-analysts. Instead, aggregate data (AD), such as group means and the associated standard errors of the original outcomes are readily accessible through published literature. These AD carry important distributional information about components of combined outcomes. The question now becomes whether one can make inferences about treatment effects on combined outcomes by exploiting AD of the original outcomes with limited or no IPD.

When more than one outcome is of interest, multivariate meta-analysis (MVMA) methods can be employed to jointly estimate treatment effects on several outcomes. MVMA extends the two-stage estimation procedure from univariate meta-analysis, where each study supplies a vector of treatment effect estimates together with an estimated variance-covariance matrix. Based on the hierarchical multivariate normality for study-specific treatment effect estimates on multiple outcomes, parameters of interest can be estimated through maximum likelihood,^6,7 restricted maximum likelihood,^6,8 profile likelihood⁷ or Bayesian methods.^9–11 Other estimating procedures based on the method of moments^12–14 and the use of U-statistics¹⁵ have also been developed.

One main advantage of MVMA over separate univariate meta-analyses is the improvement in efficiency resulting from joint modeling multiple outcomes and accounting for their correlations.^16,17 Correctly specifying the correlations facilitates the “borrowing of information” across multiple outcomes and leads to efficiency gain.^16,18 It has been demonstrated through both analytical and simulation studies that ignoring within-study correlations can result in increased mean squared errors and standard errors of the pooled estimates, especially when the between- and within-study covariances are of comparable scale.^18,19 However, within-study correlations are typically assumed known without error in MVMA and concerns have been raised about the unavailability of within-study correlations from study reports.^6,16,18,20 Wei and Higgins²¹ derived analytical formulae for estimating within-study correlations between study-specific treatment effect estimates on bivariate outcomes. Their method is able to handle various types of effect measures including the standard difference in means, log odds/risk ratio, etc, but requires knowledge of the correlation between the original outcome measures. Alternative options for MVMA when within-study correlations are unknown¹⁸ include using approximation techniques,²² obtaining IPD,^23,24 narrowing the range of possible values,²⁵ conducting sensitivity analyses over the entire parameter space,²⁶ and employing an alternative model that does not require the specification of within-study correlations.^27,28

Although MVMA makes use of correlations among multiple outcomes, inference is typically made for each original outcome separately. It is possible to make inference about a smooth function of the treatment effect vector through the use of the Delta method.²⁹ In some settings MVMA can be used to make inference about combined outcomes. For example, in a bivariate meta-analysis of two continuous outcomes U and V, suppose that treatment effects on both outcomes are estimated using mean differences between intervention groups, and the pooled estimates are $\left({\widehat{\Delta }}_U,{\widehat{\Delta }}_V\right)$ with an estimated variance-covariance matrix $\widehat{\Sigma }$. Based on the results of MVMA, one can make inference about a combined outcome of the form aU + bV where a, b are constants.^13,16,27 However, settings like this are limited. One key difference is that we consider a function of the original outcomes, while the MVMA methods work with the vector of study-specific treatment effects and the functions thereof. It is not obvious how the existing MVMA methods would handle outcomes that combine information from two original outcomes in a non-linear fashion. Take our data application in Section 4.2 for example, where the original outcomes are systolic and diastolic blood pressures (SBP and DBP). We are interested in estimating the treatment effect on the combined outcome which is a binary indicator of whether a patient’s SBP is over 130 mmHg or DBP is over 80 mmHg, i.e., 1(SBP > 130 or DBP > 80), where we use 1(·) to denote the indicator function. This combined outcome signifies whether a patient has elevated blood pressure. While standard MVMA can provide estimates of treatment effects on SBP, DBP, or more generally, a linear combination of SBP and DBP, i.e., aSBP+bDBP where a, b are fixed constants, taking into account the correlation between SBP and DBP, for outcomes such as 1(SBP > 130 or DBP > 80), they no longer apply.

In this paper, we develop meta-analysis methods for combined outcomes that are based on the reconstruction of IPD. If we view the unavailable IPD as missing values, this approach can be considered as an imputation approach. For each set of pseudo IPD, we can calculate the values of combined outcomes and apply standard random-effects methods to obtain the pooled treatment effect estimates. We then follow the multiple imputation approach³⁰ and take the average of the overall treatment effect estimates from multiple reconstructed IPD to be our final treatment effect estimate.

The proposed approach complements existing MVMA methods by expanding the variety of combined outcomes that could be meta-analyzed based on AD and/or partial IPD. Because once complete (pseudo) IPD have been generated, they can be used to construct any types of combined outcomes. Having IPD also permits the use of one-stage approaches that analyze data from all studies simultaneously under a hierarchical model without first obtaining study-specific estimates.³¹

The idea of reconstructing IPD has been previously explored in other settings. Papadimitropoulou et al³² found that fitting linear mixed effect models to reconstructed IPD led to treatment effect estimates that were comparable to those obtained through traditional aggregate data meta-analyses. Analysis of reconstructed IPD has also been shown to facilitate the detection of treatment-covariate interactions.³³ In meta-analysis of survival data, an algorithm has been developed to map digitised Kaplan-Meier (KM) curves back to the data that generate these plots using information on numbers of events and numbers at risk. The algorithm demonstrated considerable accuracy in reproducing sample statistics including survival probabilities, medians and hazard ratios.³⁴

The remainder of the article is organized as follows. In Section 2, we describe the proposed reconstruction and estimation procedure. Section 3 presents results from our simulation study. In Section 4, we illustrate the proposed method with two data examples: the first is a meta-analysis of dipeptidyl peptidase-4 inhibitors (DPP4-I) versus control in treating patients with type 2 diabetes, where the combined outcome of interest depends on both change in hemoglobin A1c (HbA1c) level and change in body weight; and the second involves a meta-analysis of the effect of positive airway pressure (PAP) in reducing blood pressure among patients with obstructive sleep apnea (OSA). Section 5 offers some discussion and concluding remarks.

2. Methods

2.1. Notation and setting

We consider a meta-analysis of J independent two-arm RCTs with two continuous original outcomes U and V . Let i = 1 or 2 denote the treatment or the control arm respectively. We use j = 1, · · · , J to index studies and k = 1, … , n_ij to index patients, where n_ij is the number of subjects assigned to arm i of study j. We assume that the studies are randomly sampled from an underlying population where the grand means of responses for individuals in intervention arm i are ${\mu }_i^U$ and ${\mu }_i^V$ respectively. Let ${\gamma }_{ij}^U$, ${\gamma }_{ij}^V$ denote the mean responses for individuals in arm i of study j. We assume that the joint distribution of $\left({\gamma }_{ij}^U,{\gamma }_{ij}^V\right)$ has finite first and second moments that are given below:

$$\begin{gathered} E\left[{\gamma }_{ij}^U\right]={\mu }_i^U, \\ E\left[{\gamma }_{ij}^V\right]={\mu }_i^V, \\ Var\left({\gamma }_{ij}^U\right)={\left({\tau }_i^U\right)}^2, \\ Var\left({\gamma }_{ij}^V\right)={\left({\tau }_i^V\right)}^2, \\ Cov\left({\gamma }_{ij}^U,{\gamma }_{ij}^V\right)=\kappa {\tau }_i^U{\tau }_i^V. \end{gathered}$$

Following convention, we use E[X] and V ar(X) to represent the marginal expectation and variance of a random variable X respectively, and Cov(X₁, X₂) to represent the covariance between random variables X₁ and X₂. We assume a random-effects model that permits heterogeneous treatment effects across studies. Such between-study heterogeneity often exists due to differences in study populations, or in the design and execution of the studies.³⁵ We further assume that, conditioning on intervention arm i and study membership j, the joint distribution of two original outcomes of the same individual satisfies the following:

$$\begin{gathered} E\left[U_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V\right]={\gamma }_{ij}^U, \\ E\left[V_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V\right]={\gamma }_{ij}^V, \\ Var\left(U_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V\right)={\left({\sigma }_{ij}^U\right)}^2, \\ Var\left(V_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V\right)={\left({\sigma }_{ij}^V\right)}^2, \\ Cov\left(U_{ijk},V_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V\right)=\rho {\sigma }_{ij}^U{\sigma }_{ij}^V. \end{gathered}$$

Lastly we assume that the marginal distribution of each original outcome conditioning on intervention arm i and study membership j, i.e. the distributions of $U_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V$ and $V_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V$, are functionally independent of ρ. The above hierarchical model allows for both the within-individual correlation (ρ) and the correlation induced by study-level characteristics (κ).

Let g(·, ·) be a user-specified known function, and Y = g(U, V) is a combined outcome constructed from the original outcomes U and V. For example, g(U, V) = U +V leads to a continuous outcome Y which is the sum of the original outcomes; and g(U, V) = 1(U > a, V > b) yields a binary outcome Y that indicates whether or not original outcomes U and V are greater than some constants a and b. For simplicity of notation, let E_j[X] denote the expectation of a random variable X conditional on study membership j (i.e. conditional on ${\gamma }_{ij}^U$, ${\gamma }_{ij}^V$). Let ${\theta }_j=h\left(E_j\left[Y_{1jk}\right]\right)-h\left(E_j\left[Y_{2jk}\right]\right)$ denote the treatment effect on the combined outcome for study j, where h(·) is the link function that specifies the metric on which the comparison between two intervention arms is made. For example, when Y_ijk is a continuous outcome, we may choose h(·) as the identity function, then θ_j represents the difference in means. When Y_ijk is a binary outcome, we may choose h(·) to be the logit function, that is, $h\left(x\right)=\text{log}\left(\frac{x}{1-x}\right)$, then θ_j represents the log odds ratio.

As in conventional random-effects meta-analyses, we assume that the study-specific effect sizes θ_j, j = 1, · · · J, are a random sample from some underlying distribution G(·). Commonly-used random-effects meta-analysis techniques, for example, the DerSimonian-Laird method,³⁶ focus on making inference about the mean of this distribution. Similarly, our objective is to estimate the overall effect size defined as:

$${\theta }_0:=E_G\left[{\theta }_j\right].$$

To achieve this goal, conventional two-stage meta-analysis methods require a treatment effect estimate ${\widehat{\theta }}_j$ together with an estimated standard error from each study. These estimates are straightforward to calculate if IPD are available from all studies. Therefore, we focus on the settings where IPD are not available for some studies. We divide participating studies into two categories based on the type of data they contribute. Let $\mathcal{A}$ denote the collection of studies for which only AD are available. That is, for $j\in \mathcal{A}$, only summary statistics of the original outcomes $\left\{\left(n_{ij},{\overline{U}}_{ij},{\overline{V}}_{ij},s_{ij}^U,s_{ij}^V\right):i=1,2\right\}$ are available, where

$$\begin{gathered} {\overline{U}}_{ij}=\frac{1}{n_{ij}}\sum _{k=1}^{n_{ij}}{U}_{ijk}, \\ {\overline{V}}_{ij}=\frac{1}{n_{ij}}\sum _{k=1}^{n_{ij}}{V}_{ijk}, \\ {s}_{ij}^U=\sqrt{\frac{{\sum }_{k=1}^{n_{ij}}{\left(U_{ijk}-{\overline{U}}_{ij}\right)}^2}{n_{ij}\left(n_{ij}-1\right)}}, \\ {s}_{ij}^V=\sqrt{\frac{{\sum }_{k=1}^{n_{ij}}{\left(V_{ijk}-{\overline{V}}_{ij}\right)}^2}{n_{ij}\left(n_{ij}-1\right)}}. \end{gathered}$$

Let $\mathcal{I}$ denote the set of studies with available IPD, that is, for $j\in \mathcal{I}$, all individual-level outcomes $\left\{\left(U_{ijk},V_{ijk}\right):k=1,\dots ,n_{ij},i=1,2\right\}$ are available.

Although our model specification shares similar hierarchical structures as the standard random-effects MVMA model, they differ substantially. We impose our modeling assumptions directly on the original individual outcomes, whereas the MVMA approaches typically postulate modeling assumptions on individual study treatment effect estimates. Furthermore, although both models involve within- and between-study correlations, these parameters refer to different quantities under the two models. For MVMA, the within-study correlation refers to correlation between treatment effect estimates on different outcomes conditional on study membership, and the between-study correlation refers to the correlation between the true treatment effect sizes on different outcomes across studies (see, for example Jackson et al¹²). Moreover, it is typical in MVMA to assume that both the study-specific treatment effect estimates and the true treatment effect parameters follow a multivariate normal distribution (or are approximately normal).¹⁹ In contrast, in the current setting, the within-study correlation refers to the correlation between original outcomes of the same individual, and the between-study correlation refers to the correlation among the underlying group-specific mean responses. We present this contrast in Table 1 for the setting with two continuous outcomes and where treatment effects are estimated by the differences in sample means.

Table 1:

Comparison of model setups for the proposed approach and the standard MVMA

	The proposed approach	MVMA
Within-study correlation	$\mathit{\text{corr}}\left(U_{ijk},V_{ijk}\mid {\gamma }_{ij}^U,{\gamma }_{ij}^V\right)$	$\mathit{\text{corr}}\left(\left({\overline{U}}_{1j}-{\overline{U}}_{2j}\right),\left({\overline{V}}_{1j}-{\overline{V}}_{2j}\right)\mid {\gamma }_{1j}^U,{\gamma }_{2j}^U,{\gamma }_{1j}^V,{\gamma }_{2j}^V\right)$
Between-study correlation	$\mathit{\text{corr}}\left({\gamma }_{ij}^U,{\gamma }_{ij}^V\right)$	$\mathit{\text{corr}}\left(\left({\gamma }_{1j}^U-{\gamma }_{2j}^U\right),\left({\gamma }_{1j}^V-{\gamma }_{2j}^V\right)\right)$

We make the comparison more explicit by writing out the model assumptions for a standard random-effects bivariate meta-analysis of two continuous outcomes using our notations:

$$\begin{gathered} \left[\begin{array}{l}{\overline{U}}_{1j}-{\overline{U}}_{2j}\hfill \\ {\overline{V}}_{1j}-{\overline{V}}_{2j}\hfill \end{array}\right]\mid \left({\gamma }_{1j}^U,{\gamma }_{1j}^V,{\gamma }_{2j}^U,{\gamma }_{2j}^V\right)~MVN\left(\left[\begin{array}{l}{\gamma }_{1j}^U-{\gamma }_{2j}^U\hfill \\ {\gamma }_{1j}^V-{\gamma }_{2j}^V\hfill \end{array}\right],D_{1j}\right), \\ \left[\begin{array}{c}{\gamma }_{1j}^U-{\gamma }_{2j}^U\\ {\gamma }_{1j}^V-{\gamma }_{2j}^V\end{array}\right]~MVN\left(\left[\begin{array}{c}{\mu }_1^U-{\mu }_2^U\\ {\mu }_1^V-{\mu }_2^V\end{array}\right],D_2\right), \end{gathered}$$

where

$$\begin{gathered} D_{1j}=\left[\begin{array}{cc}\frac{{\left({\sigma }_{1j}^U\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^U\right)}^2}{n_{2j}}& {\rho }_j^{*}\sqrt{\frac{{\left({\sigma }_{1j}^U\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^U\right)}^2}{n_{2j}}}\sqrt{\frac{{\left({\sigma }_{1j}^V\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^V\right)}^2}{n_{2j}}}\\ {\rho }_j^{*}\sqrt{\frac{{\left({\sigma }_{1j}^U\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^U\right)}^2}{n_{2j}}}\sqrt{\frac{{\left({\sigma }_{1j}^V\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^V\right)}^2}{n_{2j}}}& \frac{{\left({\sigma }_{1j}^V\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^V\right)}^2}{n_{2j}}\end{array}\right], \\ {\rho }_j^{*}=\frac{\frac{\rho {\sigma }_{1j}^U{\sigma }_{1j}^V}{n_{1j}}+\frac{\rho {\sigma }_{2j}^U{\sigma }_{2j}^V}{n_{2j}}}{\sqrt{\frac{{\left({\sigma }_{1j}^U\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^U\right)}^2}{n_{2j}}}\sqrt{\frac{{\left({\sigma }_{1j}^V\right)}^2}{n_{1j}}+\frac{{\left({\sigma }_{2j}^V\right)}^2}{n_{2j}}}}, \\ {D}_2=\left[\begin{array}{cc}{\left({\tau }_1^U\right)}^2+{\left({\tau }_2^U\right)}^2& {\kappa }^{*}\sqrt{{\left({\tau }_1^U\right)}^2+{\left({\tau }_2^U\right)}^2}\sqrt{{\left({\tau }_1^V\right)}^2+{\left({\tau }_2^V\right)}^2}\\ {\kappa }^{*}\sqrt{{\left({\tau }_1^U\right)}^2+{\left({\tau }_2^U\right)}^2}\sqrt{{\left({\tau }_1^V\right)}^2+{\left({\tau }_2^V\right)}^2}& {\left({\tau }_1^V\right)}^2+{\left({\tau }_2^V\right)}^2\end{array}\right], \\ {\kappa }^{*}=\frac{\kappa {\tau }_1^U{\tau }_1^V+\kappa {\tau }_2^U{\tau }_2^V}{\sqrt{{\left({\tau }_1^U\right)}^2+{\left({\tau }_2^U\right)}^2}\sqrt{{\left({\tau }_1^V\right)}^2+{\left({\tau }_2^V\right)}^2}}. \end{gathered}$$

${\rho }_j^{*}$ and κ* correspond to the within- and between-study correlation in the MVMA setting respectively.

2.2. The proposed method

As mentioned before, when complete IPD are available from all studies, values of combined outcomes can be computed for every individual and standard two-stage meta-analysis or IPD meta-analysis methods apply. In this section, we present our approach based on multiple reconstructed IPD for studies that provide AD only. Once pseudo IPD for every study in $\mathcal{A}$ are generated, they are combined with the observed IPD from studies in $\mathcal{I}$ to form one set of complete IPD, and standard two-stage meta-analytic methods can be carried out to obtain an overall treatment effect estimate on the combined outcome of interest. In what follows, we first present our method for the reconstruction of IPD, then describe how results based on multiple reconstructed IPD are pooled to arrive at the final treatment effect estimates.

2.2.1. Reconstructions of IPD

Suppose $j\in \mathcal{A}$ then for the k-th participant in arm i of study j, the values of original outcomes are imputed from a bivariate normal distribution with mean and variance set to be the observed sample summary statistics, and correlation set to be $\widehat{\rho }$, which is an estimate of the within-individual correlation ρ, i.e.

$$\left[\begin{array}{c}{U}_{ijk}^{*}\\ V_{ijk}^{*}\end{array}\right]~MVN\left(\left[\begin{array}{c}{\overline{U}}_{ij}\\ {\overline{V}}_{ij}\end{array}\right],n_{ij}\left[\begin{array}{cc}{\left(s_{ij}^U\right)}^2& \widehat{\rho }{s}_{ij}^U{s}_{ij}^V\\ \widehat{\rho }{s}_{ij}^U{s}_{ij}^V& {\left(s_{ij}^V\right)}^2\end{array}\right]\right).$$

While summary statistics such as sample average $\left({\overline{U}}_{ij},{\overline{V}}_{ij}\right)$ and the associated standard errors $\left(s_{ij}^U,s_{ij}^U\right)$ are often reported by individual studies, estimates of the within-study correlation ρ are not commonly provided. The within-study correlation ρ we consider here is the correlation between the original study outcomes. As we clarify in Section 2.1, this ρ is different from the within-study correlation commonly considered in MVMA, which is the correlation between the two treatment effect estimates within each study. Nonetheless, the problem of estimating within-study correlations also arises in MVMA and some of the approaches can be adapted to our setting, such as estimating the within-study correlation from IPD and conducting sensitivity analysis over a plausible range of values.

The impact of $\widehat{\rho }$ on the final treatment effect estimator depends on how the original outcomes are combined. The estimation of ρ depends on data availability. In the remainder of this subsection, we will first define linear versus non-linear combined outcomes, contrast the impact of $\widehat{\rho }$ on treatment effect estimates for these two categories of outcomes, and then propose estimators of ρ that are suitable under different data availability scenarios.

Linear versus non-linear combined outcomes

We introduce the notion of a linear combined outcome: a combined outcome is linear if it can be written in the following form:

$$Y_{ijk}=g\left(U_{ijk},V_{ijk}\right)=g_1\left(U_{ijk}\right)+g_2\left(V_{ijk}\right),$$

where g₁(·), g₂(·) are some user-specified functions. For example, Y_ijk = U_ijk + V_ijk and Y_ijk = 1(U_ijk > u) + 1(V_ijk > v), where u and v are user-specified constants representing some meaningful thresholds, are both linear combined outcomes. Note that linear combined outcomes include, but not limited to, linear combinations of the original outcomes. We term combined outcomes that are not linear as non-linear combined outcomes. For example,

$$Y_{ijk}=\mathbf{1}\left(U_{ijk}>u,V_{ijk}>v\right).$$

Suppose Y_ijk is linear and we are interested in estimating the parameter θ₀ = E_G[θ_j], where

$$\begin{gathered} {\theta }_j=h\left(E_j\left[Y_{1jk}\right]\right)-h\left(E_j\left[Y_{2jk}\right]\right) \\ =h\left(E_j\left[g_1\left(U_{1jk}\right)\right]+E_j\left[g_2\left(V_{1jk}\right)\right]\right)-h\left(E_j\left[g_1\left(U_{2jk}\right)\right]+E_j\left[g_2\left(V_{2jk}\right)\right]\right). \end{gathered}$$

Note that θ_j depends on the original outcomes only through their marginal distributions. Thus, by the assumption made in Section 2.1, consistent estimates of θ₀ can be obtained as long as the marginal distributions of the reconstructed outcomes $U_{ijk}^{*}$ and $V_{ijk}^{*}$ match those of the original data in each study. Therefore, the specification of $\widehat{\rho }$ in the reconstruction step does not affect the consistency of the final estimator. It does, however, affects its efficiency. Below we illustrate this dependence through examining the variance of the final treatment effect estimator under a simple setting.

We consider the setting where all studies provide AD only. We assume hierarchical normality for the original outcomes and let ${\left({\sigma }_{ij}^U\right)}^2={\left({\sigma }_{ij}^V\right)}^2=1$, i = 1, 2, j = 1, …, J and n_1j = n_2j = n_j for the ease of notation. We assume that all the variance parameters (between-and within-study) are known. As before, let ρ be the true underlying correlation between the two original outcomes and $\widehat{\rho }$ be the value used in IPD reconstruction. Let ${\overline{U}}_{ij}$, ${\overline{V}}_{ij}$ represent the sample means of the real (unavailable) IPD and ${\overline{U}}_{ij}^{*}$, ${\overline{V}}_{ij}^{*}$ are sample means of the reconstructed pseudo IPD. We have

$$\begin{gathered} \left[\begin{array}{c}{\overline{U}}_{ij}\\ {\overline{V}}_{ij}\end{array}\right]\mid \left({\gamma }_{ij}^U,{\gamma }_{ij}^V\right)~MVN\left(\left[\begin{array}{c}{\gamma }_{ij}^U\\ {\gamma }_{ij}^V\end{array}\right],\left[\begin{array}{cc}\frac{1}{n_j}& \frac{\rho }{n_j}\\ \frac{\rho }{n_j}& \frac{1}{n_j}\end{array}\right]\right), \\ \left[\begin{array}{l}{\overline{U}}_{ij}^{*}\hfill \\ {\overline{V}}_{ij}^{*}\hfill \end{array}\right]\mid \left({\overline{U}}_{ij},{\overline{V}}_{ij}\right)~MVN\left(\left[\begin{array}{l}{\overline{U}}_{ij}\hfill \\ {\overline{V}}_{ij}\hfill \end{array}\right],\left[\begin{array}{ll}\frac{1}{n_j}\hfill & \frac{\widehat{\rho }}{n_j}\hfill \\ \frac{\widehat{\rho }}{n_j}\hfill & \frac{1}{n_j}\hfill \end{array}\right]\right). \end{gathered}$$

We consider the simple linear combined outcome Y_1,ijk = U_ijk + V_ijk. Let ${\theta }_j=\left({\gamma }_{1j}^U+{\gamma }_{1j}^V\right)-\left({\gamma }_{2j}^U+{\gamma }_{2j}^V\right)$ and ${\theta }_0=E_{G_1}\left[{\theta }_j\right]$, where G₁ denotes the underlying distribution of the study-specific effect size θ_j. Furthermore, let ${\widehat{\theta }}_j=\left({\overline{U}}_{1j}^{*}+{\overline{V}}_{1j}^{*}\right)-\left({\overline{U}}_{2j}^{*}+{\overline{V}}_{2j}^{*}\right)$ denote the study j’s treatment effect estimate on combined outcome Y₁ calculated from a one set of reconstructed IPD, it can be verified that

$$\begin{gathered} E\left[{\widehat{\theta }}_j\right]=E\left[E\left[{\widehat{\theta }}_j\mid {\gamma }_{1j}^U,{\gamma }_{1j}^V,{\gamma }_{2j}^U,{\gamma }_{2j}^V\right]\right]=E\left[\left({\gamma }_{1j}^U+{\gamma }_{1j}^V\right)-\left({\gamma }_{2j}^U+{\gamma }_{2j}^V\right)\right]=E\left[{\theta }_j\right]={\theta }_0, \\ Var\left({\widehat{\theta }}_j\mid {\gamma }_{1j}^U,{\gamma }_{1j}^V,{\gamma }_{2j}^U,{\gamma }_{2j}^V\right)=Var\left({\overline{U}}_{1j}^{*}+{\overline{V}}_{1j}^{*}\mid {\gamma }_{1j}^U,{\gamma }_{1j}^V\right)+Var\left({\overline{U}}_{2j}^{*}+{\overline{V}}_{2j}^{*}\mid {\gamma }_{2j}^U,{\gamma }_{2j}^V\right)=\frac{4}{n_j}\left(2+\rho +\widehat{\rho }\right), \\ Var\left({\widehat{\theta }}_j\right)=\frac{4}{n_j}\left(2+\rho +\widehat{\rho }\right)+{\xi }^2,\text{ where }{\xi }^2={\left({\tau }_1^U\right)}^2+{\left({\tau }_1^V\right)}^2+{\left({\tau }_2^U\right)}^2+{\left({\tau }_2^V\right)}^2+2\kappa \left({\tau }_1^U{\tau }_1^V+{\tau }_2^U{\tau }_2^V\right). \end{gathered}$$

Consider the inverse-variance weighted pooled treatment effect estimate based one reconstruction of IPD:

$$\widehat{\theta }=\sum _{j=1}^J{w}_j{\widehat{\theta }}_j,\text{ where }{w}_j=\frac{1/Var\left({\widehat{\theta }}_j\right)}{{\sum }_{j\prime =1}^{J}1/Var\left({\widehat{\theta }}_{j\prime }\right)}.$$

We have

$$E\left[\widehat{\theta }\right]={\theta }_0,$$ (1)

$$Var\left(\widehat{\theta }\right)=\frac{1}{{\sum }_{j=1}^{J}1/Var\left({\widehat{\theta }}_j\right)}=\frac{1}{{\sum }_{j=1}^J\frac{1}{\frac{4}{n_j}\left(2+\rho +\widehat{\rho }\right)+{\xi }^2}}.$$ (2)

As can be seen from (1) & (2), the expectation of the final treatment effect estimate does not depend on $\widehat{\rho }$, the value of within-study correlation used in the reconstruction, whereas its variance does. In contrast, for non-linear combined outcomes, θ_j depends on the joint distribution of U and V and θ₀ varies across different values of ρ. Therefore, accurate characterization of ρ is essential and misspecification of $\widehat{\rho }$ could lead to substantial bias. In what follows, we describe the estimation approaches in details when some studies provide IPD, and when all studies provide AD only respectively.

Some studies provide IPD

We first consider settings where IPD are available for at least one of the studies, from which an estimate of the within-individual correlation coefficient ρ can be obtained. There are various methods to estimate ρ using IPD. In our simulation study, we used a weighted average of the sample Pearson correlation coefficients with weights proportional to sample sizes. That is,

$${\widehat{\rho }}_{IPD}=\frac{1}{{\sum }_{i=1}^2{\sum }_{j\in \mathcal{I}}{n}_{ij}}\left(\sum _{i=1}^2\sum _{j\in \mathcal{I}}\frac{n_{ij}{\sum }_{k=1}^{n_{ij}}\left(U_{ijk}-{\overline{U}}_{ij}\right)\left(V_{ijk}-{\overline{V}}_{ij}\right)}{\sqrt{{\sum }_{k=1}^{n_{ij}}{\left(U_{ijk}-{\overline{U}}_{ij}\right)}^2}\sqrt{{\sum }_{k=1}^{n_{ij}}{\left(V_{ijk}-{\overline{V}}_{ij}\right)}^2}}\right).$$ (3)

If one is willing to make fully parametric assumptions on the distribution of (U_ijk, V_ijk), maximum likelihood estimators or Bayesian estimators are viable options as well.

All studies provide AD only

When none of the studies provides IPD, we can only estimate ρ from AD. The data generating process described in Section 2.1 implies the following properties for the marginal distribution of the observed sample means:

$$\begin{gathered} E\left[{\overline{U}}_{ij}\right]={\mu }_i^U, \\ E\left[{\overline{V}}_{ij}\right]={\mu }_i^V, \\ Var\left({\overline{U}}_{ij}\right)=\frac{{\left({\sigma }_{ij}^U\right)}^2}{n_{ij}}+{\left({\tau }_i^U\right)}^2, \\ Var\left({\overline{V}}_{ij}\right)=\frac{{\left({\sigma }_{ij}^V\right)}^2}{n_{ij}}+{\left({\tau }_i^V\right)}^2, \\ Cov\left({\overline{U}}_{ij},{\overline{V}}_{ij}\right)=\frac{\rho {\sigma }_{ij}^U{\sigma }_{ij}^V}{n_{ij}}+\kappa {\tau }_i^U{\tau }_i^V. \end{gathered}$$ (4)

Hence, ρ and κ are not identifiable from AD only. Assuming κ = κ₀, we can derive the following estimator for ρ based on the method of moments:

$${\widehat{\rho }}_{MM}=\frac{1}{2J}\sum _{i=1}^2\sum _{j=1}^J\frac{n_{ij}\left[\left({\overline{U}}_{ij}-{\widehat{\mu }}_i^U\right)\left({\overline{V}}_{ij}-{\widehat{\mu }}_i^V\right)-{\kappa }_0{\widehat{\tau }}_i^U{\widehat{\tau }}_i^V\right]}{{\widehat{\sigma }}_{ij}^U{\widehat{\sigma }}_{ij}^V},$$ (5)

where ${\widehat{\mu }}_i^U$, ${\widehat{\mu }}_i^V$, ${\widehat{\sigma }}_{ij}^U$, ${\widehat{\sigma }}_{ij}^V$ are consistent estimators for ${\mu }_i^U$, ${\mu }_i^V$, ${\sigma }_{ij}^U$, ${\sigma }_{ij}^V$. One set of estimators is given below: ${\widehat{\sigma }}_{ij}^U=n_{ij}^{1/2}{s}_{ij}^U,{\widehat{\sigma }}_{ij}^V=n_{ij}^{1/2}{s}_{ij}^V$, and ${\widehat{\mu }}_i^U$, ${\widehat{\mu }}_i^V$ are the inverse-variance weighted averages of the observed group means ${\overline{U}}_{ij}$ and ${\overline{V}}_{ij}$ respectively. The weights were estimated using $s_{ij}^V$, $s_{ij}^U$ and the DerSimonian and Laird estimators³⁶ of ${\left({\tau }_i^U\right)}^2$ and ${\left({\tau }_i^V\right)}^2$:

$${\widehat{\mu }}_i^U=\frac{{\sum }_{j=1}^J{\widehat{w}}_{ij}^U{\overline{U}}_{ij}}{{\sum }_{j=1}^J{\widehat{w}}_{ij}^U},$$

with

$$\begin{gathered} w_{ij}^U={\left\{{\left(s_{ij}^U\right)}^2+{\left({\widehat{\tau }}_i^U\right)}^2\right\}}^{-1}, \\ {\left({\widehat{\tau }}_i^U\right)}^2=\text{max}\left\{0,\frac{Q_i^U-\left(J-1\right)}{{\sum }_{j=1}^J{\left(s_{ij}^U\right)}^{-2}-\frac{{\sum }_{j=1}^J{\left(s_{ij}^U\right)}^{-4}}{{\sum }_{j=1}^J{\left(s_{ij}^U\right)}^{-2}}}\right\}, \\ {Q}_i^U=\sum _{j=1}^J{\left(s_{ij}^U\right)}^{-2}{\left({\overline{U}}_{ij}-{\overline{\overline{U}}}_i\right)}^2, \\ {\overline{\overline{U}}}_i=\frac{{\sum }_{j=1}^J{\left(s_{ij}^U\right)}^{-2}{\overline{U}}_{ij}}{{\sum }_{j=1}^J{\left(s_{ij}^U\right)}^{-2}}. \end{gathered}$$

The estimation for ${\widehat{\mu }}_i^V$ can be done similarly. Note that the resulting ${\widehat{\rho }}_{MM}$ is not guaranteed to be bounded between −1 and 1. One option is to truncate it at −1 or 1 accordingly if the estimate is out of range. Alternative truncation points can be established based on prior information. For instance, if two outcomes are believed to be positively correlated, such as the systolic and diabolic blood pressure, it would be more reasonable to truncate the correlation estimates at 0 and 1.

A likelihood-based estimator can also be derived. Under mild regularity conditions, the sample means are approximately normally distributed when sample sizes are sufficiently large by the central limit theorem. Therefore we can obtain an estimate of the correlation through maximizing the approximate likelihood function $\tilde{L}$ on the interval [−1, 1]

$$\begin{array}{l}{\widehat{\rho }}_{ML}=\underset{\rho \in \left[-1,1\right]}{\text{arg}\text{max}}\tilde{L}\left(\rho \right)\\ =\underset{\rho \in \left[-1,1\right]}{\text{arg}\text{max}}\prod _{i=1}^2\prod _{j=1}^J\frac{1}{\sqrt{1-{\psi }_{ij}^2}}\text{exp}\left(-\frac{1}{2\left(1-{\psi }_{ij}^2\right)}\left[\frac{{\left({\overline{U}}_{ij}-{\widehat{\mu }}_i^U\right)}^2}{\frac{{\left({\widehat{\sigma }}_{ij}^U\right)}^2}{n_{ij}}+{\left({\widehat{\tau }}_i^U\right)}^2}+\frac{{\left({\overline{V}}_{ij}-{\widehat{\mu }}_i^V\right)}^2}{\frac{{\left({\widehat{\sigma }}_{ij}^V\right)}^2}{n_{ij}}+{\left({\widehat{\tau }}_i^V\right)}^2}-\frac{2{\psi }_{ij}\left({\overline{U}}_{ij}-{\widehat{\mu }}_i^U\right)\left({\overline{V}}_{ij}-{\widehat{\mu }}_i^V\right)}{\sqrt{\left\{\frac{{\left({\widehat{\sigma }}_{ij}^U\right)}^2}{n_{ij}}+{\left({\widehat{\tau }}_i^U\right)}^2\right\}\left\{\frac{{\left({\widehat{\sigma }}_{ij}^V\right)}^2}{n_{ij}}+{\left({\widehat{\tau }}_i^V\right)}^2\right\}}}\right]\right),\end{array}$$

with

$${\psi }_{ij}=\frac{\frac{\rho {\widehat{\sigma }}_{ij}^U{\widehat{\sigma }}_{ij}^V}{n_{ij}}+{\kappa }_0{\widehat{\tau }}_i^U{\widehat{\tau }}_i^V}{\sqrt{\left\{\frac{{\left({\widehat{\sigma }}_{ij}^U\right)}^2}{n_{ij}}+{\left({\widehat{\tau }}_i^U\right)}^2\right\}\left\{\frac{{\left({\widehat{\sigma }}_{ij}^V\right)}^2}{n_{ij}}+{\left({\widehat{\tau }}_i^V\right)}^2\right\}}}.$$

The maximize ${\widehat{\rho }}_{ML}$ is also the posterior mode under a uniform prior distribution of ρ over the interval [−1, 1]. Alternative choices of priors can be adopted to incorporate prior beliefs about the correlation (see, for example Bujkiewicz et al¹¹).

The value of κ is required for the calculation of ${\widehat{\rho }}_{MM}$ or ${\widehat{\rho }}_{ML}$, which is often unavailable in practice. In MVMA, the between-study correlation, as a parameter in the variance-covariance matrix for study-specific treatment effects, can be estimated using various methods including the maximum likelihood,^6,7 the restricted maximum likelihood^6,8 and the method of moments,¹² provided with knowledge of the within-study covariance matrices. In a Bayesian setting, Bujkiewicz et al¹¹ used an informative prior distribution of the between-study correlation based on a separate collection of studies. As mentioned in Section 2.1, the κ in our setting is different from that in the MVMA setting. For the IPD reconstruction, we only require information on ρ. Knowledge of κ, however, facilitates the estimation of ρ. When there is no external information about κ, applying the method of moments to the study-level summaries ignoring the within-study sampling variability provides a crude estimator for κ, which can be subsequently used to obtain $\widehat{\rho }$, especially when the individual study sizes are large. Lastly, because the value of κ affects the final results only through the value of $\widehat{\rho }$ used in the reconstruction, we recommend conducting sensitivity analyses for a range of plausible values of $\widehat{\rho }$ when a precise estimate of ρ is unavailable.

2.2.2. Obtain final estimates from multiple reconstructed IPD

The reconstruction procedure is repeated M times. Let $\left({\widehat{\theta }}_l,V_l\right)$, l = 1, …, M denote the point and variance estimates obtained from the l-th reconstructed dataset. To combine estimates from multiple reconstructed IPD, we follow the Rubin’s rule for combining estimates from multiple imputations to obtain the final pooled point estimate of treatment effect on the combined outcome³⁰:

$${\widehat{\theta }}_{MR}=\frac{1}{M}\sum _{l=1}^M{\widehat{\theta }}_l.$$

In the context of multiple imputation, Rubin³⁰ also proposed the following formula for obtaining the standard error estimates for the pooled estimator across multiple imputed datasets:

$$\widehat{\text{s.e.}}\left({\widehat{\theta }}_{MR}\right)=\sqrt{\frac{1}{M}\sum _{l=1}^M{V}_l+\left(\frac{M+1}{M}\right)\frac{{\sum }_{l=1}^M{\left({\widehat{\theta }}_l-{\widehat{\theta }}_{MR}\right)}^2}{M-1}}.$$ (6)

A direct naive application of this estimator does not perform well in our setting for a few reasons. First, when $\widehat{\rho }$ is estimated true from the available IPD or AD, $\widehat{s.e\cdot }\left({\widehat{\theta }}_{MR}\right)$ is likely to un-derestimate the sampling variation because it does not take into account the uncertainty in estimating $\widehat{\rho }$. Second, the accuracy of $\widehat{s.e\cdot }\left({\widehat{\theta }}_{MR}\right)$ depends on the variance V_l of $\widehat{{\theta }_l}$ obtained from each pseudo IPD. The accuracy of V_l is sensitive to mis-specifications of $\widehat{\rho }$ used in the reconstruction.

We therefore recommend the use of a bootstrap procedure to estimate the standard errors.³⁷ Since the observed data $\mathcal{D}$ consists of two parts, $\text{IPD:}\left\{\left(U_{ijk},V_{ijk}\right):k=1,\dots ,n_{ij},j\in \mathcal{I},i=1,2\right\}$, and $\text{AD: }\left\{\left(n_{ij},{\overline{U}}_{ij},{\overline{V}}_{ij},s_{ij}^U,s_{ij}^V\right):j\in \mathcal{A},i=1,2\right\}$, we generate bootstrap replicates of each part separately. We first apply non-parametric bootstrap to generate replicates of the observed IPD. The same technique has been used by Daniels and Hughes³⁸ to estimate the correlation between treatment effects on a clinical outcome and its potential surrogate marker. We then generate replicates of AD by applying non-parametric bootstrap to the study summary statistics, where we treat $\left(n_{ij},{\overline{U}}_{ij},{\overline{V}}_{ij},s_{ij}^U,s_{ij}^V\right)$, $j\in \mathcal{A}$ as a random sample from some underlying joint distribution. The specific steps for calculating the bootstrap standard errors are given below:

• Step 1: Generate a bootstrap replicate of IPD. For each $j\in \mathcal{I}$, i ∈ {1,2}, take a sample with replacement of size n_ij from {(U_ijk, V_ijk) : k = 1, …, n_ij} to obtain $\left\{\left(U_{ijk}^{†},V_{ijk}^{†}\right):k=1,\dots ,n_{ij}\right\}$;

• Step 2: Generate a bootstrap replicate of AD. Sample with replacement from $\mathcal{A}$ to get a new set of study labels $\mathcal{L}=\left\{j_1,\dots ,j_{\left|\mathcal{A}\right|}\right\}$, then form the bootstrap replicate of AD correspondingly, i.e. $\left\{\left(n_{i{j}_r},{\overline{U}}_{i{j}_r}^{†},{\overline{V}}_{i{j}_r}^{†},s_{i{j}_r}^U{}^{†},s_{i{j}_r}^V{}^{†}\right):j_r\in \left\{j_1,\dots ,j_{\left|\mathcal{A}\right|}\right\},i=1,2\right\}$;

• Step 3: Repeat the proposed reconstruction and estimation procedures on the bootstrap replicate ${\mathcal{D}}^{†}=\left\{\left(U_{ijk}^{†},V_{ijk}^{†}\right):k=1,\dots ,n_{ij},j\in \mathcal{I},i=1,2\right\}\cup \left\{\left(n_{i{j}_r},{\overline{U}}_{i{j}_r}^{†},{\overline{V}}_{i{j}_r}^{†},s_{i{j}_r}^U{}^{†},s_{i{j}_r}^V{}^{†}\right):j_r\in \left\{j_1,\dots ,j_{\left|\mathcal{A}\right|}\right\},i=1,2\right\}$, and obtain a new treatment effect estimate ${\widehat{\theta }}_{MI}^b$;

• Step 4: Repeat Step 1–3 B times and obtain ${\widehat{\theta }}_{MR}^b$, b = 1, …, B. Compute the bootstrap standard error estimate as

  $${\widehat{s.e.}}_{\mathit{\text{boot}}}\left({\widehat{\theta }}_{MR}\right)=\sqrt{\frac{{\sum }_{b=1}^B{\left({\widehat{\theta }}_{MR}^b-\frac{{\sum }_{b\prime =1}^B{\widehat{\theta }}_{MR}^{b\prime }}{B}\right)}^2}{B-1}.}$$ (7)

3. Simulation studies

We evaluated the finite sample performance of the proposed method through simulation studies. Data from J two-arm RCTs with two continuous original outcomes U and V were generated according to the following hierarchical model.

$$\begin{gathered} \left[\begin{array}{c}{\gamma }_{ij}^U\\ {\gamma }_{ij}^V\end{array}\right]~MVN\left(\left[\begin{array}{c}{\mu }_i^U\\ {\mu }_i^V\end{array}\right],\left[\begin{array}{cc}{\left({\tau }_i^U\right)}^2& \kappa {\tau }_i^U{\tau }_i^V\\ \kappa {\tau }_i^U{\tau }_i^V& {\left({\tau }_i^V\right)}^2\end{array}\right]\right), \\ \left[\begin{array}{c}{U}_{ijk}\\ V_{ijk}\end{array}\right]\mid \left({\gamma }_{ij}^U,{\gamma }_{ij}^V\right)~MVN\left(\left[\begin{array}{c}{\gamma }_{ij}^U\\ {\gamma }_{ij}^V\end{array}\right],\left[\begin{array}{cc}{\left({\sigma }_{ij}^U\right)}^2& \rho {\sigma }_{ij}^U{\sigma }_{ij}^V\\ \rho {\sigma }_{ij}^U{\sigma }_{ij}^V& {\left({\sigma }_{ij}^V\right)}^2\end{array}\right]\right), \\ i=1,2,j=1,\dots ,J,k=1,\dots ,n_{ij}. \end{gathered}$$

We set ${\mu }_1^U=2$, ${\mu }_1^V=1$, ${\mu }_2^U={\mu }_2^V=0$, ${\sigma }_{ij}^U={\sigma }_{ij}^V=1$, for all i, j, and considered a range of values for the within-individual correlation: ρ ∈ {0, 0.2, 0.5, 0.8}. The sample size of each study ranged from 20 to 200 in steps of 10 with equal number of patients in the treatment and control arms.

We applied the proposed method to analyze the following four combined outcomes:

$$\begin{gathered} Y_{1,ijk}=U_{ijk}+V_{ijk}, \\ {Y}_{2,ijk}=1\left(U_{ijk}>1\right)+1\left(U_{ijk}>1.5\right)+1\left(V_{ijk}<1\right)+1\left(V_{ijk}<2\right), \\ {Y}_{3,ijk}=1\left(U_{ijk}>1.5,V_{ijk}<1\right)+1\left(U_{ijk}>1.5,V_{ijk}<2\right), \\ {Y}_{4,ijk}=1\left(U_{ijk}>1.5,V_{ijk}>0.5\right). \end{gathered}$$

Here Y₁ and Y₂ are linear combined outcomes while Y₃ and Y₄ are non-linear combined outcomes. The corresponding parameters of interest are given by:

$$\begin{gathered} {\theta }_{10}:=E_{G_1}\left[{\theta }_{1j}\right],\text{ with }{\theta }_{1j}:=E_j\left[Y_{1,1jk}\right]-E_j\left[Y_{1,2jk}\right], \\ {\theta }_{20}:=E_{G_2}\left[{\theta }_{2j}\right],\text{ with }{\theta }_{2j}:=E_j\left[Y_{2,1jk}\right]-E_j\left[Y_{2,2jk}\right], \\ {\theta }_{30}:=E_{G_3}\left[{\theta }_{3j}\right],\text{ with }{\theta }_{3j}:=E_j\left[Y_{3,1jk}\right]-E_j\left[Y_{3,2jk}\right], \\ {\theta }_{40}:=E_{G_4}\left[{\theta }_{4j}\right],\text{ with }{\theta }_{4j}:=\text{log}\left(\frac{E_j\left[Y_{4,1jk}\right]\left(1-E_j\left[Y_{4,2jk}\right]\right)}{E_j\left[Y_{4,2jk}\right]\left(1-E_j\left[Y_{4,1jk}\right]\right)}\right), \end{gathered}$$

where G_l, l = 1, 2, 3, 4 are the underlying distributions of θ_lj, l = 1, 2, 3, 4, respectively. We investigated 20 simulation scenarios with varying parameter values. Results under scenarios 1 to 8 (see Table 2) are presented in this section. Results under scenarios 9 to 20 are included in the web supplementary materials.

Table 2:

Simulation scenarios

IPD and AD (κ = 0.5)			AD only (κ = 0)
Scenario	J	${\left({\tau }_i^U\right)}^2,{\left({\tau }_i^V\right)}^2$	Scenario	J	${\left({\tau }_i^U\right)}^2,{\left({\tau }_i^V\right)}^2$
1	7	0.05	5	13	0.01
2	7	0.5	6	13	0.05
3	30	0.05	7	50	0.01
4	30	0.5	8	50	0.05

3.1. One study provides IPD

We first investigated the case where one of the studies provided complete IPD and the rest provided AD. Data were generated under scenario 1 to 4 (see Table 2) with different configurations of the number of studies, J, and levels of the between-study heterogeneity, ${\left({\tau }_i^U\right)}^2$, ${\left({\tau }_i^V\right)}^2$, i = 1,2. The sample size of the study that provides IPD was fixed at 20 and the value of κ was set at 0.5.

We set the number of multiple reconstructions M to be 10 and the number of bootstrap replicates B to be 500, and performed 500 experiments under each parameter configuration. Study-specific treatment effect estimates on combined outcomes (calculated from the observed or reconstructed IPD) were pooled by applying the DerSimonian and Laird random-effects method.

We compared point estimates computed from the multiple reconstructed datasets when $\widehat{\rho }$ was estimated with Eq.(3), set to the true value of ρ, or set to 0, against the estimates obtained from applying the DerSimonian and Laird random-effects model to complete IPD of all studies, which corresponded to the ideal situation. The naive standard error estimates were calculated according to Eq.(6) with $\left({\widehat{\theta }}_l,V_l\right)$ obtained from applying the DerSimonian and Laird random-effects model to the l-th reconstructed dataset. We also calculated the average bootstrap standard error estimates (Eq.(7)).

Figure 1 displays the average estimates of treatment effects for the four outcomes in simulation scenario 2. Results from scenario 1, 3 and 4 were similar and were included in the web supplementary materials. Not surprisingly, for linear outcomes Y₁ and Y₂, the proposed method produced results almost identical to those based on complete IPD regardless of the value of $\widehat{\rho }$ used in the reconstruction. For non-linear outcomes Y₃ and Y₄, substantial biases were observed when $\widehat{\rho }$ was set to 0 (purple lines) but the true correlation was nonzero. In contrast, the average treatment effect estimates computed from the multiple reconstructed datasets using ${\widehat{\rho }}_{IPD}$ (blue lines) or the true value ρ (green lines) were very close to the ones obtained from complete data (red lines) across all values of ρ, even though the sample size for the study with available IPD was only 20.

Figure 1:

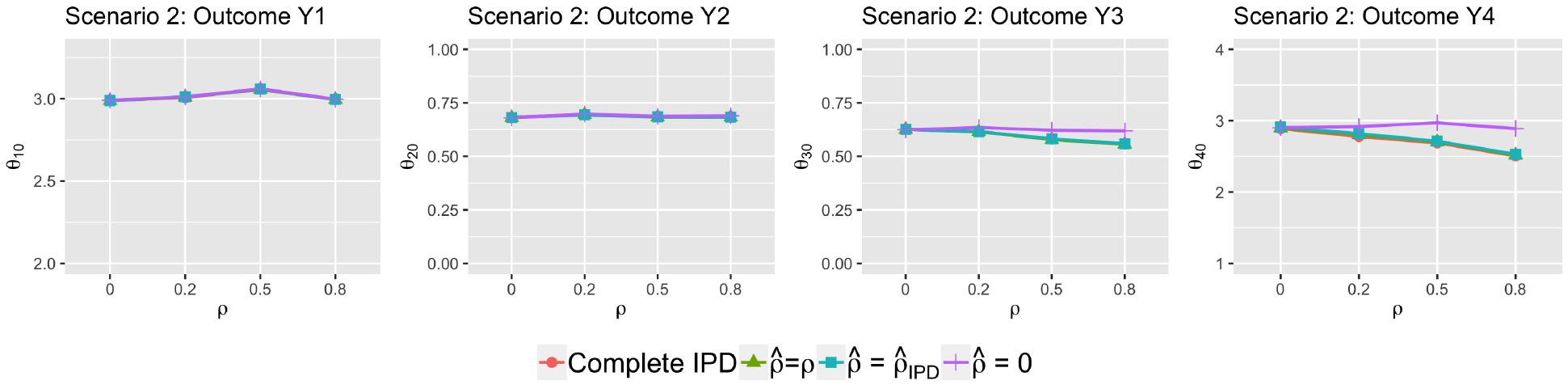
Treatment effect estimates (scenario 2)

Comparisons of average treatment effect estimates based on various $\widehat{\rho }$ versus those obtained from complete IPD. One of the studies provided IPD and the rest provided AD. The simulation parameter values were J = 7, ${\left({\tau }_i^U\right)}^2={\left({\tau }_i^V\right)}^2=0.5$, i = 1, 2, κ = 0.5.

Figure 2 compares the average naive and bootstrap standard error estimates to their empirical counterparts, which were calculated as standard deviations of the treatment effect estimates across 500 iterations. For each panel, the tabs on the right-hand side (SCN 1–4) denote simulation scenarios, the upper tabs (0, 0.2, 0.5, 0.8) represent the true values of ρ used in the data generation, and the labels on the bottom x-axis $\left(\rho ,{\widehat{\rho }}_{IPD},0\right)$ indicate the values taken by $\widehat{\rho }$ in the reconstruction. The naive standard error estimates (blue squares) were conservative under most settings, especially when the between-study variances (τ^U)², (τ^V)² were small. The bootstrap standard error estimates (red dots) in general performed well, except when the number of studies was very small (J = 7) and the between-study variances were relatively large (scenario 2). In such settings, resampling from a small number of studies was unlikely to capture the level of variability in the underlying study population, leading to the observed downward biases in the bootstrap standard error estimates.

Figure 2:

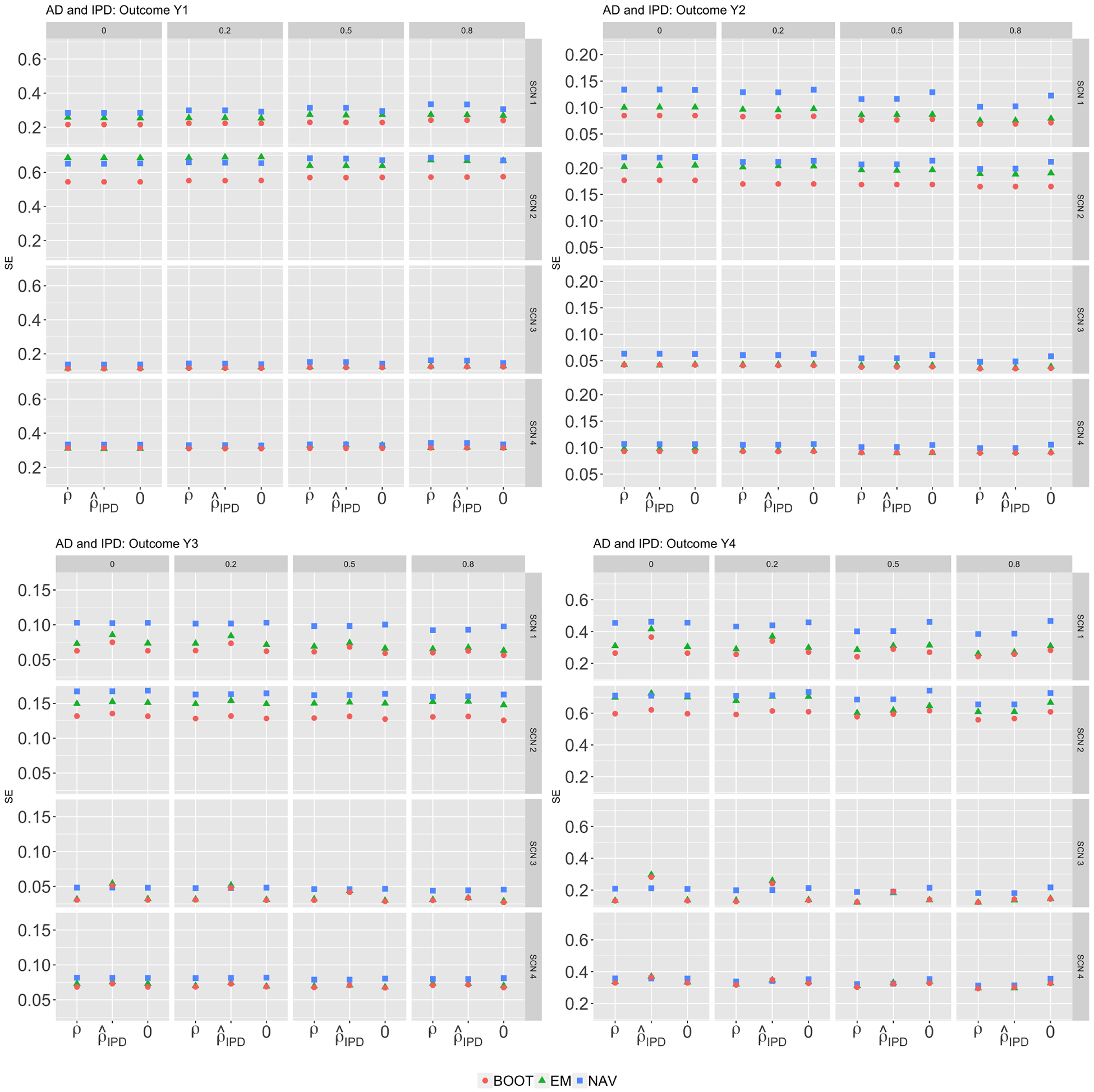
Standard errors (scenario 1–4)

Comparisons of standard error estimates of treatment effect estimates on combined outcomes for various $\widehat{\rho }$. One study provided IPD and the rest provided AD. EMP refers to the empirical standard errors, NAV refers to the average standard error estimates obtained by a naive application of the Rubin’s rule; BOOT refers to the average bootstrap standard error estimates.

3.2. All studies provide AD

We evaluated the performance of our proposed methods when only AD were available for all studies. We simulated data under scenario 5 to 8 (see Table 2 with κ set to be 0). For the $\widehat{\rho }$ required in the reconstruction step, we computed both the moment-based estimator $\left({\widehat{\rho }}_{MM}\right)$ and the likelihood-based estimator $\left({\widehat{\rho }}_{ML}\right)$ using formulae provided in Section 2.2.1 with κ₀ = 0. The truncation points for ${\widehat{\rho }}_{MM}$ were set to be −1 and 1.

Figure 3 presents the treatment effect estimates. Without any IPD, using the true correlation ρ (tan lines) in the reconstruction step yielded results virtually identical to those that would have been obtained if complete IPD were available (red lines) in all settings. Results based on ${\widehat{\rho }}_{MM}$ (the method of moments estimator; green lines) and ${\widehat{\rho }}_{ML}$ (the maximum likelihood estimator; blue lines) were also indistinguishable. For linear combined outcomes Y₁ and Y₂, all lines coincided regardless the values of $\widehat{\rho }$ used in the reconstruction. For non-linear combined outcomes Y₃ and Y₄, the results were sensitive to the misspecification of $\widehat{\rho }$: substantial biases were associated with setting $\widehat{\rho }=0$ when the true ρ deviated from 0 (purple lines). Using ${\widehat{\rho }}_{MM}$ or ${\widehat{\rho }}_{ML}$ in general performed well except when the number of studies was small (J = 13 under scenario 6). When only AD were available, accurate estimation of ρ was difficult when the number of studies was too small or when the between-study heterogeneity was large. For instance, under scenario 6 with ρ = 0, ${\widehat{\rho }}_{MM}$ was out of range and truncated at 1 or −1 in more than 40% of the 500 experiments. In the current setting, we set κ₀ = 0, based on Eq.(5)):

$${\widehat{\rho }}_{MM}=\frac{1}{2J}\sum _{i=1}^2\sum _{j=1}^J\frac{n_{ij}\left({\overline{U}}_{ij}-{\widehat{\mu }}_i^U\right)\left({\overline{V}}_{ij}-{\widehat{\mu }}_i^V\right)}{{\widehat{\sigma }}_{ij}^U{\widehat{\sigma }}_{ij}^V}.$$

Figure 3:

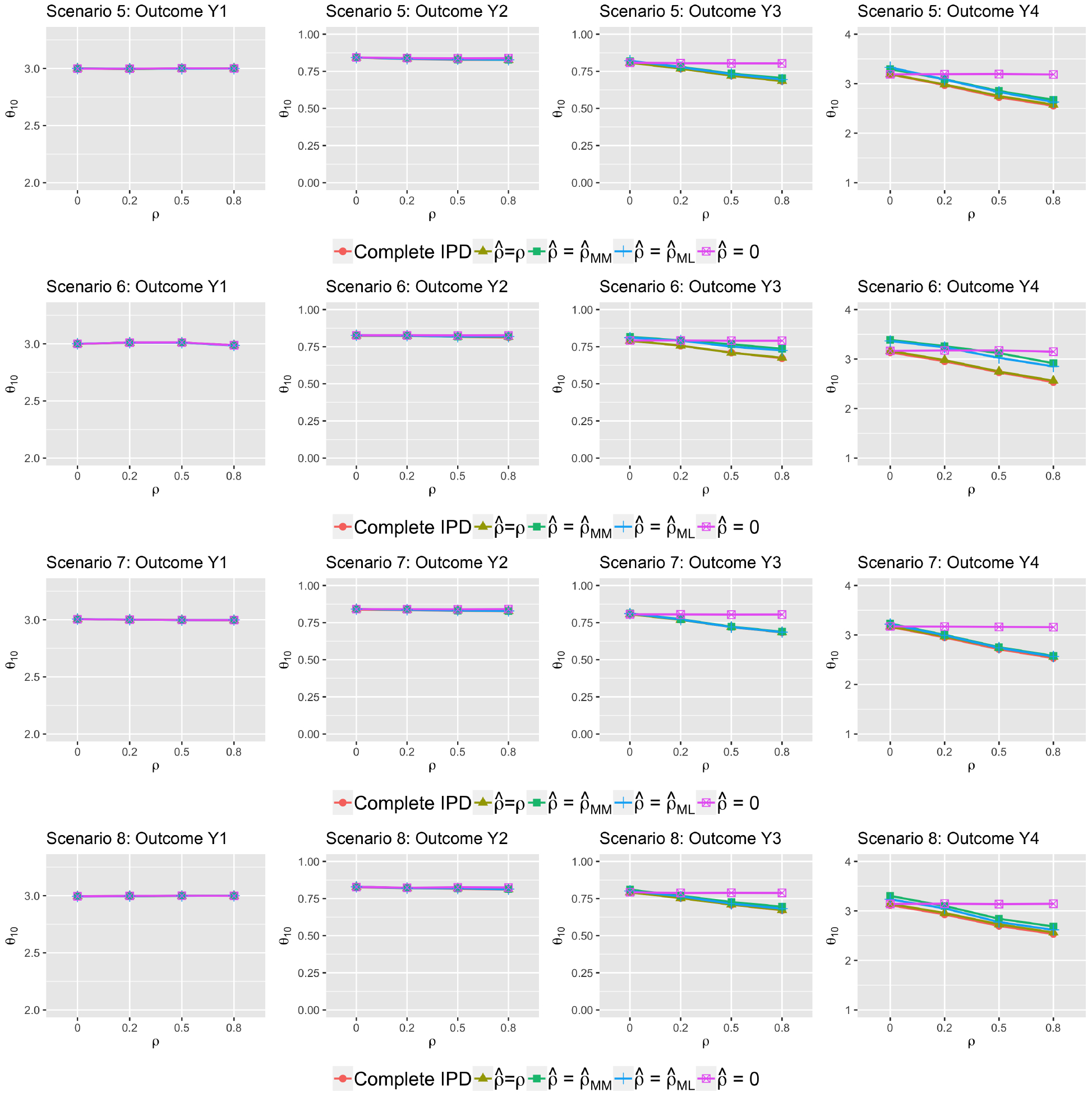
Average treatment effect estimates (scenario 5–8)

Comparisons of treatment effect estimates based on various $\widehat{\rho }$ to those obtained from complete IPD. All studies provided AD only.

Therefore, $Var\left({\widehat{\rho }}_{MM}\right)$ depends on the variance of ${\overline{U}}_{ij}$, ${\overline{V}}_{ij}$, ${\widehat{\mu }}_i^U$, ${\widehat{\mu }}_i^V$, as well as ${\widehat{\sigma }}_{ij}^U$ and ${\widehat{\sigma }}_{ij}^V$. As can be seen from Eq.(4), when the between-study heterogeneity ${\tau }_i^U$ increases, $Var\left({\overline{U}}_{ij}\right)$ increases, and the variance of ${\widehat{\mu }}_i^U$ also increases. Same holds true for outcome V. Therefore, ${\widehat{\rho }}_{MM}$ can be highly variable when the between-study heterogeneity is large.

Results for standard error estimates are presented in Figure 4. For linear combined outcomes (top panels), standard error estimates based on the bootstrap approach (red dots) closely matched the true empirical standard errors (green dots). For non-linear combined outcomes, the bootstrap performed well in general with modest underestimation when the number of studies was small. The standard error estimates obtained by a naive application of the Rubin’s rule (blue dots) were generally biased and were further away from the empirical ones compared the bootstrap standard error estimates. When the number of studies was small, ${\widehat{\rho }}_{MM}$ or ${\widehat{\rho }}_{ML}$ can be highly unstable, and estimators using ${\widehat{\rho }}_{MM}$ or ${\widehat{\rho }}_{ML}$ in the reconstruction step were associated with larger variability compared to using the true correlation ρ or a fixed value, e.g., 0. In such settings, it would be useful to consider sensitivity analyses over a range of plausible values for $\widehat{\rho }$. We illustrate this with a real-world data example in Section 4.1.

Figure 4:

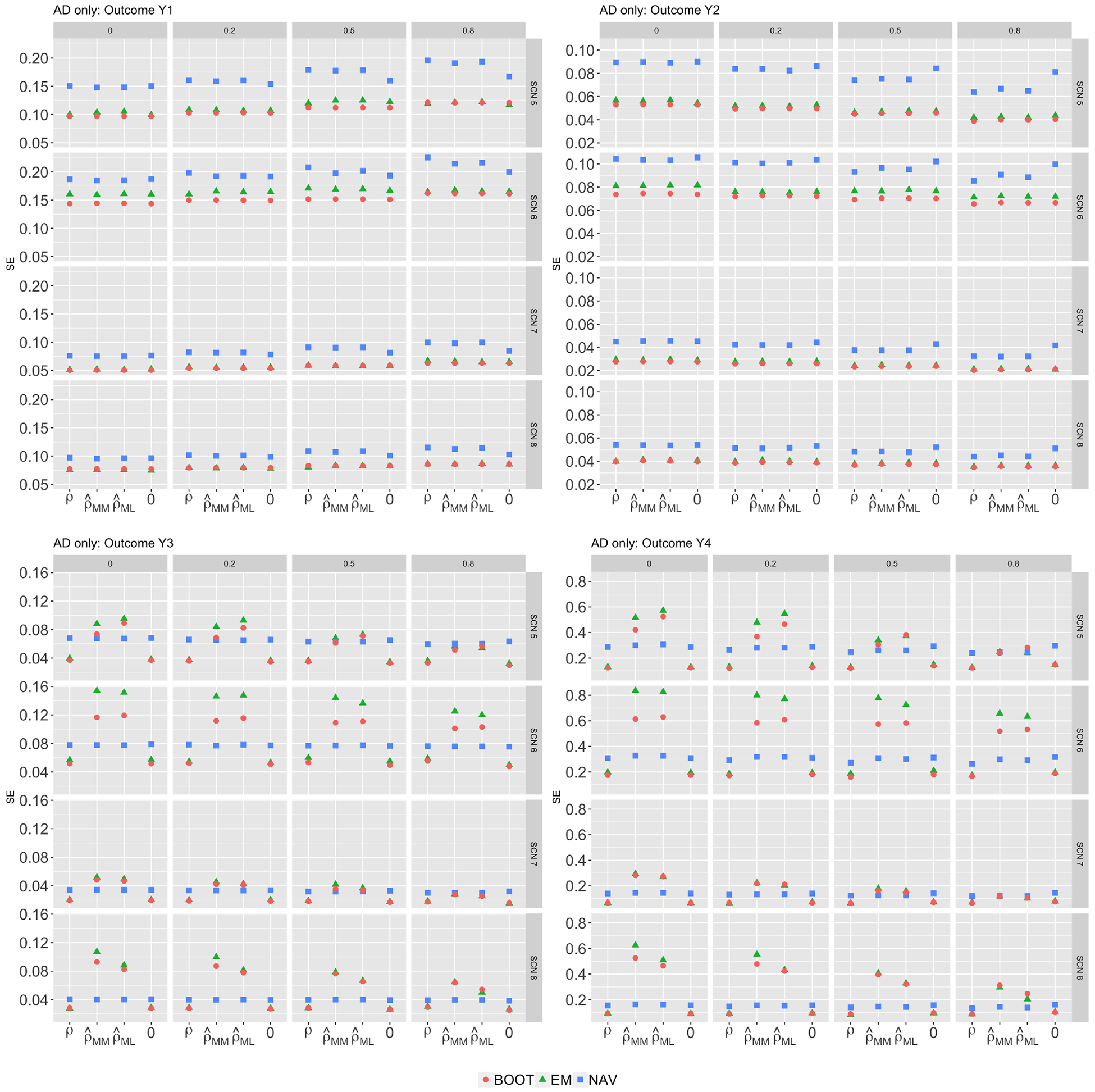
Standard errors (scenario 5–8)Comparisons of standard error estimates of treatment effect estimates on combined outcomes for various $\widehat{\rho }$. All studies provided AD only. EMP refers to the empirical standard errors; NAV refers to the average of standard error estimates obtained by a naive application of the Rubin’s rule; BOOT refers to the average bootstrap standard error estimates.

As discussed in Section 2.2.1, treatment effect estimates for linear combined outcomes remain consistent regardless of the value of $\widehat{\rho }$ used in the reconstruction whereas the efficiency can be affected. For outcome Y₁, the variance of the treatment effect estimates increases as $\widehat{\rho }$ increases (see Eq.(3))). However, this trend was not observed in Figure 4. Because the final estimate was an average over multiple sets of reconstructed IPD (here M = 10), this dependence may be diluted by averaging and became harder to detect. We conducted another set of simulations with the same set-up as scenario 18 (see Table 1 in web supplementary materials) except that we reduced M from 10 to 1. In the reconstruction step, we varied the value of $\widehat{\rho }$ from −1 to 1. The results are displayed in Figure 5. Based on a single reconstruction of IPD, the empirical standard errors of treatment effect estimates for Y₁ increased as $\widehat{\rho }$ increased, as expected from Eq.(3)). In contrast, the empirical standard errors of treatment effect estimates for Y₂ showed an downward trend as $\widehat{\rho }$ increased.

Figure 5:

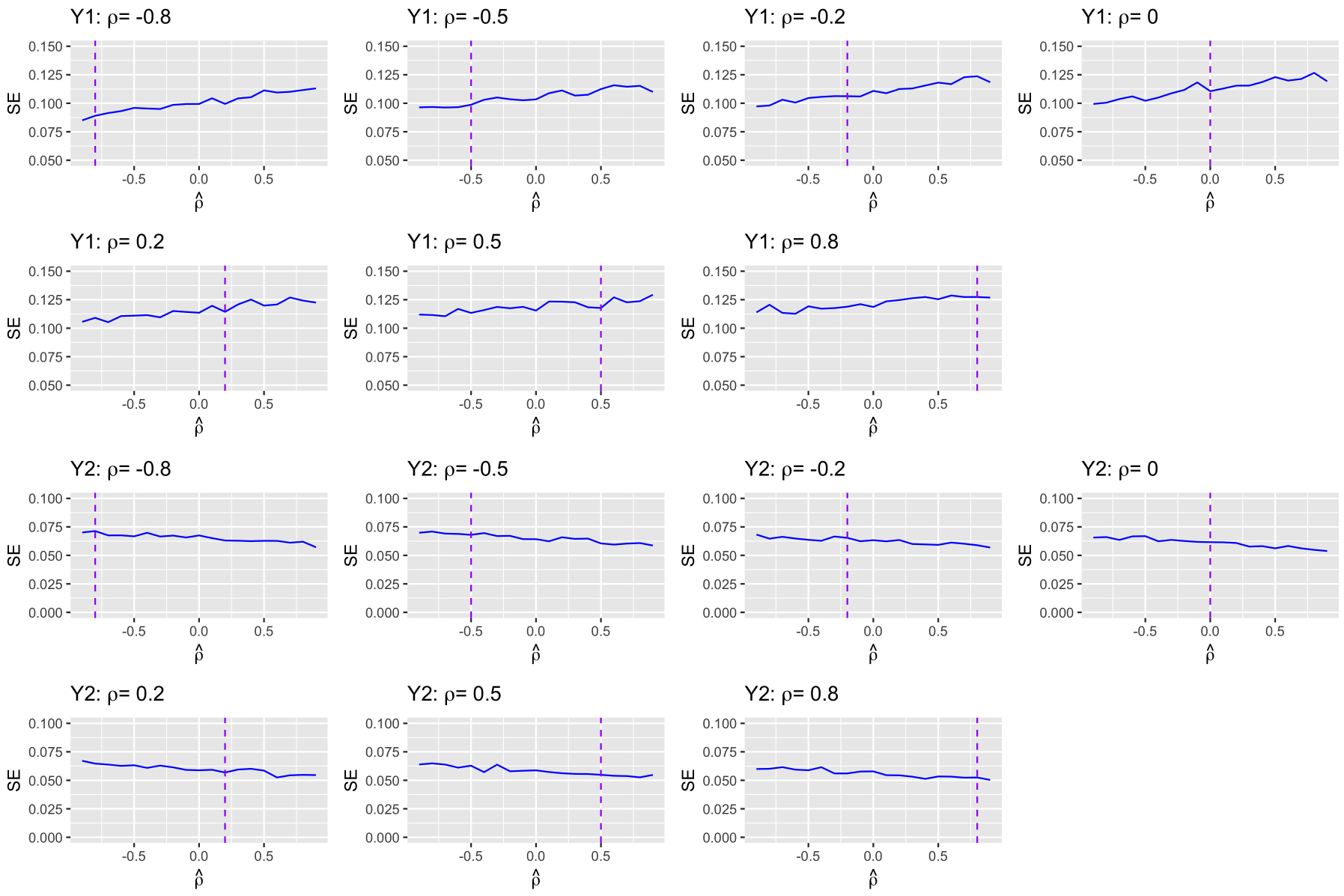
Empirical standard errors for outcomes Y₁ and Y₂ based on a single reconstruction of pseudo IPD. The vertical purple lines indicate the true ρ.

3.3. The proposed approach vs. MVMA

As discussed previously, if the parameter representing the treatment effect for the combined outcomes can be written as a smooth function of treatment effect parameters for the original outcomes, MVMA can be applied to obtain treatment effect estimates on the combined outcome without the reconstruction of IPD. An example is the outcome Y₁. We conducted a simulation study to compare the finite-sample performance of our method versus the standard random-effects MVMA. We applied two estimation approaches for MVMA: the restricted maximum likelihood (REML)^6,8 and the method of moments (MM).¹² The latter is an extension of the DerSimonian and Laird method to the multivariate setting. Data were simulated under the same parameter set-up as in scenario 18. For the ease of comparison, we assumed that within-study correlations were known. That is, following the notations in Section 2.1, we used $\widehat{\rho }=\rho$ during the reconstruction of IPD for the proposed approach, and used ${\rho }_j^{*}$ for MVMA. For both methods, the within-study variances ${\sigma }_{ij}^U$, ${\sigma }_{ij}^V$ were estimated using the sample standard deviations. Since Y₁ is just a linear combination of the two original outcomes, the true overall treatment effect for Y₁ equals θ₁₀ = 3. Table 3 and 4 present the estimated biases and the empirical standard errors. Both the proposed method and MVMA produced minimally biased point estimates with similar efficiency.

Table 3:

Comparison of biases of treatment effect estimates on Y₁ obtained from multiple reconstructions of IPD (MR) and from MVMA

	MR	MVMA-REML	MVMA-MM
ρ = −0.8	0.001	0.005	0.005
ρ = −0.5	0.001	−0.002	−0.002
ρ = −0.2	0.007	−0.001	−0.001
ρ = 0	0.001	−0.008	−0.008
ρ = 0.2	−0.007	0.004	0.004
ρ = 0.5	0.006	−0.004	−0.004
ρ = 0.8	0.002	−0.006	−0.005

Table 4:

Comparison of empirical SEs of treatment effect estimates on Y₁ obtained from multiple reconstructions of IPD (MR) and from MVMA

	MR	MVMA-REML	MVMA-MM
ρ = −0.8	0.087	0.087	0.087
ρ = −0.5	0.093	0.090	0.090
ρ = −0.2	0.098	0.096	0.096
ρ = 0	0.101	0.098	0.098
ρ = 0.2	0.107	0.104	0.104
ρ = 0.5	0.111	0.110	0.110
ρ = 0.8	0.115	0.111	0.111

4. Illustrative examples

4.1. Effect of DPP4-I on HbA1c and weight

A common side effect of anti-diabetic medications such as insulin is weight gain,³⁹ which is undesirable in most cases as over 90% of patients with type 2 diabetes are already overweight or obese.⁴⁰ However, an increasing number of therapeutic options are available that are weight neutral or even lead to weight loss in addition to their glycemic benefits.³⁹ Hence, a combined outcome that characterizes both change in glycated hemoglobin (HbA1c) and change in body weight would be useful when comparing different interventions.

Wu et al⁴¹ conducted a network meta-analysis of 360 RCTs examining the effects of incretin-based therapies on β-cell function and insulin resistance in type 2 diabetes. From their study pool, we identified 13 RCTs that compared the effect of dipeptidyl peptidase-4 inhibitors (DPP4-I, or treatment) to control and reported both change in HbA1c level (U) and change in body weight (V). Group means, standard errors and sample sizes of participating studies are summarized in Table 5. Univariate meta-analyses using the DerSimonian and Laird random-effects model revealed that patients in the treatment arms experienced a greater decline in HbA1c level by 0.67% (95% CI : [−0.90, −0.44], between-study variance estimate ${\widehat{\tau }}^2=0.16$), but a smaller reduction in body weight by 0.36 kg (95% CI : [0.05, 0.67], ${\widehat{\tau }}^2=0.11$) compared to those in the control arms. We applied the proposed method to analyzing the following non-linear combined outcome:

$$Y_{ijk}=2\times 1\left(U_{ijk}<0\right)+1\left(V_{ijk}<0\right)+1\left(U_{ijk}<0,V_{ijk}<0\right).$$

The combined outcome assigns a score in {0,1,2,4} to each of the four possible combinations of increased/decreased HbA1c level and increased/decreased body weight, with higher score being more desirable. The most desirable response is a decrease in both HbA1c and weight (score = 4), followed by a decrease in HbA1c only (score = 2), a decrease in weight only (score = 1) and an increase in both outcomes (score = 0).

Table 5:

Aggregate data on HbA1c level and body weight

Study	Intervention	N	Δ HbA1c (%)		Δ Weight (kg)
			Mean	SE	Mean	SE
Derosa, 201464	DPP4-I	101	−1.40	0.07	−3.50	0.56
	Control	96	0.50	0.12	−0.80	0.62
Derosa, 201265	DPP4-I	86	−1.40	0.08	−2.50	0.64
	Control	83	−0.70	0.07	−2.30	0.67
Ahren, 201466	DPP4-I	89	−0.56	0.12	−2.05	0.44
	Control	16	−0.46	0.21	−3.61	0.87
Iwamoto, 201067	DPP4-I	70	−0.69	0.06	0.10	0.18
	Control	73	0.28	0.06	−0.50	0.18
Mohan, 200968	DPP4-I	352	−0.71	0.05	0.60	0.09
	Control	169	0.31	0.10	0	0.19
Nonaka, 200869	DPP4-I	75	−0.65	0.08	−0.10	0.18
	Control	75	0.41	0.08	−0.70	0.15
Gul, 201170	DPP4-I	28	−0.30	0.14	−2.00	3.16
	Control	16	−0.10	0.19	−2.20	2.74
Roden, 201371	DPP4-I	223	−0.53	0.06	0.10	0.20
	Control	228	0.13	0.06	−0.43	0.20
Samocha-Bonet, 201472	DPP4-I	13	−0.20	0.08	−0.20	4.22
	Control	13	−0.10	0.11	0.10	4.34
Tian, 201673	DPP4-I	88	−0.36	0.06	−0.40	0.86
	Control	45	0.02	0.11	−0.40	0.96
Vilsboll, 201074	DPP4-I	322	−0.59	0.05	0.10	0.13
	Control	319	−0.03	0.06	0.10	0.16
Violante, 201275	DPP4-I	111	−0.68	0.08	−2.20	0.24
	Control	97	−0.38	0.09	−2.58	0.25
Yoon, 201276	DPP4-I	161	−2.37	0.09	4.80	0.51
	Control	149	−1.86	0.09	4.10	0.54

The parameter of interest θ₀ was the difference in means of the combined outcome Y between the DPP4-I and control arm, defined as follows:

$$\begin{gathered} {\theta }_j:=E_j\left[Y_{1jk}\right]-E_j\left[Y_{2jk}\right], \\ {\theta }_0:=E_G\left[{\theta }_j\right]. \end{gathered}$$

Since only AD were available and prior knowledge on κ was lacking, we calculated ${\widehat{\rho }}_{MM}$ and ${\widehat{\rho }}_{ML}$ as described in Section 2.3.2 by taking κ₀ = 0 and imputed pseudo IPD accordingly. The resulting ${\widehat{\rho }}_{MM}$ and ${\widehat{\rho }}_{ML}$ were both −1. When we plugged in a crude estimate of κ obtained by ignoring the within-study sampling variation $\left(\widehat{\kappa }=-0.756\right)$, ${\widehat{\rho }}_{ML}=1$ and ${\widehat{\rho }}_{MM}$ was out of range and close to the boundary value 1. In the current setting with only 13 studies, it was not surprising that the resulting estimates for ρ were highly variable, we therefore conducted sensitivity analyses by plugging in $\widehat{\rho }$ ranging from a very strong negative correlation $\left(\widehat{\rho }=-0.8\right)$ to a perfect positive correlation $\left(\widehat{\rho }=1\right)$. For each value of $\widehat{\rho }$, we reconstructed M = 50 sets of pseudo IPD. Table 6 shows the treatment effect estimates, the bootstrap standard error estimates, and the 95% confidence intervals. The 95% CIs were constructed assuming a normal distribution for $\widehat{\theta }$. The bootstrap standard error estimates are calculated from B = 1000 bootstrap replicates. Overall, using different $\widehat{\rho }$ yielded similar results with effect sizes ranging from 0.60 to 0.71.

Table 6:

Meta-analysis of the HbA1c-weight combined outcome

$\widehat{\rho }$	$\widehat{\theta }$	Bootstrap SE	95% CI
1	0.595	0.156	[0.290, 0.900]
0.8	0.598	0.157	[0.290, 0.905]
0.5	0.603	0.159	[0.292, 0.914]
0.2	0.608	0.160	[0.295, 0.921]
0	0.618	0.161	[0.301, 0.932]
−0.2	0.627	0.161	[0.310, 0.943]
−0.5	0.649	0.163	[0.327, 0.966]
−0.8	0.661	0.165	[0.338, 0.985]
Assume κ0 = 0
${\widehat{\rho }}_{ML}=-1$	0.699	0.153	[0.398, 0.999]
${\widehat{\rho }}_{MM}=-1$	0.705	0.160	[0.392, 1.018]

Although univariate analysis suggested that the treatment was superior in terms of lowering patients’ HbA1c level but less effective in weight reduction compared to the control intervention, meta-analysis of the HbA1c-weight combined outcome revealed that participants in the treatment arms had better outcomes when both were taken into account simultaneously. We also note that here we gave more weights to HbA1c reduction than to weight reduction in the combined outcome, out of consideration that the primary goal of diabetes treatment was glycemic control. But the choice of weights can be tailored to personal preference. If one is more concerned with weight reduction, then the weights can be adjusted accordingly. The proposed approach provides one way to assess treatment effects across multiple outcomes simultaneously.

4.2. Effect of PAP on systolic and diastolic blood pressure

Obstructive Sleep Apnea (OSA) is a sleep disorder where breathing is briefly and repeatedly interrupted during sleep, resulting in intermittent hypoxemia and sympathetic nervous system activation. It is a highly prevalent chronic condition affecting approximately 27% of men and 9% of women.⁴² Its prevalence among individuals with cardiovascular disease (CVD) is even higher.^43,44 Multiple epidemiological studies have demonstrated that OSA is a significant risk factor for CVD, including stroke, coronary artery disease, heart failure, and atrial fibrillation.^45–48 Moreover, it has been shown that OSA is an independent risk factor for the development of hypertension, a well-recognized risk factor for CVD.⁴⁹ Over 50% of OSA patients have hypertension and approximately 70% of patients with resistant hypertension have OSA.⁴³ Therefore, there is compelling evidence to identify the role of OSA treatment as a means for primary or secondary prevention of CVD.

Positive Airway Pressure (PAP) therapy is the standard first-line treatment for OSA. A PAP machine provides pressurized air to the naso-pharyngeal airway, preventing airway collapse that may occur in susceptible individuals with inspiratory breathing efforts, thus stabilizing breathing during sleep. While OSA is recognized as a cause of secondary hypertension, the extent to which PAP improves blood pressure profile has been an area of active investigation. Some research has suggested that OSA differs in its effects on diastolic versus systolic blood pressure,⁵⁰ which has implications on potential mechanisms and intervention targets. Given that adverse physiological effects of sleep apnea are most acute during sleep, there is also interest in the effect of treatment on 24-hour blood pressure profile.^51,52 Schein et al⁵³ performed a systematic review of RCTs that compared active PAP versus placebo PAP, sham PAP or subtherapeutic PAP in lowering blood pressure among patients with OSA. Six studies (620 patients in total) were identified for a meta-analysis of treatment effects on post-intervention 24-hour systolic blood pressure (SBP) and diastolic blood pressure (DBP). The comparison of PAP to control groups revealed a non-significant reduction in 24-hour SBP (−3.57 mmHg, 95% CI: [−8.58, 1.44]; between-study variance estimate ${\widehat{\tau }}^2=22.86$) but a significant reduction in 24-hour DBP (−3.46 mmHg, 95% CI: [−6.75, −0.17]; ${\widehat{\tau }}^2=10.64$). We extracted group-level aggregate data of those studies. In addition, we included individual patient data from the Best Apnea Interventions for Research (BestAIR) trial,⁵⁴ which led to a total of 7 studies (see Table 7). The BestAIR trial data are available upon reasonable request at https://sleepdata.org. Univariate meta-analyses based on the DL random-effects model from all 7 studies gave conclusions consistent with Schein et al⁵³: Compared to control arms, PAP resulted in a significant reduction in 24-hour DBP by 3.14 mmHg (95% CI: [−5.67, −0.61]; ${\widehat{\tau }}^2=6.59$), but the effect of PAP on 24-hour SBP did not reach statistical significance (treatment effect −4.01 mmHg, 95% CI: [−8.07, 0.04]; ${\widehat{\tau }}^2=16.81$).

Table 7:

Aggregate data on post-intervention 24-hour SBP and DBP

Study	Intervention	N	SBP(mmHg)		DBP (mmHg)
			Mean	SE	Mean	SE
Becker, 200377	PAP	16	126	3.50	73	2.50
	Control	16	137	2.75	82	2.25
Campos-Rodrigues, 200678	PAP	34	131	2.06	77	1.54
	Control	34	130	2.74	77	1.54
Duran-Camtola, 201079	PAP	169	128	1.00	81	0.69
	Control	171	128	0.99	82	0.69
Hui, 200680	PAP	23	123	3.13	80	2.29
	Control	23	120	6.26	81	1.88
Kohler, 200881	PAP	51	128	1.96	81	1.40
	Control	51	139	2.66	89	1.12
Robinson, 200682	PAP	16	137	4.00	84	3.00
	Control	16	139	4.50	87	3.00
Zhao, 201754	PAP	69	123	1.22	71	0.93
	Control	68	128	1.58	74	1.04

Although prior research has considered SBP and DBP separately, hypertensive burden is typically examined by considering levels of both systolic and diastolic pressures. Therefore we considered the following two combined outcomes. The first one was a binary indicator of elevated blood pressure that equals 1 if either the post-intervention 24-hour SBP is greater than 130 mmHg or DBP is greater than 80 mmHg and 0 otherwise; The second one was an ordinal outcome that equals the summation of the two indicators 1(SBP_ijk > 130) and 1(DBP_ijk > 80), i.e.

$$\begin{gathered} Y_{1,ijk}=1\left({\text{SBP}}_{ijk}>130{\text{ or DBP}}_{ijk}>80\right), \\ {Y}_{2,ijk}=1\left({\text{SBP}}_{ijk}>130\right)+1\left({\text{DBP}}_{ijk}>80\right). \end{gathered}$$

The threshold values were selected based on the guidelines published by American College of Cardiology (ACC) and American Heart Association (AHA) in 2017.⁵⁵ The guidelines classify blood pressures into 5 categories that range from normal to severe hypertension, and 130/80 mmHg is the cutoff for normal versus elevated blood pressure. Since the first outcome was binary, we chose the target parameter to be the mean log odds ratio of elevated blood pressure comparing patients treated with PAP versus control:

$$\begin{gathered} {\theta }_{1j}:=\text{log}\left(\frac{E_j\left[Y_{1,1jk}\right]\left(1-E_j\left[Y_{1,2jk}\right]\right)}{E_j\left[Y_{1,2jk}\right]\left(1-E_j\left[Y_{1,1jk}\right]\right)}\right), \\ {\theta }_{10}:=E_{G_1}\left[{\theta }_{1j}\right]. \end{gathered}$$

And for the second outcome, the parameter of interest was the difference in means:

$$\begin{gathered} {\theta }_{2j}:=E_j\left[Y_{2,1jk}\right]-E_j\left[Y_{2,2jk}\right], \\ {\theta }_{20}:=E_{G_2}\left[{\theta }_{2j}\right]. \end{gathered}$$

Our literature search revealed a positive correlation between SBP and DBP of magnitudes varying from 0.61 to 0.74.^56,57 The available IPD from the BestAIR study yielded ${\widehat{\rho }}_{IPD}=0.63$, which was consistent with published results. We generated M = 50 reconstructed datasets to obtain the treatment effect estimate and B = 1000 bootstrap replicates to obtain the bootstrap standard error estimate. For Y₁, the proposed procedure yielded a point estimate of −0.69, corresponding to an odds ratio of 0.50 for post-intervention elevated blood pressure (SBP > 130 mmHg or DBP > 80 mmHg) comparing patients in PAP groups to those in control groups. The protective effect of PAP was significant at 0.05 level, with approximate 95% bootstrap confidence interval [0.29, 0.86]. We also observed a significant treatment effect on combined outcome Y₂, where the mean response in PAP groups was estimated to be 0.26 unit lower compared to that in control groups with approximate 95% bootstrap confidence interval [−0.06, −0.46]. Meta-analyses of both combined outcomes supported the conclusion that PAP can facilitate blood pressure control among OSA patients. While univariate analysis based on DBP only did not reach statistical significance, meta-analysis based on combined outcomes revealed that PAP significantly increased the probability of a reduction in either SBP or DBP.

5. Discussion

In this paper, we develop meta-analysis methods for outcomes combining information across multiple endpoints based on reconstructions of IPD. We focus on combined outcomes that are functions of two continuous outcomes. For linear combined outcomes, treatment effect estimates obtained using the proposed procedure remain consistent regardless of misspecification of the within-study correlation ρ in the reconstruction step. In contrast, for non-linear combined outcomes, accurate estimation of ρ is essential to ensure consistency of the treatment effect estimates.When no previous knowledge of ρ is assumed, a reasonably accurate estimate can oftentimes be obtained from even a small sample of IPD. The estimation problem becomes difficult when only AD are available, in which case one needs to assume a value for the between-study correlation κ in order to estimate ρ and we found through simulations that estimators of ρ that were solely based on AD were highly unstable when the number of studies was small and the between-study heterogeneity was large. In these settings, we recommend conducting sensitivity analyses to examine treatment effect estimates for a plausible range of $\widehat{\rho }$.

When there is between-study heterogeneity in treatment effects for the original outcomes, it is reasonable to expect between-study heterogeneity in treatment effects for the combined outcomes. It would be of interest to quantify the magnitude of this between-study heterogeneity. When IPD are available from all studies, we can obtain the IPD for the combined outcomes and the usual measure such as the I² statistic⁵⁸ can be calculated in a straightforward manner. When IPD are not available from some studies, our approach is based on multiply reconstructing IPD. Although it is straightforward to calculate the I² statistic or other measures of heterogeneity for each set of pseudo IPD, pooling the estimates across multiple reconstructed datasets requires careful consideration. For measures that are asymptotically normally distributed, such as the maximum likelihood or restricted maximum likelihood estimators of the between-study variance, we can directly apply Rubin’s rule as stated in Section 2.2; For measures that are not asymptotically normally distributed, proper normalization may be used so that a pooled estimate can be computed based on the transformed values and then transformed back to the original scale. Take the I² statistic as an example, we may consider the Fisher z transformation to the square root of I². The Fisher z transformation has been suggested for R² in linear regression,⁵⁹ which is also a measure of proportion of variation. Testing the null hypothesis of homogeneity in such settings is also possible. For example, under the null hypothesis, the Cochran’s Q statistics follows a chi-square distribution with (J − 1) degrees of freedom⁶⁰ (where J is the number of studies), and methods for pooling chi-square distributed test statistics from multiple imputed datasets have been developed by Rubin³⁰ and Li et al.⁶¹ It would be useful to develop metrics that can sensibly characterize between-study heterogeneity of treatment effects on combined outcomes that are pooled from multiple reconstructed IPD in future research.

Our approach essentially approximates the joint distribution of the original outcomes with a bivariate normal distribution through matching the first and second moments. This is a convenient choice since group means and associated standard errors are the most commonly reported AD, and a normal distribution is completely specified by its first two moments. In addition, it is relatively easy to generate normal samples with specified correlations in standard statistical software. We expect this approximation to work reasonably well for original outcomes with symmetric distributions. When IPD are available for some studies, the reconstruction procedure can be generalized to accommodate skewed distributions through the use of more flexible distributions, for example, the Fleishman distribution, where the first four moments can be matched,⁶² or non-parametrically through the use of kernel density estimators.

The proposed method can be generalized to analyzing combined outcomes constructed from more than two original outcomes. It can also be adapted to scenarios where the original outcomes are discrete or a mixture of discrete and continuous outcomes, in which case, estimation of correlation parameter requires consideration of additional constraints; for example, the correlation of two binary variables is bounded above by their marginal success probabilities. Lastly, it would be useful to develop Bayesian meta-analytic methods for combined outcomes through constructing hierarchical models and placing priors on unknown parameters. Pseudo IPD can be reconstructed by sampling from the corresponding posterior distributions.

We illustrated our approach using the DerSimonian-Laird random-effects model as it is one of the most routinely-used methods for random-effects meta-analysis. However, the idea of multiply reconstructing IPD based on reported AD can also be combined with other choices of two-stage meta-analysis methods (for example, see Wang et al⁶³) or meta-analysis based on IPD directly to allow for more flexible modeling of the variance structure as well as treatment-covariate interactions. Previous work has demonstrated both feasibility and advantages of fitting regression models to reconstructed IPD when meta-analyzing reported outcomes,^32,33 we expect similar results from extending the method to combined outcomes.

Highlights.

In practice, treatment decision-making depends on an overall assessment of patient-level outcomes balancing benefit in various domains and potential risks. This calls for meta-analysis methods for combined outcomes that encompass information from different domains. When individual patient data (IPD) are available from each study, the combined outcomes can be constructed for each individual and standard meta-analysis methods would apply. However, IPD are usually difficult to obtain. In this article, we propose a new method that multiply reconstructs pseudo IPD based on the available summary statistics reported by each study and then obtains pooled treatment effect estimates for the combined outcome. This proposed method is applicable to various settings where meta-analysis of outcomes that integrates information from multiple variables is of interest.