Empirical evidence of recruitment bias in a network study of people who inject drugs

Abstract

Background:

Epidemiologic surveys of people who inject drugs (PWID) can be difficult to conduct because potential participants may fear exposure or legal repercussions. Respondent-driven sampling (RDS) is a procedure in which subjects recruit their eligible social contacts. The statistical validity of RDS surveys of PWID and other risk groups depends on subjects recruiting at random from among their network contacts.

Objectives:

We sought to develop and apply a rigorous definition and statistical tests for uniform network recruitment in an RDS survey.

Methods:

We undertook a detailed study of recruitment bias in a unique RDS study of PWID in Hartford, CT, USA in which the network, individual-level covariates, and social link attributes were recorded. A total of n=527 participants (402 male, 123 female, and two individuals who did not specify their gender) within a network of 2626 PWID were recruited.

Results:

We found strong evidence of recruitment bias with respect to age, homelessness, and social relationship characteristics. In the discrete model, the estimated hazard ratios regarding the significant features of recruitment time and choice of recruitee were: alter’s age 1.03 [1.02, 1.05], alter’s crack-using status 0.70 [0.50, 1.00], homelessness difference 0.61 [0.43, 0.87], and sharing activities in drug preparation 2.82 [1.39, 5.72]. Under both the discrete and continuous-time recruitment regression models, we reject the null hypothesis of uniform recruitment.

Conclusions:

The results provide the evidence that for this study population of PWID, recruitment bias may significantly alter the sample composition, making results of RDS surveys less reliable. More broadly, RDS studies that fail to collect comprehensive network data may not be able to detect biased recruitment when it occurs.

1. Introduction

People who inject drugs (PWID) are at increased risk of HCV, HIV, and other adverse health outcomes [1]. Reliable information about risk behaviors, access to care, and health outcomes for PWID is needed to inform intervention measures and public policy. But public health and epidemiolic research on PWID can be difficult to conduct in a rigorous way. Because PWID are a marginalized, stigmatized, and often criminalized population, potential participants in a research study may be hidden from researchers’ view; there is often no “sampling frame” by which researchers can obtain a representative sample. Instead, public health researchers have developed recruitment procedures that rely on study subjects to recruit other participants via their social network. Respondent-driven Sampling (RDS) is the most popular social network recruitment procedure for epidemiological surveys of PWID [2]. RDS is widely used in social, behavioral, epidemiological, and public health research on injection drug use.

In RDS, a few individuals called “seeds” are chosen to participate at the beginning of the study. These subjects are interviewed and receive a small number of coupons that they can use to recruit other members of the target population. The seeds recruit their social contacts by giving them a coupon, the new recruit redeems the coupon to participate in the study, and new participants are interviewed and given their own coupons. The process repeats iteratively until the desired sample size is reached. Coupons are marked with a unique code so that researchers can track who recruited whom. For confidentiality reasons, subjects in RDS surveys typically do not report on the identities of their alters in the target population social network; instead, they report their egocentric network degree, without providing identifying information about their alters. The most popular estimator of the population mean from data obtained by RDS is known as the Volz-Heckathorn estimator [3], which is consistent under conditions formalized by [4]. The properties of this estimator depends on “unbiased” recruitment of network alters by recruiters, but authors have provided differing interpretations of “unbiased” recruitment on a network [2, 5, 6, 7, 8, 9].

Despite its importance in determining the statistical properties of RDS estimates for important risk groups, there is no consensus among epidemiologists about what “biased”, “preferential”, or non-uniform recruitment actually means [10, 11]. Different authors give different or contradictory definitions of recruitment bias [12, 13, 14, 8]. Many authors confuse non-uniform recruitment of network alters with network homophily – the tendency for individuals to form social ties with others who have similar traits – or mistakenly assert that auto-correlation in the recruitment chain is evidence of one or the other [see 11, for a comprehensive list of examples]. Several authors have attempted to measure non-uniform recruitment in RDS studies of injection drug users using correlations in the trait values of recruiter-recruitee pairs [15, 13, 14, 16, 8, 17]. Empirical claims about recruitment bias in RDS studies are therefore difficult to interpret: the definitions of bias and tests for its presence may not be comparable or generalizable. To separate network characteristics from recruiters’ choices, some researchers advocate follow-up interviews of subjects to determine whom they intended to recruit and the reasons for successful and unsuccessful recruitment of those individuals, and offer different recommendations for incorporating this information into assessments of selection bias [18, 19, 9].

What would a reasonable definition of recruitment bias entail? First, recruitment bias should be defined with respect to a measured individual trait (e.g. drug use behavior, race, gender, or HIV status) or social link attribute (e.g. familial, drug sharing, co-habitation, sexual relationship) that is relevant to the scientific goals of the study. Second, researchers must be able to characterize the set of possible new recruits at each step of the RDS recruitment process. Without knowing which potential subjects are linked to a recruiter, and therefore eligible to be recruited next, researchers cannot tell whether the next recruit is chosen uniformly from this set. Third, if RDS recruitment is believed to take place across links in a population social network, then the set of possible recruits changes dynamically in time over the course of an RDS study. These challenges make it clear that formulating a sensible definition of uniform recruitment requires careful attention both to the social network upon which recruitment is supposed to operate, and the dynamics of the recruitment process conditional on that network.

In this paper, we perform an in-depth study of recruitment bias in an RDS survey of PWID in Hartford, CT, USA in which researchers conducted comprehensive sociometric mapping of recruiters and their network alters [20, 17, 11]. We first formulate a rigorous definition of uniform recruitment and construct regression-based tests that take network information into account, which can be used to test the hypothesis of uniform recruitment. For this population of PWID in Hartford, CT, we find strong evidence of recruitment bias with respect to individual traits including age, gender, homelessness, and social link characteristics. The results suggest that empirical RDS studies that do not collect such comprehensive network information may not reliably reveal the complex dynamics of recruitment, and the bias that may result.

Methods

In the RDS-net study, researchers conducted an RDS survey of 530 PWID in Hartford, Connecticut, USA [20, 17]. Six individuals with large network size were selected as seeds; these individuals were chosen to reflect the diversity of the PWID population with regard to gender, ethnicity, neighborhood of residence, and drug use. Each seed was given 3 coupons and were asked to recruit their friends who were eligible for the study. All subsequent participants also received 3 coupons until the desired sample size was nearly reached: of the 530 recruited participants, 511 received coupons. Participants received $25 upon completion of their baseline surveys, and $30 upon finishing follow-up surveys 2 months later. Each participant also received an additional $10 for each successful recruitment of eligible network alters. Coupons did not expire, but recruiters were instructed to recruit eligible subjects within two weeks. Subjects were at least 18 years old, injected drugs, and resided in the Hartford area. The study was approved by the institutional review board for the Institute for Community Research, and informed consent was obtained from all subjects.

The baseline survey included components interrogating participants’ egocentric network size (network degree) and composition, individual-level characteristics, demographics, drug use, and HIV risk behaviors, and a comprehensive ego-network assessment. Participants listed their egocentric network members’ names and identifying characteristics, and answered questions regarding relationship types and recent social activities with these members. Names and identifying characteristics of egocentric network members were later matched with other participants’ and nominees’ names via an identity resolution process [21, 22, 23, 24], to construct the “nomination network” representing the social network of PWID connected to participating subjects [25, 26]. The egocentric network assessment and subsequent identity resolution process makes the RDS-net study distinct from typical RDS studies because the entire network connecting participants – and their non-participating network alters – was reconstructed. Since this information is typically impossible to obtain using traditional RDS recruitment procedures, the RDS-net study offers a unique opportunity to study the dynamics of PWID recruitment in this population. A total of 2626 unique PWID were recruited or nominated. Figure 1 shows the RDS recruitment process overlaid on the network of 2626 PWID. Some aspects of the RDS-net study design and data collection have been described elsewhere [20, 17, 11].

Figure 1.

Pattern of RDS recruitment among people who inject drugs in Hartford, CT from the RDS-net study. The nomination network is shown overlaid with the recruitment networks at four time points (112, 190, 290, 441 days after the beginning of study). Recruited subjects are shown in red, and recruitment edges are shown as a directed edge from the recruiter to the recruitee. Edges not associated with recruitments are shown in gray. The analysis presented in this paper aims to estimate recruiter and recruitee factors associated with recruitment in this network.

Data structure

RDS recruitments are assumed to take place over social network links [2, 27, 3]. The target population social network is a simple undirected graph G = (V, E) [28, 11]. The vertex set V corresponds to members of the PWID population, and edges in E represent social links among PWID across which recruitments might take place. A recruiter is a subject who can recruit other yet-unrecruited vertices because it has at least one coupon. A susceptible individual is not yet recruited, and has at least one recruiter neighbor in G. Each recruitment of a susceptible vertex costs the recruiter one coupon, and no subject can be recruited more than once. Let M be the set of “seeds” in an RDS study whose sample size is n. Let G_R = (V_R, E_R) be the recruitment subgraph, consisting of the set V_R of recruited subjects and the set E_R of recruitment links. It follows that the sizes of these sets are |V_R| = n and |E_R| = n − |M|. Let G_S = (V_R, E_S) be the induced subgraph of recruited subjects, where E_S is the set of all edges connecting subjects in V_R. Recruitment edges E_R are a subset of the set of all edges connecting recruited subjects, E_R ⊆ E_S. Let U be the set of PWID connected to recruited subjects V_R, and let E_U be the set of links connecting vertices in U to vertices in V_R. Then define G_SU = (V_SU, E_SU) to be the augmented recruitment-induced subgraph, consisting of V_SU = V_R ∪U and E_SU = E_S ∪ E_U. Then G_SU is the network consisting of the sampled PWID and those PWID connected to members of the sampled set.

Let d = (d₁, …, d_n) be the vector of recruited subjects’ reported degrees in G. For i ∈ V_SU, let X_i be a p × 1 vector of continuous or categorical trait values of i. Likewise for i ∈ V_R and j ∈ V_SU with i ≠ j, let Z_ij be a q × 1 vector consisting of continuous or categorical trait values corresponding to the edge {i, j} ∈ E_SU. Likewise, let X_SU = {X_i : i ∈ V_SU} be the set of trait values for subjects in V_SU, and let Z_SU = {Z_ij : i ∈ V_R,j ∈ V_SU,i ≠ j} be the set of edge attributes for vertices connected in G_SU. Finally, let t = (t₁, …, t_n) be the vector of the dates of recruitment of each subject into the study.

Statistical methods

Uniform, or unbiased, recruitment occurs when a recruiter chooses uniformly at random from their currently susceptible network neighbors. When the network of all possible recruiter-susceptible pairs G_SU is known, the observed data from an RDS study can be used to test the “null” hypothesis that recruitment is uniform with respect to measured traits. If the hypothesis of uniform recruitment is rejected, this means that susceptible individuals with certain traits are recruited more rapidly than those with other traits. For a recruiter i ∈ V_SU and a susceptible individual j with {i, j} ∈ E_SU, define the edge-wise waiting time for i to recruit j as T_ij. When i recruits j, then T_ij is observed. If i does not recruit j, then T_ij is censored by recruitment of j by another recruiter, depletion of i’s coupons, or the end of the study, whichever occurs first. By parameterizing the hazard function λ_ij(t) of T_ij in terms of characteristics of i, j, and the edge {i, j} connecting them, standard regression models can be employed to learn about factors associated with more rapid recruitment, and to perform statistical tests of uniform recruitment.

We develop time-to-event regression models for the edge-wise waiting time T_ij for i to recruit j. We employ three types of covariates: characteristics X_i of the recruiter i and X_j of the susceptible vertex j; similarity of trait values |X_i − X_j|, where | · | indicates element-wise absolute value with respect to its vector argument; and attributes Z_ij of the edge connecting i and j. We specify the edge-wise recruitment hazard of i recruiting j ∈ S_i(t) at time t > t_i as

$${\lambda }_{ij}\left(t-t_i\right)={\lambda }_0\left(t-t_i\right)\exp \left[{\mathit{\beta }}^{\prime }\left|{\mathbf{X}}_i-{\mathbf{X}}_j\right|+{\mathit{\theta }}_1^{\prime }{\mathbf{X}}_i+{\mathit{\theta }}_2^{\prime }{\mathbf{X}}_j+{\mathit{\kappa }}^{\prime }{\mathbf{Z}}_{ij}\right],$$ (1)

where λ₀(·) is a non-negative propensity to recruit (baseline hazard) shared by all recruiters, and time is measured in days since recruitment of i. Below we briefly describe regression models for estimating these unknown coefficients; statistical tests that β, θ₂, κ are equal to zero follow directly. Rejection of the test constitutes evidence against uniform recruitment. The Supplementary Appendix establishes a formal statistical connection between the fitted regression models and the test of uniform recruitment.

One way to evaluate the dependence of recruitment events on recruiter, susceptible, and edge covariates is to condition on the times of recruitment events and the identity of the recruiter at each time, while treating the identity of the recruited subject as random. The likelihood L_d(β, θ₂, κ) of the discrete-time recruitment process is given by the product of the conditional recruitment probabilities, for each recruitment event. The likelihood is

$$L_d\left(\mathit{\beta },{\mathit{\theta }}_2,\mathit{\kappa }\right)=\prod _{j\notin M}\frac{\exp \left[{\mathit{\beta }}^{\prime }\left|{\mathbf{X}}_{r_j}-{\mathbf{X}}_j\right|+{\mathit{\theta }}_2^{\prime }{\mathbf{X}}_j+{\mathit{\kappa }}^{\prime }{\mathbf{Z}}_{r_{j}j}\right]}{{\sum }_{k\in S_{r_j}\left(t_j\right)}\exp \left[{\mathit{\beta }}^{\prime }\left|{\mathbf{X}}_{r_j}-{\mathbf{X}}_k\right|+{\mathit{\theta }}_2^{\prime }{\mathbf{X}}_k+{\mathit{\kappa }}^{\prime }{\mathbf{Z}}_{r_{j}k}\right]}$$ (2)

where r_j is the recruiter of j. The above expression follows because the terms λ₀(t − t_i) and $\exp \left({\mathit{\theta }}_1^{\prime }{X}_i\right)$ cancel in each conditional recruitment probability. To determine whether uniform recruitment holds, a simultaneous test over all coefficients can be conducted using a likelihood ratio test. Details of the fitting algorithm and the likelihood ratio test are described in supplementary materials.

A second way to evaluate recruitment takes a continuous-time view and jointly models the time to the next recruitment, and the identity of the next recruit, using a competing risks regression approach [29],

$$L_c\left(\mathit{\beta },{\mathit{\theta }}_1,{\mathit{\theta }}_2,\mathit{\kappa }\right)=\prod _{i=1}^n\prod _{j\in S_i\left(t_i^{+}\right)}{\lambda }_{ij}{\left(t_{ij}\right)}^{\mathbb{1}\left\{r_j=i\right\}}\exp \left[-{\mathrm{\Lambda }}_{ij}\left(t_{ij}\right)\right]$$ (3)

where r_j is the recruiter of j and Λ_ij(·) is the cumulative hazard function. Time $t_i^{+}$ is instantaneously after t_i, meaning that no recruitment events could happen between t_i and $t_i^{+}$. The continuous-time likelihood (3) corresponds to a standard survival model for edge-wise recruitment time with censoring. Allowing λ₀(t) to be unspecified suggests use of the semi-parametric Cox proportional hazards model [30]. Alternatively, letting the baseline recruitment hazard take the parametric form ${\lambda }_0(t)=\rho t^{\rho -1}$, the edge-wise waiting time T_ij to recruitment of j by i has Weibull distribution. As before, if coefficients β, θ₂, κ in the regression model are zero, then recruitment is uniform. The likelihood ratio test introduced above also applies here, and we use standard software for maximization of the likelihood [31].

Results

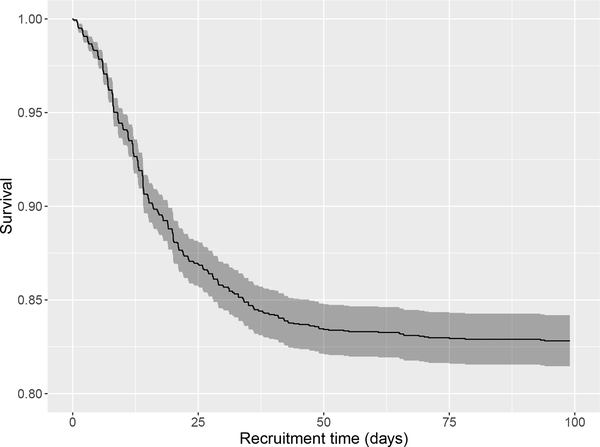
In the 441-day recruitment window, 530 people were enrolled and interviewed, of whom 527 (402 male, 123 female, and two individuals who did not specify their gender) were determined to be injection drug users eligible for the study. Therefore the RDS sample size is |V_R| = 527. After record matching to identify duplicate nominees, the nomination network G_SU contained |V_SU| = 2626 individuals eligible for the study, and |E_SU| = 3309 edges connecting individuals in G_SU. Of these edges, 1,180 connect recruited subjects and 2,129 connect recruited subjects to unrecruited subjects. The mean nomination network degree is 8.5 for recruited subjects. Among the 509 people who were successfully recruited and given coupons, 325 recruited at least one new subject. The mean number of network alters recruited by each subject is 0.98. While 184 people recruited no other subjects, 176 recruited one subject, 104 recruited two subjects, and 45 recruited three other subjects. Among all links in which a recruitment event occurred, the median time to recruitment was 13.85 days. The median times to recruiters’ first, second, and third recruitments are 12.01, 16.92, and 19.01 days, respectively. Figure 2 shows a Kaplan-Meier curve [32] for the edge-wise waiting times to recruitment. Most recruitments were made within 40 days after the recruiter was interviewed and received coupons. To test for recruitment bias, we selected several variables that have low missing rate, and are also of research interest. These variables are used in the two proposed models. Since the terms ${\mathit{\theta }}_1^{\prime }{\mathbf{X}}_i$ cancel in the likelihood, recruiters’ attributes do not enter into the discrete-time model.

Figure 2.

Kaplan-Meier survival curve for overall edge-wise recruitment showing the dynamics of recruitment across network edges in the RDS-net study. The horizontal axis measures time in days since the recruiter entered the study, and the vertical axis is the probability of no recruitment on an edge. Dashed lines show a point-wise estimated 95% confidence interval for the survival curve. The survival function corresponds to recruitment across edges, not to recruitment of individual subjects.

We first fit the discrete-time model (2) to the recruitment data in the RDS-net study. Results of the discrete-time analysis, including estimated coefficients, hazard ratios, and 95 % confidence interval for hazard ratios, are given in Table 1. Difference in homeless status has a negative regression coefficient: alters who have different homeless status from recruiters’ are only 0.61 as likely to be recruited as those who share the same status as recruiters’. Results also indicate that alters who use crack are not preferred by recruiters. Their chances of being recruited is 30% less than the alters who do not use crack. And sharing activities regarding cooker, cotton and rinse water increase recruitment probability to 2.82 times as likely. Now consider the null hypothesis that all coefficients in the discrete-time model are equal to zero. The likelihood ratio test Chi-square statistic is χ² = 61.34, with degree of freedom 19. The p-value for this test statistic is 2.37 × 10⁻⁶, indicating strong evidence that recruitment is non-uniform in the RDS-net study.

Table 1.

Estimated coefficients and confidence intervals in the discrete-time model of edge-wise recruitment. Recruiters’ attributes do not enter the likelihood for the discrete-time model, and so correposinding coefficients are not estimated here. We use γ to represent the coefficients of all types of predictors. Variables whose names are given in bold are significantly different from zero at the 0.05 level. The same notation applies to all tables in this article.

Covariate	γ	exp(γ)	95% CI of exp(γ)
drug using	−0.64	0.53	0.245, 1.134
drug injection	−0.42	0.66	0.296, 1.470
needle using	−0.18	0.83	0.347, 2.006
sharing activity	1.04	2.82	1.391, 5.715
sex	0.67	1.96	0.954, 4.030
hiv positive	0.23	1.26	0.591, 2.706
alter’s gender	−0.05	0.95	0.620, 1.466
alter’s crack using	−0.35	0.70	0.495, 0.997
alter’s homelessness	0.16	1.17	0.824, 1.674
alter’s age	0.03	1.03	1.016, 1.054
alter black	0.74	2.09	0.699, 6.269
alter white	0.99	2.69	0.885, 8.175
gender difference	0.004	1.00	0.633, 1.592
crack using difference	0.06	1.06	0.752, 1.491
homelessness difference	−0.50	0.61	0.427, 0.867
age difference	0.005	1.00	0.980, 1.029
black difference	0.85	2.35	0.682, 8.082
white difference	0.45	1.57	0.450, 5.461
hispanic difference	−0.45	0.64	0.200, 2.051

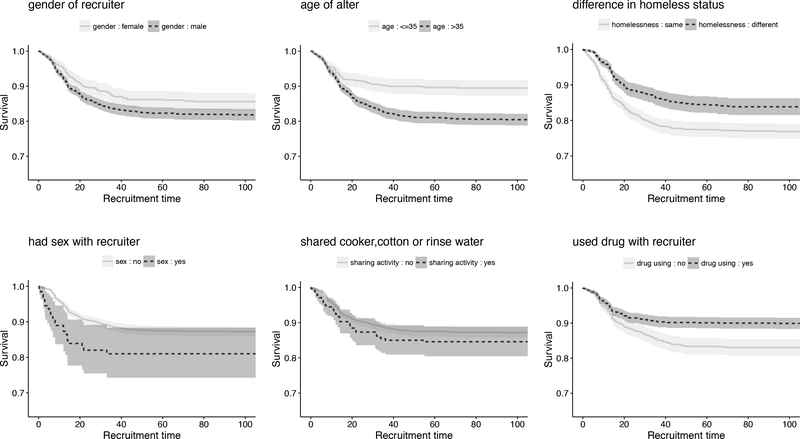
Table 2 shows results for the continuous-time Weibull model of edge-wise recruitment. The results are similar to those produced by the discrete-time model. In addition, male recruiters are more active: recruitment hazard is 1.52 times greater on an edge with male recruiter than on an edge with female recruiter. Alters who had sex with recruiters have a doubled hazard of recruitment. Recent drug-using activities together with recruiters (sharing activity) also drops the alter’s recruitment hazard to 54%. The likelihood ratio test of β, θ₂ and κ equaling zero gives Chi-square statistic χ² = 83.74 with p-value 4.19 × 10⁻¹⁰. We also performed Cox proportional hazard regression and frailty regression to assess sensitivity of the results to the hazard parameterization, with very similar results, described in Supplementary Appendix. To illustrate the presence of non-uniform recruitment, we also split edge-wise waiting times into subgroups using six variables from the Weibull continuous-time model, and compare survival patterns among subgroups. Binary variables naturally divide samples into two groups, and for continuous variable (i.e. age of alter), we use 35 as cutoff to split samples. Figure 3 shows comparisons between Kaplan-Meier curves, marginally across all subgroups.

Table 2.

Estimated regression coefficients and confidence intervals from the continuous-time Weibull model of edge-wise recruitment time. Testing β, θ₂, and κ for equality with zero gives χ² = 83.74 with degree of freedom 19, and p-value 4.19 × 10⁻¹⁰.

Covariate	γ	exp(γ)	95% CI of exp(γ)
Intercept	−4.28	0.01	0.005, 0.039
drug using	−0.61	0.54	0.335, 0.877
drug injection	−0.17	0.85	0.524, 1.369
needle using	−0.07	0.93	0.532, 1.624
sharing activity	0.56	1.75	1.117, 2.739
sex	0.73	2.07	1.262, 3.401
hivp	−0.10	0.91	0.566, 1.455
recruiter’s gender	0.42	1.52	1.078, 2.145
recruiter’s crack using	−0.13	0.88	0.669, 1.157
recruiter’s homelessness	0.08	1.08	0.814, 1.440
recruiter’s age	−0.01	0.99	0.970, 1.002
alter’s gender	0.02	1.02	0.729, 1.426
alter’s crack using	−0.25	0.78	0.595, 1.014
alter’s homelessness	0.22	1.25	0.952, 1.634
alter’s age	0.03	1.03	1.015, 1.043
recruiter black	−0.60	0.55	0.224, 1.330
recruiter white	−0.10	0.90	0.370, 2.208
alter black	0.22	1.24	0.559, 2.758
alter white	0.31	1.37	0.622, 3.015
gender difference	0.09	1.09	0.783, 1.528
crack using difference	0.20	1.22	0.937, 1.578
homelessness difference	−0.46	0.63	0.483, 0.832
age difference	−0.0028	1.00	0.980, 1.015
black difference	0.67	1.95	0.795, 4.773
white difference	−0.18	0.84	0.341, 2.051
hispanic difference	−0.19	0.83	0.358, 1.900

Figure 3.

Dynamics of edge-wise waiting time to recruitment in the RDS-net study, as a function of covariates in the continuous-time regression model. Kaplan-Meier curves represent the distribution of time to recruitment across edges connecting recruiter and potential recruitees. The horizontal axes show time in days since the recruiter entered the study, and the vertical axes show the probability of no recruitment on an edge. Dashed lines show point-wise 95% confidence intervals for the survival curves.

Discussion

How do members of stigmatized or marginalized groups like PWID recruit their network alters in real-world RDS studies? Sometimes the answer is of inherent interest in social or behavioral epidemiology [33, 13, 5, 6, 16, 7, 34, 35, 36]. More often, researchers want to know about recruitment because they wish to determine whether the assumptions required by statistical estimators for population-level quantities are met [5, 6, 7, 8, 9]. RDS is not a probability sampling design, but some researchers have argued that RDS approximates a design in which subjects are chosen with probability proportional to their network degree, either with replacement [2, 27, 3], or without replacement [37], though this approximation has been questioned in methodological and empirical work on RDS [38, 39, 5, 40, 41, 42, 28]. Researchers studying the properties of estimators have asserted that estimators for population-level quantities can exhibit bias when RDS recruitments are biased [27, 37].

In this paper, we have introduced a rigorous definition of uniform recruitment, a family of regression models for recruitment across network edges, and corresponding statistical tests for uncovering recruitment bias when the underlying network can be measured. The continuous-time analysis prives more information about the attributes of both recruiters and potential recruitees that are associated with successful recruitment. In contrast, the discrete-time approach makes fewer parametric assumptions about the edge-wise waiting time distribution, but does not estimate recruiter characteristics associated with successful recruitment. This model may be more suitable if the temporal resolution of recruitment data – times/dates of recruitment – is low, or if there are gaps in subjects’ ability to be interviewed (e.g. no recruitments on holidays or weekends).

These tools, along with data from the RDS-net study of PWID in Hartford, CT, yield insight into the dynamics of recruitment in this important risk population. The RDS-net study is unusual because it mapped the network of recruited individuals and their eligible alters. For practical and privacy-related reasons, most RDS studies do not gather this information. When researchers conduct an RDS study that does not measure any network data except the links between recruiter and recruitee, they may not be able to formulate or test a reasonable definition of uniform recruitment. As a result, claims about the presence or absence of recruitment bias in traditional RDS studies may not be falsifiable.

Our models have identified several factors that induce bias in the recruitment process in this study population of PWID, including age, homelessness, and social relationship characteristics. It is surprising that none of the race-related features were identified as important factors, because subjects with same race often demonstrate higher social closeness. It is also worth noting that some of the regression covariates are likely correlated, for example sharing activity, needle using, and joint drug injection activity. Although only sharing activity is significant in the regression model, the others also demonstrate association with recruitment marginally.

There are important limitations in our interpretation of the regression results from the RDS-net study. We have constructed the augmented recruitment-induced subgraph G_SU by taking the union of the recruitment graph G_R and the nomination network, and we treat this graph as the network of possible recruitments. However, it is possible that the true network of possible recruitments differs from the nomination network. The RDS-net study also collected information about the nominated alters that each subject intended to recruit; in a follow-up survey, many recruited subjects indicated that they received a coupon from someone other than the recruiter to whom that coupon was initially given [17]. This form of “indirect recruitment” could affect the results of our analysis: we have assumed that coupon redemption constitutes recruitment, and that the union of the actual recruitment and nomination networks represents the network of possible coupon redemptions, rather than the coupon-passing network. If many recruited individuals were not among their recruiter’s social acquaintances, or if recruitment took place on a network of starkly different topology, a core assumption of RDS recruitment may be violated. Consequently, the set of possible recruits at different times during the RDS-net study may differ from the network used in this analysis. Still, the results presented here provide an assessment of factors that appear to drive recruitment based on the characteristics of nominated – and actually recruited – individuals. In this case, the regression coefficients and tests illustrated in this paper may provide partial answers to questions about whether some individuals are more likely to be recruited than others.