Comparative roles of charge, π, and hydrophobic interactions in sequence-dependent phase separation of intrinsically disordered proteins

Significance

Mesoscopic condensates of proteins and nucleic acids, including membraneless organelles, serve myriad biological functions, whereas dysregulation of condensates can cause disease. How condensates are governed by genetically encoded biomolecular sequences is of central importance. Critical assessment of how various interactions reproduce experimental phase behaviors indicates that $\pi$-interactions’ notable facilitation of condensate formation is well reflected in established contact statistics among folded protein structures, although the condensate-driving capability of the large hydrophobic/aromatic residue phenylalanine is weaker than expected. By elucidating physical aspects of the residue–residue contacts in condensates, highlighting these contacts’ largely solvent-exposed character with ramifications such as reduced hydrophobic strengths relative to buried nonpolar contacts, fundamental conceptual and quantitative progress is made toward predictive models for biomolecular condensates.

Abstract

Endeavoring toward a transferable, predictive coarse-grained explicit-chain model for biomolecular condensates underlain by liquid–liquid phase separation (LLPS) of proteins, we conducted multiple-chain simulations of the N-terminal intrinsically disordered region (IDR) of DEAD-box helicase Ddx4, as a test case, to assess roles of electrostatic, hydrophobic, cation–$\pi$, and aromatic interactions in amino acid sequence-dependent LLPS. We evaluated three different residue–residue interaction schemes with a shared electrostatic potential. Neither a common hydrophobicity scheme nor one augmented with arginine/lysine-aromatic cation–$\pi$ interactions consistently accounted for available experimental LLPS data on the wild-type, a charge-scrambled, a phenylalanine-to-alanine (FtoA), and an arginine-to-lysine (RtoK) mutant of Ddx4 IDR. In contrast, interactions based on contact statistics among folded globular protein structures reproduce the overall experimental trend, including that the RtoK mutant has a much diminished LLPS propensity. Consistency between simulation and experiment was also found for RtoK mutants of P-granule protein LAF-1, underscoring that, to a degree, important LLPS-driving $\pi$-related interactions are embodied in classical statistical potentials. Further elucidation is necessary, however, especially of phenylalanine’s role in condensate assembly because experiments on FtoA and tyrosine-to-phenylalanine mutants suggest that LLPS-driving phenylalanine interactions are significantly weaker than posited by common statistical potentials. Protein–protein electrostatic interactions are modulated by relative permittivity, which in general depends on aqueous protein concentration. Analytical theory suggests that this dependence entails enhanced interprotein interactions in the condensed phase but more favorable protein–solvent interactions in the dilute phase. The opposing trends lead to only a modest overall impact on LLPS.

A preponderance of recent advances demonstrate that liquid–liquid phase separation (LLPS) of intrinsically disordered proteins (IDPs), proteins containing intrinsically disordered regions (IDRs), folded proteins, and nucleic acids is a general biophysical mechanism to achieve functional spatial and temporal organization of biomolecules in both intracellular and extracellular organismal space (1–9). LLPS underpins formation of a variety of biomolecular condensates (10), including intracellular bodies, such as nucleoli and stress granules, that are often referred to as membraneless organelles (4, 11), and precursor of extracellular materials as in the case of sandcastle worm adhesive (12) and elastin in vertebrate tissues (8). These dynamic, phase-separated condensates perform versatile functions, as underscored by their recently elucidated roles in synapse formation and plasticity (7, 13), organization of chromatin (14), regulation of translation (15, 16), B cell response (17), and autophagosome formation (18). The pace of discovery in this very active area of research has been accelerating (19–28).

While experimental progress has been tremendous, theory for the physicochemical basis of biomolecular condensates is still in its infancy. Biomolecular condensates in vivo are complex, involving many species of proteins and nucleic acids maintained often by nonequilibrium processes (10, 19, 29–31), rendering atomistic modeling impractical. Facing this challenge, promising initial theoretical steps using coarse-grained approaches were made to tackle simpler in vitro LLPS systems as their elucidation is a prerequisite for physical insights into more complex in vivo condensates. These recent efforts encompass analytical theories at various levels of approximation (32–42), field theory simulations (43–46), and lattice (47–50) or continuum (51–54) coarse-grained explicit-chain simulations that account for either individual amino acid residues (47, 52, 53, 55) or, at lower structural resolution, groups of residues (56, 57)—including using patchy particle representations (58, 59). The different theoretical/computational approaches are complementary and were applied to address how amino acid composition [number/fraction of hydrophobic (54), aromatic (39, 60), or charged (4) residues] and the sequence pattern of charge (34, 48, 53, 61), hydrophobic (50, 51, 54), or aromatic (60) residues affect LLPS propensity of heteropolymers as well as pertinent impact of temperature (20, 43, 51, 54), hydrostatic pressure (62–64), salt (41, 46), and osmolyte (27, 63), offering physical insights into the LLPS behaviors of, for example, the DEAD-box RNA helicase Ddx4 (34, 65), RNA-binding protein fused in sarcoma (FUS) (52), prion-like domains (60), and postsynaptic densities (64).

Developing LLPS models with transferable interaction potentials applicable to a wide range of amino acid sequences is essential for advancing fundamental physical understanding of natural biomolecular condensates and engineering of bioinspired materials (66). In this endeavor, the rapidly expanding repertoire of experimental data offers critical assessment of theoretical and computational approaches. Building on aforementioned progress (34, 41, 52, 53), the present study evaluates a variety of interaction schemes for coarse-grained residue-based chain simulations of LLPS of IDPs or IDRs, including but not limited to schemes proposed in the literature (52). We do so by first comparing their sequence-specific predictions against experiment on the RNA helicase Ddx4 for which extensive LLPS data on the wild-type (WT) and three mutant sequences are available to probe the contribution of hydrophobic, electrostatic (4), cation–$\pi$, and possibly other $\pi$-related (4, 65, 67) interactions. We use these data to benchmark the relative strengths of different types of interaction in our model. Of particular interest are the aromatic (68) and other $\pi$-related (67) interactions, which have significant impact on folded protein structure, conformational distribution of IDPs, and LLPS properties (4, 34, 39, 60, 69–73) but are often not adequately accounted for in model potentials (67). Interestingly, a simple statistical potential based upon folded protein structures (74, 75) accounts for the general trend of LLPS properties of the four Ddx4 IDR sequences, including that LLPS is more favored by arginine than lysine despite their essential identical electric charges, but that a model potential that relies solely on hydrophobicity (76) does not. This finding indicates that at the coarse-grained level of residue–residue interactions, IDP/IDR LLPS is governed largely by similar forces—including the $\pi$-related ones—that drive protein folding. Analogous agreement between statistical potential model prediction and experiment with respect to the arginine/lysine contrast is also found for the N-terminal RGG domain of P-granule RNA Ddx3 helicase LAF-1 (77). However, experimental data on tyrosine-to-phenylalanine mutants of LAF-1 and FUS (39) indicate that the contribution of the large aromatic residue phenylalanine to LLPS is overestimated by statistical potentials, most likely because the interactions involving phenylalanine in the sequestered hydrophobic core of globular proteins are not sufficiently representative of more solvent-accessible LLPS-driving interactions, pointing to a crucial aspect of LLPS energetics toward which future investigations should be directed. To gain further insights into the electrostatic driving forces for LLPS, we have conducted explicit-water simulation and developed analytical theory which suggests, at variance with previous analyses (35, 37), that the physically expected dependence of effective permittivity on IDR concentration may have a modest instead of drastic impact on LLPS propensity because of a tradeoff between solvent-mediated electrostatic interchain interactions and self-interactions. These findings and their ramifications are discussed below.

Results and Discussion

As described in Materials and Methods and SI Appendix, SI Text, our coarse-grained protein chain model for IDP LLPS basically follows the approaches in refs. 52, 53, which in turn are based on a recently proposed efficient simulation protocol (78). In the first step of our analysis, we critically assess the models against the experimental data on the Ddx4 IDR (SI Appendix, Fig. S1), which indicate that all three Ddx4 IDR mutants—the charge scrambled (CS), phenylalanine-to-alanine (FtoA), and arginine-to-lysine (RtoK) variants—have significantly reduced LLPS propensities relative to the WT (4, 65, 67). The CS, FtoA, and RtoK variants are useful probes for LLPS energetics. They were constructed specifically to study the experimental effects of sequence charge pattern (the arrangement of charges along CS sequence is less blocky than that in WT while the amino acid composition is unchanged), the relative importance of aromatic/$\pi$-related vs. hydrophobic/nonpolar interactions (all 14 Phe residues in WT Ddx4 IDR are mutated to Ala in FtoA), and the role of Arg vs Lys (all 24 Arg residues in WT IDR are mutated to Lys in RtoK) on the LLPS of Ddx4.

Assessing Biophysical Perspectives Embodied by Different Coarse-Grained Interaction Schemes for Modeling Biomolecular Condensates.

We consider the potential functions in the hydrophobicity-scale (HPS) and the Kim–Hummer (KH) models in Dignon et al. (52) as well as the HPS potential with augmented cation–$\pi$ terms (72), all of which share the same bond energy term, $U_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}}$, for chain connectivity and screened electrostatic term, $U_{\mathrm{e}\mathrm{l}}$, for pairs of charged residues, as described in SI Appendix, SI Text. We focus first on the pairwise contact interactions between amino acid residues, which correspond to the $U_{\mathrm{a}\mathrm{a}}$ energies of either the HPS or KH model (excluding $U_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}}$ and $U_{\mathrm{e}\mathrm{l}}$).

The HPS model assumes that the dominant driving force for IDP LLPS is hydrophobicity as characterized by a scale for the 20 amino acid residues. Pairwise contact energy is taken to be the sum of the hydrophobicities of the two individual residues of the pair. The HPS model adopts the scale of Kapcha and Rossky, in which the hydrophobicity of a residue is a composite quantity based on a binary hydrophobicity scale of the atoms in the residue (76).

In contrast, the KH model (79) relies on knowledge-based potentials derived from contact statistics of folded protein structures in the Protein Data Bank (PDB). As such, it assumes that the driving forces for IDP LLPS are essentially identical to those for protein folding at a coarse-grained residue-by-residue level, as obtained by Miyazawa and Jernigan (75), without singling out a priori a particular interaction type as being dominant.

The HPS model has been applied successfully to study the FUS low-complexity domain (80), the RNA-binding protein TDP-43 (81), and the LAF-1 RGG domain as well as its charge shuffled variants (77). A temperature-dependent version of HPS (HSP-T) (51) was also able to rationalize the experimental LLPS properties of artificial designed sequences (82). When both the HPS and KH models were applied to FUS and LAF-1, the predicted phase diagrams were qualitatively similar for a given sequence, although they exhibited significantly different critical temperatures (52), which should be attributable to the difference in effective energy/temperature scale of the two models. Here we conduct a systematic assessment of the two models’ underlying biophysical assumptions by evaluating their ability to provide a consistent rationalization of the LLPS properties of a set of IDR sequences.

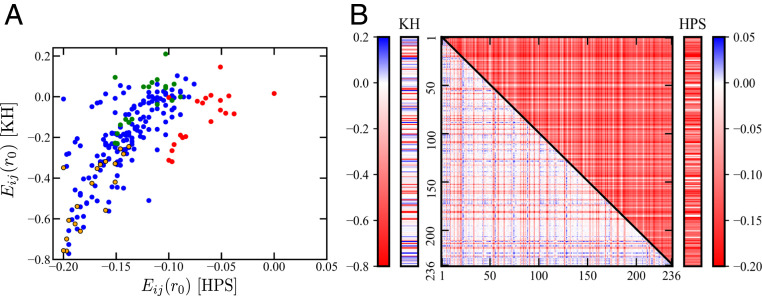
The scatterplot in Fig. 1A of HPS and KH energies indicates that despite an overall correlation, there are significant outliers. The most conspicuous outliers are interactions involving Arg (red), which are much less favorable in HPS than in KH. By comparison, most of the interactions involving Pro, as depicted by the 16 outlying blue circles as well as the single yellow and single green circles to the left of the main trend, are considerably more favorable in HPS than in KH. Interactions involving Phe (yellow) and Lys (green) essentially follow the main trend. Those involving Phe are favorable to various degrees in both models. However, some interactions involving Lys are attractive in HPS but repulsive in KH. For example, Lys–Lys interaction is attractive at $\approx -0.1$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for HPS but is repulsive at $\approx +0.2$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for KH. Fig. 1B underscores the difference in interaction pattern of the two models for the WT Ddx4 IDR. The KH pattern is clearly more heterogeneous with both attractions and repulsions, whereas the HPS pattern is more uniform with no repulsive interactions. These differences should lead to significantly different predictions in sequence-dependent LLPS properties, as will be explored below.

Fig. 1.

Comparing two amino acid residue-based coarse-grained potentials. (A) Scatterplot of 210 pairwise contact energies (in units of kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$) in the HPS (horizontal variable) versus those in the KH (vertical variable) model (52). $E_{ij}\left(r_0\right)$s are the pairwise potential energies $U_{\mathrm{a}\mathrm{a}|\mathrm{H}\mathrm{P}\mathrm{S}}\left(r\right)$ or $U_{\mathrm{a}\mathrm{a}|\mathrm{K}\mathrm{H}}\left(r\right)$ (SI Appendix, SI Text), between two residues of types $i,j$ separated by $r_{ij}=r_0$ where the Lennard–Jones component of the potential is minimum ($i,j$ here stand for labels for the 20 amino acid types). Energies of contacts involving Arg (red circles), Lys (green circles), and Phe (yellow-filled black circles) are colored differently from others (blue circles). (B) Contact energies between residue pairs at positions $i,j$ of the $n=236$ sequence of WT Ddx4 IDR [Ddx${\mathrm{4}}^{\mathrm{N}\mathrm{1}}$ (4)] in the two potentials are color coded by the scales. The vertical and horizontal axes represent residue positions $i,j\le n$. The $i\ne j$ contact energies in the HPS and KH models are provided in the 2D plot, whereas the $i=j$ contact energies are shown alongside the model potentials’ respective color scales.

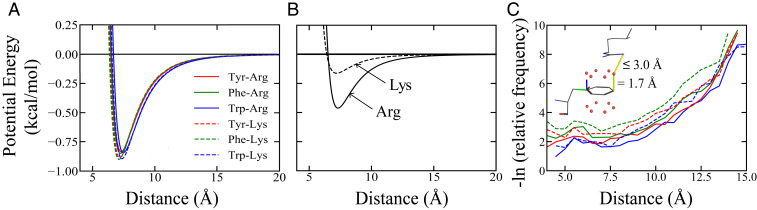
Because of the importance of cation–$\pi$ interactions in protein folded structure (69) as well as conformational distribution of IDP and LLPS (4, 39, 72, 73, 77), we study another set of model interaction schemes—in addition to HPS and KH, referred to as HPS + cation–$\pi$—that augment the HPS potentials with terms specific for cation–$\pi$ interactions between Arg or Lys and the aromatic Tyr, Phe, or Trp (Fig. 2). As explained in SI Appendix, SI Text, we consider two alternate scenarios: 1) the cation–$\pi$ interaction strength is essentially uniform, irrespective of the cation–aromatic pair (Fig. 2A), as suggested by an earlier analysis (69), and 2) the cation–$\pi$ interaction strength is significantly stronger for Arg than for Lys (Fig. 2B). The latter scheme is motivated by recent experiments showing that Arg to Lys substitutions reduce LLPS propensity, as in the cases of the RtoK mutant of Ddx4 IDR (67) and variants of FUS (39) and LAF-1 (77), as well as a recent theoretical investigation pointing to different roles of Arg and Lys in cation–$\pi$ interactions (83). Contact statistics of PDB structures, including those of Miyazawa and Jernigan (74, 75) on which the KH potential is based, may also suggest that Arg–$\pi$ attractions are stronger than Lys–$\pi$ interactions. Indeed, among a set of 6,943 high-resolution X-ray protein structures (67), we find that an Arg–aromatic pair is at least 75% more likely than a Lys–aromatic pair to be within a ${\mathrm{C}}_{\alpha }$–${\mathrm{C}}_{\alpha }$ distance of $\le 6.5$ Å (SI Appendix, Fig. S2), a separation that is often taken as a criterion for residue–residue contact (74). On top of that, given an Arg–aromatic and a Lys–aromatic pair separated by the same ${\mathrm{C}}_{\alpha }$–${\mathrm{C}}_{\alpha }$ distance (Fig. 2C), the Arg–aromatic pair (solid curves) is more likely than the Lys–aromatic pair (dashed curves) to adopt configurations consistent with a cation–$\pi$ interaction. We emphasize, however, that although a significantly stronger Arg- than Lys-associated cation–$\pi$ interaction is explored here as an alternate scenario, it is probable, as argued by Gallivan and Dougherty using a comparison between Lys-like ammonium–benzene and Arg-like guanidinium–benzene interactions, that the strengths of the pure cation–$\pi$ parts of Arg– and Lys–aromatic interactions are similar despite the relative abundance of Arg–aromatic contacts due to other factors (69) such as $\pi$–$\pi$ effects (67).

Fig. 2.

Possible cation–$\pi$ interaction potentials. (A) Sum of the coarse-grained HPS potential and a model cation–$\pi$ interaction with a uniform ${\left({ϵ}_{\mathrm{c}\pi }\right)}_{ij}=3.0$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ as a function of residue–residue distance for the residue pairs Arg–Tyr, Arg–Phe, Arg–Trp, Lys–Tyr, Lys–Phe, and Lys–Trp, wherein Tyr, Phe, and Trp are labeled as red, green, and blue, and Arg and Lys are represented by solid and dashed curves. (B) An alternate cation–$\pi$ potential in which Arg–Tyr/Phe/Trp is significantly more favorable (solid curve; ${\left({ϵ}_{\mathrm{c}\pi }\right)}_{ij}=1.85$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$) than Lys–Tyr/Phe/Trp (dashed curve; ${\left({ϵ}_{\mathrm{c}\pi }\right)}_{ij}=0.65$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$). Note that the plotted curves here—unlike those in A—do not contain the HPS potential. (C) Normalized ${\mathrm{C}}_{\alpha }$–${\mathrm{C}}_{\alpha }$ distance-dependent contact frequencies for the aforementioned six cation–$\pi$ pairs (color coded as in A) computed using a set of 6,943 high-resolution X-ray protein crystal structures (resolution $\le 1.8$ Å) from a published nonredundant set (67). Contact pair statistics are collected from residues on different chains in a given structure and residues separated by $\ge 50$ amino acids along the same chain. ${\mathrm{C}}_{\alpha }$–${\mathrm{C}}_{\alpha }$ distances are divided into 0.2-Å bins. For each bin, the relative frequency is the number of instances of a cation–$\pi$-like contact (defined below) divided by the total number of residue pairs with ${\mathrm{C}}_{\alpha }$–${\mathrm{C}}_{\alpha }$ distances within the narrow range of the bin. Thus, the shown curves quantify the tendency for a given pair of residues to engage in cation–$\pi$ interaction provided that the pair is spatially separated by a given ${\mathrm{C}}_{\alpha }$–${\mathrm{C}}_{\alpha }$ distance. Here a cation–$\pi$-like contact is recognized if either a Lys NZ or an Arg NH1 nitrogen atom is within 3.0 Å of any one of the points 1.7 Å above or below an $s{p}^2$ carbon atom along the normal of the aromatic ring in a Tyr, Phe, or Trp residue. This criterion is exemplified by the molecular drawing (Inset) of a contact between an Arg (at the top) and a Phe (at the bottom). Colors of the chemical bonds indicate types of atom involved, with carbon in black, oxygen in red, and nitrogen in blue. The red dots here are points on the exterior surfaces of the electronic orbitals farthest from the $s{p}^2$ carbons in the aromatic ring. The blue, green, and red lines emanating from a corner of the aromatic ring constitute a local coordinate frame, with the blue line being the normal vector of the plane of the aromatic ring determined from the positions of its first three atoms. The yellow lines mark spatial separations used to define the cation–$\pi$-like contact. These yellow lines do not represent chemical bonds.

Hydrophobicity, Electrostatics, and Cation–$\pi$ Interactions Are Insufficient by Themselves to Rationalize Ddx4 LLPS Data in Their Entirety.

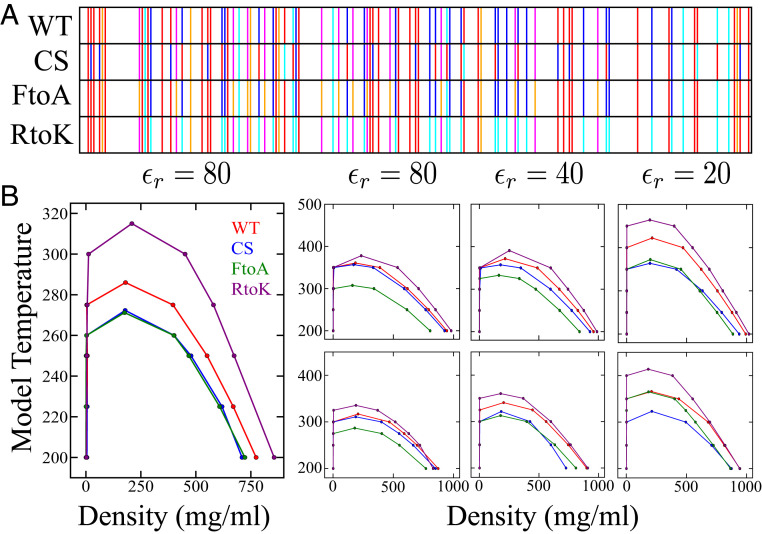
We begin our assessment of models by applying the HPS and HPS + cation–$\pi$ potentials to simulate the phase diagrams of the four Ddx4 IDRs (SI Appendix, Fig. S1), the sequence patterns of which are illustrated in Fig. 3A using a style employed previously, e.g., in refs. 4, 34, 39. The phase diagrams presented here are coexistence curves. When the overall average IDR density lies in between the left and right arms of the coexistence curve at a given temperature, the system phase separates into a dilute phase and a condensed phase with IDR densities given by the low- and high-density values, respectively, of the coexistence curve at the given temperature. When the average IDR density is not in the region underneath the coexistence curve, the system is not phase separated (see, e.g., refs. 20, 35, 84 for introductory discussions). Consistent with experiments (4, 65), the simulated phase diagrams (Fig. 3B) exhibit upper critical solution temperatures, which is a maximum temperature above which phase separation does not occur (corresponding to the local maxima of the coexistence curves at IDR density $\approx 200$ mg/mL in Fig. 3). We emphasize, however, that although the simulated critical temperatures are assuringly in the same range as those deduced experimentally (65), the model temperature (in K) of our simulated phase diagrams in Figs. 3B and 4 should not be compared directly with experimental temperature. This is not only because of uncertainties about the overall model energy scale but also because the models do not account for the temperature dependence of effective residue–residue interactions (20, 43, 51). For simplicity, our models include only temperature-independent energies as they are purposed mainly for comparing the LLPS propensities of different amino acid sequences on the same footing rather than for highly accurate prediction of LLPS behaviors of any individual sequence.

Fig. 3.

Simulated phase behaviors of Ddx4 IDR variants in a hydrophobicity-dominant potential augmented by cation–$\pi$ interactions. (A) Sequence patterns of the WT and its charge-scrambled (CS), Phe to Ala (FtoA) and Arg to Lys (RtoK) variants. Select residue types are highlighted: Ala (orange), Asp and Glu (red), Phe (magenta), Lys (cyan), and Arg (dark blue); other residue types are not distinguished. (B) Simulated phase diagrams of WT, CS, FtoA, and RtoK Ddx4 IDR at various relative permittivities (${ϵ}_{\mathrm{r}}$) as indicated, using the HPS model only (Left) and the HPS model augmented with cation–$\pi$ interactions (Right) with either (Top) a uniform ${\left({ϵ}_{\mathrm{c}\pi }\right)}_{ij}$ as described in Fig. 2A or (Bottom) different ${\left({ϵ}_{\mathrm{c}\pi }\right)}_{ij}$ values for Arg and Lys as given in Fig. 2B.

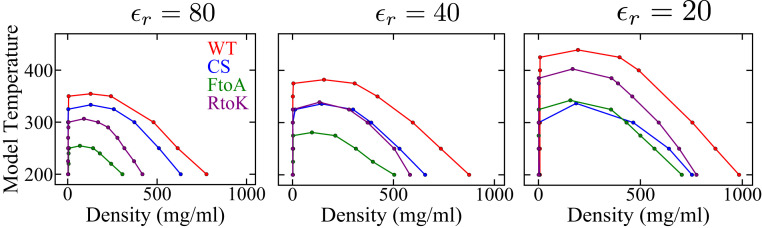
Fig. 4.

Simulated phase behaviors of Ddx4 IDR variants using an interaction scheme based largely on PDB-derived statistical potentials. Phase diagrams were computed using the KH model at three different relative permittivities (${ϵ}_r$).

Fig. 3 B, Left, provides the HPS phase diagrams at relative permittivity ${ϵ}_{\mathrm{r}}=80$ (approximately equal to that of bulk water, as in ref. 52). The predicted behaviors of the CS and FtoA variants are consistent with experiments in that their LLPS propensities are reduced relative to WT (4, 65), but the predicted enhanced LLPS propensity of RtoK is opposite to the experimental finding of Vernon et al. that the LLPS propensity of RtoK is lower than that of WT (67). This shortcoming of the HPS model is a consequence of its assignment of much less favorable interactions for Arg than for Lys, as noted in Fig. 1A.

Fig. 3 B, Right, provides the HPS + cation–$\pi$ phase diagrams. They are computed for ${ϵ}_{\mathrm{r}}=80$, 40, and 20 to gauge the effect of electrostatic interactions relative to other types of interactions. The ${ϵ}_{\mathrm{r}}$-dependent results are also preparatory for our subsequent investigation of the effect of IDR concentration-dependent permittivity ( 35, 37) on predicted LLPS properties. All of the HPS + cation–$\pi$ phase diagrams here still disagree with experiment (65, 67) as they all predict a higher LLPS propensity for the RtoK variant than for WT. Apparently, the bias of the HPS potential against Arg interactions is so strong that it cannot be overcome by additional Arg–aromatic interactions that are reasonably more favorable than Lys–aromatic interactions (Fig. 2B). The ${ϵ}_{\mathrm{r}}=80$ results for both uniform and variable cation–$\pi$ strength exhibit an additional mismatch: contrary to experiments (4, 65), they predict similar LLPS propensities for the CS variant and WT, suggesting that under this dielectric condition, electrostatic interactions are unphysically overwhelmed by the presumed cation–$\pi$ interactions. The ${ϵ}_{\mathrm{r}}=20$ results for variable cation–$\pi$ also indicate an additional mismatch; in this case they fail to reproduce the experimental trend of a significantly lower LLPS propensity of the FtoA variant relative to that of WT (4), probably because the relatively weak cation–$\pi$ contribution is overwhelmed by strong electrostatic interactions in this low-${ϵ}_{\mathrm{r}}$ situation. Taken together, although a perspective involving only electrostatic and cation–$\pi$ interactions was adequate to account for sequence-specific LLPS trend of WT and CS (and possibly also FtoA) before the RtoK experiment was performed (34), such a perspective is incomplete when RtoK enters the picture. Fig. 3B shows that the HPS + cation–$\pi$ model, which takes into account hydrophobic, charged, and cation–$\pi$ interactions, cannot account for the general trend of available Ddx4 LLPS data. It follows that these interactions—at least when hydrophobicity is accorded by the particular scale (76) adopted by HPS—are insufficient by themselves to account for LLPS of IDRs in general.

Structure-Based Statistical Potentials Provide an Approximate Account of $\pi$-Related Driving Forces for Ddx4 LLPS.

In contrast to the HPS and HPS + cation–$\pi$ models, direct application of the KH model—without augmented cation–$\pi$ terms—leads to an overall trend largely in agreement with experiments (4, 65, 67) for the ${ϵ}_{\mathrm{r}}$ values tested; i.e., all three Ddx4 IDR variants are predicted by the KH potential to have lower LLPS propensities than WT (Fig. 4). For WT at ${ϵ}_{\mathrm{r}}=80$ and $T=300$ K, the simulated condensed phase density of $\sim 500$ mg ${\mathrm{m}\mathrm{L}}^{-1}$ is comparable to the experimental value of $\sim 400$ mg ${\mathrm{m}\mathrm{L}}^{-1}$ with [NaCl] = 100 mM at the same temperature (65). Similar KH- and HPS-simulated condensed phase densities were obtained for FUS and LAF-1 IDRs (52). Illustrations of our simulated chain configurations are provided in Fig. 5. Time-dependent mean-square deviation of molecular coordinates has been used to verify liquid-like chain dynamics in the condensed phase of HPS and KH models (52). Examples of similar calculation are provided in SI Appendix, Figs. S3 and S4, for the Ddx4 IDRs examined in this work.

Fig. 5.

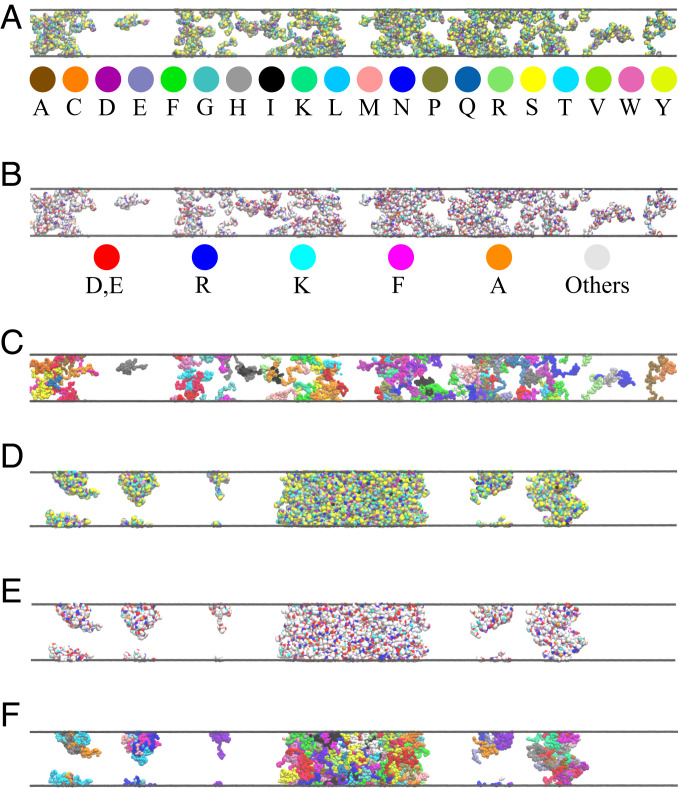
Illustrative snapshots of Ddx${\mathrm{4}}^{\mathrm{N}\mathrm{1}}$CS phase behaviors simulated using the KH potential for ${ϵ}_{\mathrm{r}}=40$. (A) A non–phase-separated snapshot at model temperature 375 K, wherein the amino acid residues are colored using the default VMD scheme (91, 92) as provided by the key below the snapshot. (B) Same as A except the color scheme (as shown) is essentially identical to that in Fig. 3A. (C) Same as A and B except all residues along the same chain share the same color. Neighboring chains are colored differently to highlight the diversity of conformations in the system. (D–F) A phase-separated snapshot at model temperature 325 K. The color schemes are the same as those in A–C, respectively.

This success of the KH model suggests that empirical, knowledge-based statistical potentials derived from the PDB may capture key effects governing both protein folding and IDR LLPS without prejudging the dominance of, or lack thereof, particular types of energetics such as hydrophobicity in the HPS model. In this respect, it would not be surprising that cation–$\pi$ and other $\pi$-related interactions are reflected in these knowledge-based potentials as well. After all, the importance of cation–$\pi$ interactions in folded protein structure (69) and $\pi$–$\pi$ interactions in IDR LLPS (67) is recognized largely by bioinformatics analyses of the PDB.

As discussed above, a major cause of the shortcoming of HPS in accounting for the LLPS of Ddx4 IDRs (Fig. 3B) is the high degree of unfavorability it ascribes to Arg interactions. Its hydrophobicity scale, based on the atomic partial charges in the OPLS (optimized potentials for liquid simulations) force field, posits that Arg has the least hydrophobicity value of $+14.5$, and the next-least hydrophobic is Asp with $+7.5$, whereas Lys has $+5.0$, and the most hydrophobic is Phe with $-4.0$ (76). This assignment results in highly unfavorable Arg-associated interactions relative to Lys-associated interactions. In the HPS model, when one of the residues, $i$, in the pairwise energy $E_{ij}\left(r_0\right)$ (Fig. 1A) is Arg, the average of $E_{ij}\left(r_0\right)$ over $j$ for all amino acids except the charged residues Arg, Lys, Asp, and Glu is equal to $-0.0762$ in units of kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, whereas the corresponding average for Lys is much more favorable at $-0.1276$. When the charged residues are included, the trend is the same with the average being $-0.0677$ for Arg and $-0.119$ for Lys. In contrast, for the KH model, the trend is opposite with Arg-associated interactions much more favorable: the corresponding average is $-0.123$ for Arg and $-0.041$ for Lys when charged residues are excluded in the averaging and $-0.0990$ for Arg and $-0.0161$ for Lys when charge residues are included. This trend echoes an earlier eigenvalue analysis of the Miyazawa–Jernigan energies (75) (which underlie the KH potential) indicating that Arg has a significantly larger projection than Lys along the dominant eigenvector (85).

Whereas correlation among hydrophobicity scales inferred from different methods is limited (86–89) with significant variations especially for the nonhydrophobic polar and charged residues (87), the extremely low hydrophobicity assigned by HPS (52, 76) to Arg relative to Lys is unusual. For instance, Lys is substantially less hydrophobic than Arg in two of the three scales tabulated and compared in ref. 89. In a commonly utilized scale based on the free energies of transfer of amino acid derivatives from water to octanol measured by Fauchère and Pliška (90) (the second scale tabulated in ref. 89), Arg is only slightly less hydrophobic ($+5.72$ kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$) than Lys ($+5.61$ kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$), and thus, essentially, Arg and Lys are deemed to possess equally low hydrophobicities. Accordingly, this scale affords a better correlation with the Miyazawa–Jernigan energies (75) (figure 3b of ref. 89) than that exhibited in Fig. 1A.

It is reasonable to expect the 210 (or more) residue–residue contact energy parameters in PDB structures-based potentials to contain more comprehensive energetic information than merely the hydrophobicities of the 20 types of amino acid residues. In this regard, it is notable that a higher propensity for Arg than Lys to engage favorably with another residue appears to be a robust feature of PDB statistics. It holds for the cation–aromatic pairs we analyze in SI Appendix, Fig. S2, for the KH potential, and also for the original Miyazawa–Jernigan energies put forth in 1985 (74). According to table V of ref. 74, the contact energies $e_{ij}$ between Arg and aromatic or negatively charged residues are $-3.54$, $-3.56$, $-2.75$, $-2.07$, and $-1.98k_{\mathrm{B}}T$ for Arg–Phe, Arg–Trp, Arg–Tyr, Arg–Glu, and Arg–Asp, respectively ($k_{\mathrm{B}}$ is Boltzmann constant, and $T$ is absolute temperature), whereas the corresponding contact energies are weaker for Lys at $-2.83$, $-2.49$, $-2.01$, $-1.60$, and $-1.32k_{\mathrm{B}}T$ for Lys–Phe, Lys–Trp, Lys–Tyr, Lys–Glu, and Lys–Asp, respectively. All 20 Arg interactions are more favorable than the corresponding Lys interactions. The average $e_{ij}$ over all Arg-associated pairs is $-2.22k_{\mathrm{B}}T$, which is substantially more favorable than the corresponding average of $-1.4795k_{\mathrm{B}}T$ for the Lys-associated pairs. It is apparent from the present application of KH to the Ddx4 IDRs that this feature is crucial, at least at a coarse-grained level, for an adequate accounting of the $\pi$-related energetics of biomolecular LLPS. Physically, the general preference for Arg–$\pi$ over Lys–$\pi$ contacts is underpinned in part by the Arg geometry which allows for favorable guanidinium–aromatic coplanar packing (71), as discussed recently by Wang et al. (ref. 39 and references therein), and that Arg–aromatic is less attenuated by the aqueous dielectric medium because it is less dominated than Lys–aromatic interactions by electrostatics (83). Consistent with this perspective, R to K mutants of FUS (39) and LAF-1 RGG (77) also exhibit substantially reduced LLPS propensity relative to WT.

Phenylalanine Interactions in Liquid Condensates, Expected to Be More Solvent-Exposed, Are Weaker than Statistical Estimates Based on Mostly Core Phenylalanine Contacts in Folded Proteins.

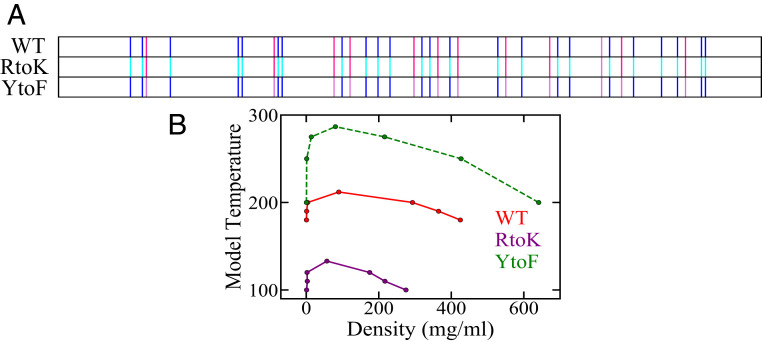
To assess further the generality of the KH model, we apply it to simulate the phase behavior of WT LAF-1 and its RtoK and tryosine-to-phenylalanine (YtoF) mutants (Fig. 6 and SI Appendix, Fig. S5). Simulation studies of LLPS of full-length and the RGG IDR (52) of LAF-1, including the latter’s charge shuffled variants (77), have been conducted extensively using the HPS (52, 77) and KH (52) models to gain valuable insights, but phase behaviors of the RtoK and YtoF LAF-1 RGG mutants have not been simulated using these models. Recent experiments indicate that the RtoK mutant does not phase separate under the conditions tested, whereas the LLPS propensity of the YtoF mutant is reduced relative to that of WT (77). As for the case of Ddx4 IDR, the KH-predicted coexistence curve for RtoK LAF-1 RGG in Fig. 6 (purple curve) is consistent with the experimental trend as it has a far lower critical temperature than that of the WT (red curve). However, KH posits a significantly higher LLPS propensity for YtoF (green dashed curve with a much higher critical temperature), which is opposite to experimental observation. On closer inspection, the basic feature that causes this shortcoming is that KH deems Phe interactions more favorable than Tyr interactions. According to KH, $E_{ij}\left(r_0\right)$ for $i=\mathrm{P}\mathrm{h}\mathrm{e}$ averaged over $j$ for all amino acids is $-0.453$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for Phe, which is significantly more negative than the corresponding average $E_{ij}\left(r_0\right)$ of $-0.281$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for Tyr. For this reason, KH is unlikely to reproduce the experimentally observed reduced LLPS propensities for any other YtoF mutant either, including the YtoF mutants of FUS (39).

Fig. 6.

Simulated phase diagrams of LAF-1 IDRs computed by the KH model at ${ϵ}_{\mathrm{r}}=40$ for the three sequences in SI Appendix, Fig. S5. (A) Sequence patterns of the WT and two variants. Highlighted residues are Phe (magenta); Lys (cyan); Arg (dark blue), as in Fig. 3A; and Tyr (pink); other residue types, including Ala, Asp, and Glu which were highlighted in Fig. 3A, are not distinguished here. (B) Phase diagrams for WT and mutant sequences are plotted in different colors as indicated.

This overestimation of the favorability of Phe-related interactions in the LLPS context also causes the KH-predicted LLPS propensity of the FtoA mutant of Ddx4 IDR (Fig. 4, green curves) to be substantially lower than that of the RtoK mutant (purple curves). Experimentally, however, FtoA mutant LLPS is observed at $\sim 350$ mg ${\mathrm{m}\mathrm{L}}^{-1}$ protein concentration, but the RtoK mutant does not phase separate up to 400 mg ${\mathrm{m}\mathrm{L}}^{-1}$ (in comparison, LLPS of WT is observed at 25 mg ${\mathrm{m}\mathrm{L}}^{-1}$) (67). In other words, the KH-predicted rank ordering of LLPS propensities of Ddx4 FtoA and RtoK is opposite to experiment. This is because the KH energy $E_{ij}\left(r_0\right)$ for Ala averaged over all 20 residue types, at $-0.160$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, is much less favorable than the corresponding $-0.453$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ for Phe and the change in average KH $E_{ij}\left(r_0\right)$ from Phe to Ala ($-0.160+0.453=+0.293$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$) is far larger than the corresponding change of $-0.0161+0.0990=+0.0829$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ from Arg to Lys.

Interestingly, while these Ala-, Tyr-, and Phe-related KH energies do not reproduce experimental observations for YtoF and FtoA mutants, the KH energies are largely in line with rank ordering in common hydrophobicity scales. For instance, in the water-to-octanol scale of Fauchère and Pliška (90), the transfer free energies for Ala, Tyr, and Phe are $-1.76$, $-5.44$, and $-10.1$ kJ ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, respectively. By comparison, the average interaction energies in the HPS model for Ala, Tyr, and Phe differ less, being $-0.141$, $-0.154$, and $-0.168$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, respectively, but Phe-related interactions are still generally more favorable than Tyr-related interactions. Thus, HPS is not only insufficient to account for RtoK experiments (Fig. 3), HPS is not expected to capture the observed YtoF trend either.

The above consideration underscores once again that the energetic contributions of amino acid residues to LLPS are not necessarily dominated by their hydrophobicities. Phe is generally considered to be more hydrophobic than Tyr. However, even for the globular proteins ribonuclease Sa and Sa3, 14 out of 16 YtoF single-site substitutions destabilize the folded state. One of the physical reasons for this behavior is that the Tyr hydroxyl group—which is absent in Phe—makes a hydrogen bond with the ${\mathrm{N}}^{ϵ}$ atom of an Arg residue (93). It would be enlightening to investigate whether similar hydrogen bonding effects account to any degree for the preference for Tyr–Arg over Phe–Arg interactions in the LLPS context.

For a relatively large residue that possesses both hydrophobic and aromatic properties such as phenylalanine, the character of its LLPS-driving contributions can also differ significantly from those stabilizing the well-packed core of a folded protein because most residue–residue contacts in the LLPS context are at least partially exposed to solvent even in the condensed phase. This observation offers a perspective to understand KH’s inability to capture LLPS behaviors of YtoF and FtoA mutants because KH is derived from statistical potentials which in turn are based upon contact frequencies in folded proteins. Since Phe is one of the most buried residues in folded proteins with on average 0.88 of its surface area inaccessible to solvent upon folding (the corresponding fractions for Tyr, Ala, Lys, and Arg are 0.76, 0.74, 0.52, and 0.64, respectively) (94), the difference in character between Phe’s LLPS-driving and folded-state-stabilizing interactions is expected to be more prominent.

Indeed, it has long been recognized that pair interactions in solvent-exposed environments have properties—including thermodynamic signatures (95, 96)—that are distinctly different from those of bulk interactions quantified by common hydrophobicity measurements (97). In this regard, computational evidence suggests that Phe-related interaction in a highly solvent accessible environment—which is more pertinent to LLPS—is not substantially stronger than Ala-related interactions. For instance, using ethane and ethylbenzene as models for Ala and Phe, respectively, explicit-TIP3P (3-point transferable intermolecular potential) water simulations of pairwise potentials of mean force (PMFs) at 298 K by Makowski et al. indicate that the lowest free energies at the ethane–ethane, ethane–ethylbenzene (98), and ethylbenzene–ethylbenzene (99) contact minima are all $\approx -1$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ [Tyr was not considered in these studies (98, 99)]. Thus, in contrast to the vastly different Ala–Ala, Ala–Phe, and Phe–Phe interaction strengths in KH, with $E_{ij}\left(r_0\right)=-0.142$, $-0.425$, and $-0.756$ kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, respectively (52), these explicit-water PMFs suggest a more modest difference in interaction strength between Ala and Phe in the LLPS context, which would be in line with the FtoA experiment. With this knowledge, future investigations should tackle hitherto overlooked features of solvent-accessible contacts among amino acid residues to improve coarse-grained interaction potentials for LLPS.

IDR Concentration Can Significantly Affect the Dielectric Environment of Condensed Droplets but Its Impact on LLPS Propensity Can Be Modest.

In recent (52, 53, 55) and the above coarse-grained, implicit-solvent simulations of LLPS of IDRs, electrostatic interactions are assumed, for simplicity, to operate in a uniform dielectric medium with a position-independent ${ϵ}_{\mathrm{r}}$. However, the dielectric environment is certainly nonuniform upon LLPS: the electrostatic interaction between two charges is affected to a larger extent by the intervening IDR materials in the condensed phase—where there is a higher IDR concentration—than in the dilute phase. Protein materials have lower ${ϵ}_{\mathrm{r}}$s than bulk water (100–102). Analytical treatments with effective medium theories suggest that a decrease in effective ${ϵ}_{\mathrm{r}}$ with increasing IDR concentration enhances polyampholytes LLPS in a cooperative manner because the formation of condensed phase lowers ${ϵ}_{\mathrm{r}}$, and that in turn induces stronger electrostatic attractions that favor the condensed phase (35, 37).

In principle, LLPS of IDR chains in polarizable aqueous media can be directly simulated using explicit-water atomic models wherein partial charges are assigned to appropriate sites of the water and protein molecules, but such simulations are computationally extremely costly because a large number of IDR chains are needed to model LLPS. Here we use explicit-water atomic simulation involving only a few IDR molecules, not to model LLPS but to estimate how the effective ${ϵ}_{\mathrm{r}}$ depends on IDR concentration. We will then combine this information with analytical formulations to provide a more complete account of the electrostatic driving forces for LLPS. The dielectric properties of folded proteins (100, 101), their solutions (103), and related biomolecular (104) and cellular (105) settings have long been of interest (106). For the current focus on biomolecular condensates, their interior dielectric environments are expected to be of functional significance, e.g., as drivers for various ions and charged molecules to preferentially partition into a condensate (107).

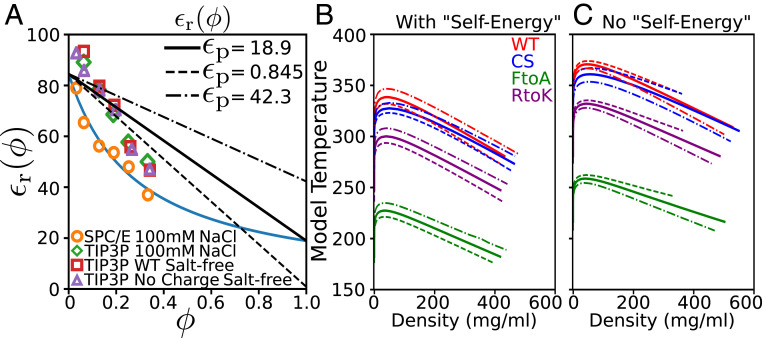
As outlined in Materials and Methods, GROMACS (Groningen Machine for Chemical Simulations) (108) and the amber99sb-ildn forcefield (109) are used for our explicit-water simulations using either the TIP3P (110) or the SPC/E (extended simple point charge) (111) model of water in simulation boxes containing WT Ddx4 IDR chains. Relative permittivities are estimated by fluctuations of the system dipole moment (101, 103). Simulations are also performed on artificially constructed Ddx4 (aDdx4) in which the side chain charges of Arg, Lys, Asp, and Glu are neutralized for possible applications when side chain charges are treated separately from that of the background dielectric medium. Methodological details are provided in SI Appendix, SI Text. Some of the simulated ${ϵ}_{\mathrm{r}}$ values are plotted in Fig. 7A to illustrate their dependence on IDR volume fraction $\varphi$ (the $\varphi \propto$ concentration relation and an extended set of simulated ${ϵ}_{\mathrm{r}}$s are provided in SI Appendix, SI Text, Fig. S6, and Table S1). The difference in simulated ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ for Ddx4 and aDdx4 is negligible except at very low IDR concentration (Fig. 7A and SI Appendix, Fig. S6), likely because the main contribution to the dielectric effect of IDR in the atomic model is from the partial charges on the protein backbone. Consistent with expectation (35, 37), simulated ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ in Fig. 7A decreases with increasing $\varphi$ for all solvent conditions considered. Permittivity is known to decrease with salt (112, 113). Here this expected effect is observed for TIP3P solution of IDR at low but not at high IDR concentration. Interestingly, the ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ simulated with SPC/E water and 100 mM NaCl exhibits nonlinear decrease with increasing $\varphi$, which is akin to that predicted by the Bragg–Pippard (114) and Clausius–Mossotti models, but the TIP3P-simulated ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ appears to be linear in $\varphi$, which is more in line with the Maxwell Garnett and Bruggeman models (37).

Fig. 7.

Effects of IDR concentration-dependent relative permittivity on phase behaviors. (A) Relative permittivity ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ values obtained by atomic simulations (symbols) using various explicit-water models (as indicated at the bottom) are shown as functions of Ddx4 volume fraction $\varphi$ ($\varphi =1$ corresponds to pure Ddx4). The blue curve is a theoretical fit of the SPC/E, [NaCl] = 100 mM explicit-water simulated data based on the Slab [Bragg and Pippard (114)] model (equation 34 of ref. 37), viz., $1/{ϵ}_{\mathrm{r}}\left(\varphi \right)=\varphi /{ϵ}_{\mathrm{p}}+\left(1-\varphi \right)/{ϵ}_{\mathrm{w}}$ with the fitted ${ϵ}_{\mathrm{p}}=18.9$ and ${ϵ}_{\mathrm{w}}=84.5$ where ${ϵ}_{\mathrm{p}}$ and ${ϵ}_{\mathrm{w}}$ are the relative permittivity of pure protein and pure water, respectively. The black solid, dashed, and dashed-dotted lines are approximate linear models of ${ϵ}_{\mathrm{r}}\left(\varphi \right)={ϵ}_{\mathrm{p}}\varphi +{ϵ}_{\mathrm{w}}\left(1-\varphi \right)$ with the same ${ϵ}_{\mathrm{w}}$ but different ${ϵ}_{\mathrm{p}}$ values as indicated (at the top right), resulting in $d{ϵ}_{\mathrm{r}}\left(\varphi \right)/d\varphi$ slopes of $-65.6$, $-83.9$, and $-42.2$. (B and C) Theoretical phase diagrams of the four Ddx4 IDR variants were obtained by a RPA theory that incorporates an ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ linear in $\varphi$. Solid, dashed, and dashed-dotted curves correspond, as in A, to the three different ${ϵ}_{\mathrm{p}}$ values used in the theory. The electrostatic contribution to the phase behaviors is calculated here using either (B) the expression for $f_{\mathrm{e}\mathrm{l}}$ given in SI Appendix, SI Text, Eq. S51 [i.e., equation 68 of ref. 35 with its self-interaction term ${\mathcal{G}}_2\left(\stackrel{\sim }{k}\right)$ excluded] or (C) the full expression for $f_{\mathrm{e}\mathrm{l}}$ (equation 68 of ref. 35 or equivalently SI Appendix, SI Text, Eq. S2). Further details are provided in SI Appendix, SI Text.

We utilize the salient features of the coarse-grained KH chain model for Ddx4 (Fig. 4) and the IDR concentration-dependent permittivities from explicit-water simulations (Fig. 7A) to inform an analytical theory for IDR LLPS, referred to as RPA + FH, that combines a random phase approximation (RPA) of charge sequence-specific electrostatics and Flory–Huggins (FH) mean-field treatment for the other interactions (34, 35). An in-depth analysis of our previous RPA formulation for IDR concentration-dependent ${ϵ}_{\mathrm{r}}$ (35) indicates that only an ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ linear in $\varphi$ can be consistently treated by RPA (SI Appendix, SI Text). In view of this recognition and considering the uncertainties of simulated ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ for different water models (Fig. 7A), three alternative linear forms of ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ (straight lines in Fig. 7A) are used for the present RPA formulation to cover reasonable variations in ${ϵ}_{\mathrm{r}}\left(\varphi \right)$.

The mean-field FH interaction parameters in our RPA + FH models for the four Ddx4 IDRs are obtained from the four sequences’ average pairwise nonelectrostatic KH contact energies. For each of the 236-residue sequences, we calculate the average of the $E_{ij}\left(r_0\right)$ [KH] quantity (Fig. 1A), for a given pair of residue types, over all pairs of residues on the sequence, including a residue with itself ($236\times 237/2=$ 27,966 pairs total), except those pairs involving two charged residues (Arg–Arg, Arg–Lys, Arg–Asp, Arg–Glu, Lys–Lys, Lys–Asp, Lys–Glu, Asp–Asp, Asp–Glu, and Glu–Glu) because interactions of charged pairs are accounted for by RPA separately. The resulting average energies in units of kcal ${\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$, $-0.1047$ for WT and CS, $-0.0689$ for FtoA, and $-0.0924$ for RtoK, are then input with an overall multiplicative scaling factor into RPA + FH theories with $\varphi$-independent ${ϵ}_{\mathrm{r}}$ for three different fixed ${ϵ}_{\mathrm{r}}=$ 80, 40, and 20. The computed RPA + FH phase diagrams are then fitted to the corresponding phase diagrams simulated by coarse-grained KH chain models in Fig. 4 to determine a single energy scaling factor from the best possible fit (SI Appendix, Fig. S7). The product of this factor and the sequence-dependent averages of $E_{ij}\left(r_0\right)$ [KH] defined above is now used as the enthalpic FH $\chi$ parameters in the final RPA + FH theories with IDR concentration-dependent ${ϵ}_{\mathrm{r}}\left(\varphi \right)$. Details of unit conversion between our explicit-chain simulation and our analytical RPA + FH formulation are in SI Appendix, SI Text.

In this connection, it is instructive to note that the corresponding averages of $E_{ij}\left(r_0\right)$ [HPS] for the HPS model are $-0.1214$ for WT and CS, $-0.1179$ for FtoA, and $-0.1294$ for RtoK. In this case, the more favorable (more negative) average energy of RtoK than WT underlies the mismatch of HPS prediction with experiment seen in Fig. 3B.

Fig. 7 B and C show the phase diagrams of the four Ddx4 IDRs predicted using RPA + FH theories with three alternative IDR concentration-dependent ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ functions and KH-derived mean-field FH parameters as prescribed above. In all cases considered, the WT sequence (red curves) exhibit a higher propensity to LLPS than the three variants, indicating that this general agreement with the experimental trend seen in Fig. 4 holds up not only under the simplifying assumption of a constant ${ϵ}_{\mathrm{r}}$ but also when the dielectric effect of the IDRs is taken into account. As discussed in SI Appendix, SI Text, we have previously subtracted the self-energy term in the RPA formulation for numerical efficiency because the term has no impact on the predicted phase diagram when ${ϵ}_{\mathrm{r}}$ is a constant independent of $\varphi$ because the self-energy contribution is identical for the dilute and condensed phases. However, with an IDR concentration-dependent ${ϵ}_{\mathrm{r}}\left(\varphi \right)$, as for the cases considered here, the self-energy—with the short-distance cutoff of Coulomb interaction in the RPA formulation corresponding roughly to a finite Born radius (115)—is physically relevant as it decreases with increasing ${ϵ}_{\mathrm{r}}$, and therefore, it affects the predicted LLPS properties as manifested by the difference between Fig. 7 B and C. It follows that the self-energy term quantifies a tendency for an individual polyampholyte chain to prefer the dilute phase with a higher ${ϵ}_{\mathrm{r}}$—because of its more favorable electrostatic interactions with the more polarizable environment—over the condensed phase with a lower ${ϵ}_{\mathrm{r}}$. This tendency disfavors LLPS. At the same time, the lower ${ϵ}_{\mathrm{r}}$ in the condensed phase entails a stronger interchain attractive electrostatic force that drives the association of polyampholyte chains. Therefore, taken together, relative to the assumption of a constant ${ϵ}_{\mathrm{r}}$, the overall impact of an IDR concentration-dependent ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ is expected to be modest because it likely entails a partial tradeoff between these two opposing effects. This consideration is borne out in Fig. 7 B and C. When self-energy is neglected in Fig. 7C, LLPS propensities predicted using ${ϵ}_{\mathrm{r}}\left(\varphi \right)$s are relatively high (as characterized by the critical temperatures), comparable to those for a fixed ${ϵ}_{\mathrm{r}}=40$ in Fig. 4B. When the physical effect of self-energy is accounted for in Fig. 7B, LLPS propensities predicted using ${ϵ}_{\mathrm{r}}\left(\varphi \right)$s are significantly lower: overall they are comparable but slightly lower than those for a fixed ${ϵ}_{\mathrm{r}}=80$ in Fig. 4A. Consistent with this physical picture, whereas the ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ with a sharper decrease with increasing $\varphi$ leads to a higher LLPS propensity when self-energy is neglected (dashed curves have higher critical temperatures than dashed-dotted curves of the same color in Fig. 7C), for the physically appropriate formulation with self-energy, a sharper decrease in ${ϵ}_{\mathrm{r}}\left(\varphi \right)$ with increasing $\varphi$ leads to a lower LLPS propensity (dashed curves have lower critical temperatures than dashed-dotted curves of the same color in Fig. 7B).

Conclusion

In summary, we have gained insights into the physical forces that drive the formation of biomolecular condensates by systematically evaluating coarse-grained, residue-based protein chain models embodying different outlooks as to the types of interactions that are important for LLPS of IDRs. By comparing model predictions against experimental data on WT Ddx4 IDR and its three variants as well as WT LAF-1 RGG and its two variants, we acquire essential knowledge from agreement as well as disagreement between simulation and experiment. Aiming to account for all observed relative LLPS propensities of the sequences, we find that hydrophobicity, electrostatic, and cation–$\pi$ interactions are insufficient by themselves. Rationalization of experiment on arginine-to-lysine variants entails significantly more favorable arginine-associated over lysine-associated contacts, an effect that is most likely underpinned by $\pi$–$\pi$ interactions. This perspective is in line with bioinformatics analysis of LLPS propensities (67) and recent experiments on other IDRs (39, 60). In this regard, it is reassuring that the balance of forces for LLPS of IDRs appears to be partly captured by common PDB-derived statistical potentials developed to study protein folding and binding. However, we found that the condensate-stabilizing contributions of phenylalanine interactions are significantly weaker than that estimated from statistical potentials, most likely because such interactions exist in highly solvent-accessible environments rather than in the sequestered cores or binding interfaces of globular proteins. We have also highlighted the reduced electric permittivity inside condensed IDR phases. Although this effect’s overall influence on LLPS propensity may be modest because of a tradeoff between its consequences on IDR self-energies and on inter-IDR interactions, the effect of IDR concentration-dependent permittivity by itself should be of functional importance in biology because of its potential impact on biochemical reactions and preferential partition of certain molecules into a given biomolecular condensate. All told, the present study not only serves to clarify the aforementioned issues of general principles, it also represents a useful step toward a transferable coarse-grained model for sequence-specific biomolecular LLPS. Many questions remain to be further investigated nonetheless. These include—and are not limited to—an adequate description of solvent-exposed interactions involving large hydrophobic/aromatic residues such as phenylalanine, a proper balance between attractive and repulsive interactions (53), devising temperature-dependent effective interactions (51), an accurate account of small ion effects (41, 116, 117), and incorporation of nucleic acids into LLPS simulations (43). Progress in these directions will deepen our understanding of fundamental molecular biological processes and will advance the design of novel IDR-like materials as well.

Materials and Methods

Our implicit-water coarse-grained explicit-chain modeling setup used in the first part of the present investigation for multiple IDP molecules follows largely the Langevin dynamics formulations in refs. 52, 53 for IDP LLPS. The simulation protocol features an initial slab-like condensed configuration that allows for efficient equilibration to produce simulated LLPS data (78). As discussed, model energy functions embodying different physical perspectives are considered. The subsequent explicit-water simulations for estimating IDR concentration-dependent relative permittivity are conducted on five WT Ddx4 IDRs using GROMACS (108) in conjunction with the amber99sb-ildn forcefield (109) and with TIP3P (110) or SPC/E (111) waters. Details of our methodology and the development of analytical RPA formulation are provided in SI Appendix, SI Text.

Data Availability.

All study data are included in the article and SI Appendix.