Observation of the Low‐Frequency Spectrum of the Water Dimer as a Sensitive Test of the Water Dimer Potential and Dipole Moment Surfaces

Abstract

Using the helium nanodroplet isolation setup at the ultrabright free‐electron laser source FELIX in Nijmegen (BoHeNDI@FELIX), the intermolecular modes of water dimer in the frequency region from 70 to 550 cm⁻¹ were recorded. Observed bands were assigned to donor torsion, acceptor wag, acceptor twist, intermolecular stretch, donor torsion overtone, and in‐plane and out‐of‐plane librational modes. This experimental data set provides a sensitive test for state‐of‐the‐art water potentials and dipole moment surfaces. Theoretical calculations of the IR spectrum are presented using high‐level quantum and approximate quasiclassical molecular dynamics approaches. These calculations use the full‐dimensional ab initio WHHB potential and dipole moment surfaces. Based on the experimental data, a considerable increase of the acceptor switch and a bifurcation tunneling splitting in the librational mode is deduced, which is a consequence of the effective decrease in the tunneling barrier.

The intermolecular modes of the water dimer in the frequency region from 70 to 550 cm⁻¹ were recorded. Observed bands were assigned to donor torsion, acceptor wag, acceptor twist, intermolecular stretch, donor torsion overtone, and in‐plane and out‐of‐plane vibrational modes. This data provides a test for water potentials and dipole moment surfaces. Calculations of the IR spectrum are presented using molecular dynamics approaches.

Introduction

Water is the most prominent solvent and of fundamental importance for chemistry and biology. After decades of research, the goal of achieving a rigorous molecular description of the underlying intermolecular and intramolecular interactions is essentially at hand. This progress is built on the analysis of the convergence of the many‐body representation of the total potential for water clusters, which shows that two‐body interactions account for 80–90 % and three‐body interactions for almost all of the remaining interaction for electronic binding energies.[ ¹ , ² , ³ ] Thus, the strategy for a general potential energy surface (PES) for arbitrary number of water monomers is based on rigorous two‐ and three‐body interaction potentials, an accurate monomer potential, and for the final “polish” a treatment of four‐ and higher‐body interactions, based on known polarizable models, for example, TTM3‐F. ^[4]

The two‐body interaction is completely described by the bonding and dynamics of the water dimer and so it is not surprising that theoretical analyses of the non‐covalent bonding in the water dimer has a long history, dating from 1976 to the present.[ ⁵ , ⁶ , ⁷ , ⁸ , ⁹ ] Much of what has been learned about the roles of permanent and induced multipole interactions, partial charge transfer, and Pauli repulsion in the water dimer is transferable to general non‐covalent interactions between molecules. For this reason and also its central importance to understanding general water interactions the water dimer is arguably the most important molecular dimer in chemistry.

Beyond important qualitative understanding of the water dimer interaction, quantitative characterization of the water dimer potential has been a major challenge for theory. Early versions of such potentials were developed for rigid monomers and their forms were guided by known long‐range and model repulsive interactions at short range. These potentials were optimized in conjunction with spectroscopic studies, which provided high‐resolution spectra of intermolecular modes, in particular tunneling splittings in the spectrum that occur owing to equivalent minima. Several such potentials were reported in the early 2000s.[ ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ ] However, these potentials do not describe the O−H stretch modes of the water dimer, in particular the strongly red‐shifted H‐bonded O−H stretch. Also, they fall short in reproducing ab initio calculations of numerous low‐lying stationary points of the water dimer that were reported in 2002. ^[17] These later became important benchmarks for new generation of fully ab initio‐based potentials for the water dimer.

A major step in this direction was made in 2007 with the introduction of the CC‐pol water dimer potential. ^[18] This is a non‐linear least‐squares fit to thousands of high‐level CCSD(T)/aug‐cc‐pVTZ energies for the water dimer with rigid monomers. This potential used numerous parameters with a physically based functional forms for the attractive and repulsive regions of the potential. (An SAPT potential for the three‐body interaction, also for rigid monomers, completed this important pioneering work.) Quantum calculations of intermolecular energies and tunneling splittings, referred to as vibration–rotation tunneling (VRT) energies, using this ab initio potential were in excellent agreement with experiment. However, the CC‐pol potential falls short in reaching the goal of a fully flexible ab initio potential for the water dimer. This was a challenge as such a potential is a function of 12 vibrational degrees of freedom and should be invariant with respect to permutation of H atoms. The first such potential was reported in 2006. ^[19] It was a mathematical fit to roughly 20 000 CCSD(T)/aug‐cc‐pVTZ electronic energies (with the standard counterpoise correction), using permutationally invariant polynomials in Morse variables. Furthermore, a full‐dimensional dipole moment surface, based on MP2/aug‐cc‐pVTZ dipole moments, at the same configurations as the electronic energies, was reported. A subsequent PES using roughly 30 000 CCSD(T)/aug‐cc‐pVTZ (AVTZ) electronic energies was reported in 2008 and used in accurate quantum calculations of intermolecular energies and tunneling splittings in (H₂O)₂ and (D₂O)₂. ^[20] The final dimer PES in this series, referred to as HBB2, was reported in 2009. ^[21] This PES reproduces the benchmark electronic dissociation energy of 4.98 kcal mol⁻¹ and was used in a rigorous calculation of the observable dissociation energy, D ₀, which was later confirmed experimentally. ^[22] The HBB2 PES is the one used in the current calculations of the far‐IR spectrum of the water dimer. Intensities are reported for the first time, using the dipole moment surface noted above. We note that the HBB2 potential is the two‐body component of the more general potential, known as WHBB, ^[23] which includes a full‐dimensional 3‐d potential. In this paper, we use WHBB and HBB2 interchangeably.

Subsequently, several other full‐dimensional, ab initio‐based water dimer potentials have been reported. One, reported in 2012 ^[24] and denoted CCpol‐8s/f, is an extension of the last version of the rigid‐monomer CC‐pol potential, denoted CCpol‐8s, ^[25] plus a flexible SAPT potential. Another one ^[26] follows the basic strategy used to develop the HBB2 potential. Namely, it used permutationally invariant polynomials. This potential is denoted MB‐Pol. All of these dimer potentials give good agreement with experiment for VRT levels and tunneling splittings of (H₂O)₂ and the six fundamental intramolecular bend and vibrational energies.[ ²⁴ , ²⁶ , ²⁷ ] Very recently, quantum calculations of the second virial coefficient over the temperature range 300 to roughly 1200 K using HBB2, MB‐Pol, and CCpol‐8s/f were reported. ^[28] In the low‐temperature region the results from CCpol‐8s/f and HBB2 are closer to each other and to experiment than are the results from MB‐Pol. At higher temperature all potentials give similar and accurate results. Overall the results using CCpol‐8s/f are the most accurate ones. In summary, these three flexible water dimer potentials appear to be highly accurate, at least for the properties examined to date. However, none of these potentials has been used in direct calculations of the IR spectrum in the far IR region, which is the focus herein.

Over several decades, high‐resolution gas‐phase measurements on the water dimer were carried out in the Saykally group, which enabled the development of accurate water dimer potentials.[ ⁹ , ²⁹ , ³⁰ , ³¹ , ³² ] The water dimer is produced in a supersonic planar expansion and probed by several FIR laser (mixed with a tunable MW source) for frequencies <150 cm⁻¹ as well as lead salt diode lasers in the frequency range from 515 to 528 cm⁻¹. This allowed to record spectra with a spectral resolution of 0.1 MHz, that is, 3×10⁻⁶ cm⁻¹ and to assign single vibrational rotational tunneling (VRT) transitions with resolved hyperfine splitting. Based on the spectra below 150 cm⁻¹, it was possible to characterize the three feasible tunneling motions that connect the 8 degenerate minima on the 12‐dim water potential (including 6 intramolecular and 3 intermolecular modes). However, despite of this enormous progress, for two degrees of freedom, which are very essential in characterizing bulk water dynamics, no information or only very limited information is available so far, owing to a lack of adequate laser sources. It is known now that the hydrogen bond breaking and reformation process in bulk water occurs via a pathway in which rotating water molecules break a hydrogen bond with an overcoordinated first shell neighbor to from an H‐bond with an under‐coordinated neighbor. ^[33] This water reorientation mechanism involves large‐amplitude angular jumps. Thus, a precise measurement of the hindered rotation (denoted as libration) of, that is, the in‐plane and out‐of‐plane tunneling mode in the water dimer is essential for a quantitative, precise prediction of the hydrogen bond network dynamics in the condensed phase. Whereas in high‐resolution studies with each radiation source only small frequency ranges can be covered, for example, from 522 to 525 cm⁻¹, in the present study the free electron laser FELIX allows coverage of the entire frequency range from 70 cm⁻¹ to 3600 cm⁻¹. In our study, the resolution of the free electron laser is restricted to the order of 1 cm⁻¹. Thus, it is not possible to resolve single VRT transitions. However, we report a comprehensive study of all intermolecular modes of the water dimer in the frequency range from 100 to 600 cm⁻¹ using helium nanodroplet isolation (HeNDI) spectroscopy. Based on our experimental results, we are able to deduce the acceptor switch (AS) tunneling for some of the excited states, including even the interchange tunneling. These full set of experimental data serves as a sensitive test for state‐of‐the‐art water dimer potentials and dipole moment surfaces. For comparison we present the results of high‐level quantum calculations fully coupled for the 6 intermolecular modes using a vibrational adiabatic potential for the 6 high‐frequency intramolecular modes (6d+6d) and quasi classical molecular dynamics (QCMD) simulations using the HBB2 dimer potential and dipole moment surfaces. Thereby, it is possible to provide now an overview of all intermolecular modes including the higher frequency librational modes for water dimer as a sensitive test for one of the most recent and accurate water potentials.

Results and Discussion

HeNDI spectroscopy is a powerful tool to record infrared spectra of single molecules and molecular clusters.[ ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ ] The technique enables stepwise aggregation and the spectroscopic characterization of molecular aggregates with well‐defined cluster sizes at ultracold temperatures of 0.37 K. ^[39] To study small water clusters in the FIR/THz region, we have combined a helium nandodroplet isolation spectrometer with the free‐electron lasers (FELs), FEL‐I and FEL‐II, at the FELIX laboratory in Nijmegen. The experimental setup BoHeNDI@FELIX, combining the helium nanodroplet isolation technique with the ultrabright radiation source FELIX and covering the entire frequency region from 66 to 3600 cm⁻¹, is described in detail in a previous publication. ^[40]

In HeNDI spectroscopy, the absorption is measured indirectly as the depletion of the ion current of a certain ionic fragment in the mass spectrum upon excitation of the embedded solute. In present study, we investigate water clusters, which are formed after sequential pick‐up of single water molecules. IR absorption results in an evaporation of helium atoms and thereby in a decrease of ionization cross section which is detected at a loss of signal on the ionic fragment [H₂O]⁺ and [(H₂O)H]⁺ at m/z=18 and m/z=19, respectively. An overview of the experimental low‐frequency spectrum of water cluster in helium nanodroplets is shown in Figure 1 a (lower trace) in gray.

Figure 1.

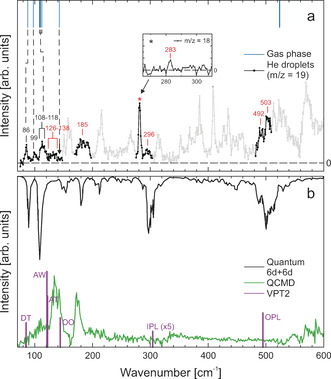
a) Overview of the FIR/THz depletion spectrum of the water cluster (H₂O)₂ in helium nanodroplets recorded at m/z=19 (lower trace, shown in gray). Bands that were assigned to water dimer are highlighted in black. The signal marked with a “*” is composed of water dimer, trimer, and higher clusters. For an assignment, we also recorded a depletion spectrum at m/z=18 (see inset), which minimizes water trimer contributions. Peak positions are given in cm⁻¹. For comparison, we show the results of previous gas‐phase studies[ ²⁹ , ³¹ , ⁴³ , ⁴⁴ , ⁴⁵ ] as blue lines (upper trace). Black numbers correspond to bands observed in previous gas‐phase studies, while red numbers correspond to newly assigned bands. b) Predictions of the low‐frequency spectrum; black line: quantum 6d+6d (upper trace); green line: QCMD calculations (lower trace) both using the HBB2 12d ab initio potential and dipole moments; and purple sticks previous VPT2 calculations ^[46] (lower trace).

In previous studies, we could show that the depletion spectrum at m/z=19 is sensitive to the water dimer as well as trimer bands, while when recording at m/z=18, the intensity of water trimer signals is significantly reduced compared to those assigned to water dimer. ^[41] Therefore, we recorded additional depletion spectra in the frequency range from 70 to 550 cm⁻¹ at the mass of the ionic fragment at m/z=19.at m/z=18. A definitive assignment of the cluster size is based on pressure‐dependent intensity measurements, so‐called pick‐up curves (see the Supporting Information). Bands which are assigned to water dimer bands are found in the following frequency regions: 70–145 cm⁻¹, 170–195 cm⁻¹, 265–310 cm⁻¹, and 480–510 cm⁻¹. These are highlighted in Figure 2 a, lower trace in black. We want to point out that the broad signal in the region from 170 to 195 cm⁻¹ is attributed to a superposition of water dimer, water trimer as well as even larger water cluster bands. The signal at 283 cm⁻¹ is found to be mainly due to water trimer. When scanning at m/z=18, we found a small peak which is assigned to the water dimer (see the Supporting Information).

Figure 2.

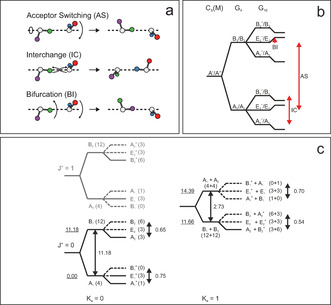
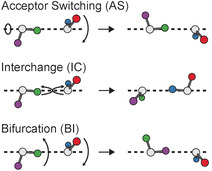
a) The three low‐barrier tunneling motions of the water dimer. The acceptor switching (AS) involving an exchange of the two protons of the proton acceptor, the interchange (IC) exchanging the proton donor and proton acceptor, and the bifurcation (BI) tunneling. b) Owing to AS, each energy level is split into two energy levels. The symmetries are denoted in the irreducible representations of the G ₄ MS group. IC tunneling leads to an additional splitting into three energy levels labeled within the irreducible representations of the G ₁₆ MS group. BI causes a shift of the energy levels. c) VRT levels for K _a=0 and K _a=1 in the vibrational ground. At 0.37 K, only VRT levels represented as solid lines are expected to be significantly populated. In parentheses, the spin statistical weights are shown.

In Figure 1 a (upper trace) we display for comparison the intermolecular modes as observed before gas phase studies of the Saykally group. As mentioned before, these high‐resolution studies are almost exclusively restricted to the frequency range below 150 cm⁻¹, with the exception of one band at 524 cm⁻¹.[ ²⁹ , ³¹ , ⁴² , ⁴³ , ⁴⁴ , ⁴⁵ ]

In Figure 1 b upper trace, we show the results of our ab initio calculations using the 6d+6d quantum calculations (Figure 1 b, upper trace) as well as predictions based upon quasi classical molecular dynamics (QCMD) simulations (Figure 1 b, lower trace). Furthermore, in purple we display the results of previous vibrational perturbation theory of second order (VPT2) calculations. ^[46] The details of the theoretical methods are described in the section Methods (see Supporting Information). The results are summarized in Table 1.

Table 1.

Predicted frequencies from different theoretical approaches as discussed in the text.^[a]

Mode	Theory				Experiment
	VPT2[b]	6d+6d[c]	Double Harmonic[c]		He droplets[c]	Gas phase[d]
	ν [cm−1]	ν [cm−1]	ν [cm−1]	μ⊥:μ∥	ν [cm−1]	ν [cm−1]
(DT)	85	89	126.7	100:0	86	52.9, 87.7
(AW)	121	109	149.6	27:73	99	97.9, 107.9
					107–120	110.0, 112.4
(AT)	122	109	139.8	99:1	108–118	109.0
					126–138
(OO)	144	152	181.5	24:76	–	142
(DT)2	–	181	–	–	185	142
(IPL)	304	300	351.2	90:10	283, 296	–
(OPL)	495	500	609.6	100:0	492, 503	524

[a] The normalized parallel and perpendicular components of the transition dipole moment obtained from double harmonic calculations are shown, as are results from experimental studies. [b] From Ref.  ^[46] . [c] This work. [d] From Ref. [ ²⁹ , ³¹ , ⁴³ , ⁴⁴ , ⁴⁵ ].

The water dimer exhibits three low‐barrier tunneling motions.[ ⁴⁷ , ⁴⁸ , ⁴⁹ ] The three modes are displayed in Figure 2 a. These are denoted as acceptor switching (AS), interchange tunneling (IC), and bifurcation (BI) tunneling. The acceptor switching involves an exchange of the two protons in the hydrogen bonded acceptor monomer. The acceptor switching has the lowest barrier. If AS tunneling is feasible, the applicable molecular symmetry group is G ₄, each rovibrational energy level is split into two energy levels (labeled as A ₁/B ₁ and A ₂/B ₂), see Figure 2 b. Previously, the AS tunneling splittings in the vibrational ground state was deduced experimentally to be 11.18 cm⁻¹ and 2.73 cm⁻¹ for K _a′′=0 and K _a′′=1 states, respectively.[ ¹³ , ⁴² ]

The interchange tunneling (IC) with a barrier of about 207 cm⁻¹ exchanges the role of the hydrogen bond acceptor and the hydrogen bond donor water molecule. ^[30] This tunneling causes an addition splitting of each state into three sublevels. These states can be labeled in the G ₁₆ molecular symmetry group (see Figure 2 b). In the vibrational ground state, the IC tunneling splitting is on the order of 0.54 to 0.70 cm⁻¹. ^[32] The bifurcational (BI) tunneling describes a proton exchange of hydrogen bond donors. The tunneling mode involves an in plane librational motion of the donor and a flip of the acceptor monomer. In the ground state the barrier is on the order of 400 cm⁻¹. ^[30] If BI tunneling is feasible, the energy levels of vibrational rotational tunneling states are shifted in energy.

Given the experimental frequency resolution of 1 cm⁻¹ in our present study, in the ground state, only the AS tunneling splitting can be resolved. The two AS tunneling levels are also denoted as (1s) and (2s) state. Recent experimental[ ²⁹ , ³¹ , ⁴³ , ⁴⁴ , ⁴⁵ ] and theoretical studies,[ ²⁷ , ⁵⁰ ] showed that the IC tunneling splitting can be dramatically increased upon vibrational excitation. The selection rules in the G ₁₆ molecular symmetry group are A₁ ⁺↔A₁ ⁻, B₁ ⁺↔B₁ ⁻, A₂ ⁺↔A₂ ⁻, B₂ ⁺↔B₂ ⁻, E⁺↔E⁻. ^[47] Note that in Figure 2 b the labeling of the E‐states as either E ₁ or E ₂ is arbitrary and does not imply any further restrictions on selection rules. Transitions between E‐states are allowed as long as the selection rule +↔− is fulfilled.

In the present study, we expect a Boltzmann population of the VRT levels with a temperature of 0.37 K. Thus, in general, only the lowest level of each symmetry will be populated. In Figure 2 c the VRT levels for K _a=0 and K _a=1 in the vibrational ground state are shown. Vibration–rotation–tunneling (VRT) levels, which are expected to be populated at 0.37 K, are displayed as solid lines, while VRT states that are expected to be not significantly populated are represented as dashed lines (Figure 2 c). Note that the K _a′′=0(2s) and K _a′′=1(2s) states are close in energy; thus both VRT levels will be populated.

In the present study, we focus on the low‐frequency spectrum including all intermolecular modes. The intermolecular vibrational modes of the water dimer are either of A′ or A′′ symmetry. In principle, parallel a‐type and perpendicular c‐type transitions are allowed from the ground state to intermolecular mode with A′ symmetry. Only perpendicular b‐type transitions are allowed from the ground states to vibrationally excited modes with A′′ symmetry. The relative intensity for parallel and perpendicular transitions can be predicted based on the ratio of the calculated parallel and perpendicular components of the transition dipole moments. These are listed in Table 1).

By comparison to previous gas‐phase studies, the absorption bands in the frequency range from 70 to 145 cm⁻¹ are assigned to the donor torsion, acceptor wag, and acceptor twist (see Table 1). An energy diagram for each of these modes along with the experimentally observed transitions in the gas phase as well as the transitions observed in the present paper are displayed in the Supporting Information.

The band at 86 cm⁻¹ is assigned to the perpendicular K _a=1←0(1s) transition from the ground state to the excited donor torsion (A′′ symmetry), in excellent agreement with previous gas‐phase measurements, which yielded a band center at 87.7 cm⁻¹. ^[43] Thus we conclude, that the matrix shift caused by the helium nanodroplet environment is very small, that is, on the order of 1 cm⁻¹ or less. In gas‐phase studies, the IC tunneling splitting of the donor torsion K _a′=1(1s) states has been determined to be 1.11 cm⁻¹. ^[43] Taking into account the resolution of our experiment of 1 cm⁻¹, for this mode, the IC tunneling is expected to cause only a broadening of the observed band, no splitting can be resolved here. This K _a=1←0(1s) transition marks the lower limit of the experimentally accessible frequency range of FELIX. Therefore, the K _a=1←0(2s) transition, which is predicted to be even about 7 cm⁻¹ lower in frequency,[ ²⁷ , ⁵⁰ ] as well as the K _a=0←1(2s) transition cannot be observed here.

For transitions from the ground state to the acceptor wag (A′ symmetry), both, parallel as well as perpendicular transitions are allowed. We assign the signal at 99 cm⁻¹ to a superposition of parallel K _a=0←0(2s) as well as perpendicular K _a=0←1(2s) transitions to the excited acceptor wag, in agreement with previous results in the gas phase (see the Supporting Information). ^[43] More specifically, the broad band at 108–118 cm⁻¹ can be attributed to a superposition of different bands, the K _a=0←0(1s), K _a=1←0(1s), K _a=1←0(2s), and K _a=1←1(2s) (see the Supporting Information). In previous studies, ^[43] it was found that the IC tunneling splitting is increased to 2.95 and 5.24 cm⁻¹, respectively, in the excited vibrational state. Thus, we expect two subbands, that is, the K _a=0←0(1s) and K _a=1←0(1 s) transition from the ground state to the acceptor. However, owing to the plethora of bands in this frequency region, this splitting cannot be further resolved here.

The acceptor twist mode has A′′ symmetry, thus only perpendicular transitions from the ground state to the excited acceptor twist are expected. Based on the results of previous gas‐phase studies, ^[43] the broad signal at 108–118 cm⁻¹ is assigned to a K _a=0←1(2s) transition (see also the Supporting Information). Based upon theoretical predictions,[ ²⁷ , ⁵⁰ ] the K _a=1←0(1s) and K _a=1←0(2s) bands are expected at approximately 125 and 142 cm⁻¹, respectively. In our study we observe a broad band between 126–138 cm⁻¹. We assign this to an overlap of two transitions, that is, the K _a=1←0(1s) and K _a=1←0(2s) transitions from the ground state to the excited acceptor twist. Thus, we conclude that the AS tunneling splitting must be overestimated by theoretical predictions. Based on our experimental results, we propose that both vibrational rotational tunneling bands lie closer in energy, that is, they are separated by less than 9 cm⁻¹.

The transitions from the ground state to the intermolecular stretch are predicted to lie in the region from approximately 140 to 150 cm⁻¹.[ ²⁷ , ⁵⁰ ] In the gas phase,[ ³¹ , ⁴⁴ ] only the K _a=0←0(2s) and K _a=0←1(2s) bands at about 142 cm⁻¹, could be were observed, see the Supporting Information. Furthermore, bands at about 142 cm⁻¹ have been reported, which were tentatively assigned to transitions from the ground state to the donor torsion overtone (A′ symmetry).[ ³¹ , ⁴⁴ ] In our experimental spectrum we find a very weak signal, indicated by an arrow in Figure 1 a), which we assign to a transition to the intermolecular stretch. Unfortunately, the region around 146 cm⁻¹ is dominated by signals attributed to water trimer. Using the ab initio 6d+6d potential (see Figure 1 b, upper trace), we predict a small intensity for transitions to the intermolecular stretch of the water dimer compared to these water trimer bands. This explains why the frequency range between 140 and 150 cm⁻¹ is dominated by trimer lines.

As was stated before, while in previous gas‐phase studies transitions at 142 cm⁻¹ were tentatively assigned to the donor torsion overtone mode, an unambiguous assignment is difficult owing to the fact that the intermolecular stretch is close in energy. In our present study, using HeNDI spectroscopy, we observe for the first time a broad signal at 170–195 cm⁻¹, which is assigned to a transitions from the ground state to the upper (2s) tunneling of the donor torsion overtone mode. The pickup curve at 185 cm⁻¹ confirms significant contributions of the water dimer (see the Supporting Information). By comparison to the spectrum based on the ab initio 6d+6d potential (see Figure 1 b, upper trace), this signal can be unambiguously assigned to the donor torsion overtone. Upon excitation in the donor torsion overtone mode, the AS tunneling, that is, the energy difference between the 1s and 2s level is expected to be considerably increased. The K _a′=0(2s) state is predicted at an energy of 185 cm⁻¹ with an increased IC tunneling splitting of 18.2 cm⁻¹. ^[50] Here, we assign the experimentally observed band to a transitions to the K _a′=0(2s) state of the donor torsion overtone. For both the K _a=0←0(2s) and K _a=0←1(2s) transitions, we expect transitions to the $A_2^{-}/B_2^{+}$ subbands in this frequency range (see Figure 3). Based on our experiment, we deduce an energy of the K _a′=0(2s, A₂ ⁻/B₂ ⁺) to be 196–197 cm⁻¹, which is 10 cm⁻¹ higher than the predictions. This implies that the AS tunneling splitting is even more increased than previously predicted.

Figure 3.

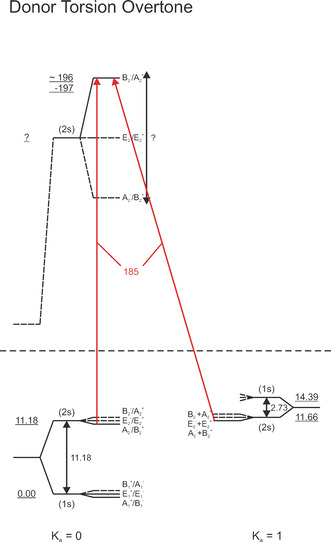
Donor torsion overtone (DT)² VRT energy level diagram. Parallel and perpendicular transitions are shown as vertical and diagonal arrows, respectively; red arrows: present study only. For bands observed in the present study, the transition frequencies are given (in red). All frequencies and energies are given in cm⁻¹.

So far, the frequency range between 150 cm⁻¹ and 520 cm⁻¹ could not be accessed experimentally. In this frequency range, the in‐plane and out‐of‐plane librational modes are predicted, which provide a most sensitive test of the accuracy of state‐of‐the‐art water dimer potential surfaces, especially in respect to the large amplitude angular motion. Using HENDI spetroscopy and cluster size determination via pick‐up curves, we assign two bands centered at 283 and 296 cm⁻¹ to the in‐plane librational mode (A′ symmetry) of water dimer. In principle, both parallel and perpendicular transitions are allowed for the in‐plane libration (Figure 4). However, the parallel component of the transition dipole moment is predicted to be much weaker than the perpendicular component (see Table 1). Therefore, the signal at 283 cm⁻¹ is assigned to the K _a=0←1(2s) and the signal at 296 cm⁻¹ to the K _a=1←0(1s) band. Depending on the magnitude of the AS tunneling splitting in the excited vibrational states, the K _a=1←0(2s) band might overlap with either the K _a=0←1(2s) or the K _a=1←0(1s) band.

Figure 4.

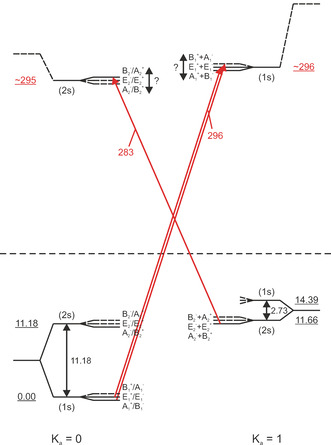
In‐plane libration (IPL) VRT energy‐level diagram. Parallel and perpendicular transitions are shown as vertical and diagonal arrows, respectively; red arrows: present study only. For bands observed in the present study, the transition frequencies are given (in red). All frequencies and energies are given in cm⁻¹.

In the frequency range of the out‐of‐plane librational mode (A′′ symmetry), we detect two signals at 492 and 503 cm⁻¹ (see Table 1). In principle, only perpendicular transitions are allowed for the out‐of‐plane libration. However, in a recent study parallel as well as perpendicular transitions could be observed. ^[45] For E‐states both transitions are allowed as long as the selection rule +↔− holds. We assign the band at 492 cm⁻¹ to the K _a=0←1(2s) transition and the band at 503 cm⁻¹ to the K _a=0(E ₂)←0(E ₁) transition from the ground state to the excited out‐of‐plane librational mode (see Figure 5). Based on our measurements we can deduce that the splitting between the K _a′=0(2s,A₂ ⁺/B₂ ⁻) and K _a′=0(2s,E₂ ⁺/E₂ ⁻) is small (1 cm⁻¹). Furthermore, we are able to prove now information on the energy of the K _a′=0(2s) state, which lies at 503 cm⁻¹. Based upon the results of our study and the previous gas‐phase study, we can deduce the size of the acceptor switch (AS) tunneling splitting in the out‐of‐plane librational mode which amounts to the energy difference between the (1s) and (2s) K _a=0 state as 34 cm⁻¹. This corresponds to an increase by a factor of three compared to the ground state, indicating a considerable coupling between the AS tunneling and this intermolecular mode.

Figure 5.

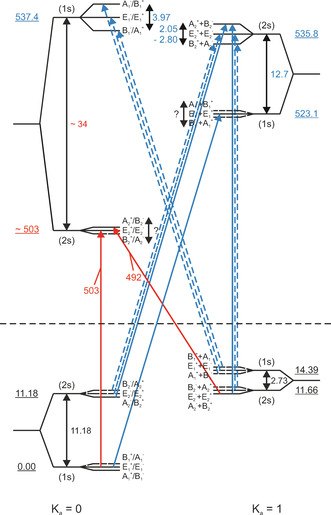
Out‐of‐plane libration (OPL) VRT energy level diagram. Parallel and perpendicular transitions are shown as vertical and diagonal arrows, respectively; red arrows: observed in the present study; blue arrows: previously observed in gas‐phase studies. For bands observed in the present study, the transition frequencies are given (in red). All frequencies and energies are given in cm⁻¹.

Conclusion

In the present study, a comprehensive spectrum in the low‐frequency range is reported, which probes the intermolecular modes of the water dimer. Upon comparison to the previous gas phase studies, we can conclude that the matrix shift of the helium nanodroplet can be neglected. The three tunneling motions are still feasible. We are able to provide for the first time information about the energy of the following intermolecular modes: (2s) K _a=0 donor torsion overtone; (2s) K _a=0 as well as (1s) K _a=1 state of the in‐plane‐librational mode; as well as (1s) and (2s) states for K _a=0 and K _a=1 of the out‐of‐plane librational mode (Table 2). We find that upon excitation of the librational modes, the tunneling splitting is increased considerably compared to the ground state.

Table 2.

Overview of the energy levels of the VRT states of water dimer.

Mode		Experiment	12d CCpol‐8s/f	6d+6d HBB2		Experiment	12d CCpol‐8s/f	6d+6d HBB2
(OPL)	(1s)	537.4[b]	–	–	(2s)	535.8[b]	–	–
	(2s)	−503[c]	–	–	(1s)	523.1[b]	–	–
(IPL)	(1s)	–	–	–	(2s)	–	–	–
	(2s)	−295[c]	‐	–	(1s)	−296[c]	–	–
(DT)2	(2s)	196–197 (B2 −/A2 +)[c]	185.01 (18.2)	–	(1s)	–	174.28(16.7)	–
	(1s)	–	128.51 (8.94)	—	(2s)	–	162.14(9.29)	–
(OO)	(2s)	153.62 (1.88)[b]	149.49 (1.13)	148.55 (1.20)	(1s)	–	152.08(1.32)	152.49(1.17)
	(1s)	–	143.15 (3.11)	145.11 (3.57)	(2s)	–	149.00(2.25)	155.78(1.07)
(AT)	(1s)	–	132.22 (1.29)	128.86 (0.78)	(1s)	–	142.09(3.82)	142.46(4.38)
	(2s)	120.19 (9.39)[b]	117.61 (8.34)	121.00 (8.54)	(2s)	–	136.33(4.50)	136.27(5.35)
(AW)	(2s)	108.89 (0.02)[b]	108.11 (0.06)	106.04 (0.02)	(2s)	123.56(3.41)[b]	132.27(3.00)	122.48(2.59)
	(1s)	107.93 (2.95)[b]	109.34 (3.04)	105.44 (1.99)	(1s)	109.98(5.24)[b]	108.49(4.58)	109.10(4.65)
(DT)	(1s)	–	113.34 (5.67)	116.47 (4.93)	(2s)	–	92.75(3.17)	94.23(2.72)
	(2s)	64.52 (2.54)[b]	61.92 (2.38)	67.24 (2.09)	(1s)	87.75(1.11)[b]	86.49(1.28)	89.63(0.56)
(GS)	(2s)	11.18 (0.65)[b]	12.58 (0.58)	10.16 (0.61)	(1s)	14.39(0.70)[b]	15.35(0.63)	14.01(0.65)
	(1s)	0.00 (0.75)[b]	0.00 (0.69)	0.00 (0.69)	(2s)	11.66(0.54)[b]	12.29(0.49)	11.53(0.50)
	K a=0				K a=1

[a] Experimental energies are compared to theoretical predictions[ ²⁷ , ⁵⁰ ] of the low‐frequency VRT levels and tunneling splittings for (H₂O)₂. Values in parentheses denote the size of the interchange tunneling splitting. All values are given in cm⁻¹. [b] Experimental results from previous gas phase studies.[ ²⁹ , ³¹ , ⁴² , ⁴³ , ⁴⁴ , ⁴⁵ ] [c] From this work.

This spectrum provides a sensitive test for water dimer potential energy surfaces as well as their dipole moment surfaces. As can be seen in Figure 1, the spectrum predicted from the ab initio 6d+6d quantum calculation using the HBB2 dimer potential and dipole moment surface is in excellent agreement with our experimental spectrum. The two strong signals observed at 86 and 107–120 cm⁻¹ are attributed to the two bands predicted at 89 and 109 cm⁻¹. The broad signal at 170–195 cm⁻¹ is close to the band predicted at 181 cm⁻¹. Additional bands are predicted at 152 and 209 cm⁻¹, which cannot be assigned unambiguously experimentally, since, this frequency range is dominated by signals attributed to larger water clusters. Bands observed in the frequency range from 265 to 310 cm⁻¹ and from 480 to 510 cm⁻¹ are assigned to the in‐plane librational (IPL) and out‐of‐plane librational (OPL) modes, respectively, which are observed for the first time experimentally.

While for the higher frequency intermolecular modes (IPL and OPL) the predictions from VPT2 calculations ^[46] are also in good agreement with the experimental band positions, we find a less good agreement for the lower frequency modes, that is, the donor torsion (DT), acceptor wag (AW), acceptor torsion (AT), and intermolecular stretch (OO; see Figure 1 b, lower trace). This can be attributed to the fact, that VPT2 calculations cannot account for the large anharmonicity caused by energy transfer between the intermolecular modes as well as coupling to large‐amplitude motions.

We want to note that excellent agreement is found for the spectrum predicted from the quantum calculations using the HBB2 potential and dipole moment surfaces and the experimental spectrum. The excellent agreement is an indication of the high accuracy of the PES and also the dipole moment surface. The predictions based upon the approximate QCMD approach, yield a spectrum that is partly blue‐shifted compared to the spectrum using the full 6d+6d approach. Furthermore, we want to note, that the intensity of the band at about 300 cm⁻¹ is too low in the QCMD approach. These are likely and (not surprising) an indication that this MD approach is not able to accurately capture the anharmonicity of the potential. We propose that the QCMD approach is too stiff. Especially for the large‐amplitude modes, the description lacks the accuracy to reproduce the experimentally observed spectrum.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

R. Schwan, C. Qu, D. Mani, N. Pal, L. van der Meer, B. Redlich, C. Leforestier, J. M. Bowman, G. Schwaab, M. Havenith, Angew. Chem. Int. Ed. 2019, 58, 13119.