ROC and AUC with a Binary Predictor: a Potentially Misleading Metric

Abstract

In analysis of binary outcomes, the receiver operator characteristic (ROC) curve is heavily used to show the performance of a model or algorithm. The ROC curve is informative about the performance over a series of thresholds and can be summarized by the area under the curve (AUC), a single number. When a predictor is categorical, the ROC curve has one less than number of categories as potential thresholds; when the predictor is binary there is only one threshold. As the AUC may be used in decision-making processes on determining the best model, it important to discuss how it agrees with the intuition from the ROC curve. We discuss how the interpolation of the curve between thresholds with binary predictors can largely change the AUC. Overall, we show using a linear interpolation from the ROC curve with binary predictors corresponds to the estimated AUC, which is most commonly done in software, which we believe can lead to misleading results. We compare R, Python, Stata, and SAS software implementations. We recommend using reporting the interpolation used and discuss the merit of using the step function interpolator, also referred to as the “pessimistic” approach by Fawcett (2006).

1. Introduction

In many applications, receiver operator characteristic (ROC) curves are used to show how a predictor compares to the true outcome. One of the large advantages of ROC analysis is that it is threshold-agnostic; performance of a predictor is estimated without a specific threshold and also gives a criteria to choose an optimal threshold based on a certain cost function or objective. Typically, an ROC analysis shows how sensitivity (true positive rate) changes with varying specificity (true negative rate or 1 – false positive rate) for different thresholds. Analyses also typically weigh false positives and false negatives equally. In ROC analyses, the predictive capabilities of a variable is commonly summarized by the area under the curve (AUC), which can be found by integrating areas under the line segments. We will discuss how interpolation between these line segments affect the visualization of the ROC curve and corresponding AUC. Additionally, partial ROC (pROC) analysis keeps a maximum specificity fixed and can summarize a predictor by the partial AUC (pAUC), integrating up to the maximum specificity, or the maximum sensitivity with the smallest false positive rate in that subset range.

Many predictors, especially medical tests, result in a binary decision; a value is higher than a pre-determined threshold or a substance is present. Similarly, some predictors are commonly collected as categorical or discrete such as low, normal, or high blood pressure while others are categorical by nature such as having a specific gene or not. These are useful indicators of presence a disease, which is a primary outcome of interest in medical settings, and are used heavily in analysis.

If one assumes the binary predictor is generated from a continuous distribution that has been thresholded, then the sensitivity of this thresholded predictor actually represents one point on the ROC curve for the underlying continuous value. Therefore the ROC curve of a binary predictor is not really appropriate, but should be represented by a single point on the curve. But alas, ROC and AUC analysis has been done on binary predictors and used to inform if one variable is more predictive than the other (E et al. 2018; TV et al. 2017; Glaveckaite et al. 2011; Blumberg et al. 2016; Budwega et al. 2016; Mwipatayi et al. 2016; Xiong et al. 2018, @shterev2018bayesian; Kushnir et al. 2018; Snarr et al. 2017; Veltri, Kamath, and Shehu 2018). For example, these cases show that researchers use ROC curves and AUC to evaluate predictors, even when the predictors are categorical or binary. Although there is nothing inherently wrong with this comparison, it can lead to drastically different predictors being selected based on these criteria if ties are treated slightly different ways. A more appropriate comparison of a continuous predictor and the binary predictor may be to compare the sensitivity and specificity (or overall accuracy) of the continuous predictor given the optimal threshold versus that of the binary predictor.

As categorical/binary predictors only have a relatively small number of categories, how ties are handled are distinctly relevant. Thus, many observations may have the same value/risk score. Fawcett (2006) describes the standard way of how ties are handled in a predictor: a probability of $\frac{1}{2}$ is given for the cases when the predictors are tied. When drawing the ROC curve, one can assume that all the ties do not correctly classify the outcome (Fawcett called the “pessimistic” approach) or that all the ties do correctly classify the outcome (called the “optimistic” approach), see Fig. 6 in (Fawcett 2006). But Fawcett notes (emphasis in original):

Any mixed ordering of the instances will give a different set of step segments within the rectangle formed by these two extremes. However, the ROC curve should represent the expected performance of the classifier, which, lacking any other information, is the average of the pessimistic and optimistic segments.

This “expected” performance directly applies to the assignment of a half probability of success when the data are tied, which is implied by the “trapezoidal rule” from Hanley and McNeil (1982). Fawcett (2006) also states in the calculation of AUC that “trapezoids are used rather than rectangles in order to average the effect between points”. This trapezoidal rule applies additional areas to the AUC based on ties of the predictor, giving a half probability. This addition of half probability is linked to how ties are treated in the Wilcoxon rank sum test. As much of the theory of ROC curve testing, and therefore testing of differences in AUC, is based on the theory of the Wilcoxon rank-sum test, this treatment of ties is also relevant to statistical inference and not only AUC estimation.

Others have discussed insights into binary predictors in addition to Fawcett (2006), but they are mentioned in small sections of the paper (Saito and Rehmsmeier 2015; Pepe, Longton, and Janes 2009). Other information regarding ties and binary data are blog posts or working papers such as http://blog.revolutionanalytics.com/2016/11/calculating-auc.html or https://www.epeter-stats.de/roc-curves-and-ties/, which was written by the author of the fbroc (Peter 2016) package, which we will discuss below. Most notably, Hsu and Lieli (2014) is an extensive discussion of ties, but the paper was not published.

Although many discuss the properties of ROC and AUC analyses, we will first show the math and calculations of the AUC with a binary predictor, which correspond to simple calculations based on sensitivity and specificity. We then explore commonly-used statistical software for ROC curve creation and AUC calculation in a variety of packages and languages. Overall, we believe that AUC calculations alone may be misleading for binary or categorical predictors depending on the definition of the AUC. We propose to be explicit when reporting the AUC in terms of the approach to ties and discuss using step function interpolation when comparing AUC.

2. Mathematical Proof of AUC for Single Binary Predictor

First, we will show how the AUC is defined in terms of probability. This representation is helpful in discussing the connection between the stated interpretation of the AUC, the formal definition and calculation used in software, and how the treatment of ties is crucial when the data are discrete. Let us assume we have a binary predictor X and a binary outcome Y, such that X and Y only take the values 0 and 1, the number of replicates is not relevant here. Let X_i and Y_i be the values of subject i.

Fawcett (2006) goes on to state:

AUC of a classifier is equivalent to the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance.

In other words, we could discern the definition AUC = P(X_i > X_j|Y_i = 1, Y_j = 0) for all i, j, assuming (X_i, Y_i) ⫫ (X_j, Y_j). Note, the definition here adds no probability when the classifier is tied, this is a strict inequality. As there are only two outcomes for X, we can expand this probability using the law of total probability:

$$\begin{gathered} P\left(X_i>X_j|Y_i=1,Y_j=0\right)=P\left(X_i=1,X_j=0|Y_i=1,Y_j=0\right) \\ =P\left(X_i=1|X_j=0,Y_i=1,Y_j=0\right) \\ \times P\left(X_j=0|Y_i=1,Y_j=0\right) \\ =P\left(X_i=1|Y_i=1\right)P\left(X_j=0|Y_j=0\right) \end{gathered}$$

Thus, we see that P(X_i = 1|Y_i = 1) is the sensitivity and P(X_j = 0|Y_j = 0) is the specificity, so this reduces to:

$$P\left(X_i>X_j|Y_i=1,Y_j=0\right)=\text{specificity}\times \text{sensitivity}$$ (1)

Thus, using the definition as P(X_i > X_j|Y_i = 1,Y_j = 0), the AUC of a binary predictor is simply the sensitivity times the specificity. We will define this as the the strict definition of AUC, where ties are not taken into account and we are using strictly greater than in the probability and will call this value AUC_definition.

Let us change the definition of AUC slightly while accounting for ties, which we call AUC_w/ties, to:

$${\text{AUC}}_{\text{w}/\text{ties}}=P\left(X_i>X_j|Y_i=1,Y_j=0\right)+\frac{1}{2}P\left(X_i=X_j|Y_i=1,Y_j=0\right)$$

which corresponds to the common definition of AUC (Fawcett 2006; Saito and Rehmsmeier 2015; Pepe, Longton, and Janes 2009). This AUC is the one reported by most software, as we will see below.

2.1. Simple Concrete Example

To give some intuition of this scenario, we will assume X and Y have the following joint distribution, where X is along the rows and Y is along the columns, as in Table 1.

Table 1:

A simple 2×2 table of a binary predictor (rows) versus a binary outcome (columns)

	0	1
0	52	35
1	32	50

Therefore, the AUC should be equal to $\frac{50}{85}\times \frac{52}{84}$, which equals 0.364. This estimated AUC will be reported throughout the paper, so note the value.

Note, if we reverse the labels, then the sensitivity and the specificity are estimated by 1 minus that measure, or $\frac{35}{85}\times \frac{32}{84}$, which is equal to 0.157. Thus, as this AUC is less than the original labeling, we would choose that with the original labeling.

If we used the calculation for AUC_w/ties we see that we estimate AUC by ${\text{AUC}}_{\text{definition}}+\frac{1}{2}\left(\frac{50+52}{169}\right)$, which is equal to 0.604. We will show that most software report this AUC estimate.

2.1.1. Monte Carlo Estimation of AUC

We can also show that if we use simple Monte Carlo sampling, we can randomly choose X_i|Y_i = 0 and X_j|Y_j = 1. From these samples, we can estimate these AUC based on the definitions above. Here, the function est.auc samples 10⁶ random samples from X_i|Y_i = 0 and X_j|Y_j = 1, determines which is greater, or if they are tied, and then calculates ${\widehat{\text{AUC}}}_{\text{definition}}$ and ${\widehat{\text{AUC}}}_{\text{w}/\text{ties}}$:

est.auc = function(x, y, n = 1000000) {
x1 = x[y == 1] # x | y = 1
x0 = x[y == 0] # x | y = 0
c1 = sample(x1, size = n, replace = TRUE)
c0 = sample(x0, size = n, replace = TRUE)
auc.defn = mean(c1 > c0) # strictly greater
auc.wties = auc.defn + 1/2 * mean(c1 == c0) # half for ties
return(c(auc.definition = auc.defn,
auc.wties = auc.wties))
}
sample.estauc = est.auc(x, y)
sample.estauc
auc.definition auc.wties
0.364517 0.603929

And thus we see these simulations agree with the values estimated above, with negligible Monte Carlo error.

2.1.2. Geometric Argument of AUC

We will present a geometric discussion of the ROC as well. In Figure 1, we show the ROC curve for the simple concrete example. In panel A, we show the point of sensitivity/specificity connected by the step function, and the associated AUC is represented in the shaded blue area, representing AUC_definition. In panel B, we show the additional shaded areas that are due to ties in orange and red; all shaded areas represent AUC_w/ties. We will show how to calculate these areas from P(X₁ = X₀) in AUC_w/ties such that:

$$\begin{gathered} P\left(X_i=X_j|Y_i=1,Y_j=0\right)=P\left(X_i=1,X_j=1|Y_i=1,Y_j=0\right)+P\left(X_i=0,X_j=0|Y_i=1,Y_j=0\right) \\ =P\left(X_i=1|Y_i=1\right)P\left(X_j=1|Y_j=0\right)+P\left(X_i=0|Y_i=1\right)P\left(X_j=0|Y_j=0\right) \\ =\left(\text{sensitivity}\times \left(1-\text{specificity}\right)\right)+\left(\left(1-\text{sensitivity}\right)\times \text{specificity}\right) \end{gathered}$$

so that combining this with (1) we have:

$${\text{AUC}}_{\text{w}/\text{ties}}=\text{specificity}\times \text{sensitivity}+\frac{1}{2}\left(\text{sensitivity}\times \left(1-\text{specificity}\right)\right)+\frac{1}{2}\left(\left(1-\text{sensitivity}\times \text{specificity}\right)\right)$$

Fig. 1:

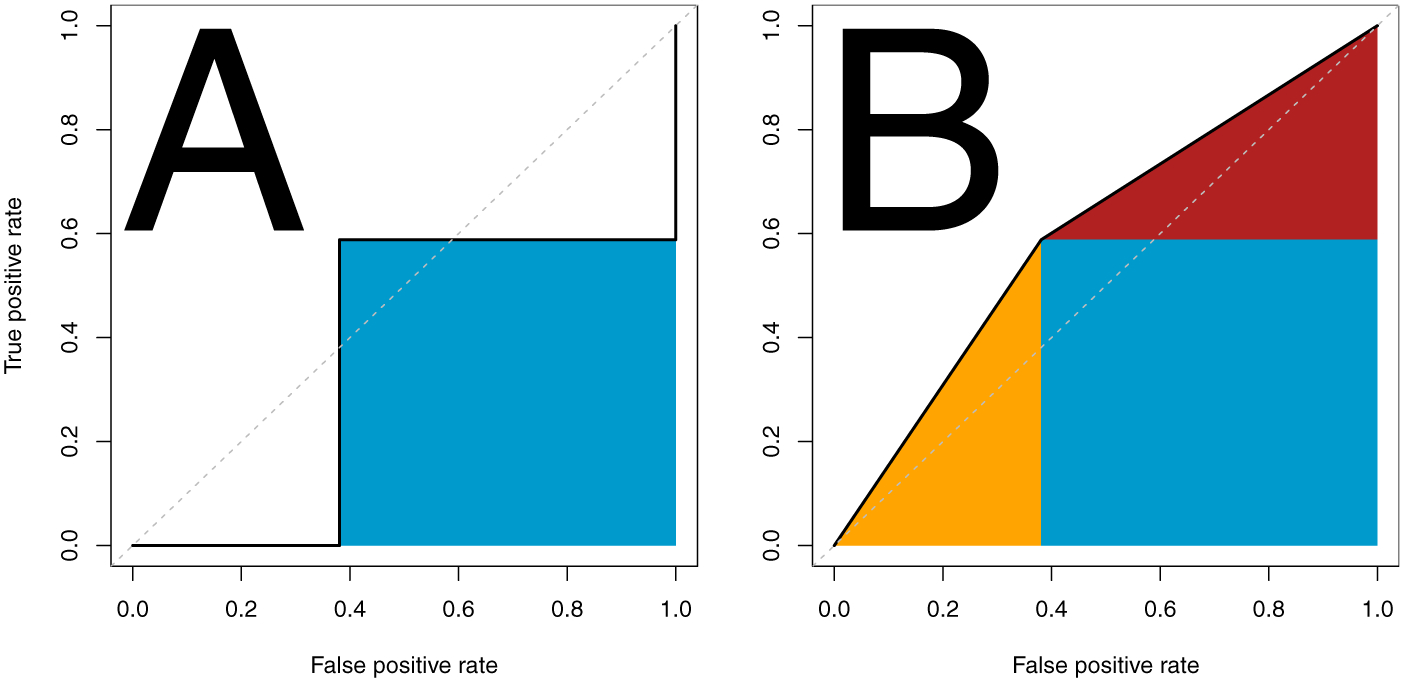
ROC curve of the data in the simple concrete example. Here we present a standard ROC curve, with the false positive rate or 1 – specificity on the x-axis and true positive rate or sensitivity on the y-axis. The dotted line represents the identity. The shaded area in panel represents the AUC for the strict definition. The additional shaded areas on panel B represent the AUC when accounting for ties.

Thus, we can see that geometrically from Figure 1:

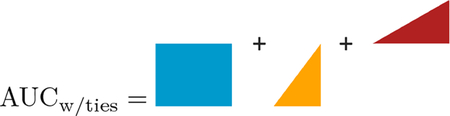where the order of the addition is the same respectively. Note that this equation reduces further such that:

$${\text{AUC}}_{\text{w}/\text{ties}}=\frac{1}{2}\left(\text{sensitivity}+\text{specificity}\right).$$

Thus, we have shown both AUC_w/ties and AUC_definition definition for binary predictors involve only sensitivity and specificity and can reduce to simple forms.

We will discuss implementations of estimating AUC in software in the next section. Though we focus on the AUC throughout this paper, many times ROC analysis is used to find optimal cutoffs for predictors to give high levels of sensitivity and specificity. The use of the linear interpolation in the ROC curve gives the false impression that varying levels of sensitivity and specificity can be achieved by that predictor. In fact, only the observed sensitivity and specificity can be observed, other than the trivial cases where sensitivity or specificity is 1. New samples of the same measurement may give different values, but the observed measurement can only achieve one point on that curve. Using a step function interpolation when plotting an ROC curve more clearly shows this fact.

2.2. AUC Calculation in Statistical Software

To determine how these calculations are done in practice, we will explore the estimated ROC curve and AUC from the implementations in the following R (R Core Team 2018) packages: ROCR (Sing et al. 2005), caTools (Tuszynski 2018), pROC (Robin et al. 2011), and fbroc (Peter 2016). We will also show these agree with the Python implementation in sklearn.metrics from scikit-learn (Pedregosa et al. 2011), the Stata functions roctab and rocreg (Bamber 1975; DeLong, DeLong, and Clarke-Pearson 1988), and the SAS software functions proc logistic with roc and roccontrast. We note that the majority of these functions all count half the probability of ties, but differences exist in the calculation of confidence intervals of AUC and note some inconsistent behavior.

3. AUC Calculation: Current Implementations

This section will present code and results from commonly-used implementations of AUC estimation from R, Python, Stata, and SAS software. We will note agreement with the definitions of AUC above and any discrepancies. This section is not to be exhaustive, but give examples how to calculate AUC in these software and show that these definitions are consistently used in AUC analysis, primarily ${\widehat{\text{AUC}}}_{\text{w}/\text{ties}}$

3.1. R

Here we will show the AUC calculation from the common R packages for ROC analysis. We will show that each report the value calculated in AUC_w/ties. The caTools (Tuszynski 2018) package calculates AUC using the colAUC function, taking in predictions as x and the binary ground truth labels as y:

library(caTools)
colAUC(x, y)
[,1]
0 vs. 1 0.6036415
which reports AUCw/ties.

In ROCR package (Sing et al. 2005), one must create a prediction object with the prediction function, which can calculate a series of measures. AUC is calculated from a performance function, giving a performance object, and giving the “auc” measure. We can then extract the AUC as follows:

library(ROCR)
pred = prediction(x, y)
auc.est = performance(pred, “auc”)
auc.est@y.values[[1]]
[1] 0.6036415

which reports AUC_w/ties. We see this agrees with the plot from ROCR in Figure 2D.

Fig. 2:

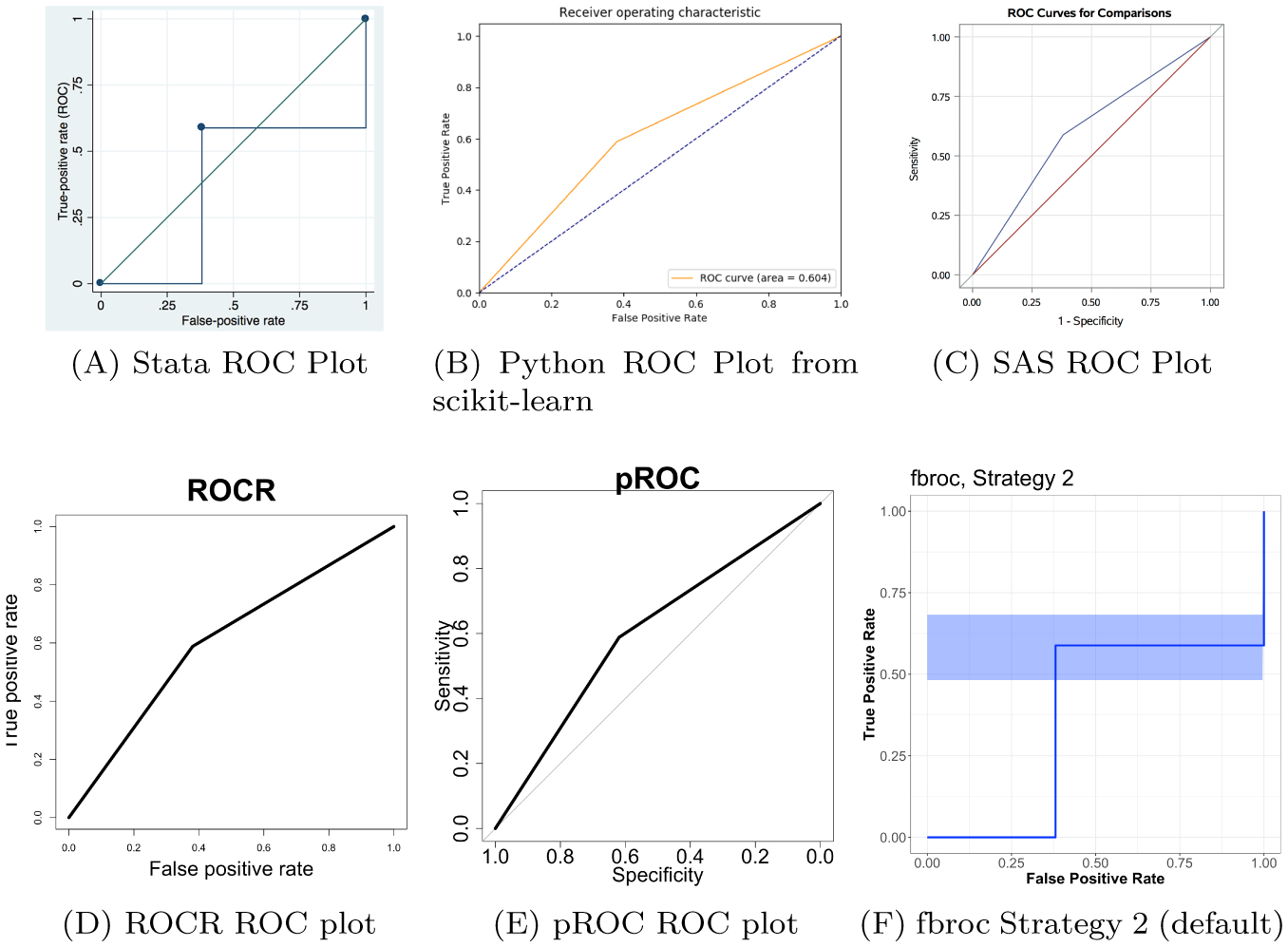
Comparison of different ROC curves for different R packages, scikit-learn from Python, SAS, and Stata. Each line represents the ROC curve, which corresponds to an according area under the curve (AUC). The blue shading represents the confidence interval for the ROC curve in the fbroc package. Also, each software represents the curve as the false positive rate versus the true positive rate, though the pROC package calls it sensitivity and specificity (with flipped axes). Some put the identity line where others do not. Overall the difference of note as to whether the ROC curve is represented by a step or a linear function. Using the first tie strategy for ties (non-default, not shown) in fbroc gives the same confidence interval but an ROC curve using linear interpolation.

The pROC (Robin et al. 2011) package calculates AUC using the roc function:

library(pROC)
pROC.roc = pROC::roc(predictor = x, response = y)
pROC.roc[[“auc”]]
Area under the curve: 0.6036

which reports AUC_w/ties and agrees with the plot from pROC in Figure 2E.

The fbroc package calculates the ROC using the boot.roc and perf functions. The package has 2 strategies for dealing with ties, which we will create 2 different objects fbroc.default, using the default strategy (strategy 2), and alternative strategy (strategy 1, fbroc.alternative):

library(fbroc)
fbroc.default = boot.roc(x, as.logical(y),
n.boot = 1000, tie.strategy = 2)
auc.def = perf(fbroc.default, “auc”)
auc.def[[“Observed.Performance”]]
[1] 0.6036415
fbroc.alternative = boot.roc(x, as.logical(y),
n.boot = 1000, tie.strategy = 1)
auc.alt = perf(fbroc.alternative, “auc”)
auc.alt[[“Observed.Performance”]]
[1] 0.6036415

which both report AUC_w/ties, though the plot from fbroc in Figure 2F, which is for strategy 2, shows a step function, corresponding to AUC_definition.

Although the output is the same, these strategies for ties are different for the plotting for the ROC curve, which we see in Figure 3. The standard error calculation for both strategies use the second strategy (Fawcett’s “pessimistic” approach), which is described in a blog post (https://www.epeter-stats. de/roc-curves-and-ties/) and can be seen in the shaded areas of the panels. Thus, we see that using either tie strategy results in the same estimate of AUC (AUC_w/ties) and are consistent for tie strategy 1 (Figure 3A). Using tie strategy 2 results in a plot which would reflect an AUC of AUC_definition (Figure 3B), which disagrees with the estimate. This result is particularly concerning because the plot should agree with the interpretation of AUC.

Fig. 3:

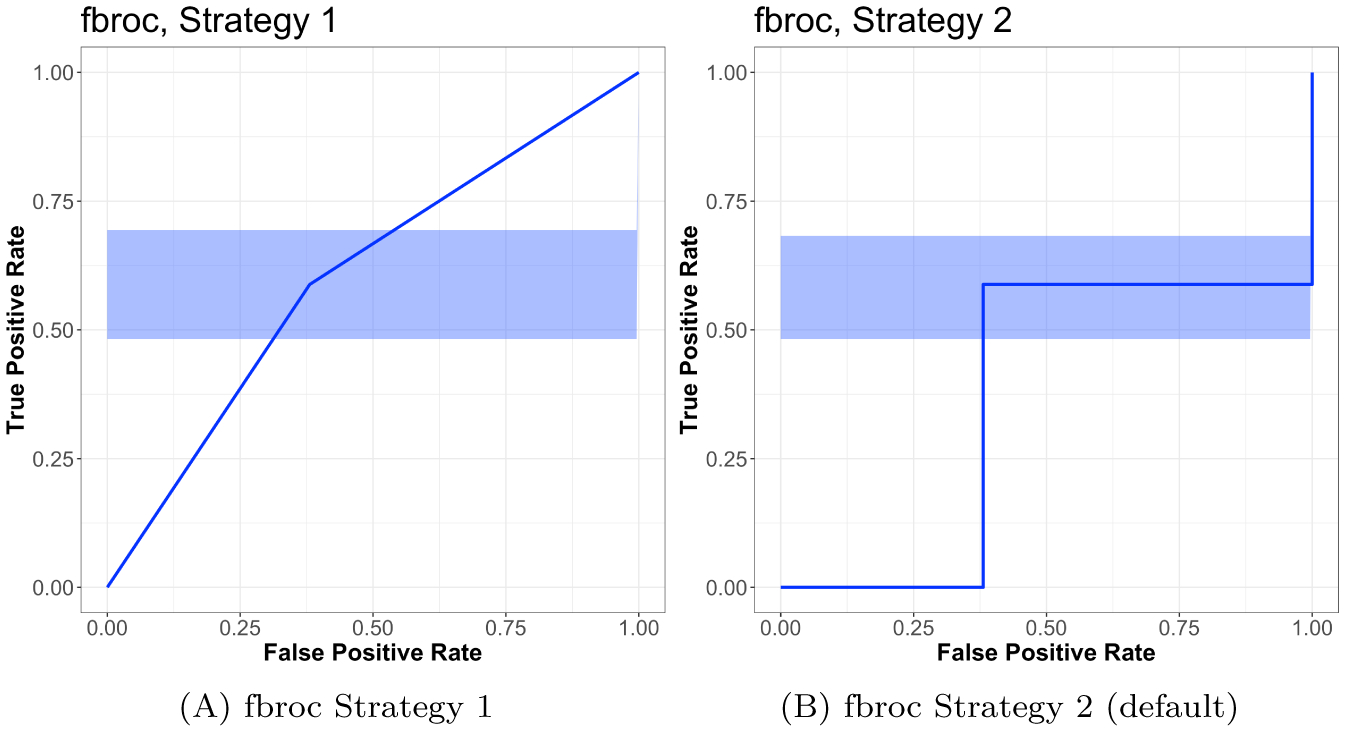
Comparison of different strategies for ties in the fbroc package. The blue shading represents the confidence interval for the ROC curve. Overall the difference of note as to whether the ROC curve is represented by a step or a linear function. Using the first tie strategy for ties (non-default) in fbroc gives the same confidence interval as the second strategy but an ROC curve using linear interpolation, which may give an inconsistent combination of estimate and confidence interval as fbroc reports the AUC corresponding to the linear interpolation.

3.2. Python

In Python, we will use the implementation in sklearn.metrics from scikit-learn (Pedregosa et al. 2011). We will use the R package reticulate (Allaire, Ushey, and Tang 2018), which will provide an Python interface to R. Here we use the roc_curve and auc functions from scikit-learn and output the estimated AUC:

# Adapted from https://qiita.com/bmj0114/items/460424c110a8ce22d945
library(reticulate)
sk = import(“sklearn.metrics”)
py.roc.curve = sk$roc_curve(y_score = x, y_true = y)
names(py.roc.curve) = c(“fpr”, “tpr”, “thresholds”)
py.roc.auc = sk$auc(py.roc.curve$fpr, py.roc.curve$tpr)
py.roc.auc
[1] 0.6036415

which reports AUC_w/ties. Although we have not exhaustively shown Python reports AUC_w/ties, scikit-learn is one of the most popular Python modules for machine learning and analysis. We can use matplotlib (Hunter 2007) to plot the false positive rate and true positive rate from the py.roc.curve object, which we see in Figure 2B, which uses a linear interpolation by default and agrees with AUC_w/ties.

3.3. SAS Software

In SAS software (version 9.4 for Unix) (SAS and Version 2017), let us assume we have a data set named roc loaded with the variables/columns of x and y as above. The following commands will produce the ROC curve in Figure 2C:

proc logistic data=roc;
model y(event=‘1’) = x;
roc; roccontrast;
run;

The resulting output reports AUC_w/ties, along with a confidence interval. The calculations can be seen in the SAS User Guide (https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/viewer.htm#statug_logistic_sect040.htm), which includes the addition of the probability of ties.

3.4. Stata

In Stata (StataCorp, College Station, TX, version 13) (Stata 2013), let us assume we have a data set with the variables/columns of x and y as above.

The function roctab is one common way to calculate an AUC:

roctab x y
			-Asymptotic Normal--
Obs	ROC Area	Std. Err.	[95% Conf.	Interval]
169	0.6037	0.0379	0.52952	0.67793

which agrees with the calculation based on AUC_w/ties and agrees with the estimates from above. One can also calculate the AUC using the rocreg function:

rocreg y x, nodots auc
Bootstrap results			Number of obs		=	169
			Replications		=	1000
Nonparametric ROC estimation
Control standardization: empirical
ROC method : empirical
Area under the ROC curve
Status: y
Classifier: x
AUC	Observed Coef.	Bias	Bootstrap Std. Err.	[95% Conf.	Interval]
	.3641457	−.0004513	.0451334	.2756857	.4526056 (N)
				.2771778	.452824 (P)
				.2769474	.4507576 (BC)

which agrees with AUC_definition and is different from the output from roctab. The variance of the estimate is based on a bootstrap estimate, but the point estimate will remain the same regardless of using the bootstrap or not. This disagreement of estimates is concerning as the reported estimated AUC may be different depending on the command used in the estimation.

Using rocregplot after running this estimation, we see can create an ROC curve, which is shown in Figure 2A. We see that the estimated ROC curve coincides with the estimated AUC from rocreg (AUC_definition) and the blue rectangle in Figure 1. Thus, roctab is one of the most common ways in Stata to estimate AUC, but does not agree with the common way to plot ROC curves.

Thus, we see in Figure 2 that all ROC curves are interpolated with a linear interpolation, which coincides with the calculation based on AUC_w/ties, except for the Stata and fbroc ROC curves, which interpolates using a step function and coincides with AUC_definition. The confidence interval estimate of the ROC curve for fbroc, which is shaded in blue in Figure 2F, corresponds to variability based on AUC_definition, but the reported value corresponds to the ROC curve based on AUC_w/ties.

Figure 3 shows that using the different tie strategies gives a linear (strategy 2, default, panel (B), duplicated) or step function/constant (strategy 1, panel (A)) interpolation. In each tie strategy, however, the AUC is estimated to be the same. Therefore, tie strategy 2 may give an inconsistent combination of AUC estimate and ROC representation and strategy 1 may give an inconsistent estimation of the variability of the ROC.

4. Categorical Predictor Example

Though the main focus of the paper is to demonstrate how using an AUC directly on a binary predictor can lead to overestimation of predictive power, we believe this relates to categorical values as well. With binary predictors, using single summary measures such as specificity and sensitivity can and should be conveyed for performance measures. With categorical predictors, however, multiple thresholds are available and simple one-dimensional summaries are more complicated and ROC curves may give insight. Let us assume we had a categorical variable, such as one measured using a 4-point Likert scale, which takes on the following cross-tabulation with the outcome in Table 2.

Table 2:

A example table of a categorical predictor (rows) versus a binary outcome (columns)

	0	1
1	31	21
2	21	14
3	11	17
4	21	33

Note, the number of records is the same as in the binary predictor case. In Figure 4, we overlay the ROC curves from this predictor and the binary predictor (black line), showing they are the same, with points on the ROC curve from the categorical predictor in blue. We also show the ROC curve with lines using the pessimistic approach for the categorical predictor (blue, dashed) and the binary predictor (red, dotted).

Fig. 4:

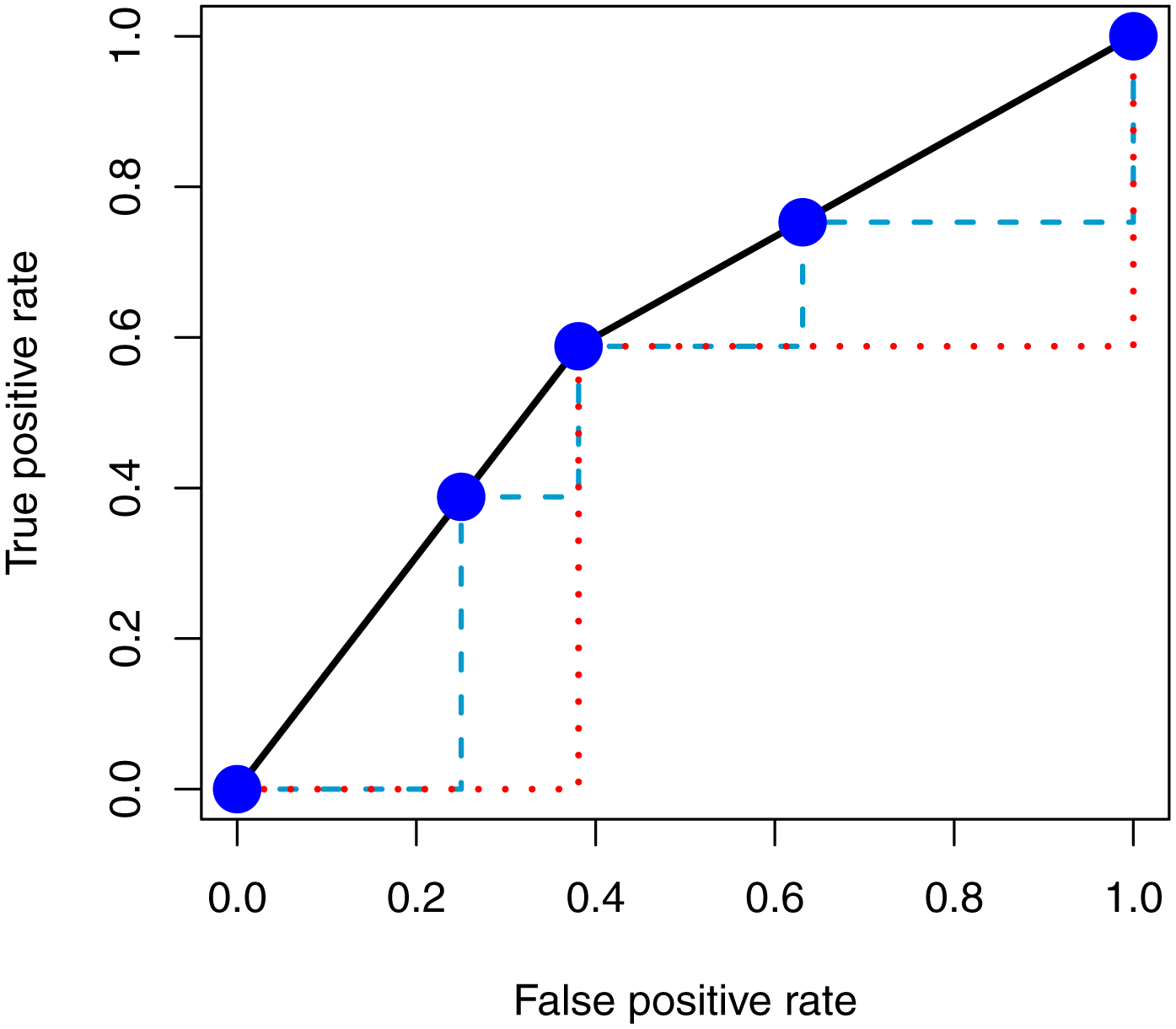
ROC curve of a 4-level categorical variable compared to the binary predictor. Here we present the ROC curve of a categorical predictor (blue points) compared to that of the binary predictor (black line). We see that the ROC curve is identical if the linear inerpolation is used (accounting for ties). The red (dotted) and blue (dashed) lines show the ROC of the binary and categorical predictor, respectively, using the pessimistic approach. We believe this demonstrates that although there is more gradation in the categorical variable, using the standard approach provides the same AUC, though we believe these variables have different levels of information as the binary predictor cannot obtain values other than the 2 categories.

We see that using the the linear interpolation in Figure 4, the AUC for the categorical predictor and the binary predictor would be nearly identical. The AUC is not exact due to the fact that the cells in the table must be integers. This result is counterintuitive as the categorical variable can take on a number of values with varying sensitivities and specificities, whereas the binary predictor cannot. With more samples, we could extend this example to a variable which had hundreds of values like a continuous predictor, but give the same ROC shape and identical AUC when using linear interpolation. We show an example in the supplemental material. Using the pessimistic approach (red dotted and blue dashed lines in Figure 4) for the categorical and binary predictors, we see that the AUC would be different in this estimation.

5. Conclusion

We have shown how the ROC curve is plotted and AUC is estimated in common statistical software when using a univariate binary predictor. There are inconsistencies across software platforms, such as R and Stata, and even within some packages, such as fbroc. We believe these calculations may not reflect the discreteness of the data. We agree that using a binary predictor in an ROC analysis may not be appropriate, but we note that researchers and users may still perform this analysis.

We believe the critiques depend partially of the nature of the predictor. Some predictors are fundamentally discrete or categorical, such as the number of different alleles at a gene or a questionnaire using Likert scales. Others are continuous but empirically discrete either by rounding or a small set of unique values. For predictors that are not fundamentally discrete, we believe that linear interpolation would be reasonable if unobserved values in between those observed are theoretically possible.

Otherwise, we believe using the step function interpolation and not counting ties would be more appropriate. We believe additional options for different calculations accounting for ties should be possible or warnings for discrete data may be presented to the user. We hope that indicating how ties are handled would become more common, especially for discrete data in practice. Using different methods for ties poses different issues, such as AUC values that are below 0.5 and some tests may not have the same theoretical properties or connections to Wilcoxon rank-sum tests. Though these new issues arise, we believe the current methodology has the potential for misleading users.

All code required to generate this paper is located at https://github.com/muschellij2/binroc.